Abstract
Glutathione peroxidase (GPx) is a well-known seleno-enzyme that protects cells from oxidative stress (e.g., lipid peroxidation and oxidation of other cellular proteins and macromolecules), by catalyzing the reduction of harmful peroxides (e.g., hydrogen peroxide: H2O2) with reduced glutathione (GSH). However, the catalytic mechanism of GPx kinetics is not well characterized in terms of a mathematical model. We developed here a mechanistic mathematical model of GPx kinetics by considering a unified catalytic scheme and estimated the unknown model parameters based on different experimental data from the literature on the kinetics of the enzyme. The model predictions are consistent with the consensus that GPx operates via a ping-pong mechanism. The unified catalytic scheme proposed here for GPx kinetics clarifies various anomalies, such as what are the individual steps in the catalytic scheme by estimating their associated rate constant values and a plausible rationale for the contradicting experimental results. The developed model presents a unique opportunity to understand the effects of pH and product GSSG on the GPx activity under both physiological and pathophysiological conditions. Although model parameters related to the product GSSG were not identifiable due to lack of product-inhibition data, the preliminary model simulations with the assumed range of parameters show that the inhibition by the product GSSG is negligible, consistent with what is known in the literature. In addition, the model is able to simulate the bi-modal behavior of the GPx activity with respect to pH with the pH-range for maximal GPx activity decreasing significantly as the GSH levels decrease and H2O2 provides a key component for an integrated model of H2O2 levels increase (characteristics of oxidative stress). The model balance under normal and oxidative stress conditions.
Keywords: enzyme kinetics, glutathione peroxidase, hydrogen peroxide, redox biology, mathematical modeling
Introduction
Reactive oxygen species (ROS), such as superoxide anion and hydrogen peroxide (H2O2), are the byproducts of normal O2 consuming respiration in the cell and their regulation has a significant impact on health and disease. Several cellular sources of have been identified [1-7], with the mitochondrial electron transport chain (ETC) as the dominant source in cardiomyocytes [8-11]. Upon its production, is rapidly dismutated to H2O2 by the catalytic actions of superoxide dismutases (SODs). H2O2 serves as a signaling molecule, and thereby play an important role in regulating diverse set of physiological processes [12-14]. However, excess H2O2 emission (where production significantly exceeds removal) leads to oxidative stress, and this has been implicated in numerous pathological conditions [15-18], as well as in aging [19,20]. Maintaining normal cellular H2O2 concentrations is, therefore, vital for the proper physiological function of the cell. To maintain normal cellular H2O2 levels and protect against oxidative damage, cells have developed a network of detoxifying compounds and enzymes consisting of catalase, glutathione (GSH), and thioredoxin (Trx) systems [21-23]. The Trx and GSH systems buffer H2O2 via peroxiredoxin (Prx) and glutathione peroxidase (GPx), respectively. In the present study, the kinetics and catalytic mechanisms of GPx (specifically, GPx-1) in the removal of H2O2 and various hydroperoxides are investigated.
GPxs in mammals constitute a family of selenoenzymes consisting of up to eight distinct isoforms [24]. They all reduce a variety of organic and inorganic hydroperoxides to the corresponding hydroxyl compounds, utilizing GSH, and/or other reducing equivalents. The reactivity of these enzymes differs considerably depending upon the hydroperoxides and thiol cofactor. Majority of the GPxs in mammals constitute selenocysteine in its active site (human GPx 1–4 and 6), which facilitates catalysis. It is thought that during the catalytic cycle, selenium of the selenocysteine in the enzyme catalytic site undergoes a redox cycle involving the selenol (ESeH) as the active/reduced form [25]. The selenol is first oxidized by the hydroperoxides to a selenic acid derivative (ESeOH). This intermediate is subsequently reduced by the electron donor GSH, resulting in a seleno-disulfide (ESeSG). A second GSH molecule cleaves the seleno-disulfide bond to regenerate the reduced GPx and simultaneously produce the product, an oxidized glutathione (GSSG) [26,27]. Several mimics for GPx enzyme have been developed by incorporation of selenocysteine through chemical modification or genetic engineering that shows a similar mechanism of catalytic action [28-32].
The majority of experimental studies on the catalytic mechanism of GPx-1 and GPx-like enzymes reported by several groups [26,31-38] are consistent with a ping-pong mechanism. Initial velocity experiments first performed with GPx-1 from bovine erythrocytes by Flohé et al. [26] suggested that the catalytic mechanism is simple pong-pong with indefinite Michaelis-Menten constants, indefinite maximum velocities, and no significant product inhibition. A similar kinetic pattern was observed with various hydroperoxides (ethyl, cumene, and t-butyl) as substrates with bovine GPx-1 [34], which also suggested that a ping-pong mechanism was involved. Furthermore, experiments performed on different forms of GPx from human [37], rat lung soluble GPx [38], and rat liver cytosolic GPx [36] with various hydroperoxides were all consistent with a pingpong mechanism for GPx. A ping-pong mechanism is also observed with selenium-containing glutathione transferase (GST) with cumene hydroperoxides (CumOOH), and t-Butyl hydroperoxides (tBuOOH) with parallel lines in their double reciprocal plots [31]. However, the observed Michaelis-Menten constants were not indefinite for the GPx-mimic. In contrast to the above studies, initial velocity experiments performed by Carsol et al. [39], with soluble and membrane-immobilized GPx-1 derived from bovine erythrocytes, resulted in nonparallel double-reciprocal plots, indicating that a sequential-ordered mechanism rather than a ping-pong mechanism is involved. The sequential mechanism was further corroborated by their product inhibition studies. Although a similar kinetic pattern was observed by Little et al. [33], they were not certain about the mechanism of GPx due to the mixture of parallel and nonparallel lines observed in their double-reciprocal plots.
Mathematical models have been developed for the catalytic mechanism of GPx that show the dependency of GSH on the rate of H2O2 removal [40-43]. Though these models were based on the observed ping-pong mechanism for GPx-1, they did not include the pH effects in their models, and hence cannot describe the observed bi-modal pH-dependency of the GPx-1 activity. Furthermore, none of the models were used to identify the precise values of the rate constants associated with each individual step in the catalytic cycle of GPx. In the current study, we developed a thermodynamically balanced mathematical model for the GPx-1 kinetics based on a unified catalytic scheme. We estimated the precise values of the rate constants for each individual step in the catalytic cycle using experimental data from different studies [26,34,36] and provided the corresponding Dalziel and Cleland’s coefficients for comparison. The developed model is also able to explain the bi-modal pH effects on the GPx-1 activity [26]. To characterize the pH effect, we incorporated intermediate GPx protonation states in the catalytic scheme based on observations from Flohé et al. [26]. We further show that, under relevant assumptions, the proposed GPx model based on our unified catalytic scheme can be reduced to the previously developed GPx models [26,40-43]. Finally, we used the developed GPx model to provide a plausible rationale for the contradicting kinetics of GPx in the study of Carsol et al. [39].
Methods
Three sets of independent experimental data [26,34,36] on the initial velocities of GPx-1 that include pH-dependent GPx kinetics and various hydroperoxides, such as ethyl hydroperoxide (EthOOH), cumene hydroperoxide (CumOOH), t-butyl hydroperoxide (tBuOOH), and linoleic acid hydroperoxide (LinOOH) with GSH as the donor substrate have been used here to identify the GPx catalytic mechanism and the relevant kinetic parameters of the model.
Proposed unified catalytic scheme for GPx
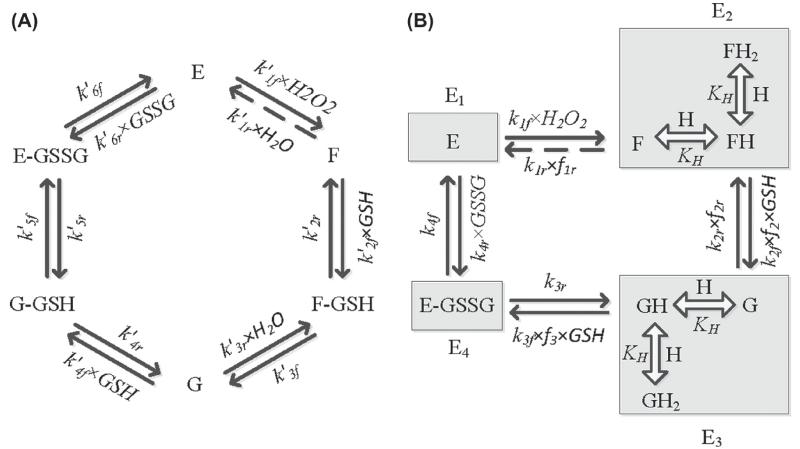
Figure 1A shows the ping-pong catalytic scheme proposed by Toppo et al. [24] based on structural information for the kinetic mechanism of GPx. Here, the reduced enzyme (E) in the vicinity of H2O2 (or various hydroperoxides) oxidizes to F, and thereby releases a H2O molecule. This step was assumed not to involve formation of a typical enzyme-substrate complex (E-H2O2). Subsequently, the oxidized enzyme undergoes several intermediate steps with the substrate GSH to generate the ground state-reduced enzyme (E) and the product GSSG. First, the oxidized enzyme F reacts with a GSH molecule to form the complex F-GSH, which is then converted to form an intermediate state G with release of a H2O molecule. State G represents the form of enzyme that is glutathionylated at the active site selenium, which then reacts with one more GSH molecule to form the complex G-GSH. In the final step, G-GSH converts to E-GSSG and the product GSSG is released while regenerating the reduced enzyme E. Although some of the steps in the reaction scheme, like oxidation of enzyme E by hydroperoxides (first step in Figure 1A), are typically assumed to be irreversible, our model strictly adheres to the laws of thermodynamics, thus all steps in the reaction scheme are considered reversible.
Figure 1.
(A) Basic kinetic scheme for the catalytic mechanism of glutathione peroxidase (GPx). E, F, and G represent reduced and oxidized forms of the enzyme GPx. F-GSH, G-GSH, and E-GSSG represent intermediate enzyme–substrate/product complexes. k′if and k′ir represent the forward and reverse rate constants for the respective interactions. (B) Reduced kinetic scheme for GPx catalytic action under rapid equilibrium assumption for selective decay reactions in Figure 1A. F, FH, and FH2 represent the oxidized, single protonated, and diprotonated form of the enzyme, respectively. G, GH, and GH2 represent the oxidized, single protonated, and diprotonated intermediate form of the enzyme, respectively. kif and kir represent the forward and reverse rate constants for the respective interactions. E1, E2, E3, and E4 represent enzyme states and fi indicates the associated binding polynomial for each enzyme state transition. Broken arrows show a reversible reaction is considered for the first step for thermodynamic constituency though theoretically considered negligible.
The catalytic scheme shown in Figure 1A contains 12 rate constants. In order to reduce the model complexity, we used fast kinetics for some of the reaction steps as described by Flohé et al. [26] and Toppo et al. [24], as shown in Figure 1B. Specifically, Figure 1B shows the reduced catalytic scheme for the kinetic mechanism of GPx based on rapid equilibrium assumptions for some reaction steps in Figure 1A. For example, the decay of the intermediate complexes F-GSH and G-GSH to form the products are believed to be much faster than their formation steps with states F and G binding to GSH. In other words, states F-GSH and G are indistinguishable and can be assumed as a single-state G. Similarly, G-GSH and E-GSSG can be assumed as a single state E-GSSG. In addition, we incorporated rapid protonation of the oxidized enzymes F and G to form activated enzyme states in the catalytic scheme, while unprotonated and diprotonated forms of F and G were considered to be inactive to explain the observed bi-modal pH-dependent behavior of the GPx activity [26]. These assumptions reduce the complexity of the GPx kinetic scheme to only four rate-limiting steps (eight rate constants).
Kinetic flux expression for GPx
The net reaction velocity equation is derived for GPx based on steady-state assumption for the unified catalytic scheme shown in Figure 1B using our freely available KAPattern Matlab tool for generating rate equations [44]. Assuming A, B, and P are concentrations of H2O2 (or hydroperoxides), GSH and GSSG, respectively, the net reaction velocity equation is given by:
| (1) |
where kif and kir (i = 1–4) represent the forward and reverse rate constants for the interactions shown in Figure 1B; E0 is the total initial concentration of the enzyme; f1r, f2r, f2, and f3 indicate the corresponding fractional occupancies associated with each state:
| (2) |
where KH represents the H+ binding constant for the enzyme. We note here that as H2O is one of the product of GPx reaction, the GPx rate Equation (1) that is based on a ping-pong mechanism resemble to a rate equation that is based on a sequential mechanism (characterized by the appearance of a constant term in the denominator of the rate equation).
For convenience, the net reaction velocity expression given by Equation (1) can be expressed using Cleland’s nomenclature [45] with appropriate relations between Cleland coefficients and the rate constants. The transformed net reaction velocity equation can be written as:
| (3) |
where the Cleland coefficients are defined according to the Cleland’s nomenclature as given below:
| (4) |
where we have used shorthand notation from Segel [46]; for example, num1 = k1f k2f k3f k4f f2 f3, num2 = k1r k2r k3r k4r f1r f2r, CoefAB2 = k1f k2f k3f f2 f3, and so on. Some of these Cleland coefficients are functions of pH through their dependencies on f1r, f2r, f2, and f3 (see Table I for detailed definitions).
Table I.
Correlation between the rate constants, the Cleland coefficients, and the Dalziel coefficients.
| Cleland coefficients (k1r ≠ 0) |
Dalziel coefficients (k1r ≠ 0) |
||||
|---|---|---|---|---|---|
| Parameter | Definition | (k1r ≈ 0) | Parameter | Definition | (k1r ≈ 0) |
| Vf | k 4f | Φ 0 | |||
| Vr | ≈0 | Φ 1 | |||
| KmA | ≈0 | Φ 2 | |||
| K mA1 | ≈0 | Φ 12 | ≈0 | ||
| K mA2 | Φ 22 | ||||
| K mB1 | Φ 122 | ≈0 | |||
| K mB2 | |||||
| K iB1 | |||||
| K iB2 | |||||
| K mP | ≈0 | ||||
k1rp= k1r f1r (H); k2rp=k2r f2r (H); k2fp=k2f f2 (H); k3fp=k3f f3 (H).
As many GPx models in the literature [26,31,39-43] present the rate expression in terms of Dalziel coefficients [47] in the absence of products, we converted the GPx rate expression obtained from the unified catalytic scheme in Figure 1B in terms of Cleland and Dalziel coefficients. Thus, under no product present condition (P = 0), the velocity and reciprocal velocity equation in terms of Cleland and Dalziel coefficients, respectively from Equation (1) can be written as:
| (5) |
| (6) |
where Φ0, Φ1, Φ2, Φ12, Φ22, and Φ122 are the Dalziel coefficients and are defined as functions of rate constants. As in the case of Cleland coefficients, some of the Dalziel coefficients are also functions of pH through their dependencies on f1r, f2r, f2, and f3. The detailed definitions for the Cleland and Dalziel coefficients and their dependencies on pH are given in Table I.
Equilibrium constant Keq for GPx
The enzyme GPx reduces H2O2 to H2O using the GSSG/GSH redox couple as shown in the overall biochemical reaction:
| (7) |
We calculated the equilibrium constant for the GPx reaction based on its biochemical reaction, for which the standard Gibb’s free energy is computed as:
| (8) |
where the Gibb’s free energy of formation of each species was obtained from Alberty’s thermodynamic database [48], and corrections for pH, ionic strength, and temperature were applied where appropriate. The equilibrium constant for the GPx reaction is then calculated as:
| (9) |
Thermodynamic constraints
All the model parameters cannot vary independently. At equilibrium, the net reaction rate in Equation (1) is zero, and correspondingly, the ratio of the product of forward rate constants and the product of the reverse rate constants is equal to the equilibrium constant, resulting in the following thermodynamic constraint for the kinetic parameters:
| (10) |
Parameter estimation and sensitivity analysis
Equation (1) contains nine unknown parameters and two known parameters of enzyme concentration (E0) and thermodynamic equilibrium constant (Keq,GPx). One unknown parameter can be obtained from the thermodynamic constraint of Equation (10). We constrained parameter k3r using the thermodynamic constraint, and remaining eight unknown parameters, including parameter for the inhibitory effects of pH (KH), were estimated using some of the available experimental data [26,34,36] from the literature. A combined least-square estimation technique was used to fit the model simulated outputs to the experimental data:
| (11) |
where Nexp is the number of experiments and Ndata is the number of data points in a particular experiment; are the experimental data and are the corresponding model simulation outputs. The accuracy and robustness of the model fitting to the data are assessed based on the value of mean residual error E(φ) and sensitivities of J(φ) to perturbations in the optimal parameter estimates, respectively.
The normalized local sensitivity coefficients with respect to the model parameters are computed as:
| (12) |
where φi is the ith parameter; Jj is the model simulation for jth data point; Mi is the number of non-zero sensitivity coefficients (Si,j) for the parameter φi; and Si is the normalized sensitivity coefficient with respect to the parameter φi. A higher sensitivity value indicates that a small change in a given parameter value will result in a significant change in the model output. On the other hand, a small sensitivity value for a given parameter indicates that the parameter should be fixed and removed from the parameter estimation procedure.
Results
In this section, we present detailed parameterization and validation of the proposed unified GPx model based on some of the available experimental data on the kinetics of GPx-1 from the literature [26,34,36]. We independently estimated all the unknown parameters of the model using initial-velocity data in the absence of products for each experimental data set [26,34], integrated time data [36], and pH-mediated kinetic data from Flohé et al. [26]. Since these experimental studies did not include product-inhibition data, we fixed parameters related to product inhibition based on sensitivity analysis. The resulting estimated parameter values along with their local sensitivity coefficients are tabulated in Table II and the corresponding Cle-land and Dalziel coefficients are tabulated in Table III. The model fittings to the initial-velocity data from bovine erythrocytes GPx-1 [26,34], in the absence of products, are illustrated in Figures 2 and 5. The estimated parameter values from Flohé et al. [26] were further used to simulate the fractional enzyme levels in each state and effect of pH on the activity of GPx under various scenarios are shown in Figures 3 and 4. The model simulations of the time course profiles of hydroperoxides along with model description of the experimental data from rat liver cytosolic GPx-1 is shown in Figure 6. Finally, the developed model is used to test under what conditions the experimental data from Carsol et al. [39] can be described and a plausible rationale to their contradicting results on catalytic mechanism of GPx is given in Figures 7 and 8 and in Supplementary Figures 1 and 2 to be found online at http://informahealthcare.com/doi/abs/10.3109/10715762.2014.886775. The corresponding model parameters, which describe the Carsol et al. data, are presented in Table IV.
Table II.
Estimated rate constants for the unified GPx kinetic model for different experimental data sets
| Flohé et al. [26] (H2O2) |
Günzler et al. [34] |
Forstrom et al. [36] |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (EthOOH) |
(CumOOH) |
(tBuOOH) |
(CumOOH) Value |
(LinOOH) Value |
||||||
| Parameter | Value | (S)* | Value | (S) | Value | (S) | Value | (S) | ||
| k1f (M−1 s−1) | 6.7 × 107 | 0.47 | 3.7 × 107 | 0.57 | 1.5 × 107 | 0.64 | 6.2 × 106 | 0.59 | 5.5 × 106 | 2.11 × 107 |
| k1r (s−1) | 1 × 10−4 | 1 × 10−4 | 1 × 10−4 | 4 × 10−5 | 1 × 10−4 | 1 × 10−5 | 1 × 10−4 | 8 × 10−4 | 1 × 10−4 | 1 × 10−4 |
| k2f (M−1 s−1) | 1.4 × 108 | 0.15 | 1.3 × 108 | 0.17 | 1.25 × 108 | 0.15 | 1.2 × 108 | 0.18 | 6.4 × 107 | 8.4 × 107 |
| k2r (s−1) | 1 × 10−4 | 1 × 10−4 | 1 × 10−4 | 4 × 10−5 | 1 × 10−4 | 1 × 10−5 | 1 × 10−4 | 6 × 10−6 | 1 × 10−4 | 1 × 10−4 |
| k3f (M−1 s−1) | 1.0 × 108 | 0.22 | 9.6 × 107 | 0.24 | 9.8 × 107 | 0.2 | 1.0 × 108 | 0.21 | 7 × 106 | 7.4 × 106 |
| k3r (s−1)a | 1.7 × 10−3 | N/A | 8 × 10−4 | N/A | 3 × 10−4 | N/A | 1.3 × 10−4 | N/A | 5 × 10−6 | 2.9 × 10−5 |
| k4f (s−1) | 7.5 × 104 | 0.15 | 7.5 × 104 | 6 × 10−3 | 7.5 × 104 | 5 × 10−3 | 7.5 × 104 | 2 × 10−3 | 7.5 × 104 | 7.5 × 104 |
| k4r (M−1 s−1)b | 4.1 × 102 | N/A | 4.1 × 102 | N/A | 4.1 × 102 | N/A | 4.1 × 102 | N/A | 4.1 × 102 | 4.1 × 102 |
| KH (M) | 1.5 × 10−9 | N/A | 1.5 × 10−9 | N/A | 1.5 × 10−9 | N/A | 1.5 × 10−9 | N/A | 1.5 × 10−9 | 1.5 × 10−9 |
| Keq (M−2) | 1.0 × 1037 | N/A | 1.0 × 1037 | N/A | 1.0 × 1037 | N/A | 1.0 × 1037 | N/A | 8.2 × 1036 | 8.2 × 1036 |
N/A: Not applicable as they are fixed parameters.
(S)-Sensitivity.
Parameter was calculated based on the thermodynamic constraint.
Indicates unidentifiable parameters for the respective data sets due to the absence of product inhibition data and fixed at a random value.
Table III.
Cleland and Dalziel coefficients calculated from the estimated rate constants for different experimental datasets.
| Parameter | Flohé et al. [26] (H2O2) pH = 6.7 (7.7)* |
Günzler et al. [34] |
Forstrom et al. [36] |
|||
|---|---|---|---|---|---|---|
| (EthOOH) pH = 6.7 (7.7) |
(CumOOH) pH = 6.7 (7.7) |
(tBuOOH) pH = 6.7 (7.7) |
(CumOOH) pH = 7.2 (7.7) |
(LinOOH) pH = 7.2 (7.7) |
||
| Cleland coefficients | ||||||
| Vf (s−1)a | 7.5 × 104 | 7.5 × 104 | 7.5 × 104 | 7.5 × 104 | 7.5 × 104 | 7.5 × 104 |
| KmA3 (M)a | 1.1 × 10−3 | 2 × 10−3 | 4.9 × 10−3 | 1.2 × 10−2 | 1.3 × 10−2 | 3.5 × 10−3 |
| KmB2 (M) | 0.15 (0.017)* | 0.17 (0.018)* | 0.17 (0.018)* | 0.17 (0.018)* | 0.49 (0.16)* | 0.45 (0.15)* |
| Dalziel coefficients | ||||||
| Φ0 (s)a | 1.3 × 10−5 | 1.32 × 10−5 | 1.32 × 10−5 | 1.32 × 10−5 | 1.32 × 10−5 | 1.32 × 10−5 |
| Φ1 (M.s)a | 1.4 × 10−8 | 2.6 × 10−8 | 6.5 × 10−8 | 1.6 × 10−7 | 1.8 × 10−7 | 4.7 × 10−8 |
| Φ2 (M. s) | 2.0 × 10−6 (2.2 × 10−7)* | 2.2 × 10−6 (2.4 × 10−7)* | 2.3 × 10−6 (2.4 × 10−7)* | 2.2 × 10−6 (2.4 × 10−7)* | 6.5 × 10−6 (2.1 × 10−6)* | 6 × 10−6 (2 × 10−6)* |
The Km values reported here are the Cleland coefficients as defined in Equation (4) and they may not be equivalent to the experimentally derived apparent Michaelis–Menten constants.
Values in the parentheses represent for pH 7.7.
Independent of pH. The values of the Cleland and Dalziel coefficients not mentioned in the table are estimated to be zero.
Figure 2.
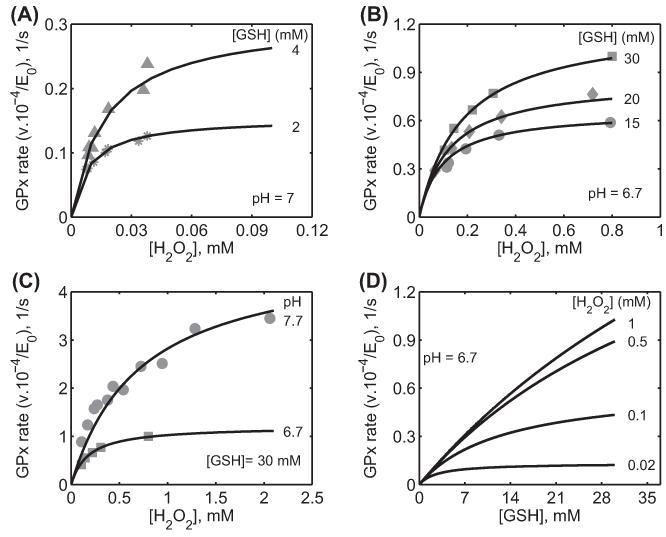
Characterization of the initial velocity data of GPx-1 for Flohé et al. [26] from bovine erythrocytes. Here, the enzyme assays were carried out at 0.15 M ionic strength and 37 °C. (A) Model fits to the initial velocity data with varying [H2O2] for two different [GSH] (2 and 4 mM) at pH 7 using phosphate buffer. (B) Model fits to the initial velocity data with varying [H2O2] for three different [GSH] (15, 20, and 30 mM) at pH 6.7 using MOPS buffer. (C) Model fits to the initial velocity data with varying [H2O2] for a fixed [GSH] (30 mM) and for different pH (6.7 and 7.7) using MOPS buffer. (D) Model simulation of initial velocity data with varying GSH for four different fixed [H2O2] (0.02, 0.1, 0.5, and 1 mM) at pH 6.7 under MOPS buffer conditions.
Figure 5.
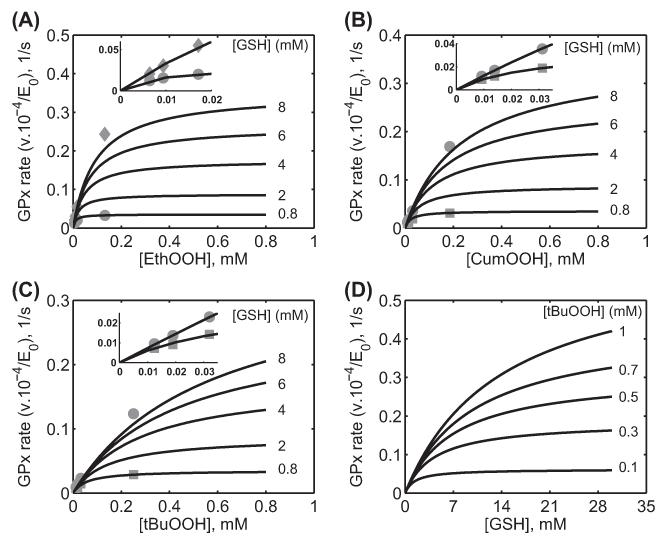
Characterization of the initial velocity data of GPx-1 for Günzler et al. [34] for different hydroperoxides. Here, the enzyme assays were carried out at 0.15 M ionic strength and 37°C at pH 6.7 in MOPS buffer. (A) Model fits to the initial velocity data with varying [EthOOH] for two different [GSH] (0.8 and 8 mM) and model prediction for three different [GSH] (2, 4, and 6 mM) using the estimated parameter values. (B) Model fits to the initial velocity data with varying [CumOOH] for two different [GSH] (0.8 and 8 mM) and model prediction for three different [GSH] (2, 4, and 6 mM) using the estimated parameter values. (C) Model fits to the initial velocity data with varying [tBuOOH] for two different [GSH] (0.8 and 8 mM) and model prediction for three different [GSH] (2, 4, and 6 mM) using the estimated parameter values. (D) Model simulation of initial velocity data with varying GSH for five different fixed [tBuOOH] (0.1, 0.3, 0.5, 0.7, and 1 mM) using the estimated parameter values for tBuOOH at pH 6.7. The figures in the inset show the model description of the experimental data for low hydroperoxide concentrations.
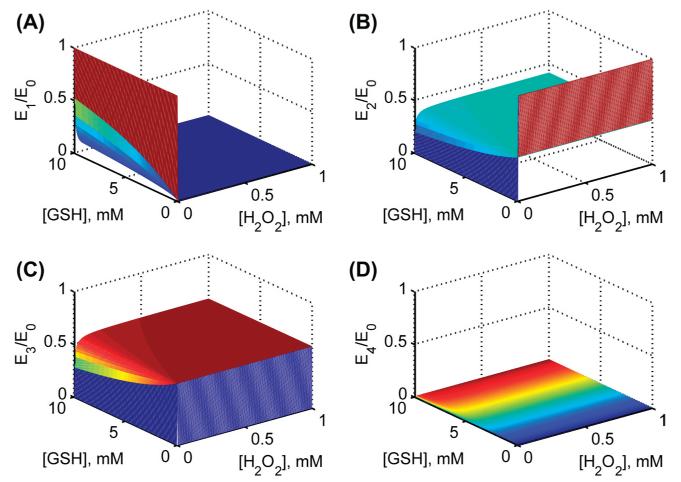
Figure 3.
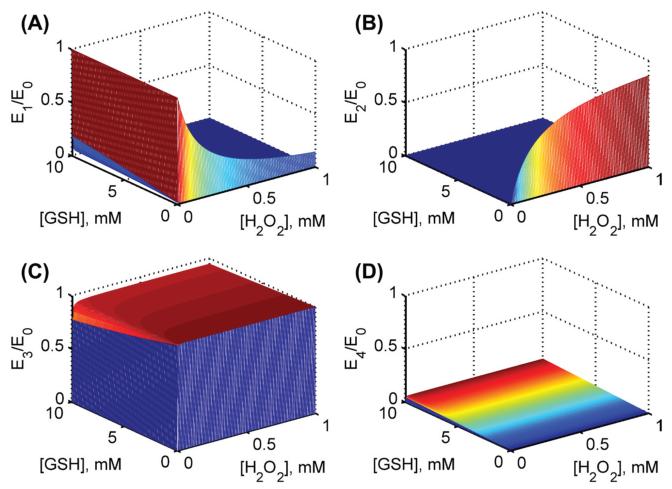
Model simulations for the fractional concentrations of individual enzyme states using estimated parameter values from Flohé et al. [26] at pH 7.2. Surface plots for fractional enzyme states with both varying substrates [H2O2] and [GSH] in the absence of product GSSG for (A) enzyme state E1 (B) enzyme state E2(C) enzyme state E3 and (D) enzyme state E4.
Figure 4.
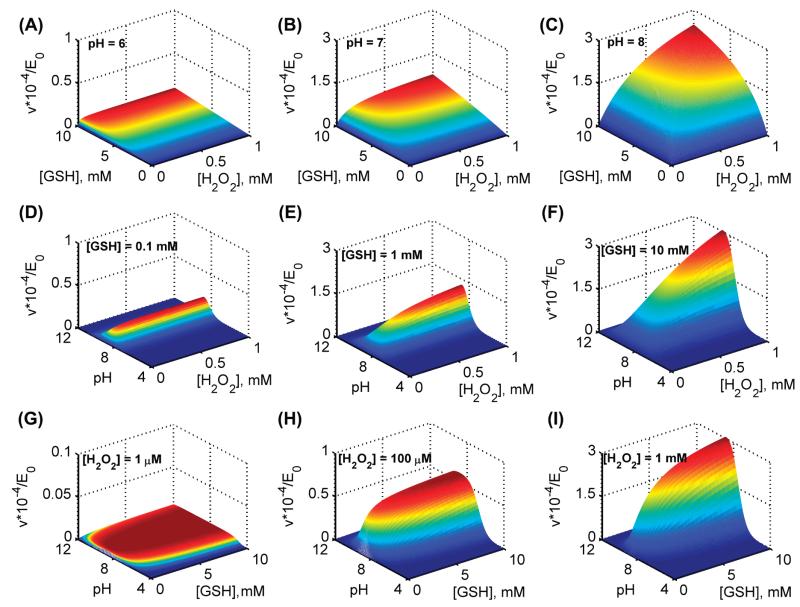
Model simulations for the effect of pH using estimated parameters values from Flohé et al. [26]. (A–C) surface plots for variation in initial velocities with both varying substrates [H2O2] and [GSH] in the absence of product GSSG for three different pH values of 6, 7, and 8, respectively. (D–F) surface plots for variation in initial velocities of GPx with both varying [H2O2] and pH in the absence of the product GSSG for three different [GSH] of 0.1, 1, and 10 mM, respectively. (G–I) surface plots for variation in initial velocities of GPx with both varying [GSH] and pH in the absence of the product GSSG for three different [H2O2] of 0.001, 0.1, and 1 mM, respectively.
Figure 6.
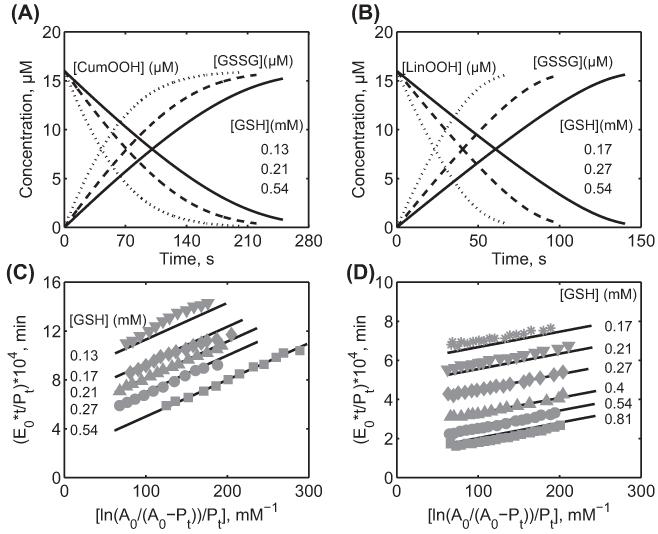
Characterization of the integrated time data from rat liver cytosolic GPx-1 for Forstrom et al. [36] for different hydroperoxides. Here, the enzyme assays were carried out at 0.15 M ionic strength and 37°C at pH 7.2 in Tris-HCl buffer. (A) Removal and generation of CumOOH (16 μM) and the product [GSSG], respectively, by rat liver GPx with time for three different [GSH] of 0.13 mM (solid line), 0.21 mM (dashed line), and 0.54 mM (dotted line). (B) Removal and generation of LinOOH (16 μM) and the product [GSSG], respectively, by rat liver GPx with time for three different [GSH] of 0.17 mM (solid line), 0.27 mM (dashed line), and 0.54 mM (dotted line). (C) Model description of the integrated time data for CumOOH (A0) for different [GSH] of 0.13, 0.17, 0.21, 0.27, and 0.54 mM. (D) Model description of the integrated time data for LinOOH (A0) for different [GSH] of 0.17, 0.21, 0.27, 0.4, 0.54, and 0.81 mM. Pt represents product [GSSG]. E0 is the concentration of enzyme used 5.2 nM.
Figure 7.
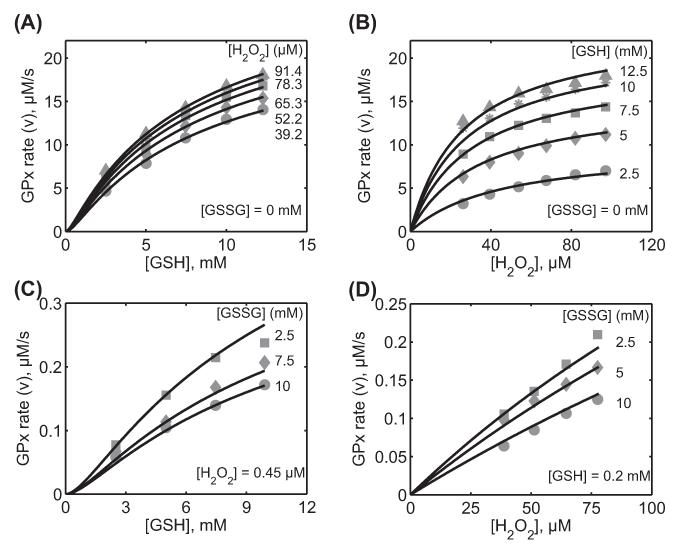
Characterization of the initial velocity data for Carsol et al. [39] using soluble GPx-1 from bovine erythrocytes. Here, the enzyme assays were carried out at 0.1 M ionic strength, pH 7.0, and 37°C. (A) Model fits to the initial velocity data with varying [GSH] for five different [H2O2] (39.2, 52.5, 65.3, 78.3, and 91.4 μM) in the absence of the product GSSG. (B) Model fits to the initial velocity data with varying [H2O2] for five different [GSH] (2.5, 5, 7.5, 10, and 12.5 mM) in the absence of the product GSSG. (C) Model fits to the initial velocity data with varying [GSH] for three different products [GSSG] (2.5, 7.5, and 10 mM) at a fixed estimated [H O] of 0.45 μM. (D) Model fits to the initial velocity data with varying [H2O2] for three different products [GSSG] (2.5, 5, and 10 mM) at a fixed estimated [GSH] of 0.2 mM.
Figure 8.
Model simulations for the fractional concentrations of individual enzyme states using estimated parameters values from Carsol et al. [39] at pH 7.2. Surface plots for fractional enzyme states with both varying substrates [H2O2] and [GSH] in the absence of product GSSG for (A) enzyme state E1 (B) enzyme state E2 (C) enzyme state E3 and (D) enzyme state E4. E0 is the total concentration of the enzyme used.
Table IV.
Estimated rate constants for the unified GPx kinetic model for different experimental data sets.
| Carsol et al. [39] | ||||||||
|---|---|---|---|---|---|---|---|---|
| Value |
Value |
|||||||
| Parameter | Value | Sensitivity | Parameter | pH = 7.0 | pH = 7.7 | Parameter | pH = 7 | pH = 7.7 |
| k1f (M−1 s−1) | 2.2 × 105 | 0.53 | Vf (s−1)a | 4.46 | 4.46 | Φ0(s)a | 0.22 | 0.22 |
| k1r (s−1) | 9.8 × 107 | 0.41 | KmA (M) | 0.1 (2.5) | 2.5 | Φ1 (M. s)a | 4.4 × 10−6 | 4.4 × 10−6 |
| k2f (M−1 s−1) | 1.3 × 108 | 0.41 | KmA1 (M) | 35 × 10−6 | 832 × 10−6 | Φ2 (M. s) | 1.5 × 10−3 | 3.2 × 10−4 |
| k2r (s−1) | 3.6 × 103 | 0.17 | KmA2 (M)a | 20 × 10−6 | 20 × 10−6 | Φ12 (M2. s) | 5.4 × 10−8 | 2.7 × 10−7 |
| k3f (M−1 s−1) | 4 × 104 | 0.42 | KmB1 (M) | 0.45 × 10−6 | 2.27 × 10−6 | Φ22 (M2. s) | 6.9 × 10−10 | 7.3 × 10−10 |
| k3r (s−1)b | 4.0 × 10−33 | N/A | KmB2 (M) | 6.8 × 10−3 | 1.45 × 10−3 | Φ122 (M3. s) | 7.4 × 10−11 | 1.8 × 10−9 |
| k4f (s−1) | 4.47 | 0.32 | KiB1 (M) | 1.3 × 10−3 | 6.9 × 10−3 | |||
| k4r (M−1 s−1) | 4.1 × 102 | 0.32 | KiB2 (M) | 12 × 10−3 | 60 × 10−3 | |||
| KH (M) | 1.5 × 10−9 | N/A | KmP(M) | 10 × 10−3 | 10 × 10−3 | |||
| Keq (M−2) | 9.0 × 1036 | N/A | Vr (s−1) | 0 | 0 | |||
N/A: Not applicable as they are fixed parameters.
Independent of pH.
Parameter was calculated based on the thermodynamic constraint.
Characterization of catalytic mechanism of GPx from bovine erythrocytes [26,34]
To study the catalytic mechanisms of GPx, Flohé et al. [26] investigated the kinetic properties of GPx-1 purified from bovine erythrocytes with H2O2 as the acceptor substrate. Using the method of quenching type rapid flow approach, they obtained parallel lines in the double-reciprocal plots of the initial velocity with varying substrate [H2O2] for the range of [GSH] used. They concluded that such a typical behavior in the double-reciprocal plots represents a classical ping-pong mechanism. Furthermore, they showed that the initial velocity of GPx increases with pH initially, but results in a typical bi-modal behavior with increasing pH. These data are used here to identify the unknown rate constants of our unified GPx model with H2O2 as the acceptor substrate.
Figure 2A-C show the experimental data of Flohé et al. [26] and the corresponding model simulations that enabled us to estimate the values of the unknown rate constants of the unified GPx model for this data set. The model fits are in agreement with the [H2O2]-dependent initial-velocity data for different [GSH] and pH values used (see figure legend for details). As shown in Figure 2A, the initial velocity was increased with increasing [GSH] (2 and 4 mM) and saturated for high concentrations of the other substrate H2O2. A similar behavior observed at high initial concentrations of GSH (15, 20, and 30 mM), where the initial velocity saturated for high concentrations of the other substrate H2O2. However, the initial velocities were not saturated with respect to GSH even for high concentrations (Figure 2B). Figure 3C shows the initial velocities for increased pH from 6.7 to 7.7 for a fixed [GSH] of 30 mM. Here, the developed model was able to describe the pH-dependent GPx kinetics adequately. The estimated values of the rate constants along with their sensitivity coefficients are tabulated in Table II. The value of the forward rate constants (k1f) estimated to fit the data at low [GSH] for Figure 2A was slightly different (2-fold higher) due to the different buffer conditions and method used to measure the initial velocities.
We used the estimated values of the rate constants for bovine erythrocytes for H2O2 in Table II to perform model simulations and predict (for which experimental data were not available) the initial velocities with varying [GSH] for four different [H2O2] and a fixed pH of 6.7 in the absence of the product GSSG (Figure 2D). The model simulations show that at low [H2O2], the initial velocity was saturated with respect to [GSH], but as [H2O2] increased, the saturating behavior disappeared. In order to see which enzyme states in the catalytic site are accumulating under steady-state (Figure 1B), we also simulated the fractional concentrations of each enzyme state with both varying substrates at a fixed pH of 7.2 (Figure 3). The figure shows that initially in the absence of H2O2, enzyme resides in reduced form (E1), which quickly disappears as both substrates increased. Similarly, in the absence of GSH, the enzyme resides in the oxidized form (E2) and settles around 50% levels for higher concentrations. The simulations show that the fractional concentrations of oxidized enzyme states (E2 and E3) are predominant under steady-state while enzyme-product complex (E4) may not be accumulating significantly.
We also further used the model-estimated parameters in Table II for H2O2 to simulate the initial velocities of the enzyme for both varying pH and substrate concentrations (Figure 4). The model simulations in Figure 4A-C show the effect of a fixed value of pH 6, 7 and 8, respectively, on the initial velocities with varying H2O2 and GSH. The initial velocities were reduced drastically under acidic pH conditions (Figure 4A) and gradually reached maximum levels as pH were increased (Figure 4B, and C). A similar behavior was observed as shown in Figure 4D-F with varying pH and H2O2 at three different fixed [GSH] of 0.1, 1, and 10 mM, respectively. Here at low [GSH] (0.1 mM), the initial velocities were minimal and activity was observed in the narrow range of pH. However, the initial velocities were increased for a higher fixed [GSH] and the enzyme was active for a broader range of pH. In contrast, for a fixed low [H2O2] (0.1 μM) with both varying pH and [GSH] (Figure 4G), though the observed initial velocities were minimal they were active under a broader range of pH. The range of pH under which the most enzyme activity observed was decreased as the fixed [H2O2] is increased as shown Figure 4H and I. Thus, the simulations show that the observed bi-modal behavior of the GPx-1 activity with varying pH, in which the bi-modal pH behavior spans broader range under low [H2O2] and high [GSH], but narrows down for the substrate combination of increased [H2O2] and decreased [GSH], representing oxidative stress conditions.
Figure 5 shows the model description of the experimental data on the reaction of GPx-1 with different hydroperoxides [34]. Here, the experiments were performed with varying hydroperoxides (EthOOH, CumOOH, and tBuOOH) for a fixed [GSH] of 0.8 and 8 mM. We used these data to estimate the unknown values of the rate constants (Table II). Figure 5A-C show respectively the model description of the initial-velocity data for EthOOH, CumOOH, and tBuOOH for a fixed [GSH] of 0.8 and 8 mM. The figures also show the model predictions of the initial velocities from the estimated rate constant values for different [GSH] (2, 4, and 6 mM) for the three hydroperoxides. We also further used the estimated parameter values to perform an example simulation (for which the experimental data are not available) with varying [GSH] for different [tBuOOH] as shown in Figure 5D. The experimental data and the model simulations show that with varying hydroperoxides, at low [GSH], the initial velocities were saturating and the saturation behavior disappeared as the [GSH] increased, indicating infinite maximum velocities and half-saturation constant values.
In order to compare the developed unified GPx model in our study with the reported flux expressions in Flohé et al. [26] and Günzler et al. [34], we used the flux expression derived in Equation (6) in terms of the Dalziel coefficients. It has been reported in Flohé et al. that the absence of terms 4, 5, and 6 in their flux expression from Equation (6) were due to no formation of ternary and quaternary complexes during catalysis. In our study, we quantitatively show that under conditions of negligible reverse rate constant, k1r (assumed a low fixed value in the model for thermodynamic consistency) and estimated low value of the k2r, the calculated values of the Dalziel coefficients Φ12, Φ22, and Φ122 turns out to be zero indicating no formation of ternary and quaternary complexes (Table I). Furthermore, Flohé et al. suggest the absence of Dalziel coefficient Φ0 in their flux expressions. Using the definition of Dalziel coefficients in terms of rate constants (Table I) and based on the estimated value of the rate constants (Table II), we show that Φ0 depends on the value of the rate constant k4f. Thus, it can be negligible given the rate of dissociation of the product GSSG from the enzyme-product complex is large. In fact, under physiological range of [GSH] (2–15 mM) [49], the Term 1(Φ0) in Equation (6) is 10-fold smaller compared to Term 3 (Φ2) based on the estimated values of the rate constants, and has small contribution to the initial velocity, which can be negligible. Furthermore, we show that the estimated values of the rate constant k1f and Dalziel coefficients Φ1 and Φ2 are identical to the reported values in Flohé et al. and Günzler et al. Thus, under the assumption of no ternary and quaternary complex formation (or negligible reverse rate constants), the flux expression for GPx from Equation (6) is equivalent to the flux expression derived in Flohé et al., with negligible contribution from Φ0 to the initial velocity of GPx.
Characterization of catalytic mechanism of rat liver cytosolic GPx [36]
Forstrom et al. [36] in their kinetic experiments determined the reaction rates of rat liver GPx-1 with two hydroperoxides using integrated rate equations. They showed that the reactivity of GSH is not altered by different hydroperoxides and concluded that GPx operates via a ping-pong mechanism. Although the experimental data did not provide initial velocities, we used the flux expression derived in our study (Equation 1) to simulate the time profiles of hydroperoxides and the product GSSG. The time profiles are then used to derive integrated rate data and compared to their data to estimate the unknown rate constants.
Figure 6 shows the formation and disappearance of the product GSSG and hydroperoxide substrates, respectively, and model description of the time profile derived data to the experimental data from Forstrom et al. [36] at different [GSH] for pH 7.2. Figure 6A shows the consumption of 16 μM CumOOH at three different [GSH] of 0.13, 0.21, and 0.54 mM. As shown in the figure, the relative consumption times depend on the [GSH], with the faster consuming times at the higher [GSH]. A similar behavior was observed with LinOOH with an initial concentration of 16 μM at three different [GSH] of 0.17, 0.27, and 0.54 mM (Figure 6B). Figure 6C and D shows the corresponding time profile derived data from model simulations for CumOOH and LinOOH, respectively, at different [GSH]. Here, the good agreement of model-derived data (solid lines) with the experimentally derived data (symbols) for various GSH concentrations suggests that the mechanism of GPx-mediated reaction is via a ping-pong mechanism. Based on the estimated values of the rate constants (Table II) and rate constant derived values of the Cleland and Dalziel coefficients (Table III), the zero values of the Dalziel coefficients (Φ12, Φ22, and Φ122) suggested no formation of intermediate ternary and quaternary complexes for rat liver GPx. The Dalziel coefficients Φ1 obtained for the unified GPx model in our study is similar to the reported value in Forstrom et al. [36]. Thus, under relevant assumptions of very low reversible rate constants (k1r and k2r), the flux expression in our unified GPx model in the absence of products can be reduced to the reported equation for flux expression in Forstrom et al.
Characterization of catalytic mechanism of soluble GPx from Carsol et al. [39]
Carsol et al. [39] performed kinetic experiments on both soluble and membrane-immobilized GPx-1 from bovine erythrocytes. Unlike other studies [26,34,36], the initial velocity measurements performed by Carsol et al. showed non-parallel lines with respect to both substrates GSH and H2O2. Furthermore, the product inhibition studies showed that the product GSSG is competitive with respect to H2O2 and non-competitive with respect to GSH. Based on these results and the observation of non-parallel lines in the double-reciprocal plots of the initial velocity with substrates, they suggested that a sequential-ordered mechanism rather than a ping-pong mechanism is involved in the catalysis of GPx. Here, the kinetic scheme presented in our study (Figure 1) is used to test the relevance of the data to the known mechanistic details of GPx mechanism and under what conditions the kinetic data of Carsol et al. can be described.
The developed model with the kinetic scheme presented above with negligible reverse rate constants (Figure 1) was not able to describe the initial velocity and productinhibition data from Carsol et al. (Supplementary Figure 2 to be found online at http://informahealthcare.com/doi/abs/10.3109/10715762.2014.886775). Thus, though thermodynamically not feasible, we assumed the reverse rate constant k1r is not vanishingly small (broken arrow in Figure 1) and used the experimental data to estimate its value along with the other rate constants. Figure 7A and B shows the model description of the initial velocity data of Carsol et al. [39] with GSH and H2O2 as the variable substrates for five different concentrations of the other substrate, respectively, in the absence of the product GSSG. The model was able to accurately describe the observed initial-velocity data given the reverse rate constants (k1r, k2r, and k4r) allowed to change. Similarly, Figure 7C and D shows the model reproduction of the effects of the product GSSG on the activity of GPx. Here, the initial velocity was measured with varying substrates [GSH] and [H2O2] for three different concentrations of the product GSSG at a fixed concentration of one of the substrates. However, the fixed [H2O2] (Figure 7C) and fixed [GSH] (Figure 7D) used in the study were not reported. We estimated these values based on the initial velocity measurements as 0.45 μM and 0.2 mM for [H2O2] and [GSH], respectively. The values of the seven unknown rate constants were estimated by simultaneously fitting both initial velocities in the absence and presence of product inhibition. The pH-mediated inhibition constant (KH) was fixed based on the value from Flohé et al. [26].
We further used the estimated parameters from Carsol et al. to determine the fractional concentrations of each enzyme state under steady-state. Figure 8 shows the model simulations of the fractional enzyme states at pH 7.2 with both varying [H2O2] and [GSH]. The simulations show that states E1 and E2 were dominant in the absence of either of the reaction substrate (Figure 8A and B) and no significant accumulation of state E4 observed as the reaction substrates increased (Figure 8D). However, with increased concentrations of both substrates, only state E3 (Figure 8C) was dominant indicating the formation of a rate-limiting intermediate enzyme complex resulting in the observed sequential mechanism. Furthermore, due to this accumulation of intermediate complex, the Dalziel coefficients Φ12, Φ22, and Φ122 from Carsol et al. [39] resulted in much higher values (Table IV) in contrast to the zero values of the Dalziel coefficients from the above studies with a ping-pong mechanism. In particular, the Dalziel coefficient Φ0 from Carsol et al. is considerably larger compared to other studies due to a small dissociation constant value of k4f (Table IV). However, as noted earlier, these results were the consequence of a hypothetical scenario where k1r is assumed to be significant. The analysis shows that the Carsol et al. data does not comply with the known details of the GPx mechanism and may be subjected to additional experimental reevaluation. Thus, the developed model based on the known aspects of the mechanism provides an opportunity to understand different data sets and validate their accuracy if contradicting experimental results were obtained under identical conditions.
Discussion
A number of experimental and modeling studies have been previously performed to characterize the catalytic mechanism of GPx [26,31-38,40,41,50]. The kinetic models developed so far for GPx kinetics are based on a simple ping-pong mechanism with no reversible reactions. Although these models were able to describe some initial velocity data, they were not able to describe the pH-mediated GPx kinetics, and hence are not complete. Since a number of integrated ROS-/H2O2-handling models [42,43,51,52] have been developed using the aforementioned catalytic mechanism for GPx yielding several conclusions, it is foremost important to understand the true catalytic mechanism of GPx-mediated reactions, which can explain both initial velocity and pH-mediated GPx kinetics [26,34,36-38,50]. Also it requires carefully choosing the relevant model in the event of contradicting experimental findings. In the current study, we present a unified catalytic scheme with the incorporation of pH regulation mechanism of GPx based on known details of the mechanism [24,26,32,34,36-38,53] and demonstrated that GPx follows a ping-pong mechanism. The analysis gave the opportunity to estimate the precise values of the rates constants for the individual reaction steps in the catalytic scheme for H2O2 and for various hydroperoxides. In addition, we show that the model is able to describe the experimental data of Carsol et al. [39] only under a hypothetical scenario which is against the known details of the GPx mechanism and reaction thermodynamics.
It was Flohé and colleagues [26,34] who first performed experiments on GPx-1 from bovine erythrocytes and proposed a kinetic mechanism based on the mechanism IV of the systemic bimolecular reactions compiled by Dalziel [47]. The resulting kinetic pattern obtained was a simple ping-pong mechanism with infinite maximal velocity and infinite Michaelis-Menten constants with the following interaction steps and the corresponding flux expression:
| (13) |
The reaction in Equation (13) contains two independent events with the reduced enzyme (E) oxidized by H2O2 and the reduction of the oxidized enzyme (F and G) by GSH. Φ1 and Φ2 are the apparent rate constants (Dalziel coefficients) for the net forward oxidative and reductive part of the catalytic cycle, respectively. A similar mechanism was corroborated by several studies [32,34-38,50]. Furthermore, based on the basic chemistry of the GPx reaction and structural information, Toppo et al. [24] suggested that GPx catalysis in reality is a complex three-substrate reaction involving a minimum of six forward and five reverse steps and suggested that the catalysis by GPx is certainly the hybrid of Dalziel’s mechanisms of IVi (formation of enzyme-substrate complexes) and IVii (no formation of enzyme-substrate complexes) [47].
For the development of a unified kinetic model for GPx, we assumed the ping-pong catalytic scheme proposed by Toppo et al. [24] (Figure 1A) based on structural information on the enzyme. We further assumed that all steps in the reaction scheme are reversible leading to six forward and six reverse steps. The catalytic scheme in Figure 1A results in a complex flux expression with 12 unknown rate constants to be estimated. In order to reduce the model complexity, as described by Flohé et al. [26] and Toppo et al. [24], we incorporated some steps in the catalytic scheme are in rapid equilibrium (fast). The substrate-binding steps involving H2O2 and GSH are believed to be rate-limiting, as opposed to substrate-independent reactions of the complexes (F-GSH and G-GSH). Furthermore, release of the product GSSG is also considered to be a rate-limiting step. Formation of the intermediate complex E-H2O2 can be ruled out assuming its rapid dissociation to form oxidized enzyme F. Furthermore, since the reaction of F-GSH to form G and H2O and G-GSH to form the state E-GSSG is considered very fast, these states can be lumped with the states G and E-GSSG, respectively, resulting in a reduced catalytic scheme presented in Figure 1B. In order to explain the observed bi-modal effects of pH on the activity of GPx [26], we incorporated the oxidized enzyme states F and G need to be in a single protonated form to react with GSH while unprotonated and diprotonated forms of F and G are considered inactive. The reduced catalytic scheme for GPx (Figure 1B) contains only eight unknown parameters for estimation after fixing one parameter from the thermodynamic constraints (Equation 10). Thus, the reduced catalytic scheme in Figure 1B was used to develop the GPx kinetic model and to characterize the available experimental data [26,34,36].
The proposed unified catalytic mechanism and the corresponding flux expression derived for the GPx kinetics in our study accurately describes the experimental data reported in Flohé et al. [26] with varying substrates (H2O2 and GSH) and pH (Figure 2). The model results are also in agreement with the Günzler et al. [34] experimental data with different hydroperoxides as the acceptor substrates (Figure 5). In fact, the flux expression reported in their studies is a special case of the flux expression derived from the unified GPx catalytic scheme in the current study. Specifically, the flux expression proposed in Flohé et al. can be obtained from Equation (6) under the assumption of negligible reverse rate constants k1r and k2r. In fact, the fitting of the model to the Flohé et al. data provides only very small estimates for k1r and k2r and can be fixed at a low value based on their local sensitivity coefficient values (Table II). The comparisons of the rate constant derived Dalziel coefficient with their reported values in the literature are in excellent agreement indicating the accuracy of the estimated values of the rate constants. Furthermore, the estimated value of the rate constant k1f is similar to the known value in the above studies. The calculated large values of the Cleland coefficients (Table III) suggest infinite half-saturation constant values for the substrates as indicated by the experimental study.
The model description of the experimental data and the corresponding values of the rate constants for H2O2 and hydroperoxides suggest that the bovine erythrocytes GPx reacts with these various hydroperoxides only slightly differently. The estimated values of the rate constant k1f were marginally different for each hydroperoxide with maximum reactivity for H2O2 followed by EthOOH. The values of k1f were only modified less than 10-fold for different hydroperoxides compared to H2O2 (Table II). Furthermore, the identical values of other rate constants (k2f, k3f, and k4f) for different hydroperoxides are consistent with the suggestion that only the first step in the reaction scheme involves hydroperoxides for oxidation of the enzyme. Subsequent steps involve GSH as the donor substrate for all hydroperoxides resulting in no change in the parameter values. The experimental data of Forstrom et al. [36] on rat liver cytosolic GPx and the corresponding model estimated parameter values for two different hydroperoxides (CumOOH and LinOOH) also suggest that the first step in the reaction scheme involves reaction with only H2O2 or hydroperoxides. However, the estimated value of the rate constant k1f for CumOOH with rat liver cytosolic GPx is 2.7-fold smaller compared to its value with bovine erythrocyte GPx (Table II, compare columns 5 and 9). The corresponding differences in the values of the other estimated rate constants (k2f and k3f) for rat liver cytosolic GPx suggest that the differences could be either due to different buffer conditions used in their experiments or due to the different source of GPx.
The basic kinetic scheme of the unified GPx model with incorporation of the pH effects was qualitatively able to show the observed bi-modal behavior of GPx activity with respect to variable pH (Figures 4 and Supplementary Figure 1A to be found online at http://informahealthcare.com/doi/abs/10.3109/10715762.2014.886775). The effect of pH on the enzyme activity was incorporated into the GPx kinetic scheme using a trial and error method. Initially, only the first enzyme state in Figure 1B (E1) assumed to be in protonated activated form and the resulted flux expression was used to fit the data. However, such assumption was not able to fit the data. Subsequently, we assumed protonation of each individual state of the enzyme independently and in combined form and repeated the fitting process. The assumption of enzyme states F and G need to be in a single protonated form to react with GSH while unprotonated and diprotonated forms of F and G are assumed inactive yielded successful description of the experimental data (Figure 2). Flohé et al. [26] also attributed the pH dependency of the bi-modal behavior of the velocity by at least two dissociations of groups in the active center of the enzyme and suggested that pH dependency is not related to the mechanism of substrate binding. The model simulation study further shows that the activity of GPxs is considerably reduced under acidic pH, indicating that under oxidative stress conditions, an acidic environment reduces the activity of GPx, thereby the rate of H2O2 removal may be hindered leading to further H2O2 emission, which has significant implications in oxidative stress conditions such as ischemia/reperfusion injury. Indeed, studies have shown increased H2O2 emission in the isolated perfused heart during ischemia, a period in which intracellular pH is low as a result of increased lactic acid build up [54,55].
The observations in Carsol et al. [39] that the GPx kinetics can be explained by a sequential-ordered mechanism cannot be true, given that the complex E-H2O2 is never formed in the catalytic cycle or reacts too fast to be detectable. Furthermore, experimental evidence is not available on the formation of ternary (E-H2O2-GSH) and quaternary (E-H2O2-(GSH)2) complexes as described in their study. Instead, the flux expression derived from the unified GPx catalytic scheme proposed in our study mimics the flux expression for sequential-ordered mechanism given the fact that the concentration of the product H2O is not explicitly used and is lumped into the rate constants. However, as expected, the current model in our study based on negligible reverse rate constants was not able to describe the experimental data of Carsol et al. [39] (Supplementary Figure 2 to be found online at http://informahealthcare.com/doi/abs/10.3109/10715762.2014.886775). We were able to describe the Carsol et al. data only when the reverse rate constants (k1r, k2r, and k4r) were allowed to change significantly, which may be thermodynamically impossible for the GPx reaction. It is also unlikely that a complex E-H2O2 is built to allow significant dissociation to form E and H2O2 through a reverse reaction. As described in various experimental studies [26,34,36,38], the enzyme is fairly unspecific with regard to various soluble peroxide substrates. Furthermore, the enzyme shows pronounced specificity for GSH with binding occurring only to the oxidized enzyme form [53]. Thus the formation of enzyme–substrate complex with GSH is probable, but may not be accumulating even at high [GSH]. The model-estimated rate constant values and the corresponding values of Cleland and Dalziel coefficients (Table III) clearly show that formation of enzyme–substrate complexes were absent. In addition, model simulations of the fractional enzyme states in the catalytic cycle clearly show that the enzyme resides predominantly in three states E1, E2, and E3 (Figure 3), based on the availability of its reactants. Given the various scenarios discussed above, it is clear that the mechanism of GPx follows a ping-pong mechanism, which is corroborated by several studies [26,32,34,36-38,56], and the model simulations presented here espouses this conclusion. Although experimental data are not reported on the effect of product GSSG on the activity of GPx, it is believed that product inhibition is negligible [26]. Interestingly, for the estimated values of the forward and fixed reverse rate constants, the model shows that the product, GSSG, has no effect on the initial velocities. The model shows product inhibition only at unrealistically high values of the reverse rate constants (e.g., parameter space of k4r, (Supplementary Figure 1B to be found online at http://informahealthcare.com/doi/abs/10.3109/10715762.2014.886775).
In conclusion, we have developed a thermodynamically balanced kinetic model for the catalytic mechanism of GPx that explains the experimental data on H2O2 and the different hydroperoxides under varying conditions [26,34,36]. Using a unified catalytic scheme, which includes an appropriate mechanism for pH, we were able to precisely determine the values of the individual rate constants for each step in the catalytic scheme. We used a systematic approach to derive flux expression in terms of Cleland and Dalziel nomenclature from general rate expression and provided the exact correlations between the rate constants, the Cleland coefficients, and the Dalziel coefficients. The analyses provided quantitative assessment for which steps in catalytic scheme are deemed to be absent based on the experimental data. Therefore, the developed model provides an opportunity to question the experimental results by Carsol et al. [39]. The requirement of the high value of the reversible rate constant k1r to describe the initial velocity measurements suggests that oxidation of free enzyme by H2O2 is reversible, which may not be feasible under physiological conditions. Thus, the sequential mechanism as described by the Carsol et al. cannot be accurate to describe the GPx kinetics. As suggested by Toppo et al. [24] and the kinetic flux expression derived in our study, the mechanism of GPx certainly follows a combination of reaction mechanisms IVi (formation of intermediate complexes) and IVii (no formation of enzyme-substrate complexes) described by Dalziel [47]. Specifically, the current model presents a unique opportunity to understand the effects of the product GSSG and pH on the activity of GPx. However, complete experimental data may still be required to estimate product-related rate constant values accurately even though product inhibition is considered negligible. Thus, the developed model in our study depicts various scenarios observed in the literature and integrating this into current models of cellular H2O2 handling can provide crucial insights into H2O2 redox balance in cells under different conditions.
Supplementary Material
Acknowledgments
The authors are thankful to Dr. Daniel A. Beard for his helpful discussions regarding the development of the model. The authors are also thankful to the reviewers for their useful comments and suggestions, which has helped in improving the manuscript significantly.
This work was supported by the National Institute of Health grants R01-HL095122 and P50-GM094503. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Footnotes
Declaration of interest
The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.
Supplementary material available online
Supplementary Figures 1 and 2.
References
- [1].Loschen G, Flohé L, Chance B. Respiratory chain linked H2O2 production in pigeon heart mitochondria. FEBS Letters. 1971;18:261–264. doi: 10.1016/0014-5793(71)80459-3. [DOI] [PubMed] [Google Scholar]
- [2].Loschen G, Azzi A, Richter C, Flohé L. Superoxide radicals as precursors of mitochondrial hydrogen peroxide. FEBS Letters. 1974;42:68–72. doi: 10.1016/0014-5793(74)80281-4. [DOI] [PubMed] [Google Scholar]
- [3].Freeman BA, Crapo JD. Biology of disease. Free radicals and tissue injury. Laboratory Investigation. 1982;47:412–426. [PubMed] [Google Scholar]
- [4].Rosen GM, Pou S, Ramos CL, Cohen MS, Britigan BE. Free radicals and phagocytic cells. FASEB Journal. 1995;9:200–209. doi: 10.1096/fasebj.9.2.7540156. [DOI] [PubMed] [Google Scholar]
- [5].Ichihashi M, Ueda M, Budiyanto A, Bito T, Oka M, Fukunaga M, et al. UV-induced skin damage. Toxicology. 2003;189:21–39. doi: 10.1016/s0300-483x(03)00150-1. [DOI] [PubMed] [Google Scholar]
- [6].Szocs K. Endothelial dysfunction and reactive oxygen species production in ischemia/reperfusion and intrate tolerance. Gen Physiol Biophys. 2004;23:265–295. [PubMed] [Google Scholar]
- [7].Novo E, Parola M. The role of redox mechanisms in hepatic chronic wound healing and fibrogenesis. Fibrogenesis Tissue Repair. 2012;5(Suppl 1):S4. doi: 10.1186/1755-1536-5-S1-S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Turrens JF. Mitochondrial formation of reactive oxygen species. J Physiol. 2003;552:335–344. doi: 10.1113/jphysiol.2003.049478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Andreyev AY, Kushnareva YE, Starkov AA. Mitochondrial metabolism of reactive oxygen species. Biochemistry (Moscow) 2005;70:200–214. doi: 10.1007/s10541-005-0102-7. [DOI] [PubMed] [Google Scholar]
- [10].Murphy MP. How mitochondria produce reactive oxygen species. Biochem J. 2009;417:1–13. doi: 10.1042/BJ20081386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Brand MD, Affourtit C, Esteves TC, Green K, Lambert AJ, Miwa S, et al. Mitochondrial superoxide: production, biological effects, and activation of uncoupling proteins. Free Radic Biol Med. 2004;37:755–767. doi: 10.1016/j.freeradbiomed.2004.05.034. [DOI] [PubMed] [Google Scholar]
- [12].Kamata H, Hirata H. Redox regulation of cellular signalling. Cell Signal. 1999;11:1–14. doi: 10.1016/s0898-6568(98)00037-0. [DOI] [PubMed] [Google Scholar]
- [13].Rhee SG. H2O2, a necessary evil for cell signaling. Science. 2006;312:1882–1883. doi: 10.1126/science.1130481. [DOI] [PubMed] [Google Scholar]
- [14].Veal EA, Day AM, Morgan BA. Hydrogen Peroxide Sensing and Signaling. Mol Cell. 2007;26:1–14. doi: 10.1016/j.molcel.2007.03.016. [DOI] [PubMed] [Google Scholar]
- [15].Andersen JK. Oxidative stress in neurodegeneration: cause or consequence? Nat Med. 2004;10:S18–S25. doi: 10.1038/nrn1434. [DOI] [PubMed] [Google Scholar]
- [16].Jones DP. Disruption of mitochondrial redox circuitry in oxidative stress. Chem Biol Interact. 2006;163:38–53. doi: 10.1016/j.cbi.2006.07.008. [DOI] [PubMed] [Google Scholar]
- [17].Lesnefsky EJ, Moghaddas S, Tandler B, Kerner J, Hoppel CL. Mitochondrial dysfunction in cardiac disease: ischemia—reperfusion, aging, and heart failure. J Mol Cell Cardiol. 2001;33:1065–1089. doi: 10.1006/jmcc.2001.1378. [DOI] [PubMed] [Google Scholar]
- [18].Wallace DC. A mitochondrial paradigm of metabolic and degenerative diseases, aging, and cancer: a dawn for evolutionary medicine. Annu Rev Genet. 2005;39:359–407. doi: 10.1146/annurev.genet.39.110304.095751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Balaban RS, Nemoto S, Finkel T. Mitochondria, oxidants, and aging. Cell. 2005;120:483–495. doi: 10.1016/j.cell.2005.02.001. [DOI] [PubMed] [Google Scholar]
- [20].Lin MT, Beal MF. Mitochondrial dysfunction and oxidative stress in neurodegenerative diseases. Nature. 2006;443:787–795. doi: 10.1038/nature05292. [DOI] [PubMed] [Google Scholar]
- [21].Arnér ESJ, Holmgren A. Physiological functions of thioredoxin and thioredoxin reductase. Eur J Biochem. 2000;267:6102–6109. doi: 10.1046/j.1432-1327.2000.01701.x. [DOI] [PubMed] [Google Scholar]
- [22].Chaudière J, Ferrari-Iliou R. Intracellular antioxidants: from chemical to biochemical mechanisms. Food Chem Toxicol. 1999;37:949–962. doi: 10.1016/s0278-6915(99)00090-3. [DOI] [PubMed] [Google Scholar]
- [23].Hayes JD, McLellan LI. Glutathione and glutathione-dependent enzymes represent a co-ordinately regulated defence against oxidative stress. Free Radic Res. 1999;31:273–300. doi: 10.1080/10715769900300851. [DOI] [PubMed] [Google Scholar]
- [24].Toppo S, Flohé L, Ursini F, Vanin S, Maiorino M. Catalytic mechanisms and specificities of glutathione peroxidases: variations of a basic scheme. Biochim Biophys Acta. 2009;1790:1486–1500. doi: 10.1016/j.bbagen.2009.04.007. [DOI] [PubMed] [Google Scholar]
- [25].Epp O, Ladenstein R, Wendel A. The refined structure of the selenoenzyme glutathione peroxidase at 0.2-nm resolution. Eur J Biochem. 1983;133:51–69. doi: 10.1111/j.1432-1033.1983.tb07429.x. [DOI] [PubMed] [Google Scholar]
- [26].Flohé L, Loschen G, Günzler WA, Eichele E. Glutathione peroxidase, V. The kinetic mechanism. Hoppe Seylers Z Physiol Chem. 1972;353:987–999. doi: 10.1515/bchm2.1972.353.1.987. [DOI] [PubMed] [Google Scholar]
- [27].Tosatto SCE, Bosello V, Fogolari F, Mauri P, Roveri A, Toppo S, et al. The catalytic site of glutathione peroxidases. Antioxid Redox Signal. 2008;10:1515–1525. doi: 10.1089/ars.2008.2055. [DOI] [PubMed] [Google Scholar]
- [28].Luo G, Zhu Z, Ding L, Gao G, Sun Q, Liu Z, et al. Generation of selenium-containing abzyme by using chemical mutation. Biochem Biophys Res Commun. 1994;198:1240–1247. doi: 10.1006/bbrc.1994.1175. [DOI] [PubMed] [Google Scholar]
- [29].Mugesh G, Singh HB. Synthetic organoselenium compounds as antioxidants: glutathione peroxidase activity. Chem Soc Rev. 2000;29:347–357. [Google Scholar]
- [30].Ren X, Jemth P, Board PG, Luo G, Mannervik B, Liu J, et al. A semisynthetic glutathione peroxidase with high catalytic efficiency: selenoglutathione transferase. Chem Biol. 2002;9:789–794. doi: 10.1016/s1074-5521(02)00167-9. [DOI] [PubMed] [Google Scholar]
- [31].Yu H, Liu J, Liu X, Zang T, Luo G, Shen J. Kinetic studies on the glutathione peroxidase activity of selenium-containing glutathione transferase. Comp Biochem Physiol B Biochem Mol Biol. 2005;141:382–389. doi: 10.1016/j.cbpc.2005.05.003. [DOI] [PubMed] [Google Scholar]
- [32].Maiorino M, Roveri A, Coassin M, Ursini F. Kinetic mechanism and substrate specificity of glutathione peroxidase activity of ebselen (PZ51) Biochem Pharmacol. 1988;37:2267–2271. doi: 10.1016/0006-2952(88)90591-6. [DOI] [PubMed] [Google Scholar]
- [33].Little C, Olinescu R, Reid KG, O’Brien PJ. Properties and regulation of glutathione peroxidase. J Biol Chem. 1970;245:3632–3636. [PubMed] [Google Scholar]
- [34].Günzler WA, Vergin H, Müller I, Flohé L. Glutathione peroxidase VI: the reaction of glutahione peroxidase with various hydroperoxides. Hoppe Seylers Z Physiol Chem. 1972;353:1001–1004. [PubMed] [Google Scholar]
- [35].Martinez JI, Garcia RD, Galarza AM. The kinetic mechanism of glutathione peroxidase from human platelets. Thromb Res. 1982;27:197–203. doi: 10.1016/0049-3848(82)90199-2. [DOI] [PubMed] [Google Scholar]
- [36].Forstrom JW, Stults FH, Tappel AL. Rat liver cytosolic glutathione peroxidase: reactivity with linoleic acid hydroperoxide and cumene hydroperoxide. Arch Biochem Biophys. 1979;193:51–55. doi: 10.1016/0003-9861(79)90007-9. [DOI] [PubMed] [Google Scholar]
- [37].Takebe G, Yarimizu J, Saito Y, Hayashi T, Nakamura H, Yodoi J, et al. A comparative study on the hydroperoxide and thiol specificity of the glutathione peroxidase family and selenoprotein P. J Biol Chem. 2002;277:41254–41258. doi: 10.1074/jbc.M202773200. [DOI] [PubMed] [Google Scholar]
- [38].Chiu DTY, Stults FH, Tappel AL. Purification and properties of rat lung soluble glutathione peroxidase. Biochim Biophys Acta. 1976;445:558–566. doi: 10.1016/0005-2744(76)90110-8. [DOI] [PubMed] [Google Scholar]
- [39].Carsol MA, Pouliquen-Sonaglia I, Lesgards G, Marchis-Mouren G, Puigserver A, Santimone M. A new kinetic model for the mode of action of soluble and membrane-immobilized glutathione peroxidase from bovine erythrocytes: effects of selenium. Eur J Biochem. 1997;247:248–255. doi: 10.1111/j.1432-1033.1997.00248.x. [DOI] [PubMed] [Google Scholar]
- [40].Antunes F, Han D, Cadenas E. Relative contributions of heart mitochondria glutathione peroxidase and catalase to H2O2 detoxification in in vivo conditions. Free Radic Biol Med. 2002;33:1260–1267. doi: 10.1016/s0891-5849(02)01016-x. [DOI] [PubMed] [Google Scholar]
- [41].Ng CF, Schafer FQ, Buettner GR, Rodgers VGJ. The rate of cellular hydrogen peroxide removal shows dependency on GSH: mathematical insight into in vivo H2O2 and GPx concentrations. Free Radic Res. 2007;41:1201–1211. doi: 10.1080/10715760701625075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Aon MA, Stanley BA, Sivakumaran V, Kembro JM, O’Rourke B, Paolocci N, et al. Glutathione/thioredoxin systems modulate mitochondrial H2O2 emission: an experimental-computational study. J Gen Physiol. 2012;139:479–491. doi: 10.1085/jgp.201210772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Cortassa S, Aon MA, Winslow RL, O’Rourke B. A mitochondrial oscillator dependent on reactive oxygen species. Biophys J. 2004;87:2060–2073. doi: 10.1529/biophysj.104.041749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Qi F, Dash RK, Han Y, Beard DA. Generating rate equations for complex enzyme systems by a computer-assisted systematic method. BMC Bioinformatics. 2009;10:238. doi: 10.1186/1471-2105-10-238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Cleland WW. The kinetics of enzyme-catalyzed reactions with two or more substrates or products. I. Nomenclature and rate equations. Biochim Biophys Acta. 1963;67:104–137. doi: 10.1016/0006-3002(63)91800-6. [DOI] [PubMed] [Google Scholar]
- [46].Segel IH. Enzyme kinetics: behavior and analysis of rapid equilibrium and steady-state enzyme systems. Wiley; New York: 1975. pp. xxii–957. [Google Scholar]
- [47].Dalziel K. Initial steady state velocities in the evaluation of enzyme-coenzyme-substrate reaction mechanisms. Acta Chem Scand. 1957;11:1706–1723. [Google Scholar]
- [48].Alberty RA. Thermodynamics of biochemical reactions. Wiley-Interscience; Hoboken, NJ: 2003. [Google Scholar]
- [49].Griffith OW, Meister A. Origin and turnover of mitochondrial glutathione. Proc Natl Acad Sci USA. 1985;82:4668–4672. doi: 10.1073/pnas.82.14.4668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Mueller S, Riedel HD, Stremmel W. Direct evidence for catalase as the predominant H2O2-removing enzyme in human erythrocytes. Blood. 1997;90:4973–4978. [PubMed] [Google Scholar]
- [51].Yang L, Korge P, Weiss JN, Qu Z. Mitochondrial oscillations and waves in cardiac myocytes: insights from computational models. Biophys J. 2010;98:1428–1438. doi: 10.1016/j.bpj.2009.12.4300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Zhou L, Aon MA, Almas T, Cortassa S, Winslow RL, O’Rourke B. A reaction-diffusion model of ROS-induced ROS release in a mitochondrial network. PLoS Comput Biol. 2010;6:e1000657. doi: 10.1371/journal.pcbi.1000657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Flohé L, Schaich E, Voelter W, Wendel A. Glutathione peroxidase. 3 Spectral characteristics and experiments for the reaction mechanism. Hoppe Seylers Z Physiol Chem. 1971;352:170–180. [PubMed] [Google Scholar]
- [54].Aldakkak M, Stowe DF, Lesnefsky EJ, Heisner JS, Chen Q, Camara AKS. Modulation of mitochondrial bioenergetics in the isolated guinea pig beating heart by potassium and lidocaine cardioplegia: implications for cardioprotection. J Cardiovasc Pharmacol. 2009;54:298–309. doi: 10.1097/FJC.0b013e3181b2b842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Camara AKS, Bienengraeber M, Stowe DF. Mitochondrial approaches to protect against cardiac ischemia and reperfusion injury. Front Physiol. 2011;2:13. doi: 10.3389/fphys.2011.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Chance B, Sies H, Boveris A. Hydroperoxide metabolism in mammalian organs. Physiol Rev. 1979;59:527–605. doi: 10.1152/physrev.1979.59.3.527. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.