Concurrent Tumor Segmentation and Registration with Uncertainty-based Sparse non-Uniform Graphs

Abstract

In this paper, we present a graph-based concurrent brain tumor segmentation and atlas to diseased patient registration framework. Both segmentation and registration problems are modeled using a unified pairwise discrete Markov Random Field model on a sparse grid superimposed to the image domain. Segmentation is addressed based on pattern classification techniques, while registration is performed by maximizing the similarity between volumes and is modular with respect to the matching criterion. The two problems are coupled by relaxing the registration term in the tumor area, corresponding to areas of high classification score and high dissimilarity between volumes. In order to overcome the main shortcomings of discrete approaches regarding appropriate sampling of the solution space as well as important memory requirements, content driven samplings of the discrete displacement set and the sparse grid are considered, based on the local segmentation and registration uncertainties recovered by the min marginal energies. State of the art results on a substantial low-grade glioma database demonstrate the potential of our method, while our proposed approach shows maintained performance and strongly reduced complexity of the model.

1. Introduction

Gliomas are the most common type of primary brain tumors and arise from glial cells. They are classified in 4 grades by the World Health Organization (WHO), grade I corresponding to benign tumors with excellent prognosis and Grade IV gliomas (Glioblastoma Multiforme) being the most common and lethal. WHO grade II Low Grade Gliomas (LGG) are a specific kind of glioma that represent about 30% of the brain tumors and can affect younger patients (Soffietti et al., 2010). They are characterized by a continuous slow growth and yield mild symptoms. They generally undergo anaplastic transformation into a fast growing malignant tumors and therefore have to be monitored closely via frequent MRIs. Knowing the size and extent of a brain tumor is of extreme importance in order to evaluate its growth, its reaction to therapy and for surgery planning Currently, the physicists compute the main tumor diameters and approximate it as an ellipsoid, a highly imprecise measure that tends to overestimate the volume of the tumor (Pallud et al., 2012). The current gold standard is manual segmentation, which on top of being a tedious and time consuming task, is also subject to a high inter and intra operator variability. Automatic tumor segmentation is thus an active research field that aims at obtaining fast and robust segmentations. It is a particularly difficult subject due to the extreme heterogeneity between the tumors in appearance, shapes and size and their overlapping intensities with the healthy tissue. LGG are diffusively infiltrative tumors with extremely irregular and fuzzy boundaries, rendering the segmentation task even more difficult.

Fuzzy clustering and knowledge based methods were amongst the first considered for tumor segmentation with limited success (Clark et al., 1998; Fletcher-Heath et al., 2001). Level sets and Active Contours have been a popular approach (Ho et al., 2002; Cobzas et al., 2007; Taheri et al., 2010), but suffer from their strong sensitivity to initialization. The idea is to model the tumor boundary as a parametric curve that evolves depending on the image properties and curvature constraints. Statistical classification methods offer an efficient way of detecting tumor voxels. The voxels are treated independently and separated by a classifier that is learned from a set of training samples. Examples refer to the Support Vector Machines (SVM) (Verma et al., 2008; Zhang et al., 2004; García and Moreno, 2004), Boosting (Xuan and Liao, 2007) or the Decision Forests (Zikic et al., 2012). Despite promising performance, those methods are plagued by the i.i.d assumption that treats each voxel independently, leading to irregular segmentations. Morphological filtering (Zhang et al., 2004) or neighborhood dependent features (Zikic et al., 2012) offer limited improvement on the local consistency of the segmentation. Notable improvement is observed when coupling the statistical classification with local neighborhood dependencies (Lee et al, 2008; Gorlitz et al., 2007; Wels et al., 2008; Bauer et al., 2011), modeled by a random field (Markov Random Field (MRF), Conditional Random Field (CRF)) (Wang et al., 2013) based spatial prior. In this context, the segmentation is locally smoothed by penalizing neighbors that are assigned different segmentation labels, but still lacks global information regarding the tumor's position and the brain boundaries. Stronger dependencies can be modeled via a hierarchical approach. Gering et al. (2002) proposed a multi layer MRF approach where the tumor is detected as an outlier from manually selected training voxels. At each layer, the segmentation is refined based on higher level information and the previous layer's segmentation. Corso et al. (2008) combine Bayesian classification using Gaussian Mixture Models with a hierarchical graph affinity model, where the spatial dependencies are modeled by assigning an affinity to each graph edge.

Atlas-based segmentation methods rely on the registration of an annotated volume to the subject in order to segment the structures of interest. The use of a brain atlas allows for structural spatial prior information, but the task is more difficult when the structure to segment is a tumor since it cannot be matched in the atlas. That is often addressed through a model for tumor detection. Kaus et al. (2001) alternate kNN classification based on intensity and anatomical location with a registration step based on the structures' segmentation, the tumor being labeled as white matter in the registration process. In (Prastawa et al., 2003) a probabilistic atlas is affinely registered to the patient, enabling to define prior probabilities on the expected intensities of the structures. The atlas is modified to account for tumor presence (detected by contrast enhancement) and edema. Similarly to Gering et al. (2002), the tumor voxels can be detected as outliers from the healthy voxels (Menze et al., 2010; Prastawa et al, 2004). The healthy structures' features are estimated from a registered healthy atlas. Additional local spatial constraints are modeled via Markov Random Fields (Menze et al., 2010) or level sets (Prastawa et al., 2004).

Atlas based methods depend on the quality of the registration. Rigid or affine registration methods are not sufficient to recover the inter patient anatomical differences, while traditional non-rigid registration methods fail in this context by attempting to find correspondences between the tumor and the healthy voxels. An efficient atlas based segmentation thus requires a registration scheme that accommodates for the presence of the tumor.

Despite extensive work in deformable image registration (Zikic et al., 2010; Ou et al., 2011; Berendsen et al., 2013; Sotiras et al., 2013), there has been limited work dedicated to registration with missing correspondences. Such a registration task is of high interest for the study of brain tumors through statistical atlases and longitudinal studies. A tumor specific probabilistic atlas, constructed through affine registration of a large database to the same reference coordinates, was notably proposed in (Parisot et al., 2011). It enabled the identification of preferential locations for the tumors and could lead to unraveling position dependent behaviors and origins. Deformable registration would enable to go further and study the interactions between the tumors and the brain structures and functional areas. Understanding the tumors growth patterns and their impact on the brain's functional organization is of key importance for therapy and surgery planning.

We can distinguish two groups of methods for registration in the presence of a tumor. The first relies on modeling the tumor growth to evaluate the tumor induced deformation (Kyriacou et al., 1999; Mohamed et al., 2006; Zacharaki et al, 2008; Cuadra et al., 2004). Kyriacou et al. (1999) proposed a biomechanical finite element model to simulate the tumor induced deformation while assuming a radial uniform growth of the tumor. Using the tumor growth model, a healthy brain was simulated by contracting the tumor, allowing for a normal registration process. Cuadra et al. (2004) also assumed radial growth of the tumor. The registration is performed using the demons algorithm (Thirion, 1998) between healthy voxels and is based on the distance from a manually selected seed in the tumor area (that has been segmented prior to the registration process). Mohamed et al. (2006) decomposed the deformation as inter subject and tumor induced deformations. The latter was modeled via a biomechanical finite element model whose parameters are learned by statistical learning. The tumor growth is then simulated in the healthy atlas, enabling normal registration. This method was extended in (Zacharaki et al., 2008) towards a computationally efficient biomechanical model taking into account the potential infiltrative parts of the tumor by limiting the tumor growth. Growth models require either user interaction or extensive computations to evaluate the model parameters and are mostly adapted to space occupying lesions. Low grade gliomas are infiltrative tumors with little to no mass effect and edemas. The limited amount of deformation caused by the tumors renders the use of growth model not adapted and possible prone to errors assuming the tumor pushes tissue instead of infiltrating it. The second group of methods (Brett et al., 2001; Stefanescu et al, 2004) adopts a simpler approach and masks the pathology towards excluding it during registration. The tumor area is discarded during the computation of the similarity criterion and deformed by interpolation. This kind of approach offers a better modularity with respect to the pathology since no assumption is made about the pathological area nor the progression of the tumor. Both approaches require a reliable segmentation of the tumor, making the registration dependent on the quality of the segmentation of the tumor.

Registration and tumor segmentation appear as two fundamentally correlated problems, where one could benefit from the other if performed simultaneously. The idea of coupling segmentation and registration is not a new concept. Yezzi et al. (2003) used an active contour framework, estimating the registration parameters and reference volume's segmentation curve by minimizing a joint energy depending on both images. The floating image is segmented by registering the reference's segmentation. A maximum a posteriori framework was presented in (Wyatt and Noble, 2003) where the segmentation and rigid registration parameters are determined alternatively. The segmentation relies on Gaussian Mixture Models coupled with an MRF prior, while the registration relies on the segmentation by minimizing the joint class histogram between both images. Mahapatra and Sun (2012) proposed an MRF based framework where each voxel of the image has to be assigned a displacement and segmentation label. The different classes are separated based on the intensities in both images while the registration relies on minimizing conventional similarity metrics. The registration and segmentation fields are smoothed by enforcing similar displacement among voxels of the same class. Ashburner and Friston (2005) proposed a statistical model, where a probabilistic atlas plays the part of a spatial prior for segmentation and bias field correction. The different classes are separated via a mixture of Gaussians, allowing for several modes per class. The atlas is globally registered by affine registration then locally deformed. Last but not least, Pohl et al. (2006) developed an Expectation Maximization (EM) Bayesian framework, alternatively estimating the segmentation probabilities and the rigid registration and bias field parameters.

All those methods rely on the concept that the structures to be segmented appear in both images. The joint segmentation and registration problem becomes far more challenging in the presence of a pathology due to the absence of a match in the second image. Most methods alternatively estimate the registration and segmentation maps. Chitphakdithai and Duncan (2010) proposed an EM Bayesian framework in the context of a surgical tumor resection. The resection area was detected by statistical learning on a training set based on the intensity values and deformed by interpolation (constant registration cost in the resection area). In the same clinical context, Risholm et al. (2009) coupled the demons algorithm with level sets. They alternate segmentation of the resected area by evolving a level set based on the image gradient and intensities disagreements, with a demons based registration that accommodates the resection by only allowing displacement towards the area. The problem is more challenging in the context of tumors that have complex intensity profiles. Gooya et al. (2011), inspired from the work of Zacharaki et al. (2008) and Pohl et al. (2006) introduced a method to to deal with the presence of a tumor. The tumor is simulated in a probabilistic atlas via a biomechanical model of tumor growth. The EM algorithm is used to iteratively estimate segmentation posterior probabilities and the tumor growth and registration parameters. While growth models are able to simulate the mass effect, they suffer from the computational burden of estimating the model parameters and are hardly generalizable to other pathologies. Furthermore, the quality of the registration directly depends on the quality of the model which implies extended knowledge on the pathology.

In (Parisot et al, 2012), we introduced a concurrent segmentation and registration framework that exploits the dependencies between the two problems in order to adapt the registration task to the presence of the tumor as well as increase the segmentation quality. The concurrent registration and segmentation framework is embedded in a discrete graphical model, where a sparse grid is superimposed to the volume domain and each node will be simultaneously displaced and classified. The registration term is relaxed in the tumor area that is detected by statistical classification. Pairwise constraints ensure the smoothness of the segmentation and deformation fields. This discrete approach raises the problem of defining the discrete displacement set and resolution of the sparse grid that have to be high enough to capture small details and remain computationally efficient. In this paper, we extend the proposed method through a novel content-driven hierarchical coarse to fine approach exploring segmentation and registration uncertainties as determined by the min-marginal energies. The displacement set sampling relies on the local structures anisotropy while the grid refinement is controlled by the local homogeneity of the region and the segmentation uncertainties. This yields non uniform high resolution grids with a much lower complexity. The proposed MRF based individual tumor detection and registration framework and their coupling is described in Section 2 while the uncertainty driven adaptive sampling method is introduced in Section 3. The experimental validation is part of Section 4 and is carried out on a large low-grade glioma database as well as the publicly available BRATS dataset. Discussion and future directions conclude the paper.

2. Concurrent Tumor Segmentation and Registration

2.1. Statistical Classification based Tumor Segmentation

Let us consider a volume V featuring a tumor that we seek to segment. The tumor can be efficiently detected via the construction of a classifier separating tumor voxels from healthy voxels. We adopt the Gentle Adaboost algorithm (Friedman et al., 2000) that builds a strong classifier as a linear combination of weak classifiers. Let us consider a set of N training samples {x_i, y_i}, i ∈ {1, N}, where x_i is a voxel extracted from a tumor bearing volume, and y_i is its corresponding label (tumor or background). To each pair is associated a feature vector Π(x_i) and a weight $W_i=\frac{1}{N}$.

At each iteration t, the algorithm selects a feature and a threshold, in order to build a weak classifier h_t(x_i) as a decision stump that minimizes the classification error:

$$\mathit{\text{err}}=\sum _{i=1}^N{W}_i|h_t({\mathbf{x}}_{\mathbf{i}})-y_i|$$ (1)

The weights W_i are then updated as W_i = W_i exp(−y_ih_t(x_i)) in order to give more importance to misclassified voxels at the next iteration. The strong classifier H(x) is obtained by summing the weak classifiers, and yields a classification score that can be converted to probabilities as:

$$\begin{array}{l}{p}_{\mathit{\text{tm}}}(\mathbf{x})=\frac{1}{1+exp(-2H(\mathbf{x}))}\\ p_{\mathit{\text{bg}}}(\mathbf{x})=1-p_{\mathit{\text{tm}}}(\mathbf{x})\end{array}$$ (2)

The key element of the boosting algorithm is the selection of the feature vector. We adopt a high dimensional space exploring visual, phase and geometric properties. First, we rely on the intensity values using patches (9 × 9 × 5) centered on the sample voxel x_i Median, entropy and standard deviation values are extracted from another set of patches of sizes k × k × 3, where k = {7, 9, 11}. Second, we compute Gabor features (Manjunath and Ma, 1996) on 2 scales and 10 orientations. We adopt the method of Zhan and Shen (2003) that approximates the 3D Gabor filters by computing two orthogonal 2D filter banks. Eventually, we compute a symmetry based feature, since the presence of the tumor will introduce an asymmetry between the hemispheres of the brain. Assuming a symmetry plane is known, the symmetry feature is computed as 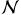$\mathit{\text{S ym}}({\mathbf{x}}_{\mathbf{i}})=\frac{1}{n}{\sum }_{{\mathbf{x}}_{\mathbf{j}}\in \mathcal{N}({\mathbf{x}}_{\mathbf{i}})}I({\mathbf{x}}_{\mathbf{j}})-\frac{1}{n}{\sum }_{{\mathbf{x}}_{\mathbf{j},\mathbf{s}}\in \mathcal{N}({\mathbf{x}}_{\mathbf{i},\mathbf{s}})}I({\mathbf{x}}_{\mathbf{j},\mathbf{s}})$. (.) is a neighborhood introduced to compensate the approximate symmetry plane, x_i,s is the symmetric of voxel x_i and I(.) is the intensity value.

Spatial dependencies are introduced through an MRF model on a graph where each voxel of the image is a node and the edges connect the node to its 6 immediate neighbors. In this model, we define a binary label set 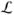_s = {0, 1}. Each node x (i.e image voxel) is to be assigned one label, tumor (l_x = 1) or background (l_x = 0). The optimal labeling is recovered by minimizing the MRF energy (Boykov and Funka-Lea, 2006):

$$E_{\mathit{\text{seg}}}(\mathbf{l})=\sum _x{V}_x(l_x)+\sum _x\sum _y{V}_{x,y}(l_x,l_y)$$ (3)

The unary potentials V_x(.) correspond to the classification likelihoods, seeking the most probable label according to the boosting classification decisions:

$$V_x(\mathbf{l})=-l_{x}log(p_{\mathit{\text{tm}}}(\mathbf{x}))-(1-l_x)log(p_{\mathit{\text{bg}}}(\mathbf{x}))$$ (4)

And the pairwise term plays the part of a smoothing prior on the segmentation field, and is defined as a Potts model that penalizes neighboring nodes labeled differently:

$$V_{\mathit{\text{xy}}}(l)=\beta (1-\delta (l_x,l_y))$$ (5)

where β is a constant parameter describing the amount of smoothing.

The main drawback of this approach is the lack of global information on the brain structure, the spatial dependencies being encoded in a strictly local manner. Coupling segmentation with registration adds global information, but requires an efficient registration scheme.

2.2. Graph based Registration

Let us consider a source image A and a target image V defined on a domain Ω. In our case, the source image is a healthy brain and the target image is a diseased brain featuring a tumor. In the task of image registration, we want to find the geometric transformation 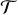that will map the source image to the target image:

$$V(\mathbf{x})=A\circ \mathcal{T}(\mathbf{x})$$ (6)

We adopt the Free Form Deformation (FFD) approach (Rueckert et al., 1999), where a sparse grid ⊂ Ω is superimposed to the volume. The transformation will be evaluated on the grid's control points, and then on the whole volume by interpolation.

$$\mathcal{T}(\mathbf{x})=\mathbf{x}+\sum _{p\in \mathcal{G}}\eta (\Vert \mathbf{x}-\mathbf{p}\Vert ){\mathbf{d}}_{\mathbf{p}}$$ (7)

where d_p is the displacement of control point p and η(.) is the projection function that describes the influence of each control point on voxel x.

The most likely displacement should minimize the differences between the deformed image A( 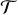(x)) and target image V(x), evaluated by a similarity measure ρ(.):

$${\mathcal{T}}^{\mathit{\text{opt}}}(\mathbf{x})=arg\underset{\mathcal{T}}{min}\sum _{p\in \mathcal{G}}{\int }_{\mathrm{\Omega }}\overline{\eta }(\Vert \mathbf{x}-\mathbf{p}\Vert )\rho (V(\mathbf{x}),A(\mathcal{T}(\mathbf{x})))\mathit{\text{dx}}$$ (8)

The similarity measure is evaluated on the whole domain Ω. This information is back projected on the control points via the function η̅(.).

In order to recover the optimal control points' displacements, we adopt a discrete MRF model (Glocker et al, 2008a, 2011). Let us consider a discrete set of labels 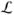= {1, …, n}, and a set of discrete displacements Δ = {d¹, …, dⁿ}. We seek to assign a label l_p to each grid node p, where each label corresponds to a discrete displacement d^lp ∈ Δ. In this setting, the deformation field is rewritten as:

$$\mathcal{T}(\mathbf{x})=\mathbf{x}+\sum _{p\in \mathcal{G}}\eta (|\mathbf{x}-\mathbf{p}|){\mathbf{d}}^{{\mathbf{l}}_{\mathbf{p}}}$$ (9)

In order to recover the optimal labeling, we need to minimize the MRF energy:

$${\mathbf{l}}^{\mathbf{\text{opt}}}=arg\underset{l}{min}{E}_{\mathit{\text{reg}}}(\mathbf{l})$$ (10)

where

$$E_{\mathit{\text{reg}}}(\mathbf{l})=\sum _{p\in \mathcal{G}}{V}_p(l_p)+\lambda \sum _{\mathbf{p}\in \mathcal{G}}\sum _{\mathbf{q}\in \mathcal{N}(\mathbf{p})}{V}_{p,q}(l_p,l_q)$$ (11)

where 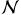(.) represents the neighborhood system, defined here as a 6-neighbors configuration. V_p,q(.) is a pairwise potential, that imposes certain smoothness on the deformation.

The unary potential V_p(.) is only dependent on node p's configuration and represent the likelihood of the node being assigned a label. To preserve the independence assumption, we can approximate the unary potentials as:

$$V_p(l_p)\approx {\int }_{\mathrm{\Omega }}\overline{\eta }(\Vert \mathbf{x}-\mathbf{p}\Vert )\rho (V(\mathbf{x}),A(\mathbf{x}+d^{l_p}))\mathit{\text{dx}}$$ (12)

This approach shows great performance for the registration of healthy brains (Glocker et al., 2008a), but performs poorly in the tumor area where the similarity metric is not reliable. The most straightforward solution is to mask the pathology and not take the tumor voxels into account during the evaluation of the similarity criterion ρ(.). This requires a very reliable segmentation map and would introduce a bias for the registration.

2.3. Concurrent Tumor Segmentation and Registration

Our approach aims at simultaneously performing tumor segmentation and atlas to diseased subject registration. The coupling of the segmentation with the registration of an atlas introduces global information on the brain structure, while the registration quality is improved by acknowledging the presence of the tumor and treating it differently than healthy tissue during registration. The registration and segmentation energies are coupled in a single MRF framework, where the tumor is detected concurrently to the registration. In this combined framework, we seek to recover the optimal transformation 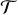(x) and the segmentation map 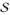(x).

Let us consider a sparse grid superimposed to the volume, a discrete set of labels 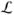_c = {1, …, 2n}, a predefined discrete set of displacements Δ, and the tumor p_tm(x) and background p_bg(x) prior probabilities learned via boosting. Each label l ∈ 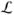_c is associated to a pair segmentation/displacement {s^l, d^l} ∈ {0, 1} × Δ, where we define:

$$\begin{array}{ll}{\mathbf{d}}^{{\mathbf{l}}_{\mathbf{p}}}\hfill & ={\mathbf{d}}^{\mathbf{k}}\text{where}k=l_p(modn)\hfill \\ s^{l_p}\hfill & =\lceil \frac{l_p}{n}\rceil \hfill \end{array}$$ (13)

We seek to assign a label l_p to each control point p of , simultaneously displacing the grid node and characterizing it as tumor or background. The segmentation and deformation fields are then evaluated on the whole volume by interpolation:

$$\begin{array}{ll}\mathcal{T}(\mathbf{x})\hfill & =\mathbf{x}+\sum _{p\in \mathcal{G}}\eta (|\mathbf{x}-\mathbf{p}|){\mathbf{d}}^{{\mathbf{l}}_{\mathbf{p}}}\hfill \\ \mathcal{S}(\mathbf{x})\hfill & =\sum _{p\in \mathcal{G}}\eta (|\mathbf{x}-\mathbf{p}|){\mathbf{s}}^{{\mathbf{l}}_{\mathbf{p}}}\hfill \end{array}$$ (14)

The MRF energy consist of segmentation and registration terms that are interdependent:

$$E_{\mathit{\text{reg}},\mathit{\text{seg}}}(\mathbf{l})=\sum _{p\in \mathcal{G}}\underset{\text{Unary terms}}{\underbrace{\alpha V_{\mathit{\text{reg}}}(l_p)+(1-\alpha )V_{\mathit{\text{seg}}}(l_p)}}+\sum _{\mathbf{p}\in \mathcal{G}}\sum _{\mathbf{q}\in \mathcal{N}(\mathbf{p})}\underset{\text{Pairwise terms}}{\underbrace{\alpha V_{\mathit{\text{pq}},\mathit{\text{reg}}}(l_p,l_q)+(1-\alpha )V_{\mathit{\text{pq}},\mathit{\text{seg}}}(l_p,l_q)}}$$ (15)

where α is a parameter balancing the importance of the segmentation and registration terms.

The pairwise costs ensure that the segmentation and registration are locally smooth. They are set as:

$$V_{\mathit{\text{pq}},\mathit{\text{seg}}}(l_p,l_q)=\frac{|s^{l_p}-s^{l_p}|}{\Vert \mathbf{p}-\mathbf{q}\Vert }$$ (16)

$$V_{\mathit{\text{pq}},\mathit{\text{reg}}}(l_p,l_q)=\lambda \frac{{\left(({\mathbf{d}}^{{\mathbf{l}}_{\mathbf{p}}}-{\mathbf{d}}^{{\mathbf{l}}_{\mathbf{q}}})\right)}^2}{\Vert \mathbf{p}-\mathbf{q})\Vert }$$ (17)

The strength of the pairwise cost depends on the distance between the connected nodes, taking into account a possible anisotropy as the distance between nodes would then differ. The closer the nodes are, the stronger the penalty imposing similar labels. The registration regularization's role is to preserve the anatomical structure of the brain. Important deformations can occur in and around the tumor area, requiring a relaxation of the pairwise cost to allow for those strong deformations.

Let us now proceed with the definitions of the unary potentials. Outside the tumor area (s^l_p = 0), the registration term seeks correspondences between the atlas and the target's healthy tissues via the similarity metric ρ(.). However, this metric is not reliable in the tumor area (s^l_p = 1) since there are no existing correspondences. We use instead a constant cost C_tm that is independent of the chosen displacement:

$$\begin{array}{r}\hfill V_{\mathit{\text{reg}}}(l_p)={\int }_{\mathrm{\Omega }}\overline{\eta }(\Vert \mathbf{x}-\mathbf{p}\Vert )\\ \hfill \left(s^{l_p}{C}_{\mathit{\text{tm}}}(\mathbf{x})+(1-s^{l_p})\rho (V(\mathbf{x}),A(\mathbf{x}+d^{l_p}))\right)\mathit{\text{dx}}\end{array}$$ (18)

The tumor probabilities and the similarity metric are evaluated on the whole volume and back projected on the control points. The use of a constant cost causes the displacement within the tumor area to be determined by interpolation with the neighboring nodes at the tumor boundary, through the pairwise regularization term. While the main role of this potential is registration of the two volumes, it allows detection of part of the tumor through the similarity measure. Indeed, if a strong dissimilarity between voxels is observed, it is likely that the area belongs to the tumor.

This potential alone is however not sufficient for a precise segmentation of the tumor, due to the fact that the tumor's local appearance can be similar to healthy tissue and that dissimilar voxels do not necessarily correspond to tumors. Additional information on the position of the tumor is introduced by coupling this registration term with a segmentation unary term. This term relies on the prior probabilities introduced in section 2.1, imposing the label that has the maximum likelihood probability:

$$\begin{array}{r}\hfill V_{\mathit{\text{seg}}}(l_p)={\int }_{\mathrm{\Omega }}\overline{\eta }(\Vert \mathbf{x}-\mathbf{p}\Vert )\\ \hfill \left(-s^{l_p}log(p_{\mathit{\text{tm}}}(\mathbf{x}+{\mathbf{d}}^{{\mathbf{l}}_{\mathbf{p}}}))-(1-s^{l_p})log(p_{\mathit{\text{bg}}}(\mathbf{x}+{\mathbf{d}}^{{\mathbf{l}}_{\mathbf{p}}}))\right)\mathit{\text{dx}}\end{array}$$ (19)

The tumor segmentation will therefore be determined taking into account anatomical prior knowledge based on the healthy reference (introduced through the registration term) and the classification decisions. The segmentation is determined on the sparse grid associated to the moving target image, it is therefore dependent on the registration as the probability maps are not aligned with the target image at the start of the process. The position of the node after its displacement corresponds to the area that is segmented. As the registration improves, the segmentation quality does as well.

The optimal labeling is recovered using a linear programming based optimization method (Komodakis et al., 2008) that offers a great compromise between speed and accuracy.

3. Uncertainty-driven Adaptive Resampling

The main drawback of discrete approaches is the trade-off between precision and computational complexity. The search space (displacement label set) for registration would ideally cover the entire area, while a high grid resolution is required to register fine details and most importantly, to detect the tumor's irregular boundary. However, both are limited in order to maintain the computational burden manageable.

These drawbacks are usually dealt with using a hierarchical approach through the use of coarse to fine grid resolutions. This enables to cover large and precise deformations with a limited search space, and makes the segmentation more robust by propagating segmentation decisions that are less sensitive to small variations in the image. In this context, several grid resolutions _j are considered, with a series of iteration t at each resolution. At level { _j, t}, the new MRF energy is computed, based on the deformed source image, evaluated at iteration t-1:

$$l_t^{\mathit{\text{opt}}}=arg\underset{l}{min}{E}_{\mathit{\text{reg}},\mathit{\text{seg}}}(l|V,A\circ T^{t-1})$$ (20)

The displacement information is propagated from one level to the next by composing the new displacement field with the one obtained at iteration t−1. There are two main challenges in this approach: (i) the sampling of the discrete deformation space at each iteration and (ii) the grid resolutions. The most straightforward approach is a uniform refinement of the label set and grid resolution. This allows for precise results but ignores the local anisotropy of the structures. Furthermore, quasi voxel-level resolutions are necessary for segmentation, which cannot be considered in the context of uniform grids. Shi et al. (2012) proposed the Sparse Free Form Deformations: the multi-level grids are optimized simultaneously with a sparsity constraint across levels, ensuring that nodes in high resolution levels are given more importance in areas with discontinuities, and low importance otherwise.

Relying on local segmentation and registration uncertainties offers an alternative and enables to define an adaptive content-driven grid refinement. Such measurements can lead to computationally efficient voxel level resolutions while capturing the local anisotropy of the structure for a more efficient registration. The min-marginals measure the variations of the energy under different constraints (Kohli and Torr, 2008) and have been considered in the context of a discrete registration framework (Glocker et al., 2008b) to evaluate the local uncertainty and adapt the displacement sampling accordingly. We are inspired by this approach that we combine with segmentation uncertainty in order to define an adaptive displacement and node sampling.

3.1. Min-marginals and Displacement Sampling

Let us consider a control point c_j ∈ _j at iteration t, and its corresponding optimal labeling $l_{c_j}^{\mathit{\text{opt}}}$. We aim at defining the displacement sampling at the next iteration as well as the resolution of the next grid level _j+1 based on the volumes' local properties.

Our approach exploits the min-marginal energies (Kohli and Torr, 2008) that evaluate the minimum value of the MRF energy under different constraints. By imposing a label k, different from the optimal label $l_{c_j}^{\mathit{\text{opt}}}$, to control point c_j, the min-marginals indicate how much a label swap costs.

$${\mathrm{\Psi }}_{{\mathbf{c}}_{\mathbf{j}},k,t}=\underset{l,l_{c_j}=k}{min}{E}_{\mathit{\text{reg}},\mathit{\text{seg}}}(\mathbf{l}|V,A\circ {\mathcal{T}}^{t-1})$$ (21)

Let us recall that the label l_cj corresponds to a pair {d^l_cj, s^l_cj}, therefore, both segmentation and registration uncertainties can be extracted from the min-marginals. If the segmentation label is constant (s^k = s^l_cj), a label swap represent a local perturbation from the optimal displacement. A small energy variation means that displacement d^k is almost as likely as the optimal displacement ${\mathbf{d}}^{{\mathbf{l}}_{{\mathbf{c}}_{\mathbf{j}}}^{\mathbf{\text{opt}}}}$, highlighting the uncertain labeling with respect to that direction. Inversely, the labeling is quite certain in a direction where a perturbation yields a high increase of energy. By normalizing the min-marginals over all the possible displacements associated to the same segmentation label, we can compute the registration uncertainty:

$$U_{\mathit{\text{reg}}}({\mathbf{c}}_{\mathbf{j}},k)=\frac{exp(-{\mathrm{\Psi }}_{{\mathbf{c}}_{\mathbf{j}},k,t})}{{\sum }_{l\in {\mathcal{L}}_c,s^l=s^{l_{c_j}^{\mathit{\text{opt}}}}}exp(-{\mathrm{\Psi }}_{{\mathbf{c}}_{\mathbf{j}},l,t})}$$ (22)

The highest U_reg(.) correspond to the most likely labels. The registration uncertainty computed over all the possible displacements can be approximated to a Gaussian distribution (see Fig.[1]), whose covariance evaluates the local anisotropy. The search space is resampled following the covariance matrix main axes and scales, allowing for a more thorough evaluation of the deformation space in the uncertain areas. The registration uncertainty is not taken into account for the tumor label and when the parameter α is low where the deformation is mostly driven by the pairwise cost, yielding a spherical covariance matrix.

Figure 1.

Registration uncertainty and displacement set resampling for one control point: (a) Min-marginal values per displacement label (blue: low, red: high energy) associated covariance matrix centered at the optimal label, (b) Min marginals visualization on a 2D slice, (c) Original isotropic displacement set and (d) Uncertainty driven displacement set, following the brain boundaries.

3.2. Uncertainty-driven Graph Refinement

Consider a uniform grid _j,max of resolution M × N × P, and 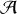_j : _j,max → {0, 1} an activation function describing the resolution of the current adaptively sampled grid _j ⊂ _j,max. At the next resolution level, _j,max is refined as a grid _j+1,max of resolution 2M − 1 × 2N − 1 × 2P − 1, splitting all existing edges in two. The grid _j+1,max represents the new level's maximal resolution, corresponding to a uniform sampling. The new grid _j+1 resolution is determined by activating relevant nodes while ignoring the ones that are not necessary to increase the quality of the registration or segmentation.

A node p ∈ _j+1,max can be activated ( 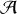_j+1(p) = 1) if it satisfies at least one of those three conditions: (i) the node has a direct correspondent c_j ∈ _j,max (same coordinates) that is activated ( 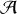_j(c_j) = 1), (ii) it is connected to nodes in _j that have a high segmentation uncertainty (segmentation activation), (iii) it is connected to nodes in _j that have a high registration uncertainty (registration activation). The registration and segmentation activations are determined via the definition of two activation terms A_r(p) and A_s(p) respectively, both taking value in {0, 1}. 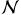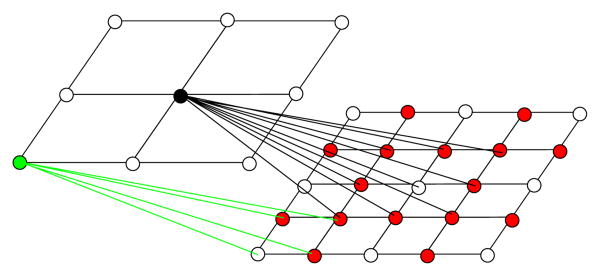To propagate the min-marginals and activation information, we define an inter level neighborhood system _i(.) by connecting c_j ∈ _j,max to its 27 closest neighbors (based on the image's spatial coordinates) in _j+1,max. The neighborhood system is shown in Fig.[2]

Figure 2.

Visual representation of the grid refinement from level j (left) to level j+1 (right). Grid resampling: the nodes that have direct correspondences appear in white, and the new nodes are red. The edges connecting the 2 grids represent the nodes' neighborhood. The grid is shown in 2D for increased visibility.

The registration activation criterion relies on the idea that small and precise displacements are necessary around salient structures, while increasing the resolution on homogeneous regions is not necessary. A node should be activated if it is at the interface of adjacent structures. Considering a node c_j ∈ _j, it covers an image region delimited by its maximum displacement. If the region is not homogeneous, there will be strong min-marginal energies variations with respect to the displacement label. The activation criterion is based on the node's energy range and is defined as:

$$A_r(\mathbf{p})=H\left(\sum _{{\mathbf{c}}_{\mathbf{j}}\in {\mathcal{N}}_i(\mathbf{p})}\frac{1}{N}\left(\underset{\underset{s^k=s^{l_{c_j}^{\mathit{\text{opt}}}}}{k\in {\mathcal{L}}_c,}}{max}{\mathrm{\Psi }}_{{\mathbf{c}}_{\mathbf{j}},k,t}-\underset{\underset{s^k=s^{l_{c_j}^{\mathit{\text{opt}}}}}{k\in {\mathcal{L}}_c,}}{min}{\mathrm{\Psi }}_{{\mathbf{c}}_{\mathbf{j}},k,t}\right)-\mu \right)$$ (23)

μ is the mean value over all activated nodes in _j, H(.) is the heaviside step function, and N is the number of nodes in the neighborhood of p. The node p will be activated if the mean energy range among its neighbors in _j is higher than the mean range over all nodes.

Similarly, the segmentation node activation is based on the segmentation uncertainty that can be evaluated by measuring the energy variation when the segmentation label changes. The uncertainty with respect to one segmentation label S can be computed by normalizing over all labels:

$$U_{\mathit{\text{seg}}}({\mathbf{c}}_{\mathbf{j}}|S)=\frac{{\sum }_{l\in {\mathcal{L}}_c,s^l=S}exp(-{\mathrm{\Psi }}_{{\mathbf{c}}_{\mathbf{j}},l,t})}{{\sum }_{l\in {\mathcal{L}}_c}exp(-{\mathrm{\Psi }}_{{\mathbf{c}}_{\mathbf{j}},l,t})}$$ (24)

In the case of a binary segmentation, we can simply reformulate the uncertainty as:

$$U({\mathbf{c}}_{\mathbf{j}})=1-|U_{\mathit{\text{seg}}}({\mathbf{c}}_{\mathbf{j}}|S)-0.5|$$ (25)

This term measures how certain the chosen label is. A low value of U(c_j) infers a highly reliable labeling. We seek to propagate the segmentation decisions to the next grid level _j+1 based on their reliability, so that the focus is on uncertain areas. This is achieved by adding an inter-level pairwise potential to the global energy :

$$V_{\mathit{\text{ucy}}}(l_{c_j}^{\mathit{\text{opt}}},l_p)=\{\begin{array}{ll}0\hfill & \text{if}{s}^{l_{c_j}^{\mathit{\text{opt}}}}=s^{l_p}\hfill \\ -log(U({\mathbf{c}}_{\mathbf{j}}))\hfill & \text{Otherwise}\hfill \end{array}$$ (26)

where c_j is a control point in G_j in the neighborhood of p. This potential penalizes nodes in G_j+1 that are assigned a label different than their neighbor in _j. The amount of penalty depends on how certain the labeling of _j is. In this neighborhood configuration, a node in _j+1 can be influenced by several nodes in _j, so that there is no penalty when the nodes labels are different and equally likely, the new node being situated at the tumor boundary. The segmentation activation criterion is controlled by the strength of the penalty and defined as:

$$A_s(\mathbf{p})=H\left(\left|\sum _{{\mathbf{c}}_{\mathbf{j}}\in {\mathcal{N}}_i(\mathbf{p})}{(-1)}^{s^{l_p}}{V}_{\mathit{\text{ucy}}}(l_{c_j}^{\mathit{\text{opt}}},l_p)\right|-\mathit{\text{tsh}}\right)$$ (27)

Where N is the number of nodes in 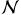_i (p), tsh is a threshold parameter and H(.) is the Heaviside step function. This term measures how strong the penalty is on node p, taking into account the fact that there is no penalty if its neighbors are labeled differently with equally confident labels. Nodes with a low overall penalty will be activated.

Eventually, we can rewrite the MRF energy at resolution level j and iteration t:

$$E_{\mathit{\text{reg}},\mathit{\text{seg}}}(l|V,A\circ {\mathcal{T}}^{t-1},{\mathcal{G}}_j)=\frac{1}{|{\mathcal{G}}_j|}\sum _{p\in {\mathcal{G}}_j}{V}_p(l_p|V,A\circ {\mathcal{T}}^{t-1})+\sum _{p\in {\mathcal{G}}_j}\sum _{q\in \mathcal{N}(\mathbf{p})}{V}_{\mathit{\text{pq}}},(l_p,l_q)+\sum _{p\in {\mathcal{G}}_j}\sum _{c\in {\mathcal{N}}_i(\mathbf{p})}\frac{1}{N}{V}_{\mathit{\text{ucy}}}(l_c^{\mathit{\text{opt}}},l_p)$$ (28)

where N is the number of nodes in _j that are connected to node p ∈ _j+1, and _i(p) is the corresponding neighborhood.

4. Experimental Validation

Our data set consisted of 110 3D FLAIR MRI volumes of different patients featuring a low-grade glioma prior any treatment. The complete tumors have been manually segmented in all volumes by experts. Although additional modalities would have offered increased segmentation quality, there were not systematically available and provided by our clinical partners. We therefore focused on the FLAIR modality.

36 volumes were randomly selected for boosting learning. We tested our joint segmentation and registration framework on the 74 remaining volumes. The reference pose for registration was a 3D FLAIR MRI volume of a single healthy subject of size 256 × 256 × 24 and resolution 0.9 × 0.9 × 5.5 mm³. The absence of existing multi subject healthy atlases of FLAIR modality has motivated the use of a single subject as reference pose to evaluate the algorithm.

We ran an additional set of experiments on the 10 real low-grade gliomas cases of the BRATS training database for an easier comparison with existing methods. We segmented the complete tumors (including active tumor, necrotic core and occasional edema). The results can be compared for the low-grade glioma case (complete tumor) with the results presented on the training set in the BRATS proceedings. In order to maintain consistency with our FLAIR database, only FLAIR images were considered for boosting training which was carried out through leave one out cross validation experiments. Registration was performed using the T2-weighted images due to the insufficient quality of the FLAIR images. Furthermore, this allows the use of the T2-weighted MNI-ICBM multi subject atlas (Fonov et al., 2009) of size 193 × 229 × 193 and resolution 1 × 1 × 1 as reference for registration, which is more adapted to anatomical differences between subjects than a single subject reference pose. This results in exploiting two of the four available modalities for segmentation and the T2-weighted modality for registration. The reference poses for registration are shown in Fig. [3].

Figure 3.

Healthy reference poses used for registration. FLAIR (First row) and T2 MNI-ICBM atlas (second row). Bottom row: MNI atlas Probability maps, from left to right: White Matter, Gray Matter and CSF.

As preprocessing, all volumes were skullstripped and rigidly registered to their reference pose (Ourselin et al., 2000). Their intensity was regularized by simply setting all volumes to the same median and interquartile range as the reference pose. Since all volumes are rigidly registered, an approximate symmetry plane of the reference pose is used for all volumes to evaluate the boosting symmetry feature. We compared the joint registration and segmentation framework with a sequential approach, where the tumor is segmented using the single boosting based MRF method and the segmentation is used as a mask for registration (not taking into account the segmented area). To demonstrate the potential of the adaptive resampling framework, we compared the results without uncertainties where the segmentation is propagated from one resolution to the next using a manually set penalty cost:

$$V_{\mathit{\text{pen}}}^t(l_p)={\int }_{\mathrm{\Omega }}\overline{\eta }(\Vert \mathbf{x}-\mathbf{p}\Vert )s^{l_p}{\mathcal{S}}^{t-1}(\mathbf{x})\frac{2}{exp(j)}\mathit{\text{dx}}$$ (29)

where j is the resolution level and t the current iteration. The uncertainty based framework was compared with this approach at the maximal and same final grid resolution.

4.1. Implementation

The same set of parameters were used for all volumes in the FLAIR database and were determined heuristically in order to obtain the best possible results over the whole database. Our coarse to fine hierarchical approach consisted of 3 image levels and 4 grid levels, where the resolution of the image increases with the grid resolution. The maximal grid resolution increased from 9 × 9 × 5 to 65 × 65 × 37. In accordance with the Free Form Deformation framework, the projection function used was cubic B-splines. We set the parameter α so that the presence of the tumor has an increasing impact on the registration. It is progressively diminished from 1 to 0.015, the focus being on segmentation at the finest level. This setting enables to focus on aligning the main brain structures at coarse resolutions where the tumor is only roughly detectable then progressively increase the segmentation precision. The constant cost C_tm for registration is progressively increased, initially set to 5 and 6 times the mean value of the similarity criterion without and with uncertainties respectively. The parameter λ describing the influence of the registration smoothing was set to 20 and relaxed in the tumor area to allow for the potentially important displacements induced by the tumor. The threshold tsh for node activation was set to 1.6.

We perform 3 iterations at each grid level. Without exploitation of the uncertainty information, the displacement sampling is sparse (31 labels, sampled along the main axes) and refined at each iteration by reducing the maximum displacement. We adopt a dense sampling (1331 labels) to compute the local uncertainties at the first iteration, and a sparse sampling at the 2 remaining iterations, the labels being sampled along the covariance matrix main axes. This enables to exploit the uncertainty information with limited impact on the run time. When α is low, the local anisotropy cannot be captured efficiently by the min marginals. A sparse sampling is adopted for all iterations at the last 2 grid levels.

The parameters were adapted to the BRATS dataset, setting the maximal grid resolution from 11 × 12 × 11 to 81 × 96 × 81, the constant cost to 6 and 7 times the mean value of the similarity criterion and progressively increased and the threshold for grid activation as the mean penalty value over all active nodes. The same parameters were used for the 10 volumes. Experiments were only carried out with sparse sampling.

4.2. Uncertainty based Grid Nodes Activation

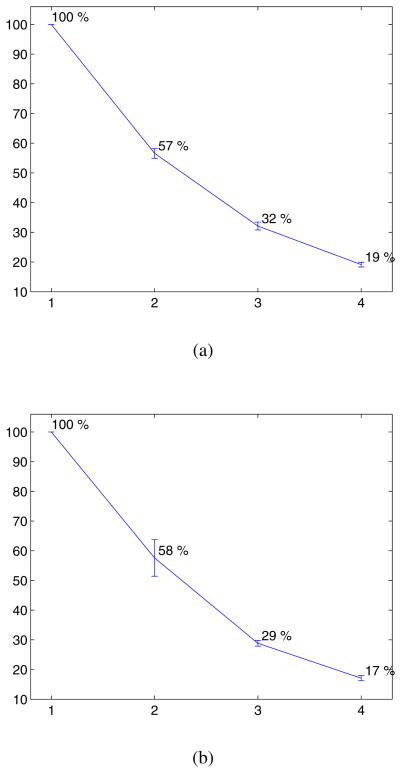
The percentage of activated nodes, with respect to the maximum uniform resolution is shown in Fig.[4]. The complexity of the framework is considerably reduced, only activating less than 20 % of the nodes at the last level for both datasets. Our current implementation associates changes of labels of inactive nodes with infinite costs and runs for less than a minute (sparse sampling) or 2 to 4 minutes (sparse/dense sampling) on the FLAIR database, and 3 to 8 minutes on the BRATS database of higher resolution. A direct construction of the grid would significantly impact the run time and memory cost. Considering an MRF with L, E and N being respectively the number of labels, edges and nodes, we provide a complexity analysis (excluding the time required to build the data term potentials):

• Computational cost:

  (L × 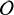(E × N²)) ∼ 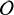(L × E × N²) per iteration

• Memory cost: 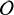(L × 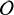(N + E))

  Reducing the number of nodes to approximately 20% at the finer resolution scale leads to:

• Computational cost:

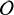  (L × 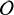(0.2E × (0.2N)²)) ∼ 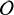(0.008L × E × N²)

  When taking into account the number of iterations, we can obtain a complexity that is approximately 3-4 orders of magnitude lower.

• Memory cost: 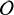(L × 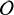(0.2(N + E))), approximately one order of magnitude lower.

Figure 4.

Mean percentage of activated nodes per level. (a) FLAIR database, (b) BRATS database.

Fig. [11] shows visual examples of the last two grid levels' resolution. Nodes are activated around the brain's structures and the tumor's boundary, demonstrating the adequacy of the registration and segmentation activation terms.

Figure 11.

Visual examples of the activated nodes for the last 2 levels of the incremental approach. The nodes are superimposed to the target image.

4.3. Segmentation Evaluation

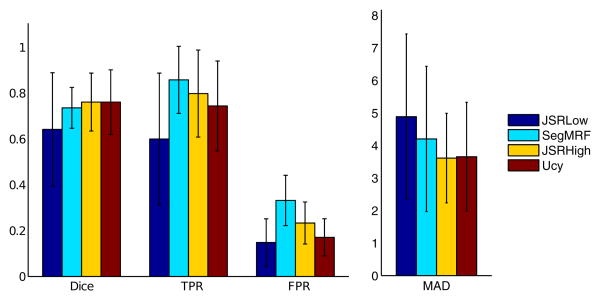
The segmentation results were evaluated by comparing the automatic segmentation AS to the manual segmentation M. To this end, we compute the Dice score $\mathit{\text{Dc}}=\frac{2\Vert M\cap \mathit{\text{AS}}\Vert }{\Vert M\Vert +\Vert \mathit{\text{AS}}\Vert }$, the rate of false positives $\mathit{\text{FPR}}=\frac{\Vert \mathit{\text{AS}}\Vert -\Vert M\cap \mathit{\text{AS}}\Vert }{\Vert \mathit{\text{AS}}\Vert }$ and the rate of true positives $\mathit{\text{TPR}}=\frac{\Vert M\cap \mathit{\text{AS}}\Vert }{\Vert M\Vert }$ and mean absolute distance between contours (MAD). Segmentations were evaluated after reverting to the patient's space (before rigid registration) where the manual segmentations were performed. Segmentations of higher quality are obtained using the joint framework on the FLAIR dataset (especially highlighted by the MAD score), and are equivalent with a high resolution uniform grid and an adaptively sampled low resolution grid, while the low resolution uniform grid yields poor tumor detection. Among the test set, 27 volumes have been manually segmented by 2 different experts. The inter expert Dice score reaches 89 % in median and gets as low as 76 %, which highlights the high inter expert variability with respect to the manual segmentations of tumors and is close to the obtained automatic segmentations (81% median over the 27 volumes). Error bars of the different scores are shown in Fig.[5].

Figure 5.

Quantitative Segmentation Results, FLAIR database: Error bars (mean and standard deviation) of the Dice score, False Positive (FPR) and True Positive (TPR) rates and MAD score (in millimeters) for the joint framework with low (JSRLow) and high resolution (JSRHigh), the individual segmentation framework (SegMRF) and the uncertainty based approach (Ucy).

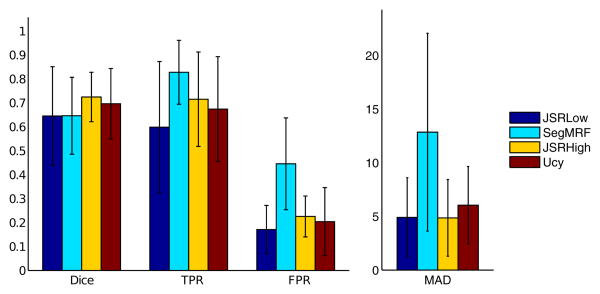
Segmentation results on the BRATS dataset are on par with results obtained by the BRATS 2012 challenge winners, (mean Dice score 70-72 %, median 72-73 % with and without uncertainties respectively), while a strong increase of quality is obtained with respect to the regularized boosting results (mean Dice score 65 %). The tumors are poorly detected using a low uniform resolution (mean Dice score 64 %, reduction of the true positive rate of 7% (with uncertainties) and 11% (without uncertainties)). Error bars of the different scores are shown in Fig.[6].

Figure 6.

Quantitative Segmentation Results, BRATS database: Error bars (mean and standard deviation) of the Dice score, False Positive (FPR) and True Positive (TPR) rates and MAD score (in millimeters) for the joint framework with low (JSRLow) and high resolution (JSRHigh), the individual segmentation framework (SegMRF) and the uncertainty based approach (Ucy).

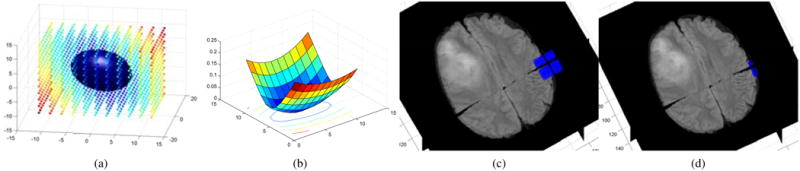
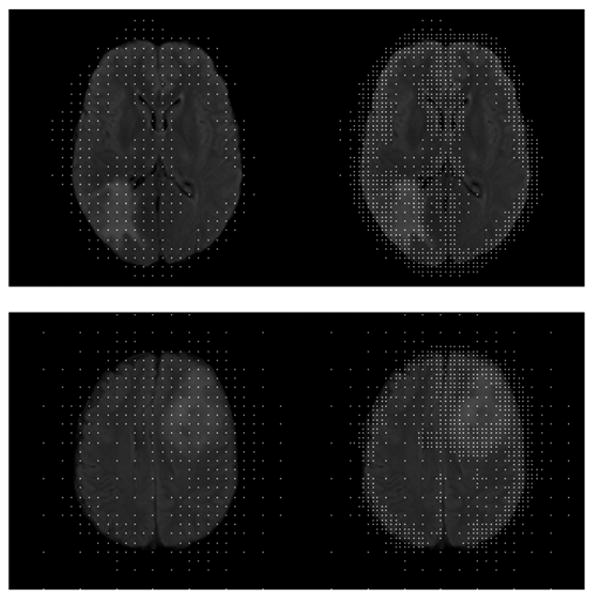
Visual segmentation results for both datasets are shown in Fig.[8].

Figure 8.

Visual Segmentation results on the FLAIR database (first two rows) and the BRATS database (bottom row, T2 volume). (a) individual framework, (b) Joint framework, high resolution, (c) Joint framework, with adaptive sampling. Automatic segmentations (blue) are compared to the manual segmentation

4.4. Registration Evaluation

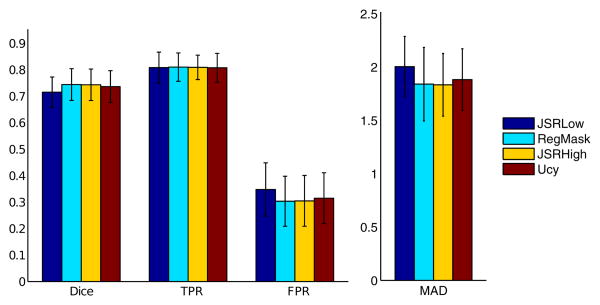
The registration was evaluated mostly qualitatively. For quantitative analysis, the ventricles where manually segmented for 33 volumes of the FLAIR dataset and the Dice score, False and True Positive rate, and MAD were computed between the registered source image and the target image outside the tumor area and are shown in Fig.[7]. Fig.[9] shows visual registration results comparing the joint registration and segmentation framework to the individual registration where the pathology has been masked. Quantitative results show equivalent performance outside the tumor area, while visual examples show a high increase in quality of registration in and around the tumor area, in cases where the individual framework fails. Quantitative results also highlight the maintained performance outside the tumor area using an adaptively sampled grid, and a lower quality registration considering a uniform grid of equivalent low resolution.

Figure 7.

Quantitative Registration results, FLAIR database: Error bar graphs of the Dice, True Positives (TPR), False Positives (FPR) and MAD scores (in millimeters) obtained for the joint framework with low (JSRLow) and high resolution (JSRHigh), the individual registration framework with masked pathology (RegMask) and the uncertainty based approach (Ucy)

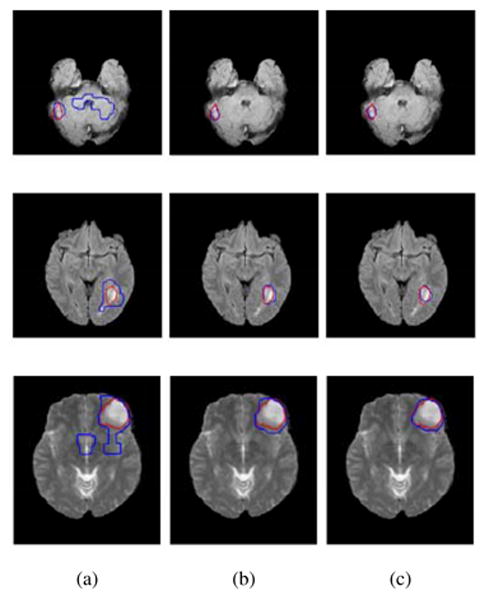
Figure 9.

Visual Registration results, FLAIR dataset. (a) Target image, (b) individual framework, (c) Joint framework, high resolution, (d) Joint framework, with adaptive sampling.

Visual examples of registration results on the BRATS dataset are shown in Fig. [10]. Cases where the individual framework and low resolution registration fail are illustrated, as well as the obtained complete segmentation of an image.

5. Conclusion and Discussion

In this paper we have presented a concurrent registration and tumor segmentation framework that exploits the interdependencies between the two problems. We adopt a discrete graphical model on a sparse grid superimposed to the image domain. Each grid node is simultaneously classified and displaced based on a boosting classifier and image similarity. The detected tumor area is registered by interpolation with the neighboring nodes. The progressive impact of the tumor segmentation on the registration allows to deal with the presence of the tumor without the introduction of an initial bias that can lead to registration errors, while the introduction of spatial information on the brain structures significantly reduces the false detections. The inclusion of uncertainties enables to deal with the main drawback of discrete approaches, that is the trade off between precision and computational complexity. Adaptive refinement of the sparse grid yields a much lower complexity framework. While our current implementation simply discards inactive nodes, direct construction of the non uniform grid would lead to significant diminution of the run time.

The framework offers great modularity with respect to the similarity measure for registration, the segmentation prior probabilities estimation, the image modality and the clinical context. We presented the method in the context of diffuse low-grade gliomas and registration/segmentation of a healthy subject/atlas to a subject with a tumor. Aside for enhanced segmentation quality through the healthy brain's anatomical information (obtained segmentation results are close to the inter expert variability), this offers the possibility to build statistical atlases of tumor appearances in the brain and to evaluate the impact of the tumors on the brain's functional organization. Furthermore, the method's modularity allows easy adaptation to different problems where correspondences are missing, such as registration between pre operative and intra/post operative images with tumor resection for surgical guidance.

The choice of pathology masking (instead of growth models) is justified by the infiltrative nature of the low-grade gliomas, and coupled with the discrete formulation and adaptive sampling, results in a fast algorithm that shows great performance. It is however not adapted to fast growing and space occupying tumors that yield strong deformation that would have to be modeled accordingly.

One limitation of the method is its dependency on the boosting classification output. It is progressively refined through increasing resolution levels and segmentation propagation/penalty across levels but still constitutes the baseline of the obtained segmentation. Two natural extensions of the algorithm are the inclusion of multimodal information and multiclass segmentation (to separate tumor core, necrosis and edema). Both can easily be introduced in the model through the boosting feature vector and by increasing the number of labels (both during boosting classification and construction of the MRF model). Such extensions are likely to increase the quality of the detection and segmentation.

Last but not least, a drawback of the method is its requirement for manual setting of important model parameters that can have a strong impact on the results. Optimal learning of the weights ( (Komodakis, 2011) of the graphical model being considered in this paper from training data will allow to eliminate the need of manual parameter setting.

Figure 10.

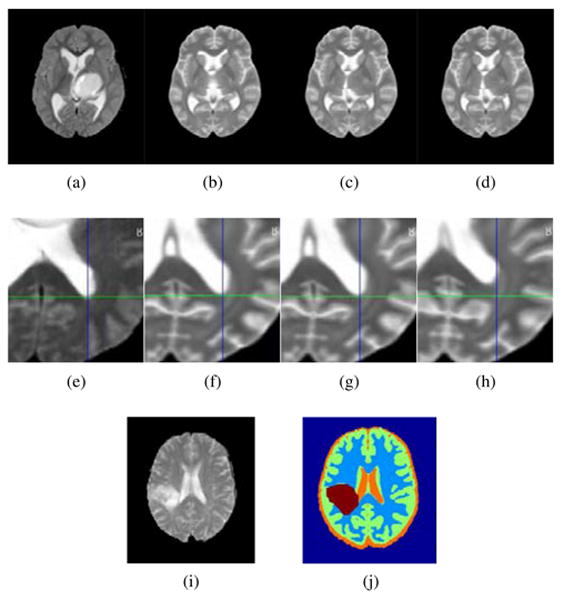
Visual Registration results, BRATS dataset. First row: comparison with the individual registration scheme. (a) Target image, (b) individual framework, (c) Joint framework, high resolution, (d) Joint framework, with adaptive sampling. Second row: close up comparison with low uniform resolution. (e) Target image, (f) Joint framework, high resolution, (g) Joint framework, with adaptive sampling, (h) Joint framework, low uniform resolution. Errors in registration can be seen with respect to the cross lines. Bottom row: example segmentation using the registered MNI-ICBM probabilities. (i) Target image, (j) Segmented image.

Highlights.

• Discrete MRF model for concurrent tumor segmentation and deformable registration

• Content-driven non-uniform sampling of the parametric space and displacement set

• Modularity with respect to matching criterion and tumor detection method

• Easily adaptable to other clinical contexts

• Assessment on a large Low-grade gliomas database