Assessing Dynamic Spectral Causality by Lagged Adaptive Directed Transfer Function and Instantaneous Effect Factor

Abstract

It is of significance to assess the dynamic spectral causality among physiological signals. Several practical estimators adapted from spectral Granger causality have been exploited to track dynamic causality based on the framework of time-varying multivariate autoregressive (tvMVAR) models. The non-zero covariance of the model’s residuals has been used to describe the instantaneous effect phenomenon in some causality estimators. However, for the situations with Gaussian residuals in some autoregressive models, it is challenging to distinguish the directed instantaneous causality if the sufficient prior information about the “causal ordering” is missing. Here, we propose a new algorithm to assess the time-varying causal ordering of tvMVAR model under the assumption that the signals follow the same acyclic causal ordering for all time lags and to estimate the instantaneous effect factor (IEF) value in order to track the dynamic directed instantaneous connectivity. The time-lagged adaptive directed transfer function (ADTF) is also estimated to assess the lagged causality after removing the instantaneous effect. In the present study, we firstly investigated the performance of the causal-ordering estimation algorithm and the accuracy of IEF value. Then, we presented the results of IEF and time-lagged ADTF method by comparing with the conventional ADTF method through simulations of various propagation models. Statistical analysis results suggest that the new algorithm could accurately estimate the causal ordering and give a good estimation of the IEF values in the Gaussian residual conditions. Meanwhile, the time-lagged ADTF approach is also more accurate in estimating the time-lagged dynamic interactions in a complex nervous system after extracting the instantaneous effect. In addition to the simulation studies, we applied the proposed method to estimate the dynamic spectral causality on real visual evoked potential (VEP) data in a human subject. Its usefulness in time-variant spectral causality assessment was demonstrated through the mutual causality investigation of brain activity during the VEP experiments.

I. Introduction

In the field of neuroscience and many other fields of science and engineering, the connectivity or causality between two observed signals in a multivariate system is of great interest [1]–[3]. As a kind of statistical methodology for time series inference, Granger causality (GC) analysis made it possible to uncover dynamic interactions in a complex nervous system from a statistical point of view [4]. Wiener [5] originally conceived the notion of relation between prediction error and its causality in time series analysis. Granger proposed the idea to introduce the multivariate autoregressive (MVAR) models of stochastic processes and proposed the time-domain measurement [6]. As the MVAR modeling is an efficient tool for locating the origins of fluctuations in a variety of processes, most of the previous linear causality analysis techniques have been based on MVAR models [7]–[12]. Since many measured electrophysiological signals were usually characterized by their spectral properties, spectral GC analysis approaches have received considerable attention [13]–[20]. To extend its application to the nonstationary measured signals, some time-dependent causality analysis methods have been proposed to track the dynamic causality and to unveil the time-varying relationship between signals [21]–[27]. These time-dependent causality analysis methods are mainly based on the construction of time-dependent coefficients of time-varying multivariate autoregressive (tvMVAR) models, which can be used to describe a system where the signals can jointly explain each other, and the dynamic interactions of the system could be analyzed from the model structure.

In many cases, the non-zero covariance of model residuals can be observed during the tvMVAR modeling, partially due to the blurring of the neuronal activity with the sluggish latent response. This phenomenon can be viewed as the presence of the potential instantaneous effect or contemporaneous causality in a sense. It has been shown that this zero-lag correlation does “leak” into estimates of time-lagged causality [28]. Hence, Erla and Faes et al. have proposed the utilization of an extended MVAR model that combines the instantaneous and lagged effects to improve the assessment of causality through Cholesky decomposition of model’s residuals [29]–[31]. Meanwhile, Deshpande et al. have introduced the method of calculating the correlation-purged GC, which is also free of the zero-lag correlation effect [28]. It must be noted that, for the above estimations of instantaneous effect, identification based on the directed acyclic graph assumption such as Cholesky decomposition is appropriate only if the direction of the instantaneous transfer pathways is known in advance so that the measured signals can be arranged accordingly [32]. Unfortunately, the prior information is hardly available in many biomedical applications. To overcome this serious problem, Shimizu and Hyvarinen et al. proposed alternative approaches in non-Gaussianity pattern [33]–[35]. The idea of these alternative approaches has been exploited for frequency domain connectivity analysis based on extended MVAR models in [36], and they demonstrated that the non-Gaussian structural vector autoregressive model can be successfully identified without any restrictions on the network structure [35].

The structural vector autoregressive model with non-Gaussian assumption was proven to be working effective when the residual terms are assumed to be independent [33]–[35], however, it is still interesting and necessary to explore the situations when the residuals in tvMVAR model are Gaussian [36]. It is believed that for the situation with Gaussian signals, there is no way to clearly and completely distinguish the directed instantaneous causality if the prior information about the “causal ordering” is not available. Consequentially, a fitted directed acyclic graph method which can find model’s dynamic causal ordering is required in order to provide another solution to the correlated Gaussian residuals in the tvMVAR models.

In the present study, we propose a new algorithm of estimating dynamic causal ordering and instantaneous effect factor (IEF) for the tvMVAR model in Gaussian residuals. We also examine their performance with different number of signal variables and model orders. The estimation of IEF values can be used to track the dynamic instantaneously coupled strength between signals. The study also suggests applying the time-lagged adaptive directed transfer function (ADTF) method to assess the lagged spectral causality in addition to applying the conventional ADTF method. Furthermore, we applied the proposed approach to assess the dynamic spectral causality in real visual evoked potentials (VEP) data of one healthy subject.

II. Methods

A. Spectral tvMVAR Modeling with Instantaneous Effect

Let X(n) denote the column vector of observed signals in arbitrary ordering,

$$X(n)={[\begin{array}{cccc}{x}_1(n)& x_2(n)& \cdots & x_N(n)\end{array}]}^T,$$ (1)

where N is the number of signals and superscript T denotes matrix transpose. If X(n) can be described as a tvMVAR model with instantaneous effect and time dependent coefficients, it can be constructed as follows

$$B_0(n)X(n)=\sum _{k=1}^p{B}_k(n)X(n-k)+E_1(n),$$ (2)

where p is the order of this model and can be determined by some criterions such as Schwarz Bayesian criterion (SBC) or Akaike information criterion (AIC) [37], [38]. E₁(n) is a N×1 column vector of uncorrelated zero-mean residuals with instantaneous covariance matrix V₁(n). B_k(n) is the time-dependent coefficient matrix of dimension N×N, and B₀(n) is a dynamic directed acyclic matrix which describes the instantaneous causal relationships between all variables and it might be a non-identity matrix when the instantaneous connectivity exists. However, it is difficult to accurately obtain the matrix B₀(n) if the prior information about model’s causal ordering is missing. Hence, we proposed a new algorithm to estimate the instantaneous effect matrix B₀(n). Firstly, we can build a conventional model as follows,

$$X(n)=\sum _{k=1}^p{A}_k(n)X(n-k)+E_2(n),$$ (3)

where A_k(n) is the lagged coefficient matrix, and E₂(n) is a correlated Gaussian noise that is different from E₁(n). In such situation, the unknown time-dependent coefficient matrices A_k(n) and correlated Gaussian residuals E₂(n) can be estimated by the well-known discrete Kalman filtering algorithm [39], [40]. By multiplying B₀(n) in equation 3 and compare it with equation 2, we can easily find the following existing relationships B₀(n)A_k(n)=B_k(n) and B₀(n)E₂(n)=E₁(n).

In order to analyze the spectral properties of the investigated process, the signals have to be transformed to the frequency domain. Therefore, we can obtain the time variant spectral formulation as follows

$$X(n,f)=H(n,f)E_2(n,f),$$ (4)

where

$$H(n,f)={\left(\sum _{k=0}^p-A_k(n)e^{-i2\pi f\mathrm{\Delta }tk}\right)}^{-1}.$$ (5)

The function H(n, f) is a time-varying transfer matrix at time point n and at frequency f, and its element H_ij(n, f) represents the directional connection from the jth to the ith signal of the system; Δt is the sampling interval and A₀(n) = −I_N.

B. Estimation of Dynamic IEF and Time-lagged ADTF

It’s apparent that normalized ADTF developed from the DTF formulation can be defined as

$${{\gamma }_{ij}}^2(n,f)=\frac{{\left|H_{ij}(n,f)\right|}^2}{{\displaystyle \sum _{k=1}^N}{\left|H_{ik}(n,f)\right|}^2}.$$ (6)

γ_ij(n, f) is the estimated spectral causality value from the jth signal to ith signal at the specific time point n and specific frequency f. It is obvious that the ADTF method cannot measure the instantaneous effect and the obtained ADTF values may only represent the fused results from instantaneous effect and time-lagged causality.

As we know, the instantaneous covariance matrix V₂(n) of residuals E₂(n) is directly influenced by matrix B₀(n) on the instantaneous covariance matrix V₁(n) of residuals E₁(n),

$$V_2(n)=B_0^{-1}(n)V_1(n)B_0^{-T}(n),$$ (7)

However, the matrix B₀(n) is not unique when any additional prior knowledge is not given. If the causal ordering of signals is well identified in advance, we can easily find a certain solution by performing an orthogonal decomposition. For the general case with unknown causal ordering, we suggest to obtain B₀(n) through traditional Cholesky decomposition after estimating the dynamic causal ordering. The steps of the proposed estimation process are described as follows,

1. Initialize the signals’ ordering arbitrarily as in equation 1 and calculate the mean value of γ_ij(n, f_band) over the frequency band f_band at time point n.

2. For each signal i=1,2,3,…, N-1, and for each signal j = i+1, i+2, …, N, compare the value γ_ij(n, f_band) and value γ_ji(n, f_band). If γ_ij(n, f_band) is larger than γ_ji(n, f_band), put the jth variable just in front of ith variable; if not, maintain the current ordering. This comparison procedure would repeat N(N-1)/2 times in total. Here, we have the assumption that the connectivity information follows the same acyclic causal ordering for all time lags, which means the instantaneous causality and all the lagged causality shall share the same acyclic direction when they exist between two signals.

3. Check the outcome ordering, and accordingly produce the time-varying permutation matrix P(n). The original signals X(n) will be arranged in the right causal ordering at time point n after left-multiplying it with P(n).

4. After the time dependent permutation matrix P(n) is determined, we can perform the Cholesky decomposition on the re-ordered covariance matrix, P(n)V₂(n)P(n)^T=L(n)V₃(n)L(n)^T, where L(n) is a lower triangular matrix and V₃(n) is a diagonal matrix, which also can be transformed from another diagonal matrix V₁(n), V₃(n)=P(n)V₁(n)P(n)^T.

5. Consequentially, we can obtain the instantaneous directed effect matrix B₀(n)=(P⁻¹(n)L(n)P(n))⁻¹.

This dynamic ordering estimation algorithm is based on the assumption that the signals follow the same acyclic causal ordering for all time lags, in which case, the causal ordering is not altered by the neglect of instantaneous effect [35]. As a consequence, the estimations of ADTF value can be used to obtain the appropriate time-varying causal ordering. The f_band can be determined by selecting the frequency band of interest in the time-frequency representation of the signals. Here, we simply select the frequency band as the overall band without specifying any particular frequency band. But in general, specific frequency band can be used when the prior information of interesting frequency band can be obtained.

After obtaining B₀(n), we can rewrite (4) by replacing the E₂(n, f) with B₀⁻¹(n)E₁(n, f),

$$X(n,f)={\left(B_0(n)-\sum _{k=1}^p{B}_k(n)e^{-i2\pi f\mathrm{\Delta }tk}\right)}^{-1}{E}_1(n,f),$$ (8)

The estimation of IEF is defined as follows,

$${\text{IEF}}_{ij}(n)=-B_{0ij}(n),$$ (9)

Its elements, IEF_ij(n), represent the instantaneous directed connection from the jth to ith elements of the system for each time point n. Meanwhile, the normalization of time-lagged ADTF value is presented,

$${{\overline{\gamma }}_{ij}}^2(n,f)=\frac{{\left|{\overline{H}}_{ij}(n,f)\right|}^2}{{\displaystyle \sum _{k=1}^N}{\left|{\overline{H}}_{ik}(n,f)\right|}^2},$$ (10)

where

$$\overline{H}(n,f)={\left(I_N(n)-\sum _{k=1}^p{B}_k(n)e^{-i2\pi f\mathrm{\Delta }tk}\right)}^{-1},$$ (11)

H̄(n, f) is considered as the time dependent transfer matrix in frequency domain after removing all the instantaneous effect from the system.

C. Simulation Study

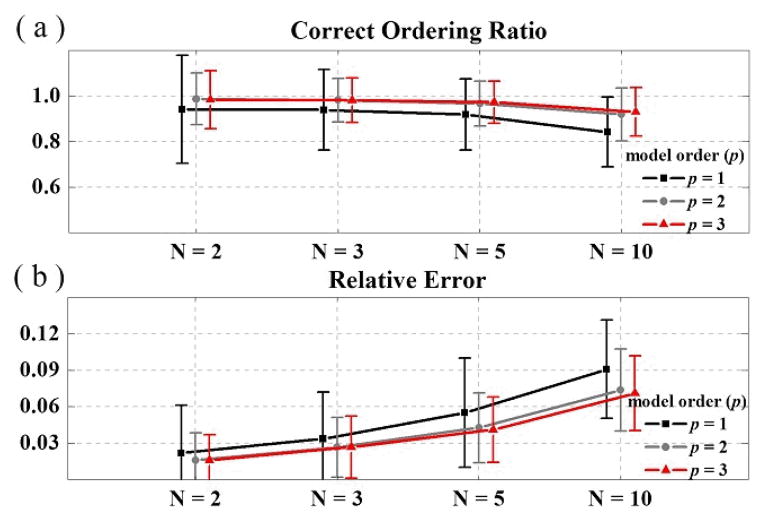
To investigate the performance of the proposed causal ordering estimation method, we firstly conducted simulations using model 1 which consists of a series of simulations with different number of variables and orders. In the model 1, we randomly constructed the tvMVAR model in which the directed causal connectivity between signals is concomitant, i.e. directions of all the lagged effects and instantaneous effect are the same. Two thousands of stochastic signals were generated according to different factors: different number of signals N=[2, 3, 5, 10], and different model’s order p=[1, 2, 3]. To ensure model’s stability and robustness, all the coefficients in lower triangular matrices B₀(n) and B_k(n) are uniformly distributed between −0.3 and 0.3. To test the confidence level of the proposed ordering estimation, we then randomly permuted the ordering of the simulated causality among signals. In order to evaluate the results of instantaneous effect direction by our ordering estimation algorithm, we defined an evaluating index Correct Ordering Ratio (COR) as the ratio between the number of correctly estimated instantaneous directed connectivity (N_e) to the number of model’s real instantaneous directed connectivity (N_r),

$$\mathit{COR}=\frac{N_e}{N_r}.$$ (12)

We also used another evaluating index, i.e. Relative Error (RE) to evaluate the precision of the estimated elements of B₀(n), which is defined as follows,

$$RE=\frac{\sqrt{{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}{(B_{0ij}-{\widehat{B}}_{0ij})}^2}}{\sqrt{{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}{(B_{0ij})}^2}},$$ (13)

where B̂_0ij is the estimation value of B_0ij.

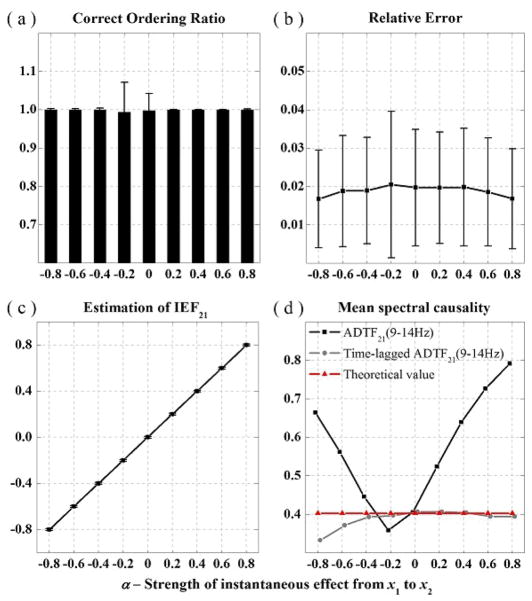
After evaluating the performance of the dynamic causal ordering estimation algorithm, we applied IEF and time-lagged ADTF method to assess the spectral causality in model 2, and compared with the results obtained by the conventional ADTF method. The model 2 was constructed with different levels of instantaneous connectivity strength and the results were compared with the theoretical values of the simulation. This causal model consisted of two nodes, in which the first signal caused the second signal in both the time-lagged pattern and the zero-lagged pattern. Mathematically, this model was described at a sampling rate of 200 Hz as follows,

$$\{\begin{array}{l}{x}_1(n)=0.55x_1(n-4)-0.81x_1(n-8)+{\epsilon }_1(n)\hfill \\ x_2(n)=\alpha x_1(n)+0.31x_1(n-4)+{\epsilon }_2(n)\hfill \end{array}$$ (14)

where ε₁(n) and ε₂(n) are the uncorrelated Gaussian white noise with constant variance. Five hundred sets of test signals were generated in order to respect imposed α levels = [−0.8, −0.6, −0.4, −0.2, 0, 0.2, 0.4, 0.6, 0.8]. It should be noted that when there is no instantaneous directed connectivity between two signals, the COR is set as 1 if both of the estimated directed IEF values are smaller than 0.05, and the COR is set as 0 if any of the estimated IEF values is larger than 0.05.

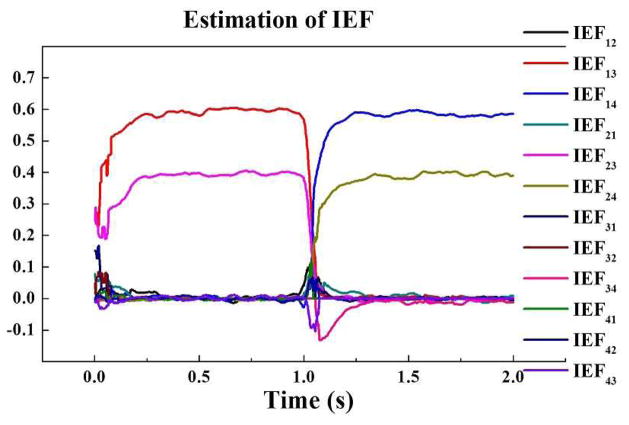
To investigate the dynamic property of the IEF and time-lagged ADTF method, analysis on a third time-varying model was performed. The construction of the model 3 is shown in Fig. 1. It consisted of 4 nodes and its sampling frequency was 400 Hz. One thousand simulated signals were generated in a dynamic pattern, in which the primary source signal was a stochastic signal described as x(n)=0.55x(n-4)-0.81x(n-8)+ε(n). During the first half of the time (0–1s), node 3 was the primary source and generated a signal of a main frequency band of 18–24 Hz. Node 4 was directly caused by node 3 in a time-lagged pattern, node 1 was directly caused by node 3 in a zero-lagged pattern, and node 2 was caused by node 3 in a fused pattern with lagged and instantaneous effects (see Fig. 1(a)). During the later portion of the time (1–2s), node 4 became the main source meanwhile there were a time-lagged propagation from node 4 to node 3, a zero-lagged propagation from node 4 to node 2, and a fused propagation from node 4 to node 1 (see Fig. 1(b)).

Fig. 1.

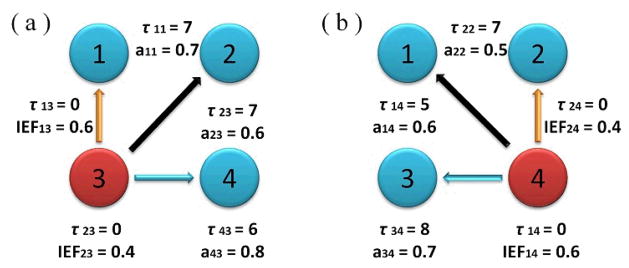
Graphical illustration of the model 3. (a) During the first half of the time (0–1s), node 3 is the primary source. It propagates to node 4 in the time-lagged pattern, propagates to node 1 in the zero-lagged pattern, and propagates to node 2 in the fused pattern. (b) During the later portion of the time (1–2s), node 4 becomes the main source and causes the other nodes in different propagation patterns. a_ij is the time dependent amplitude of the connection between ith and jth node, τ_ij denotes the constant delay in the propagation from the jth to the ith node, and IEF_ij is the instantaneous connectivity strength.

D. Statistical Significance Testing

Statistical analysis must be performed to the estimated causality values in order to test out the statistical significance of the estimation. In other words, non-zero causality values can be obtained from arbitrary sets of time series, but these values are meaningless unless they are statistically significant [4]. Thus, all multivariate causality estimators require a level of significance in order to differentiate between true connections and the connections caused by noise.

However, the dynamic spectral estimators such as time-lagged ADTF and ADTF have a highly nonlinear relationship to the time series from which they are derived. As such, the distribution of their values under the null hypothesis of no connectivity is not well established. Some nonparametric statistical tests have been utilized to overcome this issue. The “Surrogate data method” and the “leave one out method” are two common numerical methods to determine the significance of the particular causality measure [41], [42]. In the present simulation model 2 and model 3, the “surrogate data method” at a significant level of 0.05 was used for the statistical test. In our surrogate data method, the original time series were firstly transformed into the Fourier space, and then their phases were randomly and independently shuffled without changing the magnitude in order to produce a new surrogate time series. It had been shown that this process of phase shuffling preserved the spectral structure of the time series but randomized the spectral causality between artificial signals. Both the ADTF and time-lagged ADTF methods were subject to the surrogate data analysis. The shuffling and causality estimation procedures were repeated 200 times so that we could build an empirical distribution of the causality measurement values under the null hypothesis that no connectivity existed between the signals. Only the causal values that were above the significant level of 0.05 during the surrogate testing were considered as statistically significant connectivity.

E. Experimental Evaluation in Human

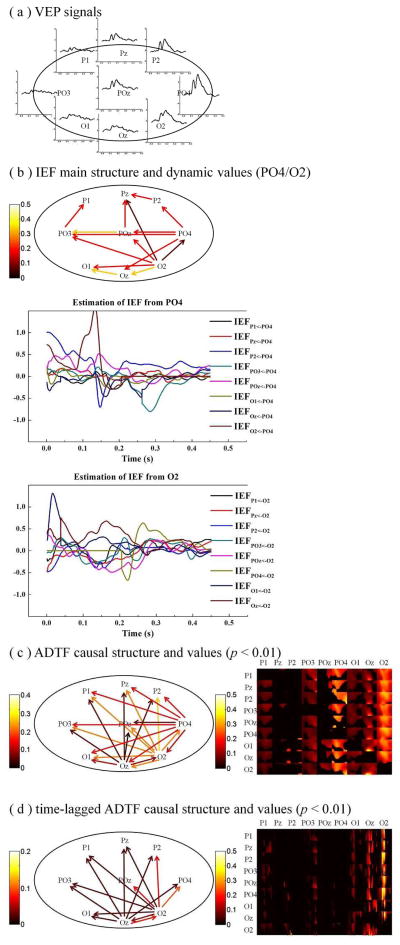
We also applied our method to estimate the dynamic spectral causality on real VEP data of a human subject. Experiments were carried out by stimulating the lower-left visual field of the healthy subject. The visual stimulus consisted of circular black-and-white checkerboards within the visual field on a homogenous grey background: the visual stimulus had a diameter of 8° visual angles and was placed along a downward diagonal at 10° visual angles as measured from the central fixation point to the center of each stimulus. The recordings were made following the international 10/20 system from 62 electrodes (Compumedics Neuroscan, El Paso, TX, USA) according to a protocol approved by the IRB of the University of Minnesota. EEG signals were digitized at 1000 Hz and the VEP data were averaged from 300 trials with each trial 500 ms long. Artifact rejections and linear detrending were performed before signal averaging to discard epochs with eye blinks or other obvious EEG noise. The scalp EEG is a mixture of activity from various sources, which include cortical activations, background brain activity, artifacts and measurement noise [43], [44]. Studies have shown that the ADTF and time-lagged ADTF methods may be immune to volume conduction, thus we can directly perform the connectivity analysis on the scalp EEG signals. Here, we selected the waveforms from nine electrodes (P1, Pz, P2, PO3, POz, PO4, O1, Oz and O2) that are mainly belonging to the parieto-occipital zone (shown in Fig. 6(a)). The purpose of the present study was to evaluate the dynamic causality of these scalp signals and the mutual influence between left and right cerebral hemispheres during the brain activation of VEP signals. In the experiment evaluation process, the “surrogate data method” at a significant level of 0.01 was also performed for the statistical test.

Fig. 6.

(a) The averaged VEP signals of the nine electrodes (P1, Pz, P2, PO3, POz, PO4, O1, Oz and O2) in lower-left condition. (b) The main structure of IEF and the plots of IEF values from PO4 and O2 to the other signals. (c) The main connectivity structure and the time-frequency distribution of the significant (p < 0.01) causality values by the ADTF method. (d) The main connectivity structure and the time-frequency distribution of the significant (p < 0.01) causality values by the time-lagged ADTF method. The color of the arrows codes the averaged strength of the absolute connectivity values over the time and the interesting frequency band (1–30Hz).

III. Results

A. Simulation Study

Two thousands of sets of simulated data representing the activations in three models were generated under different conditions. A series of fitted tvMVAR models were reconstructed based on the discrete Kalman filtering algorithm and the model orders were determined by SBC method. For such spectral tvMVAR models with instantaneous effect, we investigated the performance of dynamic causal ordering estimation algorithm, and then calculated the IEF values and the dynamic spectral causality values by using time-lagged ADTF method. We also compared the causality values with the results obtained from the conventional ADTF method.

Fig. 2 shows the plots of COR and RE corresponding to different number of variables and different number of model orders in model 1. The averaged results from two thousand sets of simulated stochastic signals are displayed. It can be noted that the mean COR decreases as the number of variables increases. For the same number of variables, the COR value is larger when the order p is higher. The averaged RE also shows similar pattern as the number of variables and orders changes (see Fig. 2(b)).

Fig. 2.

The plots show the (a) correct ordering ratio and (b) relative error with different number of variables (N) and model orders (p) from the causal ordering estimation algorithm in simulated model 1.

For the model 2, the plots of COR and RE corresponding to instantaneous strength factor α can be seen in Fig. 3(a) and Fig. 3(b), respectively. The plot of IEF₂₁ values vs. instantaneous connectivity strength factor α, estimated by our method is shown in Fig. 3(c). As the factor α increases from −0.8 to 0.8, the estimation of IEF₂₁ values matches well with the simulated instantaneous factor. In the fused pattern, including instantaneous effect and time-lagged causality, the IEF₂₁ values have been precisely detected and presented. Fig. 3(d) shows the plots of means for the causality values (x₂ < - x₁), averaging a frequency band of 9–14 Hz from the methods, compared with the theoretical time-lagged causality values. It shows that the time-lagged causality values obtained by the time-lagged ADTF method, in which the instantaneous effect could be effectively removed, are more accurate and closer to theoretical values than the results obtained by the ADTF method. It can be noted that when the factor α is zero, which means there is no zero-lag interference between the two signals, the time-lagged ADTF values are equal to the ADTF values.

Fig. 3.

The results of the simulated model 2: The plot of COR (a), RE (b) and the estimation of IEF₂₁ (c) vs. instantaneous connectivity strength factor α. (d) The plot of means for the significant (p < 0.05) causality values (x₁ -> x₂) within the frequency band of 9–14 Hz. Black, gray, and red colors represent the ADTF values, time-lagged ADTF values and theoretical values, respectively.

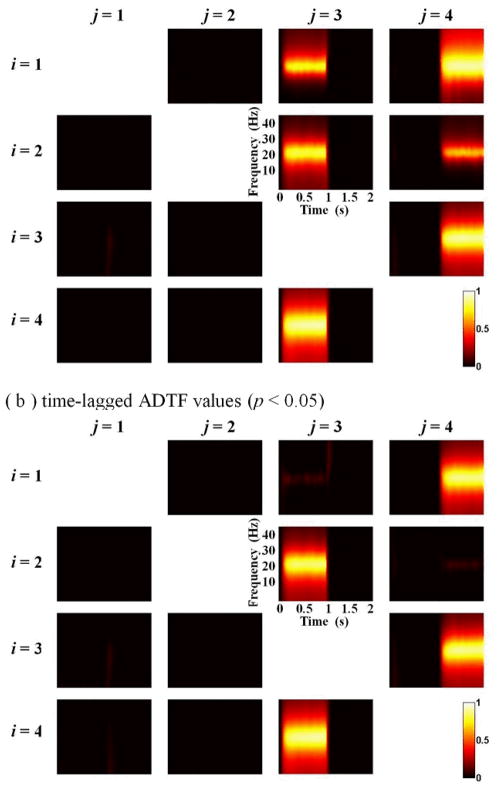
For the model 3, the plots of IEF estimations are shown in Fig. 4, and a graphical illustration of significant (p < 0.05) causality values between all signals is shown in Fig. 5. It can be seen that during the first half of the time (0–1s), IEF₂₃ is close to 0.4 and IEF₁₃ is close to 0.6, while during the later portion of the time (1–2s), IEF₁₃ and IEF₂₃ decrease to zero, IEF₁₄ increases to 0.6 and IEF₂₄ changes to 0.4. In the process of source switching from node 1 to node 2, the dynamic IEF values are well captured. Fig. 5 shows the estimated time-frequency distribution of the time-lagged ADTF values and ADTF values. The different result of estimated causality values from node 3 to node 1 and from node 4 to node 2 shows that time-lagged ADTF can separate the pure zero-lag effect from time-lagged causality and successfully describe the dynamic spectral connectivity between signals.

Fig. 4.

The estimation of the time-varying IEF values between all signals in model 3, averaged from 1000 trials.

Fig. 5.

The time-frequency distribution of the significant (p < 0.05) causality values between all the signals in simulated model 3. (a) ADTF method results, and (b) time-lagged ADTF method results.

B. Experimental Evaluation in Human

The scalp EEG signals, evoked by stimulating the lower-left visual field, were subjected to a fitted tvMVAR model that was estimated by the distribute Kalman filtering algorithm. After generating the surrogate datasets 200 times, the dynamic IEF values and time-lagged spectral causality for these nine signals was computed at a significant level of 0.01. Fig. 6(b) shows the main instantaneous effect structure and the estimation of the dynamic IEF values, which shows that PO4 and O2 have relatively large instantaneous effect to other signals. Fig. 6(c) shows the main connectivity structure and the time-frequency (1–30Hz) distribution of significant dynamic spectral causality obtained by the ADTF method. The main connectivity structure and significant dynamic spectral causality, obtained by the time-lagged ADTF method, is shown in Fig. 6(d). The color of the arrows in Fig. 6 codes the mean strength of absolute connectivity values over the whole time and the interesting frequency band (1–30Hz).

The ADTF results show that the signals of PO4, O2 and Oz are the main sources that cause the other signals. The time-frequency distributions of significant dynamic spectral causality obtained by the ADTF method indicate that the contralateral cortical activity is the primary causal source during the visual stimulation. The IEF values and time-lagged ADTF method also demonstrated this contralateral phenomenon, i.e. PO4, O2 and Oz are the primary sources. Both the ADTF results and the time-lagged ADTF results indicate that the visual cortex in the right hemisphere becomes active first and then it drives the related zones in the left hemisphere. However, different from the ADTF result, the time-lagged ADTF result reveals that the signal of PO4 might not be the main lagged causal source and the spectral causality from PO4 to other signals measured by the ADTF method is caused by the instantaneous effect (shown in Fig. 6(b)). The time-frequency distribution of time-lagged ADTF values (shown in Fig. 6(d)) is relatively smaller than the ADTF values (shown in Fig. 6(c)), which is the result after extracting the instantaneous effect. Due to the comparison in simulations, we can infer that the time-lagged ADTF values reflect the lagged causality between signals after separating the instantaneous effect while the ADTF values represent the fused results from instantaneous effect and time-lagged causality. The advantage of combination of time-lagged ADTF and IEF estimation is that they can separate the lagged causality and instantaneous causality, which cannot be provided by the conventional ADTF method.

IV. Discussion

In this study, a new method of estimating IEF value is proposed to track the dynamic instantaneous effect from the fused interactions between signals. It describes the possible zero-lag influence for the contemporaneous measured data. The study also suggests the usefulness of the time-lagged ADTF method in addition to the ADTF method in assessing the time-lagged spectral causality between signals.

For the tvMVAR model, it is convenient to observe whether the instantaneous effect exists between two signals from the covariance matrix of their residuals. The major problem in the estimation of dynamic IEF value is how to determine the time-dependent correct ordering of all the measured signals. Previous studies by Shimizu and Hyvarinen et al. have successfully tackled this problem by using independent component analysis when the model residuals are with non-Gaussian distribution [33]–[36]. Moreover, Hyvarinen et al. discussed how the coefficients of the model are changed by taking into account the instantaneous effects and definitely showed that the model’s causal ordering will not be altered by the neglect of instantaneous effect in case the signals share the same acyclic causal ordering for all time lags [35]. In mathematic principle, if A_k(n)⁻¹ and B_k(n) can be transformed into two lower-triangular matrices through a same permutation P(n), the conduct of these two matrices, B₀(n), can be also transformed into a lower-triangular matrix with the P(n). Therefore, it is reasonable to compare the time lagged causality values to estimate the time-varying causal ordering between signals when the model residuals are with Gaussian distribution. The method seems to work well under the assumption that the connectivity information flows the same causal ordering for all time lags, which means the instantaneous causality and all the lagged causality shall share the same acyclic direction when they exist between two signals. However, the current method may not work effectively when the instantaneous effect could occur randomly. Future studies considering more complicated random causal directions will be necessary to further extend the instantaneous connectivity estimation in more general cases. The time-lagged ADTF method, as well as the ADTF method, is based on the spectral tvMVAR model, which can be constructed by various algorithms. It is a linear multivariate time series model, which characterizes the interregional dependencies within data by considering the historical influence of the variables. Hence, it is the first step to build a fitted and robust spectral tvMVAR model that is consisted of optimal model order and accurate time variant coefficients. In order to avoid some of the constraints or limitations in the model construction, non-normality tests and stability tests may be necessary to improve the assessment. In addition to this linear time-varying model, the spectral causality measures also can be studied in many other nonlinear time-varying models [45], [46].

As the conventional ADTF method is based on the tvMVAR model without considering instantaneous effect, it mistakenly treated the zero-lag connectivity as time-lagged connectivity. On the contrast, zero-lag effect within all signals can be well detected and identified by estimating the IEF values. After the instantaneous effect is removed from the model, the time-lagged ADTF method could provide the pure lagged causality instead of the fused causality.

In the present simulation study, three different models are simulated to study the performances of IEF and time-lagged ADTF method. The model 1, constructed by randomly distributed coefficients with different number of signals and orders, is used to investigate the performance of the IEF estimation method. It can be observed that the COR is higher than 80% and the RE is less than 10% in most conditions. In the model 2, the estimated IEF results were compared with the theoretical IEF values in the simulation setting. The simulation result shows that the time-lagged ADTF values, distinguishing the time-lagged causality from zero-lagged influence, are much closer to the theoretical lagged causality values while the ADTF values are disturbed by the signals’ instantaneous effect. During the source switching process in model 3, the time-varying estimation of IEF values can also be used to assess the variation of instantaneous effect in a dynamic manner. It is worth noting that for a pure zero-lag effect case, time-lag causality will be given by ADTF while no such inaccurate causality could be found by the time-lagged ADTF method. These results can be explained by the incomplete tvMVAR modeling in ADTF method and its ignorance of the instantaneous effect.

There are previous studies about investigating the brain activations of the visual evoked potentials from scalp EEG [47]–[51]. Here, we study the VEP signals that are mainly located in the parieto-occipital area as these regions have most dominant evoked potentials during the experiment. Both the ADTF method and time-lagged ADTF method with IEF estimation are applied to the signals generated by stimulating lower-left visual field of the subject. The results of comparison between these two analyses are shown in Fig. 6. It can be noted that both the ADTF and time-lagged ADTF results indicate that the contralateral cortical activity is the primary causal source during the visual stimulation. In the “lower-left” condition, the visual cortex in the right hemisphere becomes active first and then it drives the left hemisphere. We studied the causal structures of the scalp recordings in lower-left visual field stimuli condition by using ADTF method and time-lagged ADTF method, which demonstrated similar results as comparing to the previous findings of the scalp phenomenon in [49]. Russo et al. studied the VEP measurements and showed that the early C1 component was maximized at the occipito-parietal midline area and the contralateral areas. They also showed the later contralateral P1 component over right occipital-temporal sites and ipsilateral component over the left hemisphere. These results indicate the initial activation of contralateral visual cortex and the later involvement of ipsilateral hemisphere, which are concordant with our findings of causal analysis. The results of the connectivity analysis for VEP data can help us understand the mutual influence between the visual areas in the left and right cerebral hemispheres. Future studies to better track the spatiotemporal functional connectivity of the human brain are still in demand to fully overcome the grand challenges and to better understand the brain function [52]–[66].

Similar to ADTF method, the time-lagged ADTF method is not suitable for distinguishing the direct and indirect causality. Compared with the time variant partial directed coherence method, the estimations by the ADTF and time-lagged ADTF methods require the matrix inversion, which may reduce the stability of the model and take more time during the computation. Nevertheless, they are still effective in estimating the dynamic spectral causalities and can be used in studying the connectivity analysis.

V. Conclusion

In summary, we have proposed a new causal ordering estimation algorithm which can handle the cases when there exist correlated Gaussian residuals in the time-varying multivariate autoregressive model, under the assumption that the signals follow the same acyclic causal ordering for all time lags. The performance of the method is investigated in a series of simulations with different number of signal variables and model orders. The dynamic estimation of instantaneous effect factor value is also proposed to track the time-varying instantaneous effect between signals. This study suggests the effectiveness of applying the time-lagged adaptive directed transfer function method to describe the lagged effect and to assess the lagged dynamic spectral causality between signals. Both computer simulation and human VEP data analysis have been performed, and the results demonstrated their usefulness in estimating the instantaneous interference and the time-lagged causality.