Multilevel modeling versus cross-sectional analysis for assessing the longitudinal tracking of cardiovascular risk factors over time

Abstract

Correlated data are obtained in longitudinal epidemiological studies, where repeated measurements are taken on individuals or groups over time. Such longitudinal data are ideally analyzed using multilevel modeling approaches, which appropriately account for the correlations in repeated responses in the same individual. Commonly used regression models are inappropriate as they assume that measurements are independent. In this tutorial, we use multilevel modeling to demonstrate its use for analysis of correlated data obtained from serial examinations on individuals. We focus on cardiovascular epidemiological research where investigators are often interested in quantifying the relations between clinical risk factors and outcome measures (X and Y, respectively), where X and Y are measured repeatedly over time, e.g., using serial observations on participants attending multiple examinations in a longitudinal cohort study. For instance, it may be of interest to evaluate the relations between serial measures of left ventricular mass (outcome) and of its potential determinants (i.e., body mass index, blood pressure etc.), both of which are measured over time. In this tutorial, we describe the application of multilevel modeling to cardiovascular risk factors and outcome data (using serial echocardiographic data as an example of an outcome). We suggest an analytical approach that can be implemented to evaluate relations between any potential outcome of interest and risk factors, including assessment of random effects and non-linear relations. We illustrate these steps using echocardiographic data from the Framingham Heart Study with SAS PROC MIXED.

Introduction

In this tutorial, we illustrate the use of multilevel modeling to perform longitudinal analysis of predictor and outcome variables that are measured repeatedly over time. Such data arise in studies such as the Framingham Heart Study (FHS), one of the largest long-running epidemiological studies of risk factors for cardiovascular disease. Participants in this longitudinal cohort study attend periodic examinations (approximately 2–4 years apart) at the Heart Study clinic, where extensive clinical data are measured. Because measurements taken within the same participant are correlated, statistical methods that account for this correlation are needed^[1–3] Data structure (also referred to as dimensionality) is a key factor that determines the choice of appropriate statistical procedures that can be used to analyze these types of data. The procedures for serial observations warrant approaches other than those used to analyze cross-sectional data, where individuals are measured only once, and thus observations are independent. Multilevel modeling is a statistical approach that is often used to analyze correlated data, such as data that is correlated within individuals or groups.^[4] For example, in the case of the FHS, there are three cohorts reflecting three generations of participants, i.e., the original cohort, the Offspring cohort and the third generation cohort.^[1–3] Considering the original cohort as an example, participants in this cohort are considered independent (from a statistical standpoint) and each participant, to date, has undergone over 30 examination cycles since the start of the study in 1948. The assessments at these examination cycles are correlated over time, and clustered or nested within each participant. As an alternative example, one might consider the outcomes of a surgical procedure in selected patients. Suppose the procedure is performed by ten different surgeons on patients within the same hospital. Patient-level outcomes are independent but they are correlated within each operating surgeon. These examples have two levels of variability. In the FHS example, we have between-participant variability (the participant is the clustering unit) and within-participant variability (over time). In the surgical example, we have between-physician variability (the physician is the clustering unit) and between-patient variability. We usually label the clustering unit as “level 2” (e.g., the participant in the FHS example, and the surgeon in the surgical example) and the individual measurement (i.e., at each examination in the FHS example, and in each patient in the surgical example) as “level 1”.^[5] In fact, it is possible to consider additional levels of hierarchy in data. For example, some of the participants in the FHS are related. One could consider parents participating in the original cohort as level 3 units, their offspring as level 2 units and repeated measurements within each offspring participant over time as level 1 units. In the surgical example, one could compare outcomes across multiple hospitals (level 3), each with different surgeons (level 2) performing procedures on their patients (level 1). For simplicity, we focus our discussion in this tutorial on two-level data structures. However, the approaches outlined here can be readily generalized to higher order data structures.

An additional feature of multilevel modeling is related to missing data, which arises frequently in longitudinal studies as individuals may not attend some examinations or may not have available data at all examinations. Multilevel models offer a reasonable option to address some of the limitations of traditional regression models in these situations because they handle correlated observations obtained at multiple levels, and also take into account the fact that all participants may not attend all serial examinations.

Motivation

Using data collected in the FHS, Cheng et al.^[6] described the correlates of echocardiographic indices of cardiac structure and function using serial data from the FHS Offspring examinations 2, 4, 5 and 6. They analyzed observations from multiple examinations (both risk factors and echocardiographic data [the latter serving as the outcome]) and applied multilevel modeling to assess the relations between risk factors and outcomes. These sequential measurements of risk factors and outcomes are not independent, because multiple measurements are obtained on the same individual over time. Here the participants represent the “level 2” units and the measurements at each examination represent the “level 1” units.

Because of the availability of multiple sequential observations on participants using serial echocardiography, FHS offers a unique opportunity to evaluate how the different parts of the heart change over the adult life course using data from the successive imaging studies. FHS investigators^[6–9] have effectively used multilevel modeling methods to evaluate the clinical correlates of cardiac structure and function using up to nearly 15,000 echocardiographic observations obtained serially in about 4,500 FHS participants. The objective of these investigations was to characterize cardiac structure and function over the adult life course by evaluating individual chamber dimensions, wall thickness and cardiac pump function separately. For instance, it is widely believed (based on cross-sectional and autopsy studies) that older individuals have greater cardiac mass, thickened heart walls and smaller ventricular cavity size.^{[10, 11]} The choice of multilevel modeling for this purpose allowed the use of serially-obtained longitudinal data and enabled the investigators to account for the fact that some participants may not attend consecutive examinations.^[6–9] From a clinical point of view, it may be important to investigate whether there are common clinical correlates for the different echocardiographic traits (translating into parallel changes in different heart chambers) by integrating the findings from these prior FHS investigations. The premise for such a comparative evaluation of tracking of cardiac chambers, wall thickness and ventricular function is that the impact of individual CVD risk factors on different parts of the heart may vary with age, sex and potentially modifiable risk factors. We illustrate herein how to analyze serial longitudinal observations on individual echocardiographic traits (see below).

Methods

Data structure and example of code

We investigated the longitudinal tracking of measures of cardiac structure and function and how variation in key biological determinants (that vary over time) influence the former in FHS participants who attended several serial examinations at which both cardiac structure/function and biological determinants were measured. Specifically, we aimed to evaluate the correlates of cardiac structure and function (outcome of interest, dependent variable), to assess the linearity of the associations between risk factors (biological factors, independent variables) and the outcome of interest, and finally to test for effect modification by one or more of the risk factors. Given the longitudinal and repeated nature of the observations, multilevel modeling was used for analyses. The SAS statistical software^[12] offers multiple procedures for analyzing correlated observations. We used PROC MIXED^[12] because it handles correlated observations obtained at multiple levels over time and accounts for the fact that participants may not attend all serial examinations (some data may be missing). PROC MIXED also fits the data into linear mixed effects models, allowing for testing of random intercepts and slopes (i.e., different baseline values and associations between risk factors and outcomes for each participant). When a model includes a random intercept, it allows for the intercepts to vary across participants, i.e., each participant may have a different starting value of the outcome of interest (e.g., left ventricular mass), before even considering the other risk factors to be included in the model. A model including a random slope for a given risk factor e.g., for age, allows for the association between age and outcome (e.g., left ventricular mass) to vary across participants.

Table 1 shows an example of the structure of a dataset appropriate for analysis using PROC MIXED. The Table displays a subset of the data used for the analysis of longitudinal tracking of left ventricular (LV) mass, where 4,217 participants contributed 11,762 person-observations (measurements).^[8] Each row represents measurements obtained from a single examination attended by a single participant; therefore, multiple rows may correspond to a single participant if they attended more than one examination (e.g., ID = 4 attended examinations 2, 4, 5, and 6). The outcome is left ventricular mass; body mass index (bmi), systolic blood pressure (sbp), and diabetes status are some of the potential risk factors associated with the outcome. We present below an example of the SAS code to analyze longitudinal tracking of left ventricular mass over time and the associations between body mass index, systolic blood pressure, and diabetes status (all of which also vary over time) as potential risk factors for left ventricular mass. Table A in the Appendix provides more detailed explanations of each of the SAS keywords used in the code below.

Table 1.

Data structure for use with SAS PROC MIXED

ID	EXAM	BMI, kg/m2	SBP, mm Hg	DIAB	LV MASS, gms
2	4	22.3	149	0	112
2	5	23.2	154	0	120
2	6	24.3	168	0	106
3	2	22.3	110	0	155
3	4	21.6	121	0	112
3	5	22.8	120	0	140
4	2	24.2	104	0	271
4	4	25.7	117	0	232
4	5	26.3	119	0	225
4	6	25.1	111	0	239

^aLVMASS as the outcome, and all other variables as the independent variables.

BMI = body mass index, DIAB = diabetes mellitus, LV = left ventricular, SBP = systolic blood pressure.

proc mixed noclprint data=dataset covtest method=ml;
 class id;
 model lvm = bmi sbp diabetes;
 random int/type=un subject=id;
run;

The SAS code above fits a model with a random intercept, and the mathematical model is as follows:

$${\mathrm{lvm}}_{\mathrm{ij}}={\mathrm{\beta }}_0+{\mathrm{\alpha }}_{\mathrm{j}}+{\mathrm{\beta }}_1\ast {\mathrm{bmi}}_{\mathrm{ij}}+{\mathrm{\beta }}_2\ast {\mathrm{sbp}}_{\mathrm{ij}}+{\mathrm{\beta }}_3\ast {\mathrm{diabetes}}_{\mathrm{ij}},$$

where lvm_ij denotes the left ventricular mass measured at each i on participant j (i denotes each serial or repeated measurement, and j denotes individual or independent participants), β₀ and α_j represent the fixed and random (varying across individuals) parts of the intercept, respectively, and β₁, β₂, and β₃ denote the slopes for bmi, sbp, diabetes, respectively.

Analytical steps

The analytical steps below outline an approach for modeling serial longitudinal measurements on participants over multiple time points. In the following examples of SAS code, we use out to represent the outcome of interest (e.g., left ventricular mass), rf to represent the main or primary risk factor of interest (e.g., BMI) and cov_1 – cov_5 to represent important covariates (e.g., age, sex, sbp, dbp, and diabetes). Figure 1 summarizes the analytical steps described below:

• 1We start by assuming that each participant has a different baseline value of the outcome of interest, or a random intercept in the model. This is particularly helpful in settings like the FHS, where participants may not attend all examinations, and therefore all participants may not have the same baseline examination. The assumption of the randomness of the intercept is tested statistically by including the “random int” statement in the model.

Figure 1.

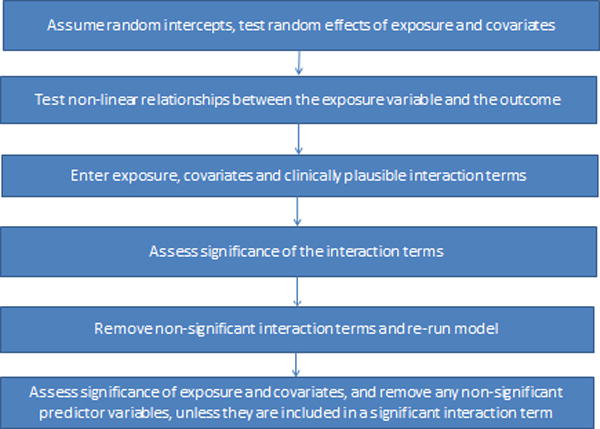
Analytical steps for applying multilevel modeling

If we are interested in testing whether the association between a risk factor and the outcome varies among participants (i.e., random slope) we can perform this in two different ways:

• a)We compare models with and without the random effect of a specific risk factor. Specifically, we run the following models, where the difference is the inclusion or omission of the random effect of the risk factor (note the difference in the two random statements below), using the maximum likelihood method (method=ml):

Model 1:
proc mixed noclprint data=dataset covtest method=ml;
 class id;
 model out = rf;
 random int/type=un subject=id;
run;

where out = outcome of interest, and

rf = main or primary risk factor.

Model 2:
proc mixed noclprint data=dataset covtest method=ml;
 class id;
 model out = rf;
 random int rf/type=un subject=id;
run;

If Model 2 (i.e., the model including the random effect of the risk factor) has a smaller Akaike Information Criterion (AIC) value, then this model has a better fit as compared to Model 1, and, therefore, we should allow for random effect of the risk factor in the SAS random statement. The significance of including a random effect is often supported by a substantial decrease in the AIC value; however, the comparison of the AIC values does not provide proof of statistical significance.

• b)Alternatively, we can perform a likelihood ratio test for the random effect of the risk factor using Restricted Maximum Likelihood (REML) estimation. Using Models 1 and 2 described above, compare the difference between the two -2*LogLikelihood values to a chi-square value with 1 degree of freedom. If the difference is larger than the critical value from the chi-square distribution, then we conclude that Model 2 is a better fit as compared to Model 1 and, therefore, we should allow for random effects of the risk factor in the SAS random statement.

• 2)Variables considered as the main or primary risk factor may not have a linear relationship with the outcome. Therefore, in the second step, we evaluate the functional form (e.g., linear versus non-linear) of the association between the primary risk factor and the outcome. This is achieved by plotting the unadjusted means of the outcome of interest for each value of the risk factor. If the plot indicates the possibility of a non-linear relation, then we can test for a non-linear effect. This is done by including a non-linear term in the model and assessing its statistical significance. For example, Figure 2 shows an example of a quadratic relation between the risk factor and the outcome; in this case, we would test the statistical significance of a quadratic relation between the risk factor and the outcome. Using the term “rf²” to denote the squared term of the risk factor of interest “rf”, we then run the following models:

  Model 3:
  proc mixed noclprint data=dataset covtest method=ml;
   class id;
   model out = rf;
   random int/type=un subject=id;
  run;
  

  Model 4:
  proc mixed noclprint data=dataset covtest method=ml;
   class id;
   model out = rf rf2;
   random int/type=un subject=id;
  run;
  

  If the p-value corresponding to rf² in Model 4 is significant, this indicates a significant quadratic relation between the risk factor and the outcome, and suggests the inclusion of the quadratic term for the risk factor in the model statement. Alternatively, we could compare the difference in -2*Log Likelihood ratio values between Model 3 and Model 4 to a chi-square value with 1 degree of freedom. If significant, we conclude that Model 4 is a better fit and, therefore, we include the quadratic term for the risk factor in the model statement. The same strategy can be followed for evaluating a potential cubic relation, or other non-linear association between the primary risk factor and the outcome of interest.

• 3)In the next step, we test whether there is effect modification. This is performed by entering all potential predictor variables (the primary risk factor and other covariates, here denoted as rf and cov_1–cov_5, respectively) in the model, along with any clinically plausible interaction terms among the predictor variables. For this example, we will assume that there are no statistically significant non-linear associations between the primary risk factor and the outcome, and that there are no random effects of the predictor variables. We will also assume that the only clinically plausible interaction term is between the primary risk factor and covariate 1 (e.g., sex), which we denote as rf*cov_1. We use the following code:

Figure 2.

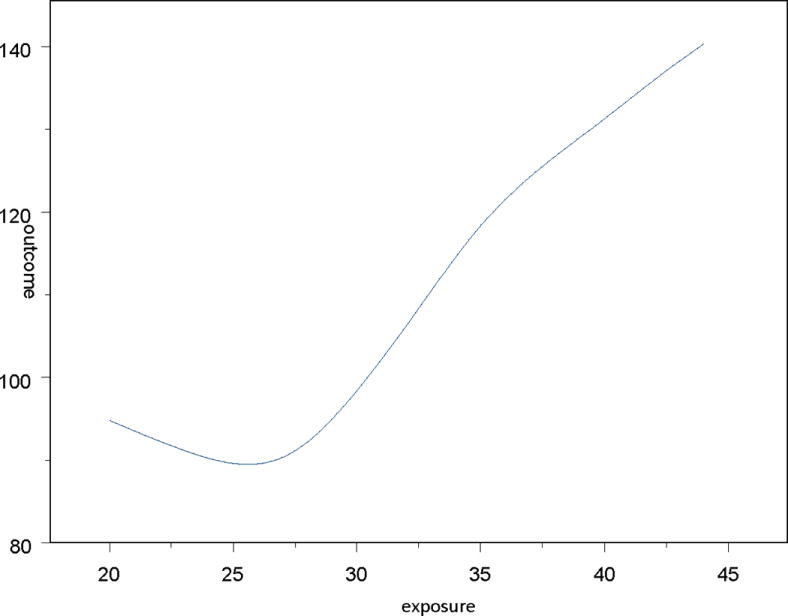
Graphic representation of a non-linear relation between a hypothetical risk factor (exposure) and an outcome of interest

Model 5:
proc mixed noclprint data=dataset covtest method=ml;
class id;
model out = rf cov_1 cov_2 cov_3 cov_4 cov_5 rf*cov_1 ;
random int /type=un subject=id;
run;

Model 6:
proc mixed noclprint data=dataset covtest method=ml;
class id;
model out = rf cov_1 cov_2 cov_3 cov_4 cov_5;
random int /type=un subject=id;
run;

We assess the statistical significance of the interaction term rf*cov_1 by either comparing the corresponding p-value from Model 5 to a pre-specified significance level or by comparing the difference in the -2*Log Likelihood ratio values between Models 5 and 6 (Model 6 does not include the interaction term rf*cov_1) to a chi-square value with 1 degree of freedom. Non-significant interaction terms can be removed from the model. Statistical tests for interaction terms are often characterized by a low power, therefore we may use a higher significance level (e.g., 0.10 instead of the widely used 0.05) to which we compare the p-value of each interaction term to assess its statistical significance. Additionally, graphical displays may be used to further evaluate the statistical significance of an interaction term. For example, if we are interested in evaluating whether the effect of age on LV mass depends on the levels of sex, we could plot LV mass versus age using a different line for men and women on the same graph, and assess whether the lines are parallel or not. If they are parallel, this means that the effect of age on LV mass does not depend on whether the participant is a man or a woman.

1. If the interaction term is statistically significant, we retain it in the model, and assess the statistical significance of other variables in the model.

2. If the interaction term is not statistically significant, we remove it from the model and re-run the model without the interaction term. We then assess the statistical significance of the remaining variables. Non-significant variables can be removed, unless they are included in a statistically significant interaction term.

Application and Results

At each of examination cycles 2, 4, 5 and 6 that occurred over a 16-year follow-up period, participants in the Framingham Offspring cohort underwent echocardiography using a standardized protocol (maximum of 4 imaging studies). Excellent inter- and intra-observer reproducibility of echocardiographic traits has been reported for the FHS echocardiographic laboratory.^[13] Clinical risk factors were defined at each of these examinations and included: age, sex, body mass index, systolic blood pressure, antihypertensive treatment, smoking, and diabetes.

Figure 3 displays examples of participants’ (“level 2”) LV mass values observed over multiple examination cycles attended (“level 1”). Each participant has a different LV mass value for each exam attended. Accordingly, the values for the risk factors are also updated at each examination cycle attended by the participant. Table 2 shows the clinical correlates of LV mass over the adult life course;^[8] LV mass was natural logarithmically transformed for these analyses to normalize its distribution and also to render comparable its variance in men versus women. We used a random intercept in the models to reflect a different baseline value of LV mass for each participant. Of note, we observed effect modification by sex and diabetes on the impact of age on LV mass (Table 2). We also observed that the impact of BMI on LV mass varied in men versus women (the interaction was statistically significant). Figure 4 displays the percent change in LV mass with increasing BMI for men and women separately. This figure was created using the regression equation formed by the parameter estimates (regression coefficients) shown in Table 2. For comparison purposes, Table 3 shows the results of a cross-sectional analysis of the same risk factors and their association with LV mass using data from a single examination cycle (FHS Offspring Cohort examination cycle 5) and multiple linear regression analysis. It is clear that using an ordinary multiple regression model such as that summarized in Table 3 (recommended for cross-sectional studies) does not allow us to capture the complex associations between the risk factors and the outcome. More specifically, when using multilevel modeling, more interaction terms between the risk factors appear statistically significant, suggesting that the associations between risk factors and the outcome vary depending on the levels of other risk factors (Table 2). Moreover, additional main effects appear to have a significant associations with LV mass (e.g., smoking status, antihypertensive treatment), therefore explaining more of the inter-individual variability in the outcome (Table 2). Table 4 summarizes the directionality of the association for these clinical covariates with echocardiographic traits, i.e., left ventricular mass (LVM), LV wall thickness, LV diastolic dimensions, fractional shortening, aortic root diameter and left atrial size.^[6–9] The use of multilevel modeling revealed interesting patterns of associations as well as interactions among the covariates (Table 4).^[6–9] For instance, systolic blood pressure (SBP) was positively associated with both LV mass and wall thickness. However, diastolic BP was inversely associated with LV diastolic dimensions, left atrial size and with fractional shortening. In contrast, aortic root diameter was inversely associated with systolic BP but directly associated with diastolic BP. Smoking was associated positively with LV mass, whereas diabetes was inversely associated with LV mass and LV diastolic dimensions, but directly associated with LV wall thickness. The effect of age on LV mass, LV wall thickness and aortic root size varied with sex. The effect of body mass index on LV mass, diastolic dimensions, left atrial size and aortic root diameter varied according to sex. The association of diabetes on LV mass, wall thickness, and diastolic dimensions varied with age. These observations suggest a complex relation among standard cardiovascular risk factors and different components of cardiac structure and function, a revelation made possible by using multilevel modeling.

Figure 3.

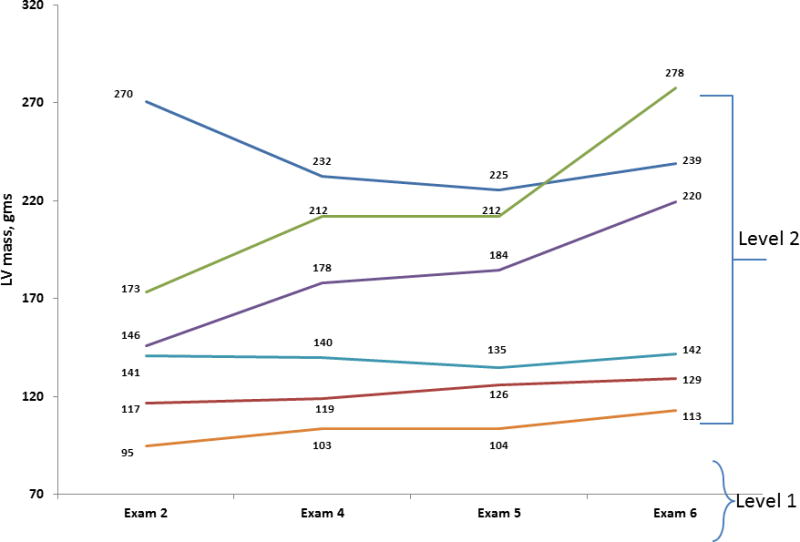
Examples of participants’ (“level 2”) LV Mass values observed over multiple examination cycles (“level 1”)

Table 2.

Clinical correlates of longitudinal tracking of LV mass over a 16-year period.

Variable	Regression coefficient	Standard error	p-value
Age 50, years	0.002073	0.00032	<0.0001
Men	0.3286	0.02814	<0.0001
Men*age 50	−0.00262	0.000381	<0.0001
Body mass index, kg/m2	0.01658	0.000602	<0.0001
Men*body mass index	−0.00209	0.001032	0.04
Systolic blood pressure, mm Hg	0.001376	0.000122	<0.0001
Antihypertensive treatment	0.02322	0.005569	<0.0001
Current smoking	0.01163	0.004752	0.01
Diabetes	−0.01628	0.01146	0.16
Age 50*diabetes	0.00338	0.000928	0.0003

Source of data in Table is reference 8.

Age 50 indicates that age was centered at the mean of all participants at all exams (50 years) to reduce multi-collinearity between regression coefficients. The regression coefficient indicates the e^beta-fold increase in LV mass in original units per one-unit-increment in the independent variable (for binary traits that corresponds to the presence vs. absence of the trait).

The effect of a variable that is included in a statistically significant term should be interpreted, accounting for the corresponding interaction term. For example, the effect of BMI depends on sex; therefore, in women, a 1-unit increase in BMI results in 0.01658 units increase in log-transformed LV mass (e^0.01658 or 1.0167–fold increase in LV mass in grams). In men, a 1-unit increase in BMI results in 0.01449 (= 0.01658–0.00209) units increase in log-transformed LV mass (e^0.01449 or 1.0146–fold increase in LV mass in grams).

Figure 4.

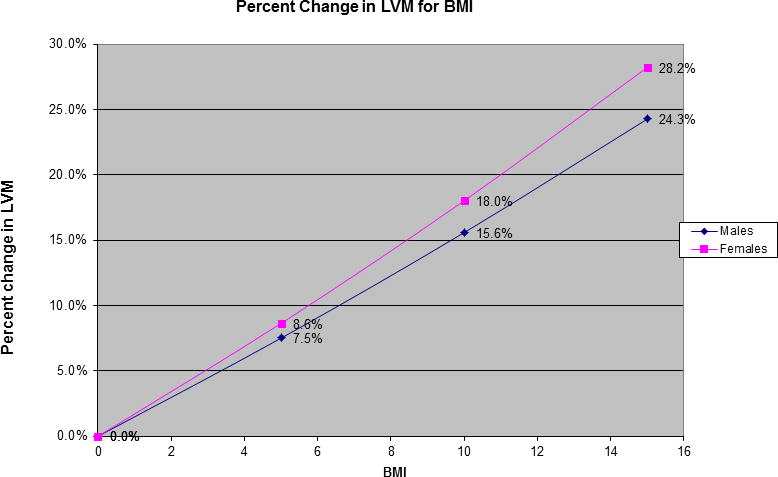
Percent change in Left Ventricular Mass for increasing BMI for men and women (source is reference 8)

Table 3.

Clinical correlates of LV mass using a cross-sectional design (single examination)

Variable	Regression coefficient	Standard error	p-value
Age 53, years	0.000343	0.00043	0.4277
Men	0.232528	0.007573	<0.0001
Body mass index, kg/m2	0.0132406	0.000886	<0.0001
Systolic blood pressure, mm Hg	0.0017879	0.0002349	<0.0001
Diabetes	−0.0205336	0.018619	0.2702
Age 53*diabetes	0.006068	0.00181455	0.0008

Age 53 indicates that age was centered at the mean of all participants at all exams (53 years) to reduce multi-collinearity between regression coefficients. The regression coefficient indicates the e^beta-fold increase in LV mass in original units per one-unit-increment in the independent variable (for binary traits that corresponds to the presence vs. absence of the trait).

The effect of a variable that is included in a statistically significant term should be interpreted, accounting for the corresponding interaction term. For example, the effect of age depends on diabetes status; therefore, in people with no diabetes, a 1-unit increase in age results in 0.000343005 units increase in log-transformed LV mass (e^0.000343005 or 1.000343–fold increase in LV mass in grams). In people with diabetes, a 1-unit increase in age results in 0.006411 (= 0.000343005+0.0060683) units increase in log-transformed LV mass (e^0.006411 or 1.00643–fold increase in LV mass in grams).

Table 4.

Directionality of Association of risk factors with Echocardiographic Traits.

Clinical Covariates	Directionality of Association with Echocardiographic Traits*
	LV mass	LV wall thickness	LV diastolic dimensions	Fractional shortening	Left atrial size	Aortic root diameter
Male sex	+	+	+	−	+	+
Age	+	+	−	+	+	+
BMI	+	+	+	NS	+	+
Systolic BP	+	+	+	+	+	−
Diastolic BP	NS	+	−	−	−	+
Antihypertensive treatment (HRX)	+	+	−	+	+	+
Smoking	+	NS	NS	NS	NS	NS
Diabetes	−	+	−	NS	NS	NS
Interactions	Age*diabetes BMI*sex Age*sex	Age*sex Age*BMI Age*diabetes	Age*diabetes BMI*sex Age*HRX	Age*HRX	BMI*sex Age* HRX DBP*sex	Age*sex Age*BMI BMI*sex BP*sex

^*+ indicates positive association, − indicates inverse association, NS indicates non-significant association.

Abbreviations: HRX, Antihypertensive treatment; BP, Blood Pressure; SBP, Systolic Blood Pressure; DBP, Diastolic Blood Pressure; BMI, Body Mass Index

The last row of the Table shows the statistically significant interaction terms for each outcome separately, e.g., for the analysis of LV mass, Age*diabetes and BMI*sex were the statistically significant interaction terms.

Discussion

Utility of multilevel modeling: A Brief Overview

Multilevel modeling is an ideal statistical approach for analyzing data that are correlated, for instance repeated measures obtained on individuals, such as longitudinal observations of biological variables in an epidemiological context.^{[14, 15]} Multilevel models can be used for continuous outcomes, and for categorical and ordinal outcomes with multinomial error distributions.^[4] The examples illustrated in this tutorial are relevant for single continuous outcomes, but the multilevel modeling method can also be applied to multivariate (multiple outcomes of interest) linear models, and to processes following a binomial or Poisson distribution, as well as for ‘time to event’ outcomes (with or without modeling of competing risks).^[4] Multivariate multilevel modeling, not discussed herein, is a special case where we can estimate associations between risk factors and an outcome that is comprised of more than one response variable. The multilevel method can also be applied to studies focused on meta-analysis^[4] that combine individual-level data with aggregate-level data, as discussed by Langford et al.^[16] It can also be used at the planning stage of multilevel studies by accounting for the choice of covariates, level of randomization (trials) and determination of sample sizes at different levels.^[4] An excellent and comprehensive resource for the various uses of multilevel modeling is reference 4.^[4]

Attractiveness of the use of multilevel modeling in epidemiological research

The multilevel modeling approach is a good option for analyzing data with missing observations. The nature of missing-ness (random versus non-random) should be evaluated to define the best strategy for handling missing-ness. It is possible that observations are missing due to study design (data obtained on a sub-sample) or other reasons unrelated to the response variable itself. In this situation, model parameters, such as level 1 or level 2 random effects, are uninfluenced by the missing values. If on the other hand, observations are missing non-randomly and are related to the values of the response variable itself, then one has to model in the missing-ness mechanism in the analytic strategy, and then proceed as though the data are missing at random.^[4] For example, individuals who are missing echocardiographic observations at FHS examinations are often not missing those observations at random, i.e., they tend to be older, and have a greater prevalence of co-morbidities such as chronic obstructive pulmonary disease or cardiovascular disease.^[17] Sensitivity analyses may be helpful in these situations, where missing values for either response or predictor variables can be imputed by assigning them select values empirically, or by estimating them from the available data. Additionally, the example of SAS code that is presented in the Methods section is easy to use and, therefore, analysis of serial measurements using the PROC MIXED^[12] procedure is recommended.

Multilevel modeling is mostly used for analyzing serial measurements over time, often obtained on participants in a longitudinal study, and is able to assess the correlates of clinically important outcomes (e.g., fractional shortening) and also evaluate the longitudinal tracking of a specific outcome, capitalizing on the wealth of information in serial observations. Applying the multilevel method in FHS studies,^[6–9] we were able to not only evaluate the associations between echocardiographic outcomes and their potential clinical risk factors, but also evaluate possible effect modification that was present among some of the risk factors. This was made possible by including corresponding interaction terms in the models and evaluating their statistical significance. Power to detect significant interaction terms was enhanced by the wealth of longitudinal observations; this may not have been possible in a smaller cross-sectional study.

Conclusion

Multilevel modeling is a suitable statistical approach for analyzing correlated risk factor data obtained from participants attending sequential examinations over time in a longitudinal cohort setting. The use of the wealth of these serial observations allows for the assessment of the associations between clinical risk factors and outcomes, offering opportunities to reveal complex relations among the risk factors with respect to their effect on the outcomes, which may have not been observed in smaller cross-sectional studies.