MCM-41 impregnated with A zeolite precursor: Synthesis, characterization and tetracycline antibiotics removal from aqueous solution

Highlights

► Adsorption of tetracycline antibiotics. ► Impregnation of one weight percentage of A zeolite on MCM-41. ► Equilibrium, kinetic and thermodynamic study of adsorption of tetracycline antibiotics onto modified MCM-41.

Abstract

In this paper, the MCM-41 has been modified by impregnation with zeolite A to prepare a kind of new adsorbent. The adsorption of TC from aqueous solutions onto modified MCM-41 has been studied. It was discovered that the adsorption capability of zeolite A modified MCM-41 (A-MCM-41) increased dramatically after modification. The modified MCM-41 was characterized by X-ray diffraction (XRD), nitrogen adsorption–desorption, Fourier Transform Infrared (FTIR) analysis, Transmission electron microscopy (TEM) images, and ²⁹Si and ²⁷Al Magic Angle Spinning Nuclear Magnetic Resonance (MAS NMR) spectra. The modified MCM-41 structure was still retained after impregnated with zeolite A but the surface area and pore diameter decreased due to pore blockage. The adsorption of TC on modified MCM-41 was discussed regarding various parameters such as pH, initial TC concentration, and the reaction time. The pH effects on TC adsorption indicated that the adsorbents had better adsorption performances in acidic and neutral conditions. The adsorption isotherms were fitted well by the Langmuir model. The adsorption kinetics was well described by both pseudo-second order equation and the intra-particle diffusion model. The adsorption behavior in a fixed-bed column system followed Thomas model. The adsorption behavior of TC was the chemical adsorption with an ion exchange process and electrostatic adsorption.

1. Introduction

Pharmaceutical antibiotics have been applied worldwide in human therapy and the farming industry. Thus, antibiotics especially tetracycline antibiotics have attracted many people’s attentions recently. Tetracycline has been considered to be a class of potential pollutants [1]. Most tetracycline antibiotics (TCs) enter the environment through municipal effluent, sewage sludge, solid wastes and manure applications. Thus, recent studies have reported the amount of TCs detected is about 0.15 μg/L in groundwater and surface water [2], 4 mg/kg in liquid manure [3], and 3 μg/L in farm lagoons [4]. In addition, even little amount of TCs can cause serious environmental pollution. The continuous release of TC into aquatic environment increases the potential for antibiotic resistance among microbial populations, and the degradation by-products have been proven even more toxic than the parents [5]. Therefore, it is urgent to develop efficient and economical technologies to remove TCs. There are many technologies available for TC removal including adsorption, oxidation, and photochemical degradation [4]. The adsorption process is a practical method for the removal of TC from wastewater in situ.

Mesoporous materials with ordered pore structure, large surface area have shown promise for applications ranging from air to water purification [6]. These materials are considered to have good potential for adsorption/separation applications because of regular hexagonal structure, uniform pore distribution, large surface area and large pore volume [7]. Untreated or functionalized mesoporous silica has been applied in different pollutants adsorption. For example, the MCM-41 was used to remove nitrobenzene, phenol, o-chlorophenol and divalent metal cations from aqueous solution [6–8]. MCM-41 was also applied to adsorb volatile organic compounds (VOCs) from indoor air [9–11]. In addition, modified MCM-41 molecular sieves were also good adsorbents for the removal of ammonia, and heavy metals [12-14]. Among these modification methods, modified MCM-41 molecular sieves with zeolite precursors attracted much attention for the removal of heavy metals. However, almost no attention has been paid to the interaction of TC with modified MCM-41.

In this study, the MCM-41 was modified through impregnation with zeolite A (A-MCM-41). The A-MCM-41-enabled batch experiments and fixed-bed column methods were used to investigate the removal of TC from aqueous solutions. The objective was to study the removal efficiency of TC by A-MCM-41 in the batch experiments and a fixed-bed system. The specific objectives of the work were to (1) investigate the interaction of tetracycline with A-MCM-41 and the fundamental adsorption behaviors of A-MCM-41 for removal of TC from a wide range of aspects including the pH effect, adsorption isotherms and adsorption kinetics. The adsorption mechanism of TC onto A-MCM-41 was discussed in detail. (2) Examine the removal performance of TC from aqueous solutions by trickling TC solution through the A-MCM-41 fixed-bed column and the efficiency of regeneration of the fixed-bed column for reuse.

2. Experimental

2.1. Materials and chemicals

Hydrochloride salt of tetracycline (TC, ⩾95% purity, MW: 480.90) was purchased from Sigma Co. and the structure of TC was presented in Fig. 1. Cetyltrimethylammonium bromide (CTAB) 98%, was supplied by Aldrich (UK). Sodium silicate (99%), sodium aluminate 99%, sodium hydroxide 99%, hydrochloric acid (99 wt.%) was provided by Fisher Scientific. All the glassware were soaked in 5% HCl overnight and cleaned with deionized water before use. All solutions were prepared with deionized water (Milli-Q) and stored at 4 °C.

Fig. 1.

A schematic flow sheet of fixed-bed column setup.

2.2. Synthesis procedures

2.2.1. Preparation of precursors of A zeolite

The precursors of zeolite A were prepared as previously reported in the synthesis of zeolite A [15]. The main process is as follows: the chemicals Na₂SiO₃·9H₂O, NaOH, and NaAlO₂ with molar ratio of Na₂O:Al₂O₃:SiO₂:H₂O equal to 3.165:1:1.926:128 were mixed in distilled water in the boiling state and stirred for 1 h. After that, aged at 298 K in a static state for 24 h to form the precursors of zeolite A.

2.2.2. Synthesis of mesoporous adsorbent

In the process of synthesizing mesoporous adsorbents, the molar ratio of (SiO₂ + Al₂O₃):NaOH:C₁₆TMABr:H₂O was equal to 1:0.24:0.12:100, and the molar ratio of SiO₂:Al₂O₃ was equal to 20:1. Exactly as follows, 70 mL C₁₆TMABr aqueous solution containing 4.37 g C₁₆TMABr was mixed with 90 mL solution of the 27.73 g Sodium silicate, 0.96 g sodium hydroxide, and 0.4 g sodium aluminate to form the original solution. 1% of weight percentage of zeolite A precursors were added to the original solution. Then the pH value of the mixture solution was adjusted to 10.5 with hydrochloric acid, resulting in a gel, after 1 h continuous stirring. The gel was transferred into a 200 mL Teflon-lined stainless autoclave and crystallized at 378 K for 48 h. After crystallization, the autoclave was cooled to room temperature naturally. Then the product was filtered out and dried at 378 K for 10 h. Eventually, the powder was calcined in air at 823 for 4 h to remove the surfactant, using a ramping rate of 2 K/min. Finally, the white powder A-MCM-41 was produced.

2.3. Characterization and analysis

The quantitative evaluation of the structural units was obtained by small-angle X-ray scattering (SAXS) measurements. A Philips X’pert powder diffractometer system with Cu Kα (λ = 1.541 A) radiation was used for X-ray studies. SAXS analysis was performed from 1.5° to 10.0°. The Brunauer–Emmett–Teller (BET) specific surface area was calculated using the standard BET method for adsorption data in the relative adsorption range from 0.05 to 0.2. The total pore volume was estimated on the basis of the amount of nitrogen adsorbed at a relative pressure (P/P₀) of ca. 0.99. The pore size distribution (PSD) was determined using the Barrett–Joyner–Halenda (BJH) method applied to the adsorption branch of the isotherm. Infrared spectra of all samples were obtained in KBr pellets in the 4000–400 cm⁻¹ region with a resolution of 4 cm⁻¹, by accumulating 64 scans using an ATI Mattson FTIR spectrophotometer. Transmission electron microscopy (TEM) images were taken on an H-8100 transmission electron microscopy operated at 200 kV. The solid states ²⁹Si and ²⁷Al Magic Angle Spinning Nuclear Magnetic Resonance (MAS NMR) spectra were recorded on a Varian Unity Inova 400 M spectrometer at 59.584 MHz and 78.155 MHz, using 1.5 μs and 0.3 μs pulse length, 3 s and 1 s recycle delays, and a spinning rate of 5 kHz and 7 kHz, respectively. ²⁷Al chemical shifts were measured relative to $\text{Al}{({\text{H}}_2\text{O})}_6^{+3}$. The concentration of TC in the solution was analyzed using High Performance Liquid Chromatography (Agilent, USA). Column: Agilent HC-C18, 5 μm, 4.6 mm × 250 mm; The mobile phase was a mixture of 0.01 M disodium hydrogen phosphate–acetonitrile (78:22, v/v); flow rate: 1 mL/min; detector: UV at 355 and sample size:5 μL. The correlation coefficient of the standard curve (n = 8) was greater than 0.999.

2.4. Adsorption batch experiments

2.4.1. Adsorption of TC at different initial pH

The influences of different initial pH to adsorption of TC onto A-MCM-41 were studied, respectively. The range of initial pH of TC aqueous solutions was 3.0–10.0. One or two drops of 0.1 mol/L HCl or NaOH solutions were added into the solution to adjust pH of solutions to different values. The initial concentrations of TC solutions were 100 mg/L. In order to reduce measurement errors in all the experiments, the residual concentration of each equilibrium solution sample was measured in triplicates and the average value was used to calculate the equilibrium concentration based on a standard calibration curve, whose correlation coefficient square was 0.9999. The experimental error was observed to be within ±2%.

The specific amount of solute adsorbed was calculated using Eq. (1) [16] as follows:

$$q_e=\frac{(C_0-C_e)\times V}{W}$$ (1)

where q_e is the adsorption capacity (mg/g) in the solid at equilibrium; C₀ and C_e are the initial and equilibrium concentrations of solution (mg/L), respectively; V is the volume of the aqueous solution (L) and W is the mass (g) of adsorbent used in the experiments.

2.4.2. Adsorption of TC at various contact time and initial concentration

The batch adsorption experiments were conducted at the temperature of 303 K. In order to study the effects of various contact time and initial TC concentrations on the adsorption of TC, A-MCM-41 was weighed and immerged into TC solutions under continuous stirring at varied initial TC concentrations. The concentrations of TC aqueous solutions ranged from 100 to 500 mg/L. The10 mL TC solution was mixed with 0.004 g A-MCM-41 in a 50 mL beaker. The beaker sealed with aluminum foil was continuously stirred (250 rpm) at initial pH 7.0. At selected time intervals (0.33, 0.66, 1, 1.33, 1.66, and 2.0 h), centrifuge tubes were centrifuged. Then, 1 mL of sample solutions was taken out and filtered through the 0.45 μm membrane filter to analyze the current TC concentration. Meanwhile, the same volume of water with pH 7.0 was added into the bulk solutions to keep the volume constant. Parallel experiments were conducted without the adsorbent (blank).

2.5. Adsorption isotherms

The batch adsorption experiments were conducted at different temperatures: 303, 313 and 323 K, respectively. The concentrations of TC aqueous solutions were 300 mg/L. The10 mL TC solution was mixed with 0.004 g A-MCM-41 in a 50 mL beaker. The beaker sealed with aluminum foil was continuously stirred (250 rpm) for 2.5 h to reach equilibrium. Then the samples were filtered with 0.45 μm membrane filter. The concentration of TC in the sample was analyzed by using HPLC.

Freundlich model supposes that uptake or adsorption of TC occurs on the heterogeneous surface by monolayer adsorption [17]. The equation of this model is described as follows [18]:

$$q_e=k_f{(c_e)}^{1/n}$$ (2.1)

The Freundlich equation can be linearized by taking logarithms and constants can be determined. The above equation can be linearized as follows:

$$\log (q_e)=\log k_f+1/n\log (c_e)$$ (2.2)

where k_f and 1/n are Freundlich constants and they are related with adsorption capacity and adsorption intensity, respectively [19]. The initial concentrations of TC were varied and adsorbent dose was the same in order to determine the equilibrium isotherms.

The Langmuir model supposes that adsorption of TC happens on the homogeneous surface by monolayer adsorption instead of interaction between adsorbed ions [20]. The model is described in the following equation form [21]:

$$q_e=q_{\max }\frac{K_L{C}_e}{1+K_L{C}_e}$$ (2.3)

The above equation can be also linearized by the following process:

$$\frac{1}{q_e}=\frac{1}{q_{\max }{K}_L}·\frac{1}{C_e}+\frac{1}{q_{\max }}$$ (2.4)

where q_e denotes the amount adsorbed at equilibrium and was calculated based on Eq. (1).

q_max is the Langmuir constant, which is equal to the adsorption capacity. The parameter K_L represents the Langmuir adsorption equilibrium constant and C_e is the equilibrium concentration.

The adsorption of TC could also be described by the Dubnin–Radushkevich (D–R) isotherm. The equation was as follows [22]:

$$\ln q_e=\ln q_m-K{\epsilon }^2$$ (2.5)

where q_m is the theoretical saturation capacity (mg/g), K is the constant related to the mean free energy of adsorption, and ε is the Polanyi potential ($\epsilon =\mathit{RT}\ln \left(1+\frac{1}{C_e}\right)$). The D–R constant can give the valuable information regarding the mean energy of adsorption by the following equation:

$$E={(2K)}^{-1/2}$$

2.6. Adsorption kinetics

The batch adsorption experiments were carried out at different initial concentrations 50,100 and 150 mg/L, respectively. The10 mL TC solution was mixed with 0.004 g A-MCM-41 in a 50 mL beaker. The beaker sealed with aluminum foil was continuously stirred (250 rpm) at initial pH 7.0 and temperature of 303 K. At selected time intervals (0.33, 0.66, 1, 1.33, 1.66, and 2.0 h), centrifuge tubes were centrifuged. Then, 1 mL of sample solutions was taken out and filtered through the 0.45 μm membrane filter to analyze the current TC concentration. Meanwhile, the same volume of water with pH 7.0 was added into the bulk solutions to keep the volume constant. Parallel experiments were conducted without mesoporous sieve (blank).

The adsorption kinetics can be judged by the pseudo-first-order model, pseudo-second order model, Intra-particle diffusion model. The equations of adsorption kinetics are as follows [23]:

$$\text{The pseudo-first-order model}\ln (q_e-q(t_i))=\ln q_e-k_{1}t$$ (2.6)

$$\text{The pseudo-second-order model}\frac{t}{q(t_i)}=\frac{1}{k_2{q}_e^2}+\frac{t}{q_e}$$ (2.7)

$$\text{Intra-particle diffusion model}q(t_i)=k_3{t}^{1/2}+C$$ (2.8)

where k₁ (1/min) is the adsorption rate constant of pseudo-first-order equation. k₂ (g mg⁻¹ min⁻¹) is the rate constant of pseudo-second-order equation. k₃ (mg g⁻¹ min^1/2) is the intra-particle diffusion rate constant and C (mg/g) is a constant that is about the thickness of the boundary layer. q_e and q(t_i) (mg/g) are the amount of A-MCM-41 adsorbed at equilibrium and at time t, respectively. The amount of adsorption at equilibrium q_e was calculated based on Eq. (1). The adsorption of TC at time t_i, q(t_i) (mg/g) was calculated from the equation as follows:

$$q(t_i)=\frac{(C_0-C_{\mathit{ti}})V_0-{\sum }_2^{i-1}{\mathit{Ct}}_{i-1}{V}_s}{m}$$

where C₀ and C_ti (mg/L) are the initial TC concentration and the TC concentration at time t_i, respectively. V₀ and V_s (L) are the volume of the bulk TC solution and the volume of the sample taken out every time for current TC concentration analysis, respectively. V_s is 1 mL. m (g) is the mass of the A-MCM-41.

2.7. Fixed-bed column experiments

Fixed-bed column experiments were used to investigate the removal of TC from water in the A-MCM-41 fixed-bed system.

A glass column of 12 cm length and 1 cm internal diameter was used to contain A-MCM-41 as a fixed-bed absorber. Fig. 1 shows the schematic flow sheet of fixed-bed column setup. The bed was supported and closed by glass wool and glass beads for good liquid distribution. The column was equipped with water baths to keep the test temperature constant at 303 K. Subsequently, the column was rinsed with distilled water and left overnight to ensure a closely packed arrangement of particles without voids, channels, or cracks. A peristaltic pump was connected at the top of the column (inlet) to regulate the flow rate. After the column system was packed, a TC solution was continuously injected to column and effluent samples collected at fixed intervals. The concentration of TC in the column effluent was then measured with HPLC and breakthrough curves built with this information. The experiment was terminated until the effluent concentration matched the initial concentration. All the column adsorption studies were performed in duplicate. The weight of adsorbent was 30, 60 and 100 mg, with corresponding bed depth of 3, 6, and 10 cm, respectively. The concentration of TC solutions was approximately 400 mg/L (pH = 7.0) and the flow rate was 1 mL/min. The amount of adsorption in column was calculated according to Eq. (2) [24] as follows:

$$q=\frac{C_0{V}_B{N}_e-V_B{\int }_0^{N_t}{C}_B{\mathit{dN}}_t}{m}$$ (2)

where C₀ and C_B (mg/L) are the initial TC concentration, and TC concentrations at a certain bed volume number, respectively; V_B (mL) is the bed volume; N_t is the bed volume number at time t (min); N_e is the bed volume number after reaching adsorption equilibrium; and m (g) is the mass of adsorbent.

2.8. Column regeneration and recycling

The A-MCM-41 fixed-bed column was used to evaluate bed regeneration and recycling efficiency. Experimental conditions of the selected column included: adsorbent dosage of 70 mg, bed depth of 10 cm, TC initial concentration of 400 mg L⁻¹ and flow rate of 1 mL min⁻¹.

To regenerate the column, the EDTA-Mcillvaine solution was injected to the fixed-bed columns until TC concentrations reached below the detection limit. Effluent samples were collected and analyzed using the same protocol as that in the column filtration experiment. The regeneration recycling was used to evaluate the viability of reuse of the A-MCM-41 fixed-bed column. After regeneration of the column, column adsorption and sample analysis were carried out under the same conditions. The regeneration was recycled up to five times and column capacity at each reuse cycle was determined. All the column regeneration and recycling studies were performed in duplicate.

3. Results and discussion

3.1. Characterization of mesoporous adsorbent

3.1.1. X-ray diffraction

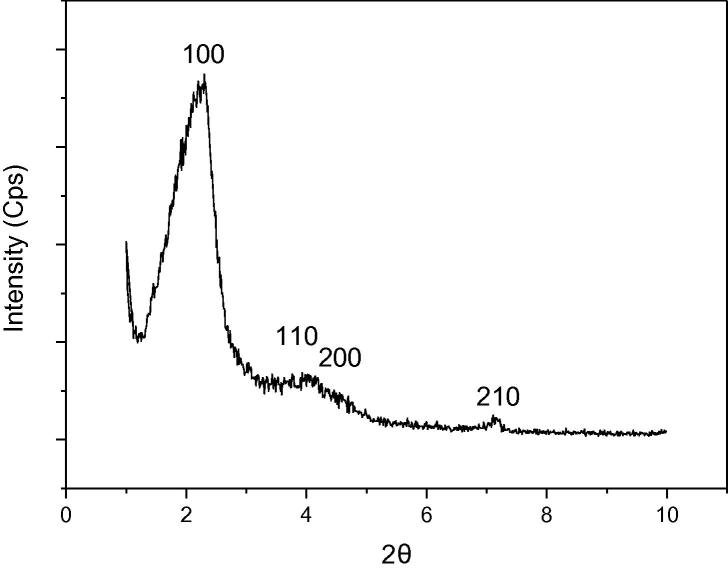
The XRD pattern of the A-MCM-41 is shown as Fig. 2. It demonstrated that the A-MCM-41 has the typical long-range ordered hexagonal mesoporous structure. The structure can be verified by the observation of four distinct diffraction peaks indexed as (1 0 0), (1 1 0), (2 0 0), and (2 1 0) in the low 2θ region [25]. In addition, the interplanar distance of the sample is 5.29 nm. The hexagonal unit cell parameter a₀ = 2d₁₀₀/1.732 of the sample is 6.11 nm.

Fig. 2.

XRD pattern of sample.

3.1.2. N₂ adsorption–desorption isotherm

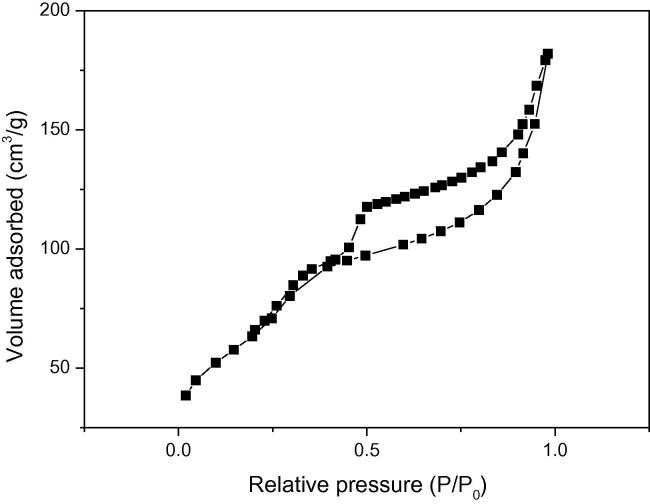
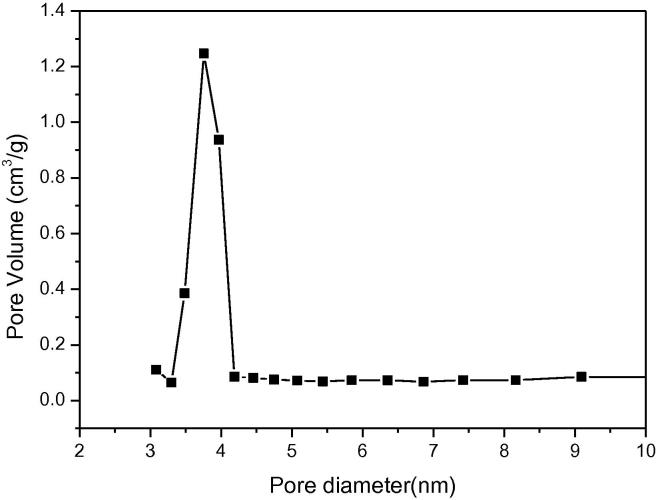
Nitrogen adsorption–desorption isotherms of the sample is illustrated in Figs. 3a and 3b. There is a deep inflection of the A-MCM-41 between relative pressure P/P₀ = 0.5 and 1.0. It demonstrated that it has the uniformity of the pores distribution due to characteristics of capillary condensation [26]. There are microporous structures in sample because the slope is at very low relative pressure. The BET surface area of molecular sieve is around 485 m²/g, and the BJH mean pore diameter is 4.60 nm. The formula T = a₀ − d_BJH calculate the pore wall thickness, and the a₀ is the hexagonal unit cell parameter. The d_BJH denotes the mean pore diameter. Thus, the pore wall thickness is 1.51.

Fig. 3a.

N₂ adsorption–desorption isotherm of sample.

Fig. 3b.

BJH pore size distribution curve of sample.

The pore distribution of molecular sieve is presented in Fig. 3. The result verified that the pores of 4 nm diameter occupied most part of pore volume of the sample. Additionally, it showed that pores of the sample are very uniform.

3.1.3. FTIR spectroscopy

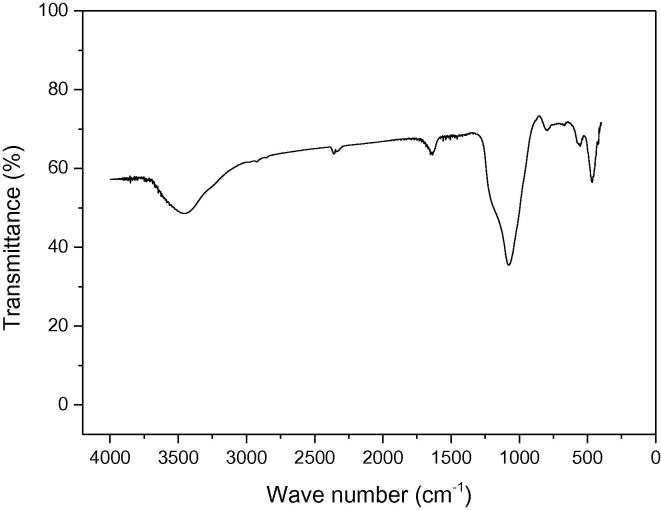
The FTIR spectrum of the molecular sieve is illustrated in Fig. 4. The vibrational band around 465 cm⁻¹ means the zeolite A is distributed in the silica framework of the molecular sieve and it is assigned as characteristic of 5-ring and 6-ring T–O–T (T can be Si or Al) in the pore walls [27]. The vibrational bands at 1087 and 465 cm⁻¹ are attributed to the characteristic silica framework in MCM-41 [28]. The band around 1634 cm⁻¹ is attributed to the characteristics of water molecules inside the framework, and the bands around 3445 cm⁻¹ correspond to OH^- groups from water molecules [29]. This illustrated that the sample is hydrophilic and it adsorbs some water when it is exposed to the air.

Fig. 4.

FT-IR spectrum of sample.

3.1.4. ²⁹Si and ²⁷Al MAS-NMR

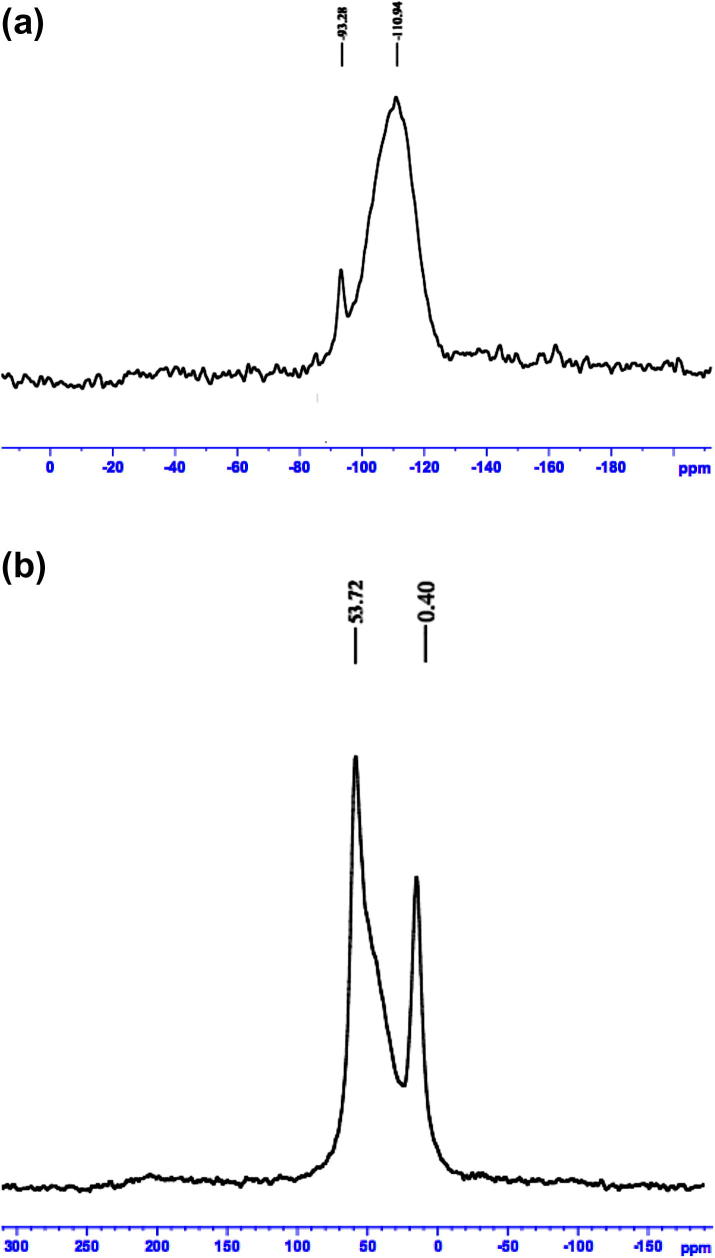
The ²⁹Si and ²⁷Al MAS-NMR spectrum of A-MCM-41 are presented in Fig. 5. From the ²⁹Si MAS-NMR spectra of the sample, ²⁹Si MAS-NMR spectra contain two signals at −93 and −110 ppm. In addition, the signal at −93 ppm and the little broad (right side) signal at −110 ppm can be decomposed three resonance peaks. Three peaks mean three structures of silicon atoms from left to right side. These structures are indexed as Q², Q³, and Q⁴ according to the Qⁿ = Si [nSi, (4-n) OH], or Si [nSi, (4-n) Al], n = 1–4 [24]. Q⁴:Q³ of A-MCM-41 was about 10.36.

Fig. 5.

²⁹Si MAS-NMR (a) and ²⁷Al MAS-NMR (b) spectra of HMAS.

Fig. 5b shows the Al coordination state of A-MCM-41 sample measured by the solid-state ²⁷Al MAS NMR. Two NMR peaks at 53.72 ppm and 0.40 ppm are observed in Fig. 5b. The peak at 53.72 ppm is attributed to aluminum species bound to four –O–Si groups covalently in tetrahedral framework and a portion of silicon in the framework was replaced by aluminum. In addition, the peak at 0.40 ppm is attributed to aluminum species in hexahedral framework and these aluminum species were extra-framework. Aluminum species in hexahedral framework generate strong acid sites and make A-MCM-41 have ion exchange capacity. As shown in Fig. 5b, some aluminum species of A-MCM-41 are in tetrahedral framework and other aluminum species are in hexahedral framework of zeolite A units which were dispersed in the pore wall of A-MCM-41.

3.1.5. Transmission electron microscope (TEM) image

The TEM image of the molecular sieve is shown as Fig. 6. The TEM image of the sample confirms that the material possesses uniform pores. The mesoporous pores distributed uniformly in the sample.

Fig. 6.

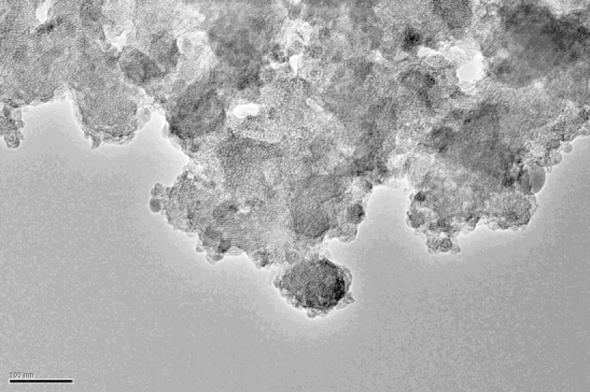
TEM image of the HMAS.

3.2. Adsorption studies

3.2.1. Untreated MCM-41 and the modified MCM-41

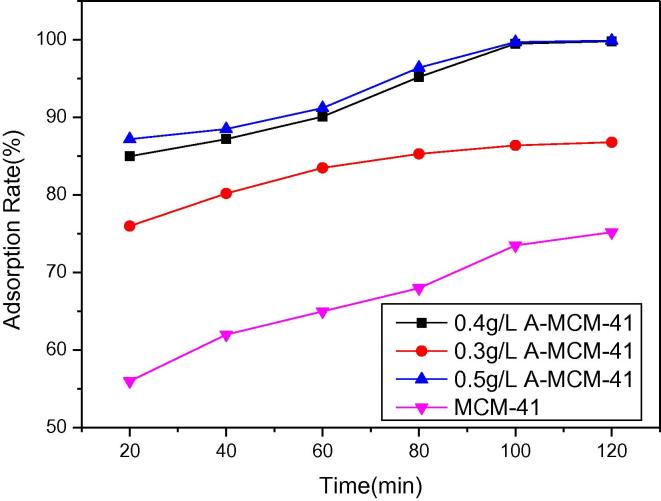
Fig. 7a shows the removal efficiency of TC with reaction time from 20 min up to 120 min under different dosages of A-MCM-41 and MCM-41. In order to investigate the removal of TC on MCM-41 and A-MCM-41, the batch experiments were carried out in 50 mL conical flasks. The 0.004 g of MCM-41 and 0.004 g of A-MCM-41 were mixed with 10 mL of the aqueous TC solutions, respectively. The beaker sealed with aluminum foil was continuously stirred (250 rpm) at initial pH 7.0 and the temperature of 298 K. The concentrations of TC aqueous solutions were 300 mg/L. After the reaction, the concentration of TC was determined by HPLC. Fig. 7a shows that the removal efficiency of TC increased with the amount of A-MCM-41 increasing from 0.003 g to 0.004 g. However, when the mass of A-MCM-41 increased from 0.004 g to 0.005 g, the removal efficiency of TC was the same. Thus, the optimum concentration of A-MCM-41 is 0.4 g/L when the TC concentration is 300 mg/L. At dosage of 0.4 g/L adsorbent, approximately 99% of TC was removed after 100 min. The removal efficiency of TC increased with A-MCM-41 dosage increasing. No decrease of TC concentration was observed in the control batch reactor containing 300 mg/L TC. The TC removal efficiency of TC by 0.4 g/L A-MCM-41 is much better than that by 0.4 g/L MCM-41.

Fig. 7a.

Adsorption rates of TC by (0.3 g/L, 0.4 g/L, 0.5 g/L) A-MCM-41 and 0.4 g/L MCM-41(initial concentration of TC, 300 mg/L; temperature, 303 K).

Thus, the following study was carried out with the modified MCM-41 as TC adsorbent due to the high efficiency of TC adsorption compared to the untreated MCM-41.

3.2.2. Effect of contact time on adsorption of TC

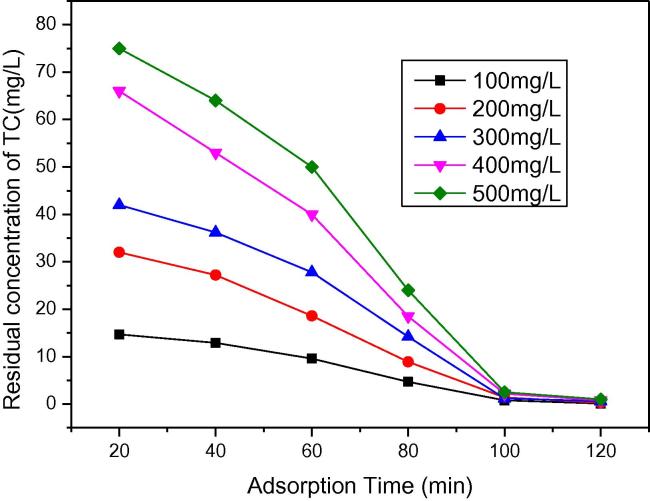
The contact time is one of the significant factors on adsorption efficiency. The effect of contact time on the adsorption of TC is shown in Fig. 7b. It is evident that time has significant influence on the adsorption of TC. The removal of TC was considerable after 100 min in the shaker and the equilibrium was also attained. Thus, the optimum contact time of 100 min could be considered for optimum adsorption of TC on A-MCM-41. The amount of TC removed increased with the increase of initial TC concentration and then reached equilibrium after 100 min. The removal of TC happened immediately at first due to the enough reactive sites available on the surface of A-MCM-41. After 100 min, when most of reactive sites were occupied, TC adsorption proceeded with very slow speed. Therefore, it is concluded that the removal rate of TC was limited because of the lake of reactive adsorption sites. Besides it, all following studies were carried out for 2.5 h duration due to obtain the optimum equilibrium results.

Fig. 7b.

Effect of initial TC concentration on the removal efficiency (dosage of A-MCM-41, 0.4 g/L; temperature, 303 K).

3.2.3. The effect of initial TC concentration

Initial concentration is one of the effective factors on adsorption efficiency. The effect of initial TC concentration on the removal of TC is shown in Fig. 7b. It showed that when the amount of molecular sieve was 0.004 g, the adsorption percentage was kept above 99% at different TC concentration. Besides it, the adsorption rate did not decrease dramatically with increasing the TC concentration and the residual TC concentration was below 1 mg/L. It may be because higher initial adsorbate concentration provided more driving force to overcome various mass transfer resistances of TC ions from the aqueous to the solid phase. Thus, the uptake of TC increased with the initial concentration of TC increasing.

3.2.4. Effect of pH

From Fig. 7c, the protonation–deprotonation transition of functional groups of TC results in the change of chemical speciation for ionizable organic compounds due to the variation of pH [28]. In addition, pH of the solution determines the different charges of TC on different sites. TC changes into a cation $({\text{TCH}}_3^{+})$ by the protonation of dimethyl-ammonium group at the pH of below 3.3. TC keeps the chemical speciation as a zwitterion $({\text{TCH}}_2^0)$ through the loss of a proton from the phenolic diketone moiety when pH is between 3.3 and 7.7. Besides it, TC transforms into anion (TCH⁻ or TC²⁻) by losing protons from the tri-carbonyl system and phenolic diketone moiety when pH is more than 7.7 [29].

Fig. 7c.

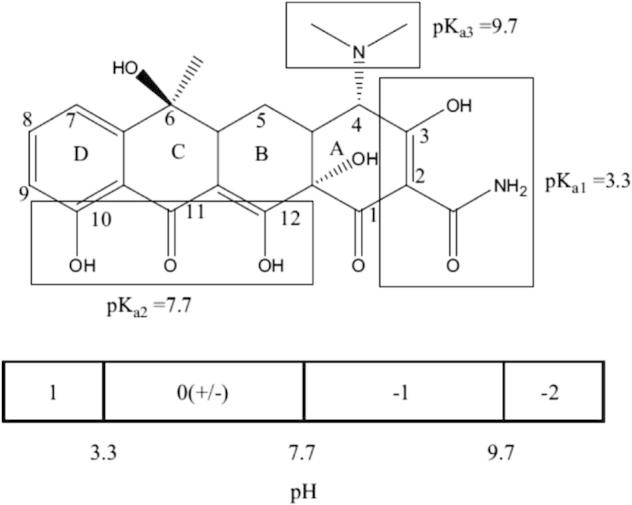
Structure of tetracycline (TC) and the pH-dependent speciation of tetracycline (TC) [28].

The pH of solution is one of the most important parameters affecting the adsorption process. Solutions were prepared at different pH values (3.0, 7.0, 8.0, and 10.0) in order to determine the effect of pH on adsorption capacity of A-MCM-41. The influence of pH on the adsorption of TC at the initial concentration of 100 mg/L is illustrated in Fig. 5c. From Fig. 7d, it is illustrated that the removal efficiency of TC was approximately 100% at pH 3.0 and pH 7.0. However, the adsorption rate of TC decreased to 85% and 75%, respectively. Thus, the TC solution without pH adjusting was appropriate and the removal of TC by A-MCM-41 was very efficient at both acidic and neutral pH.

Fig. 7d.

The adsorption rate of TC at different pH.

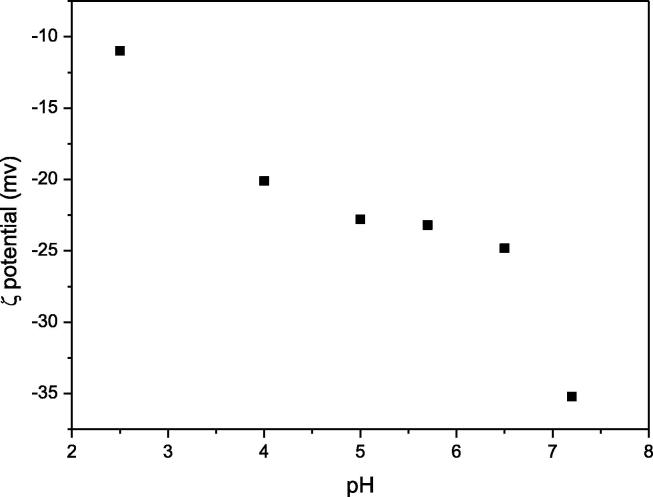
The zeta potential of A-MCM-41 is shown in Fig. 7e. The zeta potential of A-MCM-41 shows that when the pH ranges from 2 to 8, the surface of adsorbent is negative. When pH is below 3.3, ${\text{TCH}}_3^{+}$ is the main TC species in the solution and the surface of A-MCM-41 is negative. ${\text{TCH}}_3^{+}$ can be adsorbed on A-MCM-41 and it is beneficial for ion exchange between ${\text{TCH}}_3^{+}$ and the adsorbent. ${\text{TCH}}_2^0$ is the predominant TC species and A-MCM-41 surface is negative at pH between 3.3 and 7.0. ${\text{TCH}}_2^0$ with no charge can be adsorbed on negative surfaces of A-MCM-41. When pH is above 7.7, TCH⁻ and TC²⁻ are the main TC species in the solution and the surface of A-MCM-41 is negative too. Thus, TCH⁻ and TC²⁻ cannot be adsorbed on the adsorbent due to the electrostatic repulsion. It is the reason that the removal efficiency of TC decreased from 90% to 70% when the pH increased from 7.0 to 8.0 (see Fig. 7d).

Fig. 7e.

Zeta potential of A-MCM-41 at different pH of solution.

Fig. 7f.

Proposed mechanism of zeolite A impregnated into MCM-41 and TC adsorption on A-MCM-41 .

The adsorption mechanism is analyzed from ²⁷Al MAS-NMR and zeta potential of A-MCM-41. After zeolite A was impregnated into the porous walls of MCM-41, the unsaturated negative charge surface environment generated because some ions of Si⁴⁺ were instead by Al³⁺ in the pore skeleton. The sodium ion is very active in the A-MCM-41 framework. When pH is below 3.3, ${\text{TCH}}_3^{+}$ is the main TC species in the solution and the surface of A-MCM-41 is negative. According to the fundamental of ion exchange between solid and liquid phases, the ion exchange process between A-MCM-41 and ${\text{TCH}}_3^{+}$ ion in the aqueous TC solution can be expressed by the following equation.

$$\text{A-MCM-}41\text{-}{\text{Na}}^{+}+{\text{TCH}}_3^{+}\leftrightarrow \text{A-MCM-}41\text{-}{\text{TCH}}_3+{\text{Na}}^{+}$$

The A-MCM-41 removed TC through both ion exchange and electrostatic interaction. The mechanism of zeolite A impregnated into MCM-41 and TC adsorption on A-MCM-41 was illustrated as Fig. 7f.

3.3. Adsorption isotherms

The equilibrium isotherm was fundamental in describing the interactive behaviors between the solutes and adsorbents. The adsorption isotherms for TC onto A-MCM-41 at varied temperatures were presented in Table 1, respectively. Four isothermal adsorption equilibrium equations, Langmuir and Freundlich and D–R model were applied to fit the adsorption data, respectively. The fitted parameters were all listed in Table 1. These models are the most common isotherms for determining adsorption phenomena.

Table 1.

The parameters of isotherm models of TC adsorption onto A-MCM-41.

T (K)	Freundlich			Langmuir			D–R
	kf	n	R2	qmax (mg/g)	KL (L/mg)	R2	qD (mg/g)	E (kJ/mol)	R2
303	368.58	1.54	0.890	415.1	1.868	0.981	365.45	9.53	0.865
313	364.21	1.34	0.851	417.5	2.356	0.986	372.54	10.32	0.871
323	362.15	1.43	0.812	419.3	7.26	0.980	375.41	10.21	0.828

The parameters of isotherm models were calculated according to plots of log C_e versus log q, 1/C_e versus 1/q_e and ${\left[\ln \left(1+\frac{1}{C_e}\right)\right]}^2$ versus ln q_e. The regression coefficients R² of isotherms models were evaluated whether the experimental data were fitted to the Freundlich, Langmuir and R–D isotherms models.

From Table 1, it was found that the correlation coefficients R² of the linear form for Langmuir model were much closer to 1 than that of other models. It was indicated that Langmuir model was much better than other models to describe TC adsorption onto A-MCM-41. Langmuir model is based on the idealized assumption of identical adsorption heat and monolayer adsorption. It means that the monolayer coverage of TC on the surface of A-MCM-41. As shown in Table 1, the TC maximum adsorption capacity on A-MCM-41 is 419 mg/g. The obtained q_m value for A-MCM-41 material compare favorably with those using other adsorbents (Table 2). These results suggested that A-MCM-41 was effective for TC removal.

Table 2.

Maximum adsorption capacity (q_m) of various adsorbents for tetracycline.

Adsorbent	qm (mg g−1)	Refs.
Single-walled carbon nanotubes	340	[34]
Multi-walled carbon nanotubes	269.54	[28]
Montmorillonite	84	[30]
Rectorite	140	[29]
Graphene oxide	313	[31]
Smectite	462	[32]
Magnetic resin Q100	283	[33]
A-MCM-41	419	This study

In addition, the correlation coefficients R² of the Freundlich model was around 0.85. The Freundlich model was applied to describe heterogeneous system and was not restricted to formation of the monolayer. Thus, it was also illustrated that TC adsorption behaviors followed monolayer adsorption.

The values of E and q_D for the D–R isotherm model were calculated from the plot of [ln(1 + 1/C_e)]² versus ln q_e and presented in Table 1. The adsorption process will occur by chemical ion exchange if E value is between 8 and 16 kJ/mol. In addition, the adsorption will be physical type if E is less than 8 kJ/mol [30]. Thus, the process of TC adsorption involves the chemical ion exchange mechanism. The value of E is more than 8 kJ/mol according to the Eq. (2.5). The mean adsorption energy for TC was presented in Table 1. The values were all higher than 8.0 kJ/mol. It suggested that TC adsorption behaviors for A-MCM-41 were chemical adsorption. It is consistent with the mechanism of TC adsorption.

3.4. Adsorption kinetics

The uptake rate of TC and the reaction time are described by different models of adsorption kinetics. The adsorption kinetics models contain some equations such as pseudo-first order, pseudo-second order and intra-particle diffusion model. The experimental results of TC adsorption on A-MCM-41 versus time at different initial TC concentrations were shown in Table 3.

Table 3.

The kinetics model and intraparticle diffusion information of TC adsorption onto A-MCM-41.

Kinetic models	Parameters	C0 (mg/L)
		50	100	150
Pseudo-second-order parameters	qe (mg/g)	125	250	370
	K2 (1/min)	0.0139	0.0123	0.009
	R2	0.996	0.998	0.996
Intra-particle diffusion parameters	K3 (mg/g min1/2)	0.0851	0.1248	0.1542
	C (mg/g)	123.56	241.08	372.23
	R2	0.965	0.98	0.975

According to the Eq. (2.6), the plot of ln (q_e − q_t) versus time t did not show any linear relationship. it indicated that the adsorption kinetics did not follow the pseudo-first order equation.

The second pseudo second-order equation is based on the proposition that the adsorption kinetics is linearly related with the square of the number of available sites [31]. According to the Eq. (2.7), the rate constant K₂ of the second-order kinetics model was obtained through making the plot of t/q_t versus t. From R² of the linear form for various dynamic models, pseudo-second order model was much better to describe the adsorption kinetics behaviors than pseudo-first order model. It also indicated that chemisorptions were the rate controlling mechanism for TC adsorption. These results were fully consistent with those drawn from adsorption mechanism mentioned above.

The intra-particle diffusion model was adopted to investigate the controlling mechanism involved in the TC adsorption process [32]. The parameters of intra-particle diffusion model are calculated by making the plot of contact time (0–2 h) versus the amount of TC adsorbed on A-MCM-41. The plot showed that the adsorption of A-MCM-41 achieved equilibrium after about 100 min. The values of K₃ were obtained from the plot of q_t versus t. As shown in Table 3, when the initial concentration of TC increased, the value of K₃ increased. It suggests that the adsorption rate of A-MCM-41 was enhanced as the initial TC concentration increasing. The largest value of C is obtained for TC adsorption on A-MCM-41 at initial TC concentration of 150 mg/L. It indicated that the boundary layer has the greatest influence on the adsorption of TC. In contrast, the value C at TC concentration of 50 mg/L was smallest. It demonstrated that the adsorption rate of TC on the A-MCM-41 was mainly controlled by intra-particle diffusion at initial TC concentration of 50 mg/L.

3.5. Column study

The column method is one of the most common methods of adsorbents applied to wastewater treatment. The effect of the bed height on TC adsorption was studied at 303 K. The initial TC concentration was 400 mg/L and the pH was 7.0. The bed height of the column was ranged from 3 to 10 cm. The typical breakthrough curves were shown in Fig. 8. It shows that TC was completely removed by A-MCM-41 at first. This process was prolonged with bed height increase. Subsequently, TC concentration of the effluent from column increased and finally reached adsorption equilibrium. According to Eq. (2), the amount of TC adsorbed in column q was calculated and presented in Table 4. The TC adsorption was proportional to the amount of adsorbents in column. The adsorption capacity increased at higher bed depths. It is because the contact time between influent and adsorbents was increased as the bed height increased at a constant flow rate.

Fig. 8.

The effects of bed height on TC adsorption at 303 K.

Table 4.

Thomas model parameters of various adsorbents for TC adsorption in fixed-bed systems at 303 K.

M (g)	Z (cm)	kTh (mL mg−1 min−1)	qTh (mg/g)	R2	qa (mg/g)
0.02	3	0.062	388.5	0.9929	382.0
0.04	6	0.056	391.7	0.9985	388.5
0.07	10	0.057	412.7	0.9986	419.0

^aq is calculated according to the Eq. (2).

The Thomas kinetic model was used to calculate the data obtained in continuous fixed-bed systems for obtaining maximum solid phase concentration of TC on adsorbents and the adsorption rate constant [33]. Thomas model is the one of the most popular models in column performance theory. Thomas model assumes adsorption–desorption fits Langmuir model and the adsorption kinetics rate obeys pseudo-second order reversible reaction kinetics [34]. The equation of Thomas model is shown as follows:

$$\frac{C_t}{C_0}=\frac{1}{1+\exp (k_{\mathit{Th}}/f(q_{\mathit{Th}}m-C_0{V}_{B}N))}$$ (3)

where k_Th (mL min⁻¹ mg⁻¹) is Thomas rate constant, q_Th (mg/g) is the theoretical saturate adsorption capacity in Thomas model, f (mL/min) is the flow rate of the effluent, m (g) is the mass of the adsorbent, V_B (mL) is the effluent volume, C₀ (mg/L) is the influent TC concentration, C_t (mg/L) is the effluent concentration at time t and N is the bed volume number. The kinetic coefficient K_Th and the adsorption capacity of the column q_Th can be calculated using non-linear regression and their parameters are listed in Table 4.

The parameters of the Thomas kinetic model were listed in Table 4. The theoretic curves at different bed heights were simulated by the Thomas kinetic model and fit the experimental data very well. In addition, the theoretic TC adsorptions q_Th were very close to the corresponding experimental ones at varied bed heights. It showed that Thomas model can be applied to describe TC adsorption in fixed-bed column of A-MCM-41. Besides, when the bed height increased, the rate constant K_Th decreased and the adsorption capacity increased. It was because that the higher bed depth made the contact time longer and the reaction rate slower. Based on Tables 1 and 3, the adsorption capacity in column study was consistent with that in batch test.

According to the Thomas model theory, the adsorption behavior of TC on A-MCM-41 in fixed-bed systems was Langmuir-type adsorption and followed pseudo-second order kinetics. It was fully consistent with the results in the batch studies.

3.6. Column regeneration and recycling

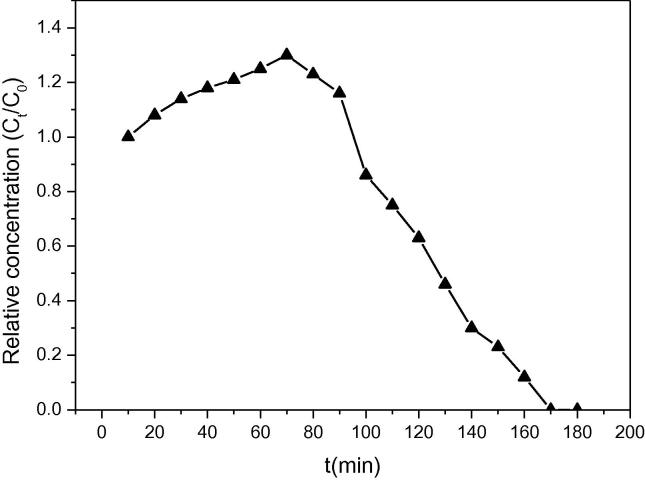
For the adsorption process to be viable, efficient regeneration and reuse of the A-MCM-41 bed is necessary. When the TC concentration (C_eff/C_inf) reached the value of 0.9 at the exhaust time, the A-MCM-41 bed was regenerated using the EDTA-Mcillvaine solution at flow rate of 1 ml/min. Fig. 9a shows the release curves of TC in the post-adsorption column during the regeneration process. It shows that the release of TC reached the maximum effluent concentration of 1.3 C/C₀ after 28 min of regeneration treatment. The mass recovery for the regeneration process was less than 100% for A-MCM-41 at each regeneration cycle. It suggests that some parts of A-MCM-41 were strongly and irreversibly bonded by the TC antibiotic at each regeneration cycle. The regeneration of A-MCM-41 fixed-bed column is expected to reduce the blocking of pores after TC adsorption and enabling the penetration of TC ions into pores after regeneration. However, some adsorption sites on A-MCM-41 were irreversibly bonded by the TC ions. It caused some adsorption sites not available for TC adsorption and caused a decrease of adsorption capacity after regeneration.

Fig. 9a.

Release of TC from the post-adsorption A-MCM-41 fixed-bed column during regeneration.

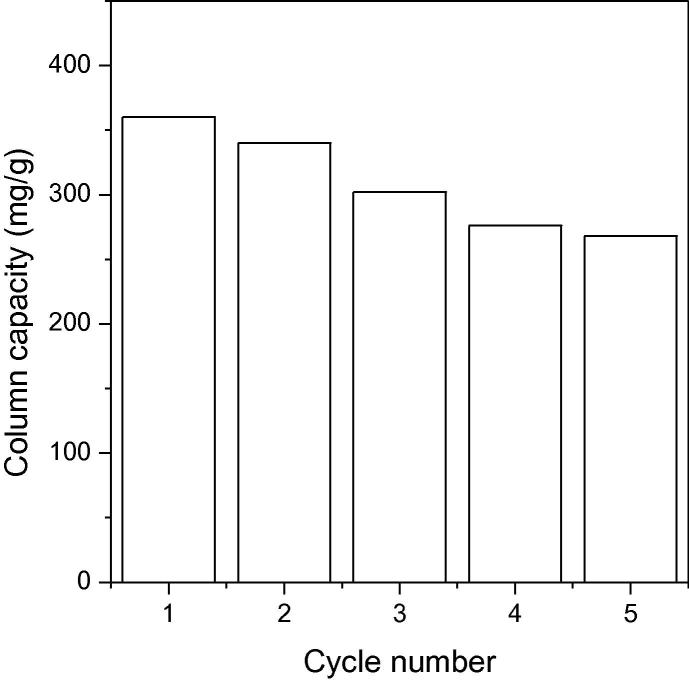
Fig. 9b presents the change of column capacity for five consecutive regeneration cycles. As shown in the figure, column capacity decreased after regeneration from 360 mg g⁻¹ to 268 mg g⁻¹ for A-MCM-41. The reduced column capacity may be due to decreased available adsorption sites and repulsion by the irreversibly adsorbed antibiotics from previous cycles. Therefore, the adsorption capacity of the fixed-bed column decreased after each adsorption-regeneration cycle. However, the fixed-bed column continued to have an acceptable capacity to remove TC from aqueous solutions after regeneration.

Fig. 9b.

Relationship between changes in column capacity (mg g⁻¹) of TC for five fixed-bed regeneration cycles. Adsorption conditions were conducted consistently for 10 cm bed depth, TC initial concentration of 400 mg L⁻¹, and 1 mL min⁻¹ flow rate.

4. Conclusion

Based on the experimental results in both batch and column studies, A-MCM-41 was proved to be an effective adsorbent for removal of TC from aqueous solutions. The adsorbent A-MCM-41 was produced through MCM-41 impregnated with A zeolite precursors. A-MCM-41 showed very high efficiency for removing TC compared to the untreated MCM-41. The batch experimental results showed that TC adsorption was pH dependent. Adsorption isotherm was well fitted by Langmuir model. The kinetics of TC adsorption was well described by both pseudo-second order and intra-particle diffusion model. Thomas model was suitable to describe TC adsorption in a fixed-bed column system. In conclusion, the adsorption behaviors were both the chemical adsorption with an ion exchange process and electrostatic adsorption. All in all, impregnation with zeolite A is a very suitable method for improving MCM-41 adsorption of TC.