Continuity of Genetic and Environmental Influences on Cognition across the Life Span: A Meta-Analysis of Longitudinal Twin and Adoption Studies

Abstract

The longitudinal rank-order stability of cognitive ability increases dramatically over the lifespan. Multiple theoretical perspectives have proposed that genetic and/or environmental mechanisms underlie the longitudinal stability of cognition, and developmental trends therein. However, the patterns of stability of genetic and environmental influences on cognition over the lifespan largely remain poorly understood. We searched for longitudinal studies of cognition that reported raw genetically-informative longitudinal correlations or parameter estimates from longitudinal behavior genetic models. We identified 150 combinations of time points and measures from 15 independent longitudinal samples. In total, longitudinal data came from 4,538 monozygotic twin pairs raised together, 7,777 dizygotic twin pairs raised together, 34 monozygotic twin pairs raised apart, 78 dizygotic twin pairs raised apart, 141 adoptive sibling pairs, and 143 non-adoptive sibling pairs, ranging in age from infancy through late adulthood. At all ages, cross-time genetic correlations and shared environmental correlations were substantially larger than cross-time nonshared environmental correlations. Cross-time correlations for genetic and shared environmental components were low during early childhood, increased sharply over child development, and remained relatively high from adolescence through late adulthood. Cross-time correlations for nonshared environmental components were low across childhood and increased gradually to moderate magnitudes in adulthood. Increasing phenotypic stability over child development was almost entirely mediated by genetic factors. Time-based decay of genetic and shared environmental stability was more pronounced earlier in child development. Results are interpreted in reference to theories of gene-environment interaction and correlation.

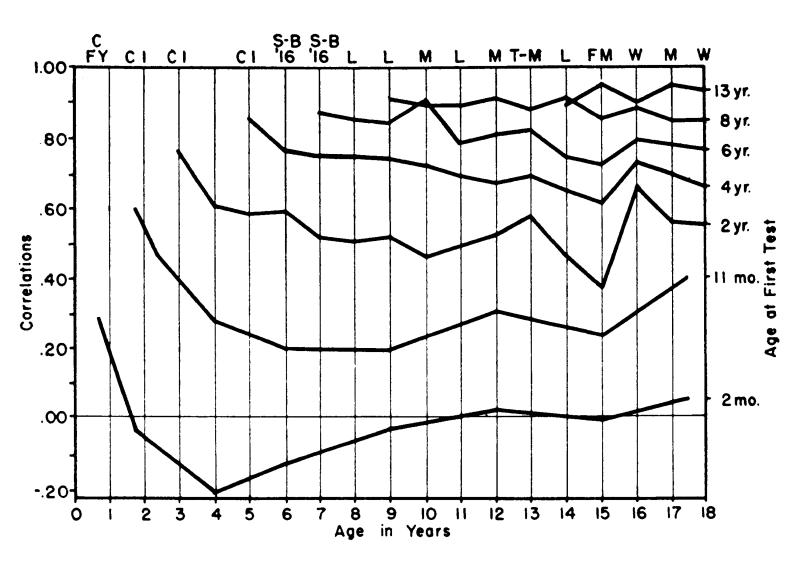
Average levels of cognitive ability change dramatically over the course of development, with impressive increases from infancy through childhood and adolescence, and gradual decreases during adulthood (Jones & Conrad, 1933; McArdle, Ferrer-Caja, Hamagami, & Woodcock, 2002; Tucker-Drob & Salthouse, 2011). Moreover, individual differences in cognitive ability undergo dramatic changes in rank-order stability over development (Bayley, 1949). When measured in infancy, individual differences in cognition are so unstable over time, that many have questioned the value of its measurement. Eschewing the view that intelligence is “inherited, or at least innate, not due to teaching or training,” (Burt, 1934, as cited in Lewis & McGurk, 1972), Lewis and McGurk (1972) wrote, “It is a sine qua non of this view that measures of intelligence have high predictive validity from one age to another. Such validity is singularly lacking in every scale used to assess intelligence during infancy” (p. 1174). They concluded that “infant intelligence scales are invalid as measures of future potential” (p. 1175). By middle childhood, individual differences in cognition become impressively stable. Based on results from a longitudinal study following individuals from age 11 to 87 years, one of the longest longitudinal studies to date, Gow et al. (2011) concluded that “childhood cognitive ability is by far the largest independent predictor of the level of cognitive ability in later life” (p. 238). By early adulthood, individual differences in cognition become so stable that some have argued that virtually no reordering occurs whatsoever. Based on results of a longitudinal study of general cognitive ability (g) that followed participants from age 20 years to 38 years, Larsen, Hartmann, & Nyborg (2008) concluded that “g measured in early adulthood predicts this very ability later in life with a precision that equals the reliability of the tests”(p. 33). One of the first reports of these dramatic increases in longitudinal stability from infancy through adolescence was by Bayley (1949) whose main findings are reproduced in Figure 1, which plots raw test-retest stability coefficients for intelligence by age, stratified by age at first testing. Also apparent in Bayley’s (1949) data is a modest degree of temporal decay of stability that diminishes with age.

Figure 1.

“Age curves of correlation coefficients between scores on selected initial tests and subsequent tests given at yearly intervals.” The x-axis (bottom) indicates participant age, and the y-axis (left) indicates the longitudinal test-retest correlation. The labels at the right indicate the age at first measurement for each corresponding connected line. From N. Bayley (1949). Consistency and variability in the growth of intelligence from birth to eighteen years. The Pedagogical Seminary and Journal of Genetic Psychology.

What are the mechanisms that underlie continuity (i.e. stability) of individual differences in cognition over time, and which of these mechanisms accounts for the dramatic increases in continuity over development? Some researchers (e.g., Sameroff, Seifer, Baldwin, & Baldwin, 1993) have suggested that the stability of individual differences in cognition over time results from the consistent exposure to the same exogenous environments over time; i.e. that stability of cognition results from stability of social, educational, and economic contexts. Others (e.g. Dickens & Flynn, 2001; Conley, 1984) have suggested that the stability of individual differences in cognition over time results from the continuous effects of endogenous factors, such as genes, and that exogenous experiences tend to be nonrecurring and produce effects that decay quickly over time. Exogenous and endogenous factors may both contribute to overall stability to varying extents, and it is possible that their relative contributions may change with age. The current article makes use of meta-analysis of longitudinal behavioral genetic studies to examine these issues. In the following sections, we review theories of developmental continuity and change, and discuss the relevance of questions concerning the genetic and environmental processes underlying cognitive stability and instability to broader questions of how genes and environments combine to influence individual differences in cognition. We then provide an overview of longitudinal behavioral genetic models, describe the specifics of our meta-analysis, report our results, and discuss their implications for theories of gene-environment coaction during cognitive development.

Theories of Developmental Continuity and Change

There are a number of theoretical perspectives on cognitive development that are relevant to the question of the continuity of genetic and environmental contributions to cognition. We describe these theories in this section, proceeding roughly from the simple theories to the more complex and dynamic: (1) genetic set-point / genetic canalization; (2) lasting effects of experience / experiential canalization; (3) stability of experience; (4) gene-environment interactions; (5) gene-environment transactions; (6) embedded dynamism.

Genetic Set-Point / Genetic Canalization

Perhaps the hypothesis most consistent with lay theories or definitions of intelligence is what might be termed a genetic set-point hypothesis. This hypothesis holds that, excepting for measurement error, short term non-systematic fluctuations in performance, and instances of neurological trauma and severe privation, (a) ability phenotypes are synonymous with ability genotypes, (b) that these same genotypes determine ability levels throughout child development and adulthood, and (c) that although normative development will entail absolute changes in cognitive performance, these changes occur uniformly throughout the entire ability distribution such that they do not result in an appreciable re-ordering of individuals over time. This perspective, namely that cognition “is stable—that is, it is determined by our genes and largely impervious to environmental influences” is what the popular science writer Malcolm Gladwell (The New Yorker, 12/17/2007) has characterized as a core tenet of “I.Q. fundamentalists.” The genetic-set point hypothesis shares a number of core features with the genetic canalization hypotheses that emerged in the mid-twentieth century, which hold that natural selection produces genotypes that buffer developing organisms against environmental heterogeneity. According to such hypotheses, a given genotype responds dynamically to varying experiential inputs encountered over the course of development to produce a relatively constant phenotypic end state (Waddington, 1942; Conley, 1984).

Lasting Effects of Early Experience / Experiential Canalization

A hypothesis that offers an altogether separate mechanism for stability of individual differences in cognitive ability holds that early experiences have persistent effects on cognition. This hypothesis is consistent with a number of related perspectives that posit critical or sensitive periods of development including life history theories, fetal programming theories, and developmental cascade theories. For instance, fetal programming theory contends that prenatal and neonatal environments, such as nutritional quality, have lasting effects on health and behavior by signaling to the organism what sorts of environments it should be prepared to encounter throughout its lifespan (Lucas, 2005). Developmental cascade theories posit that early learning confers skills that are foundational for later learning, such that differences in early cognitive performance have long lasting consequences for later performance (Duncan et al., 2007; Heckman, 2006; Knudsen, Heckman, Cameron, & Shonkoff, 2006; Rimm-Kaufman, 2004).

An illustrative, yet extreme, example of evidence indicating lasting effects of early environmental experience comes from a study of Romanian orphans (Nelson et al., 2007). Abandoned infants were randomly assigned either to remain in institutional care or to be placed in higher-quality foster care, typically before age 30 months. Deficits carried forward in time: never adopted children had IQ’s of 77 and 73, adopted children had IQ’s of 86 and 81, and a demographically matched comparison group had IQ scores of 103 and 109 at ages 42 and 54 months respectively. Another illustrative set of results was reported by Evans and Schamberg (2009). Using observational data, these authors found a significant relation between childhood poverty and adult working memory, which was mediated by a physiological composite index of allostatic load.

The experiential canalization hypothesis is not without its dissenters. Although a large body of observational data consistently indicates robust associations between quality of naturally occurring early life experiences and cognition across the lifespan (bolstered by a few notable randomized studies in which children were rescued from extremely severe privation and neglect), studies of interventions designed to boost cognition have been marked failures to evince lasting effects. In a comprehensive meta-analysis of early childhood intervention studies that used either randomized assignment or quasi-experimental methods, Leak, Duncan, Li, Schindler, & Yoshikawa (2010) found that the effects of early childhood intervention programs on cognition and achievement persisted at close to full strength for 1-2 years beyond their completion, but faded out over longer intervals. Even the randomized controlled study of the lauded Perry Preschool program, which indicated lasting program effects on numerous social and economic outcomes that persisted into adulthood, indicated complete fadeout of IQ gains by third grade (Schweinhart et al., 2005). Results of this sort have led a number of researchers to conclude that environmental influences on cognition are ephemeral, and are therefore unlikely to contribute meaningfully to stability of cognition over time.

Cross-sectional research from behavioral genetic studies has also provoked theoretical speculation about the durability of environmental influences, or lack thereof. Citing a vast array of studies that indicate that the nonshared environment (environmental influences on traits that serve to differentiate children from the same family) routinely accounts for approximately 40% or more of the variance in psychological outcomes, Plomin and Daniels (1987) asked “Why are children in the same family so different from one another?” They speculated that the answer is because of systematic effects of measured differences in their environments. However, a quantitative review by Turkheimer and Waldron (2000) indicated that only minute proportions of variation in psychological outcomes could indeed be accounted for by measurable differences in experiences. These results have led a number of researchers (e.g. Loehlin, 2007; Turkheimer, 2000) to speculate that the nonshared environment may include variance due to temporal trait fluctuation-i.e. true (internally consistent) psychological states that are short-lived, unpredictable, and either complex to the point of being empirically intractable, or entirely unsystematic. In other words, failures of measurable variables to account for psychological differences between siblings have led some researchers to suggest that the rather large differences between siblings result from little more than the short-term fluctuation of traits. If this is true, then it may indeed be no surprise that stable, measured aspects of the environment that siblings differentially experience are unable to account for much variation in behavioral outcomes.

Stability of Experience

A second environmentally-centered hypothesis holds that stability of individual differences in cognition results from stability of the exogenous determinants of ability. In other words, one possible contribution to stability of individual differences in cognition over time is that individuals are subjected to consistent social, educational, and economic contexts over long periods of time. These environmental contexts need not have effects that are particularly lasting; they simply need to recur consistently over time. This was the view championed by Sameroff et al. (1993), who wrote:

“The typical statistic reported in longitudinal research is the correlation between early and later performance of the children… The usual interpretation of such a number is that there is a continuity of competence or incompetence in the child. Such a conclusion cannot be challenged if the only assessments in the study are of the children. In [our study] we examined environmental as well as child factors… We found that the correlation between composite multiple risk scores at the two ages was… as great as or greater than any stability within the child. Those children had poor family and social environments when they were born (Sameroff, Seifer, Barocas, Zax, & Greenspan, 1987), still had them when they were 13, and probably would continue to have them for the foreseeable future.” (p. 95)

A variant of this hypothesis is that the environmental experiences that have the most appreciable effects on cognition are those that occur consistently over time. For instance, Brooks-Gunn & Duncan (1997) have reviewed evidence that environmental disadvantage compounds over time, such that poverty occurring over long durations (e.g. four or more years) produces more marked effects on cognition than shorter-term exposures to poverty. In the Romanian adoption study mentioned earlier, Nelson et al. (2007) found that infants who were randomly assigned to be adopted out of low quality orphanages at younger ages (i.e. those who spent less time in impoverished conditions) had less depressed the IQ scores than those randomly assigned to later adoption. Based on this duration hypothesis, the stability of environmental influences on cognition is nearly synonymous with the basic concept of environmental influence, in that the experiences most likely to affect cognition are precisely those that are most stable.

Genetic Differences in Sensitivity to the Environment: Gene × Environment Interaction

The theoretical perspectives reviewed thus far have all been similar to one another in that they conceptualize genetic and environmental influences as independent influences on cognitive development. Although conventional genetic perspectives and environmental perspectives do not necessarily conflict with one another –most allow genetic contributions and environmental contributions to stability of individual differences to sum together to determine overall phenotypic stability– none of the above reviewed perspectives directly addresses that possibility that the genetic and environmental mechanisms of cognitive development might interrelate and even interact in meaningful ways. Two such processes of gene-environment coactions are gene × environment interaction and gene-environment correlation. We discuss gene × environment interaction in this section and gene-environment correlation the next section. We note that these processes are not alternatives to one another or mutually exclusive in any sense.

Gene × environment interactions have been suggested as one possible resolution to the nature-nurture paradox: findings from twin and adoption studies have indicated that the effects of the shared environment (the resemblance between individuals who share common rearing experiences) decrease over development, whereas finding from studies of children rescued from poverty indicate large and lasting effects of improved rearing experiences (Turkheimer, 1991). If different people respond to the same rearing environment to differing extents as a systematic function genotypic variation, then individuals reared together may not resemble one another to an appreciable degree even though the rearing experience has true effects on them. Instead, the variation in cognitive performance associated with the shared rearing experience will be determined, in part, by genotype. Because the effect of the environment depends on genetic variation, individual differences in cognition become attributable to genetic variation as an end result. Indeed, gene × environment interactions for cognitive ability have been reported by a number of researchers (Harden, Turkheimer, & Loehlin, 2007; Rhemtulla & Tucker-Drob, 2012; Rowe, Jacobson, & Van den Oord, 1999; Scarr-Salapatek, 1971; Taylor, Roehrig, Soden-Hensler, Connor, & Schatschneider, 2010; Tucker-Drob, Rhemtulla, Harden, Turkheimer, & Fask, 2011; Turkheimer, Haley, Waldron, D’Onofrio, & Gottesman, 2003; for a review see Tucker-Drob, Briley, & Harden, 2013). If gene × (shared) environment interactions are either lasting or recurring, this would contribute to high stability of individual differences associated with genetic variation. In other words, genetic variation may account for continuity of individual variation if genetic effects present at early points in development modulate the magnitude of lasting or recurrent environmental effects. A complementary possibility is that experience-activated epigenetic processes are particularly robust over time. In other words, experiences “turn on” genes leading to heritable variation in cognition, and these genes remain “turned on” for extended periods of time.

Transactional Theories of Gene-Environment Correlation

Gene-environment correlation refers to the possibility that, rather than randomly experiencing different environments, individuals experience different environments as systematic functions of their genotypes. There are three such classes of mechanisms by which environments can come to be correlated with genotypes (Plomin, DeFries, & Loehlin, 1977). Passive gene-environment correlations occur when the rearing experiences that parents provide to their biological children are partly influenced by the same genes that the children have inherited from them. Evocative gene-environment correlations occur when children evoke or elicit experiences from others based on their genetically influenced characteristics and behaviors. Finally, active gene-environment correlations occur when children actively seek out and choose experiences on the basis of their genetically influenced preferences, motivations, and interests. Importantly, these received, evoked, and sought out experiences have the potential to have true causal effects on both cognitive development and on the noncognitive traits relevant to learning. Under transactional models (Bouchard, 1997; Hayes, 1962; Bronfenbrenner & Ceci, 1994; Collins, Maccoby, Steinberg, Hetherington & Bornstein, 2000; Scarr, 1997; Scarr & McCartney, 1983; Tucker-Drob, Briley, & Harden, 2013) a positive feedback process ensues in which child behaviors lead to experiences which reinforce those behaviors, which lead to further experiences. As Scarr & McCartney (1983, p. 425) have hypothesized, “the genotype is the driving force behind development, because, we argue, it is the discriminator of what environments are actually experienced.” Support for such processes is beginning to accumulate from a number of sources, including findings that environmental similarity covaries with genetic similarity (Kendler & Baker, 2007), and findings from cross-lagged analyses indicating reciprocal time-ordered relations between cognitive abilities and parenting (Lugo-Gil & Tamis-LeMonda, 2008; Tucker-Drob & Harden, 2012a) and between noncognitive traits and cognitive performance (Chamorro-Premuzic, Harlaar, Greven, & Plomin, 2010; Marsh, Trautwein, Lüdtke, Köller, & Baumert, 2005).

In their formalized transactional model, Dickens and Flynn (2001) have proposed that recurrence of environmental experience is a core necessity of cognitive development. Contrasting with the view that environmental influences represent little more than short term trait fluctuation, they have argued that environmental experiences have causal, albeit highly ephemeral, effects. Building on this assumption, they have argued that only environments that result from highly institutionalized processes (such as historical period, social class, or race/ethnicity) or from processes driven by endogenous (genetic) propensities are likely to recur often and systematically enough to have lasting effects on psychological traits. They argue that environments that occur fortuitously or by happenstance tend to be nonrecurring and therefore have highly time-specific effects. According to this model, environmental influences on cognition that are correlated with genes will be highly consistent over development, socially entrenched and institutionalized environmental experiences, will also be highly consistent over time, and idiosyncratic environmental influences on cognition that are uncorrelated with genes (typically nonshared environmental influences) will be highly inconsistent over development (see Dickens, Turkheimer, & Beam, 2011, for further explication of the role of the nonshared environment in the Dickens & Flynn model).

Embedded Dynamism

A final theoretical perspective comes from lifespan psychology, which has been described as a “meta-theory” (Baltes, Staudinger, & Lindenberger, 1999). Nesselroade (1991) has characterized this perspective as one in which partially stable and partially changing exogenous contexts influence individuals, individuals at the same time select and evoke contexts on the basis of their endogenous propensities, and the magnitude and enduringness of contextual influences depends on both individual factors and developmental period. He has written:

“Intraindividual change occurs in contexts: historical, cultural, societal, and so on. These various contextual strata influence the course of ontogenetic change through the conditions and events impinging on the individual. Contextual factors are themselves undergoing changes at varying rates and of differing generalities. Moreover, people are self-constructing… and are involved in selecting among possible contexts and producing new contexts to facilitate intraindividual changes… The dominant picture is one in which levels of complexity are described as ‘dynamisms within dynamisms’… or ‘embedded hierarchies’… I want to emphasize, however, that an attribute should not uncritically be assumed to manifest high stability. Rather, stability and the conditions of its maintenance should be foci of empirical examination” (p. 218-229).

To summarize, this perspective predicts that all of the mechanisms reviewed earlier (genetic set-point / genetic canalization, lasting effects of early experience / experiential canalization, stability of experience, gene-environment interaction, and gene-environment correlation) have the potential to simultaneously contribute to the stability and instability of individual differences in psychological phenotypes over time, and that empirical investigation is necessary to determine the relative contributions of each of these processes to the stability and instability of the specific phenotypes of interest. Although this perspective does not make strong empirical predictions, it highlights the likelihood that many of the mechanisms discussed above are likely to co-operate, and that the relative contributions of each mechanism may change over the course of development.

Developmental Changes in Continuity over the Lifespan

To what extents do the continuities of genetic and environmental influences on cognition change over the course of the lifespan? Moreover, to what extents do genetic and environmental factors account for increases in phenotypic stability over the course of development? Rather straightforward predictions about these issues can be derived from many of the theories reviewed above. We focus these predictions on the stabilities of three factors: genes, shared (family-level) environmental influences that serve to make children from the same family more similar to one another, and nonshared (individual-level) environmental influences that differentiate children from the same family. (Note that we provide a more detailed primer on how these factors are estimated using behavioral genetic methodology in a later section.)

Predictions

Because the genetic set-point/genetic canalization hypothesis holds that environmental effects are highly ephemeral, it would predict near zero stability of shared and nonshared environmental influences over the entirety of development. Moreover, in its most basic form, this hypothesis would predict very high stability of genetic influences over the course of development. In a somewhat elaborated form, the genetic set-point hypothesis might predict that normative biological development results in epigenetic patterns of gene activation and de-activation over development, particularly over the pubertal transition. One might refer to this as a moving set-point hypothesis, in that the genes relevant for adult cognition are somewhat different from those relevant for child cognition, and that individuals deviating from their age-specific genetic set-points will regress to that set-point. According to this moving set-point hypothesis, genetic stability would increase with child development as more of the genes associated with adult cognition become activated.

In contrast, the experiential canalization hypothesis holds that environmental influences, particularly those experiences that occur very early in development, have lasting effects. It would therefore predict small-to-moderate levels of stability for shared and nonshared environmental influences on cognition in early childhood, as young children are thought to be particularly sensitive to variability in environments. As cognitive phenotypes become canalized with increasing age, and hence resistant to de novo environmental experiences, shared and nonshared environmental influences should be expected to increase in their stability.

The stability of experience hypothesis would make opposite predictions to the experiential canalization hypothesis. This hypothesis views experiences relevant to cognition as highly determined from the family and social class circumstances into which a child is born. This hypothesis would therefore predict very high stability of shared and nonshared environmental influences on cognition at a very early age. Stability of environmental experience would remain relatively high throughout childhood and adolescence, as the quality of educational and social experiences to which children have access are thought to be strongly determined by the financial and social resources of the family. Nevertheless, some reordering of environments would be likely to occur as children develop and have access to a broader variety of extra-familial experiences, with marked discontinuities in stability likely to occur at school transitions (e.g., transitions into grade school, middle school, and high school) and life transitions (e.g. marriage and retirement). Therefore, the stability of experiences hypothesis would predict that the stability of shared and nonshared environmental influences is likely to decrease to some extent during childhood, but remain rather high due to buffering mechanisms. For example, the process of forming a personal identity over development may buffer decreasing environmental stability over age and school/life transitions because a solidified identity limits the realm of possible experiences from which a person will consider choosing (Roberts & DelVecchio, 2000). Similarly, the tracking of students into different educational programs on the basis of their past performance limits the available range of cognitively stimulating environments.

Like the experiential canalization hypothesis, a developmentally-oriented gene-environment interaction perspective would predict that early experiences have particularly lasting effects on cognition, whereas later experiences have more time-limited effects. However, this perspective adds the elaboration that early and lasting experiential effects are likely to operate differentially by genotype and/or via gene expression. Young children’s cognitive abilities are predicted to be particularly sensitive to environmentally-provoked gene-activation, whereas older children’s and adults’ cognitive abilities are predicted to be more resilient to new environmental inputs and influenced to a greater extent by lasting patterns of gene activation that have existed since very early childhood. Therefore, this perspective would predict lower stability of genetic influences on cognition in early childhood as variation in environmental experiences over time serves to activate different sets of genes, but increasing stability of genetic influences over development as later experiences become less effective in activating or deactivating genetic variation.

Transactional models of gene-environment correlation would predict that the stability of genetic factors will increase over time as environments are consistently and recurrently selected and evoked on the basis of genetically-influenced early behaviors and dispositions. This process is catalyzed because the diversity of environments that can be chosen from the “cafeteria of experiences” (Lykken, Bouchard, McGue, & Tellegen, 1993, p. 657) and the autonomy to select these environments (Scarr & McCartney, 1983) increases with development. In the Dickens and Flynn (2001) version of the transactional model, predictions are also made with respect to the shared and nonshared environment. The shared environment is predicted to represent the effects of socially entrenched and institutionalized processes, and is therefore predicted to exhibit very high stability throughout development. The nonshared environment is predicted to represent idiosyncratic, nonrecurring, and therefore nonlasting effects, and is therefore predicted to be unstable across development (although, a recent empirical study by Dickens et al., 2011, has motivated reconsideration of this prediction).

Finally, although the embedded dynamism perspective does not make strong predictions about the specific direction or magnitude of changes in genetic and environmental stability with age, it does make very clear that changes in rank-order stability over development should be expected. The core principle of this perspective is that descriptive empirical research is necessary to delineate the specific patterns of such changes.

Considering Time-Lag

It is important to note here that, unlike most statistics, continuity of individual differences cannot be measured at a single age or point in time; inherent in the definition of continuity is the repeated measurement of a phenotype over time. In considering age-differences in continuity, it is important to consider the time interval between measurements (time-lag). For instance, it does not make much sense to talk about continuity at a specific baseline age without knowing either a) the specific follow-up age, or b) the time-interval between measurements (i.e. the time-lag). The rank-ordering of cognitive test scores among a group of 2 year olds might be fairly stable after 1 month’s time, but might deteriorate to near zero after a decade. In contrast, the rank-orderings of cognitive test scores of a group of 10 year olds might be fairly stable after 1 month’s time and persist at close to full strength for many decades. This example, which bears close resemblance to the empirical trends documented by Bayley (1949) and depicted in Figure 1, illustrates a number of important considerations. First, comparing age differences in continuity, without specific attention to time-lag, is only meaningful if the average time lag is relatively constant across age groups. Second, a complete understanding of age differences in continuity should not simply hold time-lag constant, but should instead examine variability associated with both age and time-lag. Third, time-based decay of stability coefficients may differ with age. Therefore both the main effects of age and time-lag and their interactive effects are important to examine.

Other Possible Moderators of Genetic and Environmental Continuity

In addition to the possibility that the longitudinal stability of genetic and environmental influences on cognition are dependent on age and time-lag, it is also possible that stabilities depend on other person characteristics, study characteristics, or the specific form of cognition under study.

General Intelligence and Specific Abilities

One possible moderator of the stability of genetic and environmental influences on cognition is whether the form of cognition measured represents a highly generalized ability or a more domain-specific ability. Reeve and Bonaccio (2011; p. 267) for instance, have reasoned:

“Basic abilities such as g appear to be relatively stable. In contrast, skills and knowledge can, by definition, be developed (see Carroll, 1993, or Lubinski & Dawis, 1992). Thus, to the extent the focal test assesses specific skills an individual’s score could change over time due to a true change in their standing on the construct. In fact, Carroll’s (1993) three-stratum model of abilities is an effective way to conceptualize the ’ability vs. skill’ distinction. Constructs residing at the lowest levels tend to reflect specific skills and are assessed by specific types of items (Carroll, 1993, p. 634). Constructs at higher levels generally reflect abilities and are assessed by a wider range of tests and item types (Carroll, 1993, p. 633). Given that g resides at the highest stratum, it should demonstrate relative stability.”

Elaborating on this hypothesis, one might expect that the experiences relevant to specific lower-order abilities are themselves more specific (e.g. enrollment in a math course, or taking up a hobby) and amenable to short-term change, whereas the experiences relevant to general intelligence are quite broad (e.g. social class) and prone to slower change. Hence environmental influences on lower order abilities might be expected to be less stable than those on higher order abilities.

A similar set of predictions can be made for the stability of genetic influences on general intelligence vs. specific abilities. It is well agreed upon that most complex behavioral traits, including intelligence, are highly polygenic (i.e. affected by very many genes; Davies et al., 2011). However, the number of genes affecting different traits can still differ by several orders of magnitude. Empirical and theoretical work in molecular and evolutionary genetics (Kovas & Plomin, 2006; Penke, Denissen, & Miller, 2007) has posited that circumscribed sets of function-specific genes are likely to contribute to specific cognitive abilities, but that general intelligence is likely be affected by nearly any gene, anywhere on the genome, that codes for proteins relevant for physiologic function of virtually any sort. According to this mutation load hypothesis, the specific locus of a detrimental gene variant is irrelevant. Rather, the sheer number of detrimental mutations determines level of cognitive ability (or more accurately, level of cognitive impairment). Based on this hypothesis, genetic variants relevant to general intelligence should each contribute a smaller proportion to its total genetic variation than should genetic variants relevant to specific abilities. Elaborating on this reasoning, if the epigenetic changes that occur over development are localized to small portions of the genome, then one might expect genetic influences on specific cognitive abilities to be more prone to change (i.e. less stable) than genetic influences on general intelligence. One would expect that only broad epigenetic effects distributed across the genome would be able to appreciably reorder genetic effects on general intelligence.

Fluid and Crystallized Abilities

Building on a similar rationale, one might expect differential stabilities of genetic and environmental influences on different classes of specific abilities. Fluid abilities are generally conceptualized as resulting from highly generalized biologically-based cognitive capacities (Baltes et al., 1999; Cattell, 1971), although there is also strong evidence for cultural and experiential effects on tests of fluid cognition (Flynn, 2007). In contrast, crystallized abilities are generally conceptualized as knowledge acquired from cultural and educational experiences (Baltes et al., 1999; Cattell, 1971). Environmental experiences relevant for crystallized abilities confer declarative knowledge that is likely to be retained over long periods of time. Environmental experiences relevant for fluid abilities may confer shorter-term “boosts” that are not as easily retained, and instead fade more quickly over time. Moreover, compared to genetic influences on fluid abilities, genetic influences on crystallized abilities may be more substantially mediated by a host of personality, interest, and motivational factors relevant for knowledge acquisition (Tucker-Drob & Harden, 2012b,c). Because the psychological factors mediating genetic effects on knowledge acquisition may differ over time, one might expect genetic influences on crystallized abilities to be less stable than genetic influences on fluid abilities.

Social Class and other forms of Macro-environmental Opportunity

A further possible moderator of stability of genetic and environmental influences on cognition is social class and other forms of macroenvironmental opportunity. Building on the work of Bronfenbrenner and Ceci (1994), Dickens and Flynn (2001), Rowe, Almeida, and Jacobson (1999), and Scarr and McCartney (1983), Tucker-Drob and Harden (2012a,b,c) have suggested that the efficiency of reciprocal transactions between children and their proximal environments depends on the macro-environmental context in which the children and their microenvironments are embedded. Not only does this hypothesis predict that genetic variance will be larger in higher quality macro-environments, it also predicts that genetic influences on cognition will be more stable over time in higher quality macro-environments, which allow children to develop and pursue experiences that match their dispositions over prolonged periods of time. In lower quality macro-environments, consistent self-guided exposure to experiences is more difficult, and the learning experiences to which a child is recurrently exposed are predominantly exogenous. Unfortunately, the datasets identified in the current meta-analysis did not vary much in social class, and this hypothesis could not be tested.

A Primer on Behavioral Genetic Models of Stability and Instability

The longitudinal behavioral genetic methods applied in the current meta-analysis build upon the classical concept of or rank-order stability, i.e. stability of individual differences. Rank-order stability¹ refers to correlation between individual differences in a variable measured at one point in time and individual differences in the same variable measured at a later point in time (see Roberts & DelVecchio, 2000 for a discussion of other forms of trait stability). In other words, stability of individual differences refers to the extent to which the relative orderings of a sample of individuals to one another remains stable over time. When genetically informative longitudinal data are available, for instance, data from intact monozygotic and dizygotic twin pairs, one can mathematically identify quantitative behavioral genetic models that allow for the estimation of the stability of genetic and environmental influences on a given trait, and, similarly, the extent to which the stability of a trait over time stems from the continuous action of the same genes, the consistent effects of the same environmental experiences, or some mixture of the two. In this section we provide an overview of such behavioral genetic models.

Univariate Models

Before describing specific behavioral genetic models of stability and instability, it is instructive to begin by discussing behavioral genetic models of a single variable measured at a single point in time. Modern behavioral genetic models commonly make use of sibling correlations to partition variance in a phenotype, or trait, into genetic and environmental components. Typically, three variance components are estimated: an additive genetic factor (A) that accounts for variation in the phenotype associated with allelic differences between individuals, a shared (or common) environmental factor (C) that accounts for variation in the phenotype associated with influences acting at the family-level serving to make siblings from the same family more similar to one another, and a nonshared environmental factor (E) that accounts for variation in the phenotype associated with influences acting at the individual-level and serving to differentiate individuals within the same family, along with measurement error. Conceptually, these variance components are estimated by comparing the magnitudes of intraclass correlations across sibling types. For instance, if monozygotic twins (who share nearly 100% of their genes) are systematically more similar to their cotwins than dizygotic twins (who, on average, share approximately 50% of their genes) are to their cotwins, genetic factors are inferred to contribute to test scores. If monozygotic twins are more similar to the cotwins with whom they were raised than would be expected from the estimate of genetic similarity, shared environmental factors are inferred to contribute to test scores. Finally, if monozygotic twins raised together are not perfectly identical in their test scores, nonshared environmental factors are inferred to contribute to test scores.

A path diagram representing a univariate, single time point, quantitative genetic model for intact monozygotic (MZ) and dizygotic (DZ) twin pairs is represented in Figure 2 (cf. Neal & Cardon, 1992). It can be seen that this is a 2-group model in which the phenotype, Y, is represented twice: once for the member of the pair who has been randomly assigned to be “twin 1” and again for the member of the pair who has been randomly assigned to be “twin 2.” The phenotype is regressed onto latent factors representing A, C, and E. A factors are correlated at 1.0 across MZ twins, to reflect the fact that MZ twins share all of the same genes. A factors are correlated at .5 across DZ twins, to reflect the fact that DZ twins share, on average, 50% of their genes. Parameters labeled a, c, and e (which represent the regressions of Y on A, C, and E, respectively) are freely estimated, and parameters with the same label are constrained to be equivalent to one another. When Y has been standardized prior to analyses, the squares of a, c, and e, represent the proportions of variance accounted for by A, C, and E (termed heritability, shared environmentality, and nonshared environmentality) respectively. As the representation of y_tw2 and group 2 is largely redundant, it is typical for path diagrams for behavioral genetic models to only represent the portion of the diagram for a single twin. The extraneous portions of Figure 2 that do not typically appear in behavioral genetic path diagrams are depicted in gray with dashed lines. For the remaining path diagrams depicted in this article, only one twin per pair (from only one group) is represented, and the subscripts indicate wave, rather than twin number.

Figure 2.

A path diagram for a univariate behavioral genetic model for monozygotic twins reared together and dizygotic twins reared together. Portions of the figure in gray are redundant with the portion in black and are therefore often omitted from the path diagram.

Longitudinal Models

Longitudinal behavioral genetic models derive their information regarding the stability of genetic and environmental influences through cross-twin cross-time correlations (the correlation between one twin’s score at time point 1 and the other twin’s score at time point 2). A similar rationale for estimating genetic and environmental effects under the univariate model is used to estimate the longitudinal consistency of genetic and environmental effects. For instance, in using data from monozygotic twins raised together and dizygotic twins raised together, if the cross-twin cross-time correlations are larger for monozygotic than for dizygotic twins, this would be evidence for an effect of the same set of genes on the trait at the two time points. This is the same method used to estimate genetic and environmental pleiotropy (the same set of genes, or the same set of environments, affecting multiple phenotypes), except that instead of estimating commonality of genetic and environmental effects on two traits, commonalities are estimated for genetic and environmental effects on the same traits measured at two points in time (Plomin, 1986).

Three popular longitudinal behavioral genetic models are the Cholesky model (Figure 3 top panel), the Correlated Factors model (Figure 3 middle panel), and the Autoregressive Simplex model (Figure 3 bottom panel). All three models are equivalent when fit to two-wave longitudinal data, in the sense that they will fit the data equally well, and parameters from one model can be used to derive the parameters for the other models (see Appendix A). However, the three different models represent the information differently, and each therefore has unique strengths for addressing different theoretical questions (Loehlin, 1996; Loehlin, Horn, & Willerman, 1989). The Cholesky model partitions variation at the second wave into variation that is accounted for by genetic and environmental factors that contribute to variation at the first wave and genetic and environmental factors that contribute uniquely to variation in the second wave. The cross-paths a_b, c_b, and e_b provide information about the magnitudes of genetic and environmental influences carried over from the first wave, and the wave-2 paths a₂, c₂, and e₂ provide information about the magnitudes of genetic and environmental influences unique to the second wave. The question of consistency of genetic and environmental influences is not directly indexed; the cross-paths and the wave-2 paths both need to be taken into account to address this question.

Figure 3.

Path diagrams for three alternative two-wave longitudinal behavioral genetic models. Top Panel: The Cholesky model. Middle Panel: The Correlated Factors model. Bottom Panel: The Autoregressive Simplex model. For ease of presentation only one sibling per pair is depicted.

In contrast to the Cholesky model, the Correlated Factors model estimates separate parameters representing the magnitudes of genetic and environmental influences at wave 1 (a₁, c₁, and e₁) and wave 2 (a₂, c₂, and e₂), and the rank-order stabilities of genetic and environmental influences across waves (r_a, r_c, and r_e). When the phenotype (Y) has been standardized relative to its wave-specific standard deviation prior to analyses, the squares of the a, c, and e parameters represent the proportions of variances accounted by genetic, shared environmental, and nonshared environmental variance components at the respective waves. This Correlated Factors model can also be used to calculate the overall contributions of genetic, shared environmental, and nonshared environmental factors to the overall phenotypic stability (a₁×r_a×a₂, c₁×r_c×c₂, and e₁×r_e×e₂, respectively). It is important to note that these are raw contributions, rather than proportional contributions. For instance, if the phenotypic stability of cognition is .4, and genes contribute 50% to phenotypic stability, then the genetic contribution to phenotypic stability is .2. Finally, it is of note that a factor’s contribution to phenotypic stability is not a direct function of how stable that factor is. For example, ascribed characteristics of the individual (e.g., gender) are likely to be highly stable across time, but if these characteristics are relatively unimportant for cognitive development, then they will not contribute to overall stability. In terms of the correlated factors model, if the shared environment is highly stable over time (e.g., r_c = .80), but the shared environment contributes very little to the phenotype at both points in time (e.g., c² = .20), then the shared environment’s contribution to phenotypic stability will be rather small (c₁×r_c×c₂ = .16). Therefore, it is important to examine A, C, and E contributions to phenotypic stability in addition to examining the stability of A, C, and E factors.

The Autoregressive Simplex model has properties similar to both the Correlated Factors and the Cholesky models. Like the Correlated Factors model, it separates stability information from magnitude of genetic and environmental effect information. However, like the Cholesky model, because the arrows from the genetic and environmental factors at wave 1 to the corresponding genetic and environmental factors at wave 2 are directional, it is specifically concerned with accounting for genetic and environmental variance at wave 2 with genetic and environmental factors from wave 1.

Because the current project was specifically concerned with the consistency of genetic and environmental influence as separate from the magnitude of genetic and environmental influence, we used the correlated factors model as our guiding model. We focused specifically on the rank-order stability of genetic and environmental effects on cognition over time (r_a, r_c, and r_e), and on the extents to which genetic and environmental factors contributed to the phenotypic rank-order stability of cognition over time.

Goals of the Current Project

By meta-analyzing longitudinal behavioral genetic studies of samples spanning the entire lifespan, we were able to examine the following questions: 1) to what extent are genetic and environmental factors stable over time? 2) to what extent does the stability of genetic and environmental factors change across the lifespan? 3) to what extent do genetic and environmental factors underlie changes in the stability of cognitive abilities? 4) what are the other moderators of phenotypic, genetic, and environmental stability?

Method

Literature Search

We used PsycINFO to search abstracts for at least one keyword from each of three sets of keywords: genetics (twin, genetic, adoption, adopted, adoptee), longitudinal (longitudinal, aging, stability), and cognition (intelligence, cognition, cognitive, ability). Of the resulting 890 articles and chapters, we excluded those primarily focusing on clinical populations, publications in a language other than English, and publications that did not include analyses of a specific dataset (e.g. review articles). Of the 104 remaining articles and chapters, we included those that met all of the following criteria: 1) results were based on samples of siblings with varying degrees of genetic relatedness, 2) data came from at least two waves of measurement of the same cognitive ability separated in time (i.e. data were longitudinal), 3) cognition/intelligence was measured using an objective test, and 4) complete cross-time and within-time sibling correlations were supplied, or complete parameter estimates were supplied from a behavioral genetic model that produced expectations for cross-time and within-time sibling correlations (articles and chapters that only reported parameter estimates from latent growth curve models were not included, as such models estimate genetic and environmental influences on changes occurring systematically across three or more waves of data, and may therefore fail to capture dependencies between specific pairs of waves). When multiple articles made use of the same data (as is common with longitudinal studies), we retained the study that reported on the most time points, measures, or sample size. We retained studies that made use of the same sample if the article reported information that differed on one of our moderators. For example Bartels, Rietveld, Van Baal, & Boomsma (2002) and Hoekstra, Bartels, & Boomsma (2007) both report on a sample drawn from the Netherlands Twin Registry, but operationalized cognition at different levels of specificity. We included both of these studies in the meta-analysis as well as all of the measures of cognition as separate outcomes. (Implications of including multiple effects sizes from a single study and multiple studies that use the same sample are described below in the Analytic Approach section.). Finally, we asked knowledgeable colleagues if they were aware of relevant published articles that we had missed. In total, 21 articles and chapters from 15 unique samples met inclusion criteria for our meta-analysis.

Table 1 lists these articles and provides relevant characteristics. Age at wave 1 ranged from .50 to 64.10 years (mean = 15.20, SD = 22.41). The time-lag between waves of assessment ranged from .42 to 35.60 years (mean = 4.42, SD = 7.46). Age was neither linearly nor quadratically related to time-lag (R² linear term = .03, p = .44; R² quadratic term = .01, p = .76). The modal number of waves was 2 (K = 12), but number of waves ranged from 2 to 8 (mean = 3.19, SD = 1.86).

Table 1.

Included Studies and Relevant Information

Citation	Dataset	Variables Examined	Number of Waves	Age Range (years) Across Waves	Longitudinal Sample Size (pairs)
Bartels et al. (2002) a	Netherlands Twin Registry	General Intelligence	4	5.30-12.00	78 MZT and 113 DZT
Bishop et al. (2003)	Longitudinal Twin Study	General Intelligence	8	1.00-12.00	224 MZT and 189 DZT
Cherny et al. (2001) b	MacArthur Longitudinal Twin Study	General Intelligence	4	1.17-3.00	173 MZT and 143 DZT
Davis et al. (2009)	Twins Early Development Study	General Intelligence	2	3.00-8.67	2979 MZT and 5812 DZT
Dickens et al. (2011) c	Swedish Adoption/Twin Study of Aging	General Intelligence	4	64.10-77.10	162 MZT and 276 DZT
Hart et al. (2007) d	Western Reserve Reading Project	General Intelligence	2	6.00-7.20	88 MZT and 123 DZT
Hart et al. (2009) d	Western Reserve Reading Project	Expressive Vocabulary	3	6.09-8.32	128 MZT and 175 DZT
Hoekstra et al. (2007) a	Netherlands Twin Registry	Verbal and Nonverbal Ability	4 Verbal; 5 Nonverbal	5.30-12.00 Verbal; 5.30- 18.10 Nonverbal	89 MZT and 120 DZT
Lessov-Shlaggar et al. (2007)	NHLBI Twin Study	Digit Symbol Substitution, Trials B, Stroop	2 Trials B/Stroop; 3 Digit Symbol	72.70-76.60 Trials B/Stroop; 63.10-76.60 Digit Symbol	94 MZT and 91 DZT
Lyons et al. (2009)	Vietnam Era Twin Study of Aging	Armed Forces Qualification Test	2	19.80-55.40	200 MZT and 170 DZT
Malykh et al. (2003)	Moscow community sample	General Intelligence	2	6.00-7.00	32 MZT and 29 DZT
McArdle (1986)	Louisville Twin Project	General Intelligence	4	0.50-2.00	75 MZT and 75 DZT
Petrill et al. (2007)d	Western Reserve Reading Project	Phonological Awareness, Rapid Automatized Naming, Expressive Vocabulary, Letter Knowledge, Word Knowledge, Phonological Decoding, Passage Comprehension	2	6.10-7.20	88 MZT and 123 DZT
Petrill et al. (2004)	Colorado Adoption Project	General Intelligence	8	1.00-16.00	141 Adoptive and 143 Nonadoptive
Plomin et al. (1994) c	Swedish Adoption/Twin Study of Aging	General Intelligence, Blocks, Card Rotation, Figure Logic, Information, Synonyms, Analogies, Digit Span, Names and Faces, Thurstone Test, Digit Symbol, Figure Identification	2	64.10-67.10	48 MZT, 63 DZT, 34 MZA, and 78 DZA
Polderman et al. (2006) e	Netherlands Twin Registry	General Intelligence	2	5.80-12.42	97 MZT and 80 DZT
Polderman et al. (2007) e	Netherlands Twin Registry	Selective Attention; Working Memory; Sustained Attention	2	5.80-12.42	97 MZT and 79 DZT
Reznick et al. (1997) b	MacArthur Longitudinal Twin Study	Memory for Locations; Visual Attentiveness	3	1.17-2.00	176 MZT and 148 DZT
Tucker-Drob et al. (2011)	Early Childhood Longitudinal Study- Birth Cohort	General Mental Ability	2	0.83-2.03	200 MZT and 500 DZT
van den Berg et al. (2004)	Netherlands Twin Registry	Vocabulary	2	44.00-49.00	52 MZT and 63 DZT
van Soelen et al. (2011)	Netherlands Twin Registry	General Intelligence; Verbal IQ; Nonverbal IQ	2	9.10-12.10	40 MZT and 49 DZT

Note: MZT, DZT, MZA, and DZA refer to monozygotic twin pairs raised together, dizygotic twin pairs raised together, monozygotic twin pairs raised apart, and dizygotic twin pairs raised apart, respectively. Citations marked with the same letter utilized the same sample and were therefore weighted together. Sample sizes from Tucker-Drob et al. (2011) are rounded to the nearest 50 in accordance with data security regulations.

It is of particular mention that there was very little data coverage in young and middle adulthood. Very few longitudinal behavioral genetic studies have been conducted with assessments during this period. We dealt with this issue in two ways. First, we fit a series of age-based parametric models to the entire meta-analytic dataset that essentially interpolate between datapoints. Second, we focused our more complex analyses specifically on childhood, where data coverage was high. We discuss the implications of sparseness of information from this age period in the Discussion section.

Classification of Cognitive Measures

Measures included general intelligence, reasoning, memory, and verbal ability, amongst others. Studies ranged from having 1 cognitive measure to 12 cognitive measures (mean = 2.19, SD = 2.66).² Based on their descriptions, we classified each measure as either a measure of general intelligence or a measure of a specific ability by consensus method. Among the specific abilities, any measure of effortful processing (e.g. reasoning, memory, speed) was classified as fluid, and any measure of learned knowledge (e.g. verbal ability, vocabulary knowledge) was classified as crystallized. In total, 62.3% of measures were classified as general intelligence, 37.7% were classified as fluid, and 16.2% were classified as crystallized.

Estimating Parameters for Each Study Variable

Our goal was to produce a meta-analytic database containing complete sets of parameter estimates and associated standard errors from a bivariate longitudinal correlated factors model (see middle panel of Figure 3) applied to each cognitive variable for each possible pair of time points for each study. These parameters were heritability, shared environmentality, and nonshared environmentality at baseline (a₁², c₁², and e₁²) and follow-up waves (a₂², c₂², and e₂²), cross-time genetic, shared environmental, and nonshared environmental correlations (r_a, r_c, and r_e), the contributions of genes, the shared environment, and the nonshared environment to phenotypic stability (a₁×r_a× a₂, c₁×r_c× c₂, and e₁×r_e× e₂), and the overall phenotypic stability (a₁×r_a× a₂ + c₁×r_c× c₂ + e₁×r_e× e₂). We therefore began by compiling 4× 4 correlation matrices for pairs of time points for each cognitive variable from each study (2 siblings + 2 time points = 4 variables per correlation matrix), separated by sibling type (e.g. when a study was based on both monozygotic and dizygotic twins, we had separate monozygotic and dizygotic correlation matrices). When studies reported correlations or covariances, we used them (covariance matrices, which were rare, were transformed into correlation matrices). When studies only reported parameter estimates from behavioral genetic models, we produced expected correlation matrices. To determine the sample sizes to associate with each matrix, we only included the number of twin or sibling pairs that provided data for at least two time points (note that behavioral-genetic models are fit to data organized at the pair level, and the correct sample size is therefore in terms of pairs, not individuals). When publications only provided sample sizes in terms of individuals, rather than pairs, we divided the provided N in half. These decisions concerning sample size were likely to produce conservative standard errors, as the availability of individual-level data would have enabled us to use advanced missing data methods (e.g. full information maximum likelihood) to draw power from partial data patterns (e.g. incomplete twin pairs, and individuals participating only at one time point).

All correlation matrices were analyzed with a longitudinal correlated factors model using MPlus software. For four cases, our model presented convergence difficulties that we could not resolve by varying starting values. When we examined the problematic matrices, we found that either the monozygotic twin correlations were more than twice the dizygotic twin correlations (which would be consistent with a nonadditive effect of genes), or that the monozygotic twin correlations were less than the dizygotic twin correlations (which is not easily explained by genetic theory). Because these problems constituted a relatively small proportion of the total number of effect sizes, and because it would be difficult to integrate estimates from more specialized models (for instance, those that allow for genetic dominance) with those from ACE models, we chose not to attempt to model these matrices using different techniques.

In total, we attempted to compute a total of 150×3 individual estimates of r_a, r_c, and r_e, with an average of 7.14×3 estimates per study. ³ For 15 estimates of r_a and 7 estimates of r_c, an absolute value of 1.1 was exceeded. No values of r_e exceeded this value. Estimates above an absolute value of 1.1 are problematic because correlations can only realistically fall between −1.0 and 1.0 (estimates slightly lower than −1.0 and slightly higher than 1.0 were treated as within generally acceptable bounds of parameter imprecision). These problematic estimates most often occurred when one or both of the biometric components being correlated accounted for very little variance (e.g. when c² was close to 0 at both time points, the r_c estimate was often severely out of bounds). In such cases, the associated standard errors were very large. To illustrate, the average SE of out-of-bounds r_a estimates (absolute values greater than 1.1) was 1.66, which means that the 95% CI is larger than the entire possible range of correlation values (− 1 to +1). In comparison, the average SE of the in-bounds estimates (-1.1 to 1.1) was 0.19. To reduce the potential for these severely out-of-bounds estimates to exert extreme influences, we winsorized them by substituting the closest acceptable values (either −1.1 or 1.1).

Analytical Approach: Application of Meta-Regression Models

We implemented meta-regression models that predicted our parameters of interest from various study variables using the approach described by Cheung (2008), in which outputted standard errors and p values of the meta-regression parameter estimates are unbiased and do not need to be transformed by postprocessing. Separate meta-regression models were fit for each parameter of interest. Because we included multiple effect sizes per sample (i.e. multiple cognitive outcomes and multiple pairs of waves for samples with 3 or more waves), this approach required two elaborations. First, we weighted by the reciprocal number of effects sizes included for the corresponding sample, in addition to weighting by the inverse sampling variance. Second, we used the cluster option of Mplus to correct standard errors of the meta-regression parameter estimates for nonindependence of data points derived from the same sample. Our approach has a similar effect as the more conventional approach of averaging multiple effects sizes per study and not weighting by the reciprocal number of effect sizes per sample, but has the added advantage of being able to include predictors in the meta-regressions that vary across effect sizes within the same study.

Competing meta-regression models were selected by taking into account absolute fit (logliklihood), Akaike’s Information Criteria (AIC), and Bayesian Information Criteria (BIC). For all three fit indices, lower absolute values indicate better fit. Both AIC and BIC are indices that take into account both absolute fit and model parsimony (a model with fewer parameters is more parsimonious). BIC penalizes for additional model parameters more strongly than does AIC. Better fitting models were selected for further examination by plotting their expectations against scatter plots.

Results

Table 2 presents descriptive statistics for the key meta-analytic variables. The earliest assessment was at half a year old, and the latest assessment was at 77 years old. However, the age distribution was concentrated in childhood and adolescence with a mean initial assessment at 6.34 years. The time interval between measurements varied from relatively short (a third of a year) to relatively long (a third of the lifespan, 35 years). The average time interval was 5.92 years (SD = 5.53). Information about demographic composition of some studies was not well-reported. For studies that did report information about gender, females tended to be in the minority (29.08%). This under-representation of females could be attributed to the inclusion of two studies (Lessov-Schlaggar, Swan, Reed, Wolf, & Carmelli, 2007; Lyons et al., 2009) that exclusively sampled male veterans. When these two studies were excluded, females represented the slight majority (53.02%) of participants. This is likely to be closer to the female representation in the other studies that did not report on gender as they were based on general community sampling rather than military members. Very few participants were from minority racial or ethnic groups (3.36%).

Table 2.

Characteristics of Samples and Variables Meta-Analyzed

Variable	Number of contributing samples (K)	Number of contributing Datapoints (k)/Sample Size (n)	Range	Mean	SD
Age at baseline (years)	15	150/12,551	.50-72.70	6.34	13.01
Interval (years)	15	150/12,551	.33-35.60	5.92	5.53
Age at follow-up (years)	15	150/12,551	1.00-77.10	12.26	15.10
Percent Female	7	42/1,229	.00-57.00	29.08	26.48
Percent Non-White	5	56/10,547	.00-39.00	3.36	9.85
Measures of General
Intelligence	13	96/11,984	–	–	–
Measures of Fluid
Abilities	6	33/1,189	–	–	–
Measures of
Crystallized Abilities	5	21/829	–	–	–

Note: Mean and standard deviation weighted by sample size and reciprocal number of contributing datapoints.

Population Average Stabilities

We began by computing random effects meta-analytic averages for our effect sizes of interest. The estimated population-average effect sizes (and standard deviations of the associated random effects) for phenotypic stability, r_a, r_c, and r_e, were .489 (.117), .779 (.231), .655 (.078), and .165 (.112) respectively. The effect sizes were statistically significant at p < .001 for phenotypic stability, r_a, and r_c, and at p < .05 for r_e. The random effects were statistically significant at p < .001 for phenotypic stability and r_a, but not statistically significant for r_c and r_e. It is important to appreciate that the standard deviations of the random effects are not the standard deviations of the effect sizes directly observed in the meta-analytic dataset, but are instead estimates of the standard deviations of the true effect sizes after removing variation attributable to sampling error. Given the high levels of significance for the random effects of the phenotypic stability and r_a effect sizes, the nontrivial magnitudes of all random effects (including those for r_c and r_e), and given that authoritative texts on meta-analysis (Borenstein, Hedges, Higgins, & Rothstein, 2009, p. 84; Cooper, Hedges, & Valentine, 2009, p. 554) have indicated that tests of heterogeneity may be underpowered to detect subgroup differences in effect sizes, we went on to examine measured characteristics as predictors of effect sizes for phenotypic stability, r_a, r_c, and r_e.

Age Trends in Genetic and Environmental Stability

Lifespan Age trends

We fit linear, quadratic, connected-linear-spline, and exponential age-based models to the effect sizes for phenotypic stability, r_a, r_c, and r_e. Specifications for these models can be found in the top panel of Table 3. We also fit spline models that allowed for discontinuities at age 18 (the conventional marker of transition from childhood to adulthood) by using a dummy-coded variable (age<18=0, age≥18=1). However, because none of the discontinuity parameters was significant, results for the disconnected spline models are not reported. Note that we did not model time-lag in this initial set of analyses (we return to the question of time lag later on), but because time-lag was unrelated to age, time-lag should not confound these analyses. These analyses should therefore be taken to represent age differences holding time-lag constant at its weighted mean of approximately 6 years.

Table 3.

Equations for the meta-regression models fit.

Meta-Regression Model	Equation	Description of Parameters
Age-Based Models
Linear	(1) ${\widehat{y}}_i=b_0+b_1\left(ag{e}_i\right)$	b0 = y intercept b1= linear slope
Quadratic	(2) ${\widehat{y}}_i=b_0+b_1\left(ag{e}_i\right)+b_2\left(ag{e}_i^2\right)$	b0 = y intercept b1= linear slope b2= quadratic slope
Connected Linear Spline	(3) ${\widehat{y}}_i=b_0+b_1\left(ag{e}_{a,i}\right)+b_2\left(ag{e}_{b,i}\right)+b_3\left(ag{e}_{c,i}\right)$	b0 = y intercept b1= linear slope through age 8
	If agei ≤ 8, then agea,i = agei. If agei > 8, then agea,i = 8. If (agei > 8 AND age ≤ 18), then ageb,i = agei-8. If agei ≤ 8, then ageb,i = 0. If agei > 18, then ageb,i = 18-8.	b2=linear slope between ages 8 and 18 b3 = linear slope after age 18
	If agei > 18, then agec,i = agei-18. If agei ≤ 18, then agec,i = 0.
Exponential	(4) ${\widehat{y}}_i=b_0-b_1{e}^{b_2\left(ag{e}_i\right)}$	b0 = horizontal asymptote b1= age scaling factor b2=growth rate
Age- and Time-Based Models
Linear-Exponential	(5) ${\widehat{y}}_i=b_0+b_1\left(ag{e}_i\right)-b_3{e}^{\left(b_4\right(tim{e}_i)+b_5(ag{e}_i\times tim{e}_i\left)\right)}$	b0 = intercept of age function b1= age growth rate b3= time scaling factor b4=time decay rate b5=age ×time interaction
Exponential- Exponential	(6) ${\widehat{y}}_i=b_0-b_1{e}^{b_2\left(ag{e}_i\right)}-b_3{e}^{\left(b_4\right(tim{e}_i)+b_5(ag{e}_i\times tim{e}_i\left)\right)}$	b0 = horizontal age asymptote b1= age scaling factor b2=age growth rate b3= time scaling factor b4=time decay rate b5=age×time interaction

Parameter estimates and fit statistics for each of the above described models are presented in Table 4.

Table 4.

Parameter estimates and fit statistics for meta-regression models of age trends in phenotypic, genetic, and environmental stability.

Meta-Regression Model	b0 (SE)	b1 (SE)	b2 (SE)	b3 (SE)	LL (SCF)	AIC	BIC
Phenotypic Stability
Linear	.375 (.007)**	.007 (.001)**			−1939.178 (10.430)	3910.356	3958.527
Quadratic	.313 (.013)**	.0277 (.0044)**	−.00031 (.00006) **		−1920.486 (9.775)	3874.973	3926.153
Connected Linear Spline	.251 (.020)**	.048 (.007)**	.011 (.004)**	.001 (<.001)**	−1912.411 (9.165)	3860.821	3915.013
Exponential	.783 (.011)**	.559 (.028)**	−.123 (.019)**		−1913.691 (9.723)	3861.382	3912.563
Genetic Stability
Linear	.421 (.081)**	.009 (.001)**			−1909.019 (9.675)	3850.039	3898.209
Quadratic	.361 (.068)**	.0220 (.0063)**	−.00019 (.00009)*		−1900.755 (9.038)	3835.509	3886.690
Connected Linear Spline	.021 (.051)	.121 (.011)**	−.003 (.008)	.001 (.001)	−1880.977 (8.103)	3797.955	3852.146
Exponential	.993 (.003)**	1.166 (.159)**	−.222 (.040)**		−1883.950 (8.627)	3801.900	3853.081
Shared Environmental Stability
Linear	.582 (.061)**	.012 (.006)*			−1639.475 (8.243)	3310.949	3359.120
Quadratic	.518 (.082)**	.0358 (.0211)	−.00047 (.00032)		−1637.437 (7.801)	3308.874	3360.054
Connected Linear Spline	.420 (.064)**	.072 (.017)**	−.024 (.007)**	.005 (<.001)**	−1634.114 (7.175)	3304.229	3358.420
Exponential	.854 (.061)**	.546 (.096)**	−.346 (.094)**		−1633.860 (7.580)	3301.720	3352.901
Nonshared Environmental Stability
Linear	.053 (.008)**	.007 (.001)**			−1765.121 (9.485)	3562.242	3610.412
Quadratic	.049 (.010)**	.0081 (.0001)**	−.00002 (.00004)		−1765.090 (8.952)	3564.180	3615.361
Connected Linear Spline	.071 (.034)*	.001 (.012)	.011 (.006)	.007 (.001)**	−1764.968 (8.495)	3565.936	3620.128
Exponential	2.240 (5.361)	2.190 (5.355)	−.004 (.010)		−1765.095 (8.946)	3564.191	3615.372

Note:

^*p<.05

^**p<.01.

SE = Standard Error. SCF = Scaling Correction Factor for nested model comparisons.

For phenotypic stability, the two best fitting models are the spline model and exponential model. Both have very similar fits, with the spline model having a slightly lower AIC, and the exponential model having a slightly lower BIC. The age-based curves implied by these two models are superimposed on the scatterplot displayed in the top left panel of Figure 4. Note that the size of each point on the scatterplot has been scaled relative to the weight that the datapoint received in the analysis (with an upper limit imposed on the size of the points, to preserve their visibility). The larger the circle, the more heavily the datapoint was weighed in the analysis. It can be seen that the curves are highly overlapping. Both indicate that individual differences in cognition have very low stability (approximately .30) in very early life, with stability of individual differences increasing dramatically over child development. Both curves indicate stability of over .6 by 10 years of age, and stability of over .7 by 16 years of age. The exponential model has an asymptote of .78, and the spline model levels out at a similar value.

Figure 4.

Age trends in phenotypic stability (top left panel), genetic stability (top right panel), shared environmental stability (bottom left panel), and nonshared environmental stability (bottom right panel). Data points are represented as dots enclosed in circles. Larger circles indicate higher weight in the analysis and greater precision of the data point. To facilitate visualization, there was an upper limit imposed on the size of the circles. Fitted trend lines are preferred models based on AIC and BIC comparisons. Note that there are a few points outside of the visible y-axis range for genetic stability (k = 3) and shared environmental stability (k = 4). These data points tended to indicate negative stability (mean = −.85) at very young ages (mean = 2.44 years) and were not precise (mean SE = 13.34).

The spline and the exponential models were also the best fitting models for genetic stability. Both models had very similar fits, with the spline model having slightly lower AIC and BIC values. The age-based curves implied by these models are superimposed on the scatterplot displayed in the top right panel of Figure 4. It can be seen that both curves indicate very low stability (less than .20) in very early life, with dramatic increases in stability through child development. Both curves indicate stability of over .90 by 12 years of age. The exponential model has an asymptote of .99, indicating that genetic influences eventually have nearly perfect longitudinal stability over time.

The spline and exponential models were also the best fitting models for shared environmental stability, although the exponential model may be a better account of the data as it had both lower AIC and BIC values. The age-based curves implied by these models are superimposed on the scatterplot displayed in bottom left panel of Figure 4. Focusing on the exponential curve, it can be seen that stability in early life is moderate in magnitude, exceeding .40, and increases quickly in early childhood to greater than .80 by age 7, and reaching an asymptote of .85. The spline curve also indicates moderate stability in early life that increases in childhood, but the trend is somewhat jagged, perhaps attributable to model overfitting in early and middle adulthood, where data coverage is sparse.

For nonshared environmental stability, the linear model fit best by both AIC and BIC standards. The exponential model also had good fit. We plot these curves along with that implied by the spline model in bottom right panel of Figure 4. All three curves overlap considerably. They all agree in indicating continuous steady increases in nonshared environmental stability over the entire lifespan. Although data are sparse in early and middle adulthood, the datapoints in that age range fall along the curves nearly perfectly, indicating that linear increases in r_e from childhood through young, early, and middle adulthood may indeed be occurring.

Age Trends in Contributions of Genetic and Environmental Factors to Phenotypic Stability

To what extent do age-based increases in the stability of genetic and environmental factors underlie the age-based increases in the phenotypic stability of individual differences in cognition? It may be tempting to infer from the above results that increases in genetic and environmental factors each contribute to increases in phenotypic stability with age. However, as mentioned earlier, the contribution of a genetic or environmental factor to the stability of a phenotype not only depends on the stability of that genetic or environmental factor, but also on the extent to which that factor accounts for variance in the phenotype. For instance, the shared environment may be highly stable, but if it only accounts for a small amount of variance in cognition, cognition may still have very low stability. To address this question we fit a similar set of age-based curves to terms representing the contributions of A, C, and E to phenotypic stability. Recall that these terms (genetic contribution = a₁×r_a× a₂, shared environmental contribution = c₁×r_c× c₂, and nonshared environmental contribution= e₁×r_e× e₂) take into account both the stability of the genetic or environmental factor, and the influence of that factor to the phenotype at the two waves. It is also important to note that these terms represent the raw contributions to stability, as opposed to a proportional contribution. In other words, genetic, shared environmental, and nonshared environmental contributions sum to form the total phenotypic stability, not necessarily to 1.0.

Parameter estimates and fit statistics for each of the models fit to genetic, shared environmental, and nonshared environmental contributions to phenotypic stability are presented in Table 5.

Table 5.

Parameter estimates and fit statistics for meta-regression models of age trends in genetic and environmental contributions to stability.

Meta-Regression Model	b0 (SE)	b1 (SE)	b2 (SE)	b3 (SE)	LL (SCF)	AIC	BIC
Genetic Contribution
Linear	.127 (.017)**	.009 (.001)**			−1843.278 (9.640)	3718.556	3766.726
Quadratic	.049 (.027)	.0364 (.0075)**	−.00041 (.00011) **		−1830.761 (9.070)	3695.522	3746.703
Connected Linear Spline	−.043 (.024)	.068 (.007)**	.000 (.004)	.003 (.001)**	−1822.417 (8.473)	3680.834	3735.026
Exponential	.652 (.028)**	.722 (.040)**	−.132 (.017)**		−1823.210 (8.990)	3680.420	3731.601
Shared Environmental Contribution
Linear	.239 (.011)**	−.004 (.001)**			−1734.191 (9.351)	3500.382	3548.552
Quadratic	.249 (.015)**	−.0070 (.0031)*	.00006 (.00005)		−1734.008 (8.808)	3502.017	3553.197
Connected Linear Spline	.264 (.025)**	−.012 (.007)	.001 (.004)	−.003 (.001)**	−1733.873 (8.333)	3503.746	3557.937
Exponential	.047 (.079)	−.207 (.063)**	−.043 (.047)		−1734.001 (8.820)	3502.001	3553.182
Nonshared Environmental Contribution
Linear	.009 (.001)**	.002 (<.001)**			−2023.315 (9.842)	4078.631	4126.801
Quadratic	.006 (.002)**	.0025 (.0006)**	−.00002 (.00001)		−2022.976 (9.270)	4079.951	4131.132
Connected Linear Spline	.013 (.007)	.000 (.002)	.004 (.001)**	.001 (.000)**	−2022.836 (8.786)	4081.671	4135.863
Exponential	.164 (.067)*	.157 (.065)*	−.015 (.010)		−2023.046 (9.269)	4080.092	4131.273

Note:

^*p<.05

^**p<.01

SE = Standard Error. SCF = Scaling Correction Factor for nested model comparisons.

For the genetic contribution to stability, the best fitting models were the spline model and the exponential model, with the exponential model having a trivially lower AIC value, and a somewhat lower BIC value. The age-based curves implied by these two models are superimposed on the scatterplot displayed in the top panel of Figure 5. It can be seen that both curves indicate near zero contributions of genes to stability in very early life, with dramatic increases in the genetic contribution to stability through child development. According to the exponential model, genetic contributions to stability in adulthood stabilize at an asymptote of .65.

Figure 5.

Age trends in genetic contributions to stability (top panel), shared environmental contributions to stability (middle panel), and nonshared environmental contributions to stability (bottom panel). Data points are represented as dots enclosed in circles. Larger circles indicate higher weight in the analysis and greater precision of the data point. To facilitate visualization, there was an upper limit imposed on the size of the circles. Fitted trend lines are preferred models based on AIC and BIC comparisons. Note that all data points are represented.

For the shared environmental contribution to stability, the best fitting models were the linear and exponential models, with the linear model having both the lowest AIC and BIC values. These curves, along with the curve implied by the spline model, are plotted in the middle panel of Figure 5. It can be seen that the shared environment contributes moderately to stability in childhood, with an intercept of .24, but that the contribution fades slowly over development, such that by middle adulthood, the shared environment contributes little, if at all, to stability.

For the nonshared environmental contribution to stability, the best fitting models were the linear and quadratic models, with the linear model having slightly lower AIC and BIC values. These curves, along with the curve implied by the spline model, are plotted in bottom panel of Figure 5. It can be seen that the nonshared environment contributes very little to stability throughout development, although the contribution to stability is significantly greater with advancing age.

To further visualize these results, we chose the best-fitting continuous age-based models (i.e. excluding the spline model) of raw contributions of A, C, and E to phenotypic stability to produce a plot of the expected proportional contributions of A, C, and E to phenotypic stability by age. This plot is provided in Figure 6. It can be seen that the shared environment contributes the greatest proportion to stability in very early childhood, but that with child age, the shared environment contributes proportionally less, and genes contribute proportionally more. Throughout adulthood, the proportionally contribution of genes to stability is by far the largest, at approximately 75%. The nonshared environment’s proportional contribution to stability increases fairly continuously across the entire lifespan, from a near-zero contribution in early childhood to a near 20% contribution in late adulthood.

Figure 6.

Proportional genetic, shared environmental, and nonshared environmental contributions to stability across the lifespan. Estimates are based on expectations from the best fitting continuous models.

Temporal Decay of Stability over Child Development

Our next goal was to examine the extent to which phenotypic, genetic, and environmental stabilities decay over time, and the extent to which temporal decay differs with childhood age. We focused specifically on childhood (i.e. younger than 18 years) for two reasons. First, simultaneous models of the effects of both age and time are considerably more complex than simple models of age and require greater data density, and importantly, relatively uncorrelated heterogeneity in both age and time. Although our meta-analytic dataset had substantial density, age-based heterogeneity, and time-based heterogeneity across infancy, childhood, and adolescence, data were much sparser in adulthood. Second, because the analyses reported earlier indicated high asymptotic levels of phenotypic, genetic, and shared environmental stability occurring by early adulthood, we were interested in deeply examining the developmental patterns in childhood that give rise to the relatively-static adult end-states.

Our approach to simultaneously modeling influences of both age and time on temporal stability involved forming meta-regression models that included one function representing age-based growth (specifically, exponential growth for phenotypic stability, r_a, and r_c, and linear growth for r_e), a second function for time-based decay (specifically, exponential decay), along with an interaction term representing the moderation of time-based decay by age. We chose an exponential function for time-based decay specifically because this function allows for a lower-bound asymptote. We did not expect stability coefficients to decay past zero, which would be implied by a linear model. Moreover, the test-retest stability can be formalized as Autoregressive Simplex models, which have in turn been shown to imply exponential decay of stability over time (Levin, 1993). Equations for these combined age- and time- based models, along with parameter descriptions, can be found in the bottom panel of Table 3.

Parameter estimates from the combined age- and time- based models are presented in Table 6, and the curves implied by these models are presented in Figure 7. Each panel depicts a series of curves charting expected stability over time, with each curve representing stability relative to different initial age of measurement. The curves begin 1 year after the initial age. Taking the 2 year curve as an example, the curve represents the expected stability relative to age 2 beginning at a one year lag (age 3), and then along continuous increases in lag (e.g. with a baseline measurement at age 2, a 4 year lag would occur at age 6), up until age 18.

Table 6.

Parameter estimates and fit statistics for simultaneous models of age and time in childhood.

	Constant	Age growth (linear or exponential)		Time Decay (exponential)		Age × Time
Dependent Variable	b0 (SE)	b1 (SE)	b2 (SE)	b3 (SE)	b4 (SE)	b5 (SE)
Phenotypic Stability	.509	.449	−.323	−.195	−.298	.024
(exponential age function)	(.160)**	(.129)**	(.304)	(.051)**	(.306)	(.041)
Genetic Stability	1.032	1.770	−.321	−.793	.263	−.331
(exponential age function)	(.086)**	(.278)**	(.093)**	(.140)**	(.093)**	(.094)**
Shared Environmental	.861	1.127	−.565	−1.739	−.470	−1.383
Stability	(.045)**	(.223)**	(.106)**	(.171)**	(.376)	(.198)**
(exponential age function)
Nonshared Environmental	.057	.004		−.493	1.975	−6.205
Stability	(.031)	(.011)		(.112)**	(1.935)	(4.496)
(linear age function)

Note:

^*p<.05

^**p<.01.

Figure 7.

Temporal decay of phenotypic stability (top left panel), genetic stability (top right panel), shared environmental stability (bottom left panel), and nonshared environmental stability (bottom right panel) in childhood. Each line represents a different starting age that is followed with increasing time lags. The differential temporal decay of stability at different starting ages represents the age × time interaction.

The top left panel of Figure 7 represents the model-implied age- and time- based trends in phenotypic stability. Two trends are of note. First, as was also indicated by age-based trends reported earlier, which did not include time, phenotypic stability increases as a function of baseline age. Second, as expected, phenotypic stability is higher over shorter time intervals and decays over longer periods of time. This time decay effect appears to be considerably more pronounced for earlier baseline ages. However, the age × time interaction is not statistically significant. Therefore, the question of age-differences in time-based decay of phenotypic stability cannot be answered definitively from these data alone. It is worth noting however that the overall trends, including the more pronounced time-based decay of stability at younger ages, are apparent in Bayley’s (1949) data, reproduced in Figure 1.

The top right panel of figure 7 represents the model-implied age- and time- based trends in genetic stability. Like the trends in phenotypic stability, it can be seen that stability increases with age and decays with time. It can also be seen that the time-based decay is less pronounced at increasing ages. This age × time interaction is statistically significant in the case of genetic stability. Also of note from this figure is the tremendous range of stability coefficients across ages. Genes for cognition at 2 years are practically uncorrelated with genes for cognition at 18 years (or with genes for cognition at 10 years for that matter), whereas genes for cognition at 10 years are nearly identical to genes for cognition at 18 years.

The bottom left panel of Figure 7 represents the model-implied age- and time- based trends in shared environmental stability. Again, stability increases with age, decays with time, and time-based decay decreases with age. The age × time interaction is statistically significant. The range of stability coefficients is more restricted across ages. Shared environmental stability starts off at moderate levels in very early childhood, with some time-based decay, and quickly increases to high levels with very little time-based decay.

The bottom right panel of Figure 7 represents the model-implied age- and time- based trends in nonshared environmental stability. It can be seen that stability is nearly uniformly low throughout the childhood age range. The intercept of the function is not significantly different from zero. Moreover, although there is some indication of a linear increase in stability with age, the age-based growth rate is not statistically significant. The time scaling factor is statistically significant, but the time decay rate and the age × time interaction are not. In sum, there is very little evidence for nonzero stability of nonshared environmental influences on cognition in childhood.

Different Stabilities for Different Abilities?

Next, we sought to examine the extent to which phenotypic, genetic, and environmental stabilities differ for different abilities. We were particularly interested in contrasting the stabilities of general intelligence and specific abilities (both fluid and crystallized abilities), and in contrasting the stabilities of fluid and crystallized abilities with one another. We performed our analyses exclusively for childhood (younger than 18 years). This was primarily for two reasons: (1) the majority of the identified change in stability occurred during childhood making this age period particularly relevant, and (2) data density was low for measures of general intelligence in adulthood. Therefore, results based on data obtained from children may more closely reflect the changing developmental processes for methodological (i.e., low data density) and theoretical (i.e., evaluating precursor abilities in isolation rather than mixed with adult end states) reasons.

We controlled for the age trends in the data using the best fitting continuous function from the analyses reported early (specifically, exponential growth for phenotypic stability, r_a, and r_c, and linear growth for r_e), and additionally controlled for the time-based decay of stability with an exponential model (with interaction terms for age for the models applied to genetic stability and shared environmental stability, as these terms were significant in the analyses reported earlier). Results are presented in Table 7.

Table 7.

Parameter Estimates for Moderators of Stability in Childhood.

Effect Size	General Intelligence (0) vs. Fluid Abilities (1)	General Intelligence (0) vs. Crystallized Abilities (1)	Fluid Abilities (0) vs. Crystallized Abilities (1)
Phenotypic Stability	−.194 (.062)**	−.102 (.039)*	.092 (.053)
Genetic Stability	015 (.045)	−.127 (.037)**	−.142 (.050)**
Shared Environmental Stability	−.075 (.025)**	.212 (.014)**	.287 (.034)**
Nonshared Environmental	−.087 (.033)**	.155 (.045)**	.242 (.040)**
Stability

Note

^*p<.05

^**p<.01.

General Intelligence and Specific Abilities

Compared with measures of general intelligence, fluid abilities tend to display less stability at the phenotypic, shared environmental, and nonshared environmental, but not genetic levels. For example, the phenotypic stability of general intelligence is nearly .19 correlation units higher than the phenotypic stability for abilities.

Compared with measures of general intelligence, crystallized abilities evidence lower phenotypic stability and genetic stability, but higher shared environmental stability and nonshared environmental stability. The effect for the shared environmental stability was especially pronounced representing a .21 larger cross-time correlation in comparison to that for general intelligence.

In sum, general intelligence tends to be more stable at the phenotypic and genetic levels than either fluid or crystallized abilities. However, fluid abilities tend to display less environmental stability compared to general intelligence, and crystallized abilities tend to display more environmental stability and less genetic stability.

Fluid and Crystallized Abilities

The phenotypic stabilities of fluid and crystallized abilities did not differ significantly from one another. Crystallized abilities displayed less genetic stability than fluid abilities, and appreciably greater shared and nonshared environmental stabilities (.287 and .242 correlation units higher, respectively).

Possible Publication Bias?

To examine whether publication bias might have affected our key estimates, we examined funnel plots of r_a, r_c, and r_e. Funnel plots are used to examine the distribution of individual study effect sizes as a function of the estimates’ imprecision. As expected by sampling theory, there should be greater scatter around lower precision estimates, and less scatter around higher precision estimates. Importantly, scatter should be symmetrical around the estimated population mean, representing a “funnel” shape. Because the above analyses indicated that effect sizes vary substantially with age, we first conditionalized the r_a, r_c, and r_e effect sizes on the best-fitting continuous age-based models (i.e. excluding the spline model). These were the exponential model for r_a and r_c, and the linear model for r_e. We then plotted these conditionalized effect sizes against the natural logarithm of their standard errors (the distributions of standard errors were strongly positively skewed, making funnel plots of untransformed standard errors difficult to visualize). The plot for r_a was funnel shaped and appeared symmetrical. The plot for r_c was also funnel shaped, and appeared symmetrical with the exception of there being a few highly negative effects with very large standard errors (i.e., standard errors greater than 1.0) that were not balanced out by highly positive effects. To examine whether the age trend for r_c was affected by this asymmetry, we reran the age-based exponential model for r_c with all effect sizes with standard errors greater than 1.0 removed. Parameter estimates and associated standard errors were nearly unchanged. Finally, the plot for r_e appeared haphazardly scattered. We were unable to correct r_e estimates for unreliability (articles tended not to report internal consistency estimates). It is therefore possible, if not likely, that the lack of a clear funnel shape for r_e was caused by idiosyncratic differences in measurement error.

Sensitivity Analyses

Finally, we conducted two sets of sensitivity analyses. In the first set of sensitivity analyses, we tested whether the age trends reported above were affected by two potential confounds: changing cognitive tests across measurement occasions and model trimming performed in the primary studies included in the meta-analytic dataset. Because of the dramatic developmental gains in cognitive performance that occur in infancy and childhood, longitudinal studies of infants and children may be more likely to upgrade to different (more difficult, and hence, age appropriate) cognitive tests across waves than are longitudinal studies of adolescents and adults. It is therefore possible that low cross-time correlations in early childhood, derive not from low stabilities of individual differences in abilities, but instead from the possibility that the different cognitive tests used at different waves tap slightly different abilities that are themselves influenced by somewhat different genetic and environmental factors. Moreover, because some of the effect sizes that we extracted were derived from models (fit by the original study authors) that had been trimmed (e.g. had some parameters fixed or removed), it is possible that the patterns of results obtained was biased by systematic approaches to model trimming used in the original studies. In the second set of sensitivity analyses, we were interested in the possible influence of including data not only from tests of cognitive abilities but also from tests of academic achievement (e.g. reading and math).

Complete methods and results for both sets of sensitivity analyses are provided in the online supplement to this article. Although both sets of sensitivity analyses indicated statistically significant effects of the covariates introduced into the models, the patterns of age- and time-based trends reported above (and depicted in Figures 4-7) remained. This indicates that the age- and time-based trends were unlikely to be artifacts of changing measures, model trimming, or a specific focus on cognitive (rather than achievement) variables.

Discussion

This meta-analysis represents the first quantitative synthesis of the effects of age and time on the stability of genetic and environmental influences on cognition across the life span. Although previous primary studies have reported magnitudes of genetic and environmental stabilities over circumscribed periods of development, our meta-analytic approach enabled us to synthesize effect sizes from longitudinal behavioral genetic studies spanning a wide range of ages and time-lags to estimate age- and time-based trends in the stabilities of genetic and environmental influences on cognition from infancy through old age. Our meta-analytic results confirm established findings that genetic influences on cognition are largely constant in adolescence and adulthood (Trzaskowski, Yang, Visscher, & Plomin, 2013), but more importantly highlight considerable changes in genetic and environmental stabilities over age and time in the first decade of life. We highlight four particularly novel aspects of our results below.

First, although phenotypic stability was moderate (r₁₂ = .49), genetic and shared environmental stabilities were high (r_a = .78 and r_c = .67), and nonshared environmental stability was low (r_e = .17), on average, all forms of stability were found to increase substantially from low levels in infancy to moderate or high levels in adulthood. For genetic and shared environmental effects, the increase is steep in early and middle childhood, leveling out at close to unity by early adolescence. Early in development, the genetic and family-level environmental factors that influence cognition at one point in time are largely different from those that influence cognition at later points in time. The well-known finding that genetic and family-level environmental effects on cognition are largely the same over time (Plomin, DeFries, Knopik, & Neiderhiser, 2013) pertains specifically to early adolescence forward; in the first decade of life, genetic and environmental stabilities undergoe tremendous changes. The stability of the nonshared environment did not display such a rapid rise, but instead slowly and linearly increased from very low levels in childhood to moderate levels by old age. Although the stability of the nonshared environment is typically thought to be quite low, we find that it becomes progressively more stable with age. The stability of cognition at the phenotypic level also displayed a marked increase from fairly low levels in infancy, approaching an asymptote of approximately .80 by late adolescence.

Second, we uncovered large differences in the extents to which genetic and environmental factors underlie developmental increases in phenotypic stability. Our results indicate that the primary cause of increasing phenotypic stability can be attributed to genetic influences. However, genetic influences do not contribute much to phenotypic stability in early childhood. Rather, shared environmental factors contribute predominantly to stability during this period, with these contributions declining with age. Nonshared environmental influences come to contribute a nontrivial amount to stability with age. In fact, the nonshared environmental contribution to stability is greater than the shared environmental contribution by midlife, and especially so in old age. However, the nonshared environmental contribution is much less than the genetic contribution at every age. By late adulthood, when the estimate for the nonshared environmental contribution is largest, this contribution is only a quarter of the genetic contribution. Taken as a percentage of total stability, genes account for approximately 75% of stability and the nonshared environment accounts for 20% of stability in late adulthood.

Third, stability decayed with increasing time intervals between measurement occasions. For the genetic and shared environmental effects, the time-based decay in stability was more pronounced earlier in childhood. With increasing childhood age, stability persisted to a greater extent over time. This age × time interaction was particularly pronounced for genetic stability. Our results indicated that for 2 year olds, genetic stability decayed from approximately .60 over a one year interval to approximately .20 over a six year interval, whereas for 10 year olds genetic stability remained above approximately .90, regardless of time interval.

Fourth, the type of cognition being measured mattered for stability. Measures of general intelligence tended to display greater phenotypic stability compared to measures of both fluid and crystallized abilities. Fluid abilities displayed less shared and nonshared environmental stability than did general intelligence. Crystallized abilities displayed greater shared and nonshared environmental stability than both general intelligence and fluid abilities. Finally, genetic influences on crystallized abilities were less stable than those on both fluid abilities and general intelligence. These differences between the stabilities of different abilities represent a particularly innovative set of results, as we are aware of no previous studies that have directly compared the stabilities of different cognitive abilities.

Assumptions and Limitations

Convergence of Age-Related Differences and Age-Related Changes

One major assumption of the age- and time-based analyses presented here is what Bell (1953) termed the convergence assumption, which holds that between-sample age differences are informative about within-population changes. In order to make inferences about age trends in stability across the human life span, we combined information derived from across-sample age differences with information derived from within-sample across-occasion stability. Thus, the age trends detected might not only reflect developmental changes in stability over time, but also reflect cohort or period differences in stability, as well as cross-study differences in measures, methods, and populations sampled. Importantly, these potential confounds would have to be systematically associated with age in order for the developmental trends to be biased rather than merely obscured. There is a large literature (e.g. Baltes, Reese, & Nesselroade, 1977; Glenn, 1976; Tucker-Drob & Salthouse, 2011; Yang & Land, 2013) on theoretical and methodological issues surrounding the separation of age-period- and cohort-effects from one another that we encourage the interested reader to attend to.

We relied on the convergence assumption to aggregate longitudinal studies spanning different finite periods of development because were unable to identify a single longitudinal twin or adoption study of cognition that spanned both childhood and old age. The only study that we are aware of that documents the stability of genetic effects on cognition from childhood through old age in a single sample followed over time is a highly innovative molecular-genetic study by Deary et al. (2012). This study was not included in our meta-analysis because our inclusion criteria required that studies included data from siblings of varying degrees of genetic relatedness, which this study did not. Deary et al. (2012) instead used genome-wide information and longitudinal data on a population-representative sample of unrelated individuals measured on general intelligence at age 11 years (childhood) and between ages 65-79 years (old age). The researchers were able to estimate the total R-squared contribution of measured molecular genetic variants in linkage disequilibrium with true causal variants on cognition during these two age periods, along with the correlation among genetic factors at both ages. The authors estimated this correlation to be .62, however, the standard errors of the estimate were very large, such that the 95% confidence interval included both 0 and 1.

Early and Middle Adulthood

It is apparent from the scatterplots presented in this article that there was very little data covering the periods of early and middle adulthood. We suspect that this may reflect a more general trend in the study of cognition, even outside of behavioral genetics. Researchers interested in cognitive development routinely study infants, children, and adolescents. Researchers interested in cognitive aging traditionally study older adults. A commonplace assumption in the cognitive aging literature is that cognition does not change in young and middle adulthood. In spite of a long history of challenges to this assumption (e.g. Jones & Conrad, 1933; Horn & Donaldson, 1976), including a series of publications by Salthouse (e.g. Salthouse, 2004; Salthouse, 2009) demonstrating population-average cognitive declines detectable as early as age the third decade of life, and recent work by Tucker-Drob (2011) indicating reliable individual differences in cognitive change during early adulthood, there continues to be little empirical attention placed on cognitive changes in young and middle adulthood. The ramification of this lack of attention to early and middle adulthood for the current study is that there is good data coverage in childhood and old age, but very sparse data coverage in between these age ranges. Although the functions fit in the current study can be used to interpolate patterns that might be expected for this age period, we were limited in our ability to delineate specific patterns of change that occurred between adolescence and late adulthood. We did not detect any systematic discontinuities between adolescence and adulthood, but our power to detect such discontinuities was limited by poor data coverage. As more longitudinal behavioral genetic research is conducted in young adult and middle aged populations, the patterns of genetic and environmental continuity over these age ranges will be able to be more directly examined.

Rarity of Longitudinal Genetically Informative Studies of Cognition

Our analyses were successful in detecting statistically significant age trends in our meta-analytic dataset. However, just 16 independent samples contributed to the dataset, a small amount relative to most meta-analyses. Importantly, many studies contributed multiple waves and cognitive variables, which we were able to leverage to our advantage to examine moderators, while implementing methods that corrected for nonindependence associated with multiple effect sizes per study. As more longitudinal genetically informative studies on cognition accumulate, we will be able to test for even more complex age and time functions and interactions.

Unavailability of Raw Data

Unfortunately, we did not have access to raw data from the original studies, and not all studies reported comprehensive within- and cross- time sibling correlations. For the studies that reported results of unconstrained longitudinal models, such as the complete two-wave correlated factors, autoregressive, and Cholesky models, we were able to derive relatively unbiased model-implied correlations to include in our meta-analysis. However, some studies only reported results from models that had been trimmed. This trimming might have either biased our results, or introduced a degree of smoothing to the age trends relative to what would have been obtained from raw data. Importantly, sensitivity analyses indicated that controlling for whether effects sizes were derived from trimmed models did not appreciably alter the patterns of results obtained.

Separating the Nonshared Environment from Measurement Error

The general lack of availability of information on the reliability of the measures implemented prevented us from using this information to separate systematic variance from random measurement error in our estimate of the nonshared environment. Had unreliability been isolated into separate error terms, we would have been able to statistically disattenuate our estimates of nonshared environmental stability. Our results indicated that nonshared environmental stability increases linearly from approximately .05 in childhood to approximately .50 by age 70. Had, for example, reliability been uniformly estimated at .85, the age trend for the corrected nonshared environmental stability would have been one that increased from approximately .20 in childhood to approximately 1.0 by age 70. However, because reliability estimates were not generally available, it is unknown what the appropriate correction should be. If random measurement error is systematically related to age our uncorrected estimates may be unevenly biased, leading to potentially gross distortions in the age trends obtained. However, we suspect that this was not the case, as a review of the manuals for standardized measures of cognition (e.g. the WJ-III, the WISC-IV, and the WAIS-IV) reveals very little evidence for systematic age differences in test reliability (see, e.g., Tucker-Drob, 2009). Finally, it is important to note that, although the stability of the nonshared environment is affected by random measurement error, the contribution of the nonshared environment to phenotypic stability is not affected by such error. It would be prudent for future longitudinal behavioral genetic investigations to take test reliabilities into account, particularly when investigating patterns related to the magnitude and stability of the nonshared environment.

Relating the Results to Extant Theories of Developmental Continuity and Change

Taken together, these findings appear to be most consistent with transactional models of cognitive development that emphasize gene-environment correlation and interaction. Before highlighting the consistency of our results with such models, we will first evaluate the current results relative to less complex accounts. The genetic set-point / genetic canalization hypothesis (Waddington, 1942; Conley, 1984) predicts either near perfect stability of genetic factors across time or, in the case of the more elaborate moving genetic set-point hypothesis, stability that is dependent on important biological transitions, such as puberty, that may activate new genes. Neither of these predictions was supported by our results. In early childhood, the stability of genetic effects was low. Further, examination of the linear-spline and exponential models of genetic stability highlights a fairly constant increase in genetic stability rather than an increase associated with a certain developmental transition. This trend is also borne out when the scatterplot of the data is examined. The genetic set-point/genetic canalization hypotheses also predict that environmental influences will be fleeting with time. However, the shared environment displayed only slightly less stability than genetic effects, and in old age even nonshared environmental effects, which are often dismissed as idiosyncratic time-specific effects, evidenced substantial stability.

The experiential canalization hypothesis (Knudsen et al., 2006) posits that very early in development environmental inputs can shift levels of cognitive ability to a large extent, but later in development, cognition becomes more insulated from varying environmental inputs. This would imply that the stability of environmental effects would remain relatively low in early childhood and increase substantially with age. Some evidence for this hypothesis was found in that environmental stability was low in early childhood and increased with age. However, shared environmental factors actually accounted for decreasing amounts of phenotypic stability with increasing age. Genetic factors, alternatively, accounted for large portions of stability from early adolescence onward, a finding that the experiential canalization hypothesis is by itself ill-equipped to explain.

Under the stability of experience hypothesis (Sameroff et al., 1993), recurring environmental experiences, particularly those associated with one’s racial/ethnic background or social class, are thought to shape cognitive development. This is because these factors exert pervasive influences on almost all facets of an individual’s life. Inconsistent with this hypothesis, shared environmental effects displayed low-to-moderate stability in childhood. Additionally, this hypothesis predicts that family-level effects decrease in stability as children develop and gain increasing autonomy over their learning experiences. It is possible to observe this trend in the data as the linear model for the stability of the shared environment decreases from age 8 to age 18, and an inspection of the scatterplot does show at least one influential effect size with lower stability during this time span that may represent a discontinuity. However, the better fitting exponential model does not display a similar decrease, and none of the estimated discontinuity parameters for the linear-spline model were significant. More data, particularly covering educational, vocational, and family transitions, would be needed to convincingly address the possibility of discontinuities in stability. Most problematic for the stability of experience hypothesis is that it is by itself unable to explain the substantial developmental increases in genetic stability or the preponderance of genetic contributions to phenotypic stability.

The primary premises of the embedded dynamism model were largely supported (Baltes et al., 1999). That is, we found evidence that the stability of cognitive ability, as well as the genetic and environmental influences on cognitive ability, changed substantially over development. Further, these changes were dependent on the specificity of the measured outcome, whether fluid or crystallized abilities were assessed, and the amount of time that passed between waves of data collection. This last finding is particularly telling because it means that as greater time passes between observations there are increasing opportunities for different dynamic processes to influence development. Somewhat astoundingly though, intervening processes on genetic stability seem to be absent by age 10, at which point genetic stability approaches unity and does not appreciably decrease with increasing time lag.

Despite the advantages of the embedded dynamism model for including multiple developmental theories for different developmental periods, an explicit allowance for gene-environment interaction and correlation may provide an even richer account of the current results. A developmentally-oriented gene × environment interaction perspective would predict that the activation or expression of genes relevant for cognition is dependent on the environment in which the child is situated, but that as the child grows older, cognition becomes increasing shielded from this action. Thus, the stability of genetic effects would be low at early ages when new gene expression is occurring due to novel environmental experiences, and genetic stability would increase with age as the amount or influence of novel environmental inputs decreases. Gene-environment correlation occurs when environments are selected and evoked on the basis of genetically influenced traits, preferences, and dispositions. Thus, siblings who share greater genetic similarity will find themselves in increasingly more similar learning environments than less genetically similar siblings. As transactional processes progressively accumulate over development, genetic effects should become more highly stable. Indeed we found that genetic effects on cognition become increasingly stable with age, and these effects increasingly account for the stability of cognition.

Although theories of gene-environment correlation and interaction are largely consistent with the current findings, several unexpected findings concerning the environment do not fit neatly within this framework. For example, Dickens and Flynn’s (2001) transactional model of gene-environment correlation predicted that shared environmental effects would be stable across the lifespan and nonshared environmental effects would be unstable. However, we found that shared environmental effects were somewhat unstable in early childhood, and nonshared environmental effects increased to moderate levels of stability by old age. Of course, nonshared environmental stability would have been even higher had we been able to correct the nonshared environment for measurement error. Nevertheless, in later life, even with measurement error unaccounted for, within-MZ pair differences in cognition are largely maintained over time. Establishing what the mechanisms are that stabilize one’s cognitive ability in adulthood, even after controlling for genetic and shared environmental influences, may be particularly valuable for future research.

If theories of gene × environment interaction and gene-environment correlation are correct, how might they shape the interpretation of the current results or the results of twin studies more generally? When gene × environment interactions or gene-environment correlations are not explicitly modeled in behavior genetic analyses, there are predictable and important consequences, two of which we focus on here. First, if objectively shared environments (e.g., school quality, social class, etc.) exert cumulative causal influences on cognition over development that vary depending on the genotype of the child (i.e., gene × shared environment interaction; e.g. Tucker-Drob et al., 2011; Turkheimer et al., 2003) then effective estimates of shared environmental contributions to stability will decrease with age, as was documented here. In other words, as gene-by-shared environment interactions compound with age, the effects of objectively shared environments become ever more tied to genotypic differences. This may also help to explain why the stability of the shared environment increases to such a high level. As recurrent objectively shared experiences increasingly differentiate individuals on the basis of their genes, it is possible that the only remaining shared environmental main effects are those that have resulted from particularly severe and lasting early environmental experiences that all humans respond similarly to. Second, the accumulations of gene-nonshared environment correlations over development, commonly referred to as active or evocative gene-environment correlation, can lead to age-related increases in effective estimates of genetic contributions to stability, as was documented here. For example, genetically influenced individual differences in noncognitive traits such as intellectual curiosity and motivation may lead individuals to receive more intellectual stimulation from parents, teachers, and even peers. This stimulation is objectively an environmental influence, but because it was selected and evoked on the basis of genotypic differences, it acts to make genetically similar individuals more phenotypically similar (Tucker-Drob & Harden, 2012a; Turkheimer & Waldron, 2000). As children consistently, and perhaps even increasingly, select and evoke differential levels of stimulation on the basis of their genotypes over time, genetic stability will increase. These considerations together indicate that estimates of genetic influence are likely to reflect environmentally-mediated mechanisms. As we discuss below, ongoing research will do well to explicitly examine specific mechanisms of gene × environment interaction and gene-environment correlation.

Additional Implications: Explaining Increasing Heritability across Development

In addition to their implications for evaluating and distinguishing between different theories of developmental continuity and change, the findings reported in this paper may have important implications for explaining a finding that Jensen (1998, p. 179) has described as “among the most striking and strongly substantiated findings of behavioral genetics in recent years,” which is that genetic influences on cognition increase throughout infant, child, and adolescent development (see Tucker-Drob, Briley, & Harden, 2013, for a review of this literature). For instance, an early meta-analysis by McGue, Bouchard, Iacono, and Lykken (1993) indicated increases in heritability from approximately 40% at age 5 to close to 60% in adolescence, to over 80% in adulthood. Haworth et al. (2010), more recently, synthesized cognitive ability data from six twin studies from four different countries and found that heritability increased rather linearly from 41% at 9 years to 55% at 12 years to 66% at 17 years. Studies of very young children (e.g. Fulker, DeFries, & Plomin, 1988; Tucker-Drob et al., 2011) have also reported this pattern, with heritability increasing from virtually 0% in the first year of life to approximately 20% by toddlerhood. One possible mechanism for these increases in heritability is that “new,” previously inactive genes come to be expressed over development. A second possible mechanism is that the effects of genes that are active early in life become amplified with age, e.g. via transactional processes of gene-environment correlation. Our finding that genetic influences are unstable in infancy and early childhood, and highly stable after the first decade of life, indicate that “new” gene activation may be the predominant mechanism of increasing heritability in early development, whereas amplification of previously active genes may be the predominant mechanism of increasing heritability in middle childhood and adolescence. Indeed, longitudinal behavioral genetic models that formally distinguish between these different mechanisms of increasing heritability have produced results consistent with this interpretation (Briley & Tucker-Drob, 2013).

Prospects for Future Research

The results of our meta-analysis provide some leverage on distinguishing between various theories of continuity and change, and many of the theories reviewed, in turn, provide rich frameworks by which to interpret our meta-analytic results. Nevertheless, our results might be best described as richly characterizing, for the very first time, the complex and interactive patterns by which age and time relate to the continuities of genetic and environmental influences on cognition. Here we discuss what methods and data future research would do well to employ in order to add further explanatory clarity to these patterns.

Documentation and Explicit Modeling of Gene-Environment Correlation

Transactional models of gene-environment correlations provide a conceptually appealing perspective not only by which to account for developmental trends in longitudinal stability, but also by which to more generally conceptualize how genetic and experiential forces combine to affect cognitive development. Initial support for transactional models derives from findings that environments are themselves heritable on the part of child genotypes (Kendler & Baker, 2007), and findings that psychological factors and environmental factors have bidirectional cross-lagged associations over time (Tucker-Drob & Harden, 2012a). However, specific tests of transactional models are rare, as are principled and concerted efforts to identify the constellations of environments and experiences that are relevant to learning and come to be selected and evoked on the basis of genetically-influenced traits and preference. Moreover, it is not fully clear which genetically-influenced psychological characteristics drive selection, evocation, and attention to cognitively stimulating environments (although see von Stumm & Ackerman, 2013, for a promising step in this direction), and what the specific time-ordered dynamics are through which gene-environment-cognition feedback processes operate. Indeed, identification of specific measured environments on which siblings differ that can account for meaningful variance in psychological phenotypes has been a longstanding goal that has vexed behavioral genetic researchers for some time (see Turkheimer & Waldron, 2000). If the environments relevant for cognition are those that result from stable and enduring gene-environment correlation processes (Dickens & Flynn, 2001), it may be the case that efforts to measure genetically influenced psychological tendencies to engage with a host of stimulating experiences will prove to be more fruitful –albeit less direct-for indexing cumulative environmental effects than efforts to measure the experiences themselves. In sum, future research efforts to collect multivariate longitudinal genetically-informative data on cognition, personality, and environments, combined with sophisticated genetic and longitudinal statistical approaches will be valuable for testing and delineating specific transactional processes of gene-environment correlation and their implications for the stability of individual differences in cognition over time and for cognitive development more generally.

Longitudinal Examination of Gene × Environment Interaction

Theories of gene × environment interaction provide particular appeal to scientists attempting to fully realize a rapprochement to the classic nature-nurture debate. Indeed, a number of different developmentally-oriented theories have been used to make predictions regarding the specific patterns of interactions between genes and the environment (e.g. Belsky & Pluess, 2009; Bronfenbrenner & Ceci, 1994; Raine & Venables, 1981, Pluess & Belsky, in press). Moreover, in contrast to work on gene-environment correlation, work on gene × environment interaction has received broad attention, with many individual studies identifying interactions between genes and single measures of the environment in predicting a host of individual phenotypes. One future direction for research on gene × environment interaction will be to synthesize the results of individual studies into a coherent theoretical and empirical account of what environments interact with genes for cognitive development in what ways, and whether the directions and magnitudes of the interactions depend on the specific cognitive phenotype examined. A second important direction for future research in this area will be to move from a static methodology, in which gene × environment interaction is examined in a single cohort at a single point in time, to longitudinal approaches in which environments and phenotypes are measured repeatedly over development. Very few studies have actually examined gene × environment interactions at multiple time points (see Hanscombe et al., 2012 and Tucker-Drob et al., 2011 for two notable exceptions), and even fewer have examined whether gene × environment interactions observed at a given point in time represent previous interaction effects or new interaction effects. Rhemtulla & Tucker-Drob (2012) have demonstrated how longitudinal behavioral genetic models can be used to distinguish between persisting disadvantage and recurring disadvantage patterns with respect to the interactive effects of socioeconomic status and genetic influences on cognition. A persisting disadvantage pattern is one in which early gene × environment interactions are lasting and potentially increase in importance with development. A recurring disadvantage pattern is one in which similar gene × environment interactions occur repeatedly throughout childhood. This latter pattern is one in which children experience relatively consistent levels of (dis)advantage over time that have novel, yet qualitatively similar, effects on development. Importantly persisting disadvantage and recurring disadvantage processes have differing implications for the stability of cognition, with the former contributing to stability and the latter contributing to instability over time. Note, however, that these two patterns are not mutually exclusive. As, Rhemtulla and Tucker-Drob (2012) emphasize, a gene × environment interaction “at a specific point in time can potentially result from a combination of the maintenance or magnification of differences in gene expression that occurred earlier in development and the emergence of differences in the expression of genes that that are unique to that age” (p. 550). Future work should continue to make use of such frameworks for conceptualizing and testing the longitudinal time course and persistence of gene × environment interactions.

Toward a Developmental Molecular Genetics of Cognition

As Reik (2007) commented, “Development is, by definition, epigenetic” (p. 425). However, conventional molecular genetic research on human psychological development has generally not paid much theoretical or empirical attention to issues surrounding developmental stability and change. Observing that “quantitative genetic studies have a long history of assessing genetic continuity and change across development,” Ronald (2011) recently argued that “it is now time for the newer, more technology-enabled fields such as GWAS and DNA resequencing also to take on board the dynamic nature of human behavior” (p. 1471). Indeed, there have been recent movements in this direction (e.g. Deary et al., 2012; Trzaskowski et al., 2013). One intriguing prospect for future work in molecular genetics will be identifying epigenetic patterns (e.g. methylation patterns) that modulate genetic effects on cognition and examine how such patterns change over development. Age-associated changes in genome-wide epigenetic patterns are widespread in mammals (Reik, 2007), but such patterns have not yet been specifically linked with genetic effects on cognition. Importantly, epigenetic processes occurring proximal to the genome are only one mechanism by which genetic influences can become activated and deactivated. Another potentially important mechanism of activation and deactivation of genetic influences may be developmental or socio-contextual processes that are more proximal to the phenotype than to the genome. For instance, even if genetic code is translated into gene products there may be developmental or contextual differences in the efficiency or success at which the gene products (and further downstream intermediary structures and functions) are translated into the ultimate phenotype of interest (Tucker-Drob, Briley, & Harden, 2013). Careful longitudinal measurement of biological, psychological, and environmental variables at multiple levels of analysis is therefore likely to continue to prove invaluable as research in molecular genetics progresses.

Neurobiological Substrates as Developmental Endophenotypes

Neurobiology represents an important intermediary pathway in the complex causal chain whereby genotypes and environments combine and interact to influence individual differences in cognition over development. Neurobiological markers that have been linked to individual differences in cognitive performance include total brain volume (McDaniel, 2005), cortical thickness (Narr et al., 2007), white matter tract integrity (Penke et al., 2012), and more efficient brain activity both during task performance (Haier et al., 1988, although see qualifications by Neubauer & Fink, 2009) and at rest (van den Heuvel, Stam, Kahn, & Pol, 2009). Although early work specifically implicated frontal brain structures in cognitive ability (Gray & Thompson, 2004) more recent work implicates distributed structures across the brain. Summarizing the literature, Deary, Penke, and Johnson (2010) concluded that “intelligence does not reside in a single, narrowly circumscribed brain region such as the frontal lobe. Rather, intelligence seems to be best described as a small-world network. (p. 207).” For instance, according to Jung and Haier’s (2007) P-FIT model, “cortices within parietal and frontal brain regions which, when effectively linked by white matter structures (i.e., arcuate fasciculus, superior longitudinal fasciculus), underpins individual differences in reasoning competence in humans, and perhaps in other mammalian species as well” (p. 138).

Despite the clear progress that has been made in understanding the neurobiological correlates of individual differences in cognition, the vast majority of such research has been phenotypic in nature. Researchers have only infrequently examined whether genetic influences on neurobiology are shared with genetic influences on cognition, or alternatively put, whether neurobiology mediates genetic influences on cognition. Some notable exceptions include Toga et al. (2001), who reported high heritability of frontal brain regions that were in turn linked to general intelligence, Posthuma et al. (2002), who reported genetic mediation of the association between whole brain volume and intelligence, and Chiang et al. (2009) who reported genetic mediation of the association between white matter integrity and intelligence We are aware of no researchers, however, who have explicitly decomposed the pathways between neurobiology and cognition specified under Jung and Haier’s (2007) P-FIT model into genetic and environmental components. Moreover, very few studies have made use of repeated measures of neurobiology and cognition across development. One notable exception includes a longitudinal study of adolescents by Ramsden et al (2011), which reported couplings between changes in verbal and nonverbal intelligence and changes in grey matter volumes in verbal (speech) and digital (finger movement) sensorimotor areas of the brain, respectively, indicating a role for sensorimotor structures in adolescent cognitive development. Below we discuss the promises and complexities of future work to incorporate neurobiological methods with longitudinal behavioral genetic methods in the study of the genetics of cognitive development.

The most straightforward role that neurobiological substrates might play in the genetics of cognitive development is as candidate endophenotypes. Endophenotypes are measurable biological or psychological intermediaries along the pathway from genotype to the ultimate phenotype of interest (Gottesman & Gould, 2003). The endophenotype concept has received widespread attention because of the hope that it can boost power of genomic association studies, and hence aid in gene discovery for complex psychological phenotypes. Moreover, identifying endophenotypes can potentially enrich mechanistic accounts of how genotypes develop into phenotypes. As Gottesman and Gould (2003) put it, endophenotypes can provide “simpler clues to genetic underpinnings.” As described above, a handful of studies have employed behavioral genetic approaches to test for neurobiological endophonetypes of cognition, i.e. neurobioglocial mediators of genetic influences on cognition. Future research, however, may benefit from employing longitudinal endophenotype approaches to aid in understanding the mechanisms of cognitive development. Harden, Quinn, & Tucker-Drob (2011) suggested that longitudinal changes in neurobiology be investigated as endophenotypes for developmental change in behavior. That is, rather than operationalizing the endophenotype and phenotype as static entities, both are conceptualized and analyzed as longitudinal changes. This concept may at face seem dissonant with the fact that the very definition of endophenotype is as a mediator of genetic effects, and that (barring the emergence of the occasional mutation) genetic code does not change over development. However, there are at least two ways in which static genotypes might be associated with changing endophenotypes and phenotypes. First is that, rather than coding for probabilistic determinants of end states, genes may code for probabilistic developmental norms of reaction (i.e. rates of change). Second, is that, although genetic code may not change appreciably over time, different genes may be associated with the phenotype at different points in time. As discussed in the section above, this can occur either because the same phenotype relies on different neurobiological and psychological mechanisms (that are themselves influenced by different genes) with age, or because of age- or experience-related epigenetic events that modulate gene expression at the molecular level. Indeed, a key finding reported in the current meta-analysis is that the genes that contribute to cognition in infancy overlap very little with those that contribute to cognition later in development. A longitudinal endophenotype approach may be especially relevant to the questions of genetic and environmental stability that were the focus of the current meta-analysis. Using longitudinal genetically informative measurement of neurobiology and cognition one might test, for example, whether the stability of genetic influences on cognition are mediated by genetic influences on brain structure. In order to answer this question in the affirmative, there must be a high degree of genetic overlap between indices of brain structure and cognition across multiple waves of data collection, and the genetic influences on brain structure should themselves be relatively stable over time.

Integrating neurobiological approaches with developmental behavioral genetics of cognition may not be a straightforward matter of summing methodologies. Complicating matters, for example, is that the nature of the association between neurobiology and cognition may differ with age. For instance, a large scale study by Shaw and colleagues (2006) found negative relations between cortical thickness and intelligence in early childhood that switched to positive relations in middle childhood. In scenarios such as this, in which brain-cognition associations change with age, it is not directly apparent how one might go about testing whether neurobiology mediates stability of cognition. It is possible that different biological processes (e.g. neuronal pruning, neurogenesis, and neural atrophy) affect the same neurobiological measurement (e.g. cortical thickness) to different extents at different points in development. Future research will need to pay careful consideration to the fact that biological measures need not reflect unitary, homogenous, or developmentally invariant processes.

Lastly, any investigation of genetic influence at multiple levels of analysis (e.g. neurobiology and cognitive) should be careful not to rely on an exclusive unidirectional assumption of causality from genes to neurobiology to cognition. Although it is certainly a reality that neurobiology must undergird cognition in the most basic sense, neurobiological substrates of cognition may themselves be amenable to reciprocal and interactive processes with environmental experiences, or with cognition itself for that matter (Chiang et al., 2011). Indeed, neurobiological indices need not function as “genetic endophenotypes” per se. They may instead function as what might be termed “environmental endophenotypes” – processes, structures, or functions that are internal to the individual, are relatively low in heritability, and mediate the effects of environmental experience on the ultimate phenotype of interest (see panel 5 of Figure 1 in Walters & Owen, 2007). Cortisol, a steroid hormone that is regulated by the hypothalamic-pituitary-adrenal (HPA) axis, is one illustrative example of a potential candidate “environmental endophenotype” of the deleterious effects of environmental stress and privation on cognition and other forms of psychological well-being (Lupien, McEwen, Gunnar, & Heim, 2009). For instance, in a longitudinal study of young children, Blair et al. (2011) reported that multiple indices of socioeconomic disadvantage predicted higher chronic levels of cortisol that were in turn associated with lower scores on measures of cognition. The direct paths from disadvantage to cognition were attenuated by including cortisol as a mediator. Importantly, however, it is unclear whether the effects were environmentally mediated, a crucial requisite for cortisol to be an environmental endophenotype. Determining environmental mediation would have been possible had the authors used a genetically informative research design (Turkheimer & Harden, in press).

Conclusion

We documented dramatic age-related changes in the stability of cognition at the phenotypic, genetic, and environmental levels. Genetic and shared environmental stability quickly rose from low levels in early childhood to near unity by early adolescence, and remained at very high levels throughout adulthood. Nonshared environmental stability increased gradually from near zero in early childhood to moderate levels by late adulthood. Whereas shared environmental factors were the primary determinants of phenotypic stability in infancy and very early childhood, genetic factors primarily accounted for the increasing phenotypic stability over development. We recommend that future work clarify the specific developmental processes of gene-environment correlation and interaction, and the roles that they play in increasing stability with age, via careful, multivariate, longitudinal measurement and modeling of cognition, personality, neurobiology, and experience in genetically informative samples.

Appendix A: Deriving Correlated Factors Model Parameters from Cholesky and Simplex Model Parameters

The formulas that follow use the notation from the path diagrams depicted in Figure 3.

Cholesky → Correlated Factors

The a₁, c₁, and e₁ parameters from the Correlated Factors model are equivalent to the a₁, c₁, and e₁ parameters from the Cholesky model. The a₂, c₂, and e₂ parameters from the Correlated Factors model can be derived from the a_b, c_b, e_b, a_u, c_u, and e_u parameters from the Cholesky model as follows:

$$a_2=\sqrt{a_b^2+a_u^2},c_2=\sqrt{c_b^2+c_u^2},e_2=\sqrt{e_b^2+e_u^2},$$

and the r_a, r_c, and r_e parameters from the Correlated Factors can be similarly derived from the Cholesky parameters as:

$$r_a=\sqrt{\frac{a_b^2}{a_b^2+a_u^2}},r_c=\sqrt{\frac{c_b^2}{c_b^2+c_u^2}},r_e=\sqrt{\frac{e_b^2}{e_b^2+e_u^2}}.$$

Simplex → Correlated Factors

The a₁, c₁, e₁, a_b, c_b, e_b, a₂, c₂, and e₂ from the Simplex model are equivalent to the a₁, c₁, e₁, r_a, r_c, r_e, a₂, c₂, and e₂ parameters from the Correlated Factors model respectively.

Loehlin (1996) provides further explication of these formulas and their substantive implications.