A temporal basis for predicting the sensory consequences of motor commands in an electric fish

Abstract

Mormyrid electric fish are a model system for understanding how neural circuits predict the sensory consequences of motor acts. Medium ganglion cells in the electrosensory lobe create negative images that predict sensory input due to the fish’s electric organ discharge (EOD). Previous studies showed that negative images could be created through plasticity at granule cell-medium ganglion cell synapses provided that granule cell responses to the brief EOD command were sufficiently varied and prolonged. Here we show for the first time that granule cells indeed provide such a temporal basis, and that it is well matched to the temporal structure of self-generated sensory inputs, allowing for rapid and accurate sensory cancellation and explaining paradoxical features of negative images. We also demonstrate an unexpected and critical role for unipolar brush cells (UBCs) in generating the required delayed responses. These results provide a mechanistic account of how copies of motor commands are transformed into sensory predictions.

Weakly electric mormyrid fish emit brief EOD pulses for communication and active electrolocation. However, the fish’s own EOD also affects passive electroreceptors tuned to detect external fields. Previous studies have shown that such interference, a ringing pattern of activation that may persist for as long as the interval between EODs¹, is cancelled out in medium ganglion cells through the generation of motor corollary discharge responses that are temporally-specific negative images of the sensory consequences of the EOD². Elegant theoretical studies^{3, 4} have suggested that anti-Hebbian spike timing-dependent plasticity known to exist at synapses from granule cells onto medium ganglion cells⁵ could provide a basis for negative image formation, but this work depends on the untested assumption that granule cell corollary discharge responses exhibit a rich temporal structure spanning the approximately 200 ms period over which negative images can be generated^{2, 6, 7}(Fig. 1a). Granule cells, located in the eminentia granularis posterior (EGp) overlying the electrosensory lobe (ELL) molecular layer, receive excitatory input from extrinsic mossy fibers originating from neurons in a number of brain regions and from UBCs located within EGp itself (Fig. 1b). Though there are a small number of published recordings of delayed corollary discharge responses from unidentified elements in the EGp itself⁸, corollary discharge responses of mossy fibers appear to be extremely brief and minimally delayed, resembling literal copies of the EOD motor command^8–11. Moreover, delayed or temporally diverse corollary discharge responses have not been reported for granule cells. Therefore, we set out to determine: 1) whether delayed and temporally diverse granule cell responses exist and, if they do, 2) how they are generated and 3) if they are sufficient to support negative image formation.

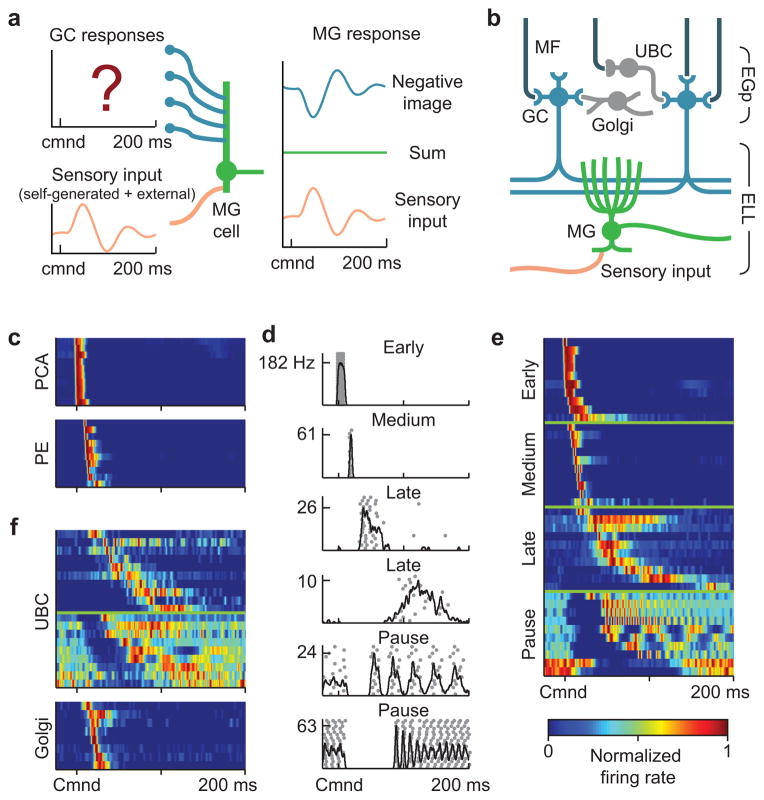
Figure 1. Corollary discharge responses in mossy fibers, UBCs, and Golgi cells.

(a) Schematic of negative image formation and sensory cancellation in a medium ganglion cell. The question mark indicates that temporal patterns of corollary discharge response in granule cells are the critical unknown in current models of sensory cancellation. (b) Schematic of the circuitry of the EGp and ELL. Corollary discharge signals related to the EOD motor command are relayed via several midbrain nuclei (not shown) and terminate in EGp as mossy fibers (MF, black inputs from top). UBCs give rise to an intrinsic system of mossy fibers that provide additional excitatory input to granule cells (GC). Golgi cells inhibit granule cells and UBCs. Medium ganglion (MG) cells in ELL receive both sensory input and granule cell input via parallel fibers. (c) Corollary discharge responses of units recorded in the paratrigeminal command associated nucleus (PCA) and the preeminential nucleus (PE). Each row shows the smoothed (5 ms Gaussian kernel) and normalized average firing rate of a single unit. In this and subsequent figures time is defined relative to the EOD motor command (Cmnd), which is emitted spontaneously by the fish at 2–5 Hz. Color bar in e applies also to c and f. (d) Example spike rasters (grey dots) and smoothed firing rates (black curves) for putative mossy fibers recorded extracellularly in EGp illustrating four temporal response classes (early, medium, late, and pause). (e) Corollary discharge responses of putative mossy fibers recorded extracellularly in EGp. Each row represents the smoothed and normalized average firing rate of a single mossy fiber, with 10 examples of each class shown. (f) Corollary discharge responses of UBCs (n = 19) and Golgi cells (n = 8) recorded intracellularly. Each row represents the smoothed and normalized average firing rate of a single cell. Note the similarity with late and pause mossy fibers, shown in e.

As in previous studies, we take advantage of an awake preparation in which fish continue to emit the motor command to discharge the electric organ, but the EOD itself is blocked by neuromuscular paralysis, allowing corollary discharge responses, i.e. neural activity in sensory areas that is time-locked to the EOD motor command, to be studied in isolation from sensory effects.

Results

Corollary discharge responses in mossy fibers and UBCs

Consistent with previous studies^8–11, extracellular recordings from two midbrain nuclei that are the main sources of corollary discharge input to granule cells revealed responses restricted to short delays after the EOD motor command (Fig. 1c, PCA, n=12; PE, n=31). To further characterize corollary discharge inputs to granule cells we used high-impedance glass microelectrodes to record from putative mossy fiber axons within EGp itself (see Methods for details of mossy fiber recordings). Most mossy fibers recorded in EGp exhibited responses restricted to short delays, termed early and medium, that closely resembled the responses recorded in midbrain neurons that send mossy fibers to EGp (Fig. 1d, e; early, n=54; medium, n=28). Thus corollary discharge inputs to EGp appear insufficient for cancelling the effects of the EOD over their entire duration. However, we also found other putative mossy fibers within EGp, termed late and pause, that exhibited far more delayed and diverse corollary discharge responses (Fig. 1d, e; late, n=26; pause, n=27). Late mossy fibers fire bursts or single action potentials at long delays after the EOD command (>50 ms), while pause mossy fibers show highly regular tonic firing that ceases abruptly around the time of the command. Resumption of firing is often marked by precise time-locking of spikes at long delays relative to the EOD command (Fig. 1d, bottom).

A candidate for the source of late and pause responses recorded in EGp are the UBCs that, in mormyrid fish as in the mammalian cerebellum and dorsal cochlear nucleus¹², give rise to an intrinsic system of mossy fiber axons that provides additional excitatory input to granule cells^{13, 14}. Whole-cell recordings from UBCs provided direct support for this idea. UBCs (n=54), granule cells (n=184), and Golgi cells (n=11) could be clearly distinguished on the basis of their electrophysiological properties and morphology (Supplementary Figs. 1–3). Strikingly, corollary discharge responses in UBCs are delayed and diverse, and they closely resemble late and pause responses recorded extracellularly (compare Fig. 1e and Fig. 1f). An objective classification algorithm supports our conclusion that early and medium responses are extrinsic mossy fiber axons originating from midbrain nuclei while late and pause responses are intrinsic mossy fiber axons originating from UBCs (Supplementary Fig. 4).

Possible mechanisms for generating diverse and delayed responses in UBCs were revealed by our intracellular recordings. Prominent post-inhibitory rebound firing was observed in a subset of UBCs (Fig. 2a, Supplementary Fig. 2), so rebound evoked by an inhibitory input arriving at a short delay after the EOD command (Fig. 2b, Supplementary Fig. 5a) could account for their delayed firing. Suggestive of such a mechanism, the morphologically identified UBC shown in Figure 2a, b fired bursts at a long delay after the command that were stronger when the preceding membrane potential was more hyperpolarized. Other UBCs exhibit regular tonic firing (Supplementary Fig. 2) that, when terminated by hyperpolarization, is followed by precisely time-locked spikes (Fig. 2c). This firing pattern is similar to pause responses recorded extracellularly and could also be explained by inhibition arriving at a short delay after the command (Fig. 2d, Supplementary Fig. 5a). Golgi cells respond at short delays after the EOD command (Fig. 1F, Supplementary Fig. 5b) and could be the source of such inhibition.

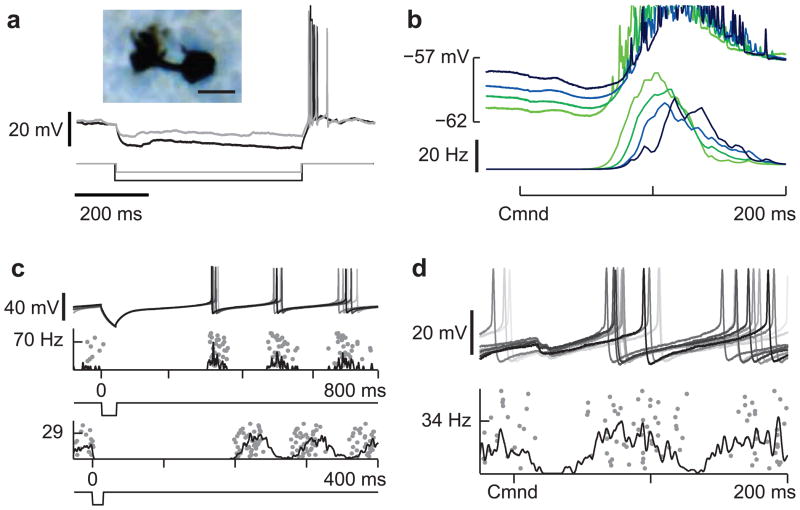
Figure 2. Mechanisms for delayed and diverse corollary discharge responses in UBCs.

(a) Two overlaid traces illustrating prominent rebound firing in response to hyperpolarizing current injections (−10 and −20 pA) in a UBC. This cell was filled with biocytin allowing for post-hoc morphological identification (inset, scale bar 10 μM). (b) Late corollary discharge response in the same UBC recording shown in a. The strength of late action potentials bursts (bottom traces) is related to the degree of preceding membrane potential hyperpolarization (top traces), suggesting rebound from command-locked hyperpolarization as a possible mechanism underlying late responses observed in UBCs. (c) Two UBCs in which a brief hyperpolarizing current injection (−50 pA, top; −200 pA, bottom) results in an entrainment of tonic firing, similar to temporal patterns of action potential firing observed in pause mossy fibers. Similar effects were seen in 7 additional UBCs. (d) Pause-type corollary discharge response in a UBC, note the small hyperpolarization time-locked to the command and the entrainment of tonic action potential firing after the pause.

Corollary discharge responses in granule cells

We next catalogued corollary discharge responses in a large number of granule cells using whole-cell recording. Corollary discharge responses were observed in 170 of 184 granule cells and consisted of prominent depolarizations with temporal patterns that are highly consistent across commands (Fig. 3a, b-left, Supplementary Fig. 5c, d). Granule cell depolarizations closely resemble early, medium, late, pause, or in some cases, apparent mixtures of these responses (Fig. 3b-right, Supplementary Fig. 5d). Action potential firing consistent mainly of single spikes (1.25 spikes/command for the roughly 20% of granule cells that fired on greater than 10% of commands) and always occurred at the peak of the subthreshold membrane potential (Fig. 4, Supplementary Fig. 6). These observations led us to hypothesize that the temporal structure of subthreshold granule cell corollary discharge responses is shaped primarily by summation of excitatory inputs, rather than by phasic Golgi cell inhibition or the intrinsic properties of the granule cells themselves. To test this, we modeled granule cell depolarizations as sums of excitatory postsynaptic potentials (EPSPs) computed from the spike trains of up to three of the recorded EGp mossy fibers (Fig. 1e), including UBCs (Fig. 1f). The small number of excitatory inputs is consistent with anatomical observations that mormyrid granule cells have, on average, three claw-like dendritic endings (N.S. unpublished observations) and previous physiological observations indicating that granule cells receive other sources of mossy fiber input in addition to corollary discharge, e.g. proprioceptive input from spinocerebellar mossy fibers¹⁵. By choosing an appropriate set of inputs from the recorded data and adjusting their excitatory synaptic strengths within a reasonable range (Fig. 3b-right; see Methods), we were able to fit the membrane-potential responses of the recorded granule cells with high accuracy (average MSE = 4.6%, n = 169; Fig. 3b-left; Supplementary Fig. 6). This provides strong support for the view of granule cell recoding as excitatory input summation stated above.

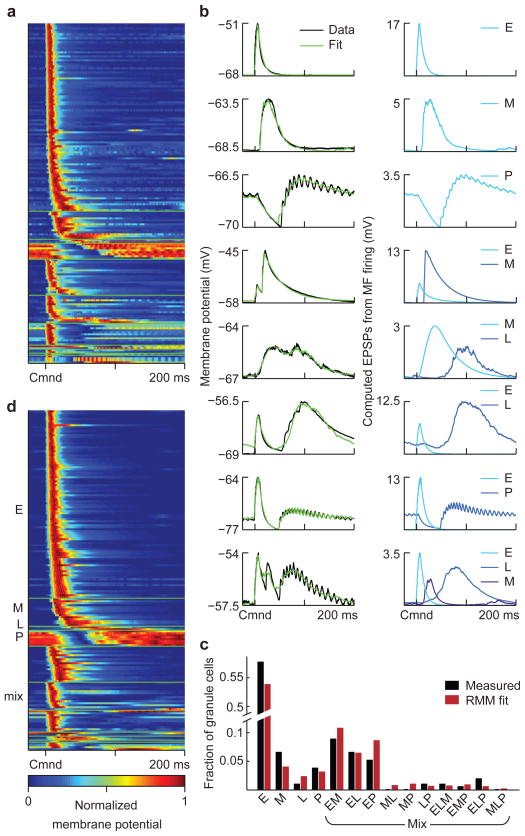
Figure 3. Experimental characterization and modeling of corollary discharge responses in granule cells.

(a) Average subthreshold corollary discharge responses of 170 granule cells. Responses are grouped by category (see d) and then sorted by the latency of their peak membrane potential. (b) Left, examples of recorded granule cell subthreshold responses (black trace) and model fits (green). Right, EPSPs computed from the recorded mossy fiber inputs used to fit each granule cell, labeled according to the class to which they belong. (c) The distribution of response categories assigned to recorded granule cells based on model fits (black bars). Bars labeled E, M, L and P indicate the fraction of early, medium, late and pause inputs used to fit the recorded granule cell responses. “Mixed” bars show these fractions for combinations of inputs used in the same way. These fractions are consistent with a four-parameter random mixing model (RMM; parameters are the probability of early, medium, late, and pause inputs) in which each input to a granule cell is assigned independently of the others (red bars). This suggests that the combinations of inputs granule cells receive are random. (d) Average subthreshold corollary discharge responses of 170 randomly constructed model granule cells selected from a total of 20,000. In this sample, the number of model cells from each granule cell category was matched to the experimental data, but the selection process was otherwise random. Note that the temporal response properties of the model granule cells closely resemble those of the recorded granule cell shown in a.

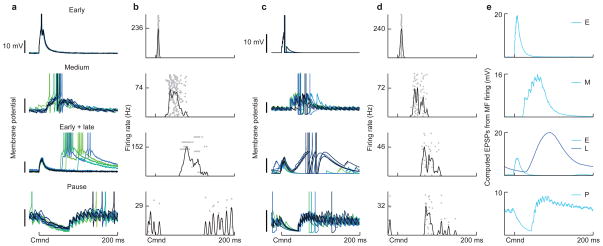
Figure 4. Patterns of corollary discharge-evoked action potential firing in recorded and model granule cells.

(a) Corollary discharge responses of four recorded granule cells that spiked in response to the EOD command. Granule cell membrane potentials from several commands are shown overlaid. Spikes are truncated to show details of subthreshold membrane potentials. (b) Spiking responses of the recorded granule cells shown in a. Spike trains on 50 individual trials are shown in gray, and the smoothed (5 ms Gaussian kernel) trial-averaged firing rate of the cell is overlaid in black. (c, d) Corollary discharge responses of four model granule cells selected from among the pool of 20,000 generated cells. Displays for model granule cells are the same as for recorded cells. e, Sources of mossy fiber input to each model granule cell, as computed EPSPs from the trial-averaged mossy fiber firing rates. Both subthreshold corollary discharge responses and spiking in model granule cells closely resembles that seen in recorded granule cells.

The similarity of the constructed and recorded granule cell responses also provides a powerful tool for addressing the central question of whether granule cell responses can support negative image formation and sensory cancellation. Given the sparseness of granule cell firing that we observed (both a small percentage of granule cells that fire and a small number of spikes per EOD in those that do), cancellation likely depends on large numbers of granule cell inputs; indeed, anatomical estimates are on the order of 20,000 granule cell inputs per medium ganglion cell¹⁶. To expand the data to this number, we constructed model granule cells. This was aided by the fact that the distribution of inputs found in our fits of recorded granule cell responses is consistent with a random mixing process in which each granule cell dendrite samples the different functional input classes (early, medium, late, and pause) independently (Fig. 3c). We extracted the probability of a granule cell receiving an input from each functional class from these fits (see Methods). Drawing randomly from these input probabilities and from the distribution of synaptic weights obtained during fitting allowed us to construct model granule cells with corollary discharge responses that closely match those of the recorded granule cells (Fig. 3d, Supplementary Fig. 6; note that these are not granule cells fit to the data, but randomly constructed and sampled model cells). The remarkable similarity between these model responses and the data provides additional support for the hypothesis that granule cell recoding of corollary discharge inputs can be explained by random mixtures of small numbers of excitatory inputs conveyed by extrinsic mossy fibers and UBCs.

Spiking in model granule cells was implemented by randomly assigning action potential thresholds sampled from a normal distribution fit to the thresholds of the recorded granule cells (average distance to threshold 20.2 ± 5.97 mV). The resulting temporal firing patterns and distribution of average spike counts per EOD in the model granule cells were statistically consistent with those of the recorded granule cells (Fig. 4, Supplementary Fig. 6).

Granule cells provide a basis for sensory cancellation

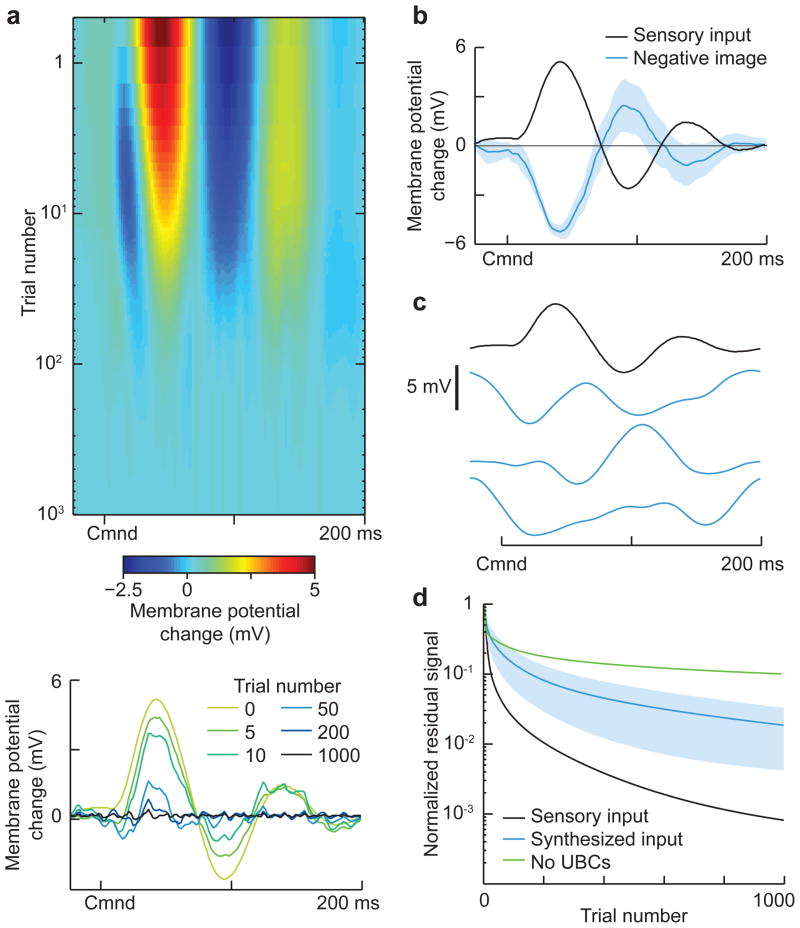
Previous experimental work has revealed a combination of anti-Hebbian spike-timing dependent long-term synaptic depression and non-associative long-term potentiation at granule cell-medium ganglion cell synapses^{5, 17}. To determine whether this form of plasticity can cancel self-generated sensory input using realistic granule cell responses, we drove a passive model medium ganglion cell with 20,000 model granule cell inputs through plastic synapses. The granule cell to medium ganglion cell synapses were strictly positive and their strengths were initially set so that granule cell responses in the absence of EOD-driven sensory input generated a roughly flat medium ganglion membrane potential, consistent with recordings from medium ganglion cells in regions of ELL involved in passive electrosensory processing^{2, 6, 7}. Next, we added a temporally varying sensory input to the model medium ganglion cell to mimic the responses of passive electroreceptors to the fish’s own EOD recorded in a previous study¹(Fig. 5a, bottom). As in previous modeling work³, the strength of the granule cell-medium ganglion synapses evolved according to the experimentally described plasticity rule^{5, 17}: synaptic strength is increased for each presynaptic action potential, corresponding to experimentally described non-associative potentiation, and decreased when a postsynaptic action potential occurs shortly after a presynaptic action potential, corresponding to experimentally described associative depression. Over the course of about 1000 EOD commands (approximately 5 minutes at EOD command rates typical of paralyzed fish), the membrane potential fluctuation caused by the sensory input is cancelled by the corollary discharge inputs conveyed by granule cells (Fig. 5a), consistent with the time-course over which negative images are formed in vivo^{2, 6}. The resulting negative image closely matches the inverse of the sensory input (Fig. 5b) and has small command-to-command variations (Fig. 5b, blue shading; standard deviation of ~1 mV) despite the sparseness of the granule cell firing. We also confirmed the stability of negative images formed using the granule cells as a temporal basis (see Supplementary Materials) and that the changes in synaptic strength underlying negative images were within a physiologically plausible range (Supplementary Fig. 7). Finally, because our estimates of both the number of granule cells active at long delays and the number of command-locked action potentials fired by granule cells were based on limited data, we tested the effects of systematically varying these properties of the model granule cells on negative images and sensory cancellation (Supplementary Figs 8–9). Rapid cancellation and negative images with small command-to-command variations were observed even when numbers of late and pause inputs used to generate model granule cells were reduced and when the number of action potentials fired by granule cells was reduced.

Figure 5. Granule cell corollary discharge responses provide an effective basis for cancelling natural patterns of self-generated sensory input.

(a) Top, Cancellation of the change in membrane potential caused by sensory input locked to the EOD motor command in a model medium ganglion cell. The medium ganglion cell receives 20,000 model granule cell inputs with synaptic strengths that are adjusted by anti-Hebbian spike-timing dependent plasticity. Bottom, select trials showing the time course of cancellation. The temporal profile of the sensory input (trial 0) was chosen to resemble the effects of the EOD on passive electroreceptors recorded in a previous study¹. (b) The negative image (blue line) effectively cancels the sensory input (black line), with small command-to-command variability (shaded region shows ± 1 std across trials.) (c) Different input signals used for the tests of sensory cancellation rates shown in d. The top trace is the same input used in a, and resembles natural self-generated inputs due to the EOD. The blue traces are selected from a set of 1,000 synthesized inputs with the same power spectrum as the natural input but with randomized phases. (d) Comparison of the time course of cancellation for the natural sensory input (black) versus the synthesized inputs (blue; shaded region is ± 1 std). Note that cancellation is faster for the natural input, suggesting that the structure of granule cell responses is matched to the temporal pattern of the self-generated signal. Cancellation is also much slower and less effective if the model granule cells are generated without UBC inputs (green line).

The effectiveness of the cancellation in the model is notable given the highly non-uniform temporal structure of the granule cell population response, in particular the fact that most granule cells are active at short delays. Rather than a general-purpose temporal basis, such as the delay-line model considered in previous theoretical work³, the structure of granule cell corollary discharge responses appears to be matched to the temporal patterns of self-generated sensory input that the fish encounters in nature, i.e. the particular pattern of ringing that the large EOD evokes in electroreceptors tuned to detect much smaller signals¹. To test this idea more directly we generated synthetic inputs with different temporal profiles but the same power spectrum as the electroreceptor response (Fig. 5c). Synthetic inputs are cancelled more slowly than inputs resembling the electroreceptor response (Fig. 5d), suggesting that the structure of granule cell responses is particularly suited to natural patterns of self-generated input. Furthermore, the rate and accuracy of sensory cancelation in the granule cell basis is comparable to that of an idealized uniform delay line basis with tuning widths approximately equal to that of granule cells receiving medium and late inputs (Supplementary Fig. 10). Finally, we note that model granule cell populations lacking late and pause inputs provide a far less effective basis for cancellation (Fig. 5d, green line), indicating an important role for the temporally diverse and delayed corollary discharge responses generated by UBCs.

Granule cell responses predict features of negative images

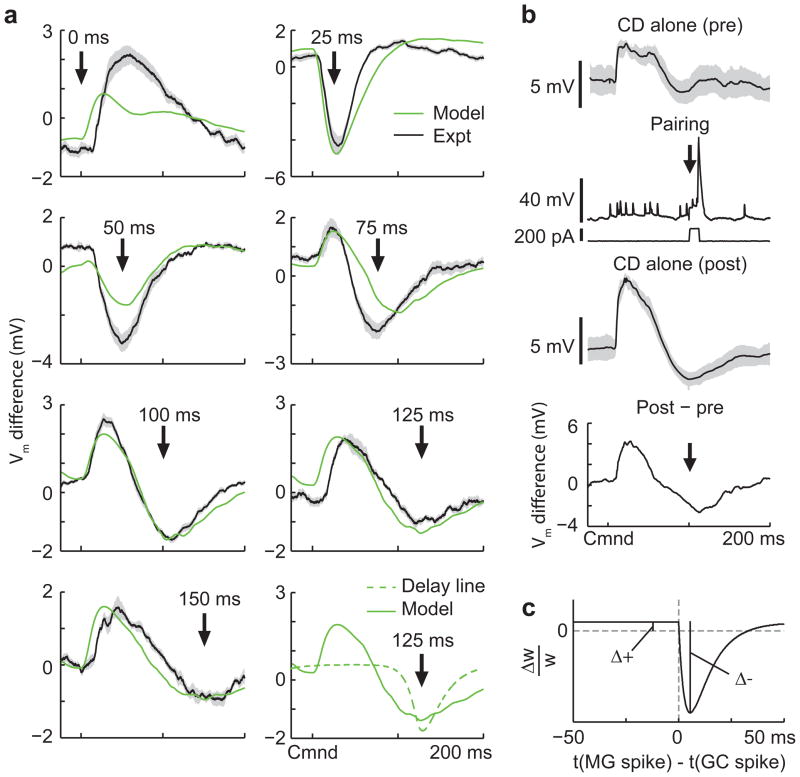
Our knowledge of the temporal structure of granule cell responses allowed us to make specific predictions about the shapes of negative images induced in experiments in which a single dendritic spike in a medium ganglion cell is paired with the EOD command at fixed delays. Previous studies have shown that such dendritic spikes are the key triggers for associative depression at granule cell synapses^{5, 18}. Our predictions based on the measured granule cell responses were twofold (Fig. 6a, green curves). Medium ganglion cell spikes evoked at short delays should induce a brief hyperpolarization peaked around the spike time due to associative depression of early granule cells inputs. More complex, bi-phasic changes were predicted for medium ganglion cell spikes evoked either at longer delays or at zero delay. At such delays, associative depression should induce a hyperpolarization around the medium ganglion cell spike time, while non-associative potentiation of the numerous early granule cell inputs should cause a “paradoxical” medium ganglion cell depolarization at short delays after the EOD command. In contrast, a model with a temporally uniform delay line basis predicts that negative images induced by medium ganglion cell spikes at different delays would always have the same shape, determined by the temporal window of the synaptic plasticity, and differ only by time translation (Fig. 6a, bottom right, dashed curve).

Figure 6. Non-uniform temporal structure of granule cell responses predicts specific features of negative images in medium ganglion cells.

(a) Changes in corollary discharge responses induced by pairing with medium ganglion dendritic spikes at 7 different delays after the EOD command. Green traces are membrane potential differences derived from the model with fitted values for the magnitudes of associative depression and non-associative potentiation (panel c). Black traces are experimentally observed membrane potential differences averaged across medium ganglion cells (outlines represent SEM; 0 ms, n = 6; 25 ms, n = 8; 50 ms, n = 6; 75 ms, n = 6; 100 ms, n = 10; 125 ms, n = 4; 150 ms, n = 3). The bottom right panel compares these predictions with those for a delay line basis (dashed green line). (b) Design of the pairing experiment. Intracellular traces from an medium ganglion cell showing the average (black) and standard deviation (gray outline) of the corollary discharge (CD) response before (pre) during (pairing), and after (post) three minutes of pairing during which a brief (12 ms) intracellular current injection evoked a dendritic spike at a fixed delay after the EOD command (arrow). The small spikes are axonal spikes and do not contribute to plasticity⁵. The bottom trace (post-pre) shows the difference in the membrane potential induced by the pairing, corresponding to the traces shown in a. Note the complex pattern of change—a relative hyperpolarization around the time of the paired spike as well as a large relative depolarization just after the command, as predicted by the model. (c) Synaptic plasticity rule and parameters used for the fits shown in a. Δ₊ is the magnitude of the non-associative potentiation and Δ− is the magnitude of the associative depression.

To test these model predictions, we recorded intracellularly from medium ganglion cells, and compared corollary discharge responses before and after 3 minutes of pairing (approximately 600 commands) with a brief current injection that evoked a dendritic spike at a fixed delay after the EOD command (Fig. 6b). The shapes of the resulting negative images exhibit a strong dependence on the delay during pairing, in agreement with our qualitative predictions (Fig. 6a, black traces). Furthermore, close quantitative agreement between our model and the experimental medium ganglion cell response changes (Fig. 6a, compare green and black traces) could be achieved by fitting just two parameters of the synaptic plasticity rule (Fig. 6c; see Methods). The similarity of the modeled and measured changes in medium ganglion cell responses indicates that the measured granule cell responses and previously measured anti-Hebbian plasticity at granule cell-medium ganglion cell synapses accurately describe negative image formation.

Discussion

Using intracellular recordings and modeling of granule cells in mormyrid fish we provide a relatively complete description of granule cell recoding, far more complete than that available in other systems. The remarkably close agreement between recorded and model granule cells (shown in Figure 3) strongly suggests that the simple rules we used to transform mossy fiber inputs into granule cell responses, i.e. summation of randomly selected excitatory inputs, are essentially correct and complete. Such a complete understanding of how inputs are transformed into output in vivo is remarkable in its own right and places us in a unique position to explore the relationships between input coding, an experimentally defined synaptic plasticity rule^{5, 17}, and a well characterized adaptive network output in the form of negative images^{2, 6, 7}. Though input coding and plasticity are the critical elements for the functioning of many neural circuits, including other cerebellum-like circuits^19–21 and the cerebellum itself ^22–25, there are few cases in which these elements are understood so thoroughly.

The function of EGp circuitry demonstrated here closely parallels longstanding, but still untested, expansion recoding schemes posited for the granular layer of the mammalian cerebellum^{22, 23}. Whereas most models of cerebellar granular layer function, posit pivotal roles for Golgi cell inhibition of granule cells in expansion recoding²⁴, our study suggests a key role for UBCs. Though we had no way to specifically target UBCs and hence cannot provide a complete account of their properties, our in vivo intracellular recordings suggest that they generate temporally diverse and delayed responses that are faithfully recoded in granule cells. Though in vivo responses to discrete inputs have yet to be described for UBCs in the mammalian cerebellum or dorsal cochlear nucleus, in vitro studies have documented a variety of synaptic and intrinsic mechanisms capable of generating prolonged and/or delayed responses^26–30. These include rebound firing²⁹, regular tonic firing²⁹, and inhibitory synaptic input from Golgi cells³⁰—the key ingredients for delayed responses suggested by our in vivo intracellular recordings. Hence the functions for UBCs established here may extend to other circuits in which they are found. Finally, though the capacity to generate temporally diverse responses in granule cells may be useful for a variety of cerebellar computations, the density of UBCs varies widely across different regions of the cerebellum and across different species³¹. Whether other circuit mechanisms, e.g. phasic Golgi cell inhibition of granule cells, function to generate temporally diverse granule cell responses for regions of the cerebellum in which UBCs are scarce is an important question for future studies.

An unexpected finding of this study is that rather than a general temporal basis, such as delay-line models considered in previous theoretical work³, the temporal structure of granule cell responses is highly non-uniform. Despite the preponderance of granule cells active at short delays, our modeling suggests that they provide a highly effective basis for sensory cancellation. The explanation to this apparent paradox is that the temporal structure of granule cell responses, though not necessarily optimal or superior to a delay-line basis, is well-suited to cancel natural patterns of self-generated sensory input. How such apparent matching might occur and whether it could be modified by experience are interesting questions for future investigations. The non-uniform temporal structure of granule cell responses also provides a simple explanation for unusual features of medium ganglion cell negative images formed in response to artificial inputs. The ability to accurately predict detailed features of negative images based on modeled granule cell responses, and previously described anti-Hebbian plasticity, also provides an additional experimental validation for the links we establish between input coding, plasticity, and adaptive network output. Finally, the apparent matching between granule cell responses and natural patterns of self-generated sensory input does not imply that the system cannot provide effective cancellation when conditions change. Indeed, EOD amplitude along with passive electroreceptor responses to the EOD are expected to change on multiple timescales due to growth of the fish, seasonal changes in water conductivity, and the presence of large nonconducting objects near the fish. However, as has been shown in a previous study on the effects of water conductivity on passive electroreceptor responses¹, such changes will primarily affect the size rather than the temporal structure of sensory responses to the EOD. Hence the matching between the temporal structure of granule cell responses and self-generated sensory input described here is expected to hold over a wide range of behaviorally relevant conditions.

Though the notion that motor corollary discharge signals could be used to predict and cancel the sensory consequences of an animal’s own behavior has a long history^{32, 33}, there are few cases in which such functions have been characterized at the level of neural circuits³⁴. In particular, it has proven challenging to understand how copies of motor commands are translated into an appropriate format to cancel sensory inputs. This problem takes a particularly clear and tractable form in the case of mormyrid ELL, where copies of a brief, highly stereotyped motor command must be delayed and diversified in order to provide a basis for cancelling sensory effects that are extended in time. A major contribution of the present study is to directly demonstrate that such a temporal expansion indeed occurs in granule cells and that, along with previously described anti-Hebbian plasticity^{5, 17}, is sufficient to account for negative images. Our results hence provide the critical missing piece in a relatively complete mechanistic account of how motor commands are used to predict sensory consequences at the levels of synaptic plasticity, cells, and circuits.

Methods

Experimental preparation

All experiments performed in this study adhere to the American Physiological Society’s Guiding Principles in the Care and Use of Animals and were approved by the Columbia University Institutional Animal Care and Use Committee. Mormyrid fish (7–12 cm in length) of the species Gnathonemus petersii were used in these experiments. Surgical procedures to expose EGp for recording were identical to those described previously¹⁵. Gallamine triethiodide (Flaxedil) was given at the end of the surgery (~20 μg/cm of body length) and the anesthetic (MS:222, 1:25,000) was removed. Aerated water was passed over the fish’s gills for respiration. Paralysis blocks the effect of electromotoneurons on the electric organ, preventing the EOD, but the motor command signal that would normally elicit an EOD continues to be emitted by the electromotoneurons at a variable rate of 2 to 5 Hz. The timing of the EOD motor command can be measured precisely (see below) and the central effects of corollary discharge inputs can be observed in isolation from the electrosensory input that would normally result from the EOD.

Electrophysiology

The EOD motor command signal was recorded with an electrode placed placed over the electric organ. The command signal is the synchronized volley of electromotoneurons that would normally elicit an EOD in the absence of neuromuscular blockade. The command signal lasts about 3 ms and consists of a small negative wave followed by three larger biphasic waves. The latencies of central corollary discharge or command-evoked responses were measured with respect to the negative peak of the first large biphasic wave in the command signal. Extracellular recordings from mossy fibers in EGp were made using glass microelectrodes filled with 2M NaCl (40–100 MΩ), as described previously^{8, 15}. For in vivo whole-cell recordings from EGp neurons and from medium ganglion cells in ELL electrodes (9–15 MΩ) were filled with an internal solution containing, in mM: K-gluconate (122); KCl (7); HEPES (10); Na2GTP (0.4); MgATP (4); EGTA (0.5), and 0.5% biocytin (pH 7.2, 280–290 mOsm). No correction was made for liquid junction potentials. Only cells with stable membrane potentials more hyperpolarized than −50 mV and access resistance < 100 MΩ were analyzed. Membrane potentials were filtered at 3–10 kHz and digitized at 20 kHz (CED power1401 hardware and Spike2 software; Cambridge Electronics Design, Cambridge, UK).

Extracellular mossy fiber recordings

Several independent lines of evidence suggest that early, medium, late, and pause responses obtained using extracellular recordings in EGp (Fig. 1d, e) reflect the activity of mossy fiber axons (either extrinsic mossy fibers originating from sources outside of EGp or intrinsic mossy fibers arising from UBCs), rather than granule cells or Golgi cells. (1) Recordings attributed to mossy fibers had characteristics similar to those made previously from known fiber tracts, including tracts containing mossy fiber axons destined for EGp. These include very large, mainly positive spike waveforms^{8, 15}, as well as sudden and often brief isolation. (2) Firing properties of putative mossy fiber recordings closely matched those of units recorded in mossy fiber nuclei of origin in the midbrain and those of UBCs, but differed markedly from those of granule cells, in which action potential firing was much sparser. (3) Characteristic early, medium, late, and pause responses of putative extracellular mossy fiber recordings were also observed in a much smaller number of whole-cell recordings from mossy fiber axons. The latter can be identified, unambiguously, based on distinctive electrophysiological properties similar to those reported for mossy fiber bouton recordings in the mammalian cerebellum³⁵, including: spikes with prominent afterdepolarizations, lack of repetitive firing in response to sustained depolarizing current injections, and complete lack of synaptic activity.

Objective classification of mossy fibers

To classify mossy fibers, we fit a multinomial logistic regression model to features of the corollary discharge responses of cells recorded in PCA (n = 12), PE (n = 28), and UBCs (n = 10), and used this model to assign labels of early, medium, or late to the recorded mossy fibers. We selected three response features that gave low classifier error on a validation set (5-fold cross validation error: 2.67%): (1) Time of first rise: the first time relative to the EOD at which the smoothed (Gaussian kernel, τ = 5 ms), trial-averaged firing rate achieves 75% of its maximum. (2) Half-width of response: the width of the first peak for which the smoothed, trial-averaged firing rate is above 50% of its maximum rate. (3) Spiking variability: the variance of the cell’s spike times relative to the EOD, given by $(1/N){\displaystyle \sum _{i=1}^N}{(t_i-\overline{t})}^2$, where t_i is the time of the i^th recorded spike relative to the most recent EOD command, and $\overline{t}=(1/N){\displaystyle \sum _{i=1}^N}{t}_i$.

Dendritic spike pairing experiments

Methods for dendritic spike pairing experiments in medium ganglion cells were similar to those described previously¹⁵. Effects of pairing on corollary discharge responses were evaluated based on averages of 60 seconds (responses to approximately 200 EOD motor commands) of data taken immediately before and after the pairing period. In some cases, narrow spikes were removed using a median filter before averaging. Dendritic spikes were induced by brief (12–15 ms) intracellular current injections (100–600 pA). The duration of the pairing period was 3 minutes. Baseline rate of broad spike firing were extremely low such that during pairing, few if any spontaneous broad spikes occurred. Cells in which resting membrane potential, access resistance, or spike height changed substantially over the course of the experiment were excluded from the analysis. Consistent with previous results, plastic changes decayed gradually over the course of approximately 3–5 minutes after the end pairing. Because medium ganglion cell recordings were difficult to obtain, but often extremely stable, multiple pairings at different delays were conducted in some cells after allowing effects of the previous pairing to decay.

Histology

After recording, fish were deeply anesthetized with a concentrated solution of MS:222 (1:10,000) and perfused through the heart with a teleost Ringer solution followed by a fixative, consisting of 2% paraformaldehyde and 2% glutaraldehyde or 4% paraformaldehyde in 0.1 M phosphate buffer. The brains were postfixed, cryoprotected with 20% sucrose and sectioned at 50 μM on a cryostat. Sections were reacted with avidin-biotin complex and diamino-benzidine or a streptavidin-conjugated fluorescent dye to reveal the biocytin filled cells.

Data analysis and statistics

Data were analyzed off-line using Spike2 and Matlab (MathWorks, Natick, MA). Data are expressed as means ± SD, unless otherwise noted. Paired and unpaired Student’s t-tests were used to test for statistical significance, as noted. Differences were judged to be significant at P < 0.05.

Fitting measured granule cell responses

We modeled the granule cell as a passive unit with leak potential E_L, which received excitatory input from 1–3 mossy fibers (including UBCs) with firing rates rⁱ(t). The membrane potential V(t)of the model granule cell is determined by its mossy fiber inputs, filtered by the mossy fiber-granule cell EPSP 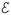, where 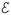is the convolution of synaptic and membrane filters. The synaptic filter was modeled as a weighted sum of a fast and slow exponential filter, giving the model

$$V(t)=E_L+\sum _{i=1}^N{w}_{\text{fast}}^i({\mathcal{E}}_{\text{fast}}\ast r^i)(t)+w_{\text{slow}}^i({\mathcal{E}}_{\text{slow}}\ast (r^i)(t)$$

The time constants of the synaptic filters were fit by hand to give τ_fast= 0.2 ms and τ_slow = 37.8 ms. The membrane time constant of the recorded granule cells was determined experimentally to be τ_m = 8.7 ms.

To fit the responses of the recorded granule cells, we first found a set of candidate mossy fiber inputs by finding $w_{\text{fast}}^i$ and $w_{\text{slow}}^i$ that minimize $C(w_{\mathit{fast}/\mathit{slow}}^i)=\frac{1}{2T}{\displaystyle \sum _{t=0}^T}{\left(\stackrel{\sim }{V}(t)-V(t)\right)}^2+{\alpha }_1({\left|\right|{\mathbf{w}}_{\text{slow}}\left|\right|}_1+{\left|\right|{\mathbf{w}}_{\text{fast}}\left|\right|}_1)$, where T is the length of the command cycle, and Ṽ(t) is the voltage of the model granule cell. We chose the smallest value of α₁ that produced 10 nonzero mossy fiber inputs. We constrained weights to be non-negative using an adjusted Least-Angle Regression (LARS) solution of the LASSO problem³⁶ that selects only inputs which are positively correlated with the granule cell response. We next cut our candidates down to 1–3 mossy fibers by finding $w_{\text{fast}}^i$ and $w_{\text{slow}}^i$ that minimize $C(w_{\mathit{fast}/\mathit{slow}}^i)=\frac{1}{2T}{\displaystyle \sum _{t=0}^T}{\left(\stackrel{\sim }{V}(t)-V(t)\right)}^2+{\alpha }_0({\left|\right|{\mathbf{w}}_{\text{slow}}\left|\right|}_0+{\left|\right|{\mathbf{w}}_{\text{fast}}\left|\right|}_0)$. Here, we apply the L₀ norm to the weight vectors, which is the number of nonzero elements contained within them. Adjusting the value of α₀ gives the lowest-MSE model fits that use one, two, or three mossy fiber inputs. For each granule cell fit, we manually selected the value of α₀ that best captured all features of the recorded cell’s average corollary discharge response. A subset of late mossy fibers fired action potentials on only a fraction of commands. We also observed prominent late subthreshold responses on only a fraction of commands in a subset of granule cells. For purposes of accurately fitting responses to such inputs, average mossy fiber spiking and average granule cell corollary discharge responses were computed using only those trials on which late spikes and synaptic responses were observed. For purposes of generating model granule cells, such non-spiking trials were included (see below).

Random Mixing Test

Granule cell categories (E, M, L, P, EM, EL, EP, ML, MP, LP, EML, EMP, ELP, MLP, and N, where E = early, M = medium, L = late, P = pause, and N = none) were assigned to the 169 recorded granule cells depending on the mossy fibers selected as inputs to the fit model granule cells. We constructed a random mixing model with the following assumptions: (1) Each granule cell has three sites for mossy fiber synaptic inputs; (2) The probabilities of a given input being of E, M, L, and P type are given by p_e, p_m, p_l, and p_p, with p_e + p_m + p_l + p_p ≤ 1 and (3) The type of input received at one mossy fiber-granule cell synapse is independent of that received at any other synapse. We fit the input type probabilities to the model granule cell fits by minimizing the Chi-squared statistic. The category frequencies included all possible input combinations that produced a granule cell of a given category; for example, E_EM was calculated as $3p_e^2{p}_m+3p_e{p}_m^2+6p_e{p}_m(1-p_e-p_m-p_l-p_p)$.

Generating Model Cells

We introduced two sources of variability to our model based on observed sources of variability in recorded cells. We found trial-to-trial variability in peak height of recorded single EPSPs to be normally distributed with σ = 0.224 mV; during simulation of model granule cells, we sampled this distribution for each mossy fiber spike. As shown previously¹⁵, in addition to receiving corollary discharge inputs, some granule cells (84 of 212 recorded in the present study) also receive input from mossy fibers that fire at high rates, independent of the EOD command. Many such “tonic” mossy fibers convey proprioceptive information^{8, 15}. We added tonic input to our model based on 72 tonic mossy fibers recorded in a previous study¹⁵. The probability of a granule cell receiving tonic input was computed under the assumption of random mossy fiber mixing, and we set the synaptic weight of tonic inputs to model granule cells by sampling a Gaussian distribution fit to observed tonic EPSP sizes (2.5 ± 0.9 mV). Using the mossy fiber input probabilities fit from our random mixing model, we randomly determined whether each “dendrite” of a given model granule cell received early (p_e = 0.425), medium (p_m = 0.075), late (p_l = 0.050), pause (p_p = 0.050), tonic (p_t = 0.157), or no input (p_n = 0.243). We then chose a particular mossy fiber response of the previously-determined class as the source of input to that “dendrite”; we assumed that a “dendrite” is equally likely to choose any of the mossy fibers within a given class. For each synapse, we set the fast and slow components of the synaptic weight by randomly sampling from the pool of all fast + slow weight pairs obtained from fitting the granule cell model to recorded granule cell responses. Finally, if a model granule cell received input from one or more late mossy fibers, we set for each such fiber a probability of that mossy fiber being active after a given command; this probability was drawn from a uniform distribution. This choice was motivated by the observation that the probability of spike firing varied widely across recorded late mossy fibers (unlike the other response classes, which fired after every command).

We then added a spiking threshold V_thresh to model cells, measured relative to the average granule cell membrane potential measure before the EOD command, V_rest. In model granule cells receiving only early, medium and/or late mossy fiber input, V_rest = E_L. In model granule cells receiving pause or tonic input, $V_{\text{rest}}=E_L+{\displaystyle \sum _i}{\overline{r}}^i\left(w_{\text{slow}}^i\int {\mathcal{E}}_{\text{slow}}(t)dt+w_{\text{fast}}^i\int {\mathcal{E}}_{\text{fast}}(t)dt\right)$, where r̄ⁱ is the average firing rate of each pause/tonic input. We measured V_rest and V_threshs in 196 granule cells, and fit the distribution of V_thresh – V_rest with a Gaussian with μ = 20.2 mV, σ = 5.97. To set the threshold of model granule cells, we calculated V_rest and then sampled granule cell V_thresh = V_rest + N (μ, σ), resampling if V_thresh < V_rest. Upon spiking, the cell was clamped to E_L for 4 ms. To simulate the activity of our model granule cell on a single trial, we randomly drew one recorded trial (25 ms before to 200 ms after the EOD command) from each of its presynaptic mossy fibers to be used as input.

Simulating Negative Image Formation

We modeled the medium ganglion cell as a passive, current-based leaky unit receiving excitatory input from 20,000 model granule cells (rⁱ(t)) and sensory input (s(t)), with anti-Hebbian spike timing-dependent plasticity at granule cell-medium ganglion cell synapses (wⁱ), and EPSP (E) fit to granule cell-evoked EPSPs recorded intracellularly in medium ganglion cells³⁷. Because the timescale of learning is slow, we assumed the wⁱ-s to be constant over a single command cycle. s(t) was taken from Figure 1b of ref. 1.

The granule cell- medium ganglion cell learning rule has the form 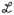(t) = Δ⁺ − Δ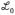⁻ (t) where t = t_{MG spike} − t_{GC spike} and 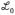(t) determines the time dependence of associative depression. Theoretical analysis (Supplementary material) has shown that negative images are guaranteed to be stable when 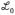= 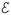. The timescale of 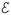agrees learning rules fit to experimental data³, thus we use 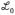= 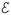here. Scaling of the weights by 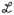was chosen to be multiplicative; because the change in synaptic weights during negative image formation was small, we simply scale 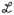by the weight prior to learning ( $w_0^i$) for each synapse. We set $w_0^i={\left({\displaystyle \sum _i}(\mathcal{E}\ast r^i)(t_{max}^i)\right)}^{-1}$ where $t_{max}^i={\text{argmax}}_t(r^i(t))$, which brings the weighted granule cell input to the medium ganglion cell close to constant over time. Thus, with the approximation of linearizing the medium ganglion cell spiking response about the equilibrium voltage V₀ (see Stability Analysis in Supplementary Materials), wⁱ evolves as $d{w}^i/d\tau =-w_0^i\left({\mathrm{\Delta }}^{+}\int r^i(t)dt-{\mathrm{\Delta }}^{-}\int V(t)({\mathcal{L}}_0\ast r^i)(t)dt\right)$, where τ is the period of each EOD cycle. We fit Δ⁺ and Δ⁻ to negative images recorded experimentally: given experimentally-recorded membrane potential changes ΔV_tD(t) induced by a broad spike at time t_D ∈ {0,25,50,75,100,125,150}ms, and predicted membrane potential change $\mathrm{\Delta }{\stackrel{\sim }{V}}_{t_D}(t)={\displaystyle \sum _i}{w}_0^i(\mathcal{E}\ast r^i)(t)\left({\mathrm{\Delta }}^{+}\int r^i(s)ds+{\mathrm{\Delta }}^{-}\int \delta (s-t_D)({\mathcal{L}}_0\ast r^i)(s)ds\right)$, we chose Δ⁺ and Δ⁻ to $\text{minimize}C({\mathrm{\Delta }}^{+},{\mathrm{\Delta }}^{-})={\displaystyle \sum _{t_D}}{min}_{c_{t_D}}\int {\left(\mathrm{\Delta }{V}_{t_D}(t)-\mathrm{\Delta }{\stackrel{\sim }{V}}_{t_D}(t)+c_{t_D}\right)}^{2}dt$ using standard linear least squares, where c_tD is a constant offset term used to remove the effect of any net drift in membrane potential. To monitor the degree of negative image formation during simulation, given a total change to each weight, Δwⁱ, we defined the residual signal error as [∫(s(t) + Δwⁱ ( 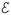* rⁱ)(t))² dt]/∫ s(t)² dt.

Supplementary Material

Supplementary Figures 1-10

Supplementary Figure 1. Morphology of intracellularly recorded Golgi cells, UBCs, and granule cells. Maximum intensity projections of cells labeled with biocytin during in vivo whole-cell recording. Fixed sections were cut at 50 microns on a cryostat, reacted with a streptavidin-conjugated fluorescent dye, and imaged on a confocal microscope. All scale bars are 10 microns. Filled Golgi cells (n = 3) were multipolar and had cell bodies that were large relative to granule cells or UBCs. Filled UBCs (n = 11) had small ovoid cell bodies, a single distinctive filamentous brush-shaped process (open arrows) and in some cases an additional long, winding process with multiple swellings (filled arrows), similar in appearance to mossy fiber axons. Filled granule cells (GC) (n = 20) had small cell bodies and 2–5 short processes with claw-like endings. An additional thin process (filled arrow), presumably the axon, could often be traced to the ELL molecular layer.

Supplementary Figure 2. UBCs exhibit characteristic electrophysiological properties. UBCs could be distinguished from Golgi cells and granule cells based on characteristic responses to intracellular current injections and, for a subset of UBCs, highly regular tonic firing. a, A subset of UBCs (30/54) exhibited prominent rebound firing in response to hyperpolarizing current injections. Such prominent rebound firing was never observed in granule cells or Golgi cells. Depolarizing current injections often evoked bursts of spikes followed by a decrease in firing rate (top trace). Five UBCs of this type were identified morphologically. b, Spontaneous firing in UBCs that exhibited prominent rebound tended to be irregular. Scale bar: 20 mV and 200 ms. c, Other UBCs (22 of 54) lacked prominent rebound firing in response to hyperpolarizing current injection (not shown). In response to depolarizing current injections such cells exhibited a delayed onset to spike firing accompanied by a distinctive “hump” and “sag” pattern during the delay (arrow in c). This pattern of response to current injections was never observed in Golgi or granule cell recordings. d, UBCs that lacked rebound and displayed a delayed onset to firing also exhibited extremely regular tonic firing (average CV = 0.139; n = 22). Similar regular tonic firing patterns were seen in pause mossy fibers recorded extracellularly in EGp. Such highly-regular firing was never observed in granule cells or Golgi cells. Four UBCs of this type were morphologically identified. Scale bar: 10 mV and 100 ms. Two additional UBCs were identified based on morphology alone.

Supplementary Figure 3. Basic electrophysiological properties of Golgi cells, UBCs, and granule cells. Basic electrophysiological properties were analyzed for all intracellularly recorded Golgi cells (n = 11), UBCs (n = 54), and a subset of recorded granule cells (GC) (n = 40). Input resistance and membrane time constants were measured at the resting membrane potential in response to 10–50 pA hyperpolarizing current pulses. Spike width was taken as the width at half-height, with threshold defined as the point at which the second derivative of the voltage waveform reaches 50% of its maximum. Afterhyperpolarization (AHP) amplitude was defined as the distance between threshold and the most hyperpolarized potential following the action potential peak. Golgi cells exhibited much lower input resistance and a shorter membrane time constants than UBCs or granule cells (left, P < 0.0001; two-tailed Student’s t-test), allowing them to be identified unambiguously based on these characteristics alone. UBCs exhibited substantial variation in their intrinsic properties, but on average they had longer time constants, broader spikes, and larger AHPs than Golgi cells or granule cells. Consistent with the possibility that UBCs comprise distinct functional classes, UBCs with regular tonic firing exhibited action potentials with significantly larger AHP amplitudes than UBCs exhibiting rebound firing (arrow, top traces, P < 0.0001; two-tailed Student’s t-test).

Supplementary Figure 4. Objective classification of extracellular mossy fiber recordings. Putative mossy fibers recorded extracellularly in EGp were subjected to a classifier analysis by multinomial logistic regression to determine the similarity of their corollary discharge responses to those recorded from identified sources. The sources were neurons recorded from two midbrain nuclei (PCA and PE) known from anatomical studies to provide mossy fiber input to EGp and intracellular recordings from UBCs, which are thought to give rise to a system of intrinsic mossy fibers. Three features of the corollary discharge spiking responses of the identified neurons were used as input to the classifier (see Methods). The classifier was trained to predict the probabilities of the class-labels PCA, PE, and UBC from these features. EGp mossy fiber spike trains were then converted to this feature representation and classified by the previously-trained classifier. EGp mossy fibers classified as most similar to PCA, PE, and UBC were called early, medium, and late mossy fibers, respectively. The blue lines represent the discrimination boundaries of the classifier. Pause mossy fibers were treated separately, as they were unique among EGp mossy fibers in exhibiting both a corollary discharge response (i.e. a pause) and regular, tonic firing (>4 Hz) independent of the EOD command. UBCs were the only other identified neural elements that shared these properties.

Supplementary Figure 5. Subthreshold corollary discharge responses in UBCs, Golgi cells, and granule cells. Average and SEM of subthreshold corollary discharge responses for ten representative UBCs (a) and Golgi cells (b). For comparison, a single representative granule cell (GC) response is shown in c on the same scale. In some cases a small amount of hyperpolarizing current was used to prevent spiking. UBCs often exhibited depolarizations that were much more prolonged than those seen in granule cells or Golgi cells (top 5 traces in a). Hyperpolarization time-locked to the EOD command (bottom 5 traces in a), suggestive of synaptic inhibition, was also much more commonly observed in UBCs than in Golgi cells or granule cells. d, Temporal features of granule cell corollary discharge responses closely resemble firing patterns of individual mossy fibers (MFs) and UBCs. Each panel shows the responses of a granule cell to ten consecutive EOD commands overlaid (black traces) along with the average taken from a larger number of commands (blue). The gray traces above are average command-evoked firing rate for selected mosy fibers recorded extracellularly in EGp smoothed with an exponential filter with width (10 ms) similar to the average granule cell membrane time constant. From top to bottom: granule cell with a subthreshold response that resembles temporal firing patterns characteristic of early mossy fibers, as seen in the inset. Timing of inflections on the rising phase of the granule cell EPSP closely match the timing of mossy fiber spikes. Middle, granule cells with subthreshold responses resembling temporal firing patterns characteristic of pause mossy fibers, spikes are truncated. Time-locking of mossy fiber spikes after the pause matches the periodicity of granule cell membrane potential changes. Bottom, granule cell with subthreshold response that appears to reflect a combination of an early response and a pause response. Individual mossy fibers or UBCs with firing patterns resembling such mixed responses were never observed, suggesting that this granule cell integrates two different corollary discharge inputs.

Supplementary Figure 6. Properties of granule cell model fits and generated granule cells. a, Normalized MSE of model fits to granule cell responses; average MSE was 4.61%. b, Histogram of EPSP amplitudes in fit mossy fiber - granule cell synapses. This distribution is in line with the range of EPSP amplitudes observed in recorded granule cells. c, average number of spikes fired per EOD command in experimentally recorded granule cells (left), and in 20,000 generated model granule cells (right); note log scale of y-axis on right. As in recorded granule cells, the model cells fired a small number of spikes per command and none of the model cells were tonically active. A comparison of the two samples using a Kolmogorov-Smirnov test (granule cells firing zero spikes per command were included in the analysis but not shown in the display) failed to reject the null hypothesis that the two samples were drawn from the same distribution. d, Histogram of the time relative to the command of maximum depolarization for recorded (left) versus model (right) granule cells. The similarity of these distributions again confirms that the model granule cells we generated are very similar to the granule cells recorded experimentally.

Supplementary figure 7. Learning-evoked changes in EPSP amplitude. Histogram of changes in EPSP amplitude from model granule cells (GCs) to the model medium ganglion cell, following cancellation of self-generated sensory input (initial amplitude 8 mV).

Supplementary Figure 8. Effects of varying the fraction of UBC inputs on negative images and sensory cancellation. UBCs exhibit temporally diverse and delayed responses, termed late and pause, that play an important role in cancelling the later components of the sensory response evoked by the fish’s own EOD. We estimated the probability of late and pause inputs from our model fits of granule cell responses, and found the probability of both late-to-granule cell and pause-to-granule cell synapses (pl and pp) to be around 5%. To ensure that sensory cancellation and negative image formation did not depend critically on this exact value, we varied this value between 1 and 9% and studied model performance. a, The rate at which the granule cell basis was able to cancel self-generated input due to the EOD was comparable for pl and pp = 3, 5, 7, and 9%. The rate of cancellation was slightly lower for pl = pp = 1%, but still substantially higher than that of a granule cell basis lacking late and pause input entirely, indicating that only a small fraction of granule cells need receive late/pause input to form a sufficient basis. b, We also verified that altering the fraction of late/pause inputs to granule cells did not substantially alter the trial-to-trial variability of negative images. Plots show trial-averaged negative images, with shaded blue regions indicating +/− 1 standard deviation.

Supplementary Figure 9. Effects of granule cell response properties on negative image formation. Though the distributions of spikes per EOD command and time of peak membrane potential (Vm) in recorded and model granule cells (GCs) are not statistically different (Suppl. Fig. 6), we wanted to confirm that negative image formation was not sensitive to any differences between real and model cells. First, a small number of model granule cells averaged more than three spikes per command, a firing rate which was not observed in the experimentally recorded granule cells; we removed these more active granule cells from our simulations to ensure that our results still held. Second, only a small fraction (1.18%) of recorded granule cells had peak Vms occurring later than 125 ms relative to command time. We divided the command interval into thirds and measured the fraction of recorded cells peaking in each third, and removed granule cells from our model population to match these proportions. a, The rate of signal cancellation of the original granule cell population is not substantially different from that of granule cell populations with highly active (>3 spikes per command) model cells removed. The cancellation rate drops for a more restricted population (cells with <=1 spikes per command), though this may be due to the smaller number of cells remaining. b, While the variability of the negative images increased when highly-active cells were removed, the overall shape of the negative image is not affected. c, The learning rate of the granule cell population matched to the observed peak Vm distribution was not substantially different from that of the original granule cell population. d, The shape and variability of the negative image formed by the modified granule cell population was also unaffected. e, Proportion of granule cells with Vm peak in each third of the command interval (20,000 model cells, 170 real cells. Real cell proportions were scaled to sum to 20,000.)

Supplementary Figure 10: Analysis of learning dynamics and comparison to delay line basis. We characterize learning in terms of the eigenmodes and eigenvalues of the learning dynamics, as outlined in the Supplementary Methods. a, First three eigenmodes of the three bases considered in this study: the model granule bell (GC) basis (blue), a delay line of uniform Gaussian bumps with with standard deviation s (green), and the model basis without UBC input (gray). The eigenmodes of a uniform delay line are the Fourier basis, regardless of the shape of individual basis functions. b, Decreasing the learning rate l increases the number of trials needed for sensory input cancellation, but decreases the amplitude of negative image variability arising from learning-induced weight fluctuations (see Supplementary Modeling; we assume h takes the form of Gaussian white noise.) Regardless of l, the relative rates of cancellation of the different bases remain the same; we therefore set the learning rate of each basis such that the negative image variability was 10–5 (noting that other values would yield the same results.) See panel e for legend. c, Decay rate of the eigenmodes of the granule cell and delay line bases, on log (left) and normal (right) scales. Increasing s decreases the number of modes of the delay line basis which can be canceled on ethologically relevant timescales. See panel e for legend. d, Projection of the sensory input to be cancelled onto the eigenmodes (sorted by rate of decay); in both bases the first twenty (or fewer) modes are sufficient to capture almost all of the sensory input. Note that the shape of the delay line eigenmodes does not depend on s. e, Combining panels c and d, we plot the decay rate of each eigenmode n against the fraction of the sensory signal canceled by modes 1 to n, providing an estimate of the learning rate of each basis. f, Time to 95% signal cancellation as a function of s. The delay line outperforms the granule cells provided that s is sufficiently small. Inset shows an example delay line basis function with s = 5 ms, for reference. g, We fit a Gaussian to the trial-averaged response of each model cell, revealing a drop in temporal precision of model cell responses at long delays to the EOD command. The green line shows a standard deviation of 24 ms, which in a delay line learned at a rate comparable to the model cell basis.