Lateral Motion and Bending of Microtubules Studied with a New Single-Filament Tracking Routine in Living Cells

Abstract

The cytoskeleton is involved in numerous cellular processes such as migration, division, and contraction and provides the tracks for transport driven by molecular motors. Therefore, it is very important to quantify the mechanical behavior of the cytoskeletal filaments to get a better insight into cell mechanics and organization. It has been demonstrated that relevant mechanical properties of microtubules can be extracted from the analysis of their motion and shape fluctuations. However, tracking individual filaments in living cells is extremely complex due, for example, to the high and heterogeneous background. We introduce a believed new tracking algorithm that allows recovering the coordinates of fluorescent microtubules with ∼9 nm precision in in vitro conditions. To illustrate potential applications of this algorithm, we studied the curvature distributions of fluorescent microtubules in living cells. By performing a Fourier analysis of the microtubule shapes, we found that the curvatures followed a thermal-like distribution as previously reported with an effective persistence length of ∼20 μm, a value significantly smaller than that measured in vitro. We also verified that the microtubule-associated protein XTP or the depolymerization of the actin network do not affect this value; however, the disruption of intermediate filaments decreased the persistence length. Also, we recovered trajectories of microtubule segments in actin or intermediate filament-depleted cells, and observed a significant increase of their motion with respect to untreated cells showing that these filaments contribute to the overall organization of the microtubule network. Moreover, the analysis of trajectories of microtubule segments in untreated cells showed that these filaments presented a slower but more directional motion in the cortex with respect to the perinuclear region, and suggests that the tracking routine would allow mapping the microtubule dynamical organization in cells.

Introduction

The eukaryotic-cell cytoskeleton plays a key role in the intracellular organization, connects the cell physically and biochemically to the external milieu, and generates coordinated forces that enable the cell to move and change shape (1). Different chemical and mechanical stimuli trigger the remodeling of this network, leading to changes in the morphology and mechanical properties of the cell that are also extremely important in launching disease processes, such as for cancer invasion (see, for example, Mouneimne et al. (2) and Goldstein et al. (3)). In this context, understanding the mechanical behavior of the biopolymers that compose the cytoskeleton is essential for describing cell mechanics and organization.

The cytoskeleton is composed of three different protein polymers with different mechanical properties and functions: actin filaments, microtubules, and a group of polymers collectively named as “intermediate filaments”. Microtubules are hollow, flexible tubes with an outer diameter of ∼25 nm, which are formed by polymerization of α- and β-tubulin heterodimers (see references in Howard (4)). During interphase in many cells, microtubules are organized in radial arrays with their minus-ends nucleated at the microtubule-organizing centers and plus-ends extended toward the cell margins. Microtubules are not stable structures; they present periods of growth and rapid shrinkage, which behavior has been named “dynamic instability” (5). These filaments are the stiffest component of the cytoskeleton. Their persistence length (i.e., the length of the filament over which thermal bending becomes appreciable (4)) is ∼5 mm, which is ∼2- and 3-orders higher than that of actin and intermediate filaments, respectively (4,6).

Microtubules in cells are decorated by MAPs (microtubule associated proteins), which stabilize them and promote their assembly (reviewed in Mandelkow and Mandelkow (7)). Samsonov et al. (8) showed that binding of tau—the major microtubule associated protein in neurons—varies according to the microtubule curvature and suggested that the interaction of this protein with the microtubule may modify local mechanical properties of the biopolymer. Also, Felgner et al. (9) and Mickey and Howard (10) demonstrated that different MAPs, including tau, increased the flexural rigidity of purified microtubules. More recently, Portran et al. (11) showed that MAP65/Ase1 from Arabidopsis thaliana has the opposite effect because they decrease the persistence length of microtubules in vitro, suggesting that the effect of MAPs on microtubule mechanical properties cannot be generalized.

Optical microscopy combined with contrast-enhancing techniques such as dark-field, differential interference contrast (DIC), and fluorescence microscopy are widely used to follow the motion of single microtubules and actin filaments (see for example, Gittes et al. (12), Mizuno et al. (13), and Brangwynne et al. (14)). By analyzing the thermally driven fluctuations of filament shapes through a Fourier decomposition technique, several authors measured the persistence length and relaxation timescales of actin filaments and microtubules either in vitro or in living cells (see, for example, Gittes et al. (12), Brangwynne et al. (14,15), and Käs et al. (16)). Surprisingly, microtubules in living cells presented an apparent persistence length ∼100 times smaller than that observed in vitro (15), indicating that mechanical properties of the filaments in living cells cannot be completely understood by only considering the in vitro observations. By studying the microtubule dynamics in living cells, Brangwynne et al. (15) also suggested that during microtubule growth, the tip fluctuations lead to microtubule bends that are frozen-in by the elastic microenvironment. This indicates that large nonthermal forces govern the growth of microtubules, and could explain the highly curved shapes and small persistence lengths of these filaments in living cells. On the other hand, Bicek et al. (17) studied events of microtubule bending and proposed that neither polymerization nor acto-myosin contractility play a relevant role in these bending events. They suggested that microtubule molecular motors are responsible for generating most of the strain energy stored in the microtubule lattice.

Although several algorithms have been described to locate and follow pointlike and spherical particles with nanometer precision (see, for example, Levi et al. (18), Cheezum et al. (19), and Yildiz et al. (20)), recovering the position of a filament that continuously changes its shape and position is extremely difficult—made even more difficult in the presence of an heterogeneous background such as that observed in living cells. Particularly, Gittes et al. (12) designed a routine based on locating with high precision a small number of points within the DIC image of a filament, and interpolating linear segments between these points to recover the whole polymer shape. Later, Janson and Dogterom (21) used DIC microscopy to study the changes in shapes of filaments using an algorithm that traced lines perpendicular to the main filament axis and recovered its position by deconvolution of the intensity profiles in these lines. Brangwynne et al. (14) designed a tracking method that consisted of binarizing the image of the filament, fitting a polynomial to the resulting image and further refining the filament position by locating with subpixel precision the intensity maximum along perpendicular lines across the filament using Gaussian deconvolution. Valdman et al. (22) also proposed a method that considers the biopolymer shape as a contour expanded on an orthogonal polynomial basis. This last approach has the advantage of simultaneously fitting the whole image of the filament, and thus it is less sensitive to the noise and heterogeneities of the filament intensity.

In this work, we introduce a believed new filament-tracking algorithm that allows recovering the coordinates of microtubule segments with 5–10 nm precision in in vitro conditions. To illustrate possible applications of this, to our knowledge, new method, we used the tracking algorithm to obtain the curvature distribution of microtubules in Xenopus laevis melanophores and observed that these shapes followed a thermal-like distribution that is not affected by the presence of a Xenopus homolog of tau protein or actin depolymerization. Surprisingly, we found that the intermediate-filaments network plays a key role in the curvature of microtubules. Finally, the tracking method allowed us to explore the motion of microtubules and to map the dynamical organization of the microtubule network in living cells.

Materials and Methods

Cell culture and samples preparation for imaging

Immortalized X. laevis melanophores were cultured in L-15 medium (Sigma-Aldrich, St. Louis, MO) supplemented with bovine fetal serum, as described in Rogers et al. (23). Some of the experiments described below were done using a cell line of melanophores stably expressing EGFP-tagged XTP, a Xenopus homolog of tau protein (18,24). This cell line is a kind gift of Dr. Vladimir I. Gelfand (Northwestern University, Chicago, IL).

Melanin production was inhibited by treatment with phenylthiourea (25). For microscopy measurements, cells were grown for 2 days on sterilized 25-mm coverslips and placed onto 35-mm plates in 2 mL of complete medium. Before observation, the coverslips were washed in serum-free 70% L-15 medium (Sigma-Aldrich) and mounted in a custom-made chamber specially designed for the microscope. Actin depolymerization was achieved by incubation of the cells with 10 μM latrunculin B (Sigma-Aldrich) for 30 min before observation (26,27). Samples were observed during 30 min.

Cells grown on coverslips were transfected using Lipofectamine 2000 (Invitrogen, Carlsbad, CA) following the vendor instructions and observed 24 h after transfection. Three different plasmids were used: a EGFP-tagged α-tubulin; a GFP-tagged full-length Xenopus vimentin, which coassembles with endogenous vimentin; and a Xenopus vimentin dominant-negative construct containing the head and α-helical domain 1A of vimentin [GFP-vim(1-138)], which disrupt the endogenous vimentin filaments network (28,29). These plasmids were a kind gift of Dr. Vladimir I. Gelfand (Northwestern University, Evanston, IL).

In vitro polymerization of microtubules

Microtubules were prepared using a tubulin polymerization protocol previously described in Lee and Timasheff (30). Briefly, 300 μL of 1 mg/mL bovine brain tubulin and 0.1 mg/mL rhodamine-labeled tubulin (Cytoskeleton, Denver, CO) was incubated at 37°C in buffer BRB80 (80 mM PIPES, 0.5 mM EGTA, 2 mM MgCl, 1 mM DTT, and 1 mM GTP, pH 6.9). The polymerization reaction was monitored by measuring the absorbance of the sample at 340 nm. During the incubation, stepwise additions of taxol (Invitrogen) were done to reach a final concentration of 10 μM.

Confocal microscopy

Confocal images were acquired in a model No. FV1000 confocal microscope (Olympus, Tokyo, Japan). EGFP fusion proteins were observed using a multi-line Ar laser tuned at 488 nm (average power at the sample, 700 nW) as excitation source. The laser light was reflected by a dichroic mirror and focused through an UPlanSApo 60× oil immersion objective (NA = 1.35; Olympus) onto the sample. Fluorescence was collected by the same objective, passed through the pinhole, reflected on a diffraction grating, and passed through a slit set to transmit in the range of 500–600 nm.

Rhodamine-labeled microtubules and actin filaments were observed using as excitation source a diode laser of 543 nm and collecting the fluorescence in the range of 555–655 nm.

In all the cases, fluorescence was detected by a photomultiplier set in the photon-counting detection mode and the pixel size was set in the range of 80–100 nm except where indicated.

Fourier decomposition of filament shapes

We used the filament coordinates (x_k, y_k) recovered from the images to calculate tangent angles as

$${\theta }_k={\text{tan}}^{-1}\left(\frac{y_{k+1}-y_k}{x_{k+1}-x_k}\right)$$ (1)

and segment lengths as

$$s_k=\sqrt{{\left(x_{k+1}-x_k\right)}^2+{\left(y_{k+1}-y_k\right)}^2}.$$ (2)

The tangent angle is then decomposed into a large number of Fourier modes and expressed as a sum of cosines (12),

$$\theta \left(s\right)=\sqrt{\frac{2}{L}}\sum _{n=0}^{\infty }{a}_n\text{cos}\left(q_{n}s\right),$$ (3)

where q_n represents the wave vector and is defined as q_n = nπ/L. The zero-order term a₀ corresponds to the average orientation of the filament, s is the arc length along the filament, and L is the total segment length.

Lateral motion of microtubules

We defined the segment lateral position (LP) as the mean y coordinate of the studied filament segment. The mean lateral square displacement (MLSD) was calculated as

$$\text{MLSD}\left(\tau \right)=\langle {\left(LP\left(t\right)-LP\left(t+\tau \right)\right)}^2\rangle ,$$ (4)

where t and τ are the absolute and lag times, respectively, and the brackets represents the time average. This calculation was done for τ < 10% of the total time of the trajectory (31).

Statistical analyses

Wilcoxon rank-sum test was used to compare the distributions of the parameters α and A obtained for control, latrunculin-treated, and vimentin-disrupted EGFP-XTP cells. Statistical analyses were performed using the rank-sum test in the software MATLAB (The MathWorks, Natick, MA).

Results and Discussion

Algorithm for filament localization and tracking

The analysis of the motion and shapes of the filaments that constitute the cytoskeleton provides relevant information to understand the cell mechanics and organization. Fig. 1 A and Movie S1 in the Supporting Material show confocal images obtained at different time lags of a representative X. laevis melanophore cell with EGFP-labeled microtubules that illustrate the complex dynamics of microtubules in living cells. Moreover, these images also show that the background presents an inhomogeneous distribution of the fluorescence, which adds even more complexity to the analysis.

Figure 1.

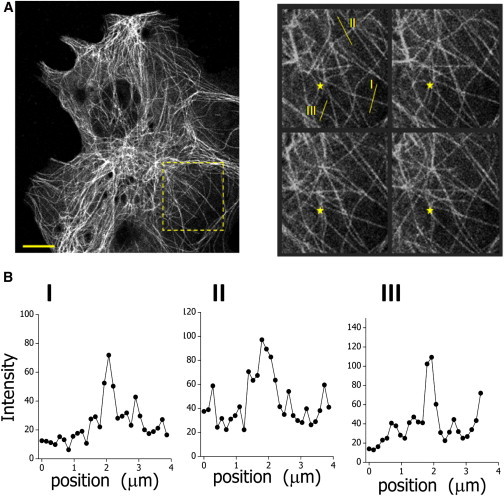
Motion of microtubules in living cells. (A) Dynamics of microtubules in a small region of the cell (yellow square in left panel); the time lag between frames was 60 s. (Yellow star) Fixed reference point. Scale bar, 10 μm. (B) Intensity profiles recovered along the yellow lines for the microtubules observed in the zoom-in images. The S/N of these filaments was ∼10. To see this figure in color, go online.

To overcome these problems, we designed what we believe to be a new tracking algorithm to follow the motion of filaments in the presence of a complex background. The tracking program displays the first image of the loaded image-stack and the user clicks on top of the selected filament to roughly set the initial positions for the algorithm. The program then applies a rotation transformation of the image in such a way that each x_c coordinate of the filament is univocally associated to a single y_c value. To determine the angle of rotation, the program fits a linear function to the (x_c,y_c) coordinates selected by the user and calculates the angle as the arctangent of the slope. We found the IMROTATE script in MATLAB to be adequate for the rotation transformation because it does not introduce artifacts in the tracking routine (see Fig. S1 in the Supporting Material). Importantly, pixilation could also introduce artifacts when rotating images with angles different from multiples of 90° in cases in which the pixel size is similar or bigger than the radial waist of the point spread function (PSF) of the microscope. Although we used a pixel size smaller than the PSF waist, we tested the algorithm performance for different rotation angles and a pixel size similar to the waist of the PSF and found that rotation introduced small errors in these conditions (see Fig. S1).

Next, the local fluorescence intensity profile in the vertical direction is extracted for the selected x_c positions of the microtubule. This profile may not follow a simple Gaussian distribution function due to the intracellular background and the presence of nearby microtubules (Fig. 1 B). Thus, it is not always possible to recover the microtubule position by Gaussian deconvolution, as was previously used (14,32–34).

Therefore, we approximated the intensity profile recovered at each x_c position to a continuous expression using a generalized regression neural network, which is a type of radial basis network that is often used for function approximation (35,36). Briefly, the method consists of a convolution of weighted Gaussian functions centered at each y_c position with amplitudes that depend linearly on the intensity value at this position. To execute this, we used the function NEWGRNN from the MATLAB Neural Network Toolbox.

The routine uses the neural network interpolation procedure to precisely locate the y_c coordinates of the selected points. These corrected (x_c, y_c) coordinates are then interpolated using a third-order polynomial to set approximate y_k coordinates for the interpolated x_k positions, where k = 1:m, and m is the number of pixels along the filament segment. This interpolation is only done to get the approximate position of the filament in the first image of the stack. The subpixel y_k coordinates are then calculated using the neural network interpolation procedure to find the maximum of the intensity distribution at every x_k position.

In the next cycle of the tracking routine, the algorithm repeats the procedures described before using the coordinates of the microtubule determined in the previous frame as initial positions. To improve the performance and speed of the algorithm, the search of the maximum at each x_k coordinate is constrained to 6–7 pixels centered in the y_k positions determined for the filament in the previous frame.

Evaluation of the tracking routine

To test the performance of the tracking routine, we simulated 20 confocal images of a single filament (see the Supporting Material for details of these simulations) and recovered the position of the filament in each image of the stack either using the proposed tracking routine or a Gaussian deconvolution-based algorithm similar to that used in Bicek et al. (17). The tracking error (σ) and the accuracy (a) of the position determination were calculated as

$$\begin{array}{c}{\sigma }^2=\frac{1}{m}\sum _{x=1}^m\sum _1^N\frac{{\left(y_k-{\overline{y}}_k\right)}^2}{N},\\ a^2=\frac{1}{m}\sum _{x=1}^m\sum _1^N\frac{{\left(y_k-y_{ks}\right)}^2}{N},\end{array}$$ (5)

where N is the number of frames, y_ks and y_k are the axial positions simulated and recovered for the microtubule at each x_k coordinate (in pixels), and m is the number of x_k positions along the tracked segment of the microtubule.

We explored the performance of the algorithm at different signal to noise ratios (S/N) because the precision on the localization of single fluorescent molecules and particles depends on the number of collected photons (37).

Fig. 2 A shows that the error on the filament position determination decreases with S/N, as expected (37). Noticeably, the error of our neural network-based routine was lower than that of the Gaussian routine for S/N < 60, suggesting that our routine could work better at the low S/N observed for filaments in the intracellular environment (inset, Fig. 2 A). In addition, the Gaussian-based method had a better performance for higher S/N (not shown); however, the precision achieved with our routine in this situation was also very good (≅1 nm).

Figure 2.

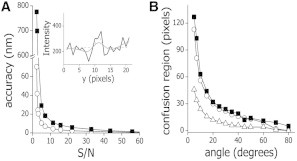
Performance of the filament-tracking routine. (A) We simulated 20 confocal images of a single, fluorescent filament and used the proposed neural network-based tracking routine (○) or a Gaussian deconvolution-based algorithm (■) to track its position. The error on the filament position determination was calculated using Eq. 5. (Inset) A representative intensity profile obtained perpendicular to a microtubule labeled with EGFP-XTP (S/N = 5) in X. laevis melanophores was fitted using the neural network-based tracking routine (continuous line) or a Gaussian function (dotted lines). (B) Twenty confocal images of two intersecting filaments (S/N = 10) were simulated and tracked using the neural network-based tracking routine (○) or a Gaussian deconvolution-based algorithm (■). The confusion regions predicted according to the diffraction limit (▵) and those obtained with the tracking routines are plotted as a function of the intersecting angle.

Fig. 1 also shows that the intensity of the background immediately surrounding the filaments is not homogeneous. To explore the performance of the routine in the presence of an inhomogeneous background, we simulated images of filaments in which the intensity of the background linearly increased in the direction perpendicular to the filament axis; if the background changes parallel to the filament, the local S/N will change with the background and the local precision is that observed in Fig. 2 A. Fig. S2 shows that whereas the error on the filament position determination increased with the slope of the background, the performance of the new routine in the low S/N regime was better than that expected for the Gaussian-based method.

Filaments in cells frequently overlap with each other, and this may affect the performance of the tracking algorithm. Therefore, we simulated two intersecting filaments with S/N = 10 (e.g., similar to that observed for cells, Fig. 1 B) and evaluated whether the algorithm is able to track one of these filaments without jumping to the other filament. With this aim, we compute the accuracy on the filament localization (Eq. 5) and calculated the confusion region as the number of x_k positions along the studied filament in which the accuracy is higher than a threshold value set as 21 nm (i.e., three times the accuracy determined for an isolated filament with the same S/N, not shown). Fig. 2 B shows that the confusion region decreases as the intersecting angle increases. Also, we found that this region is higher than expected according to the diffraction limit (i.e., the region in which the microtubules are closer than the optical resolution limit, and thus it is not possible to resolve them). This result is because the program requires 6–7 pixels (i.e., 600–700 nm) to correctly reconstitute the intensity profile in each x_k position, and this is not possible when microtubules are closer than this distance. Fig. 2 B also shows that the Gaussian-deconvolution routine behaves similar to our routine.

Taken together, these simulations suggest that the algorithm based on the generalized regression neural networks could be suitable for tracking single filaments in the intracellular environment.

The filament-tracking algorithm allows locating single microtubules with subpixel precision

To quantify experimentally the precision achieved with the believed new algorithm described in the previous section, we prepared rhodamine-labeled microtubules as described in Materials and Methods and adsorbed them onto a coverslip previously modified with diethylaminoethanol. The S/N of individual microtubules was calculated using the average intensity of the microtubule because the fluorescence intensity presented slight variations along the microtubules, probably due to local inhomogeneities in the probe distribution.

We acquired confocal stacks of 20 images of these fixed microtubules and then partially photobleached their fluorophores using a higher laser power, repeating this sequence until the S/N was ∼5. Different microtubules in each image stack were tracked and the trajectories recovered were used to calculate the tracking error (σ), as described before.

To determine the tracking error in the complex intracellular environment, we fixed melanophore cells with EGFP-labeled microtubules and acquired stacks of images as described for the in vitro microtubules. Fig. 3, A and B, shows that the algorithm allowed tracking filaments with subpixel precision. As we mentioned before, the intensity of the microtubules was not homogenous, and this fact affected the error on the localization of the microtubule: the position of the microtubule in those regions presenting higher intensity is recovered with higher precision (Fig. 3 A).

Figure 3.

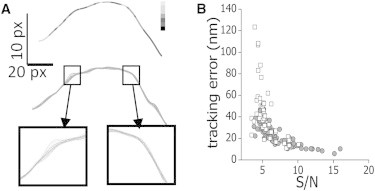
Tracking precision. Rhodamine-labeled microtubules adsorbed onto a coverslip were imaged as a function of time (frame time = 3.3 s) following the sequence of photobleaching and imaging described in the text. The image stacks were analyzed with the filament-tracking routine and the tracking error was determined for microtubules presenting different S/N values as described in the text. (A) Pseudocolor image of a representative microtubule showing the intensity recovered at each position (from black to white, white representing high intensities) (top panel). Recovered shapes of the microtubule in 20 consecutive frames (middle panels). Zoom-in of the shapes recovered in regions of the microtubule presenting low and high intensities (bottom panels). (B) Tracking error for fixed microtubules (●) and of EGFP-XTP-labeled microtubules in formaldehyde-fixed melanophore cells (□) as a function of the signal/noise. The pixel size was 100 nm.

Fig. 3 B shows that the precision on the position determination increased with the S/N, as expected; for high S/N values, the precision reaches a value of ∼9 nm very similar to the precision that can be achieved when tracking pointlike or spherical particles (18–20) and slightly better that those previously measured for microtubules (e.g., 20 nm (14), and 50–70 nm (32)). Moreover, we found that the tracking performance did not depend on the curvature of the microtubule because it worked equally well for straight or curved segments (not shown). These results indicate that the algorithm allows locating single microtubules with very high precision in the complex intracellular environment.

Analysis of the shapes of single microtubules in X. laevis melanophores: influence of actin, intermediate filaments, and MAPs

Microtubules are rigid polymers with millimeter persistence lengths. However, they are extremely curved in living cells and these curvatures have been associated to their biological function (38–40). To show potential applications of the new tracking algorithm to studies of the cytoskeleton architecture in cells, we determined the distribution of microtubule curvatures in different experimental situations.

In a previous article, Gittes et al. (12) explored the shapes of microtubules in vitro and decomposed these shapes into component Fourier modes. These authors found that the variance of the mode amplitudes averaged over uncorrelated microtubule shapes (i.e., Var(a_q)) is given by

$$\text{Var}\left(a_q\right)=\frac{1}{l_p}\times \frac{1}{q^2},$$ (6)

where q = nπ/L is the wave vector, and l_p is the persistence length.

Despite this equation being only valid in thermal equilibrium, Brangwynne et al. (15) found that the distribution of microtubule shapes in fixed CHO cells surprisingly followed Eq. 6 with an apparent persistence length (l_p^∗) of 30 μm.

Considering that the noise of the measurements and the routine of tracking could introduce artifacts on these determinations, we simulated images of filaments (L = 8 μm; S/N = 10) with curvatures determined by a thermal distribution with l_p^∗ = 15 μm (see the Supporting Material for details on these simulations), and tracked these images using the filament-tracking routine. We decomposed the obtained filament shapes into component Fourier modes and calculated the variance for each mode. Fig. 4 A shows that the variance of the simulated filaments decreases with the wave vector presenting clear deviations from the linearity for wave vectors >3.6 μm⁻¹ (i.e., n > 9). This indicates that the method does not allow obtaining the correct amplitudes of the high-frequency components. We fitted the simulated data for n < 9 and recovered l_p^∗ = 16 ± 3 μm; this value is not significantly different from the simulated l_p^∗ value, suggesting that the tracking method allows the quantitative study of the filament-shape distributions in this frequency range.

Figure 4.

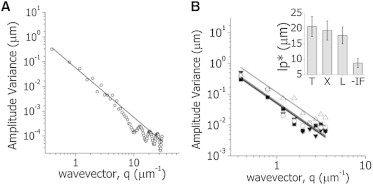
Fourier analysis of microtubule shapes. (A) Images of 8 μm-long filaments (N = 50) with shapes following a thermal distribution with l_p^∗ = 15 μm were simulated as described in the Supporting Material setting S/N = 10. Equation 6 was fitted to the simulated data in the range 1< n < 9 (continuous line) obtaining l_p^∗ = 16 ± 3 μm. (B) The variance of the Fourier mode amplitudes of microtubules was determined for cells transfected with EGFP α-tubulin (■, T), EGFP-XTP cells (▼, X), and EGFP-XTP cells treated with latrunculin to disrupt the actin filament network (○, L) or EGFP-XTP cells transfected with a dominant-negative construct of EGFP-vimentin that disrupts the intermediate-filament network (▵, −IF). (Solid lines) Least-squares fit to a thermal-like behavior (Eq. 6). The figure includes data from 80 to 110 filaments and from 15 to 50 cells in each experimental condition. (Inset) Apparent persistence lengths obtained in the assayed conditions.

We acquired confocal images of X. laevis melanophores expressing EGFP-tubulin and used the tracking routine to locate segments of these polymers with high precision. Fig. S3 shows an example of this decomposition and the distribution of the amplitudes (a_q) of different modes. Fig. 4 B shows that the variance of the mode amplitudes averaged over different microtubules presents an approximate thermal-like behavior, which agrees with Brangwynne et al. (15). We fitted Eq. 6 to this experimental data and obtained l_p^∗ = 21 ± 3 μm for microtubules labeled with EGFP-tubulin in living cells. This value is on the order of the persistence length of microtubules in fixed CHO cells (15) and significantly smaller than the persistence length of microtubules in vitro.

We also evaluated the effect of XTP, a tau-like protein of Xenopus melanophores, on the persistence length of microtubules in living cells and repeated the experiments described above using melanophore cells expressing EGFP-XTP (Fig. 4 B). The variance of the mode amplitudes presented a thermal-like behavior; the apparent persistence length was 19 ± 3 μm, which was not significantly different from the value determined in cells expressing EGFP-tubulin.

As mentioned before, Brangwynne et al. (15,38) proposed that the elastic microenvironment modulates the shape and buckling of microtubules in living cells. Because a key component of the elastic cytoskeleton is the actin filament network (reviewed in Gardel et al. (41)), we explored the role of these filaments on the persistence length of EGFP-XTP labeled microtubules in Xenopus melanophores.

With this aim, we measured the curvatures of microtubules in cells expressing EGFP-XTP treated with latrunculin (as described in Materials and Methods) to depolymerize actin filaments (see Fig. S4) and analyzed them by Fourier decomposition. Fig. 4 B shows that the variance of the mode amplitudes approaches a thermal-like behavior with l_p^∗ = 18 ± 3 μm, which is not significantly different from the value measured in the untreated cells. These results agree well with those obtained by Bicek et al. (17), who observed that microtubule bending events in cells are not correlated to acto-myosin function. Also, Brangwynne et al. (38) showed that actin depolymerization slightly affects the buckling wavelength of microtubules in living cells, and suggested that other cytoskeleton components, such as intermediate filaments, are important for determining the buckling behavior of microtubules.

To explore the influence of intermediate filaments on the mechanical properties of microtubules, we repeated the studies mentioned above in cells expressing a dominant negative version of the intermediate-filament protein vimentin. It has been demonstrated that this mutant version of vimentin induces the depolymerization of intermediate filaments in X. laevis melanophores ((28,29) and see Fig. S4). Cells expressing this mutant version of vimentin could be easily detected by their fluorescence in the nucleus (see Fig. S5 (28,29)). Fig. 4 B shows that the variance of the mode amplitudes also followed approximately a thermal-like behavior. We calculated the apparent persistence length of microtubules in this condition and obtained a value of 9 ± 1 μm, which is significantly lower than that obtained in the presence of intermediate filaments. This result shows that this cytoskeleton component has an important role in determining the shape distribution of microtubules in living cells.

Influence of actin and intermediate-filament networks on the motion of microtubules in living cells

To explore the complex motion of microtubules in cells and the influence of other cytoskeleton networks on this motion, we acquired movies of regions of cells expressing EGFP-XTP using a relatively high temporal resolution (0.6–5 frames/s) during 30 s. These movies were analyzed with the tracking routine to obtain the position of 5-μm-long microtubule segments and their average LP, which was calculated as described in Materials and Methods. Fig. 5 A shows a representative LP trajectory obtained for a microtubule segment.

Figure 5.

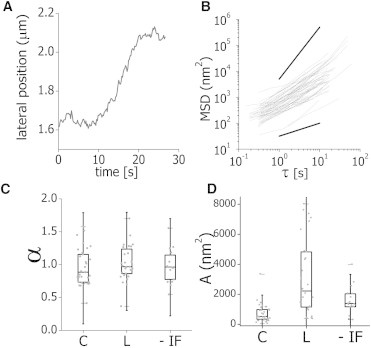
Microtubule lateral motion. (A) Representative time course plot of the average lateral position (LP) of a microtubule segment. (B) MLSD data (Eq. 4) as a function of the time lag obtained for 96 filaments. (Black lines) Representative behavior expected for subdiffusion with α = 0.5 (bottom) and ballistic motion (α = 2, top). (C and D) The MLSD data were fitted using the anomalous diffusion model (Eq. 7). Box plots of the anomalous diffusion coefficient α (C) and preexponential factor A (D) obtained for control (C), latrunculin-treated (L), and vimentin-disrupted (−IF) EGFP-XTP cells. The figure includes data from 80 to 110 filaments and from 15 to 50 cells in each experimental condition.

We quantified the deformation of segments in the studied temporal window using a deformation index defined as the ratio between the segment end-to-end distance and its length. For the analysis given below, we only considered filament segments for which the deformation index values change <7%, and thus LP only reflects the translation of the studied segment.

A widely used parameter to extract quantitative information from trajectories of single particles is the mean-square displacement. This parameter indicates how far a particle traveled after a time lag τ, and thus its behavior is related to the motion properties of the particle and its microenvironment (reviewed in Levi and Gratton (42)). Similarly, we defined the mean lateral square displacement (MLSD, see Materials and Methods) to analyze microtubule trajectories. Fig. 5 B shows the time evolution of MLSD calculated from the trajectories of 96 segments. We fitted these data with the following anomalous diffusion model similar to that proposed in our previous works (29,43),

$$\text{MSLD}\left(\tau \right)=A{\left(\frac{\tau }{{\tau }_o}\right)}^{\alpha }+{\text{MLSD}}_o,$$ (7)

where A represents a generalized diffusion coefficient; τ is the time lag; τ₀ = 1 s; and MLSD_o is the residual value of the MLSD.

The parameter α is an exponent that characterizes the motion: α = 1 corresponds to a random trajectory and α = 2 describes a processive motion with constant velocity (31). In those cases, the preexponential factor is related to the diffusion coefficient and the velocity, respectively (31).

Due to the complexity of the cell cytoplasm, these limit values of α and A are rarely obtained for particles moving in living cells. Instead, particles passively moving present 0 < α < 1, which represents a subdiffusive regime typically observed for thermally jittered particles in a viscoelastic medium while actively-moving particles show a superdiffusive behavior (i.e., 1 < α < 2) (44). In those cases, the preexponential factor A is a transport coefficient due to a combination of the directed forces driving the motion of the particle and the viscoelastic response of the cytoplasm (45,46). This factor has units of squared distance (45), which allows us to compare the effective motility of trajectories with different values of α. Microtubule segments cannot be considered single particles (e.g., the studied segments are part of a polymer and thus cannot move independently from it); however, the analysis of the MLSD can be useful to quantify the overall motion of the microtubule network in different experimental conditions.

To further explore the influence of the different cytoskeleton networks on microtubule motion, we repeated these analyses in cells treated with latrunculin or expressing the dominant negative form of vimentin, as described before. In every assayed condition, we found that α-values were in the range 0.4–1.7, with averages values slightly lower than 1 that were not significantly different in the three analyzed cases (Fig. 5 C).

On the other hand, the preexponential factor A for latrunculin-treated and vimentin-disrupted XTP-cells had a significantly larger median than that observed for control cells, as determined by the Wilcoxon rank-sum test (Fig. 5 C). These results suggest that the disruption of actin or intermediate filaments increased significantly the overall displacements of microtubules, showing that these filament networks restrain the motion of the microtubule network in living cells.

Mapping the organization of microtubules in living cells

We mentioned in the Introduction that both internal and external forces act through the cytoskeleton to affect local mechanical properties and cellular behavior (1). Therefore, mapping how different regions of the cell (and, as a consequence, of the cytoskeleton) sense these forces can provide important clues regarding the mechanical response of the cell. As far as we know, most previous works on microtubule mechanics in living cells were based on the analysis of wide-field microscopy images of the microtubule network (see, for example, Brangwynne et al. (15), Bicek et al. (17), Wu et al. (33), and Zhou et al. (47)). In this work, we used confocal microscopy to analyze microtubule dynamics in different cellular regions because out-of-focus light collected in wide-field microscopy could decrease the S/N value of microtubules and thus, the precision of their localization.

To map the dynamics of microtubules, we acquired image stacks of whole cells expressing EGFP-XTP with a temporal resolution of 0.1–0.3 frames/s during ∼12 min, recovered the coordinates of 4-μm segments of microtubules located either in the perinuclear region or near the cortex, and calculated their average lateral displacement. As described in the previous section, we only studied the motion of microtubule segments that do not present significant changes in their curvature. Fig. 6 A shows an image of a cell with some representative tracked microtubules. The arrows show the lateral displacement of these segments during the assayed temporal window. The overall trajectories of these microtubule segments are not correlated in direction or in magnitude of motion, thereby suggesting that the studied dynamics in this specific cell is not due to a global cell motion.

Figure 6.

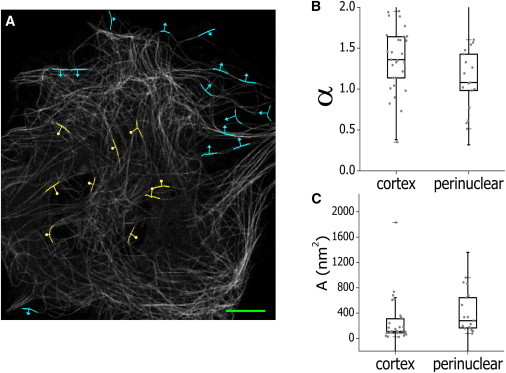
Microtubules motion depends on their relative position within the cell. (A) (Grayscale image) EGFP-XTP cell showing some tracked filament segments in the perinuclear region (circleheads) or near the cortex (arrowheads). (Lines) Vectors defined by the initial and final positions determined for each segment. Scale bar, 10 μm. The MLSD data were fitted using the anomalous diffusion model (Eq. 7). Box plots of the anomalous diffusion exponent α (B) and preexponential factor A (C) obtained by fitting Eq. 7. The figure includes data from 51 filaments from five different cells. To see this figure in color, go online.

We calculated the MLSD of segments located in the different cellular regions, as described in the previous section, and fitted the data with Eq. 7. Fig. 6 B shows that the anomalous diffusion exponents measured in both regions were >1, indicating that active forces are involved in the motion of these cytoskeletal filaments both in the cell periphery and near cortex. The values of α measured in these experiments (i.e., with lower temporal resolution) were higher than those described in Fig. 5 C for control cells, suggesting that the processes involved in the directed motion of microtubules develops in a temporal window of seconds. In this direction, it has been previously demonstrated that microtubule bending events in cells occur on the same timescale (17,49).

It is worth mentioning that the mean-square displacement of different probes in living cells frequently presents crossovers between different anomalous regimes (see, for example, Robert et al. (44), Brangwynne et al. (46), and Caspi et al. (50)). These crossovers are the consequence of the different timescales of the processes driving the motion of the studied particle/filament. For example, a micrometer-sized probe immersed in the cytoplasm may present a diffusivelike motion at short timescales, becomes more hindered by the cytoskeleton at intermediate timescales, and resumes its motion on even longer timescales due to the active remodeling of the cytoskeleton (46). The proposed equation (Eq. 7 (51–53)) assumes a single power-law behavior, and thus it represents the average anomalous behavior observed in a particular temporal window.

In addition, the value of α determined in the cell periphery was significantly higher than that observed near the nucleus as assessed by the Wilcoxon rank-sum test. Because microtubules are cross-linked to the cortex by molecular motors (54), the higher values of α may reflect either more frequent buckling events driven by the molecular motors attached to the cortex or the local changes in cell shape. Also, the preexponential factor A was significantly higher in the perinuclear region than in the cortex, as determined by the Wilcoxon rank-sum test (Fig. 6 C). Taken together, these results show that the forces involved in the cytoskeleton motion are not homogeneous in space and time.

Conclusions

In this work, we presented what we believe to be a new, automated algorithm designed to track filaments with high spatial resolution and applied it to study the microtubule dynamical organization in living cells. We believe that this new routine presents clear advantages with respect to previous methods because it can precisely locate filaments even in the presence of an inhomogeneous background. As we mentioned previously, different authors described excellent algorithms to follow microtubules in vitro with precisions as high as 1–4 nm (34). Unfortunately, we could not use these algorithms to track microtubules in living cells due to the complexity and inhomogeneity of the environment.

To illustrate potential applications of this algorithm, we explored the influence of the actin and intermediate-filaments networks on microtubule organization in interphase cells. We studied the curvature distributions of fluorescent microtubules in living cells and found that this distribution follows a thermal-like behavior, as previously reported for microtubules in fixed cells (15). We found that the effective persistence length of microtubules in cells is significantly smaller than that measured in vitro.

The Fourier analysis of microtubule segments in latrunculin-treated cells showed that the apparent persistence length was not affected by depolymerization of the actin network, suggesting that actin-related mechanisms do not contribute significantly to the formation of curved microtubule, agreeing with the observations of Bicek et al. (17). These authors explored the mechanisms involved in microtubule bending in epithelial cells and found that acto-myosin contractility and other actin-related mechanisms do not play a significant role in bend formation. Instead, they propose that most of the forces responsible of these buckling events are related to microtubule-dependent molecular motors (see also Kulic et al. (49) and Brito et al. (54)).

Surprisingly, we measured a lower apparent persistence length of microtubules in the absence of intermediate filaments than in control conditions. We hypothesize that these filaments probably obstruct buckling events driven by active processes such as those related to microtubule-motors-dependent transport. As far as we know, this is the first report on the influence of intermediate filaments on microtubule network mechanics.

In addition, we recovered trajectories of microtubule segments in actin or intermediate-filament-depleted cells, and verified a significant increase of their motion with respect to untreated cells, showing that these filaments restrict the motion of microtubules in living cells and significantly contribute to the overall dynamical organization of the microtubule network.

Microtubules constitute an interconnected network and active forces acting on one filament will contribute to the motion of other filaments within the network. The analysis of trajectories of microtubule segments in melanophore cells showed that microtubules in the perinuclear regions move faster and less directionally with respect to those located near the cortex region, showing that the algorithm allows mapping the microtubule dynamical organization in cells.

The filament-tracking algorithm runs within a MATLAB environment and can be downloaded from http://www.gdti.df.uba.ar/. We also included in the program a tip-tracking subroutine that can be used in combination with the filament-tracking algorithm to follow the motion of the extreme of a single filament (e.g., the plus-end of microtubules). This routine is very similar to that previously described by Demchouk et al. (55). Briefly, the tip-tracking subroutine allows locating with high precision the coordinates of the extreme of a single filament (tip) in an image stack; these positions are recorded in the tracking program. Then, for each frame of the stack, the filament-tracking routine sets the initial x position to that previously determined for the tip. Once the trajectory of the filament is obtained, the trajectory is replotted in the original image coordinates to get the two-dimensional motion of the filament (see further details in the Supporting Material and Fig. S6).

It is important to mention that the experimental procedure used in this work does not give information regarding the longitudinal dynamics of microtubules. The tip-tracking subroutine could also overcome this limitation if one of the extremes of the region to track is selectively tagged. There are different procedures to do that; for example, a small region of the filament could be photobleached by line-scanning a high power laser perpendicularly to the filament to track. It is also possible to label specific regions of microtubules with photoactivatable or photoswitchable fluorescent proteins.

In conclusion, we presented a tracking algorithm that allows locating single filaments in living cells with nanometer precision and demonstrated the suitability of this method to explore the organization of the microtubule network in living cells. We believe that this algorithm could constitute an important tool to elucidate the behavior of the cytoskeleton in living cells, and thus to explore the mechanical organization of the cell and its response to specific stimuli.