Arterial Extracellular Matrix: A Mechanobiological Study of the Contributions and Interactions of Elastin and Collagen

Abstract

The complex network structure of elastin and collagen extracellular matrix (ECM) forms the primary load bearing components in the arterial wall. The structural and mechanobiological interactions between elastin and collagen are important for properly functioning arteries. Here, we examined the elastin and collagen organization, realignment, and recruitment by coupling mechanical loading and multiphoton imaging. Two-photon excitation fluorescence and second harmonic generation methods were performed with a multiphoton video-rate microscope to capture real time changes to the elastin and collagen structure during biaxial deformation. Enzymatic removal of elastin was performed to assess the structural changes of the remaining collagen structure. Quantitative analysis of the structural changes to elastin and collagen was made using a combination of two-dimensional fast Fourier transform and fractal analysis, which allows for a more complete understanding of structural changes. Our study provides new quantitative evidence, to our knowledge on the sequential engagement of different arterial ECM components in response to mechanical loading. The adventitial collagen exists as large wavy bundles of fibers that exhibit fiber engagement after 20% strain. The medial collagen is engaged throughout the stretching process, and prominent elastic fiber engagement is observed up to 20% strain after which the engagement plateaus. The fiber orientation distribution functions show remarkably different changes in the ECM structure in response to mechanical loading. The medial collagen shows an evident preferred circumferential distribution, however the fiber families of adventitial collagen are obscured by their waviness at no or low mechanical strains. Collagen fibers in both layers exhibit significant realignment in response to unequal biaxial loading. The elastic fibers are much more uniformly distributed and remained relatively unchanged due to loading. Removal of elastin produces similar structural changes in collagen as mechanical loading. Our study suggests that the elastic fibers are under tension and impart an intrinsic compressive stress on the collagen.

Introduction

Arteries consist of three layers: the intima, media, and adventitia. The intimal layer is closest to the lumen, composed of a layer of endothelial cells, and important for providing hemocompatibility with blood (1). The endothelial cells are attached to the internal elastic lamina, which is the first of many concentric layers of elastic fibers (elastic lamellae) that compose the medial layer. Sandwiched between the fenestrated lamellae are smaller interconnecting elastic fibers, bundles of collagen fibers, smooth muscle cells, and proteoglycans (PGs) (2). The outermost layer of the artery is divided from the media by the external elastic lamina and is called the adventitia. It consists primarily of fibroblast cells and large crimped collagen fiber bundles, which are primarily type I collagen. In contrast, the media contains a ratio of around 30% type I and 70% type III collagen (3). The structural proteins elastin and collagen account for ∼50% of the dry weight of the vessel (2), and are often referred to as the extracellular matrix (ECM).

The ECM is essential to accommodate deformations encountered during physiological functions. The elastic lamellae and interconnecting elastic fibers keep loads evenly balanced throughout the tissue (4). Larger bundles of collagen fibers in the adventitia layer play an important role in preventing artery rupture at high pressures (5). In addition to providing structural support, ECM also acts as cellular microenvironment and plays important roles in modulating cell function (6,7). The pathogenesis of many cardiovascular diseases has been associated with loss of organization and function of the ECM. For example, hypertension results in stiffening of the artery wall and this disease is often associated with ECM changes including the collagen/elastin ratio, increased media thickness, and reduced fenestration of the elastic lamina (8–10). Large losses of elastin content along with fragmentation of the elastic laminae/fibers are reported characteristics of aneurysm, a disease state characterized by stiffer and dilated artery walls (11).

Because collagen fibers are almost three orders of magnitude stiffer than elastic fibers (12,13), it is commonly assumed that elastic fibers support the initial lower loads on the artery, whereas at higher pressures collagen fibers are recruited and become the major load bearing component (14). The recruitment of the larger collagen fiber families would explain the increase in stiffness of normal arteries and the adventitial collagen is important in preventing artery rupture at high pressures. Attempts have been made to determine the onset of collagen engagement based on the curvature of the J-shaped pressure diameter curves (15). Simultaneous mechanical loading and imaging methods have been employed to understand the structure-function relationship. Previous studies have quantitatively shown increased collagen fiber straightness as a result of mechanical loading (16–18). The changes in both collagen and elastin orientation has also been evaluated (17,19,20).

Determining how the ECM components contribute to the mechanical behavior of an artery is essential for understanding the mechanisms of vascular remodeling and disease progressions. However, the interactions of collagen and elastin and the effect of ECM structural changes on vascular function are not well understood. Through improved medical imaging and biomechanical testing methods, this information would be useful in the understanding of remodeling associated with diseases. Such information can also be incorporated into structurally based constitutive models in future diagnostic interventions (21). To this end, multiphoton microscopy is used to image both adventitial and medial layers of porcine thoracic aortas to capture the structural changes of ECM during mechanical loading. Two-dimensional (2-D) fast Fourier transform (FFT) and fractal analysis provide quantitative and complementary information on the orientation and fiber engagement of the ECM structure. Equal and unequal biaxial deformations are applied to the tissue to examine structural changes during physiologically relevant loads. A second set of samples undergo a gradual elastin degradation process to assess the resulting changes in the remaining collagen structure. This experimental protocol should allow for a better understanding of the interactions between the elastic and collagen fibers in the mechanics and mechanobiology of arteries.

Methods

Sample preparation

Porcine thoracic aortas ranging from 12–24 months of age at the time of harvest were obtained from a local abattoir. Approximately 30 mm sized square samples (n = 6) were cut so that one edge is parallel to the longitudinal direction and the other edge is parallel to the circumferential direction of the artery. The anatomic axis of the square samples was recorded for mechanical testing and imaging. Samples were placed in 1× phosphate buffered saline solution at 4°C and all samples were imaged within 24 h of cleaning/preparing the tissue.

For the elastin degradation samples, a 5 units/mL ultrapure elastase solution (MP Biomedicals, LLC, Solon, OH) was used to gradually degrade tissues at 37°C with gentle stirring following the methods detailed by Chow et al. (22). Samples (n = 6) were imaged after 0, 6, 12, 24, and 48 h of digestion. Elastin content was measured using a Fastin elastin assay kit (Biocolor, www.biocolor.co.uk) and expressed as μg of elastin/mg of wet tissue weight (22). The average elastin content for fresh tissue is 51.23 ± 7.73 μg/mg. After digestion for 6, 12, 24, and 48 h, the elastin content decreases to 38.65 ± 5.26, 20.86 ± 4.51, 9.98 ± 2.29, and 6.09 ± 2.29 μg/mg, respectively.

Multiphoton microscopy

A mode-locked Ti:sapphire laser (Maitai-HP, excitation wavelength 800 nm, 100 fs pulse width, 80 MHz repetition rate, Spectra-Physics, Santa Clara, CA) was used to generate second-harmonic generation (SHG) from collagen at 400 nm (417/80 nm) and two-photon-excited fluorescence (2PEF) from elastin (525/45 nm) (23). A quarter-wave plate was placed just before the objective (60X, NA1.0 W, LUMPlanN, Olympus) to generate a quasicircular polarization (1.8 dB) to alleviate the excitation polarization dependence of the SHG. Due to the differences in the strength of signal from the media and adventitia sides, the average power at the sample was consistently set to 40 mW for the medial images and 25 mW for adventitial images. Laser power settings were selected to image as deep as possible without causing saturation of the second harmonic generation signal from collagen at the sample surface.

Due to the thickness of the porcine aorta and penetration limits of the imaging, samples were imaged from both the adventitial and medial surfaces to assess the adventitial collagen, medial collagen, and elastin. Image acquisition was performed on a multiphoton video-rate microscope (24) and a three-dimensional volume was recorded with a field of view of 360 μm. Each sample was imaged at nine locations spread over a 1 cm square to obtain an average view of the structure for that sample. The adventitial side was imaged to a depth of 60 μm, whereas the medial side was imaged to a depth of 40 μm. A maximum intensity projection of the Z-stacks was made and images were cropped from 360 × 360 μm to 110 × 110 μm to focus on regions with better fiber coverage. The cropped projections were used in the subsequent image analysis methods.

A custom tissue stretching device was made that allows for equal and unequal biaxial deformation to be applied to tissue samples while being imaged by a multiphoton microscope (Fig. 1). All tissue samples were imaged with the circumferential direction of the tissue parallel to the horizontal direction of the images. Thus, fibers oriented at 0° and 90° are in the circumferential and longitudinal anatomic directions of the artery, respectively. Tissues were imaged at the unstretched condition and then at 5% strain increments to a max strain of 45% for equal biaxial strain imaging (n = 6). The strain used in this study is engineering strain defined as (l-L)/L, where L and l are the original and deformed lengths, respectively. For unequal biaxial deformation, samples (n = 4) were imaged at strains of 0%C-0%L, 30%C-30%L, 30%C-15%L, and 15%C-30%L where the C and L refer to the circumferential and longitudinal directions, respectively. Validation studies were done to confirm that the fiber waviness was not affected by opening and flattening the arteries in the stretching device. The elastase treated samples were imaged at unstretched condition.

Figure 1.

The custom built tissue stretching device allowing for multiphoton microscopy to be performed while tissue undergoes equal and unequal biaxial strain. To see this figure in color, go online.

Image analysis

2-D FFT analysis was performed on SHG and 2PEF images with the Directionality plug-in (developed by Jean-Yves Tinevez, http://pacific.mpi-cbg.de/wiki/index.php/Directionality) in FIJI (http://fiji.sc/Fiji, Ashburn, VA) following the developer’s instructions. Directionality has been used previously to determine the orientation of cortical myelination (25). Similar FFT analysis through ImageJ plug-ins has also been successfully performed on multiphoton images of collagen and elastic fibers in skin to determine the changes in orientation due to aging or scarring (26,27). The 2-D FFT determined the spatial frequencies within an image in radial directions and the output of the plug-in was a normalized histogram that reports the amount of structures at angles between −90° and 90° with a bin size of 2° (Fig. S1 in the Supporting Material). To compare differences in the degree of alignment of the structures in the main anatomic axis of the artery, the areas under the distribution curves from 0° ± 20° and 90° ± 20° were categorized to be circumferentially and longitudinally oriented, respectively (20).

The fractal analysis was accomplished with a box counting protocol of ImageJ (http://rsbweb.nih.gov/ij/), which gives the fractal dimension, a measure of the degree of self-similarity of the image (28). The fractal number, D, was defined as

$$D=\mathit{li}{\mathit{m}}_{r\to 0}\left\{\log \left(N_r\right)/\log \left(1/r\right)\right\},$$ (1)

where r is the box size and N_r is the number of boxes required to cover the image with the box size of r. As r approaches zero, the fractal number can be approximated as

$$D\approx \log \left(N_r\right)/\log \left(r\right),$$ (2)

so a plot of log(N_r) vs. log(r) can be best fitted and the slope will be an approximate value of D (Fig. S7). In our study, the absolute and normalized difference in fractal number was reported as abs(D – D₀)/D₀, where D and D₀ were the average fractal number of the samples at deformed and undeformed states, respectively. This limited the sensitivity to sample-to-sample variation and allowed for changes in fractal number to be interpreted as a broad measure of fiber engagement. The fractal analysis method has been used to quantify changes in the collagen network organization due to pancreatitis and fibrillogenesis after tendon injury (29,30).

Verification of the fractal analysis method as an effective means to measure fiber waviness was performed by concurrently measuring the adventitial fiber waviness with NeuronJ (31), which has been successfully used in examining the waviness of collagen fibers (32,33). The end-to-end distance L_o, and total fiber length, L_f, can be measured. The waviness of the fiber is defined as P_s = L_o/L_f, with a perfectly straight line having a straightness parameter of 1. Although this manual tracing method is successful for the analysis of larger diameter adventitial collagen fibers, the network of finer fibers in the media layer do not allow for the use of NeuronJ in those image groups. The effects of other structural changes on the image analysis, such as fiber waviness/alignment as well as image intensity/noise, were also investigated (Figs. S2–S6, S8, and S9).

Statistical analysis

Experimental data were summarized with mean ± standard error of the mean (SE), unless otherwise mentioned. Amounts of circumferentially and longitudinally oriented fibers from the FFT analysis in the equal and unequal biaxial strain tests as well as the elastin degradations were compared using a factorial analysis of variance. Post hoc testing with the Tukey’s method was used to adjust for multiple comparisons. Statistical analysis was performed using the JMP statistical package (version 9.0.2, 2010 SAS Institute Inc., Cary, NC).

Results

Representative SHG and 2PEF images from equal biaxial strain studies are shown in Fig. 2. Qualitatively the adventitial collagen is crimped initially, and then at high strains the fibers straighten out and the fiber families become more apparent. The medial collagen fibers are much smaller in diameter but also have a wavy configuration in the unstretched state and then gradually become straightened when stretched. Due to the fiber diameter and weaker 2PEF signal of the medial elastin, qualitative changes in structure are difficult to be directly visualized.

Figure 2.

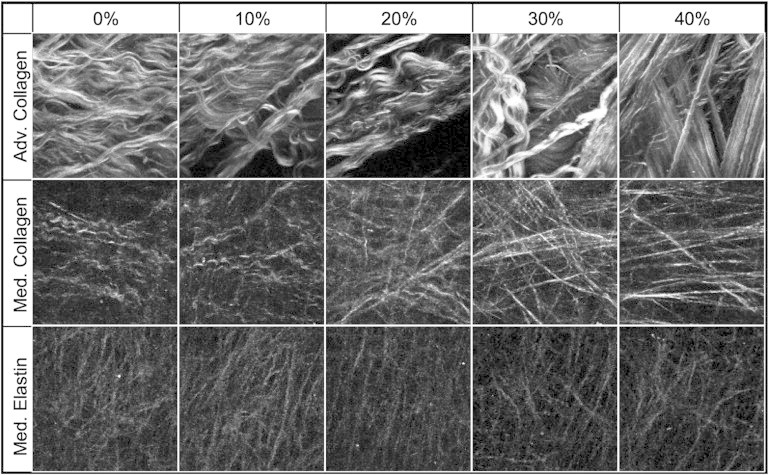
Multiphoton images of adventitial collagen (top), medial collagen (middle), and medial elastin (bottom) during equal biaxial strain. Images are 110 × 110 μm.

FFT and fractal analysis results from equal biaxial strain imaging are shown in Fig. 3. FFT analysis is presented with a three-dimensional plot with the fiber angle on the x axis (0° being the circumferential, and 90° being the longitudinal direction), equal biaxial strain on the y axis, and normalized fiber count on the z axis. Adventitial collagen appears circumferentially oriented at zero strain. The fiber orientations at 45% strain consist of circumferentially as well as ±∼70° oriented collagen families as expected for thoracic adventitial collagen (34). The medial collagen fibers remain circumferentially oriented with deformation but become significantly more aligned at 45% strain (p < 0.05). There is no significant change in elastin fiber distribution during deformation. However, it is noted that elastin is more uniformly distributed compared to the collagen and has a large longitudinally oriented fraction. Fractal analysis shows that the adventitial collagen structure is unchanged until the fibers begin to straighten after 20% strain. In contrast, the fractal number changes throughout the stretching process for the medial collagen indicating that the collagen in the media is continuously being recruited. The medial elastic fibers straighten at the onset of loading but after the 20% strain condition, changes in the fiber network appear to plateau as collagen becomes the load bearing component.

Figure 3.

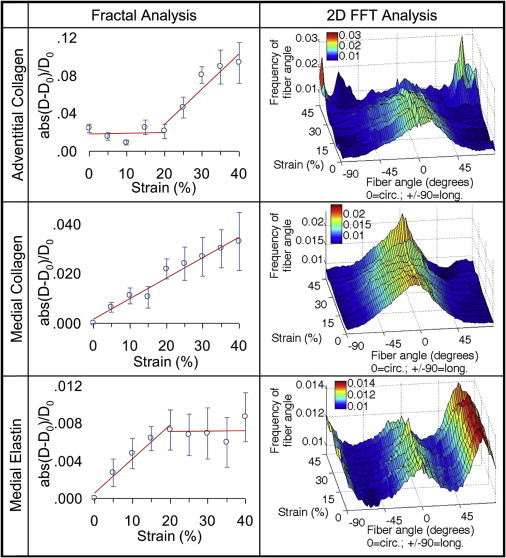
Fractal (left column) and FFT (right column) analysis of equal biaxial strain images of adventitial collagen, medial collagen, and medial elastin. Fractal analysis is plotted with the mean of the normalized absolute difference in fractal number ± SE along with increasing strain. FFT analysis is plotted with the fiber angle on the x axis (fibers oriented at 0° and 90° are in the circumferential and longitudinal anatomic directions of the artery, respectively), increasing strain on the y axis, and amount of fibers on the z axis. To see this figure in color, go online.

Analysis of the adventitial collagen fibers with NeuronJ showed the same trend as fractal analysis. No significant difference in the waviness was observed from 0% to 15% equal biaxial strain. However, all strains >20% resulted in fibers having a significantly higher straightness parameter (Fig. 4). The straightness parameter is close to its maximum at 40% strain.

Figure 4.

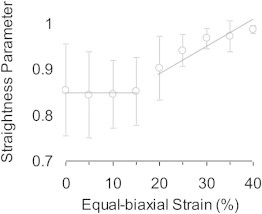
Straightness parameter of adventitial collagen fibers as measured with NeuronJ. Compared with the fractal analysis in Fig. 3, both methods consistently show a lack of structural change initially and then a decrease in fiber waviness at higher strains.

The FFT analysis of arteries subjected to the unequal biaxial stretching indicates that both medial and adventitial collagen fibers will realign in the major direction of loading. In the average normalized distribution curves (Fig. 5), there is an increase in circumferentially oriented fibers when the loading ratio is favoring the circumference direction (30%C-15%L). Likewise, the peak in the circumferential direction is diminished and there is a small rise of peaks in the longitudinal direction when loading is skewed favoring the longitude direction (15%C-30%L). Medial elastin does not appear to have a change in fiber orientation due to unequal biaxial loading. To compare the orientation distributions, the fiber orientation ratio of circumferential to longitudinal fibers, defined as the number of fibers oriented between 0° ± 20° divided by the number of fibers oriented at 90° ± 20°, are presented in Fig. 6. The 30%C-30%L equal biaxial strain condition does not result in any significant changes in fiber orientation ratio for any of the elastin and collagen in the medial and adventitia. However, both medial and adventitial collagen have significant changes in alignment as a result of the unequal biaxial strain (p < 0.05). With increased strain in the longitude direction (15%C-30%L) there is a decrease in the fiber orientation ratio. Likewise, the fiber orientation ratio increases with larger strain in the circumferential direction (30%C-15%L). Medial elastin has a fiber orientation ratio around one, which suggests a relatively uniform distribution of the elastin fibers. There is a significant increase in the fiber orientation ratio in the 30%C-15%L strain condition but no change for the 15%C-30%L state for elastin.

Figure 5.

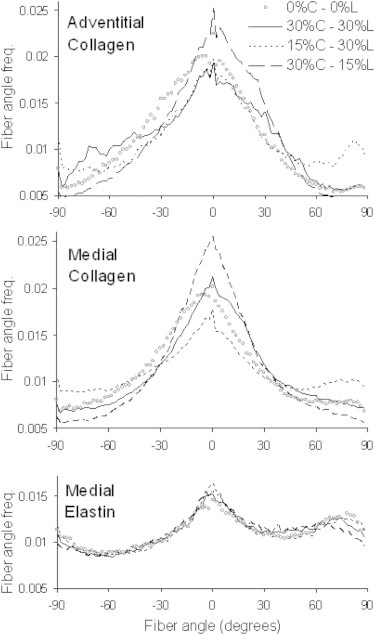
Average normalized distributions of fiber orientation with biaxial strains of 0%C-0%L, 30%C-30%L, 15%C-30%L, and 30%C-15%L applied to the tissue. Fibers oriented at 0° and 90° are in the circumferential and longitudinal anatomic directions of the artery, respectively. C and L represent the circumferential and longitudinal directions, respectively.

Figure 6.

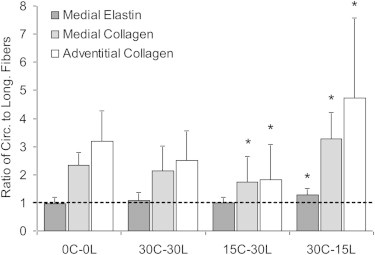
Ratio of circumferential to longitudinal distributed fibers, defined as the number of fibers oriented between 0° ± 20° divided by the number of fibers oriented at 90° ± 20° from Fig. 5, of medial collagen, medial elastin, and adventitial collagen during biaxial deformation. The 0, 15, and 30 denote strain levels; and C and L represent the circumferential and longitudinal directions, respectively. Comparisons between the stretched states and the unloaded (0C-0L) condition are shown (^∗p < 0.05).

Fig. 7 shows the example SHG images of the adventitial and medial collagen during the removal of elastin. Similar to the mechanical stretching experiment, qualitatively collagen fibers are initially wavy and as elastin is removed from the ECM, the fibers straighten. The presence of large diameter bundles in the adventitia and smaller fibers in the media is again confirmed. Fig. 8 shows the fiber distribution functions as the elastin content is decreased in the tissue. In the adventitial collagen, notable peaks indicate families of fibers that become more evident when elastin is digested away. In the medial collagen, there is a significant increase in alignment of fibers to the circumferential direction when elastin content was reduced to 9.98 and 6.09 μg of elastin/mg wet tissue weight (p < 0.05). The increase in alignment is qualitatively similar to what occurs in the collagen structure due to mechanical stretching. Due to elastin degradation, analysis of the changes in medial elastin structure is not possible.

Figure 7.

Multiphoton images of adventitial collagen (top) and medial collagen (bottom) during elastin removal from the ECM. The average elastin content was reported as μg elastin/mg wet tissue weight. Images are 110 × 110 μm.

Figure 8.

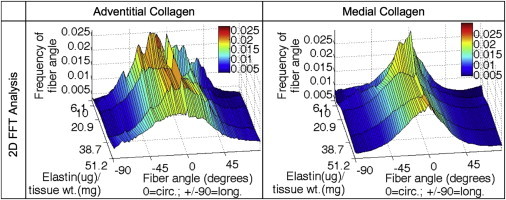
FFT analysis of elastin degradation images with the fiber angle on the x axis (fibers oriented at 0° and 90° are in the circumferential and longitudinal anatomic directions of the artery, respectively), decreasing elastin content on the y axis, and amount of fibers on the z axis. To see this figure in color, go online.

Discussion

The combination of 2PEF and SHG imaging provides detailed images of the ECM structure without the need for staining or excessive tissue processing. The FFT analysis is able to provide structural information on the main fiber orientation and degree of alignment. In contrast, the fractal analysis is a general measure of fiber engagement that occurs due to loss of undulation in the fibers under equibiaxial strain. The fractal analysis is particularly useful when the complexity of the fiber microstructure does not allow for more common analysis techniques, as was the case with the medial collagen and elastin images. The combination of FFT and fractal analysis as complementary methods allows for a more complete understanding of structural changes.

Our study provides the direct quantitative evidence on the sequential engagement of different ECM components in response to mechanical loading. The medial and adventitial collagen fibers engage differently during mechanical loading. The medial collagen continues to straighten throughout the stretching process, whereas the adventitial collagen shows a delay in the fiber straightening and only begins to lose its waviness after 20% strain (Fig. 3). As mentioned earlier, the media contains a much greater fraction of type III collagen, which is more extensible compared to type I collagen in the adventitia (35). In addition, type III collagen typically forms an elastic network structure that is important in the storage of kinetic energy (36). The medial elastic fibers are engaged at the onset of loading and the engagement plateaus at ∼20% strain, which further indicates that collagen is now the major load bearing component (Fig. 3). Our study suggests that the assumption that arterial tissues transition from being elastin- to collagen- supported should be interpreted carefully, as our data indicate that the medial collagen structure is changing at the onset of mechanical loading.

The fiber orientation distribution function from the FFT analysis also shows remarkably different changes of the ECM structure in response to mechanical loading. The adventitial collagen appears to be oriented in the circumferential direction at low or no mechanical loading, similar to the results from polarized light studies of human arteries (37,38). However, the main orientation of adventitial collagen fibers changes when deformed with multiple families of collagen fibers becoming evident at high strains (Figs. 2 and 3). Because the analyzed images are maximum intensity projections at single locations, the multiple families of collagen fibers are likely due to the varying orientation of adventitial collagen fiber through the thickness (20). Another important aspect of the orientation analysis is these fiber families are obscured by their waviness at no or low mechanical strains (Fig. S3). For use in constitutive modeling, determining the fiber family directions when the fibers are straightened is suggested due to the masking effect of the crimping. Measurements of orientation on wavy collagen fibers often appear uniform, and only after pressurizing the vessels can the preferred direction of the fiber families be determined (32,39). Although not the focus of this study, the results also suggest that fiber waviness should be considered in verifying the affine assumption by comparing the measured family angles with and without strain to those predicted by models for some biological tissues.

FFT analysis of the medial collagen images show a relatively normal distribution of the collagen fibers centered in the circumferential direction similar to previous studies (2,40). During high equal biaxial strains, there is a significant increase in the amount of fibers in the circumferential direction (Fig. 3). This could be due to the straightening of fibers because the collagen fibrils are arranged in a loosely connected array between the lamellae and uncrimping can lead to higher and narrower peak measurements in the distribution (Fig. S2). Realignment of fibers in the direction of loading during the unequal biaxial deformation is observed for both medial and adventitial collagen. The ratio of circumferentially to longitudinally oriented fibers is significantly increased or decreased when the unequal biaxial loading favors the circumference or longitude directions, respectively (Figs. 5 and 6). Evidence of fiber realignment and the dependence of fiber alignment on the direction of loading are likewise shown by Timmins et al. (20).

Although the collagen fibers display changes in fiber orientation and degree of alignment in response to mechanical deformation, the elastic fibers are not significantly affected. Elastic fibers form a dense interconnected network (Fig. 2), which is relatively uniformly distributed compared to collagen (Figs. 3 and 5). Elastic fibers and lamellae serve to evenly distribute loads through the artery wall and are closely associated with the collagen fibers (41,42). It is possible that the uniformly distributed network may facilitate the load distribution in the arterial wall.

Our study suggests there is an important intrinsic interaction between the two major ECM components, elastin and collagen, which is crucial to the proper mechanical functioning of arteries. Removal of elastin results in similar structural changes in the collagen as in mechanical deformation. The adventitial fiber families are initially masked and then become more apparent after elastin degradation (Figs. 7 and 8). The medial collagen again shows an increase in alignment in the circumferential direction as a result of elastin removal (Fig. 8). Our earlier study shows that removal of elastin leads to straightening of collagen fibers and nearly 30% increases in tissue length (22,33). Together, these results suggest that the elastic fibers are under tension and impart an intrinsic compressive stress on the collagen. The tissue level residual stresses are the sum of the intrinsic stresses in all ECM components. Thus, the intrinsic stresses within individual ECM components are not necessarily zero in the so-called stress-free configuration of the tissue.

Limitations

The collagen fibers in the adventitia appear larger in diameter compared to the ones in the media (Figs. 2 and 7), which is consistent with the difference in fiber structure found in rat carotid arteries (43). However, this difference in fiber thickness cannot be quantified with SHG because individual collagen fibers are not always resolved (44). In addition, type III collagen is thinner compared to type I fibers (35) and studies on second harmonic generation have shown that type III collagen produces a much smaller signal compared to type I collagen (36,45). Thus, the different ratios of collagen types in the media and adventitia are not truly reflected with SHG as the contribution of type I collagen is weighted more heavily.

The fractal analysis method is very sensitive to small microstructural changes, which makes it useful for studies of biological images. Previous studies have often reported the average fractal number from different experimental groups to quantify changes in complexity of fiber networks and cell shapes (29,30,46). However, the high sensitivity makes the sample-to-sample variation large, hence restricting comparisons of the actual fractal numbers. For this reason, stretched samples are compared to their nonstretched states with a normalized change in fractal number. Manual tracing of adventitial collagen fibers with NeuronJ and tests of synthetic images confirm the ability of fractal analysis to measure changes in fiber waviness (Fig. 4). However, it is noted that fractal analysis also detects other potential mechanisms of fiber recruitment such as realignment in the direction of loading (Fig. S4). Changes in fiber orientation, degree of alignment, amount of fiber waviness, as well as density of the fiber network have all been reported to occur as a result of stretching the tissue (20,32). Thus, the absolute value of the normalized difference in fractal number should be interpreted more as an encompassing measure of fiber engagement than a strict measure of fiber waviness. The effects of image intensity and noise on the FFT and fractal methods were also investigated and shown not to affect the results due to the range of intensity and noise of our images (Fig. S9).

It is noted that the clamping method in the tissue stretcher will result in stress concentrations at the edges and the inner region will not be fully loaded or stretched (47). In addition, the stretch in the tissue was measured based on the distance between the grips, which provides only a rough measure of strain compared to more accurate surface speckling and dot tracking techniques (19). However, this study sought to examine sequential and different engagement of elastin and collagen during loading and for such purposes the strain estimates are sufficiently precise.

Porcine pancreatic elastase is known to degrade PGs which surround and stabilize the elastin and collagen matrix (48–50). Removal of PGs will likely affect the ECM structure and it may contribute to the collagen straightening. Other studies have also shown that the residual stresses differ in the intima, media, and adventitia (40,51,52). Removal of elastin could cause a redistribution of residual stresses and contribute to the straightening of the collagen as well.

Conclusions

Multiphoton microscopy paired with equal/unequal biaxial deformation and elastin degradation show several important findings about the roles of elastic and collagen fibers in the mechanics and mechanobiology of arteries. The combination of fractal and FFT analysis provides complementary information on the complex interactions between the two ECM components. The sequential and different engagement of medial and adventitial collagen and elastin offers insights into the biomechanical function of the arterial wall. The orientation of collagen fiber families in the adventitia is suggested to be obscured due to crimping of the fibers in the unloaded state. Mechanical loading and elastin removal allows for better identification of fiber family. The reorientation of collagen fiber families in the direction of loading differs from elastic fibers, which maintained a relatively uniform distribution. Our study suggests that elastic fibers are prestretched and impart an intrinsic compressive stress on the collagen structure. Overall, these results pose important considerations in developing constituent-based constitutive models and in understanding vascular remodeling and disease progressions.