Abstract
Mathematical models are extensively employed to understand physicochemical processes in biological systems. In the absence of detailed mechanistic knowledge, models are often based on network inference methods, which in turn rely upon perturbations to nodes by biochemical means. We have discovered a potential pitfall of the approach underpinning such methods when applied to signaling networks. We first show experimentally, and then explain mathematically, how even in the simplest signaling systems, perturbation methods may lead to paradoxical conclusions: for any given pair of two components X and Y, and depending upon the specific intervention on Y, either an activation or a repression of X could be inferred. This effect is of a different nature from incomplete network identification due to underdetermined data and is a phenomenon intrinsic to perturbations. Our experiments are performed in an in vitro minimal system, thus isolating the effect and showing that it cannot be explained by feedbacks due to unknown intermediates. Moreover, our in vitro system utilizes proteins from a pathway in mammalian (and other eukaryotic) cells that play a central role in proliferation, gene expression, differentiation, mitosis, cell survival, and apoptosis. This pathway is the perturbation target of contemporary therapies for various types of cancers. The results presented here show that the simplistic view of intracellular signaling networks being made up of activation and repression links is seriously misleading, and call for a fundamental rethinking of signaling network analysis and inference methods.
Introduction
Mathematical models in molecular, cellular, and developmental biology, representing intracellular networks organized into modular components that interact positively (activation) or negatively (inhibition or repression), are extensively employed to understand physicochemical processes in biological systems (1–4). The lack of mechanistic knowledge presents a challenge to constructing accurate models and establishing rigorous links to experimental data (5), and has led to the widespread adoption of reverse engineering and network inference methods that aim to unravel network topology from quantitative data gathered from perturbations (e.g., small-molecule kinase inhibitors, over- or underexpression of enzymes, gene knockdowns, siRNAs) (6–10). However, underlying all these methods is the assumption that perturbations to a node will uniquely determine the sign of its direct effects on other nodes. Here we report on a surprising discovery that contradicts this widespread assumption: perturbation methods may lead to paradoxical conclusions, with either an activation or a repression of a second component being inferred, depending upon the particular type of intervention performed on the first component.
We carried out our experiments on an in vitro reconstituted system involving the proteins from the canonical mitogen-activated protein kinase/extracellular signal-regulated kinases (MAPK/ERK) pathway. This comprises a set of phosphorylation/dephosphorylation covalent modification cycles found in all eukaryotes (11–17), and is involved in the regulation of proliferation, gene expression, differentiation, mitosis, cell survival, apoptosis, and other processes (18). Our rationale for testing our ideas on an in vitro system is that, if a method fails there, there is no justification for believing that it will work in a more complicated in vivo context. We also analyzed a generic mathematical model that shows the generality of the phenomenon for other enzymatic systems. Our results show that the simplistic view of signaling networks through activation and repression links is seriously misleading, calling for a fundamental rethinking of network analysis and inference methods. This is especially urgent because the perturbation of pathway activities (and, specifically, the targeting of MAPK/ERK components) is the focus of current-generation drugs to treat advanced melanomas and a wide range of tumors including lung and thyroid cancers (19).
Perturbation methods
A widely used strategy for reverse engineering, and indeed a common feature of many popular approaches, relies on the following simple principle: to deduce the character of a directed interaction from a network node Y to another node X, apply a perturbation that locally affects Y, and quantify the change in X (20). The perturbation used experimentally might be performed through small-molecule kinase inhibitors, over- or underexpression of enzymes, siRNAs, or other interventions. If (positively) first-order correlated effects are observed, an arrow Y → X is drawn, in the network being studied, to graphically represent an activation. If the effects are of opposite sign, a blunt arrow Y ⊣ X is drawn, to represent an inactivation, repression, degradation, or inhibition. Otherwise, no arrow is drawn between these nodes (Fig. 1, a–c).
Figure 1.
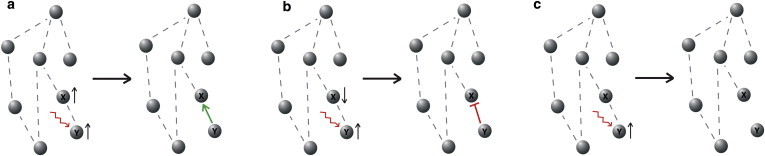
Perturbation experiments. (a) Correlated response suggests activation. (b) Anti-correlation suggests repression. (c) If no response, no edge drawn in graph. To see this figure in color, go online.
In this work, we undertook to test experimentally the following question: is it possible that the nature of the specific perturbations may affect the results? We discovered that, indeed, perturbation methods often lead to paradoxical conclusions, that is, different perturbations, on the same node, may lead to opposite conclusions. Specifically, even for the simplest systems, it is possible that, for the same pair of components X and Y, depending upon the specific type of intervention on Y, either an activation Y → X or a repression Y ⊣ X might be inferred. We emphasize that this effect is of a completely different nature from the well-studied issue of incomplete network identification due to underdetermined data (21). It is a phenomenon intrinsic to perturbation approaches, no matter how much data is collected.
Experiments and Theory
Experiments
We carried out our experiments on an in vitro reconstituted system involving the proteins from the canonical Raf/Mek/Erk MAPK/ERK pathway, a cascade of phosphorylations in which Raf activates Mek, which, when active, in turn activates Erk. An example in which MAPK networks are used as a subject of perturbation-based reverse engineering is Santos et al. (22).
Specifically, our system consists of
-
1.
Constitutively active Raf;
-
2.
Unphosphorylated Mek;
-
3.
Unphosphorylated Erk with Threonine T188 in the activation loop mutated to Valine (Erk-T188V), leaving only Tyrosine Y190 to be phosphorylated by Mek;
-
4.
Protein Phosphatase 2A (PP2A); and
-
5.
Protein Tyrosine phosphatase (PTP).
For simplicity, we refer to Erk-T188V simply as “Erk”. The possible enzymatic reactions between these proteins are as follows:
-
1.
Constitutively active Raf will doubly phosphorylate Mek to form activated Mekpp,
-
2.
Mekpp in turn will phosphorylate Erk to form Erkp,
-
3.
PTP will only dephosphorylate Erkp, and
-
4.
PP2A will only dephosphorylate Mekpp.
The choice of Erk-T188V ensures that PP2A does not also dephosphorylate Erkp. In the context of our general discussion of perturbation methods, X is Mekpp, and Y is Erkp. Our perturbations consist of modifying the total amounts of Erk or PTP.
We measured doubly-phosphorylated Mek and singly-phosphorylated Erk using an MS method, which we have previously shown to be significantly more accurate than quantitative Western blots with phosphospecific antibodies (23). When the concentration of PTP is increased in the reaction conditions (see Materials and Methods), we observed decreased Erkp and increased Mekpp. In contrast, when the concentration of Erk is increased in the reaction conditions (see Materials and Methods), we observed increased Erkp and increased Mekpp (Fig. 2 a). Western blots supported the MS results with less quantitative discrimination (Fig. 2 b).
Figure 2.
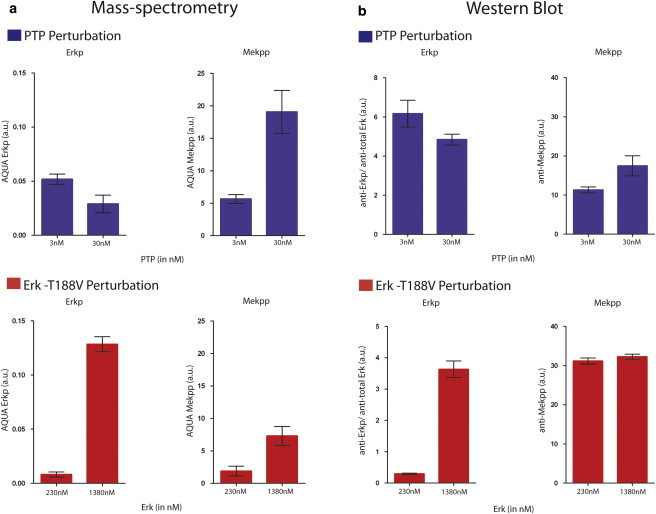
(a) Mass-spectrometry-based quantitation of Erkp and Mekpp under PTP perturbation (top) and Erk perturbation (bottom). The amounts of Erkp and Mekpp at 30 min, quantified by the AQUA method (see Materials and Methods and Gerber et al. (41)), are plotted at the indicated concentrations of the perturbed enzymes. Error bars show the standard error of the mean of three technical replicates (same sample, three different reaction tubes). (b) Western blot-based quantitation of Erkp and Mekpp under PTP perturbation conditions and Erk perturbation conditions. Amounts of Erkp and Mekpp, quantified as described in Materials and Methods, are plotted at the concentrations of the perturbed enzymes after 30 min of reaction time. Error bars show the standard error of the mean of three technical replicates (same sample, three different reaction tubes). To see this figure in color, go online.
Thus, our minimalist, in vitro system clearly shows that opposite inferences between two nodes in a reaction (X as Mekpp and Y as Erkp) can be inferred depending upon experiment: a perturbation in which we increase PTP leads to concluding an inhibitory edge Y ⊣ X, while a perturbation in which we increase Erk would lead to an inference of an activation Y → X. Every network reverse engineering algorithm based on these experiments and using active Mekpp and Erkp as nodes will suffer from this paradoxical result. The only solution to the ambiguity is to add to the network description the various phosphorylation states, and to measure these as well.
Modeling
To understand these experimental results, we formulated and analyzed a minimal mathematical model that suggests an explanation for the ambiguous effects. We employ a widely-used model of enzymatic transformation of a substrate, in our case Erk, to a product, in our case Erkp:
| (1) |
The letters α,β,… denote reaction constants, which are allowed to be arbitrary positive numbers. In this model, a kinase is constitutively activated and inactivated. The inactive form of the enzyme is, in our case, Mek. Its active form, Mekpp, drives a phosphorylation reaction in which a target or substrate, Erk in our case, is converted to an active or phosphorylated form, Erkp, the product of the reaction. Finally, a constitutively active phosphatase, PTP in our case, dephosphorylates Erkp back into inactive form Erk. The model includes two intermediate enzyme-substrate complexes, Mekpp:Erk and Erkp:PTP. Some limitations of these assumptions are discussed in the Materials and Methods. We denote by X the total amount of active Mek (Mekpp) and by Y the total amount of active Erk (Erkp). In our experimental system, these are the total measured amounts. Note that the total amounts of Erk and PTP, in any form, are
We assume that protein is synthesized and degraded over long timescales, so that the total protein concentration can be regarded as constant over the system’s equilibration timescale. We can show the following for the model (details are provided in the Materials and Methods).
Suppose that the system is allowed to reach steady state and the amounts of X (total active Mek, in our experimental system) and Y (total active Erk, in our experimental system) are measured. If the total amount of substrate ErkT is increased, and the system is allowed to reach steady state, then it will be found that the levels of both Y and X have increased: perturbation analysis would suggest that Y → X. If, instead, the total amount of Erk phosphotase PTPT is decreased, and the system is allowed to reach steady state again, then it will be found that the amount of Y has once again increased, but the amount of X has now decreased: perturbation analysis would instead suggest that Y ⊣ X.
An intuitive and mechanistic interpretation of this behavior is as follows: When the total substrate ErkT is overexpressed, its active form Erkp increases at steady state, so Y is higher, but there is also more inactive Erk that can sequester the enzyme (MekPP), thus insulating it from dephosphorylation and resulting in higher total active enzyme X as well. On the other hand, if the total phosphatase amount PTPT is decreased, there is again more active form Erkp and hence higher total active substrate Y, but now there is less inactive target (Erk) to sequester enzyme (Mekpp), thus insulating it less from dephosphorylation and resulting in lower steady-state value of total active enzyme X. Of course, this intuitive interpretation has to be rigorously proved, because it is conceivable that there could be, for example, less inactive Erk in the first case, with all additional Erk taking active form. It is important to note that the model displays the same behavior at intermediate time points (simulations shown in the Supporting Material). We can also be more specific about the changes in every individual quantity: Fig. 3 shows the changes in all the components of the system.
Figure 3.
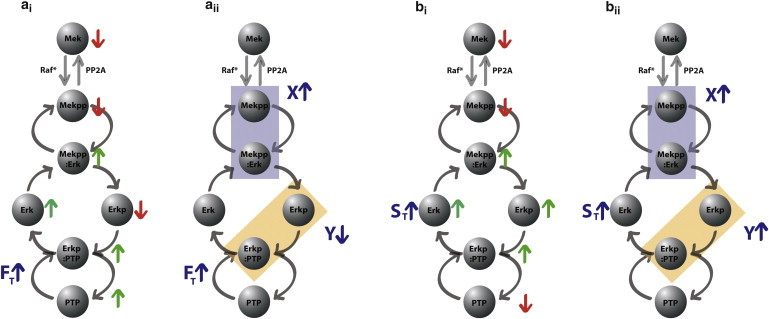
Predictions of theorem. (a) Results of perturbation in total phosphatase FT: (i) changes in individual nodes and (ii) in total active enzyme and substrate. (b) Results of perturbation in total substrate ST: (i) changes in individual nodes and (ii) in total active enzyme and substrate. To see this figure in color, go online.
Relation to retroactivity
Network reconstruction algorithms differ widely in the statistical and mathematical methods used to analyze the information gleaned from perturbation experiments. A typical example is the modular response analysis (MRA) method introduced in Kholodenko et al. (6,20) and Andrec et al. (24) for deriving local response coefficients from global response data. MRA uses linear algebra techniques to distinguish local interactions from confounding effects that propagate throughout intermediate nodes in a network and cause global changes that are hard to distinguish from local effects. Other algorithms for the same purpose use information-theoretic tools, graphical Bayesian models, numerical approximations that damp long-distance effects, or network deconvolution techniques (25–27). Recent work using MRA uncovered topological differences in the MAPK core network in rat adrenal pheochromocytoma (PC-12) cells, which were dependent upon whether cells were activated with epidermal or neuronal growth factor (22) (see our Fig. 4).
Figure 4.
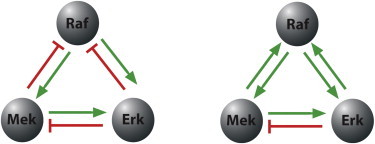
Graphical representation of MAPK networks (Raf, Mek, and Erk) in PC-12 cells, illustrating the reconstruction done in Santos et al. (22) based on data collected in different experiments. (Left) After 5′ epidermal growth factor stimulation; (right) after 5′ neuronal growth factor stimulation. (Sharp arrows) Positive effects; (blunt arrows) negative effects. Protein amounts were perturbed by RNAi downregulation of mRNA. Network reconstruction was based on the algorithm from Andrec et al. (24), a variant of MRA. To see this figure in color, go online.
It was hypothesized in Santos et al. (22) that the different topologies arise from pathways that involve other players in the cell, such as PKC phosphorylation of RKIP, promoting Erk1/2 activation by modifying the affinity of RKIP for Raf-1 as well as other PKC feedback mechanisms (28,29). Our results show that even in isolated in vitro systems, such ambiguous effects may take place, including a minimal system involving proteins from the canonical MAPK pathway. The self-contradictory aspect that we discovered potentially impacts a broad range of methods, raising questions to be considered when evaluating the resulting networks.
Our mathematical analysis predicts that such ambiguous effects will typically appear in backward-pointing interactions that superficially contradict the cascade view of cell signaling, in which substrates are the targets of enzyme activity but the substrates themselves do not actually affect enzyme activity. In the traditional view, backward arrows are often explained through hypothetical signaling nodes that might mediate the feedbacks and/or cross-talk between pathways (30). An alternative, or at least complementary explanation, lies in the retroactivity phenomenon, akin to impedance in electrical and mechanical networks, in which the mere act of transmitting a signal produces a reaction due to the load imposed by the substrate (31–36). The biochemical basis for retroactivity may be the competition among kinases and phosphatases for binding to docking sites (37), resulting in a sequestration-induced feedback (see also Blüthgen et al. (38)). Various experimental demonstrations of retroactivity have been performed, ranging from an in vitro covalent modification cycle based on a reconstituted uridylyltransferase/uridylyl-removing enzyme PII cycle (a model system derived from the nitrogen assimilation control network of Escherichia coli (39)), to an in vivo study of a MAPK kinase pathway regulating the terminal patterning system of the Drosophila embryo (40).
Our primary focus here was not on the existence of such apparent feedbacks but rather, on the apparently contradictory appearance of effects of opposite signs, such as the different-color arrows among respective components in Fig. 4. Our experimental results also serve to illustrate the retroactivity phenomenon, but with the added insight that retroactivity may lead to paradoxical network reconstructions. These contradictory effects may be obscured in other experiments by the use of phosphospecific antibodies for the detection and quantitation of protein modifications, a technology that is inherently biased and error-prone compared to mass spectrometry (23).
Materials and Methods
Proteins
N-terminal GST-tagged recombinant human Raf-1 (∼65 kDa) residues, 306-end, containing the mutations Y340D and Y341D rendering it constitutively active, were purchased from Millipore (Cat. No. 14-352; Billerica, MA). N-terminal GST and C-terminal His6-tagged, recombinant full-length human Mek1 (∼71 kDa) were expressed and purified from bacteria using Ni/NTA columns (see Fig. S1 in the Supporting Material). N-terminal His6-tagged p42 MAP kinase (Erk2) from Xenopus laevis expressed on a pT-T7 (∼43 kDa) plasmid (gift from Jim Ferrell) was mutated on Threonine188 to Valine (Erk-T188V), by site-directed mutagenesis using a QuikChange II Site-Directed Mutagenesis Kit (Cat. No. 200524; Stratagene, La Jolla, CA) according to the manufacturer’s instruction. It was expressed and purified as described in Prabakaran et al. (23) (see Fig. S1). For simplicity, we refer to Erk-T188V simply as “Erk”. Both Mek and Erk were purified to almost 95% purity.
Protein phosphatase 2A (PP2A) was purchased from Millipore (Cat. No. 14-111) and protein tyrosine phosphatase (PTP) was purchased from New England Biolabs (Cat. No. P0752S; Ipswich, MA).
In vitro reactions
All reactions were done in 20 mM MOPS, 5 mM EGTA, 1 mM dithiothreitol, 150 mM NaCl, 0.1 mM ATP, 15 mM MgCl2, pH 7.2 and at 25°C. Briefly, the reactions were set in three different 1.5-mL Eppendorf tubes. The proteins were added in the sequence Raf, Mek, Erk, and PP2A, followed by PTP to a final volume of 25 μL, and the reaction mixture was shaken at 350 rpm at 25°C for 30 min. Then the reactions were stopped with the addition of sample buffer (Cat. No. np0007; Invitrogen, Carlsbad, CA).
For PTP perturbations, the reactions were carried out at two different concentrations of PTP, at 3 nM and 30 nM. The rest of the constituents in the reactions are 80 nM Raf, 300 nM Mek, 920 nM Erk, and 20 nM PP2A. For Erk perturbation, the reactions were carried out at two different Erk concentrations, 230 and 1380 nM. The rest of the constituents are 80 nM Raf, 300 nM Mek, 30 nM PTP, and 20 nM PP2A.
Mass spectrometry analysis
Synthetic phosphopeptide internal standards, corresponding to the tryptic phosphopeptides of Erkp (VADPDHDHTGFLVE(pTyr)VAT(RC13N15)) and Mekpp (LCDFGVSGQLID(pSer)MAN(pSer)FVGT(RC13N15)) with C-terminal arginines fully labeled with 13C and 15N were purchased from New England Peptide (Gardner, MA) at 95% purity. Stock solutions were prepared for each peptide according to the manufacturer’s instructions.
For mass spectrometry (MS), a reaction mixture containing both Erk and Mek in sample buffer was loaded on a 12% 29:1 sodium dodecyl-sulfate polyacrylamide-gel electrophoresis gel, washed with water, and stained with SimplyBlue (Cat. No. LC6065; Invitrogen, Carlsbad, CA). A blank lane was used for background correction.
Bands corresponding to Erkp (∼43 kDa) and Mekpp (∼71 kDa) were excised, washed with 100 mM ABC (ammonium bicarbonate) buffer and ACN (acetonitrile) (Honeywell Burdick and Jackson, Muskegon, MI), reduced with 10 mM dithiothreitol at 56°C for 45 min and then alkylated with 50 mM iodoacetamide in the dark for 30 min. After washing with ABC and ACN (2:1 mixture) for 15 min three times and then 5 min shrinking with ACN, 12 ng/mL of sequencing-grade modified trypsin (Cat. No. V5111; Promega, Madison, WI) was added and the mixture left on ice for 1 h.
A quantity of 500 fmol of each of the internal standards was added and the mixture incubated at 37°C for 18 h. The digested tryptic peptides were extracted with ABC buffer. After drying in a speed vac, the sample was reconstituted in 20 μL of 50% water (containing 5% formic acid) and 50% ACN. Aliquots of 5 μL were analyzed by liquid chromatography/mass spectrometry (LC/MS).
The LC/MS system comprised a micro-autosampler, a nanoLC-2D nanoflow HPLC pump (both from Eksigent Technologies, Dublin, CA), and a LTQ XL-Orbitrap high-accuracy/resolution mass spectrometer (Thermo Fisher Scientific, Waltham, MA). A 100-μm PicoTip Emitter column (New Objective, Woburn, MA) was packed in-house using 5 μm, 10-nm pore size Magic C18 beads (Michrom BioResources, Auburn, CA). A 60-min gradient, 95–20% A, 5–80% B, in the first 10 min for Mekpp doubly-charged phosphopeptide (LCDFGVSGQLID(pSer)MAN(pSer)FVGTR) to elute was utilized for quantifying Mek phosphorylation, along with two targeted full-scan windows ± 2.5 m/z for the doubly-phosphorylated peptide and its corresponding internal standard (A = 0.2% formic aid in water and B = 0.2% formic acid in ACN). Fig. S2 illustrates a representative chromatogram, mass spectrum of doubly-charged Mekpp and mass-spectrum of its internal standard. A 60-min gradient, 95–65% A, 5–35% B was utilized for Erkp triply-charged phosphopeptide (VADPDHDHTGFLVE(pTyr)VATR) to elute with two targeted full-scan windows ± 2.5 m/z for the monophosphorylated peptide and its corresponding internal standard. Fig. S3 illustrates a representative chromatogram, mass-spectrum of triply-charged Erkp and mass-spectrum of its internal standard. The amounts of both Mekpp and Erkp were quantified using the AQUA method (41) by taking the peak-area ratio of the phosphorylated peptide to its corresponding internal standard.
Peak-area integration of extracted ion chromatograms (±0.17 m/z of the most abundant isotope), blank correction, and calculation of sample/internal standard ratios were programmed in the software XCALIBUR (Thermo Scientific). The intensities of the phosphorylated peptides of Mek and Erk, normalized to their corresponding internal standards, are plotted in Fig. 2 using the software GRAPHPAD PRISM Ver. 4 (GraphPad Software, La Jolla, CA).
Western blot analysis
For the antibody analysis of Fig. 2 b, samples in sample buffer were heated at 70°C for 10 min and 100 pg/well of each sample was loaded in triplicate on a 15-well 12% 29:1 sodium dodecyl-sulfate polyacrylamide-gel electrophoresis gel (nine technical replicates for each data point). For the antibody analysis of Fig. S4, Fig. S5, and Fig. S6, three technical replicates were loaded for each reaction. After separation, proteins were transferred onto transfer membranes (Cat. No. IPVH00010; Millipore) for 1 h, incubated with blocking buffer (Cat. No. 92740-000; LI-COR Biosciences, Lincoln, NE) for 60 min at room temperature, and then incubated with rabbit anti-phospho-Mek antibody (Cat. No. 2338; Cell Signaling Technology, Beverly, MA) at 1:2000 dilution and mouse anti-phospho-tyrosine-Erk (monoclonal anti-MAP kinase, monophosphorylated tyrosine produced in mouse (Cat. No. M3682; Sigma, St. Louis, MO)) along with rabbit anti-total Erk (Cat. No. 06-182; Millipore) antibody at 1:2000 overnight at 4°C.
Membranes were washed four times with PBS (phosphate-buffered saline) and incubated with IRDye 680, goat anti-rabbit IgG (Cat. No. 926-32221; LI-COR Biosciences) at 1:1000 dilution, and IRDye 800, goat anti-mouse IgG (Cat. No. 926-32210; LI-COR Biosciences) at 1:10 000 dilution and for 1 h at room temperature in the dark. Finally, membranes were washed four times with PBS and scanned with the Odyssey Infrared Imager (LI-COR Biosciences) at 169-μm resolution, medium-quality, and intensity level 3 for both 680 and 800 channels. Bands were quantified with ODYSSEY software (Ver. 2.3; LI-COR). Each band was five times zoomed, manually outlined and default background correction settings (median, border width 2, top-down) used to determine the integrated intensity. Fig. S4 illustrates a representative Western blot used for the experiment. Mek and Erk due to their different molecular weights run to different positions on the gel. Red bands indicate IRDye680 channel and green bands indicate IRDye800 channel. Their overlaid images are also shown in Fig. S4. Intensity from the red channel is used for the Mekpp quantitation while the relative intensity of the green channel to the red one is used for quantitation of Erkp ((23)). The intensity of the 680 channel for Mekpp and the 800 channel for Erkp were plotted using GRAPHPAD PRISM, Ver. 4.
Details of model
Assuming that protein is synthesized and degraded over long timescales, so that the total protein concentration can be regarded as constant over the system’s equilibration timescale, the mass-action kinetics’ differential equations governing the time evolution of the components in the chemical reaction (1) is given by the set of ordinary differential equations shown in Eq. 2. For simplicity, we use the following lower-case variables to indicate the molar concentrations of components: cm∗e = [Mekpp : Erk]; cpe∗ = [Erkp : PTP]; e = [Erk]; e∗ = [Erkp]; m = [Mek]; m∗ = [Mekpp]; and p = [PTP].
| (2) |
The letters α, β, … denote reaction constants, which are allowed to be arbitrary positive numbers for the purpose of our mathematical arguments. The amounts of constitutively active Raf and protein phosphatase 2A (PP2A) are subsumed by the values of α and β. Total concentration of active kinase, in free (Mekpp) or bound (Mekpp:Erk) form, is denoted by x. Total concentration of active target, in free (Erkp) or bound (Erkp:PTP) form, is denoted by y.
The following three conservation laws hold along any solutions of the system
| (3) |
where m∗T is the total amount of enzyme in any form (inactive, active but free, or bound to complex),
| (4) |
where pT is total amount of phosphatase (free or bound), and
| (5) |
where eT is the total amount of substrate in any form.
We will show next that, for the model in Eqs. 1 and 2, from a perturbation in total phosphatase pT, one would deduce a repression arrow Y ⊣ X, but from a perturbation in total substrate eT, one would deduce an activation arrow Y → X. Specifically, if pT is increased, then, at steady state, y decreases and x increases; if, instead, eT is increased, then both y and x increase.
A theorem
Any vector of steady-state concentrations
is obtained by setting to zero the right-hand sides of the differential equations, and solving these seven algebraic equations for m,…. Equivalently, for any given values of the total concentrations m∗T, pT, and eT, steady states are characterized by the three conservation constraint Eqs. 3–5 together with the following four additional relations:
| (6) |
| (7) |
| (8) |
| (9) |
The existence and uniqueness of steady states, for any given values of the conserved quantities m∗T, pT, and eT, follows from the existence and uniqueness of steady states for the system obtained by removing the equation, the terms “αm-βm∗” in the equation, and replacing in the conservation relation for m∗T the value of m determined from m∗ by Eq. 6. This reduced system was shown to have unique steady states in Angeli and Sontag (42). A very useful tool for the study of dynamics for such enzymatic systems is that of contraction theory (43,44).
At any given steady-state vector of concentrations, let us denote by x the total concentration of active kinase, free or bound,
and by y the total concentration of product, free or bound,
We want to show that x and y both increase (respectively, decrease) if the amount of substrate is increased (respectively, decreased), and, instead, that x increases (respectively, decreases) and y decreases (respectively, decreases) if the amount of phosphatase is increased (respectively, decreased). Mathematically, we want to compare the signs of the derivatives x′ and y′ to those of p′T or e′T. We formulate the question more precisely as follows.
Suppose that we consider a one-parameter family of positive steady-state concentrations
and respective total active kinase and products
The parameter θ may be thought of as pT, or eT, but for the analysis is arbitrary. We suppose given a certain value θ0 of this parameter, and compute
where we are using primes to indicate the derivatives with respect to θ, evaluated at the parameter θ0, and we omit the parameter from now on (thus, when writing e∗ below, we mean e∗(θ0), and so forth). Note that if the one-parameter family π(θ) describes steady states that correspond to same total phosphatase PT, we have p′T = 0, and if instead the substrate amount is constant, then e′T = 0.
Mathematically, we show the result in the Theorem stated below, which can be summarized symbolically as follows:
Theorem
The following relations hold for the derivatives with respect to θ, under the assumption that m∗′T = 0:
In general,
however, when e′T = 0,
and when p′T = 0,
Proof
From Eq. 6, we have that sign m∗′ = sign m′, which, combined with Eq. 3 and m∗′T = 0, gives that sign c′m∗e = −sign m∗′.
From the definition x = m∗ + cm∗e together with Eq. 3, we have m + x = m∗T, from which it follows, because m∗T = 0, that sign x′ = sign m∗′.
Also, differentiating Eq. 7 gives c′m∗e = −sign c′pe∗.
Differentiating Eq. 8 gives
| (10) |
so, because we already proved that sign c′m∗e = sign (−m∗′), it follows that sign e′ = sign c′m∗e. This completes the proof of the first assertion.
Suppose now that e′T = 0. Because Eq. 5 says that
it gives that y′ = −(c′m∗e + e′).
Because sign c′m∗e = sign e′, it follows that (cm∗e + e)′ = c′m∗e + e′ has the same sign as c′m∗e, and hence –sign y′ = sign(cm∗e + e)′ = sign c′m∗e = sign x′.
And because we already know that sign c′pe∗ = sign x′, this also implies that sign y′ = sign(−c′pe∗). From
we conclude that sign e∗′ = sign y′.
Differentiating Eq. 9:
Because sign c′pe∗ = sign (−e∗′), it follows that sign p′ = sign c′pe∗.
Finally, because p′T = p′ + c′pe∗, also sign p′T = sign p′. This completes the proof of the second assertion.
Now take the case p′T = 0. From Eq. 4, c′pe∗ = −p′, so sign c′pe∗ = −sign p′. Differentiating Eq. 9:
so also sign e∗′ = sign c′pe∗.
Because y = e∗ + cpe∗, it follows that also sign y′ = sign e∗′.
Finally, because e′T = e′ + c′m∗e + e∗′ + c′pe∗, and the four terms in this sum all have the same sign as x′, it follows that sign e′T = sign x′. This completes the proof of the theorem.
It is also possible to formally prove that a perturbation in total enzyme (Mek) will result in changes in X and Y in the same direction as this perturbation. The proof is similar, but this conclusion is far less interesting, because it is evidently true from the form of the reactions.
In the model and proof, we assumed that both enzymes are strongly irreversible, in the sense of Xu and Gunawardena (45). As long as equilibria are nondegenerate (Jacobian is nonsingular), it then follows, by continuity of steady states on reaction constants, that a sufficiently small rate for a reverse reaction will not change the conclusions.
Another generalization of the theorem would be to explicitly model the phosphorylation and dephosphorylation of Mek, through a full Michaelis-Menten set of reactions including complex formation. The same conclusions hold in that case, with a very similar but substantially longer proof.
Our theorem shows that the sign of the derivatives (m′ and so forth) are constant at all steady states. This implies a global change as well, along any smooth curve connecting steady states. In other words, the theorem is proved formally for first-order perturbations, but the same result holds for all perturbations. Indeed, suppose that we want to compare the values of the steady-state concentrations π(θ1) and π(θ2) at two values θ1,θ2 of the parameter θ. Because, coordinatewise, we have, for example
then it follows that, if m′(θ) > 0 for all parameter values θ, also m(θ2) > m(θ1).
Our result is justified by a mathematical proof, and hence is valid for all parameters. Simulations that illustrate dynamic behavior as well as the effect of noninfinitesimal perturbations are shown in the Supporting Material.
Discussion
A plethora of sophisticated reverse engineering methods are routinely used to generate valuable data in the form of networks of players interconnected by edges indicating positive and negative interactions. Nonetheless, our results emphasize that a naive and simplistic view of enzymatic networks, through positive and negative arrows interconnecting what are inherently complex nodes, does not tell the whole story in signal transduction. We have shown that even in simple in vitro systems, such a view is misleading; clearly, if a method fails there, there is no justification for believing that it will work in a more complicated in vivo context. Approaches that are more sophisticated are called upon, in order to address the pitfalls of perturbation techniques, which may, by themselves, lead to false conclusions. Seriously erroneous conclusions may derive from considering only discrete classes of connections while ignoring the intricate nonlinear mechanisms underlying processes such as phosphorylation (17,46,47).
To avoid incorrect interpretations of data obtained from inhibitor or activator chemical screenings, it is imperative to enrich analysis by considering the dynamics of such processes in more mathematical and modeling detail. This analysis might include, for example, enlarging network descriptions to take into account sequestration effects, stoichiometric constraints imposed by binding of transcription factors to different promoter sites, competition for mRNA polymerase, or competition for ribosome binding sites. More powerful methods might require the introduction of new perturbations that modify rate constants and other parameters. This task leads to challenging theoretical and experimental questions in systems biology.
Acknowledgments
We thank Professor Hanno Steen at Children’s Hospital, Boston for use of mass-spectrometry facilities and Ruchi Chauhan for experimental assistance. We also thank E. Nikolaev for a very useful suggestion regarding the design of Figure 3.
S.P. carried out the experiments. E.S. conceived the project and carried out the theoretical development. S.P., J.G., and E.S. performed the analysis and wrote the paper.
E.S.’s research was supported in part by National Institutes of Health grants No. NIH 1R01GM100473 and No. 1R01GM086881. S.P. and J.G. were supported in part by National Science Foundation grant No. 0856285.
Supporting Material
References
- 1.Lauffenburger D.A. Cell signaling pathways as control modules: complexity for simplicity? Proc. Natl. Acad. Sci. USA. 2000;97:5031–5033. doi: 10.1073/pnas.97.10.5031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hartwell L.H., Hopfield J.J., Murray A.W. From molecular to modular cell biology. Nature. 1999;402:C47–C52. doi: 10.1038/35011540. [DOI] [PubMed] [Google Scholar]
- 3.Bhalla U.S., Iyengar R. Functional modules in biological signaling networks. Novartis Found. Symp. 2001;239:4–13. doi: 10.1002/0470846674.ch2. discussion 13–15., 45–51. [DOI] [PubMed] [Google Scholar]
- 4.Aldridge B.B., Burke J.M., Sorger P.K. Physicochemical modeling of cell signaling pathways. Nat. Cell Biol. 2006;8:1195–1203. doi: 10.1038/ncb1497. [DOI] [PubMed] [Google Scholar]
- 5.Jaqaman K., Danuser G. Linking data to models: data regression. Nat. Rev. Mol. Cell Biol. 2006;7:813–819. doi: 10.1038/nrm2030. [DOI] [PubMed] [Google Scholar]
- 6.Kholodenko B.N., Kiyatkin A., Hoek J.B. Untangling the wires: a strategy to trace functional interactions in signaling and gene networks. Proc. Natl. Acad. Sci. USA. 2002;99:12841–12846. doi: 10.1073/pnas.192442699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.de la Fuente A., Brazhnik P., Mendes P. Linking the genes: inferring quantitative gene networks from microarray data. Trends Genet. 2002;18:395–398. doi: 10.1016/s0168-9525(02)02692-6. [DOI] [PubMed] [Google Scholar]
- 8.Gardner T.S., di Bernardo D., Collins J.J. Inferring genetic networks and identifying compound mode of action via expression profiling. Science. 2003;301:102–105. doi: 10.1126/science.1081900. [DOI] [PubMed] [Google Scholar]
- 9.Stark J., Callard R., Hubank M. From the top down: towards a predictive biology of signaling networks. Trends Biotechnol. 2003;21:290–293. doi: 10.1016/S0167-7799(03)00140-9. [DOI] [PubMed] [Google Scholar]
- 10.Prill R.J., Saez-Rodriguez J., Stolovitzky G. Crowdsourcing network inference: the DREAM predictive signaling network challenge. Sci. Signal. 2011;4:mr7. doi: 10.1126/scisignal.2002212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen Z., Gibson T.B., Cobb M.H. MAP kinases. Chem. Rev. 2001;101:2449–2476. doi: 10.1021/cr000241p. [DOI] [PubMed] [Google Scholar]
- 12.Shaul Y.D., Seger R. The MEK/ERK cascade: from signaling specificity to diverse functions. Biochim. Biophys. Acta. 2007;1773:1213–1226. doi: 10.1016/j.bbamcr.2006.10.005. [DOI] [PubMed] [Google Scholar]
- 13.Huang C.-Y., Ferrell J.E., Jr. Ultrasensitivity in the mitogen-activated protein kinase cascade. Proc. Natl. Acad. Sci. USA. 1996;93:10078–10083. doi: 10.1073/pnas.93.19.10078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Asthagiri A.R., Lauffenburger D.A. A computational study of feedback effects on signal dynamics in a mitogen-activated protein kinase (MAPK) pathway model. Biotechnol. Prog. 2001;17:227–239. doi: 10.1021/bp010009k. [DOI] [PubMed] [Google Scholar]
- 15.Widmann C., Gibson S., Johnson G.L. Mitogen-activated protein kinase: conservation of a three-kinase module from yeast to human. Physiol. Rev. 1999;79:143–180. doi: 10.1152/physrev.1999.79.1.143. [DOI] [PubMed] [Google Scholar]
- 16.Bardwell L., Zou X., Komarova N.L. Mathematical models of specificity in cell signaling. Biophys. J. 2007;92:3425–3441. doi: 10.1529/biophysj.106.090084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Futran A.S., Link A.J., Shvartsman S.Y. ERK as a model for systems biology of enzyme kinetics in cells. Curr. Biol. 2013;23:R972–R979. doi: 10.1016/j.cub.2013.09.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pearson G., Robinson F., Cobb M.H. Mitogen-activated protein (MAP) kinase pathways: regulation and physiological functions. Endocr. Rev. 2001;22:153–183. doi: 10.1210/edrv.22.2.0428. [DOI] [PubMed] [Google Scholar]
- 19.Ledford, H. 2013. First-in-class cancer drug approved to fight melanoma. http://blogs.nature.com/news/2013/05/first-in-class-cancer-drug-approved-to-fight-melanoma.html. Nature News Blog. Posted 30 May 2013, Accessed January 2014. Nature, International Weekly Journal of Science, Nature Publishing Group, Macmillan Publishers, London, UK. http://www.nature.com
- 20.Kholodenko B., Yaffe M.B., Kolch W. Computational approaches for analyzing information flow in biological networks. Sci. Signal. 2012;5:re1. doi: 10.1126/scisignal.2002961. [DOI] [PubMed] [Google Scholar]
- 21.Godsey B. Improved inference of gene regulatory networks through integrated Bayesian clustering and dynamic modeling of time-course expression data. PLoS ONE. 2013;8:e68358. doi: 10.1371/journal.pone.0068358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Santos S.D., Verveer P.J., Bastiaens P.I. Growth factor-induced MAPK network topology shapes Erk response determining PC-12 cell fate. Nat. Cell Biol. 2007;9:324–330. doi: 10.1038/ncb1543. [DOI] [PubMed] [Google Scholar]
- 23.Prabakaran S., Everley R.A., Gunawardena J. Comparative analysis of Erk phosphorylation suggests a mixed strategy for measuring phospho-form distributions. Mol. Syst. Biol. 2011;7:482. doi: 10.1038/msb.2011.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Andrec M., Kholodenko B.N., Sontag E. Inference of signaling and gene regulatory networks by steady-state perturbation experiments: structure and accuracy. J. Theor. Biol. 2005;232:427–441. doi: 10.1016/j.jtbi.2004.08.022. [DOI] [PubMed] [Google Scholar]
- 25.Margolin A.A., Nemenman I., Califano A. ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics. 2006;7(Suppl 1):S7. doi: 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Barzel B., Barabási A.L. Network link prediction by global silencing of indirect correlations. Nat. Biotechnol. 2013;31:720–725. doi: 10.1038/nbt.2601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Feizi S., Marbach D., Kellis M. Network deconvolution as a general method to distinguish direct dependencies in networks. Nat. Biotechnol. 2013;31:726–733. doi: 10.1038/nbt.2635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bhalla U.S., Ram P.T., Iyengar R. MAP kinase phosphatase as a locus of flexibility in a mitogen-activated protein kinase signaling network. Science. 2002;297:1018–1023. doi: 10.1126/science.1068873. [DOI] [PubMed] [Google Scholar]
- 29.Lorenz K., Lohse M.J., Quitterer U. Protein kinase C switches the Raf kinase inhibitor from Raf-1 to GRK-2. Nature. 2003;426:574–579. doi: 10.1038/nature02158. [DOI] [PubMed] [Google Scholar]
- 30.Cirit M., Wang C.C., Haugh J.M. Systematic quantification of negative feedback mechanisms in the extracellular signal-regulated kinase (ERK) signaling network. J. Biol. Chem. 2010;285:36736–36744. doi: 10.1074/jbc.M110.148759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Saez-Rodriguez J., Kremling A., Gilles E. Dissecting the puzzle of life: modularization of signal transduction networks. Comput. Chem. Eng. 2005;29:619–629. [Google Scholar]
- 32.Del Vecchio D., Ninfa A.J., Sontag E.D. Modular cell biology: retroactivity and insulation. Mol. Syst. Biol. 2008;4:161. doi: 10.1038/msb4100204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ventura A.C., Sepulchre J.A., Merajver S.D. A hidden feedback in signaling cascades is revealed. PLOS Comput. Biol. 2008;4:e1000041. doi: 10.1371/journal.pcbi.1000041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kim K.H., Sauro H.M. Measuring retroactivity from noise in gene regulatory networks. Biophys. J. 2011;100:1167–1177. doi: 10.1016/j.bpj.2010.12.3737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Alexander R.P., Kim P.M., Gerstein M.B. Understanding modularity in molecular networks requires dynamics. Sci. Signal. 2009;2:pe44. doi: 10.1126/scisignal.281pe44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jayanthi S., Nilgiriwala K.S., Del Vecchio D. Retroactivity controls the temporal dynamics of gene transcription. ACS Synth. Biol. 2013;2:431–441. doi: 10.1021/sb300098w. [DOI] [PubMed] [Google Scholar]
- 37.Bardwell A.J., Abdollahi M., Bardwell L. Docking sites on mitogen-activated protein kinase (MAPK) kinases, MAPK phosphatases and the Elk-1 transcription factor compete for MAPK binding and are crucial for enzymic activity. Biochem. J. 2003;370:1077–1085. doi: 10.1042/BJ20021806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Blüthgen N., Bruggeman F.J., Kholodenko B.N. Effects of sequestration on signal transduction cascades. FEBS J. 2006;273:895–906. doi: 10.1111/j.1742-4658.2006.05105.x. [DOI] [PubMed] [Google Scholar]
- 39.Jiang P., Ventura A.C., Del Vecchio D. Load-induced modulation of signal transduction networks. Sci. Signal. 2011;4:ra67. doi: 10.1126/scisignal.2002152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kim Y., Paroush Z., Shvartsman S.Y. Substrate-dependent control of MAPK phosphorylation in vivo. Mol. Syst. Biol. 2011;7:467. doi: 10.1038/msb.2010.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gerber S.A., Rush J., Gygi S.P. Absolute quantification of proteins and phosphoproteins from cell lysates by tandem MS. Proc. Natl. Acad. Sci. USA. 2003;100:6940–6945. doi: 10.1073/pnas.0832254100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Angeli D., Sontag E. Translation-invariant monotone systems, and a global convergence result for enzymatic futile cycles. Nonlin. Anal. B Real World App. 2008;9:128–140. [Google Scholar]
- 43.Russo G., di Bernardo M., Sontag E.D. Global entrainment of transcriptional systems to periodic inputs. PLOS Comput. Biol. 2010;6:e1000739. doi: 10.1371/journal.pcbi.1000739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Barton J.P., Sontag E.D. The energy costs of insulators in biochemical networks. Biophys. J. 2013;104:1380–1390. doi: 10.1016/j.bpj.2013.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Xu Y., Gunawardena J. Realistic enzymology for post-translational modification: zero-order ultrasensitivity revisited. J. Theor. Biol. 2012;311:139–152. doi: 10.1016/j.jtbi.2012.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wang L., Sontag E.D. On the number of steady states in a multiple futile cycle. J. Math. Biol. 2008;57:29–52. doi: 10.1007/s00285-007-0145-z. [DOI] [PubMed] [Google Scholar]
- 47.Thomson M., Gunawardena J. Unlimited multistability in multisite phosphorylation systems. Nature. 2009;460:274–277. doi: 10.1038/nature08102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


