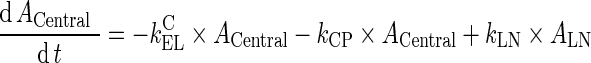Abstract
Monoclonal antibodies (mAbs) exhibit biexponential profiles in plasma that are commonly described with a standard two-compartment model with elimination from the central compartment. These models adequately describe mAb plasma PK. However, these models ignore elimination from the peripheral compartment. This may lead to underestimation of the volume of distribution of the peripheral compartment and thus over-predicts concentration in the peripheral compartment. We developed a simple and physiologically relevant model that incorporates information on binding and dissociation rates between mAb and FcRn receptor, mAb uptake, reflection, and catabolic degradation. We employed a previously published PBPK model and, with assumptions regarding rates of processes controlling mAb disposition, reduced the complex PBPK model to a simpler circular model with central, peripheral, and lymph compartments specifying elimination from both central and peripheral. We successfully applied the model to describe the PK of an investigational mAb. Our model presents an improvement over standard two-compartmental models in predicting whole-body average tissue concentrations while adequately describing plasma PK with minimal complexity and physiologically more meaningful parameters.
Electronic supplementary material
The online version of this article (doi:10.1208/s12248-014-9591-x) contains supplementary material, which is available to authorized users.
Key words: compartmental models, monoclonal antibodies, PBPK
INTRODUCTION
Monoclonal antibodies (mAbs) have become vital therapeutic modalities as anti-cancer, anti-inflammatory, or immune-modulatory agents (1,2). More than 26 mAbs are approved by the FDA and many antibody-based therapies are undergoing different phases of preclinical and clinical development (3). These molecules exhibit complex pharmacokinetic and pharmacodynamic properties which provide different challenges than those encountered with small molecules (4). Accurate description of these processes is crucial for both understanding drug disposition and for an efficient drug development process answering typical questions arising on the mechanisms of action through binding the intended target, especially in tissues.
Monoclonal antibodies display bi, or tri, phasic profile in plasma (5). A common and successful approach to describe mAb concentrations in plasma is fitting classical compartmental models, e.g., two-compartment model with linear or nonlinear elimination from the central compartment, to plasma or blood data (6). Fitting a two-compartmental model to plasma mAb PK data typically yields estimates of the volume of central compartment, VC, of 2.4 to 5.5 L, close to that of plasma (6). This estimate is considered to be physiologically reasonable given the hydrophilic nature and large molecular size of mAbs which are expected to be distributed mainly in plasma. However, estimates of the volume of the peripheral compartment Vp are typically underestimated at 1.3 to 6.8 L (6), given the volume of interstitial space is 11.3 L for a 71 kg male (7). Underestimation of the volume of distribution at steady state (VSS) of mAbs by classical models is explained, at least partially, by the fact that these models assume elimination from the central compartment only. This assumption is not adequate in the case of large molecules where VP, not VC, represents the main elimination site (8).
MAbs are predominantly eliminated via proteolytic catabolism after transit and sorting through endosomes (4). During this process, mAbs are taken into the endosome via fluid-mediated endocytosis where they bind to the Fc receptor of the neonate (FcRn) (9). FcRn-unbound mAbs in the endosomes are destined for lysosomes, where they are degraded. Owing to the ubiquitous presence of endosomes and FcRn expression in the human body, primarily in endothelial cells, elimination of mAbs can occur from either side of the endothelial cells, that is, from tissue interstitial spaces as well as from plasma. Thus, PK models that ignore elimination from peripheral compartments are simplistic and primarily designed to describe the PK in the central compartment. Further, classical models do not consider lymphatic circulation and uptake from endothelial space in peripheral tissues back to the vasculature (i.e. central compartment). Underestimation of Vp by the classical model leads to over predicting whole-body average peripheral tissue concentrations. This hinders the use of classical models in tissue target-mediated disposition models or predicting pharmacodynamic response to mAb based on in vitro estimates of binding affinities or effective concentrations in cellular assays.
A more mechanistic approach is the use of physiologically based PK (PBPK) models. Few PBPK models have been developed to integrate in vitro and in vivo data to describe mAb disposition in compartments such as the plasma, lymph node, as well as major peripheral organs (10). Models describing disposition in vascular, interstitial, and endosomal subcompartments of each organ were published (11–14). These models provide a useful tool to predict tissue concentrations, understand mAbs disposition in different compartments, and for extrapolation or prediction. However, these models are characterized by large number of parameters and differential equations. The high complexity and dimensionality of PBPK may exceed the capabilities of some simulation software and certainly take far longer to write and explain to team members. Finally, the large number of parameters makes PBPK models less suitable for estimation of individual parameters in a population analysis of clinical trial data.
An intermediate approach that reflects the physiological processes of mAb binding, transfer, and elimination in a simple compartmental model can be helpful. For example, Cao et al. proposed a general minimal PBPK model that incorporates physiological and anatomical information (15) and recently extended this approach to mAbs (16). In the current work, a previously published PBPK model (13) has been employed with several simplifying physiological assumptions regarding mAb disposition. The simplified physiological model was applied to describe the PK of an illustrative mAb in a patient cohort using the population approach and compared with a classical two-compartment model.
MATERIALS AND METHODS
Overall Simplification Methodology
Simplification of the full PBPK model was conducted via several broad classes of assumptions which fall under one of the following broad classes:
-
A.
Comparing the time scale of a process relative to others (e.g. fast transfer from one compartment to another, one organ to another, or fast receptor binding/dissociation). Both physiological and numerical factors were considered in each assumption.
-
B.
Similarity of transfer rates of mAb/IgG between body organs, within a predefined range, to allow lumping of body organs.
-
C.
Assumptions to rearrange inter-compartmental transfer rates, reduce model dimensions, and improve identifiability. These assumptions considered the numerical similarity of transfer rates as well as the direction of each process. This allowed for grouping of several processes in one term.
In each of the seven steps described below, assumptions are applied to the differential equations and a new set of differential equations was derived (Appendices 1–9). Simulations from each intermediate step were performed and plasma profile was used to compare the effects of each simplification step.
Full PBPK Model
We applied a previously published PBPK model that describes mAb PK in plasma, lymph, and body tissues (13). Transfer of mAbs is mediated via plasma and lymphatic flow (Fig. 1a, b). Each tissue was divided into three subcompartments (vascular, endosomal, and interstitial spaces). The endosomal space was described as a series of transit compartments with different pH levels. Following mAb uptake from vascular and interstitial spaces to the initial endosomal subcompartment, mAb is transferred through endosomal subcompartments with the same transit time, τ which was calculated as:
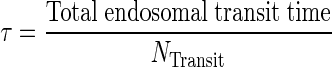 |
1 |
where NTransit is the number of transit events. In the initial endosomal subcompartment (pH 7.4), negligible binding is assumed (kon and koff are set to 0). Through the intermediate and terminal subendosomal compartments, pH decreases and thus binding affinity increases. In the terminal compartment, FcRn-bound mAb is recycled to vascular and interstitial compartments while unbound mAb is degraded via proteolytic clearance (13). Endogenous IgG and mAb compete for FcRn binding and were assumed to have the same FcRn binding affinity.
Fig. 1.
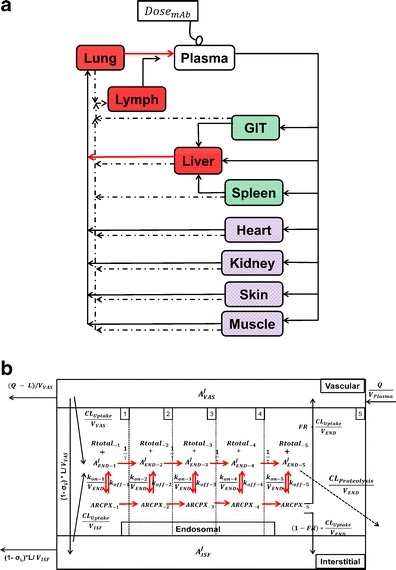
a Schematic representation of the PBPK model of mAb disposition. Plasma flow is represented by solid arrows and lymph flow by dashed arrows. Organs are shaded in groups to demonstrate the lumping and/or fast transfer assumption applied. Heart, kidney, skin, and muscle are lumped in one compartment. GIT and spleen are lumped in one compartment. Fast transfer assumption was applied from liver to lung, from lung to plasma, and from lymph node to plasma (red arrows). b Intra-tissue compartmental model. Each tissue is divided into vascular, endosomal, and interstitial spaces. The endosomal space is subdivided into five compartments with pH ranging from 7.4 to 6.0, to represent gradual acidification of endosomes
Convective movement from vascular to interstitial space and from interstitial space back to the circulation were represented using vascular and lymph reflection coefficients (σVAS and σLY, respectively). Interstitial fluid from all organs was drained by the lymphatic circulation and collected in the lymph node compartment. A fraction of the mAb collected in the lymph node (Freturn) was returned to the systemic circulation with a transit time (TauLN).
The physiological values for plasma flow rate, vascular, interstitial, and total tissue volume were obtained from the literature (10). Other model-specific parameters such as tissue-specific FcRn expression, tissue endosomal volume, uptake rate of mAb from vascular to endosomal compartments, reflection coefficients, and binding/dissociation rate constants were obtained from the original model (13). The fraction of FcRn-bound IgG recycling to the vascular compartment was obtained from (11). Parameters and variables used in the full model and the simplification steps are defined in Table I. Model equations were written for the amounts of mAb or endogenous IgG (Appendix 1). Rate constants were obtained by dividing clearances by the volume of the appropriate compartment. The volume of each endosomal subcompartment (VOrganEND) was calculated as:
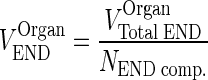 |
2 |
where VOrganTotal END is the volume of the endosomal compartment obtained from (13), and NEND comp. is the number of endosomal subcompartments per organ (i.e., 5).
Table I.
Glossary for Parameters and Variables
| Parameter/variable (unit) | Definition | References/remarks |
|---|---|---|
| Full PBPK model | ||
| - Parameters | ||
| K 0 (M/h) | Endogenous IgG production rate | (13) |
| Q organ (L/h) | Plasma Flow rate to each organ | (10) |
| L organ (L/h) | Lymphatic Flow rate to each organ | (10) |
| CLOrganUptake (L/h) | Endosomal uptake rate of unbound antibody | (13) |
| CLOrganProteolysis (L/h) | Clearance rate of unbound antibody via proteolytic degradation in the endosome | Same value for CL OrganUptake. |
| k on-X (M−1 h−1) | mAb-FcRn association constant in each subendosomal compartment X | (13) Assumed similar for IgG and mAb |
| k off-X (h−1) | mAb-FcRn dissociation constant in each subendosomal compartment X | (13) Assumed similar for IgG and mAb |
| KA (M)−1 | Equilibrium binding association affinity |
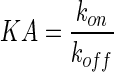
|
| RtotalOrgan ‐ X (moles) | Initial amount of free FcRn receptor in subendosomal compartment X | obtained by multiplying FcRn concentration reported in (13) by V OrganEND |
| F return (no units) | Fraction of antibody returning from lymph node to plasma |
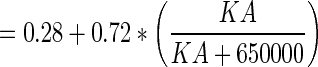 (13) (13) |
| τ (h) | Transit time between endosomal compartments | (13) (0.045) |
| TauLN (h) | Transit time from lymph node to plasma | (13) (9.1) |
| σ VAS (no unit) | Vascular reflection coefficient | Same for all organs (0.95) (11) |
| σ LY (no unit) | Lymph reflection coefficient | Same for all organs (0.2) |
| FR (no unit) | Recycling fraction of the bound antibody from endosomal to vascular and interstitial subcompartments | (11) (0.715) |
| V OrganVAS (L) | Volume of vascular compartment in each organ | (11) |
| V OrganISF (L) | Volume of interstitial compartment in each organ | (11) |
| V OrganEND (L) | Volume of each endosomal subcompartment in each organ | (11) |
| V Plasma (L) | Volume of plasma | (11) |
| - Variables | ||
| A JPlasma (moles) | Amount of endogenous IgG or mAb in plasma | |
| A JLN (moles) | Amount of endogenous IgG or mAb in lymph node | |
| A JVAS Organ (moles) | Amount of endogenous IgG or mAb in vascular space | |
| A JISF Organ (moles) | Amount of endogenous IgG or mAb in interstitial space | |
| A JEND Organ ‐ X (moles) | Amount of endogenous IgG or mAb in subendosomal compartment X | |
| ARCPXJOrgan ‐ X (moles) | Amount of endogenous IgG -FcRn or mAb-FcRn receptor complex in subendosomal compartment X | |
| Step 1 (Fig. 2) | ||
| - Parameters | ||
| k OrganVAS ‐ circul. (h−1) | Transfer rate from vascular compartment to lung or, in case of lung, from lung to plasma |
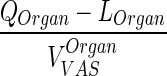
|
| k Organcircul. ‐ VAS (h−1) | Transfer rate from plasma to vascular compartment |
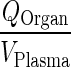
|
| (1 − σ VAS) × k OrganLY VAS ‐ ISF (h−1) | Transfer from vascular to interstitial compartment via lymphatic flow |
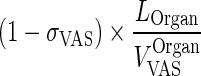
|
| k OrganVAS ‐ EL (h−1) | Elimination from vascular compartment |

|
| k OrganVAS ‐ VAS (h−1) | Input from vascular compartment to itself. Reflect endosomal contribution to vascular compartment |
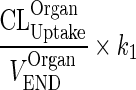
|
| k OrganVAS ‐ ISF (h−1) | Transfer from vascular to interstitial compartment |
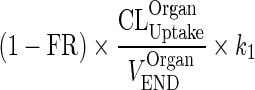
|
| k OrganISF ‐ VAS (h−1) | Transfer from interstitial to vascular compartment |
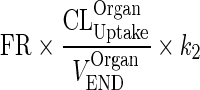
|
| (1 − σ LY) × k OrganLY ISF ‐ LN (h−1) | Transfer from interstitial compartment to lymph node via lymphatic flow |
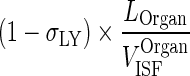
|
| k OrganISF ‐ EL (h−1) | Elimination from interstitial compartment |
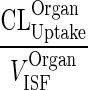
|
| k OrganISF ‐ ISF (h−1) | Input from interstitial compartment to itself. Reflect endosomal contribution to interstitial compartment |
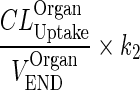
|
| KDEND (moles) | Equilibrium dissociation constant for mAb binding to FcRn receptor in amounts |
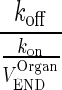
|
| K 0 (M/h) | Endogenous IgG production rate | (13) |
| - Variables | ||
| A JEND Total Organ ‐ X (moles) | Total amount of endogenous IgG or mAb (bound and free) in subendosomal compartment X | |
| Steps 2 and 3 (Fig. 3a and b) | ||
| - Parameters | ||
| Q Visceral (L/h) | plasma Flow rate to the visceral compartment | Q Heart + Q Kidney + Q Skin + Q Muscle |
| Q Splanchnic (L/h) | plasma Flow rate to the splanchnic compartment | Q GIT + Q Spleen |
| L Visceral (L/h) | Lymph Flow rate to the visceral compartment | L Heart + L Kidney + L Skin + L Muscle |
| L Splanchnic (L/h) | Lymph Flow rate to the splanchnic compartment | L GIT + L Spleen |
| - New compartments resulting from model simplification | ||
| Splanchnic | GIT and spleen | |
| Visceral | Heart, kidney, skin, and muscle lumped | |
| Steps 4, and 5 (Fig. 3c and d) | ||
| - Parameters | ||
| Q Peripheral (L/h) | Plasma Flow rate to the Peripheral compartment | Q Visceral + Q Splanchnic |
| L Peripheral (L/h) | Lymph Flow rate to the Peripheral compartment | L Visceral + L Splanchnic |
| - New compartments resulting from lumping | ||
| Peripheral | Visceral and splanchnic | |
| Step 6 (Fig. 3e) | ||
| - Parameters | ||
| k CentralEL (h−1) | Elimination rate from the central compartment | |
| (1 − σ VAS) × k CentralLY Central ‐ Per (h−1) | Transfer rate from the central to interstitial (i.e., peripheral) compartment via lymphatic flow | |
| k CentralCentral (h−1) | First-order input from central compartment to itself which reflects the impact of recycled drug from endosomal compartment | |
| k CentralCentral ‐ ISF (h−1) | First-order input from central to interstitial (i.e., peripheral) compartment | |
| k PeripheralISF ‐ Central (h−1) | Transfer from interstitial (i.e., peripheral) to central compartments | |
| (1 − σ LY) × k PeripheralLY ISF ‐ LN (h−1) | Transfer from interstitial (i.e., peripheral) compartment to lymph node via lymphatic flow | |
| k PeripheralISF ‐ ISF (h−1) | Input from Peripheral compartment to itself. Reflect endosomal contribution to interstitial compartment | |
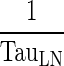 (h−1) (h−1) |
Transfer from lymph node to Central compartment | |
| Variables | ||
| A Central (moles) | Amount of mAb in the central compartment (i.e., plasma and Vascular subcompartments in equilibrium) | |
| A Peripheral (moles) | Amount of mAb in the Peripheral compartment | |
| Step 7 (Fig. 3f) | ||
| - Parameters | ||
| k CEL (h−1) | Elimination rate from the central compartment after subtracting the contribution of the endosomal compartment | |
| k PEL (h−1) | Elimination rate from the peripheral compartment after subtracting the contribution of the endosomal compartment | |
| k Cen ‐ Per (h−1) | Reflection of the fraction mAb-FcRn complex recycled | |
| (1 − σ VAS) × k CentralLY ‐ ISF (h−1) | Transfer of the mAb from Central to Peripheral compartments via lymphatic flow | |
| k CP (h−1) | Transfer of the mAb from Central to Peripheral compartments via two processes, a- the lymphatic flow and b- the reflection of the fraction mAb-FcRn complex recycled | (1 − σ VAS) × k CentralLY ‐ ISF + k CentralCentral ‐ ISF |
| (1 − σ LY) × k PeripheralLY ISF ‐ LN (h−1) | Transfer from interstitial (i.e., peripheral) compartment to lymph node via lymphatic flow | |
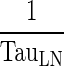 (h−1) (h−1) |
Transfer from lymph node to Central compartment | |
| Final simplified model (Fig. 4) | ||
| - Parameters | ||
| V C (L) | Volume of the Central Compartment | |
| k EL (h−1) | Elimination rate from the central and peripheral compartments | |
| k CP (h−1) | Transfer of the mAb from Central to Peripheral compartments via two processes, a- the lymphatic flow and b- the reflection of the fraction mAb-FcRn complex recycled | (1 − σ VAS) ∗ k CentralLY − ISF + k CentralCentral − ISF |
| k LN (h−1) | Transfer from interstitial (i.e., peripheral) compartment to lymph node via lymphatic flow and Transfer from lymph node to Central compartment | |
In this study, initial FcRn concentration in each tissue was used as a model parameter (Rtotal) and the free receptor is calculated as the difference between Rtotal and FcRn-bound mAb and endogenous IgG complexes. The dose used for simulations was 8 mg/kg assuming a 25-g mouse. The initial condition for mAb in the plasma compartment was the dose. For all other mAb compartments, the initial condition was set to 0. Endogenous IgG plasma amounts were fixed to 5.8 nmol (determined via enzyme-linked immune-sorbent assay (ELISA) in (13)) and steady state values were obtained by simulations of IgG levels for 200 days and used as initial conditions.
In the original publication, the authors estimated two coefficients (F1 and F2) to reflect the non-FcRn dependent tissue uptake of mAb (e.g., surface charge) which was not explained by the model (13). In our study, simulations were performed without these coefficients to be able to compare the effects of different simplification assumptions on processes explained by the model. The impact of removing F1 and F1 on mAb plasma PK is displayed in Supplementary Fig. 1.
Rapid Binding and Fast Endosomal Transfer (Step 1) (Appendix 2)
In order to simplify the subendosomal compartments, several assumptions were made. First, we assumed that the rate of inter-endosomal compartment transfer rate 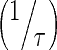 is faster than other processes such as the uptake process to the endosome and FcRn binding (17). Thus, input from vascular and interstitial compartments in the initial endosomal compartment was rapidly transferred to the terminal compartment (Appendix 9). This assumption holds true for earlier compartments where FcRn binding is considered negligible (in the first endosomal subcompartment) or low (in intermediate compartments). As the drug transfers to later compartments, rate of binding increases. Thus, rapid equilibrium between the binding and dissociation is assumed in the terminal compartment where the majority of FcRn binding occurs (18). This allowed the equations for the complex to be solved in terms of the free drug and the total FcRn receptor. Simulations from the full PBPK model supported the following assumptions: free mAb/IgG amounts (AJEND Organ ‐ 5) was 4,000- to 6,000-fold lower than the equilibrium dissociation constant, KDEND, in the terminal subendosomal compartment (Supplementary Figures 2 and 3), and that the total mAb in the terminal compartment was in equilibrium (Supplementary Figure 4). This allowed solving the complex in compartment 5 (ARCPXJOrgan ‐ 5) , which was recycled to vascular and interstitial compartments, as a function of the free amounts in vascular and interstitial compartments. This solution was then used to substitute ARCPXJOrgan ‐ 5 in differential equations for the vascular and interstitial compartments. Model equations to reflect the simplified model are provided in Appendix 3 (Fig. 2).
is faster than other processes such as the uptake process to the endosome and FcRn binding (17). Thus, input from vascular and interstitial compartments in the initial endosomal compartment was rapidly transferred to the terminal compartment (Appendix 9). This assumption holds true for earlier compartments where FcRn binding is considered negligible (in the first endosomal subcompartment) or low (in intermediate compartments). As the drug transfers to later compartments, rate of binding increases. Thus, rapid equilibrium between the binding and dissociation is assumed in the terminal compartment where the majority of FcRn binding occurs (18). This allowed the equations for the complex to be solved in terms of the free drug and the total FcRn receptor. Simulations from the full PBPK model supported the following assumptions: free mAb/IgG amounts (AJEND Organ ‐ 5) was 4,000- to 6,000-fold lower than the equilibrium dissociation constant, KDEND, in the terminal subendosomal compartment (Supplementary Figures 2 and 3), and that the total mAb in the terminal compartment was in equilibrium (Supplementary Figure 4). This allowed solving the complex in compartment 5 (ARCPXJOrgan ‐ 5) , which was recycled to vascular and interstitial compartments, as a function of the free amounts in vascular and interstitial compartments. This solution was then used to substitute ARCPXJOrgan ‐ 5 in differential equations for the vascular and interstitial compartments. Model equations to reflect the simplified model are provided in Appendix 3 (Fig. 2).
Fig. 2.
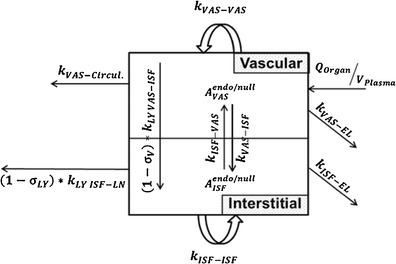
Intra-tissue compartments after simplification with rapid binding and fast transfer between endosomal compartments. Contribution of endosomal compartment to vascular and interstitial compartments is represented by first order rate inputs (k VAS ‐ VAS) and (k ISF ‐ ISF). The self-input to vascular and interstitial compartments is a reflection of the input to the first endosomal compartment, rapid binding to FcRn, fast endosomal transit, and recycle of the mAb-FcRn complex from the terminal endosomal compartment. Elimination at this stage is assumed to occur from vascular and interstitial compartments (k VAS ‐ EL) and (k ISF ‐ EL)
Lumping Tissues with Similar Transfer Rate Constants (Step 2) (Appendix 4)
In this step, rate constants governing the transfer of species in tissues sharing similar anatomical locations within the full model were compared. Processes within 20-fold difference between tissues were assumed to be kinetically similar. Thus, these tissues can be explicitly lumped. Median of the rate constants for the original tissues was used to describe the lumped compartment. Two groups of tissues were distinguished. First, the gastrointestinal tract (GIT) and spleen can be lumped into a “splanchnic” compartment which feeds into the liver via entero-hepatic circulation. The second group is the heart, kidney, skin, and muscle that can be lumped into a “Peripheral” compartment. Rate constants governing transfer of species in GIT and spleen, and that for heart, kidney, skin, and muscle are provided in Supplementary Tables 1 and 2, respectively (Fig. 3a).
Fig. 3.
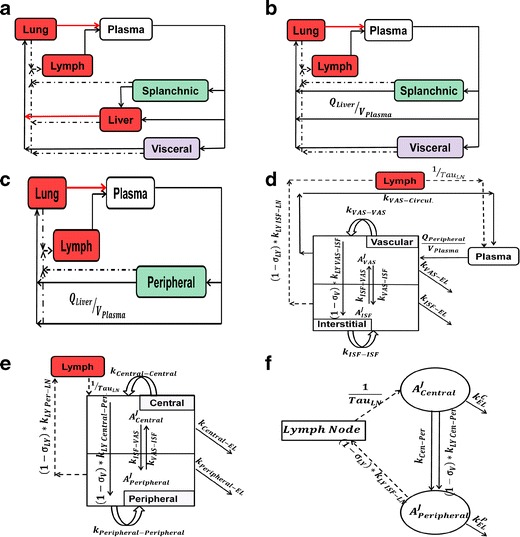
Schematic representation of simplification steps. a (Step2), lumping GIT and spleen to splanchnic and lumping heart, kidney, skin, and muscle to visceral. b (Step 3), fast transfer from liver to lung. c (Step 4), lumping splanchnic and visceral to Peripheral. d (Step 5), fast transfer from lung to plasma, intra-tissue compartments are shown. e (Step 6), equilibrium between plasma and Vascular compartments forming a Central compartment. f (Step 7) final simplified model
Fast Transfer from Liver to Lung (Step 3) (Appendix 5)
In this step, fast transfer from liver vascular compartment to lung was assumed. Thus, amount in the liver compartment was neglected and input into the liver was introduced to the lung compartment. Input into the liver, which comes from two processes namely the entero-hepatic circulation and systemic circulation, were introduced into the following sequential compartment, i.e., lung. In this case, direct input from the plasma was introduced to the lung via a first-order rate constant 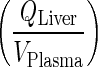 (Fig. 3b).
(Fig. 3b).
Lumping Splanchnic and Visceral Compartments into a Peripheral Compartment (Step 4) (Appendix 6)
Similar to Step 2, rate constants governing the transfer of species in splanchnic and visceral compartments were compared (Supplementary Table 3) (Fig. 3c).
Fast Transfer from Lung to Plasma (Step 5) (Appendix 7)
In this step, fast transfer from lung to plasma was assumed. Thus, the amount in the lung compartment was neglected and input into the lung was introduced to the plasma compartment. Input into the lung, which comes from two processes, namely the venous return and the remaining input to the liver compartment, were introduced into the following sequential compartment, i.e., plasma. In this case, the remaining input to liver compartment from plasma will cancel out in the plasma equation (Fig. 3d).
Rapid Equilibrium Between Plasma and Vascular Compartments to Form Central Compartment (Step 6) (Appendix 8)
In this step, we assume that the rate of transfer from plasma to vascular compartment  was of the same order as transfer rate from the vascular compartment back to plasma (KPeripheralVAS ‐ circul.) while both rates are faster than vascular-interstitial transfer rates. Further, we assume that the vascular compartment is in rapid equilibrium such that the rate of change is negligible. Further, these two rates were considered faster than rates governing transfer between vascular and that the vascular compartment is in rapid equilibrium
was of the same order as transfer rate from the vascular compartment back to plasma (KPeripheralVAS ‐ circul.) while both rates are faster than vascular-interstitial transfer rates. Further, we assume that the vascular compartment is in rapid equilibrium such that the rate of change is negligible. Further, these two rates were considered faster than rates governing transfer between vascular and that the vascular compartment is in rapid equilibrium 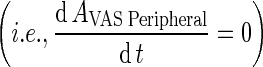 (Supplementary Table 3) (Fig. 3e).
(Supplementary Table 3) (Fig. 3e).
Rearrangement of Inter-Compartmental Transfer Rates (Step 7) (Appendix 8)
Further reduction in model dimensionality and number of parameters was achieved by regrouping the rates of inter-compartmental transfer processes that act in similar or opposite directions. The following regrouping was considered: (a) recycling of mAb from endosomal back to central compartment (kCentralCentral) acted in opposite direction and slower magnitude compared with the elimination from the central compartment, kCentralEL (see Supplementary Table 4). Thus, kCentralCentral was subtracted from kCentralEL yielding a slower elimination rate, kCEL. (b) Similar consideration was applied to the peripheral compartment, (c). transfer from central to peripheral compartments via lymphatic flow and the reflection of the fraction mAb-FcRn complex recycled are combined into one term that describes the sum of the 2 processes. Finally, the rate of return of mAb to the lymph node via lymphatic flow was considered faster than the reflection of the fraction mAb-FcRn complex recycled (kPeripheralISF ‐ Central) (Fig. 3f).
Identifiability Assumptions
To be able to identify the simple physiological model and estimate model parameters with appropriate precision from biexponential plasma profile, the following assumptions were made: (a) rate of return from peripheral compartment to lymph node was proportional to rate of return from lymph node to central compartment, and (b) rates of elimination from both peripheral and central compartments were similar, yielding one elimination rate from both compartments, kEL. One rate constant, kC ‐ P, was used to describe the sum of two processes: transfer from central to peripheral compartments was estimated as the sum of two processes, i.e., convection via lymphatic flow, (1 − σV) × kLY Cen ‐ Per, and reflection of the fraction of mAb-FcRn complex that recycles to the peripheral compartment, kCen ‐ Per. This model was then used to describe population PK of mAb in patients (Fig. 4).
Fig. 4.
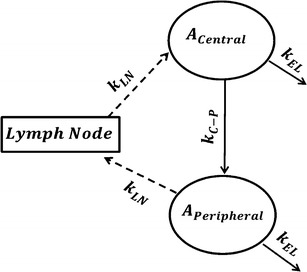
Final identifiable model for estimation of population PK parameters. Four parameters will be estimated k EL, k LN, k C ‐ P, and V C
Non-Compartmental and Population Pharmacokinetic Analysis of mAb in Patients
In a phase I study, an investigational mAb was administered at doses of 0.3, 1, 3, and 10 mg/kg as IV infusion at days 1 and 14. Plasma samples (n = 594) were obtained from 25 patients (5 to 6 patients/dose level) and analyzed for mAb concentrations using ELISA. The clinical protocols were approved by Institutional Review Boards and informed consent was obtained from every patient prior to enrollment. Non-compartmental analysis was conducted to test for linear PK. Two models were used to fit the data: (a) a standard two-compartmental model with linear elimination from the central compartment, and (b) our simplified physiological model. The model fittings and simulations were performed by nonlinear mixed effect modeling using Phoenix Version 6.4 (Pharsight, St. Louis, MO). An exponential model was used to describe the inter-individual variability (IIV) in PK parameters. Proportional and combined additive and proportional residual error models were tested. Full covariance matrix for the IIV was estimated. All estimations were carried out using the quasi-random parametric expectation maximization option (QRPEM).
RESULTS AND DISCUSSION
Simulations from Full PBPK Model Reveal Contribution of Different of Compartments to mAb Disposition
Simulations using an adapted PBPK model (13) were performed (Supplementary Figure 3). A biexponential profile in plasma was observed. Non-compartmental analysis revealed a half-life of 25.9 days consistent with typical mAb PK. The lymph node contributed highly to the mass of mAb in the body which highlights the importance of the lymph node as a transit compartment where mAb is collected from peripheral tissues. Tissue PK profiles were consistent with the observed data reported in (11). Peripheral tissues concentrations were lower than plasma concentration.
Amounts in the interstitial spaces of individual tissues were ∼100-fold lower than that in plasma reflecting a slow and inefficient transfer of mAb from plasma to peripheral tissues. The amount of mAb in the vascular compartment was higher than that in the interstitial compartment. Concentrations in the vascular compartments of all tissues rapidly equilibrated with plasma concentrations (Supplementary Figure 3).
Formation of FcRn-mAb complex was higher in the terminal compared to intermediate subendosomal compartments while free mAb disposition was similar in the first four subendosomal subcompartments and dropped 10-fold in the terminal compartment where high degree of binding to FcRn and proteolytic elimination of the free mAb occurs. It is worth mentioning that the contribution of the endosomal compartment as a whole to the amounts of mAb was negligible relative to that of interstitial and vascular compartments (Supplementary Figure 2 and 3).
Rapid Binding and Fast Endosomal Transfer Assumptions Simplifies Intra-Tissue Compartment Model
Applying fast endosomal transfer, rapid binding, and negligible free endosomal mAb amounts compared to KDEND, allowed reduction of the PBPK model by eliminating the endosomal compartment (Appendices 2 and 3) (Fig. 2). Contribution of endosomal compartment to vascular and interstitial compartments was represented by first-order rate input from vascular compartment to itself (kVAS ‐ VAS) and from interstitial compartment to itself (kISF ‐ ISF) . In contrast to classical models which assume elimination from the central compartment only, elimination was assumed to occur from vascular and interstitial compartments accurately reflecting the physiology of mAb elimination. The rate of elimination from vascular and interstitial compartments (kVAS ‐ EL) and (kISF ‐ EL), is within two- to three-fold of each other. Transfer from the vascular to the interstitial compartment is governed by two processes namely, the convective movement via lymphatic flow, and the reflection of the fraction mAb-FcRn complex recycled (kVAS ‐ ISF) and (kISF ‐ VAS), with the former process being ∼4,000-fold faster than the latter (Supplementary Tables 2–4). Simulations from the reduced model showed similar plasma profiles to full PBPK model (Fig. 5).
Fig. 5.
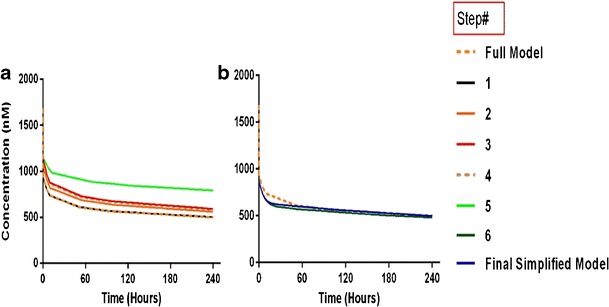
Simulations comparing the effect of consecutive simplifying assumptions on plasma concentrations. Concentrations are shown on linear scale. For Steps 6 and 7, amount of drug in plasma is calculated as a proportion of the drug in the central (i.e., vascular and plasma) compartments
PBPK Tissues Lumped into Two Compartments (Splanchnic and Visceral) (Appendix 4)
A common conundrum in tissue lumping in PBPK is how close time constants of a certain group of tissues should be to be considered for lumping. Nestorov et al. emphasized that no universal rule can be applied for PK equivalence since each case should be considered separately. In our case, most transfer rates compared were within two- to three-fold difference with the exception of the transfer rate from the interstitial compartment to the LN which is 12- and 19-fold higher for heart than skin and muscle (Supplementary Tables 1–2). This reflects physiological differences in structural properties of skin and muscle tissues which possess continuous capillary structure with an uninterrupted lining rich in tight junctions. Further, pore size of lymphatic vessels is likely smaller in skin and muscle compared to highly perfused organs such as heart and kidney (19). However, the relatively high concentrations observed in skin, as reported in (11) and supported by simulations from the full PBPK model (Supplementary Figure 5), reflects some model insensitivity for these two parameters and the difficulty of identifying distinct set of tissues with significantly different concentration profiles compared to others. Consequently, we decided to lump the skin and muscle to the rest of the tissues to provide a whole-body average tissue concentration. This approach is different from that of Cao et al. where body tissues were categorized according to their endothelial vessel structure into leaky (e.g., spleen and liver) and tight (e.g., skin and muscle) (16). The model proposed by Cat et al. assumes a tri-phasic distribution which might not be distinguished from the commonly observed biexponential plasma profile for mAbs.
Thus, GIT and spleen were explicitly lumped into a single compartment (splanchnic) which feeds into the liver via entero-hepatic circulation. Heart, kidney, skin, and muscle were lumped into another compartment (visceral). This step can be modified to express the concentration in a certain tissue of interest. For example, if the purpose of the study is to determine mAb disposition in the muscle, other organs (i.e., heart, kidney, and skin) can be lumped while muscle remains as distinct compartment. This will result in additional compartment and thus data from the tissue of interest is needed to resolve the additional complexity from additional parameters incorporated in the model. Simulations from the reduced model showed slight deviation from the full model (98% AUC agreement with full PBPK) (Fig. 5).
Fast Transfer from Liver Shows Minimal Impact on Plasma Profile (Appendix 5)
Nestorov et al., showed that for PBPK models where tissue disposition is governed via simple processes such as tissue to plasma partition coefficient, ratios of the Laplace transforms of the input and output transfer functions can be used to obtain the equivalent transfer function for the lumped compartment (20). This transfer function can be expressed as the sum or the product of the Laplace transform for the individual tissues arranged in parallel or series, respectively. However, with the complexity of the current mAb PBPK that exhibits nonlinear binding behavior and more than eight different processes controlling mAb tissue disposition, derivation of Laplace transforms is not feasible. Thus, to bypass lumping of tissues arranged in series, the rate of transfer from the liver to lung (kLiverVAS ‐ circul.) was assumed to be faster than the input rate to the liver 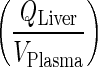 . Numerical evaluation showed that (kLiverVAS ‐ circul.) is eight-fold higher than
. Numerical evaluation showed that (kLiverVAS ‐ circul.) is eight-fold higher than 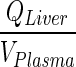 . This assumption suggests that liver does not contribute to the mass of mAb. While we acknowledge that this assumption is inaccurate, large molecules are not specifically eliminated from the liver as opposed to small molecules where liver may represent an important elimination compartment. Interestingly, fast transfer assumption from the liver lead to a minimal increase in plasma profile (Fig. 5) since all input to the liver was added to the next serially located compartment in the model (i.e. lung) and thus, negligible amount of drug is lost from the system. The slight increase in plasma PK can be attributed to the loss of liver space (volume) from the model.
. This assumption suggests that liver does not contribute to the mass of mAb. While we acknowledge that this assumption is inaccurate, large molecules are not specifically eliminated from the liver as opposed to small molecules where liver may represent an important elimination compartment. Interestingly, fast transfer assumption from the liver lead to a minimal increase in plasma profile (Fig. 5) since all input to the liver was added to the next serially located compartment in the model (i.e. lung) and thus, negligible amount of drug is lost from the system. The slight increase in plasma PK can be attributed to the loss of liver space (volume) from the model.
Lumping Splanchnic and Visceral to Peripheral Compartment (Appendix 6)
Similar to Step 2, transfer rates in splanchnic and visceral compartments were found to be within three-fold difference (Supplementary Table 3) and thus they were lumped into a single compartment (peripheral). Simulations showed slight deviation from the full model (97% AUC agreement with full model and 99% with Step 3) (Fig. 5).
Fast Transfer from Lung to Plasma (Appendix 7)
Transfer from lung to plasma (kLungVAS ‐ circul.) was assumed to be faster than the input rate into the lung (kPeripheralVAS ‐ circul.). Numerical evaluation of these rates showed that kLungVAS ‐ circul. is more than 19-fold higher than (kPeripheralVAS ‐ circul.) and 161-fold higher than the input rate to the liver 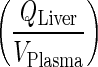 . Thus, amount in the lung compartment was neglected and input into the lung was introduced to the plasma compartment. The remaining input from the liver was introduced in the plasma equation where it canceled out. This step resulted in relatively high deviations from the full model which can be attributed to the additional amount introduced into the plasma compartment and the loss of a distribution compartment (i.e., lung) (Fig. 5).
. Thus, amount in the lung compartment was neglected and input into the lung was introduced to the plasma compartment. The remaining input from the liver was introduced in the plasma equation where it canceled out. This step resulted in relatively high deviations from the full model which can be attributed to the additional amount introduced into the plasma compartment and the loss of a distribution compartment (i.e., lung) (Fig. 5).
Plasma and Vascular Compartments in Rapid Equilibrium (Appendix 8)
The plasma compartment was assumed to be in rapid equilibrium with the vascular compartment in tissues. This assumption was supported by three observations. First, the rate transfer from plasma to vascular compartment of peripheral organs 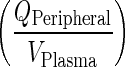 is proportional to the transfer rate from the vascular compartment of peripheral organs to plasma (kPeripheralVAS ‐ circul.). Second, these two rates are more than 9,000-fold faster than other processes. Finally, simulations showed that concentrations in plasma and vascular compartment of the peripheral organs are in rapid equilibrium (Supplementary Figure 3). Thus, the total amount of mAb in plasma and vascular compartments are represented by a new variable (ACentral). Amount of mAb in plasma was represented as a fraction of the total amounts in the central compartment. Simulations of plasma concentrations showed a biexponential profile close to that of the full PBPK model. Given this model structure, the “central” compartment resembles the rapid distribution compartment in classical two-compartment models as it includes spaces with rapid distribution properties (plasma and tissue vasculature). However, in contrast to two-compartmental models, the central compartment in our model exhibits clear physiological/anatomical definitions and retains the elimination of mAb from the central compartment, kCEL.
is proportional to the transfer rate from the vascular compartment of peripheral organs to plasma (kPeripheralVAS ‐ circul.). Second, these two rates are more than 9,000-fold faster than other processes. Finally, simulations showed that concentrations in plasma and vascular compartment of the peripheral organs are in rapid equilibrium (Supplementary Figure 3). Thus, the total amount of mAb in plasma and vascular compartments are represented by a new variable (ACentral). Amount of mAb in plasma was represented as a fraction of the total amounts in the central compartment. Simulations of plasma concentrations showed a biexponential profile close to that of the full PBPK model. Given this model structure, the “central” compartment resembles the rapid distribution compartment in classical two-compartment models as it includes spaces with rapid distribution properties (plasma and tissue vasculature). However, in contrast to two-compartmental models, the central compartment in our model exhibits clear physiological/anatomical definitions and retains the elimination of mAb from the central compartment, kCEL.
Final Simplified Physiological Model with Identifiable Parameters (Appendix 8)
In the final step, we considered regrouping transfer processes by adding processes that act in similar transfer direction or subtracting these that act in opposite direction (e.g., subtracting the rate of recycling of mAb from the endosomal space to peripheral and central spaces (kCentralCentral and kPeripheralPeripheral) from the elimination rate from these compartments). This implies that kCentralEL > kCentralCentral and that kPeripheralEL > kPeripheralPeripheral, which was confirmed by numerical evaluation (Supplementary Table 4). This simplification results in slower elimination rates (kCEL and kPEL). Data collected in routine clinical trials usually involve samples from plasma but not from tissues and thus kPEL would be unidentifiable. Given that kCEL and kPEL are within two-fold difference, we assumed that rates of elimination from both central and peripheral compartments were similar, yielding one identifiable elimination rate from both compartments, kEL.
Comparing the rates of processes involved in the transfer of mAb from the peripheral compartment, namely, the return to the lymph node via lymphatic flow and the reflection of the fraction mAb-FcRn complex recycled (kISF ‐ VAS), showed that the return via convective movement is dominant (>2 E + 07 fold higher) and thus kISF ‐ VAS was considered negligible and the loss of drug from the peripheral compartment was assumed to take place only via convective movement to the lymph node. Finally, the rate of return from peripheral compartment to lymph node, (1 − σLY) × kPeripheralLY ISF ‐ LN), was found comparable to rate of return from lymph node to central compartment, 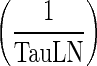 . Thus, we assumed these two rates to be equal and the term kLN (calculated as the average of the two rates) was used. This renders the lymph node as a transit compartment that reflects the delayed return of mAb to the circulation. Simulation from the final model was almost identical to that of the full model.
. Thus, we assumed these two rates to be equal and the term kLN (calculated as the average of the two rates) was used. This renders the lymph node as a transit compartment that reflects the delayed return of mAb to the circulation. Simulation from the final model was almost identical to that of the full model.
Neither the full PBPK model nor the simplified model consider binding to the specific target. Target-mediated clearance represents an important elimination pathway for mAbs and is responsible for the rapid clearance of mAbs observed at lower doses in dose escalation trials. This nonlinear clearance pathway can be considered, if needed, within the proposed physiological model. The elimination rate, kEL, can be replaced by Michaelis–Menten elimination terms VMAX and KM and or more complex TMDD models. Estimability of these parameters depends on the type and richness of the data (for example multiple doses before and after target saturation and at long sampling intervals with low concentrations).
Population Analysis and Model Parameters Estimation
Non-compartmental analysis showed linear PK across all doses tested. Initial estimates for the two-compartmental model were obtained from the literature (13). For the simple physiological model, physiological values for the transfer rates obtained during model simplification were used and the volumes of plasma in human was used as initial estimate for the volume of central compartment (3 L). The profile of the tested mAb was well characterized by both two-compartment model and the simple physiological model (Fig. 6). The residuals plots, visual predictive checks, and model selection criteria (e.g., AIC) all suggest similar fit for both models (Fig. 6 and Supplementary Figure 6). The estimated parameter values for both models are shown in Tables II and III. The estimate for VC was the same in both models (3.8 L) with comparable IIV. Estimate for VP in the classical two-compartmental model was 4.6 L which agrees with the range reported in the literature (1.3 to 6.8 L) (13). According to the structure of the simple physiological model, VP cannot be directly estimated from our model without additional information on, for example, peripheral tissue concentrations.
Fig. 6.
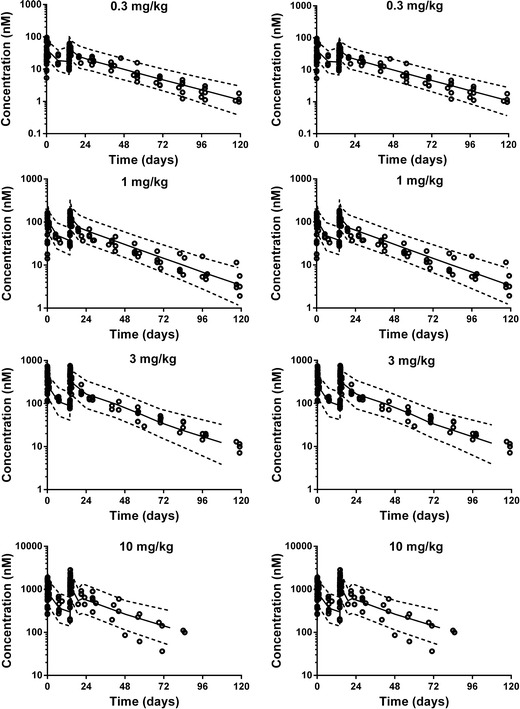
Visual predictive check for different dose levels, open symbols represent the observed plasma concentrations, solid line represents the 50th percentile and the dotted lines represent the 5th and 95th percentiles of the model predicted data
Table II.
Estimated Classical Two-compartment Model Parameters for the Population
| Parameter (unit) | Population mean final estimate (%CV) | Inter-individual variance final estimate (%CV) |
|---|---|---|
| Volume of central compartment, V C, (L) | 3.8 (7.4) | 33.9 (28.9) |
| Volume of peripheral compartment, V P, (L) | 4.8 (12.7) | 45.1 (33.2) |
| Elimination clearance, CL, (L/h) | 0.29 (7.4) | 30.3 (30.47) |
| Distributional clearance, Q, (L/h) | 1.47 (15.4) | 23.1 (37.68) |
| Model AIC | 5797 |
Table III.
Estimated Simple Physiological Model Parameters for the Population
| Parameter (unit) | Population mean final estimate (%CV) | Inter-individual variance final estimate (%CV) |
|---|---|---|
| Volume of central compartment, V c, (L) | 3.8 (7.3) | 33.9 (29.1) |
| k Cen ‐ Per (day)−1 | 0.36 (16.87) | 17.1 (30.2) |
| k LN (day)−1 | 0.51 (16.09) | 43.6 (31.6) |
| k EL (day)−1 | 0.044 (3.9) | 22.8 (30.7) |
| Model AIC | 5,796 |
However, the volume of the peripheral compartment (VP) can be inferred as a secondary parameter from the simple physiological model by considering the convective clearance for mAbs from the tissues to lymph. Human plasma flow rate (4,368 L/day) can be referenced from the literature (7). Applying the same assumptions from the full PBPK model that lymph flow is proportional to plasma flow (i.e., lymph flow = 0.2% of plasma flow), and that the lymphatic reflection coefficient is 0.2, the convective clearance from the peripheral compartment to the lymph node, (CLPer ‐ LN) can be calculated as (1 − σLY) × L (i.e., 6.9 L/day), which allows calculation of VP as the ratio between the convective clearance and 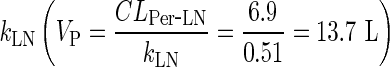 . This estimate is a much better approximation of the reported estimate of the physiological volume of the interstitial space (∼11.7 L) (7) and allows better prediction of the peripheral tissue concentrations compared to two-compartmental models (Supplementary Figure 7).
. This estimate is a much better approximation of the reported estimate of the physiological volume of the interstitial space (∼11.7 L) (7) and allows better prediction of the peripheral tissue concentrations compared to two-compartmental models (Supplementary Figure 7).
The utility of any model depends on the purpose of the modeling exercise. Both classical and simple physiological models were capable of capturing the plasma concentrations of the example used. However, if the model aims to predict whole-body average concentrations in peripheral tissues, classical models will underestimate the volume of distribution at steady state (VSS) which is calculated as the sum of VC and VP (common (VSS) estimates for mAbs are ∼5–7 L) which is almost half of the volume of interstitial space (∼11.3 L) (8). Underestimation of VSS in classical compartmental models will lead to over predicting whole-body average peripheral tissue concentrations as shown in (Supplementary Figure 7). This might be explained, at least partially, by the following two reasons: First, the classical model assumes elimination from the central compartment only. The impact of ignoring peripheral elimination on estimation of PK parameters of muscle relaxants which undergo extensive peripheral elimination has been studied. Ignoring peripheral elimination in a classical two-compartment model resulted in underestimation of several exit-site dependent PK parameters of which VSS is the most clinically significant (21). According to the physiological and PK of mAbs, both VP and VC, represents an elimination site which is misrepresented in classical models. Second, classical models do not consider lymphatic circulation and uptake from endothelial space in peripheral tissues back to the vasculature (i.e., central compartment). On the other hand, the physiological model provided reasonable representation of the whole-body average tissue concentrations. This was confirmed by calculating the ratio between average tissue and plasma concentrations from the full PBPK model (0.1) and comparing it to that obtained from the simple physiological model predictions (0.18). The classical model showed much higher ratio (0.92).
CONCLUSION
In this work, our goal was to reduce the dimensionality and complexity of a PBPK model into a simple compartmental model. The full PBPK model used provides close description of several important processes in mAb disposition such as the gradual change in endosomal pH, the change in mAb and FcRn association and dissociation affinities, mAb uptake in to the endosome, convective movement of mAb into tissue, and convective return of the antibody to blood via the lymphatic circulation (13). Using a series of physiologically plausible and consecutive assumptions, we employed a top-down approach to translate prior physiological information from the full PBPK model to a simple compartmental model. This model provides fewer compartments than PBPK but more physiologically meaningful parameters than traditional mammillary systems that can be estimated in a population approach with minimal complexity. The final model was successfully applied to describe the PK of a development mAb using the population approach.
Electronic Supplementary Material
(DOCX 894 kb)
Acknowledgments
This work was supported by NIH Grant GM57980 and the University at Buffalo-Novartis Fellowship. We would like to acknowledge thoughtful comments from Dr. Joseph P. Balthasar and Dr. Yang Chen.
Conflict of Interest
The authors declare no conflict of interest
Appendices
Appendix 1: Original Model Equations
Notes:
A superscript J is used to denote endogenous IgG or mAb in most equations. If the equations describing the mAb and IgG are different two independent systems of equations are used.
Dependent variables are described in amounts, not concentrations, as in (13).
The original model (13) described binding to FcRn receptor as the change from initial FcRn concentration in different tissues and the initial conditions for this change is set to 0. In this work, FcRn receptor amounts were expressed as RfreeOrgan ‐ X.
The original model used two estimated coefficients to reflect the non-FcRn dependent tissue uptake of mAb (13). In our study, simulations were performed without these coefficients.
I. plasma
Endogenous IgG
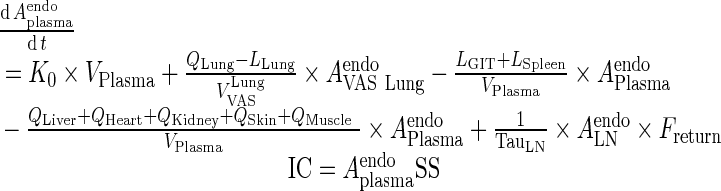 |
3 |
Exogenous mAb
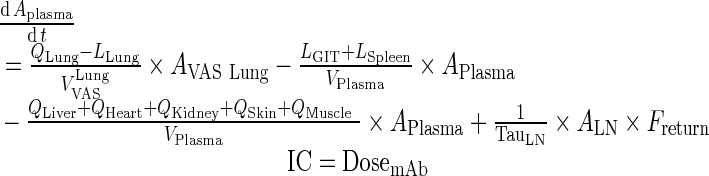 |
4 |
II. Organs
A. Vascular Space
Equations for the vascular compartment in liver and lung are different from other organs.
i. lung
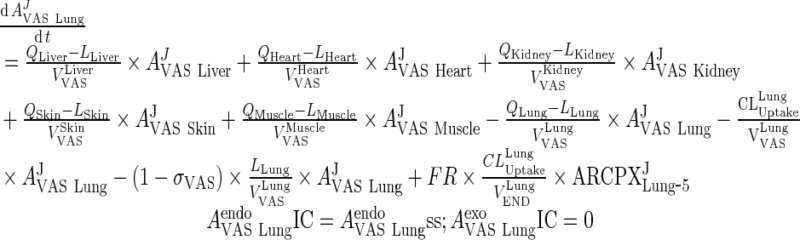 |
5 |
ii. liver
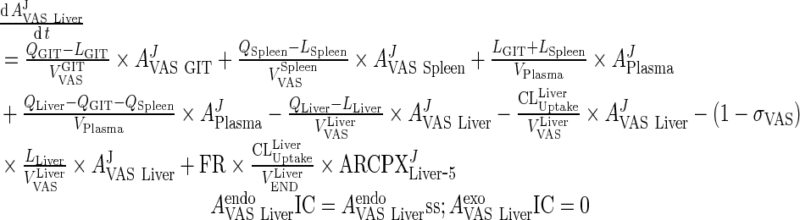 |
6 |
iii. Other Organs (heart, kidney, skin, muscle, GIT, spleen)
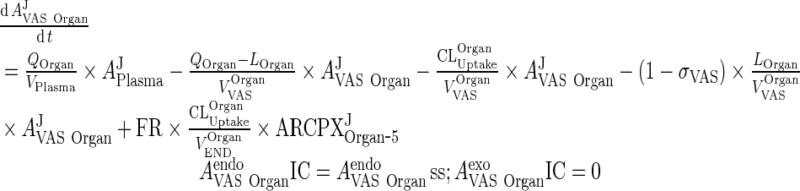 |
7 |
B. Interstitial Space (Applies for all organs including liver and lung, all termed “Organ”)
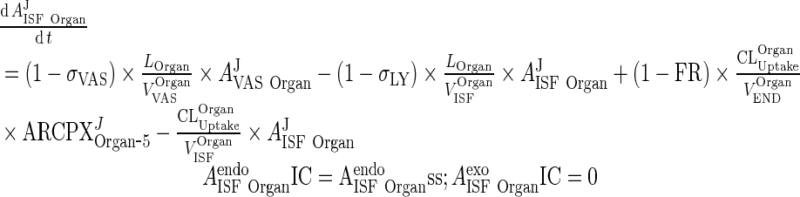 |
8 |
C. Endosomal Space (Applies for all organs including liver and lung, all termed “Organ”)
i. Subcompartment 1
Endogenous IgG
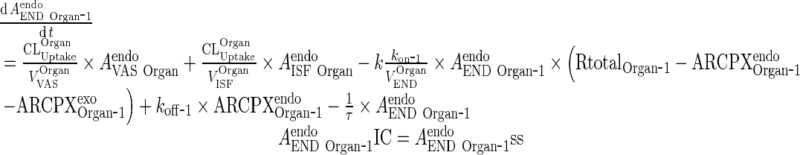 |
9 |
Exogenous mAb
 |
10 |
Endogenous IgG-FcRn complex
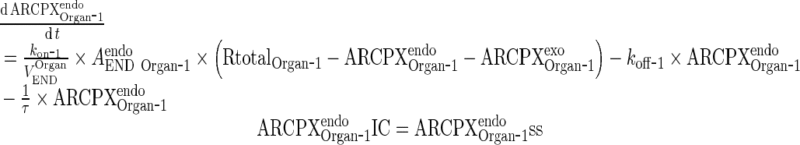 |
11 |
Exogenous mAb-FcRn complex
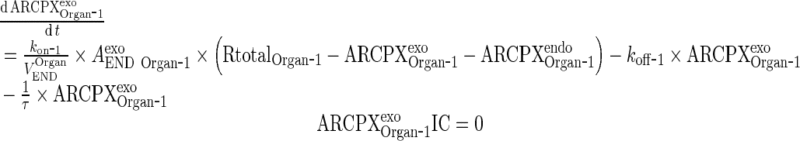 |
12 |
ii. Subcompartments 2, 3 and 4 (i = 2, 3, 4)
Endogenous IgG
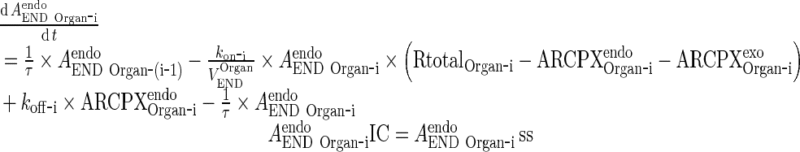 |
13 |
Exogenous mAb
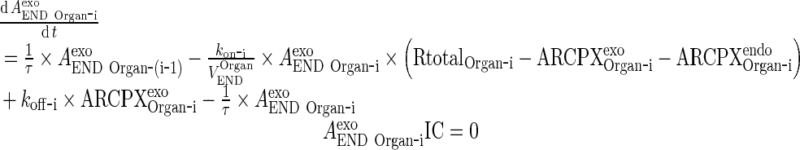 |
14 |
Endogenous IgG-FcRn complex
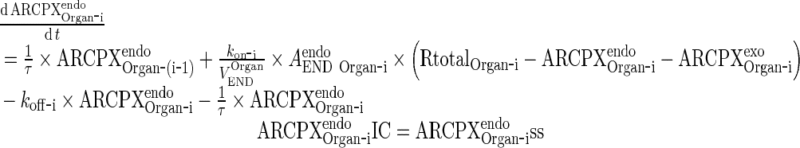 |
15 |
Exogenous mAb-FcRn complex
 |
16 |
iii. Subcompartment 5
Endogenous IgG
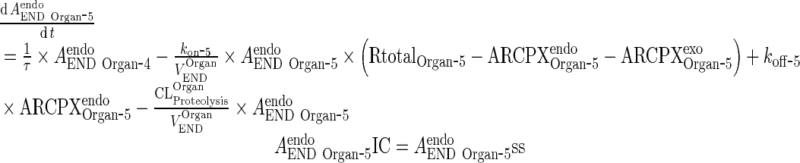 |
17 |
Exogenous mAb
 |
18 |
Endogenous IgG-FcRn complex
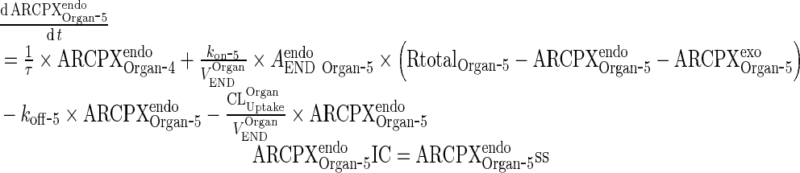 |
19 |
Exogenous mAb-FcRn complex
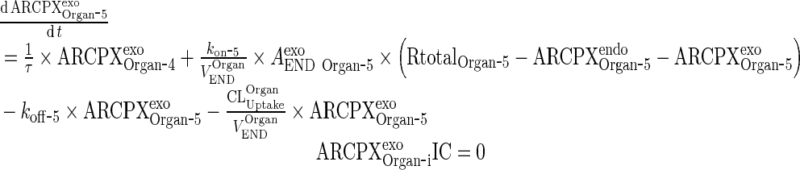 |
20 |
III. Lymph Node
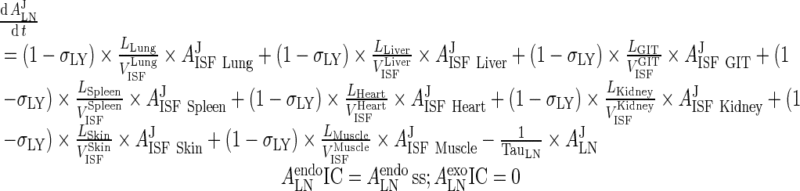 |
21 |
Appendix 2: Fast Endosomal Transfer and Rapid Binding Assumptions
Transfer of mAb/IgG between endosomal compartments is fast relative to the time scale of other processes such as changes in plasma and lymph as well as the rate of binding of mAb/IgG to FcRn. The assumption that the endosomal transfer rate is faster than FcRn binding process holds true for earlier compartments where FcRn binding is considered negligible (in the first endosomal subcompartment) or low (in intermediate compartments). As the drug is transferred to later compartments, rate of binding increases and thus rapid binding assumption is applied to the last compartment where the majority of binding to FcRn takes place. Physiologically these 2 processes (transfer and binding) might interfere with each other. However, since these 2 assumptions (i.e., fast endosomal transfer and rapid binding) are applied sequentially, the 2 assumptions do not contradict each other, at least from a theoretical aspect.
Assumption: Endosomal transfer of mAb/IgG between endosomal compartments is very fast relative to the time scale of other processes:
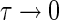 |
22 |
It can be shown that input in to the first endosomal compartment will be transferred to the terminal compartment as τ → 0 (Please refer to Appendix 9),
 |
23 |
Thus, equation for free mAb/IgG in the terminal compartment can be expressed as:
 |
24 |
and the equation for complex mAb/IgG in the terminal compartment can be expressed as:
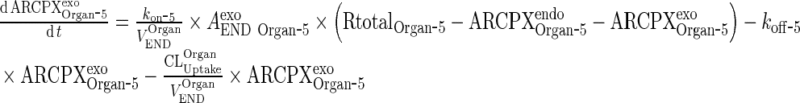 |
25 |
Assumption: Free drug, the target and the complex are at rapid equilibrium meaning that the binding and dissociation rates are much faster than other processes (18).
Thus,
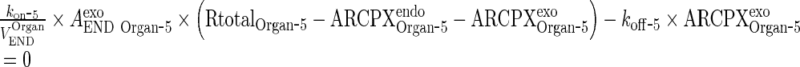 |
26 |
And
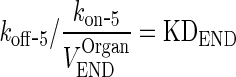 |
27 |
Solve for ARCPXexoOrgan ‐ 5
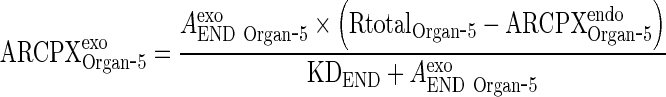 |
28 |
Similarly,
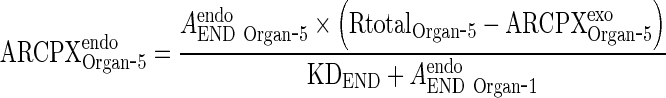 |
29 |
Substitute ARCPXendoOrgan ‐ 5 in Eq. 27 to solve for ARCPXexoOrgan ‐ 5 in terms of the free amounts of endogenous (AendoEND Organ ‐ 5) IgG and exogenous mAb (AexoEND Organ ‐ 5)
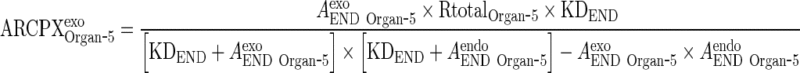 |
30 |
and AEND Organ ‐ i and AendoEND Organ ‐ i are negligible compared to KDEND (AexoEND Organ ‐ 5 < < KDEND and AendoEND Organ ‐ 5 < < KDEND) (Please refer to Supplementary Figure 2)
Thus, Eq. 29 for ARCPXJOrgan ‐ 5 can be simplified to
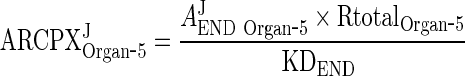 |
31 |
Equations derived for ARCPXJOrgan ‐ 5 showed that the IgG/mAb-FcRn complex is proportional to the free IgG/mAb. In the following section, equations for free IgG/mAb (Eq. 27) and complex (Eq. 28) are added to get AJTotal END Organ ‐ 5
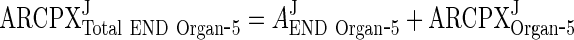 |
32 |
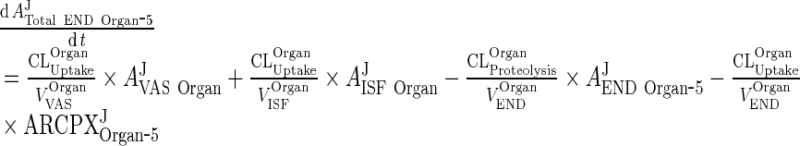 |
33 |
Assumption: total mAb/IgG in compartment 5 is in equilibrium, i.e.
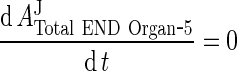 |
34 |
Consequently,
 |
35 |
Substituting ARCPXJOrgan ‐ 5 by Eq. 31 allows one to solve Eq. 43 for AEND Organ ‐ 5
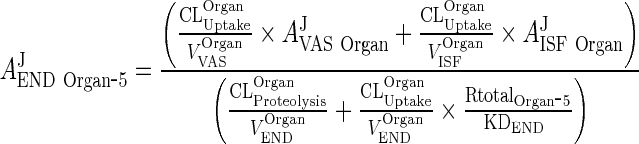 |
36 |
Substituting AJEND Organ ‐ 5 from Eqs. 38 and 34 allows solving for ARCPXJOrgan ‐ 5 in terms of vascular and interstitial amounts
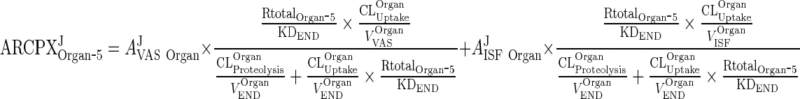 |
37 |
Let the terms multiplying AJVAS Organ and AJISF Organ be k1 and k2, respectively. Thus,
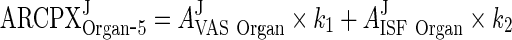 |
38 |
Substitute ARCPXOrgan ‐ 5 in the equation for vascular and interstitial compartments (Please refer to Fig. 3):
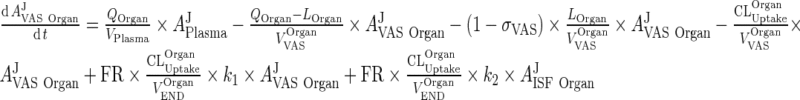 |
39 |
Introduce the input term from the vascular to the interstitial compartment: (This term appears in the interstitial compartment)
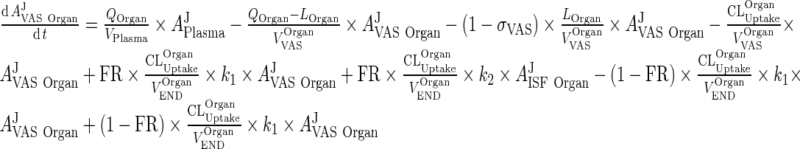 |
40 |
which can be simplified to:
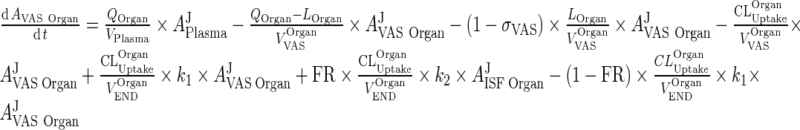 |
41 |
A similar substitution of ARCPXJOrgan ‐ 5 in the equation for the interstitial compartment yields:
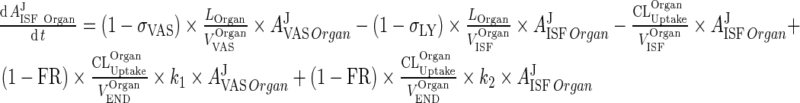 |
42 |
Introduce the input term from the interstitial to the vascular compartment: (This term appears in the vascular compartment and should be accounted for)
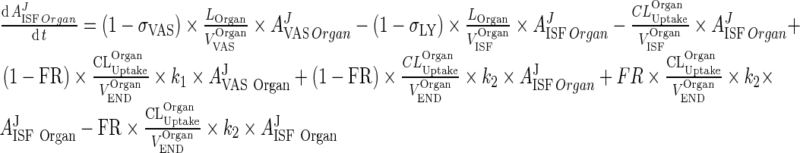 |
43 |
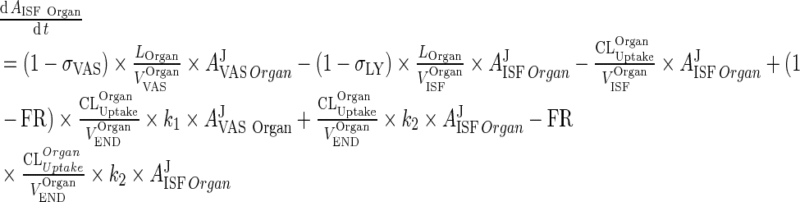 |
44 |
Let 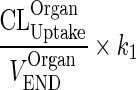 be a first-order input from the vascular compartment to itself (kOrganVAS ‐ VAS)
be a first-order input from the vascular compartment to itself (kOrganVAS ‐ VAS)
Let 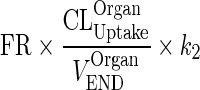 be a first-order input from interstitial compartment to vascular compartment (kOrganISF ‐ VAS)
be a first-order input from interstitial compartment to vascular compartment (kOrganISF ‐ VAS)
Let 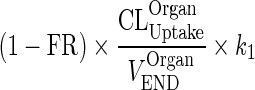 be a first-order input from vascular compartment to interstitial compartment (kOrganVAS ‐ ISF)
be a first-order input from vascular compartment to interstitial compartment (kOrganVAS ‐ ISF)
Let 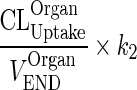 be a first-order input from the interstitial compartment to itself (kOrganISF ‐ ISF).
be a first-order input from the interstitial compartment to itself (kOrganISF ‐ ISF).
The final equations for vascular and interstitial compartments can be written as:
A. Vascular Space
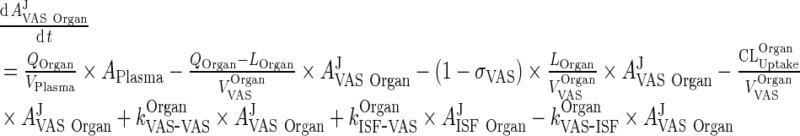 |
45 |
B. Interstitial Space
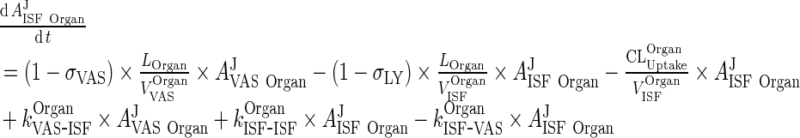 |
46 |
Appendix 3: Simplified Model Equations After Rapid Binding and Fast Endosomal Transfer Assumptions (Step 1)
I. plasma
Endogenous IgG
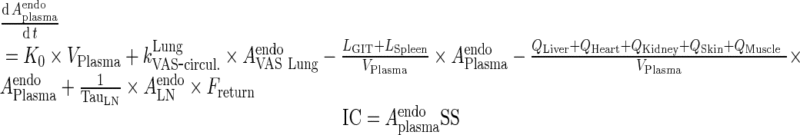 |
47 |
Exogenous mAb
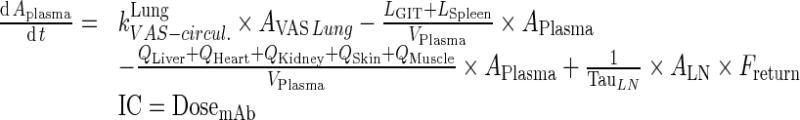 |
48 |
II. Organs
A. Vascular Space
Equations for the vascular compartment in liver and lung are different from other organs.
i. lung
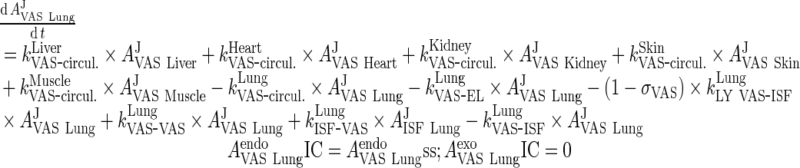 |
49 |
ii. liver
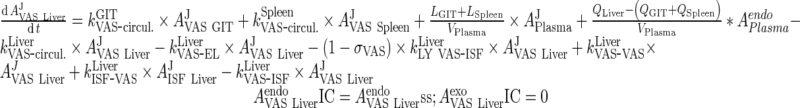 |
50 |
iii. Other Organs (heart, kidney, skin, muscle, GIT, spleen)
 |
51 |
B. Interstitial Space (Applies for all organs including liver and lung, all termed “Organ”)
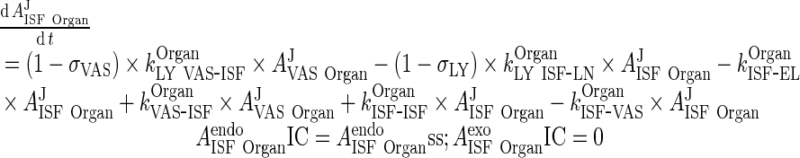 |
52 |
III. Lymph Node
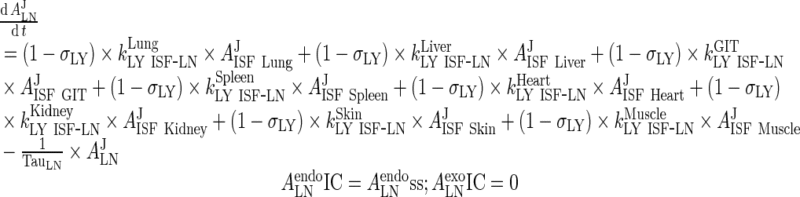 |
53 |
Appendix 4: Model Equations for Lumping of GIT and Spleen (Splanchnic) and Heart, Kidney, Skin, and Muscle (Visceral)
This is Step #2 in the model development. Please refer to Fig. 3 for model structure and Table I for model parameters.
I. plasma
Endogenous IgG
For the lumped compartment, the lymphatic can be described as the sum of flow for each individual organ as:
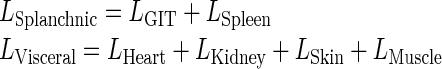 |
Similarly, the plasma flow for the lumped compartment can be described as:
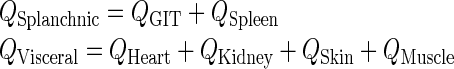 |
Then the equation for endogenous IgG in plasma becomes:
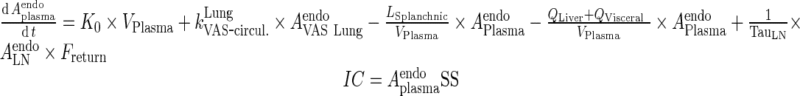 |
54 |
Exogenous mAb
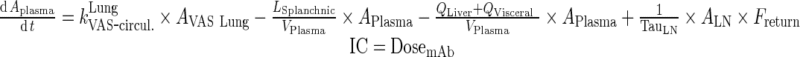 |
55 |
II. Organs
A. Vascular Space
Equations for the vascular compartment in liver and lung are different from other organs.
i. lung
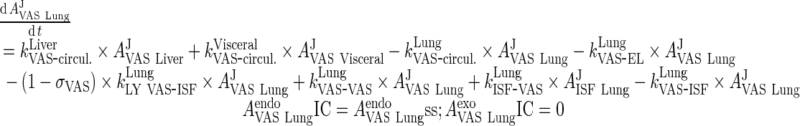 |
56 |
ii. Liver
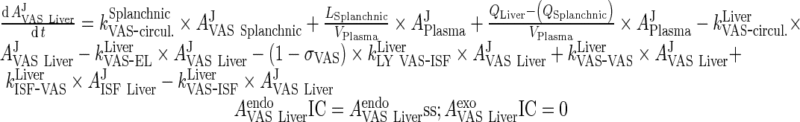 |
57 |
iii. splanchnic (GIT and spleen lumped)
 |
58 |
iv. visceral (heart, kidney, skin, muscle lumped)
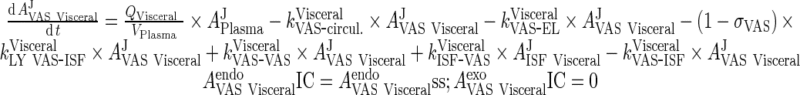 |
59 |
B. Interstitial Space
i. lung, liver
(All organs but splanchnic and visceral)
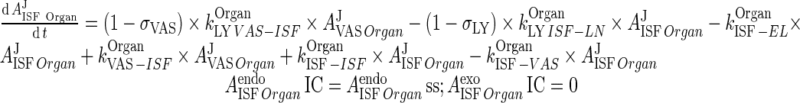 |
60 |
ii. splanchnic (GIT and spleen lumped)
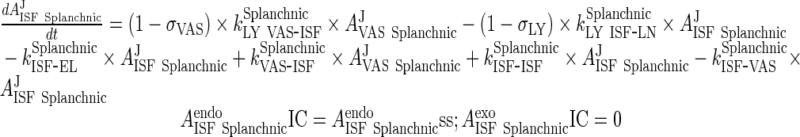 |
61 |
iii. visceral (heart, kidney, skin, muscle lumped)
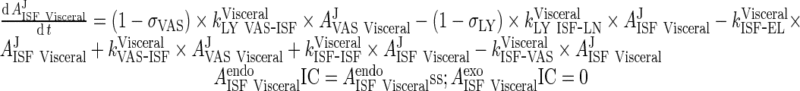 |
62 |
III. Lymph Node
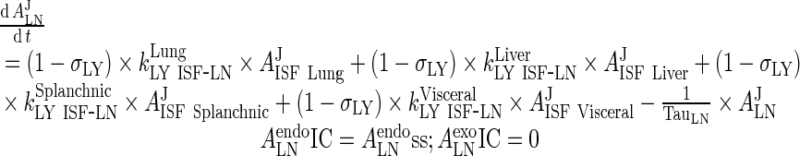 |
63 |
Appendix 5: Model Equations after fast transfer from liver to lung (Step#3)
Liver compartment no longer exists and the appearance of 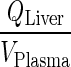 is solely indicative of the transfer from plasma to lung. Finally, splanchnic is now positioned to be parallel to other organs, i.e., visceral.
is solely indicative of the transfer from plasma to lung. Finally, splanchnic is now positioned to be parallel to other organs, i.e., visceral.
I. plasma
Endogenous IgG
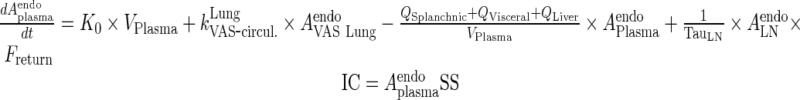 |
64 |
Exogenous mAb
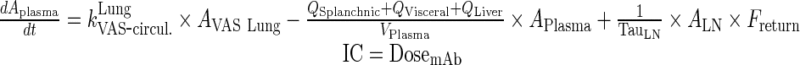 |
65 |
II. Organs
A. Vascular Space
Equations for the vascular compartment in lung are different from other organs.
i. lung
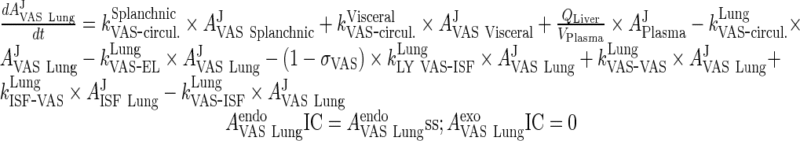 |
66 |
ii. splanchnic (GIT and spleen lumped)
 |
67 |
iii. visceral (heart, kidney, skin, muscle lumped)
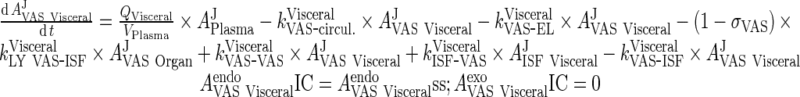 |
68 |
B. Interstitial Space
i. lung
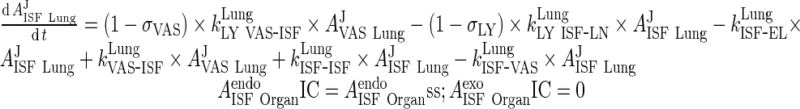 |
69 |
ii. splanchnic (GIT and spleen lumped)
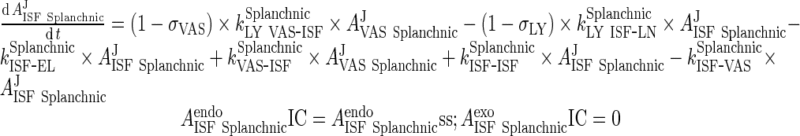 |
70 |
iii. visceral (heart, kidney, skin, muscle lumped)
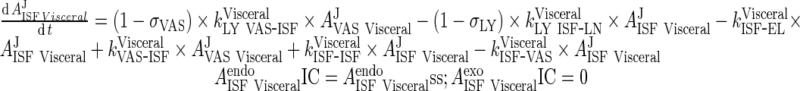 |
71 |
III. Lymph Node
Endogenous IgG
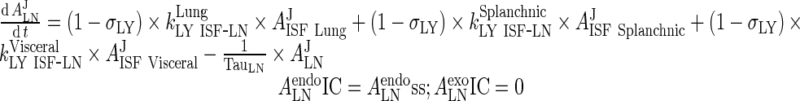 |
72 |
Appendix 6: Model Equations for Lumping Splanchnic and Visceral into Peripheral (Step#4)
I. plasma
Endogenous IgG
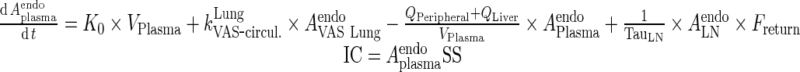 |
73 |
Exogenous mAb
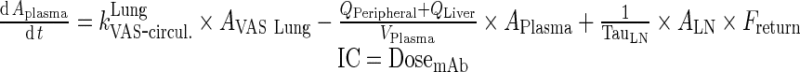 |
74 |
II. Organs
A. Vascular Space
Equations for the vascular compartment in lung are different from other organs.
i. lung
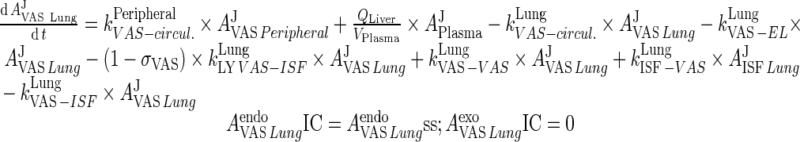 |
75 |
ii. Peripheral (splanchnic and visceral lumped)
 |
76 |
B. Interstitial Space
Peripheral
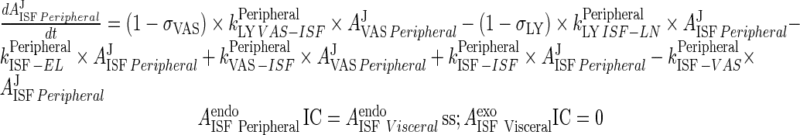 |
77 |
III. Lymph Node
Endogenous IgG
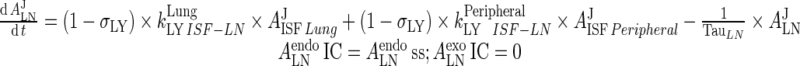 |
78 |
Appendix 7: Model Equations for Fast Transfer from Lung to Plasma (Step#5)
(Figure 4d)
I. plasma
Endogenous IgG
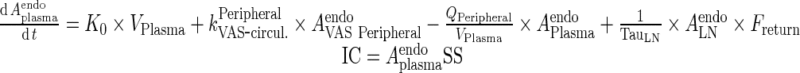 |
79 |
Exogenous mAb
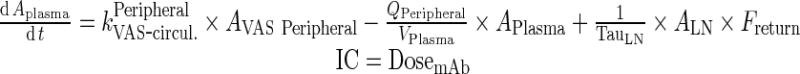 |
80 |
II. Peripheral
A. Vascular Space
 |
81 |
B. Interstitial Space
Peripheral
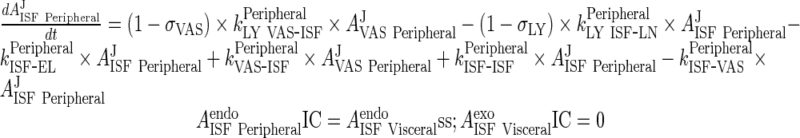 |
82 |
III. Lymph Node
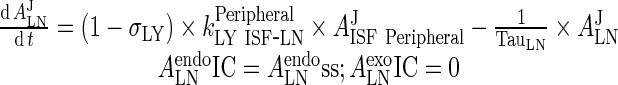 |
83 |
Appendix 8: Rapid equilibrium between plasma and Vascular compartments forming Central compartment (Model Equations) (Step#6)
(Figure 5) (Supplementary Table 4)
In this step, rapid equilibrium from plasma to vascular compartment is assumed. The rate of transfer from plasma to vascular compartment of Peripheral organs 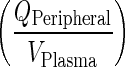 is of the same order as transfer rate from the vascular compartment of Peripheral organs to plasma (kPeripheralVAS ‐ circul.). These two rates are assumed to be faster than rates governing transfer between vascular and interstitial spaces:
is of the same order as transfer rate from the vascular compartment of Peripheral organs to plasma (kPeripheralVAS ‐ circul.). These two rates are assumed to be faster than rates governing transfer between vascular and interstitial spaces:
 |
(Table III):
Further, we assume that the vascular compartment is in rapid equilibrium such that the rate of change is negligible (i.e., 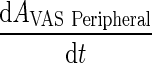 is much smaller than the right hand side of the differential equation)
is much smaller than the right hand side of the differential equation)
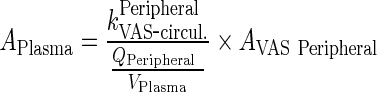
Dividing Eqs. 114/115 by kPeripheralVAS ‐ circul. leads to
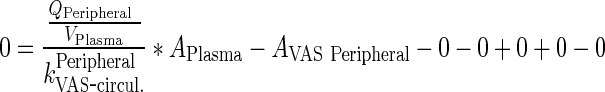 |
84 |
After rearrangement
 |
85 |
Introduce a new variable for the total amount in vascular and plasma compartments (Central)
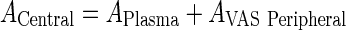 |
86 |
Then
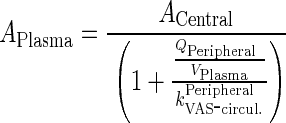 |
87 |
and
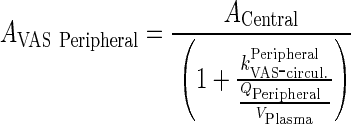 |
88 |
Adding differential equations for vascular and plasma compartments to get the differential equation for ACentral results in
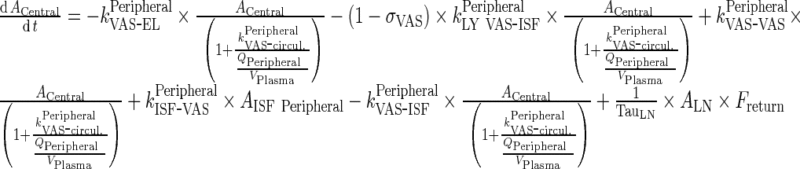 |
89 |
Regroup rates and change parameter names to reflect new model structure
Let
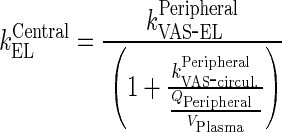 |
be elimination rate from the central compartment
Let 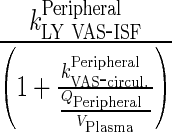 be transfer rate from the central to interstitial (i.e., peripheral) compartment via lymphatic flow
be transfer rate from the central to interstitial (i.e., peripheral) compartment via lymphatic flow
Let 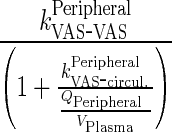 first-order input from central compartment to itself which reflects the impact of recycled drug from endosomal compartment
first-order input from central compartment to itself which reflects the impact of recycled drug from endosomal compartment
Let 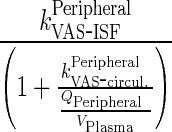 be first-order input from central to interstitial compartment
be first-order input from central to interstitial compartment
Let kPeripheralISF ‐ VAS be termed kPeripheralISF ‐ Central to reflect the updated model structure
Thus equations for Central, Peripheral and lymph node compartments are provided as follows,
Central Compartment
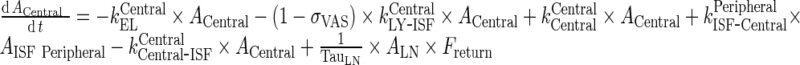 |
90 |
Peripheral Compartment
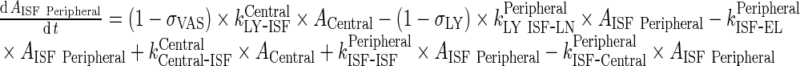 |
91 |
Lymph Node
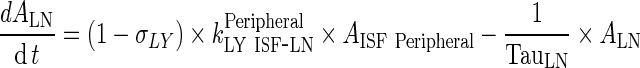 |
92 |
Rearrange equation for ACentral and AISF Peripheral
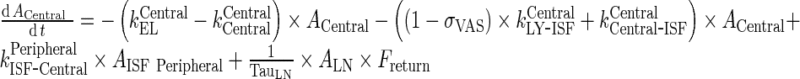 |
93 |
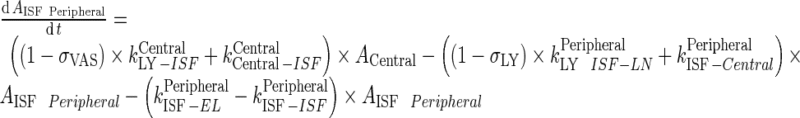 |
94 |
Subsequently, the following rearrangements and assumptions were made:
-
Rearrangement: Subtracting the rate of recycling of mAb from the endosomes back to the central compartment (kCentralCentral, 5.8E-06 h−1) which acts as an input to the central compartment from the central compartment elimination, (kCentralEL, 6.1E-06 h−1) results in a slower elimination rate termed, kCEL (3E-07 h−1).
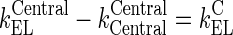
95 Similarly, subtracting the rate of recycling of mAb from the endosomes back to the peripheral compartment (kPeripheralPeripheral, 2.73E−06 h−1) from the peripheral compartment elimination, kPeripheralEL (2.85E−06 h−1) results in a slower peripheral elimination rate termed, kPEL (1.2E−07 h−1).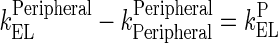
96 - Rearrangement: Transfer from central to peripheral compartments via lymphatic flow and the reflection of the fraction mAb-FcRn complex recycled are combined into one term that describes the sum of the two processes.
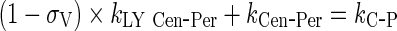
97 - Assumption: Rate of return of mAb to the lymph node via lymphatic flow ((1 − σLY) × kPeripheralLY ISF ‐ LN, 0.39 h−1) is faster than the reflection of the fraction mAb-FcRn complex recycled , (kPeripheralISF ‐ Central, 1.95E-06 h−1)
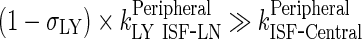
98 - Assumption: Rate of return from peripheral compartment to lymph node ((1 − σLY) × kPeripheralLY ISF ‐ LN , 0.39 h−1) is comparable to rate of return from lymph node to central compartment (
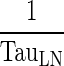 , 0.11 h−1)
, 0.11 h−1)
99 -
Assumption: 100% of the drug in the lymph node is subject to return to the central compartment (i.e., Freturn = 1)
Further, kCEL ∼ kPEL = kEL. Thus, Final model equations can be written as:
A. Central Compartment
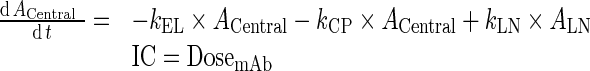 |
102 |
B. Peripheral Compartment
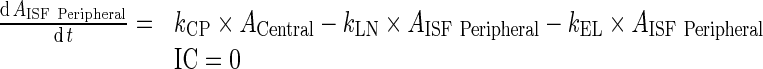 |
103 |
C. Lymph node Compartment
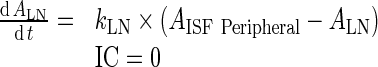 |
104 |
Appendix 9: Derivation of the Output Function in Transit Compartment System with Fast Transfer
In this appendix, we show that the output from the last of N transit compartments equals to the input, if the transfer rate between transit compartments is fast compared to other processes. We assume that all model variables describing amounts are nonnegative. We also skip the proofs of the following statements:
 |
105 |
and
 |
106 |
and there exist positive constants Mendo and Mexo such that
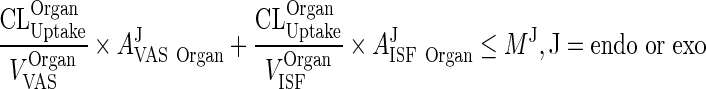 |
107 |
First we will show that for i = 1, 2, 3, 4, J = endo or exo
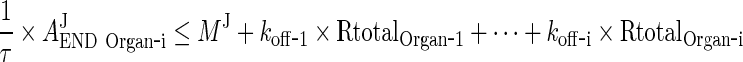 |
108 |
and
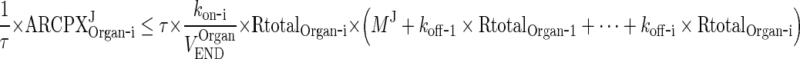 |
109 |
Applying the integrating factor et/τ to (9) and (10) one can obtain the following solution for AJEND Organ ‐ 1:
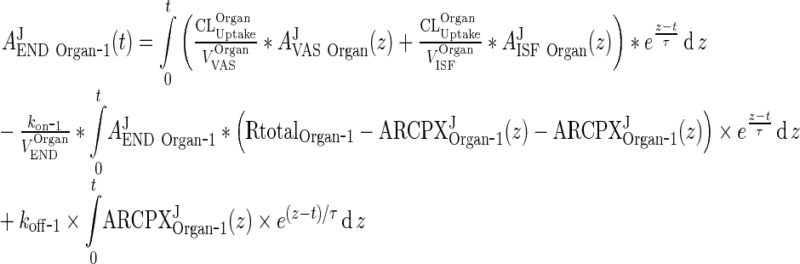 |
110 |
and
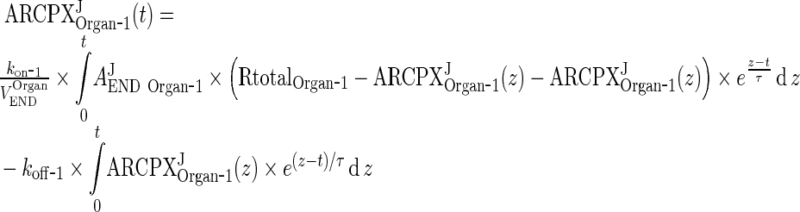 |
111 |
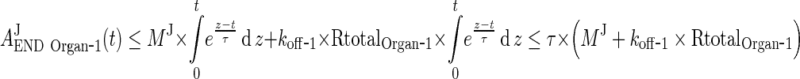 |
112 |
and
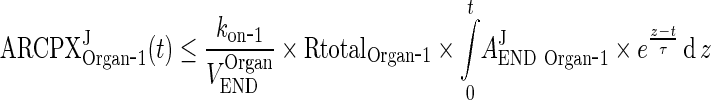 |
113 |
From (113) it follows
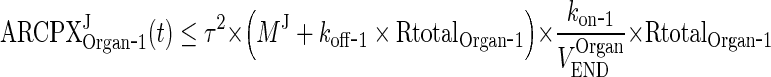 |
This proves (109) and (110) for i = 1. The proof of cases i = 2, 3, 4 is analogous.
In the next step we will show that for i = 1, 2, 3, 4, J = endo or exo
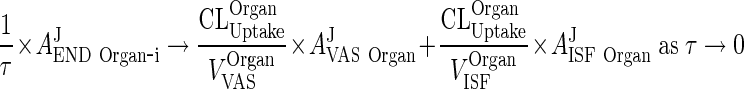 |
114 |
That will yield (23) for i = 4. Consider first the case i = 1. Multiplying (110) by 1/τ results in
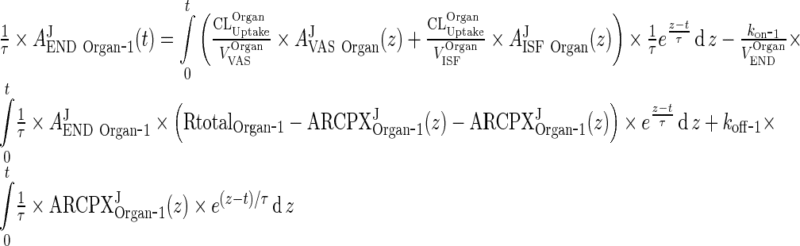 |
115 |
From (107) and (112) the following bound applies to the integral
 |
116 |
This means that the integral in (117) approaches 0 as τ → 0. Similarly, (110) implies that the last integral in (116) can be bound as follows:
 |
117 |
which implies that this integral approaches 0 as τ → 0. To conclude that
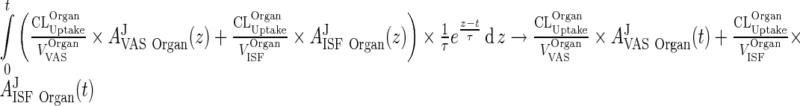 |
118 |
we observe that
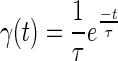 |
is the gamma probability density function which possesses the approximate identity property (22,23)
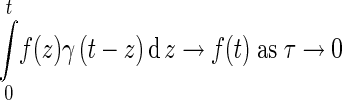 |
119 |
for any continuous function f(t). This completes proof of (114) for i = 1. The proof of cases i = 2, 3, 4 is differs only in the part:
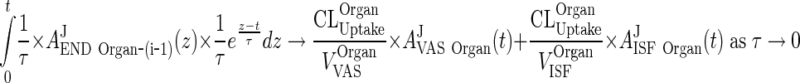 |
120 |
However, by induction, (107) implies (108) which concludes Appendix 9.
References
- 1.Scott AM, Wolchok JD, Old LJ. Antibody therapy of cancer. Nat Rev Cancer. 2012;12(4):278–287. doi: 10.1038/nrc3236. [DOI] [PubMed] [Google Scholar]
- 2.Shah B, Mayer L. Current status of monoclonal antibody therapy for the treatment of inflammatory bowel disease. Expert Rev Clin Immunol. 2010;6(4):607–620. doi: 10.1586/eci.10.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Reichert JM. Marketed therapeutic antibodies compendium. MABS. 2012;4(3):413–415. doi: 10.4161/mabs.19931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wang W, Wang EQ, Balthasar JP. Monoclonal antibody pharmacokinetics and pharmacodynamics. Clin Pharmacol Ther. 2008;84(5):548–558. doi: 10.1038/clpt.2008.170. [DOI] [PubMed] [Google Scholar]
- 5.Tang L, et al. Pharmacokinetic aspects of biotechnology products. J Pharm Sci. 2004;93(9):2184–2204. doi: 10.1002/jps.20125. [DOI] [PubMed] [Google Scholar]
- 6.Dirks NL, Meibohm B. Population pharmacokinetics of therapeutic monoclonal antibodies. Clin Pharmacokinet. 2010;49(10):633–659. doi: 10.2165/11535960-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 7.Shah DK, Betts AM. Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. J Pharmacokinet Pharmacodyn. 2012;39(1):67–86. doi: 10.1007/s10928-011-9232-2. [DOI] [PubMed] [Google Scholar]
- 8.Garzone PD, Atkinson AJ., Jr In search of physiologically based distribution volume estimates for macromolecules. Clin Pharmacol Ther. 2012;92(4):419–421. doi: 10.1038/clpt.2012.156. [DOI] [PubMed] [Google Scholar]
- 9.Brambell FW, Halliday R, Morris IG. Interference by human and bovine serum and serum protein fractions with the absorption of antibodies by suckling rats and mice. Proc R Soc Lond B Biol Sci. 1958;149(934):1–11. doi: 10.1098/rspb.1958.0046. [DOI] [PubMed] [Google Scholar]
- 10.Baxter LT, et al. Biodistribution of monoclonal-antibodies—scale-up from mouse to human using a physiologically-based pharmacokinetic model. Cancer Res. 1995;55(20):4611–4622. [PubMed] [Google Scholar]
- 11.Garg A, Balthasar JP. Physiologically-based pharmacokinetic (PBPK) model to predict IgG tissue kinetics in wild-type and FcRn-knockout mice. J Pharmacokinet Pharmacodyn. 2007;34(5):687–709. doi: 10.1007/s10928-007-9065-1. [DOI] [PubMed] [Google Scholar]
- 12.Urva SR, Yang VC, Balthasar JP. Development and validation of an enzyme linked immunosorbent assay for the quantification of carcinoembryonic antigen in mouse plasma. J Immunoass Immunochem. 2009;30(4):418–427. doi: 10.1080/15321810903188227. [DOI] [PubMed] [Google Scholar]
- 13.Chen Y, Balthasar JP. Evaluation of a catenary PBPK model for predicting the in vivo disposition of mAbs engineered for high-affinity binding to FcRn. AAPS J. 2012;14(4):850–859. doi: 10.1208/s12248-012-9395-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Abuqayyas L, Balthasar JP. Application of PBPK modeling to predict monoclonal antibody disposition in plasma and tissues in mouse models of human colorectal cancer. J Pharmacokinet Pharmacodyn. 2012;39(6):683–710. doi: 10.1007/s10928-012-9279-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cao Y, Jusko WJ. Applications of minimal physiologically-based pharmacokinetic models. J Pharmacokinet Pharmacodyn. 2012;39(6):711–723. doi: 10.1007/s10928-012-9280-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cao Y, Balthasar JP, Jusko WJ Second-generation minimal physiologically-based pharmacokinetic model for monoclonal antibodies. J Pharmacokinet Pharmacodyn. 2013 [DOI] [PMC free article] [PubMed]
- 17.Ober RJ, et al. Exocytosis of IgG as mediated by the receptor, FcRn: an analysis at the single-molecule level. Proc Natl Acad Sci U S A. 2004;101(30):11076–11081. doi: 10.1073/pnas.0402970101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mager DE, Krzyzanski W. Quasi-equilibrium pharmacokinetic model for drugs exhibiting target-mediated drug disposition. Pharm Res. 2005;22(10):1589–1596. doi: 10.1007/s11095-005-6650-0. [DOI] [PubMed] [Google Scholar]
- 19.Tabrizi M, Bornstein GG, Suria H. Biodistribution mechanisms of therapeutic monoclonal antibodies in health and disease. AAPS J. 2010;12(1):33–43. doi: 10.1208/s12248-009-9157-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nestorov IA, et al. Lumping of whole-body physiologically based pharmacokinetic models. J Pharmacokinet Biopharm. 1998;26(1):21–46. doi: 10.1023/A:1023272707390. [DOI] [PubMed] [Google Scholar]
- 21.Laurin J, et al. Assuming peripheral elimination: its impact on the estimation of pharmacokinetic parameters of muscle relaxants. J Pharmacokinet Biopharm. 1999;27(5):491–512. doi: 10.1023/A:1023286329945. [DOI] [PubMed] [Google Scholar]
- 22.Krzyzanski W. Interpretation of transit compartments pharmacodynamic models as lifespan based indirect response models. J Pharmacokinet Pharmacodyn. 2011;38(2):179–204. doi: 10.1007/s10928-010-9183-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rudin W. Functional analysis. New York: McGraw-Hill; 1973. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX 894 kb)