The Mediating Effect of Parental Neglect on Adolescent and Young Adult Anti-Sociality: A Longitudinal Study of Twins and Their Parents

Abstract

The causes of correlation between parental treatment and offspring behavior are ambiguous since genetic and social factors are correlated in typical family studies. The problem is complicated by the need to characterize the effects of genes and environment on both juvenile and adult behavioral outcomes. A model is developed for the resemblance between juvenile and adult twins and their parents that allows some of these effects to be resolved. Data on childhood adversity, parental antisocial behavior, and longitudinal adult and juvenile anti-social behavior were obtained from 1,412 families of adolescent and young adult twins. A structural model is fitted that allows for the effects of genetic and social transmission of information from parents to children. Environmental effects of parents may be mediated through measured features of the home environment. Parameters were estimated by diagonal weighted least squares applied to the 33 distinct polychoric correlations between relatives and between variables within and between ages. Sub-hypotheses were tested. Results confirmed that effects of genes and environment were both highly significant. Genetic effects were large in juveniles and largely age and sex-specific. Approximately 30% of the variation due to the shared environment was due to the effect of childhood adversity. The remaining shared environmental effects are unexplained. Adversity is affected significantly by maternal anti-social behavior. The correlation between paternal ASP and adversity may be explained by antisocial fathers selecting (or creating) antisocial mothers. All significant environmental effects of parental ASP are mediated through the measure of adversity. Though transmission of ASP is both genetic and social, passive genotype–environment correlation is very small. Assortative mating for ASP has barely detectable consequence for the genetic correlation between siblings. The longitudinal study of twins and their parents makes it possible to demonstrate there is a direct causal effect of childhood adversity on child conduct disorder over and above any indirect genetic correlation.

Introduction

Family-level risk factors such as inter-parental violence, inconsistent parenting and parental neglect are important to understanding the development of conduct disorder (CD, e.g., Rutter et al. 1998; Farrington and Loeber 2000; Johnson et al. 2004; Hoeve et al. 2009; Jaffee et al. 2009). A recurrent problem in epidemiological studies is the ambiguity attending the attribution of cause, especially when the salient environmental factors involve the behavior of parents. In theory, the association between childhood outcomes and parental treatment may be a secondary consequence of the indirect genetic correlation (IGC) between anti-social parents and their children and have nothing to do with the direct causal environmental treatment effect (DCE) of antisocial parents on their children (see e.g., review in Silberg and Eaves 2004). The problem of resolving the genetic and social correlation between children and their parents is especially potent in the study of anti-social behavior since indices of the home environment, such as maternal smoking or child neglect may themselves be manifestations of genetic liability to anti-social behavior in parents. The current paper illustrates one approach to resolving IGC from DCE through the longitudinal study of twins and their parents, “LTAP.”

There is no “perfect” strategy for resolving the effects of parental genes and treatment. However, the longitudinal study of adoptees with their foster- and biological parents has compelling simplicity. Limiting factors are sample size and representativeness in a culture where adoption is relatively infrequent and atypical. Furthermore, non-random placement of adoptees with respect to genetic similarities with their adopting parents vitiates most of the inherent appeal of the adoption paradigm.

The search for alternatives to the adoption study has led in two main directions. A first alternative is the study of the children of twins (“COT”, Nance and Corey 1976; Haley et al. 1981; Eaves 1982; Heath et al. 1985; Silberg and Eaves 2004; Rutter et al. 2001; D’Onofrio et al. 2003) in which MZ and DZ uncles and aunts are informative about the roles of non-genetic factors in parent–offspring similarity. The COT has obvious appeal for its apparent simplicity and for the fact that, at first sight, it avoids the problem that parents and offspring may be assessed at different stages of development. A deeper examination of the COT design reveals complications that, while not necessarily insoluble with care, mitigate what are often perceived as transparent advantages. The first problem is that mating may not be random. Correlations between husbands and wives undermine the simple pattern of genetic correlations between generations on which the success of the simplest analysis of COT data depend. This difficulty has long been recognized and the COT design, together with the spouses of twins provides, in theory, one method for identifying the genetic and social causes and consequences of assortative mating (Eaves and Heath 1981; Heath et al. 1985; Heath 1987). The second problem has been less widely understood and has only recently been recognized (Eaves et al. 2005b), namely, that the usual models for the role of the environment in COT depend critically on the assumption that the measured environment does not depend on the behavior of both parents. If the home environment is dyadic, i.e., depends on the behavior of both parents, conventional regression analyses of COT data do not resolve the ambiguity of the causes of association between home environment and juvenile outcome. The implications of this problem for the modeling and resolution of the family environment have still to be explored rigorously.

A further strategy is the study of twins and their parents (TAP) (Young et al. 1980; Fulker 1982) in which (juvenile) twins are studied to resolve the genetic and shared environmental components of juvenile behavior and their parents are assessed to provide indices of family genetic risk and parental treatment. However, the simple regression of offspring behavior on measures of the home environment does not identify the causal effect of parental treatment on the behavior of their children (Turkheimer et al. 2005). This problem is critical if TAP is used to discriminate genetic and environmental effects of parents because parents and children are typically assessed at different stages of development so that different genetic effects may be expressed at different ages leading to under-identification of critical genetic and environmental parameters. Meyer et al. (2000) attempted to circumvent this problem in the study of conduct disorder by using retrospective assessments of parental conduct disorder. The problem of assessment leaves some uncertainty about the validity of otherwise compelling conclusions about the direct effect of the measured home environment.

Pending solution of how best to model data on children of twins, we present an alternative approach that appears to circumvent some of the problems of both TAP and COT as they are currently conceived. The approach introduces much of the basic algebra needed to resolve the genetic and non-genetic bases of parent–offspring association and is applied to existing data on the effect of childhood adversity on the development of anti-social behavior expressed in symptoms of juvenile conduct disorder adult anti-social personality.

The LTAP design has numerous elements that, considered separately, are unable to identify the environmental and genetic effects of parents on children. However, when these are combined in the LTAP design it is possible to resolve the DCE and IGC theories of association between parental treatment and offspring outcome. Incorporating the measured environment and the (adult) parental phenotype provides information about mate selection and the magnitude (though not the cause) of the association between parental anti-social behavior and their treatment of their children. Juvenile and adult twins provide a vehicle for resolving the effects of genes and overall family environment on individual differences in the juvenile and adult behavior. If the assessments of behavior in parents and adult children are isomorphic, then assuming there are no residual interactions of genetic differences with age or secular trends, the adult “TAP” design yields critical insight about the role of genetic differences in adult parental behavior in creating the association between measures of the family environment and parental psychopathology. The information gleaned may then be used to help identify the model for the impact of parental genes and treatment on the behavior of the same twin subjects as juveniles. Thus, cross-sectional studies of juvenile twins and their parents cannot answer the critical causal question and studies of adult twins tell us nothing about juveniles. However, when adult and juvenile twins are incorporated in a single longitudinal design, the individual components are synergistic in combination and offer significant insight about the causes of parent–offspring association.

Assessment

The structure, demographics and assessment of the VTSABD have been described elsewhere (Meyer et al. 1996; Hewitt et al. 1997; Eaves et al. 1997; Simonoff et al. 1997). The critical feature of the VTSABD is the fact that the same twins, originally assessed during adolescence with their parents have themselves been assessed in a large-scale follow up as young adults (Silberg et al. 2007). For the purposes of this analysis, we focus on three principal measures from this study.

Childhood adversity

Three measures of negative family environment associated with CD indexed childhood adversity, specifically parental neglect, exposure to inter-parental violence and inconsistent parental discipline. Childhood adversity was assessed from combined reports of mother and father (see Foley et al. 2004) and utilized three items to determine a lack of care severe enough to be recognized by individuals outside the home, including notification by others about the lack of general care for the children, illness due to insufficient parental care and failure to seek medical attention for the children when such care was necessary. Exposure to inter-parental violence was measured by child report and utilized two items to determine whether parents make physical contact (i.e., pushing, shoving or hitting) with one another during disagreements. Inconsistent parental discipline was obtained by child report to determine whether each parent maintained consistent responses to child rule breaking. Responses to the binary items were summed and used as a scale ranging from 0 to 7.

Conduct disorder

At each of the four waves of the original VTSABD twins were assessed using the parent and child versions of the Child and Adolescent Psychiatric Assessment (“CAPA”, Angold et al. 1995). At the first wave, both parents were interviewed. Subsequently, only the mother was interviewed except in cases where she was not the custodian of her children. For the purposes of this analysis, we base the assessment of juvenile CD only on the available assessments by biological mothers of the twins, to avoid complications generated by heterogeneity in the relationship between mother and child. During the longitudinal study, repeated measures were secured from the families. For the purposes of this analysis, we attempted to minimize the effects of age heterogeneity in the causes of juvenile differences. We used the DSMIII-R symptoms of conduct disorder reported by mothers for twins closest to 14.5 years of age, with a maximum deviation of 1 year in either direction from the chosen optimal age of assessment.

Antisocial personality symptoms

Adult ASP symptoms in twins and their parents were measured separately as the sum of the following seven binary items: inconsistent work behavior, failure to conform to social norms and laws, irritability/aggression or involvement in fighting or assault, failure to honor financial obligations, impulsivity, recklessness in the safety of self or others, and no long-term (>1 year) monogamous romantic relationships. Responses to the binary items were summed to form a measure of ASP, having a scale ranging from 0 to 7. Parental data were gathered by face-to-face interview at the same home visit at which the CAPA interviews were secured. Twins were assessed as young adults using the same instrument administered as part of a telephone follow-up of the original VTSABD study.

Data summary

There is no obviously superior approach to scaling the raw symptoms and indicators of adversity. Sum scores or root-transformed sum sores assume the equivalence of items. More subtle approaches to scoring, such as estimating latent trait scores using an IRT model prior to genetic analysis, were not considered because of the heterosced-asticity of scores arising from the clustering of item difficulty for psychiatric symptoms (see e.g., Eaves et al. 2005a). Although it is theoretically possible to estimate the parameters of the IRT model at the same time as those of a model for family resemblance using Markov Chain Monte Carlo methods (Eaves et al. 2005a). The programming required to accomplish this goal with the current data structure has still to be accomplished. For the purposes of this analysis, the raw symptom counts for adult anti-social personality, juvenile conduct disorder and indicators of environmental adversity were recoded into three ordered categories: 0, 1 and >1 symptoms. Some information is sacrificed by collapsing all subjects displaying >1 symptom into a single category but the proportion of extreme subjects is relatively small. All the approaches to scaling considered here make the untested assumption that the latent trait is continuous and unidimensional.

The similarity between relatives for the measures was summarized by computing the polychoric correlation for each relationship. Correlations were computed using every possible pairing that could be generated for a given relationship. Thus, a pair of twins and their mother contributed two observations to the estimated correlation. Polychoric correlations and estimates of their asymptotic standard errors (a.s.e’s) were obtained by adding the option “PLCORR” to the SAS “FREQ” procedure (SAS 2003). This procedure treats all pairs as independent. This is not the case in our application because the same observation may contribute to several correlations. Our subsequent analysis does not take into account the loss of precision and correlations between raw statistics associated with this familial clustering of observations.

The design of the study yields the 33 unique raw poly-choric correlations summarized by category in Tables 1, 2, 3, and 4. Table 1 shows the pattern of correlation between the measured environment and behavioral outcome in adult (ASP) and juvenile (CD) male and female offspring.

Table 1.

Polychoric correlations between childhood adversity and anti-social behavior of adult and juvenile offspring

Outcome	Statistic
	N	r	a.s.e.
Adult male	476	0.1506	0.0770
Adult female	513	0.2986	0.0659
Juvenile male	364	0.2276	0.1045
Juvenile female	406	0.3183	0.0824

Table 2.

Polychoric correlations between parental (adult) anti-social behavior (ASP) and childhood adversity

Relationship	Statistic
	N	r	a.s.e.
Mother–father ASP	942	0.4006	0.0370
Father ASP-adversity	489	0.2805	0.0707
Mother ASP-adversity	577	0.4121	0.0565

Table 3.

Polychoric correlations between anti-social behavior of (adult) parents and adult (ASP) and juvenile (CD) anti-social behavior of their offspring

Relationship	Statistic
	N	r	a.s.e.
Mother–adult son	977	0.2368	0.0398
Mother–adult daughter	1158	0.2126	0.0380
Mother–juvenile son	662	0.1475	0.0583
Mother–juvenile daughter	746	0.2454	0.0558
Father–adult son	761	0.1507	0.0471
Father–adult daughter	869	0.2558	0.0442
Father–juvenile son	525	0.2035	0.0671
Father–juvenile daughter	568	0.1450	0.0681

Table 4.

Polychoric correlations for juvenile conduct disorder and adult anti-social personality in YAFU/VTSABD twins

Relationship	Statistic
	N	r	a.s.e.
Twins (as adults)
MZm	243	0.5654	0.0615
MZf	333	0.5093	0.0611
DZm	137	0.2646	0.1078
DZf	154	0.4069	0.0960
DZmf	209	0.3069	0.0875
Twins (as juveniles)
MZm	169	0.8003	0.0572
MZf	225	0.8023	0.0552
DZm	101	0.5153	0.1498
DZf	92	0.4189	0.1565
DZmf	132	0.0150	0.1809
Twins (adult–juvenile)
MZm	288	0.1751	0.0879
MZf	394	0.1126	0.0848
DZm	168	0.1526	0.1284
DZf	164	0.3596	0.1101
DZmf	115	0.0595	0.1474
DZfm	113	0.0647	0.1630
Within subject (adult–juvenile)
Males	569	0.2452	0.0632
Females	674	0.1103	0.0643

The correlations are all greater than zero, confirming the widely published association between childhood adversity and anti-social behavior. The correlations are larger for juvenile outcomes and females showing modest effects of age and sex on the association. Differences in correlation may, in part, be a function of age and sex differences in measurement error.

Table 2 shows that there is marked similarity between spouses for adult ASP, foreshadowing the need to allow for the effects of assortative mating in subsequent analyses of genetic and environmental transmission.

ASP of mothers and fathers correlates significantly with their treatment of their offspring. The correlation is greater for mothers than fathers. At first sight, this finding could indicate that some of the father-treatment association is a secondary consequence of assortative mating because ASP fathers may choose ASP spouses who then provide adverse environments to their children. This issue will be addressed in more detail in the subsequent model for family resemblance.

Parent–offspring resemblance for ASB (Table 3) is generally significant, indicating that risk to anti-social behavior is transmitted, genetically or socially, from parents to their offspring. The correlations do not differ markedly or consistently as a function of the age. The mechanism of inter-generational transmission will be a focus of the ensuing model-fitting analysis.

The twin data yield correlations between twins for adult and juvenile ASB (Table 4). The longitudinal design of the study provides estimates of the cross–twin, cross–age correlations and the longitudinal stability of ASB within male and female subjects. The patterns of twin correlations by zygosity are informative about the relative contributions of genes and shared environment. Sex differences in the pattern of twin correlation indicate heterogeneity between males and females in the effects of genes and/or environment Low correlations between unlike-sex pairs with like-sex DZ pairs suggest that different genetic and/or shared environmental effects influence males and females.

The correlations in Table 4 presage some of the issues that emerge from the more rigorous analysis. The MZ correlations for conduct disorder are very large and greatly exceed the correlations for DZs. Thus, genetic factors appear to play a substantial role in risk to ASB in this age group. The correlations for DZs in juveniles are slightly, but not markedly, greater than half the corresponding MZ correlations, suggesting that the relative contributions of the shared environment to juvenile ASB, at least at this age, are small relative to the effects of genes. For adult twins, the overall correlations between MZ twins are substantial, but smaller than their counterparts in the same subjects assessed as juveniles. The DZ correlation for males is smaller, suggesting some role for genetic factors, but that for female DZ twins is only modestly less than that for MZs, implicating shared environmental factors in the etiology of ASP in women.

The correlation between juvenile unlike sex twins is close to zero, implying strongly that genes that contribute to variation in boys are different from those that affect girls. Finally, the cross–age correlations between juvenile CD and adult ASP in girls and boys are much lower than the MZ correlations within adults and juveniles. This pattern gives very strong support to a markedly different etiology for adult and juvenile anti-social behavior.

Model

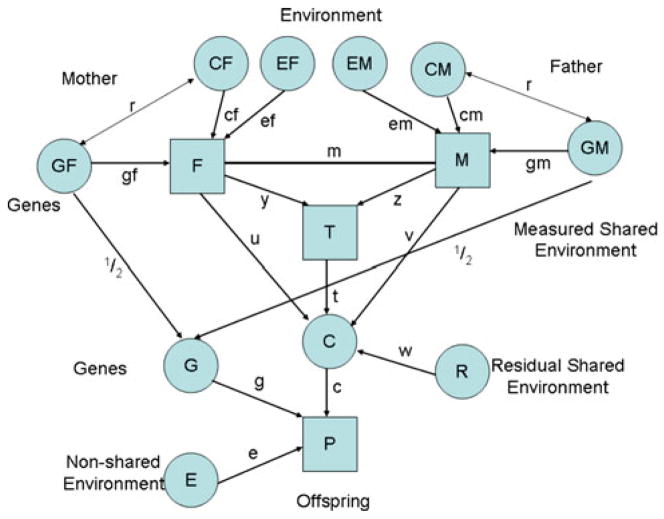
The above informal considerations may be embodied more formally in a linear structural model (“path model”, Wright 1921) for family resemblance, elements of which are summarized in Fig. 1. Measured variables are denoted by squares. Unmeasured, latent variables are denoted by circles.

Fig. 1.

Conceptual model for the effects of genes and the family environment on anti-social behavior

The figure represents one model for how latent genetic and environmental factors contribute to the correlation between the adult phenotypes of spouses and the phenotypes of their adult or juvenile offspring. The measured variables (in squares) are the phenotypes of the female (F) and male (M) parents, the phenotypes of their offspring (P) and the measured index of environment (T). The same diagram, mutatis mutandis, is applicable to both adult and juvenile outcomes.

The offspring phenotype, P, is assumed to be a (linear) function of three latent variables: (additive) genetic differences (G), “common” environment (C) shared by offspring of the same parents and unique environmental influences (E) that are not-shared with siblings in the same family. The corresponding path coefficients, g, c and e, may depend on sex and age at measurement. The full model allows for such differences.

The effects of genes and the shared environment of offspring may be traced back, in part, to the genes and phenotypes of their female and male parents. In order to maintain consistency in referencing the effects of sex on genetic and environmental pathways we use the letter “M” to refer to “male” phenotypes and paths and “F” to females. Thus, the phenotype of an (adult) mother is denoted by “F” for “female” and not “M” for “mother”. Effects of the non-shared environment, E, are assumed to be specific to individuals and uncorrelated between relatives. The genetic effects of children may be traced back to the genetic differences between their female and male parents (F and M, respectively). If genetic effects are purely additive, polygenic and autosomal, Mendelian inheritance constrains to ½ the path from parental to offspring genetic effects in both sexes. Sources of the shared environment, C, may be more complicated. Some may arise outside the family due, for example, to the fact that twins may go to the same school and shared similar social networks independently of other, measured, family influences. These residual effects on C are denoted by the latent variable R in the diagram, with path w to the shared environment. The quantity w² is the proportion of variance in C that does not depend on the parents.

The model reflects the possibility that at least some of the shared environment depends on measured aspects of the family environment. In the current application, the home environment is represented by the ASP phenotypes of mothers and fathers, F and M, respectively and by the measure of parental treatment, T. The figure represents to pathways linking F, M and T. The correlation between spouses is m. Correlations between mates are widely reported for a variety of indices of psychopathology (e.g., Merikangas 1982; Maes et al. 1998). Assortative mating has numerous consequences for familial risk. Firstly, it creates ambiguity in attempts to resolve the non-genetic influences of mothers and fathers on treatment. Second, phenotypic assortment between mates leads to spousal correlations between any latent sources of variation. For example, assortment leads to a correlation between the genetic effects of husbands and wives. In so far as the sources of variation in parents are transmitted to children, assortment will affect the next generation. If the parental phenotype is partly genetic, assortment increases the genetic correlations between siblings and parents and offspring. For traits affected by a large number of genes, assortment inflates genetic variance by producing correlations (linkage disequilibrium) between genes (Fisher 1918).

The figure shows a model for the pathways from parents to the shared environment. C may be affected directly by the ASP phenotypes of mother and father, these effects are represented by the paths u and v in the diagram for female and male parents, respectively. In addition, there are expected to be direct effects of the measured family environment, T, that are reflected in the path t from T to C. Our data (Table 2) show that T is correlated with the ASP of both parents. Thus, the model allows for the possibility that some of the environmental effects of parental ASP are mediated through the measured treatment, T. Paths y and z represent the contributions of female and male ASP, respectively, to T. We note that setting y and z to zero yields a zero correlation between T and parental phenotype. Setting t to zero does not necessarily preclude a correlation between treatment and child outcome because of the possibility that T is an index of parental ASP that may be correlated, genetically and/or socially with offspring behavior.

The possibility that parents transmit information to their children genetically and socially may lead to correlation between the genes and shared environment in offspring. This so-called “passive” genotype environment correlation is expected to persist over generations (since parents have parents of their own) and accumulate to an equilibrium value, denoted explicitly by r for parents in the figure. The equilibrium value of r is a function of other model parameters. Examples of its derivation, and the mathematical consequences of biological and cultural inheritance for family resemblance in the presence of assortative mating have been widely explored in the literature (Cloninger et al. 1979; Heath et al. 1985; Fulker 1988; Truett et al. 1994).

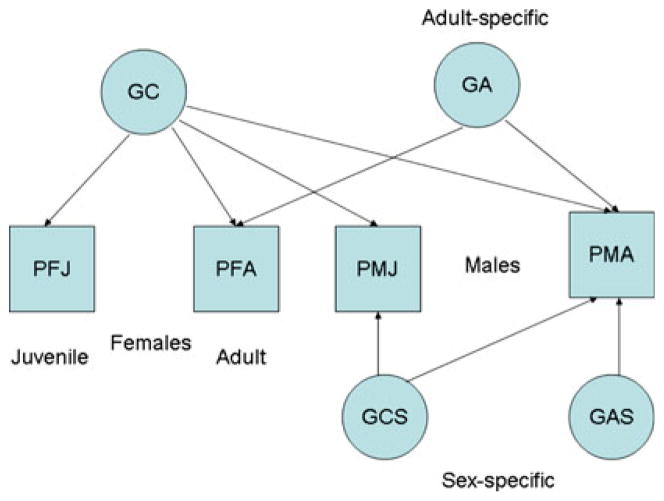
Although Fig. 1 summarizes the conceptual framework of the model, the data require a further complication. Different genes may affect the phenotypes of males and females and some genetic effects may also be age-specific. The diagram, however, assumes that the phenotypes of males and females are affected by the same, single, common set of genetic influences, G, regardless of age.

The effects of sex-limited and age-limited gene expression are incorporated by adding additional genetic components to the model (see Fig. 2). In this application we assume that there is one set of genes, GC, that has common effects on the phenotypes of both adult and juvenile males and females. Four path coefficients are estimated for this component, being the paths from GC to CD and ASP of males and females. These effects are expressed at both ages and may thus be termed “life-course persistent” genetic effect. A second set of genes, GA, is assumed to have effects specific to adult subjects, whether male or female. Two path coefficients represent the contribution of GA to male and female adult outcomes. The paths from GA to juvenile outcomes are zero because these genes only affect the adult phenotype. The effect of sex-limitation are incorporated by including two additional latent genetic effects which, while present in both males and females, are assumed only to affect the male phenotype. GCS denotes genes with life-course persistent, specific effects on males, with non-zero paths (in males) to both adult and juvenile outcomes. GAS, with a single nonzero path to the adult, male phenotype. Thus, a full model for genetic effects may involve 4 + 2+2 + 1 = 9 nonzero path coefficients.

Fig. 2.

Initial model for genetic effects

The choice to assign the sex-specific effects to males rather than females is arbitrary. The same applies to the assignment of the age-specific effects to adults. In either case, the pattern of zero and non-zero paths could be reversed, estimating instead genetic effects specific to girls and juveniles. Statistical considerations alone cannot justify the selection of either alternative. Specific hypotheses about the heterogeneity of genetic effects by age and sex may be tested by setting subsets of the “genetic” path coefficients to zero.

The genetic components are assumed to be independent in randomly mating populations. However, assortative mating will generate correlations between any genetic effects affecting the adult male and female phenotypes. Thus, sex-specific genetic effects on adults will be correlated if there is assortative mating and life-course persistent genetic effects (GC) are expected to correlate with adult-specific genetic effects (GA) if spouses are correlated. Furthermore (positive) correlation between spouses’ genetic effects will inflate the genetic correlation between siblings. In the final model (see Fig. 5; Table 6 below) in which genetic effects are sex- and age-specific, the additive genetic effects will These correlations all have equilibrium values under regular and sustained assortative mating that may be expressed in the form of non-linear constraints on the path coefficients of the model (e.g., Cloninger 1980; Heath et al. 1985; Fulker 1988; Truett et al. 1994).

Fig. 5.

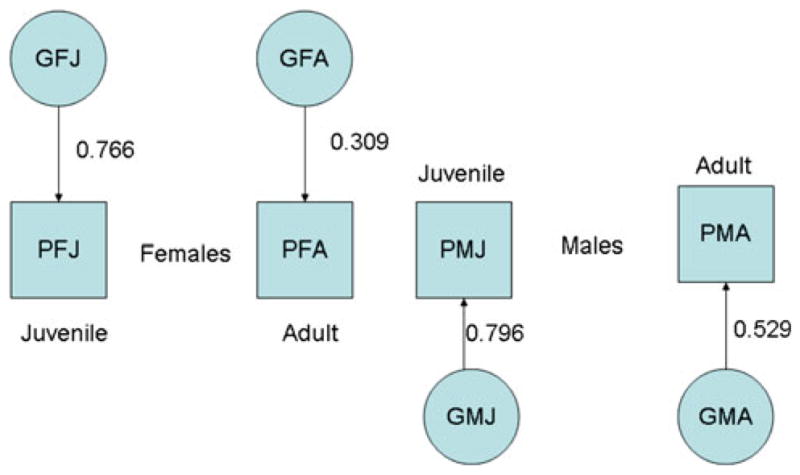
Sex- and age-specific genetic influences on adult and juvenile anti-social behavior in males and females. Note: For simplicity, the figure omits the correlations between genetic effects generated by assortative mating. The correlation between sex-specific genetic effects on adult males and females (omitted from the diagram) is estimated to be 0.0406 (c.f. Table 6)

Table 6.

Estimated passive genotype–environment correlations and sibling correlations between additive genetic components at equilibrium under assortative mating and non-genetic parent–child transmission

Component	Second sibling
	GAF	GJF	GAM	GJM	C
First sibling
GAF	0.5033	0.0000	0.0406	0.0000	0.0683
GJF	0.0000	0.5000	0.0000	0.0000	0.0000
GAM	0.0406	0.0000	0.5082	0.0000	0.0101
GAF	0.0000	0.0000	0.0025	0.5000	0.0000

Under random mating, the diagonal genetic correlations are expected to be 0.5 and the off-diagonals zero. In the absence of either genetic or non-genetic transmission the genotype–environment correlations (the last column in the table) are expected to be zero

The effects of the shared environment, c, are also allowed to be sex-specific in the full model. For the purposes of this analysis, which focuses on the effect of parental ASP and neglect we assume that the shared environmental effects are not age-specific, but we do allow the magnitudes of the shared environmental influence to be different between adults and juveniles. The residual environmental effects, e, may also be age- and sex-specific. The full model includes a path, f, from the unique environmental experiences of juveniles to adult ASP, reflecting “life-course persistent” effects of the unique juvenile environments of twins.

Model-fitting

Algebraic expectations for the 33 raw correlations were derived in terms of the model parameters and the parameters estimated numerically by constrained non-linear optimization applied to an appropriate function (“loss function”) measuring discrepancies, Δ, between the observed and predicted polychoric correlations. We minimized the weighted sum of squared residuals, using the ase’s of the raw correlations (Tables 1, 2, 3, and 4) to generate the weights. Writing s_i for the ase of the ith correlation we set the corresponding weight $W_i=1/s_i^2$ and obtain the parameter estimates that minimize $S^2={\mathit{\sum }}_i{W}_i{\mathit{\Delta }}_i^2$ subject to the non-linear constraints on the passive genotype correlation and the genetic correlations resulting from assortative mating.

The expected correlations and constraints were coded in Dr. Mike Neale’s Mx program for fitting structural models to multivariate kinship data (Neale et al. 2002). Annotated electronic copies of the code, and hence the algebraic derivations, may be obtained from the first author.

Polychoric correlations are not typically used for model-fitting to kinship data. Irregular families with multiple relatives undermine the assumption of independence between the raw correlations and tend to inflate their sampling variances while imparting undue apparent precision to parameter estimates derived from them. In principle, these problems can be accommodated by application of full maximum-likelihood to the raw response vectors (see e.g., Lange et al. 1976). However, full ML has its own practical and pedagogical drawbacks. These include: (1) the difficulty of constructing an overall test of goodness of fit of the model for a large number of correlations between relatives and variables; (2) the need to estimate “nuisance” parameters such as multiple thresholds whose (mis-)specification may contribute to errors of inference about family resemblance based on likelihood ratio; (3) the relatively large amount of computer time required for evaluation of a single model. This problem is exacerbated by the need to compare different sets of starting values in the attempt to check model identification. By contrast, fitting virtually any version of the model to the polychoric correlations takes only a few seconds on the typical laptop computer by diagonal weighted least squares (DWLS). From a pedagogical perspective, raw correlations provide a convenient basis for discussion of the data and its likely interpretation and yields a simple approach evaluating the fit of the model by comparing observed correlations with their expectations under a given model. Such information is usually less accessible in approaches that rely on fitting models to raw data from complex data structures.

Results

Model comparison statistics based on imposing additional constraints on the full model are summarized in Table 5. The goodness of fit χ² is given for each sub-model with its associated df (k) and the change, Δχ², associated with each potential model simplification is reported with its associated df Δk. The residual sums of squares are expected only to approximate the chi-square distribution because the errors are not truly independent and normally distributed when DWLS is applied to estimates of polychoric correlations. Typically, estimates and tests based on WLS are not greatly misleading when compared with those derived by applying full ML to the same data although tests of significance tend to be conservative (c.f. McGue et al. 1987). In conducting tests of significance, we confine ourselves to inferences based, for the most part, on strategically important groups of parameters that have substantive implications for how the relationship between parents and offspring are construed. Since final estimates are based on some post hoc model reduction, parameter estimates may be biased by the effects of parameters dropped from the model and their estimated sampling errors may appear misleadingly small.

Table 5.

Model comparison statistics

Constraints	Model description	χ2	k	< P%	Δχ2	Δk	< P%
1. Nonea	Full model	24.870	12	2½	NA	NA	NA
2. c = u = v = t = w = 0	No shared environment	47.315	20	½	22.445	8b	½
3. u = v = 0	No direct parent–child environment transmission	25.517	14	2½	0.647	2	75
4. t = 0	No direct effect of adversity on shared environment	33.479	13	½	8.609	1	½
5. y = z = 0	No parental effects on adversity	92.782	14	½	67.912	2	½
5a. z = 0	No direct paternal effect on adversity	27.074	13	2½	2.204	1	25
5b. y = 0	No direct maternal effect on adversity	46.249	13	½	21.379	1	½
6. w = 0	No non-parental effects on shared environment	29.484	13	1	4.614	1	5
8. f = 0	No persistence of unique environmental effects	26.096	14	2½	0.613	2	75
9. t = 1	All shared environment mediated through adversity	35.371	13	½	10.501	1	½
10. g = 0	No genetic effects	115.659	21	½	90.789	9	½
10a.	Genetic effects all age- and sex-specific	27.936	17	½	3.066	5	75

^aWhenever implied by the model, genotype–environment correlations and sibling correlations for additive genetic effects are constrained at their equilibrium values throughout

^bSee textual comment on df for this change in the model. Tests that involve setting c and/or g to zero assume that all shared environmental or genetic effects are set to zero, for both sexes and ages. Setting f to zero implies that effects of the individual unique environment, e, are entirely age-specific

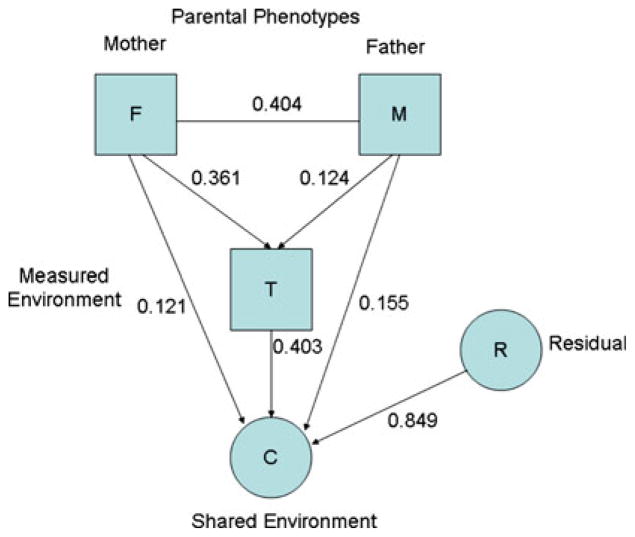
DWLS estimates of the parameters of the full model are summarized diagrammatically in Figs. 2, 3, and 4. Assortative mating is expected to increase the additive genetic correlation between siblings above the value (½) expected under random mating and to generate genetic correlations between components that are otherwise genetically independent, such as age-specific genetic effects. In so far as the treatment provided by parents depends on genetic differences in their ASB it is expected that there will be passive genotype-environment correlation. Values of the passive genotype and environmental correlations and the sibling correlations for the genetic components that satisfy the equilibrium constraints can be derived from their algebraic expectations. These are given in Table 6, based on parameters of the full model.

Fig. 3.

Estimated contributions of parents and residual effects to the shared environment of twin offspring

Fig. 4.

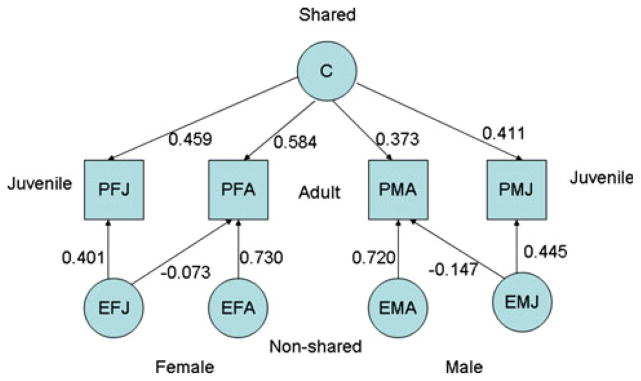
Effects of the unique and shared environment on adult and juvenile anti-social behavior and females

The overall goodness-of-fit ${\chi }_{(12)}^2$ is 24.87 for the full model (P < 2.5%, c.f. Table 5) indicating a marginally poor fit. Much of the residual SS is attributable to a handful of correlations for which the weighted deviations are large. The most prominent discrepancy is that for the adult father-son correlation (observed r = 0.151, expected r = 0.280, $W_i{\mathit{\Delta }}_i^2=7.546$) and, by itself, is sufficient to explain the significance of the goodness-of-fit chi-square. There is no a priori reason for this difference.

The fit of the model is significantly worse when all the “shared environment” parameters are set to zero ( ${\chi }_{(8)}^2=22.45$, P < 0.5%, Model 2, Table 5). The “8 df” for this change is conservative, based on counting all the parameters affecting C. However, as the four paths from C to phenotype approach zero, the other parameters (t, u, v and w) are undefined. The direct effects of parental ASP (paths u and v in Fig. 1) are close to zero and not significant (Model 3, ${\chi }_{(2)}^2=0.65$, P < 75%) and support the view that any non-genetic effects of parental ASP on the anti-social behavior of their offspring are mediated through their influence on the measured treatment variable. The effect of the measured treatment, T, is significant ( ${\chi }_{(1)}^2=8.61$, P < 0.5%, P < 0.5%, Model 4) with the significant contribution of maternal ASP (Model 5b, y = 0.355, ${\chi }_{(1)}^2=21.38$, P < 0.5%) exceeding the non-significant contribution of fathers (Model 5a, z = 0.134, ${\chi }_{(1)}^2=2.24$, P < 25%). Setting w to zero is a test of whether all shared environmental effects can be attributed to the effects of parental ASP and treatment. The residual effects on the shared environment, though numerically large, are only marginally significant (Model 6, ${\chi }_{(1)}^2=4.61$, P < 5%).

Effects of the unique environment, which include errors of measurement, are mainly age-specific since the paths, f, from EJF and EJM to PAF and PAM respectively are small and non-significant (Model 8, ${\chi }_{(2)}^2=0.61$, P < 75%). Effects of the shared environment on anti-social behavior are greater in females and males in adults and juveniles, and virtually absent in adult males.

The full model for genetic and environmental effects (Table 5, Model 1) is complex. Considered as a whole, genetic effects cannot be deleted from the model (Table 5, Model 10, ${\chi }_{(9)}^2=90.79$, P < 0.5%). However, the individual contributions of genetic effects are highly idiosyncratic in our data. Genetic effects on liability to CD in juveniles are large, but the DZmf correlation is close to zero implying profound sex differences in the biological origins of juvenile anti-social behavior. Genetic effects on juvenile ASB show very little persistence into young adulthood, each explaining less than 10% of the total variance in adult ASP. The data are consistent with a model that assumes genetic effects are completely specific by age and sex as the cross-age, cross-sex paths can be set to zero without adverse effect on fit (Model 10a, ${\chi }_{(5)}^2=3.07$, P < 75%). Subsequent discussion of the results is based on this Model (10a) which is the full model described under “Model” above, with the added constraint that all the genetic effects are age- and sex-specific.

Model 10a yields coherent estimates for the parameters of the model and may be adopted as a working model for the transmission of risk to ASB from parents to their juvenile and adult offspring. To simplify discussion, the parameters are summarized separately for measured and unmeasured components of the shared environment (Fig. 3), effects of the shared and unique environment on phenotypic outcomes (Fig. 4) and genetic effects on the outcomes (Fig. 5).

The model summarized in Figs. 3, 4, and 5 has implications that are not immediately apparent from the figures. Assortative mating will generate correlations between any otherwise independent genetic components that affect the adult phenotype involved in mate selection. Assortment also inflates the genetic correlation between siblings (DZ twins) for genes that affect choice of mate. These effects are proportional to the intensity of assortative mating and the heritability of the phenotype (Fisher 1918). The combined effect of genetic transmission and non-genetic influence of the parental phenotype is expected to generate passive genotype-environment correlation (e.g., Cloninger 1980; Fulker 1988). Table 6 summarizes the impact of these two processes on individual differences in ASP and CD. Assortative mating will not have any effect on genetic factors that are expressed only before the age of mate selection. Thus, the sibling correlations between “juvenile-specific” genetic factors (GJF and GJM) are expected to be ½ (c.f. Table 6). Assortment will not lead to any correlation between the juvenile-specific effects and other genetic components (c.f. Table 6). In our data with relatively marked assortment but only modest genetic effects on adult ASP the genetic consequences of assortment are slight, leading to a virtually undetectable excess in the sibling correlation and the correlation between functionally independent genetic components of the adult phenotype. The findings for passive rGE are comparable. The rGE is expected to be zero for any genetic effects that do not influence the parental phenotype (i.e., the juvenile-specific effects, Table 6). Even though there is a significant genetic component to the adult phenotype and detectable non-genetic transmission mediated through the measured environment, the ultimate magnitude of the genotype–environment correlation is very small. This result is seen in the small correlations between C and the adult genetic components, GAF and GAM (Table 6).

Discussion

Methodologically, the TAP design had been all but “written off” as a vehicle for disentangling the role of the measured home environment in mediating parental effects on the behavior of juvenile behavior because it could not be assumed that the same genetic effects were affecting both adult and juvenile measures. By itself, TAP cannot resolve the direct causal effect (DCE) of the measured home environment on juvenile outcome from the secondary, indirect genetic correlation (IGC) due to the fact that the same genes that affect the way parents treat their children also affect the outcome in their offspring. One attempt to overcome some of these problems involved the use of retrospective assessments of juvenile behavior in the parents (Meyer et al. 2000). Given the difficulties attending the acquisition of large adoption samples, the children of twins (COT) study had been widely assumed to provide the necessary resolution of genetic and non-genetic effects of parents on children. However, if the home environment is dyadic, i.e., an aggregate of the behavior of both parents, the attribution of causation even in the COT is far from straightforward (Eaves et al. 2005a, b).

Our analysis illustrates a complementary approach that promises additional tests of causal hypotheses that have so far eluded proponents of other family-based approaches. We show that the study of twins and their parents, when the twins are assessed both as juveniles and adults, provides additional leverage on the causes of intergenerational correlation that may allow us to resolve genetic effects and the direct and mediated non-genetic effects of parental behavior on the behavior of their juvenile offspring.

When the various components of the design are present in the same overall study, they have a synergistic effect on our ability to resolve different components of parent–offspring correlation. The use of MZ and DZ twins provides the initial leverage on the contributions of genes and shared environment. Assessment of the parental phenotype and shared environment allow aspects of the otherwise unspecified shared environment to be explored. However, the possible confounding effect of passive genotype–environment correlation cannot be identified without making additional assumptions about the genetic relationship between adult and juvenile behavior. By including adult twins as well as juveniles, it becomes possible to assess the roles of the parental phenotype on the measured environment and identify any possible source of passive genotype–environment correlation. The final critical component of the longitudinal TAP design is the assessment of the same twins as adults and juveniles. The pattern of cross-temporal correlation provides an opportunity to resolve genetic effects that persist over the assessment period from those that are expressed only in adulthood.

Although we have underscored the advantages of comparable assessments of parents and twins as adults, there is no final guarantee that the same genetic differences are expressed in parents and their adult children because of long-term age-dependent genetic effects and the interaction of genetic differences with secular changes. Our ability to resolve the various components of the model is critically dependent on the assumption of equilibrium under assortative mating and non-genetic inheritance. Rapid inter-generational changes in the pattern of mate selection or the form of non-genetic transmission will undermine the validity of this assumption. In practice, we note that the degree of assortment for ASP has very little impact on the genetic resemblance between relatives (Table 6) and that the passive genotype–environment correlations generated by the impact of differences in parental rearing practice are generally small.

Generally, the parameter estimates of the full model are sensible and do not violate, or attempt to violate, any obvious numerical or intuitive boundaries. Our results for different models are broadly consistent with the patterns in the data. However, the model for the correlations is nonlinear and subject to complex non-linear constraints imposed by the equilibrium conditions on the passive genotype–environment correlations (“r” in Fig. 1; see Table 6) and the correlations between genetic effects implied by assortative mating (Table 6). The problems of escaping local minima and establishing model identification are not trivial. Convergence was rapid from some sets of trial values, and standard numerical criteria gave no hint of an identification problem. However, from other trial values convergence was slow, or not apparent, or on a worse solution that those shown.

The study employed instruments based on recognized assessments of symptoms of adult anti-social personality and juvenile conduct disorder. Many of the components of child adversity are incorporated in the assessment of ASP. These items were excluded from the symptom counts for ASP. Application of the “OR” rule to maternal and paternal interviews for determining the presence of specific items of adversity may result in a bias towards maternal influence because there are more missing fathers than missing mothers. In principle, the maternal and paternal components of the adversity assessment could be separated and the model modified. However, separation of the maternal and paternal assessments of adversity would generate more than 20 further unique correlations within and between assessments and necessitate many additional model parameters and comparisons that may not add greatly to the overall pattern of results.

A critical issue for understanding and treating adolescent anti-social behavior is the extent to which apparent “environmental” correlates of child behavior are indeed environmental and causal. In typical family and epidemiological designs, the causal effects are confounded with secondary associations due to the correlation between the way parents treat their children and the genetic risk they transmit to their children. Our analysis of longitudinal data on twins and their parents (“LTAP”) provides both methodological and substantive insight about the complex causes of association between parental treatment and juvenile behavior.

Substantively, the data imply that genetic differences in parental anti-social personality alone cannot explain the correlation between parental treatment and offspring conduct disorder. The model-fitting results imply strongly that there is a significant direct path from adversity to offspring anti-social behavior because the path “t” in the model cannot be set to zero.

The design and analysis yield further insight about the effects of the shared environment on juvenile anti-social behavior. Firstly, a significant proportion, perhaps as much as 70% (w² = 0.72), of the shared environment is due to factors that are not explained by the measurement of childhood adversity.

Second, the small and non-significant estimates of the direct paths from parental ASP to shared environment (u and v can be set to zero without marked deterioration in fit) imply that the impact of parental ASB on adversity is, apparently, sufficient to account for the environmental effect of the parental ASB phenotype on the behavior of their children.

Third, the raw correlations between parental ASP and adversity are significant for both mothers and fathers, using the definition of “adversity” we adopted through use of the “OR” rule applied to reports by both parents to assess components of adversity. However, spouses are highly correlated and the raw correlation between adversity and paternal ASP is lower than that of maternal ASP. It is not certain whether the apparent influence of fathers on adversity is the direct effect of their own behavior or, at least in part, a secondary affect of the fact that ASP fathers choose ASP mothers who create adversity for their children. There is no doubt that maternal selection of fathers who create adversity cannot explain the association since the path from maternal ASP to adversity (y in Fig. 3) cannot be set to zero. On the other hand, the direct effect of fathers on treatment is smaller and barely reaches statistical significance in these data. This result is also theoretically important because it implies that parental treatment is a dyadic variable, depending on the behavior of both parents and the actual causal association between parental behavior and the way they treat their children needs to be resolved from any secondary association resulting from the process of mate selection.

Fourth, although there has been considerable theoretical attention to the potential importance of “passive genotype–environment correlation”, P-rGE, as a factor in behavioral development, our data suggest that the effects of P-rGE are relatively small even in a context where we might expect effects to be larger. Similarly, even though there is a marked and significant correlation between mates for antisocial behavior, our analysis shows that it has little effect in the distribution of genetic differences among children in the next generation.

All these critical facets of parent–child interaction must be viewed on the context of the other sources of variation in risk to adolescent conduct disorder. A substantial portion of the environmental influences on ASB are specific to individuals (the paths from the “E” variables in Fig. 3 are quite large). However, there is little indication that the individual, non-shared, environmental influences in adolescence have any lasting effect (the cross-age paths from EFJ and EMJ to the adult outcomes are relatively small). The model for the shared environment, however, is consistent with the effects of the shared environment, including those of adversity, are substantial and persistent especially in girls. Those in boys, though not trivial, are more modest and confined more to adolescence.

Finally, the data show that genetic effects on anti-social behavior cannot be ignored. Deletion of all genetic effects from the model leads to greater discrepancies between observed and predicted correlations than any other reduction of the model. Beyond this, however, we see that genetic effects on ASB are markedly sex- and age-dependent. The implications of this finding are profound. Firstly, any correlation between parental ASP and offspring CD is likely to be better understood in terms of environmental transmission than in terms of secondary genetic resemblance. On the other hand, as children mature into young adults, hitherto unexpressed genetic liability to anti-social behavior may be expressed. The increase in the genetic component of the parent–offspring correlation as children grow up has been noted many times in studies of IQ (e.g., discussion in Fulker 1979). Paradoxically, errors of measurement notwithstanding, the genetic contribution to liability in CD is large in both boys and girls. However, it is almost entirely age and sex-specific. Any attempt to “find” specific genes affecting risk to adolescent anti-social behavior has to deal with this specificity and recognize that solving the “genetic” problem in adolescence may have little to do with long-term outcomes. On the other hand, if the model is to be believed, the data are consistent with a relatively long-term impact of environmental adversity and imply that a focus on environmental prevention and intervention may bear more lasting fruit.

It is vital not to overstate potential preventive or therapeutic implications of any model for family resemblance. The way a model is drawn is not atheoretical and may influence the way its conclusions are translated. For example, in our case, the apparently greater path from the maternal phenotype to treatment might target intervention through counseling mothers about how better to care for their children. The role of fathers emerges as quantitatively smaller and statistically barely significant. The principal source of father–treatment correlation is identified with the phenotypic correlation between spouses that, under our model, is attributed to the relatively neutral and long-term influence of assortative mating. Our view of the etiological and therapeutic issues would change if the spousal correlation were viewed as a consequence of the direct effect of male ASP on that of their partners. In this case, the path to avoidance of adversity may be helping mothers to resolve the complication of living with an anti-social spouse. Other models and approaches are needed to resolve the effects of assortative mating from spousal interaction (e.g., Heath 1987).

Although the VTSABD is one of a handful of relatively large LTAP studies and has many strengths, we recognize that the sampling errors attached to parameter estimates are large and that the power of tests of subtle effects such as those of age and sex on the expression of genes and environment may be relatively low. We also recognize that no one study design can yield assured conclusions that are likely to be trustworthy when realized from the convergent evidence of difference designs, such as the LTAP and COT. At this point, however, few studies, if any, have all the characteristics desirable for a fully credible answer. That being said, the LTAP design, allied to some form of the model we present, offers a striking opportunity to resolve critical issues about the causal impact of parents on children that remain elusive in more conventional studies of family resemblance and cross-sectional studies of juvenile twins and their parents.