Modeling Extended Twin Family Data I: Description of the Cascade Model

Abstract

The classical twin design uses data on the variation of and covariation between monozygotic and dizygotic twins to infer underlying genetic and environmental causes of phenotypic variation in the population. By using data from additional relative classes, such as parents, extended twin family designs more comprehensively describe the causes of phenotypic variation. This article introduces an extension of previous extended twin family models, the Cascade model, which uses information on twins as well as their siblings, spouses, parents, and children to differentiate two genetic and six environmental sources of phenotypic variation. The Cascade also relaxes assumptions regarding mating and cultural transmission that existed in previous extended twin family designs. The estimation of additional parameters and relaxation of assumptions is potentially important, not only because it allows more fine-grained descriptions of the causes of phenotypic variation, but more importantly, because it can reduce the biases in parameter estimates that exist in earlier designs.

Perhaps the most salient characteristic of behavioral genetics vis-à-vis other social science fields is its extensive use of structural equation models as a means of testing hypotheses of interest. This represents a significant strength of the field, but is not without its drawbacks. Among the advantages of using such models is that they necessitate consideration and description of hypothesised causal processes, they direct focus to effect sizes rather than p values, and they lend themselves to explicit disclosure (and hopefully testing) of assumptions upon which model conclusions rest. A potential drawback of such models could be termed ‘parameter reification’, which occurs when researchers become lulled into viewing parameter estimates — usually from time tested, widely used models — as being the underlying parameters themselves rather than imperfect and potentially biased reflections of the true parameters. The quality of estimates always depends upon how well a particular model and its assumptions reflect reality. Thus, a worthwhile goal of behavioral scientists in general and behavioral geneticists specifically should be the development of models that require fewer and less stringent assumptions, increasing the accuracy and decreasing the bias of parameter estimates.

The purpose of the present article is to introduce a new extended twin family design (ETFD) model — the Cascade model — which makes fewer assumptions than previous ETFD models and therefore potentially produces less biased and more accurate parameter estimates. However, the Cascade is by no means the definitive model of individual differences, and to this end we present the logic and algebra underlying this and other ETFD models so that future researchers can build on the Cascade in the same way that we have built on previous (e.g., the Stealth) models. ETFD models, including the Cascade, are not overly difficult conceptually, but they are complex and the algebra can be tedious, which may explain why papers have not previously described such ETFD models in the detail we do here. We will attempt to provide insight into the Cascade and how it works when possible, but no amount of explanation can substitute for working through the path diagrams and algebra first hand. As such, this paper serves as a guide and tutorial for those wanting to learn about the Cascade and ETFD models. Our treatment assumes basic knowledge of behavioral genetic methods and structural equation modeling; for an introduction, see Carey (2002).

We begin by examining the logic, algebra, assumptions and potential biases of the classical twin design (CTD), the nuclear twin family design (NTFD), and the Stealth model. We use these, and particularly the NTFD, as springboards for explaining the Cascade model. As we progress, the number of assumptions for the models decreases. This should correspond to parameter estimates that are less biased. However, fewer assumptions also means more complicated models, creating a potential for over-fitting (‘reading into the tea leaves’). We therefore keep one eye on the benefits and another on the costs as the complexity of the models increases.

The Classical Twin and Nuclear Twin Family Designs

By far, the most commonly used model to infer genetic and environmental causes of variation in behavioral genetics is the classical twin design (CTD), which uses observed covariances between just two types of relatives, monozygotic (MZ) and dizygotic (DZ) twins, to estimate the variation due to additive genetic (V_A), dominance genetic (V_D), and common (V_C) and unique (V_E) environmental effects. The interpretation of these and other variance components are shown in Table 1. However, a model has no unique solutions, or is under-identified, when the number of parameters to be estimated is greater than the number of non-redundant pieces of information used to estimate them. The CTD is such a model: there are more parameters to be estimated — V̂_A, V̂_D, and V̂_C — than pieces of information to estimate them — the MZ covariance, CV̂(MZ, MZ), and DZ covariance, CV̂(DZ, DZ). (We follow the convention that V̂_O is the estimate via observation of a sample or deduction of the unknown population parameter V_O). V̂_E is estimable in all models simply from V̂_P – CV̂(MZ, MZ) and so is not focused on here-after. To circumvent this under-identification problem, behavioral geneticists routinely assume that either V_D (when CV̂(MZ, MZ) < 2CV̂(DZ, DZ)) or V_C (when CV̂(MZ, MZ) > 2CV̂(DZ, DZ)) is zero when using the CTD. However, the ratio, CV̂(MZ, MZ): 2CV̂(DZ, DZ), in no way implies that either V_D or V_C are actually zero; this is simply an assumption born from the mathematical necessity of making the model identified, and it leads to consistent biases in V̂_A (upward) and V_D̂ and V_Ĉ (downward) when the assumption is wrong (Keller & Coventry, 2005). The CTD must make numerous additional simplifying assumptions, nine of which are listed in Table 2 along with the effects on parameter estimates when these assumptions are violated. These assumptions are rarely testable with only CTD data, and to the degree that they are not met, the CTD will produce parameter estimates that are biased, sometimes wildly so.

Table 1.

Explanation of variance components in ETFD models.

Parameter	Interpretation
VP, σ2	Phenotypic variance.
VP̃	Variance of latent phenotype upon which mates choose each other.
VA	Additive genetic variance; variance of marginal or average allelic effects.
VD	Dominance genetic variance; variance of effects attributable to combinations of alleles at the same locus.
VS	Sibling environmental variance; variance in nongenetic effects (e.g., peers, cohort, school, parenting style, and so on) shared between siblings and twins but not between parents and offspring.
VT	Twin environmental variance; variance in nongenetic effects (e.g., peers, cohort, classrooms) shared by twins but not siblings.
VF	Familial environmental variance; variance in nongenetic effects (e.g., SES, social mores, education) passed (via ‘vertical transmission’) from parents to offspring.
VC	VS + VF; typically estimated in CTD or NTFD models.
VE	Unique or residual environmental variance; variance in nongenetic effects (e.g., peers, unique experiences, somatic mutation) that are unshared with any other relative class.
CV(A, F)	Covariance between additive genetic and familial environmental effects; arises if vertical transmission (causing VF) is a function of the parental phenotype because, for example, higher values on A create higher phenotypic values, which are passed to offspring F via vertical transmission.

Table 2.

Effects of Violating Assumptions on Parameter Estimates From the Classical Twin Design (CTD), Nuclear Twin Family Design (NTFD), Stealth, and Cascade Models

	Assumptions	Models	Typical biases if assumptions are not met
			Overestimated	Underestimated
1	Either VC = 0 or VD = 0	CTD	VA	VD, VC
2	CV(spouse) = 0	CTD	VC	VA, VD
3	CV(A, C) = 0	CTD	VC	VA, VD
4	Either VS = 0, VF = 0, or VD = 0	NTFD	VA	VF, VD
5	CV(spouse) due to primary phenotypic assortment	NTFD, Stealth	variable	variable
6	VEpi = 0	All	VD, maybe VA (CTD), VA (Stealth)	VEpi, maybe VA (CTD), VS (Stealth)
7	VA × C = 0	All	VA	VC, VA × C
8	VA × E = 0	All	VE	VA, VA × E
9	VA × age = 0	All	VA (CTD), VD (Stealth), VS (Stealth)	VA × age (CTD), VA (Stealth), VA × age (Stealth)
10	VTW(MZ) = 0	All	VA, VD	VTW(MZ)

Note: V_x = variance of X; CV (X, Y) = covariance between X and Y; X × Y = nonscalar interaction between X and Y; A = additive genetic; D = dominant genetic; F = familial environment, due to vertical transmission from parents; S = sibling environment, C = S + F = common environment; E = unique environment; Epi = epistasic; TW(MZ) = special MZ twin environment.

Since its inception, the CTD has largely been used as a way of estimating broad-sense heritability (V_A + V_D)/V_P) of human traits (Jinks & Fulker, 1970). But beginning in the 1970s and continuing to today there has also been interest in characterizing how environmental factors affect variation, and particularly in understanding how environmental influences are transferred from parent to offspring in a process referred to as ‘vertical transmission’ (Cavalli-Sforza & Feldman, 1973), a cultural (albeit blending) analog to genetic transmission (Cloninger, Rice, & Reich, 1979a, 1979b; Eaves, 1976a, 1976b). Because the CTD is poorly suited to resolving such issues, researchers sought additional sources of information and developed new models around them, including the nuclear twin family design (NTFD), which offers finer resolutions to genetic and environmental causes of human variation (Fulker, 1982).

The NTFD uses data on parents of twins in addition to MZ and DZ twins to garner two additional pieces of information — the covariance between parents, CV̂(spouse), and the covariance between parents and children, CV̂(Par, Child). These additional covariances obviate the need for three of the CTD assumptions (rows 1–3, Table 2), allowing: (1) V̂_A, V̂_D, and V̂_C to be estimated simultaneously (assuming that V̂_C is completely due to either V̂ _S or V̂_F; see next paragraph and row 4, Table 2); (2) the effects of assortative mating, measured from CV(spouse), on parameter estimates to be accounted for; and (3) the covariance between A and C that arises from assortative mating and combined genetic and vertical transmission to be differentiated from the effects of V̂_C.

There are many ways the NTFD can be parameterized (Heath, Kendler, Eaves, & Markell, 1985). Here we focus on a particular parameterization, written by the authors and similar to the Cascade model, which divides V̂_C into that which is shared between siblings and twins but not parents (V̂_S) and that which is transmitted via vertical transmission from parents to offspring (V̂_F). It should be noted that, because only three pieces of data, CV̂(MZ, MZ), CV̂(DZ, DZ), and CV ^(Par, Child) provide information on four parameters, V̂_A, V̂_D, V̂_S, and V̂_F, only three of these parameters can be estimated simultaneously in any model (row 4, Table 2). Again, if the parameter assumed to be zero is not truly zero, the estimated parameters from the NTFD will be biased, although not to the degree that CTD parameters are biased in the analogous (row 1, Table 2) situation. Some NTFD models include data on non-twin siblings, which greatly increases power of parameter estimates (Posthuma & Boomsma, 2000) and allows estimation of environmental effects shared only by MZ and DZ twins (V̂_T), but does not otherwise change the number of assumptions (Table 2) the NTFD must make.

Path Analysis of a Nuclear Twin Family

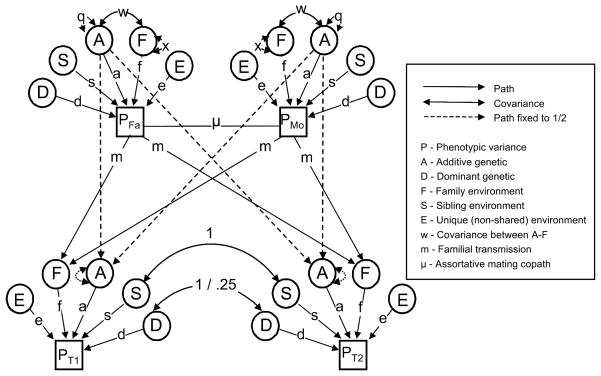
Because the Stealth and Cascade models are extensions of the NTFD, and because most of the fundamental concepts are shared between the three models, it is useful to focus first on the logic and algebra of the NTFD. Figure 1 presents the path diagram for our NTFD model. Squares denote observed and circles latent (unmeasured) variables; upper case letters simply identify variables whereas lower case letters represent path coefficients to be estimated or fixed; single-headed arrows signify causal relationships from one variable to another and double headed arrows signify covariation between two variables or between the variable and itself (i.e., variation); finally, the line connecting the two parents is a ‘copath’, representing selection between parents for similarity on the phenotype (‘like choosing like’), and has special rules as described below.

Figure 1.

Path diagram of Nuclear Twin Family Design. Note that all latent variances equal 1 (except for A and F, which equal q and x respectively) and are not shown.

Path analysis provides a systematic method for generating expected variances and covariances. To derive the expected covariance between two variables, one identifies all pathways or ‘chains’ that start at the first variable and end at the second, such that (1) a chain begins by tracing backwards, against the direction of one or more (single- or double-headed) arrow(s), (2) a chain changes direction at a double-headed arrow, and move thereafter only in the direction of single-headed arrow(s), (3) no chain goes through more than one double headed arrow (which implies that no chain changes direction more than once), and (4) no chain is counted twice. With respect to this last rule, it should be noted that order matters, such that fwa is not counted as the same chain as awf, even though algebraically they are equivalent (for an example, see equation [1] below). The expected covariance is found by multiplying the coefficients in all possible, non-redundant chains that connect two variables and summing them. Variances are found in the same manner, except that the goal is to find all chains that begin at a variable and arrive back at the same variable. As per rule 4 above, for variance caused by two other variables that are correlated, the covariance is counted in both directions.

The phenotypic variance in the NTFD is assumed to be the same for all relative classes, and so we demonstrate the above tracing rules for finding expected phenotypic variances by tracing all pathways that start and end at the paternal phenotype P_FA (top left, Figure 1). For example, consider the first chain to be aqa (the unique phenotypic variance due to the additive effects of genes) the second and third awf and fwa (the sum of the two is the phenotypic variance attributable to covariance between A and F), the fourth fxf (phenotypic variance due to familial environment), and so forth, such that the expected phenotypic variance, summing over all possible nonredundant chains, is:

$$V_P={\mathrm{\sigma }}^2=a^{2}q+f^{2}x+2\mathit{awf}+e^2+d^2+s^2$$ (1)

Note that, other than those expressed in equation (1), no other chain starting and ending at the phenotype exists that would not break one of the four tracing rules above. Note also that the latent variance of all variables is set to 1 except for A (variance of q) and F (variance of x), and that, not coincidentally, A and F are the only latent variables that have a covariance (w). The reasons for this are discussed below. Finally, note that parents, indeed all individuals, also have a sibling (S) component to their phenotypic variance, but that only siblings and twins share this variance component. For example, influences of schools might contribute to phenotypic differences in some trait; everyone, including single children, are potentially influenced by their schools, but siblings and twins are the only types of relatives likely to routinely share such influences, and to the degree this is so, school influences will be part of S.

The covariance between spouses, which is modeled as ‘primary phenotypic assortment,’ or spouses choosing partners who are like (or unlike) themselves based on their phenotypes, is:

$$CV(\mathit{spouse})={\mathrm{\sigma }}^2\mathrm{\mu }{\mathrm{\sigma }}^2$$ (2)

where μ is the assortative mating copath coefficient. Assortative mating between spouses has consequences for the variances and covariances of A and F as well as the expected relative covariances (Crow & Kimura, 1970; Eaves, 1976b), and the special rules of the copath allow these to be modeled appropriately (Van Eerdewegh, 1982). In particular, as with other paths, copaths can only be traced once in any chain, but once traversed, the four tracing rules described above are ‘reset’, allowing, for example, a second double-headed arrow to be traced.

We demonstrate the copath rules by finding the expected variance of the latent variable F (x in Figure 1). An assumption of the NTFD (required for identification but also plausible) is that the variance components in the parental generation are the same as those in the offspring generation (i.e., that the variances have reached an equilibrium). Thus, to find x, we set it to be equal to all the chains that can be traced from and back to the same F latent variable in offspring. Starting at, say, the F of twin 1, the first chain (paternal vertical transmission) travels up to the paternal phenotype (m), then up to and back from all individual latent variables affecting the father (which we have already found in equation (1), and so we can just reuse this parameter, σ²), and then back down again (m), or simply m²σ². The second chain, maternal vertical transmission, is the same, m²σ² (the assumption that maternal and paternal vertical transmission path coefficients are the same is usually relaxed in the NTFD, but it is presented this way here for simplicity). The third chain again goes to the paternal phenotype (m), up and down again to all latent variables (σ²), and then traverses the copath (μ), resetting the rules to their ‘initial state’ once across. From here it might seem legitimate to move directly back down to F (m), but this breaks the first tracing rule from above: a chain always begins by tracing backwards against an arrow. Thus, the only legitimate paths are to go up to and back from all latent variables (σ²), and finally back down to the F (m). It can therefore be seen that the final variance of F is:

$$x=2m{\mathrm{\sigma }}^{2}m+2m{\mathrm{\sigma }}^2\mathrm{\mu }{\mathrm{\sigma }}^{2}m$$ (3)

The variance of F is increased by anything that increases the phenotypic variance over time, and especially by assortative mating. At first it might seem mistaken that x is displayed in the parental generation in Figure 1 but is missing in the offspring generation. This is no mistake: the makeup of the variance in F among offspring is already implicit in Figure 1 in the form of the vertical transmission paths coming into F; to place an explicit x for the variance of F for offspring in Figure 1 would be redundant, doubling its variance over what it should be.

It might also seem mistaken that three parameters (m, x, and f,) are all used to estimate a single variance, V_F. Obviously such a situation would be under-identified. There are many workarounds; the approach taken here is to fix f = 1 and allow m to be freely estimated. x is not truly estimated, since its value is fully determined by m, σ², and μ (equation 3). Notice the circularity: σ² in equation (1) is a function of x, and x (equation 3) is a function of σ². Thus, σ² and x (along with q, discussed below) comprise a set of nonlinear constraints. Nonlinear constraints are hallmarks of most ETFD models. They describe, and constrain, the inter-relationships between estimated parameters in a way that keeps the entire model internally and logically consistent. Their values are not estimated, strictly speaking, but instead are determined by (and help to determine) estimated parameters and other non-linear constraints. Because of this, close-form solutions to ETFD models are typically impossible; their solutions usually require iterative (e.g., maximum likelihood) approaches, such as those employed in Mx (Neale, 1999).

The variance of the A latent variable, q, is also a nonlinear constraint in the context of assortativemating. The average value of offspring A is simply ½A_Fa + ½A_Mo. However, parents do not pass on their average A effects to any particular child but rather one of two discrete allelic effects per locus, and hence there is variation around the above expectation which can be found using tracing rules. In the absence of assortative mating:

$$q_{\mathit{Child}}=¼q_{Fa}+¼q_{Mo}+q_{\mathit{Seg}}$$ (4)

The q_Seg term above is called the segregation variance, representing the within-family variance in additive genetic effects caused by the randomness in which of two alleles parents pass to offspring. Since additive genetic variance will be the same across generations at equilibrium, q_Child = q_Fa = q_Mo = q, and if there is no assortative mating, q contains no nonlinear constraints and so can be set at 1. Given equation (4), this implies that q_Seg = ½ when q = 1 (i.e., when there is no assortative mating).

It has been shown that assortative mating does not change the within-family additive genetic variance, q_Seg, in polygenic characters (Rogers, 1983). Hence, we set q_Seg = ½ regardless of whether assortative mating occurs or not, denoted by dashed double-headed arrows, pointing into A of offspring in Figure 1. However, the total additive genetic variance, driven by the between-family additive genetic variance, will be altered by primary phenotypic assortment. Given that q equals 1 without assortative mating, it will be greater than 1 as a function of primary phenotypic assortative mating (Crow & Kimura, 1970; Eaves, Last, Young, & Martin, 1978). This is because spouses who are phenotypically similar tend to also have similar additive genetic effects, creating a covariance between the values of A in each parent. Offspring A is a weighted sum of the parental A values, and the variance of the offspring A will be larger for the same reason that the variance of sums is always increased by positive covariation between terms. Intuitively, inheriting positive A effects from one parent increases the probability of inheriting positive A effects from the other parent when mates choose similar mates, increasing the variance of A in offspring and hence in the population. This increase can be quantified using the tracing rules:

$$q=q_{\mathit{Seg}}+½q+½(qa+wf)\mathrm{\mu }(qa+wf)=1+(qa+wf)\mathrm{\mu }(qa+wf)$$ (5)

given that q_Seg = ½. Thus, primary phenotypic assortative mating increases the additive genetic variation by (qa + wf)²μ over what it would be without assortative mating.

Furthermore, a covariance will develop between A and F anytime both are non-zero. This is because vertical transmission passes all the constituents of the parental phenotype, including A effects, to the offspring, inducing a covariance between A and F that is accentuated in the presence of assortative mating. By tracing all the pathways from A in twin 1 to F in twin 1, or A in twin 1 to F in twin 2 (surprisingly, they are equivalent), we can find the nonlinear constraint for the covariance between A and F:

$$w=(qa+wf)m+(qa+wf)\mathrm{\mu }{\mathrm{\sigma }}^{2}m$$ (6)

The genetic and environmental variances being sought are not estimated directly, but rather are calculated by multiplying the squared path coefficients by the variances of the latent variables (V_A = a²q, V_D = d², and so on). Note the terminology: q is the variance of latent variable A whereas V_A is the additive genetic variance, and q ≠ V_A.

The covariances of the three relative types are determined using the same tracing rules discussed above, but chains are traced from one observed phenotype to another. The covariance between S of siblings are always equal to 1 and those between D of siblings are 1 for MZ twins and .25 for DZ twins.

$$CV(MZ,MZ)=a^{2}q+d^2+s^2+f^{2}x+2\mathit{awf}$$ (7)

$$CV(DZ,DZ)=a^2(q-q_{\mathit{Seg}})+¼d^2+s^2+f^{2}x+2\mathit{awf}$$ (8)

$$CV(\mathit{Par},\mathit{Child})=½a(qa+wf)+½a(qa+wf)\mathrm{\mu }{\mathrm{\sigma }}^2+m{\mathrm{\sigma }}^2+m{\mathrm{\sigma }}^2\mathrm{\mu }{\mathrm{\sigma }}^2$$ (9)

Observed MZ, DZ, and parent–child covariances or raw data can be entered into Mx or other structural equation modeling programs that can handle non-linear constraints, which typically use maximum likelihood to arrive at parameter estimates. To simplify, these programs find the fit of the solution (how close the implied relative covariances from equations 7 to 9 are to the observed relative covariances) at the start values supplied by the user. An algorithm then moves parameters in a direction that tends to increase the fit (i.e., decrease the difference between the implied and observed covariances). This process is iterated until parameter estimates converge, or change very little from one iteration to the next. In a model that fits the data well, implied and observed covariances will be similar; comparing the two can suggest places where the model is failing.

The Stealth Model

The Stealth model was developed from the NTFD as a way to improve upon its shortcoming in differentiating environmental effects within the family and to increase the power to test parameter estimates and sex effects. It was principally developed by Lindon Eaves in the mid 1980’s, and was first discussed in a paper on Church Attendance (Truett et al., 1994). The name, ‘Stealth’, comes from Lon Cardon, who commented that the path diagram looked like a ‘Stealth bomber’ (L. Eaves, personal communication). Originally written in FORTRAN, the model was transported to Mx once Mx could handle nonlinear constraints (Maes, Neale, & Eaves, 1997), and has since been extended to multivariate phenotypes (Maes, Neale, Martin, Heath, & Eaves, 1999).

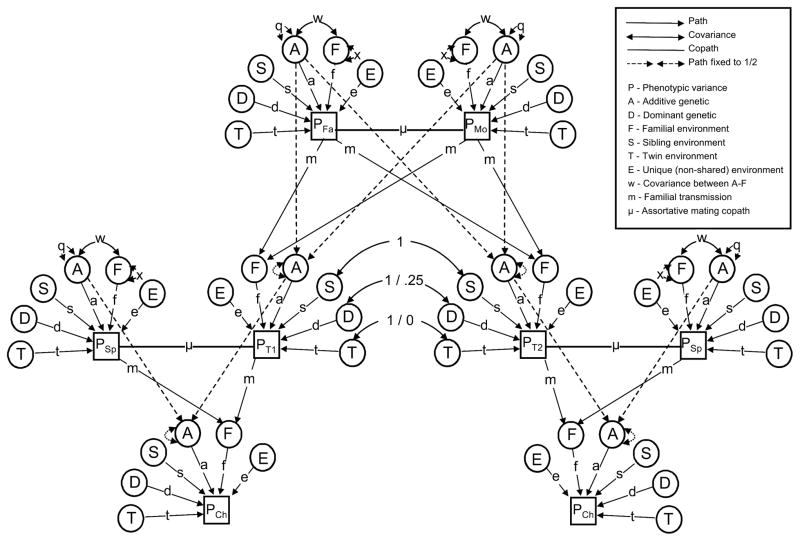
The Stealth model introduces no new concepts beyond those discussed above with respect to the NTFD. However, the amount of information and number of equations to be solved is greatly increased. By including data from twins, their parents, their offspring, and their spouses, the Stealth model models 88 relative covariances, which supplies sufficient information to simultaneously estimate sex-specific V̂_A, V̂_D, V̂_S, V̂_F, V̂_T, and V̂_E (see Table 1) as well as additive genetic variation unique to males/females and correlations between other sources of variance across sex. Many of these 88 relative classes are identical except for the fact that sex-differences must be accounted for. For example, the Stealth differentiates nephew–aunt covariances that are between sons of DZ females and female DZ co-twins from those that are between sons of DZ males and female DZ co-twins. To simplify, we do not further discuss sex effects, which reduces the number of relative classes from 88 to 17. These are shown in Appendix 1.

Figure 2 shows the Stealth model. The path diagram is identical to Figure 1 except that spouses of twins and children of twins have been added. To keep the diagram uncluttered, siblings of twins are not shown, but their covariances are simple to derive, being nearly the same as DZ twins. The same path analysis rules set forth above with respect to the NTFD are sufficient for finding the expected covariances for all 17 relative classes in the Stealth.

Figure 2.

Path diagram of the Stealth model. Note that all latent variances equal 1 (except for A and F, which equal q and x respectively) and are not shown.

There are currently three datasets with information on enough relative classes to be usable in the full Stealth model. The first consists of roughly 30,000 twins and relatives (the ‘Virginia 30K’) from the Virginia Twin Registry and from a volunteer sample through the American Association of Retired Persons, the second consists of roughly 25,000 twins and relatives from the Australian Twin Registry (Lake, Eaves, Maes, Heath, & Martin, 2000), and the third from 35,000 twins and relatives in the Netherlands Twin Registry (Boomsma, 1998). Extensive data on demographics, physical characteristics, alcohol and tobacco use, depression, personality, religious and political beliefs, intelligence, cognitive measures, and social relationships exist for these datasets.

The Stealth model has been used to analyze at least 17 phenotypes to date (Coventry & Keller, 2005), almost all on the Virginia 30K data. In general, these studies have found higher dominance and lower additive genetic effects (but only slightly lower levels of broad-sense heritability) than CTD studies on the same phenotypes, demonstrating the biases expected to exist in parameter estimates from the CTD (Keller & Coventry, 2005). Estimates of common environmental variance (V̂_S + V̂_F) were little changed (Coventry & Keller, 2005).

The Cascade Model

A potential limitation of the Stealth model is that it relies upon one particular model of mating — primary phenotypic assortment — and one particular model of vertical transmission — transmission to offspring from the full parental phenotype. Several other possibilities exist, and if they are true, then Stealth estimates will be biased in various, often difficult to predict ways (Keller et al., in prep.). With respect to mating, one possibility is that mates do not choose each other based on phenotypic similarity, but rather become more similar to each other over time. If such convergence explains spousal similarity, many of the predicted dynamics in the Stealth model, such as increases in V_A and V_F, will be incorrect, leading to biased estimates (e.g., estimates of V_A that are too high). Another commonly discussed possibility for mate similarity is social homogamy (Heath & Eaves, 1985), such that mates choose each other based on similar environmental backgrounds. For example, if people marry within religions and choice of religion is not heritable, than any similarity induced between spouses that is due to religious choice (e.g., similar views on abortion) would be due to social homogamy rather than primary phenotypic assortment. With respect to vertical transmission, it is possible that parents pass only certain (e.g., environmental) aspects of their phenotype to offspring. For example, parents might ‘pass on’ their education to their children not directly through their own education level, but indirectly, through nongenetically mediated aspects of their environment that are related to their education.

The purpose of the Cascade model is to provide a general framework for relaxing the assumptions regarding mate choice and vertical transmission made by the Stealth. The way that this is done is through use of latent phenotypes upon which spouses mate or upon which parents pass on their phenotypes. For clarity of presentation, we focus here on the mating aspect of the Cascade rather than the vertical transmission aspects of it, but it is straightforward to apply the same principles to vertical transmission. Figure 3 shows the path diagram and Appendix A shows the algebra (excluding sex effects) for the version of the Cascade that relaxes the assumptions about assortative mating but in which vertical transmission is passed from parental phenotype to offspring. The path diagrams and algebra for the model that includes sex effects and for the model that relaxes both the assortative mating and vertical transmission mechanisms are available online at the first author’s website (www.matthewckeller.com).

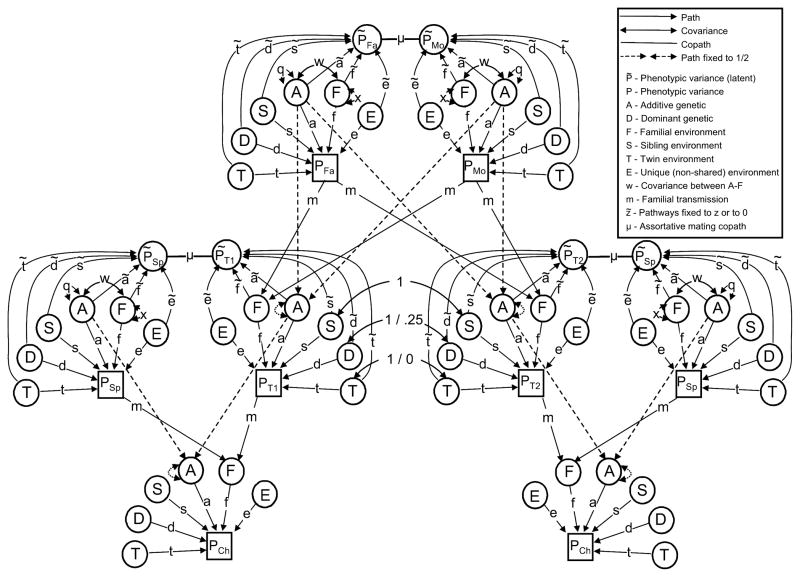
Figure 3.

Path diagram of the Cascade model. Note that all latent variances equal 1 (except for A and F, which equal q and x respectively) and are not shown.

The only difference between Figure 2 (the Stealth model) and Figure 3 (the Cascade model) is the addition of the latent phenotype (P̃) upon which mates assort. There is not sufficient information to estimate the path coefficients (e.g., ã) leading to this latent phenotype. Rather, these coefficients are set a priori by the user to reflect the type of mating system that is to be modeled. While any choice is possible, for ease of interpretation it is best to set the path coefficients to P̃ to either be equal to the path coefficients to P or to be equal to zero. For example, to model social homogamy, all genetic path coefficients to P̃ can be set to zero and all other path coefficients to P̃ can be set to the values of those to P, such that ã = 0, d̃ = 0, f̃ = f = 1, s̃ = s, t̃ = t, and ẽ = e (recall that either m or f must be fixed in order for the variance of F to be identified; here we set f to 1). The fit of this model can then be compared to a model of primary phenotypic assortment, in which ã = a, d̃ = d, f̃ = f = 1, s̃ = s, t̃ = t, and ẽ = e, and the best fitting of the two models can be chosen. In addition, convergence can be modeled (or at least approximated) by setting ẽ = e and all other path coefficients to P̃ to zero. This removes the effects of assortative mating on the genetic and familial variation, as it should, and makes intuitive sense, in that convergence is an environmental factor that uniquely affects the spouses, leading to no expected covariances between in-laws and decreasing similarity between MZ twins.

Although not shown in Figure 3, the generalization of the way in which vertical transmission occurs follows the same principles as those explained above with respect to assortative mating. This is accomplished by adding an additional latent variable, P̈, directly analogous to P̃, from which parents pass on aspects of their phenotype to offspring F via vertical transmission. The m pathways to offspring F leave from P̈ rather than from P. Again, path coefficients (e.g., ä) are set to be equal to those going to P or set to zero, and fits of the competing models can be compared.

The Stealth and Cascade models are identical when assortative mating is due to primary phenotypic assortment and when vertical transmission includes all aspects of the parental phenotype. However, by using the latent mating and vertical transmission phenotypes as explained above, the Cascade offers a much more general model of assortative mating and vertical transmission than possible in the Stealth. In this framework, the Stealth conforms to a particular subset of the models available to the Cascade. To the degree that the Stealth assumptions are unmet, the Cascade allows them to be relaxed, which should reduce bias in estimated parameters.

We have used simulation to explore the degree to which assumptions regarding mating and vertical transmission, as well as additional assumptions, including those that must be made by all extended twin family designs (e.g., no A-by-age interaction effects), affect the CTD, NTFD, Stealth, and Cascade models (Keller et al., in prep). These results demonstrate that each of these four models produce unbiased estimates when assumptions are met, but that they produce various levels of biases when assumptions are not met. These results also demonstrate that, in trying to estimate so many parameters, Stealth and Cascade models can produce estimates with higher variance than equivalent CTD or NTFD estimates, despite the huge increase in information. Despite this, estimates from the Cascade tend to be more accurate under a wider range of situations than any previous extended twin family model.

In writing this article, we have attempted to present a new extended twin family model, the Cascade, in a way that enables researchers to understand its fundamental concepts and the algebra underlying it. Our motivation has not only been to encourage researchers to use the Cascade model (the full Mx Cascade script is available at www.vipbg.vcu.edu/~sarahme/cascade/ and the extended algebra is available at www.matthewckeller.com), but also to have researchers build upon it; the Cascade is but a step in what we hope will be a longer pathway toward better, more realistic models of extended kinship. We also hope that the development of this and similar models encourages collection of datasets that include other relative classes in addition to twins. As several behavioral genetics methodologists have stressed over the years, twins alone cannot resolve many of the issues of greatest interest to behavioral scientists.

Appendix A. Algebraic Expectations From the Cascade Model

τ²: covariance between the true phenotype and the latent phenotype on which mates assort

δ: covariance between additive genetic latent factor and phenotype

μ: copath between spouses

a: additive genetic path

d: dominance genetic path

s: sibling-specific environmental path

t: twin-specific environmental path

e: unique environmental path

f: familial path – set to 1

x: variance of familial environment

q: variance of common additive genetic latent factor

w: covariance between additive genetic latent factor and familial latent factor.

z̃: pathways to latent mating phenotype (P̃). Set equal to 0 or to z to model different modes of mating.

NON-LINEAR CONSTRAINTS AND SHORTCUTS

Non-linear constraints

$q=CV(A_{MZ1},A_{MZ2})=1+{\stackrel{\sim }{\delta }}^2\mu$

$x=CV(F_{T2},F_{T2})=2m^2{\sigma }^2+2m^2{\tau }^2\mu {\tau }^2$

$CV(A,F)=CV(A_{T1},F_{T2})=CV(A_{\mathit{SIB}},F_{\mathit{SIB}})=w=\delta m+\stackrel{\sim }{\delta }\mu {\tau }^{2}m$

${\sigma }^2=a^{2}q+f^{2}x+2\mathit{awf}+e^2+s^2+d^2+t^2$

$CV(P,\stackrel{\sim }{P})={\tau }^2=aq\stackrel{\sim }{a}+fx\stackrel{\sim }{f}+aw\stackrel{\sim }{f}+fw\stackrel{\sim }{a}+e\stackrel{\sim }{e}+s\stackrel{\sim }{s}+d\stackrel{\sim }{d}+t\stackrel{\sim }{t}$

Shortcuts

$CV(A,P)=CV(A_{MZ1},P_{MZ2})=\delta =qa+wf$

$CV(A,\stackrel{\sim }{P})=CV(A_{MZ1},{\stackrel{\sim }{P}}_{MZ2})=\stackrel{\sim }{\delta }=a\stackrel{\sim }{q}+w\stackrel{\sim }{f}$

$CV(A_{DZ1},A_{DZ2})=CV(A_{\mathit{Sib}},A_{\mathit{Sib}})=q-.5$

$CV(A_{DZ1},P_{DZ2})=CV(A_{\mathit{Sib}},P_{\mathit{Sib}})=\theta =a(q-.5)+wf$

$CV(A_{DZ1},{\stackrel{\sim }{P}}_{DZ2})=CV(A_{\mathit{Sib}},{\stackrel{\sim }{P}}_{\mathit{Sib}})=\stackrel{\sim }{\theta }=\stackrel{\sim }{a}(q-.5)+w\stackrel{\sim }{f}$

$CV(A_{MZ1},P_{MZ2.\mathit{Child}})=\xi =.5a(q+{\stackrel{\sim }{\delta }}^2\mu )+mf(\delta +\stackrel{\sim }{\delta }{\tau }^2\mu )$

$CV(A_{DZ1},P_{DZ2.\mathit{Child}})=\lambda =.5a(q-.5+\stackrel{\sim }{\delta }\mu \stackrel{\sim }{\theta })+mf(\theta +\stackrel{\sim }{\theta }\mu {\tau }^2)$

RELATIVE COVARIANCES

MZ Twins

$CV(P_{MZ1},P_{MZ2})=\mathrm{\Phi }=a^{2}q+f^{2}x+2\mathit{awf}+d^2+t^2+s^2$

$CV(P_{MZ1},{\stackrel{\sim }{P}}_{MZ2})=\stackrel{\sim }{\mathrm{\Phi }}=aq\stackrel{\sim }{a}+fx\stackrel{\sim }{f}+aw\stackrel{\sim }{f}+fw\stackrel{\sim }{a}+d\stackrel{\sim }{d}+s\stackrel{\sim }{s}+t\stackrel{\sim }{t}$

$CV({\stackrel{\sim }{P}}_{MZ1},{\stackrel{\sim }{P}}_{MZ2})=\stackrel{\sim }{\stackrel{\sim }{\mathrm{\Phi }}}={\stackrel{\sim }{a}}^{2}q+{\stackrel{\sim }{f}}^{2}x+2\stackrel{\sim }{a}\stackrel{\sim }{f}w+{\stackrel{\sim }{d}}^2+{\stackrel{\sim }{t}}^2+{\stackrel{\sim }{s}}^2$

DZ Twins

$CV(P_{DZ1},P_{DZ2})=\mathrm{\Omega }=a^2(q-.5)+f^{2}x+2\mathit{fwa}+s^2+t^2+2.5d^2$

$CV(P_{DZ1},{\stackrel{\sim }{P}}_{DZ2})=\stackrel{\sim }{\mathrm{\Omega }}=a\stackrel{\sim }{a}(q-.5)+fx\stackrel{\sim }{f}+aw\stackrel{\sim }{f}+fw\stackrel{\sim }{a}+t\stackrel{\sim }{t}+s\stackrel{\sim }{s}+.25d\stackrel{\sim }{d}$

$CV({\stackrel{\sim }{P}}_{DZ1},{\stackrel{\sim }{P}}_{DZ2})=\stackrel{\sim }{\stackrel{\sim }{\mathrm{\Omega }}}={\stackrel{\sim }{a}}^2(q-.5)+{\stackrel{\sim }{f}}^{2}x+2\stackrel{\sim }{f}w\stackrel{\sim }{a}+{\stackrel{\sim }{s}}^2+{\stackrel{\sim }{t}}^2+.25{\stackrel{\sim }{d}}^2$

Siblings

$CV(P_{\mathit{Sib}1},P_{\mathit{Sib}2})=\mathrm{\Xi }=\mathrm{\Omega }-t^2$

$CV(P_{\mathit{Sib}1},{\stackrel{\sim }{P}}_{\mathit{Sib}2})=\stackrel{\sim }{\mathrm{\Xi }}=\stackrel{\sim }{\mathrm{\Omega }}-\stackrel{\sim }{t}t$

$CV({\stackrel{\sim }{P}}_{\mathit{Sib}1},{\stackrel{\sim }{P}}_{\mathit{Sib}2})=\stackrel{\sim }{\stackrel{\sim }{\mathrm{\Xi }}}=\stackrel{\sim }{\stackrel{\sim }{\mathrm{\Omega }}}-{\stackrel{\sim }{t}}^2$

Spouses

$CV(P_{\mathit{Spouse}},P_{\mathit{Spouse}})={\tau }^2\mu {\tau }^2$

Parent-child

$CV(P_{\mathit{parent}},P_{\mathit{Child}})=\mathrm{\Delta }=.5a(\delta +\stackrel{\sim }{\delta }\mu {\tau }^2)+fm({\sigma }^2+{\tau }^2\mu {\tau }^2)$

$CV(P_{\mathit{Parent}},{\stackrel{\sim }{P}}_{\mathit{Child}})=\stackrel{\sim }{\mathrm{\Delta }}=.5\stackrel{\sim }{a}(\delta +\stackrel{\sim }{\delta }\mu {\tau }^2)+\stackrel{\sim }{f}m({\sigma }^2+{\tau }^2\mu {\tau }^2)$

MZ-Nephew/Niece (MZ twin is the Uncle/Aunt)

$CV(P_{\mathit{Nephew}/\mathit{Niece}},P_{MZ})=\mathrm{\Gamma }=fm(\mathrm{\Phi }+{\tau }^2\mu \stackrel{\sim }{\mathrm{\Phi }})+.5a(\delta +\stackrel{\sim }{\delta }\mu \stackrel{\sim }{\mathrm{\Phi }})$

$CV(P_{\mathit{Nephew}/\mathit{Niece}},{\stackrel{\sim }{P}}_{MZ})=\stackrel{\sim }{\mathrm{\Gamma }}=.5a(\stackrel{\sim }{\delta }+\stackrel{\sim }{\delta }\mu \stackrel{\sim }{\stackrel{\sim }{\mathrm{\Phi }}})+fm(\stackrel{\sim }{\mathrm{\Phi }}+{\tau }^2\mu \stackrel{\sim }{\stackrel{\sim }{\mathrm{\Phi }}})$

DZ-Nephew/Niece (DZ twin is the Uncle/Aunt)

$CV(P_{\mathit{Nephew}/\mathit{Niece}},P_{DZ})=\mathrm{\Phi }=fm(\mathrm{\Omega }+{\tau }^2\mu \stackrel{\sim }{\mathrm{\Omega }})+.5a(\theta +\stackrel{\sim }{\delta }\mu \stackrel{\sim }{\mathrm{\Omega }})$

$CV(P_{\mathit{Nephew}/\mathit{Niece}},{\stackrel{\sim }{P}}_{DZ})=\stackrel{\sim }{\mathrm{\Phi }}=.5a(\stackrel{\sim }{\theta }+\stackrel{\sim }{\delta }\mu \stackrel{\sim }{\stackrel{\sim }{\mathrm{\Omega }}})+fm(\stackrel{\sim }{\mathrm{\Omega }}+{\tau }^2\mu \stackrel{\sim }{\stackrel{\sim }{\mathrm{\Omega }}})$

Sibling-Nephew/Niece (sibling of a twin is the Uncle/Aunt)

$CV(P_{\mathit{Nephew}/\mathit{Niece}},P_{\mathit{Sib}})=.5a(\theta +\stackrel{\sim }{\delta }\mu \stackrel{\sim }{\mathrm{\Xi }})+fm(\mathrm{\Xi }+{\tau }^2\mu \stackrel{\sim }{\mathrm{\Xi }})$

Cousin-Cousin

$CV(P_{\mathit{Cous}},P_{\mathit{Cous}}\mathit{vis}\mathit{MZs})=.5a(\xi +\stackrel{\sim }{\delta }\mu \stackrel{\sim }{\mathrm{\Gamma }})+fm(\mathrm{\Gamma }+{\tau }^2\mu \stackrel{\sim }{\mathrm{\Gamma }})$

$CV(P_{\mathit{Cous}},P_{\mathit{Cous}}\mathit{vis}\mathit{DZs})=.5a(\lambda +\stackrel{\sim }{\delta }\mu \stackrel{\sim }{\mathrm{\Theta }})+fm(\mathrm{\Theta }+{\tau }^2\mu \stackrel{\sim }{\mathrm{\Theta }})$

Grandparent-Grandchild

$CV(P_{\mathit{Grandparent}},P_{\mathit{Grandchild}})=.25a(\delta +\stackrel{\sim }{\delta }\mu {\tau }^2+2\stackrel{\sim }{\delta }\mu \stackrel{\sim }{\mathrm{\Delta }})+fm(\mathrm{\Delta }+{\tau }^2\mu \stackrel{\sim }{\mathrm{\Delta }})$

Siblings-in-law

$CV(P_{MZ},P_{\mathit{Spouse}ofMZ})=\stackrel{\sim }{\mathrm{\Phi }}\mu {\tau }^2$

$CV(P_{DZ},P_{\mathit{Spouse}ofDZ})=\stackrel{\sim }{\mathrm{\Omega }}\mu {\tau }^2$

$CV(P_{\mathit{Sib}},P_{\mathit{Spouse}of\mathit{Twin}})=\stackrel{\sim }{\mathrm{\Xi }}\mu {\tau }^2$

$CV(P_{\mathit{Spouse}ofMZ1},P_{\mathit{Spouse}ofMZ2})={\tau }^2{\mu }^2\stackrel{\sim }{\stackrel{\sim }{\mathrm{\Phi }}}{\tau }^2$

$CV(P_{\mathit{Spouse}ofDZ1},P_{\mathit{Spouse}ofDz2})={\tau }^2{\mu }^2\stackrel{\sim }{\stackrel{\sim }{\mathrm{\Omega }}}{\tau }^2$

Parents-in-law

$CV(P_{\mathit{Spouse}of\mathit{Twin}},P_{\mathit{Parent}})={\tau }^2\mu \stackrel{\sim }{\mathrm{\Delta }}$

Uncle/Aunt-in-laws

$CV(P_{\mathit{Nephew}/\mathit{Niece}},P_{\mathit{Spouse}ofMZ})={\tau }^2\mu \stackrel{\sim }{\mathrm{\Gamma }}$

$CV(P_{\mathit{Nephew}/\mathit{Niece}},P_{\mathit{Spouse}ofDZ})={\tau }^2\mu \stackrel{\sim }{\mathrm{\Theta }}$

Note. Subscripts: MZ1 monozygotic twin 1; DZ1 dizygotic twin 1; T1 monozygotic or dizygotic twin 1. Superscripts: ~ pathways to the latent factor on which spouses mate assortatively