Theoretical analysis of the determinants of lung oxygen diffusing capacity

Abstract

The process of pulmonary oxygen uptake is analyzed to obtain an explicit equation for lung oxygen diffusing capacity in terms of hematocrit and pulmonary capillary diameter. An axisymmetric model with discrete cylindrical erythrocytes is used to represent radial diffusion of oxygen from alveoli through the alveolar-capillary membrane into pulmonary capillaries, through the plasma, and into erythrocytes. Analysis of unsteady diffusion due to the passage of the erythrocytes shows that transport of oxygen through the alveolar-capillary membrane occurs mainly in the regions adjacent to erythrocytes, and that oxygen transport through regions adjacent to plasma gaps can be neglected. The model leads to an explicit formula for diffusing capacity as a function of geometric and oxygen transport parameters. For normal hematocrit and a capillary diameter of 6.75 µm, the predicted diffusing capacity is 102 ml O₂ min⁻¹ mmHg⁻¹. This value is 30–40% lower than values estimated previously by the morphometric method, which considers the total membrane area and the specific uptake rate of erythrocytes. Diffusing capacity is shown to increase with increasing hematocrit and decrease with increasing capillary diameter and increasing thickness of the membrane. Simulations of pulmonary oxygen uptake in humans under conditions of exercise or hypoxia based show closer agreement with experimental data than previous models, but still overestimate oxygen uptake. The remaining discrepancy may reflect effects of heterogeneity of perfusion and ventilation in the lung.

1. INTRODUCTION

The rate of oxygen uptake from the lung into the bloodstream is a critical determinant of functional capacity and is of paramount importance under normal conditions (including exercise) as well as in disease. The rate at which oxygen is taken up by erythrocytes in pulmonary capillaries is termed lung diffusing capacity, and is affected by several geometric and functional factors. The diffusing capacity of the lung is higher than would be necessary to meet the needs of healthy individuals at rest under normoxic conditions, but can become limiting under conditions of exercise, hypoxia, or disease. Such impairment of oxygen uptake can lead to inadequate oxygen delivery, with consequences that range from short-term dependence on anaerobic metabolism to organ failure and death. The lung diffusing capacity is therefore a crucial parameter in the analysis of oxygen transport in the body under a range of physiological and pathological conditions. The main physical processes determining lung diffusing capacity are well known, and a number of theoretical models have been developed, as discussed below. However, existing methods for estimating this parameter give widely varying results, and may not be suitable for examining the effects of hemodynamic or structural changes occurring in the lung. There is a need for a model of lung diffusing capacity that takes into account such changes but is simple enough to be used as a component in multi-organ simulations.

The objective of this study is to estimate lung diffusing capacity by analyzing the fundamental processes of pulmonary oxygen transport, and to use this result to predict the rate of oxygen uptake under physiological stress (exercise and hypoxia). Lung diffusing capacity (D_LO2) is generally defined via

$${\mathrm{V̇}}_{O_2}={\mathrm{D}}_{\mathrm{L}{O}_2}\times (P_A-\overline{P_b})$$ (1)

where V̇_O2 is the oxygen consumption rate, P_A is the partial pressure of oxygen (P_O2) in alveolar air and $\overline{P_b}$ is the mean P_O2 in pulmonary capillary erythrocytes (Weibel, 1999). In this definition, D_LO2 depends on the geometry of the lung and the diffusive mass transfer properties of the alveolar-capillary membrane, plasma, and erythrocytes, but is independent of blood flow rate, ventilation, and oxygen flux.

As blood traverses capillaries in the lung, P_b varies nonlinearly, such that $\overline{P_b}$ cannot be deduced directly from measurable parameters such as arterial and venous P_O2 (P_a and P_v). Therefore, D_LO2 cannot be directly estimated from experimental data. For this reason, Foucquier et al. (Foucquier et al., 2013) proposed an alternative definition of diffusing capacity ${\mathrm{D}}_{\mathrm{L}{O}_2}^{\text{'}}$ in terms of venous P_O2:

$${\mathrm{V̇}}_{O_2}={\mathrm{D}}_{\mathrm{L}{O}_2}^{\text{'}}\times (P_A-P_v)$$ (2)

This effective mass transfer coefficient includes effects of the variation of P_b during transit through the lung as well as effects of heterogeneity of blood flow, alveolar geometry, etc. In blood traversing the lung, the P_O2 approaches alveolar P_O2, implying that $|P_A-\overline{P_b}|\le |P_A-P_v|$. Hence, the lung diffusing capacity D_LO2 provides an upper bound on the effective diffusing capacity ${\mathrm{D}}_{\mathrm{L}{O}_2}^{\text{'}}$.

As already noted, knowledge of D_LO2 is important for the quantitative understanding of oxygen transport in the lung. Since D_LO2 is not directly measurable, several previous studies have used theoretical approaches to obtain estimates (see Table 1), as briefly reviewed here.

Table 1.

Previous theoretical estimates of D_LO2 and D_MO2 (ml O₂ min⁻¹ mmHg⁻¹).

Authors	DMO2	DLO2	Notes
Gehr et al. (1978)	553–586	125–263	Morphometric method
Weibel et al. (2005)	350	158	Morphometric method
Federspiel (1989)		135	Discrete spherical erythrocytes (HD = 0.237)
Frank et al. (1997)	112–199	93–185	Axisymmetric, parachute erythrocytes, [Fig. 2] DRBC = 2.4 × 10−5 cm2/s, blood volume 162.8 ml
Foucquier et al. (2013)	86–145		Biconcave erythrocytes (HD = 0.45)

The morphometric method (Weibel, 1999; Weibel, 2009; Weibel et al., 2005) is based on the concept (Roughton and Forster, 1957) that resistance to oxygen diffusion can be represented as two components in series, one associated with the alveolar membrane (D_MO2) and one associated with erythrocytes (D_eO2):

$${\left({\mathrm{D}}_{\mathrm{L}{O}_2}\right)}^{-1}={\left({\mathrm{D}}_{\mathrm{M}{O}_2}\right)}^{-1}+{\left({\mathrm{D}}_{\mathrm{e}{O}_2}\right)}^{-1}$$ (3)

Blood is treated as a continuum and the entire membrane participates in gas exchange. The membrane component is estimated as

$${\mathrm{D}}_{\mathrm{M}{O}_2}=K_{O_2}\times \frac{\frac{1}{2}[S(A)+S(c)]}{{\tau }_{hb}}$$ (4)

where K_O2 represents the Krogh diffusion constant, $\frac{1}{2}[S(A)+S(c)]$ represents the average of the alveolar surface area S(A) and the capillary surface area S(c) (approximately 130 m² in humans), and τ_hb represents the harmonic mean of the distance between the alveolar surface and the erythrocyte surface (approximately 1 µm), which includes both the plasma and alveolar-capillary membrane compartments (Weibel et al., 1993). The erythrocyte component is calculated from

$${\mathrm{D}}_{\mathrm{e}{O}_2}={\theta }_{O_2}\times V(c)$$ (5)

where V (c) represents pulmonary capillary blood volume (approximately 194 ml) and θ_O2 represents the oxygen unloading conductance of blood (i.e. the reaction rate of oxygen with whole blood), about 1.8 ml O₂ ml⁻¹ min⁻¹ mmHg⁻¹ (Weibel, 1999). This approach yields D_LO2 = 158 ml O₂ min⁻¹ mmHg⁻¹ in humans (Weibel, 1999), independent of hematocrit (Weibel et al., 1993).

This estimate far exceeds observed diffusing capacity values for humans at rest and during exercise, which are approximately 20–60 ml O₂ min⁻¹ mmHg⁻¹ (Hsia, 2002; Hughes and Bates, 2003). Awareness of this discrepancy has motivated a number of modifications to the morphometric method and development of alternative approaches. A reexamination of the morphometric method (Crapo and Crapo, 1983; Crapo et al., 1988) concluded that Eq. 3 should be modified by including correction factors in each term to accurately represent pulmonary oxygen transport. Subsequently, the model was modified by Weibel et al. (Weibel et al., 1993) to incorporate effects of the plasma layer as well as hematocrit dependence, with a resulting ~30% reduction in predicted D_MO2.

The particulate nature of blood significantly affects intraluminal diffusion resistance (Hellums, 1977; Hellums et al., 1996). In order to account for this effect, several theoretical studies of oxygen transport from alveoli to discrete erythrocytes in the pulmonary capillaries have utilized finite element models, and have variously accounted for plasma convection between erythrocytes, the reaction rate of hemoglobin with oxygen within the erythrocyte, erythrocyte shape, and a fluid barrier (Federspiel, 1989; Fink, 2002; Foucquier et al., 2013; Hsia et al., 1995; Hsia et al., 1997; Hsia et al., 1999; Reynolds et al., 2010; Sharan et al., 1991; Singh et al., 1980; Whiteley, 2006; Whiteley et al., 2001; Whiteley et al., 2003).

The model of Federspiel (Federspiel, 1989; Federspiel and Popel, 1986) considers spherical erythrocytes surrounded by plasma within a cylindrical capillary and an annular layer of tissue representing the alveolar-capillary membrane. This model incorporates the kinetics of oxyhemoglobin binding and predicts a decrease in diffusing capacity with increasing intercell spacing (decreasing hematocrit) due to a lower relative radial flux at the plasma gaps. The resulting estimate of D_LO2 is comparable to that obtained by the morphometric method (Table 1). Frank et al. (Frank et al., 1997) use a similar approach but with axisymmetric parachute-shaped erythrocytes, and obtain estimates of D_LO2 of similar magnitude. Simulations by Hsia et al. (Hsia et al., 1995; Hsia et al., 1997) of carbon monoxide diffusion in two dimensions with circular or parachute-shaped erythrocyte shapes similarly show a strong dependence of diffusing capacity on cell spacing.

In summary, previous analyses of lung diffusing capacity considering discrete erythrocytes have successfully addressed the limitation of the morphometric model with respect to dependence on hematocrit, but the discrepancy between predicted D_LO2 and observed diffusing capacities in humans remains unresolved. Therefore, we here develop a simple theoretical model for pulmonary oxygen uptake, taking into account the particulate nature of blood. The model incorporates transport barriers for oxygen, including oxygen diffusion through the alveolar-capillary membrane, plasma and erythrocyte, and oxygen loading in the erythrocyte. The model is used to obtain a new estimate of D_LO2, which is found to be about 30–40% lower than previous estimates. With this estimate of D_LO2, predicted levels of arterial saturation under conditions of rest and exercise in normoxia and hypoxia are substantially lower than those predicted based on the morphometric estimate of D_LO2, but still overestimate the observed values.

2. METHODS

2.1 Model geometry

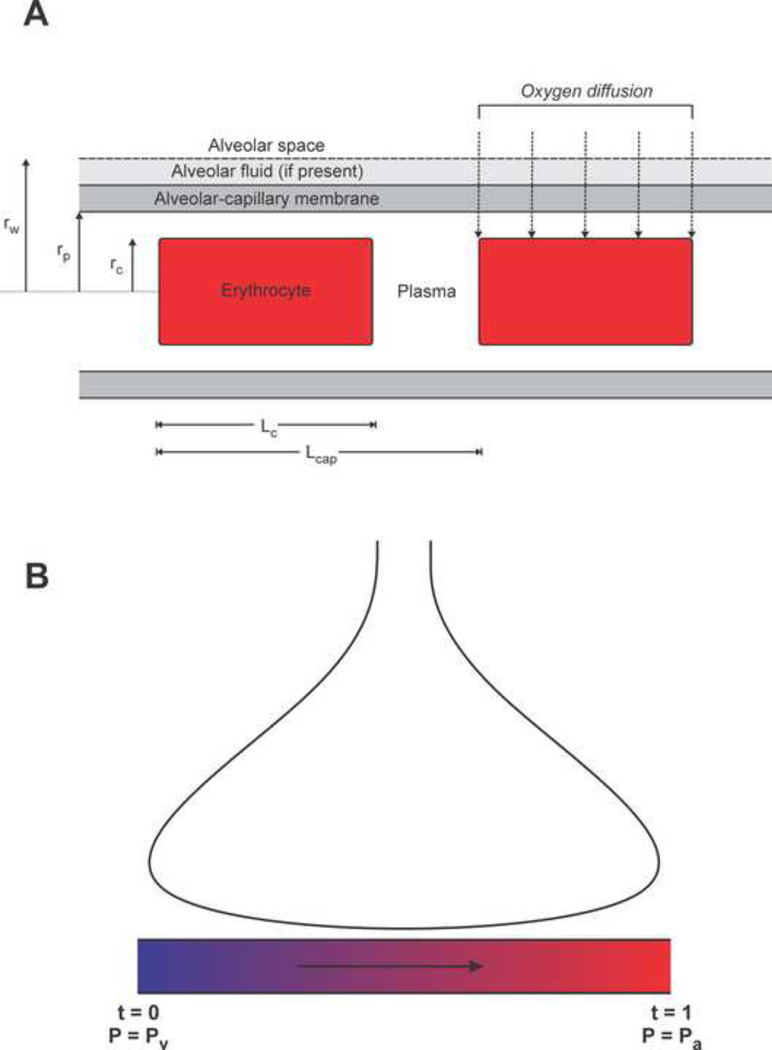
The model geometry is shown in Figure 1A. The erythrocyte is represented as a solid cylinder with fixed volume, whose length and diameter depend on the capillary diameter d_p, which is assumed to be in the range 4 to 8 µm. Observed erythrocyte shapes in capillaries range from narrow elongated bullet-like shapes in very narrow capillaries to cup or parachute shapes in larger capillaries (Gaehtgens et al., 1980). However, with regard to the transport of a highly diffusible solute such as oxygen, the exact shape is unimportant and the most relevant properties (amount of surface adjacent to capillary wall and width of plasma gap) can be represented by a cylindrical model. The dimensions of the cylindrical erythrocyte are calculated by assuming a velocity of 0.02 cm s⁻¹ and estimating cell length L_c (for a given capillary diameter) from previous detailed calculations of erythrocyte shape as a function of cell velocity and capillary diameter (Secomb, 1987) as summarized in Table 3. Assuming an erythrocyte volume V_c = 90 µm³, the corresponding diameter d_c and radius r_c of a cylindrical erythrocyte can be calculated as functions of capillary diameter.

Figure 1.

Model schematic. (A) Model geometry. Erythrocytes are represented as solid cylinders, whose length and diameter depend on vessel diameter. Oxygen is assumed to diffuse radially from the alveolar space into the erythrocytes. (B) Model for pulmonary oxygen uptake. Blood is assumed to take up oxygen from alveoli in the lung (top) during transit through a set of equivalent pulmonary capillaries arranged in parallel. The parameter t represents distance along the capillary.

Table 3.

Geometrical parameter dependence on diameter [from (Secomb, 1987)].

dp (μm)	Lc (μm)	dc (μm)	HT / HD
4	10.4	3.3	0.91
5	8.0	3.8	0.89
6	6.5	4.2	0.86
7	5.5	4.6	0.84
8	5.0	4.8	0.81

Calculations are performed for a range of discharge hematocrit (H_D) values. The tube hematocrit (H_T) is estimated from calculations of the Fåhræus effect that predict H_T / H_D for different capillary diameters as a function of cell velocity (Secomb, 1987). The capillary length per erythrocyte L_cap is then given by

$$L_{\mathit{\text{cap}}}=\frac{L_c{r}_c^2}{H_T{r}_p^2}$$ (6)

where r_p is the capillary radius (d_p / 2). Values for total capillary surface area (A_tot = 115 m²) and blood volume (V_tot = 194 cm³) from Weibel (Weibel, 2009) are used to calculate the total length of capillaries in lung (designated L_tot) and their radius r_p from A_tot = 2πr_pL_tot and V_tot = πr_p²L_tot. For a given cardiac output Q, a transit time τ can then be calculated from τ = Q / V_tot.

2.2 Oxygen transport

A key simplifying assumption of the model is that oxygen diffusion into erythrocytes is assumed to occur only in the radial direction, such that only the segments of capillary walls and alveolar membrane adjacent to erythrocytes at any given moment participate in oxygen exchange. This assumption is justified as follows. Each point in the inner surface of the capillary wall experiences an oscillating oxygen level resulting from the passage of successive erythrocytes. A well-known analysis of time-dependent diffusion in one space dimension (Carslaw and Jaeger, 1959) shows that the equation

$$\frac{\partial c}{\partial t}=D\frac{{\partial }^{2}c}{\partial x^2}$$ (7)

has solutions of the form

$$c=\Re 𝔢\left(c_0{e}^{\pm \lambda x}{e}^{i\omega t}\right)$$ (8)

where

$$\lambda =(1+i)\sqrt{\frac{\omega }{2D}}$$ (9)

These results imply that such oscillations decay exponentially with a length scale (D / ω)^1/2 where D = 1.5 × 10⁻⁵ cm² s⁻¹ is the diffusivity and ω = 2πf, where f is the frequency of erythrocyte passage (typically in the range 10 to 50 s⁻¹ in capillaries).

The resulting penetration distance of the oscillations is in the range 3.3 to 6.9 µm, significantly larger than the membrane thickness of about 1 µm. This length scale also governs the phase shift of the oscillations with distance into the tissue. Therefore, the radial oxygen flux through the membrane at any point on a capillary fluctuates approximately in phase with the passing erythrocytes. Furthermore, since the phase shift within the membrane is small, it is justified to use the steady-state diffusion equation in a reference frame moving with the erythrocyte to describe the radial diffusion of oxygen. Radial transport by convection has been shown to have a minimal impact on oxygen transport (Whiteley et al., 2001) and is not included in the model.

Within the erythrocyte, oxygen loading is assumed to occur at a constant rate T throughout the cell. This approximation is valid under the assumption that the radial variation in saturation with radius within the cell is relatively small. The equation governing oxygen diffusion into the erythrocyte is therefore

$$D_c{\alpha }_c\frac{1}{r}\frac{d}{dr}\left(r\frac{dP}{dr}\right)=T=C_{Hb}\frac{dS(P)}{dt},0\le r\le r_c$$ (10)

where D_c represents the diffusivity of oxygen in the cell, α_c represents the solubility of oxygen in the cell, C_Hb = 0.48 ml O₂ (cm³ RBC)⁻¹ represents the oxygen carrying capacity of the erythrocyte (RBC) based on an intracellular hemoglobin concentration of 0.352 g (cm³ RBC)⁻¹ (Silverman and Glick, 1969), and

$$S(P)={(P/P_{50})}^n/[1+{(P/P_{50})}^n]$$ (11)

is the oxyhemoglobin saturation according to the Hill equation. Facilitated diffusion of oxygen is not considered since the diffusivity of hemoglobin is much lower than the diffusivity of oxygen. Solving Eq. 10 within the erythrocyte results in

$$P(r)=P(0)+\frac{T{r}^2}{4D_c{\alpha }_c}$$ (12)

The mean value of P_O2 in the cell is then:

$$\overline{P}=P(0)+\frac{T{r}_c^2}{8D_c{\alpha }_c}$$ (13)

In order to quantify the effect of oxygen-hemoglobin binding kinetics on the diffusing capacity, we use a simplified kinetic model (Federspiel, 1989):

$$T=k_d{C}_{Hb}[(1-S){(P/P_{50})}^n-S]$$ (14)

where k_d represents the dissociation rate constant. This equation is derived by assuming that the dissociation rate is k_dC_HbS and choosing the binding rate to satisfy T = 0 at equilibrium. We define $\overline{S}$ and $\overline{P}$ as the spatial averages of saturation and P_O2 in the erythrocyte. Under the assumption that radial variations in saturation within the cell are small, Eq. 14 can be averaged:

$$T=k_d{C}_{Hb}[(1-\overline{S}){(\overline{P}/P_{50})}^n-\overline{S}]$$ (15)

We define P₁ and S_e as the P_O2 and saturation such that $\overline{S}=S(P_1)$ and $S_e=S(\overline{P})$. Because the binding is not in equilibrium, we expect that $P_1<\overline{P}$ during loading. Assuming that $\overline{P}-P_1$ is small, we may linearize about $\overline{P}$ to obtain $\overline{S}\cong S_e-(\overline{P}-P_1)S\prime \left(\overline{P}\right)$. Substituting this in Eq. 15 yields

$$\overline{P}-P_1=\frac{T(1-S_e)}{k_d{C}_{Hb}S\prime \left(\overline{P}\right)}$$ (16)

Combining Eqs. 12, 13 and 16 gives:

$$P(r_c)-P_1=T[\frac{r_c^2}{8D_c{\alpha }_c}+\frac{1-S_e}{k_d{C}_{Hb}S\prime \left(\overline{P}\right)}]$$ (17)

Diffusion in the plasma and the alveolar-capillary membrane are governed by

$$D_p{\alpha }_p\frac{1}{r}\frac{d}{dr}\left(r\frac{dP}{dr}\right)=0,r_c\le r\le p$$ (18)

$$D_w{\alpha }_w\frac{1}{r}\frac{d}{dr}\left(r\frac{dP}{dr}\right)=0,r_p\le r\le r_w$$ (19)

where D_p and α_p represent oxygen diffusivity and solubility in the plasma, and D_w and α_w represent oxygen diffusivity and solubility in the capillary wall. Matching the P_O2 and flux values at the erythrocyte-plasma and plasma-capillary wall interfaces results in the following expression for the P_O2 drop from the alveolar space (where P(r_w) = P_A) to the P_O2 corresponding to the mean saturation within the cell, P₁:

$$P_A-P_1=\frac{T{r}_c^2}{D_c{\alpha }_c}[\frac{1}{8}+\frac{D_c{\alpha }_c}{r_c^2}\frac{(1-S_e)}{k_d{C}_{Hb}S\prime \left(\overline{P}\right)}+\frac{1}{2}\frac{D_c{\alpha }_c}{D_p{\alpha }_p}\text{ln}\frac{r_p}{r_c}+\frac{1}{2}\frac{D_c{\alpha }_c}{D_w{\alpha }_w}\text{ln}\frac{r_w}{r_p}]$$ (20)

For a total capillary length L_tot, the number of erythrocytes is L_tot / L_cap and the rate of oxygen uptake is ${\mathrm{V̇}}_{O_2}=\pi (L_{\mathit{\text{tot}}}/L_{\mathit{\text{cap}}})r_c^2{L}_{c}T$. The diffusing capacity is defined as D_LO2 = V̇_O2 / (P_A − P₁). This definition differs from Eq. 1 in that erythrocyte P_O2 is represented by P₁, not $\overline{P}$. Using this definition allows inclusion of the erythrocyte loading kinetics as a component of diffusion resistance. As shown below, the effect of this component on D_LO2 is very small. An explicit expression for the diffusing capacity can then be obtained:

$${\mathrm{D}}_{\mathrm{L}{O}_2}=\frac{\pi L_c{L}_{\mathit{\text{tot}}}{D}_c{\alpha }_c}{L_{\mathit{\text{cap}}}}{[\frac{1}{8}+\frac{D_c{\alpha }_c}{r_c^2}\frac{(1-S_e)}{k_d{C}_{Hb}S\prime \left(\overline{P}\right)}+\frac{1}{2}\frac{D_c{\alpha }_c}{D_p{\alpha }_p}\text{ln}\frac{r_p}{r_c}+\frac{1}{2}\frac{D_c{\alpha }_c}{D_w{\alpha }_w}\text{ln}\frac{r_w}{r_p}]}^{-1}$$ (21)

Here the first term in the quantity in square brackets represents intra-erythrocyte diffusion resistance, the second term represents resistance due to hemoglobin loading, the third term represents plasma resistance, and the fourth term represents resistance of the alveolar-capillary membrane. The diffusion resistance (D_LO2)⁻¹ can then be expressed as the sum of four component resistances:

$${\left({\mathrm{D}}_{\mathrm{L}{O}_2}\right)}^{-1}=\frac{1}{8}\frac{L_{\mathit{\text{cap}}}}{\pi L_c{L}_{\mathit{\text{tot}}}{D}_c{\alpha }_c}+\frac{L_{\mathit{\text{cap}}}}{\pi L_c{L}_{\mathit{\text{tot}}}}\frac{1}{r_c^2}\frac{(1-S_e)}{k_d{C}_{Hb}S\prime \left(\overline{P}\right)}+\frac{L_{\mathit{\text{cap}}}}{2\pi L_c{L}_{\mathit{\text{tot}}}{D}_p{\alpha }_p}\text{ln}\frac{r_p}{r_c}+\frac{L_{\mathit{\text{cap}}}}{2\pi L_c{L}_{\mathit{\text{tot}}}{D}_w{\alpha }_w}\text{ln}\frac{r_w}{r_p}$$ (22)

The parameter values used are summarized in Table 2. Values for humans are used wherever available.

Table 2.

Parameter values.

Parameter	Value	Units	Ref.
P50	26.3	mmHg	(Hsia, 1998)
n	2.7	-	(Hsia, 1998)
Dc	9.5 · 10−6	cm2 s−1	(Federspiel, 1989)
Dp	2.18 · 10−5	cm2 s−1	(Hellums et al., 1996)
Dw	2.41 · 10−5	cm2 s−1	(Bentley et al., 1993)
αc	3.38 · 10−5	ml O2 cm−3 mmHg−1	(Hellums et al., 1996)
αp	2.82 · 10−5	ml O2 cm−3 mmHg−1	(Christoforides et al., 1969)
αw	3.89 · 10−5	ml O2 cm−3 mmHg−1	(Bentley et al., 1993)
Vc	90 · 10−12	cm3	(Secomb, 1987)
wt	1.0 · 10−4	cm	(Foucquier et al., 2013)
HD	0.25 – 0.55	-	-
dp	4 – 8 · 10−4	cm	-

2.3 Comparison to experimental data

The theoretical estimate of diffusing capacity D_LO2 is used to estimate P_a and P_v and compared with available experimental data under conditions of exercise and/or hypoxia. In each case, the Fick principle is used to estimate cardiac output Q from reported values of V̇_O2, P_a and P_v:

$${\mathrm{V̇}}_{O_2}=Q{C}_0[S(P_a)-S(P_v)]$$ (23)

Here C₀ = C_Hb × H_D (where H_D is the discharge hematocrit) represents the oxygen carrying capacity of whole blood, approximately 0.2 ml O₂ (cm³ blood)⁻¹. Oxygen loading in the lung is simulated by assuming that blood passes through a parallel array of identical pulmonary capillaries of length L_cap as shown in Figure 1B (Wagner, 1996). In each capillary, conservation of mass gives:

$$Q_{\mathit{\text{cap}}}{C}_0\frac{dS(P_1)}{dx}=\frac{{\mathrm{D}}_{\mathrm{L}{O}_2}}{L_{\mathit{\text{tot}}}}(P_A-P_1)$$ (24)

where Q_cap is the flow within the capillary and x represents the position along the capillary (0 ≤ x ≤ L_cap). The alveolar oxygen tension P_A is estimated from the alveolar gas equation:

$$P_A\approx F_{I{O}_2}(P_B-P_{{\mathrm{H}}_2\mathrm{O}})-\frac{P_{a\mathrm{C}{\mathrm{O}}_2}}{R}$$ (25)

which includes the inspired oxygen fraction F_IO2, barometric pressure P_B (760 mmHg), and water vapor pressure P_H2O (47 mmHg), as well as the arterial carbon dioxide tension P_aCO2 and the respiratory quotient R.

Setting t = x / L_cap and using the fact that L_tot / L_cap = Q / Q_cap = N_cap (the total number of capillaries), we obtain:

$$\frac{d{P}_1}{dt}=\frac{{\mathrm{D}}_{\mathrm{L}{O}_2}(P_A-P_1)}{Q{C}_{0}S\prime (P_1)}$$ (26)

independent of the number and length of pulmonary capillaries. This equation is integrated from t = 0 to t = 1, with P₁(0) = P_v to obtain P_a = P₁(1), and an iterative process is used to find values of P_a and P_v consistent with Eq. 23.

3. RESULTS

3.1 Lung diffusing capacity

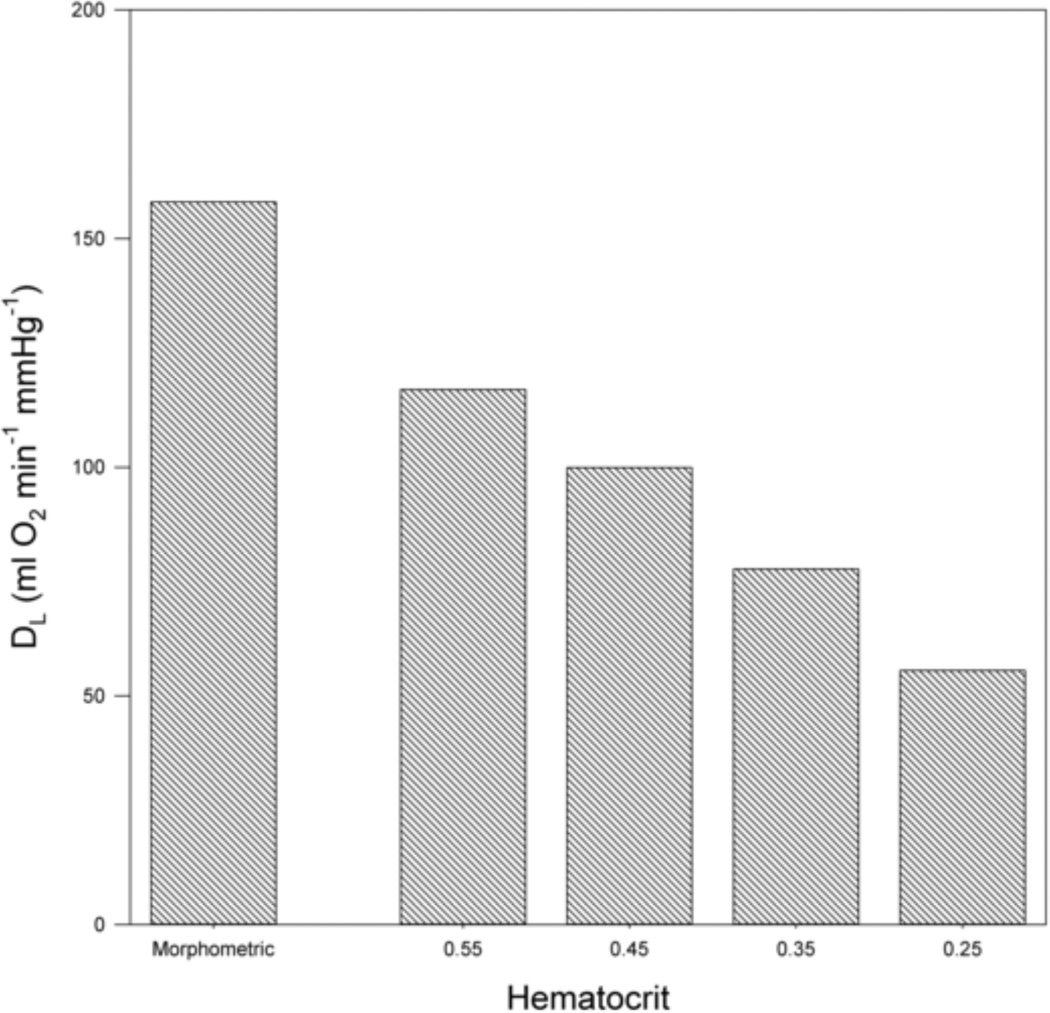
Eq. 21 allows the explicit calculation of D_LO2 for given hematocrit and capillary diameter. Estimates of total capillary length and diameter obtained based on Weibel’s (Weibel, 2009) values of capillary surface area and blood volume are L_tot = 5.4248 × 10⁸ cm and diameter d_p = 6.75 µm. The resulting estimate of D_LO2 is 102 ml O₂ min⁻¹ mmHg⁻¹. In comparison, the morphometric method (Eqs. 3 and 4) with parameter values given by Weibel (Weibel, 1999; Weibel, 2009; Weibel et al., 2005) yields an estimate for D_LO2 of 158 ml O₂ min⁻¹ mmHg⁻¹. Figure 2 shows estimates D_LO2 as a function of hematocrit at a capillary diameter of 7 µm. The values obtained range from 55 to 117 ml O₂ min⁻¹ mmHg⁻¹. As expected, D_LO2 decreases with decreasing hematocrit.

Figure 2.

Estimated lung diffusing capacity D_LO2 as a function of hematocrit values (H_D) for capillary diameter of 7 µm. Morphometric value included for comparison.

3.2 Resistances to pulmonary oxygen transport

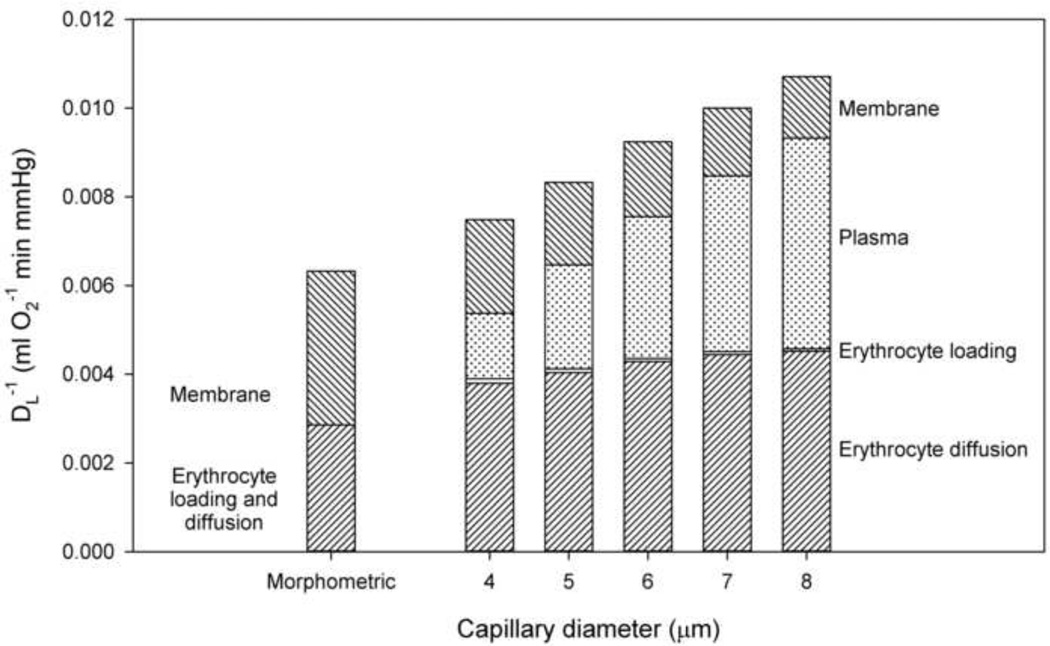
Figure 3 shows the components of the inverse diffusing capacity (D_LO2)⁻¹, representing resistances due to the transport processes from alveoli to blood, as a function of capillary diameter d_p for a fixed hematocrit (H_D = 0.45). The resistance due to oxygen diffusion within erythrocytes is higher than predicted by the morphometric method and varies only slightly with capillary diameter in this range. The resistance due to oxygen loading within the erythrocyte is insignificant for all values of capillary diameter considered, supporting the neglect of this term under normal circumstances. The resistance due to plasma increases with diameter, due to the increasing width of the plasma sleeve. With decreasing diameter, the membrane component of resistance increases. This reflects the increased length of plasma gaps between cells in small diameter capillaries, such that the fraction of membrane participating in diffusion at any instant decreases, increasing effective resistance.

Figure 3.

Components of diffusion resistance. Resistances due to different transport processes from alveoli to blood shown as a function of capillary diameter d_p (H_D = 0.45). Top to bottom: Resistance due to alveolar-capillary membrane, resistance due to plasma, resistance due to reaction of oxygen with hemoglobin, and resistance due to diffusion within erythrocyte. Values of (D_MO2)⁻¹ and (D_eO2)⁻¹ in the morphometric model are included for comparison.

3.3 Relationship between calculated and observed diffusion coefficients

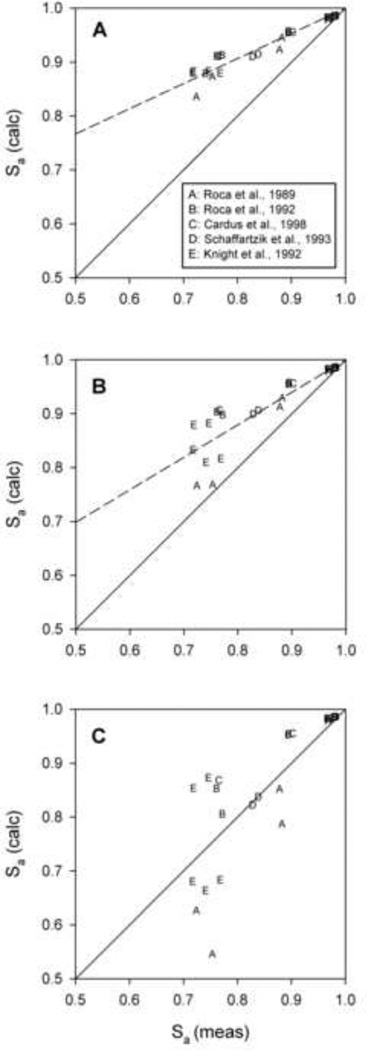
Experimental data obtained under conditions of exercise and hypoxia from a number of studies (Cardus et al., 1998; Knight et al., 1992; Roca et al., 1989; Roca et al., 1992; Schaffartzik et al., 1993) were used to predict arterial saturation, S_a = S(P_a), for three different values of D_LO2, using Eqs. 23 and 24. Results are compared with measured S_a values in Figure 4. Calculated regressions (dashed lines) are constrained to pass through the point (1,1), which corresponds to the condition that diffusing capacity is not limiting and saturation approaches 100%. When the morphometric estimate (D_LO2 = 158 ml O₂ min⁻¹ mmHg⁻¹) is used, predicted S_a values are systematically higher than measured values (Figure 4A). With the present estimate (D_LO2 = 102 ml O₂ min⁻¹ mmHg⁻¹), predicted S_a values are reduced significantly, but still exceed the measured values in most cases (Figure 4B). For comparison, further predictions were made with D_LO2 = 74 ml O₂ min⁻¹ mmHg⁻¹, for which calculated values are clustered around the line of identity with measured values, and the regression line of the calculated values coincides with the identity line (Figure 4C). These results suggest that the estimate of D_LO2 obtained from the present model, while significantly lower than predictions from previous studies, nonetheless overestimates the actual value by about 30%. Possible reasons for this discrepancy are discussed below.

Figure 4.

Calculated values of arterial oxygen saturation based on data obtained under conditions of exercise and hypoxia from a number of studies based on estimated values of lung diffusing capacity. Regression lines (dashed) shown compared to lines of identity. Panel A (Morphometric method): D_LO2 = 158 ml O₂ min⁻¹ mmHg⁻¹; Panel B (Present model): D_LO2 = 102 ml O₂ min⁻¹ mmHg⁻¹; Panel C (Optimal D_L): D_LO2 = 74 ml O₂ min⁻¹ mmHg⁻¹.

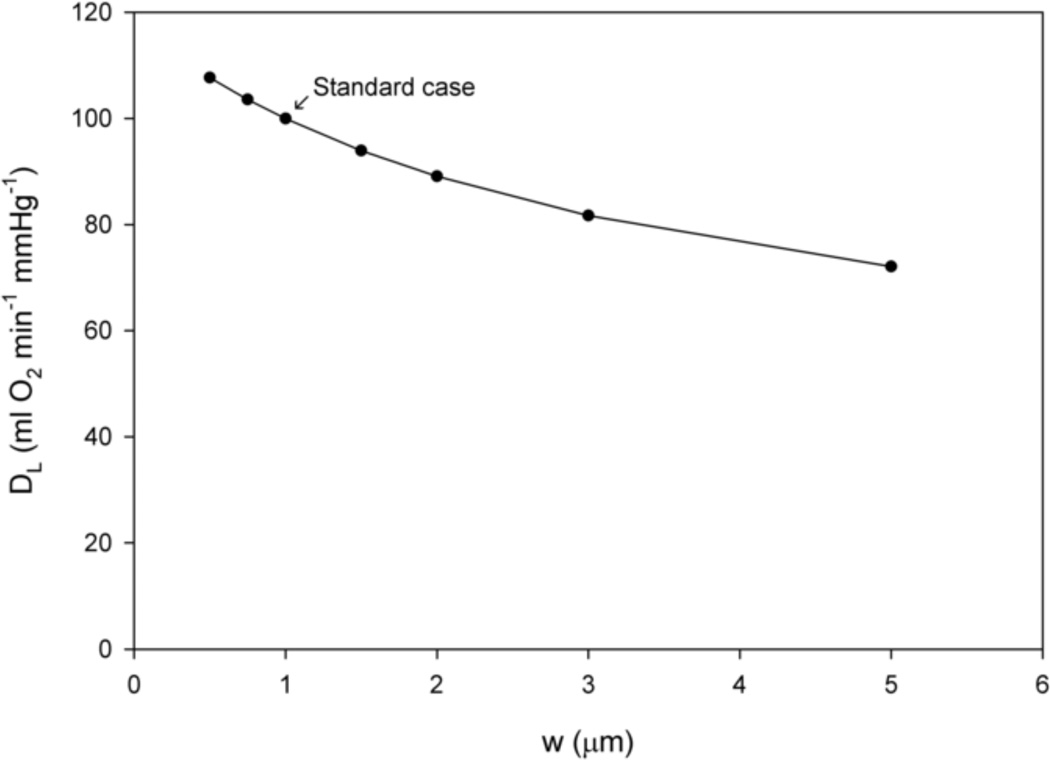
3.4 Effect of alveolar-capillary membrane thickness

Figure 5 shows lung diffusing capacity D_LO2 as a function of alveolar-capillary membrane thickness w = r_w − r_p at a capillary diameter of d_p = 7 µm and a hematocrit of H_D = 0.45. The calculations demonstrate the expected decrease in lung diffusing capacity with wall thickness.

Figure 5.

Lung diffusing capacity D_LO2 as a function of alveolar-capillary membrane thickness w at a fixed capillary diameter of d_p = 7 µm and hematocrit of H_D = 0.45.

4. DISCUSSION

In this study, a theoretical model of pulmonary oxygen uptake is used in a quantitative analysis of the factors governing oxygen transport in the lung, including the effects of the several component resistances to oxygen uptake. Because it yields a relatively simple explicit formula for diffusing capacity, it is well suited for use as an element in simulations of systemic oxygen transport and utilization to predict pulmonary performance under a variety of physiological and pathophysiological conditions such as exercise, hypoxia, and critical illness. It is also suitable for use in simulations of the important effects of heterogeneity of ventilation and perfusion on lung diffusing capacity.

Several previous models have yielded widely varying predictions for D_LO2, which appear inconsistent with experimental observations of blood oxygenation in the lungs. The challenges of understanding and simulating the actual situation with regard to oxygen transport in the lungs have been summarized by Foucquier et al. (Foucquier et al., 2013).

The present work aims to address these difficulties using a simplified model that nonetheless includes a number of important aspects of the system: (i) the particulate nature of blood and the effects of hematocrit; (ii) the dependence of erythrocyte shape on vessel diameter; (iii) the contributions of intra-erythrocyte, plasma and endothelial-alveolar membrane resistance to overall diffusion resistance; (iv) the kinetics of oxygen loading by hemoglobin. An advantage of our model is that it leads to an explicit expression for D_LO2, so that effects of varying conditions can be predicted without the need for finite-element or other numerical analysis. It has been derived without fitting any adjustable parameters to experimental data.

The main finding of this study is that the estimate of oxygen diffusing capacity of the lungs is significantly lower than predicted by models using the morphometric method, and in the lowest range of the estimates obtained by detailed numerical simulation based on discrete erythocytes. One factor contributing to this lower estimate, relative to the morphometric approach, is that it takes into account that only the portions of the plasma gap and the membrane lying adjacent to an erythrocyte at any given moment contribute significantly to radial diffusion. This is justified based on a consideration of oscillatory diffusion processes. The reasons for the discrepancy with previous discrete-cell models are less clear, but may include different assumptions about cell shapes and parameter values. Some previous studies (Federspiel, 1989; Frank et al., 1997) have indicated a significant dependence of diffusing capacity D_LO2 on saturation, as a result of the saturation-dependent rate of oxygen binding to hemoglobin. However, the present model indicates that the effect of binding kinetics on diffusing capacity is slight. The erythrocytes, plasma sleeve and endothelial-alveolar membrane all contribute significantly to overall diffusion resistance. Diffusing capacity increases with increasing hematocrit, as shown in several previous studies. Increasing alveolar-capillary membrane thickness results in lower diffusing capacity; higher values of membrane thickness can be seen under conditions of fibrosis, inflammation, or pulmonary edema (Reynolds et al., 2010).

Estimates of D_LO2 can be used together with a simple model of oxygen loading in pulmonary capillaries (Eq. 26) to predict arterial oxygen saturation S_a based on data for cardiac output and whole-body oxygen consumption. For conditions of hypoxia and/or exercise, values of D_LO2 from previous models lead to substantial overestimation of S_a relative to observed values. The lower value of D_LO2 obtained here yields predicted S_a values that are closer to but still in excess of the measured values. This implies that other factors not included in the model further limit diffusive oxygen transport in the lung.

A likely explanation for this remaining discrepancy is the presence of extensive heterogeneity in lung structure and function. According to Forster (Forster, 1999), “Nonuniformity is the greatest enemy of lung gas exchange and of the pulmonary diffusing capacity”. One such effect is diffusional screening, which lowers D_LO2 by extraction of oxygen along the diffusion path prior to reaching the alveoli (Sapoval et al., 2002). This phenomenon has been explored numerically in idealized (Grebenkov et al., 2005; Sapoval et al., 2002) as well as more realistic geometries (Felici et al., 2003; Felici et al., 2004; Felici et al., 2005). Heterogeneity of perfusion may also play a role in the lower effective D_LO2. This heterogeneity is counteracted to some extent by hypoxic pulmonary vasoconstriction that serves to improve V̇ / Q̇ matching. However, this mechanism is only stimulated at low values of P_v. Transit time heterogeneity in the pulmonary circulation has been noted to decrease with increasing cardiac output and exercise (Hughes and Bates, 2003). Therefore, the neglect of heterogeneity in alveolar and vascular structure and in distributions of perfusion and ventilation is a significant limitation of this and most other theoretical analyses of lung oxygen transport. Effects of heterogeneity should be explored in future work in this field.

Highlights.

• The process of pulmonary oxygen uptake is analyzed using a theoretical model.

• Lung diffusing capacity is expressed in terms of hematocrit and capillary diameter.

• The predicted diffusing capacity is significantly lower than previous estimates.

• The predicted diffusing capacity is higher than that suggested by experimental data.

• This discrepancy may reflect heterogeneity of perfusion and ventilation in the lung.