Summary
Identifying errors and alternate conformers, and modeling multiple main-chain conformers in poorly ordered regions are overarching problems in crystallographic structure determination that have limited automation efforts and structure quality. Here, we show that implementation of a full factorial designed set of standard refinement approaches, which we call ExCoR (Extensive Combinatorial Refinement), significantly improves structural models compared to the traditional linear tree approach, in which individual algorithms are tested linearly, and only incorporated if the model improves. ExCoR markedly improved maps and models, and reveals building errors and alternate conformations that were masked by traditional refinement approaches. Surprisingly, an individual algorithm that renders a model worse in isolation could still be necessary to produce the best overall model, suggesting that model distortion allows escape from local minima of optimization target function, here shown to be a hallmark limitation of the traditional approach. ExCoR thus provides a simple approach to improving structure determination.
Introduction
Refinement of macromolecular crystal structures is inherently limited by low data-to-parameter ratio i.e. the number of crystal model parameters relative to the quantity of measured reflection intensities (DePristo et al., 2004). In addition, calculation of crystallographic maps may be biased by phases from the current model, impeding model optimization by suppressing map features that are inconsistent with the model and rendering detection of errors or alternate conformers arduous. A related problem that impedes the development of fully automated structure determination is dealing with poorly ordered regions, such as loops, which may reflect the presence of multiple main-chain conformers.
A number of approaches have been developed to address these problems, including iterative model-building and refinement, multiple parallel refinements and model-building, and inclusion of alternative model-building procedures such as Rosetta. (Adams et al., 2011; DiMaio et al., 2011; Furnham et al., 2006; Joosten et al., 2009b; Lang et al., 2010; Langer et al., 2008; Painter and Merritt, 2006a, b; Schroder et al., 2010; Terwilliger et al., 2007; Vonrhein et al., 2007; Winn et al., 2011). Modern structure refinement approaches incorporate geometric restraints on coordinates, but interactions among these restraints and algorithms are not broadly explored. For instance, non-crystallographic symmetry (NCS) restraints can be applied between multiple copies of a protein within the crystallographic asymmetric unit (Kleywegt, 1996), and the vibration or motion of atoms can be modeled as constrained groups using TLS (translation, libration or rotation, and screw-rotation) parameterization of atomic displacement parameters (ADP) or B-factors, further improving model quality in many cases (Painter and Merritt, 2006a). Methods to refine the model in real space against electron density maps include rotamer fitting, peptide side-chain (NQH) or backbone flips to fit maps better, and global real space refinement (Adams et al., 2010; Afonine et al., 2012). These algorithms and parameters are described further in the Supplemental Information. In spite of these advances, errors in data and model parameters, model bias in associated maps and, most importantly, limited convergence radius of parameter sampling (optimization) algorithms used in refinement still limit model improvement.
The traditional approach to refinement uses a decision tree, in which a specific algorithm is tested and applied only if it improves the model, followed by the next algorithm. Another common approach is to test a few algorithms in parallel, and then incorporate those that improve the model into a single refinement run. These approaches assume that refinement algorithms are relatively independent, and that except during simulated annealing, it is not typically desirable to make the model worse during the course of refinement. We tested this hypothesis by subjecting over 50 structures to 256 distinct combinations of refinement parameters and algorithms totaling more than 12,000 independent refinement runs all together, using a process that we term, Extensive Combinatorial Refinement (ExCoR). This combinatorial approach revealed complex interactions among refinement algorithms and parameters, and led to structural diversity that can be harnessed to improve crystal structures and facilitate automated error correction.
Results
The PHENIX software suite for macromolecular structure determination presents a number of refinement options that can be switched on or off (Adams et al., 2010; Adams et al., 2011). We explored this switch for rotamer fitting, peptide side-chain (NQH) and main-chain flips, and real space refinement. We also used NCS restraints, and explored different B-factor refinements with TLS. In previous work, we tried these options in a small set of parallel refinements, and then combined the ones that most improved the model into a single refinement run. To our surprise, we found examples where combining two algorithms that individually made the model worse were beneficial when combined, and vice versa. This prompted us to see whether it was possible to identify an optimal combination of approaches for a structure to be refined. We further set out to see whether such an optimal combination of approaches would be general or specific to each case.
We tested approaches to refinement with a large set of examples. To set a high bar for improvement, test coordinates for ExCoR included 35 structures that were recently deposited in the Protein Data Bank (www.pdb.org) (Berman et al., 2000) from four Protein Structure Initiative (PSI) laboratories, representing work of very experienced crystallographers (see Supplemental Data, Table S1). We also tested a set of 18 unpublished, recently determined structures of the estrogen receptor-α (ERα) ligand-binding domain in complex with different ligands (Table S1), to determine if the optimal refinement strategy differed for late versus early stage refinements, and to compare very closely related structures. We chose to evaluate combinations of 1) rotamer fitting, 2) peptide side-chain (NQH) flips, 3) peptide backbone flips, 4) global real space refinement, and 5) NCS, using the NCS groups auto-selected by PHENIX, for a total of 32 (i.e. 25) distinct refinements. To test the effects of TLS parameterization, we compared TLS groups generated with the program phenix. find_tls_groups (Afonine, unpublished), and with different TLS grouping schemes (i.e. 0, 3, 6, 9, 12, 15 or 20 groups per chain) identified via the TLSMD server (Painter and Merritt, 2006a, b) to yield 8 × 32 = 256 refinements. Each refinement strategy included coordinate, occupancy and individual B-factor refinement, water updating, and optimization of data/restraints target weight. The 256 individual refinement strategies were specified in individual parameter text files, and then submitted for parallel refinements on a computer cluster (see Experimental Procedures).
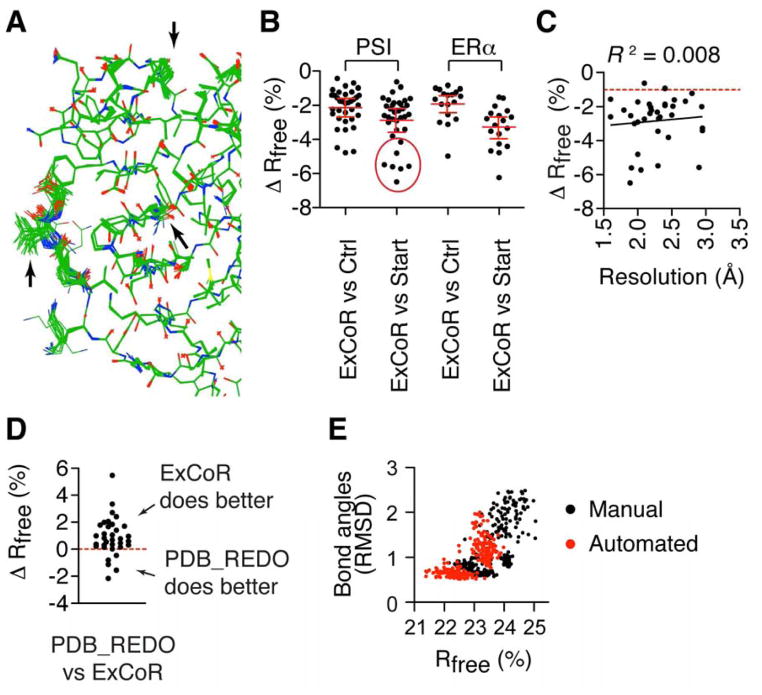
We found that the structural diversity generated by ExCoR allowed sampling of conformers with improved the free R-factor (Rfree) and corresponding improvements in electron density maps. ExCoR models typically show regions of low structural divergence and other regions with obvious heterogeneity (Figure 1A), reflecting regions where the maps are less clear. Rfree is considered the best overall statistical indicator of model quality (Brunger, 1992; Read et al., 2011). The structural diversity generated from ExCoR allowed sampling of conformers with significantly lower Rfree (paired Student’s t-test, p < 0.001) compared to both the control refinement (2% average improvement), and starting models (3% average improvement) (Figure 1B). About 20% of the recently deposited structures showed Rfree improvements greater than 4% relative to the deposited model (Figure 1B), and the degree of improvement was resolution-independent (Figure 1C).
Figure 1. ExCoR improves crystal structures.
(A) 32 ExCoR models of PDB 3MH8 refined with 3 TLS groups per chain are shown. (B) Change in Rfree from starting model or control refinement for the 35 structures from Protein Structure Initiative (PSI) laboratories and 18 ERα structures. (C) For the 35 PSI models, the change in Rfree from ExCoR is plotted as a function of resolution. The R2 value for the linear regression shows that there is no significant correlation. (D) For the 35 PSI structures, change in Rfree from ExCoR compared to PDB_REDO. (E) Comparison of all ExCoR models derived from an ERα structure immediately after model building (automated) or after manual inspection and rebuilding. (See also Figure S1)
For each structure tested there were one or more refinement strategies that improved Rfree and geometric ideality, including the RMSD from ideal bond lengths and angles (Figure S1A). For most structures, such strategies generated models that represent the intersection or the “best solutions” for these selection criteria (Figure S1A). However, some structures showed a pattern where the lowest Rfree did not correlate with the best geometry (Figure S1A), suggesting that Rfree reduction may come at the expense of model geometry in some cases. This may reflect local geometric distortions due to some errors remaining in the model. ExCoR typically lowered the number of clashes as determined by Molprobity clash score (Chen et al., 2010) (Figure S1B), as well as the percentage of residues with weak map density (Figure S1C). However, these statistics did not necessarily correlate with the lowest Rfree solutions. We also note that the structure with the best Rfree may retain specific errors that were successfully corrected in higher Rfree structures. Taken together, these data demonstrate that Rfree is not sufficient by itself to evaluate the models. This suggests that other validation parameters will need to be considered in order to combine the ensemble of ExCoR models into a single model, or to define an ensemble of models where each one represents the data equally well, thus making the entire ensemble to be the best representation of the data.
We also compared our results to prior successes in improving model quality using an advanced approach. PDB_REDO (Joosten et al., 2009a) implements a linear decision tree approach to test the effectiveness of individual algorithms sequentially, allowing its application to the entire PDB due to its relatively low computational cost. We found that ExCoR out-performed PDB_REDO in all but a few cases (Figure 1D), demonstrating the limits of even the newest algorithms when applied linearly, and suggesting that inclusion of more algorithms, into the ExCoR factorial design could lead to even greater improvements for some models. These results also suggest that ExCoR allows access to structural spaces with improved model quality.
Prior to these experiments, we manually inspected and rebuilt five of the ERα structures after molecular replacement and automated rebuilding, manually repositioning side-chains into electron density maps using Coot (Emsley and Cowtan, 2004). After seeing the results from ExCoR, we suspected that ExCoR might be sufficient to find the same rotamers without manual input. Using ExCoR, we observed significantly better solutions, with decreased Rfree and deviation from ideal bond geometry using the fully automated procedure (paired Student’s t-test, p < 0.0005) (Figures 1E and S1D), suggesting ExCoR may contribute to automation of structure determination by lifting the model out of local energy minima. Based on these results, the fully automated procedure was used for the rest of the study.
Validation of ExCoR as a Refinement Strategy
A possible trivial explanation for improved Rfree observed with ExCoR is that there is variability in the value of Rfree simply due to the limited set of reflections that are included, so that two models with essentially identical agreement with the X-ray data would normally show slight variations in Rfree (Kleywegt and Brunger, 1996). This possibility suggests that by sampling many refinements we might be observing some lower Rfree values by chance. To estimate the statistical variation in Rfree values obtained in ExCoR, we generated 2 new Rfree test sets, and ran the 265 refinements with both new Rfree test sets (Figure S1E–F), allowing us to calculate the difference between Rfree test sets for each refinement as a measure of statistical variation in Rfree. This distribution of variation in Rfree was used to generate an error distribution curve, centered on the Rfree from the control refinement for each structure (Figure S1E). The Rfree values generated by ExCoR were outside the range of the error distribution curve (Figure S1E), and more so when compared to the Rfree of the starting models. Further, the typical difference in Rfree between the different Rfree test sets was less than 1%, while the typical range of Rfree from ExCoR was much greater (Figure S1F), indicating that the Rfree improvement observed is not due to chance from increased sampling produced by many refinements.
To assess the extent to which the effectiveness of ExCoR depends on the test set, the Rfree obtained via ExCoR using test set #1 was used to rank the strategies in decreasing order, and compared with corresponding Rfree obtained in using test set #2 (Figure S1G). Using the same 256 strategies, the Rfree obtained with test set #2 (red) were not identical to those obtained with test set #1 (black), but the Rfree values for the second test set also generally decreased along with those from the first test set. To evaluate how much variability in Rfree is due to the choice of test set, we plotted Rfree from test set #1 against corresponding Rfree from test set #2 for all 256 strategies (Figure S1H). The linear correlation between corresponding Rfree values was remarkable, specifically in models that produced a substantial range of Rfree.
As previously suggested (Kleywegt, 2007), the use of Rfree as a selection criterion for evaluating parallel refinements renders Rfree itself biased. Therefore, we also implemented a separate test set (Rsleep) that was not used for selection. We found that Rsleep correlated with Rfree in ExCoR of most but not all structures tested (Figure S1I). To test whether strategies identified as effective by ExCoR remain effective when the test set is changed, we selected strategies that produced the lowest Rfree using test set #1 and compared the resulting models to starting and control-refined models (Figure S1J). We then compared models obtained from the same strategies using test set #2 to the starting and corresponding control-refined models (Figure S1J). In both cases, the selected strategies showed an average improvement in Rfree of greater than 1%, compared to control-refined models, and more than 2.5% compared to starting models (Figure S1J). Together, these findings suggest that the effectiveness of ExCoR as a refinement strategy is not an artifact of the choice of Rfree test set or variation in Rfree.
Error Correction and Hidden Alternate Conformers
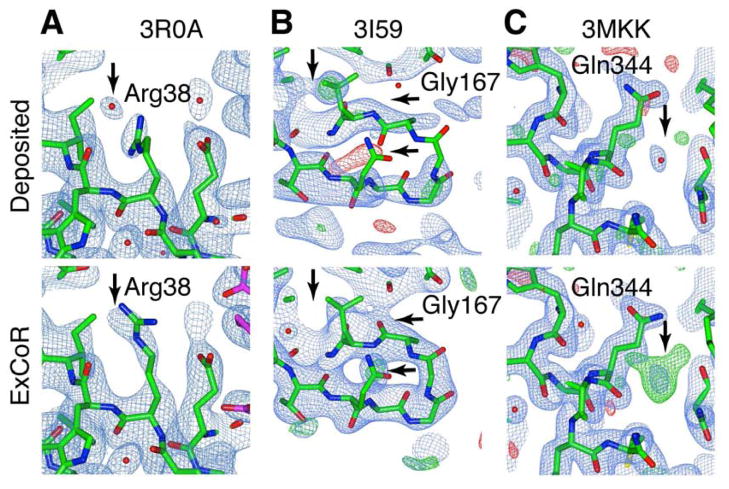
The combination of structural diversity and improved maps allows for automated error correction (Rice et al., 1998) including corrections in side-chains, main-chain and ligands (Figures 2A–B and S2A–G). We also saw many examples where the improved maps allowed identification of features and multiple conformers that were previously masked, possibly by model bias or poor phase accuracy (Figures 2C and S2B–G). These findings are consistent with the notion that ExCoR produces distinct models and allows access to structural space with improved model quality.
Figure 2. Improved maps, error correction, and identification of hidden alternate conformers.
(A–C) The top panel shows the deposited structure and the bottom one of the ExCoR models. (A) Side-chain correction with improved maps. (B) Main-chain correction with improved maps. (C) Visualization of a hidden alternate conformer (See also Figure S2). All maps are 2mfo-dfc atom density (blue) and difference maps (green/red) maps contoured at 1 sigma and ±3 sigma respectively.
ExCoR Reveals Complex Interactions Among Refinement Algorithms
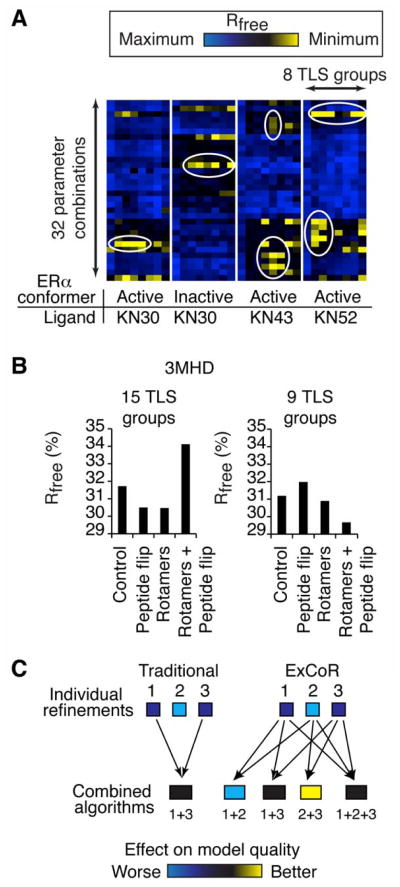
We expected the full factorial approach of ExCoR to reveal optimal refinement strategies that consistently yielded the lowest Rfree. Surprisingly, no subset of combinations consistently produced best results when Rfree was plotted as a heat map, allowing visualization of 32 parameter combinations versus the number of TLS groups (Figure 3A; Rfree values for each strategy are plotted in Figure S3), suggesting that the optimal refinement strategy is unique for each crystal. Even crystals of the same protein from the same laboratory required different refinement strategies to obtain the best structures. For instance, ERα crystallized in different conformations with the same compound (KN30) as previously described (Bruning et al., 2010), displayed distinct effective strategies (Figure 3A). The use of NCS restraints in the case of the two KN30-ERα structures dictated blocks of best and worst outcomes, and this NCS “block effect” occurred frequently in other refinements (Figure S3). This block effect might also be an artifact of the global NCS restraint algorithm used in this PHENIX version, instead of the local torsion-based NCS restraint algorithm applied in more recent versions of PHENIX. Further, compounds KN43 and KN52, which differ only by a -CH3 to -CF3 substitution, were soaked into isomorphic apo crystals of ERα. The structures of ERα bound to these compounds show RMSD’s in the 0.25 Å range, but displayed dramatic improvements with distinct strategies (Figure 3A). KN43-bound ERα improved using combinations of peptide (main-chain) or NQH side-chain flips and real space refinement, while KN52-ERα responded best to combinations with rotamer searches (Figure S3).
Figure 3. Complex interactions between approaches and models.
(A) Heat maps showing Rfree obtained upon ExCoR of 4 closely related ERα structures. (See also Table S1 and Figure S3) (B) Rfree is plotted for the indicated ExCoR of PDB 3MHD (C) The traditional refinement strategy tests a few algorithms, and combines only effective algorithms into a refinement strategy. ExCoR employs a factorial design to combine algorithms. (See also Figure S3)
Unexpectedly, we observed that application of some algorithms profoundly impacted the effectiveness of others. For example, during refinement of PDB 3MHD with 15 TLS groups per chain, the model improved when peptide flips or rotamer searches were applied. On the other hand when all of these were combined the resulting model had an Rfree that was higher (worse) by almost 4%. In contrast, during refinement of 3MHD with 9 TLS groups, peptide flips and rotamer searches did not individually improve Rfree, but produced the lowest (best) Rfree when combined (Figure 3B). Thus the full factorial design of ExCoR revealed unexpected, complex interactions among different combinations of algorithms, producing models that were uniquely improved by the full factorial design, which would not have been obtained or predicted using the traditional linear decision tree approach (Figure 3C).
TLS Refinement Generates Model Diversity
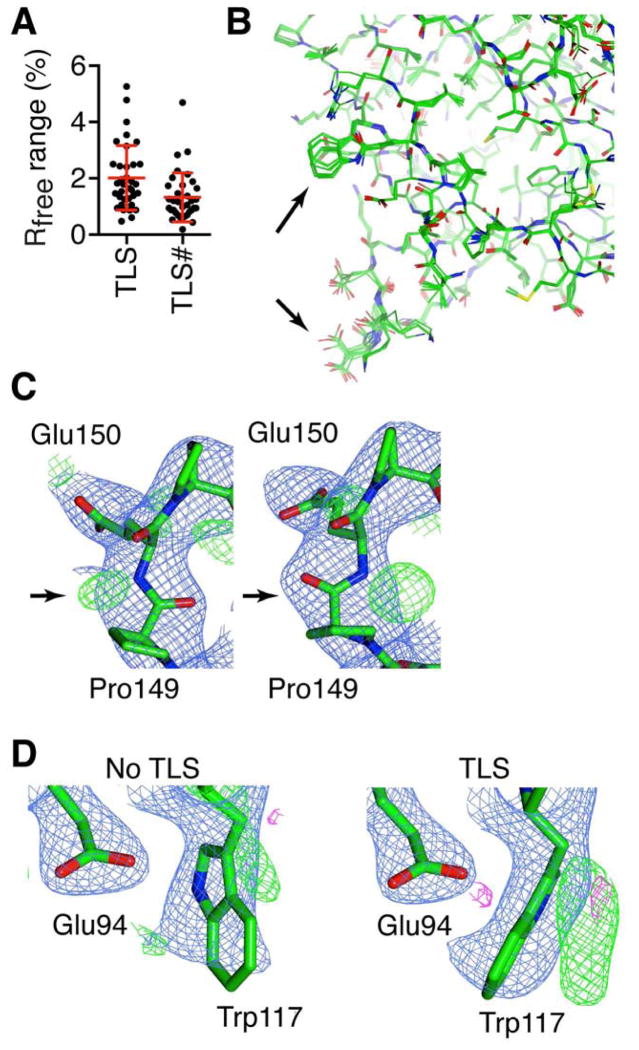
The profound > 4% improvement in Rfree from changing the TLS grouping scheme (i.e. number of TLS groups per chain) for PDB 3MHD was quite surprising (Figure 3B), prompting us to further explore the effects of TLS on generating structural diversity. For the PSI models, the range of Rfree obtained from ExCoR was calculated for refinements with and without TLS, and also for changing the TLS partitioning scheme i.e. the number of TLS groups per chain (Figure 4A). TLS refinement had dramatic effects on model quality, and Rfree was quite sensitive to the TLS partitioning scheme for many models (Figures 4A, S3 and S4A). A comparison of the Rfree range for each model shows that in most cases TLS produced changes greater than the estimated noise (Figure S4A). All of the ERα structures tested, except KNRV-ERα, showed improvement upon application of TLS refinement (Figure S3). This was also the case within the set of PSI models where a few structures (e.g. PDB 3OI7) were insensitive to TLS refinement, while most were improved by TLS refinement (Figure S3). For example, side-by-side comparison of PDB 3MJ9 models derived from otherwise identical refinements performed without or with TLS, shows that using TLS reduced Rfree, and other important indicators of model quality including Rotamer outliers, Ramachandran outliers, and Root-mean-square deviation (RMSD) from ideal bond lengths and angles (Figure S4B). A comparison of the different TLS grouping schemes for 3MJ9 shows regions with minor differences in the model, and other regions where the models differ substantially (Figure 4B). Here, changing TLS grouping schemes led to identification of an alternate main-chain conformation (Figure 4C). TLS refinement also allowed identification of a hidden alternate conformer in this structure (Figure 4D). These data demonstrate that scanning TLS partitioning schemes through ExCoR represents an important and previously unrecognized approach to generation of structural diversity and improved models.
Figure 4. Generation of model diversity from TLS refinement.
(A) For each PSI model the range of Rfree was calculated comparing with and without TLS refinement for each of the 32 combinations of ExCoR approaches. Plotted is the maximum Rfree range from implementing TLS refinement for each structure (TLS). The maximum range of Rfree is plotted for each PSI structure from changing the number of TLS groupings in ExCoR refinement (TLS#). (B) PBD 3MJ9 models generated via ExCoR using identical algorithms and different TLS grouping schemes differ substantially at specific regions (C) Shown are two ExCoR models of PDB 3MJ9, differing in the number of TLS groups used in refinement with the rotamer search and peptide flip options in common. (D) Implementation of TLS allowed the identification of an alternate side-chain conformer for PDB 3MJ9 refined with rotamer search and peptide flip options. (See also Figure S4) All maps are 2mfo-dfc atom density (blue) and difference maps (green/red) maps contoured at 1 sigma and ±3 sigma respectively.
Discussion
Ongoing problems in structure determination include model errors, which may be the result of model bias, or reflect positional uncertainty due to poor map quality or data quality. It is a common experience that most features of a structure are readily and correctly fitted, while an inordinate amount of time is spent on poorly ordered regions, such as loops, which can reflect the combined problem of positional uncertainty and existence of multiple legitimate conformations at those positions. The limited radius of convergence of most refinement approaches exacerbates these problems, such that refinements tend to stall in specific solutions that contain errors.
Solutions to these problems have increasingly focused on methods to generate multiple conformers, and their automation. Examples include Rosetta (Rohl et al., 2004), DEN (Brunger et al., 2012), and RAPPER (Depristo et al., 2005), which generate multiple models for molecular replacement and/or model building. While PHENIX Autobuild can generate multiple models of equivalent quality (Terwilliger et al., 2008), they appear to reflect positional uncertainty (Terwilliger et al., 2007). The programs Ringer (Lang et al., 2010), and qFit (van den Bedem et al., 2009), are able to successfully model alternate conformers, but require relatively high-resolution data. Recent advances to ensemble refinement may overcome the over-fitting problem by restraining simulated annealing ensemble models to the X-ray data, and improve Rfree (Burnley et al., 2012). All of these approaches share a common element in that they are specific algorithms designed to generate multiple conformers.
Here, we show that ExCoR represents a new approach to generating structural diversity by exploring refinement strategy space, using existing algorithms that are individually designed to produce a single model. It was unexpected that simply toggling the common refinement options on or off in a full factorial manner could generate significantly improved maps and models, revealing errors and hidden alternate conformations. We suspect that this is achieved by first generating an ensemble of algorithm-specific models, which then feed a set of novel models to the next algorithm, eliciting complex interactions between the tested algorithms. This allows models to explore new structural spaces, which in turn allows sampling of a wider range of structure factor phases and thus improves maps. We assumed that ExCoR would reveal evidence of optimal refinement strategies but surprisingly, no single schema consistently produced the best model, and this remained the case regardless of data resolution or the extent to which a structure had already been refined, suggesting that refinement of most – if not all - macromolecular crystal structures become trapped in local minima resulting from the particular refinement schema chosen rather than intrinsic limitations of the data, the refinement algorithms, or the scientist.
The complex interaction between approaches implies that the effectiveness of an algorithm should not be determined in isolation, as small changes in the model induced by one approach determine the effectiveness of the next applied algorithm. Thus it is not yet possible to predict which combinations of algorithms will work best for an individual structure. In addition, a linear decision tree approach would miss combinations where the first algorithm performed poorly but would have significantly improved the effects of the next algorithm if both algorithms were used sequentially. It is counter-intuitive that a refinement that appears to be proceeding poorly may actually yield the best model via the full factorial design, suggesting that the model becomes temporarily worse as it is pushed out of a local energy minima. In fact we show that very small changes in the crystal structure, such as substitution of a -CH3 with a -CF3 group, can coerce refinement to follow a completely different path to the best models. Therefore, exploration of refinement strategy space via ExCoR is a pivotal and previously unappreciated route to fundamental improvement of crystal models, which cannot be achieved through the standard linear approach.
Another strength of ExCoR is that it can be implemented with any combination of existing algorithms and refinement programs. The dramatic effects of exploring different TLS grouping schemes suggest that this is likely to be one of the more beneficial approaches to implement. It may also be worthwhile to test the order of application of different approaches, since, for example flipping peptides may alter the best fitting rotamers of neighboring residues. We performed small-scale tests on a larger set of 2,048 (211) combinations, by including Ramachandran restraints and either Cartesian or torsion simulated annealing. Our limited testing on ~3Å ERα structures suggested additional model improvement; however each ExCoR run went from several hours to several days of time on our cluster, highlighting the infrastructure requirements of dramatic expansion of the number of parallel ExCoR refinements. This approach is therefore complementary to others such as PDB_REDO, which samples fewer options and thus can be readily implemented on the entire PDB. Thus, the modular nature of the ExCoR process allows flexibility for other algorithms or programs that are beyond the scope of this work, to be combined to further explore structure improvements.
Since we observed examples of models with the best apparent refinements could retain errors that had been successfully corrected in other runs, this process would be further improved by re-combining best-fit components from multiple models. Extant scoring routines are unable to discriminate between cases in which multiple conformers represent positional uncertainty, multiple legitimate conformations, or some combination of the two. In preparing our ERα structures for publication, we retained alternate conformations only when they presented clear indications of multiple legitimate conformations. This determination was made by visual inspection of several models that ranked among the best runs, as evidenced by Rfree, Molprobity score, and other criteria. From this set we picked one structure with the best combination of validation statistics as the reference model, and then examined a handful of models and maps from this set to build obvious alternate conformers. After a few rounds of ExCoR and manual rebuilding of a given structure, certain strategies repeatedly produced lowest Rfree models, probably reflecting minor changes being introduced at these later stages. This allowed a single final refinement strategy to be applied to finish the structures.
Methods to generate models that account for both positional uncertainty and multiple structures in the crystal are required for automating structure determination. We propose that ExCoR will contribute to these efforts by providing a means to generate structural diversity and improved models. Since it can be implemented with any combination of refinement programs, algorithms and refinement parameters, ExCoR provides a broad platform to advance macromolecular structure determination.
Experimental Procedures
Data Collection
X-ray diffraction data for new ER ligand-binding domain (LBD) crystals was collected at Advanced Photon Source (APS), Argonne National Laboratory (ANL) (beam-line 23-ID-B) and Stanford Synchrotron Radiation Lightsource (SSRL) (beam-line 11-1). Data reduction was performed using HKL-2000 software (Otwinowski and Minor, 1997). Reflections were checked for anisotropy using the anisotropy server (http://services.mbi.ucla.edu/anisoscale/) (Strong et al., 2006), and other complications (e.g. twinning) using phenix.xtriage.
Model Building
All new ER LBD models were built via molecular replacement (MR) using PHENIX (version 1.7-650) (see http://www.phenix-online.org for more information and current versions) (Adams et al., 2010). MR and initial model building were performed in an automated fashion using phenix.automr and phenix.autobuild, respectively. These jobs were run on a computer cluster using the respective reflection data, and starting model coordinates. In this case, ligands and water molecules were removed from the PDB structures 2QA8 or 3OSA to generate starting models for LBDs in the agonist- or antagonist-bound conformations, respectively. The phenix.autobuild outputs were subsequently used for ligand docking and refinement.
Ligand Fitting
Coordinate files for ER ligands were generated using ChembioDraw/Chem3D software suite (Cambridgesoft) or PRODRG server (http://davapc1.bioch.dundee.ac.uk/prodrg/) (Schuttelkopf and van Aalten, 2004). Ligand restraint files were generated with phenix.elbow. For each structure, the newly built coordinate file, map file and ligand coordinates and restraints were loaded into the molecular graphic program Coot (version 0.6.1) (Emsley and Cowtan, 2004). The “Find Ligands” function of Coot was used to determine if the ligand fits the unoccupied density observed in the ligand-binding pocket of the ER structures. If so, the ligand is placed in the unoccupied density and manually adjusted to obtain the best fit. The fitted ligand coordinates were then merged with the LBD coordinates.
ExCoR
It was not feasible to test ExCoR on the entire Protein Data Bank, which would have taken some half a dozen years on our cluster to complete 18 million refinements (~70,000 × 256), so we instead defined a set of test structures. In order to obtain a set of high quality structures that was not biased by our choice, we used the most recently deposited structures from the Midwest Center for Structural Genomics, the Joint Center for Structural Genomics, the New York Structural Genomics Research Consortium, and the TB Structural Genomics Consortium. Lower resolution structures were not found in this test set. We did not seek out a lower resolution test set because we suspect it would require a different set of algorithms to test, which was beyond the scope of this work. We also tested a set of recently solved structures of ERα, in order to compare closely related structures, and structures at an early stage of refinement. Previously deposited structures were downloaded from the Protein Data Bank (http://www.pdb.org) (Berman et al., 2000). The programs phenix.elbow and phenix.ready_set were used to build ligand restraint files and prepare the models for refinement. All refinements were performed using phenix.refine, with restraints, reflections and coordinates as input. Default phenix.refine parameters, except those specified in a parameter file were used. These include ordered_solvent =True and number_of_macro_cycles =5. The basic “on/off” phenix.refine parameters varied were: ncs, fix_rotamers, flip_peptides and nqh_flips and individual_sites_real_space. Target weight optimization was used. In addition, adp groupings were specified whenever the TLS refinement strategy was used. The ADP grouping schemes for 0, 3, 6, 9, 12, 15 and 20 TLS groups were determined using the TLS motion determination server (http://skuld.bmsc.washington.edu/~tlsmd/) (Painter and Merritt, 2006a, b), while an eighth grouping scheme was obtained using the program phenix.find_tls_groups. The control refinement included refinement of xyz, individual ADP, and occupancies. Control refinement also included target weight optimization and automated water picking, and was run without TLS refinement or the other five approaches tested with ExCoR.
The 256 parameter files were placed with the mtz, pdb, and cif files, into 256 different directories, which were named with a number. A text editor was used to insert the different TLS groupings into the parameter files in batches. A sample set of parameter files is included in the Supplemental Information. To enable running the refinements on a cluster, we created 256 text files designed to launch the 256 refinements, which we called run*, where * is a number corresponding to one of the 256 directories. The refinements runs were then launched and distributed to the cluster with a command:
for x in ‘ls filepath/run*’; do qsub $x; done
The ExCoR refinements run on the PSI test sets are available for download at the following website, as are the parameter files for running the jobs and some data analysis scripts. http://media2.florida.scripps.edu/ExCoR/
Statistical Analysis
Global statistics describing model quality e.g. Rfree, Rwork, RMSD bonds and angles for both starting and refined models were calculated using the Polygon validation tool in PHENIX (Urzhumtseva et al., 2009). Molprobity clash score was obtained using phenix.clashscore, and the number of residues with some weak density obtained from phenix.get_cc_mtz_pdb is reported as a percentage of the total number of residues per structure. (Charts and graphs presented were plotted using Prism 5 (Graphpad software, Inc) or MS Excel (Microsoft Corp.). Statistical significance was determined using Student’s paired two-tailed t-test.
Model Visualization and Presentation
All the structures shown were posed using the molecular graphics programs CCP4MG (version 2.5.0) (McNicholas et al., 2011) and Coot (version 0.6.1) (Emsley and Cowtan, 2004).
Supplementary Material
Highlights.
The ExCoR strategy revealed complex interactions among refinement algorithms
ExCoR can be used to improve both unrefined and refined crystal structures
Structural diversity obtained via ExCoR facilitates automated error correction
Provides an estimate of uncertainty of refined model parameters
Acknowledgments
We are grateful to John L. Cleveland (The Scripps Research Institute) for comments on the manuscript. Terry Moore, Marketa Lebl-Rinnova and John A. Katzenellenbogen (University of Illinois at Urbana-Champaign), and Tony Durst, Christine Choueiri and Muhammad Asim (University of Ottawa) provided the compounds crystallized with ERα.
Funding
This work was supported by the US National Institutes of Health PHS CA132022, DK077085, 5U01GM102148 (KWN) and GM063210 (PDA/TCT). This work was supported in part by the US Department of Energy under Contract No. DE-AC02-05CH11231.
Footnotes
Author Contributions
JCN and KWN designed and performed all experiments and wrote the paper. PVA, PDA and TCT designed and analyzed experiments. PDA assisted in the writing of the paper. JRK designed and analyzed experiments and wrote the paper. MRS designed software/scripts for implementing ExCoR.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adams PD, Afonine PV, Bunkoczi G, Chen VB, Davis IW, Echols N, Headd JJ, Hung LW, Kapral GJ, Grosse-Kunstleve RW, et al. PHENIX: a comprehensive Python-based system for macromolecular structure solution. Acta Crystallogr D Biol Crystallogr. 2010;66:213–221. doi: 10.1107/S0907444909052925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams PD, Afonine PV, Bunkoczi G, Chen VB, Echols N, Headd JJ, Hung LW, Jain S, Kapral GJ, Grosse Kunstleve RW, et al. The Phenix software for automated determination of macromolecular structures. Methods. 2011;55:94–106. doi: 10.1016/j.ymeth.2011.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afonine PV, Grosse-Kunstleve RW, Echols N, Headd JJ, Moriarty NW, Mustyakimov M, Terwilliger TC, Urzhumtsev A, Zwart PH, Adams PD. Towards automated crystallographic structure refinement with phenix.refine. Acta Crystallogr D Biol Crystallogr. 2012;68:352–367. doi: 10.1107/S0907444912001308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunger AT. Free R value: a novel statistical quantity for assessing the accuracy of crystal structures. Nature. 1992;355:472–475. doi: 10.1038/355472a0. [DOI] [PubMed] [Google Scholar]
- Brunger AT, Das D, Deacon AM, Grant J, Terwilliger TC, Read RJ, Adams PD, Levitt M, Schroder GF. Application of DEN refinement and automated model building to a difficult case of molecular-replacement phasing: the structure of a putative succinyl-diaminopimelate desuccinylase from Corynebacterium glutamicum. Acta Crystallogr D Biol Crystallogr. 2012;68:391–403. doi: 10.1107/S090744491104978X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruning JB, Parent AA, Gil G, Zhao M, Nowak J, Pace MC, Smith CL, Afonine PV, Adams PD, Katzenellenbogen JA, Nettles KW. Coupling of receptor conformation and ligand orientation determine graded activity. Nat Chem Biol. 2010;6:837–843. doi: 10.1038/nchembio.451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnley BT, Afonine PV, Adams PD, Gros P. Modelling dynamics in protein crystal structures by ensemble refinement. Elife. 2012;1:e00311. doi: 10.7554/eLife.00311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen VB, Arendall WB, 3rd, Headd JJ, Keedy DA, Immormino RM, Kapral GJ, Murray LW, Richardson JS, Richardson DC. MolProbity: all-atom structure validation for macromolecular crystallography. Acta Crystallogr D Biol Crystallogr. 2010;66:12–21. doi: 10.1107/S0907444909042073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePristo MA, de Bakker PI, Blundell TL. Heterogeneity and inaccuracy in protein structures solved by X-ray crystallography. Structure. 2004;12:831–838. doi: 10.1016/j.str.2004.02.031. [DOI] [PubMed] [Google Scholar]
- Depristo MA, de Bakker PI, Johnson RJ, Blundell TL. Crystallographic refinement by knowledge-based exploration of complex energy landscapes. Structure. 2005;13:1311–1319. doi: 10.1016/j.str.2005.06.008. [DOI] [PubMed] [Google Scholar]
- DiMaio F, Terwilliger TC, Read RJ, Wlodawer A, Oberdorfer G, Wagner U, Valkov E, Alon A, Fass D, Axelrod HL, et al. Improved molecular replacement by density- and energy-guided protein structure optimization. Nature. 2011;473:540–543. doi: 10.1038/nature09964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emsley P, Cowtan K. Coot: model-building tools for molecular graphics. Acta Crystallogr D Biol Crystallogr. 2004;60:2126–2132. doi: 10.1107/S0907444904019158. [DOI] [PubMed] [Google Scholar]
- Furnham N, Dore AS, Chirgadze DY, de Bakker PI, Depristo MA, Blundell TL. Knowledge-based real-space explorations for low-resolution structure determination. Structure. 2006;14:1313–1320. doi: 10.1016/j.str.2006.06.014. [DOI] [PubMed] [Google Scholar]
- Joosten RP, Salzemann J, Bloch V, Stockinger H, Berglund AC, Blanchet C, Bongcam-Rudloff E, Combet C, Da Costa AL, Deleage G, et al. PDB_REDO: automated re-refinement of X-ray structure models in the PDB. J Appl Crystallogr. 2009a;42:376–384. doi: 10.1107/S0021889809008784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joosten RP, Womack T, Vriend G, Bricogne G. Re-refinement from deposited X-ray data can deliver improved models for most PDB entries. Acta Crystallogr D Biol Crystallogr. 2009b;65:176–185. doi: 10.1107/S0907444908037591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleywegt GJ. Use of non-crystallographic symmetry in protein structure refinement. Acta Crystallogr D Biol Crystallogr. 1996;52:842–857. doi: 10.1107/S0907444995016477. [DOI] [PubMed] [Google Scholar]
- Kleywegt GJ. Separating model optimization and model validation in statistical cross-validation as applied to crystallography. Acta Crystallogr D Biol Crystallogr. 2007;63:939–940. doi: 10.1107/S0907444907033458. [DOI] [PubMed] [Google Scholar]
- Kleywegt GJ, Brunger AT. Checking your imagination: applications of the free R value. Structure. 1996;4:897–904. doi: 10.1016/s0969-2126(96)00097-4. [DOI] [PubMed] [Google Scholar]
- Lang PT, Ng HL, Fraser JS, Corn JE, Echols N, Sales M, Holton JM, Alber T. Automated electron-density sampling reveals widespread conformational polymorphism in proteins. Protein Sci. 2010;19:1420–1431. doi: 10.1002/pro.423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langer G, Cohen SX, Lamzin VS, Perrakis A. Automated macromolecular model building for X-ray crystallography using ARP/wARP version 7. Nat Protoc. 2008;3:1171–1179. doi: 10.1038/nprot.2008.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNicholas S, Potterton E, Wilson KS, Noble ME. Presenting your structures: the CCP4mg molecular-graphics software. Acta Crystallogr D Biol Crystallogr. 2011;67:386–394. doi: 10.1107/S0907444911007281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otwinowski Z, Minor W. Processing of X-ray Diffraction Data Collected in Oscillation Mode. Methods in Enzymology. 1997;276:307–326. doi: 10.1016/S0076-6879(97)76066-X. [DOI] [PubMed] [Google Scholar]
- Painter J, Merritt EA. Optimal description of a protein structure in terms of multiple groups undergoing TLS motion. Acta Crystallogr D Biol Crystallogr. 2006a;62:439–450. doi: 10.1107/S0907444906005270. [DOI] [PubMed] [Google Scholar]
- Painter J, Merritt EA. TLSMD web server for the generation of multi-group TLS models. Journal of Applied Crystallography. 2006b;39:109–111. [Google Scholar]
- Read RJ, Adams PD, Arendall WB, 3rd, Brunger AT, Emsley P, Joosten RP, Kleywegt GJ, Krissinel EB, Lutteke T, Otwinowski Z, et al. A new generation of crystallographic validation tools for the protein data bank. Structure. 2011;19:1395–1412. doi: 10.1016/j.str.2011.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice LM, Shamoo Y, Brunger AT. Phase Improvement by Multi-Start Simulated Annealing Refinement and Structure-Factor Averaging. J Appl Cryst. 1998;31:798–805. [Google Scholar]
- Rohl CA, Strauss CE, Misura KM, Baker D. Protein structure prediction using Rosetta. Methods Enzymol. 2004;383:66–93. doi: 10.1016/S0076-6879(04)83004-0. [DOI] [PubMed] [Google Scholar]
- Schroder GF, Levitt M, Brunger AT. Super-resolution biomolecular crystallography with low-resolution data. Nature. 2010;464:1218–1222. doi: 10.1038/nature08892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuttelkopf AW, van Aalten DM. PRODRG: a tool for high-throughput crystallography of protein-ligand complexes. Acta Crystallogr D Biol Crystallogr. 2004;60:1355–1363. doi: 10.1107/S0907444904011679. [DOI] [PubMed] [Google Scholar]
- Strong M, Sawaya MR, Wang S, Phillips M, Cascio D, Eisenberg D. Toward the structural genomics of complexes: crystal structure of a PE/PPE protein complex from Mycobacterium tuberculosis. Proc Natl Acad Sci U S A. 2006;103:8060–8065. doi: 10.1073/pnas.0602606103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terwilliger TC, Grosse-Kunstleve RW, Afonine PV, Adams PD, Moriarty NW, Zwart P, Read RJ, Turk D, Hung LW. Interpretation of ensembles created by multiple iterative rebuilding of macromolecular models. Acta Crystallogr D Biol Crystallogr. 2007;63:597–610. doi: 10.1107/S0907444907009791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terwilliger TC, Grosse-Kunstleve RW, Afonine PV, Moriarty NW, Zwart PH, Hung LW, Read RJ, Adams PD. Iterative model building, structure refinement and density modification with the PHENIX AutoBuild wizard. Acta Crystallogr D Biol Crystallogr. 2008;64:61–69. doi: 10.1107/S090744490705024X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urzhumtseva L, Afonine PV, Adams PD, Urzhumtsev A. Crystallographic model quality at a glance. Acta Crystallogr D Biol Crystallogr. 2009;65:297–300. doi: 10.1107/S0907444908044296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Bedem H, Dhanik A, Latombe JC, Deacon AM. Modeling discrete heterogeneity in X-ray diffraction data by fitting multi-conformers. Acta Crystallogr D Biol Crystallogr. 2009;65:1107–1117. doi: 10.1107/S0907444909030613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vonrhein C, Blanc E, Roversi P, Bricogne G. Automated structure solution with autoSHARP. Methods Mol Biol. 2007;364:215–230. doi: 10.1385/1-59745-266-1:215. [DOI] [PubMed] [Google Scholar]
- Winn MD, Ballard CC, Cowtan KD, Dodson EJ, Emsley P, Evans PR, Keegan RM, Krissinel EB, Leslie AG, McCoy A, et al. Overview of the CCP4 suite and current developments. Acta Crystallogr D Biol Crystallogr. 2011;67:235–242. doi: 10.1107/S0907444910045749. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.