Abstract
A decrease in bone density at the hip or spine has been shown to increase the risk of fracture. A limitation of the bone mineral density (BMD) measurement is that it provides only a measure of a bone samples average density when projected onto a 2D surface. Effectively, what determines bone fracture is whether an applied load exceeds ultimate strength, with both bone tissue material properties (can be approximated through bone density), and geometry playing a role. The goal of this project was to use bone geometry and BMD obtained from radiographs and DXA measurements respectively to estimate fracture risk, using a two-dimensional finite element model (FEM) of the sagittal plane of lumbar vertebrae. The Canadian Multicenter Osteoporosis Study (CaMos) data was used for this study. There were 4194 men and women over the age of 50 years, with 786 having fractures. Each subject had BMD testing and radiographs of their lumbar vertebrae. A single two dimensional FEM of the first to fourth lumbar vertebra was automatically generated for each subject. Bone tissue stiffness was assigned based on the BMD of the individual vertebrae, and adjusted for patient age. Axial compression boundary conditions were applied with a force proportional to body mass. The resulting overall strain from the applied force was found. Men and women were analyzed separately. At baseline, the sensitivity of BMD to predict fragility fractures in women and men was 3.77 % and 0.86 %, while the sensitivity of FEM to predict fragility fractures for women and men was 10.8 % and 11.3 %. The FEM ROC curve demonstrated better performance compared to BMD. The relative risk of being considered at high fracture risk using FEM at baseline, was a better predictor of 5 year incident fragility fracture risk compared to BMD.
Keywords: Osteoporosis, fracture risk, finite element modelling, two dimensional, spine
Introduction
Osteoporosis (OP) is a common, complex disorder of reduced bone mass and structural deterioration of bone tissue, manifesting clinically as an increase in fracture risk [1, 2]. OP affects an estimated 1.4 million Canadians, representing 1 in 4 women and 1 in 8 men over the age of 50 [3]. Osteoporotic fractures often occur in the wrist, spine, and hip. The hip is considered the most serious fracture with a mortality rate as high as 20 percent within the first year after fracture, and a reduced functional capacity in up to 50 percent of patients [4]. The pathophysiology of OP is difficult to define, as the risk of fracture depends on many factors including the likelihood of falling, visual acuity, reaction to falling, and bone strength if a fall occurs [5, 6]. While most of these factors are difficult to measure, bone mineral density can be quantified in vivo and has been shown to be a good predictor of fracture risk [7]. A decrease of one standard deviation in bone density at the hip or spine increases the risk of fracture by a factor of two to three [8, 9]. The clinical diagnosis of OP is primarily based on previous fractures and areal bone mineral density (BMD) measured using dual energy X-ray absorptiometry (DXA), compared to a reference population database as outlined by the World Health Organization [10]. A limitation of the BMD measurement is that it provides only a measure of a bone samples average density when projected onto a 2D surface and ignores the effects of bone geometry. Two individuals may possess identical areal BMD, but have different bone geometry and structure and therefore, different fracture risks. Effectively, what determines bone fracture is whether an applied load exceeds the bones ultimate strength, with both bone tissue material properties (can be approximated through bone density), and geometry playing a role. Not accounting for bone geometry, therefore, limits the ability to predict fracture.
Finite element modelling (FEM) has been used to model the mechanical behaviour of vertebrae and has been validated with mechanical testing [11]. Previously, FEM has been shown to be computationally expensive, which has reduced its clinical use; however, it has provided significant insight into vertebral mechanical behaviour, showing that vertebral mechanical properties and BMD have a poor correlation, and that both geometry and BMD must be considered [11]. To reduce computational cost and be more clinically useful, a 2D FEM may be sufficient to predict fracture risk. Also, a 2D FEM could utilize 2D DXA and radiographs to estimate bone tissue properties and geometry. These modalities are readily available and already frequently used to determine fracture risk and diagnose vertebral fractures.
The goal of this project is to use bone geometry and BMD obtained from radiographs and DXA measurements respectively to estimate fracture risk, using FEM performed on the median sagittal plane of lumbar vertebra 1 (L1) to lumbar vertebra 4 (L4) in a large population based national cohort of men and women aged 50 and older. Bone material properties are assigned using the assumption that bone tissue Young’s modulus can be estimated using BMD, and bone tissue modulus decreases with age in an exponential fashion. Our hypothesis is that 2D FEM will provide a better prediction of 5 year fracture risk than BMD alone, indicated by having a better sensitivity at baseline, and predicting more fractures at 5 years after baseline.
Methods
Sample Selection
Initiated in 1996, the Canadian Multicenter Osteoporosis Study (CaMos) is a randomly selected, ongoing prospective cohort study of the Canadian population age 25years and older. The study population represents an age-stratified-, sex- and region-specific sample consisting of 9,423 non-institutionalized individuals (6,539 women and 2,884 men) from nine study centres across Canada (St. Johns, Halifax, Quebec City, Toronto, Hamilton, Kingston, Saskatoon, Calgary and Vancouver). CaMos participants were recruited over an 18-month period from lists of random telephone numbers from all postal codes within 50 km of each study centre. Informed consent was obtained from each individual and the study received approval by the institutional review board at each participating centre. Baseline assessments took place between February 1996 and September 1997, and the year five assessments took place between February 2001 and September 2002 [12]. Only subjects over the age of 50 years were used in this study as only these subjects received both radiographs and BMD testing. This resulted in 4194 men and women. Baseline and year five assessments included an extensive interviewer-administered questionnaire, lumbar BMD testing, and lateral lumbar and thoracic spine radiographs, in which lumbar anterior, middle, and posterior heights were measured manually [13].
Open Source Software
All of the software used to perform the modelling in this project was open source. Gmsh version 2.4.1 [14] was used as a pre-processing software to create the finite element meshes. Elmer version 5.4.1 finite element software [15] was used for solving the finite element meshes. C++ programs were developed to automatically produce all of the input and output files required for Gmsh and Elmer, and for post processing data.
Bone Mineral Density
Bone mineral density was measured at L1 to L4. Seven centres used Hologic densitometers and two centres used Lunar densitometers. All Lunar measurements were converted to equivalent Hologic values using standard reference formulas [15]. Scans were reanalyzed to insure proper positioning of the regions of interest. A single European spine phantom was circulated across study sites and the measurements were used to calibrate machines. A threshold of 1.5% was used for between-centre corrections. The resulting corrections reduced measurements in Halifax (2.18%) and St. Johns (2.49%) and increased measurements in Vancouver (2.33%), Saskatoon (2.44%) and Toronto (2.96%). A machine-specific phantom local to each site was measured at the beginning of each day. The threshold for longitudinal change was defined as a 1% difference from the calibration point and seven of the nine machines remained within the limits. Hamilton and Toronto results both required a one-time correction. Hamilton measurements were reduced by 1.5% starting in January 1998 and Toronto measurements were increased by 0.85% starting in September 1997 [13].
Fractures
Self-reported incident fractures were identified by yearly postal questionnaire or scheduled interview at Year 3, Year 5, and Year 10. Further information concerning the fracture was gathered using a structured interview which included items on date, fracture site, circumstances leading to fracture, X-ray, and medical treatment. We classified fractures by skeletal site and considered minor-trauma fractures as those that occurred without trauma, or as a result of a fall from standing height or less.
Finite Element Models
One finite element model was created from the L1 to L4 X-ray and BMD data at baseline (Figure 1). The anterior, middle, and posterior heights for L1 to L4 were obtained from lateral radiographs. Vertebral width was assumed to be constant for L1 to L4 based on the height of L1 multiplied by 1.25, as vertebral width was not measured from the radiographs in the CaMos database [16]. Middle vertebral width was assumed to be 95% of superior and inferior vertebral width [17]. As these were significant assumptions, 80 radiographs were fully measured so these assumptions could be validated. The models contained 5 vertebral discs, the disc superior to each vertebra was assigned a height one quarter of the height of the inferior vertebra. The disc inferior to L4 was assigned the same height as the disc superior to L4. These disc heights are relatively larger than would occur in vivo; however, due to varying ratios between anterior and posterior heights (some were more than one and some were less than one), room for variation was required. Using vertebral heights and the previously mentioned assumptions, the model input files were automatically generated using Gmsh and contained approximately 1000 triangular elements. Element size was determined through convergence testing and computational restrictions due to the quantity of models being solved. The Gmsh files were then automatically converted to Elmer input files. An Elmer solver file containing material properties and boundary conditions was also automatically generated. Isotropic bone tissue Young’s modulus (E) in Gigapascals (GPa) was assigned to each vertebra based on the following (Equation 1):
Fig. 1.
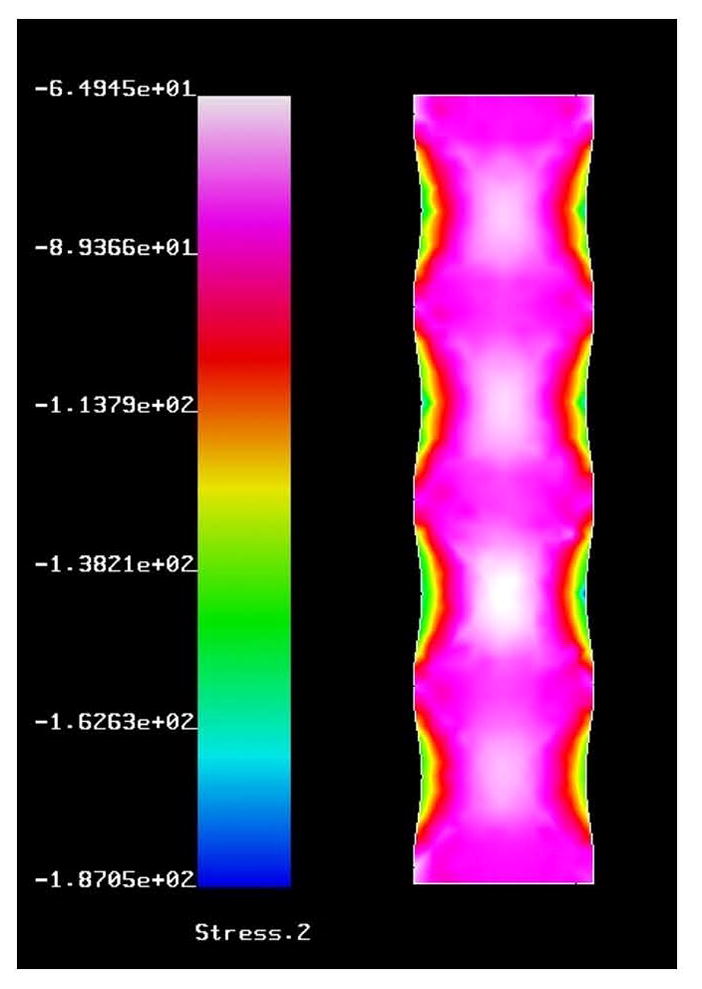
Sample finite element model. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.) Stress is shown in the vertical direction given in MPa.
Tissue stiffness varied with BMD in a polynomial fashion, and the best value for predicting fracture needed to be determined [18]. Tissue stiffness varied with age in an exponential fashion [13]. This was added into the model to incorporate the effects of ageing on overall bone strength, as bone structure could not be incorporated into this model and the effects of BMD on bone tissue strength were already incorporated. The magnitude of tissue stiffness was based on the values proposed in the paper by Schmidt et al., of 11 GPa and 0.140 GPa for cortical and trabecular bone respectively [19]. Since cortical and trabecular bone could not be segmented from the DXA images, 1 GPa was used as a baseline in equation 1 to assign both cortical and trabecular bone tissue Young’s modulus. The optimal values for the bone Young’s modulus was determined for equation 1. The discs isotropic tissue Young’s modulus of 4.2 Mpa was used as a baseline for testing for the optimal value in equation 1 [19]. Poisson’s ratios for bone and the discs were assigned 0.3 and 0.45, respectively [19]. Boundary conditions applied were axial compression based on a standing load of 800 Newtons (N) standing load for a 73 kg subject using the following equation F = BodyMass/73 * 800 N [20].
Analysis
Men and women were analyzed separately and divided into two groups: subjects with and those without minor trauma fragility fractures at any location excluding the skull, face, hands, fingers, feet, and toes. The finite element models were analyzed for reaction strain (an indication of spine stiffness). Men and women fracture and non-fracture groups were analyzed for the group mean and standard deviation. A Z-score was determined for each of the subjects in the fracture group for L1 to L4 average BMD, and reaction strain. A cutoff of 1.96 standard deviations from the healthy normal mean, was deemed an increased fragility fracture risk for testing this method. This was an arbitrary decision based on 1.96 standard deviations from the mean commonly used to indicated a significant difference (95% confidence interval). When a higher confidence interval was used (e.g. 2.54 standard deviations or 99% confidence interval) no subjects were deemed to be at increased risk of fragility fracture. Both the exponent and age normalization factors were adjusted to find optimal numbers for sensitivity. A modified receiver operator characteristic (ROC) curve was used during testing for visualization of the results. A true ROC curve was generated for DXA and FEM in predicting fractures at baseline in order to quantify the overall performance of each test. The relative risk of having an incident fracture at 5 years was found for subjects considered to be at an increased risk of fracture using both BMD and FEM. Subjects with or without a fracture at baseline were analyzed separately.
Results
There were 2957 women, with 583 of these having fragility fractures. There were 1237 men, with 203 of these subjects having fragility fractures. The characteristics of the study subjects are presented in Table 1. A sample FEM is shown in Figure 1. Each of the models solved in less than one second. The validation testing found a difference of 2.3% in reaction strain for the models in which all of the direct manual X-ray measurements were performed, and the models in which the width assumptions were used. The men and women fracture and non-fracture groups were significantly different for BMD and reaction strain. Figure 2 shows the results of the testing of Equation 1 for optimal bone and disc Young’s moduli using a cutoff of 1.96 standard deviations to indicate an increase in fracture risk. For women optimal values for Young’s modulus for bone and for the discs were 0.9 Gpa and 4.2 Mpa. For men optimal values for Young’s modulus for bone and for the discs were 1.1 Gpa and 5.2 Mpa. Figure 3 shows the testing of Equation 1 for the exponent and age normalization factors to find the optimal values for detecting the maximal number of fractured subjects at baseline. For women, a sensitivity of 3.77 % was found using BMD alone. For women, a sensitivity of 10.3 % was found for reaction strain using an exponent value of 3.375, and an age normalization factor of 40 to assign bone tissue Young’s modulus. For men, a sensitivity of 0.86 % was found using BMD alone. For men, a sensitivity of 11.3 % was found for reaction strain, using optimal parameters of 3.5 for the exponent and an age normalization factor of 50 to assign bone tissue Young’s modulus.
Table 1.
Ages, heights, and weights of the subjects without a baseline fracture (Healthy Women and Men) and subjects with a baseline fracture (Fractured Women and Men). A * symbol indicates a significant difference between healthy and fractured subjects.
| Study Subject Characteristics | ||||
|---|---|---|---|---|
| Group | Healthy Women | Fractured Women | Healthy Men | Fractured Men |
| Age | 67.01 ± 8.63* | 64.61 ± 8.65* | 65.67 ± 9.01 | 65.13 ± 8.8 |
| Height | 158.85 ± 6.48 | 159.32 ± 6.23 | 173.68 ± 7.27 | 172.84 ± 7.02 |
| Weight | 68.83 ± 13.08 | 69.0 ± 13.78 | 83.14 ± 13.23 | 81.77 ± 13.82 |
Fig. 2.
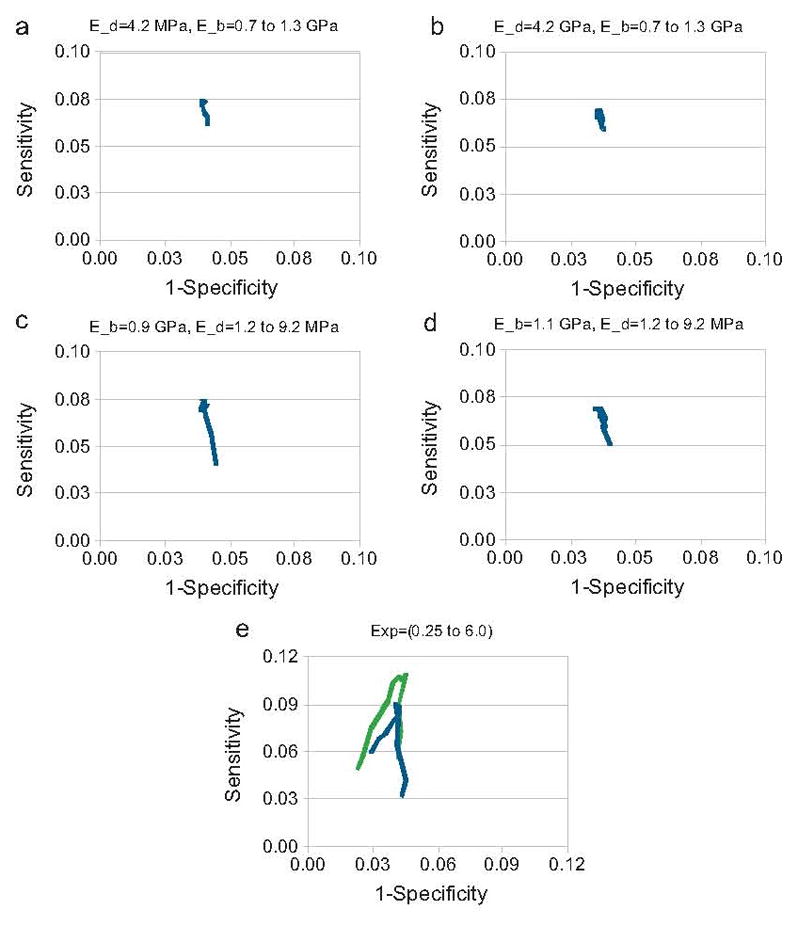
The modified ROC curves showing the testing of Young’s modulus for bone (E_b) and for the discs (E_d) in Eq. (1) are provided in figures (a)–(d). Results for females are given in figures (a) and (c) and the results for males are given in figures (b) and (d). The Young’s modulus for bone was varied from 0.7 to 1.3 GPa and Young’s modulus for the discs was varied from 1.2 to 9.2 MPa. Figure (e) shows how adding age into the model affects performance in green (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.) compared to without age in blue.
Fig. 3.
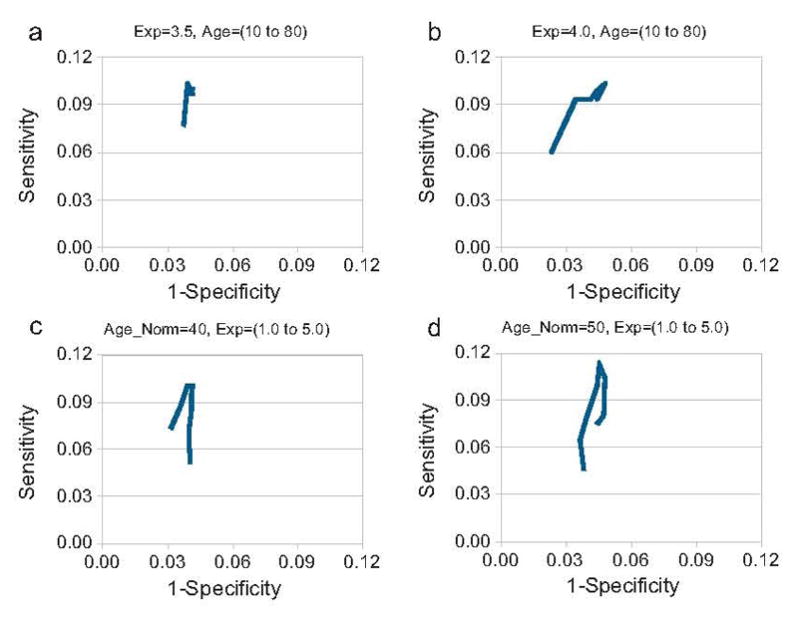
The modified ROC curves showing the testing of the exponent (Exp) in Eq. (1) are provided in figures (a) and (b). The modified ROC curves showing the testing of the age normalization factor (Age_Norm) in Eq. (1) are provided in figures (c) and (d). Results for females are given in figures (a) and (c) and the results for males are given in figures (b) and (d). The exponent was varied from 1.0 to 5.0 and the age normalization factor was varied from 10 to 80.
Figure 4 shows the ROC curves for the BMD and the FEM results. Qualitatively the FEM results were superior to BMD results as indicated by improved performance on the ROC curve. The areas under the ROC curve were found for 1-specificity values of 0.02 and 0.06 for both the BMD and FEM results. A higher area under the curve was found for women (0.0042 vs. 0.0030) and men (0.0041 vs. 0.0031) using FEM compared to the BMD.
Fig. 4.
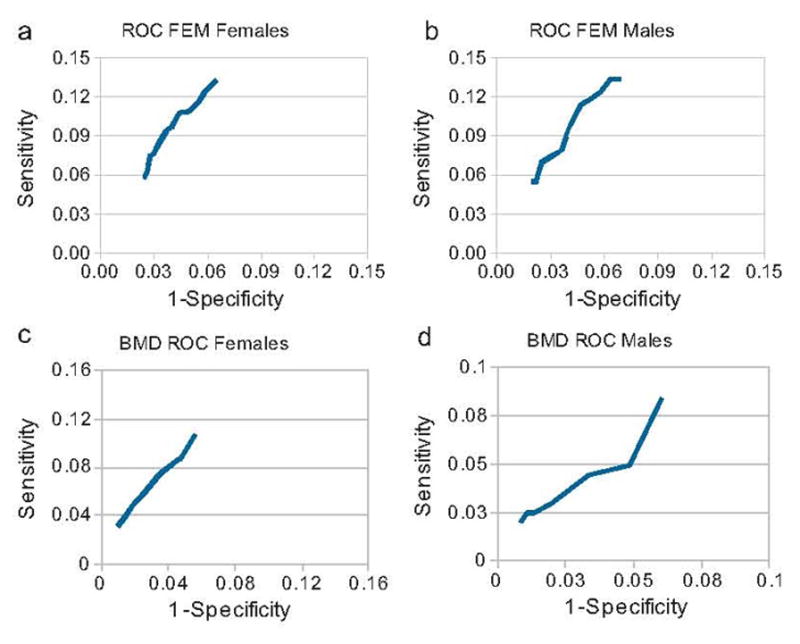
The ROC curves for the BMD results are provided in figures (a) and (b). The ROC curves for the FEM results using the optimal values for the exponent (Exp) and age normalization factors (Age_Norm) in Eq. (1) are provided in figures (c) and (d). Women are provided in figures (a) and (c) and men are provided in figures (b) and (d).
The relative risk of having a fracture at 5 years from baseline was found for subjects considered to be at high risk, with and without a baseline fracture using BMD and FEM. For women without a fracture at baseline, the relative risk of having a fragility fracture at 5 years after being considered high risk with FEM at baseline was 2.59 ± 1.58 compared to being considered high risk with BMD at baseline was 0.75 ± 0.19. For men without a fragility fracture at baseline, the relative risk of having a fragility fracture at 5 years after being considered high risk with FEM was 3.23 ± 1.43. There were no men considered high risk using BMD at baseline that went on to develop a fracture. For women with a fragility fracture at baseline, the relative risk of having a fracture at 5 years after being considered high risk with FEM at baseline, was 3.32 ± 2.22compared to being considered high risk at baseline with BMD was 3.43 ± 2.07. For men with a fragility fracture at baseline, the relative risk of having a fracture at 5 years after being considered high risk with FEM at baseline was 0.87 ± 0.12, compared to being considered high risk with BMD at baseline was 9.9 ± 2.78.
To compare our results from our population to the literature we found a 5 year relative risk, stratified by age using BMD and the reference data from a previous study using our population to obtain the T-scores [21]. For women over the age of 50 with a T-score less than 2.5, the 5 year relative risk of a minor trauma fracture was 1.57 ± 1.09, while the 5 year relative risk for men over the age of 50 with a T-score less than 2.5 was 2.02 ± 1.14.
Discussion
Finite element modelling has provided significant insight into vertebral mechanical behaviour, showing that vertebral structural properties and BMD are poorly correlated, and both must be considered in predicting vertebral strength [11]. Two dimensional finite element modelling using bone geometry from radiographs and BMD from DXA measurements to assign bone tissue properties, showed a three-fold better sensitivity at baseline in detecting subjects with fragility fracture compared to using BMD alone. The FEM results also exhibited better ROC curve performance and provided a better indication of 5 year fragility fracture risk. Men were found to have higher optimal values for Young’s modulus of the discs and bone, and had a higher age normalization factor.
The primary limitation of this project is that only some aspects of fracture risk were studied and other factors such as likelihood of falling, visual acuity, and response to falling were ignored. Z-scores were also used for the comparison between BMD and FEM as no reference data from young healthy adults was available for the FEM portion of this study. Also, multiple factors were included in the FEM (geometry, bmd, age, and weight), which was then compared to only BMD. When multiple factors were combined with BMD in a regression analysis, only BMD was a significant factor in detecting men and women with fractures at baseline. Some major assumptions were made about the geometry of the finite element models; however, the magnitude of this error was found to be only 2.3% and thus did not likely affect the outcome of the study. In this study weight, age, bone geometry and bone mineral density were combined into a single predictor of bone strength, and a 2D model of compression testing was used to predict bone strength in a 3D vertebra that experiences complex loading. In routine clinical practice, full 3D imaging of the spine using computed tomography is not performed on subjects being assessed for fracture risk due to excessive cost and radiation exposure. 3D finite element modelling of the spine is a valuable clinical research tool for studying spine mechanics and correlating spine mechanics to peripheral sites where less radiation can be used to measure 3D bone geometry and density [22,23]. The most likely future use for 3D finite element modelling of the spine based on CT scans will be retrospective analysis in patients for whom an abdominal or thoracic CT scan was performed for another medical reason [24]. Performing 3D modelling for screening purposes using peripheral sites is not available in all centres, and is more computationally expensive than 2D modelling; however, it allows for accurate and reproducible estimates of bone stiffness using linear models and can even provide an estimate of bone strength using a non-linear model [22, 25, 26].
Vertebral models in this study were used to predict fractures at all sites of the body, because vertebral data was available and other sites of the body can be more difficult to model (i.e. obtain geometry and apply boundary conditions). Although femoral neck BMD is more commonly used, it has been shown that lumbar spine BMD predicts fractures independent of femoral neck BMD and should not be ignored [27]. The 5 year relative risks of fracture found in this study were similar to the 10 year hazard ratios found using femoral neck BMD data from the Rotterdam study, which found that women older than 55 years deemed Osteoporotic using FN BMD had a 10 year hazard ratio of 2.7 (2.0 to 3.5), while men older than 55 deemed Osteoporotic using FN BMD had a hazard ratio of 2.7 (1.6 to 4.5) [28]. Vertebrae that had previously fractured were not eliminated in this study. Vertebrae that had a fracture would have an altered geometry during measurement, and could yield two possible results: very large deformities could produce an error during meshing and there would be no result (this occurred in one subject), or alternately, minor changes due to fracture may result in a smaller vertebra that would be solved normally. Based on the geometry and BMD, this would give an appropriate result because fractured vertebrae still carry load in vivo. The parameters determined in this study should be further tested in another study population to ascertain if parameters are transferable between populations. When comparing our lumbar spine BMD results to the literature we found that our relative risk of fracture was similar to values found for another Canadian population, which found a 10 year Hazard ratio for women of 1.49 (1.28 to 1.73) for each 1.0 T-score decrease in lumbar spine BMD [29]. This would give a 10 year risk of 3.75 for Osteoporotic subjects compared to the 5 year risk of 1.57 for Osteoporotic subjects found in this study. The exponent values found here were also similar to other values found in the literature for relating BMD to bone tissue strength [18, 22, 30]. The method used to adjust BMD for age is a novel technique; however, overall bone strength likely decreases with age due to factors such as a loss of collagen, and an exponential increase in fractures with age has been previously demonstrated [23].
The FEM exhibited better performance on the ROC curve compared to BMD alone, through a better sensitivity for a given 1-specificity (false positive rate) and an overall larger area under the ROC curve. The BMD ROC curve was flat at approximately 45 degrees. Therefore, any increase in sensitivity results in a proportional increase in the false positive rate. The FEM ROC curve did exhibit a minor curve in which sensitivity can be increased without a proportional increase in the false positive rate (see Figures 4c and 4d). Although the sensitivity for BMD and FEM were determined for predicting fractures at baseline, this was only for comparison and calibration. The values found for the sensitivities were relatively low and this is partly due to the fact that we did not have young healthy subjects with both BMD testing and X-rays for reference data for the FEM modelling. We were forced to use the Z-scores and unfortunately there will be many subjects without fractures that are in the healthy group that are at high risk of fracture due to their low bone quality. This decreases our sensitivity and needs to be addressed in our future work. The risk of future fracture with a positive test using both techniques was also examined and is more commonly used in the literature for comparing new tools for fracture prediction. The confidence intervals for BMD show no significant increase in risk of fracture with a positive test. Using the FEM method in this study, a relative risk of 2.59 ± 1.58 for women and 3.23 ± 1.43 for men was found and does indicate a significant increased risk with a positive test. This is a significant improvement over DXA which was not able to significantly predict which subjects were at risk of fracture. Being able to identify subjects at risk prior to losing a significant amount of their bone mass would allow treatment to begin earlier on in the disease process. Combining this new FEM method with other factors not included such as smoking and previous corticosteroid use could further improve its predictive ability.
The goal of this study was to determine if FEM could predict future fracture risk. Predicting fractures in subjects without a baseline fracture is of greater clinical use, as subjects that have already suffered a fracture are already known to be at high risk of another fracture. When the 5 year fracture data was examined, it was found that subjects deemed to be at high risk using FEM are more likely to have a fracture in 5 years than those considered to be at high risk using BMD, indicating that FEM is a better indicator of future fracture risk than BMD alone. This study has demonstrated that FEM can potentially be integrated into the clinical setting using readily available and frequently used imaging techniques for predicting future fracture risk and can improve on the use of BMD alone. In experimental studies, 3D FEM has been extensively used for measuring bone stiffness and strength. However, due to practical clinical restrictions, it is unlikely in the near future that 3D imaging methods will be used as a standard screening method to allow for 3D FEM in predicting fracture risk. Therefore, this 2D method will allow for initial work to be performed with FEM in a clinical setting to allow for parameters to be optimized and initial testing work to be performed that could benefit future 3D finite element modelling of the spine and at peripheral sites.
References
- 1.Kleerekoper M, Villanueva A, Stanciu J, Rao D, Parfitt A. The role of three-dimensional trabecular microstructure in the pathogenesis of vertebral compression fractures. Calcif Tissue Int. 1985;37:594597. doi: 10.1007/BF02554913. [DOI] [PubMed] [Google Scholar]
- 2.Peacock M, Turner C, Econs M, Foroud T. Genetics of osteoporosis. Endocr Rev. 2002;23:303326. doi: 10.1210/edrv.23.3.0464. [DOI] [PubMed] [Google Scholar]
- 3.Hanley DA, Josse RG. Prevention and management of osteoporosis: consensus statements from the Scientific Advisory Board of the Osteoporosis Society of Canada. 1. Introduction. CMAJ. 1996;155:921923. [PMC free article] [PubMed] [Google Scholar]
- 4.Cooper C, Atkinson E, Jacobsen S, OFallon W, Melton L. Population-based study of survival after osteoporotic fractures. Am J Epidemiol. 1993;137:10011005. doi: 10.1093/oxfordjournals.aje.a116756. [DOI] [PubMed] [Google Scholar]
- 5.Prudham D, Evans J. Factors associated with falls in the elderly: a community study. Age Ageing. 1981;10:141146. doi: 10.1093/ageing/10.3.141. [DOI] [PubMed] [Google Scholar]
- 6.Kelsey J, Hoffman S. Risk factors for hip fracture. N Engl J Med. 1987;316:404406. doi: 10.1056/NEJM198702123160709. [DOI] [PubMed] [Google Scholar]
- 7.Ross P, Davis J, Vogel J, Wasnich R. A critical review of bone mass and the risk of fractures in osteoporosis. Calcif Tissue Int. 1990;46:149161. doi: 10.1007/BF02555036. [DOI] [PubMed] [Google Scholar]
- 8.Marshall D, Johnell O, Wedel H. Meta-analysis of how well measures of bone mineral density predict occurrence of osteoporotic fractures. BMJ. 1996;312:12541259. doi: 10.1136/bmj.312.7041.1254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cummings S, Black D, Nevitt M, Browner W, Cauley J, Ensrud K, Genant H, Palermo L, Scott J, Vogt T. Bone density at various sites for prediction of hip fractures. The Study of Osteoporotic Fractures Research Group. Lancet. 1993;341:7275. doi: 10.1016/0140-6736(93)92555-8. [DOI] [PubMed] [Google Scholar]
- 10.Assessment of fracture risk and its application to screening for postmenopausal osteoporosis. Report of a WHO Study Group, World Health Organ Tech Rep Ser. 1994;843:1129. N. authors listed. [PubMed] [Google Scholar]
- 11.Crawford R, Keaveny T. Relationship between axial and bending behaviors of the human thoracolumbar vertebra. Spine. 2004;29:22482255. doi: 10.1097/01.brs.0000142435.90314.3b. [DOI] [PubMed] [Google Scholar]
- 12.Papaioannou A, Kennedy C, Ioannidis G, Gao Y, Sawka A, Goltzman D, Tenenhouse A, Pickard L, Olszynski W, Davison K, Kaiser S, Josse R, Kreiger N, Hanley D, Prior J, Brown J, Anastassiades T, Adachi J. The osteoporosis care gap in men with fragility fractures: the Canadian Multicentre Osteoporosis Study. Osteoporos Int. 2007 doi: 10.1007/s00198-007-0483-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Langsetmo L, Hanley D, Kreiger N, Jamal S, Prior J, Adachi J, Davison K, Kovacs C, Anastassiades T, Tenenhouse A, Goltzman D. Geographic variation of bone mineral density and selected risk factors for valueprediction of incident fracture among Canadians 50 and older. Bone. 2008 doi: 10.1016/j.bone.2008.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Geuzaine C, Remacle J. Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Int J Numer Meth Engng [Google Scholar]
- 15.Ruokolainen J, Savolainen V. ELMER Solver. http://www.csc.fi/english/pages/elmer/publications.
- 16.Masharawi Y, Salame K, Mirovsky Y, Peleg S, Dar G, Steinberg N, Hershkovitz I. Vertebral body shape variation in the thoracic and lumbar spine: characterization of its asymmetry and wedging. Clin Anat. 2008;21:4654. doi: 10.1002/ca.20532. [DOI] [PubMed] [Google Scholar]
- 17.Fan S, Ghista D, Ramakrishna K. Biomechanics of lumbar vertebrae as a functionally optimal structure. Conf Proc IEEE Eng Med Biol Soc. 2005;6:61926195. doi: 10.1109/IEMBS.2005.1615909. [DOI] [PubMed] [Google Scholar]
- 18.Homminga J, Huiskes R, Van Rietbergen B, Regsegger P, Weinans H. Introduction and evaluation of a gray-value voxel conversion technique. J Biomech. 2001;34:513517. doi: 10.1016/s0021-9290(00)00227-x. [DOI] [PubMed] [Google Scholar]
- 19.Schmidt H, Heuer F, Simon U, Kettler A, Rohlmann A, Claes L, Wilke H. Application of a new calibration method for a three-dimensional finite element model of a human lumbar annulus fibrosus. Clin Biomech (Bristol, Avon) 2006;21:337344. doi: 10.1016/j.clinbiomech.2005.12.001. [DOI] [PubMed] [Google Scholar]
- 20.Sato K, Kikuchi S, Yonezawa T. In vivo intradiscal pressure measurement in healthy individuals and in patients with ongoing back problems. Spine. 1999;24:24682474. doi: 10.1097/00007632-199912010-00008. [DOI] [PubMed] [Google Scholar]
- 21.Tenenhouse A, Joseph L, Kreiger N, Poliquin S, Murray TM, Blondeau L, Berger C, Hanley DA, Prior JC CaMos Research Group. Canadian Multicentre Osteoporosis Study. Estimation of the prevalence of low bone density in Canadian women and men using a population-specific DXA reference standard: the Canadian Multicentre Osteoporosis Study (CaMos) Osteoporos Int. 2000;11(10):897–904. doi: 10.1007/s001980070050. [DOI] [PubMed] [Google Scholar]
- 22.MacNeil Joshua A, Boyd Steven K. Bone strength at the distal radius can be estimated from high-resolution peripheral quantitative computed tomography and the finite element method. Bone. 2008;42(6):1203–1213. doi: 10.1016/j.bone.2008.01.017. [DOI] [PubMed] [Google Scholar]
- 23.Melton LJ, III, Riggs BL, Keaveny TM, Achenbach SJ, Kopperdahl D, Camp JJ, Rouleau PA, Amin S, Atkinson EJ, Robb RA, Therneau TM, Khosla S. Relation of vertebral deformities to bone density, structure, and strength. Journal of Bone and Mineral Research. 2010;25:1922–1930. doi: 10.1002/jbmr.150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Keaveny TM. Biomechanical computed tomography—noninvasive bone strength analysis using clinical computed tomography scans. Annals of the New York Academy of Sciences. 2010;1192:57–65. doi: 10.1111/j.1749-6632.2009.05348.x. [DOI] [PubMed] [Google Scholar]
- 25.MacNeil JA, Boyd SK. Accuracy of high-resolution peripheral quantitative computed tomography for measurement of bone quality. Med Eng Phys. 2007 Dec;29(10):1096–105. doi: 10.1016/j.medengphy.2006.11.002. Epub 2007 Jan 16. [DOI] [PubMed] [Google Scholar]
- 26.MacNeil JA, Boyd SK. Improved reproducibility of high-resolution peripheral quantitative computed tomography for measurement of bone quality. Med Eng Phys. 2008 Jul;30(6):792–9. doi: 10.1016/j.medengphy.2007.11.003. Epub 2008 Mar 4. [DOI] [PubMed] [Google Scholar]
- 27.Leslie WD, Kovacs CS, Olszynski WP, Towheed T, Kaiser SM, Prior JC, Josse RG, Jamal SA, Kreiger N, Goltzman D CaMos Research Group. Spine-Hip T-Score Difference Predicts Major Osteoporotic Fracture Risk Independent of FRAX(®): A Population-Based Report From CAMOS. J Clin Densitom. 2011 Jun 30; doi: 10.1016/j.jocd.2011.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schuit SC, van der Klift M, Weel AE, de Laet CE, Burger H, Seeman E, Hofman A, Uitterlinden AG, van Leeuwen JP, Pols HA. Fracture incidence and association with bone mineral density in elderly men and women: the Rotterdam Study. Bone. 2004 Jan;34(1):195–202. doi: 10.1016/j.bone.2003.10.001. Erratum in: Bone. 2006 Apr;38(4):603. [DOI] [PubMed] [Google Scholar]
- 29.Leslie WD, Lix LM. Manitoba Bone Density Program. Absolute fracture risk assessment using lumbar spine and femoral neck bone density measurements: derivation and validation of a hybrid system. J Bone Miner Res. 2011 Mar;26(3):460–7. doi: 10.1002/jbmr.248. [DOI] [PubMed] [Google Scholar]
- 30.Hangartner TN. Image-based strength assessment of bone. Conf Proc IEEE Eng Med Biol Soc. 2007;1:44254428. doi: 10.1109/IEMBS.2007.4353320. [DOI] [PubMed] [Google Scholar]


