Enhancement of crop photosynthesis by diffuse light: quantifying the contributing factors

Abstract

Background and Aims

Plants use diffuse light more efficiently than direct light. However, experimental comparisons between diffuse and direct light have been obscured by co-occurring differences in environmental conditions (e.g. light intensity). This study aims to analyse the factors that contribute to an increase in crop photosynthesis in diffuse light and to quantify their relative contribution under different levels of diffuseness at similar light intensities. The hypothesis is that the enhancement of crop photosynthesis in diffuse light results not only from the direct effects of more uniform vertical and horizontal light distribution in the crop canopy, but also from crop physiological and morphological acclimation.

Methods

Tomato (Solanum lycopersicum) crops were grown in three greenhouse compartments that were covered by glass with different degrees of light diffuseness (0, 45 and 71 % of the direct light being converted into diffuse light) while maintaining similar light transmission. Measurements of horizontal and vertical photosynthetic photon flux density (PPFD) distribution in the crop, leaf photosynthesis light response curves and leaf area index (LAI) were used to quantify each factor's contribution to an increase in crop photosynthesis in diffuse light. In addition, leaf temperature, photoinhibition, and leaf biochemical and anatomical properties were studied.

Key Results

The highest degree of light diffuseness (71 %) increased the calculated crop photosynthesis by 7·2 %. This effect was mainly attributed to a more uniform horizontal (33 % of the total effect) and vertical PPFD distribution (21 %) in the crop. In addition, plants acclimated to the high level of diffuseness by gaining a higher photosynthetic capacity of leaves in the middle of the crop and a higher LAI, which contributed 23 and 13 %, respectively, to the total increase in crop photosynthesis in diffuse light. Moreover, diffuse light resulted in lower leaf temperatures and less photoinhibition at the top of the canopy when global irradiance was high.

Conclusions

Diffuse light enhanced crop photosynthesis. A more uniform horizontal PPFD distribution played the most important role in this enhancement, and a more uniform vertical PPFD distribution and higher leaf photosynthetic capacity contributed more to the enhancement of crop photosynthesis than did higher values of LAI.

INTRODUCTION

Light in a crop canopy is heterogeneously distributed in the horizontal and the vertical plane. Due to the curvilinear response of leaf photosynthesis to light intensity, a more homogenous light distribution in the canopy could be advantageous. Solar light is composed of a diffuse and a direct component. Diffuse light arises from the scattering of light by molecules or larger particles in the atmosphere and comes from many directions simultaneously. Direct light arrives in a straight line from the sun without being scattered. Many studies suggest that plants use diffuse light more efficiently than direct light, and this is mainly attributed to a more uniform light distribution in the canopy (Cohan et al., 2002; Farquhar and Roderick, 2003; Gu et al., 2003; Alton et al., 2007; Mercado et al., 2009).

Light direction plays a pivotal role in the distribution of light in a canopy (Goudriaan and Van Laar, 1994). Light intensity usually decreases exponentially from the top to the bottom in a canopy, as described by the Lambert–Beer law (Monsi and Saeki, 2005). Diffuse light usually exhibits a lower extinction coefficient than direct solar light (Urban et al., 2007, 2012), although the effect depends on solar position (Allen, 1974; Morris, 1989). In many crop photosynthesis models, horizontal light distribution in the canopy is determined by the sunlit and shaded leaf area (Spitters, 1986; De Pury and Farquhar, 1997; Wang and Leuning, 1998; Johnson et al., 2010). At a certain canopy depth, some leaves are shaded and thus do not receive direct light, while others do (sunlit leaves).

Light distribution in the canopy is not only influenced by the direction of the light or the fraction of diffuse or direct light incident on the canopy, but also depends on crop architecture. Sarlikioti et al. (2011a, b) indicated that plant architecture has a large impact on crop light distribution and photosynthesis.

Diffuse light penetrates deeper into the canopy; thus, the lower positioned leaves will receive on average a higher light intensity when light is diffuse. This higher light intensity leads to an acclimation of the nitrogen distribution in the canopy (Johnson et al., 2010). Related to changes in nitrogen distribution, leaf photosynthetic capacity might differ in diffuse and direct light. In many plant species, the photosynthetic capacity and leaf nitrogen content depend on the prevailing light intensity within the canopy (Anten et al., 1998; Drouet and Bonhomme, 2004). Acclimation to diffuse or direct light also includes acclimation of leaf morphology and anatomy, which affect light absorption and, consequently, photosynthesis (Hemming et al., 2007; Brodersen et al., 2008; Markvart et al., 2010). Furthermore, diffuse light might also decrease leaf temperature and the extent of photoinhibition as fewer local peaks in light intensity occur.

Many studies on diffuse light have been carried out by comparing plant responses on cloudy and clear days, which implies not only a difference in the fraction of diffuse light, but also large differences in light intensity, and the subsequent changes in microclimatic parameters such as air and soil temperature, and vapour pressure deficit (VPD) (Gu et al., 2002; Farquhar and Roderick, 2003; Alton et al., 2007; Urban et al., 2007, 2012; Knohl and Baldocchi, 2008). These changes directly or indirectly influence canopy photosynthesis. Due to such large differences in microclimate, a quantitative exploration of the specific effects of light distribution on canopy photosynthesis in diffuse and direct light conditions is hardly possible in the open field.

The relative importance of the different effects of diffuse light on crop photosynthesis mentioned above has never been quantified. Many studies relevant to light distribution are based on model simulations and give a good estimation of light distribution in a canopy (Johnson and Thornley, 1984; Thornley, 2002; Johnson et al., 2010; Suwa, 2011). However, to the best of our knowledge, detailed analyses based on measurements of both the vertical and horizontal light distribution in a canopy and the consequences for crop photosynthesis are lacking. In particular, no studies have been performed in crops grown at different levels of diffuseness with similar incident light intensity on the top of the crop.

This aim of this study is to analyse the factors which contribute to an increase in crop photosynthesis in diffuse light and to quantify their relative contribution under different levels of diffuseness at similar light intensities. The hypothesis is that the enhancement of crop photosynthesis in diffuse light depends not only on the direct effects of a more uniform vertical and horizontal light distribution, but also on crop physiological and morphological acclimation. To test this hypothesis, a study was conducted in glasshouses covered with diffuse glass, converting a portion of the direct solar light into diffuse light with different degrees of diffuseness, without affecting light transmission. Tomato, often seen as a model plant (Kimura and Sinha, 2008), was used in this study.

MATERIALS AND METHODS

Plant material and growth conditions

Tomato (Solanum lycopersicum, ‘Komeett’; Monsanto, Creve Coeur, MO, USA) plants, grafted on the rootstock ‘Maxifort’ (Paramount, Quinter, KS, USA), were planted on Rockwool on 16 December 2010 in three adjacent east–west-oriented Venlo-type glasshouse compartments. Each compartment had an area of 144 m² with a gutter height of 5·5 m, and was located in Bleiswijk, The Netherlands (52°N, 4·5°E). The compartments were covered by glass (Guardian Agro, Dudelange, Luxembourg) with 0 (control), 45 and 71 % haze factor for the three compartments, respectively. The haze factor indicates the fraction of direct light converted into diffuse light. The hemispherical transmission for PPFD of the glass was 83 % for the three glass types. The haze factor and hemispherical transmission of the glass were determined in an optical sphere according to ASTM International (2007). The photostationary state of phytochrome (PSS), the R/FR ratio (the ratio between red light and far-red light) and the B/R ratio (the ratio between blue light and red light) of the penetrating light were estimated from the spectral distribution of hemispherical glass transmission and solar photon flux, based on 1 nm intervals from 400 to 800 nm (Sager et al., 1988). The PSS values of the penetrating light in 0, 45 and 71 % haze treatment were 0·718, 0·718 and 0·713, respectively; R/FR ratios were 1·25, 1·25 and 1·22, respectively; and B/R ratios were 0·44, 0·44 and 0·42, respectively. An overview of the spectral transmittance of the glass is provided in Supplementary Data Fig. S1. The greenhouse transmissivity was 66 %, measured in March 2011 on a cloudy day, and no significant difference (P = 0·07) was found among the three compartments.

Stem density was initially 2·55 stems m^–2 and increased to 3·4 stems m^–2 at 10 weeks after planting. Plants were grown on Rockwool with drip irrigation. The mean pH of the irrigation water was 6·1 and mean EC (electrical conductivity) was 5·1 dS m^–1. Plant rows were in the east to west orientation. The distance between rows was alternating between 60 and 90 cm, resulting in a double row followed by a path. A standard horticultural computer (Hogendoorn-Economic, Hogendoorn, Vlaardingen, The Netherlands) was used to control the same climate (temperature, air humidity and CO₂ concentration) in the three compartments. Solar radiation was continuously measured outside the greenhouse with a weather station system (WS-GP2 Weather station, Delta-T, Cambridge, UK) throughout the growing period. PPFD was estimated from solar radiation, assuming that half the global radiation is PPFD (Jacovides et al., 2003). Relevant measurements were mainly performed from June to September 2011. During this period, average daily outside global radiation was 15 MJ m^–2 d^–1; average day/night temperature inside the greenhouses was 22/17 °C, average daytime CO₂ concentration was 526 μmol mol^–1 and relative humidity was 72 %. During the growing period, 53 % of the global radiation was direct radiation, which was estimated from hourly values of global radiation according to Spitters et al. (1986).

Fruit production and measurements of crop morphological properties

Three double rows in the middle of the greenhouse were selected for production determination; ripe fruits were harvested weekly, starting from 13 weeks after planting. Fruit fresh weight was determined at each harvest. Crop specific leaf area (SLA) was measured four times (in April, June, July and September) during the growing season. Leaves (20–25) were randomly picked from top to bottom in the crop to estimate the leaf area of one plant (one replicate); four replicates were selected in each treatment at each time. Leaf area was measured with a leaf area meter (LI-3100C, LI-COR, Lincoln, NE, USA); leaves were dried for 48 h at 80 °C in a ventilated oven to determine their dry weights. The SLA was calculated by dividing leaf area by leaf dry weight. Crop leaf area index (LAI) was estimated non-destructively from measuring length and width at the widest point of each leaf of the six randomly selected plants; the relationship between leaf area and leaf width and length was estimated from destructive measurements of 56 leaves of comparable plants. The angle of all leaves of six plants was manually measured with a protractor in each treatment at the beginning of August; these measurements were mainly made during the morning hours (0900–1300 h). Leaf angle was determined as the angle of the leaf rachis in relation to the horizontal plane at the leaf insertion point on the stem.

PPFD distribution measurements in the canopy

The distribution of PPFD within the canopy was measured with a 75 cm long light probe, in relation to a reference sensor above the crop (Sunscan, Delta-T, Cambridge, UK). The light probe was positioned perpendicularly to the row. For characterization of the vertical PPFD distribution within the canopy, six spots in each treatment were randomly selected; PPFD was measured from the top to the bottom of the canopy at 25 cm height intervals at each spot, with four measurements taken at equal distances (15 cm) from each other at each height level. The LAI at each height was estimated from measurements of the length and width of leaves. Under clear sky conditions, the measurements were repeated on 6 d in the 0 and 71 % haze treatments, and on 3 d in the 45 % haze treatment. During the measurements, solar elevation ranged from 29 to 56° and the fraction of diffuse global radiation ranged from 12 to 28 %. Measurements under fully overcast sky conditions were repeated on 4 d.

The horizontal PPFD distribution was measured at 50 cm below the top of the crop in three double rows. Measurements were taken at 25 cm intervals over 5 m length in each double row in the 0 and 71 % haze treatments. Measurements were repeated on 2 d under clear sky conditions. During these measurements, the solar elevation ranged from 40 to 46° and the fraction of diffuse global radiation ranged from 25 to 32 %. Measurements under fully overcast sky conditions were repeated on 4 d.

Leaf photosynthesis light response curve measurements

Leaf photosynthesis light response curves were measured with a portable gas exchange device equipped with a leaf chamber fluorometer (LI-6400; LI-COR) at three canopy depths in June. Canopy depths were defined as leaf number 5 (uppermost fully expanded leaf; leaf number 1 was the uppermost leaf longer than 5 cm), leaf number 10 and leaf number 15 (this definition of canopy depth is used for all measurements herein). Measurements were carried out between 0900 and 1500 h. At each canopy depth, six leaves from different plants were randomly selected for six light response curves. On 1 d, one leaf from each treatment was measured at one specific canopy depth before 1200 h; similar measurements, but at another canopy depth, were done after 1200 h. Each canopy depth was measured on 3 d in the morning and 3 d in the afternoon. The adaxial side of the leaf was illuminated by the light source (10 % blue, 90 % red). The starting PPFD was 500 μmol m^–2 s^–1, followed by 250, 100, 50, 25, 0, 750, 1000, 1250 and 1500 μmol m^–2 s^–1; at each PPFD, the measurements were taken when the photosynthesis rate reached steady state (after about 10 min). The highest PPFD was applied at the end of measurements to avoid photoinhibition (Leverenz et al., 1990). The VPD in the leaf chamber was maintained below 1 kPa; leaf temperature and CO₂ concentration in the measurement chamber were maintained at 25 °C and 700 μmol mol^–1, respectively.

Leaf temperature measurements

Leaf temperature was measured with K-type fine-wire thermocouples at three canopy depths with three replicates in each treatment, and continuously recorded for 19 d. The thermocouples were positioned in the centre of the abaxial side of leaflets. The contact between the thermocouples and leaf surface was checked three times per day. Air temperature was measured with one thermocouple positioned in the middle of a ventilated measuring box (20 × 20 × 10 cm) per treatment per canopy depth. The measurement positions were adjusted weekly as the plants grew.

Chlorophyll fluorescence measurements

The maximum photosystem II (PSII) efficiency (F_v/F_m) was measured on four fully expanded sun-exposed leaves at each of the three canopy depths with a portable chlorophyll fluorometer (PAM-2000, Walz, Germany) at five time points (0900, 1300, 1400, 1500, 1600 and 1700 h) on clear days. Red light was used as the measuring light (2 μmol m^–2 s^–1) and saturating flashes (8000 μmol m^–2 s^–1). A leaf clip holder (DLC-8) was used for dark adaptation for 30 min prior to the measurements.

Leaf biochemical and anatomical measurements

Leaf samples were collected at the beginning of July for biochemical and anatomical measurements. Six leaf discs, 1·6 cm in diameter, were punched out of six leaves at each canopy depth in the morning; they were used to determine chlorophyll a and b content. Dimethylformamide was used as solvent, and the absorbance of the extracts was measured using a Cary 4000 spectrophotometer (Agilent Technologies, Santa Clara, CA, USA). The chlorophyll concentrations were calculated using the equations derived by Wellburn (1994). Total nitrogen content was determined with an elemental C/N analyser (model EA 1108, FISONS Instruments, Milan, Italy). Stomatal density was estimated by using a silicone rubber impression technique (Fanourakis et al., 2011). For leaf anatomical observations, six leaf samples (0·5 × 1 cm) from six plants were cut at each canopy depth and immediately fixed in 4 % neutralized formalin–acetic acid–alcohol solutions. Before being embedded in Technovit 7100 plastics, leaf samples were dehydrated in a graded ethanol series. Sections of each leaf sample, 7 μm thick, were cut with an ultramicrotome (Leica 2030 Biocut; GMI, Ramsey, MN, USA) and stained with Schiff's reagent and toluidine blue for light microscopy. Leaf thickness, palisade tissue and spongy tissue thickness were measured from microscopic photographs taken from the sections at × 100 magnification.

Statistical analysis

Treatment effects on measured plants and light characteristics were evaluated by analysis of variance (ANOVA), using GenStat 14th edition, assuming replications in the same greenhouse compartment to be independent.

A non-linear mixed effects model (Qian et al., 2012), using the non-rectangular hyperbola function (Thornley, 1976), was fitted to the measured photosynthetic light response data. The statistical software program R, version 2.14.2, package nlme was used to estimate the parameters P_max, a, Θ and R_d in the non-rectangular hyperbola function

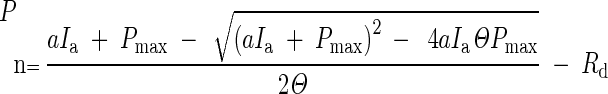(1)

where dependent variable P_n is the net leaf photosynthesis rate (μmol m^–2 s^–1) and regressor I_a is the PPFD absorbed by the leaf (μmol m^–2 s^–1); I_a was estimated from the incident PPFD multiplied by the absorption coefficient of single leaves (0·88; measurements on reflectance and transmittance of single leaves is described in the Appendix). Parameter P_max represents the light-saturated net leaf photosynthesis rate (μmol m^–2 s^–1), a is the light-limited quantum efficiency (μmol CO₂ μmol^–1 photons), Θ is the curvature parameter, and R_d is the photosynthesis rate at light intensity I_a = 0 (dark respiration, μmol m^–2 s^–1). A non-linear random coefficients model was used to accommodate the repeated photosynthesis measurements per leaf. The random part of the model specified that the four parameters have random effects per plant. In the fixed part of the non-linear mixed effect model we allowed the four parameters to be different for the nine treatment × canopy layer combinations, splitting effects into main effects and interaction. The comparison between treatments at the three individual canopy depths was of particular interest.

Crop photosynthesis calculation

An overview of the crop gross photosynthesis (from here onwards called crop photosynthesis) calculation is presented in this section, while more details are presented in the Appendix. Crop photosynthesis was calculated from the photosynthesis light response curve of single leaves, the incoming radiation, the canopy light profile and the LAI. Integrating instantaneous crop photosynthesis over time yielded the cumulative crop photosynthesis. The variables and parameters, with default values, are listed in Tables A1–A3 of the Appendix.

Leaf gross photosynthesis

The rate of leaf gross photosynthesis (P_g; μmol CO₂ m^–2 leaf s^–1) was calculated according to eqn (2), which was derived from the fitted light response curves [eqn (1)]

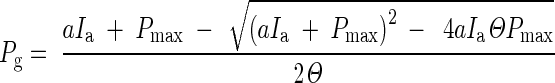(2)

Canopy light profile and crop photosynthesis

The PPFD decreases exponentially with canopy depth according to the Lambert–Beer law (Monsi and Saeki, 2005)

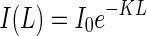(3)

where I₀ is incident PPFD at the top of the canopy (μmol m^–2 s^–1), K is the extinction coefficient, L is the cumulative LAI from the top of the canopy to a given depth in the canopy (m² leaf m^–2 ground), and I(L) is the PPFD (μmol m^–2 s^–1) at canopy depth L.

Subscripts ‘df’ and ‘dr’ denote the diffuse and direct components of PPFD. Hence, incident PPFD at the top of the canopy (I₀) is

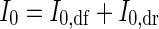(4)

Subscript ‘a’ denotes the absorption of PPFD; thus the absorbed PPFD at canopy depth L is

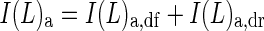(5)

For calculating canopy photosynthesis, the crop canopy was divided into three canopy depths which were selected by Gaussian integration (Goudriaan, 1986). The rate of leaf photosynthesis at each selected Gaussian canopy depth L_p [P_g(L_p)] (μmol CO₂ m^–2 leaf s^–1) is calculated according to

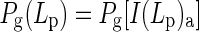(6)

The rate of whole-canopy photosynthesis [P_g,c; μmol CO₂ m^–2 ground s^–1] is calculated by integrating the weighted average of the leaf photosynthesis rate at the three canopy depths; using eqn (6) gives

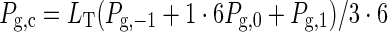(7)

where L_T is total LAI from the top to the bottom of the canopy, and P_g,–1, P_g,0 and P_g,1 are the leaf photosynthesis rate at the three Gaussian canopy depths (top, middle and bottom of the canopy, respectively). For more discussion of the Gaussian integration used for canopy photosynthesis calculation, see Spitters (1986) and Goudriaan (1986).

The canopy photosynthesis rate was calculated at 126 spots in each treatment where the horizontal PPFD distribution measurements were taken; canopy PPFD absorption at these spots was estimated according to the relative variation of PPFD in the horizontal direction. Average canopy photosynthesis rate over these spots represents instantaneous canopy photosynthesis, which was integrated from 1 April to 1 October 2011 to obtain cumulative crop photosynthesis.

Quantifying the contributing factors to crop photosynthesis in diffuse light treatment

Cumulative crop photosynthesis was calculated in both 0 and 71 % haze treatments. Afterwards, four factors (vertical PPFD distribution, horizontal PPFD distribution, photosynthesis light response curves and LAI) were considered separately in each of the treatments for calculation of the cumulative crop photosynthesis; this aims to quantify their relative contribution for crop photosynthesis enhancement in the 71 % haze treatment. When quantifying each of the four factors, the other three factors were assumed to be constant in the two treatments, using the measured values of the 0 % haze treatment. Constant LAI (Fig. 1) and leaf photosynthetic traits (Fig. 8) in each treatment were applied for cumulative crop photosynthesis calculation over the growing period from 1 April to 1 October, as based on measurements during the summer months. Furthermore, an assumption was that the horizontal variability of PPFD at the three canopy depths was similar.

Fig. 1.

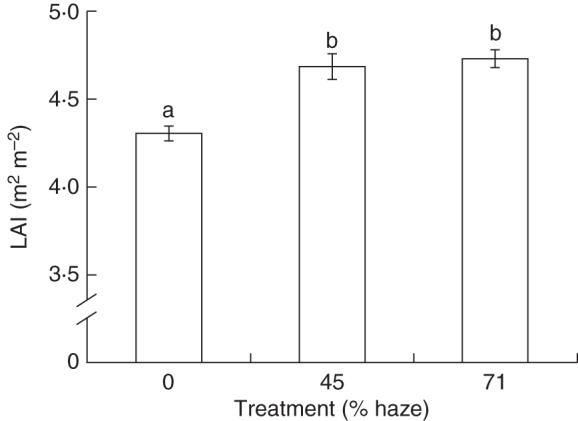
Average leaf area index (LAI) in summer months. Measurements were carried out on 25 May, and 5 and 27 July. Six plants were measured at each treatment each time. Error bars show ±s.e. (n = 18). Letters show statistically significant differences (P < 0·05).

Fig. 8.

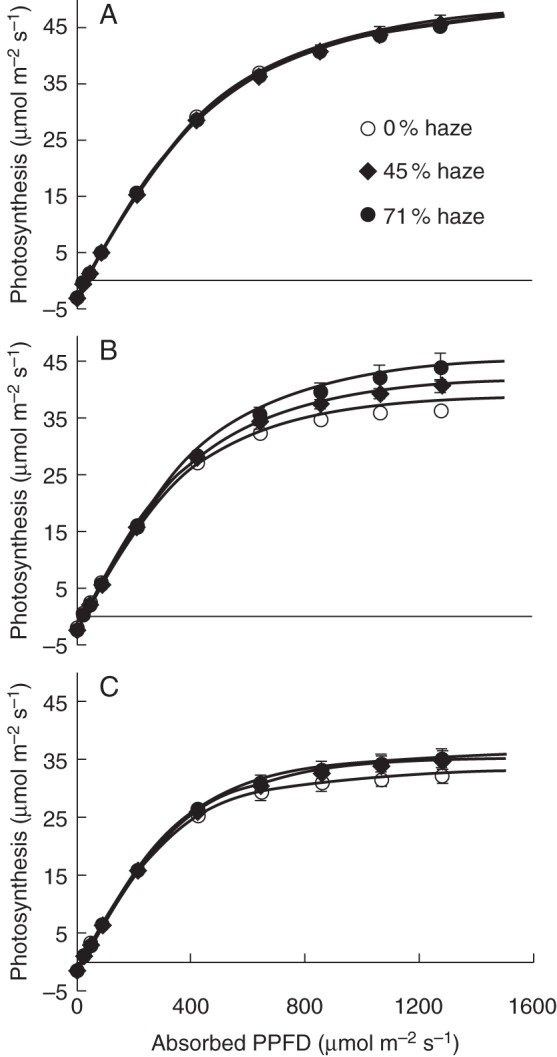
Photosynthetic light response curves of leaves at the top (A), middle (B) and bottom (C) of the canopy. These measurements were taken in June. During the measurements, leaf temperature and CO₂ concentration in the measurement chamber were maintained at 25 °C and 700 μmol mol^–1, respectively. Error bars show ±s.e. (n = 6).

RESULTS

Fruit production and crop morphological properties

The cumulative fresh weight of harvested fruits was 59·1 kg m^–2 at the end of the growing season in the control treatment. It was 8·4 % higher in the 45 % haze and 10·4 % higher in the 71 % haze treatment. For detailed information about fruit production. see Dueck et al. (2012).

In all treatments, the upper leaves of a plant showed a positive leaf angle with respect to the horizontal plane, ranging from + 50 to 0°, while the lower leaves showed a negative leaf angle, ranging from 0 to –15°. No treatment effect on leaf angle was observed (Supplementary Data Fig. S2). Furthermore, haze treatments resulted in a higher LAI (P < 0·01; Fig. 1) and a lower crop SLA (P < 0·01; Fig. 2) compared with the control.

Fig. 2.

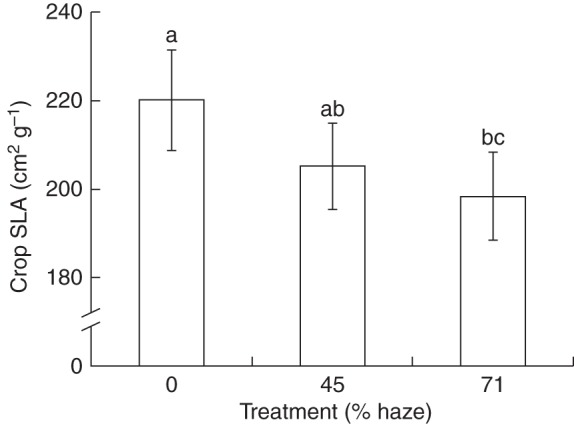
The effect of haze treatments on crop specific leaf area (SLA). Leaf samples were averaged down the canopy and over two sunny (7 April and 4 July) and two cloudy days (8 June and 1 September). On each date four replicate plants were sampled per treatment. Error bars show ±s.e. (n = 16). Letters show statistically significant differences (P < 0·05).

PPFD distribution in the crop canopy

The PPFD decayed exponentially with increasing LAI according to the Lambert–Beer law (Fig. 3). On cloudy days when PPFD was fully diffuse, the vertical distribution of PPFD in the canopy was similar in all three treatments (Fig. 3A). On clear days, however, PPFD decayed more rapidly in the control in comparison with the haze treatments (Fig. 3B). The PPFD inside the canopy was up to 9 % higher at LAI 1, 6 % higher at LAI 2 and 1 % higher at LAI 3 in the haze treatments compared with the control. Consequently, the extinction coefficient on clear days [K; eqn (3)] was significantly lower (P < 0·01) in both haze treatments (K = 0·81) than in the control (K = 0·99). The extinction coefficient in both haze treatments on clear days was similar to that on cloudy days.

Fig. 3.

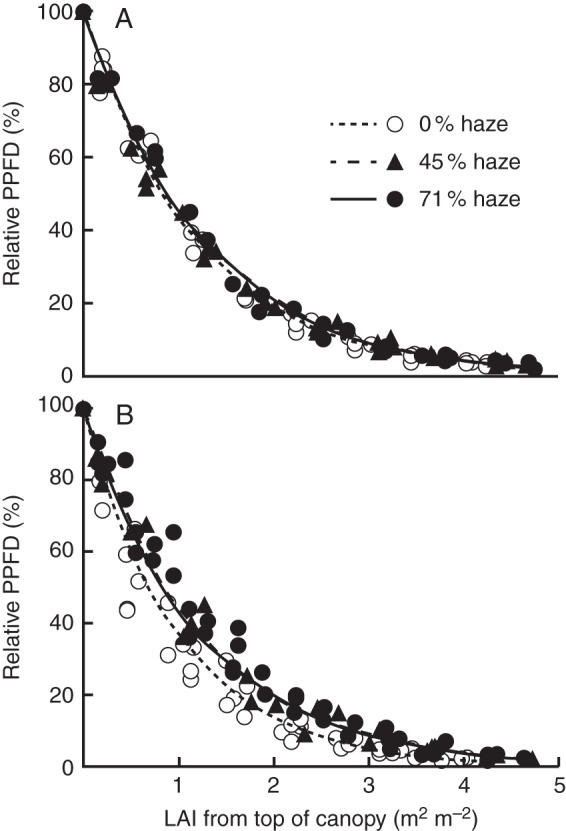
The effect of haze treatments on the vertical PPFD distribution within a tomato crop on cloudy days (A; 13, 14, 29 July, 12 September) and clear days (B; 1, 4 August, 2, 3, 29, 30 September for 0 and 71 % haze treatment; 1, 4 August, 3 September for 45 % haze treatment). Each symbol represents the average of six replicates measured in one day. Lines are fitted curves based on the Lambert–Beer law [eqn (3)].

In the horizontal plane, PPFD was homogeneously distributed in the upper part of the canopy on cloudy days in the 0 and 71 % haze treatments (Fig. 4A). On clear days, however, a large variation in PPFD in the 0 % haze treatment was observed compared with the 71 % haze treatment, as indicated by the coefficient of variation (42 and 14 %, respectively; Fig. 4B).

Fig. 4.

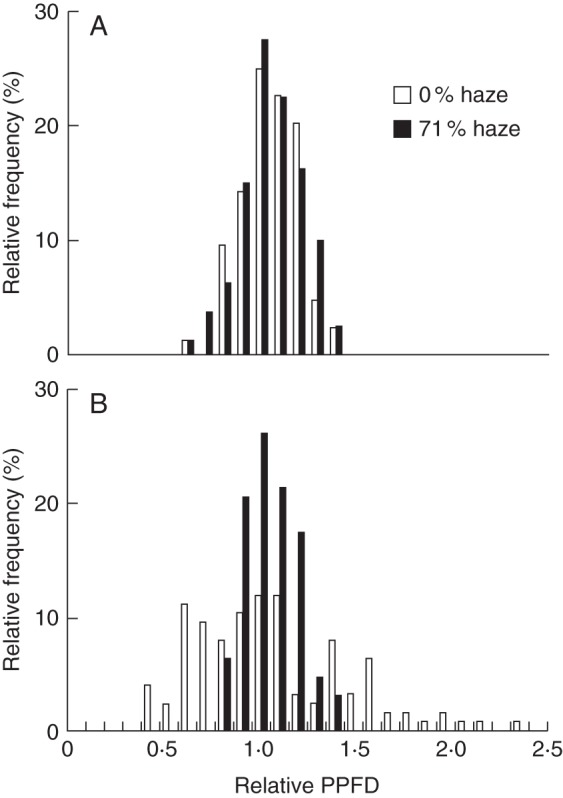
The effect of haze treatments on the horizontal PPFD distribution within a tomato crop canopy on cloudy days (A; 13, 14, 29 July and 31 August) and clear days (B; 2 and 3 September). All measurements were performed at 50 cm below the canopy top. In both panels the y-axis indicates the frequency distribution of PPFD in a horizontal plane. The x-axis indicates the relative PPFD; 1·0 represents the average PPFD on the horizontal plane.

Leaf temperature

Leaf temperature differed greatly between the control and haze treatments on clear days; this difference in leaf temperature was observed only at the top of the canopy where leaves were exposed to the sun (Fig. 5), but not in the middle and bottom leaves (Supplementary Data Fig. S3). The difference between top leaf and air temperature (ΔT) at midday on clear days was 3–5 °C higher in the control than in haze treatments. Moreover, top leaf temperature in haze treatments remained close to the air temperature on clear days.

Fig. 5.

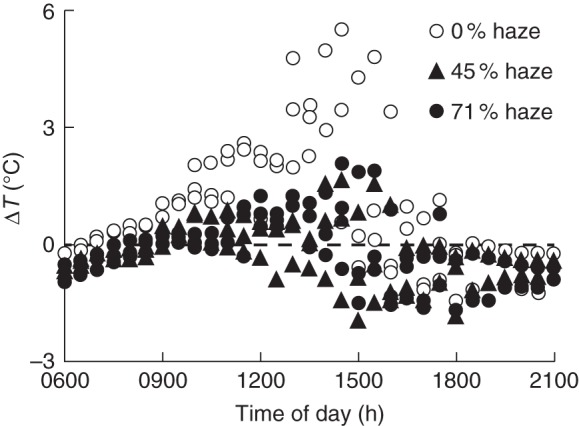
Diurnal pattern of the temperature difference between leaf and air (ΔT) at the canopy top layer on three clear days (2, 4 and 5 August; average global radiation was 18·8 ± 1·3 MJ m^–2 d^–1). Each symbol represents the average of measurements over 30 min on three leaves.

Photoinhibition

When top leaves were exposed to the full radiation (midday), maximum PSII efficiency (F_v/F_m) was reduced compared with measurements in the morning, suggesting photoinhibition. This reduction was more pronounced in the control than in haze treatments (Fig. 6). At 1400 h, when global radiation was >800 W m^–2, F_v/F_m was reduced by 21 % in the control and 12 % in haze treatments, while this difference disappeared later in the afternoon when the global radiation was low. Although F_v/F_m in the middle and bottom leaves also showed a diurnal trend with small differences between morning and midday, treatment effects were not found in these leaves (Supplementary Data Fig. S4).

Fig. 6.

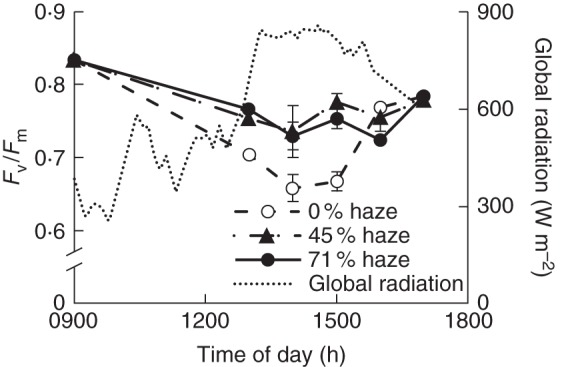
Maximum PSII efficiency (F_v/F_m) of top leaves on a clear day (15 August). Error bars represent ± s.e. (n = 4).

Leaf photosynthesis, biochemical and anatomical properties

For the parameters in the leaf photosynthesis light response curves, a significant difference in P_max in the middle canopy layer (P = 0·01) was found between treatments, but not in the top and bottom layers (P = 0·97 and 0·45, respectively) (Table 1). P_max decreased from the top to bottom canopy layer in all treatments (Table 1). For parameters a, Θ and R_d, significant differences were found between canopy layers but not between treatments (Table A3). At the crop level, significantly higher chlorophyll contents, chlorophyll a/b ratios and total nitrogen concentrations were observed in the haze treatments compared with the control treatment (Table 2). Stomatal density was not influenced by haze treatments (Supplementary Data Fig. S5). Haze treatments resulted in thicker mesophyll, palisade and spongy tissue in the bottom leaves (Fig. 7), while these differences did not occur in the top and middle leaves (Supplementary Data Fig. S6).

Table 1.

Maximum net photosynthesis rate (P_max, μmol m^–2 s^–1) in three canopy layers in response to haze treatments (n = 6)

Treatment	Top	Middle	Bottom
0 % haze	52·9	41·7	35·1
45 % haze	53·3	45·2	37·4
71 % haze	53·5	49·5	38·1
P-value	0·97	0·01	0·45

P_max was fitted from measured light response curves [eqn (1)].

P-values >0·05 were regarded as non-significant.

Fig. 7.

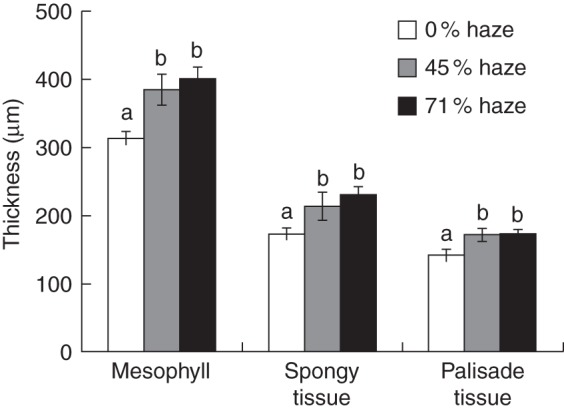
Thickness of leaf mesophyll, spongy tissue and palisade tissue in bottom leaves. Leaf samples were taken on 5 July. Error bars show ±s.e. (n = 6). Letters within each parameter show statistically significant differences (P < 0·05).

Quantifying contributing factors to crop photosynthesis

The cumulative crop photosynthesis calculated over a growing period (1 April to 1 October) increased by 7·2 % in the 71 % haze treatment compared with the control treatment. This enhancement mainly resulted from four factors: more uniform vertical and horizontal PPFD distribution (Figs 3 and 4), greater leaf photosynthetic capacity in the middle part of the crop (Fig. 8) and larger LAI (Fig. 1). Among them, horizontal PPFD distribution accounted for 33 % of this enhancement, while leaf photosynthetic capacity, vertical PPFD distribution and LAI factors accounted for 23, 21 and 13 %, respectively; the remaining 10 % was attributed to the interaction effect of the four factors (Fig. 9). Similar calculations were performed over the whole growing season (1 January to 1 November). In that case, cumulative crop photosynthesis increased by 6·6 % in the 71 % haze treatment compared with the control treatment; the relative contribution of the four contributing factors was similar to that in the calculations during 1 April to 1 October.

Fig. 9.

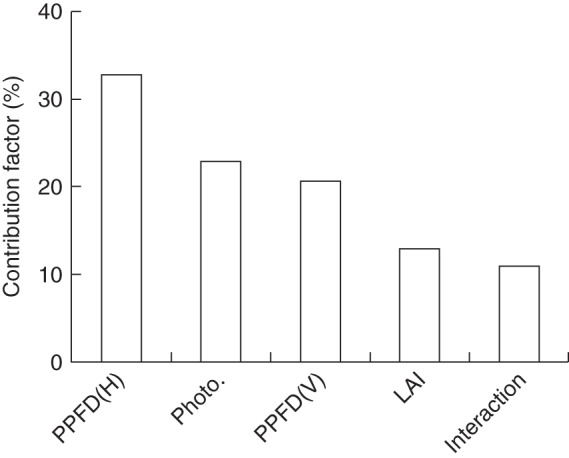
Quantification of the contributing factors to crop photosynthesis enhancement over a designated growing period (1 April to 1 October 2011) in the 71 % haze treatment. The x-axis represents the factors which have an influence: PPFD(H), horizontal PPFD distribution; Photo., leaf photosynthesis light response curve; PPFD(V), vertical PPFD distribution; LAI, leaf area index; Interaction, interaction effect of the four factors.

DISCUSSION

Plants use diffuse light more efficiently than direct light (Farquhar and Roderick, 2003; Gu et al., 2003; Mercado et al., 2009). This study is the first to show experimentally the effects of diffuse light on plant growth, while all other growth conditions remained similar. By conducting a controlled experiment in a greenhouse, this study avoided the side effects of other studies conducted on cloudy vs. clear days, such as the increased proportion of diffuse light at the expense of total global radiation (Urban et al., 2012). Furthermore, the long-term investigation of the effect of diffuse light on plant growth and acclimation is possible under such conditions and is necessary in order to discriminate the effects of diffuse light from that of other factors in interaction with diffuse light.

Crop photosynthesis is correlated with the light intensity profile within the canopy (Gonzalez-Real et al., 2007; Ninemets, 2007; Sarlikioti et al., 2011b). The horizontal PPFD distribution in the crop was directly linked to the proportion of sunlit and shaded leaf area (Spitters, 1986). Sunlit leaves are usually brightly illuminated, while shaded leaves are illuminated by diffuse light, often with relatively lower intensities. Thus, the photosynthetic light use efficiency per unit leaf area is lower in sunlit leaves than in shaded leaves due to the non-linearity of leaf photosynthetic light response (Baldocchi, 1997; Gu et al., 2002). Plants grew in treatments with diffuse light under a more uniform PPFD distribution in the horizontal plane than in the control treatment (Fig. 4). This is in consistent with Acock et al. (1970) who concluded that the variability of PPFD in the horizontal plane increases with an increase in the ratio of direct sunlight to diffuse skylight. We quantified this effect and showed that it was the most important factor for the enhancement of crop photosynthesis in diffuse light (Fig. 9). This is in contrast to Urban et al. (2012), who stated that a more uniform vertical light distribution in the canopy is the most important cause of the higher plant photosynthetic efficiency under diffuse light. However, these authors did not compare that with the effect of the horizontal light profile in the canopy. To calculate crop photosynthesis, many models artificially separate leaves into sunlit and shaded groups in the crop horizontal plane (Norman, 1980; De Pury and Farquhar, 1997; Wang and Leuning, 1998; Johnson et al., 2010). However, in this study, we measured and used the real variability of PPFD in a horizontal plane at crop level. Thus, the current calculation of crop photosynthesis might be closer to reality.

To quantify the effect of horizontal variability of PPFD on crop photosynthesis, we assumed that the relative variation of horizontal PPFD was similar at each of the three canopy depths, as we measured the horizontal PPFD distribution only in the upper part of the crop. However, Acock et al. (1970) concluded that the variability of PPFD distribution in the horizontal direction increases with increasing depth in the canopy. To test our assumption, we carried out the calculations based on relative differences in variation coefficient of horizontal PPFD distribution in the three canopy depths in each treatment according to Acock et al . (1970, fig. 2). This resulted in only 0·1 % deviation of cumulative crop photosynthesis compared with the calculation based on our assumption in both treatments. As the change in variation coefficient mainly occurred in the lowest leaf layer, this negligible effect is not surprising because the PPFD in the lower part of the crop is intrinsically low compared with the upper part of the crop. Therefore, we conclude that the assumption of equal horizontal PPFD distribution can be used for our purpose.

Increasing the fraction of diffuse light resulted in a deeper light penetration, which is characterized by a lower extinction coefficient (Fig. 3B); this is in agreement with Urban et al. (2012), who reported a lower extinction coefficient on cloudy days. This phenomenon occurred due to the properties of diffuse light which scatters in many directions and thus causes less shadow, while direct light either concentrates in a beam or casts a shadow in the canopy, which results in the upper leaves being brightly illuminated and lower leaves in deep shade, or strong lightflecks at a given canopy depth. We quantified the effect of vertical PPFD distribution on crop photosynthesis and showed that the deeper PPFD penetration in haze treatments also played a substantial role in crop photosynthesis enhancement. However, the deeper penetration of PPFD is only advantageous at a high LAI. At a low LAI, more PPFD would reach the floor and would not be absorbed by the crop. Furthermore, Sarlikioti et al. (2011b) indicated that the advantages of a deeper light penetration in the canopy depend on the seasonal distribution of leaf photosynthetic capacity over the canopy, and the seasonal pattern of light intensity due to the solar elevation changes during the year. Similarly, it changes in a diurnal pattern. Therefore, further expliotation of these effects can improve our understanding of the effect of diffuse light on plant processes.

Although the light profile in a canopy is partly linked to leaf angle (Falster and Westoby, 2003; Sarlikioti et al., 2011b), this factor can be ignored in the current study because haze treatments did not affect the leaf angle (Supplementary Data Fig. S2). This is further supported by a similar vertical light profile among the three treatments on cloudy days (Fig. 3A). Furthermore, Alton (2008) concluded from model simulations that canopy architecture plays only a minor role in the enhancement of radiation use efficiency on cloudy days. In contrast, the simulations by Sarlikioti et al. (2011b) showed that improving plant architecture leads to an increase of 6–10 % in plant photosynthesis in tomato. In this context, more investigations on plant architecture are needed to explore further the effect of diffuse light on plant photosynthesis.

Physiological and morphological properties of plant organs can be affected by their prevailing microclimate (Ellsworth and Reich, 1993; Niinemets, 2007). A homogeneous light distribution in the canopy will probably result in a higher fraction of leaves grown under relatively higher light intensities in the lower part of the crop, which is reflected by lower crop SLA (Fig. 2) and thicker bottom leaves (Fig. 7) in haze treatments. This is in accordance with the view that a lower SLA can be seen as an acclimatory response to high light intensity (Evans and Poorter, 2001; Trouwborst et al., 2010). Furthermore, higher leaf total nitrogen, chlorophyll content and chlorophyll a/b ratio at crop level (Table 2), and a higher photosynthetic capacity in the middle of the crop (Table 1) were observed in both haze treatments, which will enhance crop photosynthesis (Fig. 9). Another aspect of plant acclimation in haze treatments was the development of a higher LAI (Fig. 1). A higher LAI is highly relevant for crop photosynthesis, as long as the fraction of light interception is also increased (Wunsche and Lakso, 2000). The higher LAI in haze treatments was attributed to greater leaf width (data not shown). However, the increased LAI played a minor role in crop photosynthesis enhancement in haze treatments (Fig. 9), because the light interception was already close to saturation in the control treatment (Fig. 3).

Table 2.

Leaf chemical components in a crop in response to haze treatments (n = 6)

Treatment	Total nitrogen (g m–2)	Chl (a + b) (mg m–2)	Chl a/b ratio
0 % haze	2·05a	348a	3·28a
45 % haze	2·12b	379b	3·42b
71 % haze	2·23c	368b	3·47b
l.s.d.	0·04	17	0·07

Means followed by different letters within one column differ significantly (P < 0·05) as established by the least significant difference (l.s.d.) test.

All values are averaged values of three (top, middle and bottom) canopy layers.

Chl, chlorophyll.

When global radiation was high, the temperature of top leaves in the haze treatments was lower than in the control treatment (Fig. 5); this correlated with a lower light absorption of the top leaves under diffuse light. Furthermore, a higher maximum PSII efficiency (F_v/F_m) was observed in the haze treatments (Fig. 6) in comparison with the control treatment, suggesting less photoinhibition. This indicated that diffuse light minimized the potential for photodamage or photoprotection arising from the overexcitation of the photosynthetic apparatus. This was corroborated by a lower F_v/F_m ratio in the control treatment. In this study, a reversible change in F_v/F_m was found in the late afternoon in the control treatment (Fig. 6), suggesting photoprotection rather than photodamage. The decreased F_v/F_m at high light intensity is probably caused by the reversible inactivation or downregulation of PSII, rather than photodamage to PSII or loss of D1 protein (Long et al., 1994; Demmig-Adams et al., 1996; Demmig-Adams and Adams, 2000; Huang et al., 2006). In addition, a higher leaf temperature might further intensify the photoinhibition (Bongi and Long, 1987).

To calculate crop photosynthesis, analytical or numerical expression is commonly applied (Thornley, 2002; Johnson, 2010). In this study, we used Gaussian integration for this purpose, because Goudriaan (1986) proved that Gaussian integration is a simple and proper method to integrate photosynthesis over the canopy. Furthermore, we applied a non-rectangular hyperbola function in the Gaussian integration procedure instead of a rectangular hyperbola function which was used by Goudriaan (1986) and Spitters (1986). This is because Marshall and Biscoe (1980) indicated that the non-rectangular hyperbola is a better description of the response of photosynthesis to irradiance compared with the rectangular hyperbola. Our objective is to quantify the relative importance of each factor; therefore, the current calculation procedure should be sufficient. For the measurements of the light response curves of leaf photosynthesis, only the adaxial side of the leaf was illuminated by the light source. However, diffuseness of light may affect the fraction of light on the abaxial surface, which may have a different response curve (e.g. Paradiso and Marcelis, 2012). This might have led to a minor error in estimating the effects of diffuse light. Measurements of light absorption and photosynthesis light response curves on both the adaxial and abaxial side of leaves in the canopy in combination with functional–structural plant modelling might help to estimate these effects.

Solar radiation on the Earth's surface is the primary driver for plant photosynthesis. However, the increased anthropogenic emissions over the past century have affected solar radiation at the Earth's surface (global dimming). On the other hand, these emissions also increased the diffuse component of solar radiation (Mercado et al., 2009). According to our study and previous studies (Gu et al., 2002, 2003; Hemming et al., 2007; Zhang et al., 2011) indicating the advantages of diffuse radiation for plant photosynthesis, it stands to reason that global dimming does not negatively influence plant photosynthesis if the enhanced plant photosynthesis resulting from the increased fraction of diffuse light can sufficiently offset the reduction in the global radiation level. Furthermore, our findings have implications for improving agricultural efficiency. Crop productivity can be improved by increasing the fraction of diffuse light.

Conclusions

Transforming 71 % of direct PPFD into diffuse PPFD increased cumulative crop photosynthesis by 7·2 % in a tomato crop. Four factors contributed to this increase in crop photosynthesis. The most important factor was a more homogeneous horizontal PPFD distribution; a more uniform vertical PPFD distribution and higher leaf photosynthetic capacity contributed more to the crop photosynthesis enhancement than a higher LAI. Based on these findings, we conclude that the enhancement of crop photosynthesis in diffuse light depends not only on the direct effects of a more uniform vertical and horizontal light distribution, but also on crop physiological and morphological acclimation.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Figure S1: the hemispherical transmission of PPFD for the three glass types. Figure S2: relationship of the leaf angle to the horizontal plane. Figure S3: diurnal pattern of the temperature difference between leaf and air at the canopy of middle and bottom leaves on three clear days. Figure S4: maximum PSII efficiency of middle and bottom leaves on a clear day. Figure S5: stomatal densities on fully expanded leaves of tomato plants grown at three levels of haze treatments. Figure S6: thickness of leaf mesophyll, spongy tissue and palisade tissue in top and middle leaves.

APPENDIX

The basic set of equations for crop photosynthesis calculation was presented in the main text. The more detailed implementations are presented here. The variables and parameters, with default values, are listed in Tables A1–A3.

The outdoor intensities of direct (I_out,dr) and diffuse (I_out,df) PPFD were calculated from the total outdoor PPFD and the fraction of diffuse and direct PPFD, estimated according to Spitters et al. (1986). PPFD reaching the top of the canopy consists of a diffuse (I_o,df) and a direct (I_o,dr) component [eqn (4)]. I_o,df and I_o,dr in eqn (4) are given by

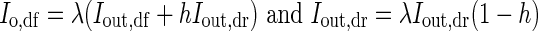(A1)

where λ is the greenhouse transmissivity (%) and h is the haze factor of the greenhouse cover.

It is assumed that both direct and diffuse components of PPFD exponentially decline through the canopy [eqn (3)]. Thus the total amount of PPFD absorbed at any given level of canopy depth L can be calculated according to eqn (5). I(L)_a,dr and I(L)_a,df in eqn (5) are given by

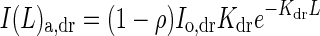(A2A)

and

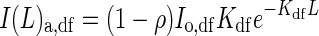(A2B)

The extinction coefficient for diffuse PPFD (K_df) was derived from fitting eqn (3) to the measured vertical PPFD distribution on overcast days in the 0 % haze treatment, when the global irradiance was fully diffuse (measurements are described in the section ‘PPFD distribution measurements in the canopy’). Similarly, an extinction coefficient for clear days (K_c) was determined on clear days in the 0 % haze treatment. On clear days, the total outdoor PPFD consists of a diffuse and direct component. Therefore, the extinction coefficient for the direct component PPFD (K_dr) was calculated as

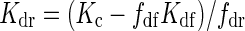(A3)

where f_df and f_dr represent the average fraction of outdoor diffuse and direct PPFD during PPFD distribution measurements on clear days, respectively.

Incoming PPFD is partly reflected by the canopy. According to Spitters [1986, eqn (1)], the reflection coefficient [ρ; in eqn (A2)] of a closed canopy is

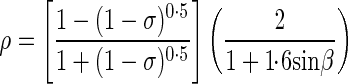(A4)

where σ is the scattering coefficient, which is the sum of reflectance and transmittance of the visible spectrum of individual leaves. Reflectance and transmittance of leaves were measured on 108 tomato leaves with a spectrophotometer (Perkin Elmer Inc., Waltham, MA, USA). β is the solar elevation above the horizon estimated from time and location (Spitters et al., 1986). The canopy reflection coefficient of diffuse PPFD [the first term in eqn (A4)] does not change with solar elevation.

For calculating canopy photosynthesis, the crop canopy was divided into three canopy depths which were selected by Gaussian integration (Goudriaan, 1986). Thus, L_p in eqn (6) is

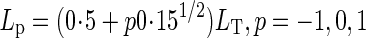(A5)

where p is a specific factor to define top (–1), middle (0) and bottom (1) canopy depth.

The leaf photosynthesis rate at each of the selected canopy depths was calculated according to eqn (6). Whole-canopy photosynthesis was calculated as a weighted average of the leaf photosynthesis rate at three Gaussian canopy depths as described in eqn (7).

According to equations presented in this Appendix and in the main text, instantaneous canopy photosynthesis can be derived. Integrating the instantaneous canopy photosynthesis rates over the designated growing period yielded the cumulative crop photosynthesis.

Note that the canopy depth defined by the Gaussian integration differs from the three canopy depths in all the measurements. Photosynthetic parameters [in eqn (1)] for the three Gaussian canopy depths were obtained by linear interpolation of the parameters derived from photosynthetic light response curve fitting (Tables 1 and A3) and the LAI where the leaf photosynthesis light response curves were measured.

Table A1.

Model variables, definitions and units

Variable	Definition	Units
Ia	PPFD absorbed by the leaflet surface [eqn (1)]	μmol m–2 s–1
Iout,dr, Iout,df	Total outside direct and diffuse PPFD [eqn (A1)]	μmol m–2s–1
Io, Io,dr, Io,df	Incident total, direct and diffuse PPFD at the top of the canopy [eqn (4)]	μmol m–2s–1
I(L)a, I(L)a,dr, I(L)a,df	Absorbed total, direct and diffuse PPFD at a given canopy depth [eqn (5)]	μmol m–2s–1
L	Cumulative leaf area index at a given canopy depth [eqn (3)]	m2 leaf m–2 ground
Lp	Leaf area index selected for Gaussian integration [eqn (6)]	m2 leaf m–2 ground
LT	Total leaf area index [eqn (7)]	m2 leaf m–2 ground
Pn	Net leaf photosynthesis rate [eqn (1)]	μmol CO2 m–2 leaf s–1
Pg	Gross leaf photosynthesis rate [eqn (2)]	μmol CO2 m–2 leaf s–1
Pg(Lp)	Gross leaf photosynthesis rate at Gaussian selected canopy depth [eqn (6)]	μmol CO2 m–2 leaf s–1
Pg,−1, Pg,0, Pg,1	Gross leaf photosynthesis rate at top, middle and bottom of the canopy [eqn (7)]	μmol CO2 m–2 leaf s–1
Pg,c	Whole-canopy photosynthesis rate [eqn (7)]	μmol CO2 m–2 ground s–1
β	Solar elevation above the horizon [eqn (A4)]	°
ρ	Canopy reflection coefficient [eqn (A2)]
p (–1,0,1)	Specific factor to define top (–1), middle (0), and bottom (1) canopy depth [eqn (A5)]

PPFD, photosynthetic photon flux density (μmol m^–2 s^–1)

The equation number following the definition indicates where the variable first occurs and is introduced.

Table A2.

Model parameters, definitions, units and default values

Parameter	Definition	Default value
Kdr	Direct PPFD extinction coefficient [eqn (A2)]	1·06
Kdf	Diffuse PPFD extinction coefficient [eqn (A2)]	0·82
Kc	PPFD extinction coefficient measured on clear days [eqn (A3)]	0·99
fdf	Average fraction of diffuse PPFD during the PPFD distribution measurements on clear days [eqn (A3)]	27·5 %
fdr	Average fraction of direct PPFD during the PPFD distribution measurements on clear days [eqn (A3)]	72·5 %
h	Haze factor of the greenhouse cover [eqn (A1)]	0 %, 45 %, 71 %
λ	Greenhouse transmissivity [eqn (A1)]	66 %
σ	Scattering coefficient of single leaves for visible radiation [eqn (A4)]	0·12

PPFD, photosynthetic photon flux density (μmol m^–2 s^–1)

The equation number following the definition indicates where the parameter first occurs and is introduced.

Table A3.

Light response curve parameters at three canopy layers (n = 6)

Canopy layer	α (μmol CO2 μmol–1 photons)	Θ	Rd (μmol m–2 s–1)
Top	0·097	0·77	3·00
Middle	0·094	0·81	2·06
Bottom	0·092	0·83	1·27
P-value	0·018	0·02	<0·01

The parameters are fitted from measured light response curves [eqn (1)].

Statistical analysis showed that light response curve parameters were not significantly different between the three treatments, except P_max; thus, these parameter values were used for crop photosynthesis calculation in all the treatments.

P-values <0·05 were regarded as significant.