Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2014 May 22;114(1):167–177. doi: 10.1093/aob/mcu087

Temporal variation in phenotypic gender and expected functional gender within and among individuals in an annual plant

Emily J Austen 1,*, Arthur E Weis 1
PMCID: PMC4071105  PMID: 24854170

Abstract

Background and Aims

Adaptive explanations for variation in sex allocation centre on variation in resource status and variation in the mating environment. The latter can occur when dichogamy causes siring opportunity to vary across the flowering season. In this study, it is hypothesized that the widespread tendency towards declining fruit-set from first to last flowers on plants can similarly lead to a varying mating environment by causing a temporal shift in the quality (not quantity) of siring opportunities.

Methods

A numerical model was developed to examine the effects of declining fruit-set on the expected male versus female reproductive success (functional gender) of first and last flowers on plants, and of early- and late-flowering plants. Within- and among-plant temporal variation in pollen production, ovule production and fruit-set in 70 Brassica rapa plants was then characterized to determine if trends in male and female investment mirror expected trends in functional gender.

Key Results

Under a wide range of model conditions, functional femaleness decreased sharply in the last flowers on plants, and increased from early- to late-flowering plants in the population. In B. rapa, pollen production decreased more rapidly than ovule production from first to last flowers, leading to a within-plant increase in phenotypic femaleness. Among plants, ovule production decreased from early- to late-flowering plants, causing a temporal decrease in phenotypic femaleness.

Conclusions

The numerical model confirmed that declining fruit-set can drive temporal variation in functional gender, especially among plants. The discrepancy between observed trends in phenotypic gender in B. rapa and expected functional gender predicted by the numerical model does not rule out the possibility that male reproductive success decreases with later flowering onset. If so, plants may experience selection for early flowering through male fitness.

Keywords: Brassica rapa, flowering time, fruit-set, phenotypic gender, hermaphrodite, hierarchical regression, ovule, phenology, pollen, sex allocation, within-plant variation

INTRODUCTION

Most flowering plants are perfect-flowered hermaphrodites (Yampolsky and Yampolsky, 1922), but hermaphrodites are not necessarily equisexual (Horovitz, 1978). Instead, pollen and ovule counts reveal continuous variation from predominantly male to predominantly female gamete production, both among plants in a population (e.g. Méndez, 1998; Wright and Barrett, 1999) and among the flowers produced by an individual (reviewed by Diggle, 2003; Herrera, 2009). This variation invites the question, why should one hermaphroditic individual (or flower) be more or less female than another?

Evolutionary stable strategy (ESS) models indentify several factors that together determine a plant's optimal sex allocation (i.e. optimal investment in male versus female function). These models find the sex allocation strategy that, if adopted by all members of the population, cannot be invaded by an alternative, initially rare, strategy. The optimum resides where the marginal gains of investment in male and female function equate (Charnov, 1982). Factors affecting sex allocation optima include the shapes of male and female gain curves (i.e. the fitness payoff of each unit investment in male or female function), the strength of competition among related pollen grains and related seeds, and the rate of self-fertilization (Charlesworth and Charlesworth, 1981; Charnov, 1982; Lloyd, 1984). When the environment is assumed to be homogenous, ESS models find a single optimum (or, where dioecy is predicted, two optima) for individuals in a population. If, however, the environment is heterogeneous, sex allocation optima may differ among plants for two reasons. First, environmental heterogeneity can alter the shape of gain curves. In wind-pollinated species, for example, the male gain curve may decelerate more rapidly in closed habitats than in open habitats (Friedman and Barrett, 2011). Second, environmental heterogeneity can induce variation in plant size, which may alter the shape of gain curves (de Jong and Klinkhamer, 2005; Friedman and Barrett, 2011), and/or lead to variation in the size of reproductive investment made. Plants making a larger absolute investment are expected to allocate relatively more to the function whose gain curve decelerates slower (Lloyd and Bawa, 1984; Zhang, 2006).

Optima can also differ among sequentially opening flowers on a plant. Like individuals, flowers that differ in reproductive investment will vary in sex allocation optima if male and female gain curves are not identical (Brunet and Charlesworth, 1995). Variation in sex allocation optima also occurs when flowers vary in selfing rates: flowers with a higher selfing rate are expected to allocate more to female function than those with a lower selfing rate when inbreeding depression (δ) < 0·5; the prediction is reversed when δ > 0·5 (Brunet and Charlesworth, 1995). The strongest driver of among-flower variation in allocation optima, however, is among-flower variation in pollen transfer probability. This can be caused by temporal shifts in the mating environment (the relative abundance of male- and female-phase flowers) arising from flower dichogamy (temporal offset of stigma receptivity and pollen dispersal within flowers) (Brunet and Charlesworth, 1995). Other causes of variation in pollen transfer probability include the tendency of pollinators to visit inflorescences from bottom-to-top (pollinator directionality) (Brunet and Charlesworth, 1995), and varying pollinator attraction as display size changes (Ishii and Sakai, 2002). All else being equal, flowers with the greatest pollen transfer probability are expected to allocate relatively more to male function (Brunet and Charlesworth, 1995).

Empirical study of sex allocation variation in hermaphroditic plants has focused largely on systems exhibiting dichogamy, or, to a lesser extent, pollinator directionality or variable selfing rates (e.g. Brunet, 1996; Vogler et al., 1999; Guitián, 2004; Huang et al., 2004; Hiraga and Sakai, 2007; Zhao et al., 2008; Brookes and Jesson, 2010; Ishii and Harder, 2012). Less attention has been paid to adichogamous, self-incompatible species lacking pollinator directionality, even though sex allocation variation can occur in such species if plants or flowers vary in reproductive investment (Brunet and Charlesworth, 1995). Moreover, a particular type of variation in investment – declining fruit-set from first to last flowers on plants – might cause variation in the mating environment of adichogamous plants by altering the quality (not, as in the case of dichogamy, quantity) of siring opportunity over time.

In their ESS model, Brunet & Charlesworth (1995) assumed a constant probability of fruit-set across all flowers, despite among-flower variation in reproductive investment. Fruit-set probability, however, frequently declines from first to last flowers on plants (Lee, 1988; Diggle, 1995), and this decline is often attributed to resource pre-emption by first flowers (e.g. Agren and Willson, 1992; Ehrlén, 1992; Kliber and Eckert, 2004). This post-fertilization decline in resources clearly lowers the expected female reproductive success of last flowers on plants. Less obvious are the effects on expected male mating opportunity. If first flowers are more likely to set fruit, then those flowers and plants that transfer pollen to the first flowers of others are more likely to fertilize ovules that successfully mature into seed. This siring advantage should fall to first flowers on plants, and to early-flowering plants in a population, because these are more likely to temporally coincide with the first flowers of others. Brunet (1996) recognized that declining fruit-set reduces the expected male success of last flowers on plants, and Weis and Kossler (2004) predicted that declining fruit-set leads to decreasing male success from early- to late-flowering plants (Weis and Kossler, 2004). The consequences of this temporal shift in mate quality for relative mating success through the two genders (i.e. for functional gender, Lloyd, 1980a) have not, however, been fully examined.

We asked the following questions. (1) Does functional gender vary within plants when fruit-set declines? (2) Does the predicted among-plant decline in male success cause appreciable variation in functional gender? (3) Are within- and among-plant trends in expected functional gender matched by within- and among-plant trends in relative male and female investment? To answer these questions, we developed a numerical model examining effects of declining fruit-set probability on expected male success and functional gender. Informed by model results, we characterized within- and among-plant variation in pollen, ovule and fruit production in Brassica rapa (Brassicaceae). We contrast temporal trends in relative male and female investment in B. rapa to temporal trends in functional gender predicted by the model.

MATERIALS & METHODS

Numerical model

We developed a numerical model to examine the effects of declining fruit-set probability within plants on male success and functional gender. Full R code (R Development Core Team, 2012) for the model is available online (Supplementary Data 1). We describe an illustrative parameterization here, and present additional cases in Supplementary Data 2.

The model assumes a large population in which flowering onset is symmetrically distributed over 5 d. Each individual produces a total of 15 flowers over a 5-d flowering duration. Flowers fall into five classes: class 1 flowers open on an individual's first day of flowering, class 2 flowers on its second day, etc. Flowering is acropetal, so that flower classes are positioned in sequence on a plant. We examined uniform, symmetrical, right-skewed and left-skewed flower production schedules (Supplementary Data 2), adopting uniform schedules in the illustrative case (Fig. 1A). In the illustrative case, flowers persist for 1 d and are adichogamous, and plants are self-compatible.

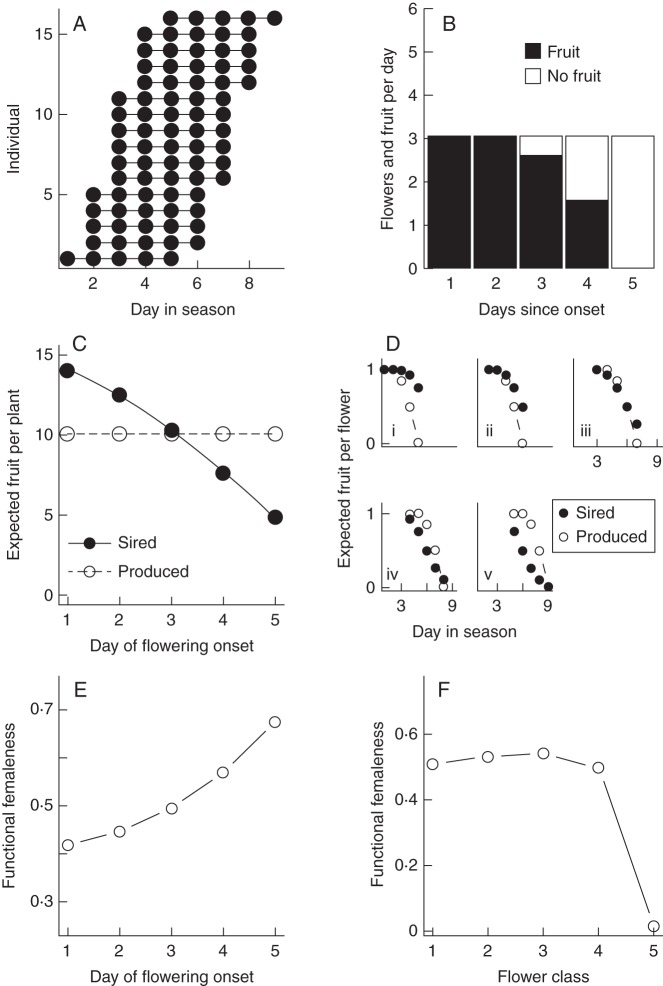
Fig. 1.

Fig. 1.

Open in a new tab

Theoretical results from the numerical model indicate that declining fruit-set probability within plants induces a decrease in expected male success with later flowering onset, and among sequentially deployed flowers on plants. (A) Sixteen individuals are sampled from a population with a 9-d flowering season. Each plant is represented by a horizontal line, and sizes of circles along the line are proportional to the number of flowers produced by that individual on a given day (flower production does not vary by day in the illustrative case). (B) Each plant displays three flowers on each day of its flowering duration in the illustrative case. Fruit-set probability of flowers open on the first few days of flowering is 100 %, of those open on a plant's third day of flowering is 85 %, of those on the fourth day is 50 % and of those open on the final day of flowering is 5 %. (C) All plants in the population produce an equal number of fruit (open circles), but the expected number of fruit sired per plant (closed circles) decreases with later flowering onset. (D) Expected male success (closed circles) decreases from first to last flowers on plants, regardless of day of flowering onset [plants beginning flowering on day 1 (i), 2 (ii), 3(iii), 4(iv) and 5(v)]. Expected female success (open circles) also decreases from first to last flowers. (E) Among plants, the fraction of reproductive success achieved through female versus male function (functional femaleness) increases with later flowering onset. (F) On average, functional femaleness of first flowers is greater than that of last flowers.

Fruit-set probability decreases from class 1 to class 5 flowers as would be expected under resource pre-emption by early classes. We examined weak, moderate and strong declines in fruit-set probability (Supplementary Data 2), and adopt a strong decline in the illustrative case (Fig. 1B). We assumed constant pollen production per flower, and constant seed production per successful fruit.

From this population, we drew 16 individuals representative of the distribution of flowering onset, and examined their expected male success and functional gender, and the expected male success and functional gender of their successive flower classes. We followed the methods of Brunet (1996) to calculate expected male success, making adjustments to identify both flower classes and individual plants. We began by summing the fruit available for siring (Rd) on each day d of the flowering season:

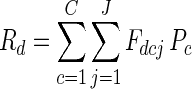graphic file with name M1.gif

where Fcdj is the number of class c flowers produced by plant j on day d, and Pc is their fruit-set probability.

The siring of Rd fruit is partitioned among plants and flower classes according to their proportional contribution to the day d pollen pool:

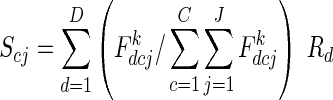graphic file with name M2.gif

where Scj is the expected number of fruit sired by class c flowers of plant j, and 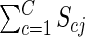Inline graphic is the total expected male success of plant j. The first term within the summation is the fraction of pollen available for siring on day d that was produced by class c flowers on plant j. Exponent k describes the relationship between the number of flowers displayed by a plant on day d and its realized contribution to the pollen pool. When k = 1, plant j's contribution to the pollen pool on day d is directly proportional to its flower, and thus pollen, production. When k < 1, realized representation in the pollen pool saturates with increasing flower display, as may occur if pollinator attraction does not increase linearly with each added flower or if larger displays promote geitonogamous pollen transfer (Ohashi and Yahara, 2001). k has no effect when flower production is uniformly distributed (illustrative case); we examine effects of k for other schedules in Supplementary Data 2.

The mean expected male success of class c flowers (Mc) is

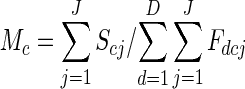graphic file with name M4.gif

and average functional femaleness (Gf) of class c flowers is

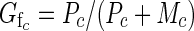graphic file with name M5.gif

When 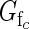Inline graphic > 0·5, class c flowers on average produce more fruit than they sire; when 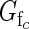Inline graphic < 0·5, they sire more fruit than they produce. A plant's expected functional femaleness is its expected female success divided by the sum of its expected male and female success.

Glasshouse experiment

We characterized temporal trends in pollen, ovule and fruit production in B. rapa, and compared these with trends in functional gender predicted by the numerical model.

Study system

Brassica rapa is a self-incompatible hermaphroditic annual that exhibits declining fruit-set within plants (Weis and Kossler, 2004). Plants grow initially as rosettes and develop a taproot. Approximately 25 d after germination, the apical meristem forms flower buds and the primary axis rapidly elongates (bolting). Although previously described as dichogamous on the basis of stigmas protruding from unopened buds (Al-Shehbaz, 1977), we saw this behaviour rarely and inconsistently, and observed dehiscing anthers and textured stigmas almost immediately upon bud opening. We therefore consider the population here to be adichogamous. Flowering is acropetal and bud production continues long after the first buds open. Rapid flower turnover and low flower production per day limit the opportunity for pollinator directionality to induce a gradient in pollen transfer probability. Being self-incompatible and adichogamous, and having little scope for pollinator directionality, B. rapa is a good system in which to examine potential consequences of declining fruit-set.

Experimental design

We characterized pollen and ovule production of sequentially produced flowers on 70 plants. To ensure good sample size for very early- and very late-flowering plants, we selected a stratified random sample of plants from a larger group of 700. From each selected plant, we collected roughly every tenth flower bud from the primary inflorescence and uppermost and lowermost secondary inflorescences, and stored them in 70 % EtOH. Buds were collected 1 d before we expected they would open. As in the numerical model, we classified buds by their day of opening (here estimated by day of collection) relative to their host plant's day of flowering onset for analysis, but we also recorded bud position within the inflorescence (1 = most basal). Days since onset and position on an inflorescence are necessarily positively correlated in an acropetally flowering plant.

The experiment took place at the University of Toronto glasshouse using seeds bulk-collected from >400 maternal families in southern California (Franke et al., 2006, population ARB97). Seeds were cold stratified for 1 week, and planted two per pot on 13 June 2009 into a 3 : 1 mixture of Pro-Mix potting soil (Premier Tech Horticulture, Rivière-du-Loup, QC, Canada) to concrete sand in super-cell sized cone-tainers (Stuewe and Sons, Corvallis, OR, USA). We thinned to a single seedling at 5 d. Plants were bottom watered, and twice fertilized with a 20 : 20 : 20 formula.

To isolate temporal variation in pollen and ovule production from variation attributable to plant size (Zhang, 2006) and resource pre-emption by developing fruit (Diggle, 1997), we imposed fertilizer and pollination treatments. In the fertilizer treatment, we supplemented the soil used to fill half of the pots with 100-d 14 : 14 : 14 slow-release ‘Nutricote’ fertilizer (Sun Gro Horticulture, Vancouver, BC, Canada) at a rate of 2·75 kg per 1000 litres, thereby introducing variation in size independent from its correlation with bolting time. We assigned plants from both fertilizer treatments to fully pollinated or unpollinated treatments, and applied mixed pollen loads to stigmas of open flowers on plants in the fully pollinated treatment every second day using a toothpick. Pollinated plants produced significantly more seed (seed mass median (range) fully pollinated: 0·14 g (0, 1·11 g), n = 39 plants – note that five plants did not set seed in this treatment; median (range) unpollinated: 0·02 g (0, 0·87 g), n = 31 plants; non-parametric Wilcoxon–Mann–Whitney test for non-normally distributed data: W = 205, P < 0·01).

Temperature (Temp, °C) and relative humidity (RH, %) were recorded every 5 min by a thermistor temperature probe and wet and dry bulb RH probes in a sensor box suspended in the glasshouse. Light intensity (LI, μmol m–2 s–1) was recorded every 5 min by a Licor quantum sensor on a rooftop weather mast. Using daytime readings (0700–2100 h), we derived an environment index through principal components analysis of the correlation matrix of these variables. Temp and LI loaded positively (loadings = 0·57 and 0·61, respectively), and RH negatively (loading RH = –0·55), onto the first principal component (PC1) accounting for 60 % of the variation. We adopted the PC1 mean on a plant's bolting day as a measure of its abiotic environment. PC1 does not necessarily correspond to the environmental variation of greatest relevance to plant performance, but our aim was to account for some component of abiotic variation without compromising power to detect temporal trends.

Data collection

We counted freshly opened flowers every second day. The sum of a plant's flower counts estimates its total flower production, and days between flowering onset and the last non-zero count estimates flowering duration. We harvested fruit as they matured, and recorded presence/absence of fruit at each floral position within the primary, top secondary and bottom secondary inflorescences of 12 fully pollinated plants from each fertilizer treatment. We interpolated the day of flower opening for all floral positions on these 24 plants from the linear regression of day of bud collection against bud position within the inflorescence.

We adopted taproot dry mass at senescence as a measure of plant size; it was positively correlated to all other measured components of plant size (rshoot.dry.mass = 0·77, rheight = 0·47, rstem.diameter = 0·86, rleaf.number = 0·49; n = 70, P < 0·01 for all correlations). Although resources stored in the taproot are exhausted by senescence, larger taproots presumably held more resources than smaller taproots.

We measured ovule and pollen content of 735 flower buds, excluding six that contained no ovary. We counted ovules and photographed the ovary and six anthers under a dissecting microscope. The length of each anther in the anther photograph, and width of the floral receptacle in the ovary photograph (Supplementary Data 3), was measured using ImageJ version 1.41o (Rasband, 2007–2014). We suspended all pollen from each of 80 buds in 1000 μL of EtOH, and counted pollen grains in five replicate 1-μL subsamples. The summed lengths of the six anthers within a bud was a strong predictor of the estimated pollen content (Pollen = –56 401 + 9417 × (Length), r = 0·88, n = 40 plants (two buds per plant); coefficient for length: t38 = 16·4, P < 0·01), and we estimated pollen content of all buds using coefficients of this regression.

To facilitate comparisons between pollen and ovule production, we expressed pollen in units of ovule equivalents using the conversion factor developed by Lloyd (1980a):

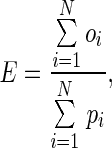graphic file with name M8.gif

where oi and pi are the ovule and pollen content of bud i, respectively, and are summed across all n = 735 measured buds. Multiplying pollen content by E converts pollen grains to units of ovule equivalents (‘adjusted pollen content’). A bud's total investment in pollen and ovules (‘total investment’) is estimated by the sum of its ovules and adjusted pollen content. Relative investment in ovules (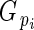Inline graphic) is estimated by:

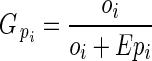graphic file with name M10.gif

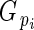Inline graphic is directly related to Lloyd's phenotypic gender (Lloyd, 1980a; Lloyd and Bawa, 1984), and is read as flower phenotypic femaleness: when 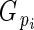Inline graphic = 1, bud i produced ovules but no pollen; when 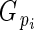Inline graphic = 0, it produced pollen but no ovules; and when 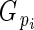Inline graphic = 0·5, its relative ovule investment was equal to the population average.

Analysis

We used hierarchical regression to examine within- and among-plant temporal trends in five response variables: ovules per flower, adjusted pollen per flower, total investment per flower, flower phenotypic femaleness and fruit-set probability. Hierarchical regression describes observations made on a single plant by a function, and simultaneously models coefficients of the within-plant functions as a function of plant-level predictors (Gelman and Hill, 2007). Although uncommon in the plant literature, this technique is well suited to the analysis of modular, ‘function-valued’ (Stinchcombe and Kirkpatrick, 2012) plant traits.

We modelled each response variable as a function of x, the day of bud collection measured as days since the plant's flowering onset. The coefficients of these within-plant regressions were simultaneously modelled as a linear function of among-plant variables. We present the regression model for adjusted pollen, and briefly describe modifications for ovules, phenotypic femaleness and fruit-set probability. The regression for total investment is identical to that for adjusted pollen.

The two-level model for adjusted pollen per flower can be represented by a system of equations (regression model 1A). First, at the within-plant level,

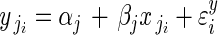Inline graphic, for i = 1 to i = nj buds in plant j.

The response 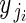Inline graphic is the adjusted pollen content (units of ovule equivalents) of bud i on plant j. The coefficients αj and βj are the within-plant intercept and partial regression coefficient for plant j, respectively. Unexplained within-plant variation in y is represented by ɛyi, which is normally distributed with mean 0 and variance σ2y. At the among-plant level:

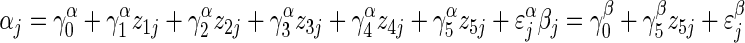graphic file with name M17.gif

for j = 1 to J = 70 plants in the experiment.

Superscripts indicate whether a coefficient predicts α or β. Within-plant intercepts αj are modelled as a linear function of the among-plant predictors days to bolting (z1), log mass taproot (z2), fertilizer treatment (z3), the major axis of environmental variation, PC1 (z4), and pollination treatment (z5), with the coefficients γα1 to γα5 reporting their respective effects. γα1 is the among-plant effect of bolting time (z1) on the response variable, holding all other among-plant variables constant. Within-plant coefficients βj are predicted by intercept γβ0 [the mean within-plant effect of day of bud collection (x), averaged across all plants], and by the effect of pollination treatment γβ5. Unexplained variation in αj and βj is conveyed by ɛαj and ɛβj, which are normally distributed with mean 0 and variances σ2α and σ2β. Correlation ρσασβ is estimated but not shown to simplify presentation of equations.

To model ovules per flower, we employed a Poisson regression at the within-plant level (regression model 1B):

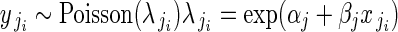graphic file with name M18.gif

for i = 1 to i = nj buds in plant j, where 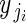Inline graphic is ovule number in bud i on plant j, and 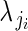Inline graphic is the single parameter of the Poisson distribution. 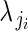Inline graphic is in turn modelled as a function of αj and βj. We modelled variation in flower phenotypic femaleness using a logistic-binomial regression at the within-plant level (regression model 1C):

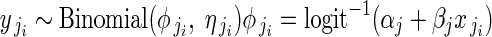graphic file with name M22.gif

for i = 1 to i = nj buds in plant j. Phenotypic femaleness is thus modelled indirectly as the number of ovules in bud i of plant j (yji) given the total reproductive investment of bud i in units of ovule equivalents (ηji). 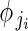Inline graphic is the probability of a given unit of total reproductive resources being invested in ovules, not pollen, and is modelled as a function of αj and βj. Regression models 1B and 1C were identical to 1A in their modelling of αj and βj at the among-plant level. Including flower size as a within-plant predictor did not meaningfully alter temporal effects (Supplementary Data 3).

The binary response variable fruit-set was modelled by logistic regression at the within-plant level (regression model 2):

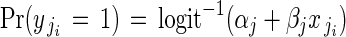graphic file with name M24.gif

for i = 1 to i = nj buds in plant j,

where yji = 1 if fruit is set, and 0 otherwise. This regression was fit using plants from the fully pollinated treatment only, and so does not include pollination treatment (z5) at the among-plant level:

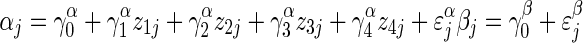graphic file with name M25.gif

for j = 1 to J = 24 plants on which we collected fruit-set data by fruit position.

We performed analyses using R packages lme4 (Bates et al., 2011) and arm (Gelman et al., 2012), and functions lmer() and glmer(). These functions process within- and among-plant models simultaneously by maximum-likelihood estimation. We tested the statistical significance of estimated coefficients using t-tests with J degrees of freedom.

RESULTS

Numerical model

In the illustrative case, the first flowers to open within a plant, and the earliest flowering plants, had greater expected male success than last flowers and plants (Fig. 1C, D). Within plants, the rate of decline in expected male success from first to last flowers on plants did not match the decline in expected female success for all flower classes. Thus, functional femaleness of first flowers remained fairly steady across earlier flower classes, but dropped in the last flower class (Fig. 1F). In contrast, at the among-plant level, functional femaleness increased steadily from early- to late-flowering plants (Fig. 1E).

Modifications to the schedule of flower deployment and the strength of fruit-set decline did not qualitatively affect these results (Supplementary Data 2). Under some circumstances, however, self-incompatibility, a diminishing relationship between flowers displayed and contribution to the pollen pool (k < 1), and flower longevity altered outcomes (Supplementary Data 2). The effects of self-incompatibility depended on population size. When the population was small (16 plants), self-incompatibility reduced the expected male success of the first flowers of early-flowering plants, and the last flowers of late-flowering plants. This removed the within-plant temporal trend in average functional femaleness, and led to a slightly convex relationship between flowering time and functional femaleness. Increasing the population size alleviated these effects (Supplementary Data 2). The effect of k < 1 depended on flower production schedules. When flower deployment followed a symmetrical distribution and k < 1, the relationship between flower class and male success was V-shaped. Functional femaleness was nonetheless greater in first flowers than last flowers, and among-plant trends were unaffected (Supplementary Data 2). Finally, if flowers persist more than 1 d, but female function is saturated on the first day, flower femaleness can increase within plants, depending on the strength of fruit-set decline (Supplementary Data 2). Flower longevity did not alter among-plant trends.

Glasshouse experiment

Flower production

Plants varied considerably in their days to bolting, flower production and flowering duration. Bolting time ranged from 15 to 55 d since planting and its distribution was not affected by fertilizer treatment (two-tailed Kolmogorov–Smirnov test, D = 0·04, n = 693 plants, P > 0·90). Total flower production per plant (sum of flower counts) ranged from 24 to 333, and increased with fertilizer availability and decreased with pollination (Supplementary Data 4). Flowering duration ranged from 14 to 60 d and increased with log-transformed flowers per plant, and decreased with pollination (Supplementary Data 5). Fertilizer addition strengthened the relationship between flower number and flowering duration (Supplementary Data 5). Log-transformed taproot mass increased with bolting time and with fertilizer addition (Supplementary Data 6).

Fruit-set probability

As expected, fruit-set probability declined from first to last flowers on plants (Fig. 2; γβ0, Table 1). We found little among-plant variation in the rate of within-plant fruit-set decline (σ2β) and no effect of bolting date (γα1), plant size (γα2), fertilizer level (γα3) or PC1 of the measured abiotic variables (γα4) (Table 1).

Fig. 2.

Fig. 2.

Open in a new tab

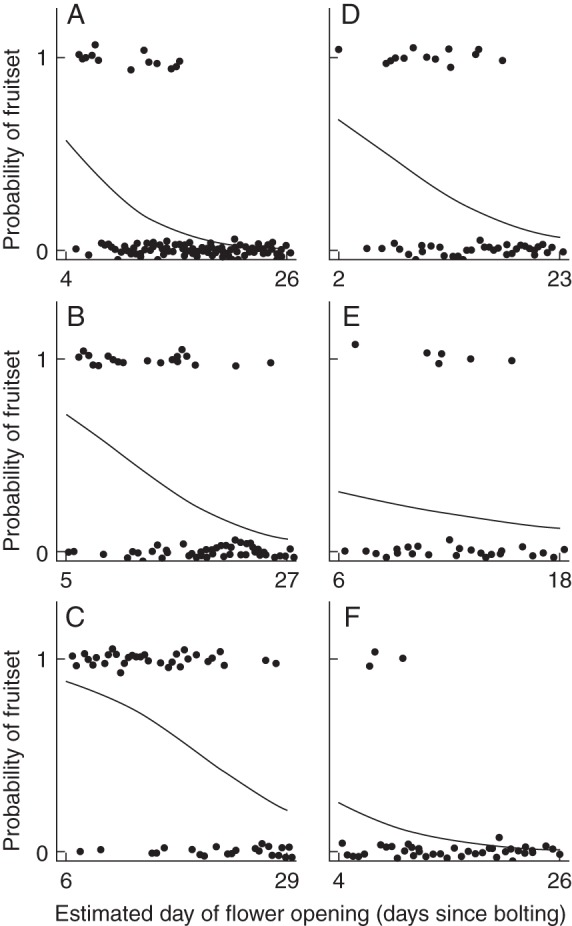
Effects of day of flower opening within a plant on fruit-set probability of the flower. Plots are shown for three fully pollinated Brassica rapa plants in the high-fertilizer treatment (A–C) and for three fully pollinated plants in the low fertilizer treatment (D–F). Curves were fit with hierarchical logistic regression.

Table 1.

Estimates (and SE) of within- and among-plant effects for hierarchical regression analyses.

Ovules Adj. pollen Gametes Femaleness Fruit-set
Regression model1 1B 1A 1A 1C 2
Family Poisson Gaussian Gaussian Logistic-binomial Logistic
Flower buds 735 735 735 735 1726
Plants 70 70 70 70 24
Within-plant:
 intercept (γα0) 3·265* (0·156) 35·237* (3·491) 60·491* (5·772) –0·375* (0·083)  –1·529 (2·835)
 days since bolting (γβ0) –0·005* (0·001) –0·487* (0·030) –0·487* (0·030) 0·017 (0·002)  –0·101* (0·024)
 pollination (full) × days since bolting (γβ5) –0·003* (0·002) –0·139* (0·043) –0·139* (0·043) <0·001 (0·002) NA
Among-plant:
 days to bolting (γα1) –0·005* (0·002) –0·021 (0·051) –0·131 (0·084) –0·005† (0·003)   0·017 (0·042)
 log mass taproot (γα2) –0·022 (0·035) 1·965* (0·776) 1·275 (1·282) –0·103 (0·041) –0·153 (0·625)
 fertilizer (high) (γα3) 0·121* (0·048) 1·081 (1·070) 4·105* (1·768) 0·079 (0·056)   0·694 (0·826)
 enviro. PC1 (γα4) 0·023 (0·019) 0·430 (0·415) 0·894 (0·686) 0·004 (0·022) <0·001 (0·300)
 pollination (full) (γα5) 0·031† (0·035) 1·965* (0·850) 2·821* (1·449) –0·024 (0·043) NA
Variances:
 plant (σ2α) 9·251 × 10–3 8·551 27·175 1·008 × 10–2   1·270
 days since bolting (σ2β) 1·370 × 10–6 0.016 0·063 1·086 × 10–9   0·010
 residual (σ2y) NA 12·686 28·796 NA NA
 covariance (ρσασβ) –0·080 –0·612 –0·665 1 –0·492
Open in a new tab

 1Regression model refers to numbering of statistical models in text

†0·045 < P < 0·05; *P < 0·03. NA, not applicable.

Within-plant variation in pollen and ovule production

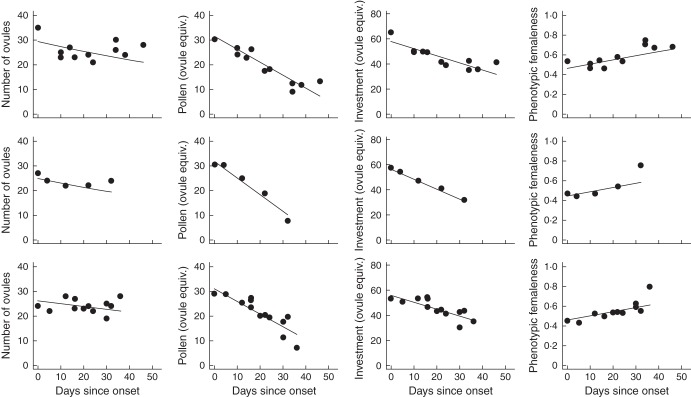
Pollen and ovule production varied substantially within plants. Estimated pollen production fell by half from first to last buds (first buds: mean ± SD = 101 179 ± 16 003 grains; last buds: 50 358 ± 16 110 grains; paired t-test, t = 20·4, d.f. = 69, P < 0·01). Ovule production declined more modestly, falling from 27·8 ± 5·0 (mean ± SD) ovules in first buds to 22·8 ± 4·8 ovules in last buds (paired t-test, t = 9·3, d.f. = 69, P < 0·01). Consequently, while adjusted pollen content (units of ovule equivalents) and ovule content both decreased with days since onset (γβ0, Table 1), adjusted pollen decreased faster (Fig. 3). Holding all predictors at their mean, adjusted pollen production decreased –0·485 ovule equivalents per day since onset, and ovule production decreased –0·153 ovules per day since onset. Pollination increased the rate of decline in ovule production (γβ5, Table 1), but it never approached the rate of change in adjusted pollen production. Flower phenotypic femaleness therefore increased from first to last buds (γβ0, Table 1, Fig. 3). These within-plant trends were largely independent of the relationship between time and flower size (Supplementary Data 3), and were highly consistent among plants (σ2β, Table 1).

Fig. 3.

Fig. 3.

Open in a new tab

Within-plant effects of time on ovules per flower bud, adjusted pollen per flower bud (ovule equivalents), total gametes per flower bud (ovule equivalents) and flower femaleness. Plots are shown for three randomly chosen Brassica rapa plants (top row: plant 181; middle row: plant 241; bottom row: plant 659). All response variables are plotted against day of flower collection, measured as days since flowering onset as estimated by the first day of bud collection. Trends estimated with hierarchical regression.

Among-plant variation in pollen and ovule production

Ovule content per flower decreased with later bolting (γα1, Table 1, Fig. 4A), while adjusted pollen content did not (γα1, Table 1, Fig. 4B). Combined, pre-fertilization flower phenotypic femaleness decreased with later bolting (γα1, Table 1, Fig. 4D).

Fig. 4.

Fig. 4.

Open in a new tab

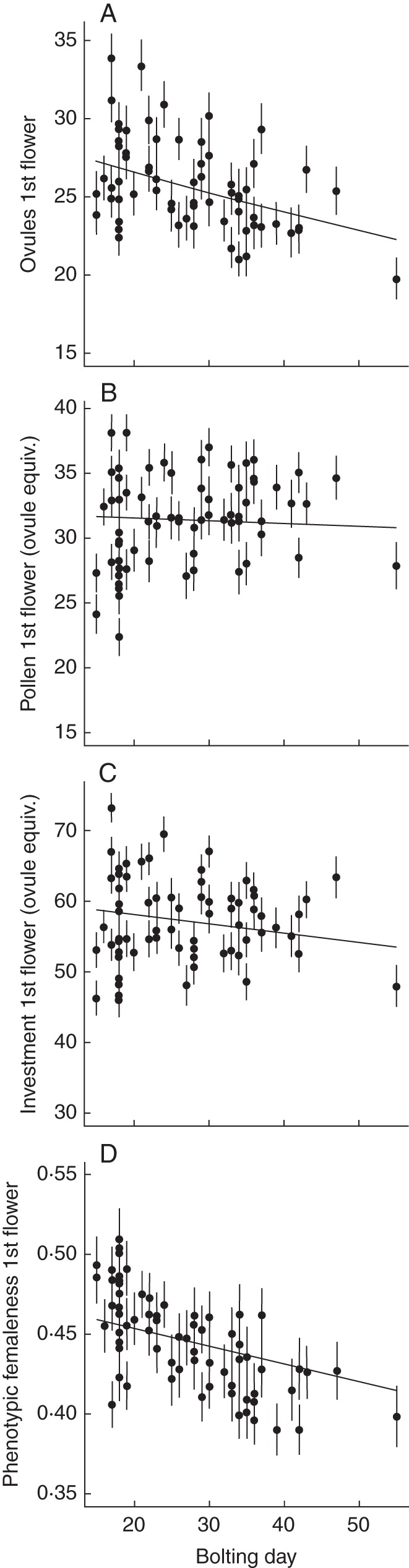
Direct effects of days to bolting on mean (±SE) pollen and ovule production and flower femaleness of first flowers within Brassica rapa plants, holding constant the effects of variation in plant size, fertilizer treatment and the abiotic environment. Trends are estimated with hierarchical regression. n = 70 plants. Pollen and investment are expressed as ovule equivalents.

When controlling for variation in other among-plant predictors, flower phenotypic femaleness decreased with taproot size (γα2, Table 1). This trend arose through increasing adjusted pollen content with size (γα2, Table 1). Ovule content per flower increased with fertilizer addition (γα3, Table 1). We did not detect statistically significant effects of PC1 of the measured environmental variables (γα4, Table 1). Note that pollination treatment, which begins after flowering onset, cannot directly influence pollen or ovule production of first flowers. Detected among-plant effects of pollination (γα5, Table 1) are a consequence of interactions between pollination and day since onset (γβ5, Table 1).

DISCUSSION

The numerical model confirmed that declining fruit-set probability from first to last flowers on plants can, under a wide range of conditions, induce temporal variation in expected male success and functional femaleness (Fig. 1, Supplementary Data 2). In most cases examined, average functional femaleness decreased sharply in the last flower class on plants. In contrast, at the among-plant level, functional femaleness increased substantially from early- to late-flowering plants in all cases where fruit-set declined (from 0·42 to 0·67 in the illustrative case). Temporal trends in phenotypic femaleness in B. rapa opposed expected trends in functional femaleness: phenotypic femaleness increased from first to last flowers on plants (Fig. 3), and decreased from early- to late-flowering plants (Fig. 4). Below, we discuss the numerical model in relation to previous ESS models, and examine the discrepancy between predicted trends in functional femaleness and observed trends in phenotypic femaleness.

Predicted effects of declining fruit-set on sex allocation optima

Variation in the mating environment of sequentially opening flowers on plants can lead to variation in their sex allocation optima (Brunet and Charlesworth, 1995). Effects of dichogamy are particularly well studied. Brunet and Charlesworth (1995) reasoned that dichogamy creates a temporal shift in the quantity of male- versus female-phase flowers (i.e. the mating environment), and therefore generates a temporal trend in total expected pollen transfer probability from first to last flowers on plants. This shift in the mating environment causes variation in sex allocation optima (Brunet and Charlesworth, 1995). This ESS model prediction is well supported by data from several dichogamous species (e.g. Brunet, 1996; Huang et al., 2004; Zhao et al., 2008; Ishii and Harder, 2012).

Dichogamy was not, however, the only scenario examined in this ESS model. Brunet and Charlesworth (1995) also reasoned that when resources decline from first to last flowers on plants, first flowers offer a higher quality siring opportunity than last flowers (see also Brunet, 1996). Flowers with a greater probability of transferring pollen to these high-quality recipients will have greater reproductive success as males, and because pollen transfer can only occur between flowers open at the same time, this advantage falls to first flowers (Brunet and Charlesworth, 1995). The optimal sex allocation of first flowers is therefore more male than that of last flowers, unless the female gain curve decelerates much more rapidly than the male (Brunet and Charlesworth, 1995: their figure 3). This scenario is similar to our numerical model, but where Brunet and Charlesworth (1995) assume an equal probability of fruit-set across flowers regardless of resource status, we instead assume that fruit-set probability decreases with resource status, and where Brunet and Charlesworth (1995) assume no variation in flowering onset, we allow onset to vary. We discuss these differences below.

In some species, declining fruit-set within plants appears to be an outcome of decreasingly female sex allocation optima (Brunet, 1996). In many others, resource shortage at least contributes to the low fruit (or seed) set of last flowers (e.g. Agren and Willson, 1992; Guitián et al., 2001; Kliber and Eckert, 2004). When we assumed that fruit-set probability decreases with resource status, we found that the drop in expected female reproductive success from first to last flowers outpaced the drop in expected male success (Fig. 1D). The average functional gender of first flowers on plants is therefore more female than that of last flowers (Fig. 1F, see exceptions Supplementary Data 2), leading us to expect that optimal sex allocation is least female in the last flowers. This expectation contrasts with Brunet & Charlesworth's (1995: their figure 3) prediction for optimal allocation under declining resources with constant fruit-set probability. Pinpointing the precise sex allocation optima of flower classes under declining fruit-set probability requires testing in an analytical ESS model. The numerical model confirmed that declining fruit-set creates conditions that could lead to selection for variable pre-fertilization sex allocation within plants. An ESS model would help predict the long-term outcome of this selection.

When flowering onset is variable and fruit-set declines, a shift occurs in the quality of male mating opportunity available to early- versus late-flowering plants. Consequently, expected male success decreases among plants across the season (Fig. 1C), and functional femaleness increases (Fig. 1E). Others have speculated that variation in the mating environment experienced by early- versus late-flowering plants in dichogamous species leads to variation in their optimal sex allocation (Brookes and Jesson, 2010; Ishii and Harder, 2012). We similarly suggest that optimal sex allocation may be increasingly female from early- to late-flowering plants in adichogamous species whose fruit-set declines. This prediction again requires testing in an ESS model.

The key finding of the numerical model was that declining fruit-set can drive temporal variation in functional gender both within and among plants. Within plants, the model revealed that the effect of declining resources among flower classes on optimal sex allocation may depend on whether resource status does (Fig. 1F, see also Brunet, 1996: her table 4) or does not (Brunet and Charlesworth, 1995: their figure 3) affect fruit-set probability. Among plants, the model presented here suggests that heterogeneity in the mating environment (i.e. the quantity and quality of available mates) may lead to among-plant variation in sex allocation optima. This contrasts with past work emphasizing effects of heterogeneity in the physical environment (Lloyd and Bawa, 1984). These two factors may lead to mechanistically different responses: whereas heterogeneity in the physical environment selects for plasticity in sex allocation (Lloyd and Bawa, 1984; Vogler et al., 1999; Friedman and Barrett, 2011), temporal heterogeneity in the mating environment resulting from declining fruit-set might instead give rise to correlational selection on flowering time and sex allocation.

Temporal variation in phenotypic gender in B. rapa

Temporal trends in phenotypic femaleness in B. rapa conflicted with trends in functional gender predicted by the numerical model. Before examining this discrepancy, we need to consider the relationship between phenotypic gender (Gp) and sex allocation. Inclusion of equivalence factor E in calculating Gp means that Gp is influenced by the population, and is not an inherent property of a plant or flower (Robbins and Travis, 1986). It therefore cannot be directly read as sex allocation. Unlike some other formulations of phenotypic gender (e.g. Thomson and Barrett, 1981), however, ours did not allow E to vary over time. Thus, the same inverse relationship between Gp and the pollen-to-ovule ratio (p:o, an inherent property of a flower) holds for all flowers in our study, meaning Gp is interpretable as an indicator of sex allocation. Varying costs per pollen grain and costs per ovule across species can complicate interpretation of p:o (and thus Gp) as sex allocation (Lloyd, 1984), but this concern does not apply when evaluating directions of change in sex allocation among flowers and plants of a single species.

The expectation that our indicator of sex allocation, Gp, would mirror trends in functional gender predicted by the model rests on the assumption that variation in functional gender causes variation in sex allocation optima. As stated above, this assumption requires testing in an analytical ESS model. Even if the assumption is correct, however, observed trends in phenotypic femaleness in B. rapa could oppose expectations for several reasons.

We first consider our experimental design. Our indicator of sex allocation includes pre-fertilization investment only, but female investment continues through seed and fruit maturation (Lloyd, 1980b). We restricted our focus to pre-fertilization investment because declining fruit-set cannot be both the cause and the consequence of among-flower variation in sex allocation optima, and because variation in pre-fertilization allocation often matches predicted variation in optima (e.g. Brunet, 1996; Huang et al., 2004; Zhao et al., 2008; Brookes and Jesson, 2010; Ishii and Harder, 2012). Also related to the experiment, plants may have plastically adjusted their allocation to the relatively constant glasshouse environment, perhaps masking temporal variation that would be expressed in the field. Discrepancy in within-plant temporal trends in sex allocation across glasshouse and field environments in some Clarkia taxa lends credence to this possibility (Delesalle et al., 2008; Mazer et al., 2009).

Second, optimal allocation in Brassica rapa might be influenced by factors not considered in the model, such as pre-fertilization decline in resource status, unequal male and female gain curves, and competition among related pollen grains and seeds (Charnov, 1982; Lloyd, 1984). Moreover, model results were sensitive to self-incompatibility, the relationship between flowers displayed and pollen export, and flower longevity (Supplementary Data 2). The first of these factors certainly applies to B. rapa, and the other two may. Because these factors affect mate availability, they interact with declining fruit-set to shape the sex allocation optima of flowers and plants. Interaction between factors is supported by Brunet's (1996) finding that when fruit-set declines, the estimated male success and functional gender of first versus last flowers depends on whether calculations take floral dichogamy into account.

Finally, some model assumptions might not apply to the study population. For example, the model assumed resource limitation of fruit production. Most species exhibit pollen limitation in at least some populations in some years (Burd, 1994; Ashman et al., 2004; Knight et al., 2005). If pollen were limiting, fruit-set probability might not decrease within plants. Predicted temporal trends in functional gender may therefore occur only in populations or years where female fitness is resource-limited. The model also assumed that flowers varied in their quality as pollen recipients, but plants did not. Selection tends to favour early flowering through female fitness (Munguia-Rosas et al., 2011), suggesting that among-plant variation in female quality may alter male mating opportunity.

The B. rapa data reported here are, to our knowledge, one of just three datasets reporting temporal variation in pollen and ovule production both within and among plants, and the only such dataset for an adichogamous species (see Brookes and Jesson, 2010; Ishii and Harder, 2012, for dichogamous species). Data describing within-plant temporal trends are, however, available for some other adichogamous species. These reveal increasing (Ishii and Sakai, 2002), decreasing (Young and Stanton, 1990; Kliber and Eckert, 2004) and constant (Cao et al., 2007) p:o from first to last flowers, suggesting multiple influences on sex allocation optima. Further data on temporal trends in adichogamous species, particularly at the among-plant level, might help resolve the potential role of declining fruit-set in shaping allocation optima.

CONCLUSIONS

The discrepancy between model expectations and our observations in B. rapa could suggest that other factors or trade-offs interact with declining fruit-set to determine allocation optima in this species. The discrepancy does not, however, rule out the possibility that male reproductive success of B. rapa decreases with later flowering onset, as predicted by the model (Fig. 1C). If declining fruit-set lowers the male reproductive success of late-flowering plants, selection could favour early flowering through male fitness. Because flowering time evolution is implicated in response to climate change (Franks et al., 2007), species invasion (Montague et al., 2007) and reproductive isolation between related species (Lowry et al., 2008), selection on flowering time is an active area of research. The empirical emphasis has been on selection through female fitness (Munguia-Rosas et al., 2011). The testable prediction regarding its action through male fitness outlined here is an exciting avenue for future work.

SUPPLEMENTARY DATA

Supplementary Data are available online at www.aob.oxfordjournals.org and consist of the following. Data 1: fully annotated R-code for the conceptual model, and instructions for its use (zip file). Data 2: numerical model results under a range of conditions relaxing assumptions made in the illustrative case. Data 3: a hierarchical regression model examining the joint effects of flower size and days since flowering onset on within-plant variation in ovule production, adjusted pollen production, total gamete production and flower femaleness. Data 4: relationships between flowering time, plant size (log-transformed taproot dry mass) and fertilizer treatment. Data 5 and 6: statistical models describing effects of pollination and fertilizer treatments on flower production and flowering duration, respectively.

Supplementary Data
supp_114_1_167__index.html (1.5KB, html)

ACKNOWLEDGEMENTS

We thank K. Nakamura for long hours spent dissecting buds; B. Petro, K. Turner, S. Hsieh and S. Wadgymar for assistance with data collection; B. Hall and A. Petrie for glasshouse support; J. Brunet, S. C. H. Barrett, J. R. Stinchcombe, L. K. Jesson, J. L. Ison, S. Wadgymar and anonymous reviewers for helpful comments on earlier drafts; and J. Forrest for enlightening conversations. E.J.A. also thanks the Chemistry/Biochemistry and Biology departments at Mount Allison University (NB, Canada) for their hospitality during the writing of this paper. This research was supported by grants from the Natural Sciences and Engineering Research Council of Canada.

LITERATURE CITED

  1. Agren J, Willson MF. Determinants of seed production in Geranium maculatum. Oecologia. 1992;92:177–182. doi: 10.1007/BF00317361. [DOI] [PubMed] [Google Scholar]
  2. Al-Shehbaz IA. Protogyny in the Cruciferae. Systematic Botany. 1977;2:327–333. [Google Scholar]
  3. Ashman T-L, Knight TM, Steets JA, et al. Pollen limitation of plant reproduction: ecological and evolutionary causes and consequences. Ecology. 2004;85:2408–2421. [Google Scholar]
  4. Bates D, Maechler M, Bolker BM. lme4: Linear mixed-effects models using S4 classes. 2011. R package version 0.999375–42 http://CRAN.R-project.org/package=lme4 .
  5. Brookes RH, Jesson LK. Do pollen and ovule number match the mating environment? An examination of temporal change in a population of Stylidium armeria. International Journal of Plant Sciences. 2010;171:818–827. [Google Scholar]
  6. Brunet J. Male reproductive success and variation in fruit and seed set in Aquilegia caerulea (Ranunculaceae) Ecology. 1996;77:2458–2471. [Google Scholar]
  7. Brunet J, Charlesworth D. Floral sex allocation in sequentially blooming plants. Evolution. 1995;49:70–79. doi: 10.1111/j.1558-5646.1995.tb05959.x. [DOI] [PubMed] [Google Scholar]
  8. Burd M. Bateman's principle and plant reproduction: the role of pollen limitation in fruit and seed set. The Botanical Review. 1994;60:83–139. [Google Scholar]
  9. Cao G-X, Kudo G, Ida TY. Floral sex allocation in a hermaphrodite herb with 1-day flowers, Hosta rectifolia (Liliaceae) Plant Species Biology. 2007;22:191–196. [Google Scholar]
  10. Charlesworth D, Charlesworth B. Allocation of resources to male and female functions in hermaphrodites. Biological Journal of the Linnean Society. 1981;15:57–74. [Google Scholar]
  11. Charnov E. The Theory of Sex Allocation. Princeton, NJ: Princeton University Press; 1982. [PubMed] [Google Scholar]
  12. de Jong TJ, Klinkhamer PGL. Evolutionary ecology of plant reproductive strategies. Cambridge, UK: Cambridge University Press; 2005. [Google Scholar]
  13. Delesalle V, Mazer SJ, Paz H. Temporal variation in the pollen:ovule ratios of Clarkia (Onagraceae) taxa with contrasting mating systems: field populations. Journal of Evolutionary Biology. 2008;21:310–323. doi: 10.1111/j.1420-9101.2007.01444.x. [DOI] [PubMed] [Google Scholar]
  14. Diggle PK. Architectural effects and the interpretation of patterns of fruit and seed development. Annual Review of Ecology and Systematics. 1995;26:531–552. [Google Scholar]
  15. Diggle PK. Ontogenetic contingency and floral morphology: the effects of architecture and resource limitation. International Journal of Plant Sciences. 1997;158:S99–S107. [Google Scholar]
  16. Diggle PK. Architectural effects on floral form and function: a review. In: Stuessy T, Horandl E, Mayer V, editors. Deep morphology: toward a renaissance of morphology in plant systematics. Konigtein, Germany: Koeltz; 2003. pp. 63–80. [Google Scholar]
  17. Ehrlén J. Proximate limits to seed production in a herbaceous perennial legume, Lathyrus vernus. Ecology. 1992;73:1820–1831. [Google Scholar]
  18. Franke D, Ellis A, Dharjwa M, et al. A steep cline in flowering time for Brassica rapa in Southern California: population-level variation in the field and the greenhouse. International Journal of Plant Sciences. 2006;167:83–92. [Google Scholar]
  19. Franks SJ, Sim S, Weis AE. Rapid evolution of flowering time by an annual plant in response to a climate fluctuation. Proceedings of the National Academy of Sciences. 2007;104:1278–1282. doi: 10.1073/pnas.0608379104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Friedman J, Barrett SCH. Genetic and environmental control of temporal and size-dependent sex allocation in a wind-pollinated plant. Evolution. 2011;65:2061–2074. doi: 10.1111/j.1558-5646.2011.01284.x. [DOI] [PubMed] [Google Scholar]
  21. Gelman A, Hill J. Data analysis using regression and multilevel/hierarchical models. New York: Cambridge University Press; 2007. [Google Scholar]
  22. Gelman A, Su Y-S, Yajima M, et al. arm: Data Analysis Using Regression and Multilevel/Hierarchical Models. 2012. R package version 1.5–04 http://CRAN.R-project.og/package=arm .
  23. Guitián J. Variation in floral sex allocation in Polygonatum odoratum (Liliaceae) Annals of Botany. 2004;94:433–440. doi: 10.1093/aob/mch163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Guitián J, Guitián P, Medrano M. Causes of fruit-set variation in Polygonatum odoratum (Liliaceae) Plant Biology. 2001;3:637–641. [Google Scholar]
  25. Herrera CM. Multiplicity in unity: plant subindividual variation and interactions with animals. Chicago: University of Chicago Press; 2009. [Google Scholar]
  26. Hiraga T, Sakai S. The effects of inflorescence size and flower position on biomass and temporal sex allocation in Lobelia sessiliflora. Plant Ecology. 2007;188:205–214. [Google Scholar]
  27. Horovitz A. Is the hermaphrodite flowering plant equisexual? American Journal of Botany. 1978;65:485–486. [Google Scholar]
  28. Huang S, Tang L, Yu Q, Guo Y. Temporal floral sex allocation in protogynous Aquilegia yabeana contrasts with protandrous species: support for the mating environment hypothesis. Evolution. 2004;58:1131–1134. doi: 10.1111/j.0014-3820.2004.tb00446.x. [DOI] [PubMed] [Google Scholar]
  29. Ishii H, Sakai S. Temporal variation in floral display size and individual floral sex allocation in racemes of Narthecium asiaticum (Liliaceae) American Journal of Botany. 2002;89:441–446. doi: 10.3732/ajb.89.3.441. [DOI] [PubMed] [Google Scholar]
  30. Ishii HS, Harder LD. Phenological associations of within- and among-plant variation in gender with floral morphology and integration in protandrous Delphinium glaucum. Journal of Ecology. 2012;100:1029–1038. [Google Scholar]
  31. Kliber A, Eckert CG. Sequential decline in allocation among flowers within inflorescences: proximate mechanisms and adaptive significance. Ecology. 2004;85:1675–1687. [Google Scholar]
  32. Knight T, Steets J, Vamosi J, et al. Pollen limitation of plant reproduction. Annual Review of Ecology, Evolution and Systematics. 2005;36:467–497. [Google Scholar]
  33. Lee TD. Patterns of fruit and seed production. In: Lovett-Doust J, Lovett-Doust L, editors. Reproductive ecology: patterns and strategies. New York: Oxford University Press; 1988. pp. 179–202. [Google Scholar]
  34. Lloyd DG. Sexual strategies in plants. III. A quantitative method for describing the gender of plants. New Zealand Journal of Botany. 1980a;18:103–108. [Google Scholar]
  35. Lloyd DG. Sexual strategies in plants. I. An hypothesis of serial adjustment of maternal investment during one reproductive session. The New Phytologist. 1980b;86:69–79. [Google Scholar]
  36. Lloyd DG. Gender allocations in outcrossing cosexual plants. In: Dirzo R, Sarukhán J, editors. Perspectives on plant population ecology. Sunderland, MA: Sinauer; 1984. pp. 277–300. [Google Scholar]
  37. Lloyd DG, Bawa K. Modification of the gender of seed plants in varying conditions. Evolutionary Biology. 1984;17:255–338. [Google Scholar]
  38. Lowry DB, Modliszewski JL, Wright KM, Wu CA, Willis JH. The strength and genetic basis of reproductive isolating barriers in flowering plants. Philosophical Transactions of the Royal Society B: Biological Sciences. 2008;363:3009–3021. doi: 10.1098/rstb.2008.0064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Mazer SJ, Dudley LS, Delesalle VA, Paz H, Galusky P. Stability of pollen–ovule ratios in pollinator-dependent versus autogamous Clarkia sister taxa: testing evolutionary predictions. New Phytologist. 2009;183:630–648. doi: 10.1111/j.1469-8137.2009.02886.x. [DOI] [PubMed] [Google Scholar]
  40. Méndez M. Modification of phenotypic and functional gender in the monoecious Arum italicum (Araceae) American Journal of Botany. 1998;85:225–234. [PubMed] [Google Scholar]
  41. Montague JL, Barrett SCH, Eckert CG. Re-establishment of clinal variation in flowering time among introduced populations of purple loosestrife (Lythrum salicaria, Lythraceae) Journal of Evolutionary Biology. 2007;21:234–245. doi: 10.1111/j.1420-9101.2007.01456.x. [DOI] [PubMed] [Google Scholar]
  42. Munguia-Rosas MA, Ollerton J, Parra-Tabla V, De-Nova JA. Meta-analysis of phenotypic selection on flowering phenology suggests that early flowering plants are favoured. Ecology Letters. 2011;14:511–521. doi: 10.1111/j.1461-0248.2011.01601.x. [DOI] [PubMed] [Google Scholar]
  43. Ohashi K, Yahara T. Behavioural responses of pollinators to variation in floral display size and their influences on the evolution of floral traits. In: Chittka L, Thomson JD, editors. Cognitive ecology of pollination. Cambridge: Cambridge University Press; 2001. pp. 274–296. [Google Scholar]
  44. R Development Core Team. R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing; 2012. http://www.R-project-org/ [Google Scholar]
  45. Rasband WS. ImageJ. Bethesda, MD: U. S. National Institutes of Health; 2007–2014. http://imagej.nih.gov/ij/ [Google Scholar]
  46. Robbins L, Travis J. Examining the relationship between functional gender and gender specialization in hermaphroditic plants. American Naturalist. 1986;128:409–415. [Google Scholar]
  47. Stinchcombe JR, Kirkpatrick M. Genetics and evolution of function-valued traits: understanding environmentally responsive phenotypes. Trends in Ecology and Evolution. 2012;27:637–647. doi: 10.1016/j.tree.2012.07.002. [DOI] [PubMed] [Google Scholar]
  48. Thomson JD, Barrett SCH. Temporal variation of gender in Aralia hispida vent. (Araliaceae). Evolution. 1981;35:1094–1107. doi: 10.1111/j.1558-5646.1981.tb04979.x. [DOI] [PubMed] [Google Scholar]
  49. Vogler DW, Peretz S, Stephenson AG. Floral plasticity in an iteroparous plant: the interactive effects of genotype, environment, and ontogeny in Campanula rapunculoides (Campanulaceae) American Journal of Botany. 1999;86:482–494. [PubMed] [Google Scholar]
  50. Weis A, Kossler T. Genetic variation in flowering time induces phenological assortative mating: quantitative genetic methods applied to Brassica rapa. American Journal of Botany. 2004;91:825–836. doi: 10.3732/ajb.91.6.825. [DOI] [PubMed] [Google Scholar]
  51. Wright SI, Barrett SCH. Size-dependent gender modification in a hermaphroditic perennial herb; Proceedings of the Royal Society B: Biological Sciences; 1999. pp. 225–232. [Google Scholar]
  52. Yampolsky C, Yampolsky H. Distribution of sex forms in the phanerogamic flora. Bibliotheca Genetica. 1922;3:1–62. [Google Scholar]
  53. Young H, Stanton M. Temporal patterns of gamete production within individuals of Raphanus sativus (Brassicaceae) Canadian Journal of Botany. 1990;68:480–486. [Google Scholar]
  54. Zhang D-Y. Evolutionarily stable reproductive investment and sex allocation in plants. In: Harder LD, Barrett SCH, editors. Ecology and Evolution of Flowers. New York: Oxford University Press; 2006. pp. 41–60. [Google Scholar]
  55. Zhao Z-G, Meng J-L, Fan B-L, Du G-Z. Reproductive patterns within racemes in protandrous Aconitum gymnandrum (Ranunculaceae): potential mechanism and among-family variation. Plant Systematics and Evolution. 2008;273:247–256. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_114_1_167__index.html (1.5KB, html)
supp_mcu087_mcu087supp2.pdf (92.6KB, pdf)
supp_mcu087_mcu087supp3.pdf (109.6KB, pdf)
supp_mcu087_mcu087supp4.pdf (12KB, pdf)
supp_mcu087_mcu087supp5.pdf (12.2KB, pdf)
supp_mcu087_mcu087supp6.pdf (38.2KB, pdf)
supp_mcu087_mcu087supp1.zip (58.1KB, zip)

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES