Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 May 12;8(6):5891–5897. doi: 10.1021/nn500978p

Patterns without Patches: Hierarchical Self-Assembly of Complex Structures from Simple Building Blocks

Michael Grünwald †,*, Phillip L Geissler ‡,*
PMCID: PMC4071109  PMID: 24816138

Abstract

graphic file with name nn-2014-00978p_0007.jpg

Nanoparticles with “sticky patches” have long been proposed as building blocks for the self-assembly of complex structures. The synthetic realizability of such patchy particles, however, greatly lags behind predictions of patterns they could form. Using computer simulations, we show that structures of the same genre can be obtained from a solution of simple isotropic spheres, with control only over their sizes and a small number of binding affinities. In a first step, finite clusters of well-defined structure and composition emerge from natural dynamics with high yield. In effect a kind of patchy particle, these clusters can further assemble into a variety of complex superstructures, including filamentous networks, ordered sheets, and highly porous crystals.

Keywords: self-assembly, computer simulation, nanoparticles, patchy particles, DNA programmed self-assembly, clusters

Living systems create and maintain their functional microscopic organization through self-assembly, the spontaneous arrangement of an initially unordered collection of biomolecular building blocks. Mimicking this behavior in the laboratory with synthetic components has proven to be a formidable challenge. A close look at the agents of self-assembly in living systems reveals a key aspect of the problem: Most biomolecular objects interact through directionally specific forces, so-called “patchy” interactions. Indeed, computer simulations of model nanoparticles with attractive patches have recapitulated much of the richness of nature’s self-assembled structures.1−6 Synthetic nanoparticles with controlled patchiness, however, are largely unavailable in the laboratory, although impressive progress has been made in specific cases.7−10

In this letter, we consider a pragmatic question, though from a theoretical perspective: Using only nanoparticle synthesis and functionalization techniques that are standard today, can self-assembled patterns be realized that share the complexity achieved by biology’s (and simulators’) patchy components? In particular, we devise and demonstrate numerically a hierarchical strategy for this purpose, which assumes control only over a few energies of interaction between spherical particles, as well as their size. Such control should be feasible in practice given well-established procedures to decorate the exterior of nanoparticles with double-stranded DNA.

Our scheme begins with a dilute solution of spherical particles, of several types, that interact isotropically and over short distances. With appropriate choice of the sizes and binding affinities of these particles, we show that a nearly uniform population of “metaparticles” can emerge: tightly bound clusters, comprising a handful of spherical monomers, with defined composition and internal structure, as illustrated in Figure 1a. These objects constitute a kind of patchy nanoparticle, with nontrivial shape and an anisotropic arrangement of monomers that can subsequently serve as sites for effectively directional interaction. In the second stage of our scheme, the emergent patchiness of metaparticles is exploited to spontaneously generate large-scale superstructures, some of which are highly ordered and reminiscent of biological assemblies.

Figure 1.

Figure 1

Open in a new tab

Self-assembly of metaparticles. (a) Three example metaparticles that can be prepared with high yield through appropriate choices of attraction strengths and glue particle size. (b) Strategy for controlling cluster size and composition. Purple contact points indicate strong attraction between glue particles (yellow) and monomers [pink (A), orange (B), and blue (C)], which dictates metaparticle size and shape. Composition and connectivity within a metaparticle are controlled through weaker interactions (green contact points) between monomers. In this example, all unlike particle types attract one another; like types do not. (c) Estimated yields (continuous curves) of the target clusters shown in (a), as a function of interaction strength ε̅ between monomers. Data points are results from simulations at ρ ≈ 0.01σ–3. (d) Snapshot from a simulation of C6 metaparticle formation (with ε̅ = 3kBT and εglue = 10 kBT) after equilibrium has been established. For clarity we show only monomers that are bound to glue particles. The yield of correctly composed octahedral metaparticles in this case is ∼90%.

Results and Discussion

The types of spherical monomers we have in mind are distinguished from one another by the strength of their interactions with other monomers. Specifically, the potential energy of two monomers, of types A and B, separated by a distance r is urep(r) + εABuatt(r). The steric repulsion urep enforces volume exclusion, strongly penalizing separations below a threshold value, r ≤ σ. At distances near contact, the attractive potential uatt provides a favorable energy, uatt(r) ≈ −1 for r ≤ σ + w, and attenuates rapidly for r > σ + w.

The specific forms of these potentials are not important, only that urep sets a well-defined particle diameter σ and that uatt acts over a short-range w ≪ σ. [We consider only attractive interactions with ε ≥ 0. Negative values of ε effectively increase the size of monomers. Because of the short-range of interactions, this modification is subtle and has little effect on assembly dynamics.] (See Methods for the specific pair potential used in our simulations.) Colloidal nanoparticles with surface-grafted DNA molecules provide one experimental realization of this system, in which the complementary sequences of DNA strands attached to monomers A and B encode the strength εAB of their attraction.11−13

Metaparticle Assembly

Building finite-sized metaparticles from a macroscopic collection of such monomers is not a trivial matter.14−16 If, say, attractions among monomers A, B, C, and D provide the cohesive energy maintaining the integrity of an ABCD cluster, then additional monomers of these four types will tend to bind at the cluster’s surface. Lacking constraints on monomer valency, it is not clear how to design against unbound growth of a close-packed crystal. Indeed, an extensive search through possible combinations of binding affinities did not yield self-limiting growth of small clusters in computer simulations.

To prepare metaparticles, we instead adopted an approach devised to build finite clusters of identical particles,17−19 modified in such a way that different monomer types can be incorporated. Here, cluster size and geometry are dictated by introducing an additional kind of particle with smaller diameter σglue < σ. This “glue particle” attracts all other monomers strongly (with contact energy εglue) and over short-range (wglue). For appropriate size combinations, the propensity to maximally coordinate each glue particle determines with great precision the structure of its shell of monomers, as illustrated in Figure 1b. Of the many convex polyhedra that can be obtained in this way (denoted Cn, where n is the number of shell particles), we focus exclusively on triangles (C3), tetrahedra (C4), and octahedra (C6), illustrated in Figure 1a. Unlike larger shapes, we can control the arrangement of monomer types within these shells through the set of attraction strengths ε ≡ {εAA, εAB, ...}, as discussed below.

The only threat to self-limiting growth in this scenario is the possibility that two glue particles bind to overlapping sets of shell monomers. This errant growth can be made irrelevant by working at low concentration of glue particles. Alternatively, they could be endowed with longer-range repulsions. Our simulations follow the latter approach, with glue particles repelling one another through a screened Coulomb interaction (see Methods).

The crux of making well-defined metaparticles lies in dictating the identities of monomers at each vertex of the shell. Out of the many possible shell compositions, illustrated for C4 clusters in Supporting Figure 2, one must be represented with dominant statistical weight. As one challenge to this task, εglue must be sufficiently weak that binding is reversible, so that inevitable mistakes in cluster composition can be corrected in reasonable time; cluster integrity may be compromised as a result. More subtly, attractions among shell particles must be sufficiently weak that they do not macroscopically condense. This constraint limits the extent to which one shell composition can dominate energetically over others. It is not obvious that these competing requirements can all be satisfied with a single choice of εglue and ε.

Approximate analytical calculations, as well as explicit Brownian dynamics simulations, indicate that high yields of certain metaparticles can in fact be made in this simple fashion. As a straightforward design, we set εij = ε̅ if monomer types i and j make contact in a desired cluster, and εij = 0 otherwise.20 Due to the limitations of short-ranged, pairwise, and isotropic interactions, this scheme does not permit access to all metaparticle compositions. For example, we cannot generate a pure population of octahedra with more than three monomer types. However, the metaparticles shown in Figure 1a can be prepared with high fidelity through spontaneous dynamics of initially dispersed monomers and glue particles.

To estimate the equilibrium yield of a metaparticle comprising n monomers, we consider a restricted ensemble of fully assembled Cn structures that differ in the assignment of k monomer types to the cluster’s n vertices. We first enumerate all (n + k – 1)!/[n!(k – 1)!] distinct compositions ν of the cluster (e.g., 2 A monomers, 1 B, and 1 C). For each ν we then enumerate all n! monomer assignments to a fixed set of vertices, as if all particles were distinguishable, calculating the energy Ei(ν) for each assignment i. The yield Y(ε̅) is then computed as a ratio of partition functions:

graphic file with name nn-2014-00978p_m001.jpg 1

where β = (kBT)−1, α(ν) = [NA(ν)!NB(ν)!NC(ν)!ND(ν)!]−1, and asterisks refer to the target metaparticle (i.e., ν* is the target composition, and E* is the minimum energy). The symmetry factor ω* accounts for the multiplicity of assignments corresponding to rotations of the desired cluster. Yields predicted in this approximate way are plotted as functions of ε̅ for all three cluster types in Figure 1c. Monomer attractions of a few kBT are sufficient to select the target composition with high probability. Results of molecular dynamics simulations, shown as data points in Figure 1c, demonstrate that the analysis described above is reasonable, but not without shortcomings. In particular, neglect of structural fluctuations en route to eq 1 tends to overestimate yields, due to the enhanced vibrational freedom of clusters lacking the maximum number of attractive interactions.

In principle, yields can be made arbitrarily close to unity by increasing the strength ε̅ of monomer attractions. Large values of ε̅, however, encourage clustering of monomers even in the absence of glue particles. Indeed, for sufficiently large ε̅ the equilibrium state of a large collection of monomers is a macroscopic crystalline aggregate. Monomer condensation thus places a practical upper limit on ε̅ and therefore also on yield. (See Supporting Information for an analytical estimate of this limit.) However, our simulations show that high yields can be achieved for values of ε̅ that are smaller than this threshold. In particular, at monomer densities of ρ ≈ 0.01σ–3, we achieve maximum yields of 94%, 78%, and 98% for C3, C4, and C6 clusters, respectively. A snapshot from a simulation of the self-assembly of C6 metaparticles is shown in Figure 1d. In the assembly of C4 clusters, the two enantiomers of an ABCD tetrahedron must appear with macroscopically identical concentrations; in simulations of superstructure assembly described below we consider the racemic mixture. In all cases, the emergent patchiness of clusters is sufficient to generate a rich variety of self-assembled superstructures.

Superstructure Assembly

To induce further assembly among many metaparticles, it is necessary at this point to modify the strengths of attraction ε between their constituent monomers, which now act as sticky patches for interactions between distinct clusters. To avoid consequent changes in the internal structure of metaparticles, it is further necessary to render the glue particle bonds irreversible. (If these latter interactions were to remain reversible, then changes in ε could greatly compromise the yield of desired metaparticles or even lead to macroscopic condensation of monomers). Both of these tasks have been accomplished in other contexts using techniques of DNA nanotechnology.13 Fortunately, elaborate combinations of monomer attraction are not needed at this stage to assemble complex patterns. On the contrary, introducing substantial attractions between more than one or two monomer types typically allows only close-packed crystals or amorphous solids as products of assembly. We have instead obtained interesting and varied assembly when ϵij = 0 for all monomer–monomer interactions except: (i) self-attraction of one monomer type, i.e., εAA > 0 (a design we denote [AA]), or (ii) self-attraction of two types, εAA > 0 and εBB > 0 (denoted [AA,BB]), or (iii) a single cross-interaction, εAB > 0 (denoted [AB]). In one special case the design [AA,BB,CC] was also conducive to nontrivial pattern formation. As is generally the case with patchy nanoparticles, the dynamical fate of assembly is very sensitive to the magnitudes of these attractions.21−23 We explored a range of values of εAA, εBB, etc., for each structure and report here on choices that yielded the most reproducible and defect-free assemblies. For an attraction range w ≈ 0.05σ, well depths of a few kBT appear to be optimal in all cases (see Methods). For some designs the energetic range between impractically slow growth and extensively defective aggregation is as narrow as 0.2kBT. The superstructures described below were assembled from metaparticles of uniform composition; their quality was only slightly degraded by including defective metaparticles at the levels indicated by simulations of cluster formation.

Given that metaparticle structures correspond to highly symmetric polyhedra and that the size of effective patches is prescribed by the monomer diameter, one might expect the variety of patterns that can be assembled from the C3, C4, and C6 clusters of Figure 1a to be meager and easily anticipated. These objects, however, are more complex building blocks than spheres decorated with symmetrically arranged interaction sites. Indeed, particle shape can be a critical factor in self-assembly, strongly influencing the structure of thermodynamic ground states as well as their kinetic accessibility.24−26

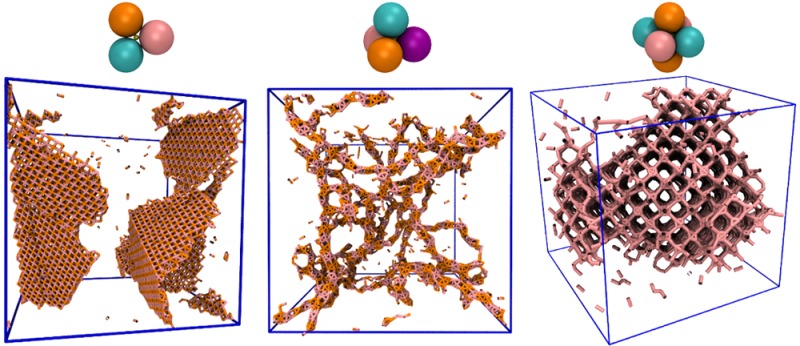
An interplay between packing and directional attraction is important in even the simplest assembly we observed in Brownian dynamics simulations of interacting metaparticles. (Simulation details are given in the Methods section.) With only one mode of self-attraction ([AA]) among monomers in different C4 clusters, the attracting species A tends to aggregate to the extent allowed by volume exclusion due to the rest of the cluster. Zero-dimensional, micelle-like superstructures thus naturally emerge (see left panel of Figure 2), and like conventional micelles, they are not uniform in size. Because of the anisotropic shape of metaparticles, the average size and polydispersity of these superstructures are the result of a complicated competition between the energetic drive to expand the A-rich cores and the entropic cost of packing (bumpy) tetrahedra at locally high density.

Figure 2.

Figure 2

Open in a new tab

Zero- and one-dimensional assemblies. (Left) Micelle-like superstructures. Attractions of type [AA] (indicated by the dashed pink line in (a)) between C4 metaparticles yield self-limiting growth of superclusters whose interiors are dense in A monomers. (b) Snapshot from a molecular dynamics simulation, showing a dispersed collection of micelles. (c) An example micelle comprising 9 C4 clusters. (d) Normalized histogram of the number of metaparticles within each micelle. (Right) Filamentous assemblies. Attractions of type [AA,BB] (indicated by the dashed pink and orange lines in (e)) between C4 metaparticles yield percolating networks of branched filaments. (f) Snapshot from simulation, showing onlyA–A and B–B bonds. An example filament segment (g) and branch point (h). The filament core consists of alternating A-rich and B-rich regions; nonattracting monomers of type C and D form a loose shell around the core. (In panels (b), (c), (g), and (h) nonattracting monomers are shown in smaller size for clarity.)

Adding a second self-attraction to C4 species ([AA,BB]) effectively encourages aggregation within and among the micellar superstructures just described. Due to constraints of packing and stoichiometry, B monomers on the micelle exterior segregate to opposite poles, where they can bind to the poles of other micelles. This linear motif may extend indefinitely, generating one-dimensional superfilaments with an internal pattern of alternating A-rich and B-rich cores, as shown in the right panel of Figure 2. The fluctuations responsible for micelle size variation in the [AA] case here produce local defects in core thickness and exposure. Some of these defects cause sufficient exposure of the cylindrical core to allow filament branching. At high metaparticle density, percolating networks of filaments reminiscent of biopolymer gels result.27

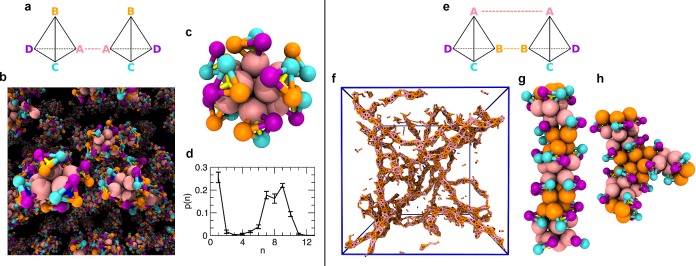
Adding a third attraction to this scenario ([AA,BB,CC]) once again increases the dimensionality of assembled superstructures. Only monomers of type D are inert in this case, and they can be sequestered to the opposing faces of an ordered sheet that is two C4 metaparticles thick, as illustrated in the right panel of Figure 3. In its ideal form this superstructure features macroscopic lines of isochiral clusters, alternating with lines of their enantiomers. Such chiral micropatterning might provide a basis for engineering unusual optical properties. Sheets forming on the time scale of our simulations possess a significant number of defects that define grain boundaries between domains of different orientation.

Figure 3.

Figure 3

Open in a new tab

Two-dimensional assemblies. (Left) Bilayer sheets of C4 metaparticles. Attractions of type [AA,BB,CC] (indicated by the dashed pink, orange, and blue lines in (a)) yield sheets two metaparticles thick. (b) Snapshot from a molecular dynamics simulation, showing a collection of sheets linked at grain boundaries. (Only A–A, B–B, and C–C bonds are shown.) (c) Top view of an example sheet, whose attracting monomers are arranged in groups of 12 in a regular pattern. Metaparticles with different chirality alternate in the sheet plane. (d) Side view of the same example sheet, highlighting its corrugation. (Centers of enantiomers are shown yellow and blue.) (e) Each cluster is bound to its mirror image in the opposite layer of the sheet. (Right) Bilayer sheets of C3 metaparticles. Attractions of type [AB] (indicated by the dashed lines in (f)) yield sheets that are flat and highly ordered. (g) Snapshot from a molecular dynamics simulation, showing only A–B bonds. Of the two disconnected sheets, one exhibits extended kink defects. Top (h) and side views (i) of an example sheet highlight the face-centered-cubic-like bonding geometry. (In panels (c), (h), and (i) monomers that can engage in attractive interactions are shown at their volume-excluding size; in all other cases, monomers are drawn as smaller objects for visual clarity.)

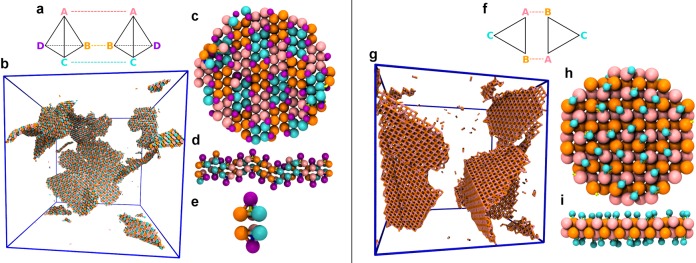
Triangular metaparticles were similarly observed to form sheets (with [AB] and [AA,BB] attractions, see Supporting Information) and micelles (with [AA] attractions), as illustrated in the right panel of Figure 3 and Supporting Figure 4. Octahedral clusters, on the other hand, generate exotic three-dimensional superlattices. In one such crystal ([AA]), C6 metaparticles maintain complete rotational freedom about the axis connecting attractive monomers (see left panel of Figure 4). Another crystal (obtained with [AB] and [AA,BB]) is highly porous, with a packing fraction of ∼0.12, and is traversed by hexagonal channels (see right panel of Figure 4 and Supporting Figure 5). Both offer intriguing design possibilities for molecular adsorption and metamaterials.

Figure 4.

Figure 4

Open in a new tab

Three-dimensional assemblies. (Left) A rotator phase with cubic symmetry. Attractions of type [AA] (indicated by the dashed pink lines in (a)) between C6 metaparticles yield a cage-like supercrystal. (b) Snapshot from a molecular dynamics simulation, showing only the bonds between A monomers. (c and d) An example vertex of the superlattice viewed from two different perspectives. Each vertex involves six C6 clusters, bound through A–A attractions in a cross-like geometry. Metaparticle centers occupy the Wyckoff 3d positions of a cubic crystal with space group 221 (Pm3̅m). The maximal packing fraction of the crystal is ∼0.42. Each metaparticle can rotate freely around its A–A axis, as indicated by arrows. (Right) Honeycomb supercrystal. Attractions of type [AB] (indicated by the dashed pink lines in (e)) between C6 metaparticles yield a superstructure featuring extended channels arranged in a hexagonal pattern. (f and g) Simulation snapshot, showing only A–B bonds, viewed from two different perspectives. (h and i) Excerpts from the honeycomb viewed along the channel axis and from its side. Channels are defined by circular arrangements of six C6 clusters; nonattracting particles of type C point toward the center of the pore. (In panels (c), (d), (h), and (i) nonattracting monomers are shown in smaller size for clarity.)

Conclusions

While this survey of assemblies is not necessarily exhaustive, we believe it to be thorough for metaparticles accessible with high yield through the procedures we have described. Mixtures of metaparticles with varying composition are in fact easier to prepare, at least in the proportions dictated by their thermodynamic stabilities. Such mixtures expand the range of superstructures that can be achieved through our hierarchical protocol. As one example, C6 clusters of uniform composition ABCBCD cannot be prepared with high yield from our strategy. However, a mixture of ABCBCD, ABCBCA, and DBCBCD clusters (in average proportions 2:1:1) can be straightforwardly generated, specifically by adding a fourth monomer type D to the collection of monomers that would otherwise form pure ABCBCA clusters, with interactions εBD = εCD = ε̅ and εAD = εDD = 0. In simulations, this mixture assembles into yet another distinct porous supercrystal, shown in Figure 5. Many more such scenarios are possible and, more importantly, should be realizable using existing synthetic technologies.

Figure 5.

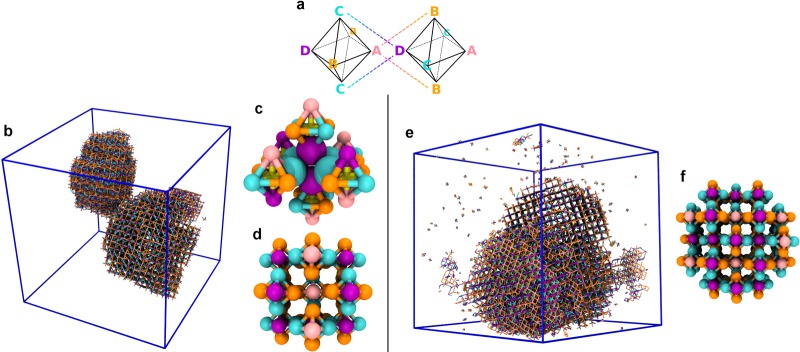
Figure 5

Open in a new tab

Assemblies of metaparticles with varying composition. A porous crystal of C6 metaparticles comprising four distinct monomer types, assembled with attractions of type [AB,CD] (indicated by the dashed lines in (a)). This crystal is obtained in simulations of metaparticles with identical composition ABCBCD and εAB = εCD = 3.9kBT (left) and simulations of mixtures of ABCBCD, ABCBCA, and DBCBCD metaparticles (in average proportions 2:1:1) with εAB = εCD = 4.0kBT (right). Snapshots from simulation show two disconnected crystalline aggregates (b) and a single aggregate with two crystalline domains (e). (Only A–B and C–D bonds are shown.) The crystal has near cubic symmetry, with metaparticle centers occupying the sites of a face-centered cubic (fcc) lattice and monomers positioned on the Wyckoff 3d sites of a cubic lattice with space group 221 (Pm3̅m). (c and d) Excerpts from the crystal illustrate that metaparticle orientations are highly ordered. Within a single (100) plane of the fcc lattice, nearest neighbor metaparticles have antiparallel orientations with respect to the A–D axis and orthogonal orientations with respect to the C–C axis. The same pattern of metaparticle orientations is observed in the case of the mixture (f), but there is no long-range order with respect to the composition of metaparticles. (In panel (c) four C and two D monomers are shown at their volume-excluding size to highlight binding geometry; in all other cases, monomers are drawn as smaller objects for visual clarity.)

Methods

Pair Potential

The repulsive and attractive interaction potentials used in our simulations have the specific forms

graphic file with name nn-2014-00978p_m002.jpg

where

graphic file with name nn-2014-00978p_m003.jpg

and

graphic file with name nn-2014-00978p_m004.jpg

The repulsive part, a shifted Lennard-Jones potential whose steepness is set by the length scale αrep, vanishes continuously at r = σ. The attractive part, a well of approximately unit depth whose steepness near r = σ + w is set by the length scale αatt, vanishes continuously at r = σ + 2w. Examples of the total interaction potential are plotted in Supporting Figure 1a. The standard mixing rule σ = (σ1 + σ2)/2 was used to determine interactions between particles with different diameters σ1 and σ2.

Simulation Details

In all simulations we adopt kBT as a unit of energy, monomer diameter σ as a unit of length, monomer mass m as a unit of mass, and τ = (mσ2/kBT)1/2 as a unit of time. Our systems are then specified by the following dimensionless parameters: (a) glue particle diameter, σglue/σ, which we set to (4/3)1/2 – 1, (3/2)1/2 – 1, and √2 – 1, for C3, C4, and C6 clusters, respectively; (b) glue particle mass, mglue/m = (σglue/σ)3, proportional to its volume; (c) monomer friction coefficient γτ/m = 10; and (d) glue particle friction coefficient γglueτ/m = 10σglue/σ, proportional to its diameter. Dynamics were advanced by numerically integrating the underdamped Langevin equation, as implemented in the HOOMD-blue simulation package.28 Images of clusters and assemblies were rendered with VMD.29

Cluster Assembly

For simulations of metaparticle formation, we set w = 0.035σ, αrep = 0.2σ, and αatt = 0.01σ. Initial conditions were constructed by randomly placing 500 glue particles and 1000 monomers (2000 in the case of C6 clusters) of each type in a periodically replicated cubic simulation box at packing fraction 0.005. Trajectories of length 104τ were generated with an integration time step Δt = 10–4τ. Binding of monomers to multiple glue particles was suppressed by a pairwise repulsion uglue–glue(r) = 40 kBT e–r/σ(r/σ)−1. We calculate assembly yields as Nt/N, where Nt is the number of clusters with desired composition and N is the total number of clusters with the maximum number of monomers. Clusters that are not fully assembled are disregarded, as their population can be made negligible by an appropriate choice of εglue. Maximum yields were achieved with εglue = 10kBT and ε̅ = 4kBT for C4 and C6 metaparticles, and ε̅ = 4.4kBT for C3 clusters.

Superstructure Assembly

Simulations of the second stage of assembly included 1000 to 8000 metaparticles, initially placed on a simple cubic lattice at densities between 0.04σ–3 and 0.01σ–3. Metaparticles were treated as rigid bodies.30 Monomer interaction parameters were set as w = 0.075σ, αrep = 0.3σ, and αatt = 0.02σ (which allow use of a larger integration time step Δt = 0.005τ). Glue particle repulsions were omitted at this stage. Time was advanced in each assembly trajectory by 5 × 105τ.

The following attraction strengths resulted in the structures depicted in Figures 2, 3, and 4:

  • •

    C4 micelles: εAA = 5.8kBT

  • •

    C4 filaments: εAA = εBB = 4.5kBT

  • •

    C4 sheets: εAA = εBB = εCC = 3.7kBT

  • •

    C3 sheets: εAB = 3.7kBT

  • •

    C6 cubic rotator phase: εAA = 4.7kBT

  • •

    C6 hexagonal channels: εAB = 4.15kBT

These values resulted in structures of the highest quality in our simulations. We note, however, that different values are likely to be optimal for different choices of pair potential (in particular, for a different range w of attraction, as discussed above) and for assembly trajectories that are substantially longer than the time scales accessible with current hardware.

Acknowledgments

We thank Michael Brenner, Todd Gingrich, Sharon Glotzer, and Patrick Varilly for useful discussions. This work was supported by the Austrian Science Fund (FWF) under Grant J 3106-N16. Calculations were in part performed on the Vienna Scientific Cluster (VSC). We acknowledge computational resources obtained under NSF award CHE-1048789.

Supporting Information Available

Additional discussion and figures. This material is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.

Supplementary Material

nn500978p_si_001.pdf (2.3MB, pdf)

References

  1. Zhang Z.; Keys A.; Chen T.; Glotzer S. Self-Assembly of Patchy Particles into Diamond Structures through Molecular Mimicry. Langmuir 2005, 21, 409–413. [DOI] [PubMed] [Google Scholar]
  2. Vissers T.; Preisler Z.; Smallenburg F.; Dijkstra M.; Sciortino F. Predicting Crystals of Janus Colloids. J. Chem. Phys. 2013, 138, 164505. [DOI] [PubMed] [Google Scholar]
  3. Bianchi E.; Blaak R.; Likos C. N. Patchy Colloids: State of the Art and Perspectives. Phys. Chem. Chem. Phys. 2011, 13, 6397–6410. [DOI] [PubMed] [Google Scholar]
  4. Hagan M. F. Modeling Viral Capsid Assembly. Adv. Chem. Phys. 2014, 155, 1–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ouldridge T. E.; Louis A. a.; Doye J. P. K. Structural, Mechanical, and Thermodynamic Properties of a Coarse-Grained DNA Model. J. Chem. Phys. 2011, 134, 085101. [DOI] [PubMed] [Google Scholar]
  6. Munaò G.; Preisler Z.; Vissers T.; Smallenburg F.; Sciortino F. Cluster Formation in One-Patch Colloids: Low Coverage Results. Soft Matter 2013, 9, 2652. [Google Scholar]
  7. Wang Y.; Wang Y.; Breed D. R.; Manoharan V. N.; Feng L.; Hollingsworth A. D.; Weck M.; Pine D. J. Colloids with Valence and Specific Directional Bonding. Nature 2012, 491, 51–55. [DOI] [PubMed] [Google Scholar]
  8. Chen Q.; Bae S. C.; Granick S. Directed Self-Assembly of a Colloidal Kagome Lattice. Nature 2011, 469, 381–384. [DOI] [PubMed] [Google Scholar]
  9. Pawar A. B.; Kretzschmar I. Fabrication, Assembly, and Application of Patchy Particles. Macromol. Rapid Commun. 2010, 31, 150–168. [DOI] [PubMed] [Google Scholar]
  10. Yi G.-R.; Pine D. J.; Sacanna S. Recent Progress on Patchy Colloids and Their Self-Assembly. J. Phys.: Condens. Matter 2013, 25, 193101. [DOI] [PubMed] [Google Scholar]
  11. Knorowski C.; Travesset A. Materials Design by DNA Programmed Self-Assembly. Curr. Opin. Solid State Mater. Sci. 2011, 15, 262–270. [Google Scholar]
  12. Geerts N.; Eiser E. DNA-Functionalized Colloids: Physical Properties and Applications. Soft Matter 2010, 6, 4647. [Google Scholar]
  13. Di Michele L.; Eiser E. Developments in Understanding and Controlling Self Assembly of DNA-Functionalized Colloids. Phys. Chem. Chem. Phys. 2013, 15, 3115–3129. [DOI] [PubMed] [Google Scholar]
  14. Manoharan V. N.; Elsesser M. T.; Pine D. J. Dense Packing and Symmetry in Small Clusters of Microspheres. Science 2003, 301, 483–487. [DOI] [PubMed] [Google Scholar]
  15. Licata N.; Tkachenko A. Self-Assembly of DNA-Coded Nanoclusters. Phys. Rev. E 2006, 74, 040401. [DOI] [PubMed] [Google Scholar]
  16. Licata N.; Tkachenko A. V. How to Build Nanoblocks Using DNA Scaffolds. Europhys. Lett. 2008, 84, 20010. [Google Scholar]
  17. Soto C. M.; Srinivasan A.; Ratna B. R. Controlled Assembly of Mesoscale Structures using DNA as Molecular Bridges. J. Am. Chem. Soc. 2002, 124, 8508–8509. [DOI] [PubMed] [Google Scholar]
  18. Fan J. A.; He Y.; Bao K.; Wu C.; Bao J.; Schade N. B.; Manoharan V. N.; Shvets G.; Nordlander P.; Liu D. R.; etal. DNA-Enabled Self-Assembly of Plasmonic Nanoclusters. Nano Lett. 2011, 11, 4859–4864. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Schade N. B.; Holmes-Cerfon M. C.; Chen E. R.; Aronzon D.; Collins J. W.; Fan J. A.; Capasso F.; Manoharan V. N. Tetrahedral Colloidal Clusters from Random Parking of Bidisperse Spheres. Phys. Rev. Lett. 2013, 110, 148303. [DOI] [PubMed] [Google Scholar]
  20. Hormoz S.; Brenner M. P. Design Principles for Self-Assembly with Short-Range Interactions. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 5193–5198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hagan M. F.; Chandler D. Dynamic Pathways for Viral Capsid Assembly. Biophys. J. 2006, 91, 42–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jack R.; Hagan M.; Chandler D. Fluctuation-Dissipation Ratios in the Dynamics of Self-Assembly. Phys. Rev. E 2007, 76, 021119. [DOI] [PubMed] [Google Scholar]
  23. Grant J.; Jack R. L.; Whitelam S. Analyzing Mechanisms and Microscopic Reversibility of Self-Assembly. J. Chem. Phys. 2011, 135, 214505. [DOI] [PubMed] [Google Scholar]
  24. Henzie J.; Grünwald M.; Widmer-Cooper A.; Geissler P. L.; Yang P. Self-Assembly of Uniform Polyhedral Silver Nanocrystals into Densest Packings and Exotic Superlattices. Nat. Mater. 2012, 11, 131–137. [DOI] [PubMed] [Google Scholar]
  25. Miszta K.; de Graaf J.; Bertoni G.; Dorfs D.; Brescia R.; Marras S.; Ceseracciu L.; Cingolani R.; van Roij R.; Dijkstra M.; etal. Hierarchical Self-Assembly of Suspended Branched Colloidal Nanocrystals into Superlattice Structures. Nat. Mater. 2011, 10, 872–876. [DOI] [PubMed] [Google Scholar]
  26. Damasceno P. F.; Engel M.; Glotzer S. C. Predictive Self-Assembly of Polyhedra into Complex Structures. Science 2012, 337, 453–457. [DOI] [PubMed] [Google Scholar]
  27. Fletcher D. A.; Mullins R. D. Cell Mechanics and the Cytoskeleton. Nature 2010, 463, 485–492. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Anderson J. A.; Lorenz C. D.; Travesset A. General Purpose Molecular Dynamics Simulations Fully Implemented on Graphics Processing Units. J. Comput. Phys. 2008, 227, 5342–5359. [Google Scholar]
  29. Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
  30. Nguyen T. D.; Phillips C. L.; Anderson J. A.; Glotzer S. C. Rigid Body Constraints Realized in Massively-Parallel Molecular Dynamics on Graphics Processing Units. Comput. Phys. Commun. 2011, 182, 2307–2313. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn500978p_si_001.pdf (2.3MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES