A personalized committee classification approach to improving prediction of breast cancer metastasis

Abstract

Motivation: Metastasis prediction is a well-known problem in breast cancer research. As breast cancer is a complex and heterogeneous disease with many molecular subtypes, predictive models trained for one cohort often perform poorly on other cohorts, and a combined model may be suboptimal for individual patients. Furthermore, attempting to develop subtype-specific models is hindered by the ambiguity and stereotypical definitions of subtypes.

Results: Here, we propose a personalized approach by relaxing the definition of breast cancer subtypes. We assume that each patient belongs to a distinct subtype, defined implicitly by a set of patients with similar molecular characteristics, and construct a different predictive model for each patient, using as training data, only the patients defining the subtype. To increase robustness, we also develop a committee-based prediction method by pooling together multiple personalized models. Using both intra- and inter-dataset validations, we show that our approach can significantly improve the prediction accuracy of breast cancer metastasis compared with several popular approaches, especially on those hard-to-learn cases. Furthermore, we find that breast cancer patients belonging to different canonical subtypes tend to have different predictive models and gene signatures, suggesting that metastasis in different canonical subtypes are likely governed by different molecular mechanisms.

Availability and implementation: Source code implemented in MATLAB and Java available at www.cs.utsa.edu/∼jruan/PCC/.

Contact: jianhua.ruan@utsa.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Recently, large-scale profiling techniques such as microarray and next-generation sequencing have enabled systematic screening of genomic, epigenomic and transcriptomic changes associated with cancer. These data have been used for disease prognosis and outcome prediction with an accuracy comparable or superior to conventional histological grading-based methods (Chang et al., 2004; Sorlie et al., 2001; Sotiriou et al., 2006; van de Vijver et al., 2002; Wang et al., 2005). However, it is well known that cancer is a heterogeneity disease and that cancers occurring at the same tissue or organ can have multiple subtypes with distinct molecular signatures and likely have different prognosis and treatment responses (Bianchini et al., 2010; Heiser et al., 2011; Prat et al., 2010; Sorlie et al., 2001; Sotiriou et al., 2006). Therefore, the overall performance of such prognostic models is still poor.

An intuitive solution to address the aforementioned problem is to design prognostic models separately for each cancer subtype. This simple solution poses two problems. Firstly, the number of available training samples becomes smaller, especially for relatively rare subtypes, which unavoidably reduces the reliability and stability of the classification models. Secondly and more importantly, this solution depends on well establishment of predefined cancer subtypes and unambiguous assignment of each patient to some subtype. However, the definition of subtypes may be ambiguous and evolve with time. For example, in a series of studies, Perou and colleagues analyzed gene expression profiles of primary breast tumors and defined the subtypes of breast cancer, termed luminal A, luminal B, normal breast-like, basal, ErbB2 and more recently, claudia-low, which have different survival rates and responses to hormone treatment (Hennessy et al., 2009; Sorlie et al., 2001, 2003). Studies on other datasets have confirmed some of the subtypes such as the basal-like and ErbB2, but the definitions of the other subtypes are not always consistent and are sensitive to the set of genes used and the set of samples analyzed (Kapp et al., 2006; Mackay et al., 2011). It was suggested that the ‘molecular subtypes’ of cancer may be a continuum (Lusa et al., 2007). Hence, attempting to identify distinct subtypes may not be always appropriate.

In this article, we propose a generalization of the subtype-based classification idea. Instead of relying on explicit definition of subtypes, we simply treat each patient as if he/she belongs to a different subtype and then construct multiple, personalized, predictive models for each patient. These models are evaluated for their performance in predicting the outcomes of the specific patient, and only the good models are retained. When a new patient comes, a set of patients of similar molecular characteristics are chosen, so are their predictive models. The final decision is made by considering the predictions from all the selected models.

Applying our method to three publicly available microarray datasets of breast cancer for prediction of metastasis, we found that our proposed personalized classification method has much better prediction accuracy than standard methods that either do not use cancer subtype information or use only the predefined cancer subtypes. Importantly, we found that our proposed method significantly improves cross-dataset prediction accuracy, which is critical in clinical practice to predict disease outcomes. Furthermore, our results show that different breast cancer subtypes require different metastatic classification models, suggesting that the metastasis process in these different subtypes are governed by different molecular mechanisms.

2 MATERIALS AND METHODS

2.1 Breast cancer datasets

In this study, we used three breast cancer microarray datasets (see Supplementary Table S1 for cohort information). The first dataset, downloaded from the Netherland Cancer Institute (NKI) website (http://bioinformatics.nki.nl/index.php), (van de Vijver et al., 2002), contains 295 primary breast carcinoma patients, where all patients were <53 years old and had stage I or II breast cancer. Among them, 151 had lymph node–negative disease and the rest had lymph node–positive disease. In this dataset, 78 patients had metastasis within 5 years of follow-up visit. Therefore, we considered these 78 patients as metastatic patients and the remaining ones as non-metastatic patients. The microarray platform used for this dataset was Agilent Hu25K. To make the NKI dataset compatible with the other two datasets, we used Entrez gene ID to map different gene entries among the three datasets. In the NKI dataset, gene expression values represent the log ratios between the signal intensities in each patient relative to the average signal intensities of all patients. Table 1 shows the number of patients in each subtype defined in Chang et al. (2005) and Sorlie et al. (2003), with the total number of metastatic and non-metastatic patients in each subtype. It is important to note that this subtype information was never used in our model; rather, it was used only for evaluation purposes. We only considered the top 1500 genes that had the highest variances in NKI dataset among samples; however, increasing the number of genes did not change the results significantly.

Table 1.

Subtype information for NKI dataset

Subtype	Number of patients	Metastatic	Non-metastatic
Normal	31	3	28
Basal	46	16	30
Luminal A	88	15	73
Luminal B	81	24	57
ErbB2	49	20	29

The second dataset, referred to as Wang dataset, contains 286 lymph node–negative breast cancer patients who had not received any adjuvant systemic treatment (Wang et al., 2005). Among them, 106 patients had distant metastasis within 5 years of follow-up checkup and were considered as metastatic patients in our analysis, whereas the rest were considered as non-metastatic patients. The microarray platform used was Affymetrix HG-U133a. This dataset was obtained from Gene Expression Omnibus with the accession number GSE2034 (Edgar et al., 2002). To make the dataset compatible with the NKI dataset, the signal intensities in the Wang dataset were converted to log ratios, where the ratio was calculated between the signal intensity of a gene in a particular patient to the average intensity of that gene in all patients. Then z-score transformation was performed for each patient for both datasets, so that the mean log ratio for each patient was 0 and the standard deviation was 1.

The last dataset was downloaded from the University of North Carolina (UNC) Microarray Database, and contains 337 samples, but we only used 116 patient samples that had at least 5-year follow-up clinical data (Prat et al., 2010). Similar to the previous two datasets, we considered 5-year follow-up disease status to distinguish between metastatic and non-metastatic patients and obtained 75 metastatic and 41 non-metastatic patients. The microarray platform used for this dataset was Agilent oligo microarray and was downloaded from Gene Expression Omnibus with the accession number GSE18229 (Edgar et al., 2002). Similar to the NKI and Wang datasets, a z-score transformation was performed to each patient in the dataset. The Wang and UNC datasets were used to evaluate models learned from the NKI dataset.

2.2 Personalized committee classification algorithm

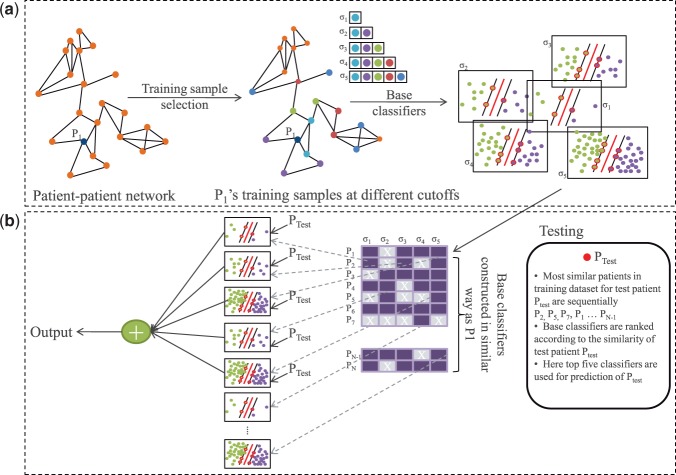
Figure 1 shows an overview of our approach. For each patient (P_Train) in the training dataset (NKI), we constructed a set of classifiers, known as base classifiers, using only patients whose gene expression profiles were similar to that of P_Train as training samples. We call P_Train a representing patient for these base classifiers. To select training samples, we created a patient–patient network based on co-expression, and used a well-known graph algorithm to identify patients that are topologically close to the representing patient in the network. Each base classifier was then evaluated for its prediction accuracy on its representing patient and was discarded if the prediction was incorrect. This procedure was repeated for all patients in the training dataset, resulting in a rich pool of classifiers that could be used for predictions in the test dataset. New patients were classified by a subset of these base classifiers chosen based on the similarity between the target patient and the representing patients of the base classifiers, and predictions from individual base classifiers were combined to form the final decision. We call the whole classification model as personalized committee classifier or PC-classifier for short. Details of our method are described below.

Fig. 1.

Overview of our approach. (a) Steps to construct PC-classifier for patient P₁ are shown. The classifiers for the remaining patients are constructed similarly. (b) An external patient P_Test is classified based on top ranked five base classifiers. Note that P_Test is never included in the construction of any classifiers in (a)

2.2.1 Training sample selection

We believe that patients with similar genetic characteristics may share common molecular mechanisms in disease development and progression, and can provide more accurate models to predict disease outcomes of other similar patients, rather than using all patients. Therefore, we only selected the most similar patients to a target patient to construct its base classifier. To retrieve the most relevant patients to construct the classifiers, we constructed a patient–patient network, where each patient is connected to its nearest three patients based on Euclidean distance between patients’ gene expression profiles (Supplementary Fig. S1). Patient–patient co-expression networks have been shown capable of preserving the topological relationship among patients and capturing cancer subtype information well (Ruan et al., 2010). Given the network, we used a well-known graph algorithm, random walk with restart, to calculate the similarity between every pair of patients, measured by the probability for a random walker starting from one node to reach another node in the network (Tong et al., 2006).

Formally, let A be the adjacency matrix of the patient–patient network, where 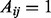if there is an edge between patient i and j, and let P be the row normalized adjacency matrix, i.e. 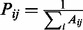. Assume that a random walker starts from node v with a uniform probability to visit each of its neighboring nodes, and with a fixed probability c to revisit the starting node v at any time point during the walk. The random walk with restart algorithm can be applied to all patients simultaneously, with a matrix form 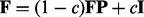, where I is an identity matrix. On convergence, the element F_ij of the square matrix F represents the probability for a patient i randomly walking on the network to reach patient j, given sufficient amount of time (Tong et al., 2006). A higher probability means topologically higher similarity between the two patients.

After calculating the similarity scores between all patients, we used a set of user-defined cutoffs (σ = 0.001, 0.0005, 0.0002, 0.0001 and 0.00005 in this study) to select five sets of neighbors for each patient (see Supplementary Materials for rationale and supporting data on parameter selection). A smaller cutoff will result in more neighbors being selected (see Supplementary Figs S2 and S3 for example and Supplementary Table S2 for statistics). Note that even with the same cutoff, each patient may end up with different number of neighbors, depending on the topology of the network (Supplementary Fig. S4). Also, the only information used in this step is gene expression profiles, without considering the predefined cancer subtypes and the metastatic status.

2.2.2 Base classifier construction

As mentioned above, our method established a pool of base classifiers, each of which was trained from a subset of similar patients from the training dataset and personalized for a specific patient. To improve robustness of the models, for each patient, we identified several sets of similar patients using different cutoffs in the training sample selection step and constructed one base classifier from each set of training samples. For example, with σ = 0.001, we built 295 such classifiers, where each classifier was built using a different number of patients depending on the number of training samples a patient had in the training sample selection step (Supplementary Fig. S4). Therefore, we built (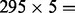) 1475 such classifiers with five cutoffs. Next, we removed those base classifiers that failed to predict the metastatic status of the representing patient. Finally, to make better use of all data points, we retrained each of the remaining correct base classifiers using both, the representing patient and the previously selected training samples. This gives us a pool of validated base classifiers for future classification of new patients.

For example, as illustrated in Figure 1, for patient P₁, we collected five sets of training samples that can be reached from P₁ with certain probabilities. These samples were used to construct five base classifiers for P₁. As the classifier resulted from 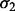-selected samples had incorrect classification result for P₁, it was removed from further consideration. We then retrained the four remaining classifiers after adding P₁ to the original training data and stored the new classifiers for future uses. We repeated this procedure for every patient in the training dataset. In this work, we used NKI dataset as training dataset and established 991 base classifiers.

Support vector machine (SVM) was used as the underlying base classifier. We used the SMO implementation of SVM in WEKA (version 3.6.3; Hall et al., 2009) and used its linear kernel with all default parameter settings. Classification output was fitted using a logistic regression model, which is included in the WEKA implementation, to predict the probability of metastasis (Hall et al., 2009).

2.2.3 Committee-based classification

To use the pool of base classifiers to classify new patients, we developed a committee classification approach. As illustrated in Figure 1, to classify a new patient (P_Test), we ranked all the available base classifiers based on the similarity between P_Test and the representing patients used to construct these base classifiers. Ties were broken according to the decision probability to make a correct prediction for the representing patient. Then we used the top-ranked N models to classify P_Test and used the average decision probability to predict its metastatic status. Note that using weighted average does not change the results significantly.

2.3 Performance evaluation and comparison with competing methods

To measure the intra-data classification performance for PC-classifiers, we used the leave-one-out evaluation technique. Briefly, we took out one patient (P_test) from the NKI dataset and constructed a PC-classifier with the remaining patients as training samples, and used the classifier to predict the probability for P_test to develop metastasis. This step was repeated for all patients in the NKI dataset, and the predictions for all patients were pooled to measure the performance. It is worth mentioning that in this evaluation, P_test was never used in any step for constructing the PC-classifier. For comparison, standard SVM classifiers and subtype-based SVM classifiers were also constructed. For standard classifiers, we constructed a SVM classifier for each P_test patient using the remaining K −1 patients as training data, where K is the total number of patients in NKI dataset. For subtype-based classifiers, we constructed an SVM classifier for P_test by using only the patients of the same subtype as P_test as training samples. In other words, if P_test is a basal type patient, then for subtype-based classifier, we constructed an SVM classifier with the other basal type patients except P_test.

To evaluate the performance of PC-classifier in cross-data scenario, we constructed base classifiers using the whole NKI dataset, and later used them to classify patients in the Wang and UNC datasets based on the committee classification approach. To compare, we also constructed a single standard SVM classifier using the entire NKI dataset and tested its performance on the Wang and UNC datasets. The subtype-based classifiers were not tested here as subtype information for the Wang cohort, and some patients in the UNC cohort are not available.

Several ensemble classifiers were also constructed and evaluated both for intra-data and inter-data classification. We tested four popular ensemble classifiers:Bagging, Dagging, AdaBoost and Random Forest (Beriman, 1996; Freund and Robert, 1996; Ting and Witten, 1997). Both Bagging and Dagging work by randomly selecting a subset of samples to construct base classifiers. The difference between the two is that Bagging allows sampling with replacement, whereas Dagging only permits sampling without replacement, and as a result, the latter creates a number of disjoint partitions from the data. AdaBoost builds multiple base classifiers by iteratively giving priority to previously misclassified samples. Random Forest constructs a multitude of decision trees and outputs the class label predicted by these trees. To have a fair comparison with our method, we used SVM as the underline base classifier for these ensemble classifiers except for random forest, which uses decision tree as underlying base classifier by design. For Dagging, we used 10 partitions to ensure having enough number of training samples in each base classifier. For AdaBoost, we used 500 classifiers, as the performance seems to be independent of the number of classifiers after some initial burn-in period. For all other ensemble classifiers, we varied the number of base classifiers from 1 to 900 and compared the performance of the algorithms as the number of base classifiers increased. Similarly, as for the standard SVM classifier, leave-one-out cross-validation was used for the NKI dataset, whereas Wang and UNC datasets were tested using models developed from the NKI dataset.

Classification performance was measured using several commonly used evaluation methods including positive predictive value, negative predictive value, kappa statistic and area under receiver operating characteristic (ROC) curve (area under curve, AUC). Let N be the total number of patients, and TP, TN, FP and FN be the numbers of true-positive (metastatic patient), true-negative (non-metastatic patient), false-positive and false-negative predictions, respectively, made by a classifier at a certain threshold of the decision probability. Positive predictive value (PPV) is defined as 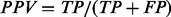, and negative predictive value (NPV) defined as 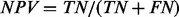. To enable a straightforward comparison among all methods, the decision probability was set differently for each classifier so that the positive predictive rate (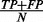) is approximately the percentage of metastatic patients in the three datasets combined (37%). The kappa statistic (Landis and Koch, 1977) is a ‘corrected’ version of accuracy, defined as 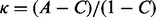, where 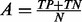is the overall accuracy, and C is the expected accuracy that a classifier can achieve by chance and can be calculated by 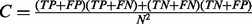. Finally, the ROC curve plots the true-positive rate (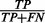) versus false-positive rate (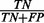) at various threshold settings of the decision probability and shows the trade-off between sensitivity and specificity. The AUC is a widely used statistic for model comparison. A perfect model will have an AUC of 1 and random guessing will score an AUC around 0.5. For each classifier, we repeated the experiment 100 times and measured the mean AUC and standard error of the mean.

2.4 Biological significance analysis

To reveal the biological significance of PC-classifiers, we clustered the base classifiers based on the similarity of their normalized SVM coefficients. For this analysis we used the correct base classifiers with σ = 0.0005. The SVM coefficients for each base classifier were normalized to z-scores. For clustering, we used the hierarchical clustering algorithm implemented in the MATLAB 8.0 Bioinformatics Toolbox (The MathWorks, Inc.). For literature mining, we searched the PubMed abstracts with the gene name together with the term ‘metastasis’ or ‘metastatic’ and reported the number of published articles retrieved.

3 RESULTS AND DISCUSSION

3.1 Performance of PC-classifier on NKI dataset

We first compared PC-classifier with standard SVM classifier and subtype-based SVM classifier for their performance on the NKI dataset using the leave-one-out evaluation technique (see Section 2). Figure 2a shows the AUC scores for these classifiers. As shown, PC-classifier with as few as two base classifiers in the committee had similar performance as the standard or subtype-based classifiers, and significantly outperformed them when at least five base classifiers were present in the committee. The best performance of our method was achieved with 150–600 base classifiers. Compared with the standard SVM classifier, the PC-classifier achieved an 11.4% performance improvement (AUC 0.78 versus 0.70). Using other evaluation methods including kappa static, PPV, NPV and ROC curves, we found similar trends that confirmed the superior performance of PC-classifier (Supplementary Table S3 and Supplementary Fig. S5).

Fig. 2.

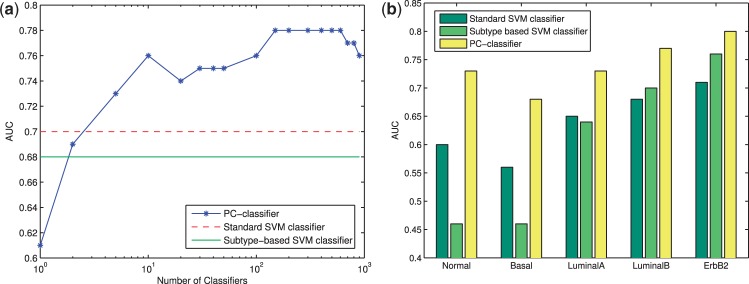
Performance of different classifiers on NKI dataset. (a) AUC scores for the whole dataset. (b) AUC scores for each subtype separately

Next, we investigated how these classifiers performed for patients falling in each of the five predefined breast cancer subtypes (Sorlie et al., 2003). To this end, we calculated the AUC scores by considering the patients in each predefined subtype separately. Figure 2b shows the classification performance for the five subtypes. It can be seen that PC-classifier significantly outperformed the other methods for all subtypes, but especially for basal and normal breast-like subtypes, two of the most difficult subtypes to be predicted by the standard classifier. On the other hand, although the subtype-based classifier performed slightly better than the standard classifier for luminal B and ErbB2 subtypes, its performance on normal breast-like and basal subtypes was much worse. The subtype-based classifier performed poorly for the normal-like subtype probably because of the small number of training samples for this subtype (Table 1) and the intrinsic difficulty in defining the subtype (Supplementary Fig. S1). Intriguingly, basal subtype is the most coherent subtype among all studies (Hennessy et al., 2009; Kapp et al., 2006; Mackay et al., 2011; Sorlie et al., 2001, 2003) (as also suggested by the patient–patient network shown in Supplementary Fig. S1). Consequently, the patients selected to construct the base classifiers for patients in the basal subtype were mostly of basal subtype as well (Supplementary Figs S2 and S4). Therefore, the dramatic performance difference between the subtype-based classifier and the PC-classifier for the basal subtype indicates that the basal subtype is also heterogeneous, as our model only used a subset of all basal patients to construct each base classifier but had better accuracy than the subtype-based classifier that used all basal patients. Overall, by dynamically controlling the number of training samples for each patient, regardless of its subtype designation, and combining decisions from multiple base classifiers learned on similar patients, our method is able to improve performance significantly for all subtypes.

It is worth noting that PC-classifier may improve breast cancer treatment by restraining unnecessary adjuvant systematic therapies. According to previous studies, 70–80% lymph node–negative breast cancer patients may undergo adjuvant chemotherapy, which is in fact unnecessary and these patients may potentially suffer from lethal side effects (van’t Veer et al., 2002). For example, the Luminal subtype is known to be the least lethal, and yet, many patients still go through advanced treatments while they would not have developed distant metastasis. Therefore, to minimize the degree of secondary damage to Luminal subtype patients, an ideal classifier should have a low false-positive rate. Further analysis revealed that for Luminal subtype (including both Luminal A and Luminal B), at a fixed 75% sensitivity level, our method achieved a false-positive rate of 31.5%, as compared with 43.1% for the standard SVM classifier (41 versus 56 incorrectly classified patients, respectively). Therefore, 15 (11.6%) additional Luminal patients are correctly classified into non-metastatic group by our method and may not be going through unnecessary adjuvant chemotherapy.

3.2 Validation of PC-classifier using two additional datasets

A more challenging and yet realistic task in cancer outcome prediction is to use the models developed in one cohort to classify patients in other cohorts. Because of the differences in patient characteristics, sample collection protocols, microarray platforms and data preprocessing steps, microarray gene expression data obtained from different studies for the same disease are often not directly comparable. For example, the three datasets used in this study consist of patients of different age groups, pretreatments, lymph node status and metastatic potentials (Supplementary Table S1). When conducting cross-dataset validations, the existing studies in breast cancer metastasis prediction usually avoid these issues by reusing only the features rather than the classification models across datasets (Chuang et al., 2007; Jahid and Ruan, 2012; Su et al., 2010). More specifically, with two datasets, A and B, the existing methods attempt to find informative genes from dataset A in a supervised way (i.e. considering the disease outcomes), and then build a new model using dataset B filtered to have only the list of genes selected from A. Cross-data classification accuracy was then measured using 10-fold cross-validation or leave-one-out within dataset B. This is in contrast to our study, where the model constructed from dataset A was directly used to classify the patients in dataset B. Our evaluation procedure is more realistic, as it reflects how well a model is expected to perform in a clinical setting where every new patient needs to be classified by the same existing model.

Here we report the performance of the PC-classifier developed on the NKI dataset and tested on Wang and UNC datasets. Figure 3a shows the results for Wang dataset. It can be seen that the cross-data AUC score for standard SVM classifier is 0.60 for this dataset. In contrast, PC-classifier with as few as two base classifiers performed similarly as standard SVM classifier and significantly outperformed standard SVM classifier with five or more base classifiers in the committee. PC-classifier had the highest accuracy with ∼100 classifiers in the committee and outperformed the standard SVM classifier significantly with 14.28% performance improvement. Figure 3b shows the AUC scores for PC-classifier and standard SVM classifier for UNC dataset. The standard SVM classifier had an AUC score of 0.67, while the PC-classifier with 20 base classifiers had similar accuracy. The highest classification accuracy was achieved with ∼400 base classifiers, which outperformed the standard SVM classifier by 17.3%. Also, from Kappa static and ROC curves, we can validate again that the performance improvement by PC-classifier in both datasets is genuine (Supplementary Figs S6 and S7 and Supplementary Tables S4 and S5).

Fig. 3.

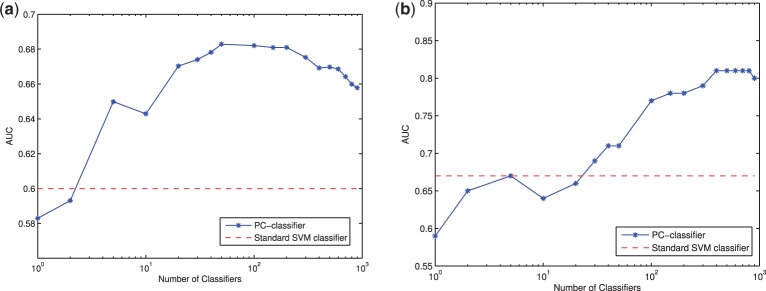
Performance of PC-classifier and standard classifier on (a) Wang and (b) UNC datasets

It is interesting to note that the number of base classifiers needed to achieve the best accuracy is much larger in the UNC dataset than in the other two datasets. This is likely because of the fact that the ratio of metastatic patients in the UNC dataset is much higher than that in the NKI and Wang datasets (64.6, 26.4 and 37.1%, respectively) and that the pretreatments received by patients in the UNC cohorts are much more heterogeneous than those in the other two data sets (Supplementary Table S1). In fact, one of the advantages that PC-classifier has over the standard methods that use the whole dataset to construct a single model is its relative insensitivity to overall sample characteristics. In PC-classifier, as only the most relevant patients in the training cohort will be used to classify a target patient, the difference in sample characteristics between the training and test cohorts does not necessarily cause as much degradation of performance as in other methods, as long as the training dataset itself contains a sufficient number of samples that are similar to the target patients.

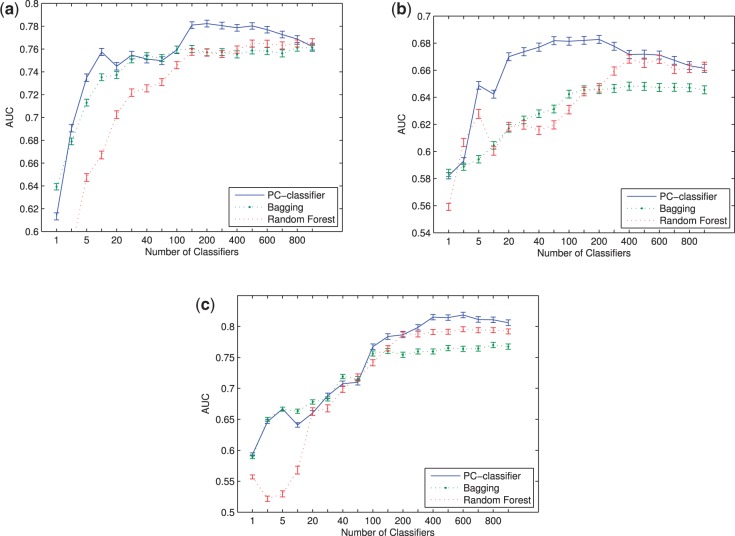
3.3 Performance comparison with other ensemble classification approaches

We also compared the performance of PC-classifier with four popular ensemble classification approaches: Bagging, Dagging, AdaBoost and Random Forest (see Section 2). Similar as in the above results, leave-one-out cross-validation was used for the NKI dataset, whereas Wang and UNC datasets were tested using models developed from the NKI dataset. Figure 4 shows the AUC scores of PC-classifier, Bagging, Random Forest with different numbers of base classifiers. From the figure it can be seen that for all the datasets, PC-classifier significantly outperformed Bagging and Random Forest. For Wang dataset, with only <20 base classifiers, PC-classifier had 9% performance improvement compared with Bagging and Random Forest. For NKI and UNC dataset, the performance of PC-classifier was similar to Bagging and Random Forest with <100 base classifiers but improved significantly when the number of base classifier increased from 100 to 400. We also report the kappa, PPV and NPV for these classifiers (Supplementary Tables S3, S4 and S5) and find that PC-classifier shows the most promising results compared with other ensemble classifiers. The performance of two other competing ensemble classifiers, Dagging and AdaBoost, are much worse than Bagging and Random Forest as well as PC-classifier (Supplementary Table S6). Bagging and Random Forest performed comparatively better than standard SVM because some of the base classifiers by chance may have subtype-specific samples. Interestingly, despite the large number of classifiers created, AdaBoost actually had even worse performance than the standard SVM classifier. As AdaBoost gives additional weights to previously misclassified samples in each new iteration (see Section 2), the results suggest that the additional focus by AdaBoost on the hard-to-classify examples actually had an adverse effect to the overall model performance. In contrast, in our algorithm, because these patients are probably the ones without enough representations in the training cohort, they have had a lower probability to be selected as training samples for other patients; in addition, the base classifiers constructed for them may also have had a higher probability to be deleted from the pool due to incorrect classifications. Consequently, these patients were relatively discounted in our model, which resulted in the improved performance of our algorithm on the overall population.

Fig. 4.

Performance of PC-classifier and different ensemble classifiers on (a) NKI (b) Wang and (c) UNC datasets. Error bars represent one standard error of the mean

3.4 Biological significance of PC-classifiers

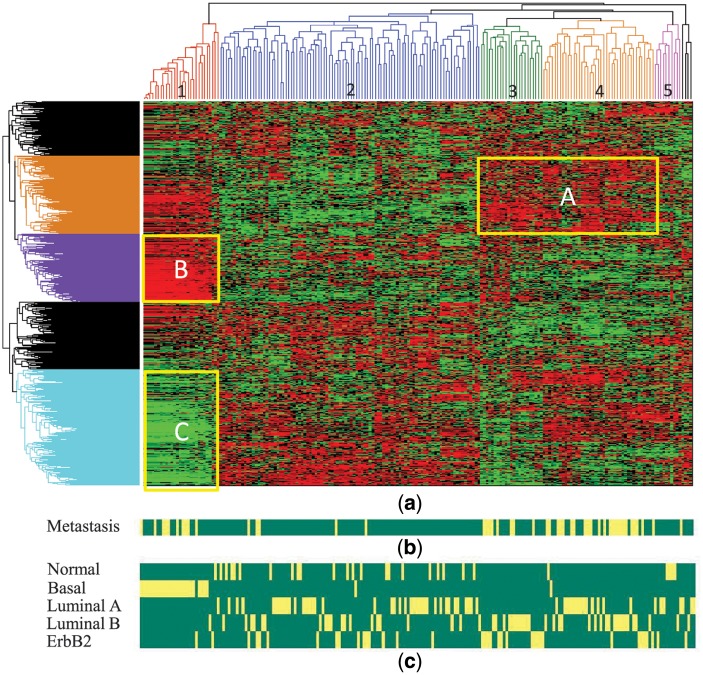
To reveal the biological significance of PC-classifiers and investigate the relationship among the base classifiers for different patients, we clustered the base classifiers based on the similarity of their normalized SVM coefficients. Because we used linear kernel SVM, each classifier is defined by a vector of coefficients, or weights, for the selected features (genes). A higher weight means that the expression level of that gene is positively correlated with metastatic potentials. Figure 5 shows the hierarchical clustering result of the validated base classifiers constructed at 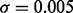. Also shown in the figure are the subtype designation of each patient given by Chanrion et al. (2007) and Sorlie et al. (2003) and the 5-year metastatic status of each patient. Remarkably, five major clusters can be easily identified from the patient dendrogram. Cluster 1 contains almost exclusively and all of the basal subtype patients. Cluster 3 contains only ErbB2 and luminal B patients, whereas cluster 4 contains mostly luminal A and luminal B patients. Cluster 5 contains mostly normal breast-like and luminal A patients. Cluster 2 is the largest and most complex, with members from all five subtypes, despite a relative overrepresentation of normal breast-like and luminal A patients. The partial overlap between the clusters and the subtype designations suggests that the molecular profiles in the luminal/ErbB2 breast cancer is a continuum rather than discrete distribution, as demonstrated in several recent studies (Lusa et al., 2007; Mackay et al., 2011).

Fig. 5.

Hierarchical clustering of PC-classifier models from NKI dataset. (a) Dendrogram and heatmap of the base classifiers, where each column corresponds to a patient and each row to a gene. Each pixel in the heatmap corresponds to SVM coefficient value of the gene in the base classifier model for a particular representing patient. Low values are in green, and high values are in red. (b) Metastasis status of the corresponding patients. (c) Cancer subtype for each patient defined by van de Vijver et al. (2002)

Most of the metastatic patients are distributed in clusters 1, 3 and 4. The overrepresentation of metastatic patients in cluster 1 and 3 is mainly because of basal and ErbB2 patients, respectively, and is expected. Interestingly, while cluster 2 and cluster 4 both have mostly luminal A/B patients, cluster 4 has the highest ratio of metastatic patients, whereas only a small number of patients in cluster 2 are metastatic.

Our results suggest that different breast cancer subtypes need different metastatic classification models. For patients in cluster 1 (basal subtype), metastasis is driven by group B genes while suppressed by group C genes. The pattern is almost the opposite for cluster 3/4 patients (luminal A, B and ErbB2 subtypes), where group A genes promote metastasis. The main difference between cluster 2 and cluster 4 patients, both of which contain mainly luminal subtypes but cluster 4 is much more aggressive, is that group A genes promote metastasis in cluster 4 but not in cluster 2. These results suggest that the metastasis processes in different subtypes are likely governed by different molecular mechanisms, especially between the patients in cluster 1 and the other four clusters. We therefore performed a functional enrichment analysis for the three groups of genes that seem to make up the difference between the clusters (Supplementary Table S7). Interestingly, while all three groups of genes are enriched in defense response and response to wounding, group B genes are more specifically enriched in cell proliferation (P < 2.6E-07) and migration (P < 7.8E-06), whereas group C genes are more specifically enriched in response to estrogen stimulus (P < 2.8E-10), cell proliferation (P < 4.4E-07), anti-apoptosis (P < 5.1E-04) and cell adhesion (P < 3.6E-04).

To further investigate the significance of PC-classifiers, we analyzed the top-ranked genes in different clusters. We identified top 30 ranked genes (disregarding their signs) in cluster 1, 3 and 4 based on their average SVM weights and searched their association with disease recurrence using literature mining (see Section 2). Table 2 lists genes that are top ranked in the standard or PC-classifiers and with at least three PubMed hits. (A complete list of all genes used by the classifiers and their ranks in different models are included in Supplementary Table S8.) As shown in Table 2, many of the top-ranked genes are already known to be metastasis-related. For example, MMP9, PDGFRA and CCL21 are well known to be involved in breast cancer recurrence. Remarkably, our results identified many genes with subtype-specific roles in metastasis development, which are difficult to be discovered with the standard classifiers. For example, ID1, HEY1 and MST1R have high ranks in cluster 1 (basal) models but low ranks in the other clusters and standard SVM models. ID1 is a well-known mediator of breast cancer lung metastasis for basal subtype patients (Gupta et al., 2007). HEY1 is a target gene for Notch signaling inhibitor for basal group (Debeb et al., 2012). Overexpression of MST1R is a strong indicator of metastasis in breast cancer patients (Welm et al., 2007). Similarly, NDRG1 is top ranked in cluster 3 and 4 but not so in cluster 1 models and is known to be related to luminal subtype (Nagai et al., 2011); TFF1 is top ranked only in cluster 3 and is known to be associated and responsible for luminal stability (Yamachika et al., 2002). We also identified some genes that show subtype specificity with high ranks in standard SVM classifiers, including PDGFRA, which is a drug target for basal-like tumor (Koboldt et al., 2012), and BMPR1B, which is known to be associated with ER-positive breast cancer subtype (Bianchini et al., 2010). Our results confirmed the specificity for BMPR1B as a target for ER-positive breast cancer and suggested that PDGFRA can also be an effective target for LuminalB/ErbB2 patients.

Table 2.

Comparison of top ranked genes in different classifiers

Gene name	PubMed hits	Rank in classifiersa
		Standard SVM	Basal	LumB/ ErbB2	LumA/ LumB
ID1	38	878	19	770	686
ATP1B1	5	88	22	459	1182
CCL19	33	252	10	704	696
HEY1	4	372	8	368	680
MST1R	3	783	6	741	1456
ANO1	3	490	9	528	652
FABP7	3	358	30	371	380
KLK7	6	990	6	916	144
KLK6	9	645	29	229	759
NDRG1	56	414	1383	22	33
FLT3	48	395	873	199	26
SPP1	26	324	334	47	18
TFF1	24	99	181	30	231
HOXB13	7	89	659	21	1214
ITGA2	5	64	247	12	12
PEG10	5	97	745	28	53
CKB	5	286	16	27	1254
IGFBP2	6	774	25	545	29
PDGFRA	144	43	26	82	1131
GP5	12	23	18	120	311
PBX1	8	28	407	134	21
NUPR1	6	15	348	18	20
ANXA3	4	18	1519	51	3
BMPR1B	2	30	1086	24	6
MMP9	323	7	572	29	4
ADAM8	15	24	160	3	2
CYP1B1	14	26	43	34	170
IGFBP5	11	33	23	11	104
PRAME	9	35	20	4	409
CCL21	58	20	227	519	79

^aBasal, LumB/ErbB2 and LumA/LumB represent the models displayed in cluster 1, 3 and 4, respectively, in Figure 5. Bold values indicate ranks less than 50.

4 CONCLUSION

In this article, we proposed a personalized committee classification approach for disease outcome prediction that was based on the decisions from multiple base classifiers, where each base classifier was developed from training patients with similar molecular characteristics. We applied our method to predict the metastatic risk of breast cancer patients for three publicly available breast cancer datasets. For all three datasets, our method significantly outperformed other methods that either do not use subtype information (standard SVM classifier) or only use predefined subtypes (subtype specific SVM classifier). Our method has superior cross-dataset prediction accuracy, which shows a clear distinction that our method will perform well in actual clinical setup. Furthermore, our method has better prediction performance compared with other popular ensemble classification approaches. Finally, analysis of the models showed that the personalized committee classifiers are consistent with the current knowledge of breast cancer subtypes and identified difference between the metastatic processes underlying different subtypes. Therefore, the classification approach proposed in this article shows that we can better design classifiers based on personalized training samples, and those classifiers could be used for developing better prediction models that can be used for better disease prognosis and treatment. Although our method is only used to predict metastasis in breast cancer patients in this article, we believe it is general and can be applied to other cancer types and other molecularly heterogeneous diseases.