FISH: fast and accurate diploid genotype imputation via segmental hidden Markov model

Abstract

Motivation: Fast and accurate genotype imputation is necessary for facilitating gene-mapping studies, especially with the ever increasing numbers of both common and rare variants generated by high-throughput-sequencing experiments. However, most of the existing imputation approaches suffer from either inaccurate results or heavy computational demand.

Results: In this article, aiming to perform fast and accurate genotype-imputation analysis, we propose a novel, fast and yet accurate method to impute diploid genotypes. Specifically, we extend a hidden Markov model that is widely used to describe haplotype structures. But we model hidden states onto single reference haplotypes rather than onto pairs of haplotypes. Consequently the computational complexity is linear to size of reference haplotypes. We further develop an algorithm ‘merge-and-recover (MAR)’ to speed up the calculation. Working on compact representation of segmental reference haplotypes, the MAR algorithm always calculates an exact form of transition probabilities regardless of partition of segments. Both simulation studies and real-data analyses demonstrated that our proposed method was comparable to most of the existing popular methods in terms of imputation accuracy, but was much more efficient in terms of computation. The MAR algorithm can further speed up the calculation by several folds without loss of accuracy. The proposed method will be useful in large-scale imputation studies with a large number of reference subjects.

Availability: The implemented multi-threading software FISH is freely available for academic use at https://sites.google.com/site/lzhanghomepage/FISH.

Contact: zlbio12@gmail.com; pyf0419@gmail.com; hdeng2@tulane.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Genotype imputation refers to a process in which missing genotypes at un-typed markers in a test sample are statistically inferred by knowledge of genotypes observed at the same markers in a reference sample (Li et al., 2009; Marchini and Howie, 2010). The principle underlying genotype imputation is that modern human genomes share segments of haplotypes with each other, as reflected by linkage disequilibrium (LD) patterns (Reich et al., 2001). Imputed genotypes have been widely used to fill sporadic missing genotypes, to integrate multiple studies with different genotyping platforms into meta-analysis, and to fine-map causal, but un-typed, disease loci. Genotype imputation has significant potential to greatly enhance our capacity to integrate and extend the scope of current existing datasets at no additional expense. Consequently, it has become a standard toolkit in large-scale genetic-association studies, and this has facilitated the discovery of a remarkable number of genetic loci responsible for a variety of complex traits and diseases (Li et al., 2009; Marchini and Howie, 2010).

A variety of statistical methods, including MACH (Li et al., 2010), IMPUTE (versions 1 and 2) (Howie et al., 2009; Marchini et al., 2007), BEAGLE (Browning and Browning, 2007) and others (Chi et al., 2013; Liu et al., 2013; Pasaniuc et al., 2012; Purcell et al., 2007; Scheet and Stephens, 2006), have been developed and used widely for genotype imputation. These methods provide excellent accuracy for imputing common variants (minor allele frequency (MAF)>5%) derived from genome-wide association studies (Duan et al., 2013a, b; Pei et al., 2008). However, as next-generation sequencing technology is getting mature and more widely applied, an increasing number of less common (1% < MAF < 5%) and rare variants (MAF < 1%) have been uncovered. It has been hypothesized that these less common and rare genetic variants represent another potential mechanism by which variations in the human genome influence complex diseases. Consequently, it has become increasingly important to be able to impute fast and accurately this increasing number of these variants in existing genome-wide association studies in order to facilitate gene-mapping studies and to study a variety of genomic structures.

The accuracy of genotype imputation is influenced greatly by the size of reference panel (Pei et al., 2008); larger reference samples increase imputation accuracy. When imputing common variants, reference panels of small to moderate size (e.g. 200) may be sufficient to attain an acceptable level of imputation accuracy. When imputing less common or rare variants, however, the accuracy of imputation will be considerably lower than that for common variants with reference panels of small to moderate size. Consequently, it is critical to use an expanded reference panel when imputing less common or rare variants in order to attain an acceptable level of accuracy. Fortunately, a continuously increasing resource of reference datasets based on next generation sequencing, e.g. 1000 genomes project (Abecasis et al., 2012), is becoming publicly available. Eventually, these well-validated datasets will provide a comprehensive set of reference samples that can support accurate genotype imputation of an extensive range of genetic variants, from common to rare ones.

One practical limitation of existing imputation methods is that they can be computationally intensive when operating with large reference samples. For example, both MACH and IMPUTE have quadratic computational complexity to the number of reference haplotypes used in the hidden Markov model (HMM), a level of complexity which actually prohibits them from making full use of all available reference haplotypes. In practice, both MACH and IMPUTE (version 2) compensate for this limitation by selecting only a subset of reference haplotypes to use for imputation. Obviously, this approach may cause a potential loss of accuracy under certain conditions, and this loss of accuracy may become particularly severe when imputing less common and particularly rare variants. Alternatively, they both have a haploid model implementation with linear complexity, which is achieved by imputing on pre-phased haplotypes rather than diplotypes (Howie et al., 2012). Nonetheless, phasing diplotypes into haplotypes introduces additional computation demanding as well as phasing uncertainty (Howie et al., 2012). In the context of a growing number of large sequencing datasets, it is becoming critically important to develop computationally efficient imputation methods that can use large reference datasets in order to retain imputation accuracy, particularly for rare variants, at a reasonably high level. Though a variety of alternative solutions have been proposed (Chi et al., 2013; Howie et al., 2012; Pasaniuc et al., 2012), they fall short regard to either accuracy or extensive computational demand.

Both MACH and IMPUTE are based on Li and Stephen’s haploid HMM (Li and Stephens, 2003). Their heavy computational demand in imputing diplotypes is attributable to modeling hidden states on pairs of reference haplotypes rather than on single haplotypes. In the present article, we propose an alternative and efficient model to impute diplotypes with linear complexity. Basically, we extend the same HMM, but we model hidden states on single haplotypes so that the computational complexity is ‘linear’ to the size of reference haplotypes. We take into account unphased genotypes through marginalization and decomposition. In addition, we develop an efficient computing algorithm to further speed up the execution of the proposed method. Through simulation as well as real data analyses, we show convincingly that the proposed method is much faster than existing methods, and yet is comparable in terms of imputation accuracy. A typical genome-wide imputation analysis for thousands of individuals, using the largest reference panel derived from the 1000 genomes project and routine computing devices can be accomplished within only a few hours with the method we developed.

2 METHODS

2.1 Definitions

Let H_R = {h₁, … , h_R} be a set of R haplotype vectors in the reference sample, each of which is fully genotyped at L markers, h_r = {h_r1, … , h_rL}, where h_rl ∈ {0, 1}, r = 1, … , R, l = 1, … , L. Let G_T = {g₁, … , g_T} be a set of T diplotype vectors in the test sample, each of which is partially genotyped at the same L markers, g_t = {g_t1, … , g_tL}, t = 1, … , T. Let 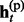= {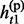, … , 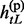} and 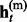= {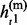, … , 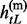} be the vectors of paternal and maternal haplotypes of the subject so that g_tl = 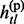+ 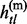, where 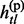and 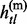∈ {0, 1, missing} and g_tl ∈ {0, 1, 2, missing}. When g_tl is heterozygous, 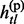and 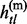may be ambiguous between alleles 0 and 1.

Given the above sample structure, our mission is to infer missing genotypes in each element of G_T with information of H_R. We infer every element in turn and focus on a single element in the following. For simplicity, we omit the subject subscript and denote the diplotype and haplotype vectors as g = {g₁, … , g_L}, h^(p) = {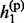, … , 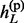} and h^(m) = {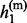, … , 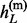}. We will first review the haploid imputation model based on the Li and Stephen’s HMM, and will then extend the model to impute diploid genotypes.

2.2 Haploid model

When the phases of h^(p) and h^(m) are a priori known, the two haplotype vectors are independent and could be imputed separately. Here we work on a single haplotype for illustration and denote it as h = {h₁, … , h_L}. The HMM assumes that h emerges from an imperfect mosaic of haplotypes in H_R, i.e. emitted from a sequence of hidden states that transit along haplotypes in H_R (Li and Stephens, 2003). Let s = {s₁, … , s_L} be a vector of hidden states emitting h, where s_l = 1, … , R indexes which reference haplotype is the hidden state at the l-th marker. We aim to sample s from its posterior distribution given the observed h and H_R, which is defined as,

(1)

In the above formula, the initial probability P(s₁) has the following form

(2)

The transition probability P(s_l|s_{l – 1}) has the following form

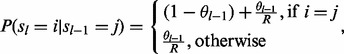(3)

where θ_{l – 1} is a locus specific parameter modeling genetic recombination events.

At last, the emission probability P(h_l|s_l) has the following form

(4)

where e_l is a locus specific parameter modeling mutation events.

Similar extensions of the above model have been implemented in IMPUTE (version 2) and presumably in the haploid implementation of the MACH algorithm MINIMAC (Howie et al., 2012).

2.3 Diploid model

When the phases of h^(p) and h^(m) are a priori unknown, imputation could not be performed on them directly. Some of the existing methods, including MACH and IMPUTE, avoid this uncertainty by taking pairs of reference haplotypes as hidden states, i.e., modeling on R² hidden states. Obviously, this strategy introduces additional computational complexity and may become prohibit in settings of large reference panels. Here we propose a new method that models on the R haploid hidden states even for the diploid genotype vector g so that the computational complexity remains linear to R. Similarly, let s^(p) = {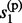, … , 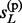} and s^(m)={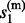, … , 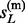} be two vectors of hidden states emitting h^(p) and h^(m), respectively. We aim to sample the sequences of s^(p) and s^(m) from their posterior distribution given g and H_R, that is, P(s^(p), s^(m)|g, H_R).

The joint posterior distribution of s^(p) and s^(m) given g and H_R is defined as

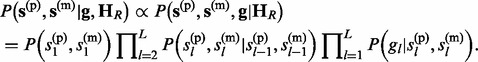(5)

Under the assumption of random mating, the prior distributions of two parental haplotypes are independent, and so are the two hidden states. Therefore,

(6)

and,

(7)

The non-missing genotype g_l is the sum of two parental alleles g_l = 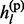+ 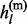. Conditioning on 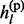and 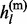, each of the two states 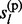and 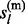is independent with the other and with the other parental allele. Therefore,

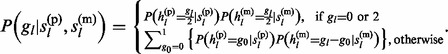(8)

Terms in probabilities (6)–(8) have the same forms as those in equations (2)–(4), respectively.

Sampling from the above HMM is performed with standard forward–backward algorithm (Rabiner, 1989). We adopt a forward-calculation-backward-selection approach. In the forward pass, the joint prior pro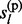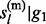babilities P(, , … , g_{l – 1}) and posterior probabilities P(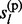, , 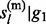… , g_l) at each non-missing marker are of interest. To achieve a linear computational complexity, we decompose them into functions of marginal prior and posterior distributions of 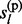and . 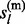Under the random mating assumption and large reference sample size, the following equation approximately holds (see Supplementary Material S1 for details)

(9)

where,

(10)

P(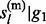, … , g_{l – 1}) is calculated in the same way, and is equals to P(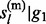, … , g_{l – 1}) due to the symmetry.

Rather than calculating the posterior distribution P(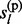, , 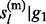… , g_l) directly, we calculate the marginal posterior distributions P(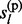|g₁, … , g_l) and P(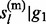, … , g_l). Let 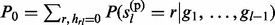and 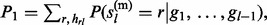then (see Supplementary Material S2 for details)

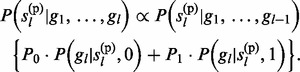(11)

In the backward pass, a pair of hidden states at each non-missing marker is sampled according to either of the following two probabilities: (i) P(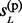, , 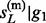… , g_L) or (ii) P(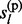, , 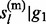… , g_l, 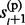, 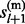). The first probability is decomposed into two forms that can be sampled sequentially. For example (Supplementary Material S3),

(12)

The second probability has the form

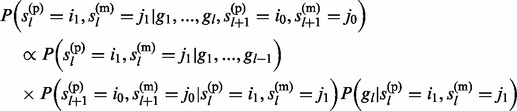(13)

To sample, all individual probabilities are summarized into four possible events: (i) neither parental haplotype recombines P_nn; (ii) only paternal haplotype recombines P_rn; (iii) only maternal haplotype recombines P_nr; and (iv) both parental haplotypes recombine P_rr. An event is sampled first and then a new pair of hidden states is updated/sampled accordingly (Supplementary Material S4).

Model parameters including recombination parameters θ and mutation parameters e could be set in accordance with (Li and Stephens, 2003), or fitted by the data (Li et al., 2010).

2.4 Compact representation of reference haplotypes

Both of the above haploid and diploid models have a linear computational complexity to reference haplotype size. Since different reference haplotypes may have the same type, they could be merged together and represented in a more compact manner (Delaneau et al., 2012) so that the size of states used in the HMM could be reduced further. Here we adopt the compact representation proposed by Delaneau et al. (2012). Briefly, a chromosome is partitioned into multiple non-overlapping segments. Within each segment, haplotypes with the same type are merged together, which we call a block. In partitioning segments, a sliding window starts at the first marker. The window size increases step-wise until the number of blocks within the window exceeds the preset size. A segment is then determined by the window’s boundaries. The window starts at the next marker, and the same process repeats until arriving at the last marker. HMM are primarily performed on merged blocks rather than on original individual haplotypes. However, the unit of transition is still individual haplotypes. At block-wise level, two types of transition are involved: within-segmental and between-segmental. Let B = {h₁, … , h_c} and B′ be two particular blocks within a same segment. In the Supplementary Material S5, we prove that the within-segmental transition probability has the form

(14)

which is essentially the equation used in the Delaneau et al. (2012).

For between-segmental transition, Delaneau et al. (2012) used the same transition formula, which is equivalent to assigning equal probabilities to all the c individual haplotypes when leaving the segment. Nonetheless, individual haplotypes may have different probabilities when entering the segment, so their probabilities will not necessarily be equal when leaving the segment. Consequently, this formula could only provide an approximation for between-segmental transitions, and the performance may vary for different partitionings of segments.

To overcome this limitation, we here develop a different and improved algorithm to always obtain an exact form of transition probabilities regardless of how segments are partitioned. In the Supplementary Material S6, we show that block transition probability is composed of two components: one contributed by each haplotype equally and the other contributed by each haplotype proportionally to its probability when entering the segment. We therefore develop a corresponding merge-and-recover (MAR) algorithm. Specifically, we merge individual haplotypes into blocks and use Equation (14) to calculate within-segmental transition probabilities; but we record the two probability components separately. We recover individual haplotypes’ probabilities by the two components at the end of the segment. We then calculate between-segmental transition probabilities at individual haplotype level with Equation (3). At the beginning of the next segment, individual haplotypes are again merged into blocks, and initial block probabilities are summarized according to individual haplotype probabilities (Fig. 1). Our algorithm keeps transition probabilities exact regardless of how segments are partitioned so that the accuracy will not be affected.

Fig. 1.

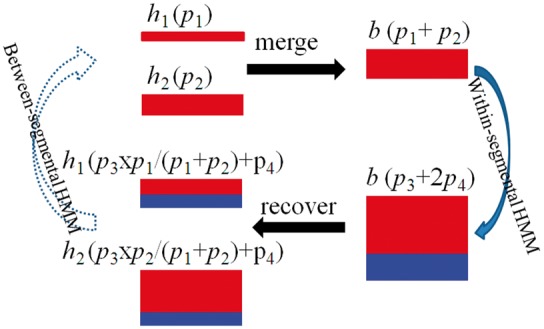
Illustration of the MAR algorithm. Two haplotypes are presented for simplicity. They are of same type and are merged into one block b. Initially the two haplotypes have the probability p₁ and p₂. Initial block probability is the sum of the two haplotype probabilities p₁ + p₂. Within-segmental HMMs are performed on the block. Block probability is partitioned into two components p₃ and 2p₄. The contribution of each haplotype in p₃ is proportional to its initial probability, and the contribution in p₄ is equal. At the end of the segment, the two haplotype probabilities are recovered with p₃ and p₄. Between-segmental HMM is then performed on individual haplotypes

2.5 Implementation

Both of the haploid and diploid models have been implemented in a user-friendly java package: fast imputation via segmental HMM (FISH). It has a variety of useful features, including support of multiple input/output data formats and support of multi-threading. The software is publicly available.

2.6 Simulation study

To evaluate the performance of the proposed method, we conducted a series of simulation studies. We randomly selected one genomic region of one mega base (MB) length on the human genome, and simulated population sequencing data with the software cosi (Schaffner et al., 2005). Specifically, we used the ‘best-fit’ model of the software and generated a pool of 10 000 population haplotypes. Two haplotypes were randomly selected from the pool to generate genotype of a simulated subject. Two samples, reference sample and test sample, were simulated each with 1000 subjects. SNPs failed to pass the Hardy–Weinberg equilibrium (HWE) test (P < 0.05) were removed from both samples. In the test sample, SNPs with MAF < 5% were removed, and were further removed randomly to retain the final number to ∼300 so that the marker density is scalable to 1 million per genome, a reasonable density for commercial genotyping arrays.

2.7 Real dataset

The real dataset that we analyzed was from the 1000 genomes project phase 1 release (as of June 2012). We focused on 379 subjects of European ancestry and analyzed the entire chromosome 22. We adopted the leave-one-out strategy and imputed each subject by the reference panel formed by remaining 378 subjects. We filtered out rare variants (MAF < 1%) because of the limited sample size. SNPs failed to pass the HWE test (P < 0.05) were also removed. To model a typical GWAS sample, SNPs that existed in the Affymetrix SNP6.0 genotyping array were kept in the to-be-imputed subject.

2.8 Comparison with other methods

We included three most popular methods for comparison: MACH, IMPUTE2 and BEAGLE. They are widely used in the community and usually outperform other methods under a variety of settings. For a fair comparison, all methods including FISH run on 100 iterations. Most of the other parameter settings were set to the default of the software. We keep in mind that these settings may not represent their best performance. Commands were listed as following:

• MACH

• mach1 -d test.dat -p test.ped -snps ref.snp –haps ref.hap –states states –burnin 10 –rounds 100 –dosage –geno –quality

• IMPUTE2

• impute2 -g test.geno -m rec.txt -int 0 100000000 -allow_large_regions -h ref.hap -l ref.map -k states -burnin 10 -iter 100

• BEAGLE

• java -jar beagle.jar unphased=test.geno out=“out” niterations=100 phased=ref.hap markers=ref.map

2.9 Comparison criteria

We evaluated the performance of various methods by imputation accuracy and running time. Two imputation accuracy measures were used: the first one was r², which was defined as the correlation coefficient between true genotype and imputed allele dosage; the second one was genotype discordance rate (GDR), which was defined as the proportion of genotypes whose type is incorrectly inferred (Marchini et al., 2007). Running time was measured on a unified computing configuration of Intel Xeon 2.4GHz CPU E5620.

3 RESULTS

In this section, we investigated the performance of the proposed method, namely FISH, as well as compared it with several existing popular methods, through simulated and real datasets.

3.1 Simulated dataset

Basic characteristics of the simulated dataset are presented in Table 1 (left). We first compared the imputation accuracy r² between diploid and haploid models. For the haploid model, in order to study the effect of phasing uncertainty on imputation accuracy, we simulated phased haplotypes with different levels of haplotyping switch error rate, which was defined as the proportion of heterozygote positions whose phase is incorrectly inferred relative to the previous heterozygote position (Lin et al., 2002; Stephens and Scheet, 2005).

Table 1.

Characteristics of the simulated and real datasets

	Simulated		Real
	Reference sample	Test sample	Reference sample	Test sample
Length (MB)	1.0	1.0	35.2	35.2
Numbe r of subjects (N)	1000	1000	379	379
Number of SNPs	6894	282	109 721	9406
MAF > 5%	2392	282	75 995	8396
MAF > 1%	1045	–	33 726	1010
MAF < 1%	3457	–	–	–

While the accuracy of the diploid model was not affected by switch error, the accuracy of the haploid model was dependent upon switch error in that imputation accuracy dropped consistently as switch error rate increased (Fig. 2). The diploid model was more accurate than the haploid model under most conditions tested. When switch error rate was below 0.2%, the diploid model was slightly inferior to the haploid model, and under these conditions, haplotypes were nearly perfectly inferred. Thus, when using the haploid model, the accuracy of pre-phase haplotypes is critical.

Fig. 2.

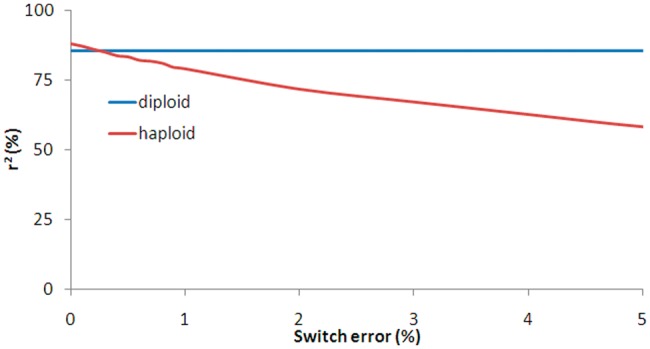
Diploid versus haploid imputation accuracies on the simulated dataset. A total of 1000 reference subjects and 1000 test subjects were simulated. Haplotypes in the reference samples were assumed known. For the diploid model, imputations were performed on diploid genotypes. For the haploid model, imputations were performed on haploid genotype. We simulated haplotypes in the test sample with various levels of switch error

As stated earlier, the MAR algorithm that we developed calculated an exact form of transition probability matrix regardless of the structure of compact representation of haplotypes. Therefore, compact representation did not affect imputation accuracy; what was being affected was running time. Here, we studied the reduction in running time from compact versus uncompact representation when all reference haplotypes were used for imputation. Both representations used the total number of R reference haplotypes. The uncompact representation therefore had an constant state size R and running time; it served as a benchmark. The running time for both models is displayed in Figure 3. For both diploid and haploid models, running time under compact representation decreased initially then increased, as the number of states increased. The gain in computational efficiency was highly correlated with compact ratio (see Section 4 for details). Shortest running times for both diploid and haploid models were approximately equal, and were observed in the range between ∼50 and 300 states. Compared to uncompact representation, compact representation could decrease running time by ∼3-fold under its best performance. Running time also elevated moderately as state size fell below 50, and MAR event occurred frequently under these conditions. Consequently, for most practical applications, we recommended an intermediate value of 50–100 states in order to optimize computational efficiency.

Fig. 3.

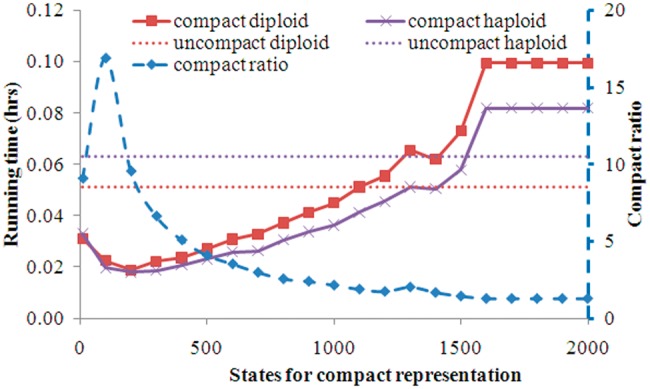
Running time of compact representation of reference haplotypes on the simulated dataset. Both compact and un-compact used the total number of R = 2000 reference haplotypes. Uncompact representation severs as a benchmark. The x-axis was only for compact representation. Difference partitionings of segments produced different on average numbers of blocks within segment, which were the states used in the HMM

The imputation accuracies of various methods are presented in Table 2. As a benchmark, we also imputed with the haploid model on the simulated haplotypes of the test sample so that haplotypes were perfectly phased, and we considered this analysis an ‘Ideal’ model as we expected it to give the highest accuracy. BEAGLE and FISH used all the R reference haplotypes, so they were not influenced by state size. The performance of MACH got better as state size increased. Interestingly, the performance of IMPUTE2 was less sensitive to state size. Its accuracy was only observed to get better slightly when state size increased from 50 to 100. For common variants (MAF > 5%), all methods had very high accuracies that was close to the ‘Ideal’ model of imputation on perfectly phased haplotypes, though the performance of MACH was inferior slightly at very low state sizes. For less common variants (1% < MAF ≤ 5%), FISH again had an accuracy close to the ‘Ideal’ model regardless of state size, while MACH achieved a high accuracy at state sizes >400. We observed a slight loss of accuracy for BEAGLE compared to the other methods; with the exception of MACH at low state sizes (<400). For rare variants (MAF ≤ 1%), FISH again had an accuracy that was close to the ‘Ideal’ model. Among the other methods, the performance of MACH was highly dependent on state size in that a size of >800 states was required to retain a comparable accuracy. Again, BEAGLE was slightly inferior to almost all of the other methods with the exception being its superiority to MACH with state sizes below ∼200. The accuracy of IMPUTE2 achieved to a level close to the ideal one at a size of as small as 50 states for all the three MAF intervals.

Table 2.

Imputation accuracies on the simulated dataset

MAF	States	r2 (%)					GDR (%)
		Ideal	FISH	IMPUTE2	MACH	BEAGLE	Ideal	FISH	IMPUTE2	MACH	BEAGLE
(0.00,0.01]	50	78.71	75.46	75.89	14.18	46.16	0.14	0.15	0.15	0.53	0.29
	100	78.71	75.46	76.15	27.49	46.16	0.14	0.15	0.15	0.52	0.29
	200	78.71	75.46	76.37	41.74	46.16	0.14	0.15	0.15	0.46	0.29
	400	78.71	75.46	76.65	55.96	46.16	0.14	0.15	0.15	0.39	0.29
	800	78.71	75.46	76.80	67.64	46.16	0.14	0.15	0.15	0.27	0.29
(0.01,0.05]	50	92.67	89.68	91.02	61.90	85.26	0.41	0.55	0.47	3.17	0.76
	100	92.67	89.68	91.23	72.72	85.26	0.41	0.55	0.46	1.81	0.76
	200	92.67	89.68	91.38	79.56	85.26	0.41	0.55	0.45	1.28	0.76
	400	92.67	89.68	91.42	84.58	85.26	0.41	0.55	0.45	0.92	0.76
	800	92.67	89.68	91.46	88.60	85.26	0.41	0.55	0.44	0.62	0.76
(0.05–0.50]	50	97.22	96.46	96.98	87.84	95.65	0.86	1.22	1.01	4.22	1.41
	100	97.22	96.46	97.07	90.93	95.65	0.86	1.22	0.99	3.14	1.41
	200	97.22	96.46	97.12	93.02	95.65	0.86	1.22	0.98	2.38	1.41
	400	97.22	96.46	97.16	94.72	95.65	0.86	1.22	0.96	1.80	1.41
	800	97.22	96.46	97.18	96.10	95.65	0.86	1.22	0.95	1.27	1.41

Figure 4 plotted running time of various methods on the simulated dataset. BEAGLE had a constant running time of ∼91.9 h based on its default settings. The relationship between state size and running time was quadratic for both MACH and IMPUTE2, while IMPUTE2 took slightly more time than MACH. Imputation on 1000 states took ∼74.8 and ∼66.7 h for IMPUTE2 and MACH, respectively. Most impressively, FISH took considerably less time than any of the other methods. Even when modeling the full set of 2000 reference haplotypes, FISH took only ∼1 min at its best performance. This gain in running time could be as high as hundreds to thousands fold compared to the other methods.

Fig. 4.

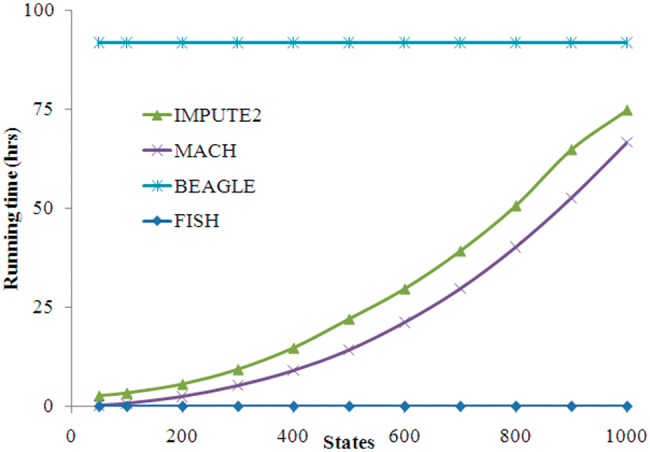
Running time of various methods on the simulated dataset

3.2 Real dataset

In order to compare the various imputation methods with a real dataset, we analyzed the entirety of chromosome 22 of the 379 sequenced European subjects from the 1000 genomes project phase 1 release (as of June 04, 2012). Basic characteristics of the data are listed in Table 1 (right). Because of the relatively limited sample size, we did not include rare variants (MAF < 1%) into the analysis. Adopting a leave-one-out strategy, we imputed each subject in turn and summarized results together. Haplotypes of all subjects were a priori inferred and were assumed known. As a benchmark, we also imputed each subject with the haploid model on the inferred haplotypes as if the subject was perfectly phased. We again called this analysis the ‘Ideal’ model. The results are summarized in Table 3. As expected, the ‘Ideal’ model analysis gave the highest r² (88.2% and 66.3%) and lowest GDR (4.0% and 1.8%) for common and less common variants, respectively. The performance of both FISH and BEAGLE was not affected by state size. Their r² were 87.0 and 64.6 and 86.9% and 59.8%, respectively, under the two MAF categories, while the GDR were 4.5 and 2.0 and 4.5% and 2.1%. The accuracy of MACH increased with increased state size, while the GDR decreased. At 200 states, its accuracy (87.1% for r² and 4.4% for GDR) for common variants was slightly higher than both FISH and BEAGLE; however those (62.9 and 2.0%) for less common variants was intermediate between FISH and BEAGLE. Increasing state size beyond 200 may increase its accuracy further. The performance of IMPUTE2 was influenced slightly by state size, with almost no differences observed with common variants and minor differences with less common variants. IMPUTE2 also produced the highest r² (87.6 and 65.2% at 200 states) and lowest GDR (4.3 and 1.9%) among all the methods, though the differences between IMPUTE2 and FISH are relatively minor.

Table 3.

Performance of various methods on the real dataset

Method	States	r2(%)		GDR (%)		Running time (h)
		MAF ≥ 5%	MAF < 5%	MAF ≥ 5%	MAF < 5%
Ideal	50	88.2	66.3	4.0	1.8	0.3
FISH	50	87.0	64.6	4.5	2.0	0.3
BEAGLE		86.9	59.8	4.5s	2.1	73.2
MACH	50	84.4	52.8	5.3	2.8	3.0
	100	85.9	58.7	4.8	2.3	8.4
	200	87.1	62.9	4.4	2.0	27.3
IMPUTE2	50	87.5	64.2	4.2	1.9	18.2
	100	87.6	64.9	4.3	1.9	25.2
	200	87.6	65.2	4.3	1.9	51.7

To estimate running time, we imputed the 379 subjects together by the reference sample formed by the same subjects. To avoid over-fitting, we disturbed the two haplotypes of each reference subject randomly with a switch error rate of 5%. As listed in Table 3, FISH took 0.3 h, while BEAGLE took 73.2 h; Again, MACH and IMPUTE2 had a quadratic computational complexity with state size. At 50 states, they took 3.0 and 18.2 h, respectively, while at 200 states, they took 27.3 and 51.7 h, respectively. Clearly, FISH was most computationally efficient among all the methods investigated. Notably, its implementation had a multi-threading feature so that the computation could be further sped up on a routine computing cluster node with multiple CPUs.

4 DISCUSSION

In this article, we have proposed a new method for performing diploid genotype imputation based on the HMM. We have also developed an algorithm MAR for efficient execution of the proposed method. Our method is comparable to most of the existing popular methods in terms of imputation accuracy and GDR, and is much preferable in terms of computational efficiency.

We model hidden states on single reference haplotypes rather than on pairs of haplotypes. Consequently, the computational complexity reduces from quadratic to linear to the number of reference haplotypes. To achieve the linear complexity, we define the Equation (9), which assumes the independence of P(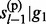, … , g_l–1) and P(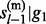, … , g_l–1). Under the random mating assumption, this independence equation holds as long as the total reference haploytypes serve as the entire population from which the test subject is sampled. In practice, it will hold approximately under large reference sample size, a condition for which our method was proposed. The computational improvement is qualitatively and quantitatively dramatic. We take into account haploid genotype uncertainty at each marker by weighted sum of both possible configurations. Our simulation studies, as well as real data analyses, showed no significant loss of accuracy compared to conventional methods modeled on pairs of reference haplotypes.

In the context of high-throughput sequencing datasets, an urgent priority for genotype imputation is to improve computational efficiency. Several alternative solutions have been proposed, one of which is to pre-phase genotypes in the test sample into haplotypes, then to impute on the inferred haplotypes (Howie et al., 2012). This reduces the computational complexity so that it is linear to the number of reference haplotypes. However, haplotype phasing itself is a computation-demanding process in large-scale settings. Moreover, the success of imputation on phased haplotypes relies largely on the availability and accuracy of statistical inference of haplotypes and may lose accuracy in certain conditions (Howie et al., 2012), though recent developments on haplotype phasing may ease this limitation (Delaneau et al., 2012, 2013; Rao et al., 2013; Williams et al., 2012). Compared to the pre-phasing approach, our proposed method does not require haplotypes to be known. It has another potential to impute on data types that could not be pre-phased, though we did not consider that situation in the current study. Another recent development includes imputing via matrix operation (Chi et al., 2013). However this method may cause some potential loss of accuracy, though it may lead to increased speed of computation.

Equation (14) provides an approximation of between-segmental transition probability calculation. When operating on long segments in which recombination events dominate probability calculations, such approximations may provide reasonable accuracy because individual haplotypes within a block receive the same probabilities regarding recombination. When operating on short segments in which initial haplotype probability dominates probability calculations, however, the loss of accuracy may become severe. An ideal requirement would be that the way to split segments will influence only computational efficiency, but not the imputation accuracy. The developed MAR algorithm meets this requirement, which allows us to optimize the minimal computation without concerns on accuracy. The improvement of computation by compact representation depends on how reference haplotypes could be merged, and essentially, on MAF and LD patterns. Suppose that the total L markers are partitioned into L_s segments, and there are on average n_s blocks within segments. The computational complexity without compact representation is c₁ = L × R (for a single individual), and that with compact representation is c₂ = n_s × (L – L_s + 1) + (L_s – 1) × R. A measure of compact ratio is therefore estimated by c₁/c₂. Our simulation studies showed that the improvement in computation was highly correlated with this ratio.

In summary, we have proposed a new statistical model and method for fast and accurate genotype imputation. Our method is suitable for large-scale dataset analyses. The implemented software FISH is publicly available for academic use.