Abstract
Making robust inferences about the functional neuroanatomy of the brain is critically dependent on experimental techniques that examine the consequences of focal loss of brain function. Unfortunately, the use of the most comprehensive such technique—lesion-function mapping—is complicated by the need for time-consuming and subjective manual delineation of the lesions, greatly limiting the practicability of the approach. Here we exploit a recently-described general measure of statistical anomaly, zeta, to devise a fully-automated, high-dimensional algorithm for identifying the parameters of lesions within a brain image given a reference set of normal brain images. We proceed to evaluate such an algorithm in the context of diffusion-weighted imaging of the commonest type of lesion used in neuroanatomical research: ischaemic damage. Summary performance metrics exceed those previously published for diffusion-weighted imaging and approach the current gold standard—manual segmentation—sufficiently closely for fully-automated lesion-mapping studies to become a possibility. We apply the new method to 435 unselected images of patients with ischaemic stroke to derive a probabilistic map of the pattern of damage in lesions involving the occipital lobe, demonstrating the variation of anatomical resolvability of occipital areas so as to guide future lesion-function studies of the region.
Keywords: Lesion segmentation, Diffusion-weighted imaging, Stroke, Zeta score, Magnetic resonance imaging, Occipital lobe, Lesion-mapping
1. Introduction
1.1. Overview
To do functional neuroanatomy in the brain is to relate a discrete area, or network of areas, to a specific function, or set of functions. The strongest evidence for such a relation is the observation of disruption of a function following disruption of its putative anatomical substrate. Unfortunately, such evidence is difficult to obtain in the human brain because disrupting its activity can be done experimentally only transiently, and only for accessible regions of cortex. We must therefore rely on data derived from patients with focal brain lesions of natural, or incidental surgical, causes.
Now human lesion data is difficult to use for the purposes of functional neuroanatomy for two conflicting reasons. First, delineating the precise extent of the lesion—at a resolution commensurate with the underlying anatomical architecture—has hitherto been done manually, by trained operators, making the process extremely time-consuming and susceptible to operator bias. Most studies therefore rely on relatively small numbers of meticulously characterised cases. Second, the resolving power of a lesion study is generally limited not by the physical resolution of the images but by the resolution of the lesion sampling of the brain: effectively the anatomical scale at which the effects of the absence or presence of damage can be reliably determined. For example, if within a set of patients under study whenever a given voxel is hit a cluster of other voxels are always also hit the resolution of the resultant lesion map is not limited by the dimensions of the voxel but by the size of the cluster of invariantly affected other voxels. This limit depends not only on variations in the frequency of damage to locations across the brain but also on the multivariate pattern of damage in the population of lesions, a factor that is hard to quantify owing to the likely complexity of what is a very high-dimensional multivariate distribution (Nachev and Husain, 2007). Most studies may therefore require much larger numbers of cases than they actually use.
A further complication of lesion studies is the dynamic nature of the consequences of focal injury on the operation of what is inevitably a distributed, plastic network. Acutely, areas remote from the site of injury may be transiently affected in ways that do not necessarily reflect the functional contribution of the target. Chronically, remote reorganisation may abnormally compensate for a deficit, camouflaging the target's true role in the normal state. To obtain a synoptic picture of the role of a given area we therefore need both acute and chronic lesion studies, with image processing methodology optimised for each.
To realize in practice the power lesion-mapping has in theory we thus need methodology that permits much larger datasets to be generated; inevitably, in a fully-automated manner. This requires the development of unsupervised algorithms for the two critical steps in the processing of lesion images: distinguishing damaged from normal brain (lesion segmentation) and determining the anatomical labels of the damaged areas (lesion registration). Although a number of satisfactory algorithms exist for the latter (Crinion et al., 2007; Andersen et al., 2010; Nachev et al., 2008) no comprehensive solution exists for the former.
Here we seek to do three things. First, we show how a simple recently-described general measure of anomaly can be used to perform lesion segmentation theoretically in any imaging modality where inter-subject registration to a set of reference normal images is possible. Second, we describe and proceed to evaluate an algorithm based on this approach that is optimised for the characterisation of acute ischaemic lesions as shown by diffusion-weighted magnetic resonance imaging (MRI) (DWI). Third, we apply the new method to acute ischaemic lesions involving the occipital lobe so as to generate a map of the patterns of damage to the region, facilitating predictions about the resolvability with lesion-mapping of specific subareas within this region. In describing the general approach and our specific application we need to make a set of general points about lesion segmentation agnostically of the lesion type and imaging modality, and a set of specific points pertinent to acute stroke.
1.2. Zeta lesion segmentation
Taking the general points first, any comprehensive method for lesion segmentation has to deal with five fundamental problems. First, for any given imaging modality, the signal at any specific point in the brain will usually vary from one normal individual to another in a way that is difficult to parameterise: the population distribution is often not only not Gaussian, but multimodal. Our method is therefore non-parametric (Lao et al., 2008). Second, deciding whether or not a region is abnormal often depends on the signal not just in one imaging sequence but several different ones: where an abnormality is not replicated across more than one type of sequence it may merely reflect noise or artefact. Our method is therefore potentially multispectral (Prastawa et al., 2004). Third, although the signal properties of normal tissue may be definable, they are often not for lesions, simply because it is in the very nature of pathology to be heterogeneous in signal. Our method is therefore agnostic of the specific properties of the lesion signal: it identifies everything that is anomalous in relation to the normal reference (Prastawa et al., 2004; Shen et al., 2010). Fourth, whether or not the signal at any given locus is interpreted as normal or damaged often depends on the signal in its immediate anatomical vicinity. Our method therefore incorporates local information, in a high-dimensional manner, when determining the anomaly of each point in the brain. Fifth, the optimal properties of an image on which to perform lesion segmentation are opposite to those of an image on which to perform lesion registration: this is so because in the former normal tissue contrast interferes with the lesion contrast one needs to distinguish normal from damaged brain, whereas in the latter lesion contrast interferes with the normal tissue contrast one needs to determine the anatomical labels of the lesion. Our method therefore uses different imaging sequences for each task: one optimised for lesion segmentation and another optimised for lesion registration. Since clinical scans invariably use at least two different sequences this does not limit the application.
The core of our method is a simple measure of the anomaly of an unknown test datum in relation to a reference set of data already known to be normal. To determine the anomaly of a single datum one may simply compare it to the k instances within the reference set that resemble it most closely: its k nearest neighbours (Cover and Hart, 1967). Where the datum is a single value, a scalar, this is simply a matter of finding the k points that are closest to it on a linear scale. Where the datum has n variables describing it, a vector, this is some distance measure in n dimensional space—most simply the Euclidean—of the datum to its k nearest neighbours. To derive a unitary measure, one can take the mean of the distances of the test datum to each of the k nearest neighbours, a measure known as gamma (γ) (Harmeling et al., 2006). The attraction of gamma is that it is indifferent to the shape and number of modes of the reference population distribution, and it is determined only by the reference set, requiring no prior knowledge of the properties of anomalous data.
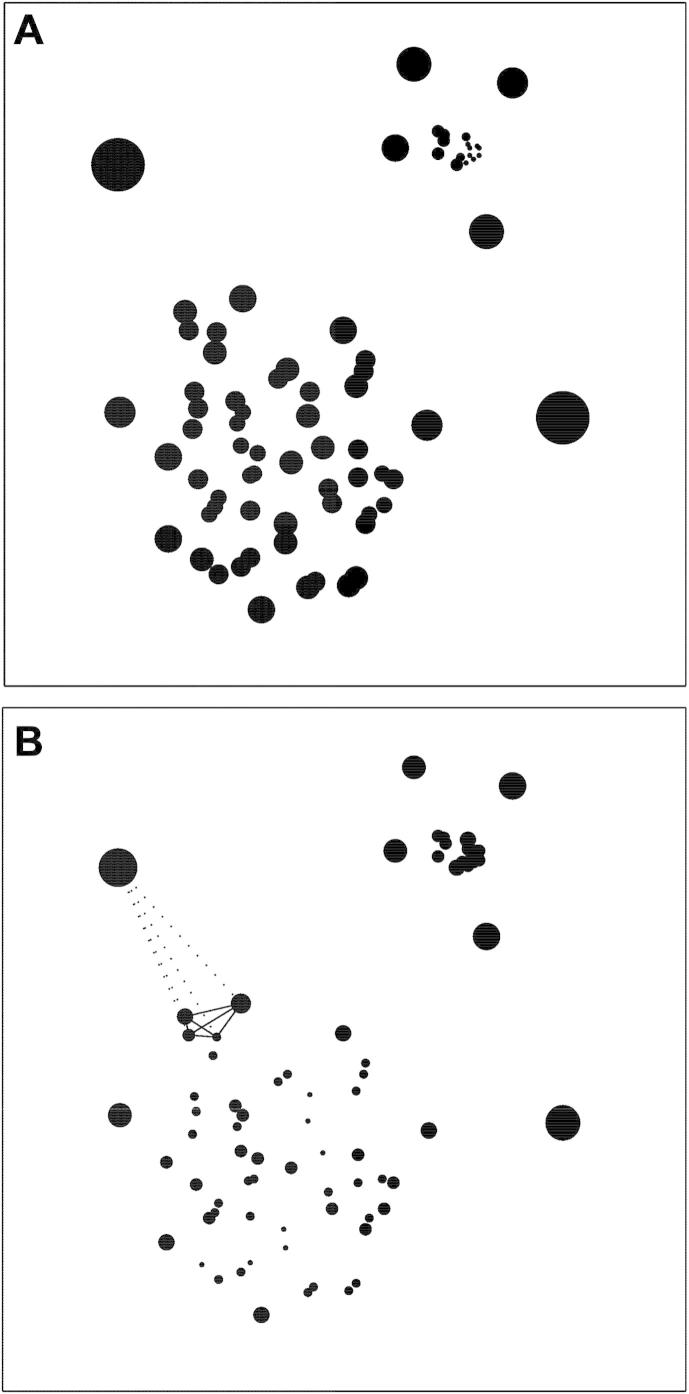
The problem with gamma, however, is that it is sensitive to variations in the density of the reference population, that is, the degree of similarity between normal points within the reference set. This is illustrated in Fig. 1A, where a heterogeneous synthetic two-dimensional dataset is labelled by the gamma score of each point: the diameter of each point is drawn in proportion to the score. It is easy to see that members of the smaller, denser cluster will generally have a smaller value of gamma than members of the larger, sparser cluster even though each belongs equally strongly to its respective cluster. Thus, if anomaly were to be determined by a fixed threshold of gamma, either too many members of the sparse cluster will be labelled as anomalous or too few of the denser one. It is thus easy to see that the score is confounded by local differences in density.
Fig. 1.
Gamma and zeta (A). A heterogeneous synthetic two-dimensional dataset with clusters differing in density labelled by gamma: the diameter of each point is proportional to the gamma score (k = 4). Note that the gamma score co-varies with the density of the neighbourhood and that a fixed criterion of anomaly would therefore either over-call points in sparse areas or under-call them in dense ones. (B). The same dataset labelled by zeta. The lines illustrate for one outlying point the distances on which zeta depends, given k = 4. Note that the anomaly score is now less dependent on density, with points equivalently anomalous to their respective clusters correctly identified as such.
So for gamma to be useful we need to find a way of correcting for such differences. As originally proposed in the context of computer network intrusion detection (Rieck and Laskov, 2006), an elegant way of doing this is to correct it by the mean of the distances between the members of the “clique” of k nearest neighbours, effectively a measure of local density. Thus, where the k nearest neighbours are sparsely distributed, gamma will have to be larger to be judged to be anomalous, and vice versa. The same dataset relabelled by this corrected score, zeta (ζ) (Rieck and Laskov, 2006), is shown in Fig. 1b. We can now see that differences in local density no longer affect the score to the same degree. In short, the zeta score embodies the simple intuition that you are an outsider if those closest to you are closer to each other than they are to you.
To apply zeta to the task of lesion segmentation, we calculate the zeta score independently for each voxel within a test image that has been brought into registration with a large set of images known to be free of lesions. The test datum is thus the signal at each voxel, and the reference data from which we choose the k nearest neighbours is the signal in each of the voxels at the same anatomical location across the reference set. Rather than using just the signal at a given voxel, a scalar value, we can also include the signal of the 26 immediately adjacent voxels (a 3 × 3 × 3 cube centred on each voxel), resulting in a vector of 27 values for each voxel. This allows us to capture information about local variations in the signal at any given point, a “searchlight” approach analogously used in multivariate functional imaging (Kriegeskorte et al., 2006). The result is a map of the brain where the anomaly of each voxel is labelled by its zeta score; appropriately thresholded this yields a binary lesion map of the brain.
1.3. Zeta lesion segmentation for acute ischaemic injury
Turning to our specific implementation of the approach, here we focus on ischaemic lesions as commonest aetiology of lesion used in neuroanatomical studies and we choose diffusion-weighted MRI as the imaging modality with the highest resolution and lesion contrast within the acute period of stroke. The relative difference in lesion contrast between diffusion-weighted and other sequences in the acute period of ischaemic damage allows us to make good use of different sequences for inter-subject registration and lesion segmentation as argued to be desirable in the foregoing. The complex distribution of the normal diffusion signal across the brain—clearly multimodal in areas of high artefact—allows us to test the approach on data bound to be ill-suited to conventional parametric methods.
1.4. Mapping ischaemic damage to the occipital lobe
Lesion-function mapping is commonly regarded as being limited primarily by the anatomical resolution of the images and the frequency at which any given area is sampled. The former depends on the product of the physical resolution of the images and the size of the inter-subject registration error, the latter on the sample size relative to the frequency of damage to the area under investigation. However, there is another, perhaps more important limit: the resolution of lesion sampling. This is not the frequency at which any given area is sampled, but the volume of brain that cannot be dissociated from any given area because it is always damaged together with it, at least in the sample under consideration. This will always arise as a theoretical problem where lesion size is substantially larger than the sampling resolution: almost invariably the case in lesion studies. The extent to which it is a problem in practice depends on correlations across voxels: essentially, the high-dimensional distribution or pattern of injury, which is unknown for vascular lesions. Our aim here is therefore to take a large sample of lesions, comparable to the largest lesion studies in the literature, and to show for the subset that involves occipital cortex how the resolvability of distinct subareas is limited by this effect. Researchers can use this map to determine whether or not a large sample of vascular occipital lesions is likely to allow them to resolve between any two subareas with the aid of lesion-mapping.
The zeta score, then, provides a simple, intuitive, and general way of segmenting lesions from images of the brain. We proceed to give a formal description of the algorithm, and go on to evaluate its performance in the context of acute ischaemic damage imaged with diffusion-weighted MRI. Finally, we apply the method to generate a probabilistic map of the damage to the brain in cases where the occipital lobe is affected, demonstrating the utility of the approach.
2. Methods
2.1. The zeta anomaly score
We have seen that the gamma score of a given point, x, is the average distance to its k nearest neighbours (nn), viz: (Harmeling et al., 2006).
| (1) |
The zeta score is the difference between gamma—an index of the anomaly of the point in relation to its neighbours—and the average inner-clique distance of its neighbours—an index of the density of the neighbourhood clique (Rieck and Laskov, 2006):
| (2) |
A key part of the elegance of this approach is that—being adaptive to the data—it has only few parameters to adjust. So to use the zeta score in the imaging domain, we need to take only two key decisions. First, we need to decide what value of k to use. The optimal value of k is determined by the smallest scale of any heterogeneity in the reference population, effectively the size of the smallest distinct cluster of values differing from the main population yet still within the normal range. Since the clustering of data has no established measure no rigid guide to the selection of k can be given. Here we arbitrarily set the value of k at 15% of the size of the number of cases within the reference set (15 images in our case). The second decision to take is how best to parameterize the signal at each voxel: since we do not need to use a scalar—we can have a vector of values—we can incorporate as few or as many parameters per voxel as is computationally practicable. For example, if one were using diffusion tensor imaging one could use each of the eigenvalues per voxel, corresponding to the magnitude of anisotropy in each plane. Similarly, one could incorporate the values of several different types of imaging sequence, coregistered so that the voxels are all matched for anatomical location, enabling multispectral lesion segmentation. Additionally or alternatively, as we do here, one can add information about the signal of adjacent voxels, thereby incorporating local pattern anatomical information in the parameterisation of the signal at each voxel.
The distance measure we compute at each voxel here is therefore the Euclidean distance in 27 dimensions—the signal at the index voxel and at the 26 voxels (a 3 × 3 × 3 cube) immediately adjacent to it—between each voxel in the test image and the homologous voxels and their adjacents in a set of reference, normal images coregistered with the index image so that anatomically homologous regions are brought into alignment. The result is a voxel-wise map of zeta values from which a binary image (lesioned vs non-lesioned) can be created by choosing an appropriate threshold zeta value. Thus though we use only one sequence to derive zeta, the b1000 image, we parameterise each voxel as the multivariate pattern of a 27 voxel cluster.
2.2. Imaging data
In order to evaluate the performance of zeta we need to generate a set of zeta maps that we can compare with a “ground truth” of what is really damaged and what is not. For this we naturally need two kinds of data: a set of target images of focally lesioned brains (in one or more imaging modality) and a set of reference images of non-lesioned brains with characteristics otherwise similar to the target set. For the former here we used DWI data derived from 38 patients with a diagnosis of acute stroke, and for the latter DWI data from 95 patients investigated for possible stroke but with no radiological evidence of that or any other focal abnormality.
The data for each patient consisted of standard clinical axially-acquired diffusion-weighted echoplanar imaging (b0 and b1000) sampled at 1 mm × 1 mm × 6.5 mm resolution, and obtained on a GE Genesis Signa 1.5T MRI scanner in a single session for each patient. The b0 images satisfactorily distinguish between cerebrospinal fluid, grey, and white matter in line with their T2-weighting while being relatively unaffected by acute ischaemic lesions in the first few hours. The b1000 images, by contrast, show little normal tissue differentiation but marked differences in signal between damaged and undamaged tissue. The complementarity between these two sequences is exploited by our method as outlined below. The lesioned brain images were unselected except for a minimum lesion size of 216 mm3. Note this value is considerably smaller than most of the lesions investigated in clinical studies, making our test more stringent than required. The patients with lesions were unselected except for the presence of a visible lesion on DWI, with a mean age of 62 years [standard deviation (SD) = 20], equal sex ratio, and were all scanned between 1 and 17 days from symptom onset (mean = 4.1 days, SD = 3.8 days). The 95 reference images were unselected except for the absence of a visible lesion on DWI, with a mean age of 67 (SD = 15) and sex ratio of 62 men to 33 women. The period from symptom onset to scan in the patients with lesions (1–17 days) is broader than the conventional notion of “acute”. For some patients, the lesion will therefore have been visible on the b0 image used in the normalisation step, where the abnormal signal may have degraded the quality of registration to some degree as previously discussed. So as to test the real-world usefulness of the algorithm, however, where a single time point within the hyperacute stage of b0 negativity is rarely practicable, we chose a spread of time points, including those in which the b0 image will have been contaminated to some degree. To the extent to which the quality of normalisation impacts on the performance of the algorithm better results might be achievable with a set of scans acquired only in the hyperacute stage.
The 75 control subjects were matched to the lesioned brains by being drawn from a similar clinical population: patients attending a transient ischaemic attack (TIA) clinic who had not been found to have any acute lesions or any chronic lesions large enough to be visible on DWI. They had a mean age of 65 years (SD = 16) and a sex ratio of 43 men to 32 women. The target and a separate set of normal images from the control population were used to create a synthetic dataset of 2850 artificially lesioned brains where each of the 38 lesions was “transplanted” into the 75 normal brains (Brett et al., 2001; Nachev et al., 2008), (see below). This was done by extracting the lesion signal—as defined by manual segmentation—and inserting it into the homologous region of the reference image (see below). The point of this manoeuvre was to evaluate the algorithm's ability to distinguish lesioned from non-lesioned signal at the same location. Unless one is fortunate enough to have a pre- and post-lesion scan for several patients—which we are not—the only way of performing such an analysis is by using “chimaeric” images of the kind we describe, an approach others have recently followed (Ripollés et al., 2012). If we had no grounds to suspect that lesion discriminability varied with location an analysis of this kind would have been unnecessary. However, it is clear that this cannot be assumed to be so, especially with DWI where some locations (e.g., frontal and temporal poles) are much more prone to artefactually abnormal signal than others.
The data used to apply the method so as to generate a probabilistic map of damage to the occipital lobe consisted of DWI volumes of 435 unselected patients with acute stroke admitted to University College London Hospitals with a lesion detectable on DWI.
2.3. Normalisation
The computation of zeta and any other voxel-wise statistic that compares a test image against a reference set of images implies knowledge of the spatial correspondence between the two. In other words, the computation must be preceded by an inter-subject co-registration step in which spatially homologous voxels in the test and reference brain images are brought into alignment: a process conventionally referred to as normalisation (Brett et al., 2001; Ashburner and Friston, 1997, 1999; Friston et al., 1995). Normalisation is commonly done by finding a set of linear and non-linear transformations of the target image such that differences in the signal at each voxel between the target and reference images are minimized at the cost of some plausible level of distortion. In the presence of a lesion, normalization can therefore be difficult since the signal within the lesioned region will inevitably tend to interfere with the signal matching process (Shen et al., 2007). One can minimize this effect by obtaining more than one imaging sequence and performing the normalization on the sequence that is least sensitive to the lesion, as we do here (see below). Alternatively or additionally, one can mask out the lesioned region (Brett et al., 2001) or fill it in with signal from the homologous region in the contralateral hemisphere (Nachev et al., 2008), but this of course implies knowing the spatial parameters of the lesion. Another option is to combine the normalization and tissue segmentation (white and grey matter, and cerebrospinal fluid) into a single generative model, explicitly modelling the lesioned area as falling within a third, abnormal class. This procedure may be used iteratively, with the lesioned class derived from one run serving as a prior for the next (Seghier et al., 2008). Since the departure of the signal at each voxel from the expected value for grey and white matter respectively determines the extent to which it is likely to disturb the matching process, this approach would seem excellent at minimizing the impact of the lesion. As a means of lesion segmentation, however, it can only be expected to be satisfactory in the special case where the optimal normalization modality and the optimal lesion identification modality are the same. Clearly this is neither inevitable nor desirable since the more the lesion disturbs the tissue contrast the worse the normalisation, and the greater the tissue contrast the more likely it is to interfere with lesion segmentation as already argued.
Our approach here is therefore to derive the normalization parameters by applying the unified normalization and segmentation procedure implemented in Statistical Parametric Mapping 5 (SPM5 – www.fil.ion.ucl.ac.uk/spm) to the b0 image—which has low lesion contrast and good grey/white matter contrast—and then to apply the resultant normalisation parameters to the corresponding b1000 image, thereby allowing much better normalisation than could be achieved from the b1000 image alone. Note that the success of the normalisation procedure is not dependent on the b0 image's being free of any lesion contrast because SPM5s routine will automatically eliminate most such voxels during the segmentation component as already explained (Seghier et al., 2008): it is simply desirable that this is kept to a minimum. We have previously shown that, in keeping with their T2-weighting, clinical b0 images of this resolution can be satisfactorily normalised (Nachev et al., 2008). Clearly, this step is only practicable if the b0 and b1000 images are already in registration. Since each pair is taken in a single run, the images are bound to be close; nonetheless we first rigid-body coregistered the b0 to the b1000 using SPM5's standard co-registration routine before performing the normalization outlined above. Note that this step is robust to the difference in lesion signal between the two scans because it is a rigid-body transformation. All further operations were performed on the normalized images, which were resliced to 2 × 2 × 2 mm voxels using 7th order spline interpolation.
2.4. Generating the chimaeric images
The set of artificially lesioned brain images was generated by replacing in each non-lesioned image and sequence (b0 and b1000) the signal intensities in the corresponding voxels within each of the lesions, resulting in 38 × 75 = 2850 chimaeric images. For the chimaeric images to be realistic the non-lesioned tissue in each donor/recipient pair must be broadly similar. Since unlike CT scans MRI images do not have a standardized intensity scale (Bergeest and Jager, 2008; Nyúl and Udupa, 1999), each transplantation step must be preceded by equating the global intensity of the donor and recipient images. This was done by calculating the mean whole brain signal—excluding voxels falling within the lesion—of the lesioned, donor image and the mean whole brain signal of the recipient image, and multiplying the signal value at each voxel within the latter image by the ratio of the two means (Brett et al., 2001). This procedure ensured that the transplanted signal was as close as possible to what abnormal signal might have looked like had it been present in the recipient; without it, unrealistic global variations in the signal would have clouded our assessment of the algorithm's performance. We confirmed that this procedure did not artificially introduce an artefactual difference between the lesion signal and the signal in the immediate vicinity of the lesion by comparing the ratios between intralesion (5 voxels inside the lesion boundary) and perilesion (5 voxels outside the lesion boundary) signal for all original lesion images and their corresponding sets of chimaerics (paired t test p value <.01 for each set).
2.5. Manual lesion segmentation
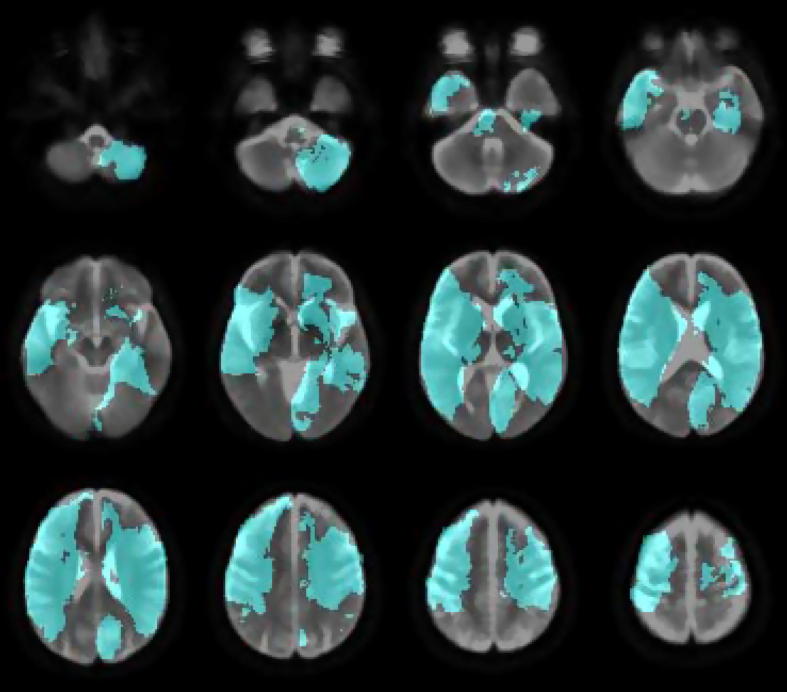
In order to evaluate our segmentation algorithm we require a “ground truth” or a standard that defines what is truly lesioned. Since even if we could have a histological reference the post-mortem specimen would be anatomically too distorted to be useable in mapping, the only standard here can be manual segmentation by eye: this is the approach every other major study in the field has taken (Brett et al., 2001; Andersen et al., 2010; Bhanu Prakash et al., 2008; Gupta et al., 2008; Hevia-Montiel et al., 2007). Each lesion was therefore segmented by hand by a trained clinician (YM) with the aid of MIPAV's gradient, magnitude and direction live-wire edge-detection tool (Barrett and Mortensen, 1997; Chodorowski et al., 2005; Falcao et al., 1998, 2000) (http://mipav.cit.nih.gov/index.php). The manual segmentation was performed on normalized versions of each image (see below). An overlap of the images is shown in Fig. 2.
Fig. 2.
Lesion coverage map. The overlay (in cyan) shows the coverage of the 38 manually segmented lesions. The underlay is the mean image created from the reference b0 dataset.
2.6. Zeta map generation
With all the images in alignment we proceeded to calculate a voxel-wise zeta map for each lesioned image (native and chimaeric). Zeta may be based on any distance measure of the signal at each voxel: here we chose the simplest: the Euclidean. So as to capture not just the signal at a specific voxel but its variation in relation to its local anatomy, we parameterized the signal at each voxel as centred within a 3 by 3 by 3 cube from the b1000 image, giving 27 dimensions for each distance measure at each voxel. Thus, the zeta map consists of a single scalar volume for each test subject where the value of each voxel is the zeta value for the vector of the signal at that location in the b1000 image and its 26 neighbours, the corresponding vectors in the normal set being the reference.
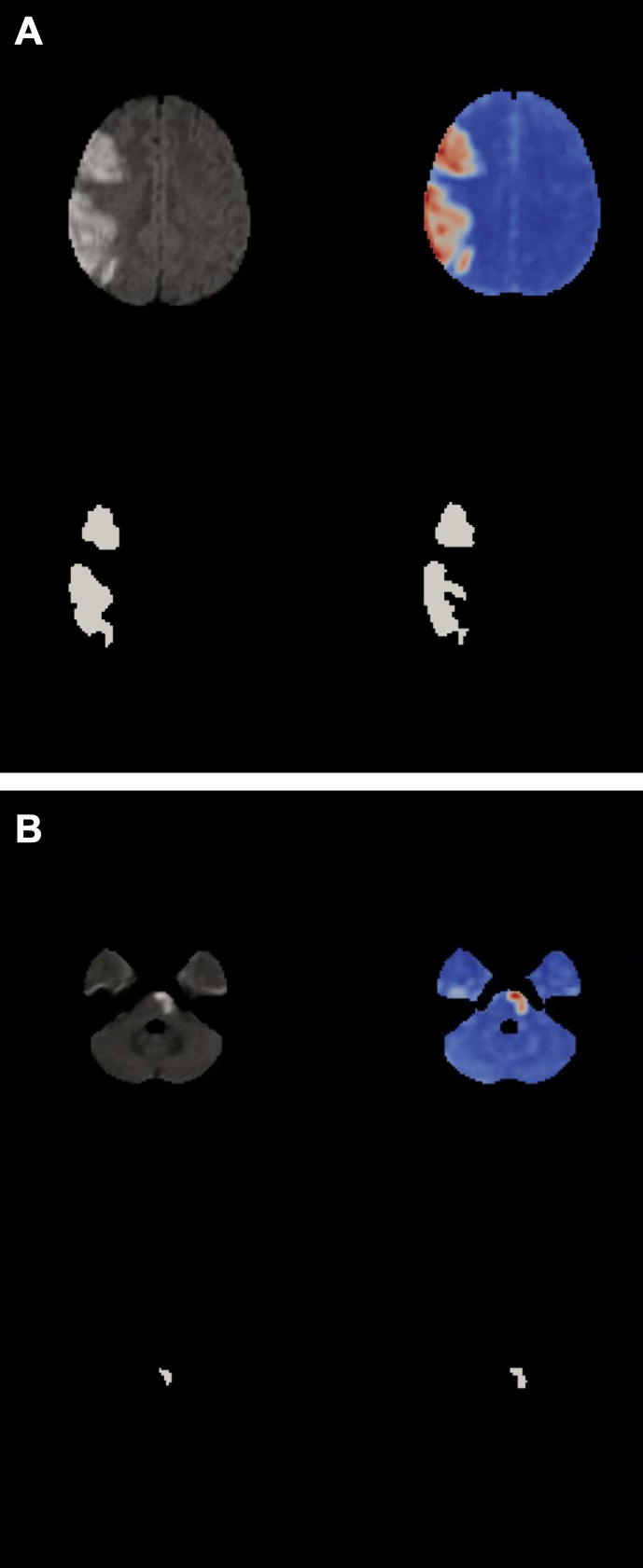
A zeta map (see Fig. 3) is real-numbered and dimensionless. One could use it directly to probe lesion–function relationships using either multivariate or mass univariate inference in the conventional way. For the purposes of validation, however, we need to compare it to manual lesion segmentation, which necessarily generates a binary mask: we must therefore find an appropriate threshold. Clearly, if our algorithm is to be unsupervised the threshold needs to be set automatically.
Fig. 3.
Zeta segmentation. All four images show the same slice from the normalized DWI brain volume of a patient with a large stroke. Diffusion-weighted image (top left). Zeta map (top right). Manual segmentation (bottom left). Thresholded zeta map (bottom right). (A). Cortical lesion. (B). Subcortical lesion. Note how the method appropriately ignores the regions of high signal artefact at the temporal poles.
2.7. Zeta map thresholding
The following procedure was used to find the optimal threshold for binarizing the zeta map into lesioned and non-lesioned tissue so as to allow comparison with the “gold standard” manual segmentation. Note that this is inevitably a heuristic process just as the manual process itself is heuristic, though of course the criterion is fixed. First, we generated a whole brain map of the reference set data only, sensitive to variations in the normal signal diversity across different parts of the brain, what we call a diversity map. This was done by iteratively calculating the zeta value of each voxel within each brain image within the reference set only, taking the remainder of the set as the reference, in essence treating each member of the set as a test volume with the remainder being the reference. This produced a set of 95 whole brain zeta maps—one map per image in the reference set—giving us a set of empirical distributions of zeta values at each voxel within the reference set. These distributions were readily parameterised as generalized extreme value distributions [equation (3)], with parameters location (μ), scale (σ), and shape (ξ) fitted using maximum likelihood estimation.
| (3) |
This diversity map allowed us to index the degree to which the normal data at each anatomical location would exhibit the characteristics of an outlier, thereby allowing better discrimination of true outliers. We thus used the diversity map to correct each test zeta image by subtracting it from the median of the diversity map, calculated independently for each voxel location.
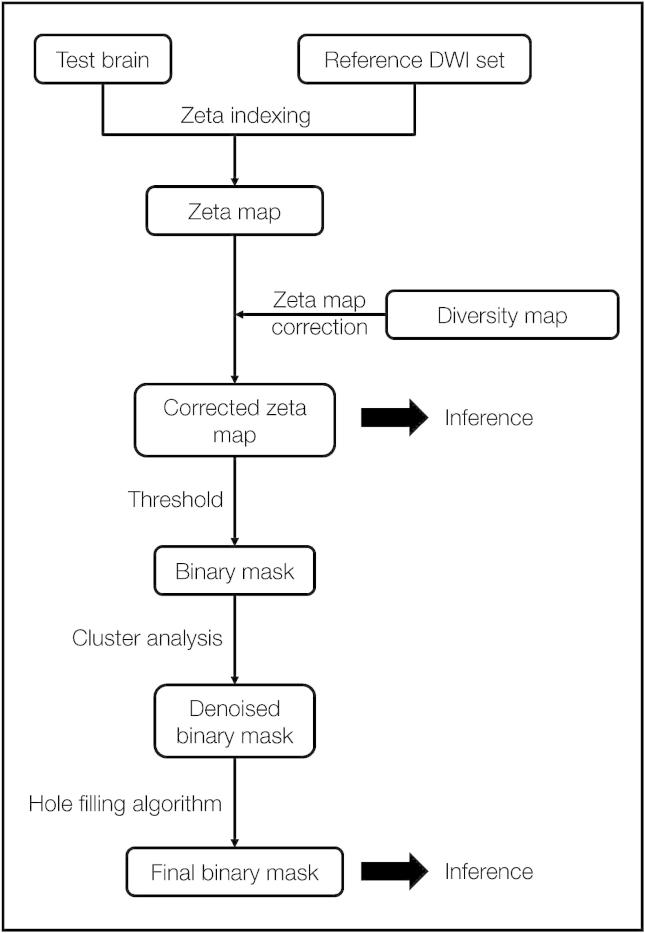
Second, this corrected zeta map was thresholded at 0, for any negative value would imply the signal at a voxel being less anomalous than that of any within the normal reference set. Third, this coarsely binarized map was then submitted to a noise removal step where clusters with fewer than 5 voxels and/or fewer than 2 voxels with a zeta score of 70% of the maximum zeta value across the brain were removed. Fourth, the surviving clusters, taken one by one, were then subjected to a further thresholding procedure, where starting at 0 and incrementally ascending the function, the zeta value was identified at which the slope of the relation between zeta and the volume of the cluster identified as anomalous at that threshold became greater than −10 voxels/zeta (for clusters smaller than 15 000 voxels) or −100 voxels/zeta (for clusters larger than 15 000 voxels). This cluster level zeta threshold was derived and applied independently for each cluster. Fifth, the denoising step above was repeated. Finally, a “hole filling” morphological operation was applied (since a completely disconnected island of normal tissue cannot possibly be functional) and linear slice artefacts were automatically removed (based on their wholly non-anatomical spatial and signal characteristics), resulting in a final binary lesion image. The procedure is illustrated in Fig. 4.
Fig. 4.
Outline of zeta segmentation method A test brain is compared with a set of reference images in a voxel-wise manner to create a zeta map. This is then corrected using a diversity map that consists of the zeta maps for each normal brain in the reference set. The corrected zeta map may be used directly for inference, however in our case it is first thresholded at 0 to create a binary mask. The resulting clusters are then assessed in turn and are either removed or modified using a heuristic. Finally a hole-filling step is applied, to create a binary mask.
2.8. Evaluation
To evaluate the performance of any lesion segmentation algorithm one requires a standard to compare it with. Ideally, this standard should be perfect. In the case of images of human brain lesions perfection is not possible because there is normally no independent way of verifying the extent of the lesion but by the appearance of the lesion on the image alone. The standard here is therefore the manual tracing of each lesion by a trained operator: this is considered the “gold standard” in the field. What we have to determine is therefore the correspondence between two binary volume images. In line with established practice, (Anbeek et al., 2004; Shen et al., 2008; Zijdenbos et al., 1994; Dice, 1945) here we use the following summary measures,
where true positives are voxels correctly identified as lesioned, true negatives are voxels correctly identified as healthy, false positives are voxels incorrectly identified as lesioned, and false negatives are voxels incorrectly identified as healthy.
For the chimaeric images, these measures were separately obtained for each lesion and each subject. For the native images, since subject and lesion are the same no such separation can be made.
2.9. Mapping damage to the occipital lobe in stroke
To generate a map of lesions that involve the occipital lobe we processed 435 diffusion-weighted images of acute ischaemic lesions and selected from this set those that involved the occipital lobe as defined by the mask supplied with MRIcron (Brodmann areas 17, 18, 19, including underlying white matter). Involvement was defined by a minimum of 30 voxels of the lesion falling within the volume of the mask which was satisfied by 120 lesions. Summary statistics were performed in a voxel-wise manner using custom Matlab scripts, and the data was visualised with MRIcron (http://www.mccauslandcenter.sc.edu/mricro/mricron).
3. Results
3.1. Zeta evaluation
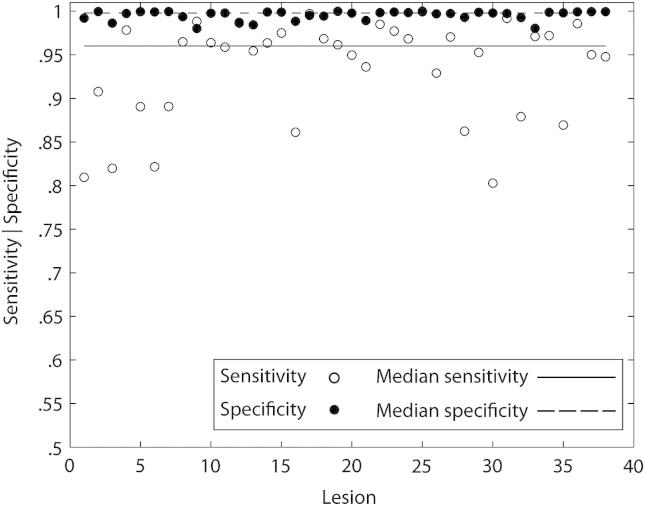
The evaluation produces a set of measures for each lesion natively, and each lesion–subject combination chimerically. In the native case, the variability of the measures can be estimated by lesion only. This analysis shows a median sensitivity of .9602, specificity of .9979 and similarity index (SI) of .7342, with corresponding standard error of the median of .0074, .0007 and .0145 respectively (Fig. 5).
Fig. 5.
Native brains performance. Plots of sensitivity and specificity scores for each native lesion. A zeta map was created for each lesion image and a thresholded version was compared against the ground truth defined by manual segmentation. Note that the median sensitivity (dotted line) and specificity (solid line) for the 38 native lesions are high at .9602 and .9979 respectively.
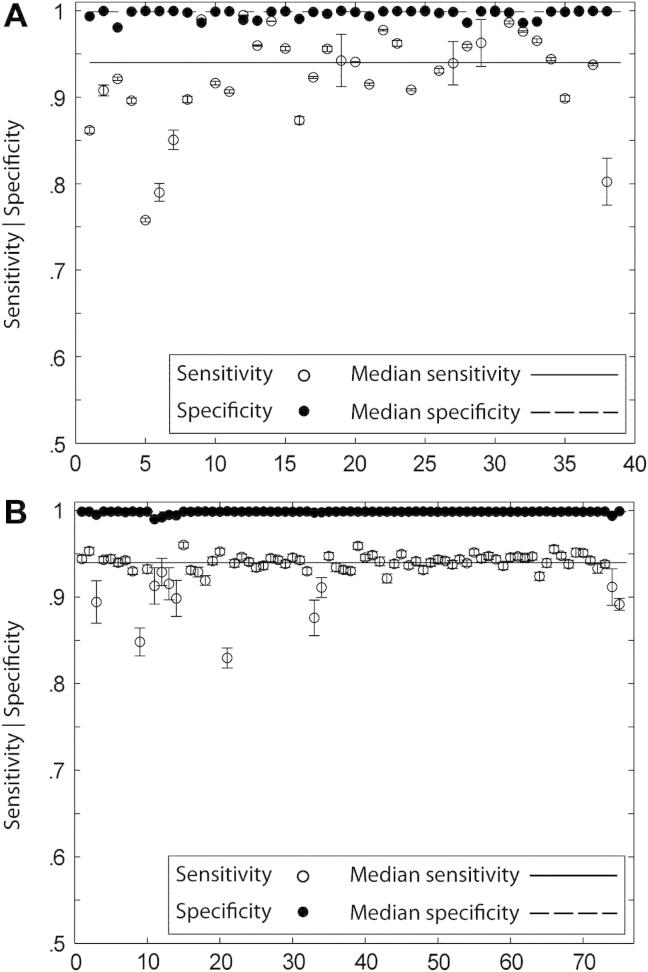
In the chimaeric case, we can obtain estimates of the variability of each measure partitioned either by lesion or by subject. In the lesion-wise analysis, there are 38 groups, corresponding to each lesion, with replications within each group corresponding to each subject. In the subject-wise analysis there are 75 groups, corresponding to each subject, with replications within each group corresponding to each lesion. This analysis shows an overall median for sensitivity of .9362, specificity of .9986 and SI of .7840. As illustrated in Fig. 6A, the range of medians for the 38 groups in the lesion-wise analysis was .7578–1.000, .9807–.9999 and .5724–.9281 for sensitivity, specificity and SI respectively. The median sensitivity, specificity and SI for the above range of values were .9400 (SE = .0069), .9988 (SE = .0002) and .7829 (SE = .0118) respectively. This narrow variability suggests a robustness of the method to variations in lesion spatial and signal characteristics. The subject-wise assessment showed median values of .9399, .9988 and .7927, with standard errors of the median now .0049, .0001 and .0084 for sensitivity, specificity and SI respectively. Fig. 6B shows the median values for the test parameters, across all lesions for each of the 75 recipient subjects. Once again, the minimal variability in the values — sensitivity .8296–.9601, specificity .9899–.9992, SI .5252– .8102 — suggests a resistance to noise and artefact. Finally the total computation time required to process a test brain image—spatially normalize the brain volume, create a zeta indexed map and segment into a binary volume—was in the order of 8 min.
Fig. 6.
Chimaeric brains performance. (A). Segmentation performance (lesion-wise). Plots of median sensitivity, specificity and SI for each lesion calculated using all 2850 chimaeric lesions, with each set containing 75 brain volumes. The error bars are standard errors of the median. Note that both sensitivity and specificity vary little across the 38 lesions. (B). Segmentation performance (subject-wise). Plots of median sensitivity, specificity and SI for each subject calculated using all 2850 chimaeric lesions, with each set containing 38 brain volumes. The error bars are standard errors of the median. Note that both sensitivity and specificity vary little across the 38 lesions, illustrating the robustness of the method to variations in normal signal and artefact.
3.2. Occipital lobe map
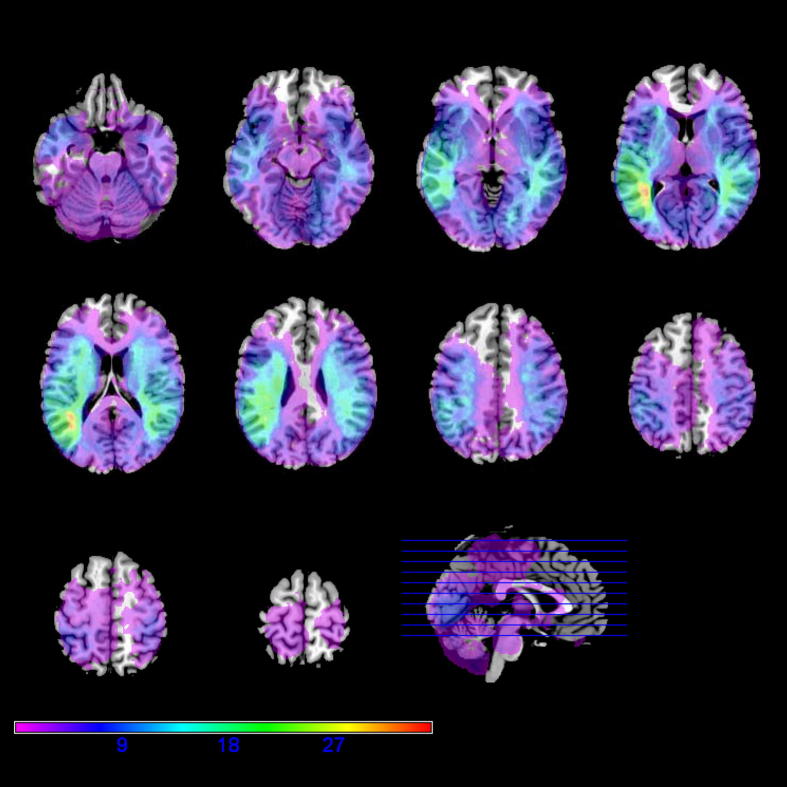
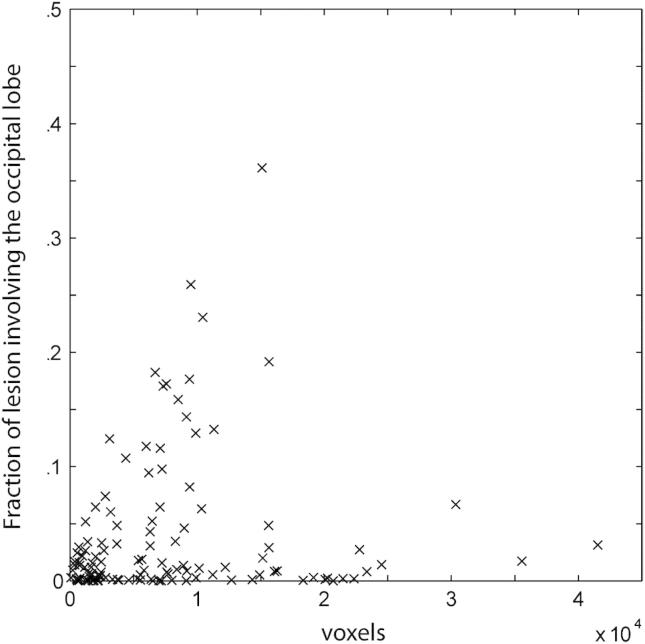
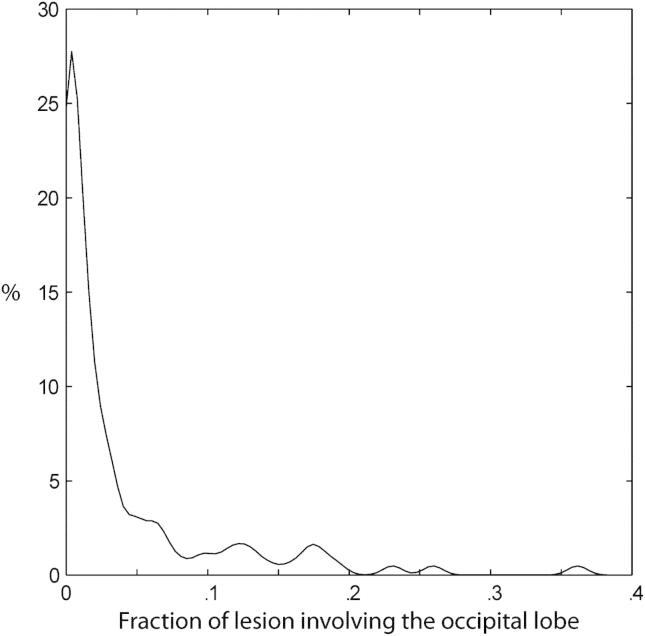
Fig. 7 shows the frequency distribution of damage in patients where the occipital lobe is affected within our dataset. Note that areas remote from the occipital lobe are frequently coincidentally damaged, and that the defining border—between occipital and other areas—is not clearly reproduced in the map. This has implications for those wishing to use lesion-mapping so as to isolate functions peculiar to the occipital lobe. So as to clarify the nature of this effect we calculated the percentage of the total volume of each lesion involving the occipital lobe at the set criterion (30 voxels or more) as a function of lesion volume (Fig. 8). Note that no lesion fell wholly within the occipital lobe and that smaller lesions were not more likely to be confined to the occipital lobe than larger ones. Indeed, the distribution of fractional occipital volume for lesions that involve the occipital lobe (Fig. 9) shows that the vast majority of lesions affect other areas preferentially. A four-dimensional (4D) version of the map (incorporating the subject dimension), allowing researchers to determine the resolvability of areas of specific interest to them within the occipital lobe can be obtained from the authors on request.
Fig. 7.
Overlay map of 120 lesions involving the occipital lobe. An overlay map for 120 lesioned brain volumes was created using a minimum involvement of 30 voxels within the occipital lobe as a selection criterion. The peak overlap was 35 lesions. The underlay is MRIcron's standard normalised colin brain.
Fig. 8.
Fraction of lesion volume involving the occipital lobe versus total lesion volume. The fraction of the lesion volume that occupies the occipital lobe is plotted as a function of the total lesion volume for each lesion. It can be seen that smaller lesions were not more likely to be confined to the occipital lobe than larger ones.
Fig. 9.
Kernel smoothing (KS) density plot for the fraction of lesion volume occupying the occipital lobe. Density plot of the fractional occipital involvement for all 120 lesions affecting the occipital lobe. The density was calculated using a kernel density estimate with a normal kernel of width .0069.
4. Discussion
We have proposed a simple, general, unsupervised method for segmenting brain lesions derived from a recently-described measure of anomaly and theoretically applicable where a reference set of normal data is available. Evaluation of its fidelity against manual segmentation in the context of diffusion-weighted imaging of ischaemic lesions has shown good performance across a range of subjects and lesion parameters; indeed no better results have been reported for diffusion-weighted imaging in stroke. The method is theoretically easy to adapt to other lesion types and imaging modalities, either alone, or in multispectral combination, and creates the possibility of high-throughput, fully-automated image processing pipelines for conducting large scale lesion–function studies. Here we consider the advantages, and disadvantages of the new method.
4.1. Advantages
First, we have shown that the performance metrics of zeta segmentation exceed those of other published algorithms for diffusion-weighted imaging, approaching the current gold standard—manual segmentation—as closely as one could reasonably expect of any automated algorithm (Table 1). Critically, there is little variability across subjects and lesions within which a bias could conceivably emerge, indeed less variability than one typically finds between observers (Fiez et al., 2000). Clearly, since manual segmentation is the gold standard here we cannot conclude that zeta is better than manual segmentation but it may be more consistent.
Table 1.
Descriptive statistics of stroke lesion segmentation results on diffusion-weighted MR images.
| Author | Sensitivity (%) |
Specificity (%) |
Similarity index |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Central tendency | Max | Min | Central tendency | Max | Min | Central tendency | |
| This study | 100.0 | 80.29 | 96.02 | 99.98 | 98.02 | 99.79 | .90 | .41 | .73 |
| (Bhanu Prakash et al., 2008) | 99.92 | 13.48 | 72.70 | 100.0 | 97.48 | 99.66 | .96 | .22 | .67 |
| (Gupta et al., 2008) | – | – | 79.30 | – | – | 99.30 | – | – | .676 |
| (Hevia-Montiel et al., 2007) | – | – | – | – | – | – | .825 | .291 | .538 |
Second, the naturally adaptive nature of the core anomaly metric theoretically allows zeta segmentation to handle highly heterogeneous data, adapting to any idiosyncrasy of a particular sequence, in our case with the prominent regional artefact seen on diffusion-weighted imaging. Zeta is able to distinguish artefactually high signal in such areas from true lesion signal elsewhere.
Third, zeta segmentation can be applied to any dataset without prior knowledge of the spatial or signal features of the lesions. It requires no priors for the number of lesions, their pattern of distribution, their signal intensity, or other features automated segmentation algorithms frequently demand from the user. Since lesions are both relatively rare—and so heterogeneous that their characteristics cannot easily be parameterized—it is advantageous that the method does not require information that is difficult or impossible to acquire.
Fourth, the high-dimensional nature of zeta makes it relatively easy to incorporate local anatomical information in the decision whether or not to label a voxel as abnormal by deriving the anomaly value not only from the signal at each voxel but also from voxels that are anatomically adjacent. The method thus becomes sensitive to variations in the local pattern of the signal, not just its point value, just as a human operator would naturally perform the task.
Fifth, zeta segmentation can easily be made multispectral: all that is required is for the different imaging modalities to be in spatial register. Since co-registering different modalities of a single subject is generally substantially easier than co-registering a single modality to a standard template this is simple to implement. For example, in the case of stroke it is possible to compensate for signal drop out in older lesions by adding another modality, such as a T2* sensitive sequence, in the distance matrix. The anomaly of each point will then be calculated on the basis of both sequences. Indeed, the only limits to the number of modalities one can add are computational, and these are likely to be modest.
Sixth, zeta segmentation naturally produces a real-numbered image where the anomaly of each voxel is given a continuous index. Since there are rarely any physiological grounds for drawing a sharp threshold at which neural tissue ceases to be active this seems to us a more appropriate instrument than any kind of binary measure. The zeta map can be directly used in making lesion-outcome inferences or relating patterns of damage to other factors of interest.
Seventh, zeta has only one parameter to adjust, the size of the clique, k. The lower the value of k the smaller the scale of signal inhomogeneity to which the algorithm is sensitive. We have not found a need to explore a wide range of k, but if this is necessary a univariate search would be quick and simple to implement. It is also theoretically possible to adjust k for each voxel independently in response to sequence-specific voxel-wise variations in the pattern of inhomogeneity, perhaps because of distortion or artefact. If binary maps are required other parameters come into play depending on the chosen heuristic for thresholding; this is not necessary if the zeta maps are used directly, as we would suggest is the best approach. Finally, zeta is computationally economical, taking approximately 8 min per image running on commodity hardware.
4.2. Disadvantages
First, our method may be taken to assume that there is a monotonic relation between signal abnormality in a region and the probability or degree of dysfunction. Naturally, it may not be so, but until we have an independent means of establishing the link between physiology and the MRI signal in a given sequence, the signal intensity is all we have. Lesion segmentation is a segmentation of images, not of the brains they imperfectly reflect. This deficit is therefore common to all segmentation algorithms.
Second, the zeta anomaly score is a continuous variable with no a priori criterion on which one could discretize it. Where binary maps are required a heuristic method of selecting a threshold is necessary. However, the performance of the heuristic we have adopted here is close to that of a trained operator, whose one criterion is by its very nature heuristic. Whether it would also do so for other modalities is a matter to be established empirically. Given the nature of the zeta score, it is to be expected that data with similar lesion contrast-to-noise ratios would perform similarly, but naturally this is not something that can be guaranteed. Although binarized data simplifies the business of inference – labelling every part of the brain as either completely lesioned or completely healthy – it involves assumptions that are neither justified empirically nor plausible a priori. While the CSF-filled centre of a chronic lesion clearly cannot have any function whatsoever, there is no reason to suppose that our arbitrary labelling of the margins of the lesion inevitably corresponds to a critical level of deterioration of physiological function, at least not for a great many lesions. Indeed, the habit of using discrete maps is arguably an artefact of the traditional way of segmenting lesions – by hand-drawn line. In any event it is a feature of the general approach to making inferences using lesions in the brain, not of this particular method.
Third, in common with any voxel-wise algorithm, zeta segmentation relies on the images already being spatially in register. Until recently, this was a major obstacle because without knowledge of the spatial characteristics of the lesion it is difficult to minimize its impact on the normalization process. If the normalization is imperfect, so necessarily will be any subsequent operation. However, SPM5's combined normalization and segmentation routine has been shown successfully to overcome this problem (Crinion et al., 2007; Andersen et al., 2010). Critically, that study used images for normalisation with very strong lesion contrast, maximally testing the algorithm's capacity to deal with lesioned images, and so one would expect their findings to extend to other modalities. The improvement in performance is roughly four times that of the preceding gold standard (cf. Brett et al., 2001), resulting in very small error values per voxel. One can further minimize the impact of this problem by deriving the normalization parameters from a separate imaging sequence with low lesion contrast, as we have done here, and as we suggest is the theoretically optimal approach.
Fourth, as with other voxel-wise methods, “islands” of normal tissue completely disconnected from the rest of the brain by damaged tissue will nonetheless be scored as normal. While in the special case of completely surrounded islands this is easily dealt with by the simple—hole-filling—morphological operation we employ here, it would be difficult to construct a method that deals robustly with intermediate cases. Once again, this is not something that any automated algorithm could easily solve without detailed knowledge of the connectivity of each brain area and the location of each connecting tract: information that we do not yet have to any degree of precision. Rather than making ad hoc decisions in each particular case – as is implicit in manual segmentation – it is perhaps best not to attempt an automated (or indeed manual) solution to this problem. Given that most lesions are more or less ellipsoidal, any distortion resulting from such effects is likely to be of relatively minor importance.
Fifth, zeta requires a set of normal images to use as a standard reference. While the relatively modest size employed here appears to be sufficient, this may not be so for other modalities and lesion types. Clearly, the performance of the algorithm will be dependent on how closely the standard set is matched to the test images: ideally, the only difference between them should be the presence or absence of lesions of the type being sought. A researcher considering our approach has two choices: either to use the standard reference set (which can be obtained from the authors) or to create a local reference set derived from normal images taken on the same scanner. These do not need to be of normal subjects but merely of patients without demonstrable acute ischaemic lesions. Indeed, it would be desirable to choose a reference cohort that is matched to the test population in all respects except the presence of acute ischaemic lesions, following the basic principles of “control” selection in experiments generally.
4.3. The pattern of ischaemic damage to the occipital lobe
We have used the new method to generate a probabilistic map of damage to the brain whenever the occipital lobe is affected. The map shows that isolated damage to the occipital lobe is rare, and that coincident damage to neighbouring areas makes the task of dissociating their function from that of occipital cortex easier for some than for others. We have provided a map that allows researchers to determine their likely ability to dissociate a given neighbouring area in a lesion-mapping study.
5. Conclusion
We have devised a simple unsupervised lesion segmentation algorithm based on zeta, a recently-described anomaly score. The algorithm places minimal demands on the experimenter and the data, and has wide potential applicability. Tested against a dataset of vascular lesions captured by DWI, it compares favourably against manual segmentation across a range of lesion sizes, locations and morphologies, and exceeds the performance of any other published algorithm. We have applied the algorithm to a set of images of vascular injury involving the occipital lobe, and derived a probabilistic map showing the resolvability of regions within occipital cortex from its neighbours.
A MATLAB (MATLAB 7.11. The MathWorks Inc. Natick, MA, 2000) implementation of the algorithm, including a reference dataset for DWI, is available from the authors on request.
Role of funding source
This work is supported by the Wellcome Trust.
References
- Anbeek P., Vincken K.L., van Osch M.J.P., Bisschops R.H.C., van der Grond J. Probabilistic segmentation of white matter lesions in MR imaging. NeuroImage. 2004;21(3):1037–1044. doi: 10.1016/j.neuroimage.2003.10.012. [DOI] [PubMed] [Google Scholar]
- Andersen S.M., Rapcsak S.Z., Beeson P.M. Cost function masking during normalization of brains with focal lesions: Still a necessity? NeuroImage. 2010;53(1):78–84. doi: 10.1016/j.neuroimage.2010.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner J., Friston K. Multimodal image coregistration and partitioning – A unified framework. NeuroImage. 1997;6(3):209–217. doi: 10.1006/nimg.1997.0290. [DOI] [PubMed] [Google Scholar]
- Ashburner J., Friston K. Nonlinear spatial normalization using basis functions. Human Brain Mapping. 1999;7:254–266. doi: 10.1002/(SICI)1097-0193(1999)7:4<254::AID-HBM4>3.0.CO;2-G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett W.A., Mortensen E.N. Interactive live-wire boundary extraction. Medical Image Analysis. 1997;1(4):331–341. doi: 10.1016/s1361-8415(97)85005-0. [DOI] [PubMed] [Google Scholar]
- Bergeest J.P., Jager F.A. Bildverarbeitung für die Medizin 2008: Algorithmen Systeme Anwendungen Proceedings des Workshops vom 6. bis 8. Informatik aktuell Springer; Berlin Heidelberg: 2008. Comparison of five methods for signal intensity standardization in MRI; pp. 36–40. April 2008 in Berlin. [Google Scholar]
- Bhanu Prakash K.N., Gupta V., Jianbo H., Nowinski W.L. Automatic processing of diffusion-weighted ischemic stroke images based on divergence measures: Slice and hemisphere identification, and stroke region segmentation. International Journal of Computer Assisted Radiology and Surgery. 2008;3(6):559–570. [Google Scholar]
- Brett M., Leff A.P., Rorden C., Ashburner J. Spatial normalization of brain images with focal lesions using cost function masking. NeuroImage. 2001;14(2):486–500. doi: 10.1006/nimg.2001.0845. [DOI] [PubMed] [Google Scholar]
- Chodorowski A., Mattsson U., Langille M., Hamarneh G., Fitzpatrick J.M., Reinhardt J.M. Color lesion boundary detection using live wire. Proceedings of SPIE. 2005;5747:1589–1596. [Google Scholar]
- Cover T., Hart P. Nearest neighbor pattern classification. Information Theory, IEEE Transactions. 1967;13(1):21–27. [Google Scholar]
- Crinion J., Ashburner J., Leff A., Brett M., Price C., Friston K. Spatial normalization of lesioned brains: Performance evaluation and impact on fMRI analyses. NeuroImage. 2007;37(3):866–875. doi: 10.1016/j.neuroimage.2007.04.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dice L.R. Measures of the amount of ecologic association between species. Ecology. 1945;26(3):297–302. [Google Scholar]
- Falcao A.X., Udupa J.K., Miyazawa F.K. An ultra-fast user-steered image segmentation paradigm: Live wire on the fly. Medical Imaging, IEEE Transactions. 2000;19(1):55–62. doi: 10.1109/42.832960. [DOI] [PubMed] [Google Scholar]
- Falcao A.X., Udupa J.K., Samarasekera S., Sharma S., Hirsch B.E., Lotufo R.A. User-steered image segmentation paradigms: Live wire and live lane. Graphical Models and Image Processing. 1998;60(4):233–260. [Google Scholar]
- Fiez J.A., Damasio H., Grabowski T.J. Lesion segmentation and manual warping to a reference brain: Intra-and interobserver reliability. Human Brain Mapping. 2000;9(4):192–211. doi: 10.1002/(SICI)1097-0193(200004)9:4<192::AID-HBM2>3.0.CO;2-Y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K.J., Ashburner J., Frith C.D., Poline J.B., Heather J.D., Frackowiak R.S.J. Spatial registration and normalization of images. Human Brain Mapping. 1995;3:165–189. [Google Scholar]
- Gupta V., Bhanu Prakash K.N., Nowinski W.L. Towards discrimination of infarcts from artifacts in DWI scans. International Journal of Computer Assisted Radiology and Surgery. 2008;2(6):385–395. [Google Scholar]
- Harmeling S., Dornhege G., Tax D., Meinecke F., Muller K.-R. From outliers to prototypes: Ordering data. Blind Source Separation and Independent Component Analysis. 2006;69(13–15):1608–1618. [Google Scholar]
- Hevia-Montiel N., Jimenez-Alaniz J.R., Medina-Banuelos V., Yanez-Suarez O., Rosso C., Samson Y. Robust nonparametric segmentation of infarct lesion from diffusion-weighted MR images. EMBS 2007–29th Annual International Conference of the IEEE. 2102–2105. 2007 doi: 10.1109/IEMBS.2007.4352736. [DOI] [PubMed] [Google Scholar]
- Kriegeskorte N., Goebel R., Bandettini P. Information-based functional brain mapping. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(10):3863–3868. doi: 10.1073/pnas.0600244103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lao Z., Shen D., Liu D., Jawad A.F., Melham E.R., Launer L.J. Computer-assisted segmentation of white matter lesions in 3D MR images using support vector machine. Academic Radiology. 2008;15(3):300–313. doi: 10.1016/j.acra.2007.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nachev P., Coulthard E., Jager H.R., Kennard C., Husain M. Enantiomorphic normalization of focally lesioned brains. NeuroImage. 2008;39(3):1215–1226. doi: 10.1016/j.neuroimage.2007.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nachev P., Husain M. Space and the parietal cortex. Trends in Cognitive Sciences. 2007;11(1):30–36. doi: 10.1016/j.tics.2006.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyúl L.G., Udupa J.K. On standardizing the MR image intensity scale. Magnetic Resonance in Medicine. 1999;42(6):1072–1081. doi: 10.1002/(sici)1522-2594(199912)42:6<1072::aid-mrm11>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- Prastawa M., Bullitt E., Ho S., Gerig G. A brain tumor segmentation framework based on outlier detection. Medical Image Analysis. 2004;8(3):275–283. doi: 10.1016/j.media.2004.06.007. [DOI] [PubMed] [Google Scholar]
- Rieck K., Laskov P. Detecting unknown network attacks using language models. Lecture Notes in Computer Science. 2006;4064:74–90. [Google Scholar]
- Ripollés P., Marco-Pallarés J., de Diego-Balaguer R., Miro J., Falip M., Juncadella M. Analysis of automated methods for spatial normalization of lesioned brains. NeuroImage. 2012;60(2):1296–1306. doi: 10.1016/j.neuroimage.2012.01.094. [DOI] [PubMed] [Google Scholar]
- Seghier M.L., Ramlackhansingh A., Crinion J., Leff A.P., Price C.J. Lesion identification using unified segmentation–normalisation models and fuzzy clustering. NeuroImage. 2008;41(4):1253–1266. doi: 10.1016/j.neuroimage.2008.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen S., Szameitat A.J., Sterr A. VBM lesion detection depends on the normalization template: A study using simulated atrophy. Magnetic Resonance Imaging. 2007;25(10):1385–1396. doi: 10.1016/j.mri.2007.03.025. [DOI] [PubMed] [Google Scholar]
- Shen S., Szameitat A.J., Sterr A. Detection of infarct lesions from single MRI modality using inconsistency between voxel intensity and spatial location: A 3-D automatic approach. Information Technology in Biomedicine, IEEE Transactions. 2008;12(4):532–540. doi: 10.1109/TITB.2007.911310. [DOI] [PubMed] [Google Scholar]
- Shen S., Szameitat A.J., Sterr A. An improved lesion detection approach based on similarity measurement between fuzzy intensity segmentation and spatial probability maps. Magnetic Resonance Imaging. 2010;28(2):245–254. doi: 10.1016/j.mri.2009.06.007. [DOI] [PubMed] [Google Scholar]
- Zijdenbos A.P., Dawant B.M., Margolin R.A., Palmer A.C. Morphometric analysis of white matter lesions in MR images: Method and validation. Medical Imaging, IEEE Transactions on. 1994;13(4):716–724. doi: 10.1109/42.363096. [DOI] [PubMed] [Google Scholar]