Game theory in the death galaxy: interaction of cancer and stromal cells in tumour microenvironment

Abstract

Preventing relapse is the major challenge to effective therapy in cancer. Within the tumour, stromal (ST) cells play an important role in cancer progression and the emergence of drug resistance. During cancer treatment, the fitness of cancer cells can be enhanced by ST cells because their molecular signalling interaction delays the drug-induced apoptosis of cancer cells. On the other hand, competition among cancer and ST cells for space or resources should not be ignored. We explore the population dynamics of multiple myeloma (MM) versus bone marrow ST cells by using an experimental microecology that we call the death galaxy, with a stable drug gradient and connected microhabitats. Evolutionary game theory is a quantitative way to capture the frequency-dependent nature of interactive populations. Therefore, we use evolutionary game theory to model the populations in the death galaxy with the gradients of pay-offs and successfully predict the future densities of MM and ST cells. We discuss the possible clinical use of such analysis for predicting cancer progression.

1. Introduction

1.1. Players: cancer and stromal cells

The emergence of therapy resistance is inevitable in multiple types of cancer and significantly affects survival of cancer patients [1]. The tumour microenvironment can influence therapy efficacy because it is not merely composed of cancer cells, but also stromal (ST) cells, a key player in cancer growth and progression [2–4]. During initial treatment, ST cells suppress the apoptosis signal of cancer cells and further prolong the survival of cancer cells [5,6]. As with many cancers, multiple myeloma (MM), a cancer of plasma cells in the bone marrow, becomes resistant to therapy by communication between the MM cells and the ST cells [7,8]. The key signalling pathways in cancer–stroma communications (i.e. interleukin 6 and stromal cell-derived factor 1) have been extensively studied. However, it is challenging to extrapolate their biomolecular network to the resulting population dynamics of cancer and ST cells. Therefore, we propose to use evolutionary game theory to interpret the interactions between cancer and ST cells [9].

1.2. Evolutionary game theory 101

Evolutionary game theory has been used for modelling interacting populations in various biological networks [10]. In evolutionary game theory, the fitness depends on the population composition of various strategies or phenotypes. For a two-player game between well-mixed player α and player β, the pay-off matrix is given by

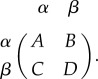1.1

When a player α encounters a player α, it receives pay-off A. A player α versus a player β receives pay-off B, whereas the other receives pay-off C. A player β versus a player β receives pay-off D. When we consider the absolute population of each type of player (α and β), then the population rate equations can be written as

1.2

1.3

where population fractions p_α = α/(α + β) and p_β = β/(α + β), and the fitness of each player is fα = Ap_α + Bp_β and f_β = Cp_α + Dp_β. If A > C and B > D, then player α dominates player β. Likewise, if A < C and B < D, then player β dominates player α. This is a classic example of frequency-dependent selection. A coordination game occurs if A > C and B < D, then both α and β are stable. In a system with more α, it will keep being dominated by α. If currently there are more β, then there will be more β. More complex dynamics occur if A < C and B > D, leading to a coexistence between the two players. In this case, a population with more α will then be dominated by β, and a population with more β will then be dominated by α (‘hawk–dove game’ [11]).

1.3. Evolutionary game theory in cancer

The evolutionary game-theoretical model has been implemented on the interaction of cancer and other cells in various stages of cancer progression. Dingli et al. [12] have explored an evolutionary game between MM cells, osteoclasts and osteoblasts, discussing disease progression and outcome of treatment. Basanta et al. [13] have used an evolutionary game to model the interaction and transformation of different stages of glioblastoma (such as glycolysis and invasive phenotypes) and predicted the stages of glioblastoma. Flach et al. [14] have studied the role of fibroblasts in melanoma growth and drug resistance from a game-theoretical point of view. However, it is very challenging to assess cancer and non-cancer populations versus time with high temporal resolution in clinical data. Because of the challenge of fitting experimental data, the current game-theoretical approach is limited in tuning parameters and discussing various scenarios in cancer progression. Even using in vitro co-culture experiments in tissue culture flasks, there is no information on complex heterogeneity in the tumour microenvironment.

1.4. Where is the game of tumour?

The tumour microenvironment highly influences the sensitivity of cancer cells to chemotherapy treatment. In solid tumours, drug diffuses into the tumour core from the blood vessels. However, the drug concentration drops significantly within hundreds of micrometres away from the blood vessels because of (i) diffusion barriers of closely packed cells, (ii) uptake by cells near the vessels, (iii) decreased activity of the drug (such as doxorubicin) owing to hypoxia, and (iv) dissociation of drug in the acidic tumour core [15,16]. The relapse usually occurs when cancer cells in the tumour core suffer less dosage of drug, survive and gradually form tumour again.

On the other hand, various cells such as tumour cells, macrophages or ST cells form highly interactive microcolonies [17]. Under different conditions, stroma can provide tumour-suppressing and tumour-promoting environments and influence cancer development and progression [17]. Combining with non-uniform distribution of drug within a tumour under treatment, one may ask whether drug distribution affects the role of ST cells on cancer survival or proliferation. Therefore, we propose to use microfluidic technology to mimic the tumour microenvironment with a drug gradient, and probe the dynamics of cancer and ST cells.

Microfluidics have been used to create versatile functions for studying various microorganisms. Microfluidics can create microfabricated landscapes, concentration gradients or dynamic switching of different chemicals [18–21]. Therefore, it is possible to reconstruct a heterogeneous microenvironment to assess the interactions such as competition or cooperation among cells. For example, a race has been held for prostate cancer cells to climb up microskyscrapers, characterizing the invasiveness of different cells [18]. The cooperation of cancer cells has been observed with the cells taking turns to lead the collective invasion through a glucose gradient across a collagen matrix [19]. Because invasion through an extracellular matrix has a metabolic cost, cancer cells tend to migrate towards a glucose-abundant region with a higher fitness and reduce the total cost via exchanging leading positions.

Likewise, a drug gradient also provides a fitness gradient for cancer cells and builds up a population gradient with time. Following a population gradient, local competition for space and metabolic resources such as glucose or oxygen drives the cancer cells to migrate towards the drug source, triggering the emergence of drug resistance [20]. The death galaxy is a microfluidic ecology with drug gradients and connected microhabitats which accelerates the emergence of antibiotic resistance in bacteria [22]. The connected microhabitats split the populations into multiple smaller populations and further increase the fixation rate of advantageous mutations [23,24]. In a death galaxy-like microenvironment with a chemotherapy gradient and microhabitats, we expect to capture the complex dynamics of MM and ST cells under simulated chemotherapy treatment.

2. Results

2.1. Cancer cells in the death galaxy

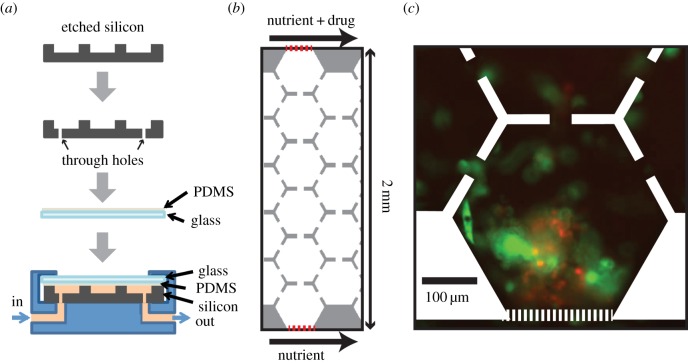
The death galaxy was originally designed for bacteria (Escherichia coli) [22,24]. Considering the difference between cancer and bacteria, such as cell size and motility (table 1), we redesign a version for cancer cells. The size of cancer cells is about 10 µm, 10 times greater than E. coli, and the motility of cancer cells is at least 100 times slower than that of E. coli. Therefore, the mammalian version is 100 µm in depth, compared with 10 µm deep for the bacterial version. The distance between neighbouring microhabitats is much shorter for the mammalian version. The mammalian version is composed of two 1 mm wide parallel channels, continuously supplying nutrient at the one side and drug plus nutrient at the other side. Between the two parallel channels, there is a culture region with arrays of hexagons (400 µm in diameter) connected to neighbouring hexagons via 40 µm channels (figure 1b), allowing cells to migrate through hexagons. The culture region and two supplying channels are separated by microslits (2.5 µm wide; figure 1b), so that cells are confined in the culture region, whereas nutrients and drug are able to diffuse in and form a linear drug gradient across the culture region.

Table 1.

Physical parameters of cancer versus bacteria.

	size (µm)	motility
Escherichia coli	1	10 µm s−1 [25]
cancer	10	10–100 µm h−1 [26]

Figure 1.

Microfluidic device configuration and micrographs of cells. (a) Fabrication and packaging process of our microfluidic device. (b) The cell region is composed of hexagonal arrays of connected microhabitats. Red dotted lines are the microposts separating the cell region from the nutrient- and drug-supplying channels. Drug gradient is constructed from the top to the bottom. (c) Image of cells after applying 6 days of doxorubicin gradient (0–2 µM 2 mm⁻¹). Red, multiple myeloma cells (8226/RFP); green, bone marrow stromal cells (HS-5/GFP).

The device structure is drawn in L-Edit, and the chromium mask is written by a laser writer (Heidelberg DWL66). We use a mask aligner (Karl Suss MA6) to expose a silicon wafer coated with a 4 µm thick photoresist (AZ4330). After development (MIF300), we use a reactive ion etcher (Samco 800) to etch 100 µm deep channels and culture region (figure 1a). We sandblast through holes in the silicon for liquid input and output (figure 1a). Then, we remove the photoresist using acetone and then oxygen plasma. The lid of the microfluidic device is made from a 1 mm thick glass slide with a 10 µm thick PDMS coating (baked at 60°C for 2 h; figure 1a). To package the device, we put the lid on top of the silicon device, use a manifold to clamp the device and introduce liquids in and out of the device (figure 1a). We coat the bottom of the silicon device with fibronectin for cell adhesion prior to loading the cells.

In the following experiments, we work with MM and bone marrow ST cells, because bone marrow cancer is incurable and the biomolecular signalling network between MM and ST is already known [7,27]. The MM cells (8226) are labelled with red fluorescent protein (RFP) and ST cells (HS-5) are labelled with green fluorescent protein (GFP). We co-culture them in the microfluidic device with a linear gradient of doxorubicin, a chemotherapeutic agent that intercalates DNA and produces oxidative stress [28], for two weeks. A representative image is shown in figure 1c, in which MM and ST cells form three-dimensional clusters near the nutrient-rich side within 6 days.

2.2. Evolutionary game theory can predict population structure

We co-culture MM and ST cells with various initial ratios and plot total populations in the death galaxy versus time in a phase portrait (figure 2). In summary, we observed

• (1) ST cells are less sensitive to drug than MM cells;

• (2) the MM cells do not survive for 5 days without ST cells in the same treatment; and

• (3) the initial ratio of MM versus ST affects the fate of MM cells: MM cells thrive if initially there were more MM than ST, but are outcompeted by ST cells if initially there were more ST than MM.

Figure 2.

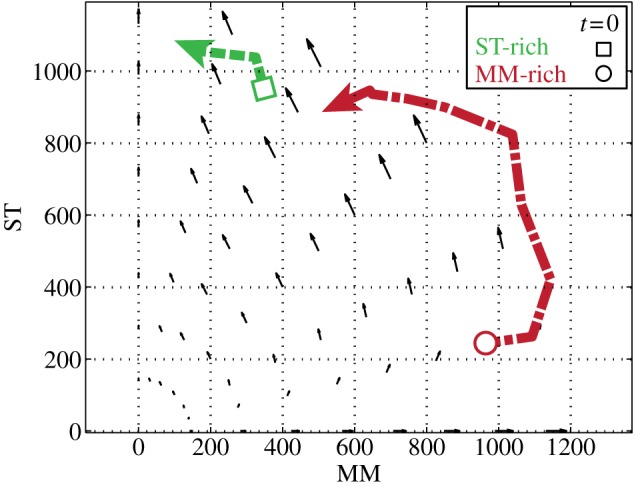
Phase portrait of total MM and ST population density (number of cells 4 mm⁻²) in the entire cell region versus time. MM and ST are co-cultured under a doxorubicin gradient from 0 to 200 nM across 2 mm. The green dotted line shows the average over five ST-rich replicates, with a square as the initial point. The red dot-dashed line indicates the average over three MM-rich replicates, with a circle showing the initial point. The counter-clockwise quivers indicate the fitness determined by slopes of semi-log growth curves in the entire cell region in the doxorubicin gradient neglecting the various drug concentrations.

The phase portrait in figure 2 shows populations of MM versus ST versus time of multiple co-culture experiments in the entire drug gradient. The MM-rich dot-dashed line (three experiments) appears red, whereas the ST-rich dotted line (five experiments) is green in figure 2. We found that a small population of ST cells desensitizes MM to drug, consistent with the previous discovery of stroma-mediated drug resistance [8]. Since we observe that the fitness of each cell depends on population fractions, evolutionary game theory is suitable for modelling this co-culture system.

We first treat the system as a well-mixed population and look for parameters of a spatial-independent evolutionary game model. Therefore, the absolute populations MM or ST can be described by the ordinary differential equations

2.1

and

2.2

where population fractions p_MM = MM/(MM + ST) and p_ST = ST/(MM + ST). If an MM cell encounters an MM cell, then it receives pay-off A; an MM cell versus an ST cell receives pay-off B. An ST cell versus an MM cell receives pay-off C; an ST cell versus an ST cell receives pay-off D. From figure 2, we can see that the system favours ST and, if initially MM is much greater than ST, there exists an anticlockwise motion towards the ST axis. Therefore, physical intuition tells us that A < C and B < D. By fitting the growth curves of each cell type with various initial population fractions, we can find the pay-offs A, B, C and D (details shown in [29,30]). The quivers in figure 2 indicate the fitness as a function of population fractions and pay-off matrix trained from our experiments (f_MM = Ap_MM + Bp_ST and f_ST = Cp_MM + Dp_ST).

2.3. Effect of drug gradient on fitness of multiple myeloma and stroma

Because doxorubicin causes DNA damage and inhibits cell proliferation [28], it affects the fitness of all cell types. A spatially resolved game-theoretical model of the system can be achieved by assuming the pay-off as a function of drug concentration. In the mammalian death galaxy with a linear drug gradient, we can simplify the system and assume the pay-off is a one-dimensional function of space (x-direction, along the drug gradient in the cell region). We also assume the pay-off is fixed with time. Here, we use finite difference time domain analysis to solve rate equations (2.1) and (2.2). We tune the pay-offs A(x), B(x), C(x) and D(x), linear functions along the x-axis, until they fit both experimental data (ST-rich and MM-rich). Note that the spatial means of the pay-offs are the same as what we used to draw the quivers in figure 2.

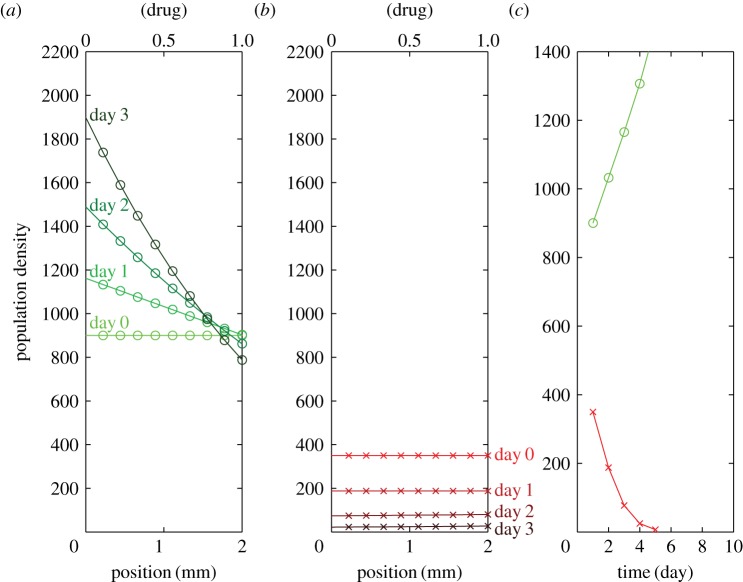
Figure 3 shows the ST-rich condition, in which the initial condition is set as a uniform distribution of 900 ST cells 4 mm⁻² versus 350 MM cells 4 mm⁻², as the starting point of the green dotted line in figure 2. The model prediction of the ST-rich population distribution within the drug gradient is shown in figure 3. The model agrees with our unpublished observations (A Wu, D Liao, G Lambert, Q Zhang, TD Tlsty, RA Gatenby, JC Sturm, RH Austin 2013) that, under ST-rich conditions, ST cells form a population gradient in response to the drug gradient, i.e. fewer cells in the regions with greater concentration of drug (figure 3a). MM cells drop monotonically with time if the initial population is much lower than that of the ST cells (figure 3b). Note that the population distribution after 3 days becomes nonlinear even if the pay-off functions are linear.

Figure 3.

Model prediction of the ST-rich population distribution within the doxorubicin gradient. (a) ST population distribution versus time (from light green to dark green). Initial condition: uniform distribution of 900 cells 4 mm⁻². (b) MM population distribution versus time (from light red to dark red). Initial condition: uniform distribution of 350 cells 4 mm⁻². (c) Total MM (red) and ST (green) population versus time.

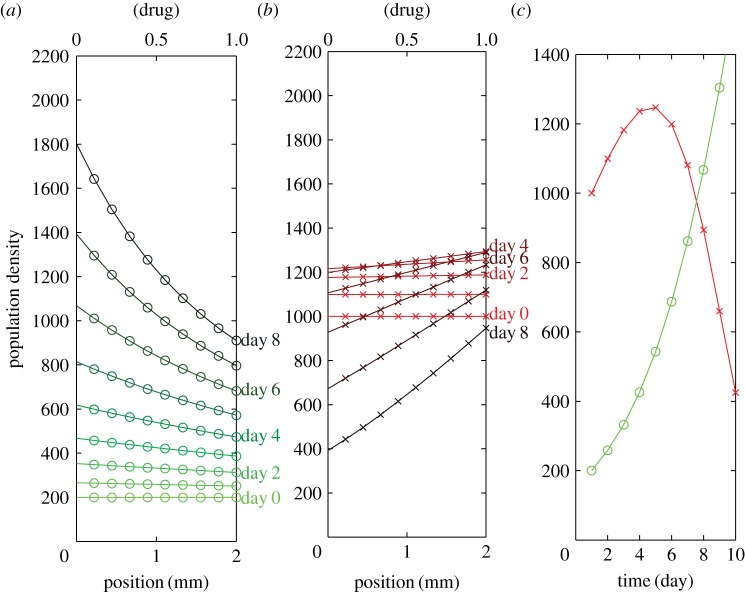
Figure 3 and figure 4 share the same linear pay-off functions, the only difference is the initial populations of MM and ST. For the MM-rich condition, the model predictions of population distribution within the drug gradient are shown in figure 4, with an initial condition of uniform distribution of 200 ST cells 4 mm⁻² versus 1000 MM cells 4 mm⁻², the starting point of the red arrow in figure 2. The model is consistent with our experiments that, under MM-rich conditions, the number of MM cells increases up to day 4 and then slowly decreases with time (figure 4b). Interestingly, one may find the MM population gradient is against the drug gradient (figure 4b). It seems that there exists competition in the region with the lower concentration of drug between MM and ST, different from our expectation that ST cells should promote cancer survival and proliferation. Therefore, ST may be cooperative or competitive depending on its population relative to the MM population and drug concentrations.

Figure 4.

Model prediction of the MM-rich population distribution within the doxorubicin gradient. (a) ST population distribution versus time (from light green to dark green). Initial condition: uniform distribution of 200 cells 4 mm⁻². (b) MM population distribution versus time (from light red to dark red). Initial condition: uniform distribution of 1000 cells 4 mm⁻². (c) Total MM (red) and ST (green) population versus time.

3. Conclusion

From a thermodynamics point of view, cell motility and drug resistance both require energy consumption. One common mechanism of drug resistance is the upregulation of the membrane drug efflux protein (P-glycoprotein 1, for example), which binds to ATP and pumps the drug molecules outside the cell membrane [31]. Under drug treatment, the environment capacity may become smaller than without drug because each cell requires more energy to be resistant or to escape [32]. Therefore, it is possible that cells were competing for nutrients in a crowded region with a lower concentration of drug.

Conventionally, one can compare the dose–response of various drugs for different types of cells in a single culture. If cancer and ST cells are independent, then applying drug to the co-culture of cancer and ST cells is a natural selection and should favour the more resistant one. However, it is more complex, because cancer cells become less sensitive to most anti-cancer drugs if they are co-cultured with ST cells [8]. The merit of evolutionary game theory is that it provides a way to model frequency-dependent selection of interactive populations—cancer and ST cells. Furthermore, if the drug concentration varies, then the pay-offs should also vary, because both players can change their strategy if they cannot bear the stress. Thus, we here simply assume the pay-offs to be a linear gradient when a linear drug gradient is applied. We found that, in regions with higher drug concentrations, ST cells grow more slowly while the most resistant cancer cells survive; this is related to the previous discovery that the most aggressive cancer cells are the least limited by environmental constraints [33].

In this paper, we introduce a simple spatial game model to describe the population dynamics of MM and ST cells in a tumour-mimicking microecology with a drug gradient. This model considers the combination of competition and cooperation among the cells as a function of drug concentration and population structure. Although we have not considered the migration of cells in the current model, we successfully predict the future densities of MM and ST cells in such a microecology. The next question is, can we apply this analytical tool to predict cancer progression in patients? If there are enough time-lapse data from medical imaging (such as magnetic resonance imaging, computed tomography and positron emission tomography) of cancer patients, it is possible to assess the dynamics of cancer and ST cells. Then, the game-theoretical model presented here would be helpful to fit the data and predict cancer progression. We hope this work can inspire more experimental validation, and eventually lead to a clinical impact on potential interventions for cancer treatment.

4. Methods

The RFP-labelled myeloma cell line (RPMI-8226/RFP) and GFP-labelled bone marrow stromal cell line (HS-5/GFP) are courtesy of the Robert H. Gatenby Laboratory from the H. Lee Moffitt Cancer Center. The cells were cultured in RPMI 1640 medium with 10% fetal bovine serum. MM and stroma cells were mixed with 33% Matrigel and dropped on the culture chamber coated by fibronectin (6 µg µm⁻²), then sealed by a PDMS-coated glass slide. The device was placed in a standard incubator under 5% CO₂ at 37°C overnight before the doxorubicin gradient was turned on. A Nikon upright microscope and Qimaging charge-coupled device camera were used to obtain images of bright field, green and red fluorescent channels.

Funding statement

The project described was supported by award U54CA143803 from the National Cancer Institute.