The effect of epistasis on sexually antagonistic genetic variation

Abstract

There is increasing evidence of segregating sexually antagonistic (SA) genetic variation for fitness in laboratory and wild populations, yet the conditions for the maintenance of such variation can be restrictive. Epistatic interactions between genes can contribute to the maintenance of genetic variance in fitness and we suggest that epistasis between SA genes should be pervasive. Here, we explore its effect on SA genetic variation in fitness using a two locus model with negative epistasis. Our results demonstrate that epistasis often increases the parameter space showing polymorphism for SA loci. This is because selection in one locus is affected by allele frequencies at the other, which can act to balance net selection in males and females. Increased linkage between SA loci had more marginal effects. We also show that under some conditions, large portions of the parameter space evolve to a state where male benefit alleles are fixed at one locus and female benefit alleles at the other. This novel effect of epistasis on SA loci, which we term the ‘equity effect’, may have important effects on population differentiation and may contribute to speciation. More generally, these results support the suggestion that epistasis contributes to population divergence.

1. Introduction

The prevalence of sexual dimorphism suggests both a longstanding history of sexually antagonistic (SA) selection and an ability of the sexes to diverge, despite a genome that is largely shared. Yet, the presence of constraints on the independent evolution of the sexes is suggested by current field studies that often point to ongoing SA selection [1]. Moreover, there is growing evidence of abundant standing genetic variance that is SA, where alleles favoured in females are disfavoured in males (reviewed in [2,3]). Evidence of substantial SA genetic variance comes from both laboratory populations [4–10] and from the wild [11–14].

The presence of SA genetic variation may at first seem difficult to reconcile with the view that the conditions for protected polymorphism of such alleles may be restrictive, requiring near equivalent selection between the two sexes [15,16], unequal dominance of alleles within the sexes [15,17,18] or X-linkage of the SA loci [19]. However, a number of recent studies suggest that the conditions for maintenance of SA variation may be less restrictive. First, Fry [17] has argued that unequal dominance effects on fitness between the sexes may be quite common, which will often lead to heterozygote advantage when fitness is summed across the sexes. Second, in the presence of unequal dominance, Arnqvist [18] demonstrated that assortative mating for fitness [20] can expand the conditions for protected polymorphism and increase the frequency of heterozygotes. Finally, even in the absence of unequal dominance or assortative mating for fitness, Patten et al. [21,22] demonstrated that the conditions for polymorphism expand when SA variation results from multiple linked loci because the effective net strength of SA selection increases.

Epistasis refers to the non-independence of genetic effects of two or more loci upon the phenotype, such that the phenotypic effect of an allele at one locus depends on the specific alleles at another locus [21–24]. Epistasis between SA loci has been widely discussed with regards to the evolution of sex chromosomes, where epistatic interactions between SA loci and sex determining loci select for reduced recombination and the origin of sex chromosomes [25–27]. Here, we suggest that epistasis between SA loci should be a general phenomenon. We expect that most traits under SA selection are highly polygenic [1,28]. Among those traits known to be under SA selection are composite traits, including locomotion [10], morphology [29,30], reproductive physiology [14] and life-history traits [31], all of which, no doubt have a polygenic basis. Given polygenic inheritance and the fact that we often expect male and female fitness functions to be concave as a result of sex-specific stabilizing selection [17], epistasis between SA loci should be pervasive. Even when allelic effects on a given trait are additive, epistasis for fitness will result when the fitness function has curvature because the recruitment of beneficial alleles at additional loci yields diminishing returns [23,32–36].

For example, imagine a single life-history trait whose value depends on two loci, and that the fitness surfaces for males and females are concave and somewhat displaced from one another (figure 1). Increases in the frequency of alleles favoured in males at one locus will bring the trait mean towards the male optimum. Because of the curvature of the fitness surfaces, however, selection in males for alleles favoured in males at the second locus will then be reduced while, at the same time, selection for the alternative alleles favoured in females will increase. Because of sexual antagonism, epistasis will be negative and selection in one locus will depend on the allele frequency at the second locus, where an increase in the frequency of male (female) benefit alleles at one locus increases the relative selection on female (male) benefit alleles at the other locus (figure 1).

Figure 1.

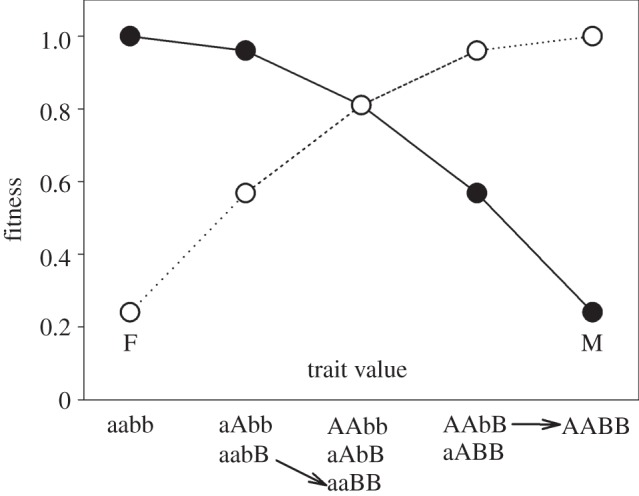
Epistasis for fitness emerges as a result of concave fitness functions even when allelic effects on traits are additive. This figure shows two bi-allelic loci that affect an arbitrary life-history trait in both sexes, where A and B are favoured in females and a and b in males. Here, allelic effects on the trait are purely additive in both loci. We make two points. First, the fitness effects of any single allelic transition will depend on the genetic background. For example, a transition from bB to BB in females (open circles) will have a much stronger fitness effect in the aa genetic background (left-hand arrow) than the AA background (right-hand arrow). Second, when selection is SA, epistasis acts to ‘even the odds’ in this genetic tug-of-war. For example, when the male benefit allele at locus A is common or fixed in a population, selection for the transition bB to BB (left-hand arrow) will be stronger in females than against this transition in males (filled circles). By contrast, when the female benefit allele at locus A is instead common or fixed in a population, selection for the same transition (right arrow) will be weaker in females than against this transition in males (filled circles). Thus, selection in one locus in a particular sex is relaxed when alleles at other loci that benefit that sex increase in frequency. The scenario visualized here represents a case where s_Am = s_Bm = s_Af = s_Bf = 0.2, h_Am = h_Bm = h_Af = h_Bf = 0.2 and ɛ_m = ɛ_f = −0.1 (table 1).

Negative frequency-dependent selection within loci can maintain genetic variation that may otherwise be lost [35–37] and therefore may play a role in the maintenance of SA genetic variation [38]. The role of positive epistasis for the simultaneous invasion of SA alleles has been explored [39–41], but the impact of negative epistasis on the maintenance of SA genetic variation has not. Here, we use individual-based simulations to explore the role that gene interactions between SA loci has on the extent and characteristics of SA genetic variation. Rather than exploring all possible scenarios, we provide an analysis of what we suggest is a set of biologically realistic situations. We focus on the effects of varying directional selection on standing genetic variation in SA loci.

2. Model

Our goal was to extend previous models aiming to understand the conditions necessary for the maintenance of SA genetic variation based on one- and two-locus population genetic models [15,17–19,21,42]. We employed forward-time individual-based simulations to examine the role of epistasis because of the difficulties involved with assessing the simultaneous effects of polygenic inheritance, recombination and epistasis in this context analytically [21,42], using the Python-based simulation program simuPOP (v. 1.1.1). This platform offers a versatile and effective modelling environment for advanced evolutionary simulations [43,44], including sexual antagonism [18]. See the electronic supplementary material for an example script.

We consider a diploid species with separate sexes where, at each of two autosomal loci with standard Mendelian inheritance and zero mutation rate, one allele is favoured by selection in males and another is favoured in females. Following Kidwell et al. [15], the most fit genotype of each sex was given the relative fitness of 1, and s_m and s_f for the two loci represent the additive selection coefficients against the less-fit homozygote in males and females, respectively. The loci- and sex-specific dominance parameters, h_m and h_f, represent the dominance of the less-fit allele in males and females, respectively, and thus refer to the dominance of different alleles in the two sexes (ranging from h = 0 (recessive) over h = 0.5 (additive) to h = 1 (dominant)). We used a multiplicative model to describe epistasis [24]. This is not only the most commonly employed population genetic model of epistasis and the one deemed most representative of natural populations [24], but it also yields fitness functions that correspond very well indeed with the biological scenario described in the introduction (figure 1). Here, epistasis was included by adding a coefficient of additive × additive epistasis, ɛ, such that the genotype-specific effects of one locus depend upon the genotype of the other. We thus assume that additive × dominance and dominance × dominance epistasis are of minor importance relative to additive × additive epistasis. The resulting sex-specific fitness matrices are given in table 1 and illustrated in figure 1 (see also the electronic supplementary material).

Table 1.

Fitness matrix for each of the nine diploid genomes in males and females under SA genetic variation, where the alleles a and b are favoured by selection in males and A and B are favoured in females, including additive × additive epistasis between the two loci. Here, h represents the dominance parameter of the less-fit allele and s the selection coefficient against the less-fit homozygote, both of which are loci- and sex-specific, and ɛ the sex-specific additive × additive epistasis coefficient. Note that forms of epistasis other than additive × additive are not considered here.

	aa	aA	AA
males
bb	1	1 − hAmsAm	1 − sAm
bB	1 − hBmsBm	(1 − hAmsAm)(1 − hBm sBm) + ɛm	(1 − sAm)(1 − hBm sBm) + 2ɛm
BB	1 − sBm	(1 − hAmsAm)(1 − sBm) + 2ɛm	(1 − sAm)(1 − sBm) + 4ɛm
females
bb	(1 − sAf)(1 − sBf) + 4ɛf	(1 − hAf sAf)(1 − sBf) + 2ɛf	1 − sBf
bB	(1 − sAf)(1 − hBf sBf) + 2ɛf	(1 − hAf sAf)(1 − hBf sBf) + ɛf	1 − hBf sBf
BB	1 − sAf	1 − hAf sAf	1

We explored two distinct forms of varying degrees of additive × additive epistasis. First, the coefficient of epistasis, ɛ, was given a fixed value ranging from 0 (no epistasis) to −0.1 (strong negative epistasis). This means that the absolute strength of the epistatic effect will be independent of the additive selection coefficients. Under such ‘absolute’ epistasis, the relative contribution of epistasis to fitness variation will thus increase as the strength of directional selection decreases. Second, the coefficient of epistasis was instead made proportional to the overall strength of additive selection, such that in each sex ɛ = ([s_A + s_B]/2) c. Here, c is a scaling coefficient ranging from 0 (no epistasis) to −1/3 (strong negative epistasis). Under such ‘relative’ epistasis, the relative contribution of epistasis to fitness variation will thus be fixed and will be independent of the additive selection coefficients.

All simulations used a stable population size of 5000 individuals and were run for 5000 generations to ensure that allele frequencies equilibrated. Points of parameter space in which at least one locus showed some polymorphism after 5000 generations were deemed to show protected polymorphism. We note here that allele frequencies stabilized after between only a few hundred and two–three thousand generations. Because of the very high dimensionality of parameter space in our models, we made two simplifying symmetry assumptions. First, we assume that the two loci ‘behave’ in a similar manner, such that they make an equal contribution to fitness variation within each sex (i.e. h_Am = h_Bm, s_Am = s_Bm, h_Af = h_Bf and s_Af = s_Bf). Second, although we allow the relative strength of directional selection to vary independently in males and females (see below), we assume that the epistatic contribution to net fitness is similar in males and females (i.e. ɛ_m = ɛ_f for absolute epistasis and c_m = c_f for relative epistasis).

We focus here on the results of 3 × 4 × 2 × 3 (i.e. 72) distinct sets of conditions. First, previous research has shown that the pattern of sex-specific dominance is critical for the zone of protected polymorphism in autosomal SA loci [15,17,18]. We thus explored the dynamics under three levels of sex-specific dominance (h = 0.2, 0.35 and 0.5 in both sexes) (see the electronic supplementary material for h = 0.8). Second, we assessed the effects of no (ɛ = 0/c = 0), weak (ɛ = −0.01/c = −0.033), intermediate (ɛ = −0.05/c = −0.166) and strong (ɛ = −0.1/c = −0.33) epistasis. Third, we compared the effects of absolute and relative epistasis (see above). Fourth, as the rate of recombination affects invasion criteria of epistatically interacting SA alleles [40], we investigated the dynamics under no (r = 0), low (r = 0.05) and maximally high (r = 0.5) recombination rates. The cases of r = 0 and r = 0.5 are given in the electronic supplementary material.

For each of the 72 sets of conditions, we ran 3000 independent replicate simulations. Previous research has shown that the relative strength of directional selection is key [15,17–19,21,42]. We thus explored the sex-specific selection space by drawing selection coefficients (s) at random from a standard uniform distribution ranging from 0 to 0.3 in each individual simulation. This focus on relatively weak selection [15] is motivated by the fact that phenotypic SA selection in the wild is typically fairly weak [1,28,45]. Finally, to ensure that our results were not affected by varying starting frequencies of alleles, the starting frequencies of the a and b alleles were drawn independently at random from a standard uniform distribution ranging from 0.05 to 0.95 in each individual simulation.

3. Results and discussion

As originally pointed out by Kidwell et al. [15], the pattern of sex-specific dominance is the most important determining factor for protected polymorphism in autosomal SA alleles [17]. Our analyses demonstrate that this is generally true also for epistatically interacting SA loci: cases where the most beneficial allele in each sex is also dominant in that sex show polymorphism in SA alleles over a much wider range of selection intensities (left column in figures 2 and 3). In the absence of epistasis (ɛ = 0/c = 0), polygenic inheritance of SA genetic variation per se led to a slightly expanded region of polymorphism at both loci (black wedge) compared with the single locus case (cf. top row 1 in figures 2 and 3 with Kidwell et al. [15]). This effect was also observed in the two-locus models of Patten et al. [21,48] and in the multi-locus models of Vellnow [46] and is no doubt due to the fact that selection across several linked loci results in an increased effective net strength of SA selection under a multiplicative fitness model [21,42]. Consequently, the variance-promoting effect of ‘heterozygote advantage’ in harmonic mean fitness across the two sexes [15,17,18] is strengthened. Similar to the one locus case, beneficial alleles in the sex under stronger selection will fix when net selection intensities become sufficiently imbalanced between the sexes.

Figure 2.

The effect of absolute epistasis on SA genetic variation. Each plot illustrates the effects of varying the strength of selection in both sexes (range of s = 0–0.3 in both sexes) for a recombination rate r = 0.05, under a given set of dominance and epistasis. Each point within plots represents the outcome of a single simulation, where the colour denotes different allelic states at the end of the run (black, polymorphism at both loci; blue, fixation of the male benefit allele in both loci; red, fixation of the female benefit allele in both loci; grey, loss of polymorphism in one locus and polymorphism at the other locus; light and dark brown, fixation of alleles in the male benefit state in one locus and the female benefit state in the other locus at alternate loci (aaBB and AAbb)). See text, table 1 and figure 1 for further details of the simulations.

Figure 3.

The effect of relative epistasis on SA genetic variation (see figure 2 for details).

Negative epistasis had a substantial impact on the maintenance of SA genetic variation as well as on the sex-specific pattern of fixation. We distinguish three effects of the general epistatic scenario explored here. First, in general, epistasis tends to increase the diversity of equilibrium states (figures 2 and 3). In fact, under some parameters for h and ɛ/c, seven possible outcomes were observed, depending on the balance between additive selection in males and females. These are: polymorphism at both loci (black), fixation of alleles at both loci in the male benefit state (blue) or female benefit state (red), fixation of alleles in the male benefit state at one locus and polymorphism at the other locus (grey zones to the right), fixation of alleles in the female benefit state at one locus and polymorphism at the other locus (grey zones to the left) and fixation of alleles in the male benefit state at one locus and the female benefit state at the other locus (light and dark brown).

Second, when beneficial alleles show sex-specific dominance for fitness, which is arguably a biologically realistic scenario [17], negative epistasis can markedly increase parameter space under which stable polymorphism is maintained in one or both alleles. This effect is most apparent under relative epistasis (figure 3). In part, the reason for this expansion of the zone of polymorphism is that epistasis represents an additional force of selection, and the conditions for the maintenance of SA genetic variation widens with increasing strength of selection [15]. However, we also found an additional polymorphic state (grey areas) that appears between those regions where both loci are fixed for male or female benefit alleles and those where both loci are polymorphic. In this domain, one locus is fixed for the beneficial allele in the sex under stronger selection, whereas the second locus remains polymorphic. This outcome is quite intuitive. It occurs because fixation at one locus results, through negative epistasis, in increased selection on the second locus in the other sex and therefore in a greater balance in net selection between males and females. This contrasts with the classic view that stable polymorphism in SA loci requires that additive selection in the two sexes approaches equivalence [15]. The effect of negative epistasis is, in fact, negatively frequency-dependent across loci, where an increase in the frequency of beneficial alleles at one locus increases selection for beneficial alleles at the other locus in the other sex (figure 4). This additional domain of polymorphism thus represents an important novel insight. Across many epistatically interacting SA loci, evolution may proceed towards an increased balance between males and females in effective net selection on such loci (and thus the maintenance of SA genetic variation), through changes in allele frequencies and the selective fixation of some of the SA loci. A direct test of this interesting possibility, however, would require a dedicated modelling effort since it is unclear precisely how well the situation we model (two interacting and similarly behaved loci) captures the dynamics of even more complex scenarios.

Figure 4.

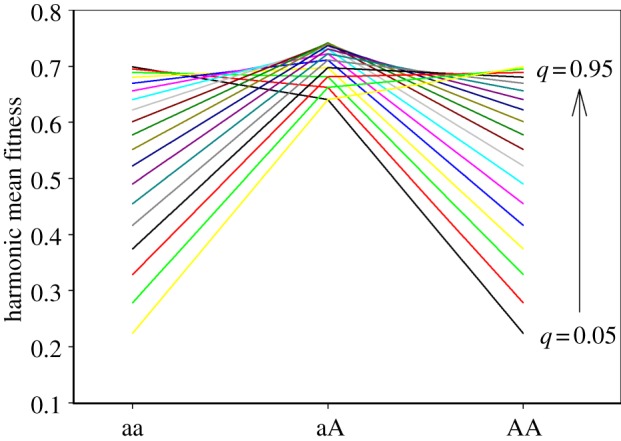
An illustration of frequency-dependent SA selection across loci under negative epistasis. Here, q denotes the frequency of the male benefit allele (b) at the B locus. The figure shows harmonic mean fitness across the two sexes (assuming Hardy–Weinberg proportions at the B locus) over the genotypes of the A locus, where a is favoured in males. As the male benefit allele at the B locus (i.e. b) increases in frequency, there is increased net selection for the female benefit allele at the A locus (i.e. A). Under intermediate frequencies, there is net balancing selection on the A locus. The scenario visualized is absolute epistasis for s_m = s_f = 0.3, h_m = h_f = 0.2 and ɛ_m = ɛ_f = −0.1.

Third, over large parts of the parameter space explored here, epistasis generated fixation of opposing male benefit/female benefit alleles at the two loci (i.e. either a and B or A and b) (see brown areas in figures 2 and 3). These sexually balanced zones emerge in different areas depending on the degree of sex-specific dominance and the type of epistasis. In the two-locus scenario modelled here, these zones often occupy a sizeable part of the selection space. Here, which of the two loci that fixed for which allele was entirely determined by the starting frequency of alleles (figure 5), illustrating the fact that selection in one locus by definition will depend upon the allele frequency at other loci under epistasis [32,47]. This sexually balanced outcome is again caused by a general and quite intuitive effect (figure 1), very similar to the grey zones discussed earlier. When, for example, the frequency of the male benefit allele in one locus increases (as a result of starting conditions, selection and/or drift), this alters selection in the other locus in two ways: selection for the male benefit allele in males is weakened, whereas selection for the female benefit allele in females is strengthened. The brown regions in figures 2 and 3 represent conditions under which such modulation of net selection does not suffice to generate a balance in net selection between males and females, leading to the fixation of opposing alleles at the two loci. In essence, an evolutionary ‘win’ at one locus for a given sex leads to an evolutionary ‘loss’ in the other locus. This interesting outcome of the SA tug-of-war between the sexes has, to our knowledge, not been observed before and we term this the ‘equity effect’.

Figure 5.

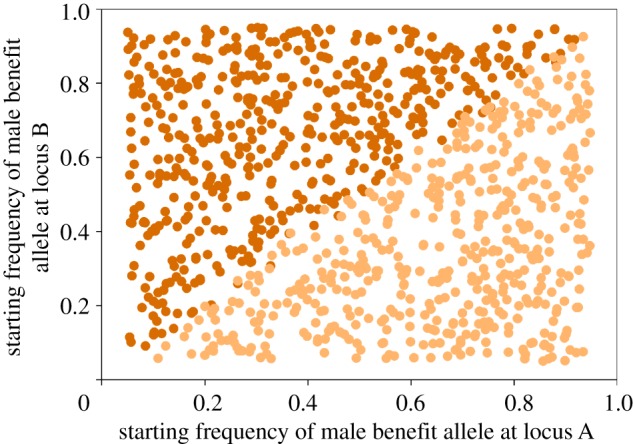
The effect of relative starting frequency of male benefit alleles on locus specific fixation, in a region of parameter space showing the equity effect (see figure 2 for colour codes). Under SA epistasis, the relative strength of net selection in males and females is affected by allele frequencies at both loci. The figure shows 1000 runs with starting frequencies drawn at random from a standard uniform distribution (0.05–0.95) and selection coefficients s_m and s_f drawn at random from a standard uniform distribution (0.0–0.15) (r = 0.05, h_m = h_f = 0.2 and ɛ_m = ɛ_f = −0.1).

The dynamics under absolute and relative epistasis differ substantially, which is unsurprising given the fact the epistatic contribution to net selection is very different under these scenarios (see the electronic supplementary material, figure S1). Which scenario is biologically generally most reasonable is debatable [35,36], but we suggest that relative epistasis should best describe the scenario we aimed to explore here. Connallon & Clark [40] showed that elevated rates of recombination reduce the probability of invasion of positively interacting SA loci, and Úbeda et al. [48] showed that recombination rate has large effects on the degree of linkage disequilibrium across non-interacting SA loci. Yet, we found that the rate of recombination had a relatively minor impact on the zone of SA polymorphism at equilibrium. Although a decreased recombination rate led to an expansion of the zone of polymorphism, in agreement with the findings of Patten et al. [21,48], this effect was very slight indeed (see the electronic supplementary material). Thus, the degree of linkage seems to have no major effects on the ultimate evolutionary fate of SA alleles across epistatically interacting loci.

It is interesting to contemplate the implications of the equity effect. First, it implies that there will be substantial variation among populations at SA loci, with alternates fixed in different populations and, consequently, pronounced interpopulation variation in SA traits. Second, gene flow across populations or within meta-populations should markedly elevate the degree of SA genetic variation and SA selection.

Interpopulation divergence is a common result of epistasis [49,50], because variation in the frequencies of any interacting alleles (due to selection or drift) in each population determines the selective consequence for other interacting alleles [51]. We have so far exemplified the scenario explored here as one where a single life-history trait is encoded by two loci. However, an alternative but entirely analogous representation is a situation where several traits are instead favoured by sex-specific selection. Imagine, for example, two sexual traits that are favoured by sexual selection in males but are costly when expressed in females, each of which is encoded by a single locus. Here, epistasis between the two SA loci will result whenever the recruitment of an additional sexual trait yields diminishing rewards to males and accelerating costs to females as a result of curved fitness surfaces (figure 1). Divergence between populations is a hallmark of sexually selected or sex-related traits, but is usually attributed to reinforcement or to differences among populations in the strength of sexual and natural selection operating upon these traits. Our analysis suggests that even in the complete absence of interpopulation differences in selection, different alleles may fix through the equity effect as a result of even relatively minor differences in allele frequencies across loci (figure 5). Such differences may result from, for example, different allele frequencies among founders or from the interaction between genetic drift and selection in small populations or during bottlenecks [41]. There is considerable evidence from population crosses that SA traits vary among populations [52], although some or all of this variation can potentially be attributable to a history of different selection regimes among populations [53], which can determine the course of SA coevolution [54,55]. Similarly, we might expect substantial interpopulation and interspecific variation in sex-biased gene expression, given that SA genes are likely to be sex-biased. Both of these patterns have been observed, primarily in male-biased genes [56–58].

Under the equity effect, SA loci will essentially remain hidden until populations are crossed to those fixed for the alternative alleles. In models with epistasis but without SA selection, crossing diverged populations often results in depressions in fitness [49,50,59]. The reason for this is that within populations, when epistasis is present, different adaptive combinations of alleles at two or more loci will evolve. When these alternative ‘coadapted gene complexes’ are crossed, heterozygotes with unfavourable combinations of alleles are created, breaking up the coadapted sets and reducing fitness (i.e. Dobzhansky–Muller incompatibilities). There would be similar effects in the cases considered here in that crossing will yield an excess of heterozygotes, at alternatively fixed loci. However, the effects on population fitness and viability are much less obvious, because some loci for some populations are fixed for male benefit alleles, and others for female benefit alleles. Production of heterozygotes will increase population fitness relative to the case where male benefit alleles are fixed, but decrease it relative to the case where female benefit alleles are fixed. Therefore, crossing may even elevate population fitness if relief from the female specific genetic load that derives from fixed male benefit alleles outweighs the deleterious effects to females from expressing heterozygotes at loci fixed for female benefit alleles, summed over multiple interacting SA loci.

The presence of interpopulation variation where alleles are fixed at alternative SA loci will contribute to speciation insofar as it contributes to population divergence, particularly in SA loci that are likely to encode for reproductive traits, which is a prerequisite for reproductive isolation [52,60–62]. Interlocus sexual conflict theory has demonstrated that the outcome of SA coevolution will vary with initial conditions and that stochastic effects, including genetic drift, should play a major role [42,63,64]. The equity effect demonstrated here adds to this general conclusion and is likely to promote divergent SA coevolution, assuming that some loci are involved in both inter- and intralocus sexual conflict, therefore contributing to population differentiation, incompatibilities and reproductive isolation. More generally, the equity effect will generate mutation-order speciation, as we expect different populations to evolve to different genetic states even under identical selective regimes [65–67] simply as a result of the order in which alleles fix across epistatically interacting SA loci.

4. Conclusion

Our results show that the incorporation of negative epistasis in a two-locus model of SA genetic variation has substantial effects on the maintenance of variation and on equilibrium conditions. In general, epistasis increases the diversity of equilibrium states for SA loci across a reasonable range of parameter space. Under a wide range of conditions, the parameter space showing polymorphism in one or both loci increases with epistasis, suggesting that epistasis may be contributing to the observed presence of segregating SA genetic variance for fitness. Finally, there were large regions of parameter space where beneficial alleles for one sex were fixed at one locus and beneficial alleles for the other sex were fixed at the second locus. Given that which locus was fixed for which alleles depended upon starting frequency, epistasis may be playing an important role in the divergence of SA traits among populations and speciation through this equity effect.

Funding statement

This work was financed by the European Research Council (to G.A.; AdG-294333), the Swedish Research Council (to G.A.; 621-2010-5266), the Canadian Natural Sciences and Engineering Research Council (to L.R.) and the Canada Research Chairs Program (to L.R.).