Experimental evolution of bet hedging under manipulated environmental uncertainty in Neurospora crassa

Abstract

All organisms are faced with environmental uncertainty. Bet-hedging theory expects unpredictable selection to result in the evolution of traits that maximize the geometric-mean fitness even though such traits appear to be detrimental over the shorter term. Despite the centrality of fitness measures to evolutionary analysis, no direct test of the geometric-mean fitness principle exists. Here, we directly distinguish between predictions of competing fitness maximization principles by testing Cohen's 1966 classic bet-hedging model using the fungus Neurospora crassa. The simple prediction is that propagule dormancy will evolve in proportion to the frequency of ‘bad’ years, whereas the prediction of the alternative arithmetic-mean principle is the evolution of zero dormancy as long as the expectation of a bad year is less than 0.5. Ascospore dormancy fraction in N. crassa was allowed to evolve under five experimental selection regimes that differed in the frequency of unpredictable ‘bad years’. Results were consistent with bet-hedging theory: final dormancy fraction in 12 genetic lineages across 88 independently evolving samples was proportional to the frequency of bad years, and evolved both upwards and downwards as predicted from a range of starting dormancy fractions. These findings suggest that selection results in adaptation to variable rather than to expected environments.

1. Introduction

Organismal persistence demands adaptation to continually varying environmental conditions. Populations may adaptively ‘track’ environmental change or, if environmental change is recurring or predictable, then adaptive phenotypic plasticity is expected to evolve. However, when environments fluctuate unpredictably, the evolution of so-called bet-hedging [1] traits is expected. Bet hedging is advantageous for the same reasons that risk-averse strategies are adopted by investors [2,3]. It is because fitness, like return on investment, is determined by a multiplicative process [4,5]—that of reproduction—and bet hedging increases the geometric-mean fitness (the nth root of the product of n fitness values) by reducing fitness variance over generations [6]. Expected fitness within generations may be ‘sacrificed’ for the geometric-mean fitness [7,8]; thus, bet-hedging strategies appear to be detrimental over the short term.

Intriguing and plausible examples of bet hedging—from heterogeneity in gene expression among genetically identical microbes [9], which is proposed to function in a malaria parasite as a hedge against unpredictable human immune response [10], to risk spreading via polyandry in female frogs [11]—are rapidly accumulating, suggesting that bet hedging may be an important and taxonomically widespread mode of response to environmental variance. However, empirical evidence for bet hedging remains scant [12]. Evidence is restricted to demonstrations of interspecific divergence [13] or population differentiation [14,15] in putative bet-hedging traits across environments that differ in predictability, or the documentation of the evolution of candidate bet-hedging traits under conditions in which they may be advantageous [16,17], with very few strong studies confirming fitness benefits of putative bet-hedging traits under fluctuating conditions [18–21]. Tests of bet hedging under field conditions are difficult because they require evaluating both environmental variance and its fitness effects over multiple generations. Furthermore, although correlational field studies are valuable, they are vulnerable to effects of uncontrolled confounding variables. A definitive test would distinguish between measures of fitness; it would ask specifically whether selection acts to increase the geometric- or arithmetic-mean fitness.

Cohen's classic model [22] of the evolution of dormancy offers an opportunity for a simple experimental test (see electronic supplementary material, figure S1) ideally suited to distinguish between measures of fitness. The model is ideal because of its simplicity: the optimal seed dormancy fraction evolves under environments that are unpredictable, but are either ‘good’ or ‘bad’. In a good year, a germinating seed survives, matures and successfully produces new seeds, whereas in a bad year, a seed that germinates will die prior to reproduction, and only dormant seeds survive. The straightforward result of the model is that, by the geometric-mean principle, dormancy fraction should evolve to equal the probability of occurrence of a bad year. By contrast, the prediction of the arithmetic-mean principle is the evolution of zero dormancy (immediate germination) under a broad range of ecological scenarios; namely if the probability of a good year is greater than 0.5. The four simplifying assumptions that make tests of Cohen's model untenable under field conditions make an experimental laboratory test feasible: environments are dichotomously ‘good’ or ‘bad’; these environments are not temporally autocorrelated; germination is not plastic to proximate environmental conditions, and thus occurs as a fixed fraction and the effect of unpredictable selection is not confounded by other potential influences on the evolution of dormancy in nature, such as density dependence [21]. An experimental selection approach to test Cohen's model [22] would obviate these difficult assumptions, and would be uniquely positioned to distinguish between the geometric- and arithmetic-mean fitness maximization principles.

The ascomycete fungus N. crassa is ideally suited to the test, and exactly parallels annual plants in relevant features: it produces ascospores with variable dormancy [23] that allow survival through conditions that are fatal to all other life stages. Whereas in angiosperms germination of non-dormant seeds is cued by appropriate conditions and dormant seeds germinate only following hostile cold or dry seasons, germination of ascospores of N. crassa is normally cued by intense heat to colonize decaying plant material following fire [24], but dormant ascospores require a second heat exposure to germinate. Heat both initiates ascospore germination and kills all life stages except ascospores that have remained dormant. This feature enables the experimental construction of sequences of good and bad environments (here referred to as ‘years’, to parallel Cohen).

In a good year, activated ascospores are allowed to complete a life cycle through to the production of new ascospores before application of a killing heat treatment; thus, dormancy would be at a selective disadvantage. In a bad year, the killing heat treatment is applied prior to successful production of new ascospores; thus, only those ascospores that remained dormant survive and are transferred to the subsequent year. The heat treatment that terminates a year also activates new or previously dormant ascospores to mark the beginning of a new year.

Dormancy fraction was allowed to evolve under five selection treatments that differed in the frequency of ‘bad’ years (0%, 25%, 30%, 40% and 50%) in 12 replicate lineages from crosses of compatible mating types from locations in Africa, Haiti and USA (table 1). It is important to note that we do not select for dormancy directly; serial transfers of standard aliquots of ascospore suspensions across years automatically contain dormant and non-dormant spores in proportion to their relative success. Thus, the crucial difference between this and previous studies is that we ask whether bet hedging evolves in response to unpredictable environments rather than asking whether a trait assumed to be bet hedging responds to selection. Five different year-type sequences (prohibiting two sequential bad years) were used for the 25–40% lines (see electronic supplementary material, table S1) to ensure that response to selection could be attributed to frequency of year type and not to specific lineages or year-type sequences. Dormancy fractions of pre- and post-selection samples were assayed simultaneously (see Material and methods).

Table 1.

Crosses used to establish selection lines.

cross no.	mating type a straina (origin)	mating type A straina (origin)
1	4832 (Eremankono, Ivory Coast)	4827 (Tiassale, Ivory Coast)
2	4712 (Leogane, Haiti)	4835 (N'Douci, Ivory Coast)
3	4712 (Leogane, Haiti)	4714 (Pescail, Haiti)
4	10654 (Franklin, Lousiana)	4837 (Sakota, Ivory Coast)
5	10654 (Franklin, Lousiana)	4711 (Haut Diquini, Haiti)
6	4712 (Leogane, Haiti)	2225 (Mauriceville, Texas)
7	4828 (Asikro, Ivory Coast)	4714 (Pescail, Haiti)
8	4828 (Asikro, Ivory Coast)	4827 (Tiassale, Ivory Coast)
9	4831 (Grabiokoko, Ivory Coast)	4834 (Issia, Ivory Coast)
10	4831 (Grabiokoko, Ivory Coast)	4837 (Sakota, Ivory Coast)
11	8876 (Franklin, Lousiana)	4837 (Sakota, Ivory Coast)
12	mass matingb

^aStrain number from Fungal Genetics Stock Center (FGSC), University of Missouri, Kansas City, MO.

^bCo-inoculation of ascospores from each of the 11 crosses.

2. Material and methods

Wild-collected strains of compatible mating types from locations in Africa, Haiti and USA (table 1) were obtained to establish 12 genetic lineages. Strains were cultured on Vogel's [25] minimal medium containing 1.5% sucrose and 1.5% agar. An aliquot of 10 ml of conidial suspension was used to inoculate pairs of strains on 1× Westergaard & Mitchell's [26] synthetic crossing medium (SCM) with 1.5% sucrose and 1.5% agar. Eleven strain crosses were performed (table 1) that produced perithecia and ejected ascospores onto the walls of the crossing tubes, including strains from all combinations of the three geographical regions. The twelfth, ‘mass mating’ lineage, was established using 100–150 heat-activated ascospores from each of the 11 strain crosses.

A heat treatment of 55°C for 45 min was established in preliminary studies to fulfil three requirements: it results in intermediate dormancy fractions (see electronic supplementary material, table S2); it kills all hyphae and conidia, but not ascospores, thus ending a ‘year’ (see §2a); and it activates dormant ascospores. Under this heat treatment, non-dormant ascospores germinate within 3–5 h, commence hyphal growth and produce a peak of new ascospores from days 19–22 (see §2b). The duration of a ‘bad’ year was thus defined as 48–60 h, and a ‘good’ year as greater than or equal to 22 days.

Five selection line treatments differing in the frequency of ‘bad years’ were established: 0%, 25%, 30%, 40% and 50%. Replicates of each of the 12 genetic lineages within each bad-year treatment line were randomly assigned to unique year-type sequences to ensure that response to selection could be attributed to frequency of year type and not to specific lineages or year-type sequences (see electronic supplementary material, table S1). The duration of the longer, good years determined the length of the study: ‘year’ corresponds to one sexual cycle, and the scale on which selection is imposed, with a much larger (and unknown) number of ‘generations’ associated with mitotic nuclear divisions occurring within an ascospore-to-ascospore cycle. Thus, 10–14 complete rounds of selection were imposed within all selection lines and year-type sequences within one calendar year (see electronic supplementary material, table S1). Because independent small-sample serial transfers are vulnerable to extinction (see below), year-type sequences were constrained by the rule that two bad years could not appear consecutively; thus, the 50% treatment alternated between good and bad years.

Immediately following each heat treatment, capture of ascospores for inoculation of the next ‘year’ was optimized by a standardized serial wash through sterile polyester fleece filters, and by allowing ascospores to settle out of solution for 30 min. All but 400 µl of the supernatant was decanted, and a 100 µl aliquot of vortexed ascospore suspension was transferred to a fresh test tube containing 1.5 ml of 1× Westergaard & Mitchell's SCM with 1.5% sucrose. Stochastic extinction of lineages was high, presumably a result of the repeated serial transfer of small aliquots containing unknown quantities of spores. However, no differences among treatments in extinction were detected (d.f. = 4; χ² = 7.163; p = 0.128), and a total of 88 independently evolved lineages were available for analysis of experimental evolution of dormancy fraction.

Dormancy fractions were assayed simultaneously for preserved original (generation zero) samples and all lineages for each of the five evolved selection lines at the termination of the experiment after propagation through one additional spore-to-spore cycle under ‘good’ conditions to eliminate possible confounding carry-over effects of the most recent environment on evolved dormancy estimates. Dormancy fraction in a sample is defined as the proportion of ascospores that germinated only following a second heat treatment. Although double-dormancy—germination only following three heat treatments—is possible, ascospores not germinating after two heat activation treatments were assumed to be non-viable.

Heat activation was performed in test tubes under conditions identical to those of the selection experiment (55°C, 45 min), whereas colony counts for germination assays must be performed on Petri plates. Therefore, after vortexing at high speed for 2.5 min, contents for each sample were partitioned equally for germination and dormancy assays following the first heat activation. Immediate germination was assayed in Petri dishes on 1× Vogel's agar medium containing 0.025% glucose, 0.025% fructose and 1.5% sorbose. Dormancy was assayed for the ascospores remaining in the test tubes by allowing germination during an incubation period at room temperature (approx. 22°C) for 48 h, applying a second identical heat treatment to the tubes, vortexing and plating for colony counts.

(a). Heat treatment

A heat treatment had to be optimized that ends a year by killing 100% of hyphae and conidia, but that does not kill ascospores. To test this, conidia and mycelial fragments were suspended in water, and 400 µl aliquots were placed in sets of tubes. These tubes were immersed in a water bath at various test temperatures, including room temperature (no heat treatment) controls. Each temperature was tested in two trials to optimize exposure time: in the first trial, tubes were removed from the bath at 5 min intervals for up to 60 min and plated in Petri dishes with 1× Vogel's medium, 1.5% sucrose, 1.5% agar and 1.5% sorbose for subsequent colony counts. In the second trial, the tubes were removed at 2.5 min intervals and plated. The suspensions for which there was no heat treatment were diluted 10 000× prior to plating. Results show that vegetative material does not survive after 40 min of exposure to 55°C. Thus, a heat treatment of 55°C for 45 min was used for the selection experiment.

(b). Duration of ‘good’ and ‘bad’ years

Ascospore-to-ascospore generation time for N. crassa ranges between 22 and 27 days, and each perithecium produces approximately 200–400 ascospores at 25°C. To find a suitable duration for a ‘good’ year, three replicates of each of four crosses were constructed and incubated at 25°C. Following inoculation, Petri dish lids were removed for observation of ejected ascospores and replaced on days 19, 22, 26, 38 and 46. This provides a cumulative total number of ascospores ejected onto the lid for the intervening periods. With the exception of one outlier, the largest number of ascospores ejected was during the 19–22 day interval. On this basis, 22 days was selected as the minimum duration for a ‘good’ year. As confirmed by preliminary assays, hyphae and conidia are highly sensitive to the elevated temperatures required to initiate ascospore germination. Following heat activation, ascospore germination initiates within 3–5 h. Thus, a ‘bad’ year was imposed by a second heat activation at 48–60 h following the first heat treatment. To maintain consistency, ascospores were germinated in test tubes containing 1.5 ml of 1× Westergaard & Mitchell's liquid SCM with 1.5% sucrose regardless of year type.

3. Results and discussion

Analyses of both final evolved dormancy fraction and of evolutionary change from initial dormancy fractions are consistent with expectations of Cohen's model and provide support for the geometric-mean principle. Final evolved dormancy fractions (table 2), measured as the proportion of ascospores germinating only following a second heat treatment, are concordant with increasing percentage of bad-year treatments (Kendall's τ = 0.23; p = 0.0032), with a slight (3%) counter-trend only for the 40% and 50% bad-year treatments. An ANCOVA to explain final dormancy fraction (figure 1) shows a highly significant effect of the covariate bad-year frequency (d.f. = 1; F = 8.430; p = 0.0051), with no evidence of effects of genetic lineage (d.f. = 11; F = 0.797; p = 0.642) or an interaction (d.f. = 11; F = 0.757; p = 0.681). Eleven of the 12 genetic lineages show a positive slope for final dormancy fraction versus bad-year frequency (figure 2), an observation that cannot reasonably (p = 0.00317) be explained by chance (see electronic supplementary material, text S1). Bad-year frequency as a categorical variable in an ANOVA is a significant predictor of dormancy (F_4,82 = 2.901; p = 0.0267), a result that is robust to pooling of levels of bad-year frequencies (see electronic supplementary material, table S3).

Table 2.

Summary of evolved dormancy fractions.

‘bad year’ selection line (%)	final dormancy fraction (±s.e.)
0	0.16 (0.029)
25	0.22 (0.038)
30	0.29 (0.069)
40	0.33 (0.043)
50	0.30 (0.037)

Figure 1.

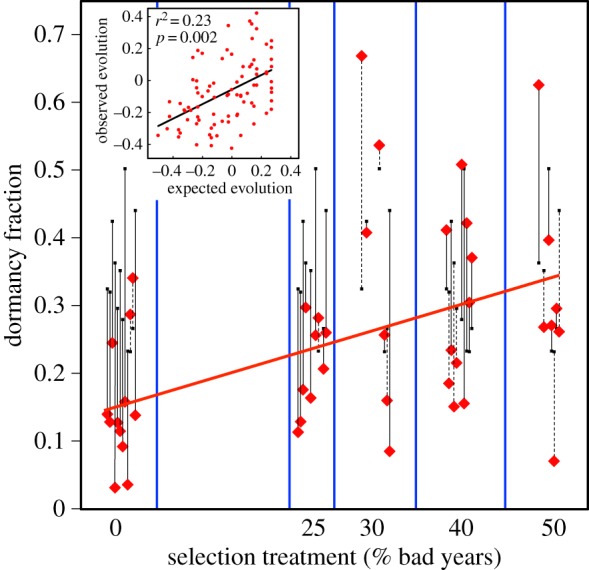
The evolution of bet-hedging dormancy in Neurospora crassa ascospores in response to five environments differing in proportion of ‘bad years’. The red line is the regression slope showing that the proportion of bad years is a significant predictor of the evolution of dormancy fraction. Initial dormancy fractions (small black squares) are connected by black lines to the final dormancy fraction (red diamonds) for each genetic lineage within each selection treatment. Solid and dashed lines indicate response in the predicted and opposite directions, respectively. Data points for each genetic lineage are offset within each ‘bad-year’ type for clarity. The inset shows the highly significant regression of the change in dormancy fraction on the expected change from initial dormancy fraction, for each replicate of each genetic lineage. This regression remains highly significant after reanalysis without the zero bad-year treatment (electronic supplementary material, figure S2).

Figure 2.

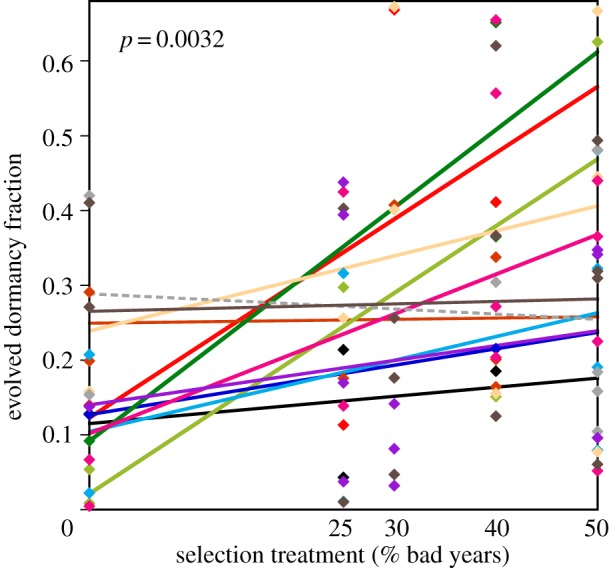
Regressions for evolved dormancy fractions across ‘bad-year’ treatments for each genetic lineage. The significant regression (figure 1) and that 11 of the 12 slopes have positive values (solid lines) reflect the consistent pattern of evolution of dormancy fraction among genetic lineages and explain the non-significant interaction of year type and genetic lineage on the evolution of dormancy. Line and symbol colours match for each lineage.

The difference between initial dormancy fractions (assayed at the termination of the selection experiment) and bad-year frequency is the expected evolutionary change in dormancy fraction, computed for each genetic lineage for each selection line. The highly significant regression of observed versus expected evolutionary change (figure 1 inset) shows that dormancy fractions evolved both upwards and downwards as predicted by the geometric-mean principle, and an ANOVA using the residuals shows no difference in evolutionary response among genetic lineages (F_11,75 = 1.222; p = 0.288).

Our results imply that, although a reduction in dormancy fraction evolves more readily than an increase, the overall agreement between observed and expected evolution is a result of both upward and downward evolution. This can be demonstrated in two ways. First, a reanalysis that completely eliminates the zero bad-year treatment confirms a highly significant positive relationship (F₆₇ = 16.83; p = 0.0001) between observed and expected evolution of dormancy despite loss of power with reduced sample size (see electronic supplementary material, figure S2). The second approach is to exclude the lineages with the most negative observed values (i.e. strongest loss of dormancy), regardless of bad-year treatment. This approach asks whether, for a dataset in which exactly 50% of lineages evolved upwards and 50% downwards, lineages evolve in the predicted direction. Again, despite reduced power, the relationship between observed and expected evolution remains positive and significant (F₅₃ = 4.640; p = 0.0358), confirming that dormancy evolved both upwards and downwards in the expected direction. Furthermore, it should be noted that observed evolutionary change in dormancy fraction—including loss of dormancy—is not similar to previous studies in which dormancy was directly selected upon; we show that dormancy fraction evolves in response to year-type frequency.

Finally, 10 of the 12 genetic lineages show a positive slope for observed versus predicted evolution, an observation unlikely (p = 0.0193) to have occurred by chance (see electronic supplementary material, text S1). By the Akaike information criterion (AIC), the geometric mean is the preferred model, with a relative likelihood 2.4 times that of the arithmetic-mean fitness model in explaining the observed evolution of dormancy.

The present results validate the considerable theoretical work endorsing the geometric-mean principle, and help resolve the paradox pointed out in the 1960s [27] that the probability of extinction may increase indefinitely even as the arithmetic-mean fitness increases. Future work will aim to reveal the genetic mechanisms underlying the observed evolutionary change in bet hedging. It should be noted that the prevalence of bet hedging in nature cannot be resolved by experimental laboratory studies because this depends on the degree of environmental unpredictability in nature, and on the relative importance of other responses to environmental change such as adaptive tracking [28,29] and adaptive phenotypic plasticity [30]. Furthermore, we did not aim to ask the less tractable question of whether evolved dormancy fractions are optimal; they may not have reached evolutionary equilibrium. In addition, the short growth periods allowed in our design excluded the effects of density-dependent competition, which has been shown to interact with abiotic unpredictability in the evolution of dormancy fraction in plants [21].

This empirical test of Cohen's model was contrived to distinguish between the arithmetic- and geometric-mean fitness principles, and is unique in providing direct evidence that environmental unpredictability results in the evolution of bet hedging. The finding that selection acts to increase geometric-mean rather than arithmetic-mean fitness affects our understanding of trait optimality (because bet-hedging traits appear to be maladaptive over the short term), substantiates the idea that bet hedging should not be considered a ‘special case’ of evolution [31,32] and carries the corollary that persistence in the face of future environmental change may depend on bet hedging that has evolved in response to variable environments of the past.

Data accessibility

Data available from the Dryad Digital Repository: doi:10.5061/dryad.8qc20.

Funding statement

This work was supported by NSERC Discovery grants to A.M.S. and M.L.S.