Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Jun 26.
Published in final edited form as: Neuroimage. 2013 Jun 11;83:335–345. doi: 10.1016/j.neuroimage.2013.06.006

Automatic hippocampus segmentation of 7.0 Tesla MR images by combining multiple atlases and auto-context models

Minjeong Kim a, Guorong Wu a, Wei Li a, Li Wang a, Young-Don Son b, Zang-Hee Cho b, Dinggang Shen a,c,*
PMCID: PMC4071619  NIHMSID: NIHMS603065  PMID: 23769921

Abstract

In many neuroscience and clinical studies, accurate measurement of hippocampus is very important to reveal the inter-subject anatomical differences or the subtle intra-subject longitudinal changes due to aging or dementia. Although many automatic segmentation methods have been developed, their performances are still challenged by the poor image contrast of hippocampus in the MR images acquired especially from 1.5 or 3.0 Tesla (T) scanners. With the recent advance of imaging technology, 7.0 T scanner provides much higher image contrast and resolution for hippocampus study. However, the previous methods developed for segmentation of hippocampus from 1.5 T or 3.0 T images do not work for the 7.0 T images, due to different levels of imaging contrast and texture information. In this paper, we present a learning-based algorithm for automatic segmentation of hippocampi from 7.0 T images, by taking advantages of the state-of-the-art multi-atlas framework and also the auto-context model (ACM). Specifically, ACM is performed in each atlas domain to iteratively construct sequences of location-adaptive classifiers by integrating both image appearance and local context features. Due to the plenty texture information in 7.0 T images, more advanced texture features are also extracted and incorporated into the ACM during the training stage. Then, under the multi-atlas segmentation framework, multiple sequences of ACM-based classifiers are trained for all atlases to incorporate the anatomical variability. In the application stage, for a new image, its hippocampus segmentation can be achieved by fusing the labeling results from all atlases, each of which is obtained by applying the atlas-specific ACM-based classifiers. Experimental results on twenty 7.0 T images with the voxel size of 0.35 × 0.35 × 0.35 mm3 show very promising hippocampus segmentations (in terms of Dice overlap ratio 89.1 ± 0.020), indicating high applicability for the future clinical and neuroscience studies.

Keywords: Automatic hippocampus segmentation, 7.0 T MRI, Auto-context model, Multiple atlases based segmentation, Label fusion

Introduction

Automatic segmentation of brain image is a critical step for quantifying the changes of anatomical structures that are highly related to brain diseases. Hippocampus is known as an important structure associated with various brain diseases such as Alzheimer’s disease, schizophrenia, and dementia. Numerous works have been proposed in the literature for automatic hippocampus segmentation (Chupin et al., 2009; Coupe et al., 2011; Khan et al., 2008; Lötjönen et al.; van der Lijn et al., 2008; Zhou and Rajapakse, 2005) by using either shape information (Joshi et al., 2002; Pizer et al., 2003; Shen et al., 2002) or image appearance (Fischl et al., 2002; Hu et al., 2011).

The recent automatic hippocampus segmentation methods generally fall into two categories. The first category includes the atlas-based segmentation methods (Collins et al., 1995; Iosifescu et al., 1997) which deploy deformable image registration as a key step to establish the spatial correspondences between each pre-labeled atlas and the new subject (under segmentation). Then, the labels in the atlas image can be propagated to the subject image for hippocampus labeling. Apparently, the segmentation performance highly depends on the accuracy of image registration, which still needs to be improved. To address the high inter-subject variations in the atlas-based segmentation, multi-atlas based methods (Artaechevarria et al., 2009; Heckemann et al., 2006; Lötjönen et al., 2011; Rohlfing and Maurer, 2004; Rohlfing et al., 2004; Sdika, 2010; Twining et al., 2005) have been investigated recently. Since multiple atlases incorporate the inter-subject variability, more reliable segmentation results can be obtained through label fusion from the multiple atlases. To further improve the segmentation performance, the techniques for optimal selection of atlases (Aljabar et al., 2009; Avants et al., 2010; Wu et al., 2007) and sophisticated label fusion (Langerak et al., 2010; Warfield et al., 2004) have been widely investigated in the literature.

The second category of hippocampus segmentation includes the learning-based segmentation methods (Morra et al., 2008a, 2008b, 2010; Powell et al., 2008; Wang et al., 2011). Specifically, the hippocampus segmentation problem is defined as the classification of each voxel in the subject image into the hippocampus or background by training a classifier to learn the correlation between point-wise image features and the associated class label. Support vector machine (SVM) (Vapnik, 1998), Adaboost (Freund and Schapire, 1997) and artificial neural networks (Magnotta et al., 1999) have been used widely for this purpose. The image features can vary from low-level features (such as image intensities, positions in the image, and gradients) to high-level features (such as Haar-like features, texture, and context information). For example, context features have been incorporated to the auto-context model (ACM) in Tu and Bai (2010) by combining the image appearance with the iteratively updated context information in a recursive manner, where the context information is calculated from a probability map produced by the previously trained classifier. Then, Adaboost is performed to learn the most distinctive features to construct a set of classifiers from a large number of the low-level image appearance features and the high-level context features.

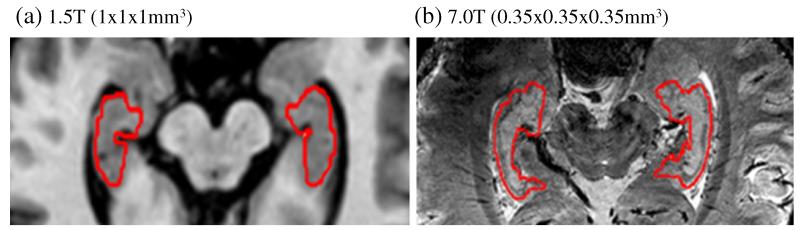
Despite the existence of intensive works for automatic hippocampus segmentation, the accuracy of segmentation is still limited by 1) the tiny size of the hippocampus (≈35 × 15 × 7 mm3), 2) low image contrast, and 3) complexity of surrounding structures (e.g., amygdala, cornu ammonis and dentate gyrus). It is worth noting that most of the existing segmentation methods have been optimized only for 1.5 or 3.0 Tesla (T) MRIs (often with voxel size of 1 × 1 × 1 mm3), which might not work well for 7.0 T images. The 7.0 T MR scanner (Cho et al., 2010) enables achieving the high signal-to-noise ratio (SNR) as well as the dramatically increased contrast and resolution compared to 3.0 T images. As demonstrated in Cho et al. (2008), 7.0 T image can clearly reveal the fine in vivo brain structures, with equivalent resolution to that obtained from the sectional slices by in vitro histological imaging. Thus, 7.0 T imaging technique can trigger the innovative development in hippocampus analysis for clinical studies due to its high capability of discovering the μm-level morphological patterns of human brain. A typical example of 7.0 T image (with the image resolution of 0.35 × 0.35 × 0.35 mm3) is shown in Fig. 1(b), along with a similar slice obtained from 1.5 T scanner (with the resolution of 1 × 1 × 1 mm3) as displayed in Fig. 1(a) for comparison.

Fig. 1.

Fig. 1

Open in a new tab

Large difference of imaging appearance between 1.5 T (a) and 7.0 T (b) MR images. For better visual comparison, the 1.5 T image has been enlarged w.r.t. the image resolution of the 7.0 T image.

Unfortunately, it is not straightforward to apply the existing hippocampus segmentation algorithms, developed for 1.5 T or 3.0 T images, to 7.0 T images. The main reasons include 1) more severe intensity inhomogeneity in the 7.0 T images compared to 1.5 T or 3.0 T images; 2) high signal-to-noise ratio (SNR) which brings forth plenty of anatomical details at the expense of troublesome image noise; and 3) incomplete brain volume (i.e., only a segment of the brain is scanned) due to practical issues such as the trade-off between acquisition time and SNR. Accordingly, no automatic hippocampus segmentation methods have been developed for 7.0 T images, except some manual or semi-automatic methods (Cho et al., 2008, 2010; Yushkevich et al., 2009). Although automatic segmentation method for hippocampal subfields (e.g., cornu ammonis fields 1–3, dentate gyrus, and subiculum) for 4.0 T MR image has been developed in Yushkevich et al. (2010), it can only deal with the subfields and additionally requires the manually labeled hippocampus.

In this paper, we propose to develop a fully automatic hippocampus segmentation method for 7.0 T MR images. Specifically, considering the difficulty in accurately aligning 7.0 T images due to considerable intensity inhomogeneity and noise, we propose employing the auto-context model (ACM), which requires only the linear registration among atlases and new subject, to learn the context information around each voxel to distinguish hippocampus and non-hippocampus voxels in the new subject. To take full advantage of the rich texture information in 7.0 T images, we further extend the ACM by integrating additional texture features as detailed below. In the training stage, a sequence of ACM-based classifiers is trained in each atlas space by borrowing the training samples from not only the underlying atlas but also all other linearly-aligned atlases. In the application stage, to segment the hippocampus in a new subject, we first map the trained classifiers on all atlases to the new subject by linearly registering each atlas to the new subject. Then, we can obtain a set of label maps, with each map representing the hippocampus classification result produced by the classifiers trained for each particular atlas. The final segmentation result is obtained by fusing all labeling results by all atlases. It is worth noting that our method trains classifiers for the left and right hippocampi separately, in order to avoid the dilemma that their intensity ranges are often quite different in the 7.0 T images.

Our learning-based hippocampus segmentation method has been extensively evaluated not only on twenty 7.0 T MR images from normal controls, but also on forty 1.5 T MR images which include 20 normal controls and 20 Alzheimer’s disease (AD) patients. Our proposed method can achieve significant segmentation improvement (p < 0.01) in terms of Dice overlap ratio (such as 6% for 1.5 T images, and 8% for 7.0 T images), compared to the method using only the conventional ACM.

Methods

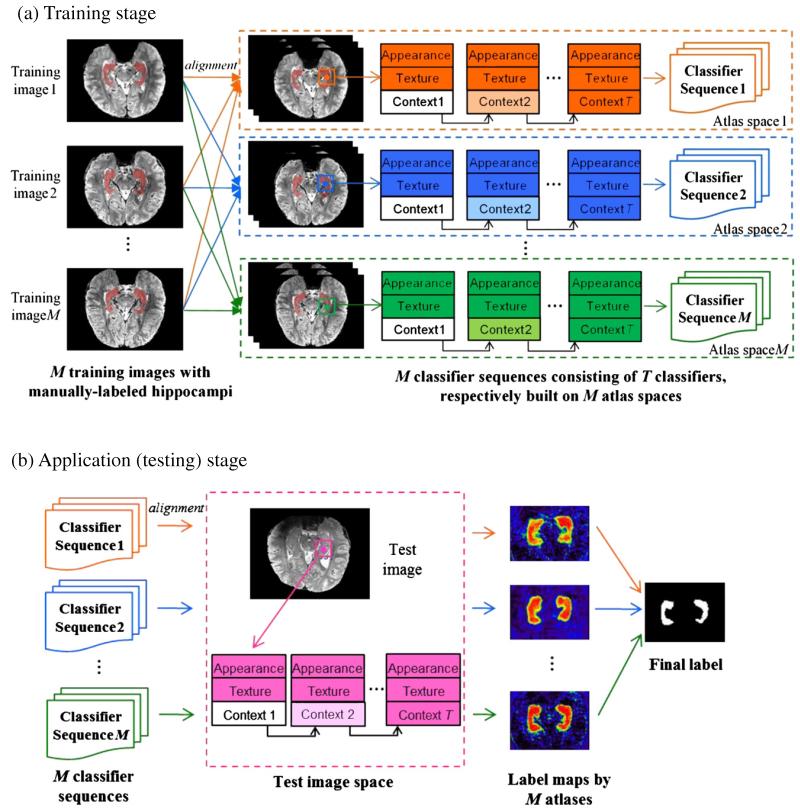
The goal of our learning-based segmentation algorithm is to accurately label each point x ∈ Ω in a new subject into either positive (i.e., hippocampus) or negative (i.e., non-hippocampus) voxels. Fig. 2 shows the overview of our proposed algorithm that consists of training (Fig. 2(a)) and application (Fig. 2(b)) stages.

Fig. 2.

Fig. 2

Open in a new tab

Schematic illustration of our proposed hippocampus segmentation framework, which includes a training stage (a) and an application stage (b). In the training stage (a), M classifier sequences are trained by performing ACM for each atlas. For clarity, we use different colors (i.e., orange, blue and green) to denote the training procedure on different atlases. In the application stage (b), we apply the classifiers (first column in (b)) built on each atlas space to produce the probability map of each point being the hippocampus (third column in (b)), according to the appearance, texture, and context features (second column in (b)) extracted from the test image. Finally, we apply the label fusion to obtain the segmentation of the hippocampus, as shown in the last column in (b).

In the training stage, M intensity images I = {Ii(x)|x ∈ Ω,i = 1,…, M} and their corresponding manually labeled hippocampal maps L = {Li(x)|x ∈ Ω,i = 1,…,M} are used as atlases A = {Ai = (Ii,Li)|i = 1,…, M} for training the ACM-based classifiers. Specifically, for each atlas Ai, we first linearly register all other intensity images Ij (j = 1,…, M, j ≠ i) in the training set, as well as their label maps Lj, toward the intensity image Ii of the current atlas Ai. Then, the classifiers for hippocampus segmentation in the space of Ii will be trained based on not only the current atlas Ai = (Ii, Li), but also on other (M-1) linearly-registered atlases Aj = (Ij, Lj), j = 1,…, M, j ≠ i. For simplicity, we use subscript i to denote for the instances (intensity image and label map) in the original atlas domain, while subscript j for the instances from other atlases after their linear transformations to the reference space (such as the atlas Ai in the training stage, and the subject image S in the applicationstage). During the training, both label map Li and the linearlytransformed label maps Lj will be used as the ground truth, and the ACM method will be used to iteratively construct the sequential classifiers from a large number of the local appearance features, texture features, and context features, as described in the Learn the classifiers by auto-context model (ACM) section. Note that we will finally obtain M sequences of cascaded classifiers, with each sequence associated with each atlas Ai(i = 1),…, M. To reduce the computation time, we only train ACM-based classifiers within a bounding box of possible hippocampal area, learned from all images in the training dataset.

In the application (testing) stage, all atlases are first linearly aligned onto the new subject image. Then, the image appearance, texture, and context features will be extracted to iteratively label each point in the new subject image by the particular sequence of cascaded classifiers that are trained for each atlas. Since each atlas contributes to label the new subject image, a label fusion procedure is further performed to integrate multiple hippocampus segmentations from all atlases, as detailed in the Multi-atlas based hippocampus segmentation section.

Learn the classifiers by auto-context model (ACM)

Before constructing the classifiers for each atlas Ai, all Ijs need to be aligned with Ii, which can be achieved by affine registration of manually-segmented hippocampi in Li and Lj. In the training stage, ACM is performed in the space of each atlas Ai to train a specific set of classifiers, by considering Li as ground truth, and both Ii and all other linearly-registered intensity images Ij as training samples. Note that only affine registration is required for our method. As mentioned earlier, the spatial context feature on classification (or confidence) map, which implicitly takes the shape priors into consideration, has been incorporated into the ACM. Therefore, the registration accuracy in our method is not the main issue for the classification performance, compared to the multi-atlases-based segmentation methods that rely on the accuracy of deformable image registration.

Conventional auto-context model

As detailed in Morra et al. (2008a, 2008b), suppose that there are totally N points in Ii, and thus Xi=(χ1i,…,χni,…,χNi) denotes the vector of all spatial coordinates in the intensity image I, where χni(n=1,…,N) represents a spatial position in Ii. Each Xi comes with a ground-truth label vector Yi=(y1i,…,yni,…,yNi), where yni∈{−1,+1} is the class label for the associated position χni. Label ‘−1’ denotes non-hippocampus voxel, and label ‘+1’ denotes hippocampus label. The training set at the iteration t is defined as ϴt={Xi,Yi,Pt−1(Xi)}∪{[Xj,Yj,Pt−1(Xj)],j=1,…,M,j≠i}, where the first part {Xi,Yi,Pt−1(Xi)} is obtained from the atlas Ai under consideration and the second part is obtained from all other atlases Aj after affine registration onto Ai. Pt−1(Xi)=(Pt−1(χ1i),…,Pt−1(χni),…,Pt−1(χNi)) is the classification map obtained at the (t - 1)-th iteration (t = 1,…,T), where each element Pt−1(χni)=pt−1(yni=+1∣χni) is the likelihood of the point χni being a hippocampus voxel.

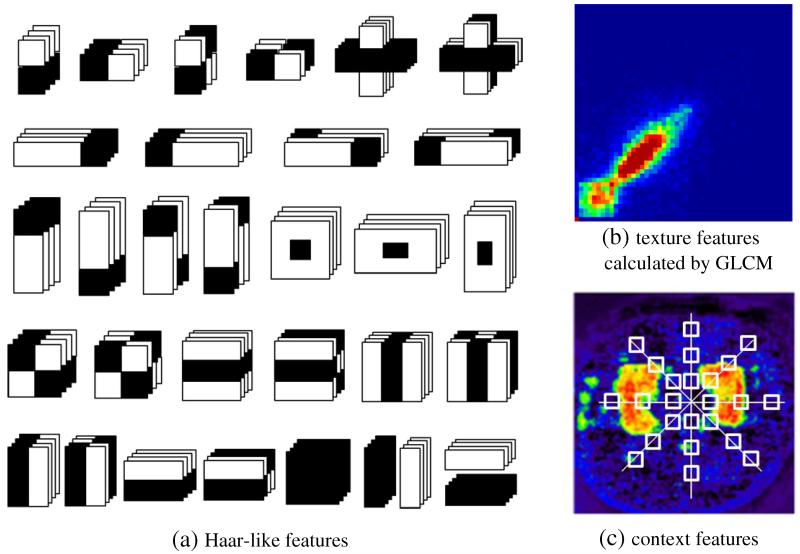
Two kinds of features can be extracted for training the classifiers: 1) local image appearance features, e.g., intensity, location, neighborhoods, and Haar-like features (Fig. 3(a)), computed from each local patch centered at point χni, and 2) context information at the t-th iteration captured from the classification map Pt−1(Xi) with the patterns shown by white boxes in Fig. 3(c). It is worth noting that the context features vary at different iterations since the context features at the t-th iteration are recursively extracted from the classification probability map Pt−1(Xi) of the (t – 1)-th iteration, which is produced by a set of classifiers trained in the (t – 1)-th iteration. Since the initial classification map P0(Xi) is unknown, we initialize it as the union of the linearly-aligned hippocampus label maps of all atlases.

Fig. 3.

Fig. 3

Open in a new tab

Demonstration of three types of features used in our method, which include (a) Haar-like features, (b) texture features calculated by GLCM, and (c) context features.

Improved multi-atlas ACM

To extract the discriminative features in 7.0 T images, we adopt three types of features, as shown in Fig. 3, for our learning-based segmentation algorithm. It is worth noting that other types of features can also be incorporated into our segmentation framework.

Image appearance features

The appearance features are employed to capture the local information around each voxel in the image. Similar to Morra et al. (2008a, 2008b), image appearance features include intensity, spatial location, and neighborhood features (such as intensity mean, variance, gradient and curvature in a small neighborhood), and Haar features at different scales. Haar features (Viola and Jones, 2004), which are widely used in object recognition, can be computed at different scales of interest with high speed by using integral images or volumes. The Haar feature considers adjacent rectangular regions at a specific location in a detection window, sums up the voxel intensities in these regions, and calculates the difference between them. In this paper, we extend 2D Haar features to multi-scale 3D Haar features (shown in Fig. 3(a)) to facilitate our classification.

Texture features

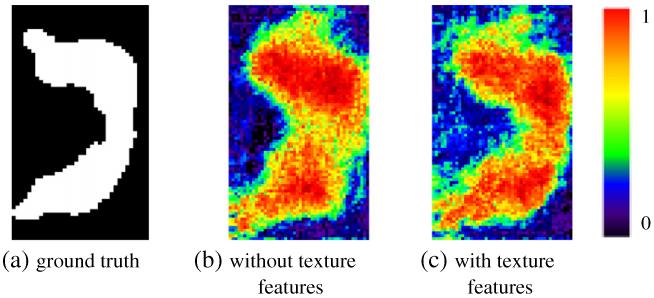
Much richer texture information in 7.0 T images is worth being extracted and further utilized as another type of discriminative features for classification. Thus, the gray level co-occurrence matrix (GLCM) (Haralick et al., 1973) is calculated for the image patch around each point χni under consideration. Overall 14 statistics can be computed, including angular second moment, contrast, correlation, variance, inverse difference moment, sum average, sum variance, sum entropy, entropy, difference variance, difference entropy, two information measures of correlation, and maximal correlation coefficient. In our method, we adopt the first 13 features as the texture features, and the last statistic, maximal correlation coefficient, is excluded due to its computational instability (Yanhua et al., 2006). The advantage of incorporating texture features into ACM model is demonstrated in Fig. 4. It is clear that the hippocampus classification map by ACM with the use of texture features (Fig. 4(b)) is much closer to the ground truth (Fig. 4(a)) than that by ACM without using texture features (Fig. 4(c)).

Fig. 4.

Fig. 4

Open in a new tab

The effectiveness of incorporating texture features for voxel classification. Compared to the ground truth (a), the hippocampus classification map by incorporation of texture features (c) shows higher similarity than that by no incorporation of texture features (b).

Context features

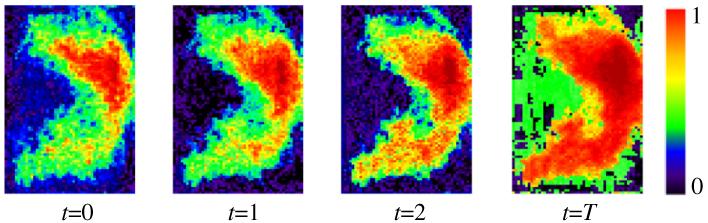
The context features are extracted from the classification probability map obtained at the previous iteration, in order to capture global anatomical information around each voxel in the image. In general, the context features are used to describe the spatial configuration of particular point w.r.t. its neighboring points. In contrast to the local appearance and texture features, the context features are extracted from a large region surrounding the current location, rather than its small neighborhood, as shown in Fig. 3. Specifically, for each point χni, a number of rays in equal-degree intervals are disseminated outward from the center point, and the context locations on these rays are sparsely sampled (white boxes in Fig. 3(b)). For each sampled location, the classification probability on the center point and the average probability within a 3 × 3 × 3 neighborhood are used as context features. As shown in Fig. 5, the hippocampus region in the sequential classification maps becomes more and more prominent and the boundary between the hippocampus and background becomes sharper and sharper, as the ACM progresses.

Fig. 5.

Fig. 5

Open in a new tab

The hippocampus classification map at each iteration of the ACM algorithm.

Training of ACM

Given the underlying atlas Ai and all other aligned atlases Aj, the initial classification map can be computed by the union of the aligned hippocampus label maps of all atlases (i.e., Li∪{⋃j=1,j≠iMLj}) as mentioned above. Then, ACM is used to iteratively find the optimal classifiers by repeating the following steps for T iterations:

  1. Update the contexture features in the training set Θt (as defined above) by using the newly-obtained classification maps Pt − 1(Xi) and Pt − 1(Xj) (j = 1,…,M,j ≠ i);

  2. Train the classifier by Adaboost using image appearance features, texture features, and the latest context features. The details for Adaboost-based training can be found in Freund and Schapire (1997).

  3. Use the trained classifier to assign the label to each point in Ii and all Ijs, thus obtaining Pt(X) and Pt−1(Xj)(j=1,…,M,j≠i) for the next iteration t + 1.

For each atlas Ii under consideration, the output of ACM is a sequence of trained classifiers, i.e., T cascaded classifiers, where each of them is associated with particular iteration. The same training procedure will be applied to all other atlases. Thus, in the end of training, we will obtain M sequences of trained classifiers, with each sequence sitting in its own atlas space and having T cascaded classifiers, as shown in Fig. 2(a). In the application stage, by registering each atlas onto the test subject image, we can apply its respective sequence of trained classifiers to determine whether the underlying point is the hippocampus or not, as shown in Fig. 5. As we can see from Fig. 5, the classification map is gradually updated as ACM processes, which will finally lead to more accurate segmentation of hippocampus.

Due to the severe intensity inhomogeneity of the left and right hippocampi in the 7.0 T MR images, we train the location-adaptive classifiers, instead of building a global classifier for the whole brain. That is, the individual sets of classifiers are generated for the left and right hippocampi separately. Moreover, to deal with large size of 7.0 T image and save the computational time, both training and testing procedures are performed in a multi-resolution fashion. That is, the final classification map at low resolution will be used as the initialization for the next high resolution.

Multi-atlas based hippocampus segmentation

In the application stage, hippocampus segmentation from a test image S is completed by three steps as described in Fig. 2(b). In the first step, all the atlases will be linearly registered onto the test image, in order to map the classifiers learned in the training stage onto the test image. Then, the local image appearance features, texture features, and context features will be computed for each point of test image. As initialization, the union of warped labels of all atlases is used as the initial classification map. In the second step, the labeling of the test image is conducted by performing each sequence of cascaded classifiers of each atlas independently upon the test image. Note that the procedure of hippocampus labeling follows exactly the training procedure of ACM, where the context features in each iteration will be recalculated based on the probability map obtained in the previous iteration. Thus, M classification probability maps will be obtained in the end of classification. In the third step, all these classification maps are integrated into the final labeling result. Although classification maps can be simply binarized and then fused together for producing the final segmentation result, this simple operation can significantly affect the final segmentation accuracy as pointed out in Warfield et al. (2004). To this end, we apply the following advanced label fusion strategy to produce segmentation result from a set of probability maps.

Label fusion

For label fusion from a set of probability maps, the simplest method is majority voting (Heckemann et al., 2006), which assumes that each atlas contributes equally to the image segmentation. Here, we go one step further to apply the local weighted voting strategy (Khan et al., 2011) to average the classification probabilities across all atlases, where the weight for each atlas is computed by image patch similarity w.r.t. the test image. Given the weighted average probability map, with the degree on each point indicating the likelihood of being hippocampus, we further apply the level sets approach (Chan and Vese, 2001) on this probability map to outline the boundary of hippocampus and obtain the final segmentation.

Summary

In summary, our segmentation framework consists of training and testing (segmentation) stages as summarized below.

Training stage

  1. For given M training images/atlases, in each atlas Ai’s space, all other intensity images Ij (j = 1,…, M, j ≠ i) as well as their corresponding label maps Lj are linearly registered onto the atlas Ai’s space.

  2. For each image resolution, repeat the following steps to train the ACM classifiers:
    1. In the lowest resolution, the classification map is initialized by the union of aligned hippocampus maps of all atlases;
    2. t = 1;
    3. The training set Θt is obtained in each atlas space, which consists of context features and also the image appearance, 3D-Haar, and texture features, calculated from all aligned images/atlases. Note that the context features are computed from the classification map of the previous iteration, Pt − 1;
    4. In each atlas space, a classifier at the t-th iteration is trained by Adaboost algorithm using the feature set Θt. Also, with this trained classifier, the new classification map Pt is obtained for the next iteration;
    5. t ← t + 1; f. If t < T, go to Step 2.c; otherwise, go to Step 3.

  3. If not reaching the finest resolution, go to Step 2.b and the latest classification map is used as the initial classification map for the next high image resolution. Otherwise, stop.

Testing stage

  1. For a given new subject image, the classifier sequences generated in all atlases will be transformed onto the subject image by linear registration.

  2. Then, the image appearance, texture, and context features are computed at each point of the subject image.

  3. The subject image is classified independently by the cascaded classifiers of each atlas in a multi-resolution way.

  4. The final probability maps obtained by all atlases are adaptively fused to build a fused probability map, according to the local image similarity between the subject image and each aligned atlas.

  5. The final label for the subject image is determined by applying a level sets algorithm to obtain the boundary of hippocampus from the locally-fused probability map.

Experimental results

In the following experiments, we evaluate the performance of our learning-based hippocampus segmentation method using twenty 7.0 T MR images. Leave-one-out cross validation is used for evaluating the generalization of our method. Specifically, at each leave-one-out case, one image is used as a test image, and all other images are used as training images (i.e., multiple atlases). In both training stage and testing stage, affine registration is used to bring the images to the same space, i.e., using the FLIRT algorithm in FSL library (Jenkinson et al., 2012). The datasets and preprocessing steps will be detailed in the following section. Then we will investigate the contribution of each component, i.e., multi-atlas framework and the image features used in our method, through both qualitative and quantitative evaluations. Moreover, due to the limited existing studies on automatic hippocampus segmentation of 7.0 T images, we also apply our method to the 1.5 T images for comparison.

Datasets and preprocessing

7.0 T MR images from 20 normal subjects acquired by the method in Cho et al. (2010) were used for evaluating our proposed algorithm. Specifically, these subjects consist of 6 males and 14 females with the age of 28.92 ± 16.51. For comparison, the same number of 1.5 T MR images was, respectively, selected from normal subjects and AD subjects in the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (Mueller et al., 2005). For the 7.0 T scan (Magnetom, Siemens), an optimized multichannel radiofrequency (RF) coil for 7.0 T image acquisition and a 3D fast low-angle shot (Spoiled FLASH) sequence were utilized, with repetition time (TR) = 50 ms, echo time (TE) = 25 ms, flip angle (FA) = 10°, pixel band width (BW) = 30 Hz/pixel, field of view (FOV) = 200 mm, matrix size = 512 × 576 × 60, 3/4 partial Fourier, and number of average (NEX) = 1. The image resolution of the acquired images is isotropic, e.g., 0.35 × 0.35 × 0.35 mm3. For all 1.5 T MR scans, spoiled gradient recalled echo/fast low angle shot (SPGR/FLASH) with 30° and 5° flip-angle and the magnetization prepared rapid gradient echo (MP-RAGE) were used with a multi-echo 3-D volume sequence and an axial dual-echo, fast spin-echo sequence. The hippocampi were manually segmented by a neurologist based on the conventional protocol (Jack et al., 1995; Pantel et al., 2000).

All images were pre-processed by the following steps: 1) inhomogeneity correction using N3 (Sled et al., 1998), 2) intensity normalization for making image contrast and luminance consistent across all subjects (Nyúl and Udupa, 1999), and 3) affine alignment. In the end of this processing procedure, all images were cropped to reduce computational burden, and further divided into the left and right parts to construct the location-adaptive classifiers.

Quantitative evaluation of hippocampus segmentation

For quantitative evaluation of our segmentation method, as well as other methods, four widely used metrics, i.e., precision (P), recall (R), relative overlap (RO), and similarity index (SI), are employed to measure the volumetric overlap of automatic segmentation with respect to the ground truth (i.e., manual labels). Moreover, we also measure the surface distance based on Hausdorff distance (HD). Let V(A) denote the volume of the ground-truth segmentation, V(B) the volume of automatic segmentation, and d(a,b) the Euclidean distance between two points a and b. Then, all above metrics can be mathematically defined as follows:

P=V(A∩B)V(B),R=V(A∩B)V(A),RO=V(A∩B)V(A∪B),SI=V(A∩B){(V(A)+V(B))∕2},HD=H1+H22, (1)

where H1 = maxa ∈ A(minb ∈ B(d(a,b))) and H2 = maxb ∈ B(mina ∈ A (d(b,a))).

The accuracy of hippocampus segmentation by our method on 7.0 T images

We performed a leave-one-out test on 20 images to evaluate the segmentation performance of our method by comparing with other methods. For each leave-one-out case, as mentioned above, we use one image for testing, and the remaining 19 images for training the classifiers. Since our method aims to improve segmentation accuracy in two ways, i.e., incorporating texture features into the conventional ACM method and taking the advantage of multi-atlas framework, it is worthwhile to evaluate the contributions from these two different ways (improved ACM and multi-atlas framework), respectively. Accordingly, we will evaluate and compare four segmentation methods: (1) conventional ACM (baseline method); (2) improved ACM (to evaluate the contribution of texture features); (3) conventional ACM + multi-atlas framework (to evaluate the contribution of multiple atlases); and (4) our complete method that incorporates the improvements in both (2) and (3). It is worth noting that the multi-atlas framework utilizes all 19 atlases to train the respective classifiers in the training stage and also segment the subject image in the application stage.

Table 1 shows the average for each of 5 evaluation metrics in the 20 leave-one-out cases by the four methods. Obviously, our complete method consistently outperforms all other three methods in all evaluation metrics. Specifically, compared to the conventional ACM, our method gains the improvements of 6%, 5%, 7% and 8% for the evaluation metrics P, R, RO, and SI, respectively. On the other hand, we find that each component in our method has its own contribution in improving the segmentation accuracy. Specifically, compared to the conventional ACM (the baseline method), the improved ACM (method 2) and the conventional ACM + multi-atlas framework (method 3) can achieve 2–4% and 3–5% improvements, respectively. These results indicate that the multi-atlas framework can have more impact in improving segmentation accuracy than the improved ACM, which leads us to examine the segmentation performance of our method w.r.t. the number of atlases used, as described next. We here further included the 5 evaluation metrics achieved by the multi-atlases framework without ACM (the second row in Table 1), which show much worse performance than all other four methods using ACM. This is mainly caused by the difficulty in accurate alignment of 7.0 T images, thus demonstrating the importance of incorporating ACM into the multi-atlases framework especially for 7.0 T cases.

Table 1.

Quantitative comparisons using 4 overlap metrics (precision (P), recall (R), relative overlap (RO), and similarity index (SI)) and Hausdorff distance (HD) for the 20 leave-one-out (LOO) cases on 7.0 T images. Here, our complete method is compared with other four methods, i.e., no ACM, conventional ACM, improved ACM, and the conventional ACM in the multi-atlases framework.

P R RO SI HD
Multi-atlases without ACM 0.74 ± 0.061 0.73 ± 0.054 0.66 ± 0.059 0.73 ± 0.051 0.59 ± 0.049
Conventional ACM 0.81 ± 0.045 0.82 ± 0.042 0.71 ± 0.048 0.81 ± 0.041 0.48 ± 0.036
Improved ACM 0.83 ± 0.042 0.84 ± 0.043 0.74 ± 0.039 0.85 ± 0.034 0.43 ± 0.035
Conventional ACM + multi-atlases 0.84 ± 0.040 0.85 ± 0.039 0.75 ± 0.042 0.86 ± 0.035 0.41 ± 0.032
Our method 0.88 ± 0.024 0.87 ± 0.038 0.78 ± 0.031 0.89 ± 0.020 0.37 ± 0.025
Open in a new tab

For further evaluation, we compute the mean and standard deviation of hippocampus volumes for the 20 leave-one-out cases by comparing our segmentation results with the manual ground truths in Table 2. The results also show that there is no significant volume difference between segmented left and right hippocampi (p > 0.3).

Table 2.

Comparison of mean volumes of hippocampi (HC) segmented by the proposed method and manual rater (used as ground truth) (unit: mm3).

Ground truth
 Our method
Left HC Right HC Left HC Right HC
Volume (mean ± std) 3368 ± 293 3436 ± 347 3327 ± 288 3391 ± 340
Open in a new tab

Effect of the number of atlases used

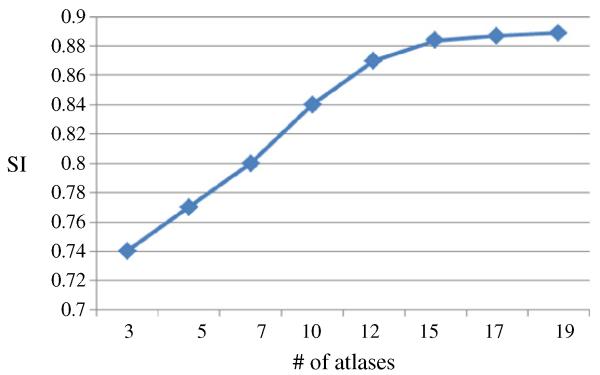
Here we investigate the effect of the number of atlases used in segmentation of hippocampus in 7.0 T images. The evolution of segmentation accuracy (e.g., SI metric) as the number of atlases used is shown in Fig. 6, which shows that the SI metric keeps increasing and then becomes stable after using 15 or more atlases.

Fig. 6.

Fig. 6

Open in a new tab

Comparison of segmentation accuracy w.r.t. the number of atlases used (3 to 19), using the similarity index (SI).

Effect of using the adaptive-weighted label fusion for the probability maps

In the multi-atlases framework, the probability maps calculated from all atlases need to be fused together for generating the final single probability map for the new subject. In our method, we propose utilizing an adaptive-weighted fusion method. That is, the final probability map for the new subject is the weighted average of all probability maps from all atlases, with the weights computed based on the patch similarity between each aligned atlas and the new subject image. To show its advantage over the simple averaging, we show the segmentation accuracy metrics by the simple averaging and our proposed adaptive-weighted averaging in Table 3, respectively.

Table 3.

Comparison of segmentation accuracy between the simple averaging and our adaptive-weighted averaging in determining the final probability map.

P R RO SI HD
Simple averaging 0.87 ± 0.031 0.85 ± 0.037 0.76 ± 0.036 0.88 ± 0.026 0.40 ± 0.030
Adaptive-weighted averaging 0.88 ± 0.024 0.87 ± 0.038 0.78 ± 0.031 0.89 ± 0.020 0.37 ± 0.025
Open in a new tab

Effect of using level sets method for final hippocampus segmentation

After combining probability maps from all atlases into a single probability map, our method further use a level sets based approach to extract hippocampal boundary and obtain the final segmentation, in order to make the segmented hippocampus have the smooth boundary. To show the advantage of using this level sets based approach over the simple thresholding based method, we list their respective segmentation accuracy in Table 4.

Table 4.

Comparison of segmentation accuracy between two binarization strategies, thresholding based method and the level sets based approach.

P R RO SI HD
Thresholding based method 0.88 ± 0.035 0.86 ± 0.041 0.77 ± 0.039 0.88 ± 0.029 0.39 ± 0.036
Level sets based approach 0.88 ± 0.024 0.87 ± 0.038 0.78 ± 0.031 0.89 ± 0.020 0.37 ± 0.025
Open in a new tab

Effect of texture features and multi-atlases framework on 1.5 T images

To show the effectiveness of our proposed method in 1.5 T images, we applied it to 1.5 T images for comparison. Especially, we selected 20 normal controls (NC) and 20 AD patients, respectively. Tables 5 and 6 show the mean and standard deviation for each of 5 evaluation metrics in 20 leave-one-out cases of 1.5 T images by the four methods (conventional ACM, improved ACM, ACM + multi-atlases, and our complete method) for NC and AD groups, respectively. The results indicate that our method still outperforms all other three methods regardless of NC or AD (with even higher improvement for AD cases). Specifically, for the normal subjects (Table 5), compared to the conventional ACM, our method gains the improvements of 4%, 6%, 5% and 5% on average for the 4 overlap metrics, P, R, RO, and SI, respectively. On the other hand, compared to the conventional ACM, other two methods (using the improved ACM with advanced texture features or using the conventional ACM in the multi-atlases framework) improve 0–1% and 2–3% for the 4 overlap metrics. Different from the influences of texture features and multi-atlases framework in 7.0 T image segmentation, the improvement by incorporating texture features appears much less than that by the multi-atlases framework. This also indicates the importance of employing texture features in dealing with rich information in the 7.0 T images.

Table 5.

Quantitative comparisons for the 20 leave-one-out (LOO) cases on 1.5 T images of normal controls by four automatic segmentation methods.

P R RO SI HD
Conventional ACM 0.81 ± 0.044 0.80 ± 0.050 0.70 ± 0.045 0.82 ± 0.048 4.2 ± 0.043
Improved ACM 0.82 ± 0.036 0.81 ± 0.042 0.71 ± 0.034 0.82 ± 0.035 4.0 ± 0.029
Conventional ACM + multi-atlases 0.84 ± 0.033 0.84 ± 0.037 0.73 ± 0.036 0.85 ± 0.032 3.7 ± 0.031
Our method 0.85 ± 0.025 0.86 ± 0.027 0.75 ± 0.031 0.87 ± 0.026 3.4 ± 0.024
Open in a new tab

Table 6.

Quantitative comparisons for the 20 leave-one-out (LOO) cases on 1.5 T images of AD patients by four automatic segmentation methods.

P R RO SI HD
Conventional ACM 0.79 ± 0.049 0.79 ± 0.053 0.69 ± 0.047 0.80 ± 0.051 4.8 ± 0.048
Improved ACM 0.81 ± 0.044 0.80 ± 0.039 0.70 ± 0.043 0.81 ± 0.042 4.4 ± 0.037
Conventional ACM + multi-atlases 0.82 ± 0.040 0.81 ± 0.038 0.71 ± 0.041 0.82 ± 0.039 4.1 ± 0.035
Our method 0.84 ± 0.034 0.84 ± 0.029 0.74 ± 0.038 0.85 ± 0.032 3.8 ± 0.033
Open in a new tab

Qualitative evaluation

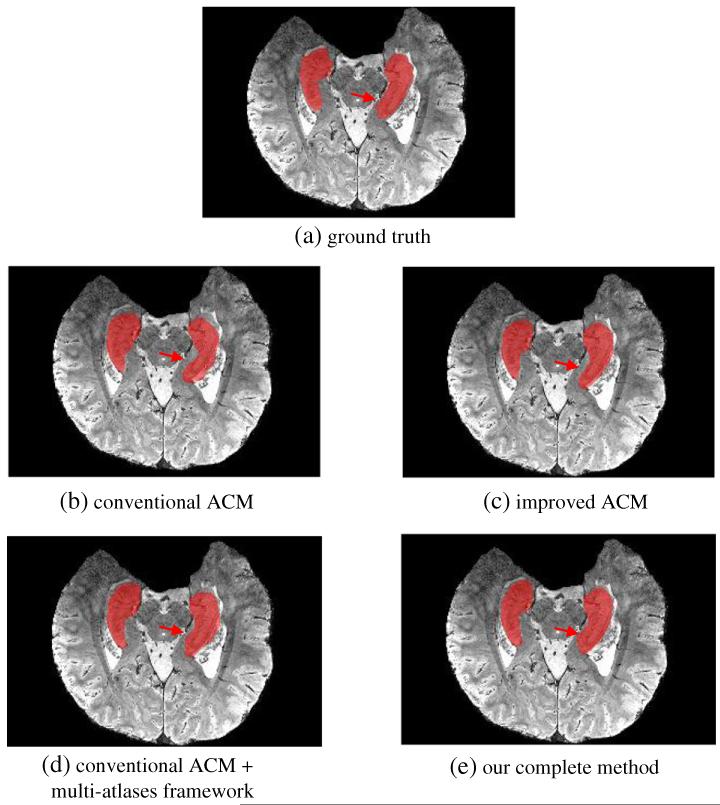
For visual comparison, we also show in Fig. 7 the segmentation results of a typical 7.0 T image by four methods (Figs. 7(b)-(e)), along with its manual segmentation (Fig. 7(a)). For fair comparison, we use the same parameters for the ACM used in all the methods, e.g., the same feature sets and the same number of iterations. It can be observed that the hippocampi segmented by our complete method (Fig. 7(e)) are more similar to the ground-truth than any other methods, e.g., the conventional ACM (Fig. 7(b)), improved ACM (Fig. 7(c)), and the conventional ACM in the multi-atlases based framework (Fig. 7(d)).

Fig. 7.

Fig. 7

Open in a new tab

Comparison of segmented hippocampus regions on a 7.0 T image by (b) the method using the conventional auto-context model, (c) the method using the improved ACM, (d) the method using the conventional ACM in the multi-atlases framework, and (e) our complete method. Compared to the ground truth (a) obtained with manual labeling, our complete method shows the best segmentation performance (especially for the area depicted by red arrows).

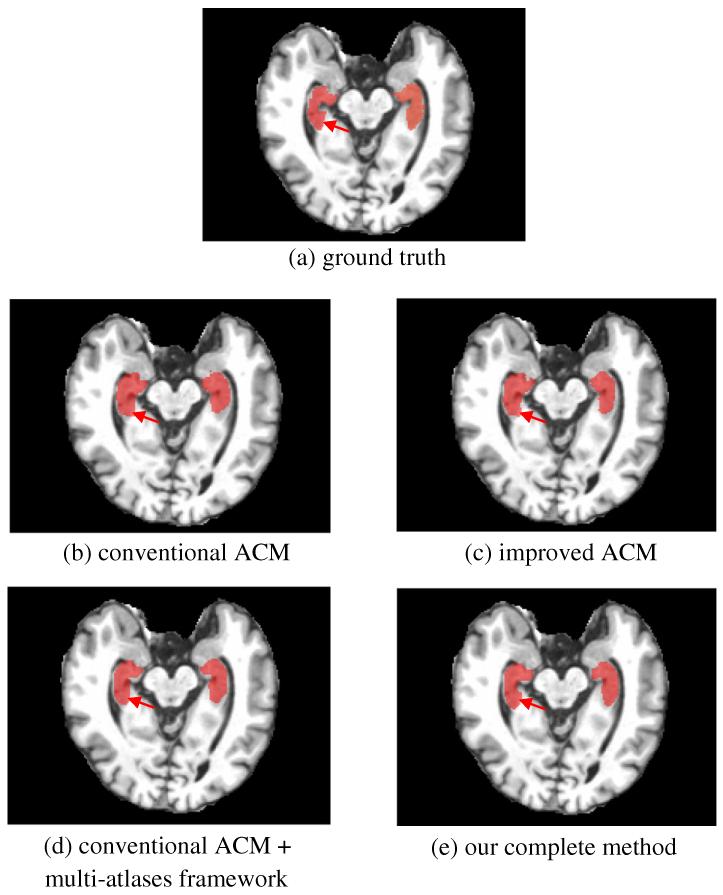
Similarly, we compare in Fig. 8 the segmentation results on a typical 1.5 T image by four different methods (Figs. 8(b)-(e)), along with manual segmentation (Fig. 8(a)). Again, it can be observed that the hippocampi segmented by our method (Fig. 8(e)) are more similar to the ground-truth than any other methods, i.e., the conventional ACM (Fig. 8(b)), improved ACM (Fig. 8(c)), and the conventional ACM in the multi-atlases based framework (Fig. 8(d)). Moreover, consistent to the quantitative result reported above, the improvement on the segmentation result by the multi-atlases appears to be larger than that by the incorporation of additional texture features.

Fig. 8.

Fig. 8

Open in a new tab

Comparison of segmented hippocampus regions on 1.5 T images by (b) the method using the conventional auto-context model, (c) the method using the improved ACM, (d) the method using the conventional ACM in the multi-atlases framework, and (e) our complete method. Compared to the ground truth (a) obtained with manual labeling, our complete method shows the best segmentation performance (especially for the area depicted by red arrows).

Discussion and conclusion

Although various methods have been proposed for hippocampus segmentation in the MR images, they were mostly developed for the 1.5 T or 3.0 T images, which contain much less anatomical structures than the 7.0 T images. Therefore, it is difficult to directly compare our method developed for the 7.0 T images with other existing methods developed for 1.5 T or 3.0 T images. Thus, in Table 7, we compare the performance of our proposed method on 1.5 T images with the representative methods in different categories, e.g., classification-based method (Powell et al., 2008), auto-context model based method (Morra et al., 2008a, 2008b), and multi-atlases based method (van der Lijn et al., 2008). We also compare with a new classification-based method that has the highest segmentation accuracy (Wang et al., 2011). Due to the use of different evaluation metrics in different methods, we take a common metric, e.g., similarity index (SI), for comparison. As we can see from Table 7, our method can achieve higher or comparable segmentation results, compared to all methods under comparison. It is worth noting that our method achieves higher segmentation accuracy in 7.0 T images (Table 1) than 1.5 T images (Tables 5 and 6).

Table 7.

Comparison of hippocampus segmentation on 1.5 T images from normal controls with other representative segmentation methods reported in the literature.

Method Method description SI
Powell ’08 Classification based 0.84
Morra ’08 Auto-context model based 0.82
van der Lijn ’08 Multiple atlases based 0.85
Wang ’11 Classification based 0.87
Our method Improved ACM + multiple atlases based 0.87
Open in a new tab

As a first attempt to explore the hippocampus segmentation on 7.0 T MR images, we found that the texture features provide greater contribution in improving the segmentation accuracy in 7.0 T cases than 1.5 T, which might be useful for the existing segmentation methods if they are planned to apply to 7.0 T images. Due to the lack of availability of 1.5 T and 7.0 T datasets from the same protocol, T1-weighted 1.5 T MR and T2-weighted 7.0 T MR images were used for comparison in our experiment. However, it is worth noting that the features used for segmenting hippocampus in our proposed framework are general enough to apply to either T1- or T2-weighted MR images. The comparison can be slightly different by applying to the same modality images but without significant difference, since none of the modality-specific image features are introduced in our method.

In conclusion, we have presented a learning-based method for accurate segmentation of hippocampus from the 7.0 T MR images. Specifically, the multi-atlases-based segmentation framework and the improved auto-context model (with advanced texture features) are employed for building multiple sequences of classifiers and further applied for hippocampus segmentation in the new test image. The experimental results show that our model can achieve significant performance improvement, compared to the baseline auto-context model.

In our future work, we will extend our proposed framework for segmentation of hippocampal sub-structures in the 7.0 T images (Cho et al., 2010). In Yushkevich et al. (2010), although it can achieve reasonable semi-automatic segmentations for hippocampal subfields in the 4.0 T MR images, it requires pre-defined hippocampus region. We believe our learning-based segmentation method will enable the fully automatic segmentation for the subfields in 7.0 T images. Moreover, in the future, we will apply our method to 7.0 T images from AD patients, which are currently under data collection.

Acknowledgment

This work was supported in part by NIH grants EB006733, EB008374, EB009634 and AG041721.

Footnotes

Conflict of interest

The authors report no biomedical financial interests or potential conflicts of interest related to this article.

References

  1. Aljabar P, Heckemann RA, et al. Multi-atlas based segmentation of brain images: atlas selection and its effect on accuracy. NeuroImage. 2009;46(3):726–738. doi: 10.1016/j.neuroimage.2009.02.018. [DOI] [PubMed] [Google Scholar]
  2. Artaechevarria X, Munoz-Barrutia A, et al. Combination strategies in multiatlas image segmentation: application to brain MR data. IEEE Trans. Med. Imaging. 2009;28(8):1266–1277. doi: 10.1109/TMI.2009.2014372. [DOI] [PubMed] [Google Scholar]
  3. Avants BB, Yushkevich P, et al. The optimal template effect in hippocampus studies of diseased populations. NeuroImage. 2010;49(3):2457–2466. doi: 10.1016/j.neuroimage.2009.09.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chan TF, Vese LA. Active contours without edges. IEEE Trans. Image Process. 2001;10(2):266–277. doi: 10.1109/83.902291. [DOI] [PubMed] [Google Scholar]
  5. Cho Z-H, Han J-Y, et al. Quantitative analysis of the hippocampus using images obtained from 7.0 T MRI. NeuroImage. 2010;49(3):2134–2140. doi: 10.1016/j.neuroimage.2009.11.002. [DOI] [PubMed] [Google Scholar]
  6. Cho Z-H, Kim Y-B, et al. New brain atlas — mapping the human brain in vivo with 7.0 T MRI and comparison with postmortem histology: will these images change modern medicine? Int. J. Imaging Syst. Technol. 2008;18(1):2–8. [Google Scholar]
  7. Chupin M, Hammers A, et al. Automatic segmentation of the hippocampus and the amygdala driven by hybrid constraints: method and validation. NeuroImage. 2009;46(3):749–761. doi: 10.1016/j.neuroimage.2009.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Collins DL, Holmes CJ, et al. Automatic 3-D model-based neuroanatomical segmentation. Human Brain Mapping. 1995;3(3):190–208. [Google Scholar]
  9. Coupe P, Manjon JV, et al. Patch-based segmentation using expert priors: application to hippocampus and ventricle segmentation. NeuroImage. 2011;54(2):940–954. doi: 10.1016/j.neuroimage.2010.09.018. [DOI] [PubMed] [Google Scholar]
  10. Fischl B, Salat DH, et al. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33(3):341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
  11. Freund Y, Schapire RE. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997;55(1):119–139. [Google Scholar]
  12. Haralick RM, Shanmugam K, et al. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973;3(6):610–621. [Google Scholar]
  13. Heckemann RA, Hajnal JV, et al. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. NeuroImage. 2006;33(1):115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
  14. Hu S, Coupé P, et al. Appearance-based modeling for segmentation of hippocampus and amygdala using multi-contrast MR imaging. NeuroImage. 2011;58(2):549–559. doi: 10.1016/j.neuroimage.2011.06.054. [DOI] [PubMed] [Google Scholar]
  15. Iosifescu DV, Shenton ME, et al. An automated registration algorithm for measuring MRI subcortical brain structures. NeuroImage. 1997;6(1):13–25. doi: 10.1006/nimg.1997.0274. [DOI] [PubMed] [Google Scholar]
  16. Jack CR, Jr., Theodore WH, et al. MRI-based hippocampal volumetrics: data acquisition, normal ranges, and optimal protocol. Magn. Reson. Imaging. 1995;13(8):1057–1064. doi: 10.1016/0730-725x(95)02013-j. [DOI] [PubMed] [Google Scholar]
  17. Jenkinson M, Beckmann CF, et al. FSL. NeuroImage. 2012;62(2):782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
  18. Joshi S, Pizer S, et al. Multiscale deformable model segmentation and statistical shape analysis using medial descriptions. IEEE Trans. Med. Imaging. 2002;21(5):538–550. doi: 10.1109/TMI.2002.1009389. [DOI] [PubMed] [Google Scholar]
  19. Khan AR, Cherbuin N, et al. Optimal weights for local multi-atlas fusion using supervised learning and dynamic information (SuperDyn): validation on hippocampus segmentation. NeuroImage. 2011;56(1):126–139. doi: 10.1016/j.neuroimage.2011.01.078. [DOI] [PubMed] [Google Scholar]
  20. Khan AR, Wang L, et al. FreeSurfer-initiated fully-automated subcortical brain segmentation in MRI using large deformation diffeomorphic metric mapping. NeuroImage. 2008;41(3):735–746. doi: 10.1016/j.neuroimage.2008.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Langerak TR, van der Heide UA, et al. Label fusion in atlas-based segmentation using a selective and iterative method for performance level estimation (SIMPLE) IEEE Trans. Med. Imaging. 2010;29(12):2000–2008. doi: 10.1109/TMI.2010.2057442. [DOI] [PubMed] [Google Scholar]
  22. Lötjönen J, Wolz R, et al. Fast and robust extraction of hippocampus from MR images for diagnostics of Alzheimer’s disease. NeuroImage. 2011;56(1):185–196. doi: 10.1016/j.neuroimage.2011.01.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lötjönen JMP, Wolz R, et al. Fast and robust multi-atlas segmentation of brain magnetic resonance images. NeuroImage. 49(3):2352–2365. doi: 10.1016/j.neuroimage.2009.10.026. [DOI] [PubMed] [Google Scholar]
  24. Magnotta VA, Heckel D, et al. Measurement of brain structures with artificial neural networks: two- and three-dimensional applications. Radiology. 1999;211(3):781–790. doi: 10.1148/radiology.211.3.r99ma07781. [DOI] [PubMed] [Google Scholar]
  25. Morra JH, Tu Z, et al. Validation of a fully automated 3D hippocampal segmentation method using subjects with Alzheimer’s disease mild cognitive impairment, and elderly controls. NeuroImage. 2008a;43(1):59–68. doi: 10.1016/j.neuroimage.2008.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Morra JH, Tu Z, et al. Proceedings of the 11th International Conference on Medical Image Computing and Computer-assisted Intervention — Part I. Springer-Verlag; New York, NY, USA: 2008b. Automatic subcortical segmentation using a contextual model. [DOI] [PubMed] [Google Scholar]
  27. Morra JH, Tu Z, et al. Comparison of AdaBoost and support vector machines for detecting Alzheimer’s disease through automated hippocampal segmentation. IEEE Trans. Med. Imaging. 2010;29(1):30–43. doi: 10.1109/TMI.2009.2021941. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Mueller SG, Weiner MW, et al. The Alzheimer’s disease neuroimaging initiative. Neuroimaging Clin. N. Am. 2005;15(4):869–877. doi: 10.1016/j.nic.2005.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Nyúl LG, Udupa JK. On standardizing the MR image intensity scale. Magn. Reson. Med. 1999;42(6):1072–1081. doi: 10.1002/(sici)1522-2594(199912)42:6<1072::aid-mrm11>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
  30. Pantel J, O’Leary DS, et al. A new method for the in vivo volumetric measurement of the human hippocampus with high neuroanatomical accuracy. Hippocampus. 2000;10(6):752–758. doi: 10.1002/1098-1063(2000)10:6<752::AID-HIPO1012>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
  31. Pizer SM, Fletcher PT, et al. Deformable M-reps for 3D medical image segmentation. Int. J. Comput. Vision. 2003;55(2-3):85–106. doi: 10.1023/a:1026313132218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Powell S, Magnotta VA, et al. Registration and machine learning-based automated segmentation of subcortical and cerebellar brain structures. NeuroImage. 2008;39(1):238–247. doi: 10.1016/j.neuroimage.2007.05.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Rohlfing T, Maurer CR., Jr. Multi-classifier framework for atlas-based image segmentation. Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition; 2004. [Google Scholar]
  34. Rohlfing T, Russakoff DB, et al. Performance-based classifier combination in atlas-based image segmentation using expectation-maximization parameter estimation. IEEE Trans. Med. Imaging. 2004;23(8):983–994. doi: 10.1109/TMI.2004.830803. [DOI] [PubMed] [Google Scholar]
  35. Sdika M. Combining atlas based segmentation and intensity classification with nearest neighbor transform and accuracy weighted vote. Med. Image Anal. 2010;14(2):219–226. doi: 10.1016/j.media.2009.12.004. [DOI] [PubMed] [Google Scholar]
  36. Shen D, Moffat S, et al. Measuring size and shape of the hippocampus in MR images using a deformable shape model. NeuroImage. 2002;15(2):422–434. doi: 10.1006/nimg.2001.0987. [DOI] [PubMed] [Google Scholar]
  37. Sled JG, Zijdenbos AP, et al. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans. Med. Imaging. 1998;17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
  38. Tu Z, Bai X. Auto-context and its application to high-level vision tasks and 3D brain image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2010;32:1744–1757. doi: 10.1109/TPAMI.2009.186. [DOI] [PubMed] [Google Scholar]
  39. Twining CJ, Cootes T, et al. A unified information-theoretic approach to groupwise non-rigid registration and model building. Proceedings of the 19th International Conference on Information Processing in Medical Imaging; SpringerVerlag, Glenwood Springs, CO. 2005; pp. 1–14. [DOI] [PubMed] [Google Scholar]
  40. van der Lijn F, den Heijer T, et al. Hippocampus segmentation in MR images using atlas registration, voxel classification, and graph cuts. NeuroImage. 2008;43(4):708–720. doi: 10.1016/j.neuroimage.2008.07.058. [DOI] [PubMed] [Google Scholar]
  41. Vapnik VN. Statistical Learning Theory. Wiley; New York: 1998. [Google Scholar]
  42. Viola P, Jones MJ. Robust real-time face detection. Int. J. Comput. Vision. 2004;57(2):137–154. [Google Scholar]
  43. Wang H, Das SR, et al. A learning-based wrapper method to correct systematic errors in automatic image segmentation: consistently improved performance in hippocampus, cortex and brain segmentation. NeuroImage. 2011;55(3):968–985. doi: 10.1016/j.neuroimage.2011.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Warfield SK, Zou KH, et al. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans. Med. Imaging. 2004;23(7):903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Wu M, Rosano C, et al. Optimum template selection for atlas-based segmentation. NeuroImage. 2007;34(4):1612–1618. doi: 10.1016/j.neuroimage.2006.07.050. [DOI] [PubMed] [Google Scholar]
  46. Yanhua H, Carmona J, et al. Application of temporal texture features to automated analysis of protein subcellular locations in time series fluorescence microscope images; Biomedical Imaging: Nano to Macro, 2006. 3rd IEEE International Symposium; 2006. [Google Scholar]
  47. Yushkevich PA, Avants BB, et al. A high-resolution computational atlas of the human hippocampus from postmortem magnetic resonance imaging at 9.4 T. NeuroImage. 2009;44(2):385–398. doi: 10.1016/j.neuroimage.2008.08.04. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Yushkevich PA, Wang H, et al. Nearly automatic segmentation of hippocampal subfields in in vivo focal T2-weighted MRI. NeuroImage. 2010;53(4):1208–1224. doi: 10.1016/j.neuroimage.2010.06.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Zhou J, Rajapakse JC. Segmentation of subcortical brain structures using fuzzy templates. NeuroImage. 2005;28(4):915–924. doi: 10.1016/j.neuroimage.2005.06.037. [DOI] [PubMed] [Google Scholar]

RESOURCES