State-Dependent Function of Neocortical Chandelier Cells

Abstract

Chandelier (axoaxonic) cells (ChCs) are a distinct group of GABAergic interneurons that innervate the axon initial segments of pyramidal cells. However, their circuit role and the function of their clearly defined anatomical specificity remain unclear. Recent work has demonstrated that chandelier cells can produce depolarizing GABAergic PSPs, occasionally driving postsynaptic targets to spike. On the other hand, other work suggests that ChCs are hyperpolarizing and may have an inhibitory role. These disparate functional effects may reflect heterogeneity among ChCs. Here, using brain slices from transgenic mouse strains, we first demonstrate that, across different neocortical areas and genetic backgrounds, upper Layer 2/3 ChCs belong to a single electrophysiologically and morphologically defined population, extensively sampling Layer 1 inputs with asymmetric dendrites. Consistent with being a single cell type, we find electrical coupling between ChCs. We then investigate the effect of chandelier cell activation on pyramidal neuron spiking in several conditions, ranging from the resting membrane potential to stimuli designed to approximate in vivo membrane potential dynamics. We find that under quiescent conditions, chandelier cells are capable of both promoting and inhibiting spike generation, depending on the postsynaptic membrane potential. However, during in vivo-like membrane potential fluctuations, the dominant postsynaptic effect was a strong inhibition. Thus, neocortical chandelier cells, even from within a homogeneous population, appear to play a dual role in the circuit, helping to activate quiescent pyramidal neurons, while at the same time inhibiting active ones.

Introduction

In the early postnatal brain, the GABAergic system has a well-established excitatory role made possible by the relative expression levels of two transmembrane chloride transporters, KCC2 and NKCC1 (Ben-Ari, 2002). By adulthood, the balance of these transporters has been inverted in pyramidal neurons, resulting in a hyperpolarizing shift in E_Cl− and consequently E_GABA (Rivera et al., 1999; Yamada et al., 2004; Romo-Parra et al., 2008), and leading to the hyperpolarizing inhibition that is characteristic of GABAergic interneurons. However, some reports show excitatory GABAergic effects in mature neurons (Alger and Nicoll, 1982; Staley et al., 1995; Chavas and Marty, 2003; Gulledge and Stuart, 2003; Choi et al., 2008; Viitanen et al., 2010). While some of these excitatory effects result from intense, prolonged GABA_A receptor activation and a breakdown in the Cl⁻ gradient, and may occur predominantly under pathological conditions (Cohen et al., 2002), others rely simply on GABA_A reversal lying between the resting membrane potential and spike threshold.

Chandelier cells, also known as axoaxonic cells, are a particularly distinctive interneuronal type characterized by their axonal morphology, with arrays of boutons—termed cartridges—that resemble the candlesticks of a chandelier (Jones, 1975; Szentagothai, 1975; Somogyi, 1977; Howard et al., 2005). These cartridges are apposed to the axon initial segment of pyramidal neurons (Somogyi, 1977; Fairen and Valverde, 1980), suggesting a critical role for ChCs in controlling the output of their postsynaptic targets. Being GABAergic, ChCs were expected to provide a strong inhibition of action potential (AP) output, but recent work has suggested a more complicated picture, with the axonal GABA_A reversal potential (E_GABA) depolarized relative to rest and to other neuronal compartments (Szabadics et al., 2006; Khirug et al., 2008; Woodruff et al., 2009). This suggests that cortical chandelier cells may provide GABAergic excitation, in addition to the expected inhibition. At the same time, in CA1 hippocampus, ChCs appear to be mostly hyperpolarizing (Glickfeld et al., 2009), the exception being a direct suprathreshold excitation that has also been described in cortex (Szabadics et al., 2006; Molnar et al., 2008) and amygdala (Woodruff et al., 2006). This functional difference may be due to the different brain structures within which the ChCs reside. Alternatively, differences in ChC function may be due to their heterogeneity (DeFelipe et al., 1985; Inda et al., 2009), with different studies sampling different ChC subtypes.

Here we re-examine the function of the ChCs and their potential heterogeneity using ChCs identified in two types of transgenic mice. We first explore the morphological and electrophysiological diversity of upper-layer neocortical ChCs, demonstrating that they form a homogeneous population. We then test the ability of cortical ChCs to provide subthreshold excitatory input to pyramidal neurons under a variety of conditions, ranging from the resting state observed in in vitro slices to a scenario designed to approximate membrane potential dynamics in the awake animal. We demonstrate a capacity for ChCs to both promote and inhibit spike generation in pyramidal neurons during quiescent conditions. However, under conditions simulating high network activity, the dominant effect is inhibition.

Materials and Methods

Slice preparation and electrophysiological recordings.

Animal handling and experimentation was performed according to NIH and local Institutional Animal Care and Use Committee guidelines. G42 (Chattopadhyaya et al., 2004) and Nkx2.1 mice (Woodruff et al., 2009) of either sex were quickly decapitated, and 300 μm coronal slices were prepared using a Leica VT1000-S vibratome. Animals used for the cluster analysis of morphological and physiological properties ranged in age from postnatal day 16 (P16) to P25. Except for the cells shown in Figure 2, D and E, those used for the remainder of this paper (including the dendrite analysis in Fig. 2) were from animals aged P18–P25. The cutting solution contained the following (in mm): 27 NaHCO₃, 1.5 NaH₂PO₄, 222 sucrose, 2.6 KCl, 3.5 MgSO₄, and 0.5 CaCl₂. Slices were incubated for 30 min at 32°C in an oxygenated (95% O₂ and 5% CO₂) artificial CSF (ACSF), pH 7.4, solution containing the following (in mm): 126 NaCl, 3 KCl, 3 MgSO₄, 1 CaCl₂, 1.1 NaH₂PO₄, 26 NaHCO₃, and 10 dextrose. Slices were allowed to equilibrate for at least an additional 30 min at room temperature before being transferred to the recording chamber. The ACSF used for recording contained the following (in mm): 126 NaCl, 3 KCl, 1.5 MgSO₄, 2.5 CaCl₂, 1.1 NaH₂PO₄, 26 NaHCO₃, and 10 dextrose. Recordings were performed at 34−36°C using Multiclamp 700B amplifiers (Molecular Devices). Whole-cell pipettes contained a solution including the following (in mm): 127 K-methylsulfate, 8 NaCl, 8 KCl, 10 HEPES, 2 MgATP, 0.3 NaGTP, and 7 phosphocreatine, adjusted to pH 7.3 with 1 m KOH. Both Nkx2.1 and G42 mice were used for the experiments pertaining to cluster analysis of electrophysiological and morphological variables. All other experiments were performed solely on G42 mice.

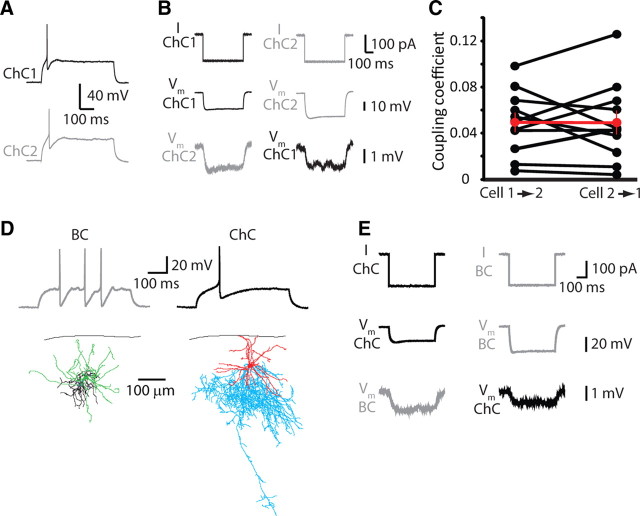
Figure 2.

Electrical coupling among chandelier cells. A, Threshold spiking response of two simultaneously recorded chandelier cells. B, Electrical coupling between a sample ChC–ChC pair. C, Summary data from 11 pairs. D, Physiologically identified basket and chandelier cells. Morphologies are shown below, with dendrites in green (BC) or red (ChC) and axons in black (BC) or blue (ChC). E, Electrical coupling was observed in the BC–ChC pair in D, taken from a P15 mouse.

Gramicidin perforated patch recordings were performed as described previously (Woodruff et al., 2009). Briefly, recording pipettes (3–5 MΩ) were filled with a solution containing the following (in mm): 140 KCl, 10 NaCl, 10 HEPES, and 20–25 μg/ml gramicidin (Sigma-Aldrich), adjusted to pH 7.3 with 1 m KOH. Gramicidin was prepared as a stock solution at 5 mg/ml and sonicated before being diluted into the pipette solution. The same solution, without gramicidin, was used to tip-fill pipettes. Both solutions were kept on ice for the duration of experiments. Following formation of a gigaseal, perforation was assessed by continuously presenting 10 mV test pulses to a cell voltage-clamped at −70 mV while recording series resistance. Recordings began once this value was below 80 MΩ (all data presented from cells with R_series 40–80 MΩ).

GABA_A reversal potential was measured in current clamp for gramicidin recordings, manipulating the holding potential of the pyramidal neuron by current injection through the patch pipette. For whole-cell measurements of E_GABA, pyramidal neurons were voltage clamped between −40 and −80 mV, in 10 mV increments. Series resistance was monitored throughout the experiment, and cells were discarded if this value changed significantly. All measurements of E_GABA were taken from the soma. For the Layer 1 (L1) stimulation experiments, we used an arbitrary cutoff value of 60 mV to represent the 100% spiking probability of a pyramidal neuron. For recordings at stimulus intensities lower than that required to generate spikes with 100% reliability, traces with spikes were digitally removed, and the remaining traces were averaged to calculate the peak EPSP.

Comparing V_m values for different internal solutions.

Whole-cell membrane potential values have not been corrected for liquid junction potential (LJP), to facilitate comparison with values obtained in previous studies using whole-cell recordings in vivo, in which junction potential (typically with K-gluconate) (Crochet and Petersen, 2006; Poulet and Petersen, 2008; Constantinople and Bruno, 2011) is not corrected for. Membrane potential values obtained using gramicidin recordings have been corrected for the calculated LJP of the gramicidin internal (+3.0 mV), for the donnan potential (−6.2 mV, Woodruff et al., 2009) formed across the cell membrane due to chloride impermeability (Kim and Trussell, 2007), and additionally for the LJP of the KMeSO₄ solution we used in whole-cell recordings (+8.36 mV). The values given for membrane potential throughout the paper are therefore equivalent for the two recording techniques and represent the value that is or would be recorded using our KMeSO₄ internal solution. Based on the difference in calculated LJP between our KMeSO₄ and reported K-gluconate solutions, our V_m values are likely ∼7 mV more hyperpolarized than the equivalent values reported for in vivo K-gluconate recordings.

Biocytin histochemistry, cell reconstruction, and morphological analysis.

At the end of an experiment, slices were fixed and kept overnight in 4% paraformaldehyde in 0.1 m phosphate buffer (PB) at 4°C. Slices were then rinsed three times, for 5 min per rinse, on a shaker in 0.1 m PB. They were then placed in 30% sucrose mixture (30 g sucrose dissolved in 50 ml ddH₂0 and 50 ml 0.24 m PB) for 2 h and frozen on dry ice in tissue-freezing medium. Following this, slices were kept overnight in a −80°C freezer. The slices were defrosted, and the tissue freezing medium was removed with three 20 min rinses in 0.1 m PB while on a shaker. Slices were kept in 1% hydrogen peroxide in 0.1 m PB for 30 min on the shaker to pretreat the tissue, and were then rinsed twice in 0.02 m potassium phosphate saline (KPBS) for 20 min on the shaker. The slices were then kept overnight on the shaker in avidin–biotin–peroxidase complex. Slices were rinsed three times in 0.02 m KPBS for 20 min each on the shaker. Each slice was then placed in DAB (0.7 mg/ml 3,3″-diaminobenzidine, 0.2 mg/ml urea hydrogen peroxide, 0.06 m Tris buffer in 0.02 m KPBS) until the slice turned light brown, then immediately transferred to 0.02 m KPBS, and finally transferred again to fresh 0.02 m KPBS after a few minutes. The stained slices were rinsed a final time in 0.02 m KPBS for 20 min on a shaker. Each slice was observed under a light microscope and then mounted onto a slide using crystal mount.

Successfully filled and stained neurons were then reconstructed using Neurolucida software (MicroBrightField). The neurons were viewed with a 100× oil objective on an Olympus IX71 inverted light microscope or an Olympus BX51 upright light microscope. The Neurolucida program projected the microscope image onto a computer drawing tablet. The neuron's processes were traced manually while the program recorded the coordinates of the tracing to create a digital, three-dimensional reconstruction. Dendrite polar plots were computed with 20 bins (18° per bin). The total dendritic length per bin was calculated using Neurolucida Explorer for each neuron, and the length per bin was averaged across all ChCs or basket cells (BCs) to create the polar plots. Statistical analysis was performed in GraphPad InStat.

Cluster analysis.

Morphological and physiological properties of chandelier cells were quantitatively characterized by 67 morphological variables describing the soma, dendrites, axons, and cell location, and by 20 physiological parameters describing both passive membrane and firing properties. For the purposes of cluster analysis, we used data from both G42 and Nkx2.1 mice (Woodruff et al., 2009) and found no effect of genotype on the morphological and physiological properties of ChCs. Although the neurons reconstructed for morphological cluster analysis were different from the ones used for the functional study, since both subsets of neurons were drawn from the same population of GFP labeled cells, we have no reason to believe that they could represent different subtypes of ChCs.

Cluster analysis was performed after dimensionality reduction using either principal component analysis (PCA) or feature subset selection (FSS) by correlation filter. The principal components (PCs) were calculated in Matlab, and the number of PCs to use for clustering was selected based on the scree test, in which a plot of the eigenvalues in descending order is examined for when the decrease in eigenvalues plateaus (Cattell 1966). FSS by correlation filter was executed with Knime software. The filter works by keeping the variable with the highest number of correlated variables and removing those correlated with it. “Correlated” is defined as having a correlation coefficient greater than or equal to a threshold set by the user, here set to r = 0.8. This process is repeated until the maximum correlation between variables is less than the selected threshold. We performed unsupervised hierarchical cluster analysis using Clustan software with Euclidean distance squared as the distance metric and Ward's method as the linkage rule. Three statistical tests were performed to determine whether there was a level of clustering with significant (p < 0.05) groups. The best-cut test does an analysis of variance on the fusion values (distance at which two clusters join) at every level in the dendrogram. The realized deviates, defined as the standardized difference between a fusion value and the mean fusion value, are compared to find significantly large realized deviates that are at least 1.96 SDs from the mean. The upper tail test applies the upper-tailed t test to the fusion values using the t statistic of realized deviate * (n − 1) over n − 2 degrees of freedom. The bootstrap test performs 1000 trials of randomizing the data and performing cluster analysis on the randomized data, and then compares the random trees to the actual tree. The data matrix was randomized by shuffling the values for each column (variable) independently. The random trees were compared to the actual tree by plotting the fusion value versus the number of clusters for the actual data and the distribution of the randomized data with a confidence interval of 1 SD around the mean. Significant departures of the actual fusion values from random, determined by the t statistic, indicate a number of clusters that are statistically significant.

The quality of clustering was also measured with silhouette analysis, which compares within-cluster and between-cluster distances (Rousseeuw, 1987). The silhouette value of a data point i in cluster A is as follows:

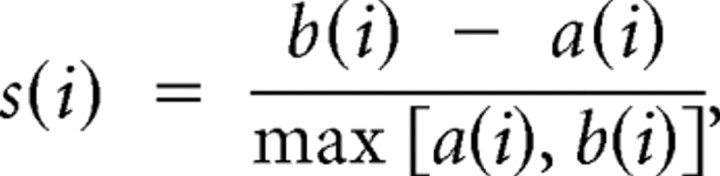where a(i) is the average Euclidean distance between i and all other data points in cluster A, b(i) is the smallest average Euclidean distance between i and all data points contained in one cluster. The value of s(i) is between −1 and 1. The silhouette width of a clustering is defined as the average of s(i) for all data points. Large positive values indicate that the cluster is compact and well separated from other clusters. To determine whether the clustering achieved a significantly better group structure than random, the data was randomized (using the same method as for the bootstrap test above), and then cluster analysis and silhouette analysis were performed on 500 randomized data sets. S(random) is the average of the 500 random silhouette widths.

In vivo-like noise stimulation.

In one set of experiments, we aimed to match the membrane voltage characteristics of the prespike depolarization (PSD) reported by Poulet and Petersen (2008) and Gentet et al. (2010). To test the effect of ChC spikes under these conditions, we subjected pyramidal neurons to repeated presentations of a 1-s-long frozen current stimulus and fired the ChC (through a short current stimulus) at different times before or after an expected pyramidal spike. The noise stimulus for the pyramidal cell was drawn from low pass filtered white noise kernels (time constant, τ = 5 ms). To mimic in vivo dynamics, we selected two sequences that produced prespike depolarizations similar to those reported in vivo and evoked single spikes rather than bursts. To facilitate later analysis, we decreased the amplitude of the stimulus kernel at the beginning and end of the stimulus and faded into/out of the stimulus slowly to avoid spiking during the initial and final 70 ms.

To create an appropriate current signal for each neuron from the stimulus kernel, we adjusted the DC offset and peak-to-peak amplitude (referred to here as “stretch”) of the signal to approximate in vivo membrane potential dynamics with mean membrane potentials of approximately −65 mV, minima of approximately −75 mV, and peak-to-peak amplitudes of ∼25 mV (excluding spikes). Additionally, we aimed for the occurrence of one to two spikes throughout a single stimulus episode with spike probabilities between ∼0.3 and 0.7. We intentionally manipulated the maximum negative value of the prespike depolarization to be below E_GABA to allow for depolarization and potential excitation from the presynaptic chandelier cell.

Having found appropriate offset and stretch parameters, the pyramidal neuron was initially subjected to 200 repetitions of the frozen noise stimulus. The resulting peristimulus spike time histograms were used to determine the expected spike times in response to the stimulus sequence.

We then chose appropriate stimulation times for the chandelier cell to fire an action potential at randomly interleaved times Δt = (−40, −20, or −5 ms), or Δt = (−30, −15, or −5 ms) before the expected pyramidal spike. We additionally interleaved control trials at Δt = +50 ms after the expected pyramidal spike. We then recorded the spiking response of the pyramidal neuron to 400–800 presentations of the same frozen current stimulus, but this time with the additional presynaptic ChC stimulation, corresponding to 100–200 trials in each of 3 + 1 randomly interleaved Δt conditions. The randomized order of four Δt intervals was chosen to eliminate time-dependent variations in pyramidal neuron spiking. Because of slow drift in the pyramidal neuron membrane potential, small positive and negative offset currents were sometimes applied during recording to prevent the pyramidal cell from firing (or not firing) on every trial. Such currents were applied when more than ∼10 consecutive trials showed the same response (spike or no spike). We reasoned that because Δt presentation was randomized, this was not deleterious to the experiment and should not greatly bias our results, and certainly the experimenter would be blind to the direction of any bias.

Results

We used both Nkx2.1 mice (Woodruff et al., 2009) and the G42 line of bacterial artificial chromosome (BAC) transgenic mice, in which parvalbumin-positive (PV+) interneurons express EGFP (Chattopadhyaya et al., 2004), to record from chandelier cells in Layer 2/3 (L2/3) of motor and somatosensory cortical slices. In brain slices from G42 mice, in contrast to the Nkx2.1 mice, the distinctive axonal arborizations of ChCs could not be seen under wide-field illumination, so prepatch knowledge of the neuron's identity as ChC or BC was not possible. By restricting our recordings to the top ∼30 μm of the layer, adjacent to Layer 1, we nevertheless estimate the probability of a targeted GFP neuron in a G42 animal being a ChC at ∼50–70%. Chandelier cells were clearly distinguished from BCs on the basis of their threshold spiking response (Woodruff et al., 2009) (Fig. 2A,D).

Anatomical homogeneity of sampled chandelier cells

We first explored the morphological and physiological diversity of our studied population of neocortical chandelier cells. For this purpose, we reconstructed the morphology of 23 ChCs, and 67 morphological variables (Table 1) describing the soma, dendrites, axon, and location of the cell were extracted from the reconstruction. To determine whether these ChCs belonged to different populations, we first used unsupervised cluster analysis to test for the existence of statistically different subtypes of neurons, based on morphological properties of the recorded ChCs. One of two dimensionality reduction techniques, either PCA or FSS using a correlation filter, was applied before cluster analysis. Three statistical tests were used to determine a significant level (p < 0.05) of clustering (see Materials and Methods). For the morphology data set, the correlation filter removed 27 variables, and cluster analysis with the remaining 40 variables had no significant divisions (data not shown). In cluster analysis with PCA, the bootstrap and two-tailed tests also failed to find any significant divisions. Nevertheless, the best-cut test found significance at the three- and two-cluster levels, indicating the potential existence of different subtypes of ChCs (Fig. 1A, purple, dark orange, light blue clusters, division marked above 6 Euclidean distance squared).

Table 1.

Morphological variables

Variable	Description
Variables describing the soma
Somatic perimeter (μm)	Perimeter of the soma
Somatic area (μm2)	Area of the soma
Somatic aspect ratio	Max. diameter of soma/min. diameter of soma
Somatic compactness	[([4/π] * area)1/2]/max. diameter
Somatic form factor	(4π * area)/(perimeter 2)
Somatic roundness	(4 * area)/(π * max. diameter 2)
Variables describing the axon
Axonal node total	Total number of axonal nodes (branching points)
Total axonal length (μm)	Sum of lengths of all axon segments, measured along tracing (not straight line distance)
Total surface area of axon (μm2)	2πr2 + 2πrh, surface area calculated by modeling axon as a cylinder with diameter defined by thickness of segment in reconstruction
Ratio of axonal length to surface area (1/μm)	Total axonal length/total surface area of axon
Highest-order axon segment	Maximum number obtained after each segment is numbered by how many nodes it is removed from the initial segment
Axonal torsion ratio	Total axonal length/total axonal length of fan in diagram where the fan in diagram is 2D projection of the neuron constructed by compiling traces swept around a vertical axis; torsion ratio = 1 corresponds to no loss of length; values larger than 1 correspond to the factor by which the processes have decreased in the fan in diagram
K-dim of axon	Fractal dimension of the axon calculated using linear regression and the nested cubes method
Axonal polar angle average	Average of polar angles of all axonal nodes; the polar angle is the angle between the two lines passing through the node and the endpoints of the next segments
Axonal polar angle SD	SD of axonal polar angles
Axonal local angle average	Average of local angles of all axonal nodes; the local angle is the angle between the two lines passing through the node and points adjacent to the node on the two following segments
Axonal local angle SD	SD of axonal local angles
Axonal spline angle average	Average of spline angles of all axonal nodes; the spline angle is the angle between the two lines passing through the node and smoothed points adjacent to the node when the following two segments are approximated by a cubic spline
Axonal spline angle standard	SD of axonal spline angles

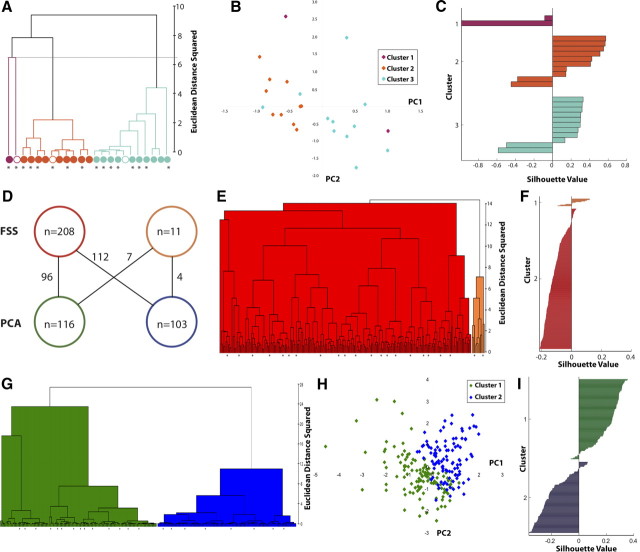
Figure 1.

Cluster analysis of chandelier cells. A, Ward's method of hierarchical unsupervised cluster analysis based on 67 morphological variables applied to 23 ChCs following PCA. The cutoff linkage for three clusters is marked with a gray line, and each cluster is given a different color. Open circles indicate the centroid of the cluster. B, Scatterplot in the principal component space of the three clusters shown in A. C, Silhouette analysis of the three clusters shown in A. D, Comparison of dimensionality reduction techniques. Map between the physiological clusters found using FSS correlation filter (top) and PCA (bottom). The numbers on the lines indicate how many cells belong to both of the clusters. E, Ward's method of hierarchical unsupervised cluster analysis based on 20 electrophysiological variables applied to 219 ChCs following correlation filter. F, Silhouette analysis of two clusters shown in E. G, As in E, but with PCA as the dimensionality reduction technique. H, Scatterplot in the principal component space of the two clusters shown in G. I, Silhouette analysis of the two clusters shown in G.

We therefore decided to further investigate the group structure of the three- and two-cluster levels found by cluster analysis with PCA, analyzing the three-cluster level for any further evidence of group structure. The data set was plotted in principal component space to search for separation of clusters. The first three principal components were used for analysis based on the scree test and on their carrying >60% of the variance (see Materials and Methods). In all three planes (PC1–PC2, PC1–PC3, and PC2–PC3) and in three-dimensional space, the clusters were not distinct and boundaries of the cluster areas overlapped (Fig. 1B). We assessed the quality of clustering with silhouette analysis (see Materials and Methods). The silhouette plot for the morphological data set showed a very weak group structure, with Clusters 2 and 3 containing cells with moderate positive and negative values, and all Cluster 1 cells having a negative value (Fig. 1C). The silhouette width of the data set was approximately zero, indicating that the clusters were not well separated and not significantly different from the average result of 500 trials of cluster and silhouette analysis on randomized data sets (see Table 3). Thus, the silhouette analysis agreed with the hypothesis that the three clusters are an arbitrary division of the data set.

Table 3.

Silhouette values

Data set	S(actual)	S(random) ± SD
219 cells, electrophysiology, two clusters, FSS	−0.107	0.081 ± 0.046
219 cells, electrophysiology, two clusters, PCA	0.044	0.117 ± 0.130
23 cells, morphology, three clusters, PCA	−0.050	0.058 ± 0.203
23 cells, morphology, two clusters, PCA	−0.031	0.020 ± 0.258

Comparison of silhouette widths of each data set to the mean silhouette width of 500 trials of clustering randomized data ± SD.

As the three-cluster division produced no valid groups, we proceeded to analyze the two-cluster division found after PCA (Fig. 1A, purple and orange vs blue cells; division at 8 Euclidian distance squared) with the same analysis method. The two-cluster division also did not have a valid group structure, with poor separation in principal component space, no distinguishing features, and a silhouette value not significantly different from random (data not shown). Based on this analysis, we concluded that there was no substructure to the morphological database, as both the two- and three-cluster PCA divisions did not withstand a more rigorous statistical examination. Therefore, the chandelier cells we recorded from appear to be morphologically homogeneous, indicative of a single, indivisible population.

Physiological homogeneity of sampled chandelier cells

We then performed a completely independent analysis of the physiological characteristics of the database of 219 recorded ChCs. We extracted 20 variables describing passive membrane properties and firing properties (Table 2) from whole-cell current-clamp recordings. The same three statistical tests were applied to determine a significant level (p < 0.05) of clustering. The FSS correlation filter did not remove any variables, and cluster analysis with all 20 variables was found to have no significant clusters by the bootstrap and two-tailed test. However, the best-cut test found significance at the two-cluster level (Fig. 1E, red and light orange clusters). For cluster analysis with PCA, the bootstrap and best-cut tests failed to find significance, while the two-tailed test found significance at the seven-, four-, three-, and two-cluster levels (Fig. 1G, green and blue clusters illustrating the two-cluster level). However, on further analysis, the two clusters found by cluster analysis with FSS correlation filter and with PCA did not correspond well to each other, with neurons from the two FSS clusters equally distributed between both PCA clusters (Fig. 1D).

Table 2.

Physiological variables

Variable	Description
Resting membrane potential (mV)	Stable membrane potential when no current applied
Input resistance (MΩ)	Calculated from small hyperpolarizing or depolarizing current steps (≤10 mV deflection)
Rheobase (pA)	Threshold current
AP1 amplitude (mV)	Amplitude of the first AP
AP1 duration (ms)	Time from onset of first AP, calculated as an increase ≥1 mV/100 ms to offset, calculated as return to same voltage as before AP onset
AP1 half-width (ms)	Time from half-amplitude during rise to halfamplitude during fall of first AP
AP1 rise time (ms)	Time from onset to peak of first AP
AP1 fall time (ms)	Time from peak to offset of first AP
AP1 rise rate (mV/ms)	AP1 amplitude/AP1 rise time
AP1 fall rate (mV/ms)	AP1 amplitude/AP1 fall time
AP drop (mV)	AP1 amplitude-AP2 amplitude
Spike frequency adaptation	t2/t1, where t1 is the time between the peaks of the first two APs (interspike interval) and t2 is the last interspike interval
Frequency (Hz)	Number of APs/0.5 s duration of 2× threshold stimulus

Action potential properties were measured from the first action potential (AP1) and second action potential (AP2) in response to 500 ms twice threshold current injection. AP2 variables not listed were calculated in the same way as AP1 variables.

As cluster analysis results using two different dimensionality reduction techniques both had significant but differing results at the two-cluster level, we chose to further analyze those divisions to test whether either could be a description of subtypes. We first analyzed the group structure of the two clusters found by cluster analysis with correlation filter (Fig. 1E). Poor separation of the clusters was evident in the silhouette plot, in which the majority of cells in the larger cluster have a negative silhouette value (Fig. 1F). The silhouette width was significantly different (p < 0.01) from random, with a more negative value than the randomized trials indicating a lack of group structure (Table 3). Thus, the physiological division of ChCs using correlation filter does not appear to be a valid division.

Next, we tested the two clusters found by cluster analysis with PCA (Fig. 1G, blue and green) for group structure using the same methods as above. We reasoned that if the two clusters found by cluster analysis with PCA demonstrated evidence of group structure, we could then analyze the finer distinctions at the three-, four-, and seven-cluster levels. Indeed, the two-cluster level appeared to withstand our initial statistical analysis: in principal component space, the two clusters roughly divided the area; however, the clusters had overlapping boundaries, so these two territories were not clearly distinct (Fig. 1H). To identify potential variables that differentiated between the two groups, we performed statistical tests, finding that rheobase was the only variable with significant difference between clusters (p < 0.05; Cluster 1, 224.26 ± 72.71 pA; Cluster 2, 170.63 ± 66.37 pA, Mann–Whitney test). To determine whether rheobase could be used as a basis to define physiological subtypes of ChCs, we analyzed the ranges of rheobase values across the two PCA clusters, finding almost identical ranges for Clusters 1 and 2 (cluster 1, 75–470 pA; Cluster 2, 60–400 pA). Therefore, cluster membership could not be determined based on rheobase, as the majority of rheobase values are included in the range of both clusters. Finally, we applied silhouette analysis, which also did not support the two clusters being distinct ChC groups. While the first cluster had predominantly positive silhouette values, the second cluster had predominately negative silhouette values, and the silhouette width was not significantly different from random (Fig. 1I; Table 3).

Overall, the electrophysiological database did not reveal clear differences among potential subtypes of ChCs. While some cluster structure was present in the two-cluster divisions of both correlation filter and PCA, these clusters were inconsistent among themselves, were not based on clearly defined differences in any electrophysiological variables, and had weak silhouette widths. Finally, even though neither clustering by morphology nor clustering by physiology variables produced meaningful subtypes of ChC, it is possible that a multiparameter analysis is needed to define ChC subtypes. Accordingly, we performed cluster analysis based on the combined morphology and electrophysiology variables, using the 23 neurons for which we had both reconstructions and patch-clamp recordings. None of the three statistical tests found a significant level of clustering in either results using FSS or PCA (data not shown). Therefore, the simplest interpretation of our morphological and physiological analysis is that the population of neocortical ChC cells that we sampled is homogeneous.

Gap junctional coupling among ChCs

Electrical coupling between GABAergic interneurons is a common network property and has been suggested to aid in the concerted activity of interneuron populations of the same subtype (Beierlein et al., 2000). Separate support for our classification of the recorded ChCs as a homogenous population came from experiments in which we recorded from two ChCs in close proximity to each other. On 11 occasions, we found weak electrical coupling between these cells (coupling coefficient, 0.05 ± 0.01; n = 11 pairs, tested bidirectionally; Fig. 2A–C). We estimate that coupling occurred in >80% of simultaneously recorded ChC pairs. Aside from the frequent heterologous coupling seen for neurogliaform cells (Simon et al., 2005; Zsiros and Maccaferri, 2005), the finding of electrical coupling among ChCs is consistent with a large volume of work indicating cell-type specific electrical coupling within interneuron subtypes (Hestrin and Galarreta, 2005). At the same time, on one occasion we also encountered gap-junctional coupling between a ChC and BC (identified electrophysiologically and morphologically; Fig. 2D,E), so, although rare, it is in principle possible to find occasional coupling between ChCs and BCs.

Dendritic polarity of ChCs

In our anatomical study, we noticed that the dendrites of the sampled ChCs were characteristically asymmetric, predominantly targeting Layer 1 (Fig. 3A). Extensive Layer 1 dendrites and minimal arborization within Layer 2/3 were not, however, consistent features, with some ChCs showing little to no preference for extending dendritic branches to Layer 1. Nevertheless, comparison of ChC dendritic trees with those of BCs (Fig. 3C) revealed distinct dendritic morphologies. Whereas basket cells appeared isotropic in their dendritic orientation, ChCs showed clear polarization and a preference for vertically projecting dendrites (Fig. 3B,D). We quantified the difference in Layer 1 dendrites, finding a considerable difference in the total length of L1 dendrites (ChC, 1365 ± 198 μm, n = 8; BC, 542 ± 199 μm, n = 6; p < 0.01), which could not be attributed to differences in overall dendritic length (ChC, 1799 ± 189 μm; BC, 1832 ± 312 μm; p = 0.92; Fig. 3F). Thus, the proportion of the dendritic arbor confined to Layer 1 differed significantly between ChCs and BCs (ChC, 76 ± 6%, n = 8; BC, 27 ± 8%, n = 6; p < 0.01 vs ChC; Mann–Whitney two-tailed test; Fig. 3G). This could not be explained simply by a difference in distance of ChC and BC somata from the Layer 1 border (ChC, −10 ± 5 mm; BC, −19 ± 6 mm; p = 0.49; Mann–Whitney two-tailed test; Fig. 3E). The chandelier cells from which we record in this study, located at the top of L2/3, therefore comprise an electrically coupled network of neurons with a preference for extending dendrites to Layer 1.

Figure 3.

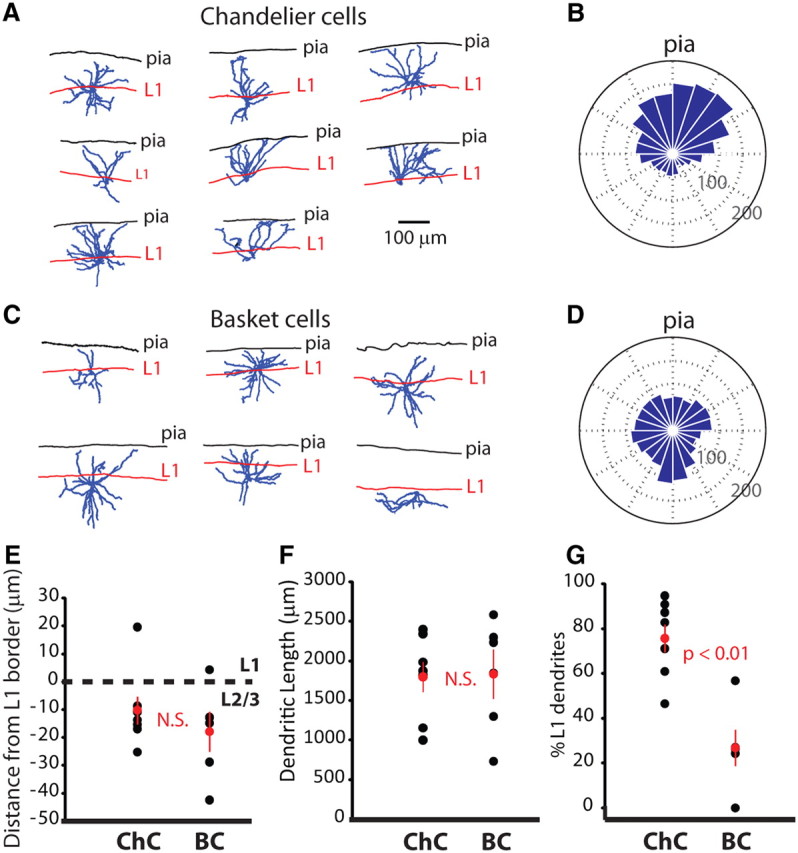
Dendritic morphology of upper Layer 2/3 chandelier and basket cells. A, Neurolucida reconstructions of ChCs used for analysis of dendritic Layer 1 preference. B, Polar plot of dendritic length and location. Neuronal somata are located at center of plots, and the average dendritic length across cells is plotted in 18° bins. The pia is at the top, and distance is indicated by dashed circles. C, D, Same as for A and B for basket cells. E, Location of ChC and BC somata relative to the L1–L2/3 border. F, Total dendritic length for ChCs and BCs. G, Proportion of ChC and BC dendrites located in Layer 1. Remaining dendrites were in Layer 2/3. Error bars indicate SEM.

Chandelier cells can promote or inhibit pyramidal neuron spiking

After this basic morphological and electrophysiological characterization, we focused on analyzing the functional effect of ChCs on the spiking of pyramidal cells. To do this, we made paired recordings and assessed their impact under different experimental conditions. The first set of experiments investigated ChC impact during static membrane potential conditions, most closely approximating the so-called DOWN state observed in anesthetized or sleeping animals (Steriade et al., 1993). The second set investigated the effect of ChC activity in response to electrical stimulation of an afferent pathway, and the third set analyzed ChC impact during awake-like membrane potential fluctuations. Although we performed some experiments using the gramicidin perforated patch technique, the majority of experiments throughout this study were performed in whole cell, using an intracellular pipette solution that contained an elevated chloride concentration. After accounting for the different ionic concentrations in the intracellular solutions (see Materials and Methods), the reversal potential of the ChC–pyramidal neuron synapse obtained in whole cell was not statistically different from E_GABA measured with gramicidin (whole-cell E_GABA, −54.0 ± 0.7, n = 23; gramicidin E_GABA, −51.4 ± 2.2, n = 17; p = 0.20; Fig. 4A).

Figure 4.

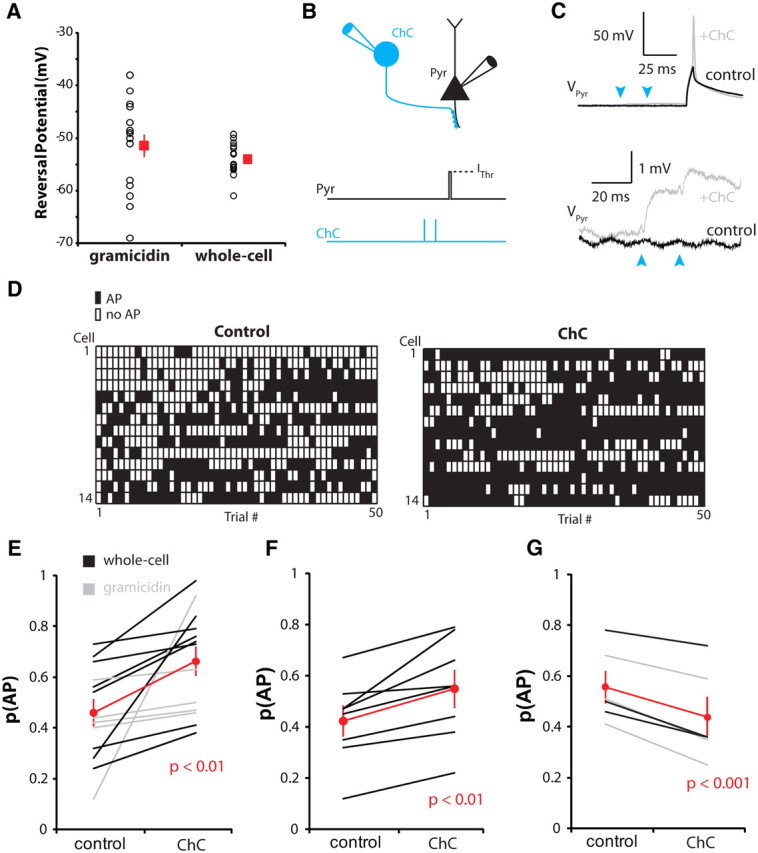
Chandelier cells can both excite and inhibit postsynaptic pyramidal neurons. A, GABA_A reversal potential recorded with gramicidin perforated patch, or in whole cell using an elevated internal chloride concentration. Inset, Traces from one pair recorded in whole cell, voltage clamped at −80 to −40 mV. Calibration: 10 pA, 10 mV. B, Schematic of the recording configuration. C, Example traces from a pyramidal neuron during control (black) and stimulation (gray) trials. Bottom, Expanded traces to illustrate depolarizing ChC input. D, Trial-by-trial plots of pyramidal neuron spiking for individual experiments. E–G, Summary graphs for pyramidal neurons at rest (E), depolarized but below E_GABA (F), and depolarized above E_GABA (G). Error bars indicate SEM.

For the first set of experiments, pyramidal neurons were stimulated from their resting membrane potential (−81.8 ± 1.4 mV) with a brief current pulse of an amplitude set to semireliably evoke APs. This amplitude varied between cells and was determined before each experiment. On alternate trials, two APs separated by 20 ms were evoked in the presynaptic ChC before pyramidal cell stimulation (Fig. 4B,C). This evoked depolarizing GABAergic PSPs (GPSPs), which typically peaked on the second of the two PSPs (peak, 1.0 ± 0.2 mV). Using this protocol, ChCs reliably increased spike probability in the postsynaptic pyramidal neuron (control, 0.46 ± 0.05; ChC, 0.66 ± 0.06, n = 13; p < 0.01; Fig. 4D,E), although the magnitude of effect varied considerably between cells. We next performed the same experiment, but after having depolarized the pyramidal neuron from rest to a level that nevertheless remained below E_GABA (V_m = −66.2 ± 1.2 mV) and that was close to reported V_m values in awake mice (Gentet et al., 2010) (different internal solutions, see Materials and Methods, Comparing V_m values for different internal solutions). The ChC synapse therefore remained depolarizing (peak GPSP2, 0.5 ± 0.1 mV) and again reliably increased pyramidal neuron spike probability (control, 0.42 ± 0.06; ChC, 0.55 ± 0.07, n = 8; p < 0.01; Fig. 4F). Depolarizing the pyramidal neuron to E_GABA or beyond reversed the ChC effect, with spike probability consistently decreasing from 0.56 ± 0.06 to 0.44 ± 0.08 (p < 0.001; n = 6; Fig. 4G). Under these slice conditions, during which the pyramidal neuron membrane potential is essentially static while receiving ChC input, chandelier cells of cortical Layer 2/3 can therefore both promote or inhibit pyramidal neuron output, depending on the pyramidal neuron membrane potential.

The above experiments were performed with the GPSP preceding the current injection by 30 ms (Δt = +30 ms). We also performed the same experiments for Δt = +5 or Δt = +15 ms, to assess the impact of the underlying GABA_A conductance change on the ability to promote spiking. For both time points, the depolarization provided by the ChC GPSP overcame the inhibitory shunt provided by channel opening, leading to increases in spike probability [normalized probability of an action potential, p(AP) +5 ms, 1.8 ± 0.5, p = 0.06 vs control; +15 ms, 1.6 ± 0.1, p < 0.001; +30 ms, 1.4 ± 0.2, p < 0.05). We expect the conductance effect to be stronger at shorter time intervals, although we did not check. However, it should be noted that the ChC synapse is quite electrotonically isolated from the source of glutamatergic excitation on dendritic spines, and that by using somatic current injection rather than dendritic inputs, we are likely overestimating the true shunt provided by the ChC synapse on excitatory synaptic inputs.

Electrical stimulation of Layer 1 enforces ChC-mediated feedforward inhibition

As described above, the ChCs from which we recorded frequently had numerous dendrites extending into Layer 1, and it would therefore seem that the majority of afferent excitation will arise through this pathway. Although in principle many other types of interneurons, such as basket cells, could be activated by Layer 1 inputs, the peculiar asymmetric dendritic morphology of ChCs could make them particularly tuned to Layer 1 activation. To study this, and because the primary target of Layer 2 ChCs is Layer 2/3 pyramidal neurons, whose apical dendrites also extend into Layer 1, we used electrical stimulation of this uppermost cortical layer to assess the impact of ChC activation on Layer 2/3 pyramidal neurons (Fig. 5A).

Figure 5.

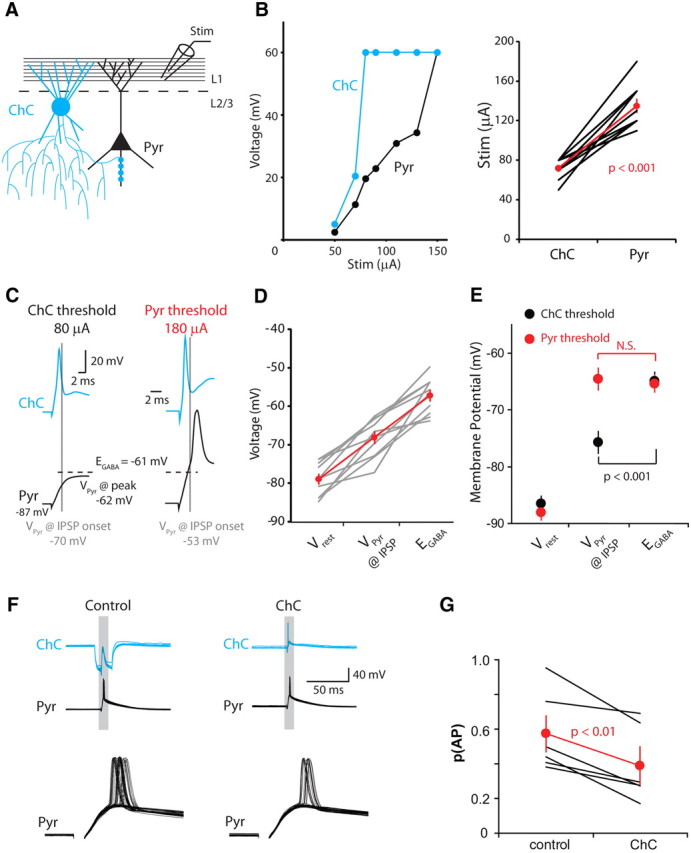
Electrical stimulation of Layer 1 recruits ChC-mediated inhibition. A, Schematic of the recording configuration. Pyramidal neurons were recorded with gramicidin. B, Left, Recruitment of ChC (blue) and pyramidal neuron to increasing stimulation strengths. Action potential amplitude is indicated by a voltage of 60 mV. Right, Summary data showing the minimum stimulation intensity required to evoke spikes in 100% of trials for ChCs and pyramidal neurons. C, Responses of recorded neurons at two stimulation intensities, ChC threshold (left) and pyramidal neuron threshold (right). D, Cell-by-cell plot of the relationship between E_GABA and the ChC GPSP at the stimulation intensity required for ChC activation. E, ChC GPSP polarity depends on the strength of afferent stimulation. F, Assaying ChC effect on pyramidal neuron spiking by applying large hyperpolarizing pulses to the ChC on alternate trials. G, At the stimulation strength required to activate pyramidal neurons, ChCs are strictly inhibitory. Error bars indicate SEM.

A glass stimulating electrode containing ACSF was placed approximately midway between the pia and Layer 2, 50–150 μm laterally displaced from the location of the ChC and pyramidal neuron cell bodies. For ChCs to influence pyramidal neurons, ChCs must be recruited both more easily than and before their postsynaptic partners. We found this to be the case for all ChC–pyramidal neuron synapse pairs recorded from (Fig. 5B). Chandelier cells required 72 ± 3 μA and pyramidal neurons 135 ± 7 μA to be activated (n = 10; p < 0.001).

At the stimulation strength required to activate ChCs, we measured pyramidal neuron V_m at the onset of the IPSP, taken here to be 1 ms after the peak of the presynaptic spike. Pyramidal neurons were consistently below E_GABA for that particular synapse at the onset of the GPSP (V_Pyr = −68.1 ± 0.1 mV; E_GABA = −57.2 ± 1.2 mV; n = 10; p < 0.001; Fig. 5C,D). The peak voltage reached by the EPSP in response to Layer 1 stimulation was −60.4 ± 2.1 mV, not significantly different from E_GABA. Thus, at IPSP onset, the ChC synapse is depolarizing, but rapidly switches to a predominantly shunting effect during Layer 1 stimulation. Although the ChC GPSP was depolarizing and thus potentially excitatory, we were unable to directly assay the impact on pyramidal neuron spiking without further increasing stimulation intensity. We increased stimulation strength to enable pyramidal neuron spiking, which decreased the latency of the ChC spike and allowed it to influence the pyramidal neuron (Fig. 5C). At this stimulation intensity, the more rapid rise of the pyramidal neuron V_m converted the ChC synapse to shunting at GPSP onset and hyperpolarizing immediately before spike generation (Fig. 5C,E). To measure the effect of ChC activation on pyramidal neurons during this protocol, we applied large hyperpolarizing pulses to the ChC on alternate trials to prevent ChC spikes (Fig. 5F). The consequent absence of ChC spikes was associated with an increase in pyramidal neuron spiking, revealing that under these conditions, chandelier cells decrease pyramidal neuron spike probability (control, 0.57 ± 0.1; ChC, 0.39 ± 0.1, n = 6; p < 0.01; Fig. 5G). This effect confirmed that the ChC was indeed firing before the pyramidal neuron and that the readout of the pyramidal neuron spike was not drastically affected by the relatively high R_series of the perforated patch configuration. Electrical stimulation of cortical Layer 1 therefore recruits a ChC-mediated feedforward inhibition of Layer 2/3 pyramidal neurons.

ChC effect during in vivo-like noise stimulation

We next performed experiments aimed at approximating, as closely as possible, the conditions under which Layer 2/3 cortical pyramidal neurons have been reported to fire in the awake animal. To do this, we generated a filtered white noise stimulus whose peak-to-peak amplitude and depolarizing offset could be adjusted (Fig. 6A, left). Although neuronal membrane potential fluctuates considerably during both the resting and actively behaving states (Crochet et al., 2011), the period immediately preceding spike generation in Layer 2/3 pyramidal neurons is highly stereotyped, being characterized by a moderately large amplitude, cell-specific depolarization (Poulet and Petersen, 2008; Gentet et al., 2010). For each recording, we adjusted both the depolarizing offset and peak-to-peak amplitude to achieve a mean membrane potential of approximately −60 mV (−62.5 ± 1.2 mV; n = 10; Fig. 6C). Thus, E_GABA at the ChC synapse (−52.3 ± 1.5 mV) lies between the mean V_m and action potential threshold (−43.7 ± 1.9 mV; Fig. 6D). In the 20 ms before the pyramidal neuron spike, the PSD averaged 16.1 ± 1.9 mV, with an average dV/dt value of 0.7 ± 0.1 mV (Fig. 6C). The PSD amplitude is comparable to but slightly larger than those recorded from awake behaving mice (Poulet and Petersen, 2008), and within the range recorded from anesthetized cats (Azouz and Gray, 2008).

Figure 6.

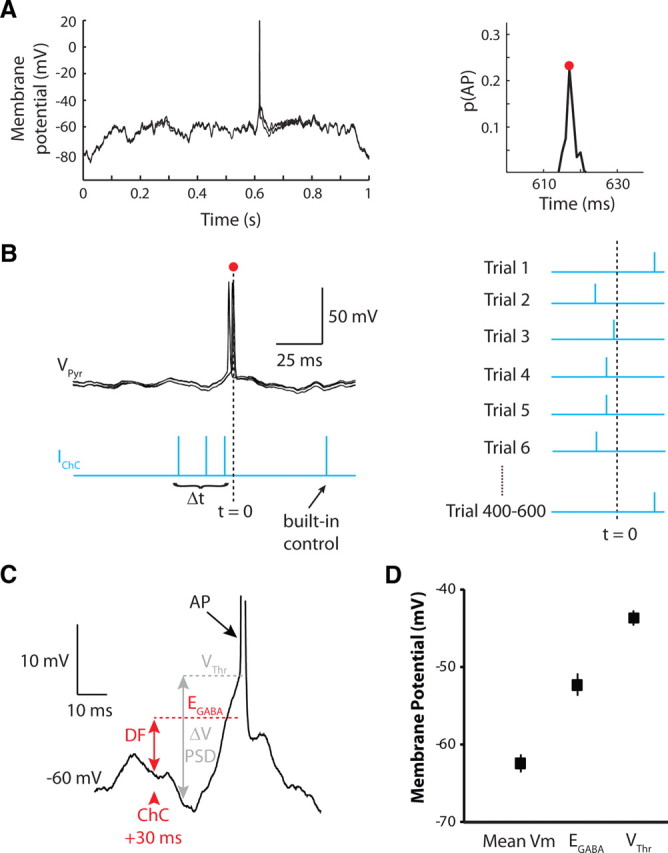
Investigating ChC impact during in vivo-like V_m fluctuations. A, Five overlaid sweeps of pyramidal neuron membrane potential during the white noise stimulation. Right, Spike-time histogram determined from 200 sweeps of the noise stimulation shown on the left. The red dot indicates center of the distribution, around which the ChC stimulation times are determined. B, Four stimulation times are defined for the ChC. Always included is a built-in control, occurring after the pyramidal neuron spike. Spike probabilities for the remaining three Δt intervals are compared to the built-in control. Right, Presentation of the ChC spike is randomized among the four Δt intervals to minimize the effect of time-dependent fluctuations in p(AP). C, Illustration of various calculated parameters. The DF is the difference between E_GABA and the pyramidal neuron V_m at the time of the ChC spike. ΔV PSD is the voltage difference between the spike threshold (V_Thr) and V_m 20 ms before spike onset. D, Plot showing the relationship between the mean V_m during white noise stimulation, E_GABA, and V_Thr across all experiments. Error bars are SEM.

After recording 200 sweeps of the white noise stimulus, we created a histogram of the pyramidal neuron spike times (Fig. 6A, right) and built a stimulation protocol to activate the ChC at various defined times before the expected pyramidal neuron spike (t_pyr). We also activated the ChC after t_pyr. This served as a control, allowing us to compare spike probability under conditions in which ChC activation preceded or followed (and could or could not influence) pyramidal neuron spikes (Fig. 6B). After defining the four Δt intervals of the ChC spikes (three before and one following the pyramid spike), the presentation of ChC spike times was randomized from trial to trial in an attempt to nullify the effect of any transient changes in pyramidal neuron excitability (Fig. 6B).

Under these conditions, ChCs produced reliable inhibition when activated shortly before the expected pyramidal neuron spike (Δt = +5 ms; Fig. 7A). Average spike probability decreased by 48.2 ± 8.1%, from 0.53 ± 0.03 to 0.27 ± 0.04, an effect that was also apparent in the majority of individual experiments (Fig. 7A). In contrast, activation of the ChC at earlier time points, either 15–20 or 30–40 ms before the pyramidal neuron spike, did not produce a consistent effect. The majority of experiments failed to show significant increases or decreases in p(AP), instead exhibiting small, statistically insignificant modulations in both directions. However, in some cells, ChC activation at these time points had robust effects on pyramidal neuron spiking, twice strongly decreasing and once strongly increasing p(AP) (Fig. 7A, black dots; p < 0.01). Across all experiments, the mean p(AP) changed by +4.6 ± 4.0% for Δt = +30–40 ms, and by −5.6 ± 6.7% for Δt = +15–20 ms (Fig. 7A).

Figure 7.

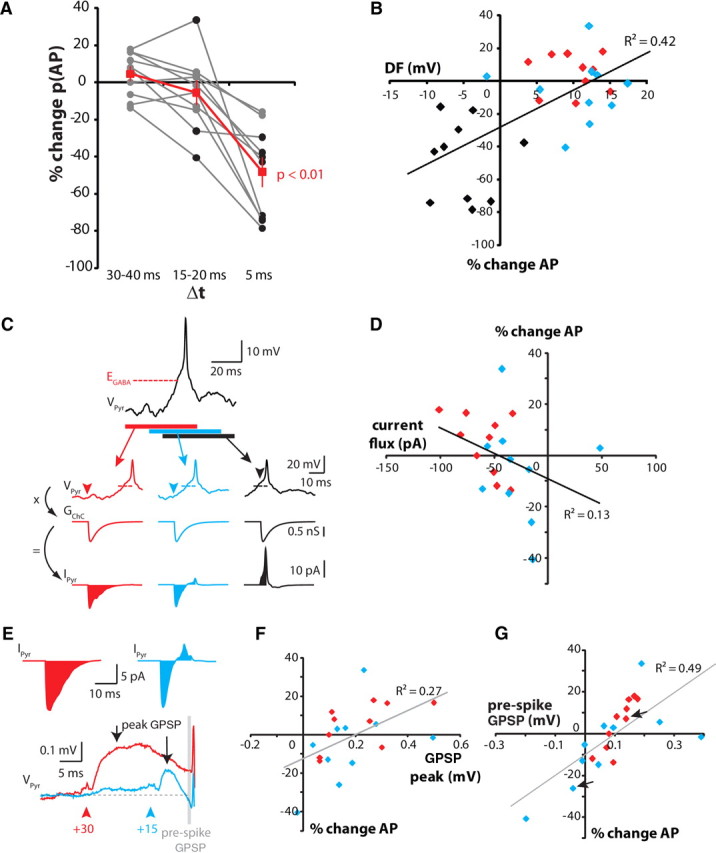
Chandelier cell effect during in vivo-like V_m fluctuations. A, Summary data for all experiments. Black symbols indicate significant deviations from control [0% change in p(AP)] for an individual experiment (χ² test). Red symbols are means across all experiments. Error bars indicate SEM. B, Relationship between driving force and p(AP) for the three time points. Black symbols, +5 ms; blue symbols, +15–20 ms; red symbols, 30–40 ms. C, Calculation of the total ChC-mediated current flux. The average spike response under control conditions (−50 ms, top trace) was zeroed at E_GABA to calculate the driving force, which was then convolved with the synaptic conductance to calculate total current flux. Arrowheads indicate time of ChC activation for each condition (colored as in B). Dashed lines indicate E_GABA. D, Relationship between total current flux and p(AP). Only data for +15–20 ms (blue) and +30–40 ms (red) time points are shown. E, Sample traces of the average ChC-evoked GPSP, showing measurement locations for peak (arrows) and prespike GPSPs (gray bar). ChC spike time is indicated by arrowheads. Top, Current flux for the two GPSPs shown below. The polarity switch for the +15 ms current flux is reflected in the isolated GPSP. F, Relationship between p(AP) and peak GPSP amplitude. G, relationship between p(AP) and prespike GPSP amplitude. Arrows indicate the GPSPs in E.

These experiments clearly show an inhibitory action of ChCs, but suggest little if any facilitatory effect, even though we observed a moderate but significant relationship between the change in p(AP) and the calculated driving force (DF) at the time of GPSP onset (Fig. 7B; R² = 0.42; p < 0.001; linear regression followed by ANOVA). Although this suggested that depolarizing GPSPs should be capable of promoting spike generation, removal of the hyperpolarizing GPSPs associated with the Δt = +5 ms condition (Fig. 7B, black diamonds) eliminated the relationship between DF and p(AP) (R² = 0.001; p = 0.88).

One would expect the driving force to be an important determinant of the effect of a synapse. However, under our conditions, as in the intact brain, the driving force is dynamic and, during the PSD, decreases with time for depolarizing GPSPs; that is, during the prespike depolarization, V_m typically starts below E_GABA, and rapidly approaches and crosses this value. Thus, for two of our three ChC stimulation conditions (Δt = +30–40 ms; Δt = +15–20 ms), the driving force changes with time from moderately positive, to zero, to negative. To address this issue, we measured E_GABA for each of the 10 cell pairs and used these values to determine the change in DF over time during the filtered white noise protocol. We convolved this DF with the ChC GPSC conductance determined for each cell (at −60 mV) to determine the current flux through the ChC synapse as a function of time. Using this approach, we routinely observed inward currents for Δt = +30–40 ms, outward currents for Δt = 5 ms, and currents that switched from inward to outward for Δt = +15–20 ms (Fig. 7C). Surprisingly, we observed only a moderate relationship between the integrated current flux and spike probability (R² = 0.13; p = 0.11; Fig. 7D), perhaps suggesting cell-to-cell variations in the activation of subthreshold voltage-gated channels.

Finally, we calculated the absolute voltage contribution of the ChC GPSP to the probability of pyramidal neuron spiking. Because average V_m and ChC synapse E_GABA have similar values, the ChC GPSP is expected to be small and is not readily detectable among the large fluctuations we used to drive the pyramidal neurons. We isolated the ChC GPSP for Δt = +30–40 and for Δt = +15–20 ms by averaging all sweeps at those two time points and subtracting from that the averaged control trace, Δt = −50 ms (Fig. 7E). In each cell, the peak GPSP was depolarizing for both time points, although this did not necessarily imply an increase in p(AP) (Fig. 7F). However, when measuring the GPSP amplitude immediately before the onset of the averaged spike envelope, we observed a robust relationship with spike probability (Fig. 7G). This is not surprising in itself, but the strength of the relationship suggests that the small and statistically insignificant changes in p(AP) are not fluctuations due simply to experimental noise or chance, but instead are due directly to the small depolarizations or hyperpolarizations provided by the ChC synapse.

Discussion

Homogeneity of upper-layer ChCs across genetic background and cortical areas

Conflicting results on the polarity of ChC E_GABA in hippocampus and cortex raise the possibility that the function of ChCs may be heterogeneous (Glickfeld et al., 2009), depending perhaps on the brain region or reflecting a basic morphological or physiological heterogeneity among chandelier cells. In our study, we therefore first explored whether different subtypes of neocortical ChCs exist by applying a rigorous series of unsupervised classification methods to a relatively large database of 219 ChCs. As clustering by both morphology and electrophysiology gives no evidence for subtypes of ChCs, we conclude that our data set of ChCs cannot be divided into statistically valid subgroups. Moreover, we used two different genetic strategies to label subsets of interneurons in the G42 and Nkx2.1 mouse lines and found no statistical difference in the morphological or physiological properties of cells from these two different genetic backgrounds. Finally, we sampled cells from 10 different cortical areas, finding no evidence that they differ systematically. Therefore the ChCs from which we recorded represent a homogeneous population that cannot be clearly subdivided according to morphological or physiological characteristics, genetic strains, or cortical areas.

A state-dependent function of ChCs

We also investigated the functional impact of this homogeneous ChC population on the firing of Layer 2/3 pyramidal neurons. We show that the ability of cortical ChCs to excite their postsynaptic targets is critically dependent on E_GABA and the membrane potential trajectory of the postsynaptic neuron. When V_m is essentially static, as in DOWN states, depolarizing GPSPs can have an excitatory influence, facilitating spike generation. Since spiking during the DOWN state is rare, our results may be more applicable to DOWN–UP state transitions, when a hyperpolarized, static V_m rapidly depolarizes due to a barrage of synaptic activity. The excitatory influence we observe occurs for latencies (or Δt) between +30 and +5 ms and is seen in a quiescent slice preparation, but also at more depolarized levels closer to the average V_m seen in vivo. The main requirement for excitation appears to be that the majority of ChC-mediated current flux occurs before the neuronal V_m crossing E_GABA. Our current injection experiments (Fig. 4), in which ChCs were activated before the pyramidal neuron being depolarized, allowed ChCs to excite their targets. In contrast, our electrical stimulation experiments (Fig. 5), in which ChCs were activated during the rising phase of the pyramidal neuron EPSP, consistently showed ChC-mediated inhibition. Under conditions of constantly fluctuating V_m, as is characteristic of neurons in awake animals, the only robust effect observed was spike inhibition, with no consistent direction of effect for time intervals of 15 ms or more. Our inability to detect an effect of ChCs—either excitatory or inhibitory—at all but the shortest Δt intervals may partly reflect the fact that we manipulate only a single ChC. Based on counts of boutons apposed to the axon initial segment (AIS), a single pyramidal neuron has been estimated to receive input from three to six ChCs (Buhl et al., 1994; Tamas and Szabadics, 2004). Temporally coordinated activation of ChCs, perhaps facilitated by the electrical coupling we describe, would therefore be expected to produce significantly larger GPSPs. In addition to producing stronger inhibition, simultaneous activation of ChCs may also enable a more overt excitatory effect on postsynaptic spiking, based on the relationship we found between prespike GPSP amplitude and spike probability.

Our results show that chandelier cells, like other interneurons, can inhibit spiking and can do so quite strongly if the pyramidal cell is active. But simple inhibition, in the absence of excitation, is unlikely to be the only function of chandelier cells. An alternative view is to consider the ChC synapse not in terms of its direct effect on spike output, but rather in terms of its impact on neuronal excitability. We took care in our experiments to make the average V_m during noise stimulation approximate that observed in vivo (our experiments, approximately −63 mV; in vivo, approximately −55 mV; different internal solutions; see Materials and Methods, Comparing V_m values for different internal solutions). The E_GABA of the ChC synapse then lies slightly depolarized relative to average V_m. This is analogous to a recent study examining the subthreshold mechanisms underlying responses of L2/3 pyramidal neurons to whisker touch (Crochet et al., 2011), in which the reversal potential of the synaptic response to whisker contact—reflecting combined excitatory and inhibitory currents—lies above the average V_m but typically below spike threshold. Variations in the reversal potential of the synaptic response correlated strongly with the excitability of the neuron. The ChC synapse may perform a similar function, helping to set the excitability of the neuron by means of its reversal potential.

Consistent with this possibility, our gramicidin recordings in fact revealed considerable variability in E_GABA, and various studies have indicated that GABA_A reversal potential is not static (Wagner et al., 1997; Woodin et al., 2003; Fiumelli et al., 2005; Choi et al., 2008). Two studies in particular relate shifts in E_GABA to activity-dependent modulation of NKCC1, the cation-chloride cotransporter present at the AIS (Khirug et al., 2008). In the first, repeated action potential activity was shown to cause a persistent increase in intracellular chloride accumulation via alterations in the Na⁺–K⁺–ATPase transporter and NKCC1 (Brumback and Staley, 2008). Since NKCC1 is expressed at the AIS, changes in E_GABA at the ChC synapse may occur naturally as a function of the spike output of the postsynaptic neuron, with high levels of activity leading to a depolarizing shift in E_GABA and increasing neuronal excitability. In the second study, near-coincident firing of presynaptic and postsynaptic cells caused a hyperpolarizing shift in E_GABA via NKCC1 alterations (Balena and Woodin, 2008), effectively increasing the strength of inhibition and decreasing excitability. Thus, mechanisms exist to bidirectionally shift E_GABA via changes in NKCC1 activity, and may explain the large variability we observe in our gramicidin recordings.

Role of ChCs in integrating Layer 1 inputs

An unexpected result from our morphological analysis is the considerable bias in the location of ChC dendrites, which are largely confined to Layer 1. The majority of previously published reconstructions of L2/3 ChCs have been located further from the L1 border (Somogyi et al., 1982; Zhu et al., 2004; Gonzalez-Burgos et al., 2005; Xu and Callaway, 2009), although one study showing ChCs situated at the top of L2/3 also appeared to demonstrate a preference for Layer 1 dendrites (Kawaguchi, 1995). We show here that despite their similar laminar position, basket cells do not display the same preference, suggesting different sources of afferent input for these two cell classes.

Layer 1 contains dense axonal projections emanating both from higher cortical areas and nonspecific thalamic nuclei (Lorente de Nó, 1949; Rockland and Pandya, 1979; Cauller et al., 1998; Douglas and Martin, 2007; Rubio-Garrido et al., 2009). Coarse-scale axodendritic overlap provides some insight into the sources of afferent input, but whether L2/3 ChCs sample equally from cortical and subcortical afferents is unknown. Interestingly, feedback, corticocortical projections from a region of extrastriate visual cortex to rat V1, did not contact PV+ dendrites of Layer 1 (Gonchar and Burkhalter, 2003). This is somewhat surprising in light of our finding regarding Layer 1 dendrites of Layer 2/3 ChCs, and whether this reflects a general scarcity of PV+ processes in Layer 1 or a direct avoidance by feedback inputs (and instead a preference for thalamic inputs) is unclear.

Chandelier cell dendrites overlapped substantially with pyramidal neuron apical dendrites, where dendritic spikes can be initiated (Yuste et al., 1994; Schiller et al., 1997; Larkum et al., 2007). Dendritic spikes are facilitated by antidromic propagation of axonally initiated spikes and can themselves propagate to the soma to facilitate spike output from the AIS (Larkum et al., 1999). This cooperativity between two distinct neural pathways may therefore constitute a mechanism to associate bottom-up and top-down inputs. The induction of dendritic spikes will depend on the local excitatory–inhibitory balance. In this regard, two important interneuron types are Martinotti cells (Silberberg and Markram, 2007; Murayama et al., 2009), whose axons extend to Layer 1 from cell bodies in deeper layers, and neurogliaform cells (Wozny and Williams, 2011), which have dense local axons and whose cell bodies are routinely found in Layer 1. Neurogliaform cells may therefore provide a feedforward inhibition of the apical tuft, while Martinotti cells, due to their different sources of excitation, may provide tuft inhibition in response to local circuit rather than interareal input. In contrast, despite their dendritic arbor overlapping with pyramidal neuron apical tufts, chandelier cells will not directly affect dendritic spike initiation. Instead, a direct impact on axonal excitability is expected. Layer 2/3 chandelier cells could therefore provide a direct link between top-down, highly processed information arriving at Layer 1 and the axonal spike output of the pyramidal neuron. In a quiet circuit, a small depolarization provided by multiple ChCs may help axonal spike initiation, which can then interact with dendritic spikes to produce axonal spike bursts. On the other hand, in an active circuit, hyperpolarization or inhibition by ChCs, perhaps the dominant effect, will prevent axonal spike initiation and therefore prevent cooperativity between bottom-up and top-down inputs.

Notes

Supplemental material for this article is available at http://hdl.handle.net/10022/AC:P:11067. This material has not been peer reviewed.