Analytical Methods to Detect Within-Individual Changes in Discounting

Abstract

Discounting, as a quantifiable measure of impulsivity, is often estimated within individuals via nonlinear regression. Here, we describe how to directly estimate within-individual change of the discounting parameter between 2 conditions and subsequently statistically test for that change using the discounting data from a single individual. To date, there has been no systematic description of how to conduct such an analysis. Employing the method allows investigators and clinicians to evaluate whether a single individual has statistically changed the way he or she discounts between 2 conditions (e.g., in the absence or presence of a pharmacologic, different time points, different rewards, etc.). We further describe a meta-analytic approach for combining estimated changes in discounting from individuals in a sample to make population inference. By providing more precise population estimates, this approach increases statistical power over traditional analytic methods.

Discounting refers to the decrease in a commodity’s subjective value as a function of cost (e.g., temporal delay, probability) to its receipt. Often, researchers study whether discounting behavior is related to the conditions an individual experiences, and use within-individual designs when addressing their questions. For example, Giordano et al. (2002) found opiate addicts to discount delayed hypothetical gains more in an opiate-deprived state than when satiated. Further, most studies have reported results at the group, rather than individual level. Giordano et al. reported that the addicts as a group discounted $1,000 at a rate of approximately k = 0.032 days⁻¹ when deprived, but that the rate was approximately half that when satiated. From a clinical point of view, understanding how the average individual’s behavior changes guides the clinician when evaluating whether an actual individual has changed. Continuing with the Giordano et al. example, if an opiate addict in mild withdrawal at least doubles his discount rate from his satiated state, a clinician might infer that the addict discounts differentially between the two states. Also important in evaluating whether an actual individual has changed is the consistency of his or her behavior in each assessment. So if the hypothetical addict above had provided erratic discounting data on which the discount rates were estimated, the clinician might decide the apparent change could well be due to chance. This report describes in detail (1) how to assess whether a single individual has statistically changed the way he or she discounts, and (2) how to use information from the individual analyses to increase statistical power at the group level. The methods described herein apply to discounting data (whether delay, probability, or otherwise) fitted with regression models, and may be used by both clinicians and researchers.

Before describing the statistical methods, we illustrate the variety of paradigms in which the methods can be used, and the mixed bag of statistical techniques used in the past. We also provide a motivating example of a well-documented phenomenon that will be used in the presentation of the statistical methods. It is our hope that this work will contribute to the standardization of methods used in discounting research and, as time passes, clinical settings.

Examples of Within-Individual Change

Many have investigated whether individuals from a particular population change the way they discount between two or more conditions. The following studies provide a flavor of the types of conditions studied and for which our proposed statistical methods are appropriate, and, in particular, the variety of statistical methods used in evaluating the changes. Though several of these studies analyzed the discounting data in other ways (e.g., analyzed AUCs—areas under the curve), we emphasize their commonality: all used nonlinear regression to obtain ks for each condition experienced by each individual, and appear to have assumed that all individuals discount with the same degree of consistency. Further a predominant discounting result presented in these studies was the average change experienced by the individuals, thus indicating the need to understand the average individual. As we show later, accounting for differing levels of consistency among individuals when characterizing the average individual can increase precision, and subsequently power in hypothesis tests.

Examining the effects of a pharmacologic on discounting in within-individual designs, Acheson and de Wit (2008); Acheson, Reynolds, Richards, and de Wit (2006); Hamidovic, Kang, and de Wit (2008); McDonald, Schleifer, Richards, and de Wit (2003); and Reynolds, Richards, Dassinger, and de Wit (2004) used the equivalent of a paired t test when comparing log-transformed ks, and de Wit, Enggasser, and Richards (2002) used the equivalent of a two-sample t test when comparing untransformed ks. Ohmura, Takahashi, Kitamura, and Wehr (2006) and Simpson and Vuchinich (2000) studied whether individuals change the way they discount across two points in time (e.g., baseline and 3 months later). Both groups used paired t tests of log-transformed ks and Pearson correlations of the pairs of log-transformed ks to ascertain group and individual reliability of discounting. Similarly, Yoon et al. (2007) and Yoon et al. (2009) assessed the discounting of individuals over time, and analyzed the log-transformed ks within a repeated-measures analysis of variance with time being the within-individual factor. Using a scatter plot, Dixon, Jacobs, and Sanders (2006) illustrated within-individual differences in untransformed ks obtained in two contextually different settings. Johnson and Bickel (2002) used Pearson correlations of log-transformed ks to learn whether individuals differ in the way they discount real and hypothetical rewards. Madden, Begotka, Raiff, and Kastern (2003) and Madden et al. (2004) also were interested in discounting differences between real and hypothetical rewards, and tested for within-individual change in untransformed ks using Wilcoxon signed-ranks test and a paired t test, respectively. Estle, Green, Myerson, and Holt (2006), among other objectives, studied whether a magnitude effect exists when discounting losses; though they fitted discounting data with a discount function, they did not use it to statistically answer their questions, but rather to illustrate group discount curves.

Assessment of Within-Individual Change

Throughout, we use illustrative delay discounting data from Bickel, Yi, Kowal, and Gatchalian (2008) that, among other results, replicates the well established magnitude effect—larger delayed magnitudes are discounted less than smaller delayed magnitudes.¹ (Though the magnitude effect is arguably an inherent construct and may not be subject to manipulation, changes in the discounting between two different amounts is represented mathematically the same as changes in discounting between two manipulatable conditions.) Specifically, we use the delay discounting data of hypothetical future gains of $10 and $1,000 collected from smokers in Bickel et al.’s study, in which details of the experimental setting can be found. Whether our interest lies in the particular smoker or in a population of smokers, the individual(s) completed the same delay discounting task for both magnitudes. We then fitted the indifference points from each task with Mazur’s (1987) hyperbolic regression function (given in the next section) to estimate κ—the discounting parameter; thus reducing the data from an individual into two k values—the estimates of κ for each magnitude.²

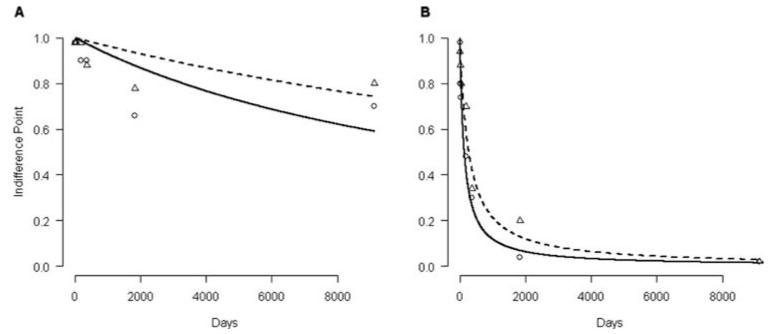
Because individuals vary, one individual may clearly discount, say $10 more than $1,000; whereas for another the distinction between the two magnitudes is less clear. To illustrate, Figure 1 contains indifference points from two smokers in the Bickel et al. (2008) study and the fitted hyperbolic curves from two conditions ($10 and $1,000) for A (left side) and B (right side). Both A and B discount $1,000 about half as much as $10 (i.e., the ratio of the k for $1,000 to the k for $10 is about 1/2 for each person). Looking at the figure, the curves fit B’s data better than A’s. Hence, more confidence goes to B’s ratio change than A’s, even though they both change by about the same amount, 1/2. This short example brings us back to our first objective in the form of the question: When the individual is of interest, how do we quantify our confidence in the estimated change within an individual?

Figure 1.

Indifference points for delay discounting of $10 (circle) and $1,000 (triangle) and their corresponding fitted hyperbolic regression lines (solid for $10 and dashed for $1,000) are plotted for two participants.

Statistical Methods for Evaluating Within-Individual Changes in Discounting

We are interested in evaluating within-individual change. With the data from a single individual, we want to statistically test whether a person has changed the way he discounts. This section contains descriptions of two such methods. The first method is an ad hoc collection of statistical routines, and we call it ad hoc estimation. Method 2, direct estimation of a difference, allows the data from two conditions within an individual to be analyzed together, and more important, enables an automatic test of within-individual change. Before describing the methods, we describe our example data and assumptions.

Describing the Data

The data come from Bickel et al. (2008), in which the experimental conditions are described in full. Briefly, each individual underwent at least two delay discounting tasks—one for a hypothetical gain of $10 and the other for a hypothetical gain of $1,000. From each task, an indifference point, y, was determined for each delay, x = 1, 7, 30.4375, 182.625, 365, 1,825, and 9,125 days. Therefore, an individual provided seven data points for each condition, for a total of 14 data points. Table 1 contains the data from Participants A and B.

Table 1. Discounting Data.

		y
w	x	A	B
0	1	0.98	0.98
0	7	0.98	0.80
0	30.4375	0.98	0.74
0	182.625	0.90	0.48
0	365	0.90	0.30
0	1,825	0.66	0.04
0	9,125	0.70	0.02
1	1	0.98	0.94
1	7	0.98	0.88
1	30.4375	0.98	0.80
1	182.625	0.98	0.70
1	365	0.88	0.34
1	1,825	0.78	0.20
1	9,125	0.80	0.02

Note. Condition (w) takes values 0 for $10 and 1 for $1,000 in hypothetical gains. Delays (x) given in days and corresponding indifference points (y) are provided.

Compared to Participant B’s data, Participant A’s data better exemplifies the features and shortcomings of the two methods. Hence, we primarily use A’s data in the following examples, relying on B’s to provide additional support. Experimentally, A and B were treated the same.

Assuming a Model

All of the previously mentioned studies used hyperbolic-like equations, such as the following proposed by Mazur (1987), to model the expected indifference point, Y, at delay x for each condition experienced by the individuals:

$$Y={(1+\kappa x)}^{-1},$$ (1)

where κ is the discounting parameter particular to the condition. An important point, however is that the methods to follow do not depend on the hyperbolic model; the methods may be applied to other possible discount functions (e.g., two-parameter hyperboloid, Myerson & Green, 1995; two-parameter power, Rachlin, 2006; exponential-power, Yi, Landes, & Bickel, 2009). See the Appendix for more technical regression assumptions.

In many discounting studies, ks are “normalized” with a logarithm transformation (for examples, see Acheson et al., 2006; Ohmura et al., 2006; Simpson & Vuchinich, 2000). Directly estimating ln(κ) saves analytical steps, and more important, allows us to estimate a relevant parameter of within-individual change later on. We need to rewrite Equation 1 in terms of κ* = ln(κ) by replacing κ in Equation 1 with e^κ*:

$$Y={(1+\exp [{\kappa }^{\ast }\left]x\right)}^{-1}.$$ (2)

Directly estimating κ* = ln(κ) is equivalent to taking the natural logarithm of k.

Defining Within-Individual Change

To identify the discounting parameters between two conditions, let κ₀ and κ₁ denote the parameters from the $10 and $1,000 conditions, respectively. Saying, for example, that A discounts $1,000 half as much as he does $10 indicates that we are interested in the ratio change of κ₁ to κ₀. We denote the ratio change with γ = κ₁/κ₀. One may also speak of an absolute change between the two parameters, say κ₁ − κ₀. Routinely though, studies report results in terms of log-transformed discounting parameters as we have noted above. This indicates that the ratio change (γ) of discounting parameters is of more interest than absolute change, because a log-transformed ratio of the original κs is the same as the difference of two log-transformed κs; that is, ln(γ) = ln(κ₁) − ln(κ₀). Indeed, many of the studies previously cited estimated this type of difference for each individual. (They subsequently performed their final analyses on the individually estimated differences.) We now present two ways to estimate the within-individual change. The first, ad hoc estimation, is the method employed by many studies in the past; the second, direct estimation, has better statistical properties than the first and appears to be novel in discounting studies.

Method 1: Ad Hoc Estimation

Plugging in previously obtained estimates into a formula for a new parameter is the essence of this technique. When using Equation 1 to individually obtain the estimates k₀ and k₁, an ad hoc estimate of the ratio change, γ, is k₁/k₀. Similarly, an ad hoc estimate of ln(γ) comes from either

1. ln(k₁) − ln(k₀), or

2. using Equation 2 to obtain $k_0^{\ast }$ and $k_1^{\ast }$ and taking their difference.

To illustrate, Participant A’s k₀ and k₁ were 7.60 × 10⁻⁵ and 3.80 × 10⁻⁵, respectively. The natural logarithm of these two estimates is the same as $k_0^{\ast }$ and $k_1^{\ast }$ from Equation 2: −9.485 and −10.179, respectively. The ad hoc estimates of γ and ln(γ) from the individually estimated discounting coefficients are 0.500 and −0.694, respectively.

For us to determine whether the estimated change (either 0.500 or −0.694) is outside reasonable random variation, we need a standard error. Determining a standard error for the estimator of γ or ln(γ) at this point will require further ad hoc calculations. However, the additional calculations are tedious and based on questionable assumptions; see the Appendix for more details. We now proceed to a more coherent method of estimating ln(γ) and its standard error.

Method 2: Direct Estimation

To directly estimate a difference, we need to incorporate an individual’s data from both conditions into one regression. We can do this by making use of a dummy variable,³ w, that indicates whether the data is coming from one condition or the other. The idea is to replace the κ* in Equation 2 (the discounting parameter for a single condition) with d(w)—a function that returns ${\kappa }_0^{\ast }$ when w = 0 and ${\kappa }_1^{\ast }$ when w = 1. Because this function alternates between two states, ${\kappa }_0^{\ast }$ for one condition and ${\kappa }_1^{\ast }$ for the other, we refer to it as a “toggle.” Incorporating the toggle in the place of the original parameter will allow us to estimate the discounting from both conditions in one analysis. We define the toggle as

$$d\left(w\right)=w\ln \left(\gamma \right)+{\kappa }_0^{\ast },$$ (3)

where $d\left(0\right)={\kappa }_0^{\ast }$ and $d\left(1\right)=\ln \left(\gamma \right)+{\kappa }_0^{\ast }=({\kappa }_1^{\ast }-{\kappa }_0^{\ast })+{\kappa }_0^{\ast }={\kappa }_1^{\ast }$. Replacing κ* with d(w) in Equation 2 gives us

$$Y={(1+\exp [d\left(w\right)\left]x\right)}^{-1}={(1+\exp [w\ln \left(\gamma \right)+{\kappa }_0^{\ast }\left]x\right)}^{-1}.$$ (4)

Myerson and Green (1995) applied this idea when estimating the difference between untransformed κ₀ and κ₁ in a hyperbola-like function; see Equation 6, page 270.

Fitting Equation 4 using a standard statistical software package will automatically estimate ln(γ) and κ₀, along with their standard errors. See the Appendix for a description of how to estimate other parameters of interest. Most statistical software (we know of none that do not) provide an automatic test of ln(γ) = 0, which is exactly the test for within-individual change. In addition, production of 95% confidence intervals (CIs) for ln(γ) is typically automatic, with the option to change the confidence level (1 − α) available.

The two methods yield the same estimates for discounting parameters; however, the primary difference between the methods is the inferential statistics that accompany direct estimation. To illustrate, directly estimating ln(γ) using Equation 4 on Participant A’s data gave the same value as the ad hoc estimate, −0.694. In addition, the regression results from using Equation 4 automatically returned the 95% CI for ln(γ), (−2.015, 0.630), and a t test of ln(γ) = 0, t(12) = 1.14, p = .2747. The decrease Participant A exhibited in discounting $1,000 from his discounting $10 could be due to chance variation in the way Participant A discounts. Turning our attention to Participant B: his estimate (95% CI) for ln(γ) was −0.7044 (−1.3864, −0.0224); thus providing statistical evidence of a change in the way he discount between $10 and $1,000, t(12) = 2.25, p = .0440.

We could stop here when evaluating information about ln(γ), and we would stop here if ln(γ) had a clear interpretation. However, because most people are not accustomed to thinking on the log scale, we want to turn our attention back to γ = κ₁/κ₀. Taking the antilog of the ln(γ) estimate and the endpoints of the 95% CI for ln(γ) give an estimate of and 95% CI for γ. To illustrate, transforming Participant A’s ln(γ) given above with the antilog gives 0.500 for γ, the same as earlier given with the ad hoc method. Similarly transforming A’s 95% CI for ln(γ) gives a 95% CI for γ of (0.1334, 1.8769). Participant B’s transformed ratio change, γ, was 0.4944 with 95% CI, (0.25, 0.9778). The appropriate null value (value of no change) for γ is 1, so our inference for Participants A and B remain the same as the inferences for ln(γ).

Estimating Population Change Parameters

Knowing whether an individual changes the way he or she discounts one condition from another is important in both research and clinical settings. Up to this point, we demonstrated how to make formal statistical inference on that change for any given individual. As demonstrated by the literature previously mentioned, knowing whether a population tends to change the way it discounts between two conditions is important. In this section we propose a method to use the results from the within-individual analyses for population inference. The method accounts for the very real possibility that the internal variability inherent to an individual differs across a sample (i.e., accounts for heterogeneity of variance among individuals).

Use Weights to Gain Power

The most common method for estimating a mean ln(γ) for a population of individuals is to compute the simple arithmetic mean of the estimated ln(γ)s from a sample of individuals. When all of the individuals’ estimates are known with the same precision (i.e., the assumption of homogeneous variance holds), the sample mean is the best linear unbiased estimator of the population mean. However, when there are consistent responders (such as Participant B) and highly variable ones (such as Participant A) in the population, the assumption of homogeneous variance is shaky at best. For example, after fitting Equation 4 to each of the 30 smokers, the standard errors of their estimated ln(γ)s ranged from 0.2 to 2; this equates to a 100-fold change in the variances among the 30 smokers. Among this sample, over half of the participants’ variances statistically differed from at least 14 other participants’ variances in the sample.

The same standard errors that provide strong reason to believe that the homogeneous variance assumption is not valid can also spare the analysis. With them, we can use the method described in Sidik and Jonkman (2005) to construct a weight associated with each individual’s estimated discounting parameter. (See the Appendix for more details.) The weight quantifies how much an individual’s estimate contributes to our knowledge of the population parameter. Those who provide “predictable” data (data with low variability/high precision about their individually estimated curves) receive more weight in our estimation of the population mean than those who do not respond as predictably. The best linear unbiased estimator of the population mean change is then the weighted mean of the estimated changes, rather than the simple arithmetic mean. In other words, the weighted mean lets us compare a hypothesized population mean to a null value with more statistical power than when using the simple mean. Two additional notes about the weighting method: (1) It is also applicable to discounting parameters other than population change; for example the mean of a single discounting parameter or a difference in discounting parameters between two populations. In such instances, the weights may often be entered into the analyses with utilities built into standard statistical software. (2) The simple and weighted mean can notably differ; this is especially true when there are extreme discounters that have low weights.

For small samples, the possibility exists of all individuals showing a statistical change within themselves, but as a group failing to provide statistical evidence of a population shift using the weighted or usual methods. In such cases, we recommend estimating the proportion of those who statistically change. If the sample is as small as five, and all have statistically changed their individual parameters in the same direction, a one-sided test that the proportion of statistical “increasers” (alternatively, “decreasers”) is 1/2—the null value—would be rejected at the .05 level; a two-sided test would be rejected if six of six statistically increased (decreased).

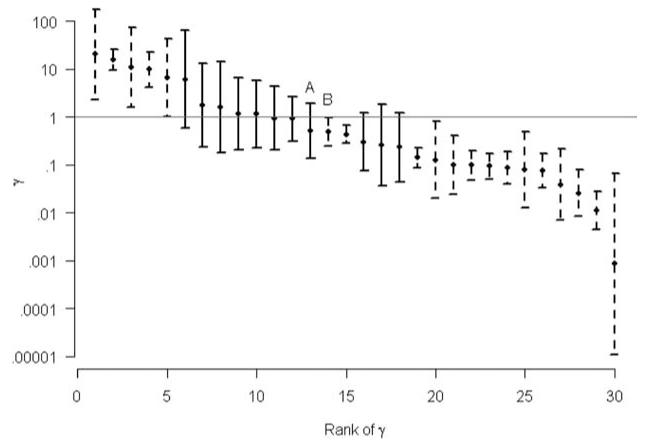
To show the differences between the simple and weighted means, we start by presenting the estimated within-individual changes and their 95% CIs for the 30 smokers in our sample (see Figure 2). The varying lengths of the individuals’ 95% CIs indicate that the changes are not known with the same amount of precision as is often assumed. The simple mean that assumes homogeneous variances among the ln(γ)s was −0.9392 with a standard error of 0.4202. Accounting for the possibility of nonhomogeneous variances (i.e., heteroscedasticity), the weighted mean was −0.8936 with a standard error of 0.2848. Speaking in terms of precision (by definition, the inverse of the variance), we gained about (0.4202/0.2848)² = 2.18 times more precision using the weighted mean to estimate the population log-ratio change than using the simple mean. As noted earlier, ratios are easier to understand than log-ratios. Translating the results into ratios is done by taking the antilog of the above means and the endpoints of their respective 95% CIs (not shown; see Figure 3). In Figure 3, we can see the 95% CI from the simple mean is about 1.5 times longer than the 95% CI from the weighted mean. Had the estimated γs in Figure 3 been shifted to the right by 0.2 units, using the proposed weights would have evidenced a statistical change; whereas with equal weighting (i.e., simple), the evidence would have been inconclusive.

Figure 2.

Individually estimated ratio changes (γ) and corresponding 95% confidence intervals after fitting Equation 4 to the indifference points from each of the 30 smokers in the sample, and taking the antilog of point and interval estimates of ln(γ). Dashed lines indicate those individuals showing a significant change in the way they discount $1,000 from $10. The “A” and “B” identify estimates for Participants A and B, respectively.

Figure 3.

Estimated population ratio change, γ, and corresponding 95% confidence intervals (CI) after antilog transformation of the simple and weighted means of log-ratio change, ln(γ). The 95% CIs not covering 1 (vertical dotted line) indicate significant change in the way $1,000 is discounted from $10.

Discussion

We described and illustrated how to make statistical inference on within-individual parameters of change in discounting. Direct estimation of the change provides automatic inference and accommodates the natural correlation among within-individual parameters, whereas the ad hoc method does not. For estimating how, on average, individuals discount or change the way they discount, we proposed weighting individuals’ estimates based on their precisions when computing the population estimate. The weighted mean tends to be more precise than the often-used simple mean. There are four points that will help put these methods in proper perspective.

First, whenever assessing whether a single individual has changed the way he or she discounts from one condition to another, the individual’s internal variability must be taken into account. For estimated change parameters like ln(γ), we recommend direct estimation of the change rather than ad hoc estimation. As noted by a referee, a lack-of-fit test in the regression context may also be used to evaluate whether an individual discounts differently among conditions. However, lack-of-fit tests cannot automatically estimate the within-individual change, nor will it provide a standard error for the change. (In a lack-of-fit context, within-individual change would likely be estimated with the ad hoc method described above.) Another possible disadvantage is reduced power in detecting change. With the lack-of-fit test, 15 of the 30 participants in our sample showed evidence that a two-parameter model (Equation 4) better fit their data from both conditions than a single parameter model (Equation 2, equivalently Equation 1). These 15 were among the 19 identified with the direct estimation method we advocate in this work (see dashed lines in Figure 2).

Second, when making population inference, one should address the heterogeneity of variance among individuals that is so often present in estimated discounting parameters. To this end, we recommend using the weights recommended in Sidik and Jonkman (2005) when analyzing the estimated discounting parameters, which consequently increases statistical precision over not using weights. Another possible method for population inference that maintains the ability to make within-individual inferences is to model the indifference points from all of the individuals in a nonlinear random coefficients regression. Explaining this sort of model is beyond the scope of this work. Davidian and Giltinan (1995) and Lindstrom and Bates (1990) are good references for these sorts of models. From unpublished simulation studies comparing nonlinear random coefficients regressions to the weighting method proposed here, the weighting method tends to have better estimation properties.

Third, all along we have considered only regression models of discounting data. Regression requires a specified form of discounting, such as Equation 1. An often-used measure of discounting that does not require a specified form is AUC as described in Myerson, Green, and Warusawitharana (2001). However, to our knowledge there is no way of obtaining a standard error for an AUC measurement (or for the change between two AUC measurements) from one individual. This lack of a standard error for AUC (or any other measure of variability for an AUC estimated from a single individual) prevents statistical comparison of two AUC values from a single individual; hence, we have not considered AUC.

Finally, a limitation of the methods proposed here lie in underlying assumptions. Inferences from these methods assume that indifference points used in the regressions are mutually independent normal random variates (about the regression function) with common variance (across delays) within an individual. These assumptions were not examined because we have only two data points at each of seven delays. Because indifference points lie between 0 and 1 and come from the same individual, these assumptions may not be valid. Indeed, the indifference points themselves are often a summarization of a series of “yes/no” (i.e., binary) questions. Wileyto, Audrain-McGovern, Epstein, and Lerman (2004) proposed logistic regression on such binary data to estimate the discounting parameter in Mazur’s (1987) equation (Equation 1). We believe their method is promising and can be extended to make within-individual comparisons by incorporating our toggle concept.

Altogether, we hope the methods recommended in this work will bring more consistency to analytic techniques used in future discounting studies.

Appendix: Assumptions and Technical Details

This appendix provides a more complete description of the assumptions and details needed to understand and implement the methods proposed in this work.

Regression Assumptions

For n indifference points, y, coming from one discounting condition experienced by one individual, we assume mutual independence among the ys and

$$Y_j\sim N\left(g\right(x_j;\kappa ),{\sigma }^2),$$ (A1)

where g(*) is a discount function (e.g., Equation 1 or 2, exponential-power, hyperboloid, two-parameter power, etc.), x_j is the j-th cost (e.g., delay, odds, social distance, etc.) for j = 1, 2, …, n, and κ is the (possibly vector-valued) parameter. (For example, in the hyperboloid model, κ= (k, s).) Most often, g(*) is a nonlinear function, and is the regression function input into nonlinear regression fitting software.

When indifference points come from two conditions experienced by an individual, we introduce an additional in-dependent variable, w, that indicates from which condition the accompanying indifference point comes. The w variable must take values 0 and 1, which may be arbitrarily assigned to the two conditions. We assigned 0 to the $10 condition and 1 to the $1,000 condition (see Table 1). Again, we assume mutual independence among the ys and

$$Y_{ij}\sim N\left(g\right(x_{ij},w_{ij};\kappa ),{\sigma }^2),$$ (A2)

where g(*) is a discount function (e.g., Equation 4), x_ij is the j-th cost from the i-th condition, for j = 1, 2, …, n_i, and i = 1, 2; w_ij indicates the i-th condition of the j-th observation; and κ is a vector-valued parameter (e.g., $\kappa =({\kappa }_0^{\ast },\ln (\gamma \left)\right)$ in Equation 4). Modeling the data from both conditions with Equation A2 assumes that the variance, σ², is the same for both conditions. Using Equation A1 as the model for the data from each condition allows for possible differences in σ² between the two conditions. Under many experimental conditions like those reviewed previously, a reasonable assumption is that σ² is the same for each condition. For our sample, 22 of the 30 participants had regression mean square errors from the two conditions that did not statistically differ when applying an F test for equal variances. Participants A and B were in the 22.

Ad Hoc Standard Errors for Estimates of γ and ln(γ)

A standard error for an ad hoc estimate of γ may be computed with either Fieller’s theorem (Cox, 1990) or the delta method (Hogg and Craig, 1994). The former assumes that k₀ and k₁ are mutually independent, whereas the latter relaxes that assumption. However, because the ad hoc method cannot estimate the covariance of k₀ and k₁, one is forced to assume independence of k₀ and k₁ when applying the delta method. Because k₀ and k₁ are coming from the same individual, this assumption is very likely violated. In addition, both methods for computing a standard error assume that k₀ and k₁ are at least approximately normal, which has been found repeatedly to not be the case (Madden et al., 2004; Myerson & Green, 1995; Simpson & Vuchinich, 2000). The violation of these two assumptions severely limits the computed standard errors’ utility.

Applying Equation 2 twice to obtain $k_0^{\ast }$ and $k_1^{\ast }$ makes computation of a standard error for the ad hoc estimate of $\ln \left(\gamma \right)={\kappa }_1^{\ast }-{\kappa }_0^{\ast }$ easier. We simply substitute the standard errors of $k_0^{\ast }$ and $k_1^{\ast }$ into the variance of a difference: ${\left[SE\right(k_1^{\ast }\left)\right]}^2+{\left[SE\right(k_0^{\ast }\left)\right]}^2-2\mathrm{cov}(k_0^{\ast },k_1^{\ast })$. The last term is forced to zero because no covariance estimate is possible with the ad hoc method. In other words, we are forced to assume independence between k₀ and k₁. Often the correlation between discounting coefficients is positive (for example, see Dixon et al., 2006; Johnson & Bickel, 2002), which means that a standard error computed as just suggested will tend to be too large. The down side of this is that some within-individual change will be missed; the upside is that any change shown with this standard error would also be shown with Method 2 in the text.

Estimating Other Parameters

To get a point estimate of ${\kappa }_1^{\ast }$, we can either add the estimates for ${\kappa }_0^{\ast }$ and ln(γ), or rewrite our toggle function in terms of ${\kappa }_1^{\ast }$ instead of ${\kappa }_0^{\ast }$ and re-run the regression. In this case, define

$$d\left(w\right)=w\ln \left({\gamma }^{\ast }\right)+{\kappa }_1^{\ast },$$ (A3)

where γ* = ${\kappa }_0^{\ast }$ - ${\kappa }_1^{\ast }$ = ln(κ₀/κ₁).

Though we focused primarily on ln(γ), a difference of two log-transformed κs, this change parameter is based on the ratio change, γ, between the two conditions. Other definitions of change exist. Using a dummy variable, a toggle such as Equation 3 can be constructed for the change parameter of interest and substituted for the original parameter, κ, in the one-condition regression function (e.g., Equation 1). One can then directly estimate the particular change of interest and obtain a standard error for it. For example, we may express a difference as a proportion of the condition 0 parameter: $\theta =({\kappa }_1^{\ast }-{\kappa }_0^{\ast })∕{\kappa }_0^{\ast }$. This may then be expressed as $\ln \left(\gamma \right)∕{\kappa }_0^{\ast }$. The toggle is defined as

$$d\left(w\right)={\kappa }_0^{\ast }[1+w(\theta +1\left)\right],$$ (A4)

checking that d(0) = ${\kappa }_0^{\ast }$ and d(1) = ${\kappa }_1^{\ast }$.

In addition, the idea of a toggle may be used for both nonlinear and linear regression. Further, a toggle can be generalized, using a series of dummy variables, to compare among more than two conditions. However, we kept our explanations to the two-condition case for the sake of brevity.

Details for Computing Weights

As noted in the text, we may “use weights to increase power” for any discounting parameter of interest, and not the within-individual change alone. Sidik & Jonkman (2005) provided the technical details for computing the weights and weighted mean; see Equations 1 to 6 (pp. 370–371). Details for confidence intervals follow with Equations 7 and 8 (p. 371). We note that their Y_i and estimated σ²_i correspond with the estimated discounting parameter of interest (e.g., k or the estimated ln(γ)) and the square of its estimated standard error. Example SAS code for computing the weights and weighted mean are available on request to the corresponding author.