Rebalancing binocular vision in amblyopia

Abstract

Purpose

Humans with amblyopia have an asymmetry in binocular vision: neural signals from the amblyopic eye are suppressed in the cortex by the fellow eye. The purpose of this study was to develop new models and methods for rebalancing this asymmetric binocular vision by manipulating the contrast and luminance in the two eyes.

Methods

We measured the perceived phase of a cyclopean sinewave by asking normal and amblyopic observers to indicate the apparent location (phase) of the dark trough in the horizontal cyclopean sine wave relative to a black horizontal reference line, and used the same stimuli to measure perceived contrast by matching the binocular combined contrast to a standard contrast presented to one eye. We varied both the relative contrast and luminance of the two eyes’ inputs, in order to rebalance the asymmetric binocular vision.

Results

Amblyopic binocular vision becomes more and more asymmetric the higher the stimulus contrast or spatial frequency. Reanalysing our previous data, we found that, at a given spatial frequency, the binocular asymmetry could be described by a log-linear formula with two parameters, one for the maximum asymmetry and one for the rate at which the binocular system becomes asymmetric as the contrast increases. Our new data demonstrates that reducing the dominant eye’s mean luminance reduces its suppression of the non-dominant eye, and therefore rebalances the asymmetric binocular vision.

Conclusions

While the binocular asymmetry in amblyopic vision can be rebalanced by manipulating the relative contrast or luminance of the two eyes at a given spatial frequency and contrast, it is very difficult or even impossible to rebalance the asymmetry for all visual conditions. Nonetheless, wearing a neutral density filter before the dominant eye (or increasing the mean luminance in the non-dominant eye) may be more beneficial than the traditional method of patching the dominant eye for treating amblyopia.

Introduction

The human brain devotes enormous resources toward providing a cyclopean view of the world, by combining the separate inputs from the two eyes ¹. This binocular combination and also stereovision depend strongly on having well balanced vision in the two eyes ^1–5. In normal vision, the two eyes exert symmetric mutual suppression on each other ^{6, 7}, thus maintaining balanced binocular vision. However, in persons with amblyopia, there is an imbalance of the two eyes and abnormal binocular vision. Specifically, the dominant eye (DE) exerts stronger suppression on the non-dominant eye (NDE) than the NDE on the DE ^8–11, even under conditions where each eye has normal monocular vision (e.g., at low spatial frequencies). However, Baker et al (2007) suggested that the binocular summation of contrast remained ‘intact’ in strabismic amblyopia if the two eyes’ inputs were normalised by their monocular contrast detection thresholds ¹², and they modelled contrast discrimination in strabismic amblyopia on the basis of signal attenuation and an increase in noise in the amblyopic eye, with ‘intact’ stages of interocular suppression and binocular summation¹³.

Ding and Sperling ^{6, 7} developed a novel psychophysical paradigm to assess interocular suppression directly. They measured the perceived phase of a binocularly-combined cyclopean sinewave, from which the relative contribution of the two eyes to the binocular combination could be calculated. Recently this paradigm was extended to the assessment of asymmetric interocular suppression in amblyopic vision ^8–11. Coherent global motion has also been used to assess the interocular suppression in both normal and abnormal binocular vision ^{14, 15}. All these studies show that the NDE of amblyopic observers is strongly suppressed, resulting in reduced or absent binocular combination under normal viewing conditions. Therefore, one possible approach to restoring their binocular vision would be to rebalance the asymmetric binocular vision of people with amblyopia. Amblyopia is a developmental visual disorder due to abnormal binocular visual experience (e.g., strabismus and anisometropia) during a sensitive period in early childhood that disrupts the neural circuitry in the visual cortex. The standard treatment for amblyopia, since first suggested by Buffon in 1743 ¹⁶, consists of occluding or penalising the fellow non-amblyopic eye ¹⁷. While patching the DE “forces” the use of the NDE to view the world, it has both physiological and psychosocial consequences ^18–21. Importantly, patching deprives the amblyope of binocular visual experience. Thus, there are important reasons to seek alternative methods that might favour the development of binocular vision. Perhaps the earliest recorded attempt at this was Worth’s advocacy of using atropine in the dominant eye to defocus the retinal image ²², thus producing an “invisible translucent patch” ¹⁷. The use of atropine (penalisation) in children is in common use today.

Over the years there have been a number of attempts to improve on patching by equalising the vision in the two eyes. For example, Maddox (1907) covered the dominant eye with smoked glass ²³, and Pugh (1936) advocated a set of calibrated filters to equalise the two eyes ²⁴. A similar approach was achieved by using graded cross polarising filters ²⁵. Others used cellotape ²⁶, optical defocus or diffusion ^27–29 to degrade the acuity of the DE and equalise the two eyes’ input. A more modern approach to re-balancing the two eyes’ input is through balancing the effective contrast in the two eyes ^{8–11, 14, 15}. Our previous study ^{8, 9} showed that it is possible to rebalance the binocular asymmetry in amblyopic vision by manipulating the two eyes’ contrast. The two eyes contribute equally to the perception of a binocular target when the DE’s contrast is reduced by a rebalance factor δ_B (NDE/DE contrast ratio at rebalanced vision). However, the rebalance factor is not a constant for an amblyopic observer, but depends on the stimulus contrast and spatial frequency. Typically, the DE’s contrast must be reduced more (larger δ_B) at higher base contrast levels and at higher spatial frequencies. Although the rebalance factor δ_B can be calculated from a binocular combination model ^{9, 30} (DSKL model, a modified Ding-Sperling model), the model is too complicated. In this study, we develop a simple formula (log-linear relationship) to calculate the rebalance factor as a function of base contrast. While it is easy to independently vary the contrast to the two eyes in the laboratory (using dichoptic stimuli), manipulating the two eyes’ contrast during natural viewing is a technical challenge. Placing a dispersing filter before the DE could be one option for this purpose, but this would degrade the vision of the DE ^{18, 19, 21}. More importantly, during natural viewing in daily life, complex images contain a broad range of contrasts and spatial frequencies, rendering a single overall contrast reduction factor unsuitable, because band-limited contrast is very different from the global contrast ³¹. On the other hand, placing a neutral density (ND) filter before the DE might better serve the purpose of balancing the two eyes’ input. For example, Zhang et al. showed that for a normal observer, the eye wearing an ND filter exerted less suppression to the other eye ³². Zhou et al found that, in normal observers, attenuation of one eye’s luminance with neutral density filters produces binocular phase combination similar to that of amblyopic subjects, and in amblyopic observers, reduction of the DE’s luminance produces binocular phase combination similar to that of normal observers³³. Previous psychophysical studies have shown that mean luminance has little effect on contrast perception ^{34, 35}, and physiological studies also suggest that luminance and contrast are processed independently in the visual system^36–38. Moreover, ND filters have been used in the simulation and treatment of amblyopia ^{12, 13, 39–42}, although there have been no clinical efficacy trials.

In this paper, we first reanalyse our previous data of perceived phase and contrast of cyclopean sinewaves, and develop a simple formula (log-linear relationship) for binocular asymmetry, and then demonstrate how to rebalance the asymmetric binocular vision of amblyopic observers by placing an ND filter before the DE.

Methods

The methods used in this paper were almost identical to our previous study ^{9, 30} except that (1) a neutral density (ND) filter was placed in front of the DE; (2) the stimuli were windowed spatially with a circular window with a blurred edge (not a square window with sharp edges); (3) the physical position of the reference line was fixed and its relative position to the cyclopean sinewave varied in a staircase from trial to trial by shifting the phases of the two eyes’ sinewaves correspondingly.

Stimuli

Horizontal gratings with sinusoidal luminance profiles, I_L = I_QL(1+m_L cos(2π_fsγ+θ_L)) and I_R = I_QR(1+m_R cos(2πf_sγ+θ_R)), were used as stimuli. I_QL and I_QR are the luminance of the background and the mean luminance of the sinewave gratings of the two eyes (=26.2 cd/m² without an ND filter); f_s is the spatial frequency, identical in both eyes; m_L and m_R are the modulation contrasts of the left- and right-eye sinewave gratings, respectively; θ_L and θ_R are the corresponding phases, which differ by 90 degree in the phase matching task (Experiment 1) but are identical in the contrast matching task (Experiment 2). The stimuli were windowed in a circular window spatially (3 deg in diameter) and a square window temporally (1s).

Procedure

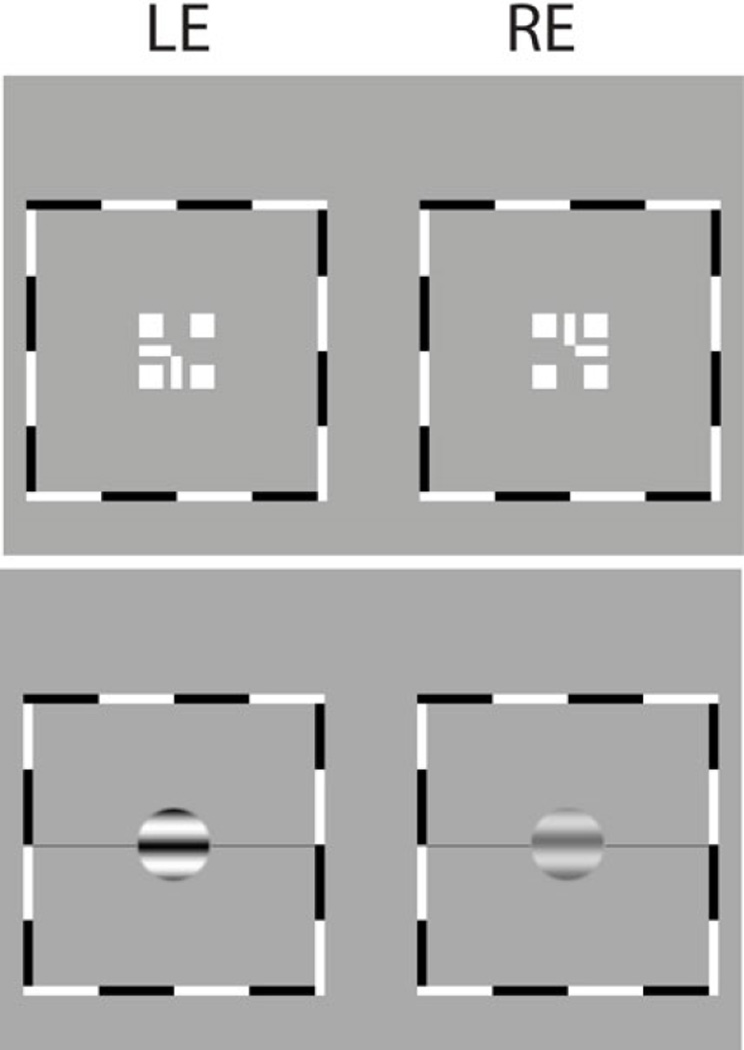
The procedure was identical to our previous studies ^{9, 30}. For Experiment 1, each trial began with presentation of a dichoptic nonius cross surrounded by a high contrast frame (Top in Fig. 1). Once the dichoptic cross appeared to be aligned and stable, the observer pressed a key to initiate the trial. Following the key press, a screen with only the surrounding high-contrast frame and reference horizontal lines appeared for 500 msec (Figure not shown), followed by sinewave gratings presented to the two eyes respectively for one second (Bottom in Fig. 1). Stimulus presentation was followed by a blank screen of mean luminance until the observer responded. The observer’s task was to indicate the apparent location of the centre of the dark stripe in the perceived cyclopean sinewave grating, relative to a black horizontal reference line adjacent to its edge. The observer pressed one of two keys to indicate whether the reference line was judged to be above or below the dark cyclopean stripe. The physical position of the reference line was fixed, always in the centre, to aid fixation, but its position relative to the dark cyclopean stripe varied from trial to trial in a staircase in order to measure the perceived phase of the cyclopean sinewave by shifting the phase of the two eyes’ sinewaves correspondingly. For Experiment 2, the procedure was similar to that used in Experiment 1 except having two stimulus intervals, one with a standard contrast (48%, 24%, 12%, or 6%) only presented to the NDE (without wearing an ND filter) and the other with a test contrast presented to both eyes with the interocular contrast ratio varying from trial to trial. Each interval lasted for 1 second and the inter-stimulus interval was 0.5 seconds. The observer’s task was to judge which interval had the sine wave with higher contrast. At each contrast ratio, two staircases were interleaved to measure the contrast of the test cyclopean sine wave depending on whether the standard contrast was in the first or second interval. The average of these two measurements was calculated as the perceived contrast at that contrast ratio. A black horizontal line was also attached to the side of a sine wave to make the stimulus identical to those used in Experiment 1. Observers were instructed to make their judgments by comparing the luminance differences of the black and white stripes within a sinewave grating, not based on the absolute darkness or brightness of a stripe.

Figure 1.

Stimuli. A dichoptic nonius cross surrounded by a high contrast frame (above) and sinewave gratings presented to the two eyes (bottom). An observer’s task was to indicate the apparent location of the centre of the dark stripe in the perceived cyclopean sinewave grating relative to reference horizontal lines adjacent to its edge. The physical position of the reference lines was fixed, and its relative vertical position to the cyclopean sinewave grating varied from trial to trial in a staircase by shifting the phases of the two eyes’ sinewaves correspondingly.

Neutral density filters

A Kodak Wratten neutral density filter was placed in front of the DE to reduce the luminance to that eye by 0 (no filter, factor = 1), 0.5 (factor = 3.16), 1.0 (factor = 10), 1.5 (factor = 31.6) and 2.0 (factor = 100) log units. The mean luminance with no filter was 26.2 cd/m² and the mean luminance with a 2.0 ND filter was 0.262 cd/m². Before testing, observers wore the ND filter for at least 5 min for dark adaptation.

Observers

Two amblyopic observers and two normal observers signed the written consent and participated in the experiment, but the new data with an ND filter placed before the DE were collected from one amblyopic observer (GD). Clinical details for amblyopic observers are provided in Table 1.

Table 1.

Clinical data for amblyopic observers

	Age	Gender	Type	Strabismus	Stereo	Eye	Refractive error	Letter Acuity (Snellen)
GJ	25	M	Strab & Aniso	R ET 4Δ	none	R(NDE) L(DE)	+3.00/−0.50x90 plano/−0.25x90	20/40−2 20/16
GD	46	F	Aniso	None	70 arcsec	R(DE) L(NDE)	+0.25/−0.50x90 +3.75/−1.00x30	20/12.5−2 20/50+2

Aniso, anisometropia; Strab, Strabismus; ET, esotropia; Δ, prism dioptres; DE, dominant eye; NDE, non-dominant eye; equivalent visual acuities are 20/12.5 (~6/4, −0.20 logMAR), 20/16 (6/5, −0.10 logMAR), 20/40 (6/12, 0.30 logMAR), 20/50 (6/15, 0.40 logMAR).

Modelling

Ding-Sperling Model: Gain-control and gain-control energy

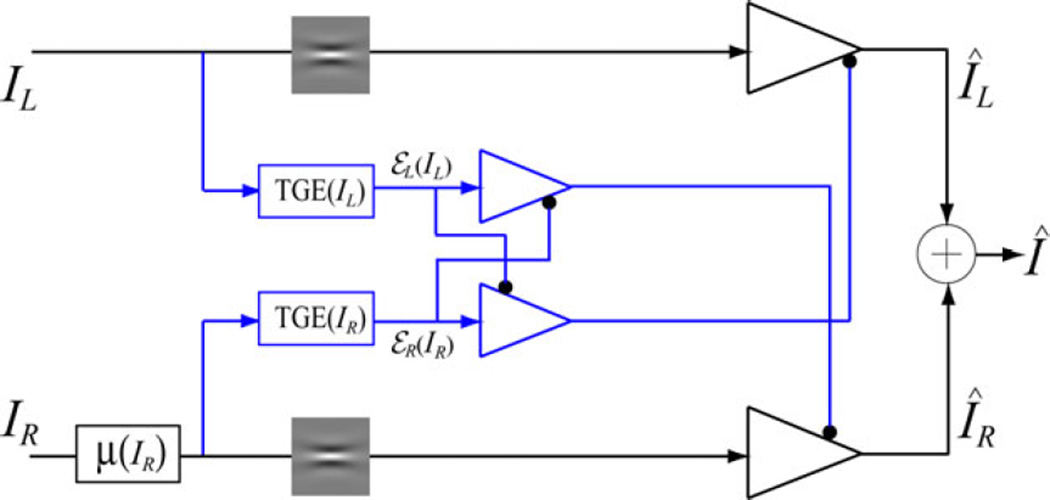
Ding and Sperling ^{6, 7} proposed a gain-control model (Fig. 2) to explain the phase-combination data. The model consists of left and right eye channels, each containing two gain control mechanisms: gain control in the signal layer (black) which is selective for orientation and spatial frequency, and gain control of the gain control in the gain-control layer (blue) which is non-selective, based on total gain-control energy (TGE) summed across all dimensions. The two TGE components exert reciprocal inhibition (gain control) on one another in the gain-control layers (blue) in proportion to their respective TGE outputs, and the outputs of those TGE components exert gain control on the other eye’s signal layer (black). The outputs are summed linearly to determine the binocular signal. The model output is given by

$$\widehat{I}=\frac{1}{1+\frac{{\epsilon }_R(I_R)}{1+{\epsilon }_L(I_L)}}{I}_L+\frac{1}{1+\frac{{\epsilon }_L(I_L)}{1+{\epsilon }_R(I_R)}}\mu I_R$$ (1)

where I_L and I_R are the inputs to the two eyes, and ε_L and ε_R are the total weighted gain-control energy (TGE) of the two eyes, which should be summed across space, time, spatial frequency and orientation ⁷. For narrow-banded stimuli, e.g.,

$$I_L=I_{QL}(1+m_L\text{sin}(2\pi f_s\chi +{\theta }_L))\text{and}{I}_R=I_{QR}(1+m_R\text{sin}(2\pi f_s\chi +{\theta }_R)),$$ (2)

the total gain-control energy is given by,

$${\epsilon }_L={\left(\frac{m_L}{g_L}\right)}^{{\gamma }_L}\text{and}{\epsilon }_R={\left(\frac{\mu m_R}{g_R}\right)}^{{\gamma }_R}$$ (3)

where I_QL and I_QR are the mean luminance of the two eyes, m_L and m_R are the two input contrast, g_L and g_R quantify the gain-control contrast threshold at which the interocular gain-control becomes apparent, γ_L and γ_R are the two exponents for the gain-control energy calculation, and μ is the contrast attenuation in the RE to account for a possible monocular asymmetry of contrast perception. A larger exponent gamma value means a faster increase of the interocular suppression (gain-control) when the input contrast increases.

Figure 2.

Ding-Sperling model, a gain-control model for binocular combination ^{6, 7, 30}. The model consists of left and right eye channels, each containing two gain control mechanisms: one is selective for orientation and spatial frequency in the signal layer (black) and the other is non-selective for those dimensions, and is based on total gain-control energy (TGE) summed across all dimensions in the gain-control layer (blue). The two TGE components exert reciprocal inhibition on one another, in the gain-control layers (blue) in proportion to their respective TGE outputs, and the outputs of those TGE components exert gain control on the other eye’s signal layer (black). The outputs are summed linearly to determine the binocular signal.

The gain-control energy plays a key role in the interocular suppression ^{9, 30}. If one eye has larger gain-control energy than the other eye, it will suppress the other eye more strongly than the converse and will dominate the binocular combination; the other eye’s signal will be suppressed and make less contribution to the summation. For normal vision, the two eyes have comparable gain-control thresholds and gamma exponents, and therefore, binocular vision remains balanced under normal viewing condition ³⁰.

Asymmetric gain-control energy causes asymmetric interocular suppression

Asymmetric interocular suppression in amblyopia has been studied using contrast discrimination¹³, coherent global motion¹⁵ and binocular phase combination^8–11. To assess the form of the amblyopic deficit in contrast discrimination, Baker et al¹³ 'lesioned' the two-stage model⁴³ of binocular contrast gain control in several ways, including asymmetric (abnormal) interocular suppression. They found that the model that most successfully accounted for contrast discrimination involves attenuation of signal and an increase in noise in the amblyopic eye, and ‘intact’ stages of interocular suppression and binocular summation¹³.

On the other hand, interocular suppression can be assessed directly either by coherent global motion^{14, 15} or by binocular phase combination^{6–11, 30, 44}. Both methods reveal that interocular suppression in amblyopia is very asymmetric even when the monocular performance is matched in the two eyes^{8–11, 15}. To account for the asymmetric binocular combination in amblyopia, several modifications of the Ding-Sperling model were proposed^8–11, including a contrast attenuator in the NDE (similar to the modified two-stage model¹³) and abnormal (asymmetric) interocular suppression in contrast to Baker et al’s modified two-stage model with ‘intact’ interocular suppression¹³.

The interocular asymmetry in amblyopia is a result of the DE’s (say LE) gain-control energy (ε_L) being much larger than the NDE’s (ε_R) under normal viewing conditions ⁹. As shown in Eq. 3, there are three factors that affect the gain-control energy: (1) the apparent contrast. The NDE (RE) might have reduced apparent contrast (μ < 1) even if the physical contrast is identical for the two eyes; (2) gain-control threshold. The NDE might have higher gain-control threshold (g_R > g_L); (3) the exponent gamma. The NDE might have smaller gamma value (γ_R < γ_L) making its gain-control energy increase more slowly as input contrast increases. Typically, all three factors contribute to the asymmetric binocular vision in amblyopic vision ⁹. However, in the literature, more studies have focused on the reduced input contrast in the NDE. Clinical treatments also generally focus on monocular treatment, e.g., trying to increase contrast sensitivity and visual acuity in the NDE. However, even though monocular vision may appear ‘normal’ (e.g., at low spatial frequencies), binocular vision may still be highly asymmetric, because of asymmetric interocular suppression ^8–11. From our previous studies ⁹, the NDE’s gain-control energy has higher gain-control threshold and smaller exponent gamma value than the normal vision, while the DE seems ‘normal’, having comparable gain-control threshold and exponent gamma with the normal vision.

Results

We first re-analyse our previous data ^{9, 30} to show how to rebalance asymmetric binocular vision by reducing the DE’s input contrast. From our previous data and modelling, we deduce a log-linear formula for the rebalanced points. Then we present new data to show how to accomplish the rebalancing by placing a neutral density filter before the DE.

Rebalancing asymmetric binocular vision by reducing the DE’s input contrast

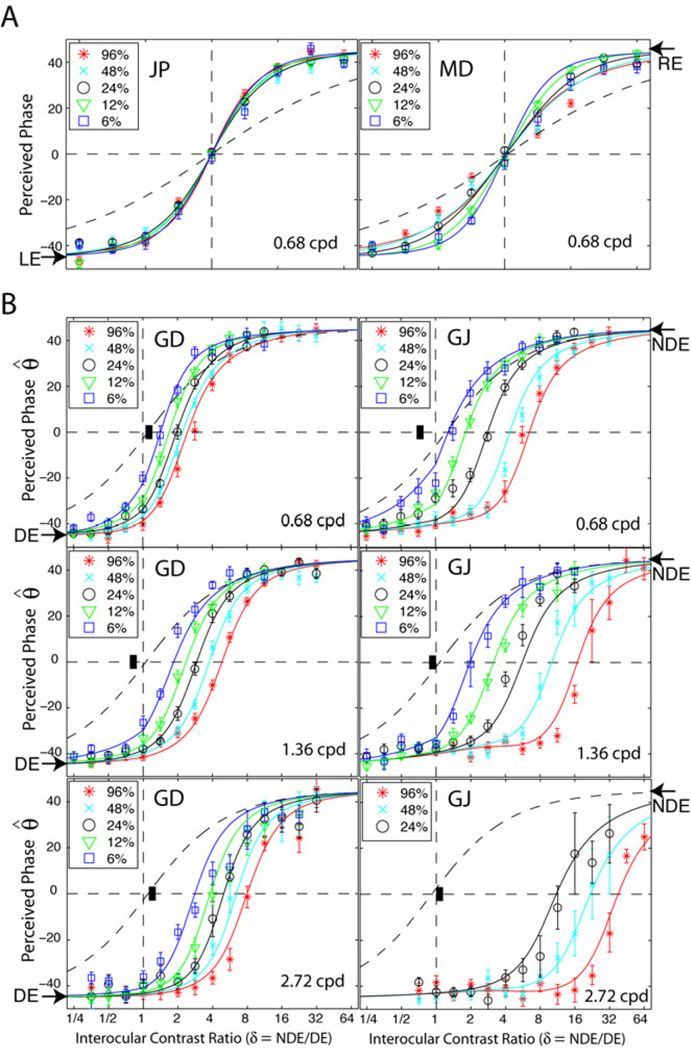
Figure 3 replots some of our previous data ^{9, 30} for the perceived phase of binocularly-combined cyclopean sinewaves as a function of interocular contrast ratio at different base contrasts and spatial frequencies. The arrow on the left side of each panel indicates the phase (−45 deg) of the LE’s (or DE’s) sinewave, and the arrow on the right side indicates the phase (45 deg) of the RE’s (or NDE’s) sinewave. The horizontal dashed line at θ̂ = 0 indicates the contrast ratio at which the two eyes equally contribute to the perceived cyclopean image. We refer to this as the “balance ratio” δ_B. When θ̂ < 0, the perceived phase is biased to the DE; when θ̂ > 0, the perceived phase is biased to the NDE. For normal observers (Fig. 3A), when the two eyes have identical contrast (RE/LE contrast ratio = 1, vertical dashed line), the gain-control energies (Eq. 3) of the two eyes are equal because the two eyes have equal gain-control threshold and exponent gamma. The perceived phase is midway between the phases of the two eyes sinewaves (= 0). However, when the two eyes have different contrast inputs, the eye with higher contrast dominates the summation, biasing the perceived phase toward that eye (Fig. 3A) by more than predicted by linear summation (black dashed curve).

Figure 3.

Results from our previous studies ^{9, 30}. Perceived phase θ̂ of binocularly-combined cyclopean sine waves as a function of the right eye/left eye (RE/LE) or non-dominant eye/ dominant eye (NDE/DE) contrast ratio (δ ) for two normal observers (A) or two amblyopic observers (B), when the base contrast m is 96% (*), 48% (x), 24% (○), 12% (∇), or 6% (□). The phase difference of the two eyes’ sinewave gratings was fixed at 90 deg; LE’s (or DE’s) was −45 deg indicated by arrows in the left side and RE’s (or NDE’s) was 45 deg indicated by arrows in the right side. When δ ≤ 1 the DE’s grating contrast was fixed at base contrast m and δ was increased by increasing the NDE’s contrast (δ m). When δ ≥ 1 the NDE’s contrast remained constant at the base contrast m, and δ was increased by decreasing the DE’s contrast (m/δ). The solid curves are the best fits from the DSKL model (a modified Ding-Sperling model). The black dashed curve is the prediction of linear summation, the asymptote of the DSKL model at zero gain-control energy. The short black bars indicate contrast threshold ratios. Error bars: ±SE.

In contrast, for an amblyopic observer (Fig. 3B), the perceived phase is biased toward the DE when the physical contrasts are identical in the two eyes (δ = 1, vertical dashed line). This DE-bias is not simply due to monocular contrast sensitivities or monocular contrast perception. At the tested spatial frequencies, both contrast sensitivity and suprathreshold contrast perception are comparable in the two eyes. The short black bar indicates the ratio of contrast sensitivity of the two eyes, and the linear summation curve (black dashed curve) is based on the apparent contrast in the two eyes (with attenuation in the NDE), which was measured in a contrast matching task (data not show, details see Ref #9). Obviously, the monocular asymmetry of either apparent contrast or contrast sensitivity in the two eyes cannot explain binocular asymmetry.

The coloured curves in Fig. 3 are the best fits of the DSKL model ^{9, 30} (a modified Ding-Sperling model ⁶) constrained by the perceived contrast of the cyclopean sinewaves (data not shown, but see our previous studies ^{9, 30}). In order for the NDE’s sinewave to contribute to the cyclopean percept, the DE’s contrast has to be reduced (NDE/DE ratio increased) and the perceived phase shifts from DE-biased (θ̂ < 0) to NDE-biased (θ̂ > 0). Rebalanced vision is achieved at NDE/DE contrast ratio δ_B (the rebalanced factor), the factor by which the DE’s contrast has to be reduced to achieve perceived phase = 0 deg, and the two eyes contribute equally to the binocular combination. The value of the rebalanced factor can be calculated from the fitted DSKL model ⁹. Normal observers have balanced vision between the two eyes when the two eyes’ sinewaves have equal contrast (δ_B = 1) (Figure 3A) and don’t need rebalancing.

From our previous modelling ⁹, the binocular imbalance in amblyopic vision is due to the elevation of the gain-control threshold (relative to the normal value) in the NDE, reducing its gain-control energy (Eq. 3) and reducing its suppression of the DE (relative to the normal level). By reducing the DE’s stimulus contrast, it is possible to equate the two eyes’ gain-control energy, and therefore to rebalance the abnormal binocular vision. However, the rebalance factor δ_B is not a constant for an amblyopic observer because the two eyes’ gain-control energies have different exponent gamma value ⁹. The gamma value in the DE is larger than in the NDE, making the DE’s gain-control energy increase more quickly than the NDE’s when the contrast increases. Therefore, when the base contrast increases, the suppression from the DE to the NDE increases more rapidly than the suppression from the NDE to the DE, and the perceived phase becomes more and more biased toward the DE, i.e., the perceived phase curve shifts down and right in Fig. 3B and the rebalance factor δ_B increases when the base contrast increases. In other words, there is no simple δ_B value to achieve rebalanced vision for all contrast levels. More importantly, the rebalance factor δ_B is also a function of spatial frequency ⁹. When the spatial frequency increases, δ_B increases and binocular vision becomes more asymmetric; the perceived phase shifts down and right in Fig. 3B and becomes more biased to the DE. This makes the correction of asymmetric binocular vision more difficult in the real world because a suitable δ_B value for one scale doesn’t work for the other scales.

Log-linear relationship of binocular asymmetry with input contrast

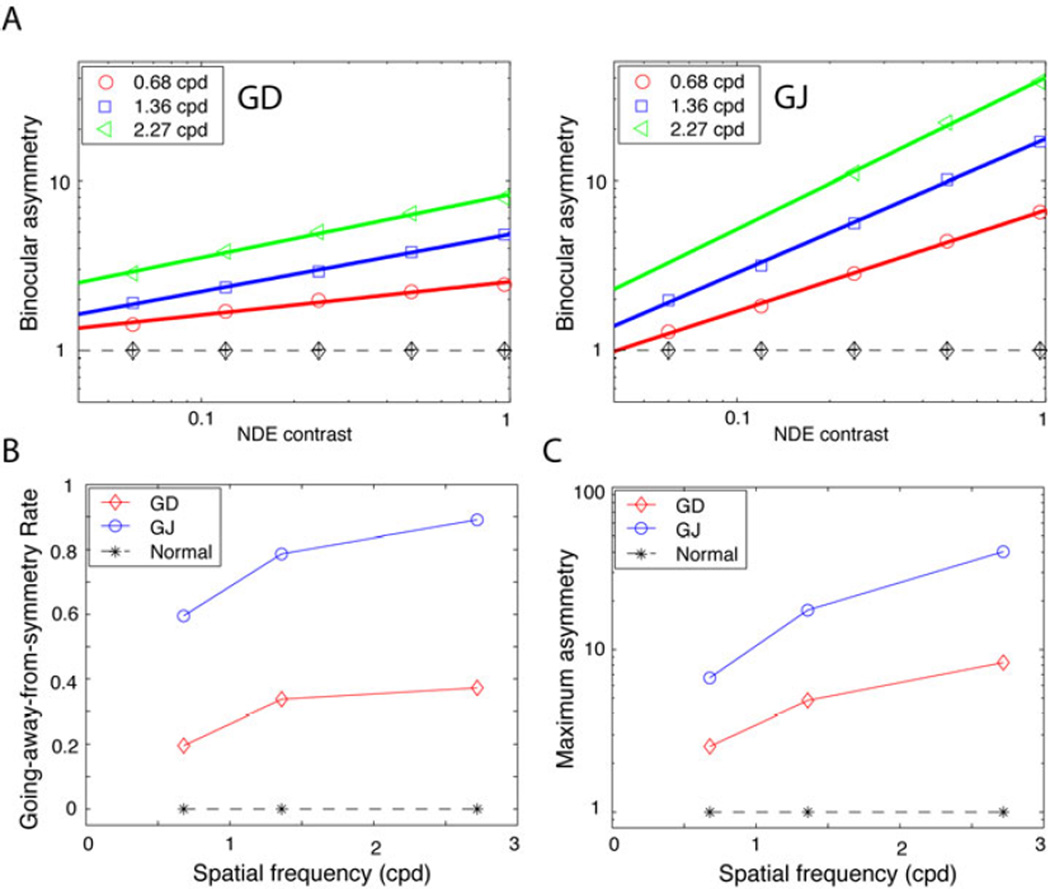
We defined binocular asymmetry as the NDE/DE contrast ratio (δ_B rebalance factor) at rebalanced vision. Although the rebalance factor can be calculated from the fitted DSKL model, it is not convenient for clinical purposes because the DSKL model is very complicated. Here we first show the rebalance factor (binocular asymmetry) as a function of the NDE’s contrast in log-log coordinates (Fig. 4A, adapted from our previous study ^{9, 30}), and then fit a straight line (the rebalance line) to the data. Normal observers have symmetric binocular vision (Fig. 4A) and their rebalance factor δ_B ≈ 1 (no need for rebalance or no asymmetry), independent of contrast and spatial frequency (black dashed lines). However, for amblyopic observers, binocular vision departs markedly from symmetry and requires rebalancing. The rebalance factor δ_B increases with increasing contrast, and reaches the maximum when the NDE’s contrast is 100%. When the spatial frequency (coded by colour) increases, δ_B also increases and binocular vision becomes more and more asymmetric. At a given spatial frequency, the data can be fit by a straight line (rebalance line) in log-log coordinates,

$$\text{log}{\delta }_B=p\text{log}{C}_{\mathit{\text{NDE}}}+{\alpha }_{\text{max}},$$ (4)

where p is the slope of the fitted line, the rate at which the line departs from that of symmetric binocular vision (δ_B = 1, the dashed horizontal line in Fig. 4A) as contrast increases, and α_max is the maximum asymmetry (in log unit) when the NDE’s contrast is 100% (C_NDE = 1). Both are functions of spatial frequency, increasing when spatial frequency increases, as shown in Figs. 4B and C. For normal observers, log δ_B ≈ 0 (no binocular asymmetry) for all contrasts and spatial frequencies (dashed horizontal line in Fig. 4A), i.e., p = 0 and α_max = 0 in Eq. 4 (dashed horizontal lines in Figs. 4B and C). Therefore, the binocular asymmetry (α = logδ_B) can be described by a log-linear formula with two parameters, the going-away-from-symmetry rate (p) and the maximum asymmetry (α_max).

Figure 4.

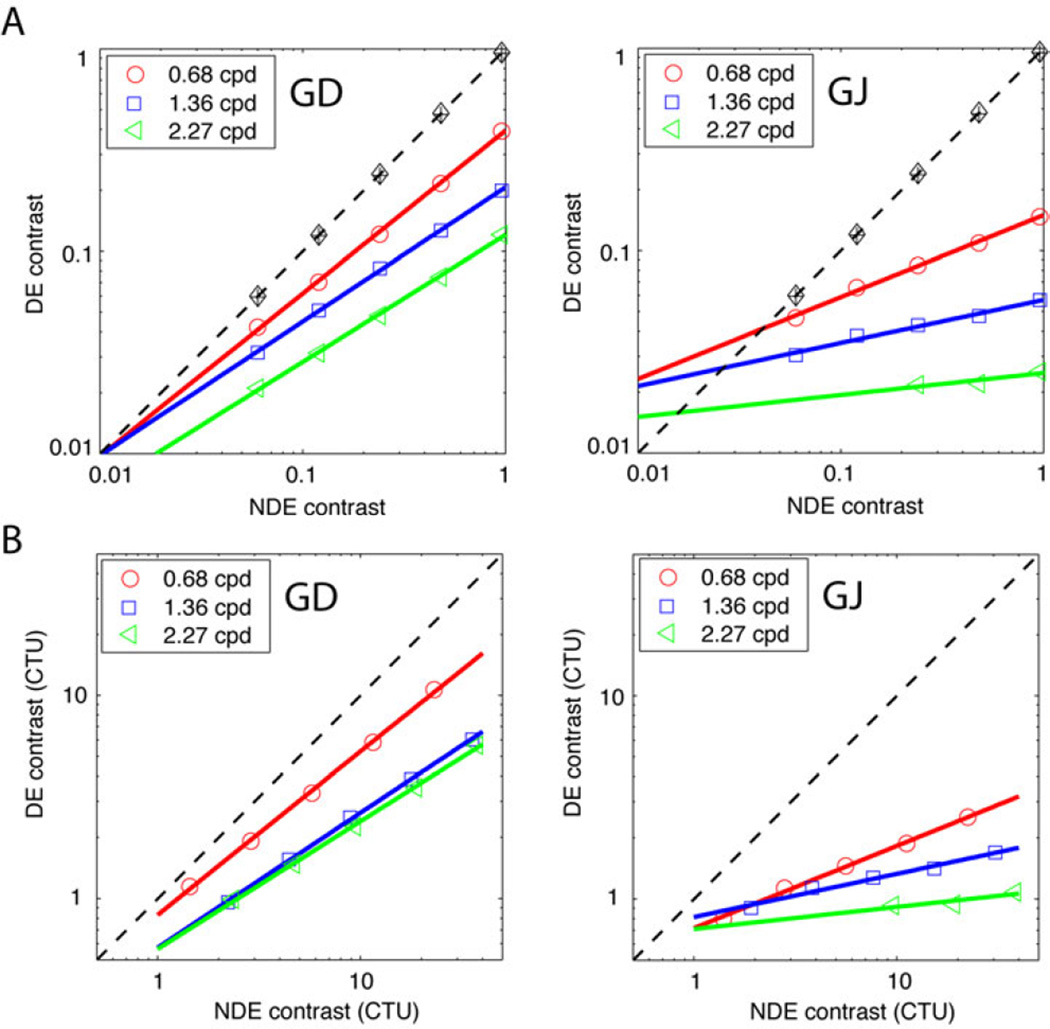
A. Binocular asymmetry (δ_B = non-dominant eye/ dominant eye or NDE/DE contrast ratio at rebalanced vision) as a function of NDE contrast for two amblyopic observers GD (left) and GJ (right), adapted from Ding, Klein & Levi ⁹. For one spatial frequency, the data can be fit by a straight line, the rebalance line (solid coloured lines), at which the imbalanced binocular vision is rebalanced. The horizontal dashed line at δ_B = 1 shows the symmetry line for normal vision, and the black markers indicate the right eye/left eye (RE/LE) contrast ratio for symmetric binocular vision. B. The going-away-from-symmetry rate (the slope of a rebalance line in A) as a function of spatial frequency. The horizontal black dashed line at 0 indicates that normal vision always remains symmetric (never going away from the symmetry). C. Maximum asymmetry (when NDE’s contrast = 100%) as a function of spatial frequency. The horizontal black dashed line at 1 indicates no asymmetry in normal vision.

Figure 5 illustrates the binocular asymmetry by plotting the contrast of the DE against that of the NDE at the rebalance points. Normal observers (black markers in Figure 5A) achieve balanced vision at all spatial frequencies when the two eyes’ inputs have identical contrast (black dashed line, the symmetry line). However, for amblyopic observers (coloured symbols), for a given NDE contrast, the DE’s contrast had to be reduced by a factor δ_B (the rebalance factor) to rebalance the asymmetry (a coloured marker), so the points all fall below the symmetry 1:1 (black dashed line) line. At a given spatial frequency (coded by colour), the rebalance points can be fit by a straight line (a rebalance line),

$$\text{log}{C}_{DE}=(1-p)\text{log}{C}_{\mathit{\text{NDE}}}-{\alpha }_{\text{max}}$$ (5)

where p is the going-away-from-symmetry rate (Fig. 4B) and α_max is the maximum asymmetry (Fig. 4C). Above threshold, all rebalance lines are below the symmetry line (black dashed line), meaning that the DE’s contrast has to be reduced to achieve rebalanced vision. The slope of the rebalance line is less than 1 (p > 0), meaning that there is no single fixed factor that can rebalance the system for all contrast levels. When the NDE’s contrast reaches the maximum value (100% C_NDE = 1), in the rebalanced binocular vision, the DE’s contrast should be 10^−α_max, the maximum-rebalanceable contrast in the DE, beyond which the system cannot be rebalanced by increasing the NDE’s contrast. Note that the binocular asymmetry is not simply a consequence of the elevated contrast thresholds (reduced contrast sensitivity) of the NDE. Fig. 5B specifies the contrasts for each eye in contrast threshold units (CTU), thus taking into account any reduction in contrast sensitivity. Thus, for example, in the most extreme case, for observer GJ to achieve rebalanced vision at 2.72 cpd with a stimulus contrast of 96% in the NDE (≈ 40 CTU), required the DE’s contrast to be just above threshold (≈ 2.3%). Therefore, contrast attenuation in the NDE is not sufficient to account for the binocular asymmetry, consistent with Harrad & Hess ⁴⁵ who found that the binocular dysfunction did not merely follow as a consequence of the known monocular loss and that it depends upon the spatial frequency of the stimulus.

Figure 5.

A. Contrast of dominant eye vs. non- dominant eye (DE vs. NDE) at rebalanced vision for two amblyopic observers measured at three spatial frequencies. Black markers show the contrast of the left eye vs. right eye (LE vs. RE) at balanced vision for normal observers. B. The same as in A but in contrast threshold units (CTU).

Rebalancing asymmetric binocular vision by reducing the DE’s mean luminance

Here we examine another method to rebalance asymmetric binocular vision by reducing the DE’s mean luminance through placing a neutral density (ND) filter before the DE. We conducted two experiments to measure the perceived phase (Experiment 1) and contrast (Experiment 2) of a cyclopean sinewave when a neutral density filter was placed in front of the DE.

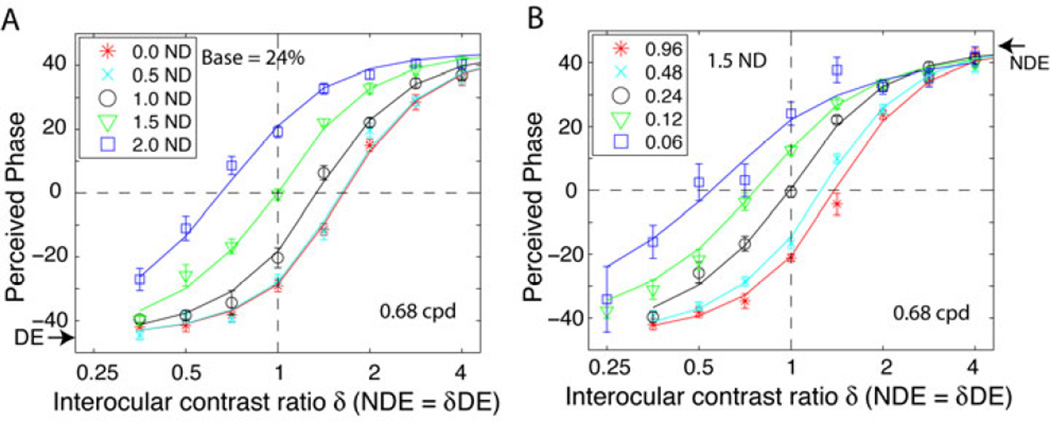
Experiment 1: Perceived phase when the DE wears a neutral density filter

Figure 6A shows perceived phase as a function of NDE/DE contrast when the DE’s luminance was reduced from 0.0 (no filter) to 2.0 log unit (factor = 100). When the DE’s luminance is reduced, the perceived phase shifts systematically toward the NDE (the phase curves shifting up and left). At a base contrast of 24%, a 1.5 ND (factor = 32) filter before the DE rebalanced binocular vision when the two eyes contrast inputs were identical (vertical dashed line). Further increasing the filter to 2.0 ND, resulted in the phase curve becoming NDE-biased. However, varying the base contrast level (from 24%), resulted in a loss of the rebalanced binocular vision (i.e. from that obtained with a 1.5 ND filter before the DE). As shown in Figure 6B, at higher contrast levels (96% or 48%), binocular vision was biased toward the DE, but at lower contrasts (12% or 6%), binocular vision was biased toward the NDE. Apparently, placing an ND filter before the DE shifts all perceived phase curves in Figure 3B towards the NDE (shifts up and left) in Figure 6B.

Figure 6.

Perceived phase θ̂ of cyclopean sinewaves as a function of the non-dominant eye/ dominant eye (NDE/DE) contrast ratio (δ) for amblyopic observer GD with a neutral density (ND) filter placed in front of her DE. A. The ND filter varied from 0 (no filter) to 2.0 log unit and the base contrast was fixed at 24%. B. The ND filter was fixed at 1.5 log unit and the base contrast varied from 6% to 96%. The mean luminance without an ND filter was 26.2 cd/m². Error bars: ±SE.

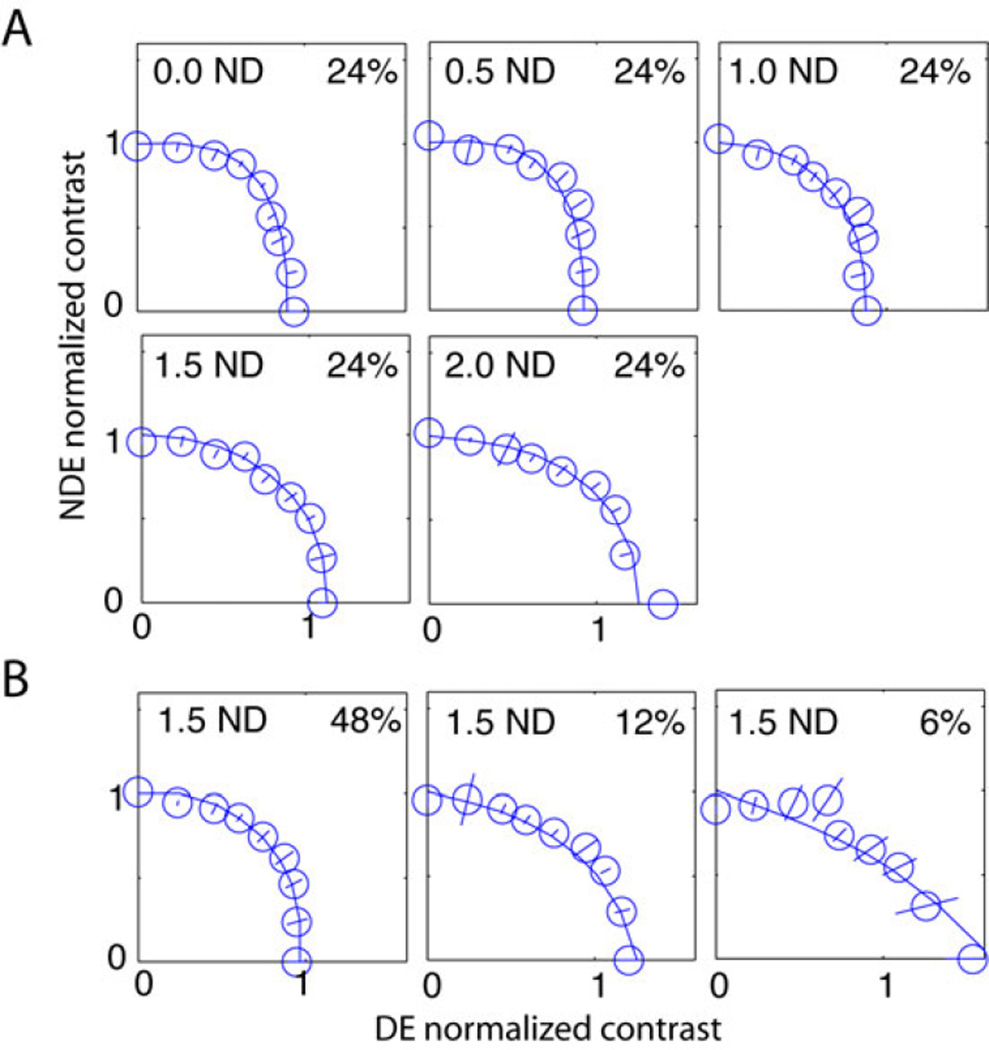
Experiment 2: Apparent contrast when the DE wears a neutral density filter

Does placing an ND filter before the DE reduce its apparent contrast and therefore rebalance binocular vision? To test this observers performed a contrast matching task between two temporal intervals (see Method for details) to measure the binocular equal-contrast contour with a standard contrast in the NDE when the DE was wearing an ND filter. The apparent contrast of the cyclopean sinewave also provided contrast constraints for fitting a model to the phase data. The contrast measured in Experiment 2 is to determine whether the same mechanisms that affect apparent monocular contrast, or the apparent contrast within binocular displays, is also responsible for the weighting of the two eyes’ inputs in the fused displays of Experiment 1.

Figure 7A shows results when the standard contrast in the NDE is 24%, the test contrast is presented binocularly, and the DE’s luminance was reduced from 0 to 2.0 log units. When ND < 1.5, the DE’s apparent contrast was almost independent of luminance, decreasing only slightly when luminance decreased, consistent with previous studies ^{34, 35}. This slightly-reduced apparent contrast is not enough to explain the phase shift towards the NDE by reducing DE’s mean luminance.

Figure 7.

A. Binocular equal contrast contour for amblyopic observer GD when a neutral density (ND) filter was placed in front of her DE. A. The ND filter varied from 0 (no filter) to 2.0 log unit and the base contrast was fixed at 24%. B. The ND filter was fixed at 1.5 log unit and the base contrast varied from 6% to 48% (the data for 24% was shown in A). The binocularly-combined contrast was measured by matching it with a standard that was always in the non-dominant eye (without wearing an ND filter). The mean luminance without an ND filter was 26.2 cd/m². Error bars: ±SE.

Modelling

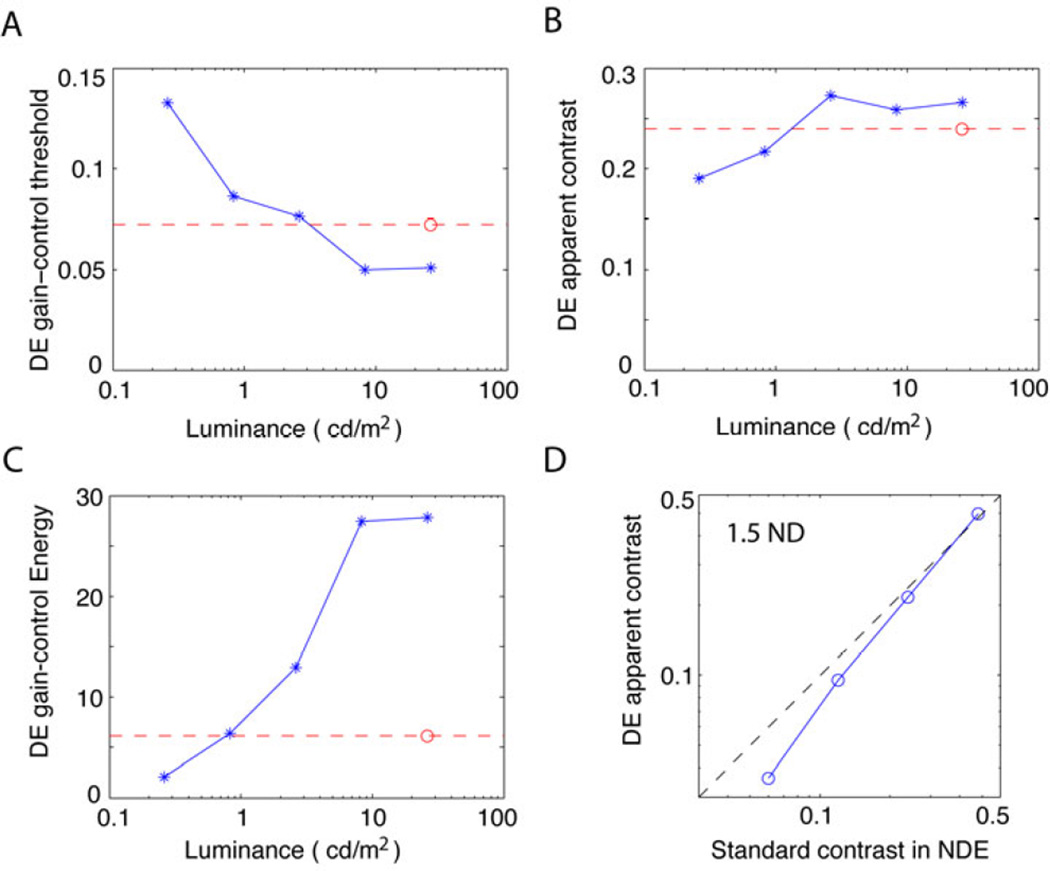
In an effort to understand how an ND filter shifts the perceived phase, we applied the Ding-Sperling model to both the perceived phase (Fig. 6) and contrast (Fig. 7) data. We assumed that placing an ND filter before the DE would elevate the DE’s gain-control threshold and reduce its apparent contrast, but have no effect on the NDE’s model parameters. Therefore, each ND filter was assigned a different DE gain-control threshold and contrast attenuation (NDE’s contrast attenuation = 1). All other model parameters were assumed to be the same for different DE’s luminance. The coloured solid curves in Figs. 6 and 7 are the best fits of the model. From this modelling, the DE’s gain-control threshold (Fig. 8A) and apparent contrast (Fig. 8B) could be calculated for each DE luminance.

Figure 8.

Results from modelling. A. Dominant eye (DE) gain-control threshold as a function of DE luminance. The non-dominant eye (NDE)’s gain-control threshold is indicated by a red circle and its luminance is fixed at 26.2 cd/m². B. DE apparent contrast as a function of DE luminance when the standard contrast in the NDE was 24% and the NDE’s mean luminance was fixed at 26.2 cd/m² (red circle). C. DE gain-control energy as a function of DE luminance. NDE luminance (26.2 cd/m²) and gain-control energy are indicated by the red circle. The physical contrasts of the two eyes were identical at 24%. D. DE apparent contrast as a function of the standard contrast in the NDE when the DE luminance was 0.83 cd/m² (wearing 1.5 ND filter) and the NDE luminance was 26.2 cd/m².

With no ND filter (0.0 ND), the two eyes have a luminance of 26.2 cd/m², at which the DE has a lower gain-control threshold than the NDE (Fig. 8A) and the apparent contrast is slightly larger than the NDE (Fig. 8B), making the DE’s gain-control energy much stronger than the NDE’s (Fig. 8C) and biasing binocular combination toward the DE (Fig. 6A). Reducing the luminance of the DE (with an ND filter), resulted in the DE’s gain-control threshold remaining constant when its luminance was > 10 cd/m², and then increasing beyond the NDE’s gain-control threshold. DE apparent contrast remained constant when its luminance was > 2.6 cd/m², and then decreased when its luminance was further reduced. At the luminance of 0.83 cd/m², DE gain-control energy reduced to equal the NDE’s (when the NDE luminance was 26.2 cd/m² - Fig. 8C), and binocular vision was rebalanced when the physical contrast in the two eyes was identical at 24%. However, wearing an ND filter failed to correct the going-away-from-symmetry rate (Eq. 4). Figure 9A shows the gain-control energy as a function of contrast. Without an ND filter, the NDE’s gain-control energy (red) is always lower than the DE’s (black). A 1.5 ND filter shifts the DE’s gain-control energy down (blue) but its slope is still steeper than that of the NDE. Actually, it is slightly steeper than with no ND filter because a 1.5 ND filter decreases apparent contrast at lower contrast, but has no effect at higher contrasts (Fig. 8D). Therefore, although the gain-control energies of the two eyes are equal at 24%, they are still imbalanced at other contrast levels because they have different slopes (different exponent gamma values). Luminance seems to have no effect on the exponent gamma value of the gain-control energy (Eq. 3).

Figure 9.

A. Gain-control energy as a function of contrast when the dominant eye (DE) luminance was 26.2 cd/m² (black star) or 0.83 cd/m² (blue diamond), and the non-dominant eye (NDE) luminance was 26.2 cd/m² (red circle) as calculated from Eq. 3 using best fit model parameters. B. Contrast of DE vs. NDE at rebalanced vision for amblyopic observer GD when the DE luminance was 0.83 cd/m² (blue) and 26.2 cd/m² (red), and the NDE luminance was fixed at 26.2 cd/m².

Because the gain-control energy increased (or decreased) more quickly in the DE than in the NDE, the rebalanced binocular vision achieved by wearing a 1.5 ND filter before the DE becomes imbalanced again when the contrast is offset from 24%. Figure 9B shows the contrast of the DE vs. the NDE at rebalanced vision when the DE wears a 1.5 ND filter; the rebalance line shifts up (from red to blue) and crosses the normal symmetry 1:1 line (black dashed line) at 24%. However, the slope of the new rebalance line (blue) is still less than 1, biasing binocular vision toward the DE when the contrast is > 24%, but toward the NDE when the contrast is < 24%. Although it is not perfect to rebalance asymmetric binocular vision, placing an ND filter before the DE can greatly improve the binocular vision of an amblyopic observer while having only a small effect on monocular contrast perception. In the case of Figure 9, with a 1.5 ND filter before the DE (blue line), a substantial range of contrasts around 24% are close to the normal symmetric binocular vision (black dashed line), making it possible to have ‘corrected to normal binocular vision’ in a large range of contrast input. In contrast, with no ND filter (red line), all rebalanced points are below the normal symmetric binocular vision (black dashed line).

Discussion

The asymmetric interocular suppression in amblyopic vision is a consequence of the asymmetric gain-control energy of the two eyes. Typically, the DE’s gain-control energy is comparable to normal, but the NDE’s gain-control energy is much reduced ⁹, resulting in binocular vision being biased toward the DE during daily life. In this paper, we examined two methods to rebalance this binocular asymmetry, either by manipulating the two eyes’ contrast or mean luminance. Manipulating the two eyes’ contrast is less practical because (1) it would reduce the input contrast range for the DE (should be less than the maximum-rebalanceable contrast), for example, for observer GJ at 2.72 cpd (Fig. 5), if the DE’s contrast is larger than 2.5% (just above the detection threshold), the binocular asymmetry could never be rebalanced (Figs. 4 and 5); (2) it would impair stereovision and impede stereo training because the best stereo performance occurs when the two eyes have equal physical contrast inputs ^{3–5, 46}; (3) the rebalance factor δ_B, by which the DE’s contrast should be reduced for rebalanced vision, is not constant when base contrast or spatial frequency varies, i.e., no simple rebalance factor works for all contrasts and spatial frequencies; (4) it is difficult to manipulate the two eyes’ contrast during daily life although it is possible in a laboratory. Wearing a dispersing filter in the DE might be one option to reduce contrast in the DE during daily life. However, this would compromise monocular vision (e.g., contrast sensitivity and visual acuity of the DE ^{18, 19, 21}). For a complex image, it might be impossible to reduce contrast equally for the whole image ³¹. On the other hand, placing an ND filter before the DE is a better choice to rebalance the binocular asymmetry. Because mean luminance has little effect on contrast perception, based on this study and previous studies ^{34, 35}, both eyes would have an almost full range of contrast input when the luminance changes over a large scale. Because the two eyes would still have comparable contrast inputs in the rebalanced vision by placing an ND filter before the DE, it might benefit stereovision and would provide an opportunity to develop stereo mechanisms. Further studies are needed to address this issue. It is also much easier to manipulate the two eyes’ mean luminance during daily life, just placing an ND filter before the DE, makes it possible to reduce luminance equally for the entire image. However, an ND filter that provides the rebalance under one set of visual conditions may not work for other conditions (e.g., at different contrasts or spatial frequencies) because the asymmetric exponent gamma of the two eyes’ gain-control energy cannot be corrected by wearing an ND filter. Although it is not perfect, wearing a suitable ND filter would partially correct the abnormal binocular system to be near the normal binocular symmetry under normal viewing conditions (Fig. 9B).

Decreasing the mean luminance in one eye reduces its gain-control energy and therefore lessens its suppression to the other eye while apparent monocular contrast remains relative constant. Gain-control energy or interocular suppression is modulated by both the mean luminance and contrast. Recent physiological studies suggests that, to some degree, contrast and luminance are processed independently^36–38, while the responses of many neurons in the primary visual cortex are strongly modulated by both the mean luminance and contrast^{37, 38}. We speculate that neurons modulated by both luminance and contrast might play an important role in interocular suppression by calculating the gain-control energy.

Decreasing the luminance to one eye also results in delayed transmission of the visual signal to the cortex^{47, 48}. If amblyopia results in delayed signals from the amblyopic eye^49–51, then one might speculate that reducing the luminance of the dominant eye’s stimulus might re-balance binocular vision by delaying the DE signals and thus reducing the asynchrony. We are exploring this possibility.

As noted previously^{12, 17, 24}, placing a suitable ND filter before the DE might provide more benefit than wearing a patch, the traditional treatment for amblyopia, especially for the treatment of abnormal binocular function. Although wearing a patch in the DE “forces” the use of the NDE to view the world, there are both physiological and psychosocial reasons to seek alternative methods ^18–21. More importantly, patching deprives the amblyope of binocular visual experience. On the other hand, wearing a suitable ND filter can substantially rebalance binocular vision; the two eyes have comparable inputs and the binocular system can experience binocular visual stimulation. How can we select a suitable ND filter? From Figs. 5 and 9, selecting a suitable ND filter would depend on contrast and spatial frequency. Generally speaking, weaker ND filters are suitable for lower contrasts and lower spatial frequencies and stronger filters are more suitable for higher contrasts and higher spatial frequencies. Image statistics, such as the spatial frequency power spectrum and contrast distribution, might provide useful information for how to select an ND filter. Although further studies are still needed for this issue, the best ND filter might be the one that is able to rebalance the two eyes at the median spatial frequency in the human spatial-frequency spectrum and the mean contrast of natural images. However, because different scenes might have different image statistics and light conditions ⁵² (e.g., outdoor versus indoor), we might need several ND filters for different conditions, which would also provide a wider range of visual channels the opportunity to experience binocular vision.

Clinically, it would be more practical to select a single ND filter. One method (which has been used in conjunction with monocular blur) would be to select a filter that equates the acuity in the two eyes. Indeed Mary Pugh (1936) suggested a similar method for selecting a filter ²⁴. She wrote (in page 42) “… the spectacle lens in front of the dominant eye may be painted with a varnish; collodion either white or coloured may be used. This varnish can be altered in density by varying the thickness of the application so that the vision of the stronger eye is reduced to the standard of that of the weaker eye. In this way fusion may still continue …”. In the current study for observer GD, we found that a 2.2 ND filter reduced the DE acuity to 0.40 logMAR (Snellen 6/15, 20/50), equal to that of her amblyopic eye. This is similar to the 2.0ND filter that re-balances her binocular vision at 1.36 c/deg (data not shown), but considerably higher than the 1.5 ND that re-balances binocular vision at 0.68 c/deg.

Recently, Zhou et al³³ made similar observations (using the method of adjustment). Their mean luminance was much higher than ours (190 vs. 26.2 cd/m²) and they tested a single base contrast (100% for amblyopic observers), and spatial frequency (0.294 cpd). Despite these substantial differences their results are comparable to ours. Their amblyopic observers could be rebalanced using filters of 2.0 – 3.0 log units, while our amblyopic observer GD required filters of 1.5 and 2.0 log units for spatial frequencies of 0.68 and 1.36 cpd, at a base contrast of 24%.

In daily life, the background luminance or the mean luminance varies from time to time. It would be helpful to know whether a suitable ND filter for one background luminance level is also suitable for other luminance levels. However, from our current data, we are not clear how a suitable ND filter would depend on the mean luminance; more data and more modelling work are required. However, by comparing the studies of Zhou et al’s³³ and ours, a suitable ND filter might be able to operate over a large range of luminance levels.

Placing an ND filter before the DE reduces the DE’s gain-control energy from a normal level to an abnormal level to match the NDE’s gain-control energy, and therefore rebalances the asymmetric binocular vision. However, this makes both eyes operate under subnormal conditions, which might be equivalent to a normal observer working under dim light. Working under such conditions might cause some problems, such as fatigue, slow reaction time, and less accurate performance ⁵³. A better way for achieving the rebalance would be to increase the NDE’s gain-control energy to the normal level through increasing its luminance, to match the DE’s gain-control energy. At least, in the laboratory, we can realize such conditions (e.g., by increasing overall luminance and placing an ND filter before the DE) to make both eyes operate under equivalent ‘normal conditions’, which would provide more promise for amblyopia treatment. However, in daily life, a device that is able to amplify the mean luminance in the NDE would be more helpful because the overall luminance cannot be conveniently adjusted in some situations. Although binocular asymmetry in amblyopic vision can be rebalanced by manipulating the two eyes’ contrast and luminance, it is very difficult or even impossible to rebalance the asymmetry for all visual conditions. Placing a neutral density filter before the dominant eye or increasing the mean luminance in the non-dominant eye would provide a method to treat amblyopia, which could have more benefit for treating both monocular and binocular functions than the traditional method of wearing a patch in the dominant eye. However, one caution that applies to any re-balancing method is that stereoacuity is best when the two eyes have equal physical contrast ⁴⁶. Re-balancing, either by contrast or luminance increases (worsens) stereo threshold. For example, GD’s stereo threshold with equal physical contrast and luminance in the two eyes is ≈ 137 ± 13 arc sec. Rebalanced by contrast it increases to 303 ± 40 arc sec and by luminance to 189 ± 24 arc sec. Finally, we note that the use of ND filters might be most effectively applied to anisometropic amblyopia. For strabismic amblyopia, the use of ND filters is complicated by the misalignment of the two eyes. Although it is unclear whether rebalancing may assist the alignment and fusion of the two eyes in strabismic amblyopes to avoid double vision in daily life, it has been shown that binocular fusion can be achieved through training in the laboratory^{9, 46}.