Normalization and extraction of interpretable metrics from raw accelerometry data

Abstract

We introduce an explicit set of metrics for human activity based on high-density acceleration recordings from a hip-worn tri-axial accelerometer. These metrics are based on two concepts: (i) Time Active, a measure of the length of time when activity is distinguishable from rest and (ii) AI, a measure of the relative amplitude of activity relative to rest. All measurements are normalized (have the same interpretation across subjects and days), easy to explain and implement, and reproducible across platforms and software implementations. Metrics were validated by visual inspection of results and quantitative in-lab replication studies, and by an association study with health outcomes

1. Introduction

A commonly used outcome measure in aging research is the capacity to engage in activities of daily living (ADLs), or sentinel behaviors required to live independently. Conventional methods for measuring ADLs include self-reported questionnaires or clinician ratings based on observed behavior (Feinstein and others, 1986; McDowell and Newell, 1987), which have several limitations. First, self-reported activity may be subject to recall bias, which can be accentuated by the decline of cognition and memory. Second, these measurements provide only a snapshot of an individual’s daily activity, while detailed minute by minute information is often missing. Thus, there is an increasing need for unbiased, detailed measurements of sentinel behaviors that describe the underlying functional capacity of the individual and are not confounded by uncontrollable bias and measurement error. One possible solution is using wearable computing devices, which allow collection of real-time, densely sampled information on movement. These devices could serve as silent, unbiased, tireless, and non-obtrusive recorders of actual human activity in a real-world context. However, translating information from high-volume and complex data from wearable sensors into acceptable measurements can be done only by careful standardization and transformation to guarantee the validity and reproducibility of the measurements. In contrast, current measurements produced by software that accompanies these devices are expressed either in “activity counts” or Metabolic Equivalent of Task “MET” units. The most commonly used device, Actigraph, produces activity counts that, while formally defined (ActiGraph), do not have a clear interpretation, and may not capture sufficient variability in older subjects. The MET units are even more problematic as they are based on population calibration equations that are severely biased at the subject level and in older adults. We propose data normalization and a set of novel, explicit, and interpretable metrics that can be used in medical and epidemiological studies.

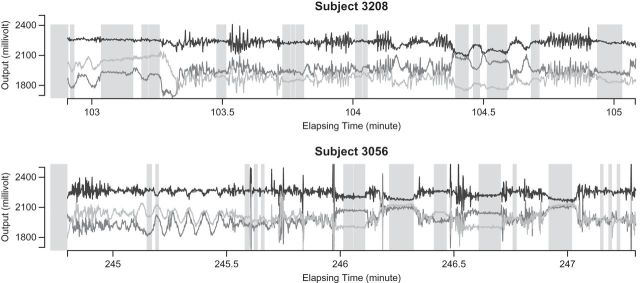
Wearable sensors for different types of activity are deployed in an increasing number of studies (Boyle and others, 2006; Bussmann and others, 2001; Grant and others, 2008; Sallis and others, 2009; Welk and others, 2000). Here, we are concerned with accelerometers worn either in-field or in-lab by older, community-dwelling adults. Our focus is providing a set of simple activity measurements from ultra large, high-density accelerometry data, and providing evidence in support of their validity and usefulness in epidemiological studies. Some metrics have been proposed to extract and summarize information from accelerometry data, especially in sleep studies (Jean-Louis and others, 1996; Blood and others, 1997; Kushida and others, 2001; Mishima and others, 1998). All these studies have focused on gross summary statistics such as: ratios of sleep/wake duration, total sleep time, proportion of wake time after sleep onset, etc. Such summaries allow researchers to apply standard statistical methods, though they over-simplify the data. Another group of metrics focuses on reducing the raw 3D accelerometry data to a 1D proxy of subjects’ activity along time. One such example is the “activity count”, which converts the raw three-axis acceleration measurements through various proprietary algorithms developed by accelerometer manufacturers. Based on activity counts, many studies categorize activities into different groups with sedentary, light, moderate, and vigorous intensity according to predefined thresholds, and obtain proportions of time spent doing each type of activity (Puyau and others, 2002; Lee and Paffenbarger, 2000; Treuth and others, 2004). There are several limitations when using “activity counts”. Indeed, the definition differs from manufacturer to manufacturer and may even differ with regard to the same manufacturer when a new device is released. Thus, it is unclear whether activity counts are comparable (Ancoli-Israel and others, 2003; Stephen and Spiro, 2001). The interpretation of “activities count” is provided by some manufacturers. For example, the Actigraph describes the process as “ActiGraph’s original activity monitor, the 7164 model, utilized a mechanical lever capable of measuring the change in acceleration with respect to time (g/s, where g is gravity or 9.806 m/s²). To suppress unwanted motion and enhance human activity, the acceleration signal was passed through an analog band-pass filter, the output of which yields a dynamic range of 4.26 g/s (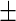2.13 g/s) at 0.75 Hz (center frequency of the filter). Using a sample rate of 10 samples-per-second, this filtered signal was then digitized into 256 distinct levels by an 8-bit solid-state analog-to-digital converter, producing 4.26 g/s per 256 levels or 0.01664 g/s/count (each level is considered one count). When each filtered sample is multiplied by the sample window of 0.1 s, a resolution of 0.001664 g/count is achieved”. While this is an excellent technical description, it leaves many questions unanswered. First, it is unclear exactly what are the formulas and whether they are applied to each axis separately or combined. Second, the transition between the quasi-continuous signal and the number of g’s in 1 s is not defined; this is a function that reduces 30 numbers (tri-axial at 10 Hz sampling) into one number. Third, methods fundamentally depend on many software parameters as well as on the sensitivity of the chip. Small changes in thresholds, sampling rates, chip sensitivity, or number of count levels can lead to dramatic batch effects within and, especially, between manufacturers. Fourth, only on rare occasions are devices validated in real data or using replication. Fifth, the interpretation of a count is, probably, “some one-epoch summary of the acceleration that is between 0.01664 and 0.03328 g/s”, whose utility in a large observational study remains to be debated. We conclude that “activity counts” are actually not counting activities or steps as their name implies; instead they are a proxy of the acceleration within a time interval. The missing piece is a paper like the one we are putting forth here; we are currently unaware of any paper starting from raw data and building explicitlyeither “activity counts” or other explicit metrics. Our paper has the following goals: (i) to propose an explicit data processing pipeline for high-dimensional accelerometer data; (ii) to present a transparent, interpretable, and implementable set of metrics; (iii) to validate these metrics via visual inspection, replicated in-lab experiments, and association studies with health outcomes.

We used data from older adults who were fitted with a high-definition three axis accelerometer “Shimmer” (ODonovan and others, 2009; Burns and others, 2010) and asked to perform standard activities in a laboratory under observation. Then, subjects were asked to wear those devices for five consecutive days during normal activity. To analyze the massive free-living data (>18 million observations per subject), we processed and summarized the data into several metrics that are intuitive and reproducible. Special attention was given to normalization to ensure comparability of measurements across subjects and visits. We investigated the validity and reproducibility of these new measurements and their association with self-reported health status.

2. Data collection

2.1. Study population

Community-dwelling men and women were recruited from an ongoing cohort study on the multilevel determinants of cognitive function in older adults, The Baltimore Memory Study (BMS, AG19604, Brian Schwartz, PI). For the LIFEmeter substudy, 125 older adult subjects were recruited and enrolled after BMS visit 4 or 5. The purpose of the LIFEmeter substudy (AG027481, Thomas A. Glass, PI) was to develop and test a sensor platform for capturing enacted function in older adults. Enrolled subjects were brought into a lab setting, given an interview, and asked to perform a series of standard activities under observation wearing a waist-mounted pouch containing several sensors. Next, subjects were asked to wear the LIFEmeter array during waking hours for three to five consecutive days, removing the device during showering, swimming, and sleeping.

2.2. Data description

Our data are generated using Shimmer^TM Unit by Shimmer Research (Burns and others, 2010), mounted on subjects’ waists. The device uses a standard tri-axial accelerometer chip found in many cell phones and other devices (Freescale MMA7361) and records acceleration in three mutually orthogonal directions with a sample rate of 10 Hz. The output consists of three voltage time series, which are proxy measures of acceleration. The time series exhibit complex variability in overall level, amplitude, frequency, correlation, and patterns along the time course of different activities.

Figure 1 displays two 2.5-min data segments representing the raw three-axis accelerometer data from two subjects, labeled 3208 and 3056. Many studies (Bai, 2011; Bussmann and others, 2001; Bao and Intille, 2004; Kozey-Keadle and others, 2011; Ravi and others, 2005; Welk and others, 2000) found that lack of accelerometer motion, which is a rough proxy for actual human activity, is characterized by low variation around stable constants for each of the three-time series. Using a simple method that will be described in this paper we have estimated periods of inactivity and shaded them in light-gray. An inspection of the time series for subject 3208 (upper panel in Figure 1) indicates that there are many periods of inactivity, each with a different length. Moreover, the accelerometer seems to be sensitive to different types of inactivity. Indeed, compare the light-gray block starting immediately after minute 103 with the one starting immediately after minute 104.5. There is low variability in both blocks, but the times series colored in light-gray and mid-gray have switched their mean levels. This probably indicates that the person is resting in different postures (e.g. on a chair vs. standing). Areas that were estimated to be active display a wide range of variation both in terms of patterns and amplitude of the signal. Inspecting such short time series is not dissimilar to listening to a new language, where we hear obvious patterns without having a clue about what is being said. However, it is quite easy to know when the person is not talking. A similar principle will be applied to identify periods of inactivity, by predicting areas of low variability above background.

Figure 1.

Two panels (from Subject 3208 and Subject 3056) of the raw three-axis accelerometer data with Active vs. Inactive prediction results. Each axis is illustrated in a different gray scale. The -axis stands for the time (in minute) from the first observation and the 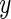-axis shows values of the raw output from the accelerometer. The inactive time periods (according to our algorithm which is also described in this section) are shaded in light-gray.

We start by introducing notation. The observed data are a collection of three time series representing proxies of acceleration in three orthogonal axes. Denote the data (sample rate 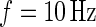) by 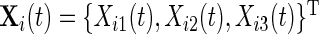, t=1,2,…,T_i, where T_i is the length of the accelerometer time series for Subject 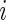. In this paper, we used field data from 34 subjects and each subject was observed for 4–5 days. So 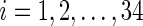and 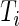is very large. For example, for a complete 5-day recording 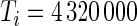. Here, we will be working directly with the raw voltage data, though our methods apply as well to data expressed in gravity units. Indeed, if 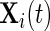is the collection of voltage time series, then the gravitation data can be obtained by the formula (Shimmer Research, 2012) 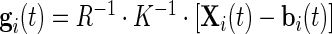. Here 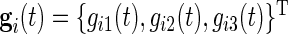is the ratio of acceleration on the three axes to gravity, 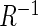is an alignment matrix, and 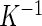is a diagonal matrix specifying the sensitivity of the sensor along each axis. In the remainder of the paper, we focus on 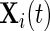and not on 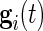. As our normalization procedure is a combination of several linear transformations of the raw signals, explicit formulas can be obtained for 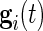, as well.

We introduce a new time series, 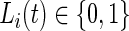, as the time series of labels, which describe whether the Subject 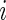is estimated to be “active” or “non-active” at each time point 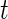. Non-active time includes both the time when the subject was resting while wearing the device and the time when the subject took the device off. Thus, 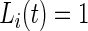if Subject 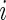is active at time point 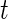and 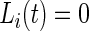otherwise. 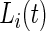is observable either by study team members or from detailed diaries. In our study, we observe 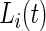only during in-lab sessions and not during the in-home data collection. We treat 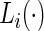’s as an unknown variable to be estimated during in-home monitoring. (Bai (2011)) introduced a method to classify accelerometry time series into active and non-active, which is essentially estimating the time-series of labels 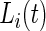. This method applies a threshold on standard deviation in each 1-s interval. More specifically, for each time point 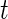of Subjec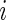t , let 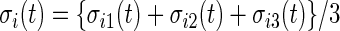, where 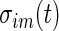(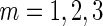) is the standard deviation of the 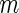th axis of the acceleration time-series 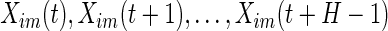in a window of length 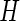. Here, we use a window of length 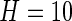, which corresponds to 1 s. We found this window size to work well in practice, as it reasonably corresponds to the temporal scale of human activity. More precisely, 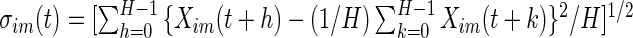. We will not use notation that depends on the window size, as 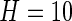is fixed throughout this paper. Also, we do not use hats to indicate that standard deviations are estimated, as we are primarily focused on prediction and algorithmic signal extraction and not on inference.

Once the subject-time specific standard deviation, 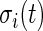, of the signal is computed, the activity label time series is estimated as 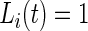if 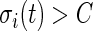and 0 if 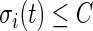. Here 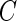is a threshold value that does not depend on the subject and is estimated from the data. Here, we investigate the impact of various choices of 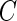and are especially interested in finding whether a common threshold is reasonable for all subjects. The threshold 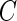will depend on the scale and type of output used in the analysis. As our data were collected in millivolts, 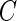is also expressed in millivolts. If data 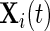were expressed in g’s, we could also specify 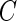in g’s. We have tried threshold approaches for both type of signals and obtained indistinguishable results; this should not be surprising given the one-to-one and monotonic relationship between the millivolt and 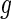scales.

To further investigate the threshold, we calculated the standard deviation, 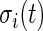, for each of the 34 subjects in each 1-s interval. For each subject, we produced a smooth histogram of standard deviation values collapsed over time. The top panel in Figure 2 displays these 34 density curves for all subjects, each in a different gray scale. A feature of these curves is that they all have a high-peak centered roughly around the same value (2–3 mV) with much of the mass concentrated between 1 and 7 mV. The reason is that people spend a lot of time resting. These plots suggest that a cut-off point of  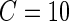mV could separate active from inactive periods in all subjects. For example, the light-gray shaded areas indicating inactive periods in Figure 1 are obtained using this decision rule. We have checked several other thresholds between 8 and 15 mV and they provided similar results. The reason is that there are few activities that are visually identifiable and correspond to a standard deviation in the range  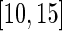mV. While some ambiguity is likely to remain even after careful visual inspection of each time series, we conclude that 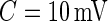works well for our data set.

Figure 2.

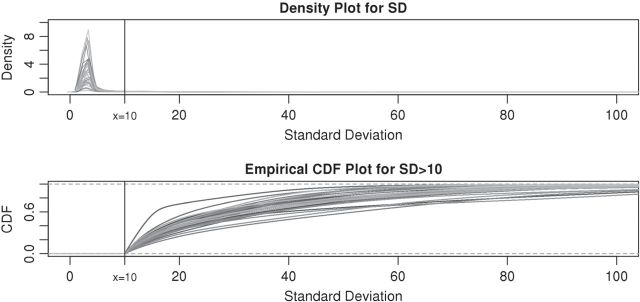
The density curves of standard deviations for all (34) subjects in different gray scale. The upper panel contains density curves of the original standard deviations and the lower panel contains density curves of standard deviations greater than 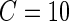. The vertical black lines in both panels are at .

All histograms have long tails, which correspond to visually identifiable activities. As accelerometer time series are likely to be dominated by inactive periods, the top panel in Figure 2 does not display enough detail to understand subject-to-subject differences in activity intensity (AI). Thus, the bottom panel displays the cumulative distribution function for standard deviations above 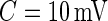. We focus on the curve that is on top of the other curves. A value of 0.7 of the cumulative distribution function at 20 mV indicates that about 70% of standard deviation values that are higher than 10 mV are between 10 and 20 mV. This implies that this person has lower intensity movements compared with the other subjects. If a subject-specific curve is higher for a given subject, it indicates that the first subject has lower level of activities across the range of observed activities. The fact that the curves do not seem to cross each other indicates a reasonable finding: if subjects tend to have fewer low-intensity movements, they also tend to have fewer high-intensity movements. This is consistent with an elderly population, though it should not be surprising to find similar patterns in other age ranges. Once the active or non-active labels 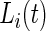’s are estimated, there were many possibilities for estimating various types of metrics to describe the rest of the data. 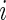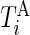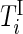We start by dividing the entire recorded time period of Subject into two sets of time points, and , corresponding to active and inactive time periods. Specifically, 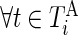, 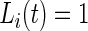and , .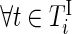

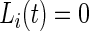3. Accelerometer metrics definition

In this section, we introduce several metrics that were found to be sensible and feasible to compute. We denote by 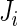the number of days when Subject 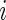is observed, while 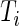is the total number of time points where the subject is observed. The number of days, 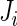, varies between 3 and 5, whereas 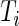is in the millions. We denote by 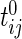the time index for start of day 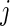, which has a total of 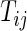data points. For subject 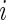on day 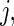we propose to extract the following 5D vector of univariate signals labeled D_ij=(T_ij,TAM_ij,TAV_ij,AIM_ij,AIV_ij). Here 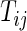is the length of time for the period estimated to be the wake time and can depend on the particular day, 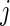, because some days have shorter recording times or missing data. The variable “Time Active Mean”, 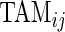, represents the fraction of total time awake, 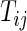, that was estimated to be active (non-rest). The variable “Time Active Variability”, TAV _ij, represents the variability of the active/non-active process. The last two variables, “AI Mean” (AIM) and “AI Variability” (AIV), are similar to 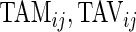, but focus on the actual intensity of movement (amplitude of signal) instead of the binary measurement active/non-active. We chose these five measurements only for simplicity, though they could be produced at much higher resolution, such as minute, hour, or time of day. A concern with reducing data sets of such complexity to a few summary measurements is whether this reduction is too aggressive. To alleviate this concern, we introduce two additional measurements, “Cumulative Relative Time Active (CRTA)” and “Cumulative Relative AI (CRAI)”. These measurements are calculated at every time point and preserve all the original information. In this paper, we use them for visualization purposes, establish their characteristics, and defer their analysis to future publications.

3.1. Time active

After 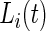, the labels denoting whether Subject 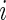is active at time 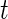, were predicted for all subjects, they can be used to calculate each subject’s “Time Active” within intervals of interest. To be specific, for Subject 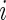, we first partition the whole time course 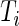into non-overlapping windows of length 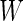, with the total number of windows equal to 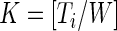, where 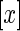denotes the highest integer smaller than 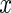. The window size can be anything, though here we focus on 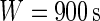, which corresponds to 15 min. 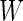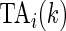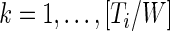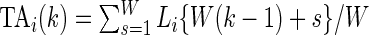For a fixed time window of length , we define the Time Active, , for every as , which is the proportion of time declared active in the time window 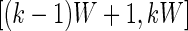using the 10 mV threshold on the 1-s window standard deviation. This measure is useful because it: (i) is explicitly measuring the active time in a particular time window without combining it with the intensity of activity during the same period; (ii) is easy to compute and reproduce given the original raw data; (iii) is interpretable across subjects and devices; (iv) is expressed on a 0–1 scale; and (v) is not dependent on black-box software.

Figure 3 displays the original tri-axial acceleration 15-min time series plots for Subject 3092 in panels 1 and 2. We display only 15 min of the raw accelerometer data, as showing the entire 5-day period would be daunting and quite useless for visual inspection. In contrast, the Time Active plot in the bottom panel provides a simple visualization tool for the entire duration of the study. 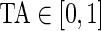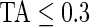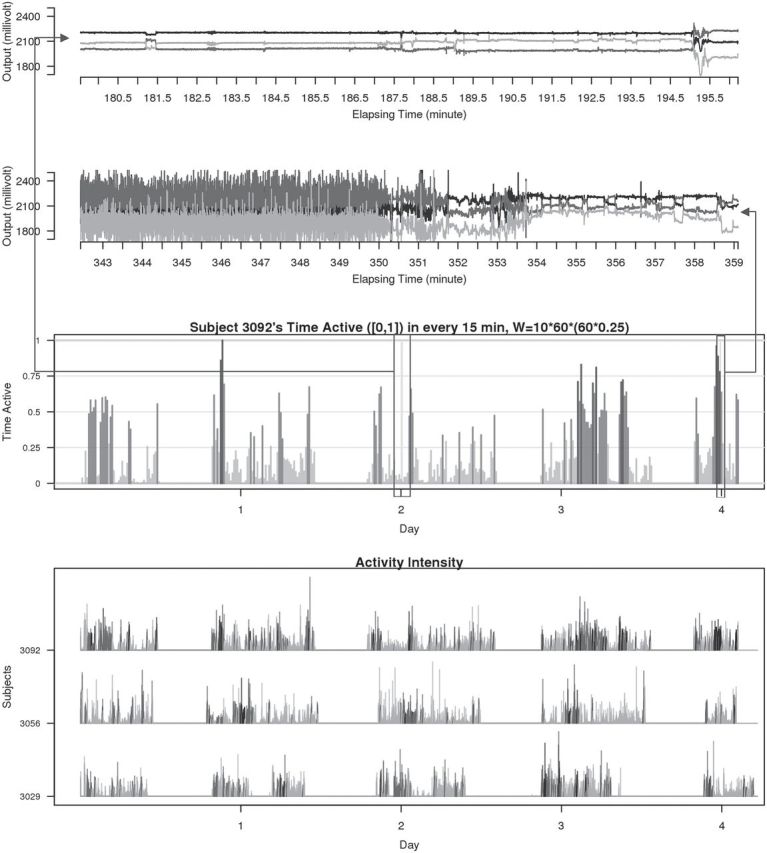In the bottom panel, the Time Active () bars of every 15-min interval for the same subject are in light gray (), mid-gray (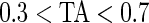), or dark gray (TA≥0.7). Note that, for example, a light gray bar means that the subject movement was distinguishable from inactivity according to the 10-mV threshold for up to 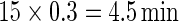out of the corresponding 15-min period. This plot corresponds to the 5-day period when Subject 3092 wore the device. As the raw and time active data are linked, one can always go back to a particular specific period for further visual inspection. TA has several long sections (i.e. between days) where it is zero, most likely during sleeping when the subject placed the device on a table. To better understand the data transformation, we placed two boxes, each with a vertical light gray bar in the background, in the third panel. Each vertical light gray bar represents a 15-min period; the corresponding raw data are shown in the panels 1 and 2. Plots indicate that the data transformation is quite sensible. Indeed, the first framed time period of Subject 3092 has much lower time active values (0.01 vs. 0.76) compared with the second framed time period. This difference can be easily observed by comparing the upper panel and mid panels in Figure 3.

Figure 3.

Two periods of raw data (panels 1 and 2), TA bars for Subject 3092 (panel 3). Each TA bar has a value between 0 and 1, and is colored light gray (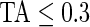), mid-gray (), or dark gray (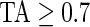). Panels 1 and 2 correspond to the light gray bars in the box frames depicted in panel 3. Panel 4 displays 3-day AI for Subjects 3029, 3056, and 3092. AI bars are colored light gray, mid-gray, or dark gray according to their TA values as in panel 3.

3.1.1. Scalar summaries of time active

The TAM is 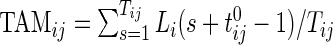, which is the average number of active periods, and 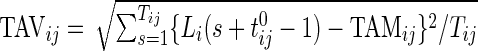, which is the standard deviation of the active periods for Subject 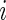on day 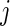. The two measurements, 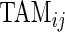and 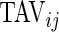are complementary. Indeed, a subject with large 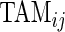and small 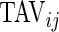would tend to have long periods of activity with few rests; a subject with small 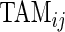and large 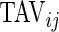would tend to be less active but with short and sustained activity periods.

3.1.2. Cumulative relative time active

Using the time active, 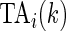, is not straightforward. Indeed, a quick inspection of the third panel in Figure 3 provides a reasonable summary, but leaves many questions unanswered: (i) how to handle the “spiky” nature of the data; (ii) what to do about the de-synchronized behavior both within and between subjects; and (iii) how to preserve the complex nature of the data without losing interpretability? To answer these questions, we follow the idea introduced for displays of actigraphy data by (Symanzik and Shannon (2008)). We introduce the 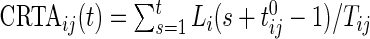, which is the fraction of active periods up to time 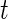of day 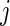for Subject 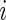out of the total time awake, 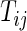. This approach provides a much smoother representation of the data while maintaining all the information. As the accelerometer is taken off during sleep, time can easily be partitioned into sleeping (non-wearing) and being awake (wearing).

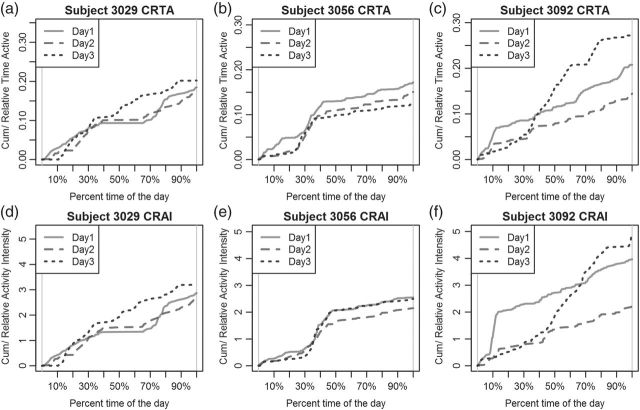
Figure 4 (top panels) provides the CRTA for three different days for three subjects. Functions are displayed with respect to the proportion of time, 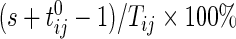, from the start of the day. Figure 4(b) indicates that Subject 3056’s has similar CRTA patterns for the 3 days. This subject is quite active in the middle of the day, which is indicated by the synchronized jumps in the day-specific curves around the 30–50% section of the 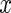-axis. Moreover, the solid curve is higher, suggesting that Subject 3056 spent more time being active on Day 1 than on either Day 2 or Day 3. Figure 4(c) suggests a different activity pattern for Subject 3092. On Day 1 and Day 2, the subject shared a similar CRTA pattern, but with different end points. After a large jump around 10% of Day 1, the solid curve remains roughly parallel to the dashed curve. This suggests that Subject 3092 had a short but active period after getting up on Day 1, but spent the rest of the day with an active/inactive pattern similar to that of Day 2. In contrast, on Day 3, the subject did not spend much time being active until the middle of the day, but then became very active for the rest of the day, leading to a high TA for that day. Such trends and differences seem obvious in Figure 4, but are hard to note in Figure 3.

Figure 4.

Top panels: CRTA for Subject 3029 (a), 3056 (b), and 3092 (c). Bottom panels: CRAI for Subjects 3029 (d), 3056 (e), and 3092 (f). There are three curves in each plot, each representing 1 day. These curves are either compressed or stretched so that they display CRTA or CRAI in the scale of percentage time of the day, instead of actual time.

3.2. Activity intensity

Time active is a measure of how long the person was active without information about how intense the activity was. Here, we propose measurements that describe the entire spectrum of activity intensities. We estimate “AI” as the standard deviation of the raw accelerometer signal relative to the standard deviation in the signal during non-wearing or rest. Thus, AI will be expressed in sigma units, where sigma is the variation of the time series during non-wearing or rest. This approach has the potential to mitigate some of the inherent problems associated with accelerometer measurements. First, data will be normalized on a scale that can be interpreted in units of intensity of activity relative to the systematic noise (non-wearing time variability of the signal). This may reduce device- and day-specific systematic deviations in measurements. Second, measurements from the same type of accelerometer from different people and locations are more comparable and have similar interpretation: observed variability relative to signal variability when the device is not perceptively moving. Third, the approach automatically mimics human information processing. Indeed, a human observer would naturally focus on areas of high, moderate, and low variability; AI quantifies this qualitative process.

We define 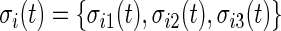as the local standard deviation at time point 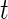calculated in each 1-s interval (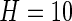). We estimate the average standard deviation of each axis during rest as 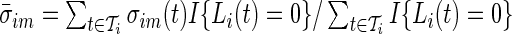. The summation 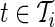stands for each time point 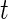in the rest period 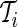. The average standard deviation 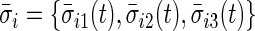quantifies the device-specific variation when the device is either not worn or the person is at rest. We estimate 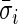using the periods when the subject was sleeping or resting. AI is defined as 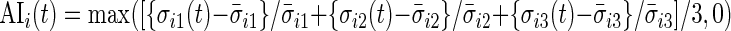. Thus, 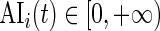and is the difference between the current observed standard deviation 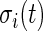and the average standard deviation 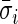during non-wearing/rest periods 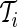, relative to 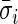. The truncation at zero is done to ensure that every standard deviation below the average standard deviation at non-wearing is set to zero and that there are no negative AI values. We used the average variability in non-wearing/rest periods as reference because it characterizes the systematic variability of the device.

AI is a complement to TA, which only focuses on time spent while active without information about how active the subject is. For example, walking and running continuously for 15 min give the same TA (which is 1 because the subject is active during the whole period), but have completely different AI. Running has much higher levels of acceleration variation compared with walking, which is characterized by a larger AI for running. To illustrate this, the bottom panel in Figure 3 displays AI for three subjects (3029, 3056, and 3092). Each bar stands for AI in a 1-s interval and is colored by their TA values (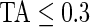: light gray; 0.3<TA<0.7TA≥0.7: dark gray). The AI and TA plots for Subject 3092 indicate that AI has a similar temporal pattern, though spikier and on a different scale. To better understand the complementarity of AI and TA, it is worth taking a closer look at the AI plot for Subject 3092. In the middle of Day 3, there are two areas with dark gray bars (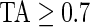) among many mid-gray bars. In the TA plot they are obvious, whereas in the AI plot they are not. Thus, Subject 3092 was performing low to moderate intensity activities continuously during the dark gray periods, while in-between the subject performed a series of high-intensity activities but with more rest periods.

3.2.1. Scalar summaries of AI

Once AI is introduced, the AIM is defined as 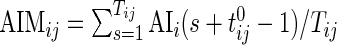, which is the average AI for day 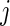of Subject 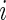. Similarly, the AIV is 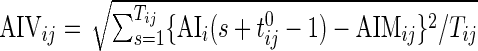, which is the standard deviation of AI. These measurements are similar to TA, though they focus more on the levels of activity and less on whether or not the subject moved.

3.2.2. Cumulative relative AI

Similar to CRTA, we introduce 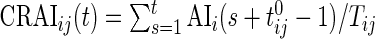, which is the cumulative sum of AI of Subject 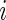up to time 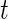in day 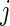. Recall that 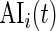is a measure of how much larger is the variability of the accelerometer time series data in a time window centered at 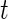relative to its variability at non-wearing time periods. Thus, 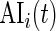is a proxy for the instantaneous intensity of human movement as measured at the hip by an accelerometer. Thus, CRAI_ij(t) is a proxy measure of cumulative energy measured at the hip during movement up to time 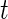of the day. To mitigate the effect of different lengths of day, we divide this cumulative sum by 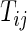. The bottom panels in Figure 4 display 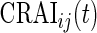for the same three subjects shown in the top panels. However, CRAI does provide something different. For example, in Figure 4(e), Subject 3056 had almost the same pattern of CRAI on Day 1 and Day 3. However, the solid curve in Figure 4(b) remains higher than the dotted one, indicating that the subject spent much more time being active on Day 1. The dotted curve catches up with the solid one in Figure 4(e) at around 35% time of the day, while the corresponding dotted curve in Figure 4(b) does not. A possible explanation is that Subject 3056 performed more intense activities late in the morning on Day 3 than on Day 1, with some rest in between. Since CRTA on Day 3 was reduced by rest, the CRAI was equal for the 2 days.

4. Evaluation of metrics

We evaluate the validity of AI and Time Active by comparing the metrics across subjects and activities. We then conduct an exploratory data analysis of the association between the proposed metrics with demographic factors and self-report quality of life (QOL) variables.

4.1. Validation of metrics

To validate the TA and AI metrics, we focus on the replication part of the study and compare the metrics within- and between subjects for the same observed activity. In addition to the free-living data collection, the subjects were also instructed to wear the device during two lab sessions. During each session, they were asked to perform a supervised battery of activities that included: walking, stair climbing, chair-standing, and lying on a bed. The start and end times of each activity were recorded by a lab technician; see (Bai and others (2012)) for a more detailed description. For a subgroup of 10 subjects, we chose two types of activities, walking and chair-standing, to perform this comparison. For each lab session, we chose two replicates of walking and three replicates of chair-stands. Figure 5 displays the raw data for these activities for Subjects 3056 and 3092. The left-hand side of Figure 5 displays four repetitions of walking for each subject, while the right-hand side displays two repetitions of chair-standing, each with three chair-stands.

Figure 5.

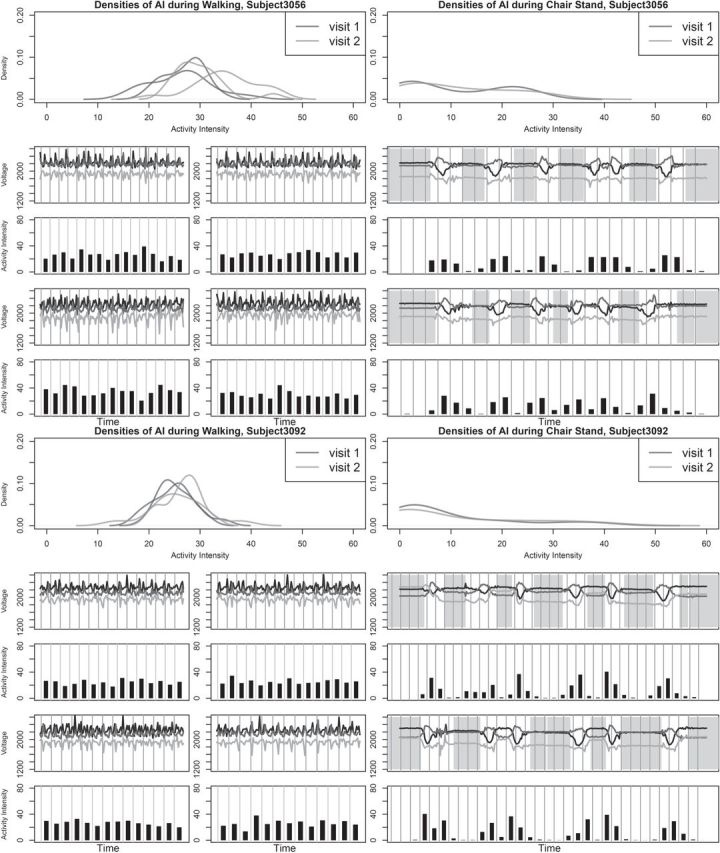
The plots for the metrics validation for Subject 3056 and Subject 3092 during two different visits. In each visit, there are two replicates of walking and three replicates of chair-stands. The raw data during these periods as well as the AI were plotted below the probability density curves of AI. In the plots of raw signals and plots of AI, each gray grid stands for 1 s. A lot of similarities of AI can be observed within and across subjects, while the modes of the distributions are very close. Also, AI picked up the change of variability of the signal during sudden movements such as standing-up-from-chair and assigned low values to the resting periods (both standing and sitting).

Methods described in Section 2.2 were used to classify the entire time series into “active” and “non-active”. The estimated inactive periods (shaded in light gray) are highly informative as the human observer only noted when the chair-standing activity started without detailed information about the exact between-activity duration. For walking, the entire period was classified as “active”, as it should be. We start by defining the AI as “the total acceleration at a particular time point after removing global average accelerations relative to rest”. Thus, any device designed to measure the AI in an unbiased way is a valid instrument. Of course, we do not actually have AI and it is hard to check whether instruments are biased. Instead, we settle for the next best thing: checking measurement reproducibility across repetitions of the same activity and across devices.

The probability density functions of AI during walking and chair stands are shown in Figure 5. AI is calculated for every second and displayed as black bars under the corresponding raw-data plots. The densities of AI during walking are quite consistent within- and between-subjects. Similar results were found for all 10 subjects with in-lab data. The density curve of AI for chair-stands is different, though it displays a lot of similarity within subjects with more variability across subjects. The difference in histogram shapes between walking and chair-standing is probably due to the fact that chair-standing consists of three different sub-activities: resting, standing-up, and sitting-down. The AI for chair-stands is low during inactive periods and high during active periods. AI during these sub-activities were quite similar within subjects across visits. In supplementary material available at Biostatistics online we also show results comparing walking normally and briskly. Results indicate that both median and standard deviation of AI increases across subjects when switching from normal to brisk walking. To quantify these differences, we calculated the intraclass correlation (ICC) for walking and chair-stands. For walking the replicates are the median AI for the first and second walking period in each visit for each of the 10 subjects, respectively. The ICC for median AI for walking was 0.92. For chair-stands, we manually identified the exact periods of the first, second, and third replicates of chair-stands in each visit. Within each replicate, we calculated the mean AI for visit 1 and 2. The ICC for mean AI for chair-stands was 0.83.

4.2. Association with health outcomes

We now conduct an exploratory data analysis on 34 subjects from the LifeMeter study who had at least three complete days of accelerometer recordings. We investigate the possible association of TAM, AIM, TAV, and AIV with several different covariates: Marital Status (Marstat), Sex, Self-Reported General Health (SRH), QOL, Age, Education (Edu), and Weekend. The age range of the 34 subjects (25 females: 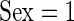) was between 59 and 80, with a mean age of 68.9. Marital status is labeled as: married, separated, divorced, widowed, never married; “married” is the baseline category. Education, SRH, and QOL are all treated as 0/1 variables. For education, 0 stands for having gone to high school or less (20 subjects), and 1 stands for having gone to some college or more (14 subjects). For SRH and QOL, 1 is for overall poor ratings (18 subjects for SRH and 21 for QOL) and 0 is for overall good ratings (16 subjects for SRH and 13 for QOL); “weekend” is 1 for a weekend day and zero otherwise.

Figure S1 in supplementary material available at Biostatistics online displays the measurements for each of 3 days plotted vs. covariates; results for different regression models are shown in Table S1 of supplementary material available at Biostatistics online. Models were fit using generalized estimating equations with an exchangeable assumption for days within subject. Several significant predictors were identified: sex (women were found to have longer time active and higher variability in intensity), age (older individuals had lower AIM and variability), 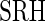(worse health status was associated with less activity), and being divorced (was associated with less activity). The weekend effect was not found to be significant (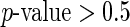) in this data set. Separate models for women confirmed both the negative effect of worse SRH and of being divorced. We found a significant association between age and all four outcomes, indicating that, as age increases, both the activity level and variability decreases. Women who were never married tend to spend more time being active and exhibit a higher variation in TA. Similar results were found when SRH was replaced with QOL. The full analysis is provided in supplementary material available at Biostatistics online.

5. Discussion

We provide a transparent, easy to use, and reproducible normalization approach to extract and summarize relevant metrics from raw tri-axial accelerometry data. Having a simple, explicit formula is a sine- qua-non for further refinements if the needed general discussion among researchers and users is to take place; we have provided a first step in the direction of increased transparency. Most importantly, the AI and TA measures have two built-in fail-safes: (i) using raw tri-axial accelerometer data allows future integration of data from multiple studies and platforms and (ii) using normalization with respect to sedentary and non-wear periods will likely mitigate small and moderate batch effects. Evaluating AI and other accelerometry measurements is difficult in the entire population, though validation in well-defined sub-populations is probably the right approach. Our perspective is different from the current scientific practice that “acceleration is a measure of energy expenditure” or that “acceleration is a measure of a level of activity”. Indeed, we consider that an accelerometer measures acceleration in three different directions at a particular part of the human body. R code is available by request and will be made available at supplementary material available at Biostatistics online.

Supplementary material

Supplementary Material is available at http://biostatistics.oxfordjournals.org.

Funding

The project described was supported by Grant Number R01EB012547 from the National Institute of Biomedical Imaging and Bioengineering and R01NS060910 from the National Institute of Neurological Disorders and Stroke. This work represents the opinions of the researchers and not necessarily that of the granting organizations.