Coupled forward-adjoint Monte Carlo simulation of spatial-angular light fields to determine optical sensitivity in turbid media

Abstract.

We present a coupled forward-adjoint Monte Carlo (cFAMC) method to determine the spatially resolved sensitivity distributions produced by optical interrogation of three-dimensional (3-D) tissue volumes. We develop a general computational framework that computes the spatial and angular distributions of the forward-adjoint light fields to provide accurate computations in mesoscopic tissue volumes. We provide full computational details of the cFAMC method and provide results for low- and high-scattering tissues probed using a single pair of optical fibers. We examine the effects of source-detector separation and orientation on the sensitivity distributions and consider how the degree of angular discretization used in the 3-D tissue model impacts the accuracy of the resulting absorption sensitivity profiles. We discuss the value of such computations for optical imaging and the design of optical measurements.

1. Introduction

The use of optical imaging to noninvasively determine the optical properties of cellular and tissue volumes provides a powerful means to determine biological structure, composition, and function. For example, fiber optic probes are increasingly employed for functional tissue imaging ranging from submillimeter to centimeter spatial scales in applications as diverse as detection of epithelial precancers,^1–4 functional neuroimaging,^5,6 and rheumatoid finger joints.⁷ Additionally, optical approaches for wide-field functional imaging using technologies, such as spatial frequency domain imaging,^8,9 laminar optical tomography,^10,11 mesoscopic epifluorescence tomography,¹² and transmission fluorescence tomography,¹³ show great promise by leveraging the detection of reflectance and fluorescent signals to provide functional information in preclinical animal models and humans.

The use of multiply scattered light to assess tissue structure and function leverages the sensitivity of the detected optical signals to changes in tissue composition, structure, and function. The radiative transport equation (RTE) provides a rigorous description of light propagation in tissue on mesoscopic and macroscopic spatial scales. However, the quantification of tissue function from optical measurements depends largely on the ability to model and predict the remitted optical signal based on knowledge of tissue optical properties. As such, a key element to the accurate quantification and assignment of optical properties is the ability to determine spatial distributions of the signal sensitivity to local tissue changes. These spatially resolved sensitivity distributions and their calculation are of key significance for optical measurement design and resolution of optical and physiological inverse problems.^14–17

Early efforts to compute measurement sensitivities include the photon hitting density¹⁸ and the photon measurement density function.¹⁹ These approaches use the diffusion approximation to the RTE and have proven invaluable for diffuse optical tomographic imaging of thick tissues using near-infrared light ^7,15,16 and provided a means for a priori measurement optimization.¹⁷ However, the limitations of the diffusion approximation prevent the application of these methods on mesoscopic spatial scales (i.e., spatial scales $\lesssim {\ell }^{\star }=1/({\mu }_a+{\mu }_s^{\prime })$) and in tissues when scattering is not dominant over absorption as these conditions often lead to light fields with a significant directional variation. In these situations, conventional Monte Carlo simulations of photon propagation have been leveraged to determine the signal sensitivity to localized changes in tissue optical properties.^6,13,20–23 These approaches assess the sensitivity of detected signals to local changes in optical absorption and/or scattering as well as measurement parameters, such as source-detector separation, source modulation frequency, and source/detector numerical aperture.

While powerful, reliance on conventional Monte Carlo simulations to obtain optical sensitivities is inefficient. This inefficiency occurs because the probability of photon detection is generally low and the probability that any given photon visits the tissue region(s) of interest is also low. Thus, the resulting three-dimensional (3-D) spatially resolved distributions provide insufficient signal to noise, and they are often integrated over the transverse dimensions and represented as depth-resolved distributions^20,22 or as 2-D projections of the complete 3-D distribution.^6,21–23 These reduced representations provide limited, and sometimes misleading, views of the characteristics of the probed tissue volume.

To mitigate the shortcomings of these conventional Monte Carlo approaches, we have developed an efficient Monte Carlo framework to predict 3-D spatially resolved sensitivity distributions. Our method performs the forward-adjoint Monte Carlo simulations by launching photons from both optical sources and detectors to determine both forward-adjoint radiance distributions. These two distributions are then coupled in location and direction using the reciprocity properties of the RTE²⁴ to provide 3-D spatially resolved sensitivity distributions. This coupled forward-adjoint Monte Carlo (cFAMC) framework effectively computes the transport circuit of photons that migrate between source and detector. Unlike conventional MC simulations, cFAMC does not suffer from a loss of efficiency when considering small detectors and/or target tissue volumes.^25,26 cFAMC methods exploit the joint probability of both spatial sampling of the tissue and subsequent detection from specific tissue region(s) of interest (ROI). Separate simulations are performed for these two aspects to compute the joint probability.²⁵ This approach improves not only the signal to noise but also the computational efficiency, especially in the case of detectors with small dimensions and/or narrow apertures. However, rigorous execution of cFAMC simulations requires both computation of the forward-adjoint radiance distributions as well as spatial and angular coupling of these distributions. Since these radiance distributions are 5-D objects (3-D in space and 2-D in direction), computational schemes must be designed carefully to reap the rewards of the efficiencies inherent in the cFAMC simulation approach as compared to conventional Monte Carlo (MC) methods.

Hayakawa et al. first introduced the cFAMC methods in the context of optical diagnostic measurements and inverse problems.²⁵ However, a comprehensive approach to angular discretization of the phase space was not implemented and 3-D spatially resolved sensitivities were not determined. Forward-adjoint MC methods have also been applied for improved simulations of fluorescence imaging.^13,26,27 However, in these studies, directional coupling is not performed for the forward (excitation) and adjoint (emission) light fields because fluorescence excitation and emission are assumed to be independent of the photon propagation direction. Moreover, while these previous manuscripts provide value, they offer few details regarding the implementation of the algorithms required to execute the computations.

Here, we develop and detail a comprehensive MC framework for the efficient evaluation and coupling of forward-adjoint radiance distributions. We used this framework to examine the effects of angular discretization on the accuracy of the resulting spatially resolved sensitivity distributions. This examination is performed in an optically thick homogeneous tissue model with either highly scattering (${\mu }_s^{\prime }/{\mu }_a=100$) or moderately scattering (${\mu }_s^{\prime }/{\mu }_a=1$) optical properties probed using a single fiber optic source-detector pair. We consider both normally and obliquely oriented detectors for source-detector separations of ${\ell }^{\star }$ and $3{\ell }^{\star }$, where ${\ell }^{\star }$ is the transport mean free path. The consideration of both moderately and highly scattering tissues at modest source-detector separations provides insight regarding the necessity of considering directional light transport in mesoscopic tissue volumes.

2. Theory

We consider time-independent radiative transfer in a homogeneous tissue using the RTE

$$\widehat{\mathit{s}}·\nabla L(\mathit{r},\widehat{\mathit{s}})+{\mu }_{t}L(\mathit{r},\widehat{\mathit{s}})={\mu }_s{\int }_{4\pi }L(\mathit{r},{\widehat{\mathit{s}}}^{\prime })p({\widehat{\mathit{s}}}^{\prime }\to \widehat{\mathit{s}})\mathrm{d}{\widehat{\mathit{s}}}^{\prime }+Q(\mathit{r},\widehat{\mathit{s}}),$$ (1)

where the radiance $L(\mathit{r},\widehat{\mathit{s}})$ represents the radiant flux per unit solid angle at position $\mathit{r}=(x,y,z)$ traveling in direction $\widehat{\mathit{s}}=(s_x,s_y,s_z)$. The scattering and absorption coefficients are ${\mu }_s$ and ${\mu }_a$, respectively, and the total attenuation coefficient is defined as ${\mu }_t={\mu }_s+{\mu }_a$. These coefficients have dimensions of inverse length and represent the mean spatial frequency at which these events occur. The scattering phase function $p({\widehat{\mathit{s}}}^{\prime }\to \widehat{\mathit{s}})$ is a probability density function that characterizes the directional redistribution of light that occurs during a single-scattering interaction, where ${\widehat{\mathit{s}}}^{\prime }$ and $\widehat{\mathit{s}}$ are the incident and scattered directions, respectively. Finally, $Q(\mathit{r},\widehat{\mathit{s}})$ accounts for any interior volumetric radiation sources. The unit-direction vector is conveniently parametrized using spherical coordinates as $\widehat{\mathit{s}}=(\sqrt{1-{\mu }^2}\cos \varphi ,\sqrt{1-{\mu }^2}\sin \varphi ,\mu )$, where $\mu$ is the cosine of the polar angle $\theta$ and $\varphi$ is the azimuthal angle. Therefore, the 3-D RTE is dependent on five variables, three that specify spatial location and two that specify the direction of photon propagation.

Using the principle of generalized reciprocity, the adjoint RTE (aRTE) governs the backward transport of radiation from a detector (or adjoint source) through the tissue ^24,28

$$-\widehat{\mathit{s}}·\nabla L^{\star }(\mathit{r},\widehat{\mathit{s}})+{\mu }_t{L}^{\star }(\mathit{r},\widehat{\mathit{s}})={\mu }_s{\int }_{4\pi }{L}^{\star }(\mathit{r},{\widehat{\mathit{s}}}^{\prime })p(\widehat{\mathit{s}}\to {\widehat{\mathit{s}}}^{\prime })\mathrm{d}{\widehat{\mathit{s}}}^{\prime }+Q^{\star }(\mathit{r},\widehat{\mathit{s}}),$$ (2)

where $L^{\star }(\mathit{r},\widehat{\mathit{s}})$ and $Q^{\star }(\mathit{r},\widehat{\mathit{s}})$ are the adjoint radiance and adjoint source, respectively. The aRTE provides a means to determine the phase space locations within the tissue of importance to a given optical detector. For this reason the adjoint radiance $L^{\star }(\mathit{r},\widehat{\mathit{s}})$ has been referred to as the importance function.²⁸ Additionally, the response, or signal, recorded by the detector can be evaluated as

$$R={\iint }_{4\pi }{\mathrm{\Xi }}^{\star }(\mathit{r},\widehat{\mathit{s}})L(\mathit{r},\widehat{\mathbf{s}})\mathrm{d}\mathit{r}\mathrm{d}\widehat{\mathit{s}}={\iint }_{4\pi }\mathrm{\Xi }(\mathit{r},\widehat{\mathit{s}})L^{\star }(\mathit{r},\widehat{\mathit{s}})\mathrm{d}\mathit{r}\mathrm{d}\widehat{\mathit{s}},$$ (3)

where $\mathrm{\Xi }(\mathit{r},\widehat{\mathit{s}})$ and ${\mathrm{\Xi }}^{\star }(\mathit{r},\widehat{\mathit{s}})$ are functions that describe the position, size, and acceptance angle of the source and detector, respectively.^25,29 The importance function provided by $L^{\star }(\mathit{r},\widehat{\mathit{s}})$ can be exploited through coupling with the forward radiance to provide a distribution of the information density or contribution³⁰ for a given source-detector pair. This coupling effectively completes the light transport circuit from source to detector within the tissue. Coupling the forward-adjoint radiances and integrating over the directional variables provides a 3-D spatially resolved contributon distribution

$${\sigma }_{{\mu }_a}(\mathit{r})={\int }_{4\pi }L(\mathit{r},\widehat{\mathit{s}})L^{\star }(\mathit{r},\widehat{\mathit{s}})\mathrm{d}\widehat{\mathit{s}}.$$ (4)

This scalar contributon function is dependent only on position and has been shown to be equivalent to the spatially resolved absorption sensitivity function.¹⁴ Thus, we will refer to the spatially resolved contributon simply as the absorption sensitivity function. Integration of the absorption sensitivity function over the transverse dimensions $(x,y)$ is useful to assess the cumulative depth-dependent sensitivity of a given source-detector pair

$${\mathrm{\Sigma }}_{{\mu }_a}(z)=\iint {\sigma }_{{\mu }_a}(\mathit{r})\mathrm{d}x\mathrm{d}y.$$ (5)

Thus, one motivation in developing a cFAMC framework is to provide an efficient means to evaluate the spatially resolved absorption sensitivity distribution. We also note that the computation of the contributon distribution provides a key element to compute the spatially resolved scattering sensitivity function.¹⁴ We first describe how to compute the forward-adjoint radiances for a given source-detector pair and spatial-angular discretization. We then describe how the forward-adjoint radiances are coupled and integrated to provide the spatially resolved absorption sensitivity function [Eq. (4)].

3. Methods

The MC method is used to simulate the transport of many photons in turbid media using probability density functions that satisfy the RTE.^29,31,32 Using variance reduction techniques, each photon can be considered as a photon packet in which weight $W$ decreases along its trajectory.^29,31,32 We use the continuous absorption weighting (CAW) method, which deposits energy fragments continuously along each path segment between collision locations. The use of CAW within a MC simulation has been shown to provide unbiased estimates of the solution to the radiative transport equation. ²⁹ Thus, photon packets begin the random walk with an initial unit weight $W_0=1$, and absorption effectively deposits weight fragments $\mathrm{\Delta }W$ throughout the medium during the transport process. The trajectory of the $m$th photon packet ${\mathbb{T}}_m$ contains $N_m$ segments, where each discrete segment $n$ is defined by a collision location ${\mathit{r}}_{m,n}=(x_{m,n},y_{m,n},z_{m,n})$ with weight $W_{m,n}$, outward propagation direction ${\widehat{\mathit{s}}}_{m,n}=({\widehat{s}}_{x,m,n},{\widehat{s}}_{y,m,n},{\widehat{s}}_{z,m,n})$, and segment length ${\ell }_{m,n}$ traveled to arrive at location ${\mathit{r}}_{m,n+1}$, such that ${\mathbb{T}}_{m,n}=\{{\mathit{r}}_{m,n},W_{m,n},{\widehat{\mathit{s}}}_{m,n},{\ell }_{m,n}\}$. We leverage the details of these trajectory segments to continuously allocate weight fragments $\mathrm{\Delta }W$ to specific spatial-angular elements within the medium. This approach enhances the spatially distributed information obtained for internal RTE quantities^31,32 while, at the same time, increasing the computational cost. A key objective of our framework is to reap the benefits of CAW for accurate calculation of the forward-adjoint radiances, while retaining computational efficiency.

In the following, we establish a ROI in which we determine the spatially resolved absorption sensitivity function. We then describe our algorithm to evaluate the 5-D radiance distribution within the ROI using a CAW MC simulation. Lastly, we describe how symmetries of the phase space can be leveraged to further enhance both the computational accuracy and efficiency.

3.1. Phase Space Representation

A discretized phase space is required to evaluate the radiances using the discrete segments of the photon trajectories generated by the MC simulation. However, increasing the granularity of the phase space may not only increase the variance of the radiance estimates, due to a reduction in the sample size for a given bin, but also requires prohibitive amounts of memory. To alleviate the latter concern, we restrict our determination of the forward-adjoint radiances to a ROI that occupies a subvolume of the tissue domain in which the photons propagate. The implementation of the ROI allows for the computation and coupling of the forward-adjoint light fields with high granularity, while allowing photons to propagate throughout a much larger domain that need not be discretized.

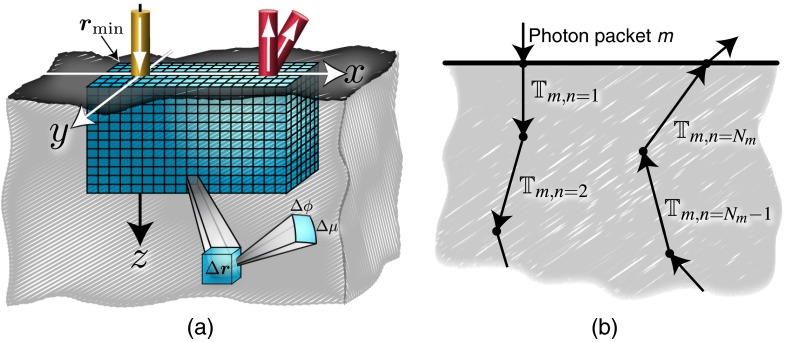
Figure 1 depicts a ROI in the form of a rectangular solid, located within a volume bordering the surface of an optically thick tissue. The optical probe employed to interrogate the tissue provides light from a normally incident source and uses two detectors located at the same location but with different orientations. The ROI is composed of a uniform 5-D spatial-angular mesh with volume elements (voxels) and solid angle elements of dimension $\mathrm{\Delta }x\mathrm{\Delta }y\mathrm{\Delta }z=\mathrm{\Delta }{l}^3$ and $\mathrm{\Delta }\mu \mathrm{\Delta }\varphi$, respectively. The total number of discrete bins contained in the ROI is $N_{\mathrm{tot}}=N_x{N}_y{N}_z{N}_{\mu }{N}_{\varphi }$, where $N_{(·)}$ is the number of elements for each phase space variable. The volume of the ROI is $l_x{l}_y{l}_z$, where the lengths are given by $(l_x,l_y,l_z)=(N_x\mathrm{\Delta }l,N_y\mathrm{\Delta }l,N_z\mathrm{\Delta }l)$, and the subvolume of tissue that the ROI encloses is further defined by the minimum vertex ${\mathit{r}}_{\min }$. We denote each voxel in the ROI as $\mathrm{\Delta }\mathit{r}=(i,j,k)\in \{[1,N_x],[1,N_y],[1,N_z]\}$, which encloses the spatial locations $\mathit{r}=(x,y,z)\in \{[x_{\min }+(i-1)\mathrm{\Delta }l,x_{\min }+i\mathrm{\Delta }l],[y_{\min }+(j-1)\mathrm{\Delta }l,y_{\min }+j\mathrm{\Delta }l],[z_{\min }+(k-1)\mathrm{\Delta }l,z_{\min }+k\mathrm{\Delta }l]\}$. The photon direction is conveniently mapped to the two angular variables specified on the unit sphere as described in Sec. 2, where $\mathrm{\Delta }\mu =2/N_{\mu }$ and $\mathrm{\Delta }\varphi =2\pi /N_{\varphi }$. Each solid angle element is then specified as $\mathrm{\Delta }\widehat{\mathit{s}}=(u,v)\in \{[1,N_{\mu }],[1,N_{\varphi }]\}$, which spans the photon propagation directions with angular variables $\mu \in [(u-1)\mathrm{\Delta }\mu ,u\mathrm{\Delta }\mu ]$ and $\varphi \in [(v-1.5)\mathrm{\Delta }\varphi ,(v-0.5)\mathrm{\Delta }\varphi ]$. The boundaries of the $\varphi$ bins are shifted by $-0.5\mathrm{\Delta }\varphi$, so that $\varphi$ values that are co-planar with the $x\text{-}z$ and $y\text{-}z$ planes occupy the center of the angular bin. To preserve this feature, we restrict the value of $n_{\varphi }$ to multiples of 4.

Fig. 1.

Illustration of the space-angle mesh contained in the region of interest (ROI) that is located within the tissue volume (a). Each volume element (voxel) if further discretized in angle, where $\mathrm{\Delta }\widehat{s}=\mathrm{\Delta }\mu \mathrm{\Delta }\varphi$ is a solid angle element, which is depicted in the closeup view of a single voxel (a). Illustration of the trajectory elements that photon packet $m$ might experience during transport through the tissue (b).

Using the spatial-angular mesh, both the discrete forward-adjoint radiances, $L(\mathrm{\Delta }\mathit{r},\mathrm{\Delta }\widehat{\mathit{s}})$ and $L^{\star }(\mathrm{\Delta }\mathit{r},\mathrm{\Delta }\widehat{\mathit{s}})$, respectively, can be estimated within the ROI. The absorption sensitivity at any given discrete location $\mathrm{\Delta }{\mathit{r}}_{i,j,k}$ is then obtained by coupling these radiances and integrating them over the solid angle elements $\mathrm{\Delta }\widehat{\mathit{s}}$ via a discrete analog of Eq. (4)

$${\sigma }_{{\mu }_a}(\mathrm{\Delta }{\mathit{r}}_{i,j,k})=\sum _{u=1}^{N_{\mu }}\sum _{v=1}^{N_{\varphi }}L(\mathrm{\Delta }{\mathit{r}}_{i,j,k},\mathrm{\Delta }{\widehat{\mathit{s}}}_{u,v})L^{\star }(\mathrm{\Delta }{\mathit{r}}_{i,j,k},\mathrm{\Delta }{\widehat{\mathit{s}}}_{u,v})\mathrm{\Delta }{\mu }_u\mathrm{\Delta }{\varphi }_v.$$ (6)

In the following section, we provide the algorithmic details of our approach to evaluate the radiances.

3.2. Radiance Evaluation

To understand how the radiance is evaluated from the detailed information of a CAW-MC simulation, we must consider the specific characteristics of ${\mathbb{T}}_{m,n}$, which records information pertaining to the $n$’th segment of the $m$’th photon packet and specifies its location ${\mathit{r}}_{m,n}$, weight $W_{m,n}$, and direction ${\widehat{\mathit{s}}}_{m,n}$ from which the photon moves a length ${\ell }_{m,n}$ to location ${\mathit{r}}_{m,n+1}$ with weight $W_{m,n+1}=W_{m,n}\exp (-{\mu }_a{\ell }_{m,n})$. It is from the location specified by ${\mathbb{T}}_{m,n+1}$ that the photon begins the next segment. Using the trajectories that result from $N_{h\nu }$ photon packets, the radiance is tallied for each segment and the photon traces within the ROI. For photon segments that take place within a single voxel, the radiance tally can be computed using

$$L(\mathrm{\Delta }\mathit{r},\mathrm{\Delta }\widehat{\mathit{s}})=\frac{1}{N_{h\nu }\mathrm{\Delta }{l}^3\mathrm{\Delta }\mu \mathrm{\Delta }\varphi }\sum _{m=1}^{N_{h\nu }}\sum _{n=1}^{N_m}\frac{\mathrm{\Delta }{W}_{m,n}(\mathrm{\Delta }{\mathit{r}}_{i,j,k},\mathrm{\Delta }{\widehat{\mathit{s}}}_{u,v})}{{\mu }_a(\mathrm{\Delta }{\mathit{r}}_{i,j,k})}.$$ (7)

According to Eq. (7), the $n$’th segment of the $m$’th photon packet deposits a weight fragment $\mathrm{\Delta }{W}_{m,n}=W_{m,n}-W_{m,n+1}=W_{m,n}[1-\exp (-{\mu }_a{\ell }_{m,n})]$ in the space-angle element $[\mathrm{\Delta }{\mathit{r}}_{i,j,k},\mathrm{\Delta }{\widehat{\mathit{s}}}_{u,v}]$, and the ratio of the deposited weight to the absorption coefficient is tallied to the radiance within the corresponding spatial.

However, Eq. (7) does not consider photon segments ${\mathbb{T}}_{m,n}$ that span multiple voxels. This case is important because accurate MC estimation of the radiance distribution requires a spatial discretization with voxel dimension $\mathrm{\Delta }l$ that is comparable to or less than the scattering length ${\ell }_s=1/{\mu }_s$.³¹ In CAW, the segment length that the photon packet traverses between its $n$’th and $(n+1)$’th collisions is sampled from ${\ell }_{m,n}=-\ln (\xi )/{\mu }_s$, where $\xi$ is a random value between 0 and 1. Thus, it is likely that many photon segments ${\ell }_{m,n}$ will span multiple volume elements. To obtain radiance estimates in this case, we must deposit the appropriate weight fragments $\mathrm{\Delta }{W}_{m,n,p}$ in each of the $p$ voxels traversed by photon segment ${\mathbb{T}}_{m,n}$. The consideration of this detail requires great care when using CAW-MC to obtain accurate internal RTE quantities. To account for these events, Eq. (7) is reformulated as follows:

$$L(\mathrm{\Delta }\mathit{r},\mathrm{\Delta }\widehat{\mathit{s}})=\frac{1}{N_{h\nu }\mathrm{\Delta }{l}^3\mathrm{\Delta }\mu \mathrm{\Delta }\varphi }\sum _{m=1}^{N_{h\nu }}\sum _{n=1}^{N_m}\sum _{p=0}^{N_n}\frac{\mathrm{\Delta }{W}_{m,n,p}(\mathrm{\Delta }{\mathit{r}}_{i,j,k},\mathrm{\Delta }{\widehat{\mathit{s}}}_{u,v})}{{\mu }_a(\mathrm{\Delta }{\mathit{r}}_{i,j,k})},$$ (8)

where $N_n$ is the number of photon segment voxel intersections.

Equation (8) provides the radiance by properly considering each voxel that is traversed by the photon segment ${\mathbb{T}}_{m,n}$. However, this requires a method to compute each of the individual weight fragments $\mathrm{\Delta }{W}_{m,n,p}$ and the corresponding voxel indices $(i,j,k)$ for each subsegment. Moreover, we must map the photon direction ${\widehat{\mathit{s}}}_{m,n}$ for segment ${\mathbb{T}}_{m,n}$ to the proper solid angle bin $(u,v)$. To efficiently evaluate $\mathrm{\Delta }{W}_{m,n,p}$ required for Eq. (8), we utilize the intersection(s) of the photon segment ${\mathbb{T}}_{m,n}$ with the spatial mesh of the ROI. Using these segment-mesh intersection locations ${\mathit{r}}_{m,n,p}$, we evaluate a series of cumulative segment lengths ${\ell }_{m,n,p}=\Vert {\mathit{r}}_{m,n,p}-{\mathit{r}}_{m,n}\Vert$, relative to ${\mathit{r}}_{m,n}$. This allows the photon weight at the segment-mesh intersections to be determined as $W_{m,n,p}=W_{m,n}\exp (-{\mu }_a{\ell }_{m,n,p})$. Finally, the evaluation of the deposited weight fragments $\mathrm{\Delta }{W}_{m,n,p}$ requires the successive photon weights, that is, $W_{m,n,p+1}$ and $W_{m,n,p}$. Therefore, if the lengths ${\ell }_{m,n,p}$ are determined sequentially, the calculation of the deposited weight fragments follows easily.

To efficiently compute both ${\ell }_{m,n,p}$ and the unique $\mathrm{\Delta }{\mathit{r}}_{i,j,k}$ voxel that correspond to weight fragment $\mathrm{\Delta }{W}_{m,n,p}$, we developed an algorithm that directly computes a complete, but unordered, list of cumulative segment lengths ${\ell }_{m,n,q}$. The ordering of this list then provides the proper sequence of cumulative segment lengths ${\ell }_{m,n,p}$. Additionally, details are extracted from each segment-mesh intersection to provide a map of the voxel indices traversed by segment ${\mathbb{T}}_{m,n}$. This approach provides for a more efficient procedure as compared to determining the segments of ${\mathbb{T}}_{m,n}$ by tracing the trajectory of the photon segment through the spatial mesh of the ROI.

Our procedure begins by leveraging the voxel indices that correspond to collision locations ${\mathit{r}}_{m,n}$ and ${\mathit{r}}_{m,n+1}$. These indices are evaluated as

$$\mathrm{\Delta }\mathit{r}({\mathit{r}}_{m,n})=\lceil \frac{{\mathit{r}}_{m,n}-{\mathit{r}}_{\min }}{\mathrm{\Delta }l}\rceil ,$$ (9)

where $\lceil ·\rceil$ is the ceiling function. The absolute difference between these indices provides the number of segment-voxel intersections for each spatial dimension as

$$\mathit{\eta }=({\eta }_x,{\eta }_y,{\eta }_z)=|\mathrm{\Delta }\mathit{r}({\mathit{r}}_{m,n})-\mathrm{\Delta }\mathit{r}({\mathit{r}}_{m,n+1})|,$$ (10)

where the number of photon segment-voxel intersections is given by $N_n=\mathit{\eta }·(1,1,1)$. To determine the intersection location(s) along the $x$-direction, $x_{m,n,q}$, we leverage the uniformity of the spatial mesh as

$$x_{m,n,q}=x_{\min }+\{i_{m,n}-1+\lfloor {\widehat{s}}_{x,m,n}\rfloor +q\mathrm{sgn}({\widehat{s}}_{x,m,n})\}\mathrm{\Delta }l,$$ (11)

where $\lfloor ·\rfloor$ is the floor function and $q=[1,{\eta }_x]$ is the range of $x$-intersections. Using a similar approach, we determine the number of $y$-voxel intersections using

$$y_{m,n,q}=y_{\min }+\{j_{m,n}-1+\lfloor {\widehat{s}}_{y,m,n}\rfloor +(q-{\eta }_x)\mathrm{sgn}({\widehat{s}}_{y,m,n})\}\mathrm{\Delta }l,$$ (12)

where the value(s) of $q=[{\eta }_x+1,{\eta }_x+{\eta }_y]$, and the number of $z$-voxel intersections as

$$z_{m,n,q}=z_{\min }+\{k_{m,n}-1+\lfloor {\widehat{s}}_{z,m,n}\rfloor +(q-{\eta }_x-{\eta }_y)\mathrm{sgn}({\widehat{s}}_{z,m,n})\}\mathrm{\Delta }l,$$ (13)

where the value(s) of $q=[{\eta }_x+{\eta }_y+1,N_n]$. The unordered list of cumulative segment lengths is first populated with values

$${\ell }_{m,n,q}=\frac{x_{m,n,q}-x_{m,n}}{{\widehat{\mathit{s}}}_{x,m,n}}.$$ (14)

This procedure is then repeated for both the $y$ and $z$ spatial variables to complete the list of ${\ell }_{m,n,q}$. However, as previously described, the evaluation of the cumulative lengths alone does not provide sufficient information to tally the radiance. Therefore, the length ${\ell }_{m,n,q}$ is stored in a structured array along with the unit vector collinear with the photon propagation direction and the mesh intersection spatial dimension. These values provide both the spatial dimension and direction of the segment-voxel intersection. For example, $x$-voxel intersection has a collinear unit vector $[\mathrm{sgn}({\widehat{s}}_{x,m,n}),0,0]$. Next, the qsort algorithm³³ is employed to produce the ordered list ${\ell }_{m,n,p}$ by sorting the structured data array according to ascending cumulative segment length ${\ell }_{m,n,q}$.

Figure 2 provides a 2-D representation of this process in the $x\text{-}z$ plane. Beginning with the photon segment ${\mathbb{T}}_{m,n}$, the unordered cumulative segment lengths ${\ell }_{m,n,q}$ are evaluated along with their collinear unitvectors. These data are first sorted to provide the contiguous cumulative segments ${\ell }_{m,n,p}$. The corresponding weight fragments are then determined and tallied to the appropriate spatial-angular bin. The first weight fragment is denoted as $\mathrm{\Delta }{W}_{m,n,p=0}=W_{m,n}-W_{m,n,p=1}$ and contributes to $\mathrm{\Delta }\mathit{r}({\mathit{r}}_{m,n})$. The voxel indices for the $p=1$ subsegment is then determined by addition of the collinear unitvector corresponding to ${\ell }_{m,n,p=1}$ to $\mathrm{\Delta }\mathit{r}({\mathit{r}}_{m,n})$. The weight fragment $\mathrm{\Delta }{W}_{m,n,p=1}=W_{m,n,p=1}-W_{m,n,p=2}$ contributes to this updated voxel index, and the process of updating the voxel index and tallying the weight fragments $\mathrm{\Delta }{W}_{m,n,p}$ is repeated until $p=N_n-1$. The last subsegment where $p=N_n$ assigns the weight fragment $\mathrm{\Delta }{W}_{m,n,p=N_n}=W_{m,n,p=N_n}-W_{m,n+1}$ to $\mathrm{\Delta }\mathit{r}({\mathit{r}}_{m,n+1})$.

Fig. 2.

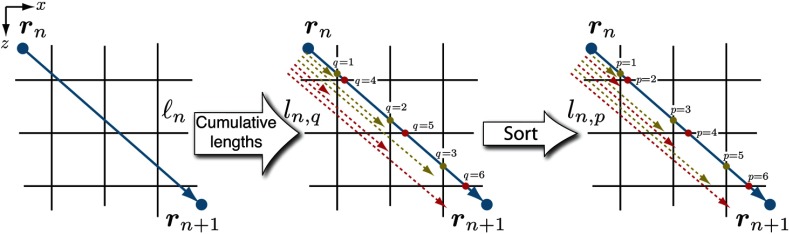
Illustration of the algorithm used to account for multiple voxel intersections, shown in 2-D for convenience. Using the segment length ${\ell }_n$, the unsorted cumulative segment lengths ${\ell }_{n,q}$ are determined for each spatial dimension. This list of lengths is sorted to provide the ordered cumulative segment lengths ${\ell }_{n,p}$. Moreover, the details regarding each mesh intersection direction are used to provide a map that traverses the voxel indices for efficient tallying, illustrated by the color-coded intersection points.

This algorithm efficiently evaluates the radiance using CAW, through the proper determination of the subsegment weight fragments $\mathrm{\Delta }{W}_{m,n,p}$ and the assignment to the appropriate spatial-angular element $(\mathrm{\Delta }{\mathit{r}}_{i,j,k},\mathrm{\Delta }{\widehat{\mathit{s}}}_{u,v})$. In cases where the source-detector pair lies in a single plane that is orthogonal to the tissue surface, the forward-adjoint radiances exhibit even symmetry about this plane, and we can exploit this symmetry to reduce the memory requirements of the cFAMC simulation. In this study, we consider cases where the source-detector pair lies in the $x\text{-}z$ plane. In all these cases, the radiances exhibit even symmetry with respect to $y$, that is,

$$L(x,y,z,{\widehat{s}}_x,{\widehat{s}}_y,{\widehat{s}}_z)=L(x,-y,z,{\widehat{s}}_x,-{\widehat{s}}_y,{\widehat{s}}_z).$$ (15)

This relationship allows us to replace the physical ROI with a memory-reduced computational ROI, while simultaneously increasing the quantity of photon tallies that contribute to the radiance in any given bin.

The proper utilization of this symmetry relationship reduces the memory requirements by nearly a factor of 2 and improves overall computational efficiency.

While this approach to evaluate the radiance applies to both forward-adjoint photon transfers, it is necessary to distinguish between forward-adjoint simulations. While a separate MC code could be developed for adjoint photon propagation from adjoint sources, this is not necessary. Rather, we leverage the reciprocity relationship of the forward-adjoint radiances²⁴

$$L^{\star }(\mathit{r},-\widehat{\mathit{s}})=L(\mathit{r},\widehat{\mathit{s}}),$$ (16)

which applies when $Q^{\star }(\mathit{r},-\widehat{\mathit{s}})=Q(\mathit{r},\widehat{\mathit{s}})$. Therefore, the algorithms that execute forward MC simulations can be used to perform adjoint simulations by constructing a source function using $Q^{\star }(\mathit{r},-\widehat{\mathit{s}})$ and evaluating the adjoint radiance using Eq. (16) on a photon-by-photon basis.

Following the determination of both forward-adjoint radiances for a given source-detector pair, the spatial distribution of the sensitivity is determined using Eq. (6). Moreover, the radiance resulting from a single forward simulation can be reused to couple with multiple adjoint radiances provided by different detector configurations, that is, changing the detector orientation and/or position.

4. Model Tissue Probe

Using this cFAMC method, we analyze the absorption sensitivity distribution when using specific source-detector configurations to probe a model tissue. We also consider the impact of angular discretization of the phase space on the accuracy of these computations. Specifically, we examine an optically thick homogeneous tissue that we model as a half-space with two sets of optical coefficients corresponding to highly scattering (${\mu }_s^{\prime }/{\mu }_a=100$) and moderately scattering (${\mu }_s^{\prime }/{\mu }_a=1$) cases, where the transport scattering coefficient, ${\mu }_s^{\prime }={\mu }_s(1-g)$, gives rise to the transport mean free path, ${\ell }^{\star }=1/({\mu }_a+{\mu }_s^{\prime })$, which we set to 1 mm. We employ a Henyey–Greenstein scattering phase function with a forward-directed scattering anisotropy of $g=0.8$ and a refractive index mismatch of $n=1.4$ characteristic of a tissue/air interface.

We model the light source as a narrow collimated Gaussian beam normally incident on the tissue surface, with radius ${\rho }_i={\ell }^{\star }/10=100\mathrm{\mu m}$ and numerical aperture $\mathrm{NA}=0.12$. We consider the collection of remitted light at source-detector separation distances ${\rho }_{\mathrm{sds}}={\ell }^{\star }$ and $3{\ell }^{\star }$. For these locations, we consider two detection angles $\alpha =0$ and 30 deg with respect to the outward-pointing surface normal. The detectors possess the same dimension and NA as the source. Figure 3 provides a schematic of the tissue and probe geometry along with a depiction of characteristic cross sections of forward-adjoint radiance distributions. These cross sections depict light fields that transition from highly asymmetric distributions proximal to the source/detector to more diffuse/isotropic distributions at distal locations.

Fig. 3.

Illustration of the model tissue with a single source and two detectors at different distances and two detection angles. Additionally, characteristic forward and adjoint radiance cross sections are displayed for the source and normally oriented detectors. The forward and adjoint radiances display the high degree of direction anisotropy in locations near the source/detector.

4.1. Simulation Details

We compute the forward-adjoint radiances and the resulting absorption sensitivity distributions using four levels of angular discretization. These levels and descriptive names are provided in Table 1. We consider the highest level of angular discretization (fine) to provide the most accurate radiances and associated sensitivity distributions. Thus, we will compare the three other levels of angular discretization to the fine case. The case of no angular discretization is an important one as this corresponds to a calculation where the forward-adjoint light fields are modeled as a scalar density function without any angular variation. To obtain the results shown below, we launched ${10}^8$ photons or ${10}^9$ photons for each forward-adjoint simulation in the cases of highly (${\mu }_s^{\prime }/{\mu }_a=100$) or moderately scattering media (${\mu }_s^{\prime }/{\mu }_a=1$), respectively. More photons were required in the moderately scattering case since the increased absorption and decreased scattering led to a reduced angular dispersion of the photon propagation direction. Additionally, we use the technique of Russian Roulette to reduce the variance and runtime of the simulations,³¹ where photons with a weight less than 0.0001 have a 10% chance of survival.

Table 1.

Levels of angular discretization used in cFAMC simulations.

Description	$n_{\mu }$	$n_{\varphi }$	$n_{\widehat{\mathit{s}}}$
None	1	1	1
Coarse	2	4	8
Moderate	8	16	128
Fine	32	64	2048

Simulations that employ a source-detector separation ${\rho }_{\mathrm{sds}}={\ell }^{\star }$ are performed with a voxel dimension of $\mathrm{\Delta }l=0.02{\ell }^{\star }$, and the physical ROI has dimensions of $1.8{\ell }^{\star }\times 1.38{\ell }^{\star }\times 1.8{\ell }^{\star }$ for a total volume of $4.47{\ell }^{{\star }^3}$. This results in a computational ROI with a total number of bins $N_{\mathrm{tot}}=n_{\mu }{n}_{\varphi }\times 90\times 35\times 90=n_{\widehat{\mathit{s}}}\times 2.835\times {10}^5$. Simulations using the larger source-detector separation ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$ employ a larger voxel size of $\mathrm{\Delta }l=0.03{\ell }^{\star }$ to accommodate the larger ROI of $5.4{\ell }^{\star }\times 4.11{\ell }^{\star }\times 5.4{\ell }^{\star }$ with volume $120{\ell }^{{\star }^3}$. This provides a computational ROI with $N_{\mathrm{tot}}=n_{\mu }{n}_{\varphi }\times 180\times 69\times 180=n_{\widehat{\mathit{s}}}\times 2.2356\times {10}^6$. Given the voxel dimensions and the ROI, the memory required for a single radiance estimate, as a function of the solid angle discretization, is $n_{\widehat{\mathit{s}}}\times 2.268\mathrm{MB}$ for ${\rho }_{\mathrm{sds}}={\ell }^{\star }$ and $n_{\widehat{\mathit{s}}}\times 17.9\mathrm{MB}$ for ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$, using double precision floating point numbers.

5. Results and Discussions

In the results that follow, we provide orthogonal slices of the 3-D spatially resolved absorption sensitivity along the $x\text{-}z$ plane at $y=0$ (symmetry plane) and the $y\text{-}z$ plane at $x={\rho }_{\mathrm{sds}}/2$, which represent the midplane between source and detector. These 2-D views of the sensitivity distributions allow the examination of the impact of angular discretization on the computations. These views are displayed using colormaps on a ${\mathrm{Log}}_{10}$ scale using fine angular discretization $[(n_{\mu },n_{\varphi })=(32,64)]$, with an overlay of contours that are computed using no $[(n_{\mu },n_{\varphi })=(1,1)]$ and coarse $[(n_{\mu },n_{\varphi })=(2,4)]$ angular discretization levels. We further provide the transverse integrated sensitivity distribution ${\mathrm{\Sigma }}_{{\mu }_a}(z)$ [Eq. (5)] that is solely a function of depth $z$, and the results for the moderate angular discretization $[(n_{\mu },n_{\varphi })=(8,16)]$ are included in these plots. Moreover, we compute the depth sensitivity distribution, ${\mathrm{\Sigma }}_{{\mu }_a}(z)$, using the photon hitting density,¹⁸ where the absorption sensitivity is approximated by the product of forward-adjoint fluence distributions provided by the standard diffusion approximation. We compute these distributions using an exponentially distributed source and treat the boundary condition at the tissue surface using the method of images.³⁴ Using these comparisons, we analyze how the degree of angular discretization impacts the accuracy of the sensitivity distributions for the various source-detector configurations and sets of optical properties. The level of agreement between results obtained using different levels of angular discretization indicates the degree of angular anisotropy of the coupled forward-adjoint light fields associated with the measurement under consideration.

Prior to analyzing the sensitivity maps provided by our cFAMC framework, we compare the quality of the cFAMC simulation results in relation to those computed using conventional MC simulations using an identical number of launched photons. Figure 4 displays the comparisons of the spatially resolved absorption sensitivity ${\sigma }_{{\mu }_a}(r)$ and depth-resolved cumulative sensitivity ${\mathrm{\Sigma }}_{{\mu }_a}(z)$ distributions for a normally oriented detector with a source-detector separation, ${\rho }_{\mathrm{sds}}={\ell }^{\star }$. The cFAMC results are provided using fine angular discretization $[(n_{\mu },n_{\varphi })=(32,64)]$. Each approach used an equivalent number of photons, where the total number of photons for the highly and moderately scattering media is $2\times {10}^8$ and $2\times {10}^9$, respectively. cFAMC uses half of this total quantity of photons for each forward and adjoint simulation, while the conventional approach launches all the photons from the source. cFAMC requires less than 1% more computational time than the conventional approach due to the additional overhead of the angular discretization and the forward-adjoint coupling step. However, it is important to note that we leverage key elements of our cFAMC framework, such as the use of photon tracking through the spatial mesh and the ROI, for the conventional MC computations as well. Thus, the additional overhead of cFAMC is solely due to the angular discretization and forward-adjoint coupling, which are small in relation to the photon tracking within the spatial mesh. The results provided in Figs. 4(a), 4(b), 4(d), and 4(e) show the dramatically enhanced spatial information obtained when using cFAMC as compared to a conventional MC approach. Additionally, the depth-resolved cumulative sensitivities provided in Fig. 4(c) and 4(f) display both improved signal to noise with the use of cFAMC and equivalence of the results provided by cFAMC and conventional MC approaches.

Fig. 4.

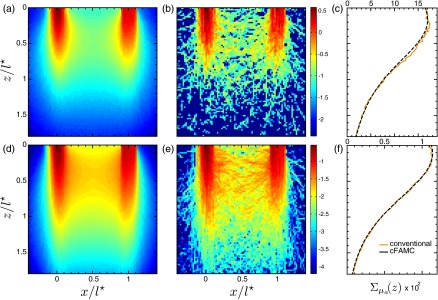
Spatially resolved absorption sensitivity distributions are displayed on a ${\mathrm{Log}}_{10}$ scale for ${\rho }_{\mathrm{sds}}={\ell }^{\star }$ and $\alpha =0\mathrm{deg}$ for highly scattering media ${\mu }_s^{\prime }/{\mu }_a=100$ (a–c) and moderately scattering media ${\mu }_s^{\prime }/{\mu }_a=1$ (d–f). Distributions are displayed for the $x\text{-}z$ plane at $y=0$ (a, b, d, and e) for cFAMC (a, d) and the conventional approach (b, e). The corresponding depth-dependent cumulative absorption sensitivity is plotted for both approaches (c, f).

5.1. Highly Scattering Media ${\mathsf{\mu }}_{\mathsf{s}}^{\prime }/{\mathsf{\mu }}_{\mathsf{a}}=$100

We first consider a highly scattering medium probed using a source-detector separation, ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$. Figures 5(a) to 5(c) display the spatially resolved absorption sensitivity ${\sigma }_{{\mu }_a}(r)$ and depth-resolved cumulative sensitivity ${\mathrm{\Sigma }}_{{\mu }_a}(z)$ distributions for the normally oriented detector, while Figs. 5(d) to 5(f) display these same results for an oblique detector oriented at $\alpha =30\mathrm{deg}$. Purely diffusive coupled forward-adjoint light transport occurs in locations where the computation of the sensitivity distribution is relatively unaffected by the degree of angular discretization used. In Figs. 5(a), 5(b), 5(d), and 5(e), this occurs at depths $z>2{\ell }^{\star }$ and lateral locations $y>{\ell }^{\star }$ for both normal and angled detectors. However, for depths $z<2{\ell }^{\star }$ and lateral locations $y<{\ell }^{\star }$, the use of no or coarse angular discretization under predicts the sensitivity distribution. The use of coarse angular discretization also under predicts the sensitivity distribution in the superficial region between the source and detector as seen in Figs. 5(a), 5(b), 5(d), and 5(e). However, the results of Figs. 5(c) and 5(f) show that the depth-resolved absorption sensitivity provided by coarse discretization agrees well with the calculations obtained using both moderate and fine angular discretizations. Figures 5(c) and 5(f) also display the photon hitting density,¹⁸ which substantially underpredicts the sensitivity for $z\lesssim 3{\ell }^{\star }$ for both normal and oblique detections. These predictions are noticeably poorer than those obtained using no angular discretization. This is the case as the photon hitting density not only ignores any angular dependence in the radiance but also utilizes the standard diffusion approximation to compute the forward and adjoint light fields, which behave poorly near boundaries and collimated sources/detectors. Comparison of Figs. 5(c) and 5(f) reveals that while the angled detector increases the sensitivity to superficial tissue structures, the differences observed between various angular discretization levels are similar. This is due to the high level of scattering, which effectively randomizes the photon propagation directions over small distances.

Fig. 5.

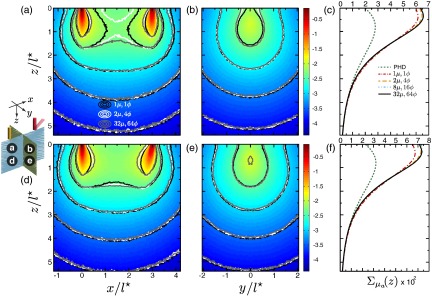
Spatially resolved absorption sensitivity distributions are displayed on a ${\mathrm{Log}}_{10}$ scale for highly scattering media ${\mu }_s^{\prime }/{\mu }_a=100$ with ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$ for $\alpha =0\mathrm{deg}$ (a–c) and $\alpha =30\mathrm{deg}$ (d–f). Distributions are displayed for the $x\text{-}z$ plane at $y=0$ (a, d) and the $y\text{-}z$ plane at $x={\rho }_{\mathrm{sds}}/2$ (b, e) where the colormap provides the results obtained using fine angular discretization. The corresponding depth-dependent cumulative absorption sensitivity is plotted for the four angular discretization cases and the photon hitting density (PHD) (c, f).

Figure 6 displays the sensitivity distributions for source-detector separation, ${\rho }_{\mathrm{sds}}={\ell }^{\star }$. In this case, the forward and adjoint radiances possess much greater directional dependence as compared to the ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$ case considered above. An examination of Figs. 6(a), 6(b), 6(d), and 6(e) reveal that the computations made with no angular discretization result in significant overestimations of the penetration and underestimation of the magnitude of the absorption sensitivity distribution. The underestimation of the sensitivity distribution at proximal depths is due to strongly direction-dependent radiance coupling at locations in the immediate vicinity of the source/detector. By contrast, sensitivity overestimation at further distances from either the source or detector arises from coupling of one strongly directed light field with the other that has become more directionally randomized. This latter scenario reduces the sensitivity, while the coupling of two isotropic fields produces an overestimation. This is consistent with recent computations that have shown the localized persistence of a strong directional dependence in the radiance distribution at distances up to $3{\ell }^{\star }$ from collimated sources at a depth of ${\ell }^{\star }$ in strongly scattering media.³⁵

Fig. 6.

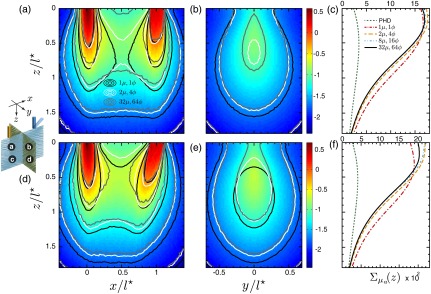
Spatially resolved absorption sensitivity distributions are displayed on a ${\mathrm{Log}}_{10}$ scale for highly scattering media ${\mu }_s^{\prime }/{\mu }_a=100$ with ${\rho }_{\mathrm{sds}}={\ell }^{\star }$ for $\alpha =0\mathrm{deg}$ (a–c) and $\alpha =30\mathrm{deg}$ (d–f). Distributions are displayed for the $x\text{-}z$ plane at $y=0$ (a, d) and the $y\text{-}z$ plane at $x={\rho }_{\mathrm{sds}}/2$ (b, e), where the colormap provides the results obtained using fine angular discretization. The corresponding depth-dependent cumulative absorption sensitivity is plotted for the four angular discretization cases and the PHD (c, f).

The use of coarse discretization provides marked improvements in prediction accuracy that begins to resemble the results obtained using fine angular discretization. This is displayed in the spatially resolved cross sections at depths $z>{\ell }^{\star }$ and lateral positions beyond the source and/or detector. However, Figs. 6(c) and 6(f) show that the coarse angular discretization still overestimates the cumulative absorption sensitivity distribution as a function of depth. Figure 6(f) shows that this overestimation is more prominent in the case of oblique detection. In the case of normal detection, Fig. 6(c) shows that the depth-dependent absorption sensitivity calculated using moderate angular discretization is in strong agreement with results computed using fine discretization. However, Fig. 6(f) shows the use of moderate angular discretization for the case of oblique detection overpredicts the results provided using fine angular discretization for depths $z\lesssim {\ell }^{\star }/2$. The lack of agreement between the absorption sensitivity functions computed using different degrees of angular discretization demonstrates the high degree of angular anisotropy in both the forward and adjoint light fields at depths up to $2{\ell }^{\star }$, when using source-detector separations on the order of ${\ell }^{\star }$. Of particular significance is the misleading picture of the absorption sensitivity obtained when using no angular discretization. These results consistently underestimate the sensitivity to superficial tissue regions while overestimating the sensitivity to deeper ($z>{\ell }^{\star }/2$) tissue volumes. Moreover, the results provided by the photon hitting density for the depth-dependent cumulative absorption sensitivity dramatically underpredict those of cFAMC, and agreement between the diffuse predictions with MC occurs at depths beyond the ROI. These photon hitting density results are consistent with the poor fluence estimates obtained using low-order approximations of light transport resulting from narrow beam irradiation of highly scattering media near the source and boundaries.^36,37

5.2. Moderately Scattering Media ${\mu }_s^{\prime }/{\mu }_a=$1

When considering moderately scattering media (${\mu }_s^{\prime }/{\mu }_a=1$), we see that the reduction in scattering relative to absorption serves to reduce the angular dispersion of the photon propagation direction and results in increased anisotropy of the forward/adjoint radiances relative to highly scattering media. Figure 7 displays the absorption sensitivity distributions in moderately scattering media for a source-detector separation of ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$. Examination of Figs. 7(a), 7(b), 7(d), and 7(e) reveals that for both normal and oblique detections, the use of no angular discretization leads to an overprediction of the absorption sensitivity at large depths and lateral positions and an underestimation of the sensitivity in regions proximal to the source/detector as well as in the proximal region between the source and detector. This underestimation at proximal locations and overestimation at distal locations occur via the same mechanism observed in Fig. 6. Specifically, both the forward and adjoint light fields are highly directionally dependent, which leads to an underestimation of the sensitivity distribution in the proximal region of the source/detector and overestimations at distal locations. Due to the reduction in scattering relative to absorption in this case, the overestimations extend over a larger region since directional dependence of the radiance persists over an extended region.³⁵

Fig. 7.

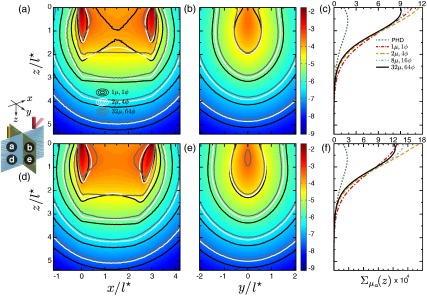
Spatially resolved absorption sensitivity distributions are displayed on a ${\mathrm{Log}}_{10}$ scale for moderately scattering media ${\mu }_s^{\prime }/{\mu }_a=1$ with ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$ for $\alpha =0\mathrm{deg}$ (a–c) and $\alpha =30\mathrm{deg}$ (d–f). Distributions are displayed for the $x\text{-}z$ plane at $y=0$ (a, d) and the $y\text{-}z$ plane at $x={\rho }_{\mathrm{sds}}/2$ (b, e), where the colormap provides the results obtained using fine angular discretization. The corresponding depth-dependent cumulative absorption sensitivity is plotted for the four angular discretization cases and the PHD (c, f).

Figures 7(c) and 7(f) display the depth-dependent absorption sensitivity in the cases of normal and oblique detections, respectively. These results emphasize the need for fine angular discretization to obtain accurate results due to the persistent directional nature of the forward-adjoint light fields in this case. While the use of coarse discretization provides improved results for proximal depths $z\le 1.5{\ell }^{\star }$, the predictions for depths $z>1.5{\ell }^{\star }$ are still overpredicted and are more pronounced when using oblique detection [Fig. 7(f)]. We also show results using the photon hitting density that dramatically underpredicts those of cFAMC at superficial depths. This is not surprising since the standard diffusion approximation, upon which the photon hitting density is based, is not valid for the case of moderately scattering media. Although it appears that the photon hitting density predictions converge with the cFAMC predictions at depths $z>3{\ell }^{\star }$, this is in fact not the case, and the predictions diverge at larger depths. This divergence leads to an overprediction relative to the cFAMC results and is consistent with fluence predictions in moderately scattering media.³⁷ These results also demonstrate the effectiveness of using oblique detection to enhance the sensitivity to superficial tissues regions. In fact, the comparison of Fig. 7(f) with Fig. 7(c) shows that the peak absorption sensitivity in the superficial tissue region predicted using fine angular discretization is enhanced nearly twofold even when using ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$.

We conclude by examining the absorption sensitivity results for moderately scattering media at a source-detector separation ${\rho }_{\mathrm{sds}}={\ell }^{\star }$ in Fig. 8. Similar to the ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$ case, Fig. 8 shows that the use of no angular discretization when coupling the forward-adjoint light fields consistently provides incorrect sensitivity distributions. Likewise, the use of coarse angular discretization improves the calculations but remains inaccurate for all locations. Moreover, the resulting depth-dependent sensitivity distributions are inaccurate regardless of detector orientation. Figures 8(c) and 8(f) provide results that display improvements when using a moderate level of angular discretization $(\mu ,\varphi )=(8,16)$ but still overpredicts the results relative to those computed using fine angular discretization at superficial depths $z\lesssim 1.5{\ell }^{\star }$. Moreover, the inaccuracies in using the photon hitting density are exacerbated for this shorter source-detector separation and again did not converge with cFAMC computations even at distal locations beyond the ROI. The differences in the results obtained using moderate and fine angular discretizations in Fig. 8(f) are amplified when using oblique detection as compared to normal detection shown in Fig. 8(c). Furthermore, similar to the ${\rho }_{\mathrm{sds}}=3{\ell }^{\star }$ case, the oblique detector is nearly twice as sensitive to the superficial region of the moderately scattering turbid medium, as seen by comparison of the peak values of the depth-dependent absorption sensitivity distributions.

Fig. 8.

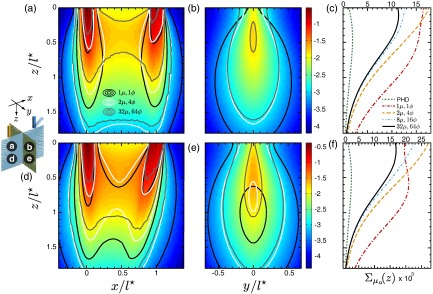
Spatially resolved absorption sensitivity distributions are displayed on a ${\mathrm{Log}}_{10}$ scale for moderately scattering media ${\mu }_s^{\prime }/{\mu }_a=1$ with ${\rho }_{\mathrm{sds}}={\ell }^{\star }$ for $\alpha =0\mathrm{deg}$ (a–c) and $\alpha =30\mathrm{deg}$ (d–f). Distributions are displayed for the $x\text{-}z$ plane at $y=0$ (a, d) and the $y\text{-}z$ plane at $x={\rho }_{\mathrm{sds}}/2$ (b, e), where the colormap provides the results obtained using fine angular discretization. The corresponding depth-dependent cumulative absorption sensitivity is plotted for the four angular discretization cases and the PHD (c, f).

5.3. Relevance of Coupled Forward-Adjoint Monte Carlo and Applications

Using our cFAMC framework, we have provided absorption sensitivity distributions computed using various levels of angular discretization for a homogeneous tissue sample. However, it is important to note that the proposed cFAMC framework can be applied to heterogeneous tissues with arbitrary boundaries. These results display the importance of angular discretization to obtain accurate predictions of coupled forward-adjoint light fields. Thus, accounting for the detailed directional dependence of light transport is critical when using optical diagnostic methods to probe mesoscopic tissue volumes. Such considerations are particularly important for moderately scattering media, that is, when probing tissues using visible wavelengths, as the tissue is less effective in randomizing the direction of light transport. This has the effect of extending the spatial region over which detailed consideration of directional light transport is required. Furthermore, the use of fine angular discretization may be insufficient in certain spatial locations. Future work will examine the use of spatially varying angular discretization schemes and/or adopt other means of angular discretization³⁸ as a means to improve the computational efficiency and accuracy. Moreover, the underlying computational efficiency of the cFAMC methods may be enhanced further by adopting advanced methods for photon propagation and tallying such as next event estimation.^39,40

Our cFAMC framework is also of value to analyze light transport over macroscopic spatial scales, even though the need for angular discretization may be limited to locations near boundaries and collimated sources/detectors. For example, the use of the ROI in which to compute and couple forward-adjoint light fields, as well as our novel method for the tracking and weight deposition of the photon paths within the ROI, provides computational efficiencies regardless of the transport domain under consideration.

The accurate computation of the absorption sensitivity distributions is not only important in the resolution of inverse problems but can also be used to assess the efficacy of different measurement configurations and/or wavelengths to probe localized tissue regions. For example, the determination of the spectral variation of sensitivity functions can identify those wavelengths that give the best contrast in their sensitivity distribution and in turn aid the a priori design of measurements for functional optical imaging. For example, such a tool could provide enhanced optical specificity in high-density optical tomography,⁴¹ while reducing the number of source-detector pairs needed for the tomographic inverse problem.

While consideration of the absorption sensitivity has dominated the field of diffuse optical tomography,¹⁴ the cFAMC approach can also provide a means to efficiently compute the scattering sensitivity and enable an evaluation of a given source-detector configuration to detect structural modifications of the cellular and extra cellular compositions.¹⁴ Furthermore, higher order light transport approximations that provide more accurate assessments than the diffusion approximation have been shown to enhance the tomographic reconstruction of absorptions and scattering⁴² and bioluminescence.⁴³ Thus, the transport rigorous approach that cFAMC offers can provide important improvements for these optical imaging modalities.

6. Conclusion

We have introduced a cFAMC framework to evaluate the spatially resolved absorption sensitivity distribution within turbid media for various source-detector configurations. This framework is designed to efficiently compute both spatially and angularly resolved light fields, the radiances, for both the forward-adjoint transport problems within a ROI. We applied this framework to study the effects of angular discretization for coupled light transport problems with source-detector separations ranging from a transport mean free path, ${\ell }^{\star }$ to $3{\ell }^{\star }$ in both highly and moderately scattering media. Furthermore, both normally and obliquely orientated detectors were examined to analyze the effects of angular anisotropy on photon transport between source and detector.

Our results demonstrate that the assumption of quasi-isotropic light fields for evaluating the spatially resolved sensitivity distributions can produce poor quality results. For most circumstances considered here, the use of a minimally anisotropic mesh of the radiant fields provides inaccurate predictions. The cFAMC framework provides a mechanism to study the directionally dependent transport of light in mesoscopic turbid systems, which has importance in measurement design and inverse problems. Thus, this approach provides sensitivity distributions in the mesoscopic regime that cannot be addressed using classical diffusion-based approaches.^18,19 Moreover, the use of both forward-adjoint radiances provides a more efficient approach in terms of computational time in relation to conventional MC simulations.²¹

Biographies

Adam R. Gardner received his BS and MS degrees in chemical engineering from the University of Nevada, Reno, and the PhD degree in chemical engineering from the University of California, Irvine. He is currently a postdoctoral scholar at the Beckman Laser Institute at UCI. His research encompasses the development of advanced radiative transport modeling and computation approaches and their application for quantitative tissue assessment.

Carole K. Hayakawa received her BA degree in applied mathematics from UC Berkeley, an MA degree in mathematics from UCLA, and a PhD degree in mathematics from Claremont Graduate University. Her research interests focus on the development of novel mathematical approaches to the solution and analysis of radiative transport problems connected to optical diagnostics and imaging in biomedicine.

Vasan Venugopalan received his BS degree in mechanical engineering from UC Berkeley, and SM and ScD degrees in mechanical engineering from MIT. He held postdoctoral positions at the Wellman Laboratories of Photomedicine, Harvard Medical School, and Princeton University. He is currently professor of chemical engineering, biomedical engineering, mechanical engineering, and surgery at the University of California, Irvine. His research examines laser-induced thermal, mechanical, and radiative transport processes relevant to medical diagnostics, therapeutics, and biotechnology.