A DCM for resting state fMRI

Abstract

This technical note introduces a dynamic causal model (DCM) for resting state fMRI time series based upon observed functional connectivity—as measured by the cross spectra among different brain regions. This DCM is based upon a deterministic model that generates predicted crossed spectra from a biophysically plausible model of coupled neuronal fluctuations in a distributed neuronal network or graph. Effectively, the resulting scheme finds the best effective connectivity among hidden neuronal states that explains the observed functional connectivity among haemodynamic responses. This is because the cross spectra contain all the information about (second order) statistical dependencies among regional dynamics. In this note, we focus on describing the model, its relationship to existing measures of directed and undirected functional connectivity and establishing its face validity using simulations. In subsequent papers, we will evaluate its construct validity in relation to stochastic DCM and its predictive validity in Parkinson's and Huntington's disease.

Highlights

• •This paper describes an efficient estimation of resting state connectivity.
• •The scheme is based on fitting observed complex fMRI cross spectra.
• •This spectral DCM grandfathers functional connectivity and Granger causality.

Introduction

The use of resting state fMRI (Biswal, Van Kylen and Hyde, 1997; Biswal et al., 1995) is now widespread (Damoiseaux and Greicius, 2009); particularly in attempts to characterise differences in functional connectivity between subject groups (or different brain states). Functional connectivity is defined as the statistical dependencies among observed neurophysiological responses. Although functional connectivity can be very useful for describing abnormal patterns of distributed activity, it cannot be used to infer the underlying effective connectivity—defined as the influence one neuronal system exerts over another (Friston, Harrison and Penny, 2003). This technical note introduces a dynamic causal model (DCM) for identifying and quantifying the effective connectivity that causes functional connectivity. This particular DCM has been used for some time in electrophysiology (Friston et al., 2012; Moran et al., 2011) and uses a neuronally plausible model of coupled neuronal states to generate the complex cross spectra among observed responses. A nice discussion of biophysical models in this context can be found in (Robinson et al. 2004). Here, we formulate the approach for resting state fMRI, with the aim of facilitating group comparisons in terms of (directed) effective connectivity.

Our motivation for developing this DCM was twofold: recently, we introduced stochastic DCM that, in principle, is well suited for characterising effective connectivity in resting state fMRI studies (Li et al., 2011). In stochastic DCM, both the effective connectivity and hidden neuronal fluctuations ‘driving’ the system are estimated from observed haemodynamic responses. This is a difficult inversion or deconvolution problem that is computationally intensive (Kloeden and Platen, 1999), because it makes minimal assumptions about the neuronal fluctuations. Furthermore, when used to characterise group differences in effective connectivity there is a potential problem: the groups could differ in terms of their effective connectivity, the form or amplitude of endogenous fluctuations, or both. For example, subjects with Parkinson's disease may have exactly the same effective connectivity as control subjects but may have neuromodulatory differences in the amplitudes or time constants of endogenous neuronal activity. An obvious candidate here is differences in the fluctuation of beta power in the cortico-basal ganglia-thalamic loops. If these differences exist, it would be nice to jointly estimate the effective connectivity and autocorrelations of neuronal fluctuations and test for differences in connectivity, neuronal fluctuations or both.

Both of these potential problems – namely, an unconstrained inversion problem and potential differences in neuronal activity – can be resolved by assuming some (parameterised) form for endogenous fluctuations. This assumption would afford constraints on the model inversion and provide parameters encoding endogenous activity that could be compared between groups. These considerations speak to the assumptions that underlie models of steady-state responses; in which variables can be characterised in terms of their correlation functions of time—or spectral densities over frequencies. In other words, instead of trying to estimate time varying fluctuations in neuronal states producing observed fMRI data, one can try to estimate the parameters of their cross correlation functions or cross spectra. This effectively means replacing the original time series with their second-order statistics (e.g., cross spectra), under stationarity assumptions.

The advantage of doing this is that the problem of estimating hidden neuronal states disappears and is replaced by the problem of estimating the spectral density of neuronal fluctuations (and observation noise). Technically speaking this means that the DCM ceases to be stochastic and becomes deterministic, because there are no unknown states to estimate. This greatly increases the computational efficiency, enabling the estimation of model parameters in seconds to minutes, as opposed to the minutes to hours required by stochastic schemes. Furthermore, the resulting parameter estimates include both the effective connectivity and potentially useful measures of endogenous neuronal fluctuations—that can be compared between groups. The disadvantage of this deterministic DCM for cross spectra rests on the stationarity assumption, which precludes state or time-dependent changes in effective connectivity (Breakspear, 2004). In other words, unlike deterministic DCM for time series, one cannot model – in a simple way – changes in effective connectivity caused by experimental manipulations or other time sensitive factors. Having said this, most applications of resting state fMRI are primarily interested in group differences—as opposed to state or set-dependent differences that are usually modelled with time-dependent (e.g., bilinear) changes in coupling. In short, DCM described below provides a simple and efficient way of estimating the effective connectivity from resting state fMRI time series, using observed cross spectra under stationarity assumptions. We anticipate that the resulting parameter estimates – for both effective connectivity and endogenous fluctuations – may be useful as summary statistics for subsequent group comparisons.

Cross spectra provide an ideal second-order statistic to model, as they are a generalisation of functional connectivity. In other words, the dynamic causal model of effective connectivity is trying to explain functional connectivity in an explicit and direct way. The cross spectra are measures of functional connectivity because their (inverse) Fourier transforms correspond to cross correlation functions—and the cross correlation function at zero lag is the conventional measure of functional connectivity used in the vast majority of studies. In other words, the cross correlation functions or cross spectra represent generalised measures of functional connectivity that retain a temporal aspect—and preserve information on directed functional connectivity, which is exploited using temporal precedence representations; for example, multivariate autoregressive models (Harrison, Penny and Friston, 2003) and Granger causality (Goebel et al., 2003).

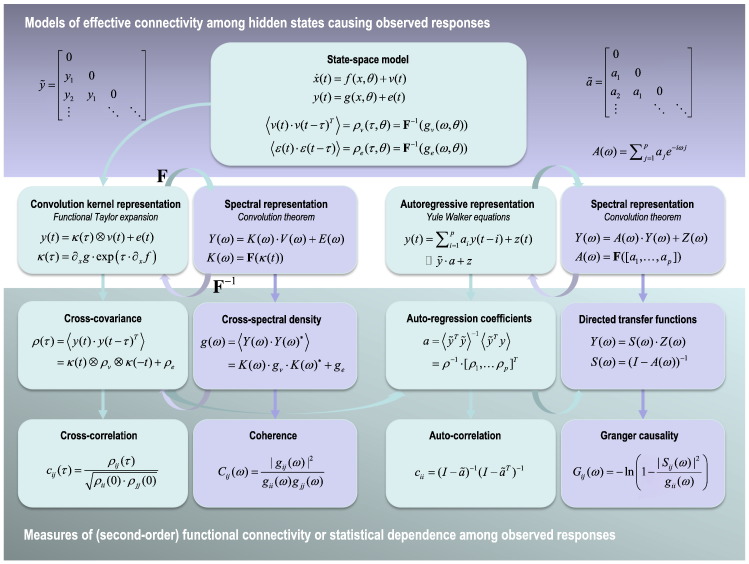
Fig. 1 tries to make this point schematically by showing how various measures of statistical dependencies (functional connectivity) are interrelated—and how they can be generated from a dynamic causal model. This schematic serves to contextualise different measures of functional connectivity and how they arise from (state space) models of effective connectivity. Although it may look complicated, it contains most descriptive measures of functional connectivity that have been used in fMRI. These include the correlation coefficient (the value of the cross correlation function at zero lag), coherence and (Geweke) Granger causality (Geweke, 1982). These measures can be regarded as standardised (second-order) statistics based upon the cross covariance function, the cross spectral density and the directed transfer functions respectively. In turn, these are determined by the first order (Volterra) kernels, their associated transfer functions and multivariate autoregression coefficients. Crucially, all these representations can be generated from the underlying state space model used by DCM. There are a number of key dichotomies implicit in Fig. 1, which we now review:

• •The first is the distinction between the state space model (upper panel)—that refers to hidden or system states, and representations of dependencies among observations (lower panels)—that do not refer to hidden states. This is important because although one can generate the dependencies among observations from the state space model, one cannot do that converse. In other words, it is not possible to derive the parameters of the state space model (e.g., effective connectivity) from transfer functions or autoregression coefficients. This is why one needs a state space model to estimate effective connectivity or – equivalently – why effective connectivity is quintessentially model based.
• •The second dichotomy is between models of the variables per se (upper two rows) and their second order statistics (lower two rows). For example, convolution and auto regressive representations can be used to generate time series, while cross covariance functions and autoregression coefficients describe the second order behaviour of time series. This is important because this second-order behaviour can be evaluated directly from observed time series—this is the most common way of measuring functional connectivity in terms of (second order) statistical dependencies.
• •The third dichotomy is between time and frequency representations. For example, the (first order Volterra) kernels in the convolution formulation are the (inverse) Fourier transform of the transfer functions in frequency space (and vice versa). Similarly, the directed transfer functions of the autoregressive formulation are based upon the (inverse) Fourier transforms of the autoregression coefficients. This is important because the Fourier transform is a linear operator, which means that exactly the same information is contained in the time and frequency domain representations.
• •The fourth distinction is between representations that refer explicitly to random (state and observation) noise and autoregressive representations that do not. For example, notice that the cross covariance functions of the data depend upon the cross covariance functions of state and observation noise. Conversely, the autoregression formulation only invokes (unit normal) innovations. In the current setting, autoregressive representations are not regarded as models, but simply ways of representing dependencies among observations. This is because (haemodynamic) responses do not cause responses—hidden (neuronal) states cause responses.
• •Crucially, all of the formulations of statistical dependencies contain information about temporal lags (in time) or phase delays (in frequency). This means that, in principle, all measures are directed – in the sense that the dependencies from one region to another are distinct from the dependencies in the other direction. However, only the autoregressive formulation provides directed measures of dependency—in terms of directed transfer functions or Granger causality. This is because the cross covariance and spectral density functions between two time series are antisymmetric. The autoregressive formulation can break this (anti) symmetry because it precludes instantaneous dependencies by conditioning the current response on past responses. Note that Granger causality is – in this setting – a measure of directed functional connectivity (Friston, Moran and Seth, 2013). This means that Granger causality (or the underlying autoregression coefficients) reflects directed statistical dependencies—such that two regions can have strong autoregression coefficients or Granger causality in the absence of a direct effective connection.
• •Finally, there is a distinction between (second order) effect sizes in the upper row of dependency measures and their standardised equivalents in the lower row. For example, the coherence is simply the amplitude of the cross spectral density normalised by the auto spectra of the two regions in question. Similarly, one can think of Granger causality as a standardised measure of the directed transfer function (normalised by the auto spectrum of the target region). This can be interpreted as the variance explained in the target by the history of the source, at a particular frequency.

Fig. 1.

This schematic illustrates the relationship between different formulations of dependencies among multivariate time series—of the sort used in fMRI. The upper panel illustrates the form of a state space model that comprises differential equations coupling hidden states (first equation) and an observer equation mapping hidden states x(t) to observed responses y(t) (second equation). Crucially, both the motion of hidden states and responses are subject to random fluctuations, also known as state v(t) and observation e(t) noise. The form of these fluctuations are modelled in terms of their cross covariance functions ρ(t) of time t or cross spectral density functions g(ω) of radial frequency ω, as shown in the lower equations. Given this state space model and its parameters θ (which include effective connectivity) one can now parameterise a series of representations of statistical dependencies among successive responses as shown in the second row. These include convolution and autoregressive formulations shown on the left and right respectively—in either time (light green) or frequency (light purple) space. The mapping between these representations rests on the Fourier transform, denoted by F and its inverse. For example, given the equations of motion and observer function of the state space model, one can compute the convolution kernels applied to state noise that produce changes in the response variables. This allows one to express observed responses in terms of a convolution of hidden fluctuations and observation noise. The Fourier transform of these convolution kernels κ(t) is called a transfer function K(ω). Note that the transfer function in the convolution formulation K(ω) maps from fluctuations in hidden states to response variables, whereas the directed transfer function in the autoregressive formulation S(ω) maps directly among different response variables. These representations can be used to generate second order statistics or measures that summarise the dependencies as shown in the third row; for example, cross covariance functions and cross spectra. The normalised or standardised variants of these measures are shown in the lower row and include the cross correlation function (in time) or coherence (in frequency). The equations show how the various representations can be derived from each other, where Fourier transforms of variables are (generally) in uppercase such that F(x(t)) = X(ω). All variables are either vector or matrix functions of time or frequency. For simplicity, the autoregressive formulations shown in discrete form for the univariate case (the same algebra applies to the multivariate case but the notation becomes more complicated). Here, z(t) is a unit normal innovation. Finally, note the Granger causality is only appropriate for bivariate time series. In this figure, ⊗ corresponds to a convolution operator, * denotes the complex conjugate transpose, 〈⋅〉 denotes expectation and ~ denotes discrete time lagged forms (as shown in the upper inserts). This particular layout of models and associated sample statistics in this figure is greatly simplified and is just meant to contextualise commonly used measures in fMRI functional connectivity research. The relationships among the sample statistics and models could be nuanced in many ways; for example, there are continuous time formulations of autoregressive models that are closely related to formulations in terms of stochastic differential equations. Furthermore, discrete time models are not necessarily linear—we have focused on linear models because the cross spectra and covariance functions (second order statistics) are derived easily under local linearity assumptions (Robinson et al. 2004).

In summary, given a state space model, one can predict or generate the functional connectivity that one would observe, in terms of cross covariance functions, complex cross spectra or autoregression coefficients (where the latter can be derived in a straightforward way from the former using the Yule–Walker formulation). In principle, this means that one could either use the sampled cross covariance functions or cross spectra as data features. It would also be possible to use the least-squares estimate of the autoregression coefficients – or indeed Granger causality – as data features to estimate the underlying effective connectivity. We have tried various combinations and find that the most accurate estimates are obtained using the cross covariance functions and complex cross spectra. This is the scheme described below and can be regarded as a generalisation of the deterministic scheme described in Di and Biswal (2013). In this previous deterministic approach to resting state fMRI, endogenous fluctuations were modelled with a Fourier basis set, using the conventional first-order data features. Here, we consider a more general form for endogenous fluctuations, focusing on second-order data features.

This technical note is divided into four sections. The first describes the generative model for resting state fMRI. This is identical to the deterministic DCM used for conventional fMRI time series analysis; however, it is used here to predict the sample (second-order) cross spectra, as opposed to the (first-order) time series themselves. The second section presents a provisional face validation of the scheme, using simulated time series and ensuing cross spectra to show that the true effective connectivity can be recovered (within certain confidence intervals). The third section repeats these simulations to see how the accuracy of the effective connectivity estimates depends upon the length of the time series. This section includes a simulated group comparison to evaluate the comparative performance of Bayesian and classical inference about group differences in effective connectivity. The final section illustrates the application of DCM for cross spectra to a standard real dataset, with a special focus on the asymmetry between forward and backward connections in the visual hierarchy.

The generative model

In this section, we described the generative model used by DCM for cross spectra and comment briefly on the inversion of these models. Dynamic causal modelling is essentially the Bayesian inversion and selection of state space models formulated in continuous time. In this section, we focus on the neuronal part of the state space model and how it provides a likelihood model for observed cross spectra (and cross covariance functions).

DCM for fMRI rests on a generative model with two components. The first is a neuronal model describing interactions in a distributed network of neuronal populations. The second maps neuronal activity to observed haemodynamic responses (Buxton, Wong and Frank, 1998; Friston, Harrison and Penny, 2003). Here, we focus on the neuronal model, because the haemodynamic part is exactly the same as described previously (Stephan et al., 2007). The basic form of the model is a linear stochastic or, strictly speaking, random differential equation that corresponds to the equations of motion in the state space model of Fig. 1:

$$\dot{x}\left(t\right)=A\cdot x\left(t\right)+v\left(t\right).$$ (1)

Here, x(t) = [x₁(t), …, x_n(t)]^T is a column vector of hidden neuronal states for n regions, whose motion depends upon the states of other regions and some endogenous fluctuations v(t). Here, there is only one hidden state for each region—although the current scheme has been implemented to accommodate multistate models (Marreiros, Kiebel and Friston, 2008). In DCM for fMRI, these hidden states are abstract representations of neuronal activity. They correspond to the amplitude of macroscopic variables or order parameters summarising the dynamics of large neuronal populations. Although the above equation may look implausibly simple, it can be motivated in a fairly straightforward way from basic principles (Friston et al., 2011); for example, the centre manifold theorem (Carr, 1981) and the slaving principle (Ginzburg and Landau, 1950; Haken, 1983) that apply to all coupled dynamical systems:

In brief, these hidden states can be regarded as encoding the slowly fluctuating amplitude of activity modes (e.g., oscillations). Conversely, the endogenous activity represents fast fluctuations about this amplitude, where the implicit separation of temporal scales is mandated by the slaving principle. Technically, endogenous fluctuations model the dynamics attributable to fast (stable) modes that become enslaved by the slow (unstable) modes, which determine macroscopic behaviour. In other words, the collective activity of coupled neuronal systems becomes organised into slow patterns, about which fast dissipative activity fluctuates. One important insight from this formulation is that the time-constants of macroscopic hidden states are much slower than the microscopic neuronal time constants (e.g., effective membrane time constants). For example, fluctuations in the characteristic frequency of each mode may be much slower (e.g., 100–10,000 ms) than the dynamics of the fast modes (e.g., 10 to 100 ms). This is important because it suggests that priors on the rate constants or effective connectivity parameters A ⊂ θ should anticipate slow dynamics. Typically, effective connectivity in fMRI falls in the range of 0.1 Hz to 1 Hz for non-trivial connections. Heuristically, these rate constants can be thought of as governing changes in the amplitude of fast (e.g., gamma band) activity (Brown, Moehlis and Holmes, 2004), which waxes and wanes on the order of seconds (Breakspear and Stam, 2005).

To equip the model with haemodynamics, we simply supplement the neuronal states above with haemodynamics states – like blood flow and deoxyhemoglobin content – using the appropriate equations of motion. The mapping to measured BOLD responses is completed with a (nonlinear) observer function, as in the upper panel of Fig. 1. This means that neuronal and haemodynamic states are treated on an equal footing, enabling the joint estimation of (global) effective connectivity and (local) haemodynamic parameters. In the time domain, haemodynamics effectively smooth the underlying neuronal fluctuations; while in the frequency or spectral domain they suppress high frequencies—by modulating the transfer function from neuronal activity to BOLD measurements. By absorbing the haemodynamics into transfer functions, we are implicitly using a linear approximation. In other words, we assume that the haemodynamic response function does not change with neuronal or haemodynamic states. Although this allows for regional variations in haemodynamics, it precludes a nonlinear modelling of haemodynamic saturation and refractoriness. However, this is exactly the same approximation used in conventional linear convolution models of fMRI time series.

To complete the specification of the likelihood model, we have to parameterise the nature of the endogenous fluctuations (and observation noise). The most parsimonious and general form, in this setting, is a power law or scale free form that can be motivated from a large body of work on noise in fMRI (e.g., Bullmore et al., 2001) and underlying neuronal activity (Shin and Kim, 2006; Stam and de Bruin, 2004):

$$\begin{array}{l}{g}_v\left(\omega ,\theta \right)={\alpha }_v{\omega }^{-{\beta }_v}+g_u\left(\omega ,\theta \right)\\ g_e\left(\omega ,\theta \right)={\alpha }_e{\omega }^{-{\beta }_e}.\end{array}$$ (2)

Under this model, the parameters control (α,β) ⊂ θ the amplitudes and exponents of the spectral density where, for example, the spectral density of white noise is flat β = 0, while pink noise has β = 1, and brown noise has β = 2. Autoregressive processes produce a similar form of coloured noise (see Fig. 1). Note that the endogenous fluctuations have an extra term. This models any spectral contribution from exogenous or experimental input u(t) that is scaled by an exogenous input parameter C ⊂ θ

$$g_u\left(\omega ,\theta \right)=\mathbf{F}\left(C\cdot u\left(t\right)\right)$$ (3)

where F(⋅) represents the Fourier transform. This allows us to accommodate designed or deterministic inputs and allows fluctuations that are externally driven to contribute to the observed cross spectra. We will see an example of this in the last section.

To fully specify the likelihood model, we now have to consider the probability of observing some data features given the model parameters θ = (A,C,α,β, …). These parameters can be used to generate the expected cross spectra g(ω,θ) = K(ω) ⋅ g(ω,θ)_v ⋅ K(ω)^∗ + g(ω,θ)_e using the equations in Fig. 1. However, the sample cross spectra g(ω) are derived from a finite realisation or time series and will differ from the expected values. In our current implementation, we assume that this difference corresponds to additive Gaussian sampling error such that:

$$g\left(\omega \right)=g\left(\omega ,\theta \right)+N\left(\omega \right).$$ (4)

Note that the sampling error N(ω) is distinct from the observation error E(ω) = F(e(t)) in Fig. 1. The observation error is generated by thermal and physiological noise processes during acquisition of the data and contributes to the observed spectra. Conversely, the sampling error models deviation of the observed spectra from their expected values under a particular set of parameters (which includes the spectra of observation noise). Clearly, the sampling error will be correlated over frequencies and this has to be accommodated in the likelihood model. We assume that the sample error has correlations over frequencies that correspond to an autoregressive process with a coefficient of one half.

By specifying the probabilistic relationship between the sample and expected cross spectra, one can evaluate the likelihood or the probability of getting some spectral observations given the parameters p(g(ω)|θ). The full generative model p(g(ω), θ) = p(g(ω)|θ)p(θ|m) is then completed by specifying prior beliefs p(θ|m) about the parameters, which define a particular model m. Because many of the parameters in these models are nonnegative (scale) parameters, we generally defined these priors as Gaussian distributions over ln(θ). Table 1 lists the priors used in DCM for fMRI cross spectra, most of which are exactly the same as used in other DCM's for fMRI (Stephan et al., 2007).

Table 1.

Priors on parameters (haemodynamic priors have been omitted for simplicity).

Parameter	Description	Prior mean	Prior variance
ln(− Aii)	Inhibitory self connections	$ln\frac{1}{2}$	$\frac{1}{256}$
Aij	Extrinsic effective connectivity	$\frac{1}{128}$	$\frac{1}{64}$
C	Exogenous input scaling	0	1
ln(α)	Amplitude of fluctuations	0	$\frac{1}{64}$
ln(β)	Exponent of fluctuations	0	$\frac{1}{64}$

Equipped with this generative model one can now invert and fit any observed cross spectra using standard variational Bayesian techniques (Beal, 2003). In our implementations we use Variational Laplace (Friston et al., 2007) to evaluate model evidence p(g(ω)|m) and the posterior density over model parameters p(θ|g(ω), m) in the usual way. In practice, we actually use both the cross spectral density and the cross covariance functions as data features, where the cross spectra are complex valued. Bayesian model inversion of nonlinear models of complex data follows exactly the same calculus as for real valued data—as shown in our previous treatment of DCM for complex cross spectra in electrophysiology (Friston et al., 2012).

In this setting, sample cross spectra and cross covariance functions can be regarded as nonlinear transformations of the original time series data that are sensitive to variations in model parameters that cause changes in slow and fast fluctuations respectively. These transformations are non-linear because sample spectra and covariances are second-order data features—that rely upon the squared values of the original data. Conceptually, converting the time series data into cross spectra is not dissimilar from any other nonlinear data transformation—like the log transformation of (nonnegative) reaction times in psychophysics. These transformations are chosen to make the model assumptions as valid as possible and to retain the data features that best inform parameter estimation.

In the examples below, sample cross spectra were estimated using a fourth order autoregressive model to ensure smooth spectral estimates—of the sort produced by the generative model. A fourth order scheme was chosen because this (relatively low) order minimised conditional uncertainty about parameter estimates—using the sorts of time series that we typically analyse. A low order autoregressive scheme produces fairly smooth sample cross spectra, of the sort predicted by the generative model. The frequencies considered ranged from $\frac{1}{128}$ Hz to the Nyquist frequency (half the sampling rate or $\frac{1}{2\cdot \mathit{TR}}$ Hz) in 64 evenly spaced frequency bins. This completes the description of the generative model for fMRI cross spectra and its inversion. Compared to stochastic DCM, the inversion of DCM for cross spectra is computationally efficient – taking a second or so per iteration – and generally converging in about 16 to 64 iterations. The iteration time scales roughly quadratically with the number of regions or nodes, taking a few hundred milliseconds for two nodes and about 30 s for 16 nodes. This also is much faster than standard (deterministic) DCM schemes, because one does not have to solve (integrate) any differential equations. In the next section, we address the accuracy and validity of this model using simulated data.

Simulations and face validity

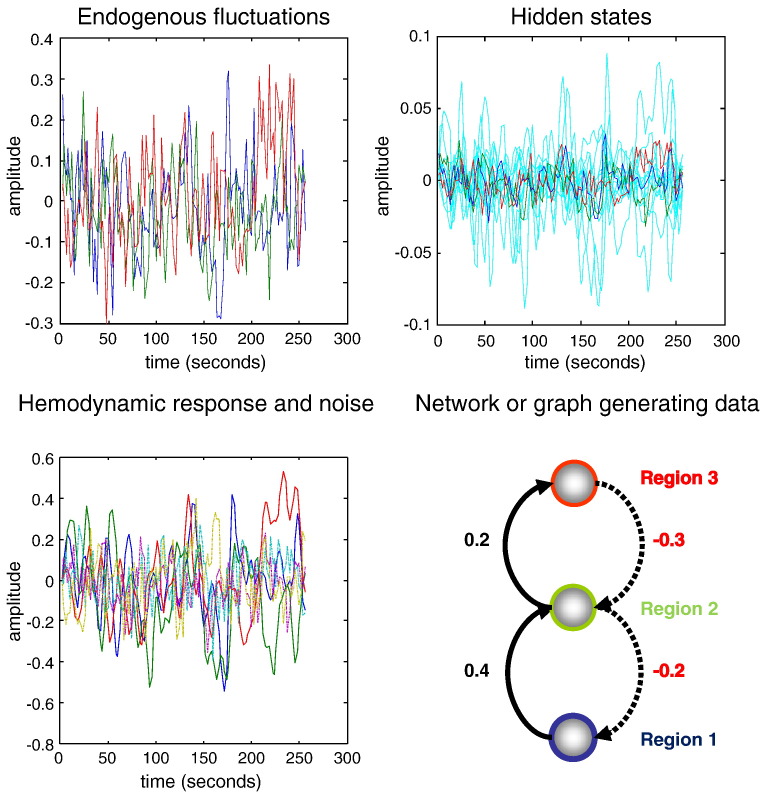
To ensure that the scheme can recover veridical estimates of effective connectivity and implicit neuronal architectures, we generated synthetic fMRI data using Eq. (1) and the usual haemodynamic equations of motion (Stephan et al., 2007). The results of these simulations are shown in Fig. 2 and exhibit the characteristic amplitude and slow fluctuations seen in resting state time-series. This figure shows the response of three regions or nodes, over 256 (2 s) time-bins, to smooth neuronal fluctuations that were generated independently for each region. These endogenous fluctuations (and observation noise) were generated using an AR(1) process with an autoregression coefficient of one half (scaled to a standard deviation of 1/8). These values were chosen to produce a maximum fMRI signal change of about 1%. The upper panels show the endogenous neuronal fluctuations and consequent changes in hidden neuronal and haemodynamic (cyan) states that generate the observed fMRI signal. Note that the fMRI signal is smoother than the underlying neuronal fluctuations, reflecting the low-pass filtering of the haemodynamic response function (that has a characteristic time constant of several seconds). This smoothing is produced by successively smoother fluctuations in haemodynamic states (like blood flow, blood volume and deoxyhemoglobin content) that accumulate fast neuronal fluctuations.

Fig. 2.

This figure summarises the results of simulating fMRI responses to endogenous fluctuations. The simulation was based upon a simple three-region hierarchy, shown on the lower right, with positive effective connectivity (black) in the forward or ascending direction and negative (red) in the backward or descending direction. The three regions were driven by endogenous fluctuations (upper right panel) generated from an AR(1) process within autoregression coefficient of one half. These fluctuations caused distributed variations in neuronal states and consequent changes in haemodynamic states – shown in cyan – (upper right panel), which produce the final fMRI response (lower left panel). These simulations were based upon 256 scans with a repetition time (TR) of two seconds (only the first 256 s are show).

The coupling parameters used for this simulation used a small hierarchy of three areas, with reciprocal connections—producing a directed and cyclic connectivity graph (see Fig. 2):

$$A=\left[\begin{array}{ccc}\hfill -.5\hfill & \hfill -.2\hfill & \hfill 0\hfill \\ \hfill +.4\hfill & \hfill -.5\hfill & \hfill -.3\hfill \\ \hfill 0\hfill & \hfill +.2\hfill & \hfill -.5\hfill \end{array}\right].$$ (7)

As often seen in empirical studies, this simulated architecture comprised positive (excitatory) forward connections and negative (inhibitory) backward connections (denoted by solid and broken lines in the figures). The use of positive and negative coupling parameters produces the anti-correlated responses seen between higher and lower nodes (see Fig. 2, lower left panel). The remaining model parameters were set to their usual priors and scaled by a random variate with a standard deviation of about 5%. This simulates regional variation in the haemodynamic response function. The resulting synthetic data were then used for model inversion to produce results of the sort shown in Fig. 3.

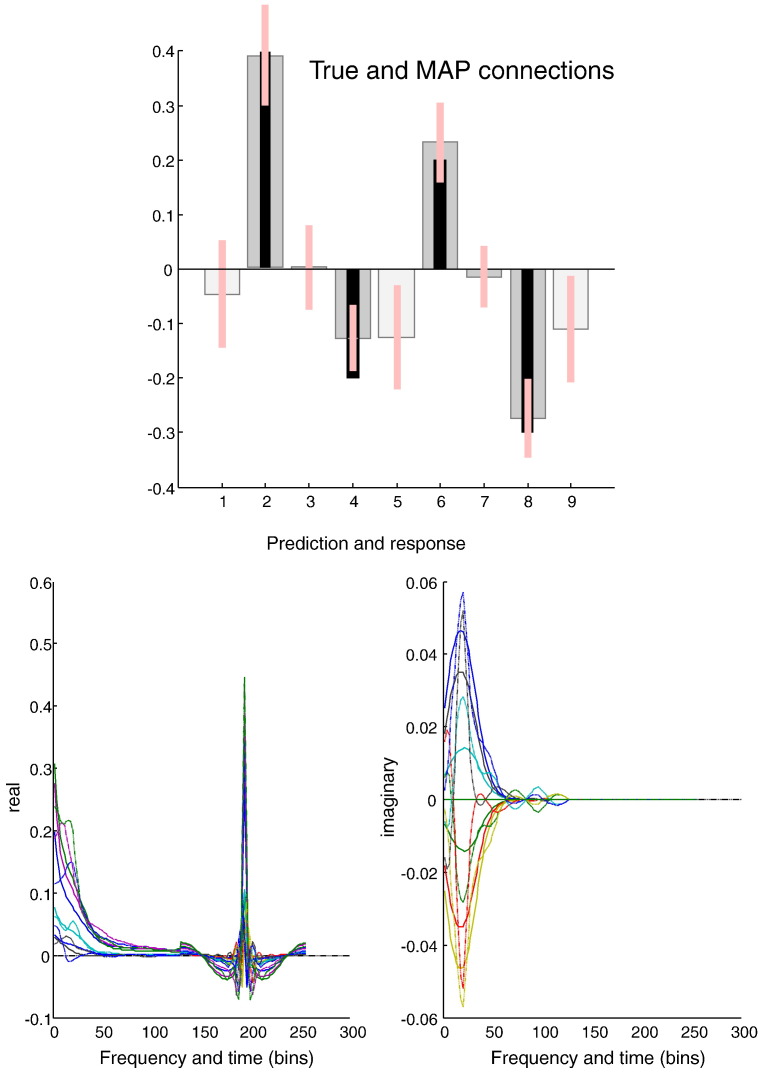
Fig. 3.

This figure reports the results of Bayesian model inversion using data shown in the previous figure. The posterior means (grey bars) and 90% confidence intervals (pink bars) are shown with the true values (black bars) in the upper panel. The light grey bars depict intrinsic or self connections in terms of their log scaling (such that a value of zero corresponds to a scaling of one). The dark grey bars report extrinsic connections measured in Hz. It can be seen that, largely, the true values fall within the Bayesian confidence intervals. These estimates produced predictions (solid lines) of sample cross spectra (dotted lines) and cross covariance functions, shown in the lower panels. The real values are shown on the left and the imaginary values on the right. Imaginary values are produced only by coupling between regions. The first half of these responses and predictions correspond to the cross spectra between all pairs of regions, while the second half are the equivalent cross covariance functions (scaled by a factor of eight).

Fig. 3 shows the posterior density over the effective connectivity parameters (upper panel) in terms of the posterior expectation (grey bar) and 90% confidence intervals (pink bars). For comparison the true values used in the simulations are superimposed (black bars). Happily, the true values of the extrinsic connection strengths fall within the 90% confidence intervals. However, the self connections (light grey) were not estimated so accurately and two areas show a log scaling parameter that is marginally too small. Note from Table 1 that the self connections are modelled as scale parameters, whereas the extrinsic parameters are free to take positive and negative values. This means that the model has underestimated self connectivity by about 10%. This corresponds to an underestimate of self inhibition and may reflect the fact that the sampled cross spectra were generated by a first-order autoregressive process, while the generative model assumes a power law distribution—which is not quite the same (see Fig. 1). The sampled (dotted lines) and predicted (solid lines) cross spectra from this example can be seen in the lower panel of Fig. 3. The agreement is self evident, if not perfect. The right and left panels show the imaginary and real parts of the complex cross spectra, superimposed for all pairs of regions. The first half of these functions corresponds to the cross spectra, while the second half corresponds to the cross covariance functions. Note that the cross covariance functions have only real values.

Simulations and accuracy

To assess the accuracy of the inversion and how accuracy depends upon the amount of data, we repeated the above simulations using time series of 128 to 1024 scans. A typical resting state fMRI experiment with a repetition time of two seconds will provide 180 scans after six min. For each run length, we performed 32 simulations using the same set of parameters as above. To score the quality of the inversions, we used the root mean square (RMS) difference between the posterior expectations and the true values of the extrinsic connectivity parameters. As noted above, a typical nontrivial effective connectivity for fMRI is about 0.1 Hz. Interestingly, this is about the same magnitude as the confidence intervals seen in Fig. 3. This means, that one would be hoping to find a RMS estimation error around 0.1 Hz or less.

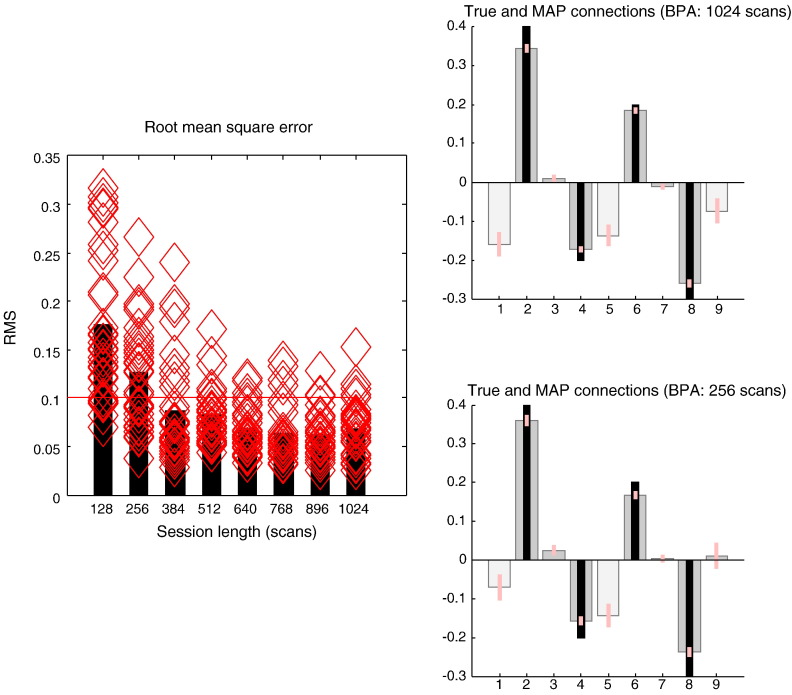
Fig. 4 shows the results of these simulations in terms of the individual RMS error for each analysis (red diamonds) and the mean (black bars) as a function of run length. It is clear that increasing the number of scans improves accuracy, which becomes acceptable after about 512 scans. At this point, the RMS error is about 0.08 Hz, with the majority of simulations falling below our heuristic threshold of 0.1 Hz. With a repetition time of 2 s, this corresponds to a run of about 17 min, which is much longer than people typically acquire. Having said this, pooling the estimates over the 32 simulations for each run length, produces remarkably accurate estimates, as shown in the right panels. These averages were obtained using Bayesian parameter averaging—for each parameter separately: i.e., ignoring posterior correlations that determine the confidence intervals over mixtures or contrasts of parameters. The results show the characteristic shrinkage of Bayesian estimators (towards the prior expectations of zero); however, this is not very severe in relation to the true values. The remarkable thing here is that the Bayesian parameter averages for long runs of 1024 scans and short runs of just 256 scans produce very similar estimates—again with a biased expectation for self connections. This suggests that even short runs of 256 scans (about 8 min) may provide accurate estimates, if averaged over a sufficient number of subjects. Similarly, one might anticipate that differences between two groups could be identified reasonably accurately—even with relatively short runs. To address this sensitivity to group differences we performed a final series of simulations:

Fig. 4.

This figure reports the results of Monte Carlo simulations assessing the accuracy of posterior estimates in terms of root mean square error (RMS) from the true value is. The left panel shows the results of 32 simulations (red diamonds) for different run or session lengths. The average root mean square error (black bars) decreases with increasing run length to reach acceptable (less than 0.1 Hz) levels after about 300 scans. The right panels report the Bayesian parameter averages of the effective connection strengths using the same format as the previous figure. Note that because we have pooled over 32 simulated subjects, the confidence intervals are much smaller. Note also the characteristic shrinkage one obtains with Bayesian estimators. Finally, note the similarity between the Bayesian parameter averages from long runs (upper panel) and shorter runs (lower panel), of 1024 and 256 scans, respectively.

Simulating tests of group differences

We repeated the above simulations with runs of 512 scans; however, for the second 16 of 32 simulations (e.g., subjects), we decreased the negative effective connectivity from the second to the first region. In other words, we increased the inhibitory effective connectivity of the first backward or descending connection and set it to 0.4. To make things more interesting, we also reduced the self inhibition of the target area (the first region) to about 20%, making it more excitable and set it to − 0.2. To see whether these differences could be estimated and detected reliably, we characterised the differences using both Bayesian and classical inference.

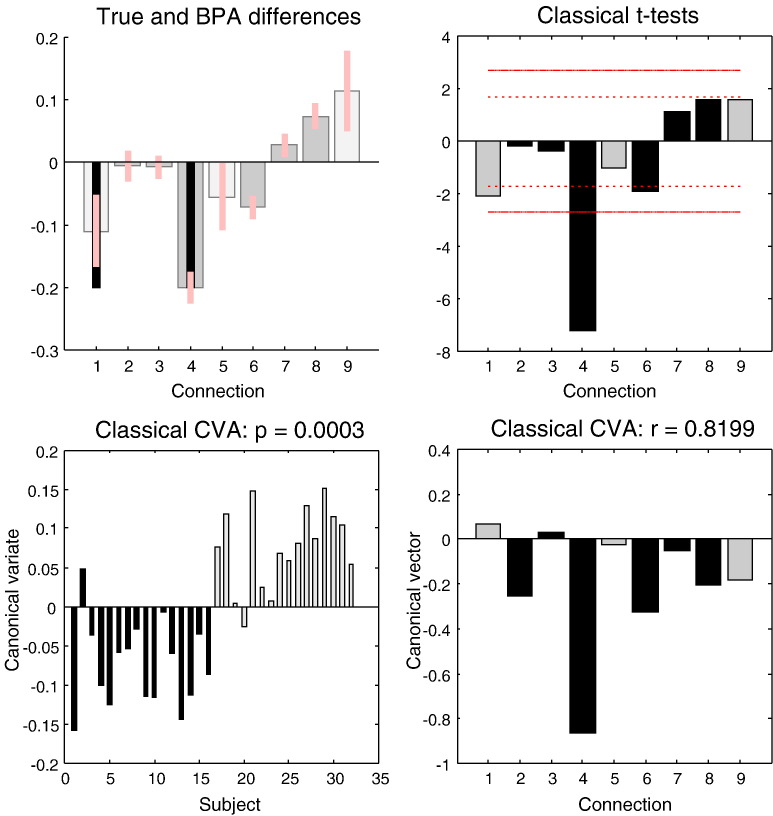
The upper left panel of Fig. 5 shows the Bayesian parameter averages of the differences between the first and second groups of 16 subjects, using the same format as the previous figures. It can be seen that the decrease in the backward connections has been estimated almost perfectly, with a high level of posterior confidence. Conversely, the change in the recurrent or self connection has been underestimated by about 50% with a greater conditional uncertainty. Interestingly, several other changes (of lesser magnitude) have been confidently identified; however, these are less than 0.1 Hz. Note that these are not false positives because we are not declaring that any difference is significant in a classical sense. The same data were then analysed using classical inference, of the sort that is typically applied in group studies using DCM parameter estimates as summary statistics for each subject. We considered univariate and multivariate tests that look for individual differences in effective connectivity or differences in mixtures of connectivity, respectively. The first would be used if one had specific hypotheses about particular connections or classes of connection (e.g., backward connections or intrinsic connections). Conversely, multivariate tests have a more inclusive nature and consider all connections collectively.

Fig. 5.

This figure reports the results of a simulated group comparison study of two groups of 16 subjects (with 512 scans per subject). The upper left panel shows the Bayesian parameter averages of the differences using the same format as previous figures. It can be seen that decreases in the extrinsic backward connections from the second to the first region (fourth parameter) have been estimated accurately, while the decrease in the self connection of the first region is underestimated. The equivalent classical inference—based upon the t-statistic is shown on the upper right. Here the posterior means from each of 32 subjects were used as summary statistics and entered into a series of univariate t-tests to assess differences in group means. The red lines correspond to significance thresholds at a nominal false-positive rate of p = 0.05 corrected (solid lines) and uncorrected (broken lines). The lower panels report the results of a canonical variates analysis (the equivalent multivariate classical inference) using the same summary statistics. The corresponding canonical variate shows reliable group discrimination (lower left), while the canonical vector has correctly identified the greatest effect in the first backward connections (lower right). The effect of group was highly significant with a canonical correlation of r = 0.0198; p = 0.0003.

The upper right panel of Fig. 5 summarises the results of classical univariate tests using the t statistic for a difference in group means. The red lines correspond to thresholds at a nominal level of p = 0.05 corrected (solid) and uncorrected (broken) for the nine tests shown. If we had had a specific hypothesis about the backward connections, then the uncorrected p-value would be extremely significant. In fact, even correcting for all comparisons, it is still very significant. Conversely, no other effective connectivity shows a significant effect at a corrected level—including the self inhibition of the first area. This is consistent with the Bayesian parameter averages, suggesting that it may be easier to detect changes in extrinsic connections than changes in intrinsic or self connections.

Finally, we applied a classical multivariate analysis to test for any differences over all connections between the two groups. The standard multivariate test here is a canonical covariate analysis. Mathematically, this reduces to the Hotelling's T-squared, when testing for a single effect—such as the difference in group means. The results of a canonical covariate analysis include canonical vectors and variates—and their significance. These are shown in the lower panels of Fig. 5 and were extremely significant with p = 0.0003. Note that because there is only one multivariate test, there is no need to correct for multiple comparisons. The canonical variate expresses the degree to which a pattern of differences – encoded by the canonical vector – is expressed in each replication or subject. The lower left panel shows that, with the exception of one subject in each group, the canonical vector was expressed positively in the second group. This vector is shown on the lower right and correctly identifies the decrease in the first backward connection. Again, there is an apparent failure to detect the decrease in the first parameter (the self connection); in fact, it is actually positive in the canonical vector. This may speak to the reduced efficiency for detecting changes in intrinsic connectivity and the effects of correlations among the parameter estimates over subjects (that do not affect the univariate tests above).

In summary, although these simulations suggest that increasing the length of the time series provides progressively more accurate estimates of effective connectivity, it appears that shorter run lengths provide sufficiently efficient estimates to detect nontrivial changes in connectivity between groups; even with relatively small numbers of subjects (here 32).

An empirical illustration

Finally, we illustrate DCM for cross spectra using an empirical dataset that has been used previously to describe developments in dynamic causal modelling and related analyses. We have deliberately chosen an activation study to show that DCM for cross spectra can be applied to conventional studies as well as (design free) resting-state studies. In what follows, we will briefly describe the data used for our analysis and then report the results of their inversion.

Empirical data

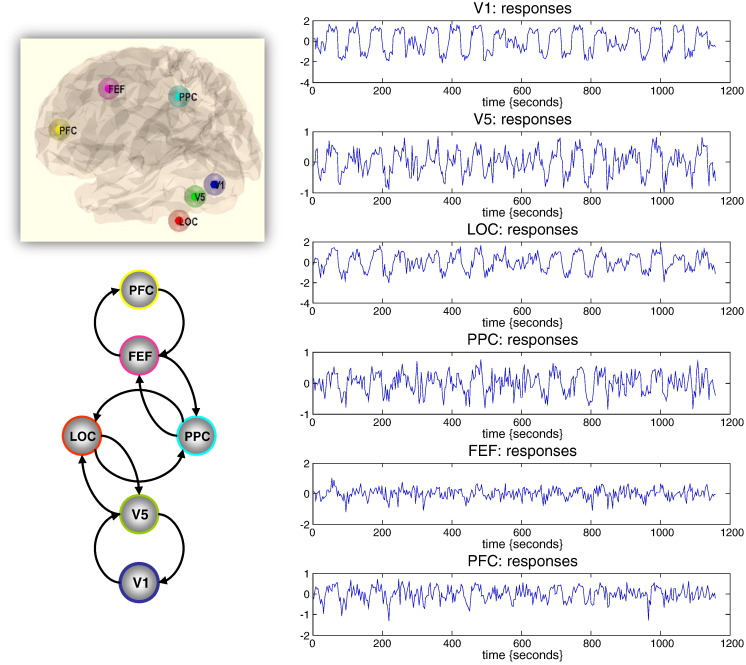
These data were acquired during an attention to visual motion paradigm and have been used previously to illustrate psychophysiological interactions, structural equation modelling, and the inversion of various dynamic causal models. The data were acquired from a normal subject at two Tesla using a Magnetom VISION (Siemens, Erlangen) whole body MRI system, during a visual attention study. Contiguous multi-slice images were obtained with a gradient echo-planar sequence (TE = 40 ms; TR = 3.22 s; matrix size = 64 × 64 × 32, voxel size 3 × 3 × 3 mm). Four consecutive 100 scan sessions were acquired, comprising a sequence of ten scan blocks of five conditions. The first was a dummy condition to allow for magnetic saturation effects. In the second condition, subjects viewed a fixation point at the centre of a screen. In an attention condition, subjects viewed 250 dots moving away from the centre at 4.7 degrees per second and were asked to detect changes in velocity. In a no attention, the subjects were asked simply to view the moving dots. Finally, in a baseline condition, subjects viewed stationary dots. The order of the conditions alternated between fixation and visual stimulation (stationary, no attention, or attention). In all conditions subjects fixated on the centre of the screen. No overt response was required in any condition and there were no actual changes in the speed of the dots. The data were analysed using a conventional SPM analysis using three designed or exogenous inputs (visual input, motion and attention) and the usual confounds. The regions chosen for network analysis were selected in a rather ad hoc fashion and are used here simply to demonstrate procedural details.

Six representative regions were defined as clusters of contiguous voxels surviving an (omnibus) F-test for all effects of interest at p < 0.001 (uncorrected) in the conventional SPM analysis. These regions were chosen to cover a distributed network (of largely association cortex) in the right hemisphere, from visual cortex to frontal eye fields (see Table 2 for details). The activity of each region (node) was summarised with its principal eigenvariate to ensure an optimum weighting of contributions for each voxel with the ROI (see Fig. 6). In this example, one can see evoked responses in visual areas (every 60 s) with a progressive loss of stimulus-bound activity and a hint of attentional modulation and other fluctuations in higher regions.

Table 2.

Regions selected for DCM analysis on the basis of an (Omnibus) SPM of the F-statistic testing for evoked responses. Regions are defined as contiguous voxels in the SPM surviving a threshold of p < 0.001 (uncorrected) within 8 mm of the locations shown. The anatomical designations should not be taken too seriously because the extent of several regions covered more than one cytoarchitectonic area, according to the atlas of Talairach and Tournoux.

Name	Rough designation	Location (mm)	Number of (3 mm3) voxels
V1	Early visual cortex	− 12 − 81 − 6	81
V5	Motion sensitive area	− 45 − 84 − 3	50
LOC	Lateral occipital cortex	− 45 − 69 − 24	39
PPC	Posterior parietal cortex	− 21 − 57 66	43
FEF	Frontal eye fields	− 33 − 6 63	18
PFC	Prefrontal cortex	− 75 − 21 33	39

Fig. 6.

Summary of empirical time series used for the illustrative analysis. The time series (right-hand panels) from six regions show experimental effects of visual motion and attention to visual motion (see main text). These time series are the principal eigenvariates of regions identified using a conventional SPM analysis (upper left insert). These time series we used to invert a DCM with the architecture shown in the lower left panel. See Table 1 for details.

Asymmetric connections and hierarchies

Network analyses using functional connectivity or diffusion weighted MRI data cannot ask whether a connection is larger in one direction relative to another, because they are restricted to the analysis of undirected (simple) graphs. However, here we have the opportunity to address asymmetries in reciprocal connections and ask questions about hierarchical organisation (e.g., Chen et al., 2009). There are many interesting analyses that one could consider, given a weighted (and signed) connectivity or adjacency matrix. Here, we will illustrate a simple analysis of functional asymmetries: Hierarchies are defined by the distinction between forward (bottom-up) and backward (top-down) connections. There are several strands of empirical and theoretical evidence to suggest that, in comparison to forward influences, the net effects of backward connections on their targets are inhibitory (e.g., by recruitment of local lateral connections, Angelucci and Bressloff, 2006; Angelucci and Bullier, 2003). Theoretically, this is consistent with predictive coding, where top-down predictions suppress prediction errors in lower levels of a hierarchy (Bastos et al., 2012). In light of this, one might hypothesise that forward effective connectivity should be positive, while backward effective connectivity should be predominantly inhibitory (negative in this DCM). To address this, we used priors on the extrinsic connectivity to estimate hierarchical forward and backward connections (see Fig. 6). In addition, we allowed the experimental effects of visual input, motion and attention to contribute to the neuronal fluctuations (visual input affected V1, motion affected V5 and attention was allowed to affect PPC, FEF and PFC).

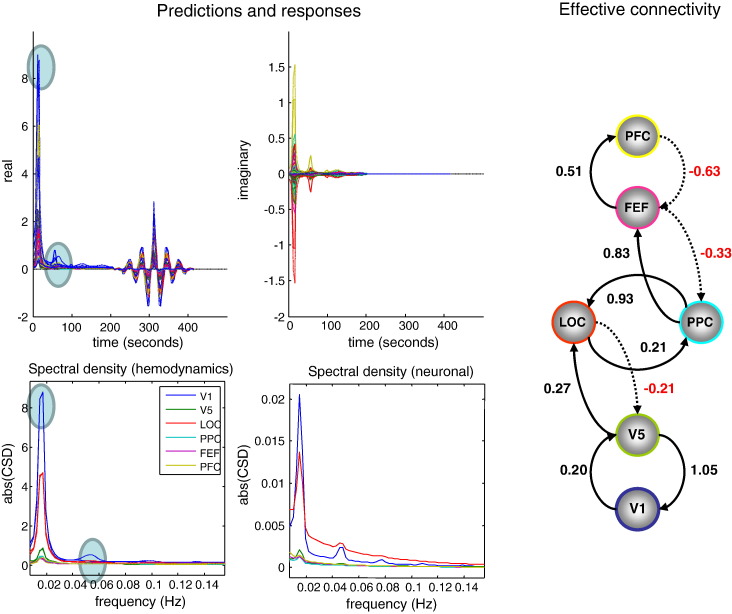
The results of model inversion are shown in Fig. 7. The upper left panels show the predicted and observed cross spectra (and cross covariance functions) using the same format as the previous figures. Here, there is a remarkably good agreement between the predicted and sample functions, which in some instances cannot be discerned by eye. In contrast to the simulations, here we see the spectral correlates of the experimental factors (visual input, motion and attention). These correlates are evident as peaks (and harmonics) in the cross spectra—highlighted with cyan circles. This experimental variance provides greater spectral density at particular frequencies and can increase the efficiency of parameter estimation.

Fig. 7.

This figure summarises the results of model inversion using the model and data of the previous figure. The upper left panel's show the predicted and observed data features using the same format as Fig. 3. The lower left panels show the predicted and observed auto spectra in the six regions, where spectral peaks induced by experimental manipulations are highlighted with cyan circles. The underlying auto spectra predicted for the hidden neuronal states (lower right) show a greater preponderance of higher frequencies with a 1/f form. The right panel reports the posterior expectations of effective connectivity using the same format as Fig. 2. The key thing to note here is that negative or inhibitory values are restricted to backwards or descending connections.

Because dynamic causal modelling characterises the system in terms of the effective connectivity and other parameters governing the dynamics of hidden states, we can reconstitute any of the characterisations in Fig. 1, either at the level of observed responses or at the level of any hidden states. For example, the lower left panel of Fig. 7 shows the auto spectra of each region predicted for haemodynamic responses. Contrast this with the equivalent auto spectra for neuronal activity (lower right panel), which possess a greater preponderance of higher frequencies, with a 1/f like form.

The estimates of effective connectivity generating these predictions are shown on the right. As predicted, all the negative or inhibitory effective connections are backwards connections. Furthermore, all but two of the backward connections are inhibitory. The two exceptions are interesting: the first is the backward connection from the posterior parietal cortex to the lateral occipital cortex, which could be construed as a lateral connection between the dorsal and ventral streams. The second exception is the backward connection from V5 to V1, which is exceptionally strong and positive. We have seen this result a number of times and had thought about it in terms of extrageniculate input to V5 that might, in some instances, render it hierarchically beneath other visual regions.

In summary, one can recover plausible results using real data with, in this example, 360 scans concatenated over four runs. The particular illustration here has only addressed model inversion; however, the usual procedures for model optimisation with Bayesian model comparison or post hoc reduction can be applied to results of this DCM, which we anticipate will find the most useful application in providing summary statistics for group comparisons in resting state fMRI studies.

Discussion

In conclusion, we hope to have introduced a dynamic causal model that could be useful in analysing resting-state studies or indeed any data reporting unknown or endogenous dynamics (e.g. sleep EEG). Being able to estimate weighted adjacency matrices summarising functional brain architectures (in terms of directed effective connectivity) also opens the door to graph theoretic analyses that may leverage important advances in network theory (Bullmore and Sporns, 2009).

Clearly, there are many issues that we have not addressed in this technical introduction. For example, we have not explored how this DCM scales with the number of nodes. However, because it uses exactly the same inversion scheme and priors as other DCMs, all previous extensions and variants should, in principle, apply. For example, one can use multiple states in each region to model inhibitory and excitatory neuronal populations explicitly (Marreiros, Kiebel and Friston, 2008). Furthermore, one can use the usual Bayesian model comparison and reduction schemes or, indeed, impose constraints to handle large numbers of regions (Seghier and Friston, 2013). These and other issues will be dealt with in subsequent publications that address construct validity—through comparative analyses with stochastic DCM (using simulated and real data). We also anticipate a series of applications to resting state fMRI data from Huntington's and Parkinson's disease—that may highlight unforeseen issues and motivate further developments.

Although most applications of resting state fMRI address differences among carefully selected subjects, there is growing interest in characterising the dynamics of functional connectivity per se (Allen et al. in press). The model we have considered does not allow for dynamic changes in effective connectivity (or the spectra of neuronal fluctuations); however, one can envisage extensions of the current scheme, in which successive epochs of resting state data are modelled. In principle, this would allow for epoch-to-epoch variations in connectivity (or neuronal spectra)—and thereby model their dynamics on a slower timescale. In fact, this sort of model is already used in the dynamic causal modelling of electromagnetic cross spectral densities, where subsets of model parameters are allowed to change in a condition or epoch-specific fashion (Moran et al., 2011).

The schemes described in this paper are implemented in Matlab code and are available freely as part of the open-source software package SPM12 (http://www.fil.ion.ucl.ac.uk/spm). Furthermore, the attentional data set used in this paper can be downloaded from the above website, for people who want to reproduce the analyses described in this paper.