Ultrafast Energy Transfer in Biomimetic Multistrand Nanorings

Abstract

We report the synthesis of LH2-like supramolecular double- and triple-stranded complexes based upon porphyrin nanorings. Energy transfer from the antenna dimers to the π-conjugated nanoring occurs on a subpicosecond time scale, rivaling transfer rates in natural light-harvesting systems. The presence of a second nanoring acceptor doubles the transfer rate, providing strong evidence for multidirectional energy funneling. The behavior of these systems is particularly intriguing because the local nature of the interaction may allow energy transfer into states that are, for cyclic nanorings, symmetry-forbidden in the far field. These complexes are versatile synthetic models for natural light-harvesting systems.

Natural photosynthetic light-harvesting systems are highly evolved for efficient energy collection, and their photophysics has been thoroughly investigated, particularly for systems from photosynthetic bacteria.¹ Many of the critical properties of these molecular assemblies have been attributed to the geometric structure of their key light-harvesting complexes (known as LH1 and LH2).²⁻⁵ Photons can be captured by a number of B800 chromophores, and their energy is funneled into a ring motif composed of B850 chromophores held in place by a protein matrix.^1,2 Experimental and theoretical studies on such chromophore systems have revealed the importance of symmetry,⁶ energy funneling, and state decoherence⁷ for the photosynthetic efficiency;⁸ however, active control over natural systems has not yet been achieved to test the relative importance of such factors.

We are intrigued by the possibility of creating synthetic biomimetic light-harvesting structures as a route to understanding, utilizing, and possibly surpassing the efficiency of the natural systems.⁹ A variety of approaches have been explored;¹⁰⁻¹² most recently, investigation of porphyrin nanorings has provided an insight into fully conjugated macromolecules with properties analogous to those of the B850 ring structures in natural LH2, which exhibit electronic delocalization around curved surfaces.¹³ Research on both natural and synthetic B850-like acceptor nanorings has revealed the importance of properties such as static and dynamic disorder-induced symmetry breaking.^6,14 However, studies of energy transfer from antenna chromophores to a synthetic nanoring have been limited by the challenges in creating such systems. Investigating the energy dynamics in synthetic LH2-like complexes may give important insights into the working mechanisms of both natural and synthetic light-harvesting systems.

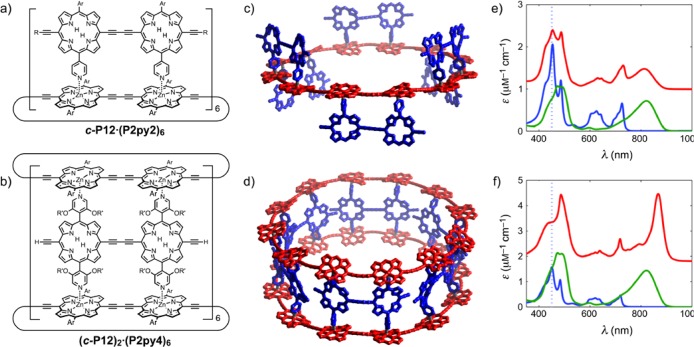
Here we report the synthesis and energy transfer dynamics of two supramolecular antenna-nanoring complexes of a 12-porphyrin nanoring, c-P12, with two different free-base porphyrin dimers, P2py2 and P2py4.¹⁵ Coordination of the pyridyl substituents to the zinc metal centers drives the self-assembly of the complexes, as shown in Figure 1. The ring–dimer complex c-P12·(P2py2)₆ (Figure 1a) consists of a porphyrin nanoring and six P2py2 dimers; these free-base porphyrin dimers have one meso-4-pyridyl substituent on each porphyrin unit to coordinate to the zinc centers of the nanoring. The 3,5-bis(trihexylsilyl)phenyl substituents on both components provide solubility and avoid aggregation. The ring–dimer–ring complex (c-P12)₂·(P2py4)₆ (Figure 1b) features analogous porphyrin dimers with four 4-pyridyl substituents allowing the coordination to two nanorings, forming a barrel-shaped architecture. To enhance the solubility of the dimers, dodecyloxy substituents are attached at the 3- and 5-position of the pyridyl moiety. Details of the synthesis and characterization of these compounds are given in the Supporting Information (SI). The association constant of each P2py2 unit for c-P12 is 5 × 10⁶ M^–1. All of the fluorescence spectra were recorded at concentrations of around 0.1 mM in toluene; under these conditions the dimer is >99% bound. The assembled complexes (shown as structural models in Figure 1c,d) have a diameter¹⁶ of 47 Å and a dimer porphyrin center to nanoring porphyrin center distance of 10.2 Å (see the SI for details). The absorption spectra of the complexes and their components are plotted in Figure 1e,f (plotted as molar absorption coefficient, scaled for the number of components). The absorption spectra of the complexes show notable shifts compared with the components, in particular a sharpening and red shift in the nanoring absorption for the ring–dimer–ring complex, which is attributed to planarization of the nanoring.¹⁷ The absorption spectrum of the nanoring undergoes less change when it forms the c-P12·(P2py2)₆ ring–dimer complex, reflecting the greater conformational heterogeneity of this complex compared with the more rigid ring–dimer–ring complex.

Figure 1.

(a, b) Chemical structures and (c, d) structural models of the ring–dimer complex c-P12·(P2py2)₆ (top) and the ring–dimer–ring complex (c-P12)₂·(P2py4)₆ (bottom). Ar = 3,5-bis(trihexylsilyl)phenyl, R = trihexylsilyl, R′ = dodecyl. (e, f) Plots of the molar absorption coefficients of the components in toluene/1% pyridine (dimer in blue, c-P12 nanoring in green), scaled for their relative numbers within the complex, as functions of wavelength. The absorption spectra of the two complexes in toluene (solid red lines, offset for clarity) are also shown. The excitation wavelength used for PL measurements (450 nm) is indicated as a dashed vertical blue line. The models shown in (c) and (d) are energy-minimized geometries calculated using the mm+ force field in HyperChem.

We found that the complexes exhibit efficient energy transfer from the dimer antennae to the nanoring (Figure 2a,b). When the complexes are assembled without additional free dimer in solution, the photoluminescence (PL) spectra are dominated by the emission from the nanoring acceptors (800–900 nm). In these measurements, the components were excited at a wavelength of 450 nm (see the dashed blue lines in the absorption spectra in Figure 1e,f), which gave approximately 2:1 (1:1) selectivity for dimer excitation in the ring–dimer (ring–dimer–ring) complex. The effective quenching of the dimer PL (710–730 nm) therefore qualitatively demonstrates the occurrence of efficient energy transfer to the nanoring acceptor. Figure 2 shows that an increase in the ratio of dimer to nanoring resulted in an abrupt onset of dimer emission at the end point of the titration, revealing the presence of unbound dimer in the solution. As expected, close to six dimers per c-P12 nanoring for the ring–dimer complex and close to three dimers per nanoring for the ring–dimer–ring complex were required (Figure 2c,d).

Figure 2.

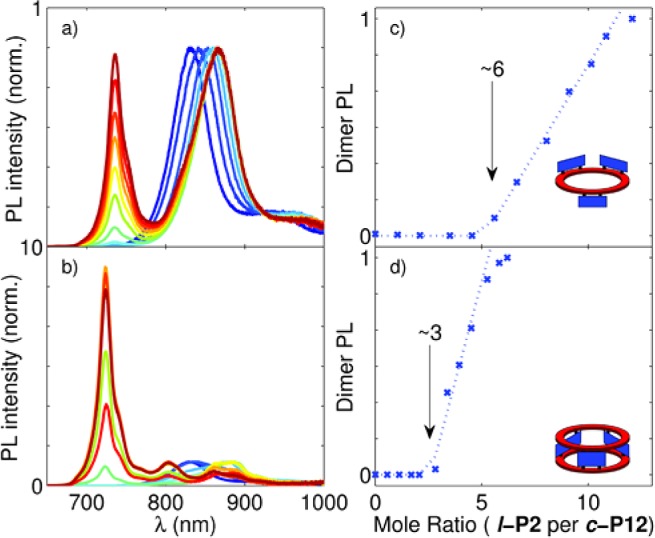
PL titrations (excitation at 450 nm) of c-P12 with (a, c) P2py2 and (b, d) P2py4, normalized to the nanoring emission peaks in (a) and (b). The end points are indicated by black arrows at approximately 6 equiv of P2py2 (c) and 3 equiv of P2py4 (d) per c-P12.

The addition of an excess of a competing ligand such as pyridine (1% by volume) effectively dissociated the complexes. In this way, we were able to achieve full control over the association state of the complexes, allowing for unambiguous isolation of electronic effects leading to energy transfer from dimers to nanorings. Figure 3a,b shows the PL spectra for the complexes in their associated state (blue line) and their dissociated state following addition of pyridine (red line). The vertical dashed red lines indicate the dimer PL emission wavelengths of 731 and 716 nm for the ring–dimer and ring–dimer–ring complexes, respectively. A qualitative comparison of the PL from the assembled and disassembled states shows the expected quenching of dimer emission for associated states. In addition, the effect of decreased planarization for the ring–dimer complex can be observed through changes in both the spectral position and intensity of the nanoring emission.¹³

Figure 3.

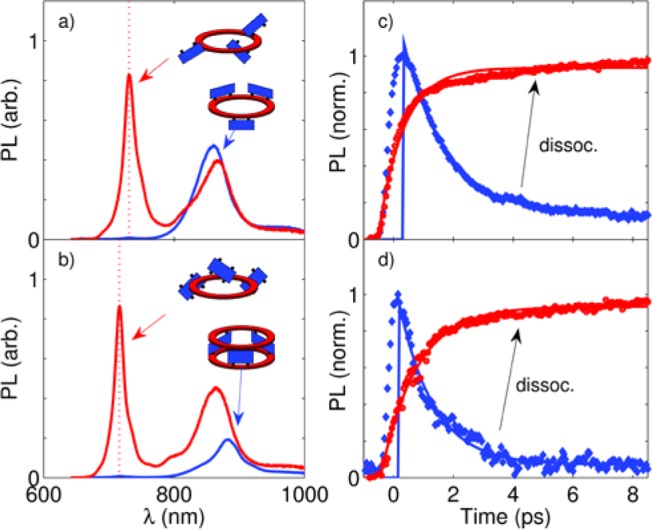
(a, b) Steady-state PL spectra for the (a) ring–dimer and (b) ring–dimer–ring complexes in the associated (blue line) and dissociated (red line) states. The dimer emission wavelength is indicated by the vertical dashed red lines. (c, d) Time-resolved PL dynamics for dimer emission for the (c) ring–dimer and (d) ring–dimer–ring structures for each association state.

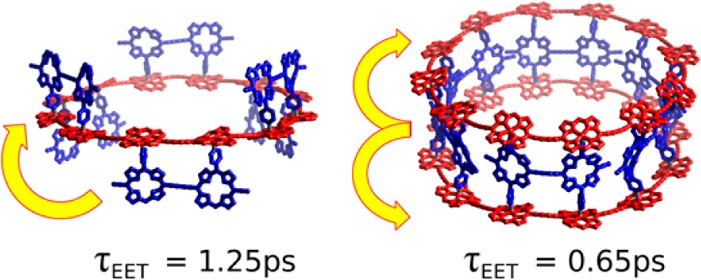
To explore the rates of energy transfer in these complexes, we employed ultrafast time-resolved PL spectroscopy. Both PL upconversion (PLUC) and time-correlated single-photon counting (TCSPC) techniques were used to provide subpicosecond time resolution and nanosecond range, respectively (a detailed experimental description is given in the SI). We experimentally assessed the dimer-to-nanoring energy transfer process by comparing the dynamics¹⁸ of dimer emission in the associated state with that of the free dimer after dissociation of the complex upon addition of excess pyridine. In the supramolecular complex, energy transfer to the nanoring provides an additional and dominant decay channel, leading to rapid PL quenching. Figure 3c,d shows that the energy transfer is remarkably fast: the dimer PL emission for the associated states (blue points and lines) drops rapidly in comparison with that for the dissociated states (red points and lines). By modeling the ratio of the dimer emissions for the assembled and disassembled states, we were able to determine energy transfer rates of (1.25 ps)⁻¹ and (0.65 ps)⁻¹ for the ring–dimer complex c-P12·(P2py2)₆ and the ring–dimer–ring complex (c-P12)₂·(P2py4)₆, respectively. The effective doubling of the energy transfer rate upon addition of the second nanoring is a striking demonstration of the effects of adding a second, symmetric acceptor deactivation channel (see further details in the SI). These synthetic ring assemblies therefore demonstrate the feasibility of both uni- and bidirectional energy funneling. Excitations on c-P12 have lifetimes of 850 and 1150 ps for the ring–dimer and ring–dimer–ring geometries, respectively (see the SI for details), comparable to the lifetimes of 600–1200 ps for the excited states of natural LH2 complexes.¹⁹ This is significantly longer than the typical time required for energy collection from natural LH2 (2–5 ps)³ or for charge transfer in synthetic porphyrin–fullerene systems,²⁰ providing ample time for efficient solar energy harvesting.

It is illuminating to compare the energy transfer rates observed for these synthetic nanoring assemblies to those of their intensively studied natural counterparts. In LH2 complexes of purple bacteria, a rate of (0.9 ps)⁻¹ for energy transfer between B800 antenna chromophores and the B850 chromophore array has been established.^8,21 Such a high rate is in general not well modeled by the standard Förster point-dipole equation and has been attributed to a variety of more complex processes. The presence of a virtual intermediate state (via the carotenoid molecule),⁵ quantum coherent transfer,^7,22 and disorder-assisted⁴ energy transfer have been proposed. It is noted that while such effects are not expected to be relevant for synthetic systems, strikingly similar energy transfer rates are found. This suggests the possibility of gaining further insight into the natural light-harvesting systems through modeling of the energy transfer in the presented complexes. In general, the lowest excited state in a molecular ring sustaining fully delocalized excitonic states is expected to be dipole-forbidden by symmetry.¹⁷ However, natural systems tend to exhibit disorder-allowed radiative transitions due to flexibility in the protein scaffold supporting the ring structure.⁶ In contrast, fully conjugated porphyrin nanorings ought to exhibit lower disorder, leading to an absorbing state that is fully delocalized around the ring²³ and an optically dark lowest exciton state.²⁴ As a result, full models of the energy transfer dynamics are likely to be complex, even in more robust synthetic systems. In particular, the simple Förster model is expected to fail,^5,25 as the emitting and absorbing moieties in the complex lie around 10 Å apart at their closest separation, while the dimer is 25 Å in length. A description in terms of a point dipole can therefore only ever be a first-order approximation as it suffers from two primary flaws: the unphysical allocation of the dipole strength to the geometric center of the nanoring and the neglect of dark absorption states (states with no far-field oscillator strength). The former may be addressed through the use of the more accurate line-dipole approximation^26,27 to distribute excitonic strength around the rim of the nanoring. The latter requires further knowledge of the electronic states of the acceptor. All of these states except for the allowed k = 1 state ought to be forbidden for the high-symmetry nanoring system and should have no far-field absorption.⁸ However, as far as energy transfer from the dimer to the nanoring is concerned, it is not reasonable to neglect these states, as the donor dimer is close enough to break the symmetry of the interaction, leading to a non-negligible energy transfer rate. Since these states are optically inactive in the far field, they cannot be easily observed experimentally, and calculations of the exciton energy level spacing will be essential to allow rigorous modeling of energy transfer in the complexes. Unfortunately, present computational techniques are not able to accurately model the large structures presented here, and a quantitative description of the energy dynamics is therefore beyond the scope of this work. Tuning of the exciton-state energies through modification of the complex size or geometry provides an example of the way that synthetic complexes may shed light upon energy transfer in natural LH2 antenna systems. In natural light-harvesting systems, such optically dark states have been suggested to be responsible for both the rapid energy transfer and high overall photosynthetic efficiency of these structures²⁵ and are an important target for further research.

In summary, we have reported two synthetic supramolecular complexes with analogies to natural LH2 antenna systems. Extremely rapid energy transfer from porphyrin dimer antenna molecules to the 12-porphyrin nanoring acceptor was observed in time-resolved PL measurements, and the energy rate doubles upon the addition of a second acceptor nanoring. These systems thus have energy transfer rates that are comparable to those observed in natural light-harvesting systems, making them interesting for understanding energy transfer in natural light-harvesting systems. In addition, both uni- and bidirectional energy transfer was shown to be feasible, highlighting the potential use of these systems for highly selective energy channeling in solar-harvesting applications.

Supporting Information Available

Synthesis and characterization of the investigated compounds and supramolecular complexes, PL quantum yield measurements, optical spectroscopy experimental details, and effects of stoichiometry on energy transfer. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.