How does the motor system correct for errors in time and space during locomotor adaptation?

Abstract

Walking is a complex behavior for which the healthy nervous system favors a smooth, symmetric pattern. However, people often adopt an asymmetric walking pattern after neural or biomechanical damage (i.e., they limp). To better understand this aberrant motor pattern and how to change it, we studied walking adaptation to a split-belt perturbation where one leg is driven to move faster than the other. Initially, healthy adult subjects take asymmetric steps on the split-belt treadmill, but within 10–15 min people adapt to reestablish walking symmetry. Which of the many walking parameters does the nervous system change to restore symmetry during this complex act (i.e., what motor mappings are adapted to restore symmetric walking in this asymmetric environment)? Here we found two parameters that met our criteria for adaptive learning: a temporal motor output consisting of the duration between heel-strikes of the two legs (i.e., “when” the feet land) and a spatial motor output related to the landing position of each foot relative to one another (i.e., “where” the feet land). We found that when subjects walk in an asymmetric environment they smoothly change their temporal and spatial motor outputs to restore temporal and spatial symmetry in the interlimb coordination of their gait. These changes in motor outputs are stored and have to be actively deadapted. Importantly, the adaptation of temporal and spatial motor outputs is dissociable since subjects were able to adapt their temporal motor output without adapting the spatial output. Taken together, our results suggest that temporal and spatial control for symmetric gait can be adapted separately, and therefore we could potentially develop interventions targeting either temporal or spatial walking deficits.

in our everyday lives we experience a variety of perturbations to movement and quickly learn to correct for predictable errors—we adjust walking for icy surfaces or hand movements for an unfamiliar computer mouse. We refer to this short-timescale motor learning process as motor adaptation. Motor adaptation is defined here as an error-driven process that allows us to adjust stored movement calibrations used to make predictions of movement outcomes. So rather than constantly correcting our movements upon sustained perturbations, motor adaptation enables us to adjust sensorimotor mappings of well-learned movements when there are changes in the environment or the body (Bastian 2008; Krakauer 2009). Motor adaptation is studied by exposing subjects to novel situations (i.e., adaptation periods), where movements are initially perturbed and errors abruptly increase (Fig. 1A). To minimize these errors, movements (i.e., motor outputs) are actively modified from a preperturbation (i.e., pattern A) behavior to a new “adapted” steady state (i.e., pattern A′), which then gradually returns to baseline behavior once the perturbation is removed (Fig. 1B) (for reviews see Bastian 2008; Krakauer 2009; Tian et al. 2009).

Fig. 1.

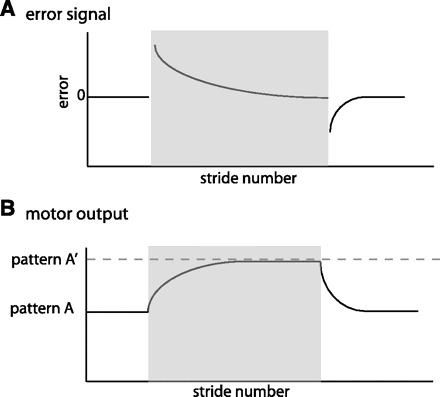
Schematic of error signal and motor output. Shaded region represents the adaptation period. A: parameters quantifying error are perturbed early in adaptation and decrease throughout adaptation. They also show the opposite perturbation in deadaptation. B: motor outputs exhibit a smooth change from a set pattern A to a new value during adaptation (pattern A′), set by the environmental conditions. They also must be actively deadapted with a smooth transient from pattern A′ to pattern A when environmental conditions change back to the original state.

Previous studies have investigated the relationship between movement perturbations, motor errors, and the subsequent alteration of motor outputs in adaptation paradigms (e.g., Fine and Thoroughman 2007; Wolpert and Kawato 1998). For many movement types, the mapping between error signals and motor outputs can be fairly straightforward (e.g., saccades: Keller and Robinson 1971; planar reaching: Krakauer et al. 1999; Shadmehr and Mussa-Ivaldi 1994). For example, in visuomotor adaptation to a 30° clockwise rotation, subjects learn to aim 30° counterclockwise to reduce the initial 30° clockwise performance error (Krakauer et al. 1999). On the other hand, in locomotion there are cyclical motions of each leg, interactions between the limbs, and the spatial and temporal control of gait to consider. Because of this, the mapping between error signals and motor outputs is less obvious in walking.

We know from prior work that healthy subjects adapt to reestablish symmetry of interlimb walking parameters during split-belt walking. Thus walking asymmetries in interlimb temporal and spatial parameters behave like an error signal and are corrected back to symmetry through adaptation. This is true for walking with split-belt perturbations of different magnitudes (Reisman et al. 2005) and in different directions (Choi and Bastian 2007). Specifically, we are referring to the antiphase movement of the legs as a symmetric temporal relationship and the similar axis about which the limbs oscillate when stepping (i.e., center of oscillation) as a symmetric spatial relationship. Our recent work further suggests that the adaptation of temporal and spatial parameters is dissociable—they show different responses to distraction during adaptation (Malone and Bastian 2010), generalize differently to natural walking (Torres-Oviedo and Bastian 2010), and show a different time course over development (Vasudevan et al. 2011).

Given these observations, we hypothesized that gait symmetry (temporal and spatial) can be achieved through the adaptation of temporal and spatial motor outputs that can be controlled separately. To test this hypothesis, we first identified temporal and spatial motor outputs that could minimize errors in gait symmetry and the specific error signals that drive them. We then tested whether the adaptation of these temporal and spatial motor outputs could be dissociated by clamping one and allowing the other to adapt.

METHODS

Subjects.

For experiment 1, we reanalyzed previously collected data from Malone and Bastian (2010) to derive parameters that behaved as motor outputs. Thirty-three healthy volunteers (19 men, 14 women; mean age 23.6 yr) participated in that study. For experiment 2, we used an additional 15 healthy volunteers (8 men, 7 women; mean age 26.3 yr) to test whether spatial and temporal adaptations were dissociable. All subjects gave informed written consent before participating. The protocols were approved by the Johns Hopkins Institutional Review Board.

Data collection.

Kinematic data were collected at 100 Hz with Optotrak (Northern Digital). Infared-emitting markers were placed bilaterally over the toe (fifth metatarsal head), ankle (lateral malleolus), knee (lateral femoral epicondyle), hip (greater trochanter), pelvis (iliac crest), and shoulder (acromion process) (Fig. 2A). Foot contacts were determined with four contact switches per foot: two on the forefoot and two on the heel. Analog data (foot switches and treadmill speed) were synchronized with the kinematic data and collected at 1,000 Hz.

Fig. 2.

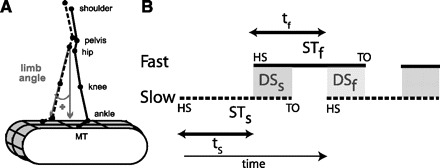
Definitions of parameters. A: marker diagram for experiments 1 and 2 with limb angle convention shown. MT, 5th metatarsal head. By convention, positive limb angles represent when the ankle is in front of the hip (flexion) and negative angles when it is behind (extension). B: schematic defining temporal parameters of locomotion during normal, symmetric walking. Time is represented along the horizontal axis, with time increasing from left to right. HS, time at heel-strike; TO, time at toe-off. Solid and dashed lines represent stance time periods (ST) for the slow (ST_s) and fast (ST_f) legs, respectively. White areas between these lines represent swing time periods (i.e., time intervals from TO to HS). Shaded areas indicate when both feet are on the ground, defined as double support periods (i.e., overlap in stance time for both legs); DS_s and DS_f are slow and fast double support periods, respectively. Slow and fast step timings (t_s and t_f) are defined as the time between consecutive heel-strikes.

Overall protocol.

Split-belt walking adaptation was investigated with a custom-built treadmill with two separate belts driven by independent motors (Woodway). Individual speed commands were sent to each motor through a custom MATLAB (MathWorks) computer interface. Subjects wore a safety harness suspended from the ceiling that did not provide additional support to the body. All subjects stood in the middle of the treadmill with one leg on each belt. Instructions were given for the subjects initially to hold onto a ground-referenced rail when the belts started moving but to lift their hands off the rail and cross their arms as soon as they felt comfortable (within 5 s). Additionally, all subjects were instructed to refrain from looking at the belts, unless specifically instructed (described below).

In experiment 1, we used previously collected data from Malone and Bastian (2010) to derive parameters that behaved as motor outputs (i.e., they exhibit a smooth transition from baseline behavior to a novel condition in the adapted state, which then returns to baseline behavior in deadaptation; Fig. 1B). Thirty-three subjects completed three epochs: baseline (tied belt), adaptation (split belt), and deadaptation (tied belt). In the “tied-belt” condition, the belts moved at the same speed (0.5 or 1.5 m/s). In the “split-belt” condition, the belt under the subject's self-identified dominant leg moved at 0.5 m/s and the other at 1.5 m/s. During this adaptation period subjects walked under different visual feedback conditions. One group of subjects were looking at the sagittal projection of their feet up to their lower calves and the belts on a television in front of them (Conscious Correction, N = 11), others were distracted with audio and visual stimuli projected on the television (Distraction, N = 11), and others were looking straight ahead (Control, N = 11) (Malone and Bastian 2010). We present the results from the Distraction group in Figs. 4, 6, and 7, A and C. This group was the slowest to adapt and deadapt (Malone and Bastian 2010), and therefore allowed us to investigate transients more clearly. One subject from the Distraction group was removed from the analysis because of missing kinematic data during the adaptation period. In deadaptation, both belts moved at 0.5 m/s (tied belts) and all distracters and feedback were removed in order to assess storage and unlearning under the same conditions.

Fig. 4.

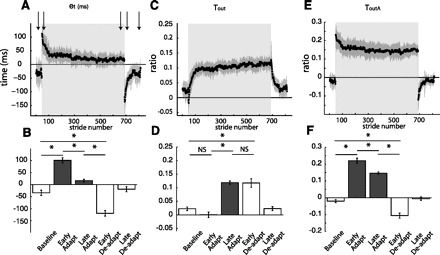
Group averages of temporal parameters throughout experiment 1. Adaptation period is represented by shaded area. Arrows represent time correspondence between bar graphs and group average curves; the first arrow corresponds to the first epoch (baseline), and so forth. A: stride-by-stride time course of the temporal error (e_t) characterized by the double support difference. e_t follows the characteristic time course of a motor error: large values during early adaptation, error reduction as subjects adapt, and aftereffects during early deadaptation that are actively washed out. B: key epochs are shown for the error parameter double support difference. Abrupt transitions in e_t values are observed when the environmental conditions change (e.g., tied to split). This is indicated by the significant differences between baseline and early adaptation and those between late adaptation and early deadaptation. Also, subjects adapted as indicated by the significant decrease in e_t from early to late adaptation and stored these changes as shown by the aftereffects demonstrating the opposite asymmetry in early deadaptation. C: stride-by-stride time course of the temporal motor output (T_out). T_out follows the characteristic time course of motor outputs. Contrary to the temporal error time course, the temporal motor output smoothly changes from zero in baseline (tied) walking to values greater than zero during adaptation, and smoothly changes back to zero during deadaptation when the belts run in tied mode. D: key epochs are shown for T_out. Two important features characterizing the behavior of motor outputs are observed. First, there are smooth transitions between tied and split conditions as shown by the similarity in T_out values from baseline to early adaptation and from late adaptation to early deadaptation. Second, there is a statistical increase in T_out values from early to late adaptation. E: stride-by-stride time course of the alternate parameter to characterize temporal motor output (T_outA) based on toe-off timings. The time course of T_outA does not follow the characteristic time course of motor outputs. F: statistical analysis on key epochs of T_outA also shows that this parameter cannot be used to characterize the adaptation of temporal motor outputs. *Significant difference between epochs. NS, nonsignificant.

Fig. 6.

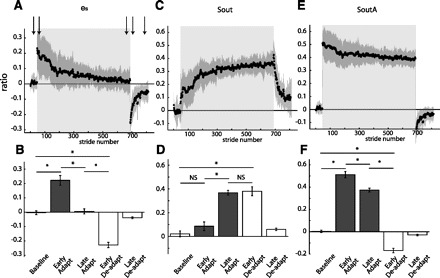
Group averages of spatial parameters throughout experiment 1 are shown similarly to the temporal parameters in Fig. 4. Adaptation period is represented by shaded area. Arrows represent time correspondence between bar graphs and group average curves; the first arrow corresponds to the first epoch (baseline), and so forth. A: stride-by-stride time course of the spatial error (e_s) characterized by the difference in angular ratios. B: key epochs are shown for the e_s. C: stride-by-stride time course of the spatial motor output (S_out) characterized by a normalized difference in limb angles at heel-strike. D: key epochs are shown for the S_out. E: stride-by-stride time course of the spatial motor output (S_outA) characterized by the normalized difference of limb angles at toe-off. F: key epochs are shown for the S_outA. Like their temporal counterparts, e_s follows the characteristic time course of a motor error and S_out of a motor output. On the other hand, the alternative motor output parameter based on toe-off timings (S_outA) does not exhibit the characteristics of motor outputs: smooth transitions when environmental conditions change and rise from one steady state to another during adaptation.

Fig. 7.

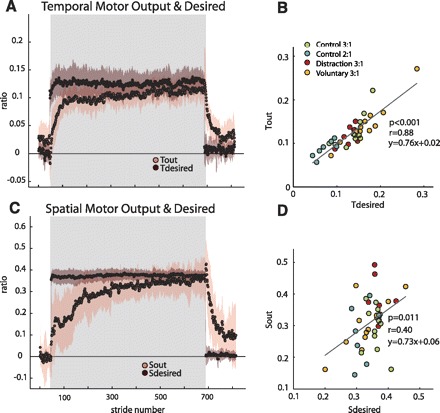
Temporal and spatial motor outputs with their respective desired values (derivation in methods and appendixes a and b, respectively). Adaptation period is represented by shaded region. Group average plots for the Distraction group are shown with shaded standard error regions in A (temporal) and C (spatial). Note that the spatial (S_desired) and temporal (T_desired) desired values change immediately upon the split-belt perturbation, while the motor outputs change on a stride-by-stride basis. On average, by the end of adaptation, the motor outputs approached the desired values. B and D: scatterplots of each subject's T_desired vs. T_out (B) and S_desired vs. S_out (D). Each group in experiment 1 is classified in different colors. Only subjects from the Control group in experiment 2 are also included in this analysis. Although regression results show that “desired” values are a good predictor of the steady-state values reached by motor outputs, the temporal correlation coefficient is larger than the spatial coefficient. This suggests that the temporal parameter is more tightly controlled in individual subjects.

In experiment 2, we investigated whether the temporal and spatial motor outputs derived in experiment 1 could be adapted separately. For the baseline condition, the belts moved at the same speed (0.7 or 1.4 m/s). After baseline, all subjects were instructed to step to markers placed on the frame of the treadmill (i.e., foot placement occurred at a symmetric spatial location), while both belts moved at 0.7 m/s. In the “split-belt” (adaptation) condition, the belt under the dominant leg moved at 0.7 m/s and the other at 1.4 m/s. Speed pairs different from those used in experiment 1 were used here in order to test the generality of our measures. Subjects in experiment 2 were randomly assigned to one of two groups who were given different instructions during adaptation. In adaptation, subjects in the “Control” group were instructed to walk on the treadmill looking straight ahead, and the markers on the treadmill were not visible (N = 7), while subjects in the “Spatial Hold” group (N = 8) were asked to step to symmetric markers placed on the frame of the treadmill and were able to look directly down at their feet (i.e., we forced foot placement to be the same on both belts even though the belts moved at different speeds). A subject in the Spatial Hold group could not follow the instructions of the task, and was therefore removed from all further analysis. All subjects completed a deadaptation period (0.7 m/s) where the markers were hidden and they were instructed to “just walk and look straight ahead.”

Data analysis.

In experiment 1, we derived interlimb parameters that could characterize temporal and spatial motor outputs. In our derivations we looked at interlimb relationships during a single stride cycle (T_stride), defined as the time between two consecutive heel-strikes (i.e., time of foot landing) of the same leg. Also, subjects maintained an alternating stepping pattern (i.e., they did not take multiple steps with one leg while the other one was on the ground). In other words, the stride cycle is the same for both legs throughout adaptation (Reisman et al. 2005).

A previous study on split-belt adaptation investigated common interlimb gait parameters that could be adapted during split-belt walking on the treadmill (Reisman et al. 2005). The authors found that neither the stance time, defined as the time from heel-strike to the same limb's toe-off (i.e., when the foot is lifted off the ground), of individual limbs nor the stance time ratio, defined as the fast stance time divided by the slow stance time, was adapted by subjects; rather, they changed abruptly between split-belt and tied-belt conditions. Similar to the stance time, the authors also demonstrated that stride length (distance traveled by the ankle marker in the anterior-posterior direction from heel-strike to toe-off of one limb) ratio does not adapt or show significant aftereffects with split-belt adaptation (Reisman et al. 2005). While the stance phase was not adapted in either space or time, the swing phase motion is unconstrained during treadmill walking. Moreover, when and where the leg starts and finishes the swing phase directly alters double support times and the orientation of leg oscillation (see appendixes a and b), which are purely temporal or spatial gait features that are equalized in the adapted state (i.e., error signals) (Choi and Bastian 2007; Malone and Bastian 2010; Reisman et al. 2005). Therefore, we investigated both the spatial and temporal control of heel-strike and toe-off to ascertain which of these events the nervous system could use as motor outputs in adaptation.

Temporal error and motor output.

In the temporal domain, we used double support time (i.e., period when both legs are on the ground) as the error because it purely characterizes temporal asymmetries in the locomotor pattern (Reisman et al. 2005). Then, we derived motor outputs that could minimize this temporal asymmetry (temporal motor error). Double support time is the transition period when the body mass is transferred between limbs. This transition time has been described to be energetically important because when both legs are on the ground, one limb is generating positive work while the other is absorbing work (Ruina et al. 2005). Therefore, equal double support times of both legs will most likely facilitate an efficient body transfer between the limbs and reduce impact forces at foot landing. While double support times are equal during symmetric gait, this equality is initially disrupted and gradually recovered during split-belt walking (Reisman et al. 2005)—like performance errors in other adaptation paradigms (for reviews see Krakauer 2009 and Tian et al. 2009). Therefore, we defined the temporal motor error (e_t) as the difference in double support times:

$${\text{e}}_{\text{t}}={\text{DS}}_{\text{s}}-{\text{DS}}_{\text{f}}$$

where DS_s and DS_f are the double support times for the “slow” and “fast” limbs, respectively. DS_s was calculated as the time from heel-strike of the “fast” limb to toe-off of the “slow” limb, and vice versa for DS_f (Fig. 2B).

We hypothesized that the temporal motor output (T_out) is adapted to recover double support symmetry and is a function of interlimb heel-strike durations or step times (t). We defined slow step time (t_s) as the time period between the heel-strike of the slow leg and the subsequent heel-strike of the fast leg. Similarly, we defined fast step time (t_f) as the time period between the heel-strike of the fast leg and the subsequent heel-strike of the slow leg (Fig. 2B). We think these timings might be updated in a feedforward manner during split-belt adaptation since it has been shown that there is a large contribution of higher centers, relative to feedback processes, in the control of heel-strike in cats (Bretzner and Drew 2005). Accordingly, we defined T_out as the difference in slow and fast step times (t_s and t_f, respectively) normalized by the stride time (T_stride):

$$T_{\text{out}}=\frac{t_{\text{s}}-t_{\text{f}}}{T_{\text{stride}}}=\frac{t_{\text{s}}-t_{\text{f}}}{t_{\text{s}}+t_{\text{f}}}$$

The full derivation of T_out is provided in appendix a. We also defined T_desired, or the value that T_out could approach to equalize double support times, as:

$$T_{\text{desired}}=\frac{{\text{ST}}_{\text{s}}-{\text{ST}}_{\text{f}}}{T_{\text{stride}}}$$

The full derivation of T_desired is also given in appendix a.

In conclusion, we proposed that the temporal motor output is determined by interlimb heel-strike durations (i.e., step times). We further suggest that during split-belt walking the temporal motor output approaches a new steady state, T_desired, specified by the difference in stance times in the asymmetric environment. This is accomplished in order to minimize the temporal motor error (e_t) characterizing the asymmetry in double support times that subjects experience during split-belt walking. To show specificity of this measure, we tested whether an alternate temporal motor output (T_outA) that also minimizes the temporal error e_t would follow the smooth transitions characteristic of a motor output. We defined T_outA as follows:

$$T_{\text{outA}}=\frac{t_{\text{s\_off}}-t_{\text{f\_off}}}{t_{\text{s\_off}}+t_{\text{f\_off}}}$$

where t_{s_off} and t_{f_off} are the slow and fast interlimb toe-off times, respectively. t_{s_off} was calculated as the time between the slow toe-off and the next fast toe-off, and vice versa for t_{f_off}.

Spatial error and motor output.

We have previously shown that the axis about which each leg oscillates (i.e., the center of oscillation) is adapted during split-belt walking (Malone and Bastian 2010). We can quantify this for each limb by computing an angular ratio (r), which indicates the proportion of limb flexion compared to the entire range of motion of the leg:

$$r_{\text{s}}=\frac{{\alpha }_{\text{s}}}{{\gamma }_{\text{s}}}\text{and}{r}_{\text{f}}=\frac{{\alpha }_{\text{f}}}{{\gamma }_{\text{f}}}$$

Here α_s and α_f are the limb angles at heel-strike of the slow and fast legs, respectively (see Fig. 5). Similarly, γ_s and γ_f are the limb angles from heel-strike to toe-off of the slow and fast legs, respectively. In other words, γ_s and γ_f values quantify the entire range of motion for each leg, or total amplitude of oscillation for each leg during one stride (see Fig. 5). Note that limb angle is defined here as the angle between a vertical line and the vector from the hip to the ankle on an x-y plane (Fig. 2A); by convention, it is positive when the ankle is in front of the hip (flexion) and negative behind (extension).

Fig. 5.

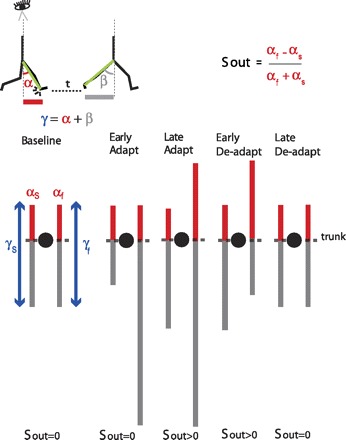
Schematic of spatial changes occurring throughout adaptation. Stick figures at top show the sagittal view of someone walking on the treadmill. The limb angle at heel-strike (i.e., α) is shown at a time period t before the limb angle is at toe-off (i.e., β). Eye icon indicates that diagrams below the sagittal schematic represent the bird's-eye view of the subject stepping on the treadmill. Lines in the bird's-eye view are projections of limb motions during stance at different points in the experimental paradigm. Trunk position is represented by black circles. Red and gray lines represent limb axis projection at angles α and β. Blue arrows represent the range of motion for a single limb's stride, which depends on the limb excursion (angle γ). In baseline, the proportion of the limb-forward placement with respect to its entire movement is the same for both legs. This symmetry is disrupted when placing the legs at the same angle α [spatial motor output (S_out) = 0] during early adaptation. Thus subjects adapt their limb-forward placement to reestablish symmetry in proportions of limb-forward placement with respect to the entire limb motion in both legs during late adaptation. In deadaptation, the belts are tied to the same speed. The nervous system still attempts to maintain the new spatial motor output in early adaptation, but now the limbs' spatial error (limb-forward placement with respect to the entire movement) is asymmetric in the opposite direction. By the end of deadaptation, S_out returns back to zero and walking is similar to what is seen at baseline.

Our prior work has also shown that people adapt their center of oscillation values to be equal on the two legs (Malone and Bastian 2010). We therefore defined the spatial error (e_s) as the difference in angular ratios:

$$e_{\text{s}}=r_{\text{s}}-r_{\text{f}}$$

We hypothesized that the spatial motor output (S_out) is adapted to recover spatial gait symmetry. We further hypothesized that S_out is a function of the limb angle (α) at heel-strike, since as previously discussed it has been shown that foot placement at heel-strike is very precise in intact cats across different speeds (Halbertsma 1983) and that high-level structures are involved in the control of the limbs at foot placement (Drew 1993; Drew et al. 2002, 2004; McVea and Pearson 2009). We defined S_out as the difference between fast and slow limb angles at heel-strike (α_f and α_s, respectively) normalized by their sum:

$$S_{\text{out}}=\frac{{\alpha }_{\text{f}}-{\alpha }_{\text{s}}}{{\alpha }_{\text{f}}+{\alpha }_{\text{s}}}$$

The full derivation of this is provided in appendix b. We also defined S_desired, or the value that the spatial motor output could approach for angular ratio symmetry, as:

$$S_{\text{desired}}=\frac{{\gamma }_{\text{f}}-{\gamma }_{\text{s}}}{{\gamma }_{\text{f}}+{\gamma }_{\text{s}}}$$

The full derivation of S_desired is also given in appendix b.

In conclusion, we propose that the spatial motor output is determined by the limbs' orientation at heel-strike. We further suggest that during split-belt walking the spatial motor output approaches a new steady state, S_desired, specified by the difference in the limbs' range of motion in the asymmetric environment. This is accomplished in order to minimize the spatial motor error (e_s) characterizing the asymmetry in orientation of the limbs' oscillations that subjects experience during split-belt walking. To show specificity of this measure, we tested whether an alternate spatial motor output (S_outA) that also minimizes the spatial error e_s would follow the smooth transitions characteristic of a motor output. We defined S_outA as follows:

$$S_{\text{outA}}=\frac{{\beta }_{\text{s}}-{\beta }_{\text{f}}}{{\beta }_{\text{s}}+{\beta }_{\text{f}}}$$

where β is the limb angle at toe-off (see Fig. 5). β_s and β_f are the slow and fast limb angles at toe-off, respectively.

It is important to mention that an interlimb gait parameter commonly used to characterize spatial asymmetries is step length symmetry, defined as the normalized difference in step lengths, where step length is the anterior-posterior distance between the ankle marker of each leg at heel-strike of the leading leg (Reisman et al. 2005). However, step length symmetry has been shown to be affected by changing both spatial and temporal coordination patterns (Malone and Bastian 2010), and here we wanted to investigate parameters characterizing purely temporal or spatial gait features. Therefore, we chose to focus on the adaptation of each limb's oscillation, which is a purely spatial parameter adapted during split-belt walking (Malone and Bastian 2010).

Statistical analysis.

We analyzed the behavior of all temporal and spatial parameters (i.e., T_out, S_out, e_t, e_s, T_outA, S_outA) across five epochs throughout the experiment: baseline, early adaptation, late adaptation, early deadaptation, and late deadaptation. Baseline values for each parameter were calculated from the last 10 strides of tied walking, prior to any perturbation. Early adaptation and deadaptation values were averages of the first 10 strides in each of these respective periods. Similarly, late adaptation and deadaptation values were averages of the last 10 strides during adaptation and deadaptation, respectively. We used repeated-measures ANOVAs to analyze changes in temporal and spatial parameters across these five epochs. Post hoc analyses were used to assess the adaptation of these parameters by comparing early adaptation versus late adaptation values. Post hoc analyses were also used to assess the storage of these adaptation effects by comparing baseline versus early deadaptation values. Additionally, a linear regression was used to determine the similarity between motor outputs values at steady state (late adaptation) and the “desired” motor output values obtained from our derivation. The Spatial Hold group was not included in this regression analysis because we wanted to investigate the natural relationship between motor outputs values at steady state and the “desired” values that would theoretically achieve spatial and temporal symmetry. Statistica (StatSoft, Tulsa, OK) was used for all statistical analysis.

RESULTS

Temporal motor output and motor error.

We found that stepping timings characterized by T_out were adapted to recover double support symmetry and a new interlimb temporal pattern (i.e., stepping rhythm) was learned during split-belt walking. In other words, subjects adapted T_out from a stepping rhythm A in Fig. 1B to a new stepping rhythm A′ to minimize the double support differences experienced during split-belt walking. Figure 3 is a schematic that illustrates the general changes that are made in the temporal motor output (T_out) and motor error (e_t) from baseline walking throughout adaptation. Note that during baseline, normal walking conditions (i.e., tied belts), the slow and fast step timings are equal (i.e., T_out = 0) and the double support periods are equal (i.e., e_t = 0). When the belts were split (i.e., adaptation), the stance times for the fast and slow legs (Fig. 3, orange lines) become different since one leg is moving faster than the other and subjects take alternating steps (i.e., multiple steps with one limb are not taken while the other limb is in contact with the ground). Consequently, equal slow and fast step timings lead to asymmetric double support durations (i.e., e_t > 0) (Fig. 3, blue regions). Therefore, as in the schematic shown on Fig. 1B, subjects changed their stepping rhythm (i.e., T_out > 0) to equalize the double support periods (i.e., to make e_t = 0). In deadaptation (tied belts), the newly learned stepping rhythm caused a marked asymmetry in double support durations (i.e., e_t < 0) since the two belts were moving at the same speeds. Subjects then had to actively unlearn the new stepping rhythm and return back to stepping with symmetric step timings (i.e., T_out = 0) to wash out the asymmetry error by the end of the block.

Fig. 3.

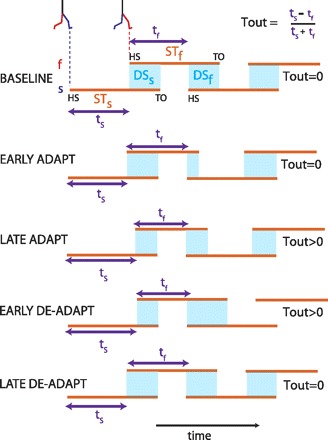
Schematic of temporal changes throughout adaptation. Stick figures show limb configuration at heel-strike for the fast (red) and slow (blue) limbs. Stance periods are shown by orange lines. Double support periods are represented by the shaded blue squares. Slow and fast step timings are shown by the purple arrows. Temporal motor output (T_out) is a normalized difference of step timings. When belts are tied during baseline walking, a temporal motor output of zero (equal purple arrows) and equal double support periods (blue regions) are apparent. In early adaptation (split belt) the temporal motor output is still zero, but double support periods (blue regions) are asymmetric. To equalize the double support periods, the slow and fast step timings are changed so that the temporal motor output is greater than zero (i.e., t_s is larger than t_f, Late Adaptation). In deadaptation, the belts are tied (i.e., move at the same speed), so the stance periods (orange lines) return back to baseline values. However, the nervous system has learned a new motor output (i.e., slow and fast step timings), which results in unequal double support periods, but the double support asymmetry is in the opposite direction (DS_f > DS_s). By the end of deadaptation, the nervous system changes the temporal motor output back to zero, and walking looks similar to baseline.

Figure 4 shows stride-by-stride behavior for temporal error e_t and temporal motor output T_out. We found that e_t and T_out are parameters that behaved as would be expected of an error and motor output, respectively, during split-belt locomotor adaptation. Figure 4A shows a stride-by-stride plot of e_t, which characterizes well the initial rise during early adaptation, reduction in late adaptation, and aftereffect in postadaptation. We found significant epoch effects on e_t [F(4,36) = 67.90, P < 0.001; Fig. 4B]. The e_t values showed a marked asymmetry early in adaptation (P < 0.001), which was reduced as subjects adapted (P < 0.001). In early deadaptation, we found the opposite asymmetry, which was significantly different from baseline (P < 0.001) and late adaptation (P < 0.001).

We found that T_out, which we derived analytically (see appendix a) can characterize the adaptation of temporal motor outputs during split-belt walking—this is shown stride by stride in Fig. 4C. We observed that the significant epoch effects on T_out [F(4,36) = 37.80, P < 0.001; Fig. 4D] throughout the experiment were characteristic of the adaptation of motor outputs in other adaptation paradigms (Fine and Thoroughman 2007; Smith et al. 2006; Wolpert and Kawato 1998). First, as expected for a motor output, baseline and early adaptation were not significantly different from one another (P = 0.10). Second, we found a significant increase from early adaptation to late adaptation (P < 0.001), which means that subjects adapted T_out to a new steady-state value for the split-belt condition. Additionally, we found a significant increase from baseline to early deadaptation (P < 0.001), meaning that there was significant storage of the new stepping rhythm for walking on the treadmill. Finally, the early deadaptation value was not different from late adaptation (P = 0.93), demonstrating a smooth change from adaptation to deadaptation.

In contrast, we found that an alternate temporal motor output parameter based on toe-off timings, T_outA, which could also minimize the asymmetry in double supports during split-belt walking, could not be used to characterize the behavior of a temporal motor output (Fig. 4E). Although there was a significant effect of epoch on T_outA values [F(4,36) = 119.90, P < 0.001; Fig. 4F], its behavior differed from that of motor outputs. There was a significant difference between baseline and early adaptation (P < 0.001), and while there was a difference between early and late adaptation (P < 0.001), it was in the wrong direction (i.e., parameter decreased as subjects adapted). Additionally, there was a significant difference between early deadaptation and baseline (P < 0.001) and late adaptation (P < 0.001), which means that while the parameter is stored, it is not unlearned smoothly in deadaptation.

Spatial motor output and motor error.

Similar to the temporal motor output, in the spatial domain we found that subjects adapted their feet placements from a stepping pattern A (i.e., interlimb spatial relationship A in Fig. 1B) to a new stepping pattern A′ to minimize the initial difference in limb oscillations during split-belt walking. Figure 5 schematically demonstrates the spatial changes that occurred during adaptation from a bird's-eye view over the treadmill. During baseline walking, subjects had equal limb angles at heel-strike (α angle, red lines, Fig. 5) (i.e., S_out = 0) and the limbs oscillations are equally centered (i.e., e_s = 0). When the belts are split, the range of motion of the leg on the fast belt becomes much larger than that of the slow leg and subjects take alternating steps. Consequently, equal α angles (i.e., S_out = 0) lead to asymmetric limb oscillations—the proportion of the limb-forward component of the fast leg becomes very different from that of the slow leg (i.e., e_s > 0) (Fig. 5, Early Adapt). Subjects adapt their stepping pattern such that the proportion of the limb-forward placement with respect to its entire movement is the same for both legs (Fig. 5, Late Adapt). In deadaptation, the opposite asymmetry occurs and subjects must unlearn the new stepping pattern to return back to stepping at symmetric locations.

Our error measure, e_s, characterized well the spatial asymmetry during split-belt walking and had the time course during adaptation and deadaptation of a typical error signal (Fig. 6A). Figure 6B shows that there was a significant epoch effect on e_s values [F(4,36) = 72.33, P < 0.001], with e_s values different between baseline and early adaptation (P < 0.001). This spatial asymmetry was reduced as subjects adapted, as shown by the significant differences between early and late adaptation (P < 0.001). In early deadaptation we found the opposite spatial asymmetry, as indicated by the significant differences in early deadaptation of e_s values compared with those in baseline (P < 0.001) and late adaptation (P < 0.001). The asymmetry in early deadaptation was in the opposite direction as early adaptation.

We found that S_out is a parameter that can characterize the adaptation of spatial motor outputs during split-belt walking (Fig. 6C). There was a significant epoch effect on S_out [F(4,36) = 41.55, P < 0.001], with features of S_out that are characteristic of motor outputs (Fig. 6D). There were no significant differences between baseline and early deadaptation S_out values (P = 0.10) or between late adaptation and early deadaptation S_out values (P = 0.75), which indicates a smooth transition in S_out when the environmental conditions changed. However, there was a significant increase between early and late adaptation S_out values (P < 0.001), indicating the adaptation of S_out. Finally, there was also a significant difference between baseline and early deadaptation S_out values (P < 0.001), meaning that there was significant storage of the new stepping pattern for walking on the treadmill.

In contrast, we found that the time course of an alternate S_out parameter based on toe-off timings (S_outA), which could also minimize the asymmetric limb orientation during split-belt walking, could not be used to characterize the behavior of a spatial motor output (Fig. 6E). Figure 6E shows the behavior of the normalized difference in limb angles at toe-off, S_outA. While S_outA showed significant changes across the epochs [F(4,36) = 301.81, P < 0.001], it did not have the characteristic behavior of a motor output (Fig. 6F). First, S_outA did not show the typical smooth transitions in motor outputs when the environmental conditions changed (e.g., tied to split and vice versa). This is shown by the significant differences between baseline and early adaptation (P < 0.001) or late adaptation and early deadaptation (P < 0.001). Also, S_outA decreased from early to late adaptation (P < 0.001), instead of increasing to a new steady state as subjects adapted. Finally, we found the opposite asymmetry in early deadaptation, which was significantly different from baseline (P < 0.001) and late adaptation (P < 0.001).

Temporal motor output is more tightly controlled than spatial motor output.

While on average subjects reached the desired temporal and spatial values by the end of adaptation (Fig. 7, A and C), there was tighter control of temporal symmetry within individual subjects compared with the control of spatial symmetry (Fig. 7, B and D). Through mathematical derivation (see methods, appendixes a and b), we proposed that the temporal motor output would approach T_desired to reestablish temporal symmetry (e_t = 0) and the spatial motor output would approach S_desired to reestablish spatial symmetry (e_s = 0). We observed that in late adaptation the averaged motor outputs approached the “desired” temporal (T_desired) and spatial (S_desired) parameters for symmetric gait (Fig. 7A, temporal; Fig. 7C, spatial). We observed that T_desired and S_desired do not adapt, and instead change rapidly when experimental conditions change (i.e., rapid jump from baseline to early adaptation and again from late adaptation to early deadaptation). Scatterplots of individual subjects' desired values versus motor output in late adaptation (i.e., last 10 strides) are shown for temporal and spatial parameters in Fig. 7, B and D, respectively. A regression was performed, and there was a significant correlation of the respective desired parameters for both temporal and spatial outputs (temporal P < 0.01 and spatial P = 0.01). Note that subjects from the Spatial Hold group were not included in this analysis because we wanted to investigate the natural relationship between motor outputs at the adapted state and their corresponding “desired” values to achieve symmetry. Although both motor outputs could be significantly predicted by their respective desired values, there was a much stronger correlation for the temporal parameters (r = 0.88) as opposed to the spatial parameters (r = 0.40). These results suggest that it might be more important for subjects to achieve temporal symmetry than spatial symmetry.

The adaptation of spatial and temporal motor outputs is dissociable.

Results from experiment 2 indicate that the temporal motor output can be adapted during split-belt walking when the adaptation of spatial motor output is consciously prevented. This finding signifies that the spatial and temporal adaptations are dissociable. Group averages of spatial and temporal motor outputs of subjects in the Control and Spatial Hold groups are shown in Fig. 8. We observed that S_out in the Spatial Hold group does not change during adaptation, whereas there was a clear change in S_out during adaptation in the Control group (Fig. 8A). This is indicated by the significant interaction between group and epoch [F(4,38) = 5.13, P < 0.01]. To verify that the Spatial Hold group did not adapt their leg configuration, we tested for epoch effects for the ankle and knee angles and found that they did not change significantly across epochs [F(4,24) = 1.03, P = 0.41 for ankle; F(4,24) = 1.37, P = 0.27 for knee]. We found that the Control group displayed a significant change in S_out from early to late adaptation (P < 0.001), while the Spatial Hold group did not (P = 0.22). Consequently, the new stepping pattern learned during split-belt walking was stored in the Control group, as indicated by the significant differences between baseline and early deadaptation S_out values (P < 0.01), but not in the Spatial Hold group (P = 0.23).

Fig. 8.

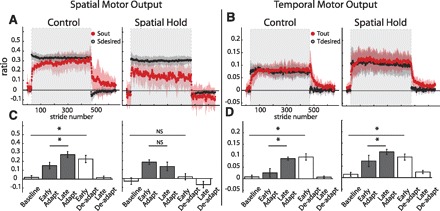
Group averages and standard errors of S_out, S_desired, T_out, and T_desired for Control (N = 7) and Spatial Hold (N = 7) groups. A: stride-by-stride time course of S_out and S_desired for both groups. Adaptation period is represented by shaded area in gray. Spatial motor output adapted normally for the Control group, while the Spatial Hold group was prevented from adapting the spatial motor output. B: stride-by-stride time course of T_out and T_desired for both groups. Adaptation period is represented by shaded area in gray. Although S_out was not adapted in the Spatial Hold group, T_out adapted normally in this group. This suggests that the adaptation of temporal and spatial motor outputs is dissociable. C: statistical analysis on the first 10 strides of S_out for key epochs in the experimental paradigm. A significant change from early to late adaptation was found for the Control but not the Spatial Hold group. Also, significant storage from baseline to early deadaptation was found for the Control but not the Spatial Hold group. D: statistical analysis on the first 10 strides of T_out for key epochs in the experimental paradigm. In both groups T_out adapted normally: there were significant differences between early adaptation and late adaptation and between baseline and early deadaptation.

Conversely, while there were differences in the adaptation of spatial motor outputs across the Control and Spatial Hold groups, both groups adapted their temporal motor outputs similarly [F(4,48) = 1.11, P = 0.36; Fig. 8, B and D]. We observed that there was a significant effect of epoch in both groups [F(4,48) = 19.44, P < 0.001]. In both groups, T_out had significantly different values between early and late adaptation (P < 0.001) and there were significant differences between baseline and early deadaptation (P < 0.001). This indicates that in both groups the changes in T_out with adaptation were stored (Fig. 8D). In conclusion, we demonstrated with this experiment that subjects can adapt their temporal motor output without adapting their spatial motor output—dissociating temporal and spatial adaptation of locomotion.

DISCUSSION

Here we describe two parameters that characterize temporal and spatial motor outputs for locomotion. The temporal motor output is a normalized difference between step timings (i.e., stepping rhythm), while the spatial motor output is a normalized difference between limb angles at heel-strike (i.e., stepping pattern). Both these motor outputs adapt in order to regain temporal and spatial symmetry. Importantly, in this study we were able to dissociate the adaptation of temporal and spatial control. Although the nervous system typically adapts both temporal and spatial parameters, we found that there is more consistent and tighter control of the temporal motor output, suggesting a priority in the adaptation of timing. Moreover, this tighter control of the temporal motor output could also suggest distinct neural structures that control more precisely the adaptation of the temporal control versus the spatial control of stepping in locomotion. In sum, these results suggest that there are separate neural mechanisms that control temporal and spatial locomotion parameters.

Numerous parameters could theoretically capture motor output behavior in walking, particularly since it is a multisegmental and bilateral cyclical movement. Here we analytically derived and systematically tested different candidate parameters and found that the motor outputs defined in this study have strong explanatory value. Furthermore, we think that heel-strike is important for the nervous system to control in a feedforward manner, whether it is the duration between heel-strikes or the limb orientation at heel-strike. When we investigated similar parameters using the toe-off time that could affect temporal and spatial errors, we found that they did not exhibit characteristic motor output behavior (see Figs. 4E and 6E). Since motor outputs have been suggested to represent feedforward adjustments of the nervous system (Smith et al. 2006), this leads us to believe that the temporal and spatial control of heel-strike utilizes feedforward mechanisms to update the subsequent heel-strike.

Although there is an important contribution of the spinal cord, brain stem, and motor cortex in the control of locomotion (Bretzner and Drew 2005; Hayes et al. 2009; Le Ray et al. 2011), the cerebellum is important for the adaptation of the locomotor pattern. The cerebellum is believed to have a role in monitoring errors and updating the motor outputs (Shadmehr and Krakauer 2008), and, not surprisingly, the cerebellum has been shown to be essential for many forms of motor adaptation (Criscimagna-Hemminger et al. 2010; Lewis and Zee 1993; Maschke et al. 2004; Tseng et al. 2007), including split-belt walking adaptation (Morton and Bastian 2006). Locomotor adaptation likely involves the interaction between the cerebellum and cortical or brain stem structures; however, we know that cerebral motor areas are less essential for this adaptation in humans, since individuals with cerebral stroke and hemiparesis can adapt normally (Choi et al. 2009; Reisman et al. 2007, 2009). Work in the cat shows that spinal circuits alone can produce rhythmic stepping patterns on a split-belt treadmill (Forssberg et al. 1980). However, without cerebellar integrity, spinal circuits cannot adapt the locomotor pattern to restore spatial and temporal symmetry (Yanigahara and Kondo 1996). Therefore, we felt it was important to determine that the errors and motor outputs described here were neural inputs/outputs of the cerebellum. For spatial coordination, neural recordings in cats have shown that signals of lower limb length and orientation during locomotion are carried in the dorsal spinocerebellar tract (Bosco and Poppele 2001). Additionally, it has been demonstrated that neurons in the dorsospinocerebellar tract respond differently to bipedal movements compared with ipsilateral movements (Poppele et al. 2003), suggesting that the spatial relationship between both limbs is important to the nervous system. With regard to temporal coordination, additional neural recording studies in cats have found that cerebellar discharges from Purkinje cells are most active at the time of foot contact (Apps and Lidierth 1989; Apps et al. 1995), possibly indicating the importance of this event in the gait cycle. Taken together, these results suggest that some of the essential elements of our model are accessible by the cerebellum for the purposes of adapting movements to predicable perturbations.

Separation of temporal and spatial control of locomotion.

Our findings show separate control of the temporal and spatial parameters of locomotion in this adaptive task. Some of our previous studies have treated these parameters as if they were controlled by overlapping neural systems and would therefore adapt together (Choi and Bastian 2007). However, our more recent work suggests that temporal and spatial parameters may be controlled, and therefore adapted, separately. Children with hemispherectomies, where one half of the cerebrum is removed, adapted their step symmetry but not their double support errors (Choi et al. 2009). Additionally, we have seen that experimental conditions such as consciously controlling the gait or dual-tasking while walking affected the adaptation rate in spatial parameters, but temporal parameters remained unaffected (Malone and Bastian 2010). In that study, we found that the temporal coordination was adapted at a rate almost two times faster than the spatial coordination, even under “control” conditions in which we asked subjects to “just walk.” Here we see similar trends: the spatial parameters take longer to adapt than the temporal parameters (compare spatial and temporal motor outputs in Figs. 4C and 6C). However, in our prior studies spatial and temporal parameters always adapted, just at different rates. While these findings led us to hypothesize separate control and distinct neural substrates of spatial and temporal control of locomotion, this study allowed us to completely dissociate the two. From our direct investigation into the independence of parameters, we found that subjects could consciously prevent their spatial motor output from adapting while the temporal motor output was unaffected.

We also observed that subjects tended to reach temporal symmetry at the adapted state more often than spatial symmetry, thereby suggesting tighter control of the temporal coordination in this locomotor task. Each motor output (temporal and spatial) tended to approach a “desired” value by the end of adaptation that we derived mathematically, using specific error parameters (see methods, appendixes a and b). For temporal coordination, the “desired” parameter was a relationship between stance times (Fig. 3, orange lines). In space, the “desired” value was a relationship between the limb ranges of motion (Fig. 5, blue arrows). Not only did group average curves for the spatial and temporal motor outputs approach the group average “desired” values, but these relationships held true with individual subjects as well. When we regressed the “desired” parameter with the final plateau of the motor output for both spatial and temporal coordination, we found significant positive correlations. Although this result was found for both temporal and spatial coordination, the temporal relationship was more tightly controlled than the spatial relationship (i.e., larger correlation coefficients). In other words, the temporal motor output was more likely to reach the “desired” value (normalized difference of stance times) than the spatial counterparts. While this suggests that temporal asymmetries are smaller than spatial asymmetries in the adapted state, it is difficult to directly compare the temporal and spatial features because temporal and spatial coordination are expressed in different units in this analysis. Future studies will investigate how temporal and spatial motor outputs can combine in order to equalize steps.

Additionally, we attempted to prevent the temporal motor output from adapting but found that this was not as easily accomplished as clamping the spatial adaptation. Subjects were provided with an auditory cue of when to land their feet—a symmetric rhythm (i.e., T_out = 0). However, we found that healthy adults were not able to prevent their temporal motor output from adapting. We hypothesize that this could be due to a number of reasons. First, subjects may not be able to consciously prevent the temporal motor output from adapting under split-belt conditions (i.e., temporal control was harder to influence with conscious efforts; Malone and Bastian 2010). Second, the temporal changes induced by a speed ratio of 2:1 on the split-belt treadmill are small (between 100 and 150 ms). It is possible that while both the subjects and experimenter perceived subjects landing on the time specified by the auditory cue, they do not have the resolution to make conscious perceptions and adjustments on that timescale. Future work will be done to investigate whether different types of feedback on timing control will allow healthy adults to consciously adjust their locomotor timing.

This more stringent control of timing agrees with previous studies in our lab in which we found that temporal control was invariant to conscious efforts (Malone and Bastian 2010) and training structure (Malone et al. 2011). Additionally, temporal adaptation was found to be fully developed by the age of 3, while spatial adaptation continued to develop well into adolescence (Vasudevan et al. 2011), leading us to believe that temporal control is more automatic and perhaps depends more heavily on subcortical circuits.

Clinical implications.

It is important for us to understand features of the gait cycle that the nervous system could use to control locomotion and what it could monitor as error signals relevant to motor outputs. Recently, we have begun to see differences in the temporal and spatial control of locomotion in humans; however, we wanted to know whether it was possible to adapt only spatial or only temporal parameters of walking. This is an important distinction to make, especially for therapeutic rehabilitation. Previous studies have shown that split-belt walking can temporarily improve asymmetries due to hemiparesis from stroke (Reisman et al. 2007). However, some patients have asymmetries in only one domain; for example, they only have a double support asymmetry (temporal). It is important to target therapeutic rehabilitation to only the area of walking that subjects experience difficulty in. Future work will be aimed at possible interventions to improve asymmetries in only one domain for our patient populations.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: L.A.M., A.J.B., and G.T.-O. conception and design of research; L.A.M. performed experiments; L.A.M. and G.T.-O. analyzed data; L.A.M., A.J.B., and G.T.-O. interpreted results of experiments; L.A.M. and G.T.-O. prepared figures; L.A.M. drafted manuscript; L.A.M., A.J.B., and G.T.-O. edited and revised manuscript; L.A.M., A.J.B., and G.T.-O. approved final version of manuscript.

APPENDIX A

Derivation of Temporal Motor Output

To reduce the timing error (i.e., double support symmetry difference, e_t = DS_s − DS_f), we hypothesized that subjects adapt their heel-strike timing. We think that the temporal motor output (T_out) for split-belt adaptation could be a function of the interlimb heel-strike durations, defined as slow (t_s) and fast (t_f) step timings (Fig. 2B, black arrows). The slow step timing is the time between a slow heel-strike and the next fast heel-strike, and vice versa for the fast step timing. Formally expressed,

$$T_{\text{out}}\left(t_{\text{s}},t_{\text{f}}\right)\to T_{\text{desired}}$$

where T_desired is the value that T_out could approach for temporal gait symmetry.

Moreover, we know that for temporal gait symmetry

$$e_{\text{t}}=0\text{or}{\text{DS}}_{\text{s}}={\text{DS}}_{\text{f}}$$

However, by definition the stance time for the slow leg (ST_s) (Fig. 2B, dashed line), or time when the foot is in contact with the slow belt, equals the sum of the slow step timing (t_s) and slow double support time (DS_s), and the same is true for the fast leg.

Therefore,

$${\text{DS}}_{\text{f}}={\text{ST}}_{\text{f}}-{\text{t}}_{\text{f}}\text{and}{\text{DS}}_{\text{s}}={\text{ST}}_{\text{s}}-{\text{t}}_{\text{s}}$$

where ST_s and ST_f are the slow and fast stance times, respectively. ST_s was calculated as the time from heel-strike to toe-off of the slow leg, and the same was done for the fast leg.

Thus for temporal gait symmetry,

$${\text{ST}}_{\text{f}}-t_{\text{f}}\text{and}{\text{DS}}_{\text{s}}={\text{ST}}_{\text{s}}-t_{\text{s}}$$

rearranging terms,

$$t_{\text{s}}-t_{\text{f}}={\text{ST}}_{\text{s}}-{\text{ST}}_{\text{f}}$$

To compare the behavior across subjects we can normalize both sides by the stride time (T_stride) to account for subjects who walked at different cadences (i.e., strides/s). Accordingly, we obtain

$$\frac{t_{\text{s}}-t_{\text{f}}}{T_{\text{stride}}}=\frac{{\text{ST}}_{\text{s}}-{\text{ST}}_{\text{f}}}{T_{\text{stride}}}$$

Note that the stride time, which is the period between two consecutive heel-strikes of the same leg, equals to the sum of step timings (Fig. 2B, black arrows).

Therefore we can define the temporal motor output as

$$T_{\text{out}}=\frac{t_{\text{s}}-t_{\text{f}}}{T_{\text{stride}}}=\frac{t_{\text{s}}-t_{\text{f}}}{t_{\text{s}}+t_{\text{f}}}$$

and T_desired, or the value that the temporal motor output could approach for temporal gait symmetry, can be defined as

$$T_{\text{desired}}=\frac{{\text{ST}}_{\text{s}}-{\text{ST}}_{\text{f}}}{T_{\text{stride}}}$$

In conclusion, we propose that the temporal motor output is the difference in interlimb heel-strikes normalized by their sum. Moreover, we hypothesize that to minimize the motor error, defined as the difference in double support times, the temporal motor output would approach T_desired, defined as the normalized stance time differences.

Since DS_s and DS_f can also be expressed as a function of slow and fast toe-off timings (t_s-off and t_f-off), a similar derivation can be performed to obtain an alternate T_outA:

$$T_{\text{outA}}=\frac{t_{\text{s\_off}}-t_{\text{f\_off}}}{t_{\text{s\_off}}+t_{\text{f\_off}}}$$

APPENDIX B

Derivation of the Spatial Motor Output

To reduce the spatial error (i.e., difference in the center of oscillation, e_s = r_s − r_f) we hypothesized that subjects adapted their heel-strike angle (α). In other words, we think that the spatial motor output (S_out) for split-belt adaptation could be a function of the limb angles at heel-strike. Formally expressed,

$$S_{\text{out}}\left({\alpha }_{\text{s}},{\alpha }_{\text{f}}\right)\to S_{\text{desired}}$$

where S_desired is the value that S_out could approach for spatial gait symmetry.

Again, we hypothesize that for spatial gait symmetry

$$e_{\text{s}}=0\text{or}{r}_{\text{f}}=r_{\text{s}}$$

also, by definition,

$$r_{\text{s}}=\frac{{\alpha }_{\text{s}}}{{\gamma }_{\text{s}}}\text{and}{r}_{\text{f}}\frac{{\alpha }_{\text{f}}}{{\gamma }_{\text{f}}}$$

Therefore we have that

$$\frac{{\alpha }_{\text{f}}}{{\gamma }_{\text{f}}}=\frac{{\alpha }_{\text{s}}}{{\gamma }_{\text{s}}}$$

Rearranging terms, we obtain the following relationship:

$$\frac{{\alpha }_{\text{f}}}{{\alpha }_{\text{s}}}=\frac{{\gamma }_{\text{f}}}{{\gamma }_{\text{s}}}$$

To avoid exaggerating differences when α_s was small (i.e., close to zero), we rearranged terms to normalize the α difference by their sum, shown below:

$$\begin{array}{c}\frac{{\alpha }_{\text{f}}}{{\alpha }_{\text{s}}}=\frac{{\gamma }_{\text{f}}}{{\gamma }_{\text{s}}}\\ \frac{{\alpha }_{\text{f}}}{{\alpha }_{\text{s}}}+1=\frac{{\gamma }_{\text{f}}}{{\gamma }_{\text{s}}}+1\end{array}$$

$$\frac{{\alpha }_{\text{f}}+{\alpha }_{\text{s}}}{{\alpha }_{\text{s}}}=\frac{{\gamma }_{\text{f}}+{\gamma }_{\text{s}}}{{\gamma }_{\text{s}}}\left(a\right)$$

Similarly,

$$\frac{{\alpha }_{\text{f}}+{\alpha }_{\text{s}}}{{\alpha }_{\text{f}}}=\frac{{\gamma }_{\text{f}}+{\gamma }_{\text{s}}}{{\gamma }_{\text{f}}}\left(b\right)$$

By inversing (a) and (b) and then subtracting (b) − (a), we obtain

$$\frac{{\alpha }_{\text{f}}-{\alpha }_{\text{s}}}{{\alpha }_{\text{f}}+{\alpha }_{\text{s}}}=\frac{{\gamma }_{\text{f}}-{\gamma }_{\text{s}}}{{\gamma }_{\text{f}}+{\gamma }_{\text{s}}}$$

Therefore we can define the spatial motor output as

$$S_{\text{out}}=\frac{{\alpha }_{\text{f}}-{\alpha }_{\text{s}}}{{\alpha }_{\text{f}}+{\alpha }_{\text{s}}}$$

and S_desired, or the value that the spatial motor output could approach for spatial symmetry, can be defined as

$$S_{\text{desired}}=\frac{{\gamma }_{\text{f}}-{\gamma }_{\text{s}}}{{\gamma }_{\text{f}}+{\gamma }_{\text{s}}}$$

In conclusion, we propose that the spatial motor output is the difference in heel-strike angles normalized by their sum. Moreover, we hypothesize that to minimize spatial motor error, defined as the difference in proportions of limb-forward placements with respect to the entire range of motion of the leg, the spatial motor output would approach S_desired, defined as the normalized difference in the limb's range of motion.

Since e_s can also be expressed as a function of slow and fast angles at toe-off (β_s and β_f), a similar derivation can be performed to obtain an alternate S_outA:

$$S_{\text{outA}}=\frac{{\beta }_{\text{s}}-{\beta }_{\text{f}}}{{\beta }_{\text{s}}+{\beta }_{\text{f}}}$$