Dynamic connectivity regression: Determining state-related changes in brain connectivity

Abstract

Most statistical analyses of fMRI data assume that the nature, timing and duration of the psychological processes being studied are known. However, often it is hard to specify this information a priori. In this work we introduce a data-driven technique for partitioning the experimental time course into distinct temporal intervals with different multivariate functional connectivity patterns between a set of regions of interest (ROIs). The technique, called Dynamic Connectivity Regression (DCR), detects temporal change points in functional connectivity and estimates a graph, or set of relationships between ROIs, for data in the temporal partition that falls between pairs of change points. Hence, DCR allows for estimation of both the time of change in connectivity and the connectivity graph for each partition, without requiring prior knowledge of the nature of the experimental design. Permutation and bootstrapping methods are used to perform inference on the change points. The method is applied to various simulated data sets as well as to an fMRI data set from a study (N=26) of a state anxiety induction using a socially evaluative threat challenge. The results illustrate the method’s ability to observe how the networks between different brain regions changed with subjects’ emotional state.

INTRODUCTION

Functional magnetic resonance imaging (fMRI) data has been extensively used to study the neural basis of perception, cognition, and emotion. Traditionally, these studies have focused on locating brain regions showing task-related changes in neural activity, for example, greater activity during an experimental task than during a baseline state (Lindquist, 2008). The voxel-wise general linear model (GLM) (Worsley and Friston, 1995) has become the standard approach for analyzing such data. However, since a significant amount of neural processing is performed by integrated networks consisting of multiple brain regions, a complete understanding of brain function should also include the study of interactions between distinct brain regions. An active area of neuroimaging research involves examining the undirected association, or functional connectivity, between two or more spatially remote brain regions (Biswal et al., 1995; Friston et al., 1993). Functional connectivity analyses allow for the characterization of interregional neural interactions during certain cognitive or motor tasks, or alternatively from brain activity during resting state experiments. Properly applied, they allow for the creation of maps of distinct spatial distributions of temporally correlated brain regions, called functional networks, and provide means for studying the mechanisms by which experimental manipulations, brain activity, and psychological/physiological outcomes affect one another.

The simplest approach to functional connectivity analyses simply compares the correlation between regions of interest, or between a “seed” region and other voxels throughout the brain. Alternative approaches include using multivariate methods, such as Principal Components Analysis (PCA) (Andersen, Gash and Avison, 1999) and Independent Components Analysis (ICA) (Calhoun et al., 2001b; McKeown et al., 1998), to identify task related patterns of brain activation without making any a priori assumptions about its form. In contrast, partial least squares (PLS; McIntosh et al., 1996; Krishnan et al., 2010) attempts to identify common patterns between brain activity and behavioral measures or experimental design.

Another approach is to simply estimate the covariance, or correlation matrix, between predefined regions of interest (ROIs). However, the process of estimating the covariance matrix can at times be difficult (Stein, 1956; Pourahmadi, 2011), due to the positive definite constraint on the matrix and the high-dimensional nature of the data. Dempster (1972) simplified the estimation procedure using the idea of covariance selection, which sets certain elements of the precision matrix (the inverse covariance matrix) to zero. Here a zero element can be interpreted as conditional independence between the corresponding variables, or ROIs, thus indicating a lack of functional connectivity between regions.

The graphical lasso, or glasso (Friedman et al., 2007), is a technique used for estimating a sparse precision matrix that uses an l₁-constraint (constraint on the absolute values of the elements of the precision matrix) to force many of the elements to zero, in a similar manner as the standard lasso forces regression coefficients to zero. Varoquaux et al. (2010) recently applied an extension of these techniques to fMRI data where they estimate sparse precision matrices for a group of subjects under the assumption that they have the same structure for all individuals in the group. In other words, the zero elements of the matrix are assumed to be fixed across all subjects.

The covariance estimation procedures discussed above are typically applied to steady-state time series data, where the experimental condition does not vary over the course of the experiment. However, under certain circumstances the dynamic manner in which ROIs interact with one another during the course of the experiment is of primary interest. For example, PPI (psychophysiological interactions; Friston et al., 1997) is a technique that investigates whether the correlation between two brain regions differs depending on psychological context, that is, whether a significant interaction exists between the psychological state and the functional coupling between two brain regions. Another recent example is statistical parametric network analysis (Ginestet and Simmons, 2011), which allows researchers to study the dynamics of functional networks under different levels of cognitive demand.

While addressing the dynamic nature of functional connectivity, both of these techniques assume that the timing of the various contexts is known. However, it is often difficult to specify the nature, timing and duration of the psychological processes being studied a priori. Hence, an important extension would be to introduce methods that can detect changes in connectivity, regardless of the nature of the experimental design. To address this issue Bassett et al. (2010) explored the dynamic organizational (modularity) changes of graphs for human learning using predefined data windows spanning multiple temporal scales (e.g. days, hours and minutes) during motor learning. Here the width of the window is chosen by the researcher prior to analysis, where it would ideally be determined from the data itself.

In this paper, we take a different approach and consider a novel data-driven technique for partitioning the experimental time course into distinct intervals based on the underlying functional connectivity patterns between ROIs. The technique, called Dynamic Connectivity Regression (DCR), detects temporal change points in functional connectivity and estimates a graph, or series of relationships between brain regions, for data in the temporal partition that falls between pairs of change points. Similar to Varoquaux et al. (2010) it is assumed that within each partition the graph structure is the same across subjects. An illustration of DCR can be seen in Figure 1A, which depicts two change points, denoted τ₁ and τ₂. At these change points, the functional connectivity between ROIs is altered due to shifts in behavior, cognitive state, or other neurobiological processes. DCR allows us to not only detect these change points, but also estimate an undirected graph using the data within each partition, thereby allowing us to dynamically measure the functional connectivity between the ROIs. These temporal partitions can be expressed equivalently as a regression tree (see Figure 1B) with a graph estimated at each terminal node.

Figure 1.

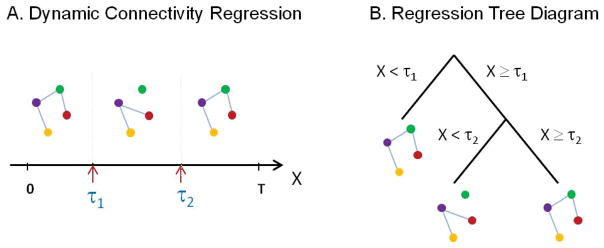
A toy example. (A) Two change points (denoted τ₁ and τ₂) exist where the functional connectivity between the 4 ROIs changes behavior. DCR allows us to not only detect the change points, but also estimates an undirected graph which measures the functional connectivity between the ROIs. Equivalently, the temporal partitions can be expressed as a regression tree (B) with a graph estimated at each terminal node.

DCR shares similarities to the Graph Valued Regression (GVR) technique introduced by Liu et al. (2010a). In both methods, the dependency structure of a random variable Y (e.g., a set of brain regions) is assessed conditional on another variable X (e.g., time or some characteristic of the subjects), and it is of interest to study the dependency structure of Y given X. The main differences between methods lie in the potential locations of the splits (or change points) and the applied penalization method. DCR is more flexible in that splits are permitted to occur anywhere along the time course, whereas GVR only considers dyadic splits (i.e. halves, quarters, eighths, etc.). The criterion for model selection used by DCR and GVR are Bayesian Information Criteria (BIC) and risk, respectively. Finally, both techniques share similarities to classification and regression trees (CART; Breiman et al., 1984) insofar as they build a regression tree on the space of covariates, but unlike CART, at each node of the tree a graph is estimated using glasso.

This paper is organized as follows. We begin by introducing the theoretical foundation of DCR and a greedy partitioning algorithm for estimating the model parameters. Next we introduce inferential procedures, based on the bootstrap, for determining statistically significant change points. Finally, we apply the method to a number of simulated data sets, as well as to an fMRI data set from a study of state anxiety, induced using a socially evaluative threat (SET) challenge. The results display DCR’s power and capability to serve as a useful tool in the high dimensional image setting.

METHODS

Background

The goal of dynamic connectivity regression (DCR) is to detect temporal change points in functional connectivity and estimate a graph, or set of relationships between ROIs, for data in the temporal partition that falls between each pair of change points. Throughout this paper, we assume that Y is a p-dimensional Gaussian random vector where each element represents one of p pre-defined regions of interest (ROIs). Before introducing DCR we briefly discuss some of the theoretical building blocks required for the development of the method. These include topics such as graphical models, the graphical lasso and regression trees.

Graphical Models

The DCR technique builds upon the extensive literature on graphical models (Whittaker, 1990; Edwards, 1995; Cox and Wermuth, 1996). Within this framework, graphical models display the dependency structure of a random vector Y (e.g., a set of p pre-defined brain regions) using a graph G. Graphs are mathematical structures that can be used to model pair-wise relationships between variables. They consist of a set of vertices V and corresponding edges E that connect pairs of vertices. A graph G=(V, E) may be defined as either undirected or directed with respect to how the edges connect one vertex to another. Directed graphs infer directionality between variables while undirected graphs do not, and in the present work we focus exclusively on the latter. Here each vertex represents a random variable, or ROI, and edges encode dependencies between the variables. In the fMRI setting, a missing edge indicates a lack of functional connectivity between corresponding regions.

A graph of Y can alternatively be represented using the precision matrix (inverse covariance matrix) of Y, with the elements of the matrix corresponding to edge weights. Here a missing edge between two vertices in the graph indicates conditional independence between the variables, giving rise to a zero element in the precision matrix. Throughout this paper we will be interested in modeling dependencies between regions through the precision matrix.

Graphical LASSO (GLASSO)

The Least Absolute Shrinkage and Selection Operator (lasso) (Tibshirani, 1996) is a shrinkage and selection method for linear regression. It minimizes the usual sum of squared errors with a bound on the sum of the absolute values of the regression coefficients. It is a method of selecting a sparse number of predictors in the usual linear regression setting by shrinking many of the β coefficients to zero.

The graphical lasso, or glasso (Friedman et al., 2007), is an extension of this thinking to the realm of graphs. Suppose Y is a p-dimensional Gaussian random vector with mean and covariance matrix Σ. If the ij^th component of the precision matrix Ω=Σ⁻¹ is zero, then variables i and j are said to be conditionally independent, given the other variables, and no edge is included in the graph between the variables. The glasso is a method of estimating sparse graphs G=(V, E) by applying an l₁-penalty to the elements of the precision matrix. Similar to the lasso technique, the glasso shrinks elements of Ω to zero, corresponding to missing edges in the graph. A sparse estimate of Ω is obtained by minimizing the penalized log likelihood

$$\widehat{\mathrm{\Omega }}=argmin\left\{tr(S\mathrm{\Omega })-log\mid \mathrm{\Omega }\mid +\lambda {\Vert \mathrm{\Omega }\Vert }_1\right\}$$ (1)

where Ω is any positive definite matrix, S is the sample covariance matrix, ||Ω||₁ is the element-wise l₁-norm of Ω, and λ is a tuning parameter. An efficient algorithm has been developed (Friedman et al. 2007) for finding Ω̂ that estimates a single row (and column) of Ω in each iteration by solving a lasso regression.

Regression Trees

Regression trees are a simple, but powerful, method for performing nonparametric regression. They are easy to compute, require virtually no assumptions, and are simple to interpret. The idea is to partition the space of explanatory variables into homogenous segments within which the response is modeled locally. For a single explanatory variable, its range is partitioned into segments and within each segment a local regression function is fit. For two or more explanatory variables, the covariate space is instead partitioned into rectangular regions. Typically the local regression function on each partition is assumed to be constant and estimated by taking the mean of the response variables whose explanatory variables lie inside the partition.

Partitioning of covariate space is performed recursively by repeatedly selecting the most relevant explanatory variable and using it to split the data into groups. Within each partition, the process is repeated until the resulting groupings are homogenous. This allows us to divide the covariate space χ into disjointed homogenous sets χ₁,…, χ_m. Recursive partitioning models are often called trees as the sequence of partitions can be represented using a tree-like structure (see Figure 1) where each terminal node, or leaf, of the tree represents a cell of the partition with a constant response associated with it. This representation is useful as it can help make the results more interpretable. The most commonly used recursive partitioning technique is classification and regression trees (CART; Breiman et al. 1984), which is a non-parametric decision tree learning method that produces either classification (the predicted outcome is the class to which the data belongs) or regression trees (the predicted outcome can be considered a real number).

Dynamic Connectivity Regression (DCR)

In Dynamic Connectivity Regression (DCR), as well as having the random variable Y, another variable X (e.g. time) is also available. The goal is now to estimate G(x), the graph of Y conditioned on the covariate X taking some value x. The space of the covariate X is divided into finitely many homogenous partitions and within each, the glasso is used to estimate a partition-specific sparse graph. The partitions are found in a similar manner as in regression trees, with split points chosen based on whether they give rise to a reduction of the Bayesian information criteria (BIC). However, while techniques such as CART estimate the mean within each partition element, DCR instead estimates an undirected graph.

The general setup of the DCR method is as follows. Suppose {(x₁, y₁),…, (x_T, y_T)} is an independent identically distributed (i.i.d.) sample from the joint distribution of (X, Y) where X is a d-dimensional and Y a p-dimensional random vector (e.g., corresponding to p ROIs). It is assumed that

$$\mathbf{Y}\mid \mathbf{X}=\mathbf{x}~N_p(\mu (\mathbf{x}),\mathrm{\sum }(\mathbf{x}))$$

where μ(x) is a p-dimensional vector-valued mean function and Σ(x) is a p×p matrix-valued covariance function. An assumption of the method is that for each x, Ω(x) = Σ(x)⁻¹ is a sparse matrix with many zero elements, indicating conditional independence between variables (regions). This assumption reflects our belief that the brain networks are sparse, with relatively few edges between regions. The goal is to find a sparse inverse covariance matrix, Ω̂, to estimate Ω(x) for any x in the domain of X denoted χ. In this work we assume that X is the 1-dimensional variable time and the domain of X is given by χ = [0,T]. However, in practice X can be any d-dimensional vector consisting of either subject-attributes or task-related information.

Assume we have a partition Π = {χ₁,…, χ_m} on that splits the domain into homogenous segments. For example, if X represents time, then χ₁ = [0, τ₁], χ₂ = [τ₁, τ₂], …, χ_m = [τ_m−1,T] for some values of 0 < τ₁ ≤ τ₂ ≤ ....≤ τ_m−1 < T. Figure 1 shows an example with m=3 partitions. Here the time points τ₁ and τ₂ represent boundaries between partitions. If each partition is homogenous, then these points represent change points in the behavior of the response variable Y. For each partition χ_j, the sample mean is estimated by taking the average value of y whose x value lies in the partition, i.e.

$${\widehat{\mathbf{\mu }}}_{{\chi }_j}=\frac{1}{{\sum }_{i=1}^{T}I(x_i\in {\chi }_j)}\sum _{i=1}^T{\mathbf{y}}_{i}I(x_i\in {\chi }_j)$$ (2)

The glasso is then used to estimate a sparse precision matrix. In other words, suppose Σ̂_χj is the sample covariance matrix for the partition element χ_j given by

$${\widehat{\mathrm{\sum }}}_{{\chi }_j}=\frac{1}{{\sum }_{i=1}^{T}I(x_i\in {\chi }_j)}\sum _{i=1}^T({\mathbf{y}}_i-{\mathbf{\mu }}_{{\chi }_j}){({\mathbf{y}}_i-{\mathbf{\mu }}_{{\chi }_j})}^{T}I(x_i\in {\chi }_j)$$ (3)

Then the estimator Ω̂_χj is found by optimizing

$${\widehat{\mathrm{\Omega }}}_{{\chi }_j}=argmin\left\{tr({\widehat{\mathrm{\sum }}}_{{\chi }_j}\mathrm{\Omega })-log\mid \mathrm{\Omega }\mid +\lambda {\Vert \mathrm{\Omega }\Vert }_1\right\}$$ (4)

where λ is a tuning parameter. In empirical work, the full regularization path of λ values is run and the optimal value is chosen based on the BIC (see Appendix A). Large values of λ yield a very sparse graph while λ=0 results in a “full” covariance matrix or graph. To reduce the bias of the glasso and improve the model selection performance when estimating graphs, it can be shown (Liu et al., 2010b) that it is best to first estimate the sparse precision matrix using l₁-regularization and thereafter refit the model without the regularization but keeping the zero elements in the matrix fixed.

DCR Algorithm

In this section we describe a greedy partitioning scheme for estimating the DCR model parameters. In particular we are interested in determining the split points, or change points, and corresponding partition specific graphs. In the description below we assume the input data is from a single subject. Hence, Y is a T×p matrix where T is the experimental time and p the number of ROIs. Similarly, X is a vector of time ranging from 1 to T. For multi-subject analyses, the same algorithm can be used with subjects stacked in a similar manner as in Group ICA (Calhoun et al., 2001). Here the N individual subjects data are stacked to make an NT×p matrix corresponding to Y and their time courses concatenated to make a vector of length NT corresponding to X. The resulting data is similar in nature to panel data commonly seen in the econometrics literature.

Throughout, we make use of the Bayesian information criterion (BIC) which is a model selection criterion based on combining the likelihood function with a penalty term that guards against over-fitting (see Appendix A). Hence, it balances the dual needs of adequate model fit and model parsimony. Alternative penalization criteria (e.g., AIC) were also tested, but the combination of glasso and BIC provided the best performance.

Our greedy partitioning scheme begins by calculating the sample mean and sample covariance for the entire data set using Eqs. (2) and (3), respectively. Estimates of the precision matrix are then obtained for the full path of possible λ values using Eq. (4). As mentioned above, large values of λ give rise to sparse graphs while small values give rise to denser graphs (i.e. containing more edges). The value of λ that minimizes the BIC is chosen, thus identifying non-zero edges, and the model is refit without the l₁-constraint while keeping the zero elements in the matrix fixed to reduce bias and improve the model selection performance. The minimum BIC score for the entire data set is recorded, providing a baseline in which to evaluate subsequent splits of the domain of X.

Upon completion of this step, the data is partitioned into two parts; a left subset consisting of time points {1:Δ} and a right subset consisting of {Δ+1:T}, where T represents the length of the experimental time course. Note Δ is usually chosen to be between 10–20 time points to ensure that there is enough data to provide reliable estimates of the sample means and sample covariance matrices. The choice of Δ is of particular importance as it also represents the minimum possible distance between adjacent change points and its value can be adjusted depending on the existence of a priori knowledge about the spacing of changes in functional connectivity. The sample mean and covariance matrices for both subsets are calculated separately using Eqs. (2) and (3), respectively. The full path of possible λ values for the glasso is run on both subsets and the final values of λ and the corresponding precision matrices are chosen using BIC. Each model is then refit, as above, keeping the zero elements in the precision matrix fixed, and the combined BIC scores for the two subsets are recorded. This procedure is repeated along the entire time path, with the data partitioned into two subsets with split points ranging from Δ+1 to T−Δ+1. The partition with the smallest combined BIC score is chosen and, if its value is less than the BIC score for the entire data set, the corresponding split point is used to partition the data, thus identifying the first change point.

The DCR procedure continues by recursively applying the same method to each individual partition element until they can no longer be split any further. In other words, if the first split occurs at time point ρ, the procedure is repeated for both the data set consisting of time points {1:ρ} and the one consisting of time points {ρ+1:T}. The procedure is repeated until no further splits reduce the BIC score. After completion, the DCR algorithm will have split into connected partitions χ₁,.....χ_m (e.g., [0, τ₁], [τ₁, τ₂], … [τ_m−1, T]) and within each partition χ_j glasso is used to estimate a graph Ĝ_j, which consists of the nodes (ROIs) and edges/connections between them. The step-by-step description of the DCR algorithm can be found in Appendix B.

Inference

In this section we discuss a series of inferential procedures that can be used in conjunction with DCR. Throughout, our focus will be on performing inference about whether or not a detected change point is significant. Since a change point is defined as a splitting time where partitioning the data set results in a decrease in BIC, we base inference on creating confidence bounds for the BIC reduction at each possible change point.

A random permutation procedure

To determine whether significant change points exist, confidence bounds for the BIC reduction at each non-zero splitting time are created using a simple permutation test procedure. The procedure is based on the assumption that the underlying data are independent (i.e. no significant splits exist), and thus can be permuted across time without decreasing evidence of a split. The procedure starts by using DCR to determine a candidate split, which we denote ρ. To test whether or not it is significant, the data is repeatedly permuted across time. For each permutation the data is split into two parts, one consisting of time points {1:ρ} and the other consisting of {ρ+1:T}. The combined BIC score from each subset is subtracted from the BIC of the entire permuted data set and the results are combined across permutations to create a permutation distribution. The entire procedure is repeated for each possible splitting time.

The (1−α/2) and α/2 quantiles of the permutation distribution for each non-zero splitting time can be plotted and interpreted as 100(1− α)% confidence bounds. For a candidate splitting time ρ, if the value of the BIC reduction for the original data is not extreme relative to confidence bounds based on random permutations of the data, then there is no evidence of a difference between the original data and the random permutations. Hence, the splitting time is not significant and the connectivity or undirected graph remains unchanged. On the other hand, if the reduction is more extreme, we conclude there is a significant splitting time at ρ with a subsequent change in connectivity.

Block and Stationary Bootstrap

The permutation procedure described above provides a quick and clean method for computing confidence bounds for the BIC reduction at each non-zero splitting time ρ under the assumption of independence. However, if there is a serial dependence structure present in the data, it fails to take this into account, thereby providing incorrect estimates of the confidence bounds. Two methods that are mindful of the dependency structure are the block bootstrap and the stationary bootstrap. While the ordinary nonparametric bootstrap assumes the data are uncorrelated and resamples the entire data set, the block bootstrap introduced by Carlstein (1986), assumes the data are stationary. Here successive time points are assumed to be correlated, but observations “far apart” are assumed to be uncorrelated. The method therefore divides the time series into blocks and resamples these blocks with replacement to create a pseudo time series. The main idea underlying this approach is that by resampling sufficiently long blocks, the dependency structure of the original time series is preserved. Many variants of this method exist, including the idea of using overlapping blocks introduced by Künsch (1989).

The stationary bootstrap is a resampling scheme introduced by Politis and Romano (1994). It is an adaptation of the block bootstrap that allows for randomly varying block sizes. For any strictly stationary time series (Y_t) the stationary bootstrap procedure consists of generating pseudo-samples Y₁^*,….., Y_T^* from the sample Y₁,….., Y_T by taking the first T elements from Y_K1,…,Y_K1+L1−1,…Y_KN+LN−1 where (K_i) is an i.i.d sequence of random variables uniformly distributed on {1,….T} and (L_i) is an i.i.d. sequence of geometrically distributed random variables with P(L₁ = k) = q(1−q)^k−1, k=1,2,…., for some q = q_n ∈ (0,1). Note that the mean block size is ξ =1/q, where the choice of ξ in the stationary bootstrap is similar to the choice of block length in the block bootstrap.

Both the block and stationary bootstrap confidence bounds are created in a similar manner as the permutation confidence bounds discussed above. For each non-zero splitting time, the (1−α/2) and α/2 quantiles of the empirical distribution of the bootstrapped replicates of BIC reduction are plotted and interpreted as 100(1−α)% confidence bounds. For a potential splitting time ρ, if the BIC reduction for the original data is more extreme (either larger or smaller) than the 100(1−α)% confidence bounds computed using repeated bootstrap replicates, we conclude there is a significant splitting time at ρ, indicating a change in connectivity.

Networks and Undirected Graphs

Once the significant splitting times have been found, the data is divided into partitions defined by the splits. For each partition, the sample mean and sparse precision matrix are calculated using equations (2) and (3), respectively. Using the full path of λ values, the edges in the undirected graph are chosen based on the value that minimizes the BIC. It is necessary to carry out these extra calculations as the actual partitioning is not finalized until after inference is performed. For example, the first split, or connectivity change point, partitions the data into two data sets and the λ values associated with this split assumes there are no further splits. If additional splits exist, the λ value associated with the partition is no longer valid as it is based on data no longer included in the partition.

Simulations

To assess the performance of the DCR method, a series of simulation studies were performed. The first two simulations illustrate the application of the DCR estimation procedure to single-subject i.i.d. data (i.e. null data). The next ten simulations illustrate the application of the DCR estimation procedure to both multi-subject null data and multi-subject simulated Vector Autoregressive (VAR) data (Zellner, 1962; Hamilton, 1995). The latter is an econometric model, generalizing the univariate AR model, commonly used to capture the evolution and the interdependencies between multiple time series. It has the property of autocorrelation in the individual time series, as well as cross correlation between time series, and is thus representative of the properties underlying fMRI data.

The objective of each simulation is to find the connectivity change points and estimate functional connectivity within each resulting partition. The value of Δ is chosen to be 10 time points to ensure that there is enough data to provide reliable estimates of the sample means and sample covariance matrices. However, we found that altering this value had minimal impact on the results. Permutation and bootstrapping procedures are used to perform meaningful inference procedures. For the stationary bootstrap, ξ=1/0.05 is used which corresponds to a mean block size of 50, 30, and 10 for the simulated data sets composed of 1000, 600 and 200 time points, respectively. This block size was chosen empirically, but investigations (not presented here) showed its value had minimal impact on the results. As an alternative, one could choose the mean block size by calculating the sample autocorrelation function (ACF) of the data and observing the dependency structure.

Table I summarizes how the data is generated in each simulation. Here N, T and p represents the number of subjects, the length of the time series, and the number of included regions, respectively. The information in the Mean change and Spikes columns indicate whether mean changes or spikes were included in the simulation, their magnitude and at what time point they occurred. The ROI connectivity column indicates which ROIs were functionally connected during each partition. For the VAR simulations, the dependency between ROIs was similar for each subject with a mean correlation of approximately 0.6. In each case, the rest of the ROIs were made up of i.i.d. Gaussian noise indicating a lack of functional connectivity.

For Simulation 7, each subject has 5 random spikes of magnitude 4 added to their ROI time series. For Simulation 8, the strength of the dependency, or connection between the ROIs specified, differs across subjects. For certain subjects, the dependency is strong (mean correlation ~ 0.7) while for others it is weak (mean correlation ~ 0.3). Also 5 subjects are simply i.i.d. Gaussian noise. For Simulation 11, half the subjects have a different connectivity change point compared to the other half, that is, the same connectivity patterns are consistent across subjects but appear at different time points. Finally, Simulation 12 is repeated 100 times to verify the consistency of the results. For each simulation the red triangles represent the .975 and .025 empirical quantiles of the BIC reduction for 1,000 stationary bootstrap replications of the data for each non-zero split unless otherwise stated.

Experimental Data

The data was taken from an anxiety-inducing experiment (Wager et al., 2009a&b; Lindquist and McKeague, 2009). The task was a variant of a well-studied laboratory paradigm for eliciting social threat, in which participants must give a speech under evaluative pressure. The design was an off–on–off design, with an anxiety-provoking speech preparation task occurring between lower anxiety resting periods. Participants were informed that they were to be given 2 min to prepare a 7 min speech, and that the topic would be revealed to them during scanning. They were told that after the scanning session they would deliver the speech to a panel of expert judges, though there was “a small chance” they would be randomly selected not to give the speech. After the start of fMRI acquisition, participants viewed a fixation cross for 2 min (resting baseline). At the end of this period, participants viewed an instruction slide for 15 s that described the speech topic, which was “why you are a good friend”. The slide instructed participants to be sure to prepare enough for the entire 7 min period. After 2 min of silent preparation, another instruction screen appeared (a relief instruction, 15 s duration) that informed participants that they would not have to give the speech. An additional 2 min period of resting baseline completed the functional run.

Data was acquired and preprocessed as described in previous work (Wager et al. 2009a). During the course of the experiment a series of 215 images were acquired (TR= 2 s). In order to create ROIs, time series were averaged across the entire region. Two separate data sets were extracted from the experiment: the first consisting of 4 ROIs and heart rate for N=23 subjects (Figure 10A) and the second consisting of 5 ROIs (Figure 11A) for N=26 subjects. The discrepancy between the numbers of subjects was due to the fact that heart rate measurements were not available for 3 subjects. The regions in the first data set were chosen due to the fact that they showed a significant relationship to heart rate in an independent data set. The temporal resolution of the heart rate was 1 second compared to 2 seconds for the fMRI data. Hence, the heart rate was down-sampled by taking every other measurement. The regions in the second data set were chosen because they each showed the presence of at least one significant change in mean intensity in a previous analysis (Lindquist et al., 2007). The regions included the visual cortex, bilateral superior temporal sulcus, ventral striatum, and ventromedial PFC.

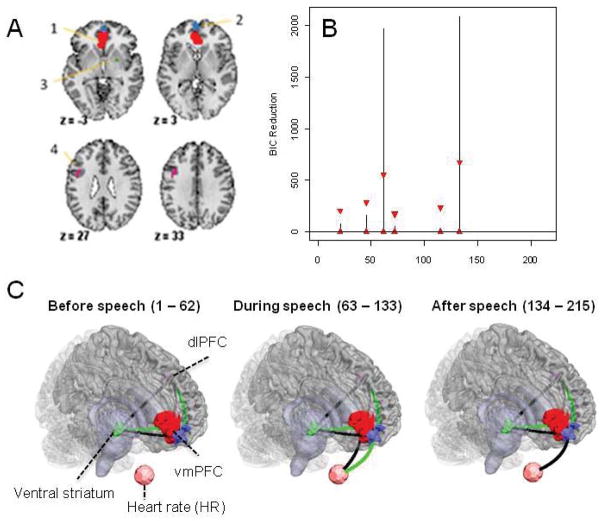
Figure 10.

(A) The 4-ROI and heart rate data set - the regions are: (1) VMPFC, (2) DLPFC, (3) Striatum. (B) The splitting times plotted against BIC reduction for the 4-ROI and heart rate data set with 99% confidence bounds computed using the stationary bootstrap. (C) The corresponding undirected graphs. Black lines indicate a positive relationship between connected regions, while green lines indicate a negative relationship. The thickness of the lines corresponds to the strength of the relationship.

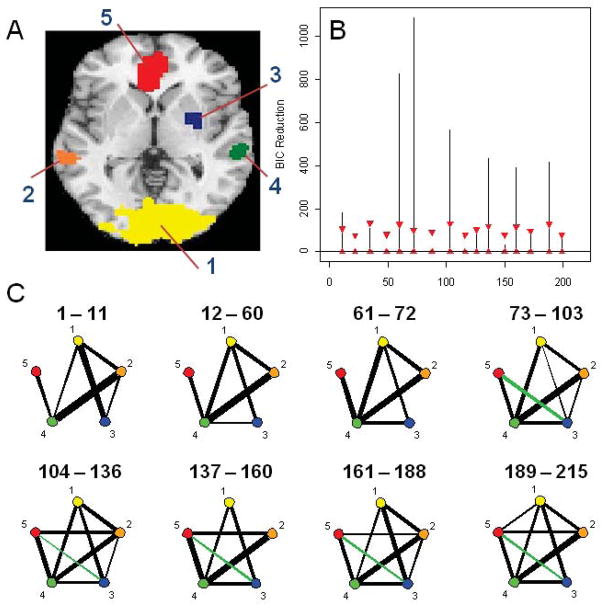
Figure 11.

(A) The 5-ROI data set - the regions are: (1) Visual cortex, (2) Superior temporal sulci, (3) Ventral striatum, (4) Superior temporal sulci and (5) Ventromedial PFC. (B) The splitting times plotted against BIC reduction with 99% confidence bounds computed using the stationary bootstrap. (C) The corresponding undirected graphs. Black lines indicate a positive relationship between connected regions, while green lines indicate a negative relationship. The thickness of the lines corresponds to the strength of the relationship.

For both data sets, subjects were stacked in a similar manner as Group ICA (Calhoun et al., 2001) before applying the DCR procedure. The order of the subjects in the stacking did not affect the results. The value of Δ was chosen to be 8 time points as this coincided with the shortest expected distance between change points. Permutation and stationary bootstrapping methods were carried out in order to perform meaningful inference procedures. Throughout we based inference on creating 99% confidence bounds for the BIC reduction at each possible change point. For the stationary bootstrap, ξ=1/0.05 was used which corresponded to a mean block size of 20. Similar results were obtained by using a mean block size of 10. The DCR approach was used to test whether stressor onset was associated with changes in a) the connectivity between the brain regions and heart rate and b) the connectivity among the brain regions in the two data sets, respectively.

RESULTS

Simulations

Simulation 1

Figure 2A shows the splitting times (in TRs) plotted against the BIC reduction for the single-subject i.i.d. data set. From the plot it is evident that there is positive BIC reduction for the data. Confidence bounds for the BIC reduction are produced using the permutation method. The superimposed red triangles represent the .975 and .025 empirical quantiles of the BIC reduction for 1000 permutations of the data. Note that the actual BIC reductions are comfortably within the bounds produced by the random permutations for all the splitting times. As there is no significant BIC reduction for any splitting time using the permutation procedure, the networks in the undirected graph or the connectivity between ROIs remain unchanged throughout the entire time course. Figure 2B shows the connectivity between the ROIs using data from the entire time course. As the data is white noise, the DCR technique correctly finds no connectivity between the ROIs.

Figure 2.

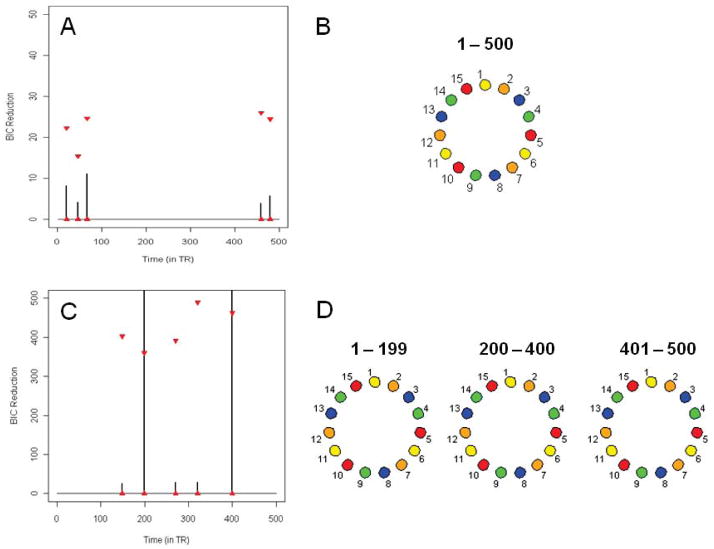
(A) The splitting times plotted against BIC reduction for the single-subject i.i.d data set (Simulation 1). The red triangles represent the .975 and .025 empirical quantiles of the BIC reduction for 1,000 permutations of the data for each non-zero split. (B) The corresponding undirected graph for the single-subject i.i.d data set. (C) – (D) Same results for the single-subject i.i.d data set with a mean change (Simulation 2).

Simulation 2

Figure 2C shows the splitting times plotted against the BIC reduction for the same single-subject i.i.d data set in Simulation 1 but with a mean change included. (If permutation confidence bounds are created there are significant splits present that do not coincide with the mean changes. This is discussed in more detail below.) The two significant splits are at time points 200 and 400 which correspond directly to the change in means. However, the presence of mean changes in the data does not pose a problem as a change in mean should have no direct effect on the change in connectivity between the ROIs. Figure 2D shows the undirected graphs for the splitting times of this data set. The data is white noise and the DCR method correctly finds no connectivity between the ROIs for each partition. Hence, the DCR method can also be used to find changes in the mean while retaining the connectivity pattern between ROIs across partitions.

Simulation 3

Similar results are found for the multi-subject i.i.d. data set shown in Figure 3A. As there is no positive BIC reduction, signifying no connectivity change points, a permutation procedure is not necessary. As the data is white noise, the DCR technique correctly finds no connectivity between the ROIs (Figure 3B).

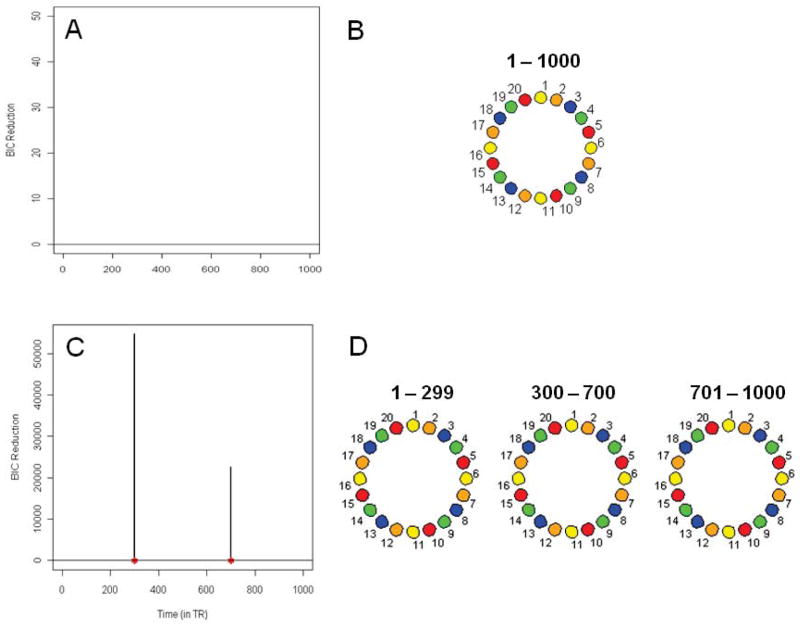
Figure 3.

(A) The splitting times plotted against BIC reduction for the multi-subject i.i.d data set (Simulation 3) with confidence bounds computed using the permutation procedure. (B) The corresponding undirected graph for the multi-subject i.i.d data set. (C) – (D) Same results for the multi-subject i.i.d data set with a mean change (Simulation 4).

Simulation 4

Figure 3C shows the splitting times plotted against the BIC reduction for the same multi-subject i.i.d data set in Simulation 3 but with a mean change included. The two significant splits are at time points 299 and 700 which correspond directly to the change in means. The DCR correctly finds no connectivity between the ROIs for each partition (Figure 3D).

Simulation 5

Figure 4A shows the splitting times plotted against the BIC reduction. The superimposed red triangles represent the .975 and .025 empirical quantiles of the BIC reduction based on 1,000 permutation replicates of the data for each non-zero split. Notice that the actual BIC reductions are not within the confidence bounds for three splitting times. The reason for this is that this resampling scheme does not take the serial dependence inherent in the data into consideration and estimates incorrect bounds. Figures 4B shows the splitting times plotted against BIC reduction for the same data except this time the red triangles superimposed represent the .975 and .025 empirical quantiles of the BIC reduction based on 1,000 stationary bootstrap replicates of the data for each non-zero split. As expected, the actual BIC reductions are comfortably within the bounds produced by this approach for all the splitting times except for the specified connectivity change point at time 500.

Figure 4.

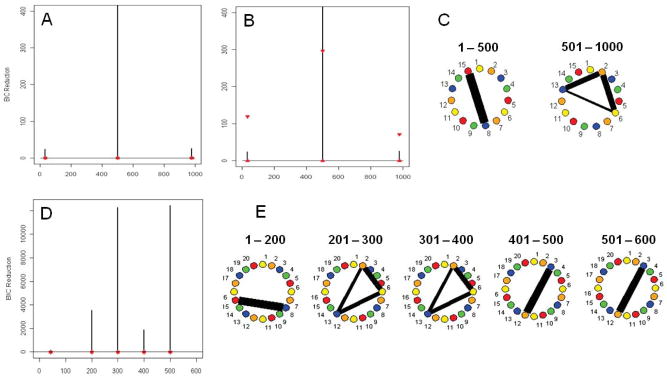
(A) The splitting times plotted against BIC reduction for the multi-subject VAR data set with one connectivity change point (Simulation 5) with confidence bounds computed using the permutation procedure. (B) The same results with bounds computed using the stationary bootstrap procedure. (C) The corresponding undirected graphs for the multi-subject VAR data set based on change points in (B). (D) The splitting times plotted against BIC reduction for the multi-subject VAR data set with a mean change (Simulation 6) with bounds computed using the stationary bootstrap procedure. (E) The corresponding undirected graphs for the multi-subject VAR data set with a mean change.

Figure 4C shows the undirected graphs for the connectivity change points specified in Figures 4B. The strength of connection between the regions or vertices is directly related to the thickness of the edges, that is, the thicker the edge the stronger the connection. In each case, the DCR method correctly identifies the splitting times and the networks in the undirected graphs.

Simulation 6

This simulation study shows how the DCR method is affected by mean changes in the presence of connectivity change points. Figure 4D shows the splitting times plotted against the BIC reduction for this simulation. The significant splits occur at time points 200, 250, 400 and 450 which coincide directly with the connectivity and mean change points. The undirected graphs for this simulation are shown in Figure 4E. The DCR correctly finds the connectivity between ROIs 8 and 15 for the first 200 time points. It also correctly identifies the connectivity between ROI 2, 6 and 13 for time points 201–400. That is, the connectivity remains constant for time points 201–400 even though there is a mean change point found at time point 250. This shows the robustness of the DCR technique to changes in mean response. The DCR method again correctly identifies the connectivity between ROI 3 and 8 for time points 401–600 even though there is another mean change at time point 450.

Simulation 7

A common artifact in neuroimaging time series data is the presence of spikes. The results shown in Figure 5 illustrate that the correct splitting times and connectivity networks are found, and that no significant splitting times are found corresponding to the spikes.

Figure 5.

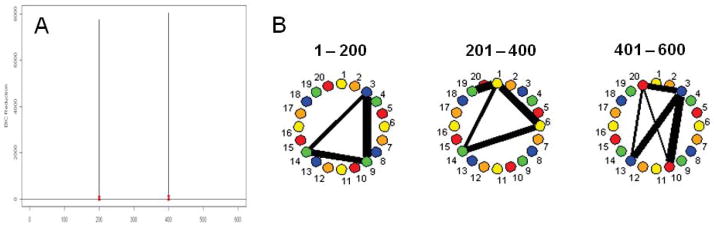
(A) The splitting times plotted against BIC reduction for the multi-subject VAR data set with spikes (Simulation 7) with confidence bounds computed using the stationary bootstrap procedure. (B) The corresponding undirected graphs.

Simulation 8

In the previous simulations all the multi-subject VAR simulations had similar dependencies between each pair of connectivity change points for each subject. In this simulation the strength of the dependency, or connection between the ROIs, is different for each subject. Figure 6A shows the splitting times against BIC reductions for this data set. The DCR method correctly identifies the connectivity change points. The correct networks are also found for subjects with significant networks, as shown in the undirected graphs in Figure 6B. Another two simulations with a similar setup were also carried out. Instead of having 10 subjects with similar dependency and connectivity change points, and 5 subjects consisting of Gaussian noise (a 10/5 split), a 1/14 split and a 5/10 split was also run. In the case of the 1/14 split, no significant splits were found while in the case of the 5/10 split, both the correct splits and undirected graphs were found. However, the magnitude of the BIC reduction was decreased, indicating reduced power to detect change points.

Figure 6.

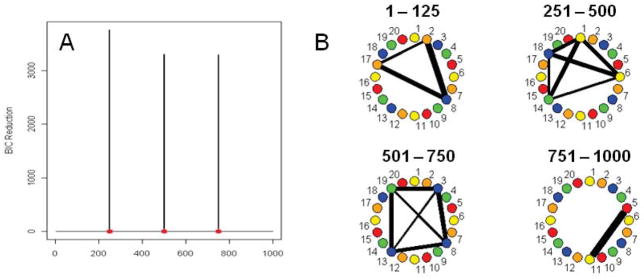
(A) The splitting times plotted against BIC reduction for the multi-subject VAR data set (Simulation 8) with confidence bounds computed using the stationary bootstrap procedure. (B) The corresponding undirected graphs.

Simulation 9

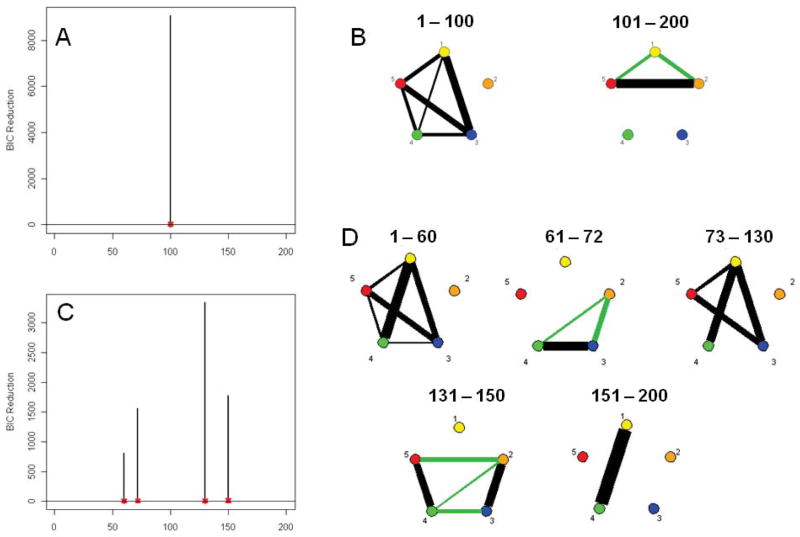
This simulated data set corresponds roughly to the number of subjects and data points present in the experimental data set discussed in the next section. Figure 7A shows the splitting times plotted against the BIC reduction. The actual BIC reductions are comfortably within the bounds produced by the stationary bootstrap resampling for all the splitting times except for the specified connectivity change point at time point 100. Figure 7B shows the corresponding undirected graphs for the connectivity change points. The DCR method correctly identifies the splitting time and the networks in the undirected graphs.

Figure 7.

(A) The splitting times plotted against BIC reduction for the multi-subject VAR data set (Simulation 9) with confidence bounds computed using the stationary bootstrap procedure. (B) The corresponding undirected graphs. (C) The splitting times plotted against BIC reduction for the multi-subject VAR data set (Simulation 10) with confidence bounds computed using the stationary bootstrap procedure. (D) The corresponding undirected graphs.

Simulation 10

Again, this simulated data corresponds to the number of subjects and data points found in our experimental data set. Figure 7C shows the splitting times plotted against the BIC reduction. Significant splits occur at time points 60, 72, 130 and 150 which coincide directly with the connectivity changes. The undirected graphs for this simulation are shown in Figure 7D. The DCR correctly finds the connectivity structure for all partitions including the partition based on only 12 time points (60–72), illustrating the glasso technique’s ability to efficiently handle even very small amounts of data.

Simulation 11

The use of multiple subjects in neuroimaging is difficult and challenging due to inter-subject variability. The DCR describes subject-level brain connectivity by imposing a common structure on the graphical model in the population. In this simulation subjects are separated into two groups with different connectivity change points, that is, the same ROIs are functionally related for all subjects but at different time points. Figure 8A shows the splitting times and their respective BIC reductions for this data set. The DCR method correctly finds the change points for both groups. Figure 8B shows the undirected graphs for each of the time regions specified by the connectivity change points. Interestingly, the DCR method finds the combined connections for all subjects at each time point. For the first 200 time points, the connections (between ROIs 2 and 14) are the same for all 20 subjects. At time point 200, the first 10 subjects have a connectivity change (from ROIs 2 and 14 to ROIs 3, 9, and 18), while the other 10 subjects remain unchanged until time 301 after which all 20 subjects have the same connectivity pattern (between ROIs 3, 9, and 18). At time 500, the first 10 subjects have another connectivity change (from ROIs 3, 9 and 18 to ROIs 2, 6, 13, and 19) while the other 10 remain unchanged until time point 601 after which the connectivity pattern is the same for all 20 subjects.

Figure 8.

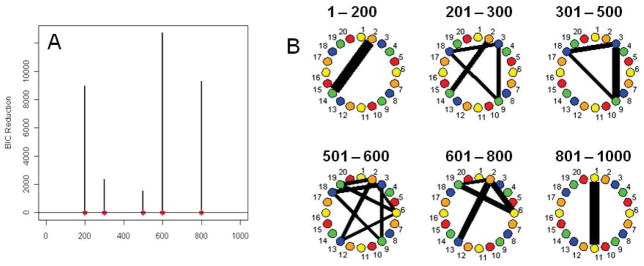
(A) The splitting times plotted against BIC reduction for the multi-subject VAR data set (Simulation 11) with bounds computed using stationary bootstrap procedure. (B) The corresponding undirected graphs.

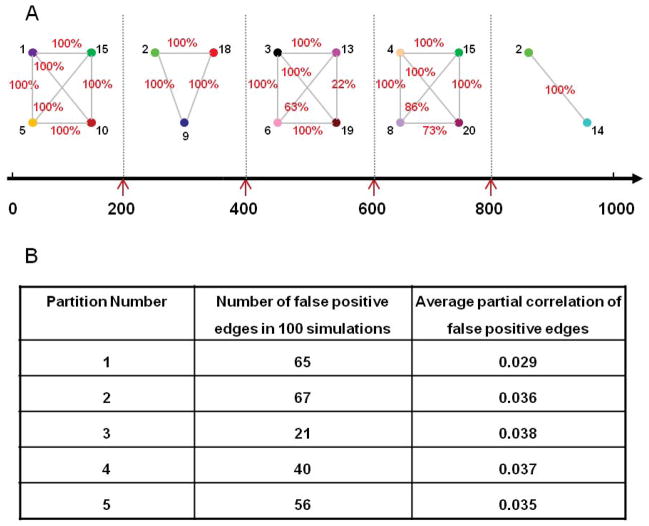
Simulation 12

The previous simulations have only considered a single iteration. Here we repeat a multi-subject VAR simulation 100 times and study how often our method is able to detect the correct connectivity change points and undirected graphs. The results show that in every case, the correct splitting times were found but that there were 4 false positives overall. However, for each false positive, the correct undirected graphs are found both before and after. Figure 9A shows the percentage of times the correct networks in the undirected graphs were found. The DCR finds 92.9% of the networks in 100 simulations. Figure 9B presents the details of the number of false positive edges for the 100 simulations for each partition. Note that the number of possible edges in 100 simulations is 100*190 (100*(19+18+…+1)) and the total number of possible edge combinations is 2²⁰, so the number of false positive edges is very small. In fact, the DCR method averages less than 1 false positive per partition with a very small partial correlation.

Figure 9.

The results of Simulation 10. (A) The percentage of times a correct connection between ROIs was detected in the 100 repetitions. (B) The number of false positive edges found in each partition with the average partial correlation of each false positive.

The same set of VAR simulations were run on single subject data and similar results were obtained. In each case the correct connectivity change points were found, although more false positive connections were identified in the undirected graphs. In general, the results from the multi-subject setting are stronger and more robust due to the increased amount of data.

Experimental Data

Figure 10B shows the splitting times (in TRs) plotted against the BIC reduction for the fMRI data set composed of 4 ROIs and heart rate data. The actual BIC reductions are comfortably within the bands produced for almost all the splitting times except at time points 62 and 133. At time point 60 (120 seconds), the first visual cue specifying the topic of the speech was shown and the first splitting time is related to the corresponding change to a state of increased anxiety. At time point 130 (260 seconds), the second visual cue stating that the participants would in fact not have to give the presentation was revealed and the second splitting time is related to the corresponding change in brain connectivity.

The undirected graphs for each partition can be seen in Figure 10C. From the graphs it is evident that heart rate is not connected to any ROI during the first partition. However, during the second partition, when the speech topic is presented and the participants begin to silently prepare their speech, there is a positive connection between HR and the VMPFC (1) and a negative connection between DLPFC (2) and HR. In the third partition, when the participants relax, the connection between HR and VMPFC (1) disappears and the connection between DLPFC (2) and HR becomes positive. These results are consistent with findings in Wager et al. (2009a).

The splitting times (in TRs) for the 5-ROI data set can be seen in Figure 11B. The actual BIC reductions are comfortably within the bounds for almost all splitting times except at time points 11, 60, 72, 103, 136, 160 and 188. At time point 60 (120 seconds), the first visual cue specifying the topic of the speech was presented and the large BIC reduction is related to the corresponding change in brain connectivity. At time point 67.5 (135 seconds), the visual cue informing the participant of the speech topic was removed, and participants began silently preparing their speeches, leading to a state change at time 72. At time point 130 (260 seconds), the second visual cue stating that the participants would in fact not have to give the presentation was revealed and the corresponding change point is related to a change away from a state of heightened anxiety. The other change points may be due to the different modes of anxiety as subjects silently prepare their speech.

The undirected graphs for each partition can be seen in Figure 11C. Of particular note is the fact that after reading and processing the speech instruction, the connectivity between the MPFC (5) and the ventral striatum (3) becomes negative and the connectivity between MPFC (5) and superior temporal sulci (4) strengthens. This period corresponds to the reading and interpretation of instructions, which causes the onset of anxiety. MPFC (5) has previously been shown to be a key region in tracking anxiety and heart-rate responses throughout the duration of the stressor; the fact that it maintains strong connectivity with bilateral superior temporal sulcus (4) during this stressful time supports this interpretation.

DISCUSSION

In this work, we introduce Dynamic Connectivity Regression (DCR), a new approach for splitting the experimental time course in a functional neuroimaging experiment into partitions based on functional connectivity changes between ROIs. The novelty of this technique lies in its dynamic nature. It finds the connectivity change points for both single and multi-subject data sets and then plots the graphical model between each pair of change points. The method assumes that the graphical model is sparse. The greedy partitioning algorithm used in the method is computationally attractive as it combines classical greedy algorithms for decision trees with recent advances in l₁-regularization techniques for graph selection.

DCR can be applied directly to data from ROI studies or to temporal components obtained from a PCA or ICA analysis. It does not require prior knowledge of the nature of the experimental design and may be particularly appropriate for studies when it is not possible to replicate experimental manipulations within subjects. These include studies of emotional responses, “ecologically valid” tasks, changes in state-related activity evoked by learning, or studies of tonic increases following solutions to “insight” problem solving tasks.

The simulations indicate that the DCR method is sensitive to both changes in mean activity and spikes, as well as changes in functional connectivity. Hence, this technique is also useful for detecting changes in mean activation level within the regions. If such changes are suspected in the data set, a mean change detection technique (e.g. Lindquist et al., 2007; Robinson et al., 2010) could be utilized. If a change point is found using both types of methods it can be assumed to be a mean change point and removed. The connectivity between ROIs can then be calculated assuming a partition does not occur at this time point. The simulations also show that the addition of noise and weaker signals do not adversely affect the results.

To date, DCR has been run on data sets with up to 40 regions. In theory it should scale up to handle data sets with more ROIs. However, of course, the inclusion of more ROIs would inevitably lead to larger computation time, especially with regard to the non-parametric inference procedures. Thus, it may become burdensome if the number of ROIs were in the order of hundreds.

The choice of Δ in DCR is of particular importance as it represents the minimum possible distance between adjacent change points. Ideally, we want to make Δ as large as possible to ensure that there is enough data to provide reliable estimates of the sample means and sample covariance matrices. However, the choice of Δ places an upper bound on the number of change points that can be found using our method, with small values allowing for more change points. Hence, we want to make Δ as small as possible to ensure that we find all possible change points. Ultimately, its value can be adjusted depending on the existence of a priori knowledge about the spacing of changes in functional connectivity. In our application, we choose Δ to be 8 time points because this coincided with the timing of the smallest known change in the experimental paradigm (the visual instruction). We would not recommend using this method without further modifications if one believed that the distance between state changes was less than Δ.

A serious challenge in using multi-subject data is the existence of subject-to-subject variability (Van Horn et al., 2008). DCR assumes that the undirected graph, or precision matrices, in a group of subjects share the same structure but contribute to it individually. This allows for situations where brain regions are functionally related only for a certain group of subjects, and where regions might be related at different times for different subjects. Simulations indicate that DCR performs very well in both settings, as it consistently finds the correct connectivity change points and identifies the correct combined networks. As an alternative, one could fit each subject separately and thereby avoid making this assumption altogether.

Permutation and stationary bootstrap inferential procedures were introduced for use with DCR, with a particular focus on determining whether or not a change point was significant. From the results of the simulations it is clear that the stationary bootstrap is preferable as it adjusts for the temporal dependency structure inherent in fMRI time series. Note also that by resampling blocks of null data using the stationary bootstrap the resulting replicated time series is again identically distributed. Thus, it has no problems dealing with the i.i.d. noise setting. In addition to inference on the change points, it would also be interesting to obtain confidence bounds on the connectivity parameters (i.e. the entries of the precision matrix) of the graphs estimated in each partition. Similarly, one may also be interested in quantifying the uncertainty associated with the estimated change-points. However, we leave both issues for later work.

In sum, DCR is a new technique for estimating functional connectivity that is capable of handling the artifacts and autocorrelated noise present in typical fMRI data. Its dynamic data-driven approach makes it ideally suited for analyzing data from experiments where the nature, timing and duration of the psychological processes being studied are not known beforehand. Hence, we believe it has the potential to become an important tool for analyzing data from emotion, stress or resting state studies.

TABLE 1.

Description of the simulation studies. The variables N, T and p represent the number of subjects, time points and ROIs in each simulated time series, respectively. The Mean Change and Spikes columns provide information on whether mean changes or spikes were added to the time series together with their magnitude and where they occurred. The ROI connectivity column provides information on the connectivity structure between ROIs during each partition.

Sim	Data Type	N	T	p	Mean Change	Spikes	ROI Connectivity
1	IID	1	500	15
2	IID	1	500	15	Size 4; 200–400
3	IID	20	1000	20
4	IID	20	1000	20	Size 3; 300–700
5	VAR	20	1000	15			8–15 (1–500); 2–6–13 (501–1000)
6	VAR	10	600	20	Size 2; 250–450		8–15 (1–200); 2–6–13 (201–400); 3–12 (401–600)
7	VAR	10	600	20		Yes	3–9–14 (1–200); 1–6–14–19 (201–400); 3–10–13–20 (401–600)
8	VAR	15	1000	20			2–8–17 (1–250); 1–6–14–18 (251–500); 3–8–13–19 (501–750); 5–11 (751–1000)
9	VAR	25	200	5			1–3–4–5(1–100); 1–2–5 (101–200)
10	VAR	25	200	5			1–3–4–5(1–60); 2–3–4 (61–72); 1–3–4–5(71–130); 2–3–4–5 (131–150); 1–4 (151–200)
11	VAR	20	1000	20			First 10 subjects: 2–14 (1–200); 3–9–18 (201–500); 2–6–13–19 (501–800); 1–11 (801–1000) Second 10 subjects: 2–14 (1–300); 3–9–18 (301–600); 2–6–13–19 (601–800); 1–11 (801–1000)
12	VAR	20	1000	20			1–5–10–15 (1–200); 2–9–18 (201–400); 3–6–13–19 (401–600); 4–8–15–20 (601–800); 2–14 (801 1000)

APPENDIX

A. Bayesian Information Criterion (BIC)

Let Π = {χ,....χ_m} denote the partition of χ and let I(·) represent an indicator function. The piecewise constant mean and precision functions are denoted by

$$\mu (x)=\sum _{j=1}^m{\mu }_{{\chi }_j}I(x\in {\chi }_j)$$

and

$$\mathrm{\Omega }(x)=\sum _{j=1}^m{\mathrm{\Omega }}_{{\chi }_j}I(x\in {\chi }_j)$$

where μ_χj is a 1-dimensional vector-valued mean function and Ω_χj is a p×p precision matrix for the partition element χ_j.

Given an induced partition Π and corresponding mean and precision functions μ(x) and Ω(x), the Bayesian Information Criterion (BIC) is defined as follows

$$\begin{array}{l}\mathit{BIC}=-2log(L)+klog(T)\\ =-\frac{2}{n}\sum _{i=1}^T\sum _{j=1}^m\left[(tr({\mathrm{\Omega }}_{{\chi }_j}((y_i-{\mu }_{{\chi }_j}){(y_i-{\mu }_{{\chi }_j})}^T)-log({\mathrm{\Omega }}_{{\chi }_j}))I(x_i\in {\chi }_j)\right]+klog(T)\end{array}$$

where T is the number of data points or the number of observations, k is the number of free parameters to be estimated and L is the maximized value of the likelihood function for the estimated model.

B. DCR Algorithm

The algorithm for performing DCR is set up as follows:

1. Consider the full data set. Calculate the sample mean and covariance matrix using equations (2) and (3), respectively. Obtain an estimate of Ω(x) = Σ(x)⁻¹ for each value of λ using equation (4).

2. Choose the value of λ and hence the estimate of Ω(x), that minimizes the BIC.

3. Refit the model without the lasso penalty term (i.e. the l₁-constraint) keeping the zero elements in the matrix fixed and record the minimum BIC.

4. Partition the data into two parts: a left subset consisting of time points {1:γ} and a right subset consisting of {γ+1:T} where γ=Δ. Repeat Steps (1)–(3) for both data sets and sum the BIC scores from the two partition elements. Repeat this procedure for γ values from Δ+1 to T−Δ+1.

5. If the sum of the combined BIC scores for any two subsets is less than the BIC of the entire data set computed in (2), the time point with the largest decrease is selected as the splitting time point, thus partitioning the data into two segments.

6. Apply Steps (1)–(5) recursively to each partition until no partition element can be further split into smaller elements.