Abstract
Mechanical stress is necessary to sustain the mineral content of bone in adults. However, in a developing neonatal mouse, the mineralization of soft tissues progresses despite greatly reduced average mechanical stresses. In adults, these reduced loads would likely lead to bone loss. Although biochemical factors may partly explain these different responses, it is unclear how mineralization is initiated in low load environments. We present here the effect of morphometric data and initial modeling supporting a hypothesis that mechanical factors across several length scales amplify stresses, and we suggest that these stresses are of a level adequate to contribute to mechanical signaling for initiation of mineralization at the developing tendon-to-bone enthesis. A mineral gradient is evident across the insertion from the onset of mineralization. This grading maintains a constant size from early postnatal time points to adulthood. At the tissue level, this grading contributes to reduced stresses in an adult animal and to a minor elevation of stresses in a neonatal animal. At the cellular level, stress concentrations around mineralizing chondrocytes are enhanced in neonatal animals compared to adult animals. The enhancement of stresses around cells at early timepoints may serve to amplify and transduce low loads in order to initiate mineralization.
Keywords: Mineralized tissue, enthesis development, enthesis, tendon-to-bone attachment
1 Introduction
Soft connective tissue, such as tendon and ligament, inserts into hard bone through a graded interface called the enthesis. Mature fibrocartilaginous entheses, such as those at the rotator cuff tendon and the anterior crucial ligament bony attachment, display four regions: a tendinous region, an unmineralized fibrocartilage region, a mineralized fibrocartilage region, and a bone region (Benjamin et al. 2002). Recent studies of entheses show a gradual increase in the amount of mineral from tendon to bone, and a gradual variation in the organization of collagen fibers (Wopenka et al. 2008; Thomopoulos et al. 2003, 2006; Genin et al. 2009). The graded structure of the enthesis appears to be optimized to achieve an effective load transfer (Liu et al. 2012; Genin et al. 2009). However, this optimized interface is not re-formed after injury, leading to poor healing outcomes, presumably due to concentrations of stress at the interface (Lui et al. 2010; Harryman et al. 1991; Galatz et al. 2004). Our paper examines mechanical loading on the developing enthesis structure over time, offering an understanding of mechanical factors that may be important for the development, homeostasis, and healing of a functional enthesis. Results from the current study may also offer guidance for tissue-engineered repair of tendon/ligament-to-bone enthesis injuries (Smith et al. 2012).
Mechanical loading affects the structure and function of mature tissues via well understood cell-mediated responses that are reviewed elsewhere (Thomopoulos et al. 2011). Skeletally mature bone adapts both its mass and its architecture to external mechanical (Tanck loads et al. 2006). Bone density increases with increased mechanical loading due to physical activity (Bailey et al. 1999), and decreases with reduced mechanical loading under microgravity conditions (Collet et al. 1997). Likewise, tendon strength is reduced when the muscle is immobilized (Amiel et al. 1982; Woo et al. 1982). In the healing process, a low level of controlled force is more beneficial than the complete removal of a mechanical load in the healing of the rotator cuff (Galatz et al. 2009). Decreased fetal movement and/or muscle loading leads to dramatic defects in skeletal development (Nowlan et al. 2010). A reduced load impairs the development of the tendon-to-bone enthesis, reducing its modulus, strength, and mineral content (Thomopoulos et al. 2010). The responsiveness of mature, healing, and developing bones, tendons, and their attachments to the mechanical environment suggests that mechanical factors play an important role for the formation and maintenance of these tissues.
How, then, does mineralized tissue form in a developing animal, especially at early postnatal time points, when stresses applied by muscles are very low? We recently characterized the development of a mineralized enthesis in a mouse model (Schwartz et al. 2012). Many of the expected elements were observed. The enthesis developed following a course similar to what has been described by others (Benjamin et al. 2006; Blitz et al. 2009). Endochondral ossification at growth plates followed a well described sequence: reserve chondrocytes proliferated and then became hypertrophic, altering the extracellular matrix and facilitating mineralization, and were eventually replaced by osteoblasts and a fully mineralized collagen matrix. At the developing rotator cuff insertions into the humeral head, we observed the expected growth of bone as the animals aged.
However, we also observed a surprising result: a mineral gradient was seen at the mineralization front from the onset of mineralization at early postnatal time-points through adulthood. The size of this graded region was nearly constant at all timepoints. In the mature enthesis, this graded region serves to reduce stress concentration and improve load transfer (Liu et al. 2012; Genin et al. 2009). What role does this gradient play at early time points when muscle loads are relatively low? We modeled stresses in the developing enthesis to gain insight into these questions. We hypothesized that the graded region serves a different role at earlier time points, namely that it combines with other morphological changes to instead elevate local stresses at early timepoints. We argue that, in addition to the effects of the many soluble factors present during development, these stress concentrations can serve to elevate stresses in the matrix surrounding cells and thereby contribute to the initiation of mineral accumulation.
In this paper, we first describe the experimental methods used to characterize the morphology of the rotator cuff tendon-to-bone enthesis in a mouse model at time points throughout postnatal development, from postnatal (as early as 7 days), to adult (56 days). We then present the morphologies observed throughout development and first-order models to explore the mechanical consequences of these morphologies. We conclude by discussing the potential role of these elevated stresses in the transduction of mineralization cues.
2 Methods
2.1 Animal model, histology, and morphometry
The use of animals for this study was approved by the animal studies committee at Washington University. Fifteen CD1 mice (Charles River Labs) were used in this study. Mice were sacrificed in a CO2 chamber at 7, 10, 14, 28, and 56 days after birth (denoted as P7, P10, P14, P28, and P56, respectively; n=3 per time point). The humerus and supraspinatus tendon with muscle attached were dissected free of all other tissues.
2.1.1 Micro-computed tomography and muscle forces
The isolated humerus and supraspinatus muscle complexes were fixed in 4% paraformaldehyde and dehydrated to 70% ethanol. Two dimensional sagittal plane images were acquired using a micro-computed tomography scanner at tube settings of 55kVp and 145μA with a 25mm diameter tube resulting in an ~20μm isometric resolution(μCT 40; Scanco Medical, Basserdorf, Switzerland). A soft tissue threshold was used throughout to distinguish unmineralized and mineralized tissue from background due to the low level of mineralization found in the humeral head of the 7-14 day time-points. Humeral head volume, supraspinatus muscle volume, and supraspinatus muscle length were calculated as previously described (Thomopoulos et al. 2007). A cross-sectional area of the tendon was determined by averaging the area of a 0.8mm2 region of interest centered about the minimum area of the tendon.
The method of Gokhin et al. (2008) was used to approximate the isometric tension generated by the supraspinatus muscle at each time point. In that study, the muscle fiber cross-sectional area and the isometric stress generated by the murine tibialis anterior at various postnatal time points were measured. Isometric tension was calculated by multiplying isometric stress by the physiological cross-sectional area of the muscle (PCSA). Consistent with Gokhin et al. (2008), we used an adjusted PCSA that accounts for muscle fiber packing:
| (1) |
V is the muscle volume determined from μCT; θ is the fiber pennation angle (11.7°) (Burkholder et al. 1994); Lf is the muscle fiber length, calculated as 0.6 times the μCT measured muscle length; and Xcsa represents the age appropriate value of the cross-sectional area fraction of contractile material, as estimated by Gokhin et al. (2008).
2.1.2 Histomorphometry
The shoulder specimens used for μCT were rehydrated and decalcified using 14% EDTA for two weeks. Samples were then dehydrated, embedded in paraffin, and sectioned to 5μm in the coronal plane. Tissue sections were stained with toluidine blue to estimate extracellular matrix area fraction. The humeral head diameter was determined by calibrating ImageJ to a scale bar to measure the widest diameter of the humeral head on the section. Tendon length was measured using ImageJ from the insertion to the beginning of muscle (i.e., where muscle fibers were identified).
The volume fraction ratio of cells and matrix was a central morphometric parameter needed both to evaluate the cell-level stress concentrations and the homogenized moduli for the gradient and unmineralized regions. To calculate the approximate matrix area fraction, we analyzed images using ImageJ software. A rectangle (~ .01mm2) was drawn over the matrix region of interest. Cells were identified by manual inspection, and regions of nuclear staining within cells were excluded to enable separation of cells from an extracellular matrix by an intensity threshold. The area fractions of cells was then used to estimate the volume fraction of cells using Delesse’s principle, which states that the mean value of the area fraction estimated from planar sections is equal to the volume fraction in three dimensions (Delesse 1847). However, the histology sample slices have finite thickness and, because the projected areas of cells are different at different planes, inaccuracies will be introduced when estimating area fraction. We used the largest of the cross-sectional areas in each toluidine blue stained histology slice, because there we could see the boundary between the brighter, more transparent cells and the dark purple matrix. With this approach, the true area fraction was likely slightly overestimated at each slice. Therefore, a correction factor k was introduced in the area fraction by the following formula (Chayes 1956):
| (2) |
where R is the average radius of cells and t = 5μm is the thickness of the histology sections. We used the average cell diameter observed from 2D sections to represent the 3D size of the spherical cell. The true mean radius of a sphere, by taking all the transection planes, is πR/4 = 0.785R, and furthermore, the tendency of the largest area in a slice observed by using toluidine blue staining method decreased the discrepancy of the 2D observed size of the cells and the real cell size.
The details for calculating the slope of the graded mineralized region and the distance from the tendon to the start of mineralization were described by Schwartz et al. (2012). The length of the gradient region was calculated by dividing the gradient slope by the average mineral content of the bone underlying the insertion and the data will be published by Schwartz et al. (2012) and listed here for reference. The cortical bone outer radius was calculated by subtracting the distance from the tendon to the start of mineralization and length of the gradient from the measured humeral head radius.
2.2 Modeling
2.2.1 Overview of multiscale modeling
We applied our cross-scale morphological data of the developmental enthesis to model how the stress environment in the vicinity of the cell-matrix interface changes over time in the mineralized region. At the tissue level, an idealized representation of was studied to estimate the amplification of stresses at points proximal to the bone relative to the stresses in the tendons. At the cellular level, a periodic unit cell model was used to estimate local stress concentrations in the direct vicinity of chondrocytes in the mineralized region. The overall amplification of stress near cells was obtained by combining estimates of the age-appropriate muscle stresses with the estimated concentrations of stress from both tissue-level and cell-level effects.
2.2.2 Tissue-level stress concentrations
The enthesis is a hierarchical structure, and is believed to present toughening mechanisms over several of these hierarchies Liu et al. (2011). The first level studied was the enthesis as a whole (tissue level). Throughout development, four regions present: (1) the tendon, (2) the unmineralized fibrocartliage region, (3) the graded mineralized fibrocartilage region, and (4) the bone, with the widths of the unmineralized and mineralized regions in the enthesis much smaller than those of the tendon and the humeral head. The graded region maintains a constant size throughout development (Schwartz et al. 2012). To determine what effect this gradient has on the tissue level scale stress field near the mineralization front, we studied a simplified one dimensional axisymmetric concentric ring model (Fig. 1).
Figure 1.
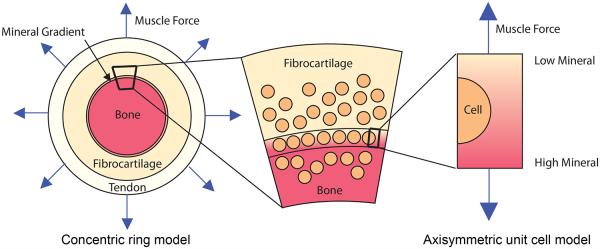
Schematic of the modeling approach to estimate the stress environment of developing tendon-to-bone enthesis at the rotator cuff of a mouse. The rotator cuff to humeral head insertion is modeled as a concentric ring model. Because the size of the enthesis (mineralized region and unmineralized region) is much smaller than that of the tendon and bone, and the size of the cells are comparable to the length of gradient region, an axisymmetric unit cell model (a spherical cell in the center of cylindrical extracellular matrix) was used to estimate the stress concentration at cell and matrix interface.
This representation approximates the structure of the entheses of the rotator cuff of the humeral head when viewed in a sagittal plane. The rotator cuff tendons insert radially into the humeral head and form a nearly complete ring around the approximately spherical humeral head (Liu et al. 2012). The concentric ring model was loaded by uniform radial tensile stress to estimate the tissue-level stress concentrations in the structure. The magnitude of this stress was estimated based upon the above measurements, and upon the assumption that peak muscle stress was approximately independent of the overall stiffness of the insertion over the age range studied. Further details of the stress analysis are listed in the Appendix.
The cortical bone core of the concentric ring model represented cortical bone was modeled with linear elastic, isotropic material properties Ebone=20 GPa and νbone=0.3 (Kaplan et al. 1994). The outermost ring represented tendon, modeled as transversely isotropic, with longitudinal modulus E1 ≈ 460 MPa, transverse modulus E2 ≈ 2.4 MPa, Poisson’s ratio ν12 ≈ 1, Poisson’s ratio in the transverse plane ν23 = 0.3, and G12 ≈7.1 MPa (Stabile et al. 2004; Lynch et al. 2003; Maganaris and Paul 1999; Weiss et al. 2002; Yin and Elliott 2004). The shear modulus was estimated from G12 = 3βE1(R/L)2, where β = 1.07 and the aspect ratio of collagen fibers (R/L) = 1 : 20 (Genin et al. 2009). Longitudinal and transverse moduli for the gradient and unmineralized regions at the enthesis were estimated by solving a boundary value problem involving the axisymmetric unit cell model as described below.
2.2.3 Cell-level stress concentrations
We studied an axisymmetric unit cell model of a cell at the tendon-to-bone enthesis to estimate how age-related changes to cell size and shape affected the stress field near these cells. We additionally applied these models to estimate homogenized mechanical moduli of tissue in the graded region.
As described below, our observations at all time points supported a model of the cells as spherical. At early time points, we observed dense hypertrophic chondrocytes with a roughly spherical shape at the mineralized region of the enthesis. Here, the average radius of hypertrophic chondrocytes was comparable to the length of the gradient region. Over the course of development, the enthesis cells became dramatically smaller.
In the axisymmetric unit cell model, the center of the spherical cell was coincident with the center of a cylinder, with the height of the cylinder two times the radius of the cylinder (schematic in Fig. 1). The radius of the spherical cell was determined from experimental data. Symmetrical boundary conditions were applied at the bottom surface of the cylinder, with zero shear traction on the lower surface and displacement prohibited along the height of the cylinder (z-direction). The top surface was loaded by a uniform displacement in the z-direction, which yielded a uniform mean strain ∊z = 0.01, and was traction-free in the azimuthal and radial directions. The circumferential surface of the cylinder was constrained so that it had uniform displacement in the radial direction, and was traction-free in the azimuthal and z directions. The applied stress σz was calculated as the total reaction force in the z direction at the top surface divided by the cross-sectional area of the cylinder, and the stress concentration factor was defined as the ratio of the maximum first principal stress to σz.
Constitutive models
Each unit cell spanned the region between the bone and the mineralization front (the mineralized region) and the region between the mineralization front and the tendon (the unmineralized region) at the enthesis, and contained a single chondrocyte. Following a review of the literature, we assumed the chondrocyte to be isotropic with Young’s modulus Ecell = 350kPa and Poisson’s ratio νcell = 0.43 (Alexopoulos et al. 2005; Kim et al. 2010; Jones et al. 1999). In the unmineralized region, the extracellular matrix was assigned the same material properties as a tendon.
The mineralized region was graded, with the accumulation of mineral beginning at the mineralization front and increasing until bone was reached at the base of the unit cell. In the mineralized region, the extracellular matrix properties were thus varied continuously, from no mineral at the mineralization front to fully mineralized at the bone side. The volume fraction of mineral increased linearly from the mineralization front to the bone. However, the material properties of partially mineralized collagen do not vary linearly with mineral volume fraction. In our recent study, we developed models predicting the material properties of mineralized collagen tissue with a variation of volume fraction, based on the nanoscopic details of the accumulation of mineral on collagen fibrils (Liu et al. 2014; Alexander et al. 2012) using linear, multiphase homogenization theory, c.f. (Genin and Birman 2009). Here, we followed a model from our earlier work, in which mineral first deposited within the gap channels of the periodic collagen fibrils structure and then accumulated randomly in the extrafibrillar regions (Liu et al. 2014). The results for moduli were derived in our earlier work from the Monte Carlo finite element simulation, and interpolated with a cubic spline function (see Appendix, Fig. S1). The extracellular matrix properties were assumed to be transversely isotropic, with the longitudinal direction in parallel with the z-direction of the unit cell model. At earlier time points, the collagen fibers in the enthesis as a whole are more disorganized than a mature structure (the results of measurement of collagen fiber orientation throughout development are not shown). However, local organization over a length scale associated with our finite element model is not known. As a first-order approximation, we ignored those effects.
Interpretation of cell-level data to estimate constitutive properties for the tissue-level model
The homogenized longitudinal modulus was obtained from unit cell models as the calculated applied stress σz divided by the nominal strain ∊z resulting from displacement boundary conditions applied to the unit cell. To obtain the homogenized transverse modulus, the circumferential surface was loaded by a uniform displacement in the r-direction, which yielded a uniform nominal radial strain ∊r = 0.01, while the model was traction-free in the azimuthal and z-direction. The top and bottom surfaces of the cylinder were constrained to have uniform displacement in the z-direction, and were traction-free in the azimuthal and radial directions. The applied stress σr was calculated as the total reaction force in the r direction at the circumferential surface divided by the circumferential surface area of the cylinder. νrθ = 0.3 was assumed for the unit cell structure and the effective transverse modulus was equal to σr(1–νrθ)/∊r because of the Poisson effect in the transverse plane. Poisson’s ratio νzr or νzθ was assumed to be 0.1, which satisfied positive definite constraint of the stiffness tensor. The homogenized moduli depended on the volume fraction of cells. The results are shown in the Appendix.
Finite element models
Finite element analysis software COMSOL (COMSOL, Inc) was used to estimate cell-level stress concentrations at the cell and extracellular matrix interface. The linear elastic axisymmetric model was described above. A ne mesh with triangular elements was used, and elements were further divided at the equator of the cell-matrix interface characterized by stress concentration. Adequate convergence was achieved by using approximately 75000 degrees of freedom.
2.2.4 Development of cell-level stresses in the mineralized region
Combining tissue-level (concentric ring model) and cell-level (axisymmetric unit cell model) scale stress concentration with the applied muscle stress yields an estimate of the stress level around cells in the gradient region. The variance of the volume fraction of cells at the gradient and the unmineralized regions introduced bounds on the total stress concentration effects at different time points. Another uncertainty came from estimates of the peak muscle stress. The combined cell-level stress level at the cell-matrix interface in the mineralized region at different time points was calculated, and normalized to the average value at 56 days.
3 Results and Discussion
3.1 Over the course of post-natal development the humeral head grows and cells shrink but the mineral gradient stays the same size
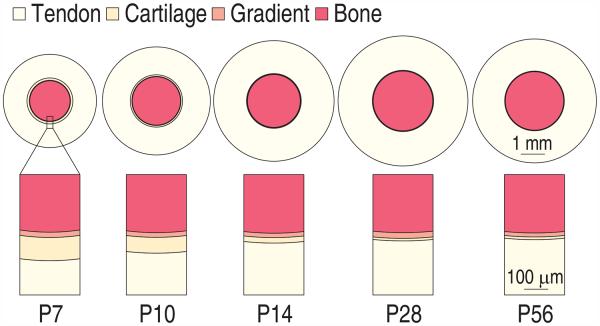
Table 1 shows the length of supraspinatus tendon, the distance from the mineralization front to the tendon, the length of the gradient region in the enthesis, the cortical bone outer radius, and the humeral head diameters (the summation of the later three) at P7, P10, P14, P28 and P56, as measured from histology sections. The data show that, during development, both the tendon and the humeral head grew, the size of the gradient region remained constant (with an average length ~ 20μm), the unmineralized region shrank, and the size of the enthesis was small relative to that of tendon and bone (schematic, Fig. 2).
Table 1.
Morphometric data for the surpraspinatus tendon, enthesis, and humeral head during post-natal development. ± indicates standard deviation (N=3). The cortical bone outer radius was calculated by subtracting the “distance from the tendon to the start of mineralization” and “gradient length” from the humeral radius, mean values are used, no standard deviation. (SS: supraspinatus tendon, HH: humeral head).
| Age (days) | SS length (mm) |
HH diameter (mm) |
distance from SS to mineralization front (μm) |
mineral gradient length (μm) |
cortical bone outer radius(μm) |
|---|---|---|---|---|---|
| 7 | 1.07±0.25 | 1.73±0.15 | 96.2±11.8 | 23.8±7.20 | 836 |
| 10 | 1.21±0.04 | 2.04±0.05 | 65.8±13.6 | 18.6±5.96 | 1000 |
| 14 | 1.39±0.16 | 2.11±0.05 | 22.9±4.4 | 22.6±10.7 | 1100 |
| 28 | 1.44±0.29 | 2.27±0.15 | 10.4±3.4 | 25.9±11.2 | 1240 |
| 56 | 1.34±0.23 | 2.27±0.14 | 11.1±5.1 | 19.1±9.98 | 1210 |
Figure 2.
Schematic of the developing tendon-to-bone enthesis at the rotator cuff of a mouse. The graded mineralized region maintained a relatively constant thickness over time, increasing while the outer radius of the cortical bone (humeral head) and tendon length grew. The unmineralized “fibrocartilage” disappeared with age. Rings are drawn to scale.
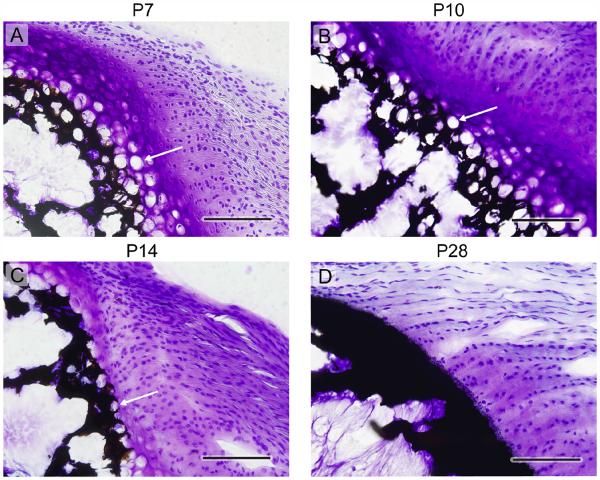
The volume fraction ratio of cells and matrix was a central morphometric parameter needed both to evaluate the cell-level stress concentrations and the homogenized moduli for the gradient and unmineralized regions. Representative histology sections at P7, P10, P14, and P28 (Fig. 3) show that the fraction of cells relative to extracellular matrix decreased throughout development (enthesis structure at P56 (not shown) was similar to that at P28). From the histology sections, the area fraction of cells was estimated (Fig. 4a,b. The area fraction was then used to estimate the volume fraction of cells using Delesse’s principle. The cells shrank over time (Fig. 4c).
Figure 3.
Histologic tissue sections of the tendon-to-bone enthesis at the rotator cuff of a mouse, showing a steady decline in the size and volume fraction of chondrocytes with age. Time points: (a) P7, (b) P10, (c) P14, (d) P28. The black/dark areas indicate mineral, the cell nuclei are stained with dark blue, hypertrophic chondrocytes appear as white circles (see arrows in (a), (b), and (c)), and the purplish/pinkish areas indicate the presence of proteoglycans, which are characteristic of cartilage. Note that the cells remain spherical throughout, and start to organize into columns at later timepoints. Although Raman spectroscopic analysis clearly indicates a gradient in mineral at all timepoints (Schwartz et al. 2012; Wopenka et al. 2008), the graded transition zone is not visible by von Kossa staining at any timepoint, as this staining yields an opaque band with even a small level of mineralization. (5 μm thick sections, von Kossa and Toluidine blue staining, scale bar = 100μm, arrows: hypertrophic chondrocytes).
Figure 4.
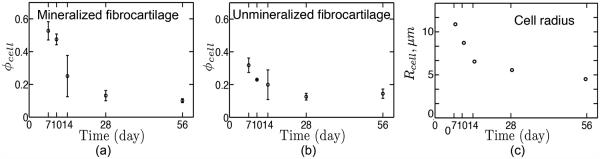
Development of the volume fraction of cells at (a) mineralized fibrocartilage (b) unmineralized fibrocartilage.The range of data indicates standard deviation (N=3). (c) Mean radius of cells as a function of age. Both the volume fraction and size of cells decrease with age. The fraction of cells decreases rapidly after 14 days in the mineralized region. The volume fraction is much larger in the mineralized region than in the unmineralized region at early development.
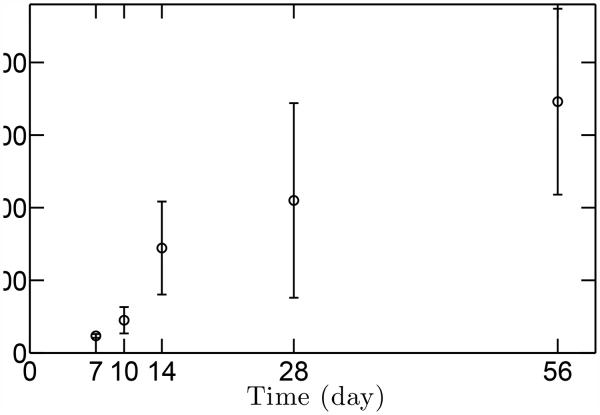
3.2 Muscle stresses increase steadily from birth through adulthood
The peak muscle stresses that were used as inputs to the stress concentration models were estimated as a function of age using micro-computed tomography data (Fig. 5). As expected, muscle volume increased through development, and consequently muscle stresses increased steadily as well. The stress ratio between P56 (maturity) and P7 was approximately 15.
Figure 5.
Estimated peak muscle stresses as a function of age. Peak muscle stresses increase with age, with the stress ratio between the P56 (maturity) and P7 (early post-natal) about 14.8. The range of data indicates standard deviation (N=3).
3.3 Cell-level stress concentrations decrease with age
First order models were used to estimate how observed morphologies affected the stress field in the vicinity of cells. Collagen is expected to nonlinear viscoelastic behavior (Pryse et al. 2003; Nekouzadeh et al. 2007), and cell mechanics are expected to change with age (Qiu et al. 2010), ECM stiffness (Marquez et al. 2010), and cell volume fraction (Marquez et al. 2005, 2006). However, because accurate, calibrated models are not available these effects could not be considered and simple linear theories were used.
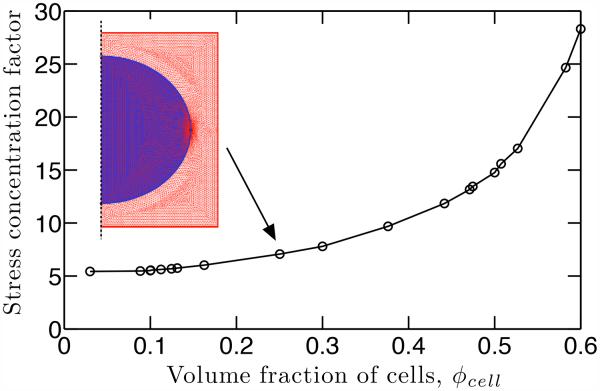
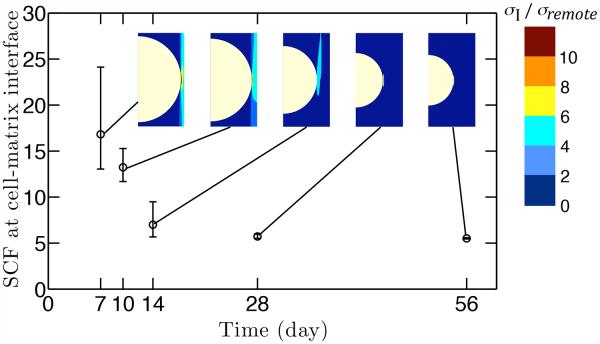
Within this framework, the stress concentration factor depended on the volume fraction of cells, with a broad range demonstrated for the axisymmetric unit cell model (Fig. 6). The cell volume fraction decreased from 60% to 10% in the mineralized region throughout development (Fig. 4a); this resulted in a cell-level SCF decrease from 28 to 5.5 (Fig. 6). The SCF and the corresponding first principal stress contour in the gradient region at different time points are shown in Fig. 7. The cell-level SCF was much higher at early time points (P7 and P10) than at later time points, and the highest stress regions around the cell were larger at early time points.
Figure 6.
As the volume fraction and the size of cells decrease over time, the SCF decreases at the cell-matrix interface. The SCF was determined numerically using finite element simulations; a schematic axisymmetric unit cell model with mesh is shown.
Figure 7.
The stress concentration at the cell-matrix interface decreased as a function of age. The stress field remained qualitatively similar over time, as shown in the contour of peak principal stresses.
3.4 Tissue-level stress concentrations decrease slightly with age
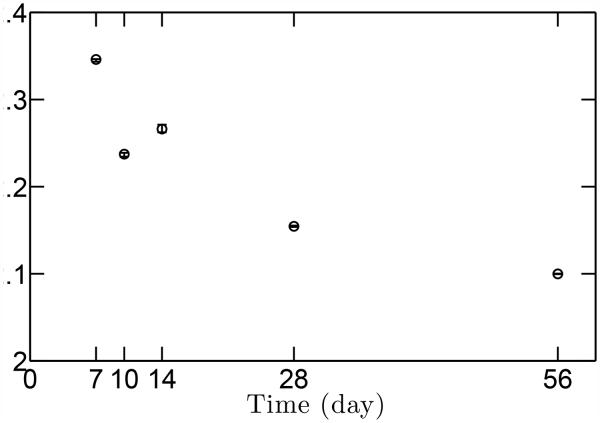
The tissue-level SCF for the concentric ring model is shown in Fig. 8. The constant gradient size and decreasing unmineralized region size over time (with the stiffness adjusted for the volume fraction of cells) led to a slight decrease in macroscopic stress at the tendon-to-bone enthesis from P7 to P56.
Figure 8.
The effect of the mineral gradient region on the macroscopic stress concentration at the tendon-to-bone enthesis is shown as a function of age. The gradient region did not change over time and the stiffness was adjusted for the volume fraction of cells using the results of the finite element analyses shown in Fig. 7. A schematic of the concentric ring model is shown above the plot.
3.5 Morphological factors combine to stress cells at adult levels during development
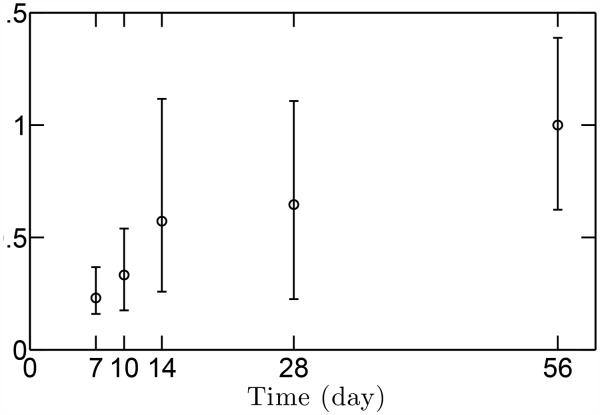
The peak principal stress at the equator of cells in the gradient region was estimated at each time point. This involved, first, estimating the combined stress concentration factor that accounts for amplification of stresses at both the cell- and tissue-level, and, second, scaling the applied muscle stresses by this combined stress concentration factor (Fig. 9). The estimated peak principal stress did not change significantly from P10 onwards; only the difference between P7 and P56 was significant statistically, with the average value at P7 0.23 times of that at P56. At all time points, the peak principal stress was not different statistically from that at young adulthood (P28).
Figure 9.
The peak principal stress surrounding cells during early development are elevated to near adult physiologic levels through stress concentrations. The estimated peak principal stress did not change significantly from P10 onwards; only the difference between P7 and P56 was significant statistically, with the average value at P7 0.23 times of that at P56. At all time points, the peak principal stress was not different statistically from that at young adulthood (P28).
Why might these morphologically elevated stresses be important? Failure to provide the appropriate local stress stimuli to cells during early enthesis development leads to severe defects in enthesis mineralization, fibrocartilage formation, and collagen organization (Thomopoulos et al. 2007; Blitz et al. 2009). Experimental results show that local mineral content in developing tissues is the same as in mature tissues, both at the mineralized region of the enthesis and at the bone, although the tissue level volume fraction is lower because of the larger volume fraction of chondrocytes at early time points (Schwartz et al. 2012). Our work suggests that the local stresses at early time points are also elevated to near adult physiologic levels, presumably to stimulate chondrocyte mineralization.
While the enthesis serves to reduce the tissue-level level of stress concentration caused by directly connecting two dissimilar materials (i.e., tendon to bone) in adulthood, its role might be different in development. The highly localized stress around cells may serve to amplify the low muscle loads present during early tendon-to-bone enthesis development. One possible effect of the highly localized stress around the cells may be to stimulate the enlargement of the chondrocytes, inducing a phenotypic change into hypertrophic chondrocytes accompanied by extracellular mineralization (Hall 2005; Coe et al. 1992). Mechanical stress might play a role in the proliferative to hypertrophic transition (Stokes 2002; Stokes et al. 2002), and our observations are consistent with this. Although the load-bearing capability is low because of the immaturity of tissues in the early time points of development, removing all muscle load is clearly detrimental to development (Thomopoulos et al. 2010; Blitz et al. 2009).
These results suggest that amplified local stresses around cells in the mineralized region are present during development, and support our hypothesis that mechanical factors across several length scales amplify stresses. The contribution of this work is to show that even in early development, stresses around cells in the mineralized region can reach levels associated with early adulthood. We suggest that these stresses are of a level adequate to contribute to mechanical signaling during mineralization.
3.6 Other interpretations
The mechanical factors we describe are likely just one of many possible explanations for the ability of cells to mineralize tissue at early time points. Early in development, the signaling factors surrounding cells at the enthesis differ from factors present in adulthood. One possibility is that all mineralization around hypertrophic chondrocytes is triggered by such soluble factors through a pathway that is completely independent of mechanical stresses, but this is not likely due to the observation that immobilization leads to development of a highly abnormal insertion of tendon to bone (Thomopoulos et al. 2010).
An important potential role of mechanical factors in signal transduction relates to the ways that gradients and associated inhomogeneities in the stress field distort cells, particularly at early time points. Studies conducted in vitro indicate a strong relationship between cell shape and mechanosensitivity, and there are typically a number of molecular mechanisms beyond shape that drive this response (e.g., level of attachment to a substrate, stiffness of substrate, etc.) (Adams et al. 1989). Although hypertrophic chondrocytes and cells within the gradient region of the enthesis do in fact retain a spherical geometry (Guilak et al. 1995), subtle, stress-induced deformation of cell shape is an important factor to consider. However, we note that these changes might be small because the stress around these cells has a large hydrostatic component due to the azimuthal constraint associated with the spherical shape of the humeral head.
Another interesting mechanical factor is that the pericellular matrix surrounding chondrocytes in cartilage is highly inhomogeneous (Guilak et al. 1995). Although the dominant factor of mineralization was included in our first order approximations to local stress concentrations around cells, potential second order contributions of the pericellular matrix are an important consideration for future work.
3.7 Caveats
Mechanical factors are well known play an important role in maintaining homeostasis during the development of tendon-to-bone attachment. Note, however, that this work is preliminary, with idealized models: (1) the geometric models ignored the spacing and size of the cells in the fully mineralized region; (2) due to the lack of experimental data, collagen fiber angular distribution was ignored in estimating the stiffness of the extracellular matrix at the enthesis. Despite the idealized nature of the modeling, stress analysis results qualitatively show that local stresses around cells are elevated in the regions where mineralization occurs. The highly localized stress level at the cell appears at early postnatal time points, suggesting that mechanical cues may be important for the initial deposition and later accumulation of mineral. This is supported by experimental evidence demonstrating that muscle loads are necessary for mineralization at the developing tendon-to-bone insertion. Elevated local stress, then, may be crucial for early development and, likewise, for the early stages of post-surgical healing.
Although physiological muscle forces are typically cyclical in nature, the model assumed static muscle loads. Cells respond to both peak and time-averaged muscle loads in vivo. Based on morphological data and finite element analyses of developing chicks, Nowlan et al. (2008) showed that high cycles of stress preceded ossification of cartilage. Furthermore, analysis of biophysical stimuli in a “muscleless” mouse model showed that passive cyclical movements (e.g., via movements of the mother) can compensate for the lack of direct skeletal muscle loading (Nowlan et al. 2012). Future studies will therefore expand the current model to include physiologically relevant cyclical loads.
Many questions remain and warrant further study. At the enthesis, there is a large volume fraction of cells in the unmineralized region, although the fraction of cells is smaller than that in the mineralized region. How is mineral retained away from these regions, after the front of mineralization has passed? At the nanoscale, where and how does mineral first form on/in the collagen fibrils? How is a gradient in the mineral content achieved from the mineralization front to the bone? It is clear that biochemical and genetic factors also play important roles in both enthesis development (Thomopoulos et al. 2010; Blitz et al. 2009) and mineralization during development (Coe et al. 1992; Yagami et al. 1999; Liu et al. 2007); these factors likely interact with the mechanical factors described in the current study to regulate enthesis development.
4 Conclusions
In a mouse, the approximately linear gradation in mineral content at the supraspinatus enthesis stays a constant size from early postnatal time points through adulthood, while the humeral head grows substantially. The morphology of the enthesis in the adult mouse is believed to serve the role of reducing stress concentrations, but the analyses presented here suggest a different role at early time points. Effects of the mineralization gradient at the tissue level may combine with effects of cell volume fraction at the cell level to compensate for extremely low muscle stresses present at earlier time points. This results in elevation of stresses at the cell-matrix interface in juveniles to levels similar to those estimated for adults. These observations have important implications for post-surgical physical therapy regiments for patients who receive engineered tissue scaffolds to guide enthesis redevelopment. Stress concentrations at the cell level, which are favorable in the early time points of enthesis development, may also be favorable for enthesis tissue engineering.
Supplementary Material
Acknowledgements
This work was supported in part by the NSF (CAREER 844607), the NIH (R01 AR055580), and the Washington University Musculoskeletal Research Center (NIH P30 AR057235). YXL acknowledges a graduate fellowship from the Fannie Stevens Murphy foundation, and AGS from the NIH (T32 AR060719). The authors thank Sandra Matteucci and Lynnea Brumbaugh for assistance with manuscript preparation.
References
- Adams SL, Pallante KM, Pacifici M. Effects of cell shape type x collagen gene expression in hypertrophic chondrocytes. Connective tissue research. 1989;20(1-4):223–232. doi: 10.3109/03008208909023891. [DOI] [PubMed] [Google Scholar]
- Alexander B, Daulton TL, Genin GM, Lipner J, Pasteris JD, Wopenka B, Thomopoulos S. J R Soc Interface. 2012. The nanometre-scale physiology of bone: steric modelling and scanning transmission electron microscopy of collagen–mineral structure. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexopoulos LG, Williams GM, Upton ML, Setton LA, Guilak F. Osteoarthritic changes in the biphasic mechanical properties of the chondrocyte pericellular matrix in articular cartilage. J Biomech. 2005;38(3):509–517. doi: 10.1016/j.jbiomech.2004.04.012. [DOI] [PubMed] [Google Scholar]
- Amiel D, Woo SLY, Harwood FL, Akeson WH. The effect of immobilization on collagen turnover in connective tissue: a biochemical-biomechanical correlation. Acta Orthop. 1982;53(3):325–332. doi: 10.3109/17453678208992224. [DOI] [PubMed] [Google Scholar]
- Bailey DA, McKay HA, Mirwald RL, Crocker PRE, Faulkner RA. A six-year longitudinal study of the relationship of physical activity to bone mineral accrual in growing children: the university of saskatchewan bone mineral accrual study. J Bone Miner Res. 1999;14(10):1672–1679. doi: 10.1359/jbmr.1999.14.10.1672. [DOI] [PubMed] [Google Scholar]
- Benjamin M, Kumai T, Milz S, Boszczyk BM, Boszczyk AA, Ralphs JR. The skeletal attachment of tendons–tendon “entheses”. Comp Biochem Phys A. 2002;133(4):931–945. doi: 10.1016/s1095-6433(02)00138-1. [DOI] [PubMed] [Google Scholar]
- Benjamin M, Toumi H, Ralphs JR, Bydder G, Best TM, Milz S. Where tendons and ligaments meet bone: attachment sites (‘entheses’) in relation to exercise and/or mechanical load. J Anat. 2006;208(4):471–490. doi: 10.1111/j.1469-7580.2006.00540.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blitz E, Viukov S, Sharir A, Shwartz Y, Galloway JL, Pryce BA, Johnson RL, Tabin CJ, Schweitzer R, Zelzer E. Bone ridge patterning during musculoskeletal assembly is mediated through scx regulation of bmp4 at the tendon-skeleton junction. Dev Cell. 2009;17(6):861–873. doi: 10.1016/j.devcel.2009.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burkholder TJ, Fingado B, Baron S, Lieber RL. Relationship between muscle fiber types and sizes and muscle architectural properties in the mouse hindlimb. J Morphol. 1994;221(2):177–190. doi: 10.1002/jmor.1052210207. [DOI] [PubMed] [Google Scholar]
- Chayes F. Petrographic modal analysis: an elementary statistical appraisal. Wiley; New York: 1956. [Google Scholar]
- Coe MR, Summers TA, Parsons SJ, Boskey AL, Balian G. Matrix mineralization in hypertrophic chondrocyte cultures:: Beta glycerophosphate increases type x collagen messenger rna and the specific activity of pp60c-src kinase. Bone Miner. 1992;18(2):91–106. doi: 10.1016/0169-6009(92)90850-d. [DOI] [PubMed] [Google Scholar]
- Collet PH, Uebelhart D, Vico L, Moro L, Hartmann D, Roth M, Alexandre C. Effects of 1-and 6-month spaceflight on bone mass and biochemistry in two humans. Bone. 1997;20(6):547–551. doi: 10.1016/s8756-3282(97)00052-5. [DOI] [PubMed] [Google Scholar]
- Delesse A. Precede mechanique pour determines la composition de roches (extrait) CR Acad Sci (Paris) 1847;25:544–560. [Google Scholar]
- Galatz LM, Ball CM, Teefey SA, Middleton WD, Yamaguchi K. The outcome and repair integrity of completely arthroscopically repaired large and massive rotator cuff tears. J Bone Joint Surg Am. 2004;86(2):219–224. doi: 10.2106/00004623-200402000-00002. [DOI] [PubMed] [Google Scholar]
- Galatz LM, Charlton N, Das R, Kim HM, Havlioglu N, Thomopoulos S. Complete removal of load is detrimental to rotator cuff healing. J Shoulder Elb Surg. 2009;18(5):669–675. doi: 10.1016/j.jse.2009.02.016. [DOI] [PubMed] [Google Scholar]
- Genin GM, Birman V. Micromechanics and structural response of functionally graded, particulate-matrix, fiber-reinforced composites. Int J Solids Struct. 2009;46(10):2136–2150. doi: 10.1016/j.ijsolstr.2008.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genin GM, Kent A, Birman V, Wopenka B, Pasteris JD, Marquez PJ, Thomopoulos S. Functional grading of mineral and collagen in the attachment of tendon to bone. Biophys J. 2009;97(4):976–985. doi: 10.1016/j.bpj.2009.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gokhin DS, Ward SR, Bremner SN, Lieber RL. Quantitative analysis of neonatal skeletal muscle functional improvement in the mouse. J Exp Biol. 2008;211(6):837–843. doi: 10.1242/jeb.014340. [DOI] [PubMed] [Google Scholar]
- Guilak F, Ratcliffe A, Mow VC. Chondrocyte deformation and local tissue strain in articular cartilage: a confocal microscopy study. Journal of Orthopaedic Research. 1995;13(3):410–421. doi: 10.1002/jor.1100130315. [DOI] [PubMed] [Google Scholar]
- Hall BK. Bones and cartilage: developmental and evolutionary skeletal biology. Academic Press; 2005. [Google Scholar]
- Harryman DT, Mack LA, Wang KY, Jackins SE, Richardson ML, Matsen FA. Repairs of the rotator cuff. correlation of functional results with integrity of the cuff. J Bone Joint Surg Am. 1991;73:982–989. [PubMed] [Google Scholar]
- Jones WR, Ping Ting-Beall H, Lee GM, Kelley SS, Hochmuth RM, Guilak F. Alterations in the youngs modulus and volumetric properties of chondrocytes isolated from normal and osteoarthritic human cartilage. J Biomech. 1999;32(2):119–127. doi: 10.1016/s0021-9290(98)00166-3. [DOI] [PubMed] [Google Scholar]
- Kaplan FS, Hayes WC, Keaveny TM, Boskey A, Einhorn TA, Iannotti JP. Form and function of bone. Orthopaedic Basic Science. 1994:127–185. [Google Scholar]
- Kim E, Guilak F, Haider MA. An axisymmetric boundary element model for determination of articular cartilage pericellular matrix properties in situ via inverse analysis of chondron deformation. J Biomech Eng. 2010;132:031–011. doi: 10.1115/1.4000938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Thomopoulos S, Chen C, Birman V, Buehler MJ, Genin GM. ? modelling the mechanics of partially mineralized collagen fibrils, fibres and tissue. J R Soc Interface. 2014:20130835. doi: 10.1098/rsif.2013.0835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu YX, Birman V, Chen CQ, Thomopoulos S, Genin GM. Mechanisms of bimaterial attachment at the interface of tendon to bone. J Eng Mater Technol Trans ASME. 2011;133:011–006. doi: 10.1115/1.4002641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu YX, Thomopoulos S, Birman V, Li JS, Genin GM. Bi-material attachment through a compliant interfacial system at the tendon-to-bone insertion site. Mech Mater. 2012;44:83–92. doi: 10.1016/j.mechmat.2011.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Lavine KJ, Hung IH, Ornitz DM. Fgf18 is required for early chondrocyte proliferation, hypertrophy and vascular invasion of the growth plate. Dev Biol. 2007;302(1):80–91. doi: 10.1016/j.ydbio.2006.08.071. [DOI] [PubMed] [Google Scholar]
- Lui PPY, Zhang P, Chan KM, Qin L. Biology and augmentation of tendon-bone insertion repair. J Orthop Surg Res. 2010;5(1):1–14. doi: 10.1186/1749-799X-5-59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch HA, Johannessen W, Wu JP, Jawa A, Elliott DM. Effect of fiber orientation and strain rate on the nonlinear uniaxial tensile material properties of tendon. J Biomech Eng. 2003;125:726–731. doi: 10.1115/1.1614819. [DOI] [PubMed] [Google Scholar]
- Maganaris CN, Paul JP. In vivo human tendon mechanical properties. J Physiol. 1999;521(1):307–313. doi: 10.1111/j.1469-7793.1999.00307.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marquez J, Genin G, Zahalak G, Elson E. The relationship between cell and tissue strain in three-dimensional bio-artificial tissues. Biophysical journal. 2005;88(2):778–789. doi: 10.1529/biophysj.104.041947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marquez J, Genin G, Pryse K, Elson E. Cellular and matrix contributions to tissue construct stiffiness increase with cellular concentration. Annals of biomedical engineering. 2006;34(9):1475–1482. doi: 10.1007/s10439-006-9160-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marquez J, Elson E, Genin G. Whole cell mechanics of contractile fibroblasts: relations between effective cellular and extracellular matrix moduli. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2010;368(1912):635–654. doi: 10.1098/rsta.2009.0240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nekouzadeh A, Pryse K, Elson E, Genin G. A simplified approach to quasi-linear viscoelastic modeling. Journal of biomechanics. 2007;40(14):3070–3078. doi: 10.1016/j.jbiomech.2007.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowlan NC, Murphy P, Prendergast PJ. A dynamic pattern of mechanical stimulation promotes ossification in avian embryonic long bones. Journal of biomechanics. 2008;41(2):249–258. doi: 10.1016/j.jbiomech.2007.09.031. [DOI] [PubMed] [Google Scholar]
- Nowlan NC, Sharpe J, Roddy KA, Prendergast PJ, Murphy P. Mechanobiology of embryonic skeletal development: insights from animal models. Birth Defects Research Part C: Embryo Today: Reviews. 2010;90(3):203–213. doi: 10.1002/bdrc.20184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowlan NC, Dumas G, Tajbakhsh S, Prendergast PJ, Murphy P. Biophysical stimuli induced by passive movements compensate for lack of skeletal muscle during embryonic skeletogenesis. Biomechanics and modeling in mechanobiology. 2012;11(1-2):207–219. doi: 10.1007/s10237-011-0304-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pryse K, Nekouzadeh A, Genin G, Elson E, Zahalak G. Incremental mechanics of collagen gels: new experiments and a new viscoelastic model. Annals of biomedical engineering. 2003;31(10):1287–1296. doi: 10.1114/1.1615571. [DOI] [PubMed] [Google Scholar]
- Qiu H, Zhu Y, Sun Z, Trzeciakowski J, Gansner M, Depre C, Resuello R, Natividad F, Hunter W, Genin G, et al. Vascular smooth muscle cell stiffness as a mechanism for increased aortic stiffness with agingnovelty and significance. Circulation research. 2010;107(5):615–619. doi: 10.1161/CIRCRESAHA.110.221846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz A, Pasteris JD, Genin GM, Daulton T, Thomopoulos S. The nanometer-scale physiology of bone: Steric modeling and scanning transmission electron microscopy of collagen-mineral structure. PLoS ONE. 2012;7(11):e48–630. doi: 10.1098/rsif.2011.0880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith L, Xia Y, Galatz L, Genin G, Thomopoulos S. Tissue-engineering strategies for the tendon/ligament-to-bone insertion. Connective Tissue Research. 2012;53(2):95–105. doi: 10.3109/03008207.2011.650804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stabile KJ, Pfaeffle J, Weiss JA, Fischer K, Tomaino MM. Bi-directional mechanical properties of the human forearm interosseous ligament. J Orthop Res. 2004;22(3):607–612. doi: 10.1016/j.orthres.2003.05.002. [DOI] [PubMed] [Google Scholar]
- Stokes IAF. Mechanical effects on skeletal growth. J Musculoskelet Neuron Interact. 2002;2(3):277–280. [PubMed] [Google Scholar]
- Stokes IAF, Mente PL, Iatridis JC, Farnum CE, Aronsson DD. Growth plate chondrocyte enlargement modulated by mechanical loading. Studies in Health Technology and Informatics. 2002:378–381. [PubMed] [Google Scholar]
- Tanck E, Hannink G, Ruimerman R, Buma P, Burger EH, Huiskes R. Cortical bone development under the growth plate is regulated by mechanical load transfer. J Anat. 2006;208(1):73–79. doi: 10.1111/j.1469-7580.2006.00503.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomopoulos S, Williams GR, Gimbel JA, Favata M, Soslowsky LJ. Variation of biomechanical, structural, and compositional properties along the tendon to bone insertion site. J Orth Res. 2003;21(3):413–419. doi: 10.1016/S0736-0266(03)00057-3. [DOI] [PubMed] [Google Scholar]
- Thomopoulos S, Marquez J, Weinberger B, Birman V, Genin G. Collagen fiber orientation at the tendon to bone insertion and its influence on stress concentrations. J Biomech. 2006;39(10):1842–1851. doi: 10.1016/j.jbiomech.2005.05.021. [DOI] [PubMed] [Google Scholar]
- Thomopoulos S, Kim HM, Rothermich SY, Biederstadt C, Das R, Galatz LM. Decreased muscle loading delays maturation of the tendon enthesis during postnatal development. J Orth Res. 2007;25(9):1154–1163. doi: 10.1002/jor.20418. [DOI] [PubMed] [Google Scholar]
- Thomopoulos S, Genin GM, Galatz LM. The development and morphogenesis of the tendon-to-bone insertion-what development can teach us about healing. J Musculoskelet Neuronal Interact. 2010;10(1):35–45. [PMC free article] [PubMed] [Google Scholar]
- Thomopoulos S, Das R, Birman V, Smith L, Ku K, Elson E, Pryse K, Marquez J, Genin G. Fibrocartilage tissue engineering: The role of the stress environment on cell morphology and matrix expression. Tissue Engineering Part A. 2011;17(7-8):1039–1053. doi: 10.1089/ten.tea.2009.0499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss JA, Gardiner JC, Bonifasi-Lista C. Ligament material behavior is nonlinear, viscoelastic and rate-independent under shear loading. J Biomech. 2002;35(7):943–950. doi: 10.1016/s0021-9290(02)00041-6. [DOI] [PubMed] [Google Scholar]
- Woo SL, Gomez MA, Woo YK, Akeson WH. Mechanical properties of tendons and ligaments. ii. the relationships of immobilization and exercise on tissue remodeling. Biorheology. 1982;19(3):397. doi: 10.3233/bir-1982-19302. [DOI] [PubMed] [Google Scholar]
- Wopenka B, Kent A, Pasteris JD, Yoon Y, Thomopoulos S. The tendon-to-bone transition of the rotator cuff: a preliminary raman spectroscopic study documenting the gradual mineralization across the insertion in rat tissue samples. Appl Spectrosc. 2008;62(12):1285–1294. doi: 10.1366/000370208786822179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yagami K, Suh JY, Enomoto-Iwamoto M, Koyama E, Abrams WR, Shapiro IM, Pacifici M, Iwamoto M. Matrix gla protein is a developmental regulator of chondrocyte mineralization and, when constitutively expressed, blocks endochondral and intramembranous ossification in the limb. J Cell Biol. 1999;147(5):1097. doi: 10.1083/jcb.147.5.1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin L, Elliott DM. A biphasic and transversely isotropic mechanical model for tendon: application to mouse tail fascicles in uniaxial tension. J Biomech. 2004;37(6):907–916. doi: 10.1016/j.jbiomech.2003.10.007. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.