Standardizing the intrinsic brain: Towards robust measurement of inter-individual variation in 1000 functional connectomes

Abstract

As researchers increase their efforts to characterize variations in the functional connectome across studies and individuals, concerns about the many sources of nuisance variation present and their impact on resting state fMRI (R-fMRI) measures continue to grow. Although substantial within-site variation can exist, efforts to aggregate data across multiple sites such as the 1000 Functional Connectomes Project (FCP) and International Neuroimaging Data-sharing Initiative (INDI) datasets amplify these concerns. The present work draws upon standardization approaches commonly used in the microarray gene expression literature, and to a lesser extent recent imaging studies, and compares them with respect to their impact on relationships between common R-fMRI measures and nuisance variables (e.g., imaging site, motion), as well as phenotypic variables of interest (age, sex). Standardization approaches differed with regard to whether they were applied post-hoc vs. during pre-processing, and at the individual vs. group level; additionally they varied in whether they addressed additive effects vs. additive + multiplicative effects, and were parametric vs. non-parametric. While all standardization approaches were effective at reducing undesirable relationships with nuisance variables, post-hoc approaches were generally more effective than global signal regression (GSR). Across approaches, correction for additive effects (global mean) appeared to be more important than for multiplicative effects (global SD) for all R-fMRI measures, with the exception of amplitude of low frequency fluctuations (ALFF). Group-level post-hoc standardizations for mean-centering and variance-standardization were found to be advantageous in their ability to avoid the introduction of artifactual relationships with standardization parameters; though results between individual and group-level post-hoc approaches were highly similar overall. While post-hoc standardization procedures drastically increased test–retest (TRT) reliability for ALFF, modest reductions were observed for other measures after post-hoc standardizations—a phenomena likely attributable to the separation of voxel-wise from global differences among subjects (global mean and SD demonstrated moderate TRT reliability for these measures). Finally, the present work calls into question previous observations of increased anatomical specificity for GSR over mean centering, and draws attention to the near equivalence of global and gray matter signal regression.

Introduction

Measurement standardization represents a key challenge for the field of functional connectomics. As researchers increase their efforts to characterize variations in the functional connectome observed across studies and individuals, concerns about the many known and unknown sources of nuisance variation present and their impact on resting state fMRI (R-fMRI) measures continue to grow (Cole et al., 2010; Kelly et al., 2012). Between studies, MR acquisition methodologies are among the most commonly cited sources of measurement variation (Friedman and Glover, 2006b); yet a multitude of experimental, environmental and subject-related factors can introduce unintended variations in measurement as well (Table 1). Few, if any, of these factors are addressed in imaging studies. Finally, head-motion and physiologic parameters (cardiac or respiratory effects) are major sources of measurement variation, which can at times be related to systematic variables of interest (e.g., age, diagnostic status) (Power et al., 2012; Satterthwaite et al., 2012; Van Dijk et al., 2012). A growing reality is that even the best efforts to standardize data acquisition and limit the number of unknowns, unwanted sources of variation in R-fMRI studies will remain.

Table 1.

Factors can introduce unintended variations in fMRI measurement.

Category	Factor
1. Acquisition-related variations	Scanner make and model (Friedman and Glover, 2006b), sequence type (spiral vs. echo planar; single-echo vs. multi-echo) (Klarhofer et al., 2002), parallel vs. conventional acquisition (Feinberg et al., 2010; Lin et al., 2005), coil type (surface vs. volume, number of channels, orientation), repetition time, number of repetitions, flip angle, echo time, and acquisition volume (field of view, voxel size, slice thickness/gaps, slice prescription) (Friedman and Glover, 2006a)
2. Experimental-related variations	Participant instructions (Hartstra et al., 2011), eyes-open/eyes-closed (Yan et al., 2009; Yang et al., 2007), visual displays, experiment duration (Fang et al., 2007; Van Dijk et al., 2010)
3. Environment-related variations	Sound attenuation measures (Cho et al., 1998; Elliott et al., 1999), attempts to improve participant comfort during scans (e.g., music, videos) (Cullen et al., 2009), head-motion restraint techniques (e.g., vacuum pad, foam pad, bite-bar, plaster cast head holder) (Edward et al., 2000; Menon et al., 1997), room temperature and moisture (Vanhoutte et al., 2006).
4. Participant-related variations	Circadian cycle (Shannon et al., 2013), prandial (Haase et al., 2009), caffeine (Rack-Gomer et al., 2009), and nicotine status (Tanabe et al., 2011), sleepiness/arousal (Horovitz et al., 2008), sleep deprivation (Samann et al., 2010), scanner anxiety (de Bie et al., 2010), and menstrual cycle status (for women) (Protopopescu et al., 2005)

In 2009, the publicly released 1000 Functional Connectomes Project (FCP) and International Neuroimaging Data-sharing Initiative (INDI) provided a stark portrayal of variability in imaging methodologies employed by the neuroimaging field. Comprised of R-fMRI samples independently collected at imaging sites around the world, notable variation in almost every aspect of imaging acquisition methodologies represented in these datasets while the majority of participant-related variables are not reported (and in most cases, were not systematically recorded). As expected, remarkable site-related variation is detectable in R-fMRI measures derived from the FCP/INDI datasets, raising understandable concerns about whether such data could be harmonized and analyzed. Fortunately, despite justifiable skepticism, feasibility analyses demonstrated that meaningful explorations of the aggregate dataset (n = 1093; 24 imaging sites) could be performed (Biswal et al., 2010). After accounting for site-related differences, discovery analyses revealed brain–behavior relationships with phenotypic variables such as sex, age, and diagnostic status, and confirmed a variety of prior hypotheses (Biswal et al., 2010; Fair et al., 2012; Tomasi and Volkow, 2010; Zuo et al., 2012). Although encouraging, the many unknown and uncontrolled factors in the FCP/INDI remain a source of concern, as they extend beyond simple site effects and can limit the utility of the datasets.

The goal of the present work is to provide a comprehensive assessment of the impact of post-acquisition standardization methodologies on common R-fMRI data analyses, using data from the original 1000 Functional Connectomes Project. Several strategies for standardization have already emerged in the field including mean division (Zang et al., 2004, 2007); Z-score standardization (Beckmann et al., 2005; Buckner et al., 2009; Calhoun et al., 2001; Zou et al., 2008; Zuo et al., 2010a, 2012, 2013); and Gaussian function fit normalization (Lowe et al., 1998). However, these methods are not consistently used and have not been systematically compared. Additional approaches can be borrowed from the molecular genetics community, which has made noteworthy strides in dealing with unwanted variation in microarray technologies and procedures (see Quackenbush, 2002 for a review). Drawing on these two sources we identified 11 standardization approaches (Table 2) to apply to the original FCP dataset and compare with respect to their impact on commonly examined R-fMRI measures, their test–retest (TRT) reliability and phenotypic relationships (sex, age), as well as nuisance variables of interest.

Table 2.

Standardization procedures examined in the current study.

	Analytic method	Post-hoc correction	Correction level	Addresses additive noise	Addresses multiplicative noise	Can introduce artifact	Non-parametric
GSR	Regression of the mean brain signal during preprocessing		I			X
Mean subtraction	Vmeasure − Meanmeasure	X	I	X		X
Mean division	Vmeasure / Meanmeasure	X	I	X	X	X
Z-standardization	(Vmeasure − Meanmeasure) / SDmeasure	X	I	X	X	X
Mean regression	Regress out Meanmeasure from Vmeasure	X	G	X
Mean regression and SD division	• Regress out Meanmeasure from Vmeasure,, resulting in y′ • y′/SDmeasure	X	M	X	X	X
Mean regression and log SD regression	• Regress out Meanmeasure from Vmeasure,, resulting in y′ • Regress out ln(SDmeasure) from ln(|y′|), resulting in y″ • Take the exponent of y″ and recover the sign resulting in ey″	X	G	X	X
Mean–IQR	(Vmeasure − Medianmeasure) / IQRmeasure	X	I	X	X	X	X
Rank	Rank Vmeasure relative to all voxels with the whole brain	X	I	X	X	X	X
Quantile standardization	Rank Vmeasure within subject. For each rank, calculate the mean across subjects and assign back	X	M	X	X	X	X
Gaussian fit	(Vmeasure − E[Meanmeasure]) / E[SDmeasure]	X	I	X	X	X

All standardization procedures were implemented for each voxel. GSR: global signal regression; V_measure: the value of a given R-fMRI measure at a given voxel; Mean_measure: the within-subject mean of a given measure; SD_measure: the within-subject standard deviation of a given measure; Median_measure; the within-subject median of a given measure; IQR_measure: the inter-quartile range of a given measure defined as the range between 25% and 75% percentile for a subject; E[Mean_measure]: the estimated mean of a given measure based on a Gaussian function (Lowe et al., 1998); E[SD_measure]: the estimated standard deviation of a given measure based on a Gaussian function; X: yes; I: individual-level; G: group-level; M: mixed-level.

As shown in Table 2, a first key distinction among standardization approaches is whether they handle factors that have additive effects, multiplicative effects, or both. Additive factors are those which sum with signals of interest, to globally shift the observed distribution for a given R-fMRI measure from one participant to another. Mean centering is the prototypic standardization approach for removing additive effects within participants. Mean centering straightly shifts the distribution of values observed across voxels to be centered at zero, by subtracting the mean of the distribution (i.e., the global mean). In contrast, multiplicative factors scale distributions of values observed for a given R-fMRI index in an individual, with a scaling factor that varies from one participant to the next, which can be treated as additive after log transformed. Mean division is a prototypic approach for correction of multiplicative effects by scaling each participant in terms of the global mean across voxels, and has been used in the R-fMRI literature for frequency-based measures and regional homogeneity (Zang et al., 2004, 2007). To handle both additive and multiplicative factors, Z-standardization shifts the distribution with its mean and scales it in terms of the standard deviation (SD). Meanwhile, a variety of non-parametric equivalents of Z-standardization are commonly used to avoid potential biases introduced by extreme outliers (median–interquartile range normalization, quantile normalization, rank) (Parrish and Spencer, 2004).

A key concern that arises with the aforementioned within-subject post-hoc approaches is their potential to introduce artifactual relationships with the distribution parameters employed for standardization. The source of the concern arises from the fact that: 1) all voxels are adjusted equivalently, regardless of whether or not their values are affected by artifact, and 2) each participant's centering or scaling factor is calculated independently. For voxels that initially have no relationship to the standardization parameters (e.g., global mean, global SD) across subjects, relationships can emerge due to their forced adjustment based upon the global parameters in each subject. To avoid such confounds, our examination will include two group-level post-hoc approaches (mean regression [additive], mean regression & log SD regression [additive + multiplicative]). Based on regressing each voxel on its distribution parameters across subjects, rather than forcing subject-wise changes, this approach is only applicable at the group level, not to single subjects.

While post-hoc statistical approaches standardize data based upon the distribution of values obtained after calculation of a given R-fMRI measure, the common practice of characterizing and removing nuisance signals in each participant's fMRI time series prior to calculating the R-fMRI measure can provide some degree of standardization. Specifically, global signal regression (GSR) has emerged as a commonly used, though controversial technique for preprocessing. At the center of this controversy is the tendency of GSR to zero-center the distribution of correlation values (Murphy et al., 2009). This tendency indicates that GSR has properties similar to the proposed standardization procedures, and therefore we evaluate its utility for reducing inter-subject and inter-site variation. Additionally, GSR is believed to afford increased tissue sensitivity (Fox et al., 2009) and decreased dependencies on motion (Satterthwaite et al., 2013; Yan et al., 2013).

In the present work, we analyzed the publically available FCP datasets to quantitatively evaluate the impact of different standardization approaches on statistical analyses of a variety of R-fMRI measures. First, we evaluate distribution parameters (global mean and global SD) to examine if there are systematic variations related to confounding factors (e.g., site and motion) and variables of interests (e.g., age and sex). Second, we evaluated the ability of different standardization procedures in reducing voxel-wise effects of confounding factors on the R-fMRI measures. Third, we investigated the impact of the standardization procedures in revealing voxel-wise effects of interests (age and sex). Fourth, we investigated the impact of standardization on TRT reliability of both global and voxel-wise measurements of these R-fMRI metrics. Given concerns about the potential for standardization approaches to introduce artifact, we complement our analyses with an examination of unintended relationships with R-fMRI distribution parameters (i.e., global mean, global SD) following application. Finally, we revisit previous claims that mean-centering approaches reduce anatomic specificity relative to GSR.

Methods

Participants and imaging protocols

We performed our analyses on publicly available imaging data from the 1000 Functional Connectomes Project (all data are available at http://fcon_1000.projects.nitrc.org). TRT reliability was assessed on the NYU TRT dataset. The corresponding institutional review boards approved or provided waivers for the submission of anonymized data, which were obtained with written informed consent from each participant.

Although datasets differ in participant demographics and scanning parameters (see Table 3 for details, data of 828 subjects entered into group analyses), the general data acquisition procedures were similar across sites. Specifically, participants were instructed to rest while awake in the MR scanner, and R-fMRI data were acquired using an echo-planar imaging (EPI) sequence. A high-resolution T1-weighted anatomical image was also obtained for each participant for spatial normalization and localization.

Table 3.

Participant and scanning parameter details for each dataset included in group analyses in the current study.

	Center	PI	n	Sex (M/F)	Age (mean/SD)	Magnet	TR (s)	Slice number	Time points	Voxel size	FOV	Eyes open vs. closed	Slice order
1	Baltimore, MD, USA	James J. Pekar/Stewart H. Mostofsky	23	15/8	29.3/5.5	3T	2.5	47	123	2.67 × 2.67 × 3	256 × 256	Open, fixation	SA
2	Bangor, UK	Stan Colcombe	17	0/17	24.0/5.6	3T	2	34	265	3 × 3 × 3	240 × 240	Open	SA
3	Beijing, China	Yu-Feng Zang	176	106/70	21.2/1.9	3T	2	33	235	3.12 × 3.12 × 3.6	200 × 200	Closed	IA
4	Berlin, Germany	Daniel Margulies	11	5/6	30.4/6.1	3T	2.3	34	195	3 × 3 × 4	192 × 192	Open, blank screen	IA
5	Cambridge, MA, USA	Randy L. Buckner	197	123/74	21.0/2.3	3T	3	47	119	2 × 2 × 4	256 × 256	Open	IA
6	Cleveland, OH, USA	Mark J. Lowe	16	12/4	37.3/9.4	3T	2.8	31	127	4 × 4 × 5.5	256 × 256	Closed	IA
7	Montreal, Canada	Alan C. Evans	36	23/13	42.1/18.6	3T	2	23	128	3.44 × 3.44 × 3.44	220 × 220	Closed	SD
8	Leiden, Netherlands	Serge A.R.B. Rombouts	11	0/11	23.2/2.5	3T	2.18	38	215	3.44 × 3.44 × 3.44	220 × 220	Closed	SD
9	Leiden, Netherlands		17	8/9	21.9/2.6	3T	2.2	38	215	3 × 3 × 4	192 × 192	Closed	SD
10	Leipzig, Germany	Arno Villringer	34	20/14	25.3/3.7	3T	2.3	34	195	3.12 × 3.12 × 4.4	200 × 200	Open, fixation	IA
11	Munchen, Germany	Christian Sorg/Valentin Riedl	10	4/6	68.3/4.2	1.5T	3	33	72	3.44 × 3.44 × 5	220 × 220	Closed	IA
12	Newark, NJ, USA	Bharat B. Biswal	18	10/8	24.2/4.0	3T	2	32	135	3.44 × 3.44 × 5	220 × 220	Closed	IA
13	New York City, NY, USA	Michael Milham/F. Xavier Castellanos	79	41/38	24.9/10.1	3T	2	39	192	3 × 3 × 3	192 × 192	Open	IA
14	New York City, NY, USA	Michael Milham/F. Xavier Castellanos	19	11/8	30.2/10.0	3T	2	33	175	3 × 3 × 4	192 × 240	Open	IA
15	Orangeburg, NY, USA	Matthew J. Hoptman	15	4/11	40.3/11.9	1.5T	2	22	165	3.5 × 3.5 × 5	224 × 224	Closed	IA
16	Oulu, Finland	Vesa J. Kiviniemi/Juha Veijola	100	65/35	21.5/0.6	1.5T	1.8	28	245	4 × 4 × 4.4	256 × 256	Open, fixation	IA
17	Queensland, Australia	Katie McMahon	18	7/11	26.3/3.7	3T	2.1	36	190	3.59 × 3.59 × 3.6	230 × 230	Open	IA
18	Saint Louis, MO, USA	Bradley L. Schlaggar/Steven E. Petersen	31	17/14	25.1/2.3	3T	2.5	32	127	4 × 4 × 4	256 × 256	Open, fixation	IA

All the datasets were selected from FCP/INDI website (http://fcon_1000.projects.nitrc.org). The following exclusion strategies were employed: 1) Using the visual inspection step within DPARSF, subjects showing severe head motion in the T1 image and subjects showing extremely poor coverage in the functional images were excluded, resulting in 895 subjects from the 18 sites; 2) subjects with motion (Mean FD Jenkinson (Jenkinson et al., 2002)) greater than 2*SD above the group mean motion (threshold: 0.192) were excluded, resulting in 862 subjects; 3) subjects with overlap with the group mask (voxels present at least 90% of the participants) less than 2*SD under the group mean overlap (threshold: 92.2%) were excluded, resulting in 828 subjects for group analyses.

IA: interleaved ascending; SA: sequential ascending; SD: sequential descending. Other details on scanning parameters like TE, flip angle, and scanner model are not available through the FCP/INDI website.

Preprocessing

Unless otherwise stated, all preprocessing was performed using the Data Processing Assistant for Resting-State fMRI (DPARSF, Yan and Zang, 2010, http://www.restfmri.net), which is based on Statistical Parametric Mapping (SPM8) (http://www.fil.ion.ucl.ac.uk/spm) and Resting-State fMRI Data Analysis Toolkit (REST, Song et al., 2011, http://www.restfmri. net). All volume slices were corrected for different signal acquisition times by shifting the signal measured in each slice relative to the acquisition of the slice at the mid-point of each TR. Then, the time series of images for each subject were realigned using a six-parameter (rigid body) linear transformation with a two-pass procedure (registered to the first image and then registered to the mean of the images after the first realignment). Individual structural images (T1-weighted MPRAGE) were co-registered to the mean functional image after realignment using a 6 degrees-of-freedom linear transformation without re-sampling. The transformed structural images were then segmented into gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF) (Ashburner and Friston, 2005). The Diffeomorphic Anatomical Registration Through Exponentiated Lie algebra (DARTEL) tool (Ashburner, 2007) was used to compute transformations from individual native space to MNI space.

Nuisance regression

Recent work has demonstrated that “micro” head movements, as small as 0.1 mm between time points, can introduce systematic artifactual inter-individual and inter-group variability in R-fMRI measures (Power et al., 2012, 2013; Satterthwaite et al., 2012; Van Dijk et al., 2012). Here we utilized the Friston 24-parameter model (Friston et al., 1996) to regress out head motion effects from the realigned data (i.e., 6 head motion parameters, 6 head motion parameters one time point before, and the 12 corresponding squared items) based on recent reports that higher-order models demonstrate benefits in removing head motion effects (Satterthwaite et al., 2013; Yan et al., 2013). We further addressed the residual effects of motion in group analyses by including mean framewise displacement (FD) derived with Jenkinson's relative root mean square (RMS) algorithm (Jenkinson et al., 2002) as a nuisance covariate; mean FD (Jenkinson) was used due to its consideration of voxel-wise differences in motion in its derivation (Yan et al., 2013).

Global signal regression (GSR), a commonly used yet controversial practice in the R-fMRI field, yields substantial increases in negative correlations (Murphy et al., 2009; Weissenbacher et al., 2009) and may distort group differences in intrinsic functional connectivity (iFC) (Saad et al., 2012). In iFC analyses, GSR also has a normalization effect by shifting the correlation distribution to be more “bell-shaped” and zero-centered (Murphy et al., 2009). Thus, we evaluated the impact of standardization effect of GSR and compared with other post-hoc standardization procedures on analyses without GSR. The signals from WM and CSF were regressed out to reduce respiratory and cardiac effects. In addition, linear and quadratic trends were also included as regressors since the blood oxygen level dependent (BOLD) signal demonstrates low-frequency drifts. Temporal filtering (0.01–0.1 Hz) was then performed on the time series except for the frequency-based R-fMRI indices: amplitude of low frequency fluctuations (ALFF) and fractional ALFF (fALFF).

A broad array of R-fMRI-based intrinsic brain function indices

We explored whether and how a broad array of R-fMRI based indices of intrinsic brain function are affected by standardization procedures. The R-fMRI indices examined were:

1. Amplitude measures: ALFF (Zang et al., 2007) and fALFF (Zou et al., 2008). ALFF is the sum of amplitudes within a specific low frequency range (0.01–0.1 Hz in the current study) from a Fourier decomposition of the time course. fALFF is the ratio of the ALFF of a given low frequency band (here, 0.01–0.1 Hz) to the sum of Fourier amplitudes across the entire frequency range. ALFF is proportional to the strength or intensity of low frequency oscillations, while fALFF represents the relative contribution of specific oscillations to the whole detectable frequency range.

2. Regional homogeneity (ReHo) (Zang et al., 2004). ReHo assesses the degree of regional synchronization among fMRI time courses. ReHo is defined as the Kendall's coefficient of concordance (KCC, Kendall and Gibbons, 1990) of the time series of a given voxel with those of its nearest neighbors (26 in the current study). A larger ReHo value for a given voxel indicates higher regional coherence.

3. Voxel-mirrored homotopic connectivity (VMHC) (Anderson et al., 2011; Zuo et al., 2010b). VMHC corresponds to the functional connectivity between any pair of symmetric inter-hemispheric voxels—that is, the Pearson's correlation coefficient between the time series of each voxel and that of its symmetrical inter-hemispheric counterpart. The resultant VMHC values were transformed into z values using Fisher's r-to-z transformation.

4. Seed-based correlation analysis (SCA).We extracted the mean time series for the posterior cingulate cortex (PCC: 0, −53, 26; 10 mm diameter sphere) (Satterthwaite et al., 2012; Van Dijk et al., 2012; Yan et al., 2013) from smoothed functional volumes in MNI152 standard space, and then calculated the Pearson's correlation coefficient between the PCC time course and every other voxel in native brain space. These correlation values were transformed into z values using Fisher's r-to-z transformation.

5. Network degree centrality (Buckner et al., 2009; Zuo et al., 2012). Degree centrality is the number or sum of weights of significant connections for a voxel. Here, we calculated the weighted sum of positive correlations by requiring each connection's statistical significance to exceed a threshold of p < 0.001 (Zuo et al., 2012).

Indices 1 and 4 (ALFF/fALFF and SCA) were calculated in native space based upon the preprocessed timeseries, and corresponding maps were then registered into MNI152 space with 3 mm³ cubic voxels by using transformation information acquired from DARTEL. The maps were further smoothed by a kernel of 4.5 mm. Indices 2 and 5 (ReHo and DC) were directly calculated in MNI152 space to ensure the same voxel size across sites in ReHo and DC calculation. Spatial maps of these measures were then spatially smoothed with the same Gaussian filter. Calculating measure 3 (VMHC) requires that data are first registered in MNI space and smoothed. For better correspondence between symmetric voxels, the individual structural image was reregistered to a group averaged symmetric template (all normalized T1 images were averaged to create a mean normalized T1 image, and then this image was averaged with its left–right mirrored version), and then this refined transformation was applied to the functional data before VMHC calculation (Zuo et al., 2010b).

Standardization procedures

Here, we employed various standardization procedures used in neuroimaging studies or micro-array studies to the R-fMRI measures (Table 2). We first generated a study-specific functional volume mask including only voxels (in MNI152 standard space) present in at least 90% of the participants. Then those subjects with coverage less than 2*SD under the mean overlapping [threshold: 92.2%] with this mask were excluded (see Table 3 for more details of exclusion criteria). This mask was used to define the whole brain for standardization procedures in final 828 participants included in this study.

• 1)GSR: This preprocessing-level procedure is reported to have a normalization effect for functional connectivity analyses. During preprocessing, the global mean signal was extracted and regressed out from the BOLD signal, then the R-fMRI measures were calculated based on data with GSR (also see Nuisance regression section).
• 2)Mean subtraction: Calculate the mean across voxels in the functional mask for R-fMRI measure and then subtract the mean from the value at each voxel.
• 3)Mean division: Calculate the mean across voxels for R-fMRI measure and divide the value at each voxel by the mean. This method has been widely used in ALFF and ReHo studies.
• 4)Z-standardization: Calculate the mean and standard deviation across voxels for R-fMRI measure, then subtract the mean from the value at each voxel and divide the value at each voxel by the standard deviation. This method has been widely used in ALFF/fALFF and DC studies.
• 5)Mean regression: Calculate the mean across voxels for R-fMRI measure for each participant and then regress out the mean at group-level.
• 6)Mean regression + SD division: Calculate the mean and standard deviation across voxels for each participant, and then regress out the mean at group-level. The residual value at each voxel is divided by the standard deviation.
• 7)Mean regression + log SD regression: As derived from the Supplementary methods, a mean regression + log SD regression model was employed to accurately address both additive noise and multiplicative noise in a two-step regression model. Specifically, first remove the additive noise and constant by regressing out global mean, resulting in y′. Log transform the SD and y′. To address the negative values within y′, first preserve the sign of y′, and then log transform the absolute value of y′, resulting in ln(|y′|). Regress out ln(SD) from ln(|y′|), resulting in y″. Take the exponent of y″, e^y″, and multiply by the preserved sign (sign of y′). Please see more details in the Supplementary methods.

The following additional non-parametric standardization procedures from micro-array analyses (Parrish and Spencer, 2004) (detailed results reported in the Supplementary materials) were performed:

• 8)Median–inter-quartile range standardization: Calculate the median and the range between 25% and 75% percentile (interquartile range), then subtract the median from the value at each voxel and divide the value at each voxel by the interquartile range.
• 9)Rank standardization: Each voxel is ranked according to value within the brain, and the rank value was assigned to each voxel.
• 10)Quantile standardization: Each voxel is ranked according to value for each participant, and then the average value across participants of each rank is computed. The voxel with the same rank for each participant is assigned that average value.

Importantly, quantile normalization (which is a mixed within-subject/group-level approach) and rank standardization approaches are more “aggressive” than others, in that they change the distribution of the data, while maintaining relative positioning (i.e., rank).

In addition to the parametric and non-parametric approaches list above, the following Gaussian function fit normalization proposed by Lowe et al. (1998) was also evaluated:

• 11)Gaussian function fit normalization. This method is firstly developed byLowe et al. (1998) for functional connectivity analyses. First fit a Gaussian function with parameters of mean, standard deviation, and area to the distribution of values (restricted to full width at half maximum), then subtract the estimated mean from the value at each voxel and divide the value at each voxel by the estimated standard deviation.

Group analyses

We employed a general linear model to examine the inter-individual differences in R-fMRI measures related to age and sex while taking the confounding effects of site and mean FD into account. Age, sex and motion effects were estimated by the t value of the corresponding repressor. Site effects were evaluated by the F value of site regressors. Group mean effects were estimated by the t value of a constant regressor. Gaussian random field theory correction for multiple comparisons was applied (voxel Z > 2.3, cluster-level p < 0.05, corrected) for the voxel-wise maps of R-fMRI derivatives.

Additionally, for each of the R-fMRI measures, we statistically compared the various standardization approaches with respect to their impact on group-analysis findings. Specifically, for each effect examined (age, sex, motion), we generate composite maps that represent the union of significant findings across the different post-hoc standardization approaches (the findings with GSR and no standardization were not included in this union, as they tended to be less conservative than those obtained with post-hocs due to global relationships with variables of interest); positive and negative effect relationships were treated separately. Then, for each composite, the Wilcoxon signed-rank test was performed across voxels to compare the statistical Z value between standardization approaches. Results were Bonferroni corrected (p < 0.05, corrected) to take into account the number of pairwise comparisons [3 (effects: motion, age, sex) * 2 (valence of findings: positive, negative) * 8 (number of standardization approaches) * 7 / 2 = 168]. Given differences in the number of voxels that may be included in a given composite map, we report effect sizes (Wilcoxon's $Z/\sqrt{N}$), which take into account the number of voxels across which the significance was determined.

Test–retest reliability of R-fMRI measures with standardization procedures

To evaluate the effects of different standardization procedures on the TRT reliability of R-fMRI indices, we computed intra-class correlations (ICC) (Shrout and Fleiss, 1979) for each of the standardized R-fMRI indices, using the NYU TRT dataset. ICC values were derived by linear mixed models (LMMs) as Zuo et al. (2013).

The NYU TRT dataset contains three scans for each subject; the first scan (scan 1) was collected 5–16 months (mean ± SD = 11 ± 4 months) before two subsequent scans (scans 2 and 3), which were collected in a single session 45 min apart. We evaluated inter-session reliability as the ICC between scan 1 and the average of scans 2 and 3. Scans 2 and 3 were averaged to improve the estimation of long-term reliability (Shehzad et al., 2009; Zuo et al., 2010a).

Results

Systematic variation in common standardization parameters: global mean and global SD

Prior to application of standardization techniques to voxel-wise R-fMRI measures, we first tested for the presence of systematic variation in key distribution parameters related to known nuisance variables (site, motion) as well as effects of interest (sex, age). Specifically, we focused on the relationship between inter-individual differences in each of these variables and differences in 1) the mean R-fMRI measure calculated across voxels (global mean), and 2) the SD for the R-fMRI measure (global SD). For all R-fMRI measures, we observed robust effects of site (across subjects) for both the global mean and SD (see Tables 4A and 4B). Similarly, significant positive correlation with motion was observed in the global mean for all R-fMRI measures except fALFF; motion-related effects on the global SD were less consistent among measures, with ALFF, ReHo and DC showing positive relationship with motion, while VMHC exhibited a significant negative relationship with motion. This negative relationship between motion and global SD in VMHC suggests that as motion increases, connectivity between homotopics increase throughout the brain, thereby decreasing variability in VMHC—in other words, motion increases connectivity and thereby reduces variability. The ubiquity of this phenomenon may be attributable to the fact that pitch (i.e., head nodding) tends to be the most prominent motion.

Table 4.

A The site, motion, age, sex effects and R2 on the whole brain mean of R-fMRI measures.
Effects on mean	ALFF	fALFF	ReHo	VMHC	PCC−iFC	DC
Site (F)	3073.71 (0.0000)	4305.97 (0.0000)	192.86 (0.0000)	46.57 (0.0000)	7.48 (0.0000)	27.61 (0.0000)
Motion (T)	3.77 (0.0002)	−0.72 (0.4741)	10.74 (0.0000)	11.51 (0.0000)	8.44 (0.0000)	9.93 (0.0000)
Age (T)	0.15 (0.8825)	−3.85 (0.0001)	−8.84 (0.0000)	−6.50 (0.0000)	−2.72 (0.0067)	−3.53 (0.0004)
Sex (T)	−0.25 (0.7993)	−0.31 (0.7532)	−0.36 (0.7172)	1.11 (0.2659)	0.75 (0.4548)	0.22 (0.8242)
R2	0.99	0.99	0.82	0.58	0.21	0.45

B The site, motion, age, sex effects and R2 on the whole brain standard deviation of R-fMRI measures.
Effects on STD	ALFF	fALFF	ReHo	VMHC	PCC−iFC	DC
Site (F)	1659.00 (0.0000)	93.95 (0.0000)	61.78 (0.0000)	106.59 (0.0000)	84.07 (0.0000)	20.05 (0.0000)
Motion (T)	3.28 (0.0011)	−0.06 (0.9548)	5.66 (0.0000)	−4.27 (0.0000)	−0.12 (0.9040)	10.37 (0.0000)
Age (T)	−0.04 (0.9710)	0.19 (0.8479)	−7.29 (0.0000)	2.71 (0.0069)	−4.68 (0.0000)	−3.62 (0.0003)
Sex (T)	−0.24 (0.8111)	2.03 (0.0422)	1.26 (0.2072)	0.43 (0.6702)	−5.65 (0.0000)	0.93 (0.3549)
R2	0.97	0.69	0.62	0.73	0.65	0.40

The first value in each cell is the F value or T value. The value in parentheses corresponds p value. A red number indicates significance after Bonferroni correction (p < 0.05) across 6 measures.

Importantly, relationships with the global mean and SD were not limited to nuisance covariates. Though notably smaller in magnitude than site and motion effects, negative effects of age were present in the global mean for all R-fMRI measures except ALFF. Interestingly, while age-related decreases in the global mean for ReHo, PCC-iFC, and DC were complemented by decreases in the global SD, VMHC alone exhibited an age-related increase in global SD. VMHC-related increases are not necessarily surprising, as prior work suggest differential age-related trajectories (Zuo et al., 2010b). In contrast to age, relationships between sex and distribution parameters were relatively limited, with only the global SD for PCC-iFC showing a relationship (negative).

In summary, although rarely reported in studies employing standardization techniques, distribution parameters for common R-fMRI measures exhibited significant relationships with both nuisance variables and variables of interests.

The impact of standardization procedures on confound variables: site and motion effects

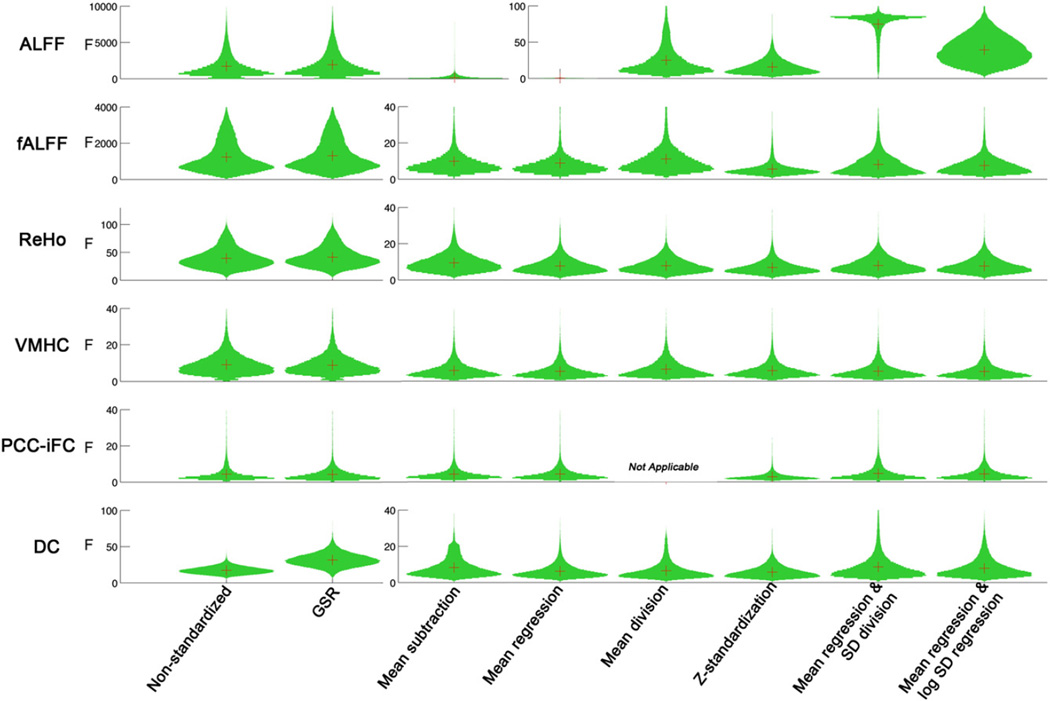
Application of post-hoc standardization approaches dramatically reduced unwanted site-related effects for all R-fMRI measures (see Fig. 1). F-scores for the effect of site were reduced by nearly two orders of magnitude for frequency-based metrics, where they were greatest – in part reflecting variation in TR and number of time points – two parameters that directly impact ALFF and fALFF values (ALFF ≫ fALFF¹) (Wu et al., 2011). Though less dramatic, F-scores for correlation-based metrics were decreased by up to 50%; PCC-iFC, which had the smallest site effects, was least affected by standardization. In contrast to posthoc standardization, global signal regression had relatively minimal impact on site-related effects.

Fig. 1.

The impact of standardization procedures on site effects for the R-fMRI measures. The distribution of F values across voxels was plotted. Given the large amount of reducing site effects for the standardized measures, different scales were used on the non-standardized and standardized measures for ALFF, fALFF, ReHo and DC.

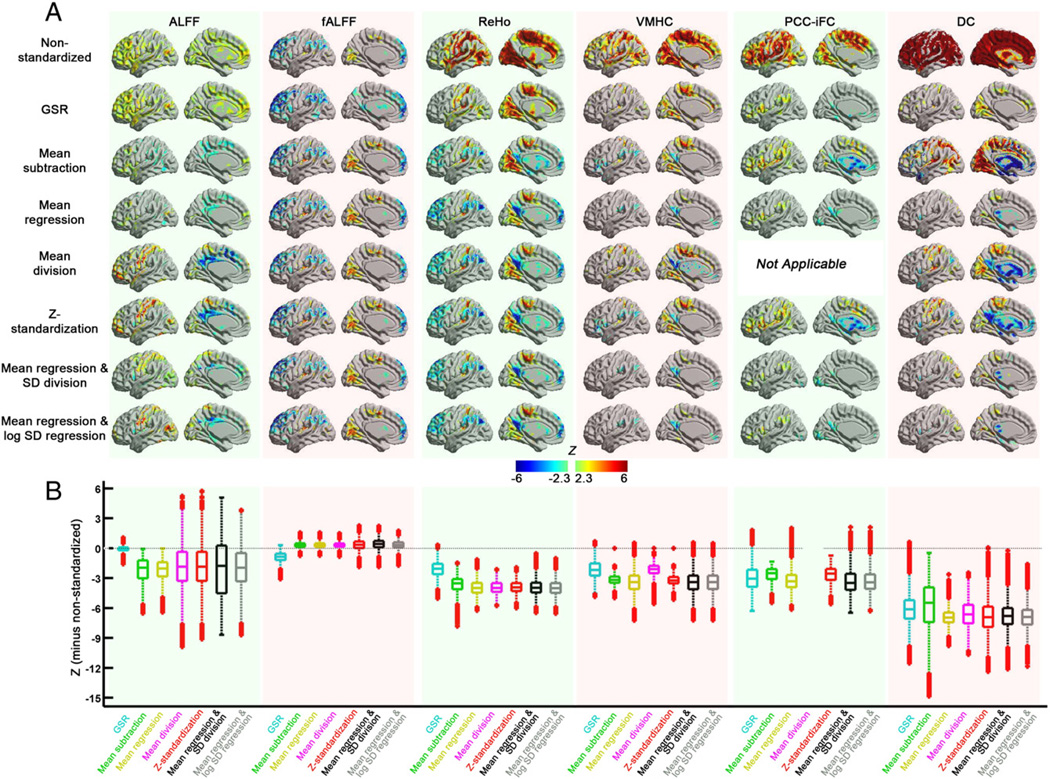
Inter-individual variation in R-fMRI measures across participants was impacted by all standardization approaches, though with notable differences in the specific effects. Post-hoc standardization approaches and GSR were similar in their tendency to reduce positive relationships between motion and R-fMRI measures, though differed regarding negative relationships (Fig. 2). Specifically, application of post-hoc standardization approaches increased negative relationships between motion and observed measures for all R-fMRI measures, while GSR had relatively little impact in this regard (PCC-iFC represents a notable exception). A natural concern is that within-subject post-hoc standardization approaches can introduce artifactual relationships with the standardization parameters. However, it is important to note that the results obtained with approaches that involve mean-centering were nearly identical to those obtained with its group-level regression (e.g., mean-centering vs. mean regression; Z-standardization vs. mean regression + SD division or mean regression + log SD regression) for fALFF, ReHo, and VMHC (Fig. S1 and Supplementary results)—thereby suggesting against the presence of such artifacts. In contrast, for PCC-iFC and DC, negative relationships appear to be artifactually exaggerated by mean-centering—particularly in subcortical areas. Finally, it is worth noting that results obtained with mean-centering alone, vs. those that include a variance normalization procedure (i.e., mean division, Z-standardization, mean regression + SD division, mean regression + log SD regression) were nearly identical for all R-fMRI measures, suggesting against the presence of meaningful multiplicative effects. A notable exception was ALFF; for this measure, only those standardizations that included variance normalization were able to reveal robust relationships between motor-strip ALFF and motion. Presence of this effect for the group-level mean regression + log SD regression approach suggested that this finding is not an artifact of the standardization approach.

Fig. 2.

The impact of standardization procedures on motion effects for the R-fMRI measures. (A) The voxel-wise motion effects (estimated from the group analysis model) of the standardization procedures for each R-fMRI measure on surface brain (left hemisphere, with BrainNet Viewer, http://www.nitrc.org/projects/bnv/). (B) Box plots of the motion effects across gray matter. To demonstrate the change in motion effects of each standardization procedure from the non-standardized measure, the differences in z value (each standardization procedure minus non-standardized) were plotted.

The impact of standardization procedures on variables of interest: age and sex effects

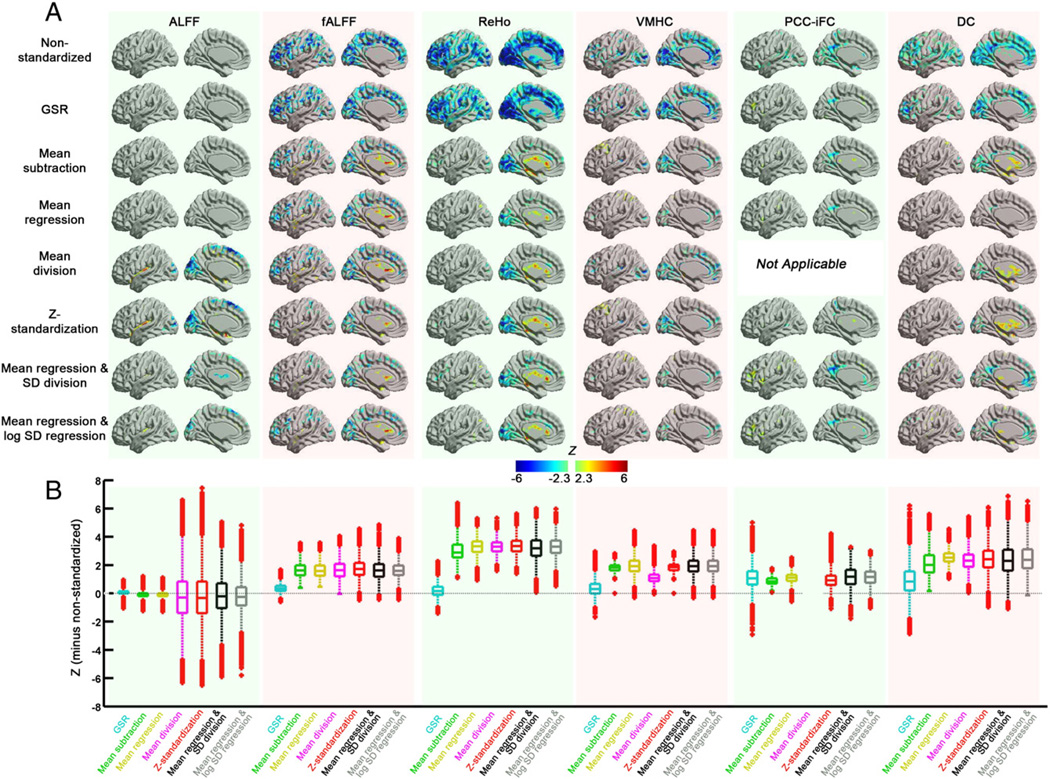
Standardization procedures increased the detection of regional associations observed with age and sex for the various R-fMRI measures included in our analysis.² For age effects, there are whole brain changes on the uncorrected data for all measures (except for ALFF) (see Fig. 3). Marked differences were observed between post-hoc approaches and GSR, which kept the similar pattern with non-standardized procedure of age effects except for PCC-iFC. Specifically, post-hoc approaches removed distributed negative-relationships between voxel-wise R-fMRI measures (particularly ReHo and fALFF), as they are better at accounting for the global mean. Application of post-hoc standardization approaches increased positive relationships between age and observed measures for all R-fMRI measures, particularly in subcortical (fALFF, ReHo, DC) and fronto-parietal areas (VMHC, PCC-iFC). The positive effects noted with mean-centering were nearly identical to those obtained with its group-level regression approaches (e.g., mean-subtraction vs. mean regression; Z-standardization vs. mean regression + SD division or mean regression + log SD regression) for fALFF, ReHo, and VMHC, which provides evidence that they are not artifactual in origin. In contrast, for DC, positive age relationships appear to be artifactually exaggerated by mean-centering—particularly in CSF regions which can be mistaken for nearby subcortical areas (see Fig. S2 for detailed statistical comparison). Similar to motion effects reported in the previous section, the results obtained with mean-centering alone, vs. those that include a variance normalization procedure were nearly identical for most R-fMRI measures, suggesting against meaningful multiplicative effects. Importantly, the age effects after mean centering and variance normalization (e.g., Z-standardization, mean regression + SD division or mean regression + log SD regression) are consistent with the findings in a previous study (Biswal et al., 2010).

Fig. 3.

The impact of standardization procedures on age effects for the R-fMRI measures. (A) The voxel-wise age effects (estimated from the group analysis model) of the standardization procedures for each R-fMRI measure on surface brain (left hemisphere). (B) Box plots of age effects across the gray matter voxels. To demonstrate the change in age effects of each standardization procedure from the non-standardized measure, the differences in z value (each standardization procedure minus non-standardized) were plotted.

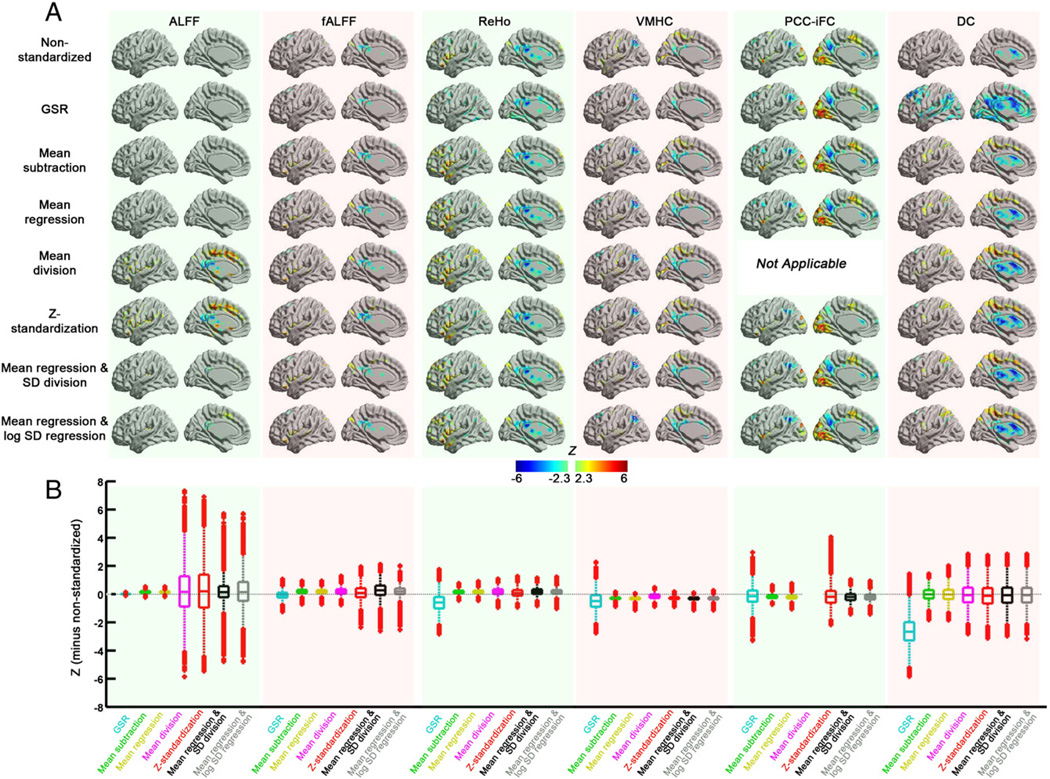
On the other hand, sex effects remained largely unchanged with the standardization procedures for fALFF, ReHo, VMHC and PCC-iFC (Fig. 4). ALFF is again an exception, as sex effects were only detectable when both mean-centering and variance standardization approaches were applied, and were consistent with the pattern reported in the previous study (Biswal et al., 2010). For DC, all the post-hoc standardization approaches yielded similar patterns consistent with the results reported in Zuo et al. (2012). Increased DC in lateral precentral and postcentral lobule regions in males were not detectable on data without standardization or only with GSR applied, suggesting increased sensitivity with post-hoc approaches.

Fig. 4.

The impact of standardization procedures on sex effects for the R-fMRI measures. (A) The voxel-wise sex effects (estimated from the group analysis model) of the standardization procedures for each R-fMRI measure on surface brain (left hemisphere). (B) Box plots of sex effects across the gray matter voxels. To demonstrate the change in sex effects of each standardization procedure from the non-standardized measure, the differences in z value (each standardization procedure minus non-standardized) were plotted.

Statistical comparison of standardization procedures

In order to provide further insights into the impact of standardization procedures and differences among them, we used the Wilcoxon signed-rank test to statistically compare findings obtained across voxels in clusters exhibiting positive and negative associations with our nuisance variable (motion) and signals of interest (age, sex) (Fig. 5).

Fig. 5.

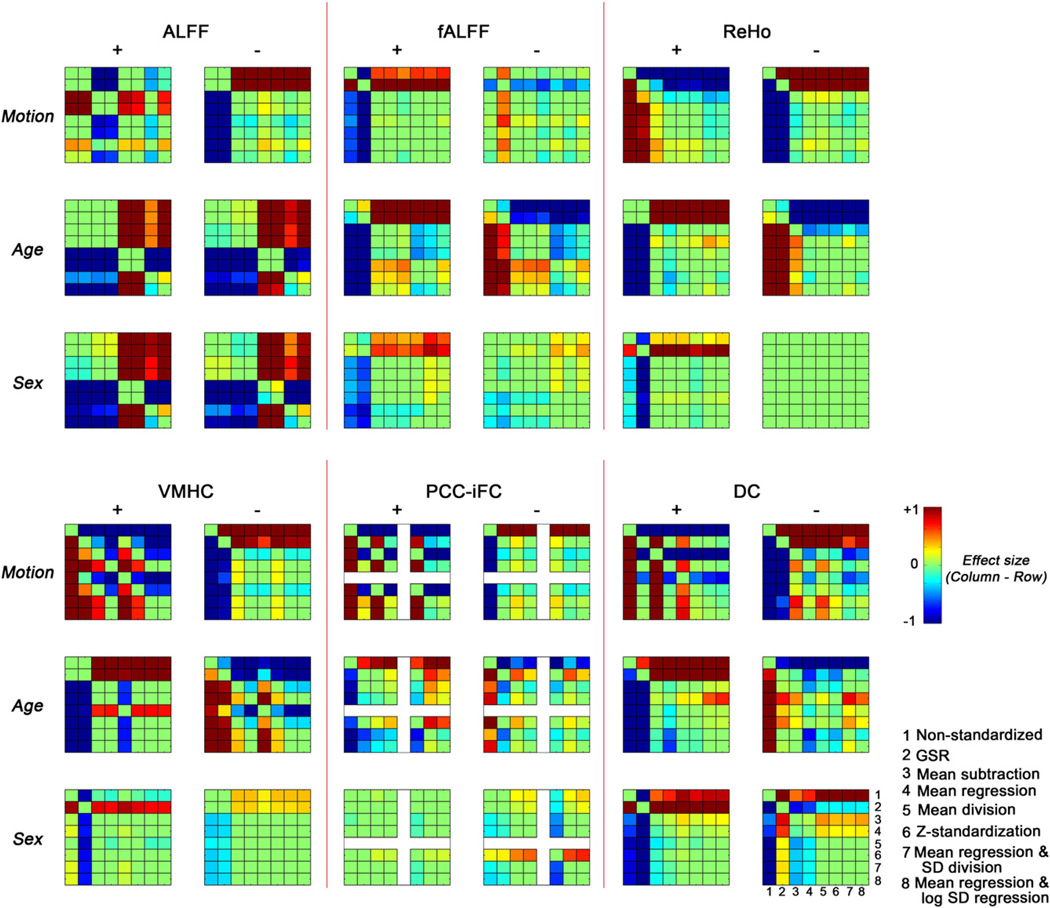
The statistical differences between different standardization approaches across voxels in clusters exhibiting positive (+) and negative (−) associations with nuisance variable (motion) and signals of interest (age, sex). For each effect examined, we generated composite maps that represent the union of significant findings across the different post-hoc standardization approaches; positive and negative effect relationships were treated separately. Then, for each composite, Wilcoxon signed-rank test was performed across voxels to compare the statistical Z value between standardization approaches. Results were Bonferroni corrected to take into account the number of pairwise comparisons [3 (effects) * 2 (positive/negative) * 8 (number of standardization approaches) * 7 / 2 = 168]. Given differences in the number of voxels that may be included in a given composite map, we plot effect sizes (Wilcoxon's $Z/\sqrt{N}$) which take into account the number of voxels across which the significance was determined.

For motion, we found that with the exception of fALFF, standardization approaches significantly decreased the magnitude of positive relationships with R-fMRI measures (relative to non-standardized data), while increasing our appreciation of negative relationships. Findings were generally more robust for post-hoc procedures than GSR, except in the case of PCC-iFC. Among the post-hoc procedures, mean regression + SD division showed a significant advantage in reducing positive motion-relationships for most measures.

Findings for age- and sex- relationships with R-fMRI measures were notably different than those obtained for motion. Positive relationships with age and sex effect were significantly more robust when standardization approaches were applied. Mean regression alone tended to be more conservative, producing significantly smaller increases than the other approaches for most measures. In contrast, when combined with SD division or log SD regression, positive relationships were significantly greater than observed with most of the other standardization approaches. For negative relationships, the impact of standardization on age and sex relationships differed, with standardization approaches tending to significantly decrease negative relationships with age, but significantly enhance negative relationships with sex. While this may at first seem discordant, it is important to note that for most measures, age but not sex demonstrated significant relationships with global distribution parameters used for standardization. Thus these findings are actually sensible, and highlight the importance of examining and reporting any relationships between the standardization parameters and signals of interest.

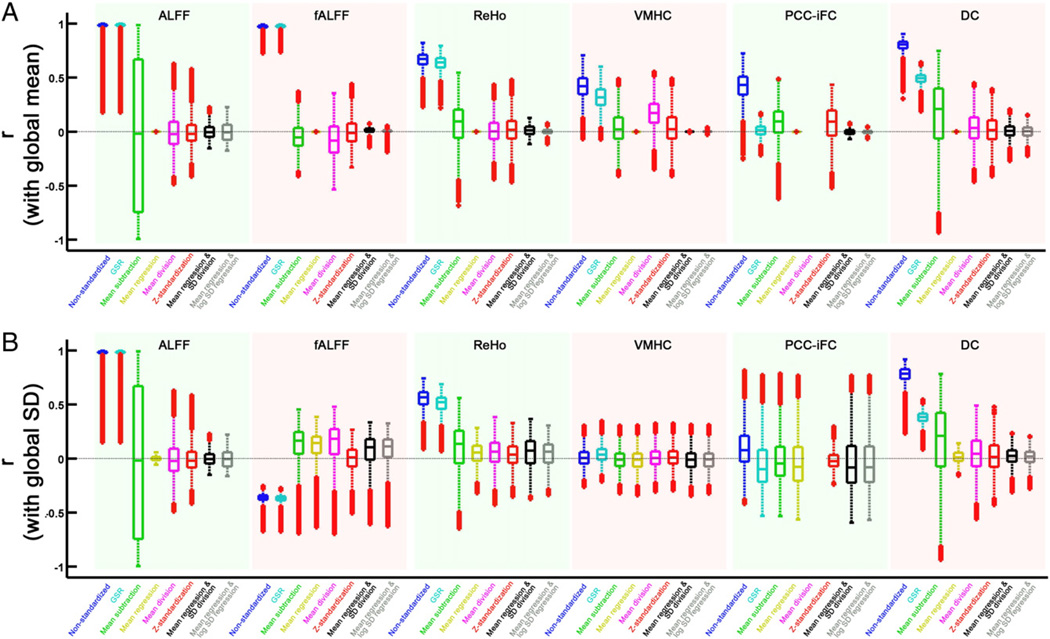
Residual relationships with standardization parameters after correction: global mean and global SD

We demonstrated the systematic variations in the global mean values of R-fMRI measures across subjects. Here, we investigated if voxel-wise values correlated with the global mean value across subjects, and how this relationship changed with standardization procedures (Fig. 6). The global mean of each R-fMRI measures is highly correlated with t he voxels across the brain, especially high for ALFF and fALFF. For VMHC and PCC-iFC, the correlation is significant within gray matter voxels, but not in white matter voxels. While, the mean subtraction procedure attenuated relationships with the global mean, it also created significant artifactual negative correlation with the global mean within white matter regions, for all the R-fMRI measures. This pattern of findings indicates that as expected, mean subtraction will add noise related to the global mean at those voxels not affected by this additive noise. Procedures of mean division and Z-standardization further decreased the relationship between global mean and voxel-wise measures, and these procedures produced less artifactual relationships than mean subtraction, but still exist in white matter regions. Of note, group-level methods (mean regression, mean regression + SD division and mean regression + log SD regression) were more conservative and eliminated the relationships with the standardization parameters. Different from mean subtraction, group-level techniques take into account variation in contribution of noise to different voxels, thus will not induce artifacts into the voxels that are less affected by the noise.

Fig. 6.

The correlation between the standardized measure and the global mean (A) or global SD (B) within gray matter voxels. For each measure, the global mean (or global SD) of each subject was firstly extracted, and then correlated with all the voxels across subjects. The correlation distribution within the gray matter voxels was plotted for each standardization procedure.

In order to more clearly demonstrate the potential for introducing artifactual relationships with standardization parameters, we carried out the various standardizations on simulated data and examined their impact on group-comparison findings obtained using a two-sample t-test (Supplementary results, Fig. S3 and Table S1). Specifically, we created artificial datasets in which “voxels” could either have a meaningful group difference across subjects or not, and have systematic noise related to the group difference applied or not. Mean subtraction (and Z-standardization, which involved mean subtraction) preserved the ability to detect the group difference in voxels where it was present (profiles 1, 2, 4 and 5) (Fig. S3). However, as expected, mean subtraction caused artifactual group differences in regions without group differences in profiles of 3 and 6. In contrast, mean regression (and the mean regression based approaches: mean regression + SD division, mean regression + log SD regression) performed optimally in our simulation. Similar to mean-subtraction, it revealed the true group differences while successfully avoiding the contribution of systematic noise. Unlike mean subtraction, for voxels in which no noise was applied (profiles 3 and 6), mean regression didn't cause false positives.

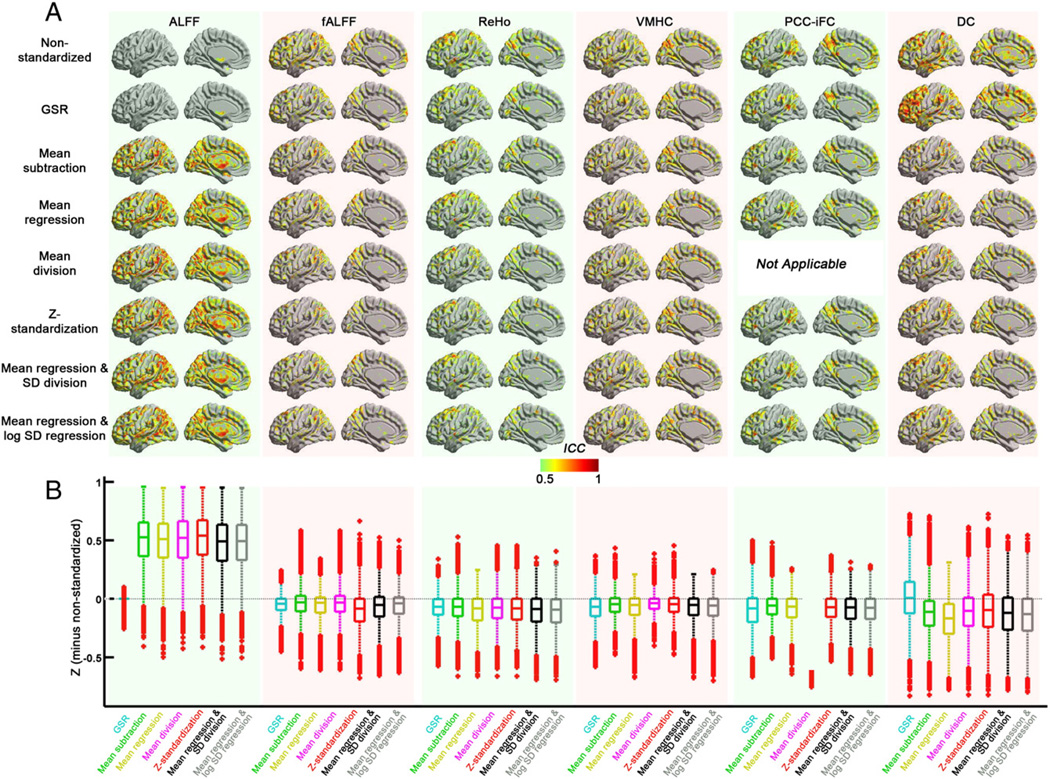
The impact of standardization procedures on test–retest reliability

With the exception of ALFF, our analyses indicated that standardization approaches served to decrease voxel-wise test–retest reliability within GM (Fig. 7). These reductions are not surprising, as the global mean and global SD for nearly all R-fMRI measures exhibited significant test–retest reliability (see Table 5). In considering the reliability of global parameters, it is important to note that nuisance signals, which contribute to the global R-fMRI measure for an individual, can be pretty reliable and could artifactualy elevate reliability of the metrics (e.g., ICC for mean FD: 0.6). As such, these reductions in reliability should not be viewed as discouraging; as demonstrated previously (Zuo et al., 2010b), meaningful variation with variables of interest can be examined for the global R-fMRI measure separately from voxel-wise analyses.

Fig. 7.

The impact of standardization procedures on test–retest (TRT) reliability (indexed by intra-class correlation [ICC] based on NYU TRT dataset) for the R-fMRI measures. (A) The voxel-wise TRT reliability of the standardization procedures for each R-fMRI measure on surface brain (left hemisphere). (B) Box plots of the TRT reliability across the gray matter voxels. The differences in the ICC value (each standardization procedure minus non-standardized) were plotted in order to demonstrate the change in TRT reliability of each standardization procedure from the non-standardized measure.

Table 5.

Test–retest reliability (ICC) on distribution parameters (global mean and global SD).

	ALFF	fALFF	ReHo	VMHC	PCC-iFC	DC
ICC on mean	0.00	0.48	0.59	0.59	0.63	0.58
ICC on SD	0.41	0.42	0.55	0.00	0.61	0.52

Standardization approaches were generally comparable with respect to long-term (5–11 months) voxel-wise test–retest reliability for the various R-fMRI measures (see Fig. 7). Here, we draw attention to key exceptions. Most notable was ALFF—consistent with prior concerns about the susceptibility of this measure to various noise sources (Zou et al., 2008; Zuo et al., 2010a) and head motion (Yan et al., 2013), this measure exhibited low reliability prior to standardization. While GSR had relatively little impact on ICC values for ALFF, marked improvements were noted for all of the post-hoc measures, whether group-level (mean regression, mean regression + SD division, mean regression + log SD regression) or applied at the individual subject level (mean subtraction, mean division, Z-standardization). Of note, the test–retest reliability of the global mean for ALFF was quite low, suggesting that global differences in ALFF are compromising voxel-wise finding. Thus, our analyses support the merits of standardization of this measure if ALFF analyses are employed. Interestingly, while test–retest reliability of ALFF's normalized counterpart (fALFF), showed less dependency on standardization, the commonly used Z-standardization was actually less optimal with respect to reliability than other post-hoc standardization approaches.

Overall, test–retest reliability for correlation-based measures was minimally affected by standardization. Degree centrality provided a notable exception, with decreases in test–retest reliability that appear to be most prominent in prefrontal and temporo-parietal areas. In trying to understand these decreases with standardization, it is important to note the high test–retest reliability of the distribution parameters (mean: ICC = 0.58; SD: ICC = 0.52) for DC, suggesting that global differences in connectivity can drive voxel-wise reliability when not accounted for.

Finally, it is worth noting that group-level approaches, which are least susceptible to the introduction of artifactual relationships, had the fewest outlier voxels in the direction of standardization-related increases of ICC. This once again highlights the more conservative nature of group-level standardization approaches.

Addressing concerns about standardization-related artifacts: negative connectivity—real or artifact?

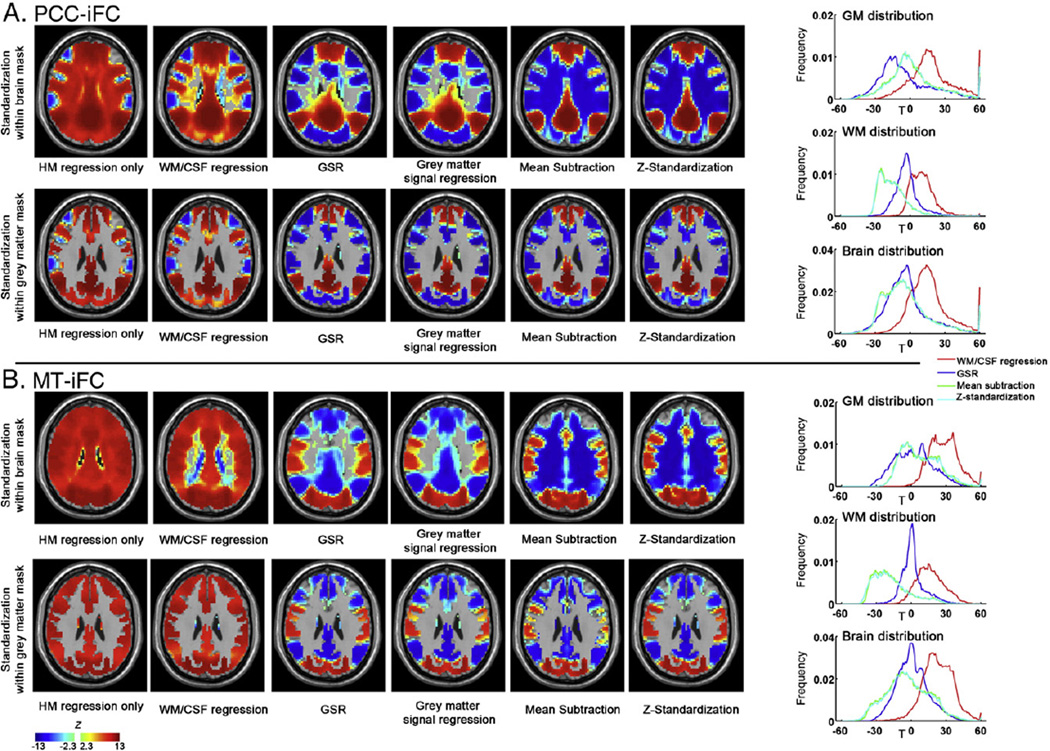
Arguably the most common standardization method employed to date, GSR, has become the source of significant controversy due to demonstrations that the method can introduce artifactual negative correlations into findings for iFC. In response, researchers using GSR have become increasingly hesitant about reporting negative functional connectivity findings. Although not the primary focus of the present work, we took the opportunity to examine negative connectivity in the FCP dataset, with and without nuisance signal correction (Fig. 8). While examination of middle temporal region (MT)-iFC did not reveal negative connections without GSR, examination of PCC-iFC in the large-scale FCP sample did in fact reveal negative connections in the absence of nuisance signal regression (WM, CSF, global signal), though these were admittedly less robust. These patterns observed for PCC-iFC were highly consistent with those revealed by Chang and Glover (2009) as well asFox et al. (2009) in the absence of nuisance signal regression. As previously noted by Chang and Glover (2009) and Van Dijk et al. (2010), regression of GS, not WM or CSF was associated with marked increases in negativity. In sum, while concerns about the potential for GSR to introduce artifactual negative relationships are valid, they should not be misinterpreted to infer that negative connectivity does not exist in the functional connectome.

Fig. 8.

The impact on group mean effects of within-subject standardization procedures for PCC-iFC (A) and MT-iFC (B). The MT seed is centered at [−47, −69, −3] (and converted from Talairach space to MNI space) as defined in Fox et al. (2009). The standardization was performed within the whole brain mask (upper row) or within the gray matter mask (bottom row) (axial slice on z = 27). The right panel demonstrates the voxel-wise distribution in T values (T values were used to avoid the inaccuracy of transforming extreme T values into Z values) within the gray matter mask (upper row), white matter mask (middle row) and whole brain (bottom row). Of note, the gray matter and white matter masks were specifically eroded for one voxel to avoid the partial voluming issue related to the gray matter/white matter boundary.

In order to understand why regression of the whole-brain signal, not the WM or CSF signal, has such a profound impact on findings, it is important to consider the relative contributions of the three brain tissue types to the global signal. High correlation between global and gray matter signals were found across all the participants (r = 0.98 ± 0.02),while the correlation between global and white matter (r = 0.34 ± 0.27, across subjects) or CSF signals (r = 0.67 ± 0.22, across subjects) was generally lower. Consistent with this finding, we found the iFC maps (PCC-iFC and MT-iFC) obtained from data that was standardized with global signal regression to be nearly identical to those generated with gray matter signal regression; both created a huge number of negative correlations, suggesting that the commonly used GSR is actually gray matter signal regression.

Addressing concerns about standardization-related artifacts: potential reductions in anatomical specificity associated with mean centering

Prior work suggests that mean centering approaches reduce anatomical specificity due to their tendency to introduce negative artifacts within white matter (Fox et al., 2009). Here we build upon the work ofFox et al. (2009) using a notably larger sample to gain further insights into changes in anatomical specificity resulting from standardization procedures. Following Fox et al. (2009), we examined voxelwise iFC for PCC and MT, replicating their group-level finding that white matter regions yield significant negative correlations after mean centering but not after GSR. Unlike their analysis, we found evidence of negative connectivity in key gray matter regions for both GSR and mean-centering—likely reflecting differences in sample size. Given that GSR is essentially gray matter regression, we repeated our analyses with standardization approaches limited to gray matter (i.e., gray matter regression, gray matter-based mean centering) (see Fig. 8).

Although highly similar at the group-level, an obvious question is how similar are these approaches with respect to their impact on individual subject data, and inter-individual differences. In this regard, we found that the average spatial Pearson correlation between GSR and global mean centering within gray matter was 0.92 ± 0.09 across subjects (for PCC-iFC); so as the average correlation between gray matter regression and gray matter centering (0.92 ± 0.09). With respect to inter-individual differences, as already reported, correlation between GSR and mean centering is generally high (0.88 ± 0.06 across gray matter voxels). When we limited our corrections to gray matter only (gray matter signal regression, gray-matter centering), correlation across subjects is also at a high level (0.88 ± 0.06 across gray matter voxels).

Finally, in order to better understand the differences in the impact of these standardization approaches, we examined the impact of each method on GM, WM and CSF distributions (Fig. 8). At the group-level, both GSR and mean-centering shift the overall distribution to be approximately zero-centered. However, GSR yielded more GM voxels to negative correlations, while mean-centering (mean subtraction and Z-standardization) yield much more WM voxels to negative correlations. Generally, the re-distribution with GM voxels shared similar patterns between GSR and mean centering.

Discussion

Our analyses suggest the presence of both additive and multiplicative effects for all R-fMRI measures. Not surprisingly these effects were most correlated with imaging site, followed by motion. Although less commonly considered, we found that global effects related to our phenotypic variables of interest as well for most measures, with age exhibiting both additive and multiplicative effects; sex effects were limited to a multiplicative effect for PCC-iFC. While all standardization approaches were effective at reducing undesirable relationships with nuisance variables, post-hoc approaches were generally more effective than GSR. Across standardization approaches, correction for additive effects (global mean) appeared to be more important than for multiplicative effects (global SD) for all R-fMRI measures with the exception of ALFF. As expected, group-level approaches for mean-centering and variance-standardization were found to be advantageous in their ability to avoid the introduction of artifactual relationships with standardization parameters; though results between group-level and within subject correction approaches were highly similar overall. While post-hoc standardization procedures increased TRT reliability for ALFF, which was otherwise overwhelmed by noise, modest reductions in TRT were found for post-hoc standardizations—a phenomena likely attributable to the separation of voxelwise from global differences among subjects. Finally, the present work called into questions previous observations of increased anatomical specificity for GSR over mean centering.

Recommendations for selecting a standardization

An obvious question that may arise is whether standardization is always advisable. As already demonstrated, standardization approaches are not without their limitations. In this regard, if we take the ideal case, where all potential nuisance covariates are known and do not differ between groups, leaving the data “untouched” would likely be preferable rather than attempting to account for nuisance variation. With that said, we rarely know the ground truth of noise signals present and cannot be sure if they are equal between groups. Thus, we argue that the more conservative decision generally is to standardize, or at least repeat analyses with standardization to determine the robustness of findings. When applied, standardization parameters should be tested for potential relationships with signals of interest, and the results reported.

The first key decision that researchers must make in the selection of which standardization approach to employ in their work is whether to use a post-hoc standardization or GSR. To address this question, we draw attention to the following considerations:

• GSR was effective in reducing motion-, but not site-related effects; post-hoc approaches removed both effectively.

• For all R-fMRI measures except PCC-iFC, residual dependencies between voxelwise R-fMRI measurements and global parameters (mean, SD) remained with GSR; regression forms of post-hoc approaches removed these effects nearly entirely.

• The relationship between signals removed with GSR and variables of interest are not easily quantifiable; the relationship between standardization parameters for post-hoc approaches can be directly examined and reported.

• Prior claims about the greater anatomical specificity of GSR vs. post-hoc mean centering were biased by inclusion of white matter in the subtraction-based post-hoc centering; additionally, mean regression-based approaches to mean centering avoid such concerns.

In light of these points, we recommend using post-hoc standardization approaches over GSR. Of note, this recommendation does not invalidate prior use of global signal regression—in fact, for iFC, the method for which GSR is most commonly applied, results obtained for our phenotypic variables of interest (sex, age) were similar to those obtained with post-hoc standardizations. Although GSR's tendency to introduce artifactual inter-individual relationships has been shown through simulation (Saad et al., 2012), we did not find evidence of standardization-induced relationships with variables of interest (age, sex) that were unique to GSR. The larger concern regarding GSR in the present work is that despite its effectiveness in reducing relationships with motion, it is insufficient as a means of standardization for most R-fMRI measures, leaving robust residual relationships with the global mean and SD. Of note, one possibility not explored in the present work is the combination of using both GSR and post-hoc approaches. Supplementary analyses (Figs. S4–S6) looking at the impact of combining GSR with the various post-hoc procedures suggest minimal difference in findings relative to our primary analyses without GSR. These findings are consistent with our suggestions that the two approaches are redundant (i.e., in mean-centering). At present, we suggest against the combination of GSR and post-hoc approaches, as it obfuscates the definitional clarity afforded by selecting one approach or the other, with unclear advantage.

While selecting among the various post-hoc approaches to standardization (mean subtraction, Z-standardization, mean division, mean regression, mean regression + SD division, and mean regression & log SD regression), it is first important to differentiate the R-fMRI measures being standardized. In the present work, ALFF was the only measure for which voxel-wise findings were strongly impacted by both additive and multiplicative noise; approaches carrying out both mean-centering and variance normalization proved critical for this measure. Specifically, mean division, Z-standardization, mean regression + SD division and mean regression + log SD regression standardization procedures were uniquely effective in accounting for the impact of noise on ALFF calculation—thereby improving test–retest reliability and power to detect relationships with variables of interest. For the other measures, multiplicative noise proved to be much less of a factor in the appreciation of differences among individuals with respect to nuisance and phenotypic variables, as well as test–retest reliability. A high degree of consistency was observed between mean subtraction and Z-standardization, as well as between mean regress and mean regression + SD division / mean regression + log SD regression.

The next key decision in selecting a post-hoc standardization approach is whether to employ a within-subject or group-level approach. In this regard, a few considerations exist. First, group-level approaches engender a natural advantage in their ability to avoid artifactual introduction of relationships with standardization parameters; one can attempt to mitigate this advantage by including the parameters in a group-level analysis, but, this does not guarantee complete removal. With respect to choosing between mean regression and mean regression + log SD regression, it should be noted that the latter inherently assumes that the true signal is centered at 0 (across participants) after any nuisance additive effect is accounted for. While this assumption did not appear to result in significant penalty for most measures in the present work, some caution needs to be taken when employing this method and future efforts to innovate this approach are merited. By avoiding such an assumption, the combination of mean regression + SD division also appears to be acceptable (with results highly consistent with those of mean regression + log SD regression), though once again the potential for introducing multiplicative artifacts in the signal must be acknowledged. For handling additive effects alone, mean regression had clear advantages over mean subtraction, as well as all other standardizations examined. Of note, one caveat that should be noted for group-level approaches, is that although optimal for appreciation of inter-individual differences, they do not facilitate one-sample t-tests (i.e., viewing of the overall group-mean), as they inherently guarantee a zero-center at each voxel. If visualization of the group mean is required, within-subject standardization approaches should be considered.

In addition to development of more robust group-level approaches to correction of multiplicative effects, future work may benefit from more comprehensive examination of sample requirements and sensitivities for group-level correction approaches. Finally, it is worth noting that although not reported in our primary analyses, an initial survey of non-parametric standardization approaches was conducted, obtaining results that were highly similar to those yielded with parametric analyses (i.e., Z-standardization) (Fig. S7). Further investigation of non-parametric approaches and exploration of the potential value of standardizations using more robust distribution characterizations may be of value.

Does standardization change interpretation of R-fMRI measures?

Central to the reporting of findings for standardized R-fMRI measures is an understanding of the impact of the method employed on the interpretation. The controversy surrounding GSR provides a key example of the confusion that can arise when the impact of data standardization on interpretation of R-fMRI measures is not fully considered. As clarified by our findings for PCC-iFC in the present work, and previously noted (Chang and Glover, 2009; Fox et al., 2009), negative connectivity can exist in the functional connectome without application of GSR or WM/CSF regression, though findings are markedly less robust. Studies employing GSR have consistently reported markedly increased sensitivity to negative correlations in the functional connectome, noting increases in negative correlations for connections that are negative prior to correction, as well as the detection of negative relationships for connections that were unrelated or positive prior to correction. Based on the assumption that the global signal is non-neural in origin (e.g. cardiovascular, respiratory, head motion and scanner-related signals), the vast majority of studies have reported findings of negative correlation after GSR as reflective of true, unqualified, negative connectivity in the connectome—sparking variably-heeded objections (Murphy et al., 2009). However, in recent years, electrophysiological studies have begun to appreciate the presence of large-scale signals in the gray matter (Scholvinck et al., 2010). Their presence would incontrovertibly force the need for a reinterpretation of findings of negative correlation only detectable after GSR to more properly state: negative connectivity was only detected after accounting for large-scale neural and non-neural signals in the gray matter. Importantly, the present work draws attention to a previously noted, though commonly overlooked aspect of the global signal—it is nearly equivalent to the gray matter signal, and variably relates to white matter and CSF signals (likely in part due to partial voluming effects). In this regard, we suggest that those considering global regression (typically carried out in addition to WM/CSF regression), carry out gray matter regression instead—thereby increasing interpretational accuracy.

Regarding the post-hoc standardization approaches, subtle nuisances regarding interpretation need to be considered. As previously discussed, whether carrying out within-subject or group-level standardization approaches, the first step should be to calculate global mean and SD and test for relationships with variables of interest (a practice commonly overlooked at present)—significant findings would suggest full-brain relationships with these variable. With respect to within-subject standardization approaches, authors need to carefully refer to the voxel-wise R-fMRI measures as differences from baseline (e.g., in terms of the R-fMRI measure specific units for mean subtraction, Z-scores for Z-standardization or fraction of the mean for mean division). Regarding group-level standardizations, relationships between a given phenotypic variable and the R-fMRI metric should be described as “being detected after accounting for individual differences in the mean (mean & SD) R-fMRI measure across voxels”.

Will we always need post-acquisition standardization?

The emphasis of the present work on post-acquisition standardization techniques is not to undermine the potential value of standardization of acquisition methodologies. Current recommendations by leading efforts in standardization emphasize the need to maintain acquisition protocols, relevant equipment and software as constants over the duration of studies. Unfortunately, this is not always feasible—particularly for large-scale multi-year studies (e.g., longitudinal studies). Innovations in imaging methodologies are rapidly advancing and researchers are continuously challenged with the question of when to “make the change” in their approaches, and to which of the emerging techniques, as no consensus exists in the field. Weekly and/or daily phantom-based quality assurance protocols are recommended as a means of detecting deviations over time and preventing large unintended variations; unfortunately such data is rarely maintained and not readily accounted for in analyses, resulting in minor variations being overlooked. The collection of respiratory, cardiac and breath-holding data is increasingly encouraged to facilitate artifact correction; however, such measures are variably collected and can increase subject burden with vulnerable populations; additionally, quality can vary markedly depending on calibration of measurement and appropriateness of application. Finally, it is worth noting that no current standards exist for the collection of participant-related factors (e.g., caffeine or nicotine consumption prior to scan, time of day, prandial status), and even when obtained, are not commonly included in analyses. While the field should be encouraged to increase the number of variables recorded for the purpose of analysis, the effectiveness of such efforts are likely to vary across studies and laboratories.

In summary, while it is of utmost importance that investigators limit sources of variation as much as possible in data acquisition, and account for as many known possible confounders, a pragmatic view of the task at hand will continue to necessitate post-acquisition standardization approaches.

Summary

The present work demonstrated the potential utility of post-acquisition standardization techniques in minimizing the influences of nuisance variables on inter-individual variation in the functional connectome. Additionally, we provided a base set of recommendations for their application and interpretation, as well as clarified previous misconceptions. Future efforts would benefit from further characterization and innovation of standardization approaches, particularly in the handling of multiplicative effects.