Abstract
Spin–torque nano–oscillators (STNOs) have outstanding advantages of a high degree of compactness, high–frequency tunability, and good compatibility with the standard complementary metal–oxide–semiconductor process, which offer prospects for future wireless communication. There have as yet been no reports on wireless communication using STNOs, since the STNOs also have notable disadvantages such as lower output power and poorer spectral purity in comparison with those of LC voltage–controlled oscillators. Here we show that wireless communication is achieved by a proper choice of modulation scheme despite these drawbacks of STNOs. By adopting direct binary amplitude shift keying modulation and non–coherent demodulation, we demonstrate STNO–based wireless communication with 200–kbps data rate at a distance of 1 m between transmitter and receiver. It is shown, from the analysis of STNO noise, that the maximum data rate can be extended up to 1.48 Gbps with 1–ns turn–on time. For the fabricated STNO, the maximum data rate is 5 Mbps which is limited by the rise time measured in the total system. The result will provide a viable route to real microwave application of STNOs.
Mobile terminals, an indispensable gadget of modern life, are becoming more compact and power efficient while serving multiple functions and operating in different standards of wireless communication. One of the main issues associated with multi–standard transceivers is how to design a compact, low–power, low–phase–noise, and wideband voltage–controlled oscillator (VCO). The rapid progress in spintronics technology suggests that the spin–torque nano–oscillator (STNO), owing to its small chip size and high tunability, can be a new solution not only for memory and but also for radio–frequency (RF) devices1,2. Compared to the LC tank–based VCO, which is generally used for conventional RF transceivers, STNOs are remarkably small (100 nm or less in diameter) without an LC resonance tank because they are based on the spin–transfer torque on nano–magnetic structures. Moreover, for reconfigurable communication, the high tunability of the STNO makes an STNO–based RF transceiver superior to an LC VCO–based RF transceiver, which requires multiple VCOs and thus consumes much more power than a single LC VCO. In one example, an STNO3 featured an ultra–wideband tuning ratio that exceeds 100% at a center frequency of oscillation of 5 GHz.
However, several issues remain that hinder the realization of an STNO–based RF transceiver. The STNOs have critical disadvantages such as lower output power and poorer spectral purity in comparison with LC voltage–controlled oscillators (VCOs). Many research groups have tried to improve the output power and spectral purity of a single or multiple STNOs4,5,6,7,8,9,10,11,12,13,14,15,16,17. For example, to increase the output power associated with STNOs, the synchronization of multiple STNOs4,5 as well as structural optimizations6,7,8,9,10,11,12,13,14,15 has all been attempted; however, these devices require a sizable amplification for wireless communication. Even with multiple amplifications of the STNO output2, modulation which uses a mixer for up– and down–conversion of the frequency cannot be realized due to the poor spectral purity, as evidenced by several MHz of the linewidth Δf and numerous spurious signals, mode hopping16, and the frequency–amplitude nonlinearity17.
Here we take an alternative approach to perform wireless communication by adopting direct modulation with binary amplitude shift keying (ASK) despite major drawbacks of STNOs. This modulation scheme enables us to demonstrate STNO–based wireless communication with a decent data rate at a distance between the transmitter (Tx) and receiver (Rx) of 1 m. We analyze the noise caused by the STNO to extract the maximum data rate theoretically and present the measured data rate experimentally.
Results
Operational principle and properties of the STNO
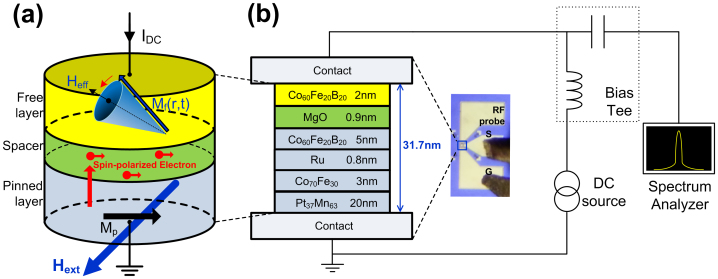
The operation of the STNO is based on the transfer of spin angular momentum from spin–polarized current to the local magnetization of a thin magnetic layer18,19,20. As shown in Fig. 1a, when DC current IDC is supplied to the STNO, the conduction electrons are polarized by the magnetization Mp of the pinned layer; the magnetization vector Mf(r,t) in the free layer continuously oscillates around the local effective magnetic field Heff. The spin torque oscillation is observed in a nanoscale structure with a high current density (~107 A/cm2). The oscillation occurs around static equilibrium at Gigahertz frequencies, which can be tuned by choosing the material parameters and device structure. The direction and magnitude of Hext also mainly influences the oscillation frequency. Fig. 1b shows that, to measure the STNO oscillation, IDC is injected via the inductive branch and the generated voltage oscillation is extracted via RF microprobes and the capacitive branch of the bias tee. A spectrum analyzer with an operating bandwidth in the range of 10 kHz–50 GHz was used in this case to extract the output spectrum of the STNO.
Figure 1. Operation and test setup of the STNO.
(a) Schematic of the STNO sample with a free layer (FL), a barrier, and a pinned layer (PL). Mp denotes the magnetization of the pinned layer, Mf(r,t) is the magnetization of the free layer, and Heff is the local effective magnetic field. (b) Schematic of the test setup for the STNO. Hext is the external magnetic field. Chip photo of the STNO (middle).
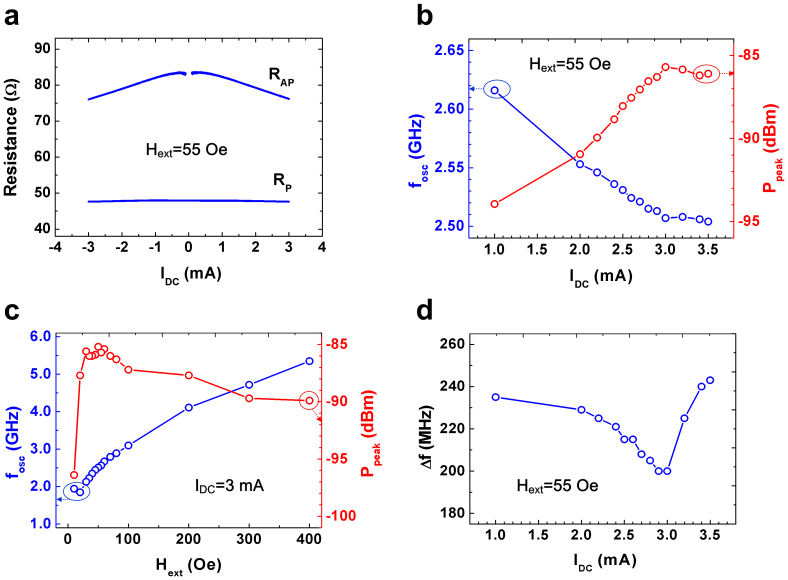
We have measured the DC and RF properties of an STNO based on MgO magnetic tunnel junction (MTJ) (See Methods for the details of the sample structure). Fig. 2a shows the magneto–resistance (MR) values of the STNO at both antiparallel (AP) and parallel (P) states between Mp and Mf(r,t) when IDC varies from −3 mA to 3 mA. When IDC is increased from 0 mA to 3 mA, RAP decreases from 83 Ω to 77 Ω. We have observed a microwave oscillation in this AP state at IDC = 1 ~ 3 mA and Hext = 55 Oe; as shown in Fig. 2b, when IDC is increased from 1.0 mA to 3 mA, the output peak power of the STNO (Ppeak) is increased from −94.0 dBm to −85.7 dBm, and the oscillation frequency of the STNO (fosc) is decreased from 2.62 GHz to 2.51 GHz. When IDC is increased further to 3.5 mA, Ppeak is slightly decreased to −86.1 dBm. Fig 2c shows the magnetic field dependence of microwave oscillation from the STNO; both fosc and Ppeak are changed notably when Hext is applied in a range of 20 Oe to 400 Oe. The frequency is tuned from 1.870 GHz to 5.350 GHz, and Ppeak ranges from −96.4 dBm to −85.7 dBm; the linewidth Δf of the oscillation output spectrum ranges from 200 MHz to 245 MHz with variation of IDC, as shown in Fig. 2d. With an IDC value of 3 mA and a Hext value of 55 Oe, the STNO generates a maximum Ppeak of −85.7 dBm with a minimum Δf of 200 MHz and resistance near 50 Ω(77 Ω) at 2.5 GHz; the STNO under these conditions will be used for wireless communication in this work.
Figure 2. Characteristics of the measurements for the fabricated STNO.
(a) Magneto–resistance of the STNO as a function of IDC (Hext = 55 Oe). P indicates the parallel (P) state between Mp and Mf, AP denotes the antiparallel (AP) state between Mp and Mf. (b) The oscillation frequency fosc and peak output power Ppeak level of the STNO as a function of IDC (Hext = 55 Oe). (c) fosc and the Ppeak level of the STNO as a function of Hext (IDC = 3 mA). (d) The linewidth Δf of the STNO as a function of IDC (Hext = 55 Oe).
Modulation for STNO–based communication
For wireless modulation and demodulation, a local oscillator (LO), which generates the carrier frequency, requires enough power (~0 dBm) to obtain the intermodulation signal using an RF mixer to perform frequency up– and down–conversion. However, the output power levels of STNOs are much lower than 0 dBm; the STNOs in the previous reports2,3,4,5,6,7,8,9,10,11,12,13,14,15 have an output power lower than −45 dBm, and the STNO in this work has an Ppeak value of −85.7 dBm. In addition, the STNO generates numerous spurious signals with the STNO output signal. Due to the low output power and the spurious signals of the STNO, wireless communication by intermodulation, which uses the STNO as an LO, cannot be performed successfully. Thus, we consider amplitude shift keying (ASK) and frequency shift keying (FSK) for STNO–based modulation, as these strategies do not require an RF mixer for wireless communication.
The wired binary FSK (BFSK) modulation or analog frequency modulation using STNOs by controlling IDC has already been demonstrated21,22,23,24,25,26. The demodulation of BFSK, however, leads to another challenge. In the BFSK demodulation, there are two types of the BFSK demodulation with no RF mixer; one is using bandpass filter (BPF) pairs, and the other is using a frequency discriminator27. The BPF pairs should separate two different frequencies clearly. However, given the oscillation characteristics of STNOs, it is difficult to separate the two different frequencies by BPF pairs due to the bandwidth limitation of BPF; a frequency discriminator increases the noise of high frequency components of the STNOs. Therefore, the demodulation through IDC–controlled BFSK is very difficult to be used with STNOs. Moreover, the STNO fabricated in this work has a broad minimum linewidth of 200 MHz as shown in Fig. 2d. In order to use the BFSK, a sufficient frequency separation between two frequencies more than 200 MHz is required, but the frequency range of the STNO that can be controlled by bias current (IDC) is only 110 MHz shown in Fig. 2b. The IDC–controlled BFSK based on this type of STNO cannot distinguish the on–state from the off–state in the demodulated STNO signal. Instead, we may consider the BFSK controlled by external field (Hext) as an alternative option for our STNO of which frequency can be controlled over a wide frequency band (1.87 ~ 5.35 GHz) by Hext. Unfortunately, the Hext–controlled BFSK additionally requires a circuit such as coplanar wave guide (CPW) for generating Hext changed continuously by the current of pulsed input28,29. As a consequence, the integrated chip size for wireless communication system becomes larger, and more DC current may be consumed in comparison with the IDC–controlled modulation.
For the binary ASK, digital data is simply represented as the presence or absence of STNO oscillation. Because the demodulation is performed by detecting the envelope of the modulated signal without BPF pairs and a frequency discriminator, it is also related to neither Δf nor the maximum frequency difference of the STNO, in contrast to BFSK. Moreover. The BFSK signal requires two frequencies representing the symbol states with a sufficient separation. In contrast, the binary ASK signal requires only one carrier frequency. Because the required bandwidth of the BFSK signal has twice larger than the bandwidth of the ASK signal under same data rate, the binary ASK has a higher data rate that can be transmitted over a given bandwidth (or higher bandwidth efficiency) than the BFSK27. Thus, we decided to take advantage of binary ASK modulation instead of BFSK for wireless communication.
There are two types of circuit structures for binary ASK modulation which do not use intermodulation; one is modulation by turning on and off the oscillator directly, and the other is the modulation by switching on and off the on–state oscillator to the antenna. By utilizing the fast turn–on time (~1 ns) of the STNO30, the direct binary ASK modulation was adopted here instead of switching binary ASK modulation in order to have low power consumption with simple circuitry31. For the demodulation stage, a simple envelope detector was implemented to recover the data from the received RF signal. Demodulation using an envelope detector avoids the poor spectral purity and weak output power of the STNO because it is noncoherent demodulation, which does not require a RF mixer for the frequency down–conversion process.
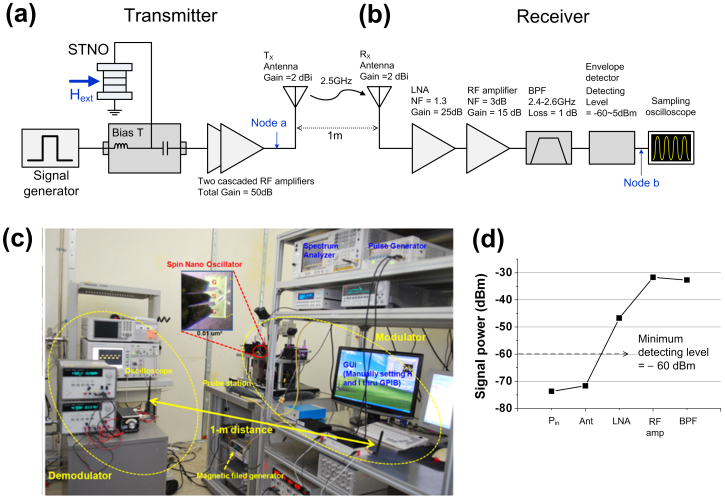
Figs. 3a and 3b show a schematic block diagram of the STNO–based direct binary ASK wireless communication system and Fig. 3c shows the measurement set–up of the system. For Tx shown in Fig. 3a, the signal generator modulates the STNO directly and the modulated signal is amplified by as much as 50 dB by two cascaded RF amplifiers. Because the amplified modulation signal (−35.7 dBm) is transmitted through the Tx antenna (−33.7 dBm with 2–dBi Tx antenna gain), which is a 2.5–GHz 2–dBi dipole antenna identical to Rx and given that the path loss of air is −40 dB (see Methods) with a distance of 1 m between Tx and Rx, the received signal power through the Rx antenna is −71.7 dBm [ = −85.7 dBm (STNO output) + 50 dB (amplifier gain) + 2 dB (Tx antenna gain) – 40 dB (the air path loss) + 2 dB (Rx antenna gain)]. For Rx shown in Fig. 3b, the total gain and noise figure NF of Rx are 39 dB and 1.4 dB, respectively, as calculated by adding each RF block's gain and NF (see Eq. (1) in Methods). Fig. 3d shows the RF block–by–block signal power flow of the received signal. The received signal power right before the demodulator is –32.7–dBm, which is within the operating range of −60 dBm to −5 dBm of the envelope detector. We designed Rx such that it has a 1.4–dB NF and a gain of 39 dB, thus satisfying the minimum sensitivity of the envelope detector (−60 dBm).
Figure 3. Configuration of the STNO–based binary ASK transceiver.
(a) Schematic of the STNO–based binary ASK transmitter (Tx). (b) Schematic of the receiver (Rx) and the gain and noise figure (NF) of the Rx chain. (c) The measurement set–up of the STNO–based binary ASK system. (d) The received signal power flow, where Pin is the received signal power of Rx and Ant, LNA, RF amp, and BPF are the measurement positions before the Rx antenna, the LNA, the RF amplifier, BPF, and the envelope detector, respectively. The signal level right after BPF is −32.7 dBm, which is within the detectable range of the demodulator (–60 ~ 5 dBm).
Demonstration of binary ASK modulation and demodulation
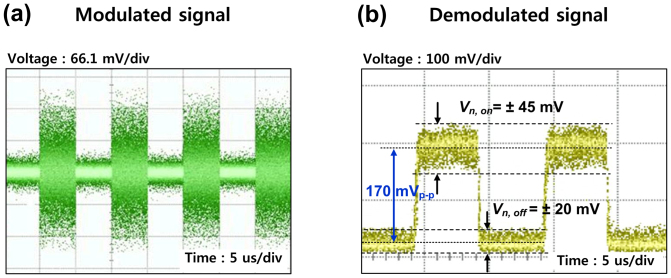
The square–pulsed signal of 230 mVp–p generates an IDC value of 3 mA to turn on and off the STNO, where Vp–p is the peak–to–peak voltage of a signal. The modulated signal is measured at node a in Fig. 3a, right before the antenna, and the demodulated signal is measured at node b in Fig. 3b on the sampling oscilloscope.
Fig. 4 reveals the successful wireless communication between Tx and Rx at 200 kbps. Figs. 4a and 4b show the modulated signal with a pulsed input frequency of 100 kHz and a demodulated signal at a distance of 1 m between Tx and Rx, respectively. The 170–mVp–p value in Fig. 4b is much larger than the noise voltage level after the demodulation process. One remarkable feature in Fig. 4b is that there is a difference in the noise voltage between the on–and–off states: ±45 mV for the on–state (Vn, on) and ±20 mV for the off–state (Vn, off). The only cause of this difference is whether the STNO is on or off. This is used to extract the STNO noise voltage and finally to determine the maximum data rate with the STNO in the forthcoming discussion section.
Figure 4. Modulated and demodulated signal in the time domain.
(a) The measured time trace of the modulated signal when the pulse frequency is 100 kHz at node a in Fig. 3a. (b) The measured time trace of the demodulated signal of 100 kHz at node b in Fig. 3b.
Dicussion
Analysis of the STNO noise
The STNO–caused noise, Vn, STNO, can be extracted from the measurement of the on–state and off–state noise voltages with the assumption that the STNO noise does not have any correlation with other noise sources in the communication system in Fig. 4b.
The total noise voltage of a system and the noise voltage from each noise source are related by the following equation,
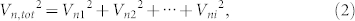 |
where Vn,tot is the total noise voltage of the system and Vni is the n–th noise voltage from the n–th noise source. All noise voltages are independent of each other in Eq. (2). Thus, the noise voltage caused by only the STNO is calculated by the equations below.
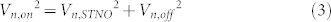 |
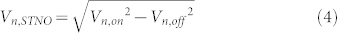 |
Here, Vn, STNO is the noise voltage amplified from the only STNO–caused noise, Vn, on is the noise voltage of the system when the STNO is turned on, and Vn, off is the noise voltage of the system when the STNO is turned off.
Using Eqs. (3) and (4), Vn, STNO is determined to be ±40.3 mV, which is observed as the largest noise source in the system, where Vn, on = ±45 mV and Vn, off = ±20 mV. The only STNO–caused noise power Pn, STNO is determined to be 16.25 μW, or −17.90 dBm from the root–mean–square (RMS) value of Vn, STNO and the 50–Ω impedance [Pn, STNO = Vn, STNO/2√2)2/50].
The noise generated only by the STNO is Vn, STNO which is amplified as much as the total gain of the system because we analyze Vn, STNO in the demodulator. The total gain of 80.3 dB is calculated by adding the subtotal gain of 53 dB before the envelope detector and the envelope detector gain of 27.3 dB. The envelope detector gain is calculated by subtracting the input signal power of −32.7 dBm from the output signal power of −5.4 dBm, as calculated from a RMS of 170 mVp–p and the 50–Ω impedance [the output signal power = (170 mVp–p/2√2)2/50 = 5.4 dBm]. Therefore, the noise generated only by the STNO itself is −98.2 dBm [−17.90 dBm (Pn, STNO) – 80.3 dBm (total gain)], and the signal–to–noise ratio (SNR) of the signal power to the STNO noise power is determined to be 12.5 dB [−85.7 dBm – (−98.2 dBm)], where the signal power of the STNO is −85.7 dBm, as shown in Fig. 2b. For ASK modulation with the STNO, because the amplitude stability of the STNO mainly determines the SNR of the system, we can improve the SNR and the data rate by eliminating the mode hopping at fosc and/or maintaining the constant oscillation amplitude of the STNO.
Extraction of the maximum data rate
The maximum data rate Dmax can be extended with the available bandwidth and the number of modulation levels which can be increased with SNR from Shannon's theorem given as
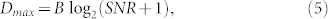 |
where B is the 3-dB bandwidth of the signal. The rise time (Tr) is typically defined as the time for the signal to rise from 10% to 90% of the step size, and B is given by 0.35/Tr32. The B is closely related to the transitional processes in STNOs30,33,34,35,36. If the turn–on of the STNO is approximately 1 ns30, the rise time Tr is approximately 1 ns, and thus B is calculated as 350 MHz. The total noise power in the SNR calculation for a communication system is the arithmetic sum of the system noise power, which results from the circuits of the signal generator, power amplifiers, antennas, LNA, and the envelope detector, and the STNO noise power. Here, the maximum date rate, where it is assumed that all circuits do not produce any noise apart from the STNO, can be extracted as 1.48 Gbps from the 12.5–dB SNR of the STNO itself by Eq. (5). From Table 1, it can be seen that the parameters and possible maximum data rate for the different types of STNOs.
Table 1. Comparison of possible maximum data rate for the different types of STNOs. Here F is the oscillation frequency, LWmin the minimum linewidth, Pout the maximum output power, Dmax the maximum data rate. For all STNOs, Dmax is evaluated with SNR (12.5 dB) through the modulator and demodulator of binary ASK modulation. All the STNOs have the 50–ohm connection to the sampling oscilloscope.
| STNOs | F (GHz) | LWmin (MHz) | Pout (dBm) | Turn–on time (ns) | Dmax (Mbps) |
|---|---|---|---|---|---|
| Ref. 30 | 3–5.2 | – | −73.0 | 1 | 1480 |
| Ref. 33 | 10.48 | 10 | −73.2 | 15 | 99 |
| Ref. 34 | 25.3 | – | – | 16* | 93 |
| Ref. 35 | 0.007–0.04 | – | – | 500 | 3 |
| This work | 1.87–5.35 | 200 | −85.7 | 350** | 5 |
*The turn–on time of Ref. 34 is assumed to 16 ns from the pulse repetition period in the measurement.
**The total rise time of the system is 350 ns which include the turn–on time of the fabricated STNO.
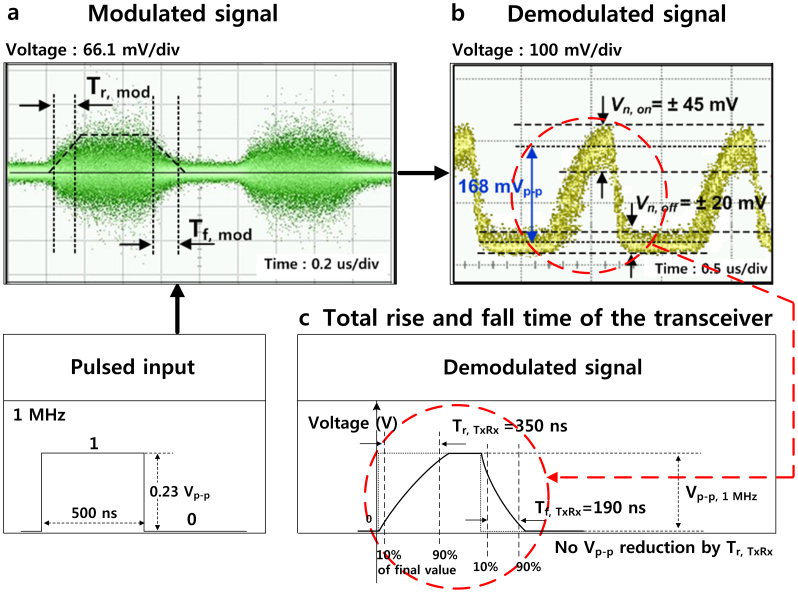
In the modulation and demodulation test of Fig. 5, the pulsed signal generated by the pulse generator has approximately only 50–ns rise time and 60–ns fall time by itself. The modulated signal has 130–ns Tr, mod and 150–ns Tf, mod in the usage of 1–MHz pulsed input signal in Fig 5a. The 80–ns increase of Tr and 90–ns increase of Tf in the modulated signals is involved in the by–pass capacitor which is parallel–connected to the inductive branch of bias tee. In Fig. 5b and 5c, the rise time of the demodulated signal by the transceiver (Tr, TxRx) and the fall time of the demodulated signal by the transceiver (T f, TxRx) are measured into 350 ns and 190 ns after the envelope detector, which are shorter than the pulse width of 500 ns corresponding to 1–MHz pulsed input frequency. Thus, the signal power decreased by the Vp–p reduction does not occur and does not degrade SNR because the Vp–p is 168 mVp–p from 1–MHz pulsed input compared with 170 mVp–p of 100–kHz pulsed input (only 2–mVp–p decrease). If the pulsed input frequency increases to more than 1 MHz, 350–ns Tr, TxRx is much longer than the pulse width and the SNR is degraded. Moreover, because the 120–ns Tr, mod is increased to 350–ns Tr, TxRx and the 150–ns Tf, mod is increased to 190–ns Tf, TxRx, the Tr of only demodulator (Tr, demod) is 230 ns and the Tf of only demodulator (Tf, demod) is 40 ns. Due to the total rise time of the system is 350 ns, the maximum data rate using the fabricated STNO is 5 Mbps.
Figure 5. Rise and fall time of modulated and demodulated signal.
(a) The rise and fall time from the measured time trace of the modulated signal when the pulse frequency is 1 MHz at node a in Fig. 3a. (b) The measured time trace of the demodulated signal of 1 MHz at node b in Fig. 3b. (c) Total rise and fall time of the transceiver from the demodulated signal.
In conclusion, STNO–based wireless communication was demonstrated for the first time successfully at a distance of 1 m at 200 kbps with the direct binary ASK modulation and demodulation. By analyzing the STNO noise, a SNR of STNO is 12.5 dB, and maximum data rate could be, theoretically, increased up to 1.48 Gbps with the STNO having the fastest turn–on time of 1 ns. The maximum data rate using the fabricated STNO is 5 Mbps which is limited by rise time and fall time of the system. Further improvement of the data rate is possible by reducing the turn–on time, the rise time, and the fall time of the system and by stabilizing and linearizing the STNO oscillation amplitude.
Methods
STNO fabrication
We fabricated STNOs using magnetic tunnel junctions (MTJs) with an MgO barrier. As shown in Fig. 1b, the MTJ stack consists of a buffer/Pt37Mn63 (20)/Co70Fe30 (3)/Ru (0.8)/Co60Fe20B20 (5) (pinned layer)/MgO (~0.9) (barrier)/Co60Fe20B20 (2) (free layer)/cap layer, where the subscript denotes the composition in atomic percent and the numbers in parentheses denote the layer thickness. Nanopillars with area of 0.053 μm2 were formed by Ar ion milling and e–beam lithography.
Numerical
The path loss is the power attenuation when an electromagnetic wave propagates through air space. The power at receiving antenna is given by Friis transmission equation as follows:
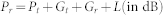 |
where Pr is the input power of the Rx antenna, Pt is the output power of the Tx antenna, Gt and Gr are the antenna gains of the Tx and Rx respectively, L is the free–space path loss, 20log10 (4πd/λ), λ is the wavelength, and d is the distance between the Tx and Rx in the same units as the wavelength). The oscillation frequency of the STNO in this experiment is 2.5 GHz and the calculated path loss of the free space is −40 dB.
For the calculation of total NF, if several devices are cascaded, the total noise factor can be obtained by the Friis formula for the noise factor, as follows:
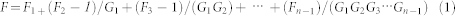 |
Here, Fn is the noise factor for the n–th device and Gn is the power gain (linear, not in dB) of the n–th device. Related to this equation, NF in the text refers to F expressed in dB.
Author Contributions
H.S.C. and C.S.P. designed the experiments and performed the analysis of the data. C.J. and B.C.M. fabricated the devices. S.Y.K., S.J.C., S.I.K. and S.Y.P. supported the experiments and I.Y.O., M.S. and H.P. supported the analysis of the data. H.S.C. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Acknowledgments
This work was supported by the National Research Foundation of Korea Grant funded by the Korean Government (No.2014-004057). The authors wish to thank Kyung-Jin Lee (Korea University) for the valuable discussion of the manuscript and Jürgen Langer, Berthold Ocker, and Wolfram Maass (Singulus Technology Ag) for the low-resistance MTJ stacks.
References
- Wolf S. A. et al. Spintronics: a spin-based electronics vision for future. Science 294, 1488–1495 (2001). [DOI] [PubMed] [Google Scholar]
- Villard P. U. et al. A GHz spintronic-based RF oscillator. IEEE J. Solid-State Circuits 45, 196–197 (2010). [Google Scholar]
- Krivorotov I. N. et al. Large-amplitude coherent spin waves excited by spin-polarized current in nanoscale spin valves. Phys. Rev. B 76, 024418 (2007). [Google Scholar]
- Ruotolo A. et al. Phase-locking of magnetic vortices mediated by antivortices. Nature Nanotechnology 4, 528–532 (2009). [DOI] [PubMed] [Google Scholar]
- KaKa S. et al. Mutual phase-locking of microwave spin torque nano-oscillators. Nature Letter 437, 389–392 (2005). [DOI] [PubMed] [Google Scholar]
- Kiselev S. I. et al. Microwave oscillations of a nanomagnet driven by a spin-polarized current. Nature 425, 380–383 (2003). [DOI] [PubMed] [Google Scholar]
- Rippard W. H. et al. Direct-current induced dynamics in Co90Fe10 = Ni80Fe20 point contacts. Phys. Rev. Lett. 92, 027201 (2004). [DOI] [PubMed] [Google Scholar]
- Rippard W. H. et al. Current-driven microwave dynamics in magnetic point contacts as a function of applied field angle. Phys. Rev. B 70, 100406 (R) (2004). [Google Scholar]
- Mistral Q. et al. Current-driven microwave oscillations in current perpendicular-to-plane spin-valve nanopillars. Appl. Phys. Lett. 88, 192507–192507-3 (2006). [Google Scholar]
- Houssameddine D. et al. Spin-torque oscillator using a perpendicular polarizer and a planar free layer. Nature Materials 6, 447–453 (2007). [DOI] [PubMed] [Google Scholar]
- Pribiag V. S. et al. Magnetic vortex oscillator driven by DC spin-polarized current. Nature Physics 3, p. 498–503 (2007). [Google Scholar]
- Gusakova D. et al. Spin-polarized current-driven excitations in spin-valve nanopillars with a synthetic antiferromagnetic pinned layer. The 53rd Annual Conf. Magnetism and Magnetic Materials proceedings, (2008). [Google Scholar]
- Mistral Q. et al. Current-driven vortex oscillations in metallic nanocontacts. Phys. Rev. Lett. 100, 257201 (2008). [DOI] [PubMed] [Google Scholar]
- Nazarov A. V. et al. Microwave generation in MgO magnetic tunnel junctions due to spin transfer effects. J. Appl. Phys. 103, 07A503 (2008). [Google Scholar]
- Houssameddine D. et al. Spin transfer induced coherent microwave emission with large power from nanoscale MgO tunnel junctions. Appl. Phys. Lett. 93, 022505 (2008). [Google Scholar]
- Muduli P. K., Heinonen O. G. & Åkerman J. Decoherence and mode hopping in a magnetic tunnel junction based spin torque oscillator. Phys. Rev. Lett. 108, 207203 (2012). [DOI] [PubMed] [Google Scholar]
- Consolo G. et al. Combined frequency-amplitude nonlinear modulation: theory and applications. IEEE Tran. on Magnetics 46, 3629–3634 (2010). [Google Scholar]
- Slonczewski J. C. Current-driven excitation of magnetic multilayers. J. Magnetism and Magnetic Mater. 159, L1–L7 (1996). [Google Scholar]
- Berger L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 54, 9353–9358 (1996). [DOI] [PubMed] [Google Scholar]
- Sun J. Z. Spin angular momentum transfer in current-perpendicular nanomagnetic junctions. IBM J. Res. & Dev. 50, 81–100 (2006). [Google Scholar]
- Manfrini M. et al. Agility of vortex-based nanocontact spin torque oscillators. Appl. Phys. Lett. 95, 192507 (2009). [Google Scholar]
- Manfrini M. et al. Frequency shift keying in vortex-based spin torque oscillators. J. Appl. Phys. 109, 083940 (2011). [Google Scholar]
- Pufall M. R. et al. Frequency modulation of spin-transfer oscillators. Appl. Phys. Lett. 86, 082506 (2005). [Google Scholar]
- Muduli P. K., Pogoryelov & Bonetti S. Nonlinear frequency and amplitude modulation of a nanocontact-based spin-torque oscillator. Phys. Rev. B 81, 140408 (2010). [Google Scholar]
- Pogoryelov et al. Spin-torque oscillator linewidth narrowing under current modulation. Appl. Phys. Lett. 98, 192506 (2011). [Google Scholar]
- Pogoryelov et al. Frequency modulation of spin torque oscillator pairs. Appl. Phys. Lett. 98, 192501 (2011). [Google Scholar]
- Watson B. FSK: Signals and Demodulation. Watkins–Johnson Company Tech–notes. vol. 7, no. 5 (1980). [Google Scholar]
- Nagasawa T. et al. Frequency transition of spin-torque oscillator under the magnetic-field pulse in nanosecond range. J. Appl. Phys. 109, 07C907 (2010). [Google Scholar]
- Nagasawa T. et al. Delay detection of frequency modulation signal from a spin-torque oscillator under a nanosecond-pulsed magnetic field. J. Appl. Phys. 111, 07C908 (2012). [Google Scholar]
- Krivorotov I. N. et al. Time-domain measurements of nanomagnet dynamics driven by spin-transfer torques. Science 307, 228–231 (2005). [DOI] [PubMed] [Google Scholar]
- Byeon C. W., Lee J. J., Eun K. C. & Park C. S. A 60 GHz 5 Gb/s gain-boosting OOK demodulator in 0.13 μm CMOS. IEEE MWCL 21, 101–103 (2011). [Google Scholar]
- Bogatin E. Bandwidth and Rise time: Signal and Power Integrity – Simplified (2nd ed.). (Prentice Hall, 2009).
- Rippard W. H., Pufall M. & Kos Time required to injection-lock spin torque nanoscale oscillators. Appl. Phys. Lett. 103, 182403 (2013). [Google Scholar]
- Zhou et al. Oscillatory transient regime in the forced dynamics of a nonlinear auto oscillator. Phys. Rev. B 82, 012408 (2010). [Google Scholar]
- Belanovsky A. D. et al. Phase locking dynamics of dipolarly coupled vortex-based spin transfer oscillators. Phys. Rev. B 85, 100409(R) (2012). [Google Scholar]
- Slavin A. & Tiberkevich V. Nonlinear auto-oscillator theory of microwave generation by spin-polarized current. IEEE Trans. Magn. 45, 1875 (2009). [Google Scholar]