The morphology of the masticatory apparatus facilitates muscle force production at wide jaw gapes in tree-gouging common marmosets (Callithrix jacchus)

SUMMARY

Common marmosets (Callithrix jacchus) generate wide jaw gapes when gouging trees with their anterior teeth to elicit tree exudate flow. Closely related cotton-top tamarins (Saguinus oedipus) do not gouge trees but share similar diets including exudates. Maximizing jaw opening theoretically compromises the bite forces that marmosets can generate during gouging. To investigate how jaw-muscle architecture and craniofacial position impact muscle performance during gouging, we combine skull and jaw-muscle architectural features to model muscle force production across a range of jaw gapes in these two species. We incorporate joint mechanics, resting sarcomere length and muscle architecture estimates from the masseter and temporalis to model muscle excursion, sarcomere length and relative tension as a function of joint angle. Muscle excursion from occlusion to an estimated maximum functional gape of 55 deg. was smaller in all regions of the masseter and temporalis of C. jacchus compared with S. oedipus except the posterior temporalis. As a consequence of reduced muscle excursion distributed over more sarcomeres in series (i.e. longer fibers), sarcomere length operating ranges are smaller in C. jacchus jaw muscles across this range of gapes. This configuration allows C. jacchus to act on a more favorable portion of the length—tension curve at larger gapes and thereby generate relatively greater tension in these muscles compared with S. oedipus. Our results suggest that biting performance during tree gouging in common marmosets is improved by a musculoskeletal configuration that reduces muscle stretch at wide gapes while simultaneously facilitating comparatively large muscle forces at the extremes of jaw opening.

INTRODUCTION

The masticatory muscles generate jaw movements and bite forces during ingestion, chewing, biting and related behaviors. Attempts to model the masticatory system have emphasized jaw-muscle and bite forces in humans (Koolstra and van Eijden, 1992; Koolstra et al., 1988; Osborn and Baragar, 1985) and other animals (e.g. van der Meij and Bout, 2008). Considerably less attention has been paid to the impact of jaw mechanics on muscle function (e.g. Koolstra and van Eijden, 1997; Weijs and van der Wielen-Drent, 1983). This shortcoming persists despite the fact that jaw kinematics, such as maximum jaw opening ability, is an important performance variable functionally related to feeding behaviors (Herring and Herring, 1974; Miller et al., 1999; Miller et al., 2000).

Studies combining muscle architecture and joint kinematics to model a muscle's functional operating range have demonstrated integrated musculoskeletal systems (Lieber, 1997; Rome and Sosnicki, 1991; Ward et al., 2006a). While some of these modeling studies have examined variation among muscles within a species, this study utilizes a model of sarcomere length operating range to examine how musculoskeletal design impacts masticatory muscle function across a range of jaw postures in two closely related species of callitrichid monkeys that engage in different ingestive behaviors. By modeling the sarcomere length operating range of the jaw-closing muscles in these two monkeys, we can examine how sarcomere behavior influences muscle function in each species. Finally, the generation of a model within a specific behavioral context between closely related species offers insight into potential functional and/or evolutionary adaptations of their masticatory muscles.

Common marmosets (Callithrix jacchus) and cotton-top tamarins (Saguinus oedipus) are closely related New World monkeys (Primates: subfamily Callitrichinae) that are broadly similar in size and diet but have divergent ingestive feeding behaviors. Common marmosets [321 g (Fleagle, 1999)] and cotton-top tamarins [411 g (Fleagle, 1999)] both feed on fruits, insects and tree exudates (e.g. Ferrari, 1993; Garber, 1984; Garber, 1992; Neyman, 1977; Smith and Jungers, 1997; Stevenson and Rylands, 1988; Sussman and Kinzey, 1984). Marmosets, however, actively gouge trees with their anterior dentition to stimulate exudate flow (Coimbra-Filho and Mittermeier, 1976; Coimbra-Filho and Mittermeier, 1977; Lacher et al., 1984) whereas tamarins feed opportunistically on exudates that have been released by other means (Ferrari, 1993; Garber, 1992; Peres, 1989; Soini, 1982). Marmosets can spend a significant portion of their daily activity cycle, up to 70% of their day, feeding on tree exudates (Fonseca and Lacher, 1984; Lacher et al., 1981; Maier et al., 1982; Sussman and Kinzey, 1984). Gouging trees to elicit exudates is hypothesized to provide marmosets with specific ecological benefits, such as a source of carbohydrates and calcium, a stable food supply and access to an under-exploited food source (Coimbra-Filho and Mittermeier, 1977; Nash, 1986; Power, 1996; Sussman and Kinzey, 1984). These divergent ingestive behaviors between marmosets and tamarins provide a natural experiment for studying the influence of anterior tooth biting on marmoset masticatory apparatus form and function (Taylor and Vinyard, 2004; Taylor and Vinyard, 2008; Taylor et al., 2009a; Taylor et al., 2009b; Vinyard et al., 2003; Vinyard et al., 2009).

Laboratory and field studies indicate that when common marmosets gouge trees, they generate relatively wide jaw gapes (Fig. 1) but not necessarily relatively large bite forces (Vinyard et al., 2009). Although bite forces during tree gouging do not approach an animal's maximum biting capability, preliminary in vivo evidence indicates that maximum bite forces during gouging can occur at relatively large jaw gapes (Fig. 2). Producing these bite forces at large gapes during gouging may extend the range over which the sarcomeres in the jaw muscles must generate significant force during ingestive functions.

Fig. 1.

The tree-gouging common marmoset (Callithrix jacchus) shown generating a wide jaw gape while gouging in a laboratory setting. Adapted from Vinyard and Schmitt (Vinyard and Schmitt, 2004).

Fig. 2.

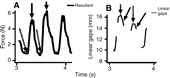
Maximum bite forces can occur at relatively large jaw gapes during tree gouging. (A) The solid arrows show peak force whereas the broken arrows indicate maximum jaw gape. Force trace showing that resultant forces are relatively low at maximum gape (broken arrows). (B) Plot of gapes, for the same two gouges as in A, illustrating that peak forces can occur at relatively large jaw gapes (solid arrows). The intermittent nature of linear gape results from teeth not being visible for digitizing in all frames (C.J.V., unpublished).

In order for an animal to successfully extract nutrients from a food, it must defeat both the internal mechanical properties, such as their elastic modulus or toughness, and external physical properties, such as their size and shape, from that food item (Lucas, 2004). Overcoming these physical properties during feeding often requires an ingestive, or procurement, phase followed by a masticatory, or breakdown, sequence prior to swallowing (Hiiemae and Crompton, 1985). Much of the research into the evolution of mammalian masticatory form has concentrated on how diet and feeding behaviors affect the masticatory apparatus. This research focus is appropriate given that food mechanical properties can modulate both jaw-muscle activity (Agrawal et al., 1998; Woda et al., 2006) and bone loading (Hylander, 1979) during ingestion and mastication. Alternatively, studies of sarcomere lengths in mammalian jaw muscles often focus on physiological relationships such as how manipulated or representative jaw movements impact sarcomere length and, hence, peak muscle forces (Anapol and Herring, 1989; Carlson, 1977; Herring et al., 1984; Mackenna and Turker, 1978; Nordstrom et al., 1974; Thexton and Hiiemae, 1975; Weijs et al., 1989; Weijs and van der Wielen-Drent, 1983; Weijs et al., 1982). The lack of behavioral and ecological specificity in these studies makes it more difficult to understand the implications of sarcomere length variation for mammalian jaw-muscle evolution. Tree gouging in marmosets provides a specific example of an ingestive behavior affecting jaw muscle form and function. Substrate size, in addition to substrate mechanical properties, also has a fundamental influence on gouging mechanics because without trees being much larger than marmosets there would be no obvious reason for large jaw gapes. Although mastication is a critical function, the size of the dietary substrate and ingestive behaviors may also play key roles in defining optimal sarcomere length operating ranges in mammalian jaw muscles.

Previous morphological comparisons have shown that marmosets possess craniofacial and jaw-muscle features that theoretically facilitate the generation of large jaw gapes during tree gouging. For example, compared with non-gouging tamarins, marmosets have lower condylar heights relative to the mandibular occlusal plane (Vinyard et al., 2003). This lower condylar position yields a more obtuse angle between the origin and insertion of the masseter muscle; thereby, reducing masseter stretch and facilitating wider jaw gapes (Herring and Herring, 1974). The masseter muscles are also positioned on the marmoset skull to reduce stretching during wide jaw opening (Vinyard et al., 2003). Marmosets have anteroposteriorly elongated mandibular condyles and temporal articular surfaces compared with tamarins. During jaw opening, the elongated condyle facilitates increased angular rotation (because condylar length tracks condylar curvature in these primates), while a longer temporal articular surface increases the translational capacity of the condyle. Both can facilitate a wider jaw gape.

Jaw-muscle architecture in tree-gouging marmosets also promotes relatively large gapes but not necessarily relatively large bite forces. Compared with cotton-top tamarins, tree-gouging marmosets have relatively longer masseter and temporalis fibers but relatively smaller physiological cross-sectional areas (PCSA) (Taylor and Vinyard, 2004; Taylor and Vinyard, 2008; Taylor et al., 2009a; Taylor et al., 2009b). Because fiber length is a measure of the number of sarcomeres in series, and the absolute excursion of a fiber is equivalent to the unit excursions achieved by each sarcomere in series (Gans, 1982; Williams and Goldspink, 1978; Williams and Goldspink, 1971), the relatively longer jaw-muscle fibers of tree-gouging marmosets reduce the amount of muscle stretch per angular degree of gape. Alternatively, maximum muscle force production theoretically reflects the sum of the cross-sectional areas of all muscle fibers lying in parallel (Powell et al., 1984) and is proportional to PCSA, suggesting that marmosets may not be able to produce relatively large muscle forces given their relatively smaller masseter and temporalis PCSA.

The performance of a muscle is also influenced by other mechanical and physiological factors, including the moment arm and the length—tension (L—T) relationship of a muscle (Gordon et al., 1966; Lieber and Boakes, 1988). The L—T relationship describes the amount of isometric force a muscle can produce at a given sarcomere length (Gordon et al., 1966). Each region of the sarcomere L—T curve has different functional consequences for a muscle. When a muscle acts on the ascending limb of the L—T curve, force in the muscle will increase with increasing muscle length until active force achieves a maximum as the muscle reaches the plateau of this curve. Conversely, when a muscle acts on the descending limb of the L—T curve, active force will decrease with increasing muscle length. This less advantageous position on the L—T curve may have consequences for maintaining active muscle force and control of movement. The muscle may not be able to generate sufficient force to counteract a length perturbation that pulls the muscle to greater lengths. Data describing joint mechanics can be combined with muscle architectural variables (e.g. sarcomere number) to model the sarcomere length operating throughout the range of joint angles over which a muscle operates (Fig. 3).

Fig. 3.

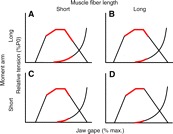
This schematic demonstrates the relationship between moment arm and muscle fiber length and the consequences for a muscle's operating range. Increasing the moment arm increases the amount of stretch imposed on the muscle, thereby increasing its operating range for a given amount of angular rotation (compare elongated red lines estimating operating range in A and B with those in C and D). Increasing the muscle fiber length increases the number of sarcomeres to take up the imposed stretch, decreasing the operating range (compare shortened red lines estimating operating range in B and D with those in A and C).

Both the architectural trade-off between excursion and force production as well as the L—T relationship for a muscle may have important functional consequences for producing bite forces at wide jaw gapes. For example, do the longer muscle fibers help maintain marmoset jaw muscles at a favorable location on the L—T curve (e.g. on or near the plateau region) when gouging trees with wide jaw gapes to help offset their relatively reduced force-generating capacity? To address this and related questions about jaw-muscle function during biting at wide gapes, we need to consider muscle architecture within the context of the larger muscle—joint system.

In this study, we model the muscle—joint system to compare sarcomere length operating ranges and muscle force production across a range of jaw gapes in regional portions of the masseter and temporalis muscles of tree-gouging common marmosets and non-gouging cotton-top tamarins. This modeling approach builds on previous studies examining changes in jaw-muscle mechanics during ontogeny in rabbits (Weijs et al., 1987) and variation in mechanical parameters among masticatory muscles in rabbits (Hertzberg et al., 1980) and rats (Hiiemae, 1971; Nordstrom et al., 1974; Rayne and Crawford, 1972). We test the hypothesis that the masseter and temporalis muscles of common marmosets are configured to generate relatively large forces at relatively wide jaw gapes during tree gouging (Taylor and Vinyard, 2004; Taylor et al., 2009a; Vinyard et al., 2003).

Based on previous work examining muscular and skeletal differences in the masticatory apparatus of marmosets and tamarins (Taylor and Vinyard, 2004; Taylor et al., 2009a; Vinyard et al., 2003), we predict that tree-gouging marmosets will operate on a more advantageous portion of the L—T curve for the masseter and temporalis. A lower condylar height relative to mandible length in the marmosets will reduce masseter stretching for a given jaw gape. Additionally, longer masseter and temporalis fibers (i.e. more sarcomeres in series) will reduce the length change each sarcomere must take up during gape, resulting in the muscles operating over a narrower range of sarcomere lengths. Assuming that marmosets and tamarins have similar sarcomere lengths on the ascending limb of the L—T curve at occlusion, these musculoskeletal features would allow marmosets to operate at sarcomere lengths that are closer to optimum length where relative isometric force is maximal during a large jaw gape, compared with the non-gouging tamarins. Thus, although tamarins have a relatively larger PCSA and would be predicted to generate higher muscle forces, force production might be compromised when the muscles operate at sarcomere lengths that are longer than optimal sarcomere length. We contend that using a model informed by both in vivo mechanics and behavioral observations may provide novel insight into the functional consequences and morphological adaptations of the marmoset masticatory apparatus.

MATERIALS AND METHODS

Samples

Formalin-fixed heads were used to generate musculoskeletal models of the masticatory apparatus for common marmosets (Callithrix jacchus Linnaeus) (N=3) and cotton-top tamarins (Saguinus oedipus Linnaeus) (N=3). Cadavers were skeletally mature and lacked obvious pathologies or deformities. Cadaveric specimens were provided by the New England Primate Research Center (Southborough, MA, USA) and the Dumond Conservancy (Miami, FL, USA). Although all specimens were captive raised, these individuals perform gouging behaviors similar to those of wild individuals (McGrew et al., 1986).

Data collection

Initially, heads were skinned and the masseter and temporalis muscles were removed. During muscle excision, we marked each skull to indicate the origin and insertion of the anterior and posterior superficial masseter, deep masseter, and anterior, middle and posterior temporalis (Fig. 4). The joint capsule and associated capsular ligaments were left intact to maintain physiologically relevant mobility of the jaw joint. The cranium was secured to a custom jig using Steinmann pins (Fig. 5). Sutures were used to approximate the path of each muscle as the jaw was opened from occlusion to a pre-determined maximum gape. A 3-0 nylon suture (Ethibond Excel, Ethicon, Inc., Sommerville, NJ, USA) was secured to the coronoid process and placed through a custom eyelet over the marked insertion of each region of the temporalis muscle. For the masseter muscle, a distal suture was secured to one of three marked insertion points on the mandible and placed through the eyelet over each region's origin on the zygomatic arch. The proximal end of the suture was pre-tensioned with a 40 g weight and placed over a potentiometer (precision=0.039 mm).

Fig. 4.

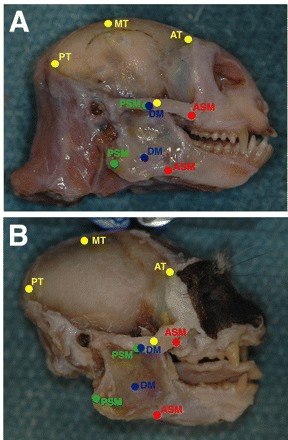
Sagittal view of Callithrix jacchus (A) and Saguinus oedipus (B) skulls with the masseter and temporalis muscles removed. The origin and insertion points of the anterior (AT), middle (MT) and posterior temporalis (PT; yellow circles) as well as the anterior superficial (ASM; red circles), deep (DM; blue circles) and posterior superficial (PSM: green circles) masseter are shown. Markings were made on the skulls as muscles were removed to approximate muscle paths.

Fig. 5.

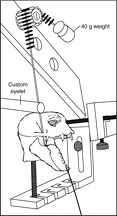
A custom jig was used to measure muscle excursion. The cranium was secured to the jig using Steinmann pins. Sutures were used to approximate the path of each muscle as the jaw was opened from occlusion to a pre-determined maximum gape (data collection for the anterior temporalis is shown here). A 3-0 nylon suture was secured to the coronoid process and placed through a custom eyelet over the marked insertion of the anterior temporalis muscle. The proximal end of the suture was pre-tensioned with a 40 g weight and placed over a potentiometer. The mandible was opened incrementally and in-plane images were used to measure joint angle while muscle excursion was measured with a potentiometer.

Because heads were formalin-fixed upon arrival, we could not quantify maximum gape for each specimen. To provide a range of functionally relevant jaw gapes for studying muscle excursion, we calculated the mean of the largest 10% of jaw gapes during gouging in four common marmosets (X̅=24.2 mm; N=18) (C.J.V., unpublished data) (see also Vinyard et al., 2009). Based on this mean of the largest gapes and a mean jaw length of 26.2 mm in C. jacchus (N=16), we converted the linear gape to an angular gape estimate of 55 deg. using a simple geometric model centered at the temporomandibular joint {2×[sin⁻¹(24.2×0.5/26.2)]}. Although not directly measured, we used the same maximum functional gape of 55 deg. in S. oedipus.

Although in this study we do not measure muscle moment arms directly (i.e. with a ruler), we have used the tendon excursion method (Brand et al., 1975) to define moment arm throughout the jaw range of motion. The excursion imposed on a muscle during joint movement is a function of the degree of joint angular rotation and the muscle's moment arm. In the tendon excursion method for measuring moment arm, tendon excursion is measured through a joint's angular range of motion (ROM) and is expressed using the following equation:

$$L=r\Phi ,$$ (1)

where L is tendon excursion, r is the radius of the joint (i.e. muscle's moment arm) and Φ is the angular rotation of the joint in radians. Using this equation, moment arm can be calculated by taking the derivative of a function describing the joint angle—tendon excursion relationship.

Serial photographs were taken while the jaw was manually opened incrementally from occlusion to the mean maximum functional gape. Jaw angle was measured from the photographs using ImageJ software (Version 1.38x; National Institute of Health, Bethesda, MD, USA). Markers were placed on the mandible to facilitate jaw angle measurements made relative to a stationary maxilla. Voltage changes measured by the potentiometer during jaw opening were acquired using a data acquisition board and custom LabVIEW software (Version 8; National Instruments, Austin, TX, USA). Synchronization of the serial photographs and potentiometer measurements allowed voltage to be measured as a function of jaw angle. Muscle excursion was calculated by converting voltage measurements to distances using a measured calibration factor (39.37 mm V⁻¹). We fit three excursion trials for each region of the temporalis and masseter muscles with a quadratic polynomial (R²=0.973±0.005; mean ± s.e.m.) and averaged the three trials using Matlab software (Matlab version 7.0; The Mathworks, Natick, MA, USA).

To integrate the modeled length changes with known muscle architecture, we used previously published data on masseter and temporalis fiber architecture [C. jacchus N=12 and S. oedipus N=10 (Taylor and Vinyard, 2004; Taylor and Vinyard, 2008)] and estimates of sarcomere lengths (L_s′ (Table 1). All jaws were fixed in a standardized posture (tip-to-tip incisor occlusion). Small (~2 mm³) tissue samples were excised from anterior, middle and posterior regions in the temporalis and the anterior and posterior superficial and deep masseter. The tissue samples were paraffin embedded, serial sectioned (5-6 m), mounted on slides and stained with phosphotungstic acid hematoxylin to facilitate visibility of muscle striations. Using either ×40 or ×100 (oil immersion) objectives (Nikon 50i compound microscope, Melville, NY, USA), one or more repeating visible structures — Z (Zwischenscheibe)-lines, A (anisotropic)-bands or I (isotropic)-bands (Young et al., 2006) were identified. Sets of 10 consecutive sarcomeres were measured to calculate a mean L_s′ for each muscle region. These sarcomere lengths were used to normalize fiber lengths (L_f).

Table 1.

Muscle architecture of the masseter and temporalis of Callithrix jacchus and Saguinus oedipus*

			Muscle length (mm)	Fiber length (mm)	Tendon length/fiber length	Sarcomere length (μm)	PCSA (mm2)
Muscle	Species	Mass (g)					Anterior	Middle	Posterior
Masseter	C. jacchus	1.11±0.05	29.70±2.27	9.57±0.67	1.15±0.09	1.63±0.10	0.33±0.03	0.34±0.03	0.35±0.03
	S. oedipus	1.29±0.09	32.57±2.13	8.45±0.75	1.59±0.09	1.51±0.11	0.39±0.04	0.46±0.04	0.44±0.04
Temporalis	C. jacchus	1.59±0.05	36.90±2.03	11.71±0.57	1.86±0.17	1.59±0.11	0.53±0.03	0.48±0.03	0.24±0.01
	S. oedipus	1.92±0.12	42.03±3.29	7.69±0.56	3.23±0.26	1.77±0.07	0.80±0.04	0.74±0.03	0.70±0.03

^*Architectural dimensions are based on conspecific individuals collected using similar protocols as the specimens examined here.

Values are means ± s.e.m.

Muscle length (L_m) and fiber length (L_f) are normalized to a sarcomere length of 2.41 μm.

PCSA = physiological cross-sectional area.

For the masseter, this is the deep region of the muscle.

Values for sarcomere number (S_n) and normalized L_f were calculated for isolated fiber bundles according to the following equations (Lieber et al., 1994):

$$S_{\mathrm{n}}=L_{\mathrm{f}}^{\prime }∕L_{\mathrm{s}}^{\prime },$$ (2)

and

$$L_{\mathrm{f}}={L_{\mathrm{f}}}^{\prime }\left(\frac{2.4}{{L_{\mathrm{s}}}^{\prime }}\right),$$ (3)

where L_f′ is the measured muscle fiber length, L_s′ is the measured sarcomere length, L_f is normalized muscle fiber length, and 2.4 μm is the optimum sarcomere length derived from myofilament lengths measured in rhesus macaque (Walker and Schrodt, 1974). The ratio of tendon length to fiber length (L_T/L_f) was calculated by dividing the total L_T by the normalized L_f.

The mass (M) of each muscle region was measured to calculate regional PCSA. PCSA (Powell et al., 1984) was calculated as:

$$\mathrm{PCSA}=\frac{M\times \cos \theta }{\rho \times L_{\mathrm{f}}},$$ (4)

where θ is pinnation angle and ρ is muscle density (1.0564 g cm⁻³) (Mendez and Keys, 1960).

Muscle architecture and joint angle—excursion data were input into a simple lumped-parameter model (Ward et al., 2006a; Zajac, 1989) to define the sarcomere length—joint angle and relative tension—joint angle relationships in each muscle region (Lieber and Boakes, 1988). Briefly, we used normalized fiber length and sarcomere length measurements to estimate the number of sarcomeres in series in each fiber. Using mean sarcomere lengths measured from specimens with jaws in occlusion as a reference (Taylor and Vinyard, 2004), the length changes measured from each muscle region were distributed evenly among the sarcomeres in that region. This allowed an entire sarcomere length—joint angle curve to be computed for each muscle region. Sarcomere length—joint angle curves were interrogated in five degree increments to make comparisons among muscles and between species.

Zajac defined a stiff tendon actuator as a ratio of tendon to fiber length of approximately 3 and lower (Zajac, 1989). Based on this definition, the temporalis and masseter of both C. jacchus and S. oedipus can be defined as stiff (Table 1). Tendon strain has a negligible effect on the sarcomere length—tension curve in stiff tendon actuators (Zajac, 1989). Thus, the contribution of tendon strain to muscle excursion in our model was ignored. Using the experimentally derived sarcomere length—joint angle curves, relative active and passive tension values as a function of jaw angle were computed using an active length—tension curve derived from rhesus macaque myofilament lengths (Walker and Schrodt, 1974) and a passive length—tension curve measured from a rabbit tibialis anterior muscle (Davis et al., 2003). A muscle's maximum force-producing capacity is proportional to its physiological cross-sectional area (PCSA) and can be calculated as the product of PCSA and muscle specific tension (22.5 N cm⁻²) (Powell et al., 1984). The relative tension—joint angle curves can be multiplied by the muscle region's maximum force-producing capacity to estimate the absolute force—joint angle relationship of each muscle region. Each sarcomere length—, relative active—, relative passive— and absolute force—joint angle curve was interrogated in five degree increments to make comparisons of these variables between C. jacchus and S. oedipus for each muscle region.

There were no significant (P>0.05) sex differences in jaw length, muscle mass or muscle length in either species. In addition, sexual dimorphism in body size is minimal in these species (Fleagle, 1999) and we have no basis for hypothesizing sex differences in tree gouging. We therefore combined males and females in all analyses. Assumptions of normality and homogeneity of variances were met. Therefore, comparisons of modeled variables (muscle fiber excursion, sarcomere length, relative active tension, relative passive tension, relative total tension and total force) between species were made using two-way (species × joint angle) repeated-measures analyses of variance (ANOVA), with joint angle as the repeated measure within each individual. Post hoc t-tests with Šidák corrections were used to determine differences when main effects were identified. Statistical tests were performed using SPSS software (SPSS, Inc., Version 13.0, Chicago, IL, USA), and an a priori significance (α) was set at 0.05.

RESULTS

Muscle fiber excursion

In both species, total muscle excursion over the range of jaw opening was greater in the anterior portion of the superficial masseter as well as the anterior and middle portions of the temporalis, compared with the deep and posterior portions of these muscles, respectively (Tables 2 and 3; Fig. 6). Maximum muscle excursion (at the estimated maximum jaw gape) was greatest in the anterior superficial masseter of S. oedipus (10.543±0.374 mm; Fig. 6A) and smallest in the posterior superficial masseter of C. jacchus (0.57±0.35 mm; Fig. 6C). Saguinus oedipus had a larger maximum muscle excursion compared with C. jacchus in all muscle regions except the posterior temporalis (Fig. 6F). This difference in excursion was significant for the anterior superficial masseter (10.54 mm vs 7.28 mm) and posterior superficial masseter (2.30 mm vs 0.57 mm; Table 2). All other muscle comparisons between C. jacchus and S. oedipus approached statistical significance but failed to achieve significance potentially because of small samples and low statistical power (Tables 2 and 3).

Table 2.

Excursion (mm), sarcomere length (L_s), relative tension and muscle force estimates as a function of joint angle in the (A) anterior superficial masseter, (B) deep masseter and (C) posterior superficial masseter of Callithrix jacchus and Saguinus oedipus. The bottom panel provides P-values for two-way (species × joint angle) repeated-measures ANOVAs comparing C. jacchus and S. oedipus

	Joint angle	Excursion (mm)*, †		Relative tension
			Ls	Active (%)	Passive (%)	Total (%)	Muscle force (N)
(A) Anterior superficial masseter
C. jacchus	0	0	1.63	53.72	0	53.72	3.99
	5	0.91±0.05	1.78±0.00	73.21±0.17	0	73.21±0.17	5.44±0.01
	10	1.77±0.09	1.93±0.00	81.81±0.28	0	81.81±0.28	6.07±0.02
	15	2.58±0.12	2.07±0.01	89.92±0.36	0	89.92±0.36	6.68±0.03
	20	3.34±0.15	2.20±0.01	97.54±0.46	0	97.54±0.46	7.24±0.03
	25	4.05±0.18	2.32±0.01	100.00±0.00	0	100.00±0.00	7.43±0.00
	30	4.71±0.21	2.43±0.02	100.00±0.00	0.13±0.00	100.13±0.00	7.43±0.00
	35	5.32±0.23	2.54±0.02	99.94±0.06	0.15±0.01	100.09±0.05	7.43±0.00
	40	5.88±0.26	2.63±0.03	96.58±2.11	0.20±0.02	96.76±2.09	7.19±0.15
	45	6.40±0.29	2.72±0.04	90.82±2.80	0.31±0.08	91.13±2.72	6.77±0.20
	50	6.86±0.33	2.80±0.05	85.61±3.60	0.58±0.27	86.19±3.34	6.40±0.25
	55	7.28±0.37	2.87±0.07	80.96±4.51	0.95±0.45	81.91±4.07	6.08±0.30
S. oedipus	0	0	1.51	34.19	0	34.19	3.00
	5	1.10±0.05	1.71±0.01	66.07±1.84	0	66.07±1.84	5.80±0.16
	10	2.16±0.09	1.90±0.02	79.81±1.25	0	79.81±1.25	7.00±0.11
	15	3.21±0.12	2.08±0.03	90.75±1.77	0	90.75±1.77	7.96±0.16
	20	4.22±0.15	2.26±0.04	98.99±1.01	0	98.99±1.01	8.69±0.09
	25	5.20±0.18	2.44±0.04	100.00±0.00	0.09±0.05	100.09±0.05	8.78±0.00
	30	6.16±0.21	2.61±0.05	96.51±1.81	0.19±0.02	96.70±1.79	8.49±0.16
	35	7.09±0.23	2.78±0.05	87.03±3.52	0.48±0.14	87.51±3.38	7.68±0.30
	40	7.99±0.26	2.94±0.06	76.42±3.72	1.38±0.41	77.81±3.32	6.83±0.29
	45	8.87±0.29	3.09±0.06	66.14±3.87	2.88±0.66	69.02±3.22	6.06±0.28
	50	9.72±0.33	3.25±0.06	56.18±3.97	5.75±1.48	61.93±2.52	5.43±0.22
	55	10.54±0.37	3.39±0.06	46.55±4.03	12.05±3.58	58.60±0.77	5.14±0.07
ANOVA (P-values)	0	NA	NA	NA	NA	NA	NA
	5	0.045	0.002	0.018	NA	0.018	0.089
	10	0.031	0.193	0.193	NA	0.193	0.001
	15	0.022	0.671	0.671	NA	0.671	0.001
	20	0.015	0.163	0.259	NA	0.259	<0.001
	25	0.011	0.057	NS	0.116	0.116	<0.001
	30	0.008	0.026	0.127	0.055	0.128	0.003
	35	0.006	0.014	0.021	0.084	0.020	0.451
	40	0.005	0.009	0.009	0.044	0.008	0.338
	45	0.004	0.007	0.007	0.018	0.006	0.111
	50	0.004	0.005	0.005	0.026	0.004	0.044
	55	0.004	0.005	0.005	0.037	0.005	0.039
(B) Deep masseter
C. jacchus	0	0	1.63	53.72	0	53.72	4.11
	5	0.43±0.06	1.70±0.01	65.74±2.30	0	65.74±2.30	5.03±0.02
	10	0.84±0.11	1.77±0.03	72.09±2.00	0	72.09±2.00	5.52±0.04
	15	1.20±0.17	1.83±0.04	76.17±2.33	0	76.17±2.33	5.83±0.02
	20	1.54±0.21	1.89±0.05	79.53±3.01	0	79.53±3.01	6.08±0.03
	25	1.84±0.26	1.94±0.06	82.57±3.65	0	82.57±3.65	6.32±0.05
	30	2.11±0.30	1.99±0.07	85.28±4.25	0	85.28±4.25	6.52±0.06
	35	2.35±0.34	2.03±0.08	87.66±4.81	0	87.66±4.81	6.71±0.07
	40	2.56±0.38	2.07±0.09	89.72±5.35	0	89.72±5.35	6.86±0.09
	45	2.73±0.42	2.09±0.10	91.45±5.88	0	91.45±5.88	7.00±0.11
	50	2.87±0.46	2.12±0.11	92.55±6.20	0	92.55±6.20	7.08±0.07
	55	2.98±0.50	2.14±0.12	92.85±6.21	0	92.85±6.21	7.10±0.00
S. oedipus	0	0	1.51	34.19	0	34.19	3.54
	5	0.48±0.01	1.60±0.00	48.04±0.18	0	48.04±0.18	4.97±0.02
	10	0.94±0.01	1.68±0.00	61.43±0.39	0	61.43±0.39	6.36±0.04
	15	1.38±0.02	1.76±0.00	71.58±0.23	0	71.58±0.23	7.41±0.02
	20	1.81±0.03	1.83±0.00	76.10±0.33	0	76.10±0.33	7.88±0.03
	25	2.22±0.04	1.91±0.01	80.45±0.44	0	80.45±0.44	8.33±0.05
(B) Deep masseter
S. oedipus	30	2.62±0.05	1.98±0.01	84.63±0.57	0	84.63±0.57	8.76±0.06
	35	3.01±0.07	2.05±0.01	88.65±0.71	0	88.65±0.71	9.18±0.07
	40	3.37±0.08	2.11±0.01	92.51±0.87	0	92.51±0.87	9.58±0.09
	45	3.72±0.10	2.18±0.02	96.21±1.04	0	96.21±1.04	9.96±0.11
	50	4.06±0.12	2.24±0.02	99.07±0.67	0	99.07±0.67	10.25±0.07
	55	4.38±0.14	2.29±0.02	100.00±0.00	0	100.00±0.00	10.35±0.00
ANOVA (P-values)	0	NA	NA	NA	NA	NA	NA
	5	0.636	0.002	0.002	NA	0.002	0.761
	10	0.560	0.026	0.006	NA	0.006	0.006
	15	0.487	0.122	0.122	NA	0.122	0.001
	20	0.418	0.320	0.320	NA	0.320	0.002
	25	0.355	0.594	0.594	NA	0.594	0.002
	30	0.298	0.887	0.887	NA	0.887	0.002
	35	0.248	0.849	0.849	NA	0.849	0.003
	40	0.205	0.634	0.634	NA	0.634	0.003
	45	0.169	0.470	0.470	NA	0.470	0.003
	50	0.140	0.349	0.355	NA	0.355	0.003
	55	0.115	0.262	0.313	NA	0.313	0.002
(C) Posterior superficial masseter
C. jacchus	0	0	1.63	53.72	0	53.72	4.23
	5	0.12±0.07	1.65±0.01	57.02±2.06	0	57.02±2.06	4.49±0.16
	10	0.22±0.14	1.67±0.02	59.94±3.89	0	59.94±3.89	4.72±0.31
	15	0.32±0.20	1.68±0.03	61.95±4.98	0	61.95±4.98	4.88±0.39
	20	0.40±0.25	1.70±0.04	63.13±5.46	0	63.13±5.46	4.97±0.43
	25	0.46±0.29	1.70±0.01	64.12±5.86	0	64.12±5.86	5.05±0.46
	30	0.51±0.32	1.71±0.05	64.90±6.20	0	64.90±6.20	5.11±0.49
	35	0.55±0.34	1.72±0.05	65.49±6.45	0	65.49±6.45	5.16±0.51
	40	0.58±0.36	1.72±0.06	65.87±6.61	0	65.87±6.61	5.19±0.52
	45	0.59±0.37	1.73±0.06	66.06±6.69	0	66.06±6.69	5.20±0.53
	50	0.59±0.36	1.73±0.06	66.04±6.68	0	66.04±6.68	5.20±0.53
	55	0.57±0.35	1.73±0.06	65.82±6.57	0	65.82±6.57	5.18±0.52
S. oedipus	0	0	1.51	34.19	0	34.19	3.38
	5	0.31±0.07	1.57±0.01	43.21±2.13	0	43.21±2.13	4.28±0.21
	10	0.60±0.14	1.62±0.02	51.65±4.05	0	51.65±4.05	5.11±0.40
	15	0.87±0.20	1.67±0.04	59.50±5.76	0	59.50±5.76	5.89±0.57
	20	1.12±0.25	1.71±0.04	64.95±5.93	0	64.95±5.93	6.43±0.59
	25	1.35±0.30	1.75±0.05	68.51±5.75	0	68.51±5.75	6.78±0.57
	30	1.56±0.34	1.79±0.06	71.44±5.49	0	71.44±5.49	7.07±0.54
	35	1.75±0.37	1.82±0.07	74.07±5.26	0	74.07±5.26	7.33±0.52
	40	1.91±0.41	1.85±0.07	76.40±5.07	0	76.40±5.07	7.56±0.50
	45	2.06±0.44	1.88±0.08	78.43±4.93	0	78.43±4.93	7.76±0.49
	50	2.19±0.47	1.90±0.08	80.07±4.96	0	80.07±4.96	7.93±0.49
	55	2.30±0.50	1.92±0.09	81.20±5.31	0	81.20±5.31	8.04±0.53
ANOVA (P-values)	0	NA	NA	NA	NA	NA	NA
	5	0.140	0.010	0.010	NA	0.010	0.471
	10	0.130	0.214	0.214	NA	0.214	0.479
	15	0.119	0.725	0.764	NA	0.764	0.218
	20	0.108	0.846	0.833	NA	0.833	0.115
	25	0.098	0.587	0.621	NA	0.621	0.077
	30	0.088	0.431	0.474	NA	0.474	0.055
	35	0.078	0.331	0.361	NA	0.361	0.040
	40	0.070	0.263	0.275	NA	0.275	0.030
	45	0.062	0.213	0.211	NA	0.211	0.023
	50	0.055	0.177	0.167	NA	0.167	0.019
	55	0.049	0.150	0.143	NA	0.143	0.018

^*Values are means ± s.e.m.

^†Bolded values indicate a significant species difference (P<0.05).

‘NA’ indicates no statistical test was applied on pre-determined values.

Table 3.

Excursion (mm), sarcomere length (L_s), relative tension and muscle force estimates as a function of joint angle in the (A) anterior temporalis, (B) middle temporalis and (C) posterior temporalis of Callithrix jacchus and Saguinus oedipus. The bottom panel provides P-values for two-way (species × joint angle) repeated-measures ANOVAs comparing C. jacchus and S. oedipus

	Joint angle	Excursion (mm) *, †		Relative tension (%)
			Ls	Active	Passive	Total	Muscle force (N)
(A) Anterior temporalis
C. jacchus	0	0	1.59	47.21	0	47.21	5.63
	5	0.53±0.13	1.66±0.01	59.02±2.31	0	59.02±2.31	7.04±0.27
	10	1.08±0.24	1.74±0.03	68.95±2.95	0	68.95±2.95	8.22±0.35
	15	1.64±0.33	1.81±0.04	74.83±2.27	0	74.83±2.27	8.92±0.27
	20	2.20±0.40	1.89±0.05	79.37±2.88	0	79.37±2.88	9.46±0.34
	25	2.78±0.46	1.97±0.06	83.99±3.42	0	83.99±3.42	10.02±0.41
	30	3.37±0.50	2.05±0.07	88.69±3.89	0	88.69±3.89	10.58±0.46
	35	3.50±0.40	2.13±0.07	93.01±3.87	0	93.01±3.87	11.09±0.46
	40	4.58±0.55	2.21±0.08	95.99±2.55	0	95.99±2.55	11.45±0.30
	45	5.21±0.55	2.30±0.08	98.72±1.28	0.04±0.04	98.76±1.31	11.78±0.16
	50	5.84±0.54	2.38±0.09	100.00±0.00	0.05±0.05	100.05±0.05	11.93±0.01
	55	6.49±0.53	2.47±0.09	98.38±1.62	0.11±0.06	98.49±1.57	11.75±0.19
S. oedipus	0	0	1.77	72.35	0	72.35	13.02
	5	0.59±0.13	1.90±0.03	80.27±1.96	0	80.27±1.96	14.45±0.35
	10	1.19±0.24	2.04±0.06	88.43±3.60	0	88.43±3.60	15.92±0.65
15	1.81±0.33	2.19±0.08	95.14±3.67	0	95.14±3.67	17.13±0.66
	20	2.44±0.40	2.33±0.10	98.23±1.77	0.05±0.05	98.28±1.79	17.69±0.32
	25	3.10±0.46	2.48±0.11	98.07±1.93	0.12±0.06	98.19±1.88	17.67±0.34
	30	3.77±0.50	2.64±0.12	92.75±4.88	0.32±0.15	93.07±4.73	16.75±0.85
	35	4.45±0.40	2.79±0.12	85.74±7.82	0.82±0.47	86.56±7.38	15.58±1.33
	40	5.16±0.55	2.96±0.12	75.22±7.67	1.78±0.87	76.99±6.81	13.86±1.23
	45	5.88±0.55	3.12±0.11	64.30±7.05	3.75±1.51	68.05±5.59	12.25±1.01
	50	6.61±0.54	3.29±0.09	53.13±6.09	8.04±3.00	61.17±3.26	11.01±0.59
	55	7.37±0.53	3.47±0.07	41.70±4.81	18.81±6.18	60.51±1.74	10.89±0.31
ANOVA (P-values)	0	NA	NA	NA	NA	NA	NA
	5	0.790	0.003	0.002	NA	0.002	<0.001
	10	0.763	0.010	0.014	NA	0.014	<0.001
	15	0.732	0.016	0.009	NA	0.009	<0.001
	20	0.696	0.017	0.005	0.374	0.005	<0.001
	25	0.656	0.015	0.023	0.134	0.022	<0.001
	30	0.610	0.013	0.551	0.102	0.515	0.003
	35	0.166	0.009	0.451	0.159	0.482	0.033
	40	0.500	0.006	0.062	0.111	0.059	0.129
	45	0.437	0.004	0.009	0.070	0.006	0.667
	50	0.371	0.002	0.002	0.056	<0.001	0.192
	55	0.306	0.001	<0.001	0.039	<0.001	0.079
(B) Middle temporalis
C. jacchus	0	0	1.59	47.21	0	47.21	5.10
	5	0.41±0.17	1.65±0.03	56.25±5.12	0	56.25±5.12	6.08±0.55
	10	0.85±0.31	1.71±0.06	62.88±6.35	0	62.88±6.35	6.79±0.69
	15	1.32±0.42	1.77±0.08	69.66±6.38	0	69.66±6.38	7.52±0.69
	20	1.83±0.51	1.84±0.10	75.53±6.28	0	75.53±6.28	8.16±0.68
	25	2.37±0.57	1.91±0.11	80.65±6.42	0	80.65±6.42	8.71±0.69
	30	2.93±0.62	1.99±0.12	85.19±6.92	0	85.19±6.92	9.20±0.75
	35	3.53±0.64	2.07±0.13	89.03±6.39	0	89.03±6.39	9.61±0.69
	40	4.17±0.66	2.16±0.13	92.60±5.53	0	92.60±5.53	10.00±0.60
	45	4.83±0.67	2.25±0.13	95.35±4.65	0.04±0.04	95.40±4.67	10.30±0.50
	50	5.53±0.70	2.34±0.13	96.92±3.08	0.09±0.04	97.01±3.12	10.48±0.34
	55	6.25±0.75	2.44±0.14	98.32±1.26	0.11±0.06	98.43±1.31	10.63±0.14
S. oedipus	0	0	1.77	72.35	0	72.35	12.05
	5	0.60±0.17	1.91±0.01	80.49±0.74	0	80.49±0.74	13.40±0.35
	10	1.21±0.31	2.05±0.02	88.79±1.25	0	88.79±1.25	14.78±0.65
	15	1.84±0.42	2.19±0.03	97.24±1.54	0	97.24±1.54	16.19±0.66
	20	2.47±0.51	2.34±0.03	100.00±0.00	0	100.00±0.00	16.65±0.32
(B) Middle temporalis
S. oedipus	25	3.12±0.57	2.49±0.03	100.00±0.00	0.14±0.01	100.14±0.01	16.67±0.34
	30	3.78±0.62	2.64±0.02	96.05±1.30	0.20±0.01	96.25±1.29	16.03±0.85
	35	4.45±0.64	2.79±0.01	85.90±0.94	0.44±0.06	86.34±0.88	14.38±1.33
	40	5.13±0.66	2.95±0.02	75.58±1.17	1.46±0.13	77.04±1.05	12.83±1.23
	45	5.83±0.67	3.11±0.03	65.09±2.16	2.97±0.44	68.06±1.72	11.33±1.01
	50	6.53±0.70	3.27±0.05	54.42±3.55	6.53±1.85	60.95±1.71	10.15±0.59
	55	7.25±0.75	3.44±0.08	43.58±5.25	17.46±8.40	61.04±3.15	10.16±0.31
ANOVA (P-values)	0	NA	NA	NA	NA	NA	NA
	5	0.465	0.001	0.009	NA	0.009	<0.001
	10	0.451	0.005	0.016	NA	0.016	<0.001
	15	0.437	0.007	0.014	NA	0.014	<0.001
	20	0.420	0.008	0.018	NA	0.018	<0.001
	25	0.403	0.007	0.039	<0.001	0.038	<0.001
	30	0.386	0.005	0.198	<0.001	0.191	0.001
	35	0.370	0.004	0.654	0.002	0.698	0.003
	40	0.357	0.003	0.040	<0.001	0.051	0.010
	45	0.353	0.003	0.004	0.003	0.005	0.151
	50	0.366	0.003	0.001	0.025	0.001	0.498
	55	0.401	0.003	0.001	0.108	<0.001	0.439
(C) Posterior temporalis
C. jacchus	0	0	1.59	47.21	0	47.21	2.55
	5	0.59±0.17	1.67±0.03	60.21±5.30	0	60.21±5.30	3.25±0.29
	10	1.15±0.32	1.75±0.06	67.49±6.99	0	67.49±6.99	3.65±0.38
	15	1.69±0.44	1.82±0.08	72.78±7.41	0	72.78±7.41	3.93±0.40
	20	2.21±0.54	1.89±0.10	78.08±7.40	0	78.08±7.40	4.22±0.40
	25	2.71±0.61	1.96±0.12	83.37±6.95	0	83.37±6.95	4.50±0.38
	30	3.18±0.67	2.02±0.13	87.14±7.54	0	87.14±7.54	4.71±0.41
	35	3.63±0.70	2.08±0.13	90.09±7.44	0	90.09±7.44	4.87±0.40
	40	4.05±0.71	2.14±0.13	92.32±6.79	0	92.32±6.79	4.99±0.37
	45	4.45±0.71	2.19±0.13	94.12±5.88	0	94.12±5.88	5.08±0.32
	50	4.83±0.69	2.25±0.12	95.42±4.58	0.04±0.04	95.47±4.61	5.16±0.25
	55	5.18±0.67	2.29±0.11	96.82±3.18	0.04±0.04	96.86±3.20	5.23±0.17
S. oedipus	0	0	1.77	72.35	0	72.35	11.40
	5	0.23±0.17	1.82±0.01	75.41±0.38	0	75.41±0.38	11.88±0.06
	10	0.48±0.32	1.88±0.01	78.83±0.58	0	78.83±0.58	12.42±0.09
	15	0.76±0.44	1.94±0.01	82.59±0.58	0	82.59±0.58	13.01±0.09
	20	1.06±0.54	2.01±0.01	86.71±0.39	0	86.71±0.39	13.66±0.06
	25	1.39±0.61	2.09±0.00	91.18±0.06	0	91.18±0.06	14.36±0.01
	30	1.75±0.67	2.17±0.01	96.00±0.58	0	96.00±0.58	15.12±0.09
	35	2.13±0.70	2.26±0.02	99.79±0.21	0	99.79±0.21	15.72±0.03
	40	2.54±0.71	2.35±0.04	100.00±0.00	0.04±0.04	100.04±0.04	15.76±0.01
	45	2.97±0.71	2.45±0.06	100.00±0.00	0.09±0.05	100.10±0.05	15.77±0.01
	50	3.43±0.69	2.56±0.08	96.92±3.08	0.18±0.05	97.10±3.03	15.29±0.48
	55	3.92±0.67	2.67±0.11	92.93±6.47	0.43±0.27	93.36±6.20	14.71±0.98
ANOVA (P-values)	0	NA	NA	NA	NA	NA	NA
	5	0.208	0.010	0.046	NA	0.046	<0.001
	10	0.207	0.096	0.181	NA	0.181	<0.001
	15	0.206	0.218	0.257	NA	0.275	<0.001
	20	0.205	0.298	0.309	NA	0.309	<0.001
	25	0.205	0.324	0.324	NA	0.324	<0.001
	30	0.204	0.306	0.306	NA	0.306	<0.001
	35	0.205	0.260	0.262	NA	0.262	<0.001
	40	0.208	0.202	0.321	0.374	0.319	<0.001
	45	0.214	0.146	0.374	0.124	0.367	<0.001
	50	0.227	0.101	0.799	0.086	0.780	<0.001
	55	0.253	0.071	0.618	0.225	0.642	0.001

^*Values are means ± s.e.m.

^†Bolded values indicate a significant species difference (P<0.05).

‘NA’ indicates no statistical test was applied on pre-determined values.

Fig. 6.

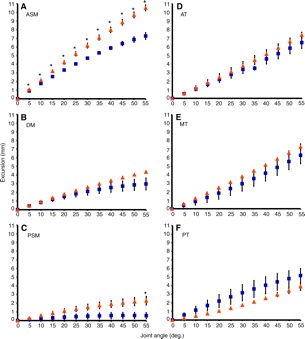
Excursion as a function of joint angle in the (A) anterior superficial (ASM), (B) deep (DM) and (C) posterior superficial (PSM) masseter as well as the (D) anterior (AT), (E) middle (MT) and (F) posterior (PT) temporalis in Callithrix jacchus (blue squares) and Saguinus oedipus (yellow triangles). Data are presented as means ± s.e.m. Significant differences (P<0.05) between C. jacchus and S. oedipus at a given joint angle are indicated with an asterisk (*).

Sarcomere length operating range

Sarcomere length operating ranges varied between 1.51-3.47 μm across all muscle regions and fell within the theoretical physiological range of 1.3-4.1 μm (Walker and Schrodt, 1974). Saguinus oedipus has significantly shorter fibers than C. jacchus (Table 1), implying that the fibers in S. oedipus have fewer sarcomeres in series. Greater muscle excursion distributed over fewer sarcomeres in series resulted in S. oedipus acting over a larger sarcomere length operating range from occlusion to our maximum functional gape estimate in all regions of the masseter and temporalis compared with C. jacchus (Tables 2 and 3; Fig. 7). The effect of excursion and sarcomere number on sarcomere length operating ranges is clearly demonstrated when considering that there were no differences in sarcomere length at occlusion between C. jacchus and S. oedipus for either the masseter or temporalis (Table 1)

Fig. 7.

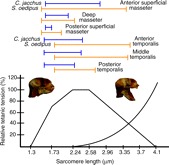
Sarcomere length operating ranges of masseter and temporalis muscle regions in Callithrix jacchus (blue) and Saguinus oedipus (yellow) from occlusion to our maximum gape estimate (55 deg.). Sarcomere operating ranges are superimposed on a sarcomere length—relative tension curve. The sarcomere length operating ranges of the anterior superficial masseter as well as anterior and middle temporalis in S. oedipus are significantly greater compared with C. jacchus as a function of longer moment arms (i.e. greater excursion) and shorter fibers.

Consistent with the fiber excursion data, the anterior superficial masseter of S. oedipus operated over the widest range of sarcomere lengths (1.51-3.39 μm; Fig. 7 and Table 2), followed by the anterior (1.77-3.47 μm) and middle (1.77-3.44 μm) temporalis of S. oedipus. The smallest sarcomere length operating ranges occurred in the posterior superficial masseter of C. jacchus (1.63-1.73 μm) and S. oedipus (1.51-1.92 μm). At maximum gape, S. oedipus exhibited significantly greater sarcomere lengths than C. jacchus in the anterior superficial masseter and the anterior and middle temporalis (Tables 2 and 3; Fig. 7).

In the anterior superficial masseter, both species are operating on the descending limb of the L—T curve at maximum gape (Fig. 7). In this masseter region, C. jacchus operated on the ascending limb and plateau region of the active L—T curve through 37 deg. of jaw gape and on the descending limb through an additional 18 deg. of gape. Saguinus oedipus acted on the ascending limb and plateau region of the active L—T curve up to 30 deg. of gape and on the descending limb through the subsequent 25 deg. of jaw ROM. Although the anterior superficial masseter of C. jacchus is acting on the descending limb for 18 deg. of jaw ROM, this muscle still has the ability to actively generate greater than 80% of maximal tetanic tension at the maximum estimated gape while S. oedipus is able to actively generate less than 50% of maximum tension at this gape (Table 2; Fig. 7). The deep and posterior superficial masseter in C. jacchus operate on the ascending limb of the L—T curve throughout the jaw ROM while the deep masseter of S. oedipus acts on the ascending limb, and the posterior superficial masseter on the ascending limb and plateau region.

The anterior, middle and posterior regions of the temporalis muscle in C. jacchus operate on the ascending limb and plateau region of the L—T curve throughout the entire jaw ROM (0-55 deg.), while these muscle regions in S. oedipus are on the descending limb at jaw angles greater than 28 deg. in anterior temporalis, 26 deg. in the middle temporalis and 52 deg. in the posterior temporalis (Table 3; Fig. 7).

Muscle tension and force generation

Combining sarcomere length operating ranges with the sarcomere L—T curve, we predicted the relative amount of active and passive tension the muscles were able to generate throughout the jaw ROM. Tree-gouging C. jacchus were able to generate significantly (P<0.05) greater active tension than the non-gouging S. oedipus at jaw angles greater than 35 deg. in the anterior superficial masseter, 45 deg. in the anterior temporalis and 40 deg. in the middle temporalis (Tables 2 and 3). Because S. oedipus is forced to operate at extremely long sarcomere lengths at large gapes in several muscle regions, passive tension plays a larger role in force generation for these muscles. Saguinus oedipus generates significantly greater relative passive tension than C. jacchus in the anterior superficial masseter at jaw angles greater than 40 deg., in the anterior temporalis at jaw angles greater than 55 deg. and in the middle temporalis at most joint angles larger than 25 deg. (Tables 2 and 3). Common marmosets exhibit significantly greater total relative tension in the anterior superficial masseter at joint angles of 35-55 deg., in the anterior temporalis from 45-55 deg. and in the middle temporalis from 45-55 deg. (Tables 2 and 3).

Using the PCSA of each muscle region and the specific tension of muscle to predict maximum force generating capacity (Powell et al., 1984), the relative amount of tension as a function of joint angle can be used to predict the absolute force-generating capacity throughout the jaw ROM (Tables 2 and 3). In the deep and posterior superficial masseter as well as the posterior temporalis, where excursion was the smallest, the non-gouging S. oedipus is able to generate significantly greater total force at most jaw angles compared with C. jacchus (Tables 2 and 3; Fig. 8). In the anterior superficial masseter, C. jacchus is able to generate significantly greater force at jaw angles of 50-55 deg. (Fig. 8). A similar pattern is observed for the force at maximum jaw gape in the anterior temporalis, although these differences only approach statistical significance (P=0.079; Fig. 8).

Fig. 8.

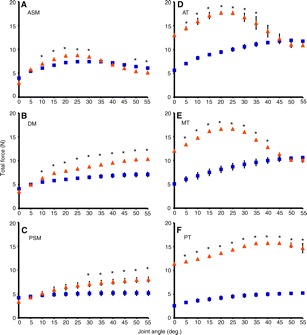
Muscle force as a function of joint angle in the (A) anterior superficial (ASM), (B) deep (DM) and (C) posterior superficial (PSM) masseter as well as the (D) anterior (AT), (E) middle (MT) and (F) posterior (PT) temporalis in Callithrix jacchus (blue squares) and Saguinus oedipus (yellow triangles). Data are presented as means ± s.e.m. Significant differences (P<0.05) between C. jacchus and S. oedipus at a given joint angle are indicated with an asterisk (*).

DISCUSSION

Circumventing architectural trade-offs in marmoset jaw muscles during gouging at wide gapes

Following on essential mathematical models, it is widely recognized that muscle architecture cannot simultaneously maximize excursion and force production holding muscle volume and other factors constant (Gans, 1982; Lieber, 2002; Lieber et al., 1997; Otten, 1988). Based on comparative muscle architecture, it appears that the masseter and temporalis of C. jacchus have been altered to facilitate larger range of motion while compromising maximum force production relative to S. oedipus (Taylor et al., 2009a; Taylor and Vinyard, 2004). Our modeling results support this observation as S. oedipus is predicted to generate larger isometric forces at optimal sarcomere lengths in each jaw-muscle region compared with C. jacchus (Tables 2 and 3; Fig. 8).

In addition to facilitating ROM, fiber length also affects force production throughout the range of jaw postures by influencing sarcomere operating range. Taylor and Vinyard (Taylor and Vinyard, 2004) previously hypothesized that the relatively longer fibers in marmoset jaw-closing muscles would reduce muscle stretch at wide jaw gapes and hence facilitate comparatively large bite forces at the extremes of jaw opening (see also Vinyard et al., 2003). Our results support this hypothesis by demonstrating that at an estimated maximum functional gape of 55 deg. the anterior superficial masseter and anterior and middle temporalis of C. jacchus are capable of generating equivalent or significantly greater muscle forces compared with S. oedipus despite having relatively smaller PCSAs. The anterior (and middle) region of the masseter and temporalis probably play key functional roles in biting at the anterior teeth in primates because they (1) possess improved leverage for biting compared to more posterior muscle regions (Turkawski et al., 1998; van Eijden et al., 1997), (2) are oriented to generate a significant vertical component of force during incisal biting (Hylander, 2006), and (3) are routinely active during incisal biting in anthropoid primates (Blanksma et al., 1997; Hylander and Johnson, 1985; Lindauer et al., 1993; Ross and Hylander, 2000), including common marmosets (C.J.V., unpublished). By incorporating muscle architecture and joint mechanics in modeling sarcomere operating ranges and muscle tension throughout a series of jaw postures, we show that the relatively longer fibers in common marmoset jaw muscles facilitate increased range of motion without negatively impacting force production in a restricted subset of jaw postures (i.e. wide gapes).

In 2001, Burkholder and Lieber reviewed published sarcomere operating ranges in mammalian muscles finding that most function over a range extending from 81-107% of their optimal sarcomere length (Burkholder and Lieber, 2001). Using our maximum functional gape estimate (55 deg.) and a minimum estimate of 10 deg. (Vinyard et al., 2009) (C.J.V., unpublished data), we found comparable ranges of relative sarcomere lengths during gouging for the anterior superficial masseter (80-120%), anterior temporalis (73%-103%) and middle temporalis (71-102%) (Table 4). Focusing on jaw muscles, our marmoset values are similar to estimated sarcomere length ranges during active contraction in the masseter and temporalis of rabbits (Weijs and van der Wielen-Drent, 1983; Weijs et al., 1982) and pigs (Herring et al., 1984) during mastication (Table 4). However, cotton-top tamarin ranges for 10-55 deg. of jaw gape in the anterior superficial masseter (79-141%) and middle/anterior temporalis (85-143/145%) markedly exceed the upper end of the reported range typical of both mammalian muscles (Burkholder and Lieber, 2001) and contracting jaw muscles during mastication (Table 4). We see a reversed situation when considering the range of jaw movements typical of mastication (0-30 deg. gape) (Vinyard et al., 2009) (C.J.V., unpublished). Tamarin relative sarcomere length ranges are similar to the mammalian muscle mean and overlap considerably with masseter and temporalis ranges in pigs and rabbits (Table 4). The marmoset model, however, suggests relatively shortened lengths with the anterior and middle temporalis not reaching optimal length during the chewing cycle (Table 4).

Table 4.

Relative sarcomere length ranges in mammalian jaw muscles during various activities

Animal	Muscle	Relative sarcomere length range (%)1	Behavior
Pig2	Anterior superficial masseter	92-117	Range of active muscle
	Anterior temporalis	88-118	contraction during chewing
	Middle temporalis	93-117
Rabbit3	Superficial masseter	92-116	Range of active muscle
	Temporalis	88-110	contraction during chewing
Rat4	Anterior masseter	78-126	Range of manipulated jaw
	Temporalis	74-95	opening during experiment
Marmoset5	Anterior superficial masseter	80-120	Gouging (10-55 deg. gape)
	Anterior temporalis	73-103
	Middle temporalis	71-102
	Anterior superficial masseter	68-101	Chewing (0-30 deg. gape)6
	Anterior temporalis	66-85
	Middle temporalis	66-83
Tamarin5	Anterior superficial masseter	79-141	Wide opening (10-55 deg. gape)7
	Anterior temporalis	85-145
	Middle temporalis	85-143
	Anterior superficial masseter	63-109	Chewing (0-30 deg. gape)7
	Anterior temporalis	74-110
	Middle temporalis	74-110

¹Relative sarcomere length ranges were calculated following Burkholder and Lieber (Burkholder and Lieber, 2001).

²Data from Herring et al. (Herring et al., 1984). We used an estimated optimal sarcomere length of 2.4 μm following Herring et al. (Herring et al., 1984).

³Data from Weijs and van der Wielen-Drent (Weijs and van der Wielen-Drent, 1982; Weijs and van der Wielen-Drent, 1983). We used an optimal sarcomere length of 2.41 μm based on thin filament length estimate of 1.16 μm from rabbit psoas muscle (Ringkob et al., 2004).

⁴Data from Nordstrom et al. (Nordstrom et al., 1974). We used an estimated optimal sarcomere length of 2.4 μm following Burkholder and Lieber (Burkholder and Lieber, 2001). Range of jaw opening does not appear to have a physiological basis.

⁵Data from this study (Tables 2 and 3).

⁶Range of chewing gape taken from Vinyard et al. (Vinyard et al., 2009).

⁷Estimated gapes are taken from marmoset behaviors and do not necessarily reflect gapes routinely used by tamarins. This chewing gape range is probably a reasonable estimate for this species.

Our modeling results suggest that the derived musculoskeletal configuration of the anterior superficial masseter and temporalis in common marmosets allows these muscle regions to produce maximal tension at wide gapes during tree gouging. This functional ‘tuning’ is similar to several previous studies documenting musculoskeletal configurations that facilitate muscle function near optimal sarcomere lengths during locomotor (Lutz and Rome, 1996; Rome and Sosnicki, 1991; Rome et al., 1993) and masticatory behaviors (Herring et al., 1984). Thus, while the architectural trade-off of reduced PCSA in marmosets may have negative performance consequences for force production during mastication (and gouging at smaller jaw gapes), consideration of the more inclusive muscle—joint system suggests that biting performance during tree gouging at wide gapes is not compromised and may be relatively improved. Furthermore, circumventing this architectural trade-off may have created an anterior to posterior functional division in these jaw muscles where the anterior muscle regions function near optimal sarcomere lengths during gouging at wide gapes while the more posterior regions of these muscles produce maximal tension during mastication (see Blanksma et al., 1997; Herring et al., 1979; Taylor and Vinyard, 2008).

Jaw-muscle ‘design’ in common marmosets

The observation that the anterior regions of common marmoset jaw muscles facilitate both jaw ROM and force production at wide jaw gapes raises questions about the functional and/or evolutionary factor(s) involved in generating this derived musculoskeletal configuration. Previously, we have linked jaw-muscle architecture in marmosets to a kinematic performance involving wide jaw gapes during gouging (e.g. Taylor et al., 2009a). It remains unclear, however, whether alterations in marmoset muscle architecture and skeletal form have been driven by functional shifts related to generating relatively wide gapes and/or bites forces at wide jaw gapes. Comparisons of skull form between tree-gouging and non-gouging callitrichids provide little evidence that common marmosets are relatively better at generating or resisting bite forces (Vinyard and Ryan, 2006; Vinyard et al., 2003). Furthermore, in vivo data show that common marmosets are not utilizing maximum bite forces but are using jaw gapes approaching their structural capacity for jaw opening during gouging (Vinyard et al., 2009). Moreover, tree-gouging marmosets exhibit musculoskeletal morphologies that facilitate the production of wide jaw gapes (Taylor et al., 2009a; Taylor and Vinyard, 2004; Taylor and Vinyard, 2008; Vinyard et al., 2003). While these comparisons cannot demonstrate that marmosets have undergone selection to increase ROM, the specializations collectively support the hypothesis that marmosets possess a musculoskeletal system configured for relatively greater excursion.

The comparative evidence suggesting that marmoset masticatory form is evolved to enhance kinematic performance does not rule out an added influence of bite force at wide gapes. We need to clarify two issues to further our understanding of the functional and evolutionary factors affecting marmoset masticatory form. While force production may be straightforwardly linked to generating sufficient force to remove tree pieces during gouging, the performance benefits of wide jaw gapes are more difficult to identify. Wide gapes and the resulting increased muscle excursion and contraction velocities may (1) help align the incisal cutting edge for removing anisotropic (i.e. grained) tree pieces and reducing bending of the incisors (Ang et al., 2006; Paphangkorakit and Osborn, 2008; Sui et al., 2006), (2) reduce the energetic cost of gouging if the relative work to fracture exceeds the work to peel tree pieces, and/or (3) increase jaw-muscle power during gouging and hence benefit extraction rates (Taylor et al., 2009a).

The relative extent that muscle architecture is the result of evolutionary vs physiological (i.e. lifetime) adaptation to gouging represents an additional, largely unknown parameter hindering our understanding of marmoset craniofacial form. While comparisons of inbred mice strains demonstrate a heritable component to jaw-muscle architecture (Taylor et al., 2008), it is well known that muscle is a highly modifiable tissue with increased excursion resulting in the addition of sarcomeres to help maintain an optimal sarcomere length [i.e. maximum tension (Williams and Goldspink, 1978)]. Thus, both evolutionary and physiological mechanisms may be responsible for the observed interspecific differences in jaw-muscle architecture among callitrichids. Future experiments comparing architecture in captive gouging and non-gouging marmosets are needed to help discriminate among these potential mechanisms.

Limitations of this study and future work

We note several limitations to our study. First, we lack in vivo data to calibrate our sarcomere length—joint angle results. Nonetheless, this does not change the relative differences between species in masseter and temporalis sarcomere length ranges. The modeled data are within the physiological range of sarcomere lengths, which provides initial support to the model. The sarcomere length—passive tension relationship used in our model was obtained from a rabbit lower extremity muscle. Passive tension is likely to be variable across muscles and thus a key future experiment to calibrate the model involves measuring in situ passive length—tension and sarcomere length—joint angle relationships for the jaw-closing muscles in these species.

There are differences in the tendon to fiber length ratios in the masseter and temporalis of C. jacchus and S. oedipus (Taylor et al., 2009b). This is important because tendons represent a source of series elasticity in a muscle—tendon unit. When tendons are long relative to the length of fibers in a muscle, tendon strain allows sarcomeres to shorten during muscle force development. The tendon to fiber length ratios in the temporalis of C. jacchus and masseter in both species are small and, therefore, the effect of tendon strain on sarcomere length is considered minimal and can be ignored (Lieber et al., 1992; Zajac, 1989). However, the tendon to fiber length ratio in the S. oedipus temporalis is slightly greater (3.23±0.26). Based on the model of muscle—tendon unit series compliance presented by Lieber and colleagues (Lieber et al., 1992), this would allow sarcomeres to shorten a maximum of ~10% during maximum isometric force production. Importantly, this model assumes that the material properties of tendons are constant between muscles, which have been shown to be inaccurate (Ward et al., 2006b). In effect, this model represents a ‘worst-case’ scenario for ignoring tendon compliance. Even if true, this means that sarcomere lengths in the S. oedipus temporalis are only slightly overestimated and force production is only slightly underestimated. Because the material properties of each tendon are unknown and the effects of tendon compliance are expected to be relatively small in these muscles, we have ignored the effect of tendon strain.

Our model did not account for the effect of muscle velocity on muscle force. We estimated active force across gapes from the isometric sarcomere length—tension curve essentially modeling a portion of the gouge as isometric biting. Given that the jaw-closing muscles of marmosets are doing work and hence changing length during gouging, our tension estimates probably overestimate the actual muscle forces generated in vivo throughout the gouging cycle.

In the absence of jaw ROM data for S. oedipus, we relied on maximum functional gapes obtained in C. jacchus to model jaw ROM in both species. If tamarins maintain relatively smaller gapes during their feeding behaviors, then both taxa could potentially act on similar portions of the length—tension curve. This possibility is clearly illustrated by the similarity in relative sarcomere length ranges for jaw muscles during chewing (0-30 deg. gape) in tamarins compared with gouging (10-55 deg. gape) in marmosets (Table 4). Additional field studies of tamarins are needed to capture jaw kinematics during feeding in these primates.

Our model did not account for fiber rotation during contraction, which may influence a muscle's force production in vivo. In pinnate-fibered muscles, only the component of muscle fiber force generated parallel to the muscle's line of action will contribute to total muscle force. During contraction, muscle fibers may rotate and increase the angle of pinnation. Increasing pinnation during a contraction decreases the percentage of fiber force contributing to muscle force. Conversely, muscle fiber rotation increases total muscle excursion and can act to increase muscle velocity. Azizi and colleagues found that the amount of fiber rotation occurring in a muscle in vivo is task-dependent (Azizi et al., 2008). Thus, when a muscle contracted against a small load, muscle thickness and pinnation angle increased as the muscle fibers rotated and facilitated increased muscle velocity. With large loads, the muscle decreased in thickness and less fiber rotation occurred, which provided relatively greater force as fibers showed smaller increases in pinnation during contraction. These dynamic changes in fiber pinnation present another trade-off in muscle performance that may influence gouging abilities, and should be considered in future attempts to model muscle mechanics during gouging.

We used a quadratic polynomial to fit joint angle—excursion data throughout the ROM. R² values between these dimensions were high in most muscle regions (0.96-0.99); however, the posterior superficial masseter was an exception. This muscle region experiences an increase in length initially (~0-15 deg.) but does not change length at larger joint angles because the muscle line of action is passing close to the joint center of rotation. Traditional polynomial curve-fitting techniques (e.g. least-squares regression) provide a poor approximation of these data. In fact, the quadratic fit suggests that excursion decreases at joint angles close to maximum gape, which is clearly at odds with the raw excursion data. Although this error probably has a negligible effect on our total muscle force estimates, this issue should be considered when interpreting the behavior of the posterior superficial masseter at large jaw gapes in our model.

Finally, it remains unclear whether the musculoskeletal differences between C. jacchus and S. oedipus are related to evolutionary adaptations and/or phenotypic plasticity related to the mechanical demands of tree gouging. The data presented in this paper are insufficient to directly answer this question despite demonstrating the functional consequences of these musculosketal differences for tree gouging across a range of jaw gapes. That said, we can note evidence in support of a heritable component to maximum jaw gape (Taylor et al., 2008; Vinyard and Payseur, 2008).

In summary, our modeled sarcomere length operating ranges and relative tension—joint angle data demonstrate that tree-gouging common marmosets are able to generate relatively greater tension in the anterior superficial masseter as well as anterior and middle temporalis muscles at jaw gapes that are consistent with the maximum gapes they generate in the wild during this feeding behavior. Although a theoretical trade-off between the force-generating capacity of a muscle and a muscle's excursion and contraction velocity is often acknowledged, this study provides a useful example of a masticatory musculoskeletal system that may be ‘designed’ to generate relatively large bite forces at wide maximum jaw gapes. It seems likely that other animals that routinely use wide jaw gapes during ingestive behaviors may have similar musculoskeletal configurations to facilitate force production at these large excursions.

ABBREVIATIONS

ASM

anterior superficial masseter

AT

anterior temporalis

DM

deep masseter

L

muscle—tendon excursion

L_f

normalized muscle fiber length

L_f′

measured muscle fiber length

L_m

muscle length

L_s

sarcomere length

L_s′

measured sarcomere length

L_T

total tendon length

L—T curve

length—tension curve

M

mass

MT

middle temporalis

PCSA

physiological cross-sectional area

PSM

posterior superficial masseter

PT

posterior temporalis

r

radius of the arc

ROM

range of motion

S_n

sarcomere number

ρ

density

Φ

joint angular rotation

θ

pennation angle