PARAMO: A Parallel Predictive Modeling Platform for Healthcare Analytic Research using Electronic Health Records

Abstract

Objective

Healthcare analytics research increasingly involves the construction of predictive models for disease targets across varying patient cohorts using electronic health records (EHRs). To facilitate this process, it is critical to support a pipeline of tasks: 1) cohort construction, 2) feature construction, 3) cross-validation, 4) feature selection, and 5) classification. To develop an appropriate model, it is necessary to compare and refine models derived from a diversity of cohorts, patient-specific features, and statistical frameworks. The goal of this work is to develop and evaluate a predictive modeling platform that can be used to simplify and expedite this process for health data.

Methods

To support this goal, we developed a PARAllel predictive MOdeling (PARAMO) platform which 1) constructs a dependency graph of tasks from specifications of predictive modeling pipelines, 2) schedules the tasks in a topological ordering of the graph, and 3) executes those tasks in parallel. We implemented this platform using Map-Reduce to enable independent tasks to run in parallel in a cluster computing environment. Different task scheduling preferences are also supported.

Results

We assess the performance of PARAMO on various workloads using three datasets derived from the EHR systems in place at Geisinger Health System and Vanderbilt University Medical Center and an anonymous longitudinal claims database. We demonstrate significant gains in computational efficiency against a standard approach. In particular, PARAMO can build 800 different models on a 300,000 patient data set in 3 hours in parallel compared to 9 days if running sequentially.

Conclusion

This work demonstrates that an efficient parallel predictive modeling platform can be developed for EHR data. This platform can facilitate large-scale modeling endeavors and speed-up the research workflow and reuse of health information. This platform is only a first step and provides the foundation for our ultimate goal of building analytic pipelines that are specialized for health data researchers.

1 Introduction

Predictive modeling is one of the most important methodologies used in clinical and healthcare research. According to PubMed (1), since 2005, over 22,000 papers have been published which include the phrase “predictive model”. The publication rate of these papers has increased every year, from 1,782 in 2005 to 3,748 in 2012.

One application of predictive modeling is to accurately derive insights from diverse sets of longitudinal patient data in a manner that can influence disease progression by recommending actions that can effectively change the clinical pathway of the patient for a more optimal outcome.(2) For example, chronic diseases emerge over time, mediated by early physiologic and pathological changes which can be measured using overt or surrogate indicators. The primary goal of predictive modeling in this context is to move detection of the disease from a frank disease state to a pre-clinical disease and to quantify the expected risk and time span of disease onset. Population-level data can be mined to detect robust signals before an event or to influence the course of events (e.g., optimizing choice of treatment) (3). The time scale for prediction depends on the clinical context. For example, effective use of a signal of future risk of chronic progressive diseases like heart failure would likely require detection one to two years before the usual diagnosis for early treatment to influence disease progression. In contrast, the time scale for predicting 30-day readmission risk is days to weeks. Quantitative signals of this type have many potential applications during routine encounters or for population level screening or management as shown in Table 1.

Table 1.

Examples of applications of predictive modeling on EHR data.

Examples	Time Scale	Value of Predictive Model	Who Benefits?
Risk of Chronic Progressive disease	12-36 months	Slowing progression, preventing onset	Patient and payer
Risk of disease progression	12-60 months	Slowing progression, preventing rapid decline	Patient and payer
Optimizing choice of interventions and treatments	Variable	Improve chance for more optimal outcome	Patient and others
Time to inpatient discharge	Days	Improve discharge preparation, reduce readmission	Hospital, payer, and patient
Risk of 30-day readmission	Days to weeks	Reduce risk of readmission	Hospital, payer, and patient
Identifying future costly patients	12-36 months	Prevention and case management to reduce cost of care	Payer and patient

Beyond early detection of disease, predictive modeling can also facilitate greater individualization of care. Predictive models can enable clinicians to distinguish between individuals who will benefit from a specific therapeutic intervention from those that will not (3,4). For example, it is known that obesity, with or without the metabolic syndrome, increases an individual's risk for developing diabetes (5), yet the majority of these individuals do not develop diabetes. The ability to refine the predictive ability for developing diabetes would allow for therapies to be better targeted to the individuals more likely to benefit. Indeed, as our understanding of genomic information increases, the combination of genomic, environmental, and clinical variables in predictive modeling will likely be critical for the individualization of care in a broad array of disease processes (6).

The increasing adoption of electronic health record (EHR) systems introduces new challenges and opportunities in the development of predictive models for several reasons. First, EHR data is collected over time on patients in a healthcare system and is becoming part of the “big data” revolution (7). EHRs are increasingly documenting a large quantity of information on a broad patient population, which varies in completeness, certainty, and detail per patient(8). Second, EHR data is often generated to support clinical operations or healthcare business processes (e.g., billing) and is not necessarily curated for biomedical research (8,9). As a consequence, researchers may need to spend significant effort to prepare EHR data for predictive modeling (10). In particular, the independent and dependent variables need to be constructed and selected carefully. Third, EHRs contain heterogeneous data such as diagnoses, medications, lab results, and clinical notes. Such data heterogeneity requires diverse modeling techniques and offers many options for their combination. The descriptive and temporal differences among patients may also be useful predictors and need to be considered.

Despite the challenges associated with the use of EHRs for research purposes, there is growing evidence that clinical phenotypes fit for scientific investigations can be extracted from EHR data. For instance, certain phenotypes, such as smoking status, can be precisely discovered through International Classification of Disease Version 9 (ICD-9) codes, with recall improved through natural language processing of text in the EHR (11,12). Other phenotypes, however, require more complex multi-modal methodologies, which incorporate laboratory reports, medication lists, and clinical narratives (e.g., cataracts (13), type 2 diabetes (14), and rheumatoid arthritis (15)).

Predictive models have been developed based on EHR data and applied successfully to a wide variety of targets including heart failure (16–19), chronic obstructive pulmonary disease (20), bipolar disorder (21), cancer (22), life expectancy and physiology status (23,24), kidney disease (25), and HIV (26).

Although the specific targets, data sets, and final models differ in each of the aforementioned studies, the predictive models are built using approaches that can be represented by a generalized predictive modeling pipeline. This pipeline is depicted in Figure 1A and has five core processing tasks:

• Cohort construction: Create a patient cohort consisting of a set of patients with the specified target condition and a corresponding set of control patients without the condition.

• Feature construction (or feature extraction): Compute a feature vector representation for each patient based on the patient's EHR data.

• Cross-validation: Partition the data into complementary subsets for use in model training and validation testing.

• Feature selection: Rank the input features and select a subset of relevant features for use in the model.

• Classification: The training and evaluation of a model for a specific classifier.

Figure 1.

A) A single predictive modeling pipeline consisting of the following computational tasks: cohort construction, feature construction, cross-validation, feature selection, and classification. The healthcare domain specific information would typically reside in the cohort construction and the feature construction components. B) The set of predictive modeling pipelines needed to evaluate two different feature selection approaches (e.g., Information Gain and Fisher Score) and three different classification algorithms (e.g., Naïve Bayes, Logistic Regression, and Random Forest) using 2-fold cross-validation on one patient data set using four different types of input features (e.g., Medication, Symptom, Lab, and Diagnosis). C) The dependency graph generated for the set of pipelines shown in Figure 1B.

To develop an accurate and useful predictive model, a researcher generally needs to build and compare many different models as part of the discovery workflow. Each model can be viewed as an instance of the modeling pipeline and consists of a unique combination of the data, algorithms, and/or certain parameter configurations in the task components.

A number of factors combine to increase the number of models that need to be explored, resulting in a large set of pipelines that have to be processed. First, the volume, variability, and heterogeneity of EHR data require significant processing in building predictive models (10). Second, there is uncertainty in knowing a priori which feature construction, feature selection, and classification algorithms are most appropriate for the specific target application (27). As such, composition of an appropriate predictive model requires exploring a potentially large space of possible algorithms and parameters and their combinations. Third, for some biomedical applications, the ability to interpret how the model works is just as, if not more, important than the accuracy of the model. Here, it is important to explore a variety of classification algorithms (e.g., decision trees, Bayesian networks, and generalized regression models) that produce trained models which can be interpreted by domain experts to verify and validate that the model is clinically meaningful (28). It is likely that multiple models can have similar performance in terms of prediction accuracy, but may differ significantly in their internal model parameters. By building multiple models, it becomes possible to select ones that have more clinically meaningful interpretations. Fourth, it is critical to statistically validate the models to ensure generalizability and accuracy. Cross-validation techniques can help with this endeavor, but can dramatically increase the number of models that need to be built and evaluated.

As a result, there is an important need for a platform that can be used by clinical researchers to quickly build and compare a large number of different predictive models on EHR data.

In this paper, we describe a scalable predictive analytics platform that can be used for many different predictive model building applications in the healthcare analytics domain. Specifically, we propose a PARAllel predictive MOdeling (PARAMO) platform that implements the generalized predictive modeling pipeline described above. PARAMO takes a high level specification of a set of predictive modeling pipelines, automatically creates an efficient dependency graph of tasks in all pipelines, schedules the tasks based on a topological ordering of the dependency graph, and executes the independent tasks in parallel as Map-Reduce (29) jobs. It is important to note that this platform is only a first step towards our ultimate goal of building analytic pipelines that are specialized for health data researchers. The platform provides the foundation on which we can build specialized functional layers that can facilitate specific biomedical research workflows, such as refinement of hypotheses or data semantics.

We demonstrate the generality and scalability of PARAMO by testing the platform using three real EHR data sets from different healthcare systems with varying types of data and detail ranging from 5000 to 300,000 patients. We build predictive models for three different targets: 1) heart failure onset, 2) hypertension control, and 3) hypertension onset. It is important to note that the scope and purpose of these experiments is to analyze the computational performance of the platform and not to perform discovery-based research. As such, we focus on the scalability of PARAMO, as opposed to the specific accuracy of the predictive models. As expected, PARAMO achieves significant speedups. Thanks to the parallel model building capability, PARAMO can, for instance, complete 800 model building pipelines on a 300,000 patient data set in 3 hours, while the same job takes over 9 days running sequentially. The reduction in processing time allows a larger number of hypotheses to be evaluated in the same amount of time which can lead to more accurate predictive models.

2 Background

Scientific workflows are used to describe multi-step computational tasks. They capture the tasks to run, the dependencies between the tasks, and the data flow among the tasks. A number of traditional scientific workflow systems such as Kepler (30), WINGS (31), Pegasus (32), and Taverna (33) have been developed for a variety of applications. More recently, a number of Map-Reduce workflow systems such as Kepler+Hadoop (34), MRGIS (35), and Oozie (36) have also been developed. However, these workflow systems are not ideal for use in the healthcare analytics domain for several reasons. First, some of these systems are specialized for different domains and the built-in assumptions and semantics around data partitioning and domain specific processing would be difficult to adapt to healthcare analytics. Second, other systems provide only low-level programming tools and APIs that are not well-suited for researchers who are not parallel programming experts. Although the general workflow systems do provide tools and support for creating workflows, the composition of the workflow is still left to the user who must either assemble the workflow manually or select and customize one from an existing inventory of workflow templates.

In the healthcare analytics domain, and especially in predictive modeling, it is common to build, evaluate, and compare many models with varying cohorts, features, algorithms, and parameters. This typically results in very large and complex workflow graphs containing thousands of nodes that would be very difficult to construct manually or to encapsulate in a set of templates. It would be more convenient to allow the user to specify a small number of high-level parameters that describe the desired set of modeling pipelines and have the system automatically generate a complete and optimized workflow graph. PARAMO is designed to fill this functionality gap. It supports Map-Reduce for efficient parallel task execution and accepts different task scheduling preferences. In addition, PARAMO includes several healthcare domain specific processing tasks such as patient cohort construction and feature vector construction that incorporate biomedical vocabularies, such as ICD (International Classification of Diseases), CPT (Current Procedural Terminology), and UMLS (Unified Medical Language System), and constraints on the data permitted, such as prediction and observation windows (37).

3 Methods

As shown in the high-level architecture diagram in Figure 2, PARAMO consists of three major components: 1) a dependency graph generator, 2) a dependency graph execution engine, and 3) a parallelization infrastructure.

Figure 2.

High level architecture of the Parallel Predictive Modeling Platform (PARAMO).

3.1 Dependency Graph Generator

The dependency graph generator facilitates the translation of a set of predictive modeling pipelines into an efficient computational workflow. It frees the user from having to 1) manually identify redundant tasks, 2) specify the dependency relationships between the tasks, and 3) partition the tasks into independent groups that can be run in parallel.

The dependency graph generator takes as input a set of pipeline specifications and automatically generates a dependency graph that efficiently implements those pipelines. The graph is a directed acyclic graph (DAG) where the nodes represent the tasks and the edges represent the dependencies between the tasks. Redundant tasks in the pipelines are collapsed into a single task that is computed once but whose output is shared by multiple tasks later in the pipeline. Dependencies between the tasks are identified and used to create the edges connecting the tasks. Tasks that can be executed in parallel are reflected in the topology of the graph. Associated with each node is the entire configuration needed for the task to be executed.

The dependency graph generator can handle a wide variety of pipeline specifications. For each pipeline task, the user can specify the methods and parameters to be used. Each task has a prebuilt set of methods but custom methods can be added.

In the cohort construction processing, predefined patient cohorts can be selected for use or new patient cohorts can be defined. The creation of a new patient cohort requires the specification of a list of patients and the following information for each patient: a unique identifier for each patient, the diagnosis date of the condition, and the target condition label (e.g., 1 for case and 0 for control). The process of identifying the case and control patients is application dependent and is outside the scope of the pipeline node. However, once the patients are identified, the cohort construction task can be used to create a new patient cohort for subsequent use in the pipelines.

The feature construction task computes a feature vector representation for each patient based on the patient's EHR data. EHR data can be viewed as multiple event sequences over time (e.g., a patient can have multiple diagnoses of hypertension at different dates). To convert such event sequences into feature variables, an observation window (e.g., one year) is specified. Then all events of the same feature within the window are aggregated into a single or small set of values. The aggregation function can produce simple feature values like counts and averages or complex feature values that take into account temporal information (e.g., trend and temporal variation). A set of basic aggregation functions (e.g., count, minimum, maximum, mean, and variance) is provided, but additional user-defined aggregation functions can be added as necessary.

In the feature selection task, a number of standard selection algorithms (e.g., information gain, Fisher score, least angle regression (LARS)) (38–40) are available, but we have also added custom algorithms such as scalable orthogonal regression (SOR) feature selection for optimally combining knowledge-based and data-driven features (41).

In the classification task, all the classifiers in the open source machine learning packages Orange (42) and SciKit-Learn (43) are available, but custom classification algorithms can also be added.

We anticipate that the majority of PARAMO users will work with the predefined configuration APIs or the web interface to specify the pipeline using the standard predefined components and algorithms. Expert users, however, can use our extension framework to programmatically add new components and algorithms.

The following is a simple pipeline specification example:

• Cohort construction: One patient data set (the Medium data set defined in section 4.1).

• Feature construction: Four types of features: diagnoses, labs, medications, and symptoms. “Mean” aggregation is used for labs and “count” for the others.

• Cross-validation: 2-fold cross-validation.

• Feature selection: Two approaches: Information Gain and Fisher Score (38,39).

• Classification: Three classifiers: Naïve Bayes, Logistic Regression, and Random Forest (38,44).

This specification results in a set of 12 pipelines, as shown in Figure 1B. The corresponding dependency graph that is generated is shown in Figure 1C. Since the feature construction task processes different feature types independently of each other, they can be run in parallel and the results merged for subsequent use. The cross-validation task partitions the data into multiple subsets. For each subset, the different feature selection and classification algorithms can be run independently and in parallel as illustrated in the dependency graph. The output tasks are used to clean up intermediate files and to put results into their final locations.

3.2 Dependency Graph Execution Engine

As shown in Figure 2, the dependency graph execution engine takes a dependency graph as input. It parses the graph, assigns priorities to the tasks, schedules the tasks based on a topological ordering of the graph, and executes the independent tasks in parallel to produce the final set of the results. The execution engine uses a list scheduling approach (45). It maintains a producer-consumer priority queue of tasks that are awaiting execution. A task in the dependency graph is added to the priority queue only if it is “ready” to be executed. A task is “ready” if it either has no dependencies or all its dependencies have already completed execution. The priority of the tasks in the queue is updated based on user preference and on the results of already completed tasks. As task execution slots become available, the highest priority tasks are removed from the queue and submitted to the parallelization infrastructure for execution. The execution engine continues processing until all tasks in the dependency graph have been executed.

Figure 3 shows an analysis of the execution of the dependency graph from Figure 1C on a Map-Reduce cluster with 20 concurrent tasks. The analysis shows the start time, end time, and duration of each task. The execution of dependent and parallel tasks is clearly visible. The cohort construction task is executed first, followed by the parallel execution of the four different feature construction tasks, and then the feature construction merge task. The processing time of the feature construction tasks can vary dramatically depending on the feature type. We observe that the cross-validation task is executed in parallel at this stage, which creates two sets of training and testing partitions of patients (i.e., 4 out-going edges). Next, the four feature selection tasks are run in parallel and, finally, the twelve classifier tasks are run in parallel. The classifier processing times can be very different depending on the classification algorithm. The time gaps between task executions are due to overhead in the Map-Reduce tasks management processing.

Figure 3.

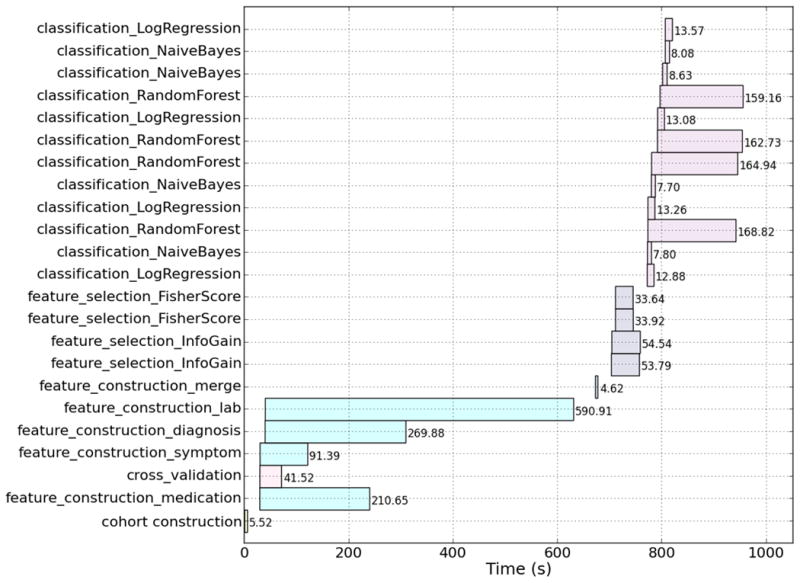
Dependency graph execution analysis showing the start time, end time, and duration of each task in the dependency graph from Figure 1C. The graph was executed on a Map-Reduce cluster with 20 concurrent tasks.

PARAMO supports different scheduling preferences that allow a researcher to influence the order in which the models are built. Flexible scheduling can be useful when there are many models and the processing times are lengthy or when the analytics are conducted in a time-constrained environment such as in a consulting engagement. Three different scheduling algorithms have been implemented: 1) uniform, 2) fast model first and 3) accurate model first. In the uniform approach, the priority of all tasks is the same. This causes the tasks to be executed solely based on the topological ordering of the dependency graph. In the fast model first approach, the priorities of the feature selection and classifier tasks are based on the average execution time of previously completed tasks of the same type. This causes models that run faster to be executed before models that take more time. In the accurate model first approach, the priority of the classifier tasks are based on the average accuracy measure of previously completed classifier tasks of the same type. The priority of the feature selection tasks is set to the highest priority of its dependent classifier tasks. This causes models that have higher accuracy to be executed before models that perform worse. The priorities of the tasks waiting in the execution queue are continually updated using information from recently completed tasks. If the researcher is evaluating a set of models where the accuracy can be vastly different, he could use the accurate models first priority to quickly get a sense of the models that work well. However, if he is refining a set of models that have similar accuracy, he could use the fast models first priority so more models are built sooner in the processing. The researcher can examine the models that have completed so far to decide whether to stop the processing to save unneeded computation without having to wait for everything to finish. We note that although PARAMO enables these workflows, it does not specify (at this time) which is the best. This is left for future research because it will need to be specialized to specific healthcare analytics problems.

A number of task schedulers have been developed for the Map-Reduce framework including performance-driven schedulers that dynamically adjust resource allocation to maximize each job's chance of meeting its runtime performance goal (46), network-aware schedulers that try to reduce network traffic by enforcing local computations (47), and resource-aware schedulers that try to improve resource utilization across machines (48). The scheduler in PARAMO differs from these in that the prioritization scheme is based on higher level application-specific objective functions that can be specified by the user instead of lower level infrastructure and application independent metrics.

3.3 Parallelization Infrastructure

Healthcare organizations have a wide range of computing architectures and capabilities. As such, PARAMO allows for execution of the dependency graph tasks on a number of different parallel systems, ranging from a single machine running a multiple worker process pool to a large compute cluster. A variety of tools may be used for parallelization on large compute clusters. Open-source tools such as Apache Hadoop's Map-Reduce (49) afford graceful handling of large data sets and built-in resilience against failures. The Hadoop API, however, is too low-level and ill-suited for implementing analytics tasks. High-level programming tools built on top of Hadoop such as Cascading (50) and NIMBLE (51) allow the programmer to specify parallel computations. Cascading supports setting up a DAG of Map-Reduce jobs but is not suited to specifying task parallelism, as is needed in our case. NIMBLE is a tool for data analytics algorithms with support for specifying data parallelism, task parallelism, and DAGs of computations, all at a higher level of abstraction than Map-Reduce. In this paper, we use NIMBLE to execute our dependency graph using task parallelism on top of Hadoop.

4 Results and Discussion

4.1 Experimental Setup

We stress tested the computational performance of PARAMO using three sets of real EHR data ranging in scale from 5000 to over 300,000 patients as described in Table 2.

Table 2.

Description of the three EHR data sets used to evaluate the performance of PARAMO. For each data set, the origin, the number of years of data, the unique number of patients, the unique number of features, and the total number of records (feature instances) are shown.

Data Set	Origin	Years of Data	Number of Patients	Number of Features	Number of Records
Small	Vanderbilt University Medical Center	3	4,758	25,932	3,312,558
Medium	Geisinger Health System	10	32,675	46,117	24,719,809
Large	Anonymous longitudinal claims database	4	319,650	49,269	33,531,311

The Small dataset was collected from the Vanderbilt University Medical Center (VUMC) de-identified EHR repository, Synthetic Derivative, which is a completely de-identified, randomly date-shifted version of the electronic health record (52). All dates are changed by a random offset per patient. At the time of this study, the MyHealthTeam (MHT) cohort consisted of 1,564 hypertension patients enrolled between 2010 and 2012 who had at least one transition point while in the program. A transition point is defined as a time point at which the clinical blood pressure assessment changes from in-control to out-of-control or vice versa. The data analyzed included MHT program-specific measures, such as control status and home blood pressures, and was supplemented by all longitudinal clinical information available in the EHR. Each patient received an average of 5 hypertension physician assessments across 158 days while in the MHT program. The 1,564 patient cohort contains 615 cases (blood pressure out of control) and 949 controls (blood pressure in control). This data set is used to predict the transition points at which hypertension is brought into, as well as pushed out of, control among those patients.

The Medium dataset comes from a case-control design study utilizing a retrospectively identified cohort of primary care patients who eventually developed heart failure (HF) and controls who did not (53). Patient EHRs dating from 2001 to 2010 within the Geisinger Health System were utilized to identify cases and controls. The Geisinger Health System is an integrated health care system that provides health services in 31 counties of central and northeastern Pennsylvania and includes 41 community practice clinics which has been utilizing the EPIC EHR since 2001. Data for this study were derived from the approximately 400,000 primary care patients served by these clinics. From these EHRs, we identified 4,644 incident HF cases with a clinical diagnosis based on meeting at least one of the following criteria: 1) HF diagnosis appearing on the problem list at least once; 2) HF diagnosis appeared in the EHR for two outpatient encounters; 3) at least two medications prescribed with the ordering provider associating that medication order with an ICD-9 diagnosis of HF; or 4) HF diagnosis appearing on one or more outpatient encounters and at least one medication prescribed with an associated ICD-9 diagnosis for HF. The diagnosis date was defined as the first appearance of a HF diagnosis in the EHR. Approximately 10 eligible clinic-, sex-, and age-matched (in five-year age intervals) controls were selected for each incident HF case. Primary care patients were eligible as controls if they had no history of HF diagnosis before December 31, 2010. Control patients were required to have had their first Geisinger Clinic office encounter within one year of the incident HF case's first office visit and had at least one office encounter 30 days before or anytime after the case's HF diagnosis date in order to ensure similar durations of observations among cases and controls. In situations where 10 matches were not available, all available matches were selected (28,031 eligible controls retained). Therefore, for the purposes of this study we extracted the clinical notes portion of the EHRs for 32,675 patients. All patient encounters preceding the diagnosis of HF in cases, and the matched date in controls were analyzed. This data set is used to predict the onset of HF 6 to 24 months prior to their clinical diagnosis.

The Large dataset comes from an anonymous longitudinal claims database and consists of 319,000 patients over 4 years. This data set used a similar study design as the Medium dataset but for hypertension disease instead of heart failure. The resulting patient cohort consists of 181,128 patients for hypertension diagnosis prediction with 16,385 cases and 164,743 controls. In particular, the cases are the patients who had (incident) hypertension diagnosis in the last 2 years of the data (not in the first 2 years); controls are group matched to the cases on age and gender but without hypertension diagnosis in all 4 years. The EHR data from first 2 years of the cases and controls are used in the predictive modeling. This data set is used to predict the onset of hypertension diagnosis.

All three data sets contain diagnoses, medications, and lab results. The Small and Large sets also contain procedure information while the Medium set contains HF symptoms extracted from clinical notes (54). Although these patient data sets have been created for use in clinical application studies, they are used in these experiments only as representatives of predictive modeling applications using real EHR data at different scales.

For our parallelization infrastructure, we use a Hadoop cluster with 160 Intel Xeon 2.13GzH processors distributed across 40 nodes with 4 GB of RAM per processor that can support running up to 160 concurrent tasks. All the nodes run Linux (kernel 2.6.18-164.el5) with IBM Java v1.7.0 and Hadoop v1.0.4.

To measure runtime performance we used elapsed time in seconds and for classifier accuracy we used the AUC (area under the ROC curve) measure.

4.2 Parallel Execution Experiments

Identical predictive modeling pipeline structures were created for all three data sets consisting of the following components:

• One patient data set: Small, Medium, or Large.

• A fixed set of input feature types: diagnoses, medications, labs, procedures, and symptoms with a mean aggregation function for the labs feature and a count aggregation function for the other features.

• Two feature selection approaches: Information Gain and Fisher Score.

• Four classification algorithms: K-Nearest Neighbor, Naïve Bayes, Logistic Regression, and Random Forest.

• 10 times 10-fold cross-validation.

The only differences in the pipeline specifications for the different data sets are in the parameter values of the cohort construction tasks, the feature construction tasks, and the feature selection tasks. An initial set of experiments, described in Appendix A, was used to determine the number of features and observation window size parameter values to use.

The dependency graph generated using this set of pipeline specifications contains 1,808 nodes and 3,610 edges. There were 200 feature selection tasks and 800 classification tasks. The graph structure is similar to the 36-node 42-edge graph shown in Figure 1C, but with many more feature selection and classification task nodes and edges.

The dependency graph execution engine was used to run the dependency graph for each data set on our Hadoop cluster. Figure 4 shows the runtime performance as the number of concurrent tasks varies from 10 to 160. The time to run the tasks serially is also plotted as a reference point. There are three graphs, one for each data set: Small (dotted line), Medium (dashed line), and Large (solid line). There are several noteworthy observations. First, as expected, processing larger data sets requires more time using the same number of concurrent tasks. Second, the processing time decreases as the number of concurrent tasks increases. The larger the data set, the larger the performance improvement. Comparing the serial and 160 concurrent task performance, the improvement is 1.6x for the Small data set, 39x for the Medium data set, and 72x for the Large data set. Third, for these dependency graphs, diminishing returns appear after 80 concurrent tasks. There is a minimum runtime for the dependency graph regardless of the number of concurrent tasks, which corresponds to the sum of the runtimes of the tasks in the “longest” single path through the graph. Fourth, for small data sets where the individual task executions take little time, it is possible for the overhead of managing the Map-Reduce tasks to be more expensive than the tasks themselves. For the Small data set, running with 40 or fewer concurrent tasks actually takes more time than serial execution.

Figure 4.

Runtime performance (in seconds) on the three different EHR data sets as a function of the number of concurrent tasks on the Map-Reduce cluster. The time to run all the tasks in the dependency graph serially is shown as a reference as the leftmost point.

Table 3 shows the average runtime of the different pipeline tasks. The feature construction and classification tasks take much more time than other tasks. In general, the same task takes longer to run when processing a larger data set. There is a notable exception for the feature construction processing on the Medium data set, which takes more time than the Large data set. This is due to the fact that although the Medium data set has fewer unique patients than the Large data set, it has many more years of data for each patient. This causes the data selection and extraction processing to be more expensive. There can be large differences in the runtimes of the various feature selection and classification algorithms both within and across data sets.

Table 3.

Average runtime (in seconds) of the different predictive modeling pipeline task types for the three different EHR data sets.

Task Type	Runtime (seconds)
	Small	Medium	Large
Cohort Construction	6.14	6.53	9.32
Feature Construction (Diagnosis)	15.77	275.05	266.64
Feature Construction (Lab)	27.94	551.49	104.29
Feature Construction (Medication)	26.43	203.75	131.47
Feature Construction (Procedure)	13.93	--	199.25
Feature Construction (Symptoms)	--	88.33	--
Feature Construction (Merge)	1.32	12.16	16.28
Cross-validation	7.00	42.37	248.41
Feature Selection (Fisher Score)	5.47	65.87	72.64
Feature Selection (Information Gain)	8.50	103.95	370.83
Classification (K-Nearest Neighbor)	0.16	64.02	1651.12
Classification (Naïve Bayes)	0.20	7.74	34.25
Classification (Logistic Regression)	0.18	24.56	342.65
Classification (Random Forest)	1.21	190.66	1649.13

Table 4 shows the AUC values for the various feature selection and classification combinations in the predictive modeling pipelines for the three different data sets. The average and standard deviation of the AUC computed across 100 classification runs (10×10-fold cross-validation) are shown. The highest average AUC value for each data set is bolded. There is considerable variability in the accuracy of the classifiers. Across the three data sets, the k-nearest neighbor classifier performs the worse, followed by the Naïve Bayesian classifier. The logistic regression and random forest classifiers are the top performers and have similar performance. The difference between the two feature selection algorithms is much smaller. Across the data sets, the information gain criterion has slightly better performance than the Fisher score criterion. Although the specific accuracy of the predictive models is not the focus of our experiments, the AUC values are reported for completeness. They are also used as in the priority scheduling process.

Table 4.

Average AUC (area under the ROC curve) performance measures for the various feature selection and classifier combinations in the predictive modeling pipelines for the three different EHR data sets. The average and standard deviation is computed over 100 classifier runs (10 × 10-fold cross-validation).

Data Set	Feature Selection	Classification	Average AUC (std)
Small	Information Gain	K-Nearest Neighbor	0.680 (0.075)
		Naïve Bayesian	0.687 (0.042)
		Logistic Regression	0.690 (0.044)
		Random Forest	0.717 (0.045)
	Fisher Score	K-Nearest Neighbor	0.655 (0.102)
		Naïve Bayesian	0.690 (0.042)
		Logistic Regression	0.689 (0.046)
		Random Forest	0.713 (0.043)
Medium	Information Gain	K-Nearest Neighbor	0.598 (0.013)
		Naïve Bayesian	0.692 (0.013)
		Logistic Regression	0.746 (0.012)
		Random Forest	0.752 (0.012)
	Fisher Score	K-Nearest Neighbor	0.616 (0.013)
		Naïve Bayesian	0.688 (0.014)
		Logistic Regression	0.741 (0.012)
		Random Forest	0.749 (0.012)
Large	Information Gain	K-Nearest Neighbor	0.602 (0.027)
		Naïve Bayesian	0.634 (0.007)
		Logistic Regression	0.706 (0.006)
		Random Forest	0.705 (0.006)
	Fisher Score	K-Nearest Neighbor	0.597 (0.023)
		Naïve Bayesian	0.632 (0.007)
		Logistic Regression	0.705 (0.006)
		Random Forest	0.704 (0.006)

4.3 Priority Scheduling Experiments

To evaluate the behavior of the different priority scheduling algorithms, we ran the dependency graphs using the uniform, fast model first and accurate model first settings. Figure 5 plots the number of completed classifier tasks as a function of runtime for the three different priority scheduling approaches for the Medium data set. Before 1000 seconds, most of the computation is spent on tasks before classification, such as feature construction and feature selection. Compared to the uniform scheduling (solid line), the fast model first scheduling (dashed line) results in more classifier tasks being completed earlier in the processing. For example, at 1500 seconds, 362 classifier tasks have completed compared to 237. This is clearly due to the scheduling algorithm prioritizing the faster running classifier tasks. On the other hand, using the accurate model first scheduling (dotted line) results in many fewer classifier tasks being completed at any given point in time. For example, at 1500 seconds, only 119 classifier tasks have completed. This is because the high accuracy classifiers, such as the random forest, generally take more processing time as we saw in Table 3.

Figure 5.

The number of completed classifier tasks as a function of runtime (in seconds) for the three different priority scheduling approaches (fast model first, uniform, and accurate model first) for the Medium data set. The dependency graph was run on a Map-Reduce cluster with 80 concurrent tasks.

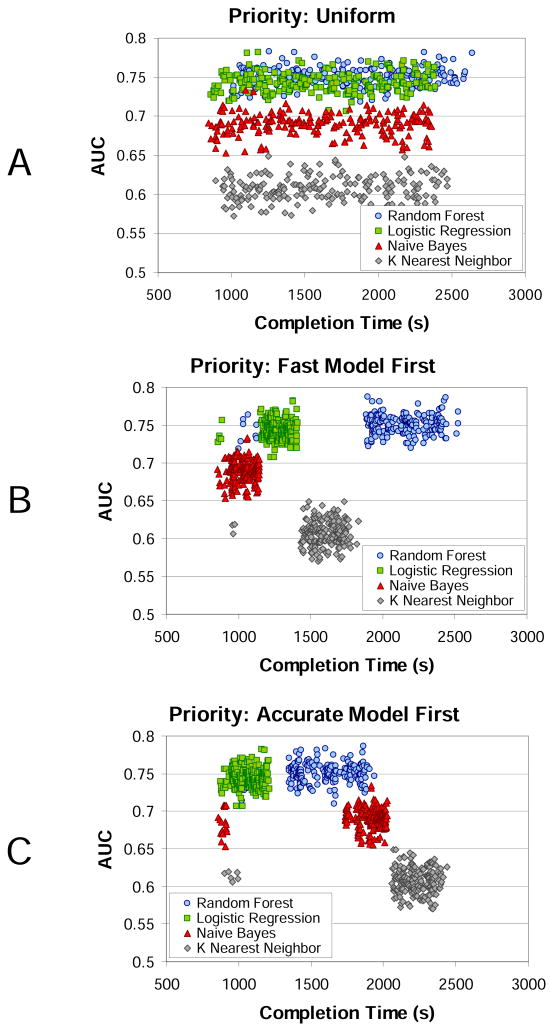
Figure 6 shows scatter plots of the AUC value for each classifier as a function of completion time for the three different priority scheduling approaches for the Medium data set. As expected, the AUC values for the uniform scheduling (Figure 6A) are evenly distributed over time since there is no preference imposed on which classifiers to execute first. The AUC values for the fast model first scheduling (Figure 6B) show a clear clustering behavior. The classifier executions are ordered by ascending runtime: naïve Bayes, logistic regression, k-nearest neighbor, and random forest with average runtimes (in seconds) of 7.74, 24.56, 64.02, and 190.66 respectively. The AUC values for the accurate model first scheduling (Figure 6C) show a different clustering behavior. In this case, the classifier executions are ordered by descending AUC value: logistic regression, random forest, naïve Bayes, and k-nearest neighbor with average AUCs of 0.74, 0.75, 0.69, and 0.61 respectively. Note that for scheduling, it is the relative values of the AUC that are important, not the absolute values. Also, since the priority is based on the average AUC value of already completed classifiers, it is possible (due to score variability) for the execution order of classifiers that have similar AUC values to be swapped (as we see here with the logistic regression and random forest classifiers). Finally, when the classifiers are initially executed (around 1000 seconds), several instances of all classifier types are run. This is because, at this time, no runtime or AUC estimates are available for changing the priorities from the default topological ordering.

Figure 6.

Scatter plot of the AUC values for each classifier model (random forest, logistic regression, naive Bayes, k-nearest neighbor) as a function of completion time (in seconds) for the three different prioritization schemes: A) uniform, B) fast model first, and C) accurate model first for the Medium data set. The dependency graph was run on a Map-Reduce cluster with 80 concurrent tasks.

5 Conclusion

Various initiatives, such as meaningful use in the United States (55), are accelerating the adoption of EHRs and the volume and detail of patient information is growing at a frenetic pace. As the healthcare community looks to develop novel therapies and personalized clinical decision support, predictive modeling over data derived from EHRs will continue to become more prevalent. To accelerate the translation of predictive analytics for use in clinical care, the healthcare community needs more efficient means of developing, building, and testing models. In this regard, we believe that a parallel predictive modeling platform like PARAMO can serve to rapidly explore applications for a diversity of health problems and health services utilities.

PARAMO is currently tailored to handle predictive modeling pipelines. However, there are additional modeling pipelines of interest in the healthcare analytics domain such as patient similarity, risk stratification, and treatment comparison (37,56,57). One area of future work is to extend the platform to handle these additional modeling pipelines. Other areas of opportunity include expanding the priority scheduling to support more complex algorithms and partitioning some of the pipeline tasks into finer grained computations that can be run in parallel to further improve computational performance. As previously mentioned, the PARAMO platform is only a first step towards our ultimate goal of building analytic pipelines that are specialized for health data researchers. Much work remains in designing and building the specialized functional layers on top of the platform that can facilitate specific biomedical research workflows.

Appendix A

We determined the appropriate number of features to use for building the predictive models in a separate set of experiments. For each type of feature (diagnosis, medication, lab, procedure, and symptom), we measured the AUC (area under the ROC curve) as a function of the number of selected features using the information gain criterion and the logistic regression classification algorithm. The goal was to determine the smallest number of features that maintained the highest classifier accuracy. In these experiments, a fixed observation window size of 720 days was used. The results are shown in Figures A1(A), A1(B), and A1(C) for the Small, Medium, and Large data sets, respectively. We note that the different feature types can have very different performance from one data set to another.

The general trend across feature types and data sets is that the AUC reaches a maximum value over a medium sized range of number of features. We use these results to determine the appropriate number of features for each feature type and data set. For the Small data set, the total number of features is 32: 10 diagnoses, 10 labs, 6 procedures, and 6 medications. For the Medium data set, the total number of features is 320: 150 diagnoses, 100 labs, 50 medications, and 20 symptoms. For the Large data set, the total number of features is 700: 300 diagnoses, 300 procedures, 75 medications, and 25 labs.

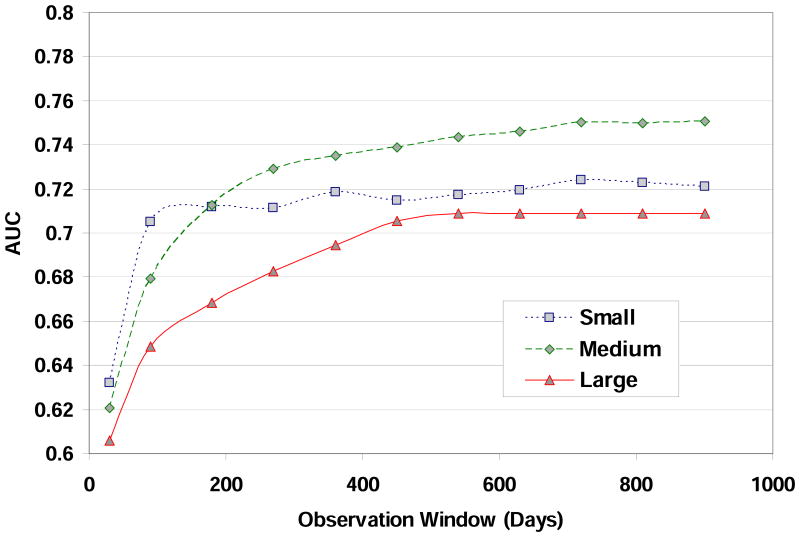
In another set of experiments, we determined the appropriate observation window size to use for building the predictive models. The observation window size determines how much data from the patient record history is used to construct the input feature vectors. We measured the AUC value as a function of the observation window size using the logistic regression classification algorithm. The goal was to determine the smallest observation window size that maintained the highest accuracy. We used the number of features for each feature type for each data set determined in the first experiment described above. The results are shown in Figure A2 for the Small (square, dotted line), Medium (diamond, dashed line), and Large (triangle, solid line) data sets. The general trend across the data sets is for the AUC to increase as the observation window size increases. The AUC improves rapidly for small window sizes and then levels off after a certain window size. We use these results to determine the appropriate observation window size for each data set. For the Small data set, the observation window size is 360 days. For the Medium data set, the observation window size is 720 days. For the Large data set, the observation window size is 720 days.

The optimal parameter values for the number of features for each feature type and the observation window size determined in these initial experiments are used in the predictive modeling experiments presented in Section 4.2 of the main manuscript.

Figure A1.

AUC for the different feature types as a function of the number of features for the A) Small data set, B) Medium data set, C) Large data sets.

Figure A2.

AUC as a function of observation window size (in days) for the Small, Medium, and Large data sets.