Abstract
The pattern of deformation of the different structural components of a muscle-tendon complex when it is activated provides important information about the internal mechanics of the muscle. Recent experimental observations of deformations in contracting muscle have presented inconsistencies with current widely held assumption about muscle behavior. These include negative strain in aponeuroses, non-uniform strain changes in sarcomeres, even of individual muscle fibers and evidence that muscle fiber cross sectional deformations are asymmetrical suggesting a need to readjust current models of contracting muscle. We report here our use of finite element modeling techniques to simulate a simple muscle-tendon complex and investigate the influence of passive intramuscular material properties upon the deformation patterns under isometric and shortening conditions. While phenomenological force-displacement relationships described the muscle fiber properties, the material properties of the passive matrix were varied to simulate a hydrostatic model, compliant and stiff isotropically hyperelastic models and an anisotropic elastic model. The numerical results demonstrate that passive elastic material properties significantly influence the magnitude, heterogeneity and distribution pattern of many measures of deformation in a contracting muscle. Measures included aponeurosis strain, aponeurosis separation, muscle fiber strain and fiber cross-sectional deformation. The force output of our simulations was strongly influenced by passive material properties, changing by as much as ~80% under some conditions. Maximum output was accomplished by introducing anisotropy along axes which were not strained significantly during a muscle length change, suggesting that correct costamere orientation may be a critical factor in optimal muscle function. Such a model not only fits known physiological data, but also maintains the relatively constant aponeurosis separation observed during in vivo muscle contractions and is easily extrapolated from our plane-strain conditions into a 3-dimensional structure. Such modeling approaches have the potential of explaining the reduction of force output consequent to changes in material properties of intramuscular materials arising in the diseased state such as in genetic disorders.
Keywords: Muscle contraction, Finite element analysis, Skeletal muscle, Muscle Material Properties, Muscle Deformation
1. INTRODUCTION
Recent developments in imaging have significantly improved the resolution of measurements of the deformations of a contracting skeletal muscle. It is now possible to observe deformations in regions of muscle with a resolution of only a few cubic millimeters in volume (Drace and Pelc, 1994; Finni et al., 2003; Maganaris et al., 1998; Pappas et al., 2002; Shin et al., 2009). Observations at these resolutions have revealed considerable heterogeneity in the changes occurring in muscle tissues during a voluntary contraction, such as different sarcomere length changes along the length of individual muscle fibers and even the simultaneous appearance of both positive and negative strain (length change) in different regions of a single aponeurosis (Finni et al., 2003; Kinugasa et al., 2008; Pappas et al., 2002; Shin et al., 2009). Such observations are at odds with current models of skeletal muscle function, suggesting major shortcomings in currently theories of muscle function. Parallel developments in computational models of muscle have hinted at such heterogeneity and efforts have successfully simulated observed heterogeneities in both muscle fibers and aponeuroses (Blemker et al., 2005; Chi et al., 2010; Johansson et al., 2000, Oomens et al., 2003, van der Linden et al., 1998a, Yucesoy et al., 2002). One implication of such efforts is that muscle morphology, the mechanical properties of the component materials of a muscle, and even the relationships between component materials impact the deformation of muscle. Conversely, it should be clear that the deformations observed in a muscle reflect the aforementioned properties, implying that a detailed study of muscle deformation provides important information about muscle structure, even at resolutions that may not be directly observed. The present paper reports our continuing efforts to develop a computational model of contracting muscle with the joint goals of better understanding the physics of three-dimensional deformation in muscle and of using that understanding to identify potential critical design features which determine intramuscular deformation. Our ultimate goal is to use an interactive process of model prediction and experimental measures to determine the most likely structure and underlying mechanics of specific muscle. Our strategy has been to begin with a very simple model with as few assumptions as possible. No efforts were made to design specific functional outcomes into the models. Simulations determined the degree to which the emergent properties of the model qualitatively describe the performance of contracting muscle. In addition, we modified the mechanical properties of the constituent materials and the morphology of the muscle to determine the degree to which changes in these values impact the performance of our computational model, thus providing clues to which properties are most critical to optimum muscle performance.
Particular questions that we wished to address were what influences the separation of aponeuroses as a muscle changes length, the distribution of sarcomere length changes along a muscle fiber and how the complex non-contractile tissue structure within a muscle may impact these measures in addition to the force and length changes as a muscle contracts.
The role of connective tissue and other passive materials within skeletal muscle seems particularly intriguing. The role of the endomysium and perimysium in force transmission has been the subject of recent interest, although the topic is still quite controversial (reviewed in Purslow, 2002). A significant portion of the controversy relates to how the endomysium may contribute to force transmission through the muscle. Implicit in all of these discussions is the notion that the non-contractile tissues transmit stress and that it must accomplish this function in the presence of significant changes in muscle and muscle fiber geometry. The presence of a (presumably stiff) load-carrying material surrounding a muscle fiber poses considerable design problems if the force is to be efficiently transferred through the endomysium due to changes in strain energy with respect to tissue deformation. We therefore asked, how passive materials distributed throughout a muscle may contribute to (or compromise) muscle performance. In order to better understand the mechanical impact of passive intramuscular materials and their elastic properties, we will present models to demonstrate the characteristics of a model responding only to hydrostatic pressure in a constant volume model and then compare this with two additional models, incorporating homogeneous distributions of isotropic elastic material, each model differing only in the stiffness of the elastic material.
1.1. Aponeurosis separation
A well accepted feature of muscle contractions is the relative constancy of aponeurosis separation and aponeurosis length as the whole muscle changes length. This observation leads to the conclusion, often implemented in models, that the area defined by these parameters remains constant, even when the muscle length changes (Otten, 1998; van der Linden et al., 1998b; Zajac, 1989). The constant area is an assumed approximation, since both aponeurosis length and separation change slightly (Maganaris et al, 1998; Maganaris and Paul, 2000). Nevertheless, the experimental observation of a (relatively) constant aponeurosis separation is not consistent with muscle behaving as a simple isotropic elastic material (see Section 1.2 and appendix 1). The mechanism of aponeurosis separation has not been fully explored in computational models which do not specifically constrain aponeurosis separation (Yucesoy et al., 2002; Maganaris and Paul, 2000). A common assumption is that the contraction of muscle fibers increases intramuscular pressure which then opposes the inward movement of the aponeuroses (Otten, 1998; van der Linden et al., 1998b). It has been hypothesized that the specific orientation of muscle fibers in the curved pattern often observed in muscle may be an adaptation to generate the pressures necessary to oppose aponeurosis separation (Otten, 1998; van Leeuwen and Spoor, 1993). High resolution muscle imaging has now evolved to the point where intramuscular fiber orientation may be surveyed, providing the raw data for a detailed investigation of this hypothesis (Heemskerk et al., 2009; Sinha et al., 2010).
In an attempt to better understand the potential physical principles behind some of these issues, we recently supplemented our experimental investigative efforts with finite element models (FEM) of muscle. Our initial efforts illustrated that it was possible to generate a model with straight muscle fibers where aponeurosis separation increased or decreased slightly in response to a simulated isometric contraction (Chi et al., 2010). These findings suggested that the control of aponeurosis separation did not require curved muscle fibers. A further interesting observation was that aponeurosis separation was influenced by muscle fiber pennation, suggesting that changes in aponeurosis separation may be an emergent property related to muscle morphology.. Consequently, we have opted to investigate two pennation angles in this study.
1.2. Muscle fiber cross sectional deformation
A related consequence of the constant area of the muscle plane defined by aponeurosis length and aponeurosis separation is that the dimension of the muscle perpendicular to that plane must also remain constant in order to satisfy the observed constant volume of muscle during a contraction (Baskin and Paolini, 1966; van Donkelaar et al., 1999). This suggests that the dimension of muscle fibers perpendicular to this plane may remain unchanged as the muscle fiber shortens, leaving only one direction of expansion in the muscle fiber cross section. Such a possibility has been recognized in previous publications (Gans, 1982; Huijing, 1999; van der Linden et al., 1998a, Kinugasa et al., 2011). Thus, a further challenge presented by the observation of relatively constant aponeurosis separation is to identify intramuscular mechanisms which control not only aponeurosis separation, but also the pattern of deformation of the muscle fiber cross section. While muscle fiber curvature may be a candidate mechanism to accomplish this, we propose an alternative and direct mechanism to control muscle fiber deformation, based upon the ‘slanted cylinder model’ described by Willems and Huijing (Huijing, 1998; Willems and Huijing, 1994). The slanted cylinder model demonstrates possible changes in geometry which may occur in a shortening muscle fiber as its cross section increases and the fiber rotates. A critical characteristic of this model is that the contact region between a muscle fiber and aponeurosis does not change in shape or area as the muscle fiber rotates. Extending this model to the whole muscle leads us to hypothesize structural planes throughout a muscle, roughly parallel to the aponeuroses, including both intra- and extracellular components and operating in a mechanically similar way to the aponeuroses. Such planes would retain a constant area as muscle length changes and also experience minimal deformation (appendix 1). Thus, extremely stiff materials oriented in a plane parallel to the aponeuroses may provide strict dimensional controls over muscle fiber deformation while requiring no deformation of their own structure and consequently minimal work absorbed by the structure as the muscle deforms. One possible candidate to implement such a structure is the costameres of the muscle (Ervasti, 2003; Sanger JM and Sanger JW, 2008). These structures provide a potential structural continuum throughout intra- and extra-cellular materials of a muscle which may be used to control patterns of deformation throughout the muscle as well as providing a means of lateral force transmission between muscle fibers and other intramuscular structures. We thus suggest that costamere orientation (and mechanical properties) may be critical for proper muscle function. A final model will thus incorporate an anisotropic elastic material with high stiffness parallel to the plane of the aponeuroses and zero stiffness along the axis perpendicular to the aponeurosis plane to simulate costameres oriented in a plane that we suggest may be optimum for proper muscle function.
1.3. Muscle fiber longitudinal strain
Physiological measures have indicated that sarcomere length changes along a contracting muscle fiber may be non-uniform (Drost et al., 2003). This has been demonstrated in vivo in human muscles undergoing length changes (Pappas et al., 2002; Shin et al., 2009). Computational models have also predicted non-uniform length changes along muscle fibers and differences between models indicate that the precise patterns of longitudinal strain heterogeneity are model dependent (Blemker et al., 2005; Huijing, 1998; Jenkyn et al., 2002; Yucesoy et al., 2002). This suggests that the specific mechanics of a muscle influences the fiber strain distribution, thus providing a further criterion for evaluating the validity of a proposed model. We will therefore examine how the material properties of our models influence the distribution of sarcomere strain along a muscle fiber.
In summary, we present a FEM investigation in which we have attempted to investigate how the presence of passive materials and the properties of such passive materials may influence the deformation and performance of contracting skeletal muscle. We were particularly interested in how simulations relate qualitatively to in vivo observations of contracting human muscle and if any special conditions need to be satisfied in order to accomplish the specific patterns of dimensional changes observed in contracting muscles. Our findings indicate that passive material properties may have a significant effect on patterns of muscle deformation and even force output. The model which introduced anisotropy along specific axes most closely reflected experimentally observed muscle deformations and also resulted in the highest force output.
2. METHODS
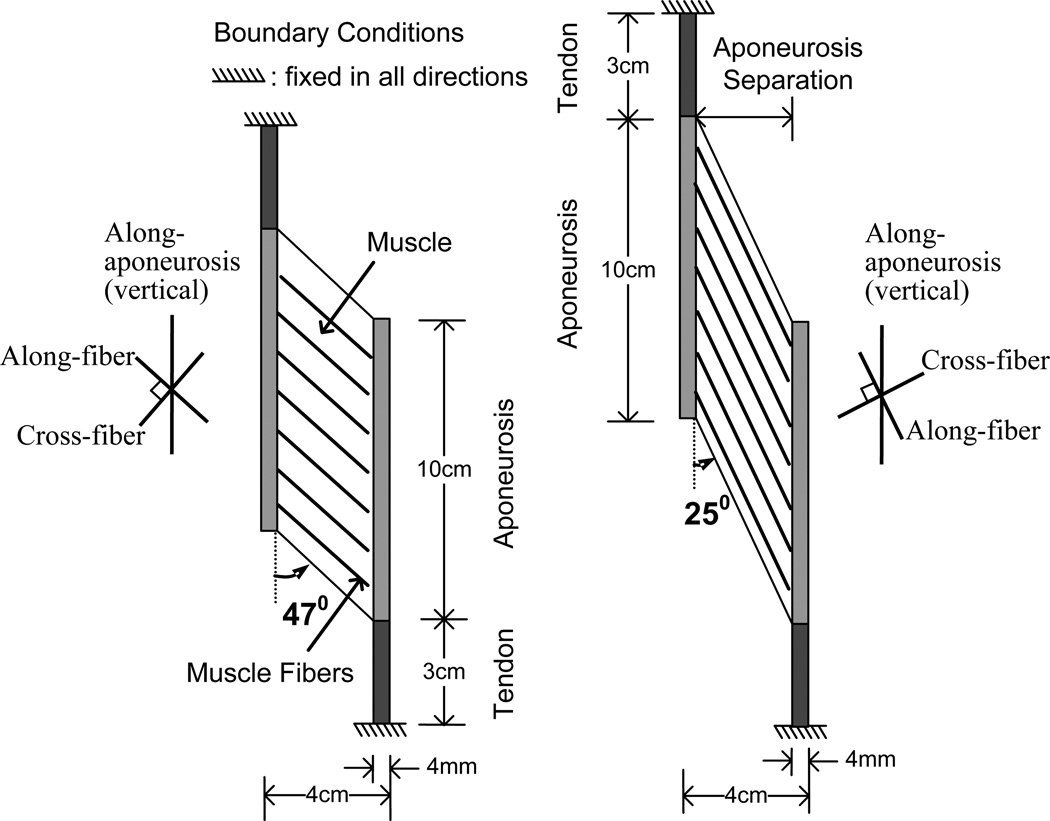
In this study, the material model was assumed to be nearly incompressible as described by Chi et al. (Chi et al., 2010). A muscle belly connected with two tendons (Fig. 1) was discretized by finite elements with a bilinear displacement field, constant pressure field and the plane strain condition with a thickness of 3 cm. Since the thickness of 3 cm was of the same order as the width of 4 cm of the muscle, and the prescribed boundary conditions were in the in-plane directions, plane strain condition was assumed. The ‘plane strain’ model utilizes the simplifying assumption that there are no changes in strain along the axis perpendicular to the surface described above (i.e. no change in muscle thickness). The through-plane constraint implicit in our plane strain model is also consistent with experimental observations showing that a majority of strain changes take place in the plane defined by our model (Gans, 1982; Huijing, 1999; van der Linden et al., 1998a, Kinugasa et al., 2011). Initially, the two end points of the tendons were fixed to simulate isometric conditions for the muscle-tendon unit. Two simulation models, with resting fiber pennation angles of θ = 25° and 47° were considered, each with the same volume of contractile tissue. The geometry of the models determined the fiber lengths as 7.572 and 4.375 cm, respectively. The muscle thickness was set at 3cm, giving physiological cross sectional areas (PCSA) of 12.679 and 21.94 cm2, respectively. The two pennation angles were chosen to sample different values in the range of pennation angles encountered in normal muscle, particularly as our previous work has demonstrated that aponeurosis strain, aponeurosis separation and intramuscular strain may be influenced by pennation angle and that the pennation angle of 45° plays a significant role in determining whether the aponeuroses stretch or shorten (Chi et al., 2010).
Fig. 1.
Diagram of the basic model.
The material properties were homogeneous throughout the muscle, and the muscle fibers were straight and parallel to each other. In the force equilibrium, the normalized fiber force is the combination of the normalized active fiber force and the normalized passive fiber force and is assumed to be in the following form (Blemker and Delp, 2006; Chi et al., 2010; van Leeuwen and Spoor, 1993):
| (1) |
and a is the muscle activation function. Muscle fibers contract and generate forces when the activation level, a in Eq. (1), rises. Unless otherwise maintained, we prescribed the following form of the activation function as the muscle contracts (Johansson et al., 2000; van Leeuwen and Spoor, 1993):
| (2) |
where t̅ = t /T is the normalized time, t is the time, and T is the duration of muscle activation.
The activation curve is shown in Fig. 2a and allowed us to investigate the development of deformation with force development. In a further series of simulations, we also shortened the muscle as activation was increased in order to explore the interactions of muscle length changes and activation. This is also shown in Fig. 2a. In this study, we considered only quasi-static cases and neglected the velocity dependency. Thus, the results of shortening would be equivalent to shortening the muscle and then activating it at the new length.
Fig. 2.
The activation function and normalized fiber force-length properties. a) The activation function (solid line) used to progressively activate the simulated muscle and the length-change function (dotted line) used to simulate muscle shortening in some simulations during activation. b) The activation level, a, was assumed to be unity in this figure. The shaded band indicates the range of fiber length change over which the models operated. The fiber rest length is indicated by the rightmost edge of the shaded band.
The stress in the fiber direction is then calculated as
| (3) |
where σmax is the maximum isometric stress which occurs at the optimal fiber stretch λ0, and is the normalized fiber force.
The force-length property of muscle fiber (Blemker and Delp, 2006; Chi et al., 2010) was employed in our modeling and is shown in Fig. 2b. The figure also illustrates the region of the force-length curve over which the simulations were performed. The same muscle fiber properties were assumed for all simulations but the passive matrix material properties were altered to explore the impact of material properties on deformation patterns in the muscle. Four different passive matrix materials were introduced and will be described in the following section.
2.1. Transversely isotropic hyperelastic model
Based on previous work (Blemker et al., 2005; Blemker and Delp, 2006; Chi et al., 2010; Oomens et al., 2003; Weiss et al., 1996), muscle can be described by a transversely isotropic hyperelastic model which is related to an anisotropic strain energy density function. Considering the nearly incompressible nature of tissues (Baskin and Paolini, 1966), the strain energy density function of the muscle-fiber assembly takes the following form:
| (4) |
where I̅1 and I̅2 are the reduced invariants of the Cauchy-Green deformation tensor C defined as I̅1 = J−2/3 I1, I̅2 = J−4/3 I2, where I1 = tr (C), , J = det (C)½, and λ is the stretch ratio along the fiber direction in the reference configuration. We consider the muscle matrix Wmatrix of a polynomial type up to the second order:
| (5) |
where Cij and K are material constants. K is the bulk modulus of the material and can be viewed as the penalty parameter for imposing incompressibility. The anisotropy of the model is introduced by the fiber stress although the isotropic strain energy is used for muscle matrix.
2.2. Tendon and aponeurosis
The tendon and the aponeurosis were modeled by an isotropic cubic hyperelastic model to simulate the well known force-length behavior of the tendon and aponeurosis, which is more compliant at low-force levels and stiffer at the high-force levels. The expression for the tendon and the aponeurosis are similar and given as (Chi et al., 2010):
| (6) |
where the materials properties are listed in Table 1.
Table 1.
Material Constants for Tendon and Aponeurosis.
| C10 (N/cm2) | C20 (N/cm2) | C30 (N/cm2) | K(N/cm2) |
|---|---|---|---|
| 30 | 80 | 800 | 2×105 |
2.3. Passive materials
To better understand passive material properties on the deformation and force output of skeletal muscle, four types of matrix models were introduced in this study. The bulk modulus K = 2×104 (N/cm2), with its value much larger than the other material constants in the strain energy density function in Eq. (4), introduces a volume constraint in the materials as shown in the following material models.
2.3.1. Model 1 – Hydrostatic model
For the hydrostatic model, the muscle matrix was designed to mimic the fluid behavior such that there was no shear resistance and near incompressibility was maintained. The strain energy density function of the muscle matrix took the following form:
| (7) |
2.3.2. Model 2 – Softer Matrix Model and Model 3 – Stiffer Matrix Model
The strain energy density functions of muscle matrices for both softer and stiffer models are described in Eq. (5). The matrix constants are given in Table 2. The stiffer material was based on the material model in our previous study (Chi et al., 2010). The material constants in this model were calibrated from the data in van der Linden, 1998c. The softer matrix model was designed to model a softer passive material response, and the corresponding material constants Cij were scaled to be one eighth of those for the stiffer model.
Table 2.
Material Constants for Muscle Matrix of Stiffer and Softer Matrix Models.
| C10 (N/cm2) | C01 (N/cm2) | C20 (N/cm2) | C11 (N/cm2) | C02 (N/cm2) | |
|---|---|---|---|---|---|
| Stiffer model | 6.43 | −3.80 | 0.94 | −0.0043 | 0.0005 |
| Softer model | 0.80 | −0.47 | 0.12 | −0.0005 | 0.0001 |
2.3.3. Model 4 (d) - Vertically reinforced model
In this model, stiffness was added in the along-aponeurosis direction only, by adding one more term to Wmatrix in the hydrostatic model. This simulates a material with elevated stiffness oriented parallel to the aponeurosis. Since the aponeurosis is oriented in the vertical direction in Fig. 1, hereafter this model is referred to as the vertically reinforced model. The specific form Wmatrix for the vertically reinforced model was
| (8) |
where
| (9) |
in which λv is the stretch ratio in the vertical direction given by λ v2 = N • C̅ • N with N the unit vector in the vertical direction and C̅ = J−2/3C. The material constant for the reinforcement was Cv = 20(N/cm2) which gives a much lower stiffness than the tendon material (Table 1).
The stress-strain relations for those four models are illustrated by a uniaxial tension test with muscles in the active and unactivated state. The stress-strain curves are shown in Fig. 3 where Fig. 3a shows the relation along the muscle fiber direction with the muscle fibers fully activated and Fig. 3b shows the relation in the vertical direction with inactive muscle fibers. For Fig. 3b, the material properties of the first 3 examples are transversely isotropic and therefore represent the passive material properties along any axis in the cross-fiber plane. The curve for the vertically reinforced material shows the properties along the axis of maximum stiffness (along-aponeurosis direction). Note that the vertically reinforced model has a larger stress response along the along-aponeurosis axis than the active muscle along the fiber direction, thus simulating a muscle with a high lateral force transmission between muscle fibers due to the passive material.
Fig. 3.
Stress-strain curves for materials used in the models. a) Stress-strain curves along the fiber orientation plotted with the muscle fully active, illustrating the dominance of the muscle material properties in the fiber direction for these simulations. b) Stress-strain curves along the cross-fiber axis of the model in a passive muscle. c) Comparison of compressive behavior to experimental data (Bosboom et al., 2001) and van Loocke’s model (van Loocke et al., 2006). The shaded area represents the variation of stress-strain behaviors from experiment data and published material models.
As will be discussed in Section 4.1, the compressive behavior of muscle models has effect on the aponeurosis separation. Therefore, the stress-strain curves in compression of the four models were validated with the data from experiments (Bosboom et al., 2001a,b) and from some published models (van Loocke et al., 2006) as shown in Fig. 3c, in which the shaded area represents the deviation of experimental data and numerical models used in van Loocke et al., 2006. Although the compressive behaviors of the four models vary slightly, they all fall within the deviation of experimental data and published models.
2.4. Change in aponeurosis separation
The changes in aponeurosis separation in Tables 3 and 4 were calculated based on the fiber straight-line length Lf and the sin value of average pennation angle θ̅, as d0 – Lf sin(θ̅), where d0 is the aponeurosis separation before deformation.
Table 3.
Changes in aponeurosis separation (mm) during isometric contractions showing the effects of material properties and pennation angle. Two locations are shown, representing aponeurosis separation at one end of the muscle (top fiber) and the middle of the muscle (middle fiber). Since the models are symmetrical, fibers at the bottom of the muscle would behave in the same way as the top fibers.
| Change in aponeurosis separation (mm) |
Constant volume (hydrostatic fluid) |
Softer material |
Stiffer material |
Vertical reinforced material |
|
|---|---|---|---|---|---|
| 25° | top fiber | 1.3620 | 1.2546 | 0.8844 | 1.4370 |
| middle fiber | −2.4634 | −1.3379 | 0.6214 | −0.5302 | |
| 47° | top fiber | −1.9044 | −1.6639 | −1.1288 | −0.1428 |
| middle fiber | −2.4520 | −2.2764 | −1.5658 | −0.7374 | |
Table 4.
Changes in aponeurosis separation (mm) for the shortened contracting muscles showing the effects of material properties and pennation angle.
| Change in aponeurosis separation (mm) |
Constant volume (hydrostatic fluid) |
Softer material |
Stiffer material |
Vertical reinforced material |
|
|---|---|---|---|---|---|
| 25° | top fiber | −0.6891 | 1.4324 | 0.3471 | 1.4818 |
| middle fiber | −2.0664 | −0.3405 | 1.4388 | −0.3241 | |
| 47° | top fiber | −2.1764 | −0.8509 | −0.3131 | 0.3437 |
| middle fiber | −1.9594 | −1.8039 | −1.1507 | −0.5504 | |
3. RESULTS
It should be noted that the simulations reported here incorporate the simplifying assumption of the ‘plane strain’ model described at the beginning of the Methods section. It provides a simpler conceptual model than a true 3-dimensional model although we will discuss extrapolations to 3-dimensional conditions where the situation warrants.
3.1. The influence of passive material properties on muscle shape and strain
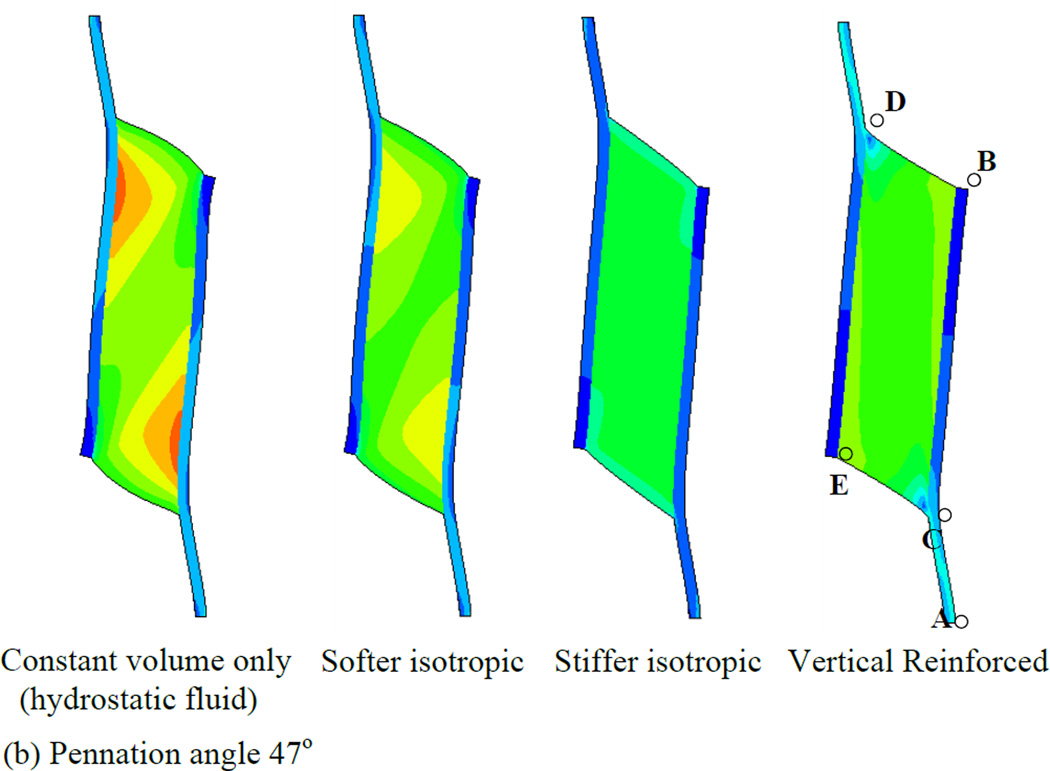
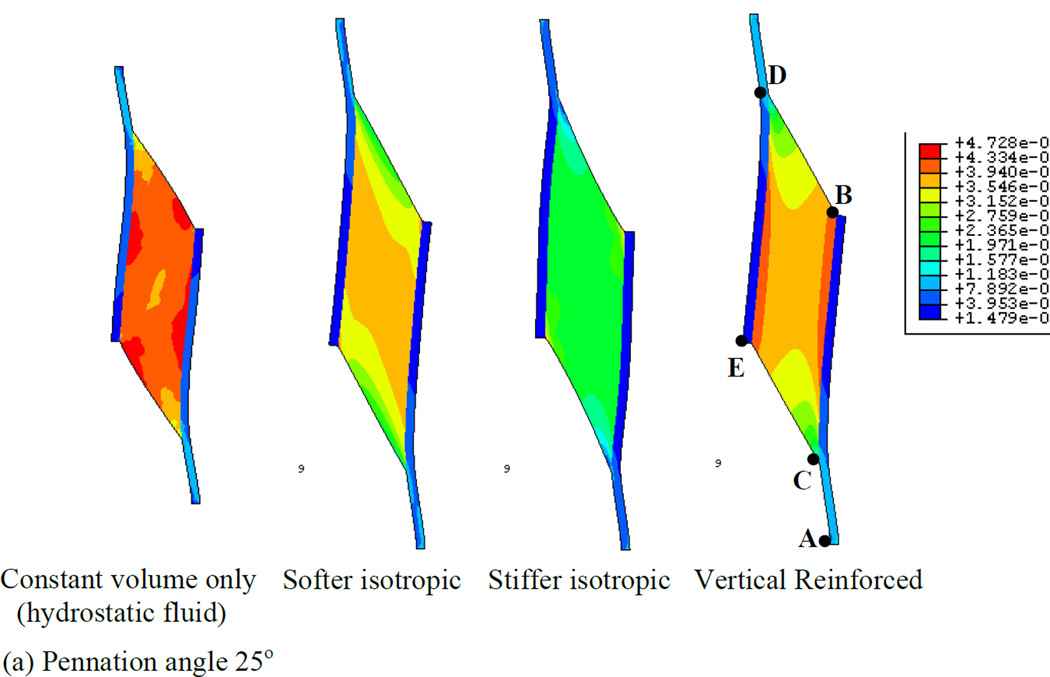
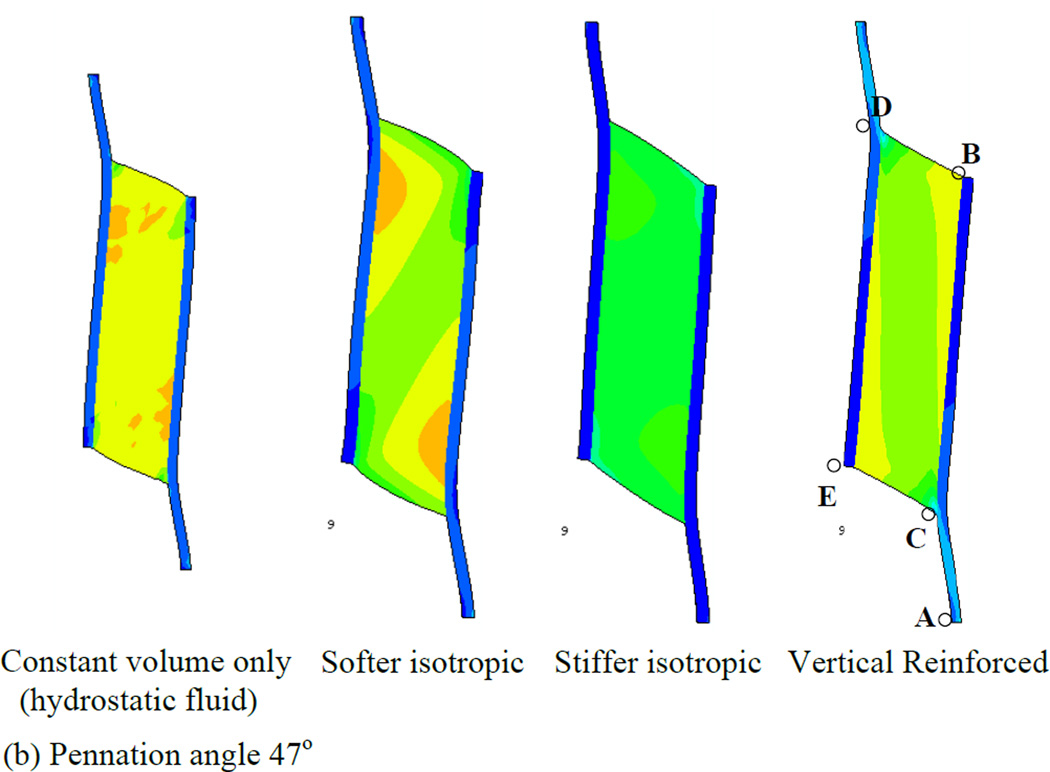
In order to first define a basis upon which to consider the various properties of the muscle, we illustrate a series of simulations in which the muscles were allowed to contract under isometric conditions (Fig. 4). Each simulation represents a maximally contracted muscle in which the fibers exert only tensile stress in the direction of the fiber orientation but the passive material properties of each muscle were altered (by using different Wmatrix, see the model description). In each case the muscle material maintained a constant volume throughout the contraction. We have also considered 2 pennation angles, 25° (top row of Fig. 4) and 47° (bottom row of Fig. 4) and show that both result in qualitatively similar patterns of deformation. The resulting whole-muscle deformations are, however more pronounced in the 47° case. In the hydrostatic model (column 1 of Fig. 4), the material making up the bulk of the muscle is designed to simulate fluid behavior with near incompressibility. As the muscle fibers exert an inward force on the aponeuroses, the pressure within the muscle increases, until the outward force due to pressure balances the inward force due to muscle fiber tension. A consequence of this model is that the ends of the muscle bulge outwards (lines BD and CE). A constant volume constraint on the muscle would require that the aponeuroses move together as the muscle maintains constant volume. In a three-dimensional model there would be additional deformation as the (through-plane) thickness of the muscle increased due to pressure induced bulging, allowing even greater collapse of the aponeuroses. The hydrostatic model also exhibits significant curvature of the aponeuroses, with an apparently higher separation at each end, indicating significant non-uniformity of aponeurosis separation along the muscle (see also Table 3). This also influenced the distribution of muscle fiber length changes (see below). A further dimension change arising from muscle contraction is the strain in the aponeurosis which lengthens between 0.5 and 0.7 cm depending upon the pennation angle (Fig. 5a). This corresponds to a strain change of 5 - 7% (note that the first 3 cm of the graphs in Fig. 5 represent tendon). In a plane-strain model, this dimensional change interacts with bulging at the ends of the muscle to determine the changes of the average aponeurosis separation to maintain constant volume.
Fig. 4.
Principal strain contours for maximally activated models with different passive material properties. Principal strain is the strain in the maximum principal direction at each point in the image. Pennation angles of 25° (top row) and 47° (bottom row) are illustrated. The initial muscle length corresponded to the length at which the passive materials were in their neutral position and therefore exerted no force before muscle activation deformed them (blue diagram, bottom right illustrates the undeformed 47° pennation angle model). The first column shows the hydrostatic model. The second and third columns show the softer and stiffer isotropic elastic matrix models respectively. The fourth column shows the vertically reinforced model.
Fig. 5.
Comparison of aponeurosis length change in response to maximal activation for all 8 examples. (a) Constant volume only (hydrostatic fluid), (b) Softer isotropic material, (c) Stiffer isotropic material, (d) Vertically reinforced material. The figures also illustrate the influence of different pennation angles.
If the fluid is replaced by an elastic material with properties similar to tendon (column 2 of Fig. 4), some resistance to flow may reduce the bulging at the ends of the muscle but not entirely remove it. The ends of the muscle bulge in this case also, suggesting that aponeuroses must move together (denoted by the negative sign in Table 3) in this case also (Fig. 4 and Table 3). This is most noticeable in the 47° pennation angle. A stiffer elastic material (column 3 of Fig. 4) resulted in a model where the ends of the muscle appear less convex. In the 25° case, the end is slightly concave, thus pulling material into the muscle which we may expect to force the aponeuroses apart (Fig. 4 and Table 3). The differences between the 47° and 25° cases in this model illustrate the impact of pennation angle alone on the mechanical performance. In this case it results in an overall outward movement of the aponeurosis at 25° and a slight inward movement of the aponeuroses at 47°. A further contributor to differences in the direction of aponeurosis movement may also be the aponeurosis strain. Figs. 5c and 6c indicate that the aponeuroses in this model experience the least length and strain changes of all the models studied and these are less in the 47° case relative to the 25° case. Note also the lower tendon strain, suggesting that the force output of this model is reduced.
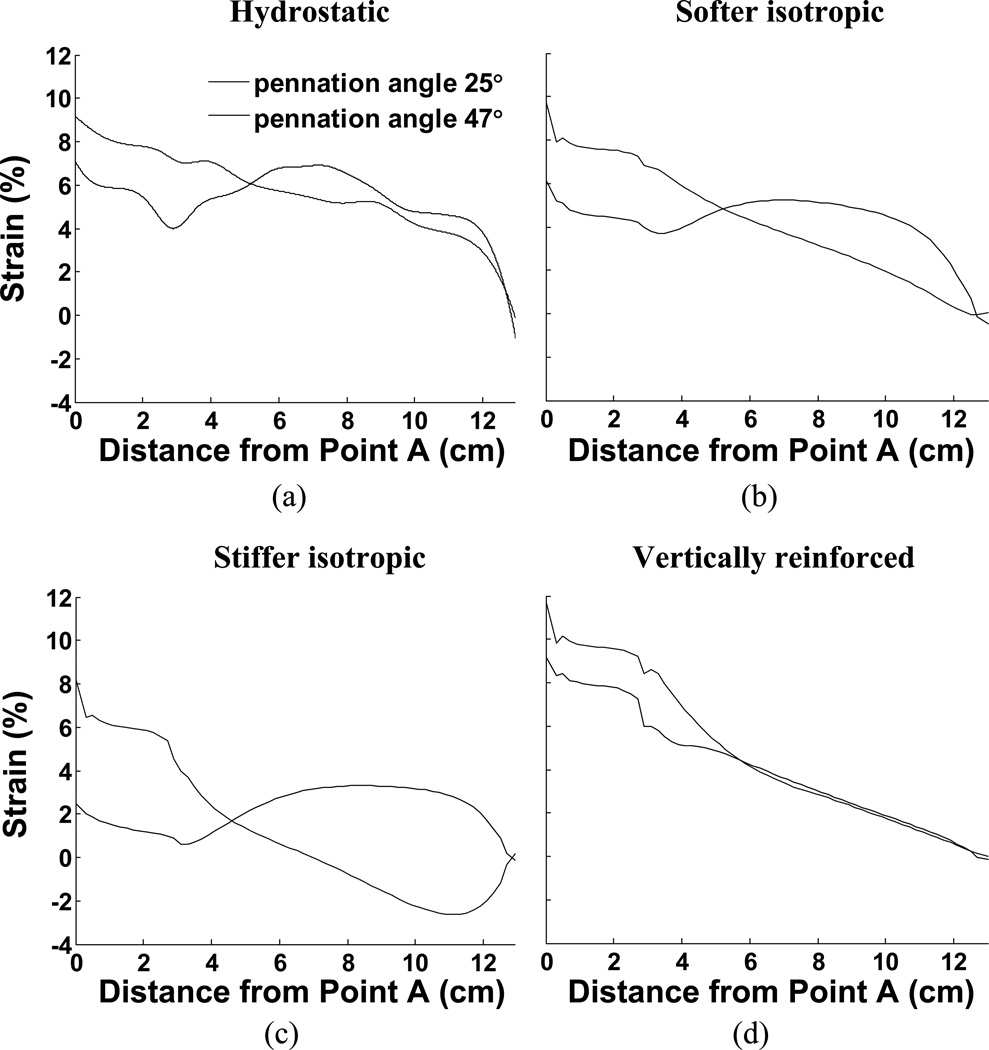
Fig. 6.
Comparison of strain along aponeuroses for all 8 examples in response to maximal activation. (a) Constant volume only (hydrostatic fluid), (b) Softer isotropic material, (c) Stiffer isotropic material, (d) Vertically reinforced material. The figures also illustrate the influence of different pennation angles.
The final example in Fig. 4 (column 4) illustrates a fluid type muscle with additional material arranged to resist deformation only in the direction parallel to the aponeuroses. Thus, it replicates column 1 of Fig. 4, but with a stiff component parallel to the aponeurosis resisting outward bulging at the ends of the muscle. In this model, the separation of the aponeuroses appears to change less than other models in the 47° instance although the 25° case still shows a substantial, region-dependent change (Table 3).
Collectively, we observe that the choice of passive intramuscular material properties have a significant impact upon the distribution and magnitude of strain within a muscle when it contracts. The overall shape changes of the muscle are influenced by the material properties. Furthermore, interactions between material properties and pennation angle upon aponeurosis separation appear to be noticeably different in the four material models.
3.2. Non-uniform strain in aponeuroses
The material properties also influence the distribution of strain along the aponeuroses and these strain curves are plotted in Fig. 6. These findings support previously published work showing that the distribution of strain along an aponeurosis may be influenced by pennation angle (Chi et al., 2010; Shin et al., 2009). Such observations strongly indicate that the aponeuroses are not the only means of transmitting fiber contractile force to the tendons, implying that other, intramuscular, materials transmit some of the muscle contractile force. The model performance also illustrates how passive intramuscular material properties may influence that distribution of strain. In our case, the aponeurosis was chosen to be uniform along the muscle and may therefore not accurately represent the strains encountered in muscle. An advantage, however is that the strains along this uniform material indicate the regional stresses encountered, illustrating that the distribution of stress along the aponeurosis is not a simple function of location but also depends upon material properties. In one case (Fig. 6c), the aponeurosis in the 25° case exhibits a region where the aponeurosis of the contracting muscle is shortened, despite the presumed increased load due to muscle contraction. This observation also was material-dependant.
3.3. Non-uniform strain in muscle fibers
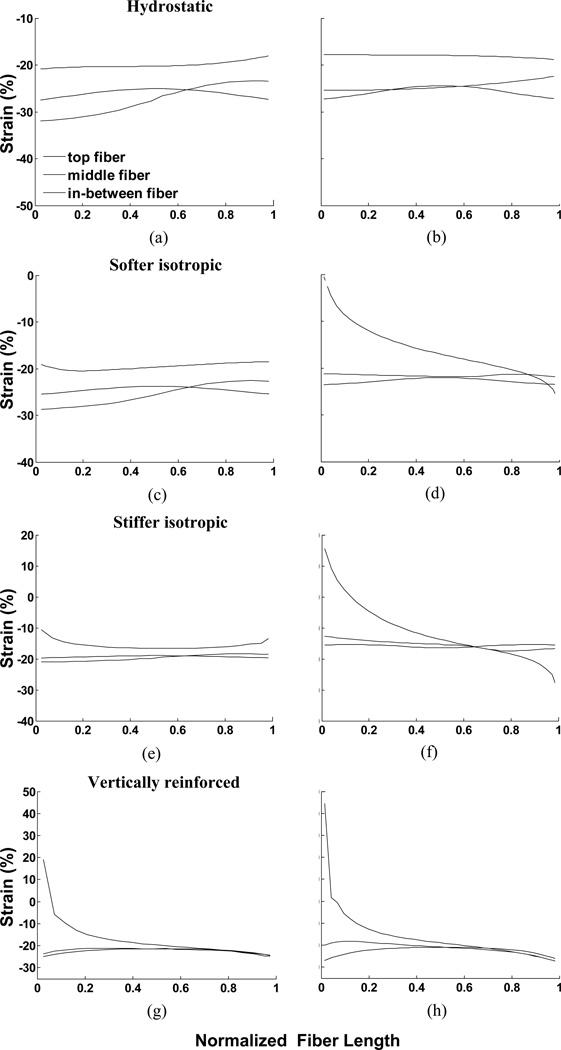
A notable feature of all of the models in Fig. 4 is the non-uniformity of strain across the muscle material. Both material properties and pennation angle influence the distribution of strain within the muscle. For example, the strain change across the hydrostatic model in Fig. 4 appears to be rather gradual whereas the strain changes in the vertically reinforced model appear to be concentrated in a region close to the aponeuroses. This suggests that muscle fibers in different regions of a muscle may experience different strains simply because of their location in the muscle. Furthermore, differences in strain along a line parallel to the muscle fiber orientation suggest that even different regions of a single muscle fiber may experience different strains (Fig. 7). The range of strains encountered in the different models differ substantially and in some examples suggests that some regions of fibers may even experience eccentric contractile conditions when the whole muscle-tendon system remains at a constant length (Fig. 7f, g, h).
Fig. 7.
Strain along fibers in muscle for all 8 examples in response to maximal activation. The three lines represent fibers at the top end of the muscle, 25% of the distance along the muscle and in the mid-region of the muscle. The left column illustrates the 47° pennation angles and the right column, 25° pennation angles. (a) and (b) illustrate constant volume only (hydrostatic fluid), (c) and (d) illustrate softer material, (e) and (f) illustrate stiffer material, (g) and (h) illustrate vertically reinforced material. As the muscle is symmetrical, the curves for the fibers in the lower portion of the muscle would be left/right reversals of the plotted curves.
3.4. Muscle force production
The different models exhibit substantial differences in the force output of the muscle (Fig. 8). The model represented by column 4 in Fig. 4 (upper and lower) appears to exhibit the greatest force output of the muscle models we have investigated. A somewhat unexpected finding in our models is that the force output of the models with an initial pennation angle of 47° did not generate higher forces than the 25° models as would have been predicted from the greater PCSA of the 47° models (21.94 vs. 12.68cm2 for the 25° model). This is a topic of ongoing investigation. Adding a constraint to our model to prevent lateral movement of the aponeuroses results in the expected relationship between PCSA and force output, suggesting that additional factors (such as non-uniform stress and pressure distribution) may influence force output in an unconstrained muscle.
Fig. 8.
Force output of the models during progressive activation of isometric contractions for (a) pennation angle 25°, and (b) pennation angle 47°.
3.5. Response of the muscle to length changes
Fig. 9 illustrates the responses of our models when allowed to shorten by 6% of their starting length. The muscle fibers are thus contracted to a shorter length, pennation angles are slightly greater and the deformations of the passive intramuscular materials are different relative to Fig. 4. As stated in the methods, velocity effects were ignored in this simulation. Effectively, the model illustrates changes which occur in isometric contractions at each incremental length. The changes in muscle outline shape and strain patterns are qualitatively similar to those plotted in Fig. 4. In general, aponeurosis separation was greater in the shortened condition (Table 4). The differences in aponeurosis separation between the two contracted muscles also illustrated that the change in aponeurosis separation caused by shortening was much less than the change caused by muscle activation under isometric conditions (compare tables 4 & 5).
Fig. 9.
maxumum principal strains for shortening cases: (top row) pennation angle 25°, and (bottom row) pennation angle 47°.
Table 5.
Differences in aponeurosis separation (mm) between the isometric and the shortened muscles. Positive values indicate greater aponeurosis separation in the shortened muscle
| Change in aponeurosis separation (mm) |
Constant volume (hydrostatic fluid) |
Softer material |
Stiffer material |
Vertical reinforced material |
|
|---|---|---|---|---|---|
| 25° | top fiber | −2.0511 | 0.1778 | −0.5373 | 0.0448 |
| middle fiber | 0.397 | 0.9974 | 0.8174 | 0.2061 | |
| 47° | top fiber | −0.272 | 0.813 | 0.8157 | 0.4865 |
| middle fiber | 0.4926 | 0.4725 | 0.4151 | 0.187 | |
The distribution of strain along the aponeurosis (Fig. 10) suggests that the amplitude and pattern of strain distribution is influenced by muscle length changes. Strain in the muscle fiber direction (Fig. 11) again shows regional differences with significant differences along the fibers in some regions. In some models, the pattern of fiber strain differs at the two muscle lengths (compare Figs. 7 and 11), suggesting that regional changes in fiber strain may depend upon muscle length and therefore may be quite dynamic as a muscle changes length.
Fig. 10.
Comparison of strain along aponeuroses for all 8 examples. (a) Constant volume only (hydrostatic fluid), (b) Softer isotropic material, (c) Stiffer isotropic material, (d) Vertically reinforced material. The figures also illustrate the influence of different pennation angles.
Fig. 11.
Strain along fibers in the middle and one end of the muscle for all 8 shortening examples. (a) and (b) illustrate constant volume only (hydrostatic fluid), (c) and (d) illustrate softer elastic material, (e) and (f) illustrate stiffer elastic material, (g) and (h) illustrate vertically reinforced material with different pennation angles.
Reaction forces computed for the shortened muscles illustrate significantly different outcomes with the different material properties. Fig. 12 illustrates the force development as the models were activated with the pattern illustrated in Fig. 2a and linearly shortened (Fig. 2a) during the rise of activation. Some of the drop in force exhibited throughout the contraction is due to fibers shortening along the descending limb of the force-length curve (Fig. 2b). The final forces developed by each model under isometric and shortened conditions are summarized in Fig. 12. The highest force outputs occur in the vertically reinforced model for both isometric and shortened conditions. Decrements due to muscle shortening appear approximately equivalent, with the exception of stiffer isotropic material model which exhibits a large force decrement at the shorter length. Thus, material properties of the passive tissues within muscle have a significant impact on the force output of the muscle and in the way that force output is influenced by changes in muscle length.
Fig. 12.
Force output of the shortening muscle models. (a)(b) Changes in force as activation increased and muscle shortened. (c)(d) Final force output at different lengths, where models 1, 2, 3, and 4 indicate constant volume only (hydrostatic fluid), softer isotropic material, stiffer isotropic material, and vertically reinforced material, respectively.
4. DISCUSSION
The results we present here illustrate an important relationship between the mechanical properties of the muscle tissue material and the pattern of deformation observed when that material is stressed. They also illustrate that passive material properties influence the force output of a muscle and influence the relationship between length changes and force output beyond that predicted from the active length-tension curve. A rather surprising outcome was that the higher pennation angle failed to reproduce the expected increase in muscle force output due to an increased PCSA. This issue will be a topic for further investigation. A major goal of this paper was to identify the critical features which could significantly influence the performance of skeletal muscle. Our first consideration was therefore to understand how the passive properties of materials within a muscle impact the functional properties of a muscle, particularly with respect to intramuscular strain and force output. We have deliberately used very simple models with minimal assumptions, to gain some insight of the potential importance of material mechanical properties. The complex emergent properties of the model were also qualitatively compared with deformation patterns observed in contracting human muscles (Pappas et al., 2002; Shin et al., 2009). Simple changes in the model definition, such as elastic moduli and even pennation angle allowed us to “experiment” computationally and better understand the sensitivity of muscle contractile output to changes in the structure of a muscle and the mechanical properties of its constituent materials.
Despite using pennation angles in this and previous papers which ranged from 25 to 60 degrees, we have observed similar responses of all our simulations. Similarly, while the models display significant differences in response to changes in fiber lengths and matrix material properties, the qualitative pattern remained similar (e.g., Figs. 4 & 9), indicating a substantial degree of robustness to changes in model parameters. These findings point to potentially significant physical principles, discussed below, which influence muscle in a consistent manner over a range of altered muscle properties.
The models presented in this paper are known as plane-strain models because their deformation is restricted to the plane of the images presented. Thus, no change in thickness of the models occurs. Our reference to isotropic materials is thus an abbreviation of “transversely isotropic” where the elastic deformation is accounted for only in the plane of the models. Deformation in the through-plane direction is ignored. It should be noted that such a model is consistent with current experimental data suggesting that through-plane dimensional changes are small compared with the in-plane changes. Nevertheless, these models illustrate the physics we wish to convey and in the following descriptions, we also consider the effects of allowing changes in the third direction insofar as it aids understanding of the behavior of muscle under stress.
4.1. Maintenance of aponeurosis separation
The present models parallel an intuitive model of muscle, where contractile forces exerted by muscle fibers apply an inward force upon the aponeuroses (Zajac, 1989). Such inward forces would be expected to increase intramuscular pressure, which, in turn opposes inward movement of the aponeuroses (Otten, 1998; van der Linden et al., 1998b). Intuitively, one may expect the mechanics of the muscle to be critical in determining the movement of aponeuroses. A reshaping of intramuscular material, evidenced as bulging at the ends of the muscle and/or increasing the through-plane thickness of the muscle as the muscle shortens along the fiber direction would require movement of the aponeuroses in a constant volume material. One explanation for the observed minimal lateral movement of aponeuroses during contraction has been that tensile loading along properly oriented curved muscle fibers applies a force vector oriented perpendicular to the contractile vector and towards the center of curvature, potentially contributing to a higher intramuscular pressure to oppose aponeurosis movement (Otten, 1998; van Leeuwen and Spoor, 1993). It should be noted that the fibers of our models are straight when the muscle is at rest. Curving of the material during a contraction (e.g., along lines BD and EC in Figs. 4 and 9) resulted in local reorientation of the muscle tensile vector, thus simulating curvature of muscle fibers as the muscle contracts. In the case of the pure hydrostatic model, the nearly incompressible material property preserves the volume of the system and the muscle fiber strain and hydrostatic pressure distribution determine the ultimate shape of the muscle. The second model introduces a uniform elastic material dispersed throughout the muscle. This material differs from a fluid since it resists shear, compression and stretch in 3 dimensions. Under isometric muscle contraction, the muscle component undergoes a nearly simple shear deformation due to its geometry. This leads to a structural deformation where the relative movement of the two aponeuroses in the width direction is considerably smaller than their relative movement along the aponeurosis axial direction. This relative motion in the width direction is further resisted by the constant volume constraint and the hydrostatic pressure built up in response to the normal strain. An alternative scheme was to introduce an intramuscular tensile material oriented parallel to the aponeuroses. This material prevents bulging at the ends of the fibers and thus does not allow a decrease of aponeurosis separation. In the 3-dimensional case, additional tensile material oriented along the through-plane axis would prevent any increase in muscle thickness due to increased intramuscular pressure. Such a material would also prevent dimensional changes along the through-plane axis of the muscle fiber, thus restricting the dimensional change of the muscle fiber cross section to the in-plane axis as has been reported experimentally (Gans, 1982; Huijing, 1999; van der Linden et al., 1998a, Kinugasa et al., 2011).
All of the models exhibit some changes in aponeurosis separation. The greatest change appeared in the isometric contraction of the hydrostatic model where the baseline aponeurosis separation of 3.8 cm was reduced by 7.7 mm, or 20% (Table 3). Table 3 illustrates that passive intramuscular material properties influence the separation of aponeuroses during a contraction, The shortened muscles generally exhibited smaller changes in aponeurosis separation (Table 4). A comparison between these differences in length of the muscle suggests that contraction has a much greater effect than muscle length change upon aponeurosis separation (Tables 4 & 5). This finding is in agreement with experimental efforts to measure the effects of contraction and length changes on transverse strain in the rat medial gastrocnemius muscle where it was shown that an isometric contraction produced ~11% change in transverse strain with very little change at different muscle lengths (van Donkelaar et al., 1999). Thus, simple, material-dependent mechanical consequences of a 2- or 3-dimensional muscle limit aponeurosis movement and force the fibers to rotate when they change length. It may also be noted that some simulations resulted in regions where aponeurosis separation increased during a contraction. This possibility was discussed in a previous publication (Chi et al., 2010) where we pointed out that a constant volume condition of a 3-dimensional material undergoing shortening along one axis requires that the dimension along at least one other axis must increase. In the case where the shortening axis is at an angle to the aponeuroses, the sign and magnitude of the aponeurosis separation depends upon the length change vector perpendicular to the aponeurosis orientation. Thus, the aponeurosis separation of muscles with a pennation angle of 25° may be more influenced by increasing girth of muscle fibers whereas pennation angles above 45° will be accompanied by decreasing aponeurosis separation reflecting the muscle fiber shortening vector.
4.2. Influence of passive material on force output
A notable difference between the models arises when there is a change in length. In the hydrostatic model, fluid will flow freely from one region of the muscle to another with some small penalty due to the energy required to move the fluid. The elastic models have resistance to deformation in all directions and will thus absorb and store elastic strain energy (and oppose contractile force) as the muscle changes shape from its resting form. This results in a lower force output of these models, with a slightly greater force loss if the muscle shortens significantly, due to higher strain energy levels. It should be noted that the elastic energy stored under such conditions may be recouped as the muscle returns to its undeformed shape. This situation occurs under both isometric and concentric contractile condition, robbing the elastic models of force potential under both conditions (Figs. 8, 12). This effect is independent of the fiber length-tension curve and due simply to deformation of an elastic material, the restoring force which opposes contractile force and the corresponding absorption of energy. The stiffness of the passive material has a significant impact upon force output and energy storage, with the stiffer material accompanied by much lower forces in the shortened condition (Fig. 12). While this may not be considered to be significant in healthy muscle, it illustrates a potential impact of changes in the mechanical properties and quantities of passive material due to muscle pathologies.
4.3. An anisotropic passive material improves model performance
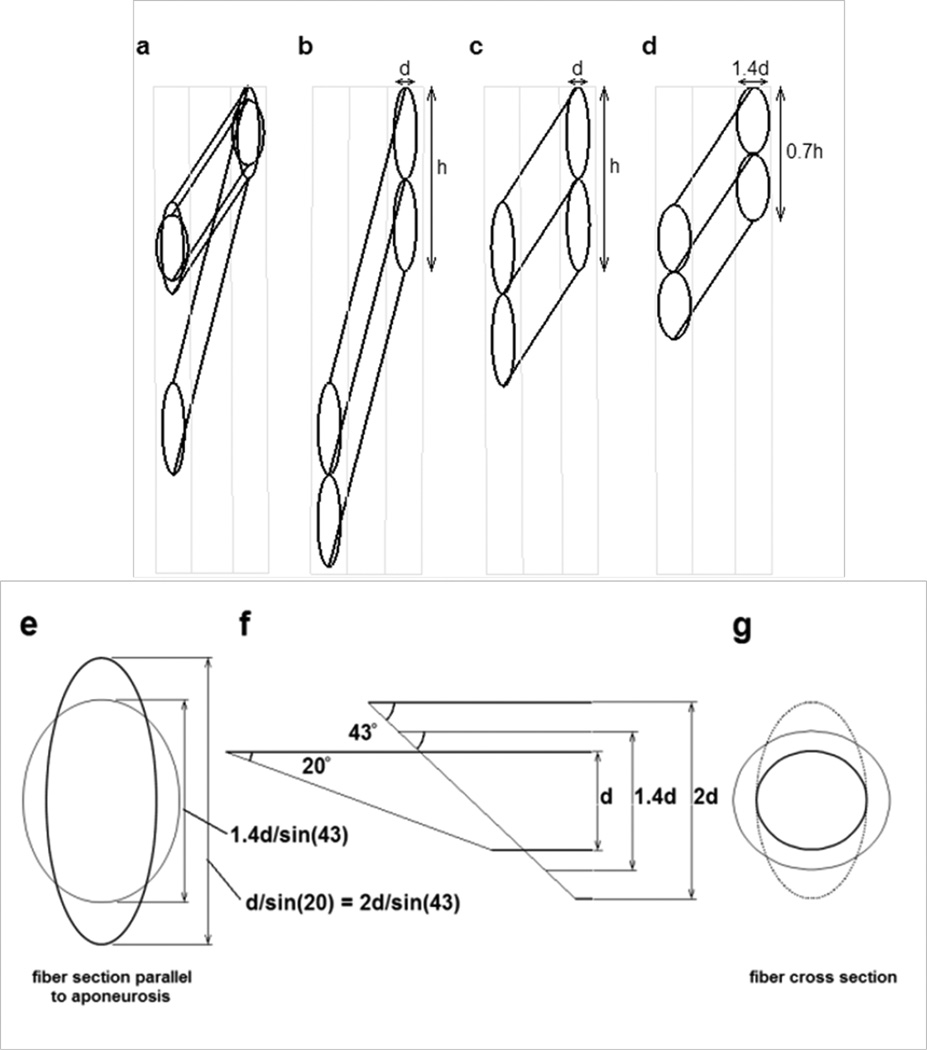
The final model offers a significant departure from a uniform orientation of material properties within the passive material. This model was created as a first attempt at simulating many of the observed features of muscle deformation. We attempted to assign a ‘structure’ to the passive material in an attempt to explore the notion that specific structural design features within a muscle may bring about the observed patterns of deformation. We were particularly challenged by the apparent need to provide control over the change in shape of the muscle fiber cross section while minimizing the detriment to muscle performance observed in the isotropic models. A few papers have proposed the idea that muscle fiber cross section does not change uniformly, and these provided significant clues about how the problem may be approached (Gans, 1982; van der Linden et al., 1998a; Willems and Huijing, 1994). Most important was the geometry originally proposed as a ‘slanted cylinder model’ by Willems & Huijing (Huijing, 1998; Willems and Huijing, 1994), providing a geometry where the cross sectional area of a muscle fiber may change without any change in the area of the oblique cross section of the fiber contacting the aponeurosis (van der Linden et al., 1998a). As a muscle fiber changes length, it rotates, thus altering its pennation angle and also the angle that the aponeurosis plane cuts through the fiber cross section. This is shown in Appendix 1 which illustrates how a hypothetically cylindrical muscle fiber may change shape and pennation angle as the muscle length changes. If the fiber remains cylindrical, the diameter of the cylinder must change in proportion to the square root of the fiber length change in order for the fiber volume to remain constant. Thus the thickness of the fiber (and muscle) must change in addition to the separation of the aponeuroses. This model predicts that when a muscle shortens, the aponeurosis would become shorter, the muscle would become fatter and the area in the plane of the fibers would decrease (Fig. 13a, d, e, f, g). Overall, however, experimental data do not support this model. Interestingly, the prediction of shorter aponeurosis in this model provides a possible alternative explanation for the observed shortening in some regions of the aponeurosis (Chi et al., 2010; Finni et al., 2003; Kinugasa et al., 2008). An alternative to the above symmetrical deformation of the muscle fiber cross section is for the fiber cross section to deform elliptically, with only one axis (lying in the plane of Figs. 4, 9) of the elliptical cross section changing dimension (Fig. 13a, c, e, f, g). The thickness of such a muscle (d in Fig. 13) would not change with fiber length changes, nor would the length of the aponeurosis, represented by the distance h in Fig. 13 (Huijing, 1999; van der Linden et al., 1998a). This model is more consistent with experimental data. In order to propagate such properties throughout the muscle, rather than just at the aponeuroses, we hypothesized a structure, or series of structures throughout the muscle which operate in a similar way to the fiber-aponeurosis interface, opposing any through-plane dimensional changes in the fiber, and resulting in the same intra-fiber dimension of the passive material due to its orientation within and between fibers as the fibers rotate. This is clearly illustrated in a review paper by Huijing (Fig. 12d in (Huijing, 1999)). This hypothesized structure was implemented in our model by specifying an anisotropic material with significant stiffness only parallel to the aponeuroses. The plane strain model adopted for this investigation simulates a very high stiffness along the through-plane axis. The costameres of muscle are a potential candidate for such structures, and illustrate a potentially important function for the abundant structural materials within muscle fibers, across the cell membranes and in the extracellular matrix (Bloch and Gonzalez-Serratos, 2003; Scott et al., 2008; Sjçbloma et al., 2008; Wolff et al., 2006; Zoghbi et al., 2008). These structures, attached to the connective tissue structures of the endomysium (Trotter and Purslow, 1992) would provide a continuous structural matrix throughout the entire intra- and extracellular regions of a muscle. As with the aponeurosis, the relationship between fiber length and the angle at which such structures cut the muscle fiber would result in minimal strain in these passive structures as the muscle changes length while strictly controlling how the muscle fibers (and muscle) change shape. Thus, we demonstrate an alternative to intramuscular pressure for controlling the shape of a muscle as it contracts. It also suggests a possible role for the abundant structural materials present in muscle and also demonstrate how a muscle may change shape significantly without significant detrimental effects from the sophisticated connective tissue structures associated with muscle fibers. For this design to work, the major loading of the endomysium would be oriented approximately along the axis of the muscle rather than parallel to the fiber direction or around the fiber circumference. High compliance in these latter directions may be accomplished by appropriate orientation of collagen fibers. The reported open “weave” observed in endomysial collagen may provide these properties, similar to the biaxial braid utilized in the gag toy commonly known as a Chinese finger trap (Purslow, 2002; Rowe, 1981; Trotter and Purslow, 1992).
Fig. 13.
Diagrams illustrating possible geometry changes in muscle fibers as a pinnate muscle shortens. a) The possible changes in a muscle fiber with a circular cross section as it rotates between the aponeuroses and shortens to 50% of its original length. Two final configurations are shown, each maintaining the same volume during shortening. (i.e. As the muscle fiber length halves, the fiber cross sectional area must double). The resting pennation angle was 20° and the pennation angle after shortening was ~43°. b) Two resting fibers of diameter d between two aponeuroses at the pennation angle of 20°. The vertical distance (labeled as h for the pair of fibers) occupied by individual fibers on the aponeurosis is d/sin(20) or ~ 2.9d. c) The shortened fibers under the constraint that the aponeurosis separation remains constant and the aponeurosis length change is negligible. Distances d and h remain constant. d) The geometry change when the muscle fiber diameter increases symmetrically. As the fiber cross sectional area doubles, the fiber diameter must increase to ~1.4d. The vertical contact distance of the fiber on the aponeurosis would be 1.4d/sin(43°), or ~2.1d. e) The hypothetical contact area of the muscle fiber onto the aponeurosis. The taller ellipse shows the contact surface of the resting fiber at an angle of 20° to the aponeurosis and also of the contracted fiber illustrated in panel c. The shorter ellipse shows the contact area of the shortened fiber in panel d. f) The geometry between a fiber and the aponeurosis. The oblique end of the fiber represents the contact area with the aponeurosis, at an angle of 20° to the fiber for the resting fiber and 43° for the shortened fiber. The thinnest fiber, height d represents the resting fiber illustrated in panel b. The intermediate fiber, height 1.4d represents the geometry of a shortened fiber in panel d. The thickest fiber, height 2d represents the geometry of the shortened fiber in panel c. Note that the length of the oblique lines across the thinnest and the thickest fiber are equal although the overall muscle geometry has changes significantly. g) The changes in fiber cross section (perpendicular to the long axis of the fiber) showing the original fiber cross section (smallest circle) corresponding to panel b, the elliptical cross section of the fiber in panel c and the larger circular cross section of the fiber in panel d.
Simulations of this model (column 4 of Figs. 4, 9) illustrate characteristically different patterns of strain which are also reflected in the strain in the muscle fiber direction (Figs. 7g, h & 11g, h).
The noticeable change in fiber strain close to the aponeurosis contrasts with the more gradual change across the muscle in our other models. The distribution of strain throughout a muscle has been measured experimentally although the spatial resolution limits our ability to make accurate comparisons with our simulations (Shin et al., 2009). Fiber strain in the medial gastrocnemius muscle changed dramatically close to the aponeuroses at each end of the muscle with smaller, more uniform changes along fibers in the middle of the muscle, similar to the results illustrated for the model in Figs. 7g, h. The MRI results also exhibited the progressive reverse of the ends of the fiber experiencing the maximum strain at the proximal and distal ends of the muscle, thus showing encouraging correspondence between this model and in vivo muscle deformation data (Shin et al., 2009).
A further persuasive property of this model is the apparent improvement in active muscle force output with this arrangement of passive tissue (Fig. 12). There is no need for significant deformation of the elastic structures, thus allowing the maximum amount of work to be done on the external world rather than absorbed by deformation of passive intramuscular elastic structures. Additionally, this model lends itself to extrapolation into the third dimension. However, while providing significant insight into muscle deformations, our plane strain model will require extension into the third dimension to accurately represent real-world muscle deformations. Interestingly, this model also exhibits the least change in aponeurosis separation as a result of muscle length changes (Table 5). Previous discussions of the role of the epimysium have considered its role as a mediator of lateral force transmission or of shear forces between fibers (Trotter & Purslow, 1992; Huijing, 1999; Purslow, 2002). Our interpretation seems to be intermediate between these two extremes, suggesting that the optimum load vector should be oriented at an angle to the muscle fiber equivalent to the pennation angle of the muscle. Also implicit in this model is the notion that it is the internal materials of the muscle fibers themselves rather than the extracellular matrix which experiences most of the shear as the muscle fibers rotate.
The mechanical response of the epimysium to dimensional changes of the muscle fiber are also impacted by restricting fiber cross sectional changes to only one axis of an elliptical or polygonal cross section. Models of an epimysium accommodating changes in muscle fiber dimensions assume identical changes in both axes of the fiber cross section (Purslow, 1989; Trotter & Purslow 1992). In a constant volume muscle fiber, this results in a circumference change proportional to the square of the fiber length change whereas changes in only one axis dimension result in a circumference change which is directly proportional to length. Thus, strains (and therefore stresses) in a spirally wound epimysial fiber will be smaller per muscle fiber length change for an ellipse (or polygon) with one constrained axis than they would be for a muscle fiber undergoing similar changes in both dimensions of the cross section.
4.4. Non-uniform muscle fiber strain
The experimental observation of non-uniform strain along the fibers of in vivo contracting muscle (Pappas et al., 2002; Shin et al., 2009) is reproduced in these models. Our models attribute force transmission properties to passive materials within the muscle. The anatomy of a pennate muscle results in a diminishing cross sectional area at each end of the muscle, thus reducing the amount of passive material through which stress must be transmitted. Therefore, higher stress densities in this region may be expected to produce higher strains. At the moment, we are unable to speculate on the mechanical consequences of such a property, but it appears that passive materials have a role in controlling the way that muscle and muscle fibers deform during a contraction. The regional strain differences suggest the distribution of sarcomere strain along a fiber is not constant and it may therefore be advantageous for some sarcomeres to be longer than others. Several publications have noted a ~20% range of sarcomere lengths in skeletal muscle (Golspink, 1968; Tameyasu et al., 1982). One survey of sarcomere lengths suggest that sarcomere lengths may cover a 2-fold range in vertebrate muscle, consistent with the range of strains reported in lengthening human muscle (Shin et al., 2009). A two-fold range of resting sarcomere lengths seems well accepted across different fiber types of insect muscle (Gronenberg et al., 1997; Stokes et al., 1975). Results from simulations and physiological experiments would thus appear to encourage an exploration of potential regional differences in resting sarcomere length.
4.5. Limitations
This model is not intended to be a precise model of muscle, rather a "test bed" to explore the influence of passive intramuscular material properties on the performance of contracting skeletal muscle. For structures with thickness close to the in-plane dimension, the two-dimensional plane-strain model offers a reasonable approximation in representing the mechanical behavior of the three-dimensional structure. For typical muscle component, the thickness is about 30~50% of the in-plane dimension and justifies the employment of the two-dimensional plane-strain model. This geometry simplification is particularly effective for parametric studies. The material properties were chosen to provide a range of behaviors from which we may begin to formalize the relationship between passive material properties and muscle behavior. In the case where the thickness or material property variation in the muscle component become significant, a three-dimensional model is required.
5. CONCLUSION
We have demonstrated that hypothesis-generating mechanical models of muscle suggest distinct patterns of intramuscular deformations that parallel in vivo physiological data. We demonstrate how changes in muscle dimension and force output can be influenced by the passive mechanical properties of intramuscular materials during a contraction. These results point to the importance of lateral force transmission within a muscle (Huijing, 1999, Purslow, 2002) and offer possible clues about the importance of individual intramuscular structural materials. A potentially important application of these findings may relate to changes in intramuscular material properties due to genetic disorders and other pathologies. We show how changes in stiffness and anisotropy of structural materials may have a significant impact upon muscle performance and that such changes are also reflected in the observed deformation of a muscle. In addition to providing a possible mechanism contributing to degradation of muscle performance, these results also suggest that observations of in vivo pathological muscle deformations may help define the major mechanical deficits present in such muscles.
ACKNOWLEDGEMENTS
This study was supported by National Institute of Arthritis and Musculoskeletal and Skin Diseases Grant RO1-AR-53343.
APPENDIX
Diagrams in Fig. 13 illustrate possible geometry changes in muscle fibers as a pinnate muscle shortens. a) The possible changes in a muscle fiber with a circular cross section as it rotates between the aponeuroses and shortens to 50% of its original length. Two final configurations are shown, each maintaining the same volume during shortening. (i.e. As the muscle fiber length halves, the fiber cross sectional area must double). The resting pennation angle was 20° and the pennation angle after shortening was ~43°. b) Two resting fibers of diameter d between two aponeuroses at the pennation angle of 20°. The vertical distance (labeled as h for the pair of fibers) occupied by individual fibers on the aponeurosis is d/sin(20) or ~ 2.9d. c) The shortened fibers under the constraint that the aponeurosis separation remains constant and the aponeurosis length change is negligible. Distances d and h remain constant. d) The geometry change when the muscle fiber diameter increases symmetrically. As the fiber cross sectional area doubles, the fiber diameter must increase to ~1.4d. The vertical contact distance of the fiber on the aponeurosis would be 1.4d/sin(43°), or ~2.1d. e) The hypothetical contact area of the muscle fiber onto the aponeurosis. The taller ellipse shows the contact surface of the resting fiber at an angle of 20° to the aponeurosis and also of the contracted fiber illustrated in panel c. The shorter ellipse shows the contact area of the shortened fiber in panel d. f) The geometry between a fiber and the aponeurosis. The oblique end of the fiber represents the contact area with the aponeurosis, at an angle of 20° to the fiber for the resting fiber and 43° for the shortened fiber. The thinnest fiber, height d represents the resting fiber illustrated in panel b. The intermediate fiber, height 1.4d represents the geometry of a shortened fiber in panel d. The thickest fiber, height 2d represents the geometry of the shortened fiber in panel c. Note that the length of the oblique lines across the thinnest and the thickest fiber are equal although the overall muscle geometry has changes significantly. g) The changes in fiber cross section (perpendicular to the long axis of the fiber) showing the original fiber cross section (smallest circle) corresponding to panel b, the elliptical cross section of the fiber in panel c and the larger circular cross section of the fiber in panel d.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Baskin RJ, Paolini PJ. Muscle Volume Changes. J. Gen. Physiol. 1966;49:387–404. doi: 10.1085/jgp.49.3.387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blemker SS, Pinsky PM, Delp SL. A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. J. Biomech. 2005;38:657–665. doi: 10.1016/j.jbiomech.2004.04.009. [DOI] [PubMed] [Google Scholar]
- Blemker SS, Delp SL. Rectus femoris and vastus intermedius fiber excursions predicted by three-dimensional muscle models. J. Biomech. 2006;39:1383–1391. doi: 10.1016/j.jbiomech.2005.04.012. [DOI] [PubMed] [Google Scholar]
- Bloch RJ, Gonzalez-Serratos H. Lateral force transmission across costameres in skeletal muscle. Exerc. Sport Sci. Rev. 2003;31:73–78. doi: 10.1097/00003677-200304000-00004. [DOI] [PubMed] [Google Scholar]
- Bosboom EMH, Hesselink MKC, Oomens CWJ, Bouten CVC, Drost MR, Baaijens FPT. Passive transverse mechanical properties of skeletal muscle under in vivo compression. Journal of Biomechanics. 2001;34:1365–1368. doi: 10.1016/s0021-9290(01)00083-5. [DOI] [PubMed] [Google Scholar]
- Chi SW, Hodgson J, Chen JS, Edgerton VR, Shin DD, Roiz RA, Sinha S. Finite element modeling reveals complex strain mechanics in the aponeuroses of contracting skeletal muscle. J. Biomech. 2010;43:1243–1250. doi: 10.1016/j.jbiomech.2010.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drace JE, Pelc NJ. Measurement of skeletal muscle motion in vivo with phase-contrast MR imaging. J. Magn. Reson. Imaging. 1994;4:157–163. doi: 10.1002/jmri.1880040211. [DOI] [PubMed] [Google Scholar]
- Drost MR, Maenhout M, Willems PJB, Oomens CWJ, Baaijens FPT, Hesselink MKC. Spatial and temporal heterogeneity of superficial muscle strain during in situ fixed-end contractions. J. Biomech. 2003;36:1055–1063. doi: 10.1016/s0021-9290(02)00461-x. [DOI] [PubMed] [Google Scholar]
- Ervasti JM. Costameres: the Achilles’ Heel of Herculean Muscle. J. Biol. Chem. 2003;278:13591–13594. doi: 10.1074/jbc.R200021200. [DOI] [PubMed] [Google Scholar]
- Finni T, Hodgson JA, Lai AM, Edgerton VR, Sinha S. Nonuniform strain of human soleus aponeurosis-tendon complex during submaximal voluntary contractions in vivo. J Appl. Physiol. 2003;95:829–837. doi: 10.1152/japplphysiol.00775.2002. [DOI] [PubMed] [Google Scholar]
- Gans C. Fiber architecture and muscle function. Exerc. Sport Sci. Rev. 1982;10:160–207. [PubMed] [Google Scholar]
- Golspink G. Sarcomere length during post-natal growth of mammalian muscle fibers. J. Cell Sci. 1968;3:539–548. doi: 10.1242/jcs.3.4.539. [DOI] [PubMed] [Google Scholar]
- Gronenberg W, Paul J, Just S, Hölldobler B. Mandible muscle fibers in ants: fast or powerful? Cell Tissue Res. 1997;289:347–361. doi: 10.1007/s004410050882. [DOI] [PubMed] [Google Scholar]
- Heemskerk AM, Sinha TK, Wilson KJ, Ding Z, Damon BM. Quantitative assessment of DTI-based muscle fiber tracking and optimal tracking parameters. Magn Reson Med. 2009;61:467–472. doi: 10.1002/mrm.21819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huijing PA. Muscle, the motor of movement: properties in function, experiment and modeling. J. Electromyogr. Kinesiol. 1998;8:61–77. doi: 10.1016/s1050-6411(97)00023-0. [DOI] [PubMed] [Google Scholar]
- Huijing PA. Muscle as a collagen fiber reinforced composite: a review of force transmission in muscle and whole limb. J. Biomech. 1999;32:329–345. doi: 10.1016/s0021-9290(98)00186-9. [DOI] [PubMed] [Google Scholar]
- Jenkyn TR, Koopman B, Huijing P, Lieber RL, Kaufman KR. Finite element model of intramuscular pressure during isometric contraction of skeletal muscle. Phys. Med. Biol. 2002;47:4043–4061. doi: 10.1088/0031-9155/47/22/309. [DOI] [PubMed] [Google Scholar]
- Johansson T, Meier P, Blickhan R. A finite-element model for the mechanical analysis of skeletal muscles. J. Theor. Biol. 2000;206:131–149. doi: 10.1006/jtbi.2000.2109. [DOI] [PubMed] [Google Scholar]
- Kinugasa R, Hodgson JA, Edgerton VR, Sinha S. Asymmetrical Deformation of Contracting Human Gastrocnemius Muscle. J. Appl. Physiol. doi: 10.1152/japplphysiol.00666.2011. 20011. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinugasa R, Shin D, Yamauchi J, Mishra C, Hodgson JA, Edgerton VR, Sinha S. Phase-contrast MRI reveals mechanical behavior of superficial and deep aponeuroses in human medial gastrocnemius during isometric contraction. J. Appl. Physiol. 2008;105:1312–1320. doi: 10.1152/japplphysiol.90440.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maganaris CN, Baltzopoulos V, Sargeant AJ. In vivo measurements of the triceps surae complex architecture in man: implications for muscle function. J. Physiol. 1998;512:603–614. doi: 10.1111/j.1469-7793.1998.603be.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maganaris CN, Paul JP. In vivo human tendinous tissue stretch upon maximum muscle force generation. J. Biomech. 2000;33:1453–1459. doi: 10.1016/s0021-9290(00)00099-3. [DOI] [PubMed] [Google Scholar]
- Oomens CWJ, Maenhout M, van Oijen CH, Drost MR, Baaijens FP. Finite element modeling of contracting skeletal muscle. Phil. Trans. R. Soc. Lond. B. 2003;358:1453–1460. doi: 10.1098/rstb.2003.1345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otten E. Concepts and models of functional architecture in skeletal muscle. Exerc. Sport Sci. Rev. 1998;16:89–137. [PubMed] [Google Scholar]
- Pappas GP, Asakawa DS, Delp SL, Zajac FE, Drace JE. Nonuniform shortening in the biceps brachii during elbow flexion. J. Appl. Physiol. 2002;92:2381–2389. doi: 10.1152/japplphysiol.00843.2001. [DOI] [PubMed] [Google Scholar]
- Purslow PP. Strain induced reorientation of an intramuscular connective tissue network: implications for passive muscle elasticity. J. Biomech. 1989;22:21–31. doi: 10.1016/0021-9290(89)90181-4. [DOI] [PubMed] [Google Scholar]
- Purslow PP. The structure and functional significance of variations in the connective tissue within muscle. Comp. Biochem. Physiol. A: Mol. Int. Physiol. 2002;133:947–966. doi: 10.1016/s1095-6433(02)00141-1. [DOI] [PubMed] [Google Scholar]
- Rowe RWD. Morphology of perimysial and endomysial connective tissue in skeletal muscle. Tissue and Cell. 1981;13:681–690. doi: 10.1016/s0040-8166(81)80005-5. [DOI] [PubMed] [Google Scholar]
- Sanger JM, Sanger JW. The Dynamic Z Bands of Striated Muscle Cells. Sci. Signal. 2008;1:e37. doi: 10.1126/scisignal.132pe37. [DOI] [PubMed] [Google Scholar]
- Scott RS, Li Z, Paulin D, Uvelius B, Small JV, Arner A. Role of desmin in active force transmission and maintenance of structure during growth of urinary bladder. Am. J. Physiol. Cell Physiol. 2008;295:324–331. doi: 10.1152/ajpcell.90622.2007. [DOI] [PubMed] [Google Scholar]
- Shin DD, Hodgson JA, Edgerton VR, Sinha S. In vivo intramuscular fascicle-aponeuroses dynamics of the human medial gastrocnemius during plantarflexion and dorsiflexion of the foot. J. Appl. Physiol. 2009;107:1276–1284. doi: 10.1152/japplphysiol.91598.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha U, Sinha S, Hodgson JA, Edgerton RV. Human Soleus Muscle Architecture at Different Ankle Joint Angles from Magnetic Resonance Diffusion Tensor Imaging. J Appl. Physiol. 2010;110:807–819. doi: 10.1152/japplphysiol.00923.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjçbloma B, Salmazoa A, Djinovic´-Carugoa K. a-Actinin structure and regulation. Cell Mol. Life Sci. 2008;65:2688–2701. doi: 10.1007/s00018-008-8080-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes DR, Josephson RK, Price RB. Structural and functional heterogeneity in an insect muscle. J. Exp. Zool. 1975;194:397–408. doi: 10.1002/jez.1401940205. [DOI] [PubMed] [Google Scholar]
- Tameyasu T, Ishide N, Pollack GH. Discrete sarcomere length distribution in skeletal muscle. Biophys. J. 1982;37:489–492. doi: 10.1016/S0006-3495(82)84695-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trotter JA, Purslow PP. Functional morphology of the endomysium in series fibered muscles. J. Morphol. 1992;212:109–122. doi: 10.1002/jmor.1052120203. [DOI] [PubMed] [Google Scholar]
- van der Linden BJ, Koopman HF, Grootenboer HJ, Huijing PA. Modelling functional effects of muscle geometry. J. Electromyogr. Kinesiol. 1998a;8:101–109. doi: 10.1016/s1050-6411(97)00026-6. [DOI] [PubMed] [Google Scholar]
- van der Linden BJJJ, Koopman HFJM, Huijing PA, Grootenboer HJ. Revised planimetric model of unipennate skeletal muscle: a mechanical approach. Clin. Biomech. 1998b;13:256–260. doi: 10.1016/s0268-0033(98)00002-3. [DOI] [PubMed] [Google Scholar]
- van der Linden BJJJ. Mechanical Modeling of Skeletal Muscle Functioning. University of Twente Press, Enschede PhD. Thesis; 1998c. [Google Scholar]
- van Donkelaar CC, Willems PJB, Muijtjens AMM, Drost MR. Skeletal muscle transverse strain during isometric contraction at different lengths. J. Biomech. 1999;32:755–762. doi: 10.1016/s0021-9290(99)00073-1. [DOI] [PubMed] [Google Scholar]
- van Leeuwen JL, Spoor CW. Modelling the pressure and force equilibrium in unipennate muscles with in-line tendons. Philos. Trans. R Soc. Lond. B. Biol. Sci. 1993;342:321–333. doi: 10.1098/rstb.1993.0162. [DOI] [PubMed] [Google Scholar]
- van Loocke M, Lyons CG, Simms CK. A validated model of passive muscle in compression. J. Biomech. 2006;39:2999–3009. doi: 10.1016/j.jbiomech.2005.10.016. [DOI] [PubMed] [Google Scholar]
- Weiss JA, Maker BN, Govindjee S. Finite element implementation of incompressible, transversely isotropic hyperelasticity. Comput. Methods Appl. Mech. Engrg. 1996;135:107–128. [Google Scholar]
- Willems MET, Huijing PA. Mechanical and geometric properties of the rat semimembranosus lateralis muscle during isometric contractions. J. Biomech. 1994;27:1109–1118. doi: 10.1016/0021-9290(94)90051-5. [DOI] [PubMed] [Google Scholar]
- Wolff AV, Niday AK, Voelker KA, Call JA, Evans NP, Granata KP, Grange RW. Passive mechanical properties of maturing extensor digitorum longus are not affected by lack of dystrophin. Muscle Nerve. 2006;34:304–312. doi: 10.1002/mus.20588. [DOI] [PubMed] [Google Scholar]
- Yucesoy CA, Koopman BHFJM, Huijing PA, Grootenboer HJ. Three-dimensional finite element modeling of skeletal muscle using a two-domain approach: linked fiber-matrix mesh model. J. Biomech. 2002;35:1253–1262. doi: 10.1016/s0021-9290(02)00069-6. [DOI] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: properties, models, scaling and application to biomechanics and motor control. Crit. Rev. Biomed. Eng. 1989;17:359–411. [PubMed] [Google Scholar]
- Zoghbi ME, Woodhead JL, Moss RL, Craig R. Three-dimensional structure of vertebrate cardiac muscle myosin filaments. PNAS. 2008;105:2386–2390. doi: 10.1073/pnas.0708912105. [DOI] [PMC free article] [PubMed] [Google Scholar]