Efficient visual-search model observers for PET

Abstract

Objective:

Scanning model observers have been efficiently applied as a research tool to predict human-observer performance in F-18 positron emission tomography (PET). We investigated whether a visual-search (VS) observer could provide more reliable predictions with comparable efficiency.

Methods:

Simulated two-dimensional images of a digital phantom featuring tumours in the liver, lungs and background soft tissue were prepared in coronal, sagittal and transverse display formats. A localization receiver operating characteristic (LROC) study quantified tumour detectability as a function of organ and format for two human observers, a channelized non-prewhitening (CNPW) scanning observer and two versions of a basic VS observer. The VS observers compared watershed (WS) and gradient-based search processes that identified focal uptake points for subsequent analysis with the CNPW observer. The model observers treated “background-known-exactly” (BKE) and “background-assumed-homogeneous” assumptions, either searching the entire organ of interest (Task A) or a reduced area that helped limit false positives (Task B). Performance was indicated by area under the LROC curve. Concordance in the localizations between observers was also analysed.

Results:

With the BKE assumption, both VS observers demonstrated consistent Pearson correlation with humans (Task A: 0.92 and Task B: 0.93) compared with the scanning observer (Task A: 0.77 and Task B: 0.92). The WS VS observer read 624 study test images in 2.0 min. The scanning observer required 0.7 min.

Conclusion:

Computationally efficient VS can enhance the stability of statistical model observers with regard to uncertainties in PET tumour detection tasks.

Advances in knowledge:

VS models improve concordance with human observers.

The prospect of better clinical outcomes is a major impetus for research in medical imaging. This motivation is formalized in the practice of task-based assessments, whereby image quality is defined by how well observers can perform a specified task with an appropriate set of test images.¹ An observer could be a human or a mathematical algorithm, undertaking diagnostic tasks such as parameter estimation or tumour detection. With tumour detection, diagnostic accuracy as measured in observer studies provides a basic measure of imaging system performance.² It has been suggested that consistent use of observer studies for evaluation and optimization in the early stages of technology development could improve both the focus of imaging research and the efficiency of later-stage studies.³

High levels of observer variance can make human-observer studies impractical for extensive assessments. A standard alternative is to employ a mathematical model observer that mimics humans for the bulk of the observing work, augmenting these data with occasional human-observer data for validation purposes. Many of these model observers in regular use trace their derivation to ideal observers from signal detection theory.⁴ An ideal observer establishes the upper bound on diagnostic accuracy for a given task when performance of the task is limited by stochastic processes such as quantum and anatomical noise. Models of human observers generally build on an ideal observer by incorporating additional sources of noise or other inefficiencies such as limited visual-response characteristics.

Among the widely used model examples are linear, Hotelling-type observers for two-hypothesis (binary) tasks. These observers are constructed by treating the image variations as a multivariate Gaussian process, with the relevant stochastic processes contributing to the total Gaussian covariance. The performance of a Hotelling observer depends solely on prior knowledge in the form of first- and second-order image statistics. Among the standard Hotelling applications are quantum-noise limited signal-known-exactly (SKE)–background-known-exactly (BKE) tasks, where prior knowledge of the mean tumour-absent (or background) image is used to classify each test image as tumour-present or tumour-absent at a specific location.

We are interested in developing model observers that can accurately and efficiently predict human performance in clinically realistic tasks. Model-observer studies for detection–localization tasks have been relatively rare in the literature, but several recent works have made extensive use of these observers in comparing the relative benefits of time-of-flight and point-response modelling in positron emission tomography (PET) reconstructions.^5–7 With regard to observer development, these works are notable for their treatment of tumour detection–localization tasks for scanning observers using real imaging data. These scanning models, derived as fundamental extensions of the Hotelling-type models,⁸ perform what may be classified as “signal-known-statistically” (SKS) tasks, accomplishing the task by examining every possible tumour location in an image. The aforementioned PET studies found good correlation between the scanning and human-observer results.

These PET studies also featured substantial differences in how the model observer was applied. Kadrmas et al^5,6 employed a scanning channelized non-prewhitening (CNPW) model, complete with background reference images, to read study images from physical phantom acquisitions. Each reference image provided a low-noise estimate of the background anatomical noise for a given study image,⁹ effectively creating a BKE task. These studies treated tumour locations in the lungs, liver, abdomen and pelvis. Schaefferkoetter et al⁷ used hybrid images (normal clinical backgrounds with simulated tumours) and the scanning observer in what may be considered a “background-assumed-homogeneous” (BAH) task. This study was limited to tumour locations in the liver.

To better understand the properties of the scanning CNPW observer as applied in these PET studies, we investigated how the BKE and BAH task assumptions can affect observer performance in PET detection–localization tasks. Our observer study evaluated tumour detectability in different organs of simulated PET images as a function of the image-display format. The study images and human-observer data were taken from a previous localization receiver operating characteristic (LROC) validation study,⁹ which compared human and scanning model observers. We shall refer to this earlier work as Study I.

The present study also included tests of a visual-search (VS) model observer. This model is motivated by the two-stage paradigm presented by Kundel et al¹⁰ for how radiologists read images. A reading with an experienced radiologist generally relies on a sequence involving quick, global impressions to identify possible abnormalities (or candidates), followed by a lengthier inspection of these candidates.¹¹ Our VS framework applies a feature-based search as a front end to analysis and decision-making processes conducted with a statistical observer (usually the scanning CNPW model).

In an earlier study,¹² comparing the scanning and VS observers for tumour detection in three-dimensional (3D) lung single-photon emission CT (SPECT), the latter provided a better fit to human data. The downside was a ten-fold increase in execution time compared with the scanning observer. Efficient algorithms for carrying out the initial search phase of the VS observer are necessary for realizing the advantages for large-scale studies, and a pair of search algorithms are compared in this work.

A standard approach to gauge model-observer effectiveness is to compare the average task performance from a group of human observers with the performance of the model. However, a truly robust human-observer model should satisfy more stringent measures of agreement. Chakraborty et al¹³ have proposed pseudovalue correlation as a possible measure. Other researchers (e.g., Abbey and Eckstein^14,15) have approached model-observer estimation based on the raw human-observer data. Herein, we consider case-by-case agreement (or concordance) in the tumour localizations provided by pairs of observers.

BACKGROUND

Tumour search tasks

A two-dimensional (2D) test image in our study is represented by the N × 1 vector f. We consider two classes of images such that f is either tumour free or contains a single tumour somewhere within specified areas of the body. The possible tumour locations are represented by the set Ω of pixel indices, which can vary with f.

With J possible locations, we can construct J + 1 detection hypotheses for a model observer. Under the tumour-absent hypothesis H₀, f comprises a background (b) and zero-mean stochastic noise (n):

Image b can be thought of as the mean obtained by averaging many reconstructions of the appropriate normal test case, whereas image n is the reconstructed quantum noise. Under each of the remaining J tumour-present hypotheses,

the image also has a tumour s_j at the jth location. Note that Equations (1) and (2) are not intended as precise statements about how f was formed. Details about the imaging simulation are provided in the Methods section.

The prior information or training that observers receive with regard to the test images is an essential component of the task definition. As a starting point, we assume that b for a given f is known and the tumour profile at a given location is fixed and known to the observer. (To varying extents, these assumptions were relaxed in actually applying the model observers.) With location uncertainty, this is an SKS task. Incorporating a tumour discrimination component into the task calls for additional subscripts on s_j (and on H_j) that relate to other sources of tumour variability. However, the observer would still have prior knowledge about the possible tumour profiles.

Observer-task performance can be assessed with LROC methodology, with each test image being assigned a localization (r) and a scalar confidence rating (λ) by an observer. The tumour locations represented by Ω may be contiguous, representing a region of interest (ROI) such as the lungs or liver. In such a case, the localization in a tumour-present image is scored as correct if r is within a fixed threshold distance from the true tumour location. An image is read as abnormal at threshold λ_t if λ  λ_t. The LROC curve relates the probability of a true-positive response conditioned on correct localization to the probability of a false-positive response as λ_t varies, and accepted performance figures of merit are the area under the LROC curve (A_L) and the fraction of tumours correctly localized (or fraction correct), which we denote as F_c.

Image class statistics

The model observers for our study are based on statistical decision theory and thus require knowledge of certain class statistics. We denote the conditional mean of f under the jth hypothesis as f_j = 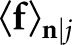, where the bracket notation indicates an average over the quantum noise n given that f has a tumour centred on the jth pixel. Thus, f₀ = b for the tumour-absent hypothesis and f_j = b + s_j for the tumour-present hypotheses.

The N × N covariance matrix K accounts for the sources of randomness in the images, which for the BKE task are quantum noise and tumour location. As is often performed in model observer studies with emission images, we make the low-contrast approximation that the presence of the tumour has a negligible effect on the pixel covariances, so that only quantum noise need to be considered. In that case, the covariance matrix is:

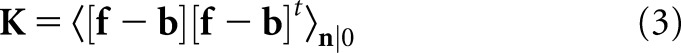Ideal and quasi-ideal observers

An ideal observer establishes the upper bound on performance for tasks in which performance is limited by stochastic processes. The mathematical form of the observer depends on the task definition and also on the performance figure of merit. In medical imaging research, ideal observers have been proposed for optimizing system hardware and data acquisition protocols and have also served as the basis for many model observers in the literature.

For our detection–localization tasks, an ideal observer that maximizes A_L is appropriate. Under fairly basic conditions, this is accomplished with the Bayesian observer that computes the location-specific likelihood ratio:^16,17

for which 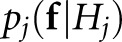is the conditional probability distribution for the image pixels under the jth hypothesis. The LROC data for f are then determined according to the following rules:

The term scanning observer has been used in the literature¹⁷ to describe this approach of selecting the maximal response of some perception statistic to identify the most suspicious location.

In practice, the exact conditional probabilities are typically unknown. A useful recourse is to substitute the multivariate normal distribution,

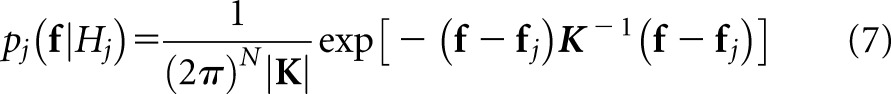for all j. By substituting this distribution into Equation (4) and transforming to log-likelihoods, one arrives at a PW observer that computes the affine test statistic given below:

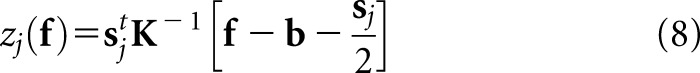We shall use the J-element vector z to denote the set of all z_j.

For most realistic tumour-detection tasks, this PW observer is only quasi-ideal; however, it preserves some ideal characteristics that are suitable as a starting point for human-observer models, such as prior knowledge about the class statistics and the ability to perform exact numerical integration over specified ROIs. In deference to similarities with the Hotelling-type observers that are widely applied for binary tasks, the scanning PW observer has also been referred to as a scanning Hotelling observer.¹⁷

METHODS AND MATERIALS

Imaging simulation

A brief overview of the imaging simulation is provided in this section. Additional details can be found in studies by Gifford et al⁹ and Lartizien et al.¹⁸ An F-18 fludeoxyglucose biodistribution was assigned to the various organs of a mathematical cardiac torso phantom¹⁹ that corresponded to a 170-cm patient weighing 70 kg. Multiple realizations of the phantom were produced by the random placement of spherical tumours in the liver, lungs and background soft tissue. The tumours were 1 cm in diameter, and the centre of a given tumour was constrained to lie at least 1 cm below the organ surface. Otherwise, the tumour placement was random. The use of five tumour contrasts per organ presented observers with a wide range of detection challenges.¹⁸ These contrasts ranged from 2.5 to 4.75 in the liver, 5.5 to 9.0 in the lungs and 6.5 to 10.5 in the soft tissue. The contrast assignment to the tumours in a particular organ was randomized.

The simulation modelled fully 3D data acquisitions. Noiseless imaging data were obtained using the ASIM (analytic simulator) projector,²⁰ which accounted for attenuation, scatter and randoms. Poisson noise was then added to the data prior to 3D reconstruction with an attenuation-weighted ordered-sets expectation maximization (AWOSEM) reconstruction algorithm. The noise level was consistent with clinical protocols utilizing a 12-mCi dose and an uptake period of 90 min.

Image reconstruction

The FORE + AWOSEM algorithm,²¹ which combines Fourier rebinning with AWOSEM, was used for image reconstruction. The 3D projection data were rebinned into 144 projection angles, and reconstructed volumes were obtained using four AWOSEM iterations. The projection angles were partitioned into 16 subsets for the iteration. Each reconstructed volume consisted of 225 transaxial slices (2.4-mm thickness), with slice dimensions of 128 × 128 (5-mm voxel width). These non-cubic voxel dimensions led to oval tumour profiles when the images were viewed in the coronal and sagittal formats. Post smoothing was performed using a 3D Gaussian filter with a 10-mm full width at half maximum.

Test image slices that were extracted for the LROC study then underwent a final image processing in the form of an adaptive, organ-specific upper thresholding.⁹ This process increased the dynamic range of the image greyscale at the count levels near those of the tumours, modelling to some extent the thresholding that nuclear medicine physicians apply to clinical images, while imposing some control over the process. Afterwards, the images were converted to 8-bit greyscale format and then zero-padded to the 256 × 256 dimensions compatible with our viewing software. Example images are shown in Figure 1.

Figure 1.

An example of positron emission tomography study images. The top row (a–c) shows a case with a liver tumour in the coronal, sagittal and transverse views. Images in the middle row (d–f) pertain to a lung tumour case, whereas the bottom row (g–i) shows a case with a soft-tissue tumour.

Scanning observers

A family of scanning observers is obtained by generalizing Equation (8) to the linear form:

where w_j is a location-specific scan template and c_j is a reference image that provides a normal (in the sense of tumour absence) calibration at the given location. The superscript t denotes the transpose. With the scanning Hotelling observer described in the Ideal and quasi-ideal observers section, w_j = K⁻¹s_j and 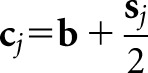. Other choices for the template and reference image will give Hotelling-type scanning models with different levels of prior knowledge.

The channelized Hotelling (CH) observer²² is an appropriate starting point for human-observer models, having been widely applied for SKE tasks. The CH model includes band-pass spatial-frequency filters intended to mimic the human visual system. In the scanning mode, the observer computes perception measurements from the filter values 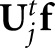at various locations, where the matrix U_j contains the spatial responses of c shift-invariant channels (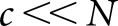) and the matrix index indicates that these responses are to be centred on the jth location. The resulting c × c channel covariance matrices 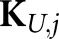are generally not location invariant, but the small number of channels greatly simplifies the calculation of z in comparison with having to estimate and invert K.

Nonetheless, the burden of computing 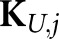from sample images can still be appreciable. Gifford et al²³ estimates of the channel covariances for all possible tumour locations in a mathematical phantom were obtained using a single set of normal training images, but even though only three channels were used, stable estimates of A_L still required several hundreds of training images. In addition, there is some evidence^7,23 that channel PW has little effect on model-observer performance for search tasks involving statistical image reconstructions in nuclear medicine.

The choice of c_j may also be grounded in computational concerns. The location-specific nature of the tumour profile for the scanning Hotelling observer will be a problem if there are extensive search areas and profile variability with respect to location is relatively high. In emission tomography, the reconstructed tumours often display noticeable spatial variations, largely owing to attenuation effects. Rather than include the full range of variations, one may treat the tumour profile as locally shift invariant over appropriate subregions of Ω. In our work, model observers consider the profile 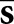generated as the average tumour profile over a given organ of interest. Note that this approach adds uncertainty to the detection task.

Based on the above considerations, a scanning CNPW observer was applied for Study I that computed:

where the shift-invariant template,

is a filtered version of the mean reconstructed tumour 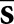. In this equation, vector 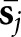represents the mean reconstructed tumour profile shifted to the jth location. A set of three 2D difference-of-gaussian (DOG) channels comprised the sparse DOG model applied in Study I.⁹ The shift invariance of the mean tumour and the channel responses allow efficient calculation of all z_j values for f by means of a 2D cross-correlation operation.

For the present study, the CNPW observer was applied under four task variants that tested the model response to anatomical noise at the organ boundaries alone and over the organs as a whole. Prior knowledge of b was one consideration, and the BKE and BAH assumptions were both tested. A second consideration was whether the model observer was made aware of the restriction that tumours lie no closer than 1 cm from the organ boundaries. (The human observers were aware of this.) Henceforth, we let Ω represent the full bounded region for a given organ. Excluding locations within the 1-cm margin, the search ROI becomes the reduced region Ω_R. Each task may be denoted by the particular combination of background and ROI knowledge (e.g., BKE- and BAH-Ω_R).

Visual-search observers

The VS observer applied in this work adds a front-end search process to the scanning observer that effectively replaces the location set Ω in Equations (5) and (6) with a considerably smaller subset. The observer framework was adapted from the VS paradigm of image interpretation for radiologists put forth by Kundel et al.¹⁰ According to these authors, a brief holistic search that identifies suspicious candidate regions is followed by more-deliberate candidate analysis and decision-making. The intent of the search process for our VS observer is to closely mimic the candidate selection that humans would make. The analysis stage for the VS observer was carried out with the CNPW observer described above.

Tumour detection in emission tomography is often concerned with locating correlated regions of high activity or “blobs.” Our original VS observer characterized blob morphology with an iterative gradient-ascent (GA) algorithm with line search.²⁴ Beginning the iteration at the centre of a given ROI pixel, one follows the greyscale intensity gradient in subsequent iterations to eventually determine a corresponding convergence point (or focal point). Starting pixels that converge to the given focal point comprise the region of attraction for that focal point and make up the blob. Repeating the iterative process for all the ROI pixels as initial guesses leads to a mapping of the focal points and their corresponding regions of attraction. The relevant blobs for a given image have focal points within the specified ROI, and the subsequent scanning-observer analysis of these candidates is conducted only at the focal points. Restricting the analysis to ROI blobs in this way makes the VS observer less susceptible to the effects of background structures compared with scanning observers.¹²

The GA algorithm is computationally intensive in treating the image gradient as a continuous field. For the 3D lung SPECT studies in Gifford¹², GA-based VS observers required 60 min to read 100 volumes compared with 7 min for the scanning CNPW observer. The computer code for both observers was written in [Interactive Data Language (IDL), Exelis Visual Information Solutions, Boulder, CO]. For this work, we used the GA algorithm but also tested the watershed (WS) algorithm²⁵ that comes with the IDL package. Both versions of the VS observer were applied for the same four tasks as the scanning observer.

Observer study

Our LROC study compared the detectability of tumours in the reconstructed images as a function of display format. The human-observer data were collected from two imaging scientists (non-radiologists) who were well versed in the purposes of the study.⁹ There were 292 images per display format, read in two sets of 146 images. Each set consisted of 42 training images followed by 104 test images. The 84 training images per format combined 14 abnormal cases per organ with an equal number of normal cases per organ. Among the 208 test images, the number of cases per organ varied, with 21 abnormal/normal pairs for the liver, 64 pairs for the lungs and 102 pairs for the tissue. For a given image, the observer (whether human or mathematical) was told which organ to search.

Each human observer, thus, read a total of six image sets (two sets per format × three formats) in the study. The order in which these sets were read varied with observer, and the reading order of the images in a given set was randomized for each observer. The images were displayed on a computer monitor, which had been calibrated to provide a linear mapping between image grayscale values and the logarithm of the display luminosity. Observers were not allowed to adjust the display but were permitted to vary both the room lighting and viewing distance. Rating data in the human study were collected on a six-point ordinal scale. With each image, an observer also marked a suspected tumour location with a set of cross-hairs that was controlled with the computer mouse.

A localization within 15 mm of a true location was scored as correct. This radius of correct localization (R_cl) was determined empirically from the human-observer data, and a single value was applied for all the studies. The threshold is determined by first calculating the fraction of tumours correctly located as a function of proposed radius for each image-display format. This produces a set of monotonically non-decreasing curves. The objective is to pick a radius within an interval where all three curves are relatively flat, ensuring that moderate variations in R_cl will not significantly affect the study results. More details on the choice of R_cl can be found in Gifford et al⁹. Because of the non-cubic voxels used in the reconstruction, the threshold radius defined an ellipsoid centred on the true location, with minor axes of three pixels in the transverse plane and a major axis of 6.25 pixels in the axial direction.

The model observers read the same images as the human observers, with confidence ratings and localizations determined according to Equations (5) and (6). Correct localizations were assessed with the same R_cl as in the human-observer study. A voxelized density map of the mathematical phantom was used to delineate the various organ regions for the model observers. The relevant statistical template components in Equations (10) and (11) are the mean reconstructed tumour profile 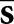and the mean background b. In this work, 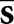for each display format was estimated from the set of 84 training images, whereas b was approximated by the average of a set of 25 noisy normal reconstructions.

A Wilcoxon estimate²⁶ of the area under the LROC curve was used as the figure of merit for all observers in this study. Each human observer's data from the two image subsets were pooled for scoring purposes. For each observer, values of A_L were calculated for the nine combinations of organ (liver, lung and soft tissue) and display format (coronal, sagittal and transverse views). An average area 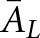for each format and organ was computed over the two human observers. Standard errors for the A_L estimates were calculated using the formula given by Tang and Balakrishnan.²⁷

Observer concordance

Comparing the A_L values from a study is a standard way of validating model observers. However, A_L is an average figure of merit that obscures case-by-case discrepancies in the raw data. A truly robust model of the human observers should satisfy more stringent measures of agreement. For this study, we also computed a measure of observer concordance that summarized the localization agreement between pairs of observers. We refer to this measure as the fraction of matching localizations (or matching fraction). This measure is similar in concept to the fraction correct (F_c) defined in Tumour search tasks section, except that the localizations from one observer are compared with the localizations from a second observer instead of the actual tumour locations. Also, F_c only considers tumour-present data, whereas this concordance measure can account for the localizations in all the images.

Two approaches to compute matching fractions for the model observers were tested. We let F_m denote the matching fraction between the two human observers or a cross-pairing of a model observer and a human observer. Concordance for a given model observer can be obtained as the average (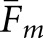) of the cross-pairings for that observer. A broader definition of concordance compares a localization from the model observer to the pool of same-case human-observer localizations. A match is assigned when the model-observer localization agrees with any of the human-observer localizations. We denote this version of the matching fraction as 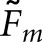. With two human observers, the two fractions are related by the following formula:

where P is the fraction of cases in which only one human observer matched with the model observer.

Scoring the localization agreement for the test images requires a matching distance threshold R_m. To set this parameter, we followed the same general approach that was described in Observer study section for determining R_cl. Further details on how R_m was selected are given in Observer concordance section.

RESULTS

Visual-search algorithms

The VS models based on the GA and WS clustering algorithms identified very different numbers of focal-point candidates per image. For example, the GA version found an average of 148.8 focal points per coronal lung image and 223.2 focal points per transverse tissue image. The corresponding statistics for these two image sets with the WS-based observer were 39.0 and 95.1 focal points, respectively. Similar reductions in the number of focal points for the other seven image sets were also seen with the WS version.

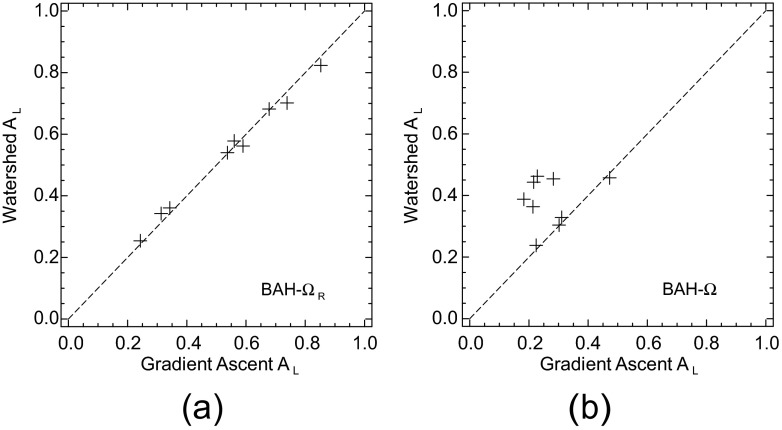
The diagnostic performances of these two VS observers were compared for the four task definitions. Some representative A_L results of these comparisons are shown in the scatter plots of Figure 2. The diagonal line in each plot is provided as a reference for equality. Despite the disparity in focal-point totals, quantitative agreement in the performances was quite high with three of the tasks. Figure 2a offers the BAH-Ω_R comparison. With both VS models, the values of A_L for this task were in the range of (0.25–0.85). Similar plots (not shown) were obtained with the BKE tasks, although the performance range for these easier tasks was (0.35–0.90). The Pearson correlation coefficient (r) exceeded 0.99 with each of these three tasks.

Figure 2.

Performance comparisons of the visual-search observers based on the gradient-ascent and watershed algorithms. Values of area under the localization receiver operating characteristic curve (A_L) are plotted for (a) the background-assumed-homogeneous (BAH)-Ω_R task and (b) the BAH-Ω task. The dotted diagonal line in each plot is included to help judge deviations from equality.

Focal-point totals were an issue with the BAH-Ω task. This was the most difficult of the four tasks, providing the least amount of prior information to the model observers. As shown in Figure 2b, both VS models yielded A_L values in the approximate range of (0.20–0.45). However, the relatively low correlation coefficient (r = 0.21) underscores how important the search quality becomes as task difficulty increases. The impact of the search on observer consistency was assessed by comparing each observer's scores from the BKE-Ω_R and BAH-Ω tasks. The correlation coefficients were, respectively, 0.14 and 0.94 for the GA and WS models.

The times required for the VS observer to read the 624 test images were 19.0 min with the GA algorithm vs 2.0 min with the WS algorithm. The scanning observer took 0.7 min. The remainder of Results section treats only the WS version of the VS observer.

Observer performance

The average human-observer performances in our study were roughly the same for tumours in the soft tissue and lungs and lower with the liver tumours. For a given organ, performances were highest with the transverse and sagittal displays and comparatively lower with the coronal images, in part because the latter images featured the largest ROIs.

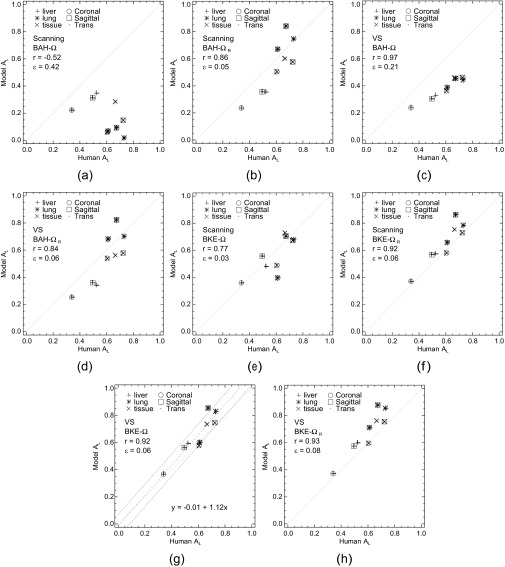
Scatter plots comparing the model and human-observer performances are given in Figure 3. With all observers, the uncertainties in A_L were approximately 0.07–0.09 for lung and soft-tissue sets and 0.10–0.12 for the liver sets. Each of the eight plots treats one combination of model observer and task. One of the plots (Figure 3g) includes a regression analysis (discussed below). As shown in Figure 3, r for these comparisons ranged from −0.52 to 0.97 for the BAH tasks (Figure 3a–d) and 0.77 to 0.93 for the BKE tasks (Figure 3e–h). Regardless of task, both model observers demonstrated consistent correlation with the humans for the liver image sets. Task definition did affect the correlation for the other image sets and the quantitative accuracy (ε) of the model-observer predictions. Accuracy was quantified for each plot by the root-mean-squared (RMS) difference between the observer performances.

Figure 3.

(a–h) A comparison of human and model observer performances. Each plot compares the nine values of from the human observers to the areas obtained from a model observer with one of the four tasks. The correlation coefficient (r) and root-mean-squared error (ε) are provided for each comparison. BAH, background-assumed-homogeneous; BKE, background-known-exactly; VS, visual search.

The highest correlation was obtained with the VS observer in the BAH-Ω task (Figure 3c). The lowest r values were associated with the scanning observer and the Ω ROI (plots shown in Figure 3a,e). Operating pixel-by-pixel, this observer does not differentiate between actual tumours and relatively hot spill-in of activity that is most apparent at the boundaries of the cooler organs (for this simulation, the lungs and soft tissue). This limitation, which is aggravated by the BAH assumption, can be addressed by working with Ω_R instead of Ω (Figure 3b,f) or by using the VS observer, which examines local pixel variations during the holistic search. The coefficients for the VS observer were the most stable, particularly for the BKE tasks (Figure 3g–h).

Disparate trends in r and ε were evident with the various combinations of model observer and task, with the lowest (and highest) RMS errors coming from the scanning observer. A separate consideration is whether a model presents minimal detection inefficiencies relative to the human observers. Such was the case in three of our BKE comparisons (Figure 3f–h), where the model observer performed at or above the level of the humans for every image set. A representative linear fit to the scatter data, along with prediction intervals [±1 standard deviation (SD)], is shown within the VS BKE-Ω plot in Figure 3g. In this case, the model observer overperformed relative to the humans at the upper end of the A_L scale, in large part because of results with the sagittal and transverse lung image sets. Quantum noise in the lungs is low compared with the liver, and with the BKE assumption, there is a high likelihood of detection if the actual location has been identified as a focal point.

Observer concordance

Values of F_m were calculated between the two human observers and for each cross-pairing of model and human observer. From these cross-pairing values, both 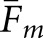and 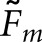were calculated for the model observers. Separate fractions were computed for the 312 abnormal test images, the 312 normal test images and all 624 test images combined. We did not perform a subanalysis on the basis of display format or organ.

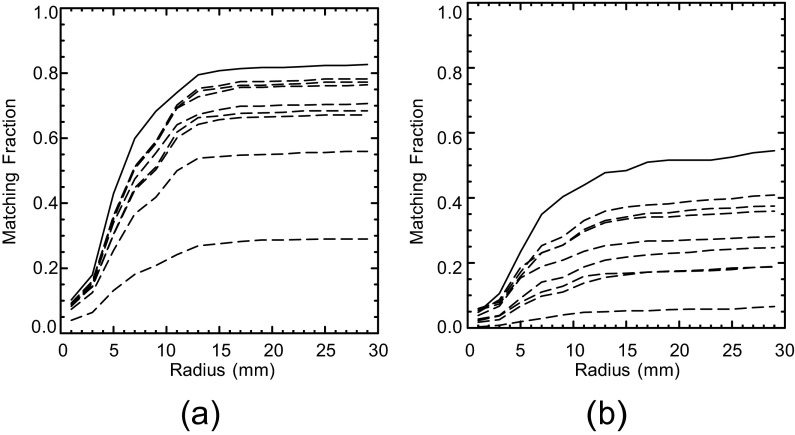
Two localizations were considered a match if their separation was within the threshold radius R_m. Figure 4 shows how F_m for the human observers and 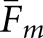for the model observers varied as a function of the prospective radius. Separate graphs address the calculations with abnormal (Figure 4a) and normal (Figure 4b) test images. The change in F_m between the human observers is indicated by the solid plot line in each graph. The remaining eight curves per graph show the variation in 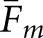for the two model observers under the four task definitions. All of the curves in Figure 4 reach a plateau at about the same radius. On this basis, R_m was set to 15 mm, the same value as R_cl. Moderate variations in R_m will have little effect on our concordance analysis.

Figure 4.

Matching fractions for the human and model observers as a function of prospective threshold radius. Plot (a) is for the abnormal test images, and plot (b) is for the normal test images. F_m between the two human observers is indicated by the solid line in each plot. The other eight curves per plot indicate 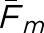for the model observers with the background-known-exactly and background-assumed-homogeneous tasks. Based on these plots, the threshold R_m was set to 15 mm.

Table 1 summarizes the computations of F_m and 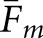for this choice of R_m. The concordance analysis was constrained by having only two human observers, although both may be regarded as experts in the context of PET and SPECT simulation studies. A larger pool of human observers would allow for concordance analyses based on observer experience. The values of F_m between the human observers were 0.81 ± 0.02 and 0.48 ± 0.03 for the abnormal and normal images, respectively. The uncertainties are the SDs assuming a binomial distribution on the number of matching localizations. The fractions are naturally higher for the abnormal images than for the normal images, which lack tumours to focus observer attention. The overall fraction was 0.65 ± 0.02.

Table 1.

F_m and 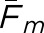values for cross-pairings of the model and human observers

Task	Observer	Human	Abnormal	Normal	Overall
	Humans		0.81 ± 0.02	0.48 ± 0.03	0.65 ± 0.02
BKE-Ω	Scan	1	0.66 ± 0.03	0.25 ± 0.02	0.46 ± 0.02
		2	0.71 ± 0.03	0.27 ± 0.02	0.49 ± 0.02
		Average	0.69 ± 0.02	0.26 ± 0.02	0.47 ± 0.01
	VS	1	0.74 ± 0.02	0.32 ± 0.03	0.53 ± 0.02
		2	0.77 ± 0.02	0.36 ± 0.03	0.56 ± 0.02
		Average	0.75 ± 0.02	0.34 ± 0.02	0.55 ± 0.01
BKE-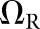	Scan	1	0.72 ± 0.02	0.33 ± 0.03	0.52 ± 0.02
		2	0.77 ± 0.02	0.34 ± 0.03	0.55 ± 0.02
		Average	0.74 ± 0.02	0.34 ± 0.02	0.54 ± 0.01
	VS	1	0.75 ± 0.02	0.35 ± 0.03	0.55 ± 0.02
		2	0.78 ± 0.02	0.39 ± 0.03	0.58 ± 0.02
		Average	0.76 ± 0.02	0.37 ± 0.02	0.57 ± 0.01
BAH-Ω	Scan	1	0.27 ± 0.02	0.05 ± 0.01	0.16 ± 0.02
		2	0.28 ± 0.02	0.06 ± 0.01	0.17 ± 0.02
		Average	0.28 ± 0.02	0.05 ± 0.01	0.16 ± 0.01
	VS	1	0.54 ± 0.03	0.15 ± 0.02	0.34 ± 0.02
		2	0.55 ± 0.03	0.18 ± 0.02	0.36 ± 0.02
		Average	0.54 ± 0.02	0.16 ± 0.02	0.35 ± 0.01
BAH-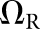	Scan	1	0.64 ± 0.03	0.14 ± 0.02	0.39 ± 0.02
		2	0.67 ± 0.03	0.20 ± 0.02	0.44 ± 0.02
		Average	0.66 ± 0.02	0.17 ± 0.02	0.41 ± 0.01
	VS	1	0.65 ± 0.03	0.19 ± 0.02	0.42 ± 0.02
		2	0.69 ± 0.03	0.25 ± 0.02	0.47 ± 0.02
		Average	0.67 ± 0.02	0.22 ± 0.02	0.44 ± 0.01

BAH, background-assumed-homogeneous; BKE, background-known-exactly; VS, visual search.

Also included in the table is the F_m value between the human observers.

The matching fractions calculated between the individual human observers and either model observer were considerably lower than those values of F_m from the human observers. Both model observers consistently demonstrated nominally higher concordance with human observer #2 regardless of the task or image type, but the largest overall fraction was 0.58 ± 0.02. The variations in the fractions with individual human observers were largely the same for both model observers.

With regard to the average values (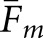) in Table 1, both model observers returned higher fractions with the BKE tasks than with the BAH tasks. Thus, a ranking of the eight observer-task combinations by matching fraction does not agree with the rankings based on either correlation coefficient or RMS error. The highest concordances as measured by overall 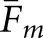were obtained from the VS observer with the BKE-Ω and BKE-Ω tasks and the scanning observer with the BKE-Ω task, which were the three observer-task combinations identified in the Observer performance section as having performed at or above the level of the human observers for every image set.

To a large extent, calculation of the 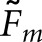matching fractions (Table 2) corroborated the trends obtained with 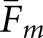. As expected from Equation (12),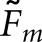  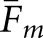  for a given observer and task. Since the human-observer localizations disagree more often with the normal images than with the abnormal images, the quantity P in Equation (12) will be larger for the normal images. Thus, the difference between 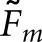and 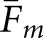will be larger for normal images. Comparison of Tables 1 and 2 also shows that with the normal images, the differences between pairs of 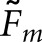are consistently greater than the corresponding differences for 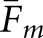. As an example, for the two model observers with the BKE-Ω task are 0.34 and 0.26, respectively. The corresponding 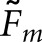values are 0.46 and 0.34. The VS observer demonstrated higher overall concordance than the scanning observer for all four tasks. Largely owing to consistently higher concordance with the normal images, this improvement would generally have only a second-order effect on the agreement in A_L between the human and model observers.

Table 2.

A summary of the 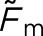values for the model observers

Task	Observer	Abnormal	Normal	Overall
BKE-Ω	Scan	0.75 ± 0.02	0.34 ± 0.03	0.54 ± 0.02
	VS	0.82 ± 0.02	0.46 ± 0.03	0.64 ± 0.02
BKE-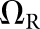	Scan	0.81 ± 0.02	0.44 ± 0.03	0.62 ± 0.02
	VS	0.83 ± 0.02	0.50 ± 0.03	0.66 ± 0.02
BAH-Ω	Scan	0.29 ± 0.02	0.07 ± 0.01	0.18 ± 0.02
	VS	0.57 ± 0.03	0.21 ± 0.02	0.39 ± 0.02
BAH-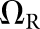	Scan	0.70 ± 0.02	0.22 ± 0.02	0.46 ± 0.02
	VS	0.71 ± 0.02	0.28 ± 0.02	0.50 ± 0.02

BAH, background-assumed-homogeneous; BKE, background-known-exactly; VS, visual search.

The statistical significance of the 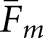and 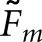data for the BKE tasks was tested through separate three-way analyses of variance that considered image class, observer model and task as fixed factors. Table 3 summarizes the outcome of the 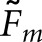analysis. We assessed statistical significance at the α = 0.0083 level, implementing a Bonferroni correction based on six comparisons (the three main effects plus three two-way interactions) to reduce the probability of a Type-I error. With 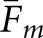, only the three main effects were significant. For 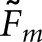, all the main effects and the class: observer and observer: task interactions were significant.

Table 3.

Results of the three-way analysis of variance conducted with concordance measure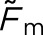

Factor	Degrees of freedom	Sum of squares	F	p-value
Class	1	0.27000	2,175,625	0.0004
Observer	1	0.00900	72,361	0.0023
Task	1	0.00600	47,961	0.0029
Class: observer	1	0.00120	9409	0.0066
Class: task	1	0.00063	5041	0.0090
Observer: task	1	0.00150	11,881	0.0058
Residuals	1	0

Image class, observer model and task were factors.

Significant effects (α = 0.0083) are indicated in bold type.

DISCUSSION

The model observers applied herein were also featured in a recent 3D SPECT lung study.¹² In that study, the VS observer resolved a fundamental difference between the scanning and human-observer results. In doing so, the VS observer demonstrated better reliability, in the sense of being less sensitive to reductions in prior knowledge compared with the scanning observer. Such reductions represent task uncertainty. One current objective was to see if similar advantages might be realized when the scanning and human observers already show good agreement. A second objective was to examine computationally efficient methods for implementing VS.

With regard to computational efficiency, the WS-based VS observer yielded equivalent results in a fraction of the time required for the GA version. Another WS advantage is that image gradients are not required. With nuclear medicine applications, the noisy quality of these gradients leads to searches with high numbers of focal points per test image. As related in the Visual-search algorithms section, the GA search identified more than twice as many focal points as the WS version, which led to degraded performance in one of the detection tasks.

As for the relative impact of task uncertainty on the scanning and VS observers, overall localization concordance with the human observers was highest with the latter observer regardless of task definition. The ability to implement a range of task uncertainties is crucial for purposes of modelling human observers. High levels of prior knowledge for statistical observers can lead to inflated estimates of human-observer performance with both localization and SKE tasks.^12,28 The errors can be magnified with localization tasks because relatively higher target contrasts are involved. A standard solution is to increase clinical realism by incorporating additional sources of observer uncertainty. With SKE tasks, one often models the covariance contributions of anatomical and internal noise, but this approach is not as effective for many localization tasks.^12,23 As an alternative approach, the VS observer provides a foundation for implementing anatomical and internal noise mechanisms with such tasks.

The lowest concordances from the model observers occurred with the BAH tasks, which were intended to approximate the scanning-observer tasks applied by Schaefferkoetter et al.⁷ Our results (Figure 3) suggest that the scanning observer in BAH form might be useful for same-organ evaluations at best. However, comparisons with Schaefferkoetter's hybrid image study are constrained by the limited variability in our simulation (e.g., a single mathematical phantom and one reconstruction method). In the hybrid study, quantitative agreement in 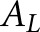was obtained between the scanning CNPW and human observers for liver tumours (tumour locations elsewhere in the body were not assessed). Modelling our study as a BAH task undoubtedly introduced some bias since the human observers had more familiarity with the normal cases than did the observers in the study by Schaefferkoetter et al.⁷

Concordances in this study were highest with the BKE tasks, which are impracticable for hybrid images. The high correlation obtained with the VS observer in one BAH task (Figure 3c) is remarkable, but further work is necessary to determine if this result reflects a capacity for cross-organ normalization of A_L. Continued development of the VS framework could lead to practical observer models based on a modified BAH assumption. The basic blob search treated in this article offers a canonical process that imposes no additional training requirements yet is applicable for a variety of imaging applications (e.g. Das and Gifford²⁹ and Lau et al³⁰). However, the non-specificity of the search is a limitation—a more-selective search process driven by both target and background features might improve concordance between the VS and human observers while overcoming the need for reference images.

CONCLUSIONS

Computationally efficient VS processes can enhance the ability of Hotelling-type observers to quantitatively predict the performance of human observers in localization tasks. The VS model observer was less sensitive to task definition than the scanning observer. Furthermore, case-by-case concordance with human-observer localizations was improved with the VS observer.

FUNDING

This work was supported by grant R01-EB12070 from the National Institute for Biomedical Imaging and Bioengineering (NIBIB) and the National Institutes of Health (NIH). The contents are solely the responsibility of the author and do not necessarily represent the views of NIBIB/NIH.