Meniscus on a shaped fibre: singularities and hodograph formulation

Abstract

Using the method of matched asymptotic expansions, the problem of the capillary rise of a meniscus on the complex-shaped fibres was reduced to a nonlinear problem of determination of a minimal surface. This surface has to satisfy a special boundary condition at infinity. The proposed formulation allows one to interpret the meniscus problem as a problem of flow of a fictitious non-Newtonian fluid through a porous medium. As an example, the shape of a meniscus on a fibre of an oval cross section was analysed employing Chaplygin's hodograph transformation. It was discovered that the contact line may form singularities even if the fibre has a smooth profile: this statement was illustrated with an oval fibre profile having infinite curvature at two endpoints.

1. Introduction

When a fibre is immersed perpendicularly into a liquid, the liquid surface deforms into meniscus embracing the fibre. Depending on the fibre wettability, the contact line, separating wet and dry parts of the fibre surface, can be located above (for the wetting fluids) or below (for the non-wetting fluids) the horizontal liquid surface. For a hollow fibre or a tube, the effect of capillary rise of the liquid surface is even more evident. This capillary rise experiment first documented by James Jurin [1] has ignited the interests of prominent scientists such as Laplace, Poisson, Gauss and Young and has led to the development of the quantitative theory of capillarity [2–4].

It appears that the meniscus height and shape are very sensitive to the surface properties of a fibre [5–9]. Therefore, the Jurin experiment and analysis of meniscus shape and height became one of the most popular techniques for characterization of fibre surfaces [5,10–13]. While menisci on circular cylinders have been well studied [14], menisci on fibres with other shapes have received much less attention [13,15–20]. The development of grooved and complex-shaped fibres and nanofibre yarns [21–28] calls for a new study of characteristic features of the menisci for interpretation of the Jurin experiments. An analysis of the meniscus shape on a complex-shaped fibre requires the development of a mathematical technique to solve the nonlinear equation of capillarity with nonlinear boundary conditions. In many cases, the contact line forms singularities on the complex-shaped substrates [29,30]. Therefore, analytical theories enabling classification of the behaviour of the contact lines at the fibre surfaces are especially critical. This classification is necessary for the successful development of the numeric algorithms for the meniscus shape characterization [17,18].

In this paper, we formulate the problem of meniscus shape when the fibres are thin, and gravity plays a secondary role in shaping the meniscus profile. Quantitatively, one assumes that the Bond number defined as $\epsilon =L_{\mathrm{m}}^2/L_{\mathrm{c}}^2\ll 1$ is small. In this definition, $L_{\mathrm{c}}=\sqrt{\sigma /(\rho g)}$ is the capillary length, σ is the surface tension of the liquid, ρ is its density and g is acceleration due to gravity; L_m is the mean fibre radius $L_{\mathrm{m}}=\sqrt{A/\pi }$, where A is the cross-sectional area of the fibre. Typical fibres are thin, i.e. the inequality ε≪1 holds true. For example, the Bond number for the water meniscus on a human hair of about 30 μm radius is estimated as ε≈10⁻⁴. The sizes of insect feeding devices, for example, proboscises of butterflies and moths, vary in the range from a few micrometres to hundreds of micrometres. For these natural fibres, the Bond number is always less than one [31–33].

In this work, the main attention is paid to the external menisci. We employ the method of matched asymptotic expansions [34] and reduce the problem of meniscus shaping on a fibre to the determination of a minimal surface constrained by the special boundary conditions. This formulation allows one to use the well-developed methods of fluid dynamics and complex variables to study menisci on the complex-shaped fibres. We traced a mathematical analogy of the nonlinear equation of minimal surfaces with the Chaplygin gas equations [35–39] or equations describing the flow of non-Newtonian fluids through porous media [40–42]. A hodograph transformation was introduced and illustrated on the one-dimensional meniscus on a cylindrical fibre and on the two-dimensional meniscus on a fibre with the cross section of a symmetric oval.

In many cases, classification of the substrate wettability is associated with the behaviour of the contact line [5]. In design of omniphobic materials, one needs to understand the effect of the fibre shape on the formation of singularities on the contact line [29,43,44]. We question whether the fibres with a smooth cross-sectional profile Γ would necessarily have a smooth contact line Γ_c. Analysing the obtained exact solution for a meniscus on a fibre with an oval cross section, we showed that the contact line may form singularities even on the smooth fibres.

2. Mathematical model

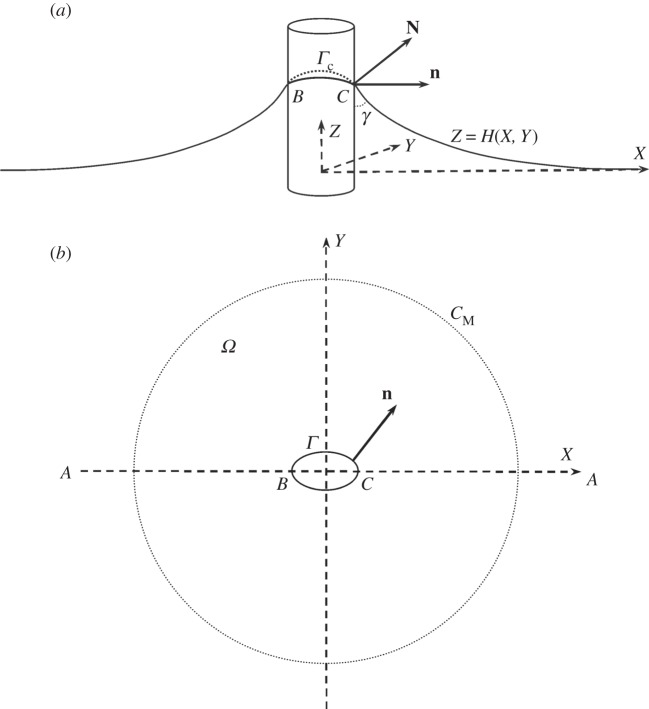
In the Cartesian system of coordinates (X,Y,Z), the meniscus profile Z=H(X,Y) describes the liquid elevation above the reference plane (X,Y), which coincides with the horizontal liquid level far away from the fibre. The centre of coordinates is chosen inside the fibre. The Laplace law of capillarity [2], σ(1/R₁+1/R₂)−ρgH=0 is employed to describe the meniscus shape where the first term in this equation is the mean curvature defined by two principal radii of curvatures R₁ and R₂; the second term is the hydrostatic pressure. The Young–Laplace equation is used to formulate the boundary condition at the fibre surface [2,5,45]. It is convenient to rewrite the mean curvature in terms of the outward normal vector N to the meniscus surface, (1/R₁+1/R₂)=∇⋅N, where this vector is expressed through the surface elevation as N=(1+|∇H|²)^−1/2(−∂H/∂X,−∂H/∂Y,1) [46], where ∇=(∂/∂X,∂/∂Y) is the two-dimensional nubla operator.

Thus, introducing the dimensionless variables (x,y)=(X/L_m, Y/L_m) and dimensionless function h(x,y)=H/L_m, the mathematical model is written as [47]

$$\begin{array}{rl}& \mathrm{\Omega }:\mathrm{\nabla }\cdot [{(1+|\mathrm{\nabla }h{|}^2)}^{-1/2}\mathrm{\nabla }h]-\epsilon h=0,\end{array}$$ 2.1

$$\begin{array}{rl}& \mathit{\Gamma }:{(1+|\mathrm{\nabla }h{|}^2)}^{-1/2}\frac{\mathrm{\partial }h}{\mathrm{\partial }n}=-\cos \gamma \end{array}$$ 2.2

$$\begin{array}{rl}\text{and}& h\to 0\text{as}{(x^2+y^2)}^{1/2}\to \mathrm{\infty }.\end{array}$$ 2.3

The set of equations (2.1)–(2.3) has to be augmented by the force balance condition

$$\epsilon {\iint }_{\mathrm{\Omega }}h\hspace{0.17em}\text{d}\mathrm{\Omega }=l\cos \gamma ,$$ 2.4

where Ω is the (x,y)-projection of the domain occupied by the liquid, and l is the dimensionless perimeter of the fibre. This equation is the first integral of models (2.1)–(2.3) [47].

3. External menisci as minimal surfaces

We will employ the method of matched asymptotic expansions [34,48,49] mostly following Lo's ideas. Lo used meniscus on a circular cylinder to illustrate a rigorous matching procedure [49]. The meniscus was subdivided onto two parts, the inner and outer parts. Both parts were described by the asymptotic series with respect to the Bond number. The inner asymptotic expansion described the meniscus profile near the fibre, while the outer expansion described the meniscus profile far away from the fibre where it meets the horizontal air–liquid interface. Each solution contains one unknown constant which are connected by matching two solutions in an intermediate zone where the solutions overlap.

As the Lo problem was one-dimensional, it was difficult to recognize the importance of the force balance condition (2.4): the Lo construction significantly used the properties of the explicit solution—catenoid [3]. That is why she never introduced or used this force balance condition. Following Lo's method for the two-dimensional case when the fibre has a complex shape and assuming the smallness of the Bond number, one can derive a two-dimensional nonlinear partial differential equation describing a minimal surface. As this equation cannot be solved analytically, it is not clear how to apply Lo's method in this case. Fortunately, the outer asymptotic solution of the two-dimensional problem can be separated and solved explicitly, and equation (2.4) can be directly employed for selection of the integration constants prior to solving the nonlinear partial differential equation describing a minimal surface. Invoking equation (2.4), one can match the inner solution with the outer solution not using any explicit form of the inner solution.

In this section, we demonstrate this matching procedure. According to this asymptotic method, we seek a solution of problems (2.1)–(2.4) by matching two asymptotic series, the inner and outer.

(a). Inner expansion

The inner zone is located closer to the fibre surface; this zone excludes the centre of coordinates (0,0) and infinity. Hence, the variables (x,y) in the inner zone are of the order of one. The meniscus height in the inner zone is assumed to be of the order of one as well, h(x,y)∼O(1). Therefore, we need to seek an asymptotic solution of the inner problem of the form

$$x,y\sim O(1):h^{\mathrm{i}}(x,y)=h^{\mathrm{i},0}(x,y)+o(1),$$ 3.1

where the superscript ‘i’ specifies the inner solution, and the superscript ‘0’ points the principal term of the asymptotic equation. Separating all terms of the order of one in the governing equation (2.1), one obtains

$$\mathrm{\Omega }:\mathrm{\nabla }\cdot [{(1+|\mathrm{\nabla }{h}^{\mathrm{i},0}{|}^2)}^{-1/2}\mathrm{\nabla }{h}^{\mathrm{i},0}]=0.$$ 3.2

And the boundary condition at the fibre surface reads

$$\mathit{\Gamma }:{(1+|\mathrm{\nabla }{h}^{\mathrm{i},0}{|}^2)}^{-1/2}\frac{\mathrm{\partial }{h}^{\mathrm{i},0}}{\mathrm{\partial }n}=-\cos \gamma .$$ 3.3

According to the method of matched asymptotic expansions, the inner solution has to be matched with the outer solution using the matching condition as [34,49]

$$r\to \mathrm{\infty }:h^{\mathrm{i},0}\cong {[h^{\mathrm{o},0}]}^{\mathrm{i}},$$ 3.4

where r=(x²+y²)^1/2, and [h^o,0]ⁱ is an inner expansion of the outer expansion as ε goes to zero [34,49,50]. In order to specify the behaviour of the inner expansion far away from the fibre, we turn back to the original boundary condition (2.3) and assume that the inner and outer solutions overlap in the region where the meniscus approaches the horizontal air–liquid interface. In this region, all derivatives of h^i,0 are small and the following asymptotic approximation of equation (3.2) holds true Δh^i,0=0+O(|∇h^i,0|²), as $r\to \mathrm{\infty }$. Therefore, at infinity, the leading term of asymptotic expansion (3.1) must satisfy the Laplace equation

$$r\to \mathrm{\infty }:\mathrm{\Delta }{h}^{\mathrm{i},0}=0.$$ 3.5

One has to mention that the form (3.1) assumes a regular behaviour of the solution in the inner zone, where x, y∼O(1). Outside this zone, the proposed solution may behave singularly [34]. In particular, the solution may have logarithmic and other singular terms [34]. These singular terms included in the far-field condition must behave regularly within the inner zone, where x, y∼O(1); they are allowed to diverge only at infinity which does not belong to this zone.

Taking into account this comment, one has to consider the general form of the boundary condition for the Laplace equation at infinity [51]

$$r\to \mathrm{\infty }:h^{\mathrm{i},0}(r,\phi )\approx B_{-1}\ln r+B_0+\sum _{k=1}^N{B}_k{r}^k\cos k\phi ,$$ 3.6

where φ=arctan(y/x) and N is the number of multipoles. In contrast to the fluid mechanics where these multipoles must be identified in the mathematical model of the given flow [51], the constants B_k, k=−1,0,1,…,N are not identified yet and must be found from the matching condition (3.4). Thus, the inner problem is reduced to the solution of equation (3.2) with the boundary condition at the fibre surface (3.3) and at infinity (3.6). As constants in equation (3.6) are not known, we have to turn to the outer expansion. One important feature of equation (3.1) is that it has a logarithmic singularity. This requires a more careful analysis of the outer expansion [49].

(b). The leading-order term of the outer expansion

Intuitive estimates based on the physical arguments allow one to guess the form of the outer variables. Indeed, far away from the fibre, all perturbations of the meniscus surface specific for the shaped fibre should fade away, and the meniscus should approach the free horizontal surface at a very small slope, |∇h^o|≪1. Therefore, at infinity the basic equation (2.1) is simplified to

$$\mathrm{\Delta }{h}^{\mathrm{o}}-\epsilon h^{\mathrm{o}}=0.$$ 3.7

As follows from the scaling analysis, the first and second terms of this equation are balanced at the distances of the order of r∼ε^−1/2.

These estimates suggest to introduce the outer variable as $\xi =r\sqrt{\epsilon }$ and define the outer zone Z_ξ as the region where the variable ξ should be of the order of one, ξ∼O(1). The boundary condition (2.3) requires the meniscus height to decrease down to zero at infinity. Therefore, one can extend the outer zone up to infinity, Z_ξ:ξ≥O(1), and require boundary condition (2.3) to be satisfied.

In the outer zone Z_ξ, we seek an asymptotic solution h^o in the following form:

$${\mathrm{Z}}_{\xi }:h^{\mathrm{o}}(\xi ,\phi )=h^{\mathrm{o},0}(\xi ,\varphi )+o(1).$$ 3.8

In this zone, interpreting the derivative of the meniscus elevation as $\mathrm{\partial }{h}^{\mathrm{o}}/\mathrm{\partial }r=\sqrt{\epsilon }\mathrm{\partial }{h}^{\mathrm{o}}/\mathrm{\partial }\xi$, and collecting only highest order terms, we rewrite equation (3.7) in cylindrical coordinates as

$$\frac{1}{\xi }\frac{\mathrm{\partial }}{\mathrm{\partial }\xi }\left(\xi \frac{\mathrm{\partial }{h}^{\mathrm{o},0}}{\mathrm{\partial }\xi }\right)+\frac{1}{{\xi }^2}\frac{{\mathrm{\partial }}^2{h}^{\mathrm{o},0}}{\mathrm{\partial }{\phi }^2}-h^{\mathrm{o},0}=0.$$ 3.9

The solution to this equation approaching zero at infinity can be represented in a Fourier series over the angular variable φ with the Bessel functions of the second kind K_n(ξ), n≥0, as the spectral ξ-functions [17,18]. In the electronic supplementary material, a full derivation of the leading-order term of this series is presented,

$${\mathrm{Z}}_{\xi }:h^{\mathrm{o},0}(\xi ,\phi )=C_0{K}_0(\xi ).$$ 3.10

Solution (3.10) satisfies the boundary condition at infinity, but it does not satisfy the boundary condition at the fibre surface. In order to find a relation between the constants C₀ and B_k in equation (3.6), we employ the matching condition (3.4) where the inner expansion of the outer expansion (3.10) takes on the form

$${[h^{\mathrm{o},0}]}^{\mathrm{i}}=C_0{K}_0\left(r\sqrt{\epsilon }\right){|}_{r\sim 1}\approx -C_0[\ln r+\ln \left(\frac{{\mathrm{e}}^{\mathrm{E}}\sqrt{\epsilon }}{2}\right)],$$

where E=0.577215 is the Euler constant. In the electronic supplementary material, we confirm that constant B₀ in equation (3.6) does not have any other terms of the order of O(1) coming from the higher-order Bessel functions of the second kind K_n(ξ), n≥1.

(c). Matching the inner and outer expansions

In order to find constant C₀, one can employ the force balance equation (2.4). We will consider a large circle C_M taking its radius M of the order of 1, M∼O(1) (figure 1b). The integral over the meniscus profile can be evaluated as

$$\epsilon {\iint }_{\mathrm{\Omega }}h\hspace{0.17em}\text{d}\mathrm{\Omega }=\epsilon {\iint }_{\mathrm{\Omega }\cap C_M}h\hspace{0.17em}\text{d}\mathrm{\Omega }+\epsilon {\iint }_{\mathrm{\Omega }\mathrm{\setminus }{C}_M}h\hspace{0.17em}\text{d}\mathrm{\Omega }\cong \epsilon {\iint }_{\mathrm{\Omega }\cap C_M}{h}^{\mathrm{i}}\hspace{0.17em}\text{d}\mathrm{\Omega }+\epsilon {\iint }_{\mathrm{\Omega }\mathrm{\setminus }{C}_M}{h}^{\mathrm{o}}\hspace{0.17em}\text{d}\mathrm{\Omega }.$$ 3.11

The first integral on the right-hand side is taken over the inner region Ω∩C_M bounded by the circle C_M, and the second integral is taken over the exterior of this circle, Ω∖C_M. According to the techniques of matched asymptotic expansions [34], the first integral does not require specification of the exact upper limits of integration. This boundary should be taken somewhere in the region where the inner and outer solutions match. Therefore, the first integral is expected to be small, $\epsilon {\iint }_{\mathrm{\Omega }\cap C_M}{h}^{\mathrm{i}}\hspace{0.17em}\text{d}\mathrm{\Omega }\ll 1$, and can be dropped.

Figure 1.

(a) External meniscus on fibre and (b) projection of the meniscus profile on the (X,Y) plane. The projection of contact line Γ_c exactly matches the fibre contour Γ.

In the second integral on the right-hand side of equation (3.11), we replaced h with h^o. This replacement is justified by the Kaplun expansion theorem of the asymptotic analysis [52]. According to this theorem, one can extend the zone of action of the outer expansion down to the boundary C_M. In other words, it can be shown that the meniscus elevation at C_M where M∼O(1) cannot be greater than O(1) (see the electronic supplementary material for the details). Therefore, the second term in equation (3.11) takes on the form [32]

$$\epsilon {\iint }_{\mathrm{\Omega }\mathrm{\setminus }{C}_M}{h}^{\mathrm{o}}\hspace{0.17em}\text{d}\mathrm{\Omega }=2\pi \epsilon C_0{\int }_M^{\mathrm{\infty }}{K}_0\left(r\sqrt{\epsilon }\right)r\hspace{0.17em}\text{d}r=2\pi C_0{\int }_{\sqrt{\epsilon }M}^{\mathrm{\infty }}{K}_0(u)u\hspace{0.17em}\text{d}u=2\pi \sqrt{\epsilon }{C}_{0}M{K}_1\left(M\sqrt{\epsilon }\right).$$

Taking into account the asymptotic approximation of the modified Bessel function of the second kind at small arguments, $K_1\left(M\sqrt{\epsilon }\right)\cong {\left(M\sqrt{\epsilon }\right)}^{-1}$, we obtain $\epsilon {\iint }_{\mathrm{\Omega }\mathrm{\setminus }{C}_M}{h}^{\mathrm{o}}\hspace{0.17em}\text{d}\mathrm{\Omega }\cong 2\pi C_0$. Substituting this value into equation (2.4), the constant C₀ is asymptotically defined through the contact angle and fibre perimeter as

$$C_0=\frac{l\cos \gamma }{2\pi }.$$ 3.12

Substituting equation (3.12) with the determined constant C₀ into equation (3.6), we finally obtain the necessary boundary condition for the inner expansion

$$r\to \mathrm{\infty }:h^{\mathrm{i},0}(r,\phi )\approx -\frac{l\cos \gamma }{2\pi }\left[\ln r+\ln \left(\frac{{\text{e}}^{\mathrm{E}}\sqrt{\epsilon }}{2}\right)\right].$$ 3.13

Thus, in the first approximation, all constants B_k in condition (3.6) having the subscript k greater than 1 must disappear, B_k=0, k≥1. Remarkably, that the constants B₋₁ and B₀ are completely defined by the outer expansion. This important conclusion was not noted in the past; in Lo's method of asymptotic analysis, the constant C₀ was obtained by directly matching the explicit solution of the inner expansion with equation (3.10) without application of equation (2.4). Hence, equation (3.13) was not discovered. Using equation (2.4), we showed that in the general case of a two-dimensional problem, the inner problem can be separated from the outer one. The explicit specification of the boundary condition (3.13) allows one to significantly expand this asymptotic methodology onto more complex two-dimensional problems of capillarity.

(d). Uniformly valid asymptotic solution

Having a solution of the inner problem, one can use the Van Dyke rule [50,53] to write down the leading-order approximation of solution h^u,0 valid everywhere in domain Ω

$$h^{u,0}(r,\phi )=h^{\mathrm{o},0}(r,\phi )+h^{\mathrm{i},0}(r,\phi )-{[h^{\mathrm{o},0}]}^{\mathrm{i}}.$$ 3.14

Substituting equations (3.10), (3.12) and (3.13), the uniformly valid asymptotic solution takes on the form

$$h^{u,0}(r,\phi )=h^{\mathrm{i},0}(r,\phi )+\frac{l\cos \gamma }{2\pi }\left[K_0\left(r\sqrt{\epsilon }\right)+\ln r+\ln \left(\frac{{\text{e}}^{\mathrm{E}}\sqrt{\epsilon }}{2}\right)\right].$$ 3.15

Thus, the model of external meniscus on a thin fibre of arbitrary shape is reformulated as a problem of minimal surfaces (3.2) with boundary conditions (3.3) and (3.13).

This asymptotic analysis allows one to understand the driving mechanism of the meniscus formation by the complex-shaped slender fibres. It appears that the shape of the meniscus is mostly controlled by the wetting forces acting at the contact line and a tensile force which is a resultant of the gravity and surface tension at infinity. In contrast to the menisci formed inside hollow fibres [1], the capillary pressure plays no role in shaping the external menisci.

4. Analogy with flow of non-Newtonian fluids through porous media

While the asymptotic model (3.2), (3.3) and (3.13) reduces the original nonlinear boundary value problem of capillarity to a more tractable form, it is still complicated. In the following analysis, we show that the proposed formulation permits a transformation of this nonlinear problem to an auxiliary domain where the boundary value problem for the h-function becomes linear. This transformation has its roots stemming from fluid dynamics. The analogy with the problems of gas dynamics and flows of non-Newtonian fluids though porous media [36,40–42,54] is helpful because it opens up new opportunities to obtain new explicit solutions of capillarity and construct more efficient numerical algorithms for studying a broad range of materials science problems.

One can note that equation (3.2) has a form of a continuity equation ∇⋅J=0 with a flux of a fictitious fluid defined as

$$\mathbf{J}=-\frac{\mathrm{\nabla }{h}^{\mathrm{i},0}}{\sqrt{1+{(\mathrm{\nabla }{h}^{\mathrm{i},0})}^2}}.$$ 4.1

This fictitious fluid flows from the higher elevation of the meniscus height to its lower elevation. Therefore, the meniscus height can be considered as a hydraulic head of this fictitious flow. The continuity equation (3.2) is automatically fulfilled when we introduce the stream function ψ(x,y) as J_x=∂ψ/∂y and J_y=−∂ψ/∂x.

In the two-dimensional fluid dynamics, it is convenient to analyse the flow in the hodograph plane (J_x,J_y) [40,42,51]. In many cases, the flow in the hodograph plane can be completely described by studying the behaviour of the flux at the fibre boundary and at infinity. When the (J_x,J_y)-pair of the flux is not specified at the boundaries, one can deal with the (θ,J)-plane complimentary to the hodograph plane. The angle θ is defined as the angle that the vector J makes with the x-axis; the flux strength J is the absolute value of vector J, hence one has the following connection between the (J_x,J_y)-plane and (θ,J)-plane J=|J|>0, $J_x=J\cos \theta$ and $J_y=J\sin \theta$.

As follows from definition (4.1), we have the following relation between the flux strength and meniscus height:

$$\mathrm{\Omega }:J=\frac{|\mathrm{\nabla }{h}^{\mathrm{i},0}|}{\sqrt{1+|\mathrm{\nabla }{h}^{\mathrm{i},0}{|}^2}},0\le J\le 1.$$ 4.2

Following the traditional formulations of constitutive equations in fluid mechanics, we rewrite equation (4.22) solving it for the gradient of hydraulic head as

$$|\mathrm{\nabla }{h}^{\mathrm{i},0}|=\mathrm{\Phi }(J),\mathrm{\Phi }(J)=\frac{J}{\sqrt{1-J^2}},\mathrm{\Phi }(J)\ge 0,{\mathrm{\Phi }}^{\prime }(J)\ge 0.$$ 4.3

With these relations in hand, one can reformulate the capillary rise problem as a problem of a flow of a fictitious non-Newtonian fluid [36,40–42,54]

$$\mathrm{\Omega }:\mathrm{\nabla }{h}^{\mathrm{i},0}=-\mathrm{\Phi }(J)\frac{\mathbf{J}}{J},\mathrm{\nabla }\cdot \mathbf{J}=0.$$ 4.4

The mathematical model (4.4) is closed by the following boundary conditions at the fibre surface Γ:

$$\mathit{\Gamma }:\mathbf{J}\cdot \mathbf{n}=\cos \gamma .$$ 4.5

And at infinity where we can use either condition for the hydraulic head

$$r\to \mathrm{\infty }:h^{\mathrm{i},0}=-\frac{Q}{2\pi }\left[\ln r+\ln \left(\frac{{\text{e}}^{\mathrm{E}}\sqrt{\epsilon }}{2}\right)\right]+O(r^{-1}),$$ 4.6a

or for its gradient

$$r\to \mathrm{\infty }:\mathrm{\nabla }{h}^{\mathrm{i},0}=-\frac{Q}{2\pi r^2}\mathbf{r}+O(r^{-2}),$$ 4.6b

where r is the radius-vector of the given point, and Q is the total discharge of a fictitious fluid $Q=l\cos \gamma$.

(a). Hodograph transformation

Following Chaplygin [36] and Khristianovich [54], the system of equation (4.4) is rewritten in terms of the hydraulic head $h^{\mathrm{i},0}(J,\theta )$ and the stream function $\psi (J,\theta )$ as

$$\frac{{\mathrm{\Phi }}^2(J)}{J{\mathrm{\Phi }}^{\prime }(J)}\frac{\mathrm{\partial }\psi }{\mathrm{\partial }J}=-\frac{\mathrm{\partial }h}{\mathrm{\partial }\theta }\text{and}\frac{\mathrm{\Phi }(J)}{J^2}\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\theta }=\frac{\mathrm{\partial }h}{\mathrm{\partial }J}.$$ 4.7

Calculating function Φ and its derivative, one obtains the following relations:

$${\mathrm{\Phi }}^{\prime }(J)=\frac{1}{{(1-J^2)}^{3/2}},\frac{{\mathrm{\Phi }}^2(J)}{J{\mathrm{\Phi }}^{\prime }(J)}=J{(1-J^2)}^{1/2}\text{and}\frac{\mathrm{\Phi }(J)}{J^2}=\frac{1}{J{(1-J^2)}^{1/2}}.$$

Substituting these relations in equation (4.7), we have

$$J{(1-J^2)}^{1/2}\frac{\mathrm{\partial }\psi }{\mathrm{\partial }J}=-\frac{\mathrm{\partial }h}{\mathrm{\partial }\theta }\text{and}\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\theta }=J{(1-J^2)}^{1/2}\frac{\mathrm{\partial }h}{\mathrm{\partial }J}.$$ 4.8

Sokolovsky noted that the system of equations (4.8) can be transformed into the Cauchy–Riemann system by introducing new function t as [55]

$$t=\ln \frac{1+\sqrt{1-J^2}}{J}\equiv \text{arccosh}\frac{1}{J}.$$ 4.9

As a result, the problem of the meniscus shaping is reduced to a problem of a flow of an ideal fluid for which the stream function and hydraulic head satisfy the Cauchy–Riemann equations

$$\frac{\mathrm{\partial }\psi }{\mathrm{\partial }t}=\frac{\mathrm{\partial }{h}^{\mathrm{i},0}}{\mathrm{\partial }\theta }\text{and}\frac{\mathrm{\partial }\psi }{\mathrm{\partial }\theta }=-\frac{\mathrm{\partial }{h}^{\mathrm{i},0}}{\mathrm{\partial }t}.$$ 4.10

In order to eliminate the stream function from equation (4.10), one needs to differentiate the first equation by θ, and the second equation by t and then sum up the results. After these transformations, the problem of minimal surfaces is reduced to the Laplace equation in the hodograph plane

$$\frac{{\mathrm{\partial }}^2{h}^{\mathrm{i},0}}{\mathrm{\partial }{t}^2}+\frac{{\mathrm{\partial }}^2{h}^{\mathrm{i},0}}{\mathrm{\partial }{\theta }^2}=0.$$ 4.11

The Cauchy–Riemann equations allow one to introduce the following complex-valued functions and variables:

$$W=-h^{\mathrm{i},0}+\text{i}\psi \text{and}\chi =t+\text{i}\theta ,$$ 4.12

and employ different methods of complex analysis to solve the problem of meniscus shape on fibres of different cross sections. As an illustration of the hodograph method, we analyse the shape of meniscus on a circular cylinder and then present a method of generation of new explicit solutions for the complex-shaped fibres.

(b). Meniscus on a circular cylinder

In the case of a circular fibre, the physical semi-infinite plane is shown in figure 1a, where contour Γ is the circle. The boundaries BA and CA are impermeable, and one can seek a solution to equation (4.11), which is independent of θ, ∂²h^i,0/∂t²=0. This equation has the following solution h^i,0=C₁t+C₂ or, taking into account representation (4.9), we find

$$h^{\mathrm{i},0}=C_1\cdot \ln \frac{1+\sqrt{1-J^2}}{J}+C_2.$$ 4.13

Following Engelund [41], we can now employ constitutive equation (4.4). Writing it in a cylindrical system of coordinates, one finds a relation between the flux and meniscus height as

$$\frac{\text{d}{h}^{\mathrm{i},0}}{\text{d}r}=-\frac{J}{\sqrt{1-J^2}}.$$ 4.14

Taking the r-derivative of the solution given by equation (4.13), one obtains $\text{d}{h}^{\text{i,0}}=-C_1{\left(J\sqrt{1-J^2}\right)}^{-1}\text{d}J$. Thus, equation (4.14) is rewritten in the form C₁J⁻²dJ=dr and its integral is J=−C₁/r. Applying boundary condition (4.5) at the fibre surface r=1, the constant C₁ is specified as $C_1=-\cos \gamma$.

With the defined constant, the asymptotic form of solution (4.13) at infinity is written as $h^{\mathrm{i},0}=\cos \gamma \ln (\cos \gamma /2r)+C_2$. Applying the boundary condition at infinity, equation (3.13), the unknown constant is set as $C_2=-\cos \gamma \ln (\cos \gamma {\text{e}}^{\mathrm{E}}\sqrt{\epsilon }/4)$.

Finally, the solution is written as

$$h^{\mathrm{i},0}=-\cos \gamma [\ln (r+\sqrt{r^2-\cos {\gamma }^2})+\ln \left(\frac{{\text{e}}^{\mathrm{E}}\sqrt{\epsilon }}{4}\right)].$$ 4.15

This solution corresponds to the leading term of asymptotic expansion given by James [48] and Lo [49]. In their representation, it takes the form

$$h^{\mathrm{i},0}(r,\epsilon )=-c\ln \sqrt{\epsilon }+c(2\ln 2-E)-c\ln [r+{(r^2-c^2)}^{1/2}]+o(1),$$

with $c=\cos \gamma$ and the elevation of the contact line

$$h_{\mathrm{C}}=-\cos \gamma [\ln (1+\sin \gamma )+\ln \left(\frac{{\text{e}}^{\mathrm{E}}\sqrt{\epsilon }}{4}\right)].$$

(c). Method of conformal mapping: an example of an explicit solution for a fibre with non-circular cross section

The hodograph transformation can be considered as a conformal mapping of the function χ=t+iθ onto the plane W=−h^i,0+iψ. After determination of function χ=χ(W), one needs to find function h^i,0(x,y). The relation between the physical plane z=x+iy and the W-plane has been derived by Khristianovich and Engelund as [40–42,54]

$$\text{d}x=-\frac{\cos \theta }{\mathrm{\Phi }(J)}\hspace{0.17em}\text{d}{h}^{\mathrm{i},0}-\frac{\sin \theta }{J}\hspace{0.17em}\text{d}\psi \text{and}\text{d}y=-\frac{\sin \theta }{\mathrm{\Phi }(J)}\hspace{0.17em}\text{d}{h}^{\mathrm{i},0}+\frac{\cos \theta }{J}\hspace{0.17em}\text{d}\psi .$$ 4.16

Taking into account equations (4.3), (4.9) and connecting flux J with t, one can rewrite equation (4.16) in terms of (θ,t)

$$\text{d}x=-\cos \theta \sinh t\hspace{0.17em}\text{d}{h}^{\mathrm{i},0}-\sin \theta \cosh t\hspace{0.17em}\text{d}\psi \text{and}\text{d}y=-\sin \theta \sinh t\hspace{0.17em}\text{d}{h}^{\mathrm{i},0}+\cos \theta \cosh t\hspace{0.17em}\text{d}\psi .$$ 4.17

With the known dependence χ=χ(W), i.e. the functions t=t(h^i,0,ψ) and θ=θ(h^i,0,ψ), equations (4.17) allow one to connect the physical z-plane with the hodograph plane by integrating equations (4.17) over any line in the W-plane. In particular, the lines of equal elevation h^i,0=const. can be found in the following parametric form: x=x(ψ,h^i,0) and y=y(ψ,h^i,0).

(i). Hodograph plane for a completely wettable fibre with a symmetric cross section

As an illustration of the strength of the hodograph transformation method, we construct the hodograph plane for a meniscus on a completely wettable fibre, γ=0. The fibre cross section is assumed of an arbitrary form with a mirror-symmetry with respect to the x and y axes. For completely wettable fibres, the flux J must be finite and normal to the fibre boundary Γ. Therefore, equation (4.5) takes on the form Γ:J=1. Or, taking into account equation (4.9), one obtains

$$\mathit{\Gamma }:t=0$$ 4.18

At the line CA in figure 1b, the angle θ is equal to zero, θ=0, and at the line BA we have θ=π. At the fibre boundary, the angle θ is not defined, but it has to change from 0 to π as one moves from C to B. In the vicinity of point A∈AC, the behaviour of the meniscus elevation and its gradient are dictated by equations (4.6a,b) where we have to substitute γ=0:

$$y=0,x\to \mathrm{\infty }:h^{\mathrm{i},0}(x,y)=-\frac{l}{2\pi }\ln \left(\frac{x{\text{e}}^{\mathrm{E}}\sqrt{\epsilon }}{2}\right)+O(x^{-1})$$ 4.19a

and

$$y=0,x\to \mathrm{\infty }:|\mathrm{\nabla }{h}^{\mathrm{i},0}|=\frac{l}{2\pi x}+O(x^{-2}).$$ 4.19b

This behaviour suggests that as x goes to infinity, function t increases as well. Collecting all the derived features of behaviour of the θ- and t-functions, one concludes that the upper half-plane in figure 1b is mapped onto a semi-infinite strip ABCA in the hodograph plane χ (figure 2a).

Figure 2.

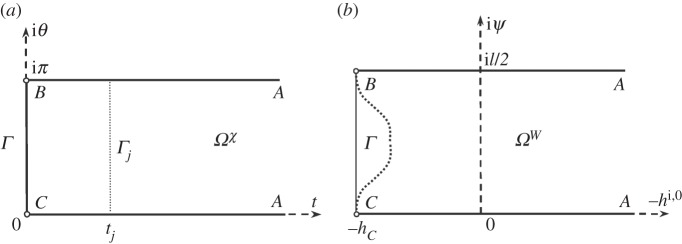
(a) Hodograph plane for a fictitious flow generated by a symmetrical completely wettable fibre shown in figure 1b. (b) A semi-infinite strip with solid boundaries ABCA in the W-plane corresponds to the meniscus on a circular fibre. When the fibre is not circular, the boundary BC deforms in a dotted line BC.

This semi-infinite strip describes menisci on fibres of different symmetrical shapes. In order to specify the meniscus shape on a particular fibre, one needs to solve a problem for the potential W. In the case of a circular cylinder, the height of the contact line is constant and the lines CA and BA are the streamlines (ψ=const.) for a fictitious flow (4.10). Hence, the shape of the W-plane is known; it is a semi-infinite strip (figure 2b). In the general case, the height of the contact line is not necessarily constant. It has to be found as a part of the solution. Therefore, the W-plane is not defined. However, one can note that the lines CA and BA remain the streamlines, and the h-function together with the height of the contact line can be represented in a Fourier series associated with equation (4.11) in the χ-plane. Therefore, a particular truncated Fourier series compatible with the spectral properties of equation (4.11) and the boundary conditions ∂h^i,0/∂θ=0 at CA and BA should generate a set of explicit solutions. This observation was the motivation for the following procedure for calculating new non-trivial solutions in an ‘inverse’ manner when one picks a particular form of the function W(χ) and finds the fibre shape corresponding to this function.

(ii). Explicit solution for a fibre with an oval cross section

We illustrate this method with a truncated Fourier series of the form

$$W(\chi )=-h_0+\frac{l}{2\pi }\chi +a({\text{e}}^{-2\chi }-1),$$ 4.20

parameterized by constants a and h₀. When a≡0, the semi-infinite strip Ω^χ is mapped onto the region ${\mathrm{\Omega }}_0^W$ having the form of a semi-infinite strip of width l/2. As shown in the electronic supplementary material, this Ω^χ→Ω^W mapping describes the shape of the meniscus on a circular fibre and gives h=h₀. The term in the parentheses in equation (4.20) deforms the boundary BC of a semi-infinite strip as shown schematically in figure 2b.

It is convenient to introduce a set of gridlines t=t_j, j=1…N, and trace the changes of function χ along these lines,

$${\mathit{\Gamma }}_j:\chi =t_j+\text{i}\theta ,\text{where}\theta \in [0,\pi ].$$ 4.21

One can track these changes in the physical plane following the changes of the triplet:

$$x=x_j(\theta ),y=y_j(\theta )\text{and}z=h_j(\theta ).$$ 4.22

The function h_j(θ) is obtained from equation (4.20) by selecting the real part of the W-function

$$h_j(\theta )=h_0-\frac{l}{2\pi }{t}_j-a({\text{e}}^{-2t_j}\cos 2\theta -1).$$ 4.23

Integrating equation (4.17) (electronic supplementary material), one obtains the gridlines as

$$\begin{array}{rl}{x}_j(\theta )& =\frac{l}{2\pi }\cosh t_j\cos \theta +a\left({\text{e}}^{-t_j}\cos \theta -\frac{{\text{e}}^{-3t_j}}{3}\cos 3\theta \right)\\ \text{and}{y}_j(\theta )& =\frac{l}{2\pi }\cosh t_j\sin \theta -a\left({\text{e}}^{-t_j}\sin \theta +\frac{{\text{e}}^{-3t_{\mathrm{j}}}}{3}\sin 3\theta \right).\end{array}\}$$ 4.24

(iii). The shapes of fibre and contact line

Specifying the boundary BC in the χ-plane by choosing t_j=0 in equations (4.24), one determines the fibre shape as

$$x_{\mathit{\Gamma }}(\theta )=\left(\frac{l}{2\pi }+a\right)\cos \theta -\frac{a}{3}\cos 3\theta \text{and}{y}_{\mathit{\Gamma }}(\theta )=\left(\frac{l}{2\pi }-a\right)\sin \theta -\frac{a}{3}\sin 3\theta .$$ 4.25

The elevation of the contact line on such a fibre is given by formula (4.23) at t_j=0 (see the details of the derivation of parameter h₀ in the electronic supplementary material)

$$h_{\mathit{\Gamma }}(\theta )=-a\left(\cos 2\theta -1\right)+\frac{l}{2\pi }\ln \left(\frac{8\pi }{l{\text{e}}^{\mathrm{E}}\sqrt{\epsilon }}\right)-a.$$ 4.26

(iv). Relationships between auxiliary and physical parameters

The fibre shape given by equation (4.25) and the contact line profile defined by equation (4.26) depend on two auxiliary parameters, a and l. One has to remember that the chosen normalization with $L_{\mathrm{m}}=\sqrt{A/\pi }$ assumes that the non-dimensional cross-sectional area of the fibre must be equal π. This gives the following constrain:

$$\frac{\pi }{2}={\int }_0^{\pi }{y}_{\mathit{\Gamma }}(\theta )\left(-\frac{\text{d}{x}_{\mathit{\Gamma }}}{\text{d}\theta }\right)\hspace{0.17em}\text{d}\theta .$$ 4.27

Taking the integral, we end up with a simple relation between these parameters

$$\frac{l^2}{4{\pi }^2}-1=\frac{2}{3}{a}^2\text{or}a=\pm \sqrt{\frac{3}{2}\left(\frac{l^2}{4{\pi }^2}-1\right)}.$$ 4.28

Another constrain is that the perimeter l cannot be less than the circumference of a unit circle,

$$l\ge 2\pi .$$ 4.29

For a unit circle, one has: l=2π and hence a=0.

Examination of the square root (4.28) reveals that the map W(χ) remains conformal if and only if the following inequality holds true:

$$|a|\hspace{0.17em}\le a_{\ast }=\frac{l}{4\pi }$$ 4.30

At the upper boundary of inequality (4.30), a=±a_*, one observes the development of singularities at the boundary Γ:

$$\mathit{\Gamma }:{\frac{\text{d}W}{\text{d}\chi }|}_{\theta =0,\pi }=0\text{ at }a=a_{\ast }\text{and}\mathit{\Gamma }:{\frac{\text{d}W}{\text{d}\chi }|}_{\theta =\pi /2}=0\text{ at }a=-a_{\ast }.$$

At these points, the map W(χ) still remains conformal inside Ω^χ.

When the modulus |a| increases further beyond boundary a_*, the function W(χ) becomes multivalent leading to a non-physical, self-intersecting surface describing the meniscus. As parameters a and l are connected by equation (4.28), the inequality (4.30) leads to the following boundaries for l:

$$2\pi \le l\le l_{\ast }=2\pi \sqrt{\frac{6}{5}.}$$

This inequality sets the range of admissible parameters l selecting menisci with a smooth contact line. The shape of the meniscus is represented by the function h_j(θ), equation (3.15), of the form

$$h_j(\theta )=\frac{l}{2\pi }[\ln \left(\frac{4\pi }{l}\right)-t_j+K_0(r_j(\theta )\sqrt{\epsilon })+\ln r_j(\theta )]-a({\text{e}}^{-2t_j}\cos 2\theta -1),$$

where $r_j(\theta )={[x_j^2(\theta )+y_j^2(\theta )]}^{1/2}$.

(v). Numerical examples

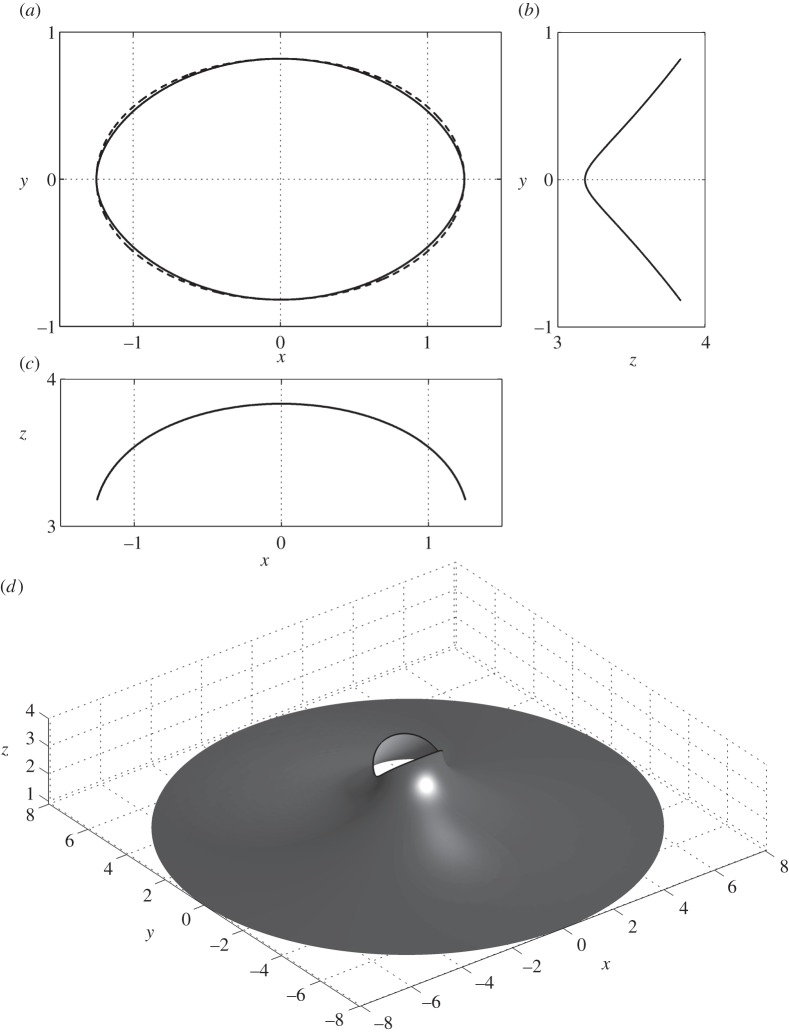
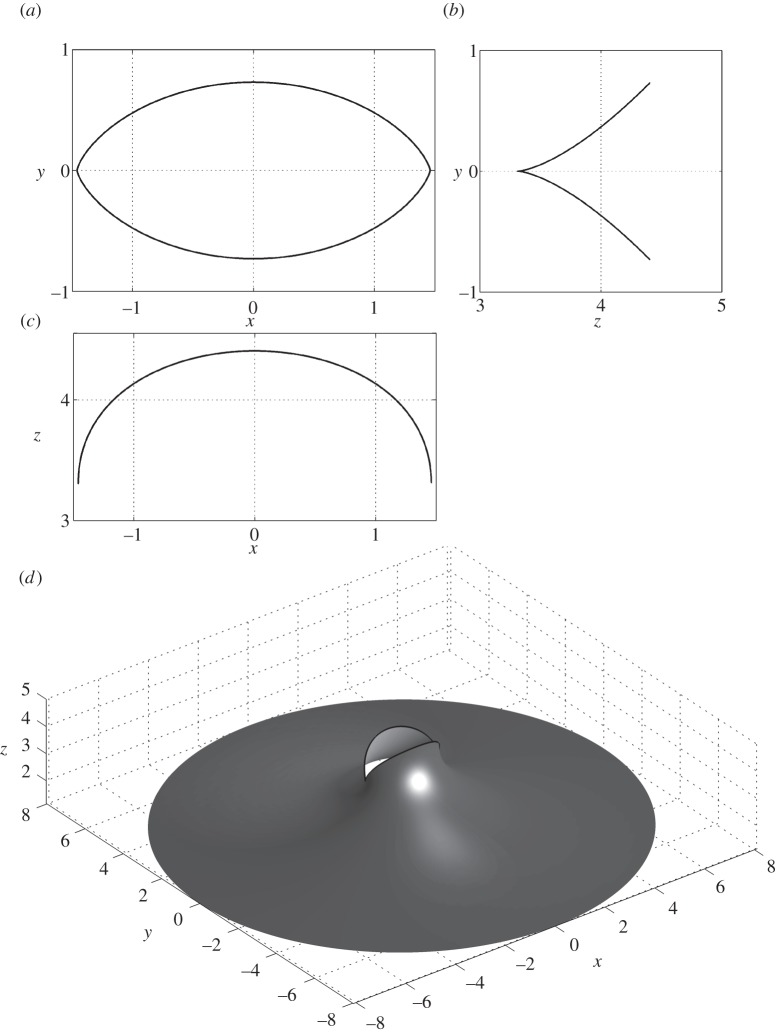
We consider two representative examples of menisci formed on fibres with cross-sectional profile (4.27) when l=6.5 (figure 3) and l=l_*≈6.8829 (figure 4). In the first case, l=6.5, the curvature of the fibre contour is always finite, in the second case, l=6.8829 the curvature of the fibre contour goes to infinity at points B and C.

Figure 3.

(a) The fibre contour described by equations (4.25) with l=6.5, the Bond number is ε=0.01. Observe that the fibre contour can be described by an ellipse x²/α²+y²/β²=1 with the semi-axes α=1.2508 and β=0.8182 shown as the dashed line; (b) the (z,y)-profile of the contact line. (c) The (x,z)-profile of the contact line. (d) The three-dimensional shape of the meniscus. The fibre is not shown.

Figure 4.

(a) The fibre contour described by equations (4.25) with l=l_*, the Bond number is ε=0.01; (b) the (z,y)-profile of the contact line. (c) The (x,z)-profile of the contact line. (d) The three-dimensional shape of the meniscus. The fibre is not shown.

These two examples show a drastically different behaviour of the contact line. When the curvature of the fibre profile at the points C and B is finite, the contact line is smooth and the meniscus is smooth as well. When the curvature goes to infinity, the contact line jumps down forming a cusp. The contact line is still continuous but the derivatives of the contact line become singular at these two points C and B. Thus, the singularities of the contact line can be developed not only at the corners, but even at smooth substrates when the fibre contour possesses some points with the infinite curvature. This discovery deserves a special attention because it reveals a lack of understanding of the behaviour of capillary surfaces on ‘smooth’ substrates without visible sharp singularities.

5. Conclusion

In many practical situations, the characterization of liquid–fibre interactions requires the knowledge of the shape of a meniscus formed on the fibres of different shapes. Available analytical solutions deal with flat plates and circular cylinders. While different numerical methods have been developed in recent years, the criteria for formation of singularities of the contact lines and menisci formed on the complex-shaped slender fibres are still unknown and are actively discussed in the literature. The lack of understanding of the mechanism of formation of singularities of the contact line, calls for the development of new analytical methods enabling such an analysis.

In this paper, the problem of meniscus shape is formulated for a slender fibre: the weight of the meniscus is assumed very small hence the capillary forces play the main role in shaping the meniscus. Using the method of matched asymptotic expansions, the problem of capillary rise of a meniscus was reduced to a nonlinear problem of determination of a minimal surface; the boundary value problem consists of equations (2.2)–(2.4), and (3.13).

The proposed formulation allows one to interpret the meniscus problem as a problem of flow of a fictitious non-Newtonian fluid through a porous medium. The Chaplygin method of a hodograph plane was introduced. This approach employs a rich arsenal of methods of fluid dynamics to solve analytically many meniscus problems. The method is based on the conformal mapping of the hodograph plane onto the physical plane. As an example, an explicit solution for a meniscus on a completely wettable oval fibre with profile (4.25) was obtained. We showed that the contact line can have either smooth shape or form some cusps; this behaviour of the contact line is very sensitive to a small variation of the fibre shape. We discovered that the cusped contact line can be formed even on a ‘smooth’ fibre without visible sharp corners. In the analysed example, the fibre curvature controls the development of the cusped contact line. We believe that the proposed methodology will be useful for the analysis of the behaviour of capillary surfaces on the complex-shaped substrates.

Funding statement

M.M.A. was supported by the Russian Foundation for Basic Research, projects nos. 12-01-00996 and 13-01-00368. K.G.K. was supported by the National Science Foundation through the grant no. PoLS 1305338.