All-Atom Polarizable Force Field for DNA Based on the Classical Drude Oscillator Model

Abstract

Presented is a first generation atomistic force field for DNA in which electronic polarization is modeled based on the classical Drude oscillator formalism. The DNA model is based on parameters for small molecules representative of nucleic acids, including alkanes, ethers, dimethylphosphate, and the nucleic acid bases and empirical adjustment of key dihedral parameters associated with the phosphodiester backbone, glycosidic linkages and sugar moiety of DNA. Our optimization strategy is based on achieving a compromise between satisfying the properties of the underlying model compounds in the gas phase targeting QM data and reproducing a number of experimental properties of DNA duplexes in the condensed phase. The resulting Drude force field yields stable DNA duplexes on the 100 ns time scale and satisfactorily reproduces (1) the equilibrium between A and B forms of DNA and (2) transitions between the BI and BII sub-states of B form DNA. Consistency with the gas phase QM data for the model compounds is significantly better for the Drude model as compared to the CHARMM36 additive force field, which is suggested to be due to the improved response of the model to changes in the environment associated with the explicit inclusion of polarizability. Analysis of dipole moments associated with the nucleic acid bases shows the Drude model to have significantly larger values than those present in CHARMM36, with the dipoles of individual bases undergoing significant variations during the MD simulations. Additionally, the dipole moment of water was observed to be perturbed in the grooves of DNA.

INTRODUCTION

DNA participates in many vital biological processes, ranging from gene expression to million-fold compaction into chromatin and genetic packaging.¹ Those processes are controlled by a delicate balance of various types of physical interactions, most notably elastic and electrostatic forces.^2,3 For example, during formation of the basic repeating unit of the chromatin fiber, a nucleosome core particle, DNA wraps around the protein histone core with penalty incurred for the bending of the DNA molecule compensated by neutralization of its residual charge.^4,5 To understand the atomistic mechanisms behind such large-scale structural transformations experimental techniques, such as X-ray crystallography and solution NMR are of great utility, but are limited by a number of problems associated with DNA crystallization and resolution issues, as well as accessibility to short lived high energy states and time domain information.⁶ To overcome these limitations as well as allow for detailed investigations of the energetics of DNA, including investigations of structural transitions and environment effects, computational modeling represents a powerful approach. During the past two decades several additive all-atom empirical force fields (FF) for DNA have been developed, including CHARMM,^7,8 AMBER,^9,10 Bristol-Myers Squibb,¹¹ and GROMOS,¹² with the CHARMM and AMBER FFs being the most commonly used in studies of nucleic acids. Presently, we report on the development of a first generation all-atom CHARMM polarizable force field for DNA based on the classical Drude oscillator model.

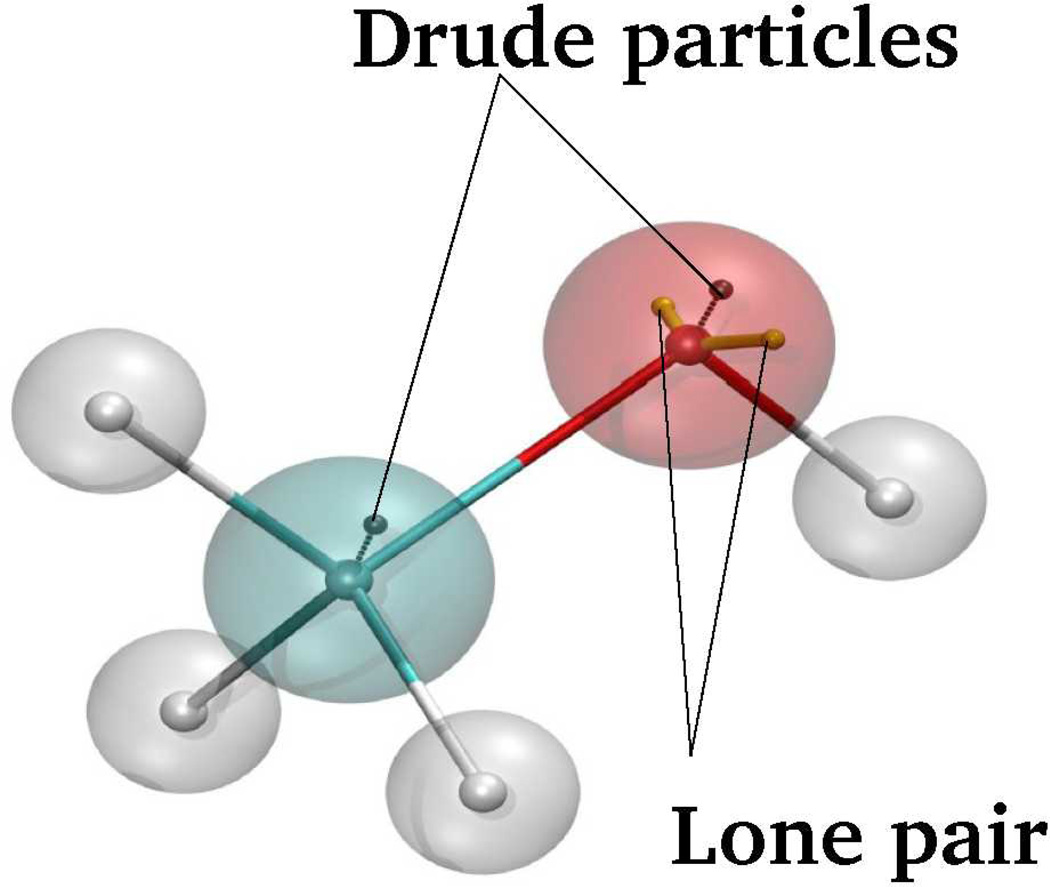
The additive all-atom force fields for nucleic acids treat electrostatics within the framework of the fixed-atomic-charge approximation where effective charges assigned to particles are independent of a system’s configuration. While this approach is very attractive from the viewpoint of computational efficiency, the underlying Coulomb electrostatic interaction potential does not allow for the system to respond to changes in the polarity of the environment via redistribution of the electron density. For such a complex biological system as polyanionic DNA immersed in an aqueous salt environment, whose conformational behavior is determined to a significant extent by solvation effects and interactions with the surrounding ionic atmosphere, the omission of polarization effects may preclude a physically correct description of its conformational behavior. In the present study electronic polarizability to represent electronic induction is explicitly included in the FF using classical Drude oscillators,¹³ where an auxiliary (Drude) charged particle is attached to each polarizable atom by a harmonic spring (Fig. 1). In practice, partial charge for the parent atom, q_A, and the Drude particle, q_D, are assigned based on the value of atomic polarizability, α, from the following equations,

$$\alpha ={(q_D)}^2/k_D,q_A=q_{tot}-q_D,$$ (1)

where k_D is the force constant on the harmonic spring connecting the Drude particle and the parent atom, and the q_tot is the net charge of the Drude oscillator.^14,15 While our earlier Drude models operated with the scalar isotropic polarizabilities, the model was extended to include anisotropic polarizabilities, to improve non-bonded interactions as a function of orientation involving hydrogen bond acceptors.¹⁶ For such atoms polarizability is a tensor of trace=3, diagonal in a local reference frame. In addition, to mimic higher order electrostatic effects, such as atomic multipoles in acceptors, and further improving the treatment of non-bonded interactions as a function of orientation, virtual particles representative of lone pairs were included in the model (Fig. 1).¹⁶ Additional extensions of the Drude model include the use of through-space Thole scaling and functions¹⁷ to avoid polarization catastrophe.^18,19 Details of the Drude model have been presented previously.^14,15,20

Figure 1.

Schematic representation of methanol including auxiliary Drude particles attached to the polarizable (non-hydrogen) atoms to model induced polarization in the classical Drude oscillator model along with the lone pair attached to the oxygen atom.

In MD simulations using the Drude model, charge redistribution as a response to the change in the local electrostatic field is approximated by updating self-consistently the positions of Drude particles. Importantly, both Drude particles and heavy atoms are explicitly considered, dynamically, within the framework of an extended Lagrangian formalism allowing for computationally efficient MD simulations.^21–23 For example, an implementation of the Drude model in NAMD²⁴ yielded a 1.6 to 2 fold increase in computational demand. This increase, along with the need to use a 1 fs integration time step, versus a 2 fs time step often used for additive MD simulations, yields an approximately 4-fold overhead for Drude polarizable simulations versus additive simulations. Accordingly, MD simulations of a Drude system comprised of ∼25,000 particles including DNA, water and mobile ions is feasible for hundred of nanoseconds and takes less than six weeks using NAMD²⁴ run on 32 AMD Opteron 2.3 GHz CPUs. In addition to CHARMM²⁵ and NAMD,²⁴ the Drude model has been implemented in ChemShell QM/MM²⁶ and efforts towards implementation of the model in the Gromacs package²⁷ and in the Open MM suite of GPU utilities²⁸ are ongoing.

Recently, Drude parameters have been presented for lipids,²⁹ proteins²⁰ and a limited collection of carbohydrates^30,31. Together with the present Drude FF for DNA and previously developed Drude models for water^32–34 and ions,^19,35 this opens a venue for numerous application studies of heterogeneous biological systems using a fully polarizable force field.

In this study we develop a Drude polarizable DNA model which faithfully captures the important conformational aspects of the B form of duplex DNA in solution, particularly, sequence-specific sugar repuckering and BI/BII transitions, with both processes occurring on a sub-nanosecond time scale. Additionally, the model is sensitive to changes in the environment and stabilizes the A form under appropriate conditions. Tests of the model demonstrate that it reproduces a range of experimental data on DNA in solution and performs similarly to the state-of-the-art additive force fields for nucleic acids. It also allows for a consistency with gas phase quantum mechanical (QM) data on model compounds representative of DNA exceeding that of the latest additive CHARMM36 FF.⁸ The presently developed DNA parameters will be included in the new Drude-2013 force field for macromolecules, which may be accessed via the MacKerell laboratory web page at http://mackerell.umaryland.edu/CHARMM_drude_ff_params.html. In addition, a new module, the Drude Prepper, has been added to the CHARMM-GUI³⁶ which allows for previously equilibrated systems based on the CHARMM36 additive FF to be converted to the Drude model along with the production of inputs for MD simulations using either CHARMM or NAMD. In the remainder of the present manuscript the Drude force field for DNA will be referred as the Drude model.

COMPUTATIONAL METHODS

Quantum Mechanical Calculations

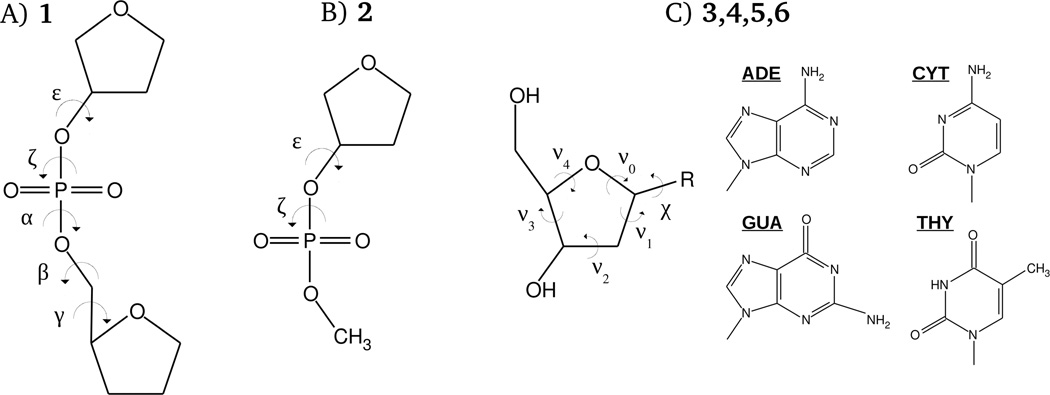
Model compounds used to study the conformational energetics of the DNA backbone, glycosidic linkage and sugar repuckering are shown in the Fig. 2. QM calculations on these systems were performed with the programs Gaussian 09³⁷ and QChem.^38,39 Model compound 1, designed to represent the DNA phosphodiester backbone, was previously subjected to extensive QM calculations.⁴⁰ A similar model compound was used in a study updating the additive AMBER force field for nucleic acids.^41,42 As described previously, 1D potential energy scans for each backbone dihedral angle were calculated by initially optimizing the structures at the MP2/6–31(+)G(d) level in Gaussian followed by a single-point energy calculations at the RI-MP2/cc-pVTZ level with QChem. Optimizations were initiated with selected dihedral angles in the sugar and phosphate moieties, constrained to values obtained from statistical surveys of DNA crystal structures in the protein⁴³ and nucleic acid⁴⁴ databases. For 1, following the initial constrained optimizations, additional optimization of sugar pucker with the backbone dihedral constraints maintained was performed at the MP2/6–31+G(d) level followed by RIMP2 single point calculations. Model compound 2, a truncated version of 1, was designed to study correlations between ε and ξ torsions in the context of BI/BII transitions in DNA.⁸ Calculation of the ε versus ξ 2D surface on this model compound was based on structure optimizations at MP2/6–31+G(d) level with no subsequent RIMP2 single-point energy evaluations. ε and ξ were sampled with an increment of 15°, with the single sugar dihedral and α dihedral restraints corresponding to B form DNA. Finally, model compounds 3, 4, 5 and 6, the deoxyribonucleosides of adenine, cytosine, guanine and thymine, respectively, were used for calculating 1D energetic profiles for rotations of purine and pyrimidine bases around glycosidic bond (glycosidic χ surfaces), as well as for studying energetics of sugar repuckering. Glycosyl surfaces were obtained from structures optimized at the MP2/6–31+G(d) level, subject to various structural restraints. Specifically, β, γ and ε dihedral angles, and also two of the five sugar torsions, ν₀ and ν₄, were restrained to the values corresponding to either A or B forms DNA, as described in Folloppe et al.⁴⁵ Additional combinations of restraints were applied to compounds 3 and 4 to model nucleoside conformations not sampled in pure A and B forms to get insights into the energetics of the A-to-B DNA transition on the nucleotide level. Those non-standard conformations include the following: A-like sugar conformation and the B-like χ torsion; B-like sugar conformation and the A-like χ torsion; O4'-endo sugar conformations with the χ corresponding to B form DNA; and planar furanose with the χ torsion characteristic of B DNA form.

Figure 2.

Model compounds used in the present study for parameter optimization. In (C), the base, R, is adenine for model 3, cytosine for model 4, guanine for model 5, and thymine for model 6, as shown. The phosphodiester dihedral angles shown in (A) and (B) are defined as follows: α = O3’-P-O5’-C5’, β = P-O5’-C5’-C4’, γ = O5’-C5’-C4’-C3’, ε = C4’-C3’-O3’-P, and ζ = C3’-O3’-P-O5’. In (C), the glycosyl dihedral angle, χ, is defined as O4’-C1’-N1-C2 and O4’-C1’-N9-C4, when R is cytosine/thymine and adenine/guanine, respectively. Definitions of the torsions of the sugar moiety are the following: ν₀ = C4’-O4’-C1’-C2’, ν₁ = O4’-C1’-C2’-C3’, ν₂ = C1’-C2’-C3’-C4’, ν₃ = C2’-C3’-C4’-O4’, and ν₄ = C3’-C4’-O4’-C1’.

Molecular Mechanical Calculations and MD Simulation Protocol

MM calculations on model compounds were performed with the program CHARMM⁴⁶, version 36. Model systems, subject to the corresponding dihedral restraints used in the QM calculations, were minimized using the adopted-basis Newton-Raphson (ABNR) algorithm before calculating dihedral potential energy scans. Dihedral harmonic restraints of 10⁵ kcal/mol/rad² were used with minimizations performed to a gradient of 10⁻⁶ kcal/mol/Ų.

MD simulations of a variety of DNA systems (Table 1) were carried out using the CHARMM⁴⁶ (version 36) and NAMD⁴⁷ (version 2.9) programs. For the majority of DNA systems initial configurations were generated by simulating the analogous additive CHARMM36 (C36) systems, solvated by a minimum of 8 Å beyond the solute non-hydrogen atoms, for several nanoseconds according to the protocol described elsewhere,⁸ taking the last snapshot from these runs as inputs for subsequent Drude simulations. All systems, except 1ZF1 (# 6 in Table 1), were solvated with the additive TIP3P (CHARMM version)^48,49 or polarizable SWM4-NDP³⁴ water models with neutralizing Na⁺ ions and an extra ∼120 mM of NaCl salt.¹⁹ In case of the 1ZF1 system, the solvent buffer was comprised of ∼75% of ethanol⁵⁰ and ∼25% of water along with the ∼120 mM of NaCl. Drude ethanol molecules⁵⁰ were generated from the standard additive EtOH molecules.⁵¹ All simulations were performed with periodic boundary conditions. Polarizable systems were generated using the CHARMM utility 'GENERATE DRUDE' that automatically adds the Drude particles and/or lone pairs to polarizable (non-hydrogen) atoms. A subsequent self-consistent relaxation of the Drude positions in the local electric filed was carried out using a combination of the steepest descent and ABNR minimization algorithms while holding all non-hydrogen atoms fixed. For each system a short equilibration of the solvent and mobile ions was then performed by running a 500 ps MD simulation with all solute particles fixed, followed by an additional 1 ns equilibration of the whole system without any restraints, after which the production MD simulations were initiated. All equilibration and some of the production MD runs were conducted with the CHARMM program, utilizing the Velocity-Verlet integrator (VV2)²⁵ in conjunction with the TPCONTROL (“Temperature-Pressure Control”) command, allowing for efficient simulation of the motion of Drude oscillators. In particular, a Nose-Hoover thermostat was applied to all real atoms to control the global system temperature of 300K, and a separate low-temperature thermostat at 1K was applied to Drude particles to ensure that their time course approximates the self-consistent field (SCF) regimen.²⁵ A constant pressure (1 atm) was maintained via a modified Andersen-Hoover barostat, and SHAKE⁵² was used to constrain covalent bonds involving hydrogens. Electrostatic interactions were treated using the particle-mesh Ewald (PME) summation⁵³ with a coupling parameter of 0.34 and a sixth-order spline for mesh interpolation. Non-bonded pair lists were maintained out to 16 Å, and a real space cutoff of 12 Å was used for the electrostatic and Lennard-Jones (LJ) terms, with a long-range correction applied to LJ interactions.⁵⁴ A recently implemented ‘HARDWALL’ feature of the CHARMM program enabled use of a 1 fs time step in MD simulations.²⁹ The name of this feature comes from the “hard wall” reflective term in the potential energy function that has been added to resolve the polarization catastrophe problem in Drude MD simulations, as previously described.²⁹ An analogous simulation protocol was used in all production MD runs with NAMD where an alternate dual thermostatting approach is applied based on Langevin dynamics.²⁴

Table 1.

DNA Systems Used for Parameter Training and Validation ^a

DNA sequence	Comment/Refrence
(1) d(CGCGAATTCGCG)	EcoR1 dodecamer, MD for 150 ns with Drude and C36 FFs, X-ray/NMR77–83
(2) d(GCATTCTGAGTCAG)	JunFos, experimental BII content 69,72,84
(3) d(ACACTACAATGTTGCAAT)	3BSE, B form, X-ray 1.60 Å; disordered region 85
(4) d(GAAGAGAAGC)	1AXP, NMR, high purine content strand 87
(5) d(CCGTCGACGG)	1ZF7, B form, X-ray (1.5 Å) 86
(6) d(CCGGGCCCGG)	1ZF1, A form, X-ray (1.35 Å) 86
(7) d(CGCATGCTACGC)	2L8Q, B form, NMR 88

^aOf these, EcoR1 and 1ZF1 were used as training systems. Other sequences were utilized for the force field validation. All simulations were performed for 100 ns unless noted. Comment/Reference includes the PDB or NDB identifiers.

Analysis of the DNA Structure and Dynamics

All simulated DNA structures were subject to the following analysis. First, RMS differences were calculated for all non-hydrogen DNA atoms in the non-terminal nucleotides relative to the A and B forms to characterize the structure of the molecule with respect to the canonical A or B forms DNA in the course of MD simulation. Next, the fidelity of the hydrogen bonds among complementary DNA bases was monitored by plotting the time series for the N1…N3 distances for each base step. An N1…N3 probability distribution over all the sequences was compared with the corresponding data from a survey of B form DNA crystal structures. Included in the survey were only double helical DNA duplexes with unmodified DNA bases or backbones, no protein or RNA in the structure, and with a resolution less than 2.5 Å. Terminal nucleotides were excluded from the analysis. DNA helicoidal parameters (rise, tilt, twist etc.)^55–57 were calculated and compared to experimental survey data. Additional analysis included calculation of the distributions of DNA backbone dihedral angles, glycosidic torsions and pseudorotation angle (sugar pucker distribution) from MD simulations and comparing them with the corresponding crystal survey data. As prominent features of DNA dynamical behavior include sugar puckering and BI/BII transitions, special attention was paid to time series of the ε and ξ torsions, as well as the evolution of the pseudorotation angle (P). Based on those data, correlation times for the base step to remain in a BI (BII) state and the sugar moiety be in the north (south) conformation were estimated by computing corresponding dynamic correlation functions. For EcoR1 and JunFos systems additional details of DNA structural behavior were analyzed by computing sequence dependence for the percent of the BII state from MD simulations with the comparison to experimental data. BI versus BII populations were computationally obtained by simple counting, i.e., BI if ε – ζ < 0 and BII if ε – ζ > 0; this method, however, differs from that used to obtain BII population estimates from NMR, as discussed below. For EcoR1 the sequence specific population of the N conformation by the sugar moiety was calculated assuming a two-state equilibrium between N (P=270…90°) and S (P=90…270°) states, a definition adopted in related J-coupling and residual-dipolar-coupling (RDC) NMR experiments.^58,59 Dynamics of the force field was tested on the basis of the reproduction of NMR order parameters for all C1', C3', C6 and C8 sites in EcoR1.⁶⁰ Finally, dipole moment analysis for the nucleic acid bases and the water molecules around major and minor DNA grooves in the EcoR1 system was carried out to demonstrate dipole moments vary in the polarizable model as compared to the additive C36 model.

For the analysis described in this section we used the following software. CHARMM analysis tools⁴⁶ were used for calculation of a majority of DNA characteristics, such as RMSD, N1…N3 distance and dihedral angle distributions. The Curves package^55,56 was used for computing time series of DNA helicoidal parameters from MD trajectories. The Biochemical Algorithms Library (BALL)⁶¹ was utilized for computing dynamical correlation functions, analysis of sequence specific effects, such as sugar repuckering and BI/BII transitions, and also for the structural and dipole moment analysis of the water in the major and minor DNA grooves. In particular, an in-house program was written to uniquely define the separation of the water molecule from DNA atoms based on the closest approach to the surface of the DNA groove; accordingly, the same approach was adopted to properly normalize the water-DNA radial distribution function. Additionally, BALL was used for writing code for reimaging/recentering of MD trajectories in cases when DNA strands (treated as independent segments) appeared separated in the course of simulation because of the periodic boundary conditions. This post-processing was necessary for subsequent calculations of the overall DNA properties, such as RMS deviations and helicoidal parameters, and also for computing water-DNA RDF.

RESULTS AND DISCUSSION

Parametrizaton strategy

The present study is based on more than a decade of work conducted in our lab, in collaboration with Roux and coworkers, on the development of a Drude polarizable force field for water,^32–34 ions^14,24 and various model compounds, such as nucleic acid bases, tetrahydrofuran, dimethylphosphate anion and others that represent components of nucleic acids as well as other biological molecules.^50,62–67 Applying preliminary Drude parameters for these model compounds in combination with the CHARMM27 all-atom nucleic acid FF directly to DNA and simulating the resulting oligomer in solution, the overall DNA structure deviated significantly from canonical conformation in less than 5 ns of MD simulation time,⁶⁸ indicating that critical aspects of DNA structural behavior are not captured by the force field. Among those aspects are the conformations of the phosphodiester backbone and repuckering of the sugar moiety. To overcome this, additional optimization of the parameters was performed on the basis of more complex model compounds. As seen in Fig. 2, compounds 1, 2 and 3–6 represent combinations of the nucleic acid bases, sugar and dimethylphosphate anion. The majority of parameters for those compounds were transferred from the simpler compounds with empirical optimization performed mainly on phosphodiester backbone dihedral angles and glycosidic and sugar group torsions. In addition, adjustments were necessary for some valence angles along the phosphodiester backbone and in all of the nucleic acid bases. Those adjustments led to a better representation of the vibrational frequencies of the bases and, based on results from preliminary calculations of DNA in solution, to closer agreement with experimental data on DNA helicoidal parameters. Also, alteration of the transferred partial atomic charges for selected backbone and sugar atoms, as well as adjustments of some of the Lennard-Jones parameters, were made based on model compound 2. The adjustments were again made following preliminary DNA simulations to obtain satisfactory agreement with QM and experimental data on the energetics of the correlated ε and ζ dihedrals. As for DNA electrostatic model in general, an independent extensive study has been conducted based on transport and thermodynamic properties of aqueous solutions of different cations and anions, solvation properties of various model compounds, and the interplay between mobile ionic atmosphere and DNA oligomer. Results from these investigations will be presented in a forthcoming manuscript with the remainder of the present work focusing on the final optimization of the DNA dihedral parameters and subsequent validation MD simulations.

Optimization of the Drude FF for DNA in the present study is based on balancing the energetic properties of the underlying model compounds and the overall conformational and dynamical properties of DNA in condensed phase. The same strategy was adopted in prior efforts on the development of both the additive and Drude polarizable CHARMM FFs. It is important to note that this strategy is more physically sound, though significantly more demanding, than approaches based on empirically adjusting parameters targeting only condensed phase experimental data on DNA, or approaches aimed at reproducing solely QM data on small model compounds. Indeed, the first approach does not guarantee sufficient fidelity of the important local DNA motions, while the latter one does not capture correlations among various motional modes and other many-body effects in the DNA polymer. For example, applying dihedral parameters optimized by direct fitting to the QM data on model compounds, 1 and 3–6, which were designed specifically to represent DNA backbone and glycosydic linkages, while stabilizing an overall DNA structure did not result in a model capable of reproducing critical aspects of DNA structural behavior in solution (Fig. S1 of the Supporting Information). Thus, while those parameters may serve as an initial guess, optimization of the parameters for the highly correlated DNA molecule needs to simultaneously target both QM and experimental data, allowing for a compromise between the level of agreement with the two types of target data. While this approach was previously applied during additive DNA FF development, the increased sensitivity of the polarizable FF to changes in the environment increases the degree of difficulty in balancing the reproduction of the gas phase QM and experimental condensed data.

Following the history of additive CHARMM force field development for nucleic acids,^7,8,69 we presently focus on the two main aspects of duplex DNA conformational behavior: (1) the equilibrium between A and B forms of DNA and (2) the BI/BII conformational equilibrium within the B form of the DNA. The BI and BII sub-states are defined on the basis of the two phosphodiester dihedral angles, ε and ξ, with the difference ε – ξ ≤ 0° corresponding to BI and ε – ξ > 0° corresponding to BII. The equilibrium between BI and BII states influences the overall DNA conformation by altering its helicoidal parameters and modulating the width of the major groove.⁷⁰ As a result, BI/BII equilibrium has direct consequences for a myriad of the groove binding processes, e.g. protein-DNA recognition,⁷¹ and may even contribute to the ability of DNA sequences to form nucleosomes.⁷² Experimental data indicates that around 20% of the base steps in duplex DNA alone populate the BII state, with the percentage decreasing in DNA bound to proteins.⁷³ NMR experiments allow for evaluation of the percent of the BII as a function of sequence for some DNA molecules,^72,74,75 and this information can be readily used for FF optimization and validation. Interestingly, when correlations between ε and ξ torsions are investigated on the model compound level from a QM two-dimensional (2D) energetic profile for these dihedral angles, a minimum corresponding to the BII state is not present (see below). This indicates that transitions between BI and BII is a cooperative process driven by correlation effects in the DNA.

Equilibrium between the A and B forms of the DNA is significantly impacted by the energetics of repuckering of the sugar moiety.⁴⁵ The C2'-endo (south, or S) conformation of the ribose dominates B form DNA, while the C3'-endo (north, or N) conformation is characteristic of the A form of DNA as well as the A form of RNA. NMR investigations have been interpreted in terms of the two-state equilibrium, N vs. S, providing information on the sequence specific extent of the N population in the EcoR1 Dickerson-Drew dodecamer.^58,59 Computational results indicate cytosine to favor the N sugar pucker, contributing to GC base pairs leading to an increased propensity of sampling of the A form of DNA.⁴⁵ Additionally, NMR order parameters, S², for the EcoR1 duplex are available⁶⁰ for direct comparison with predictions from MD simulations, allowing for a test of the ability of the FF to capture the kinetics of the local DNA motions. Similarly to BI/BII transitions, DNA’s sugar repuckering is a highly cooperative process, not amenable to study using only simple model compounds. For example, when the parameters optimized for DNA in solution are applied to β-ribose, a model compound used to investigate sugar repuckering in prior studies,⁷⁶ the barrier between the N and S sugar conformations is overestimated relative to QM data. At the same time, use of those parameters in MD simulations results in the frequent sugar repuckering on a sub-nanosecod time scale, in very good agreement with NMR data.⁶⁰ As discussed below, understanding sugar repuckering in DNA requires accounting for consideration of the role of other local structural transformations, such as rotation about the glycosidic bond and the population of the BII state which anti-correlates with the north conformation of the sugar.

Another important aspect of DNA conformational behavior involves the α and γ phosphodiester backbone dihedrals. For example, enhanced sampling of non-canonical α/γ states was identified in DNA simulations longer than 10 ns using the AMBER Cornell et al. force field.⁷⁷ The problem was solved using QM data on model compounds.⁷⁸ In the present study we encountered a similar problem leading to destabilization of the DNA duplex after ∼8 ns of simulation. However, direct parameter fitting targeting the QM data did not correct the situation with the Drude polarizable model, and subsequent manual adjustments were necessary.

Survey of the DNA Systems Studied

Target and validation data for the polarizable force field involved various aspects of DNA structural behavior using a number of DNA systems varying in length and sequence. Those are listed in the Table 1. The EcoR1 dodecamer was a natural choice as it has been among the most extensively studied DNA sequences.^79–85 For this system a variety of experimental data are available, including sequence specificity of the BII content⁷⁵ and repuckering of the sugar moiety,^58,59 as well as data on the dynamics of the local DNA motions.⁶⁰ The JunFos sequence was selected because it has been subjected to explicit analysis of the BII content in solution.^71,74,86 A longer oligonucleotide, 3BSE, was chosen in part due to unique dynamic aspects of the molecule in solution.⁸⁷ Sequences 1ZF7 and 1ZF1 were of interest as they crystallize in the B and A forms, respectively, despite their similar sequences.⁸⁸ System 1AXP was selected to test the overall DNA stability in a duplex where the strands are rich in purine or pyrimidine content.⁸⁹ Among other simulated DNA systems was the 2L8Q sequence, a recently resolved structure by solution NMR.⁹⁰ Except for the 1ZF1 system, simulations of all sequences were initiated from the B form of DNA in an aqueous salt solution, according to the MD protocol elaborated above. For 1ZF1, two independent MD simulations initiated from the A form conformation were performed – one in water and another in 75%-ethanol solution, with the addition of ∼120mM of NaCl in both systems – to test the sensitivity of the FF to changes in DNA environment and, specifically, the ability of the Drude FF to maintain the A form in a low water activity environment. Because the equilibrium between A and B form DNA and BI/BII transitions are the two critical features we targeted during optimization of the Drude model, 1ZF1 and EcoR1 duplexes were chosen as training sequences, while the rest of systems were used for the force field validation. Unless noted, MD simulations were run for 100 ns.

Model Compound Calculations

Results in this section focus on the energetic properties of model compounds 1–6 using the final parameters derived for DNA, with emphasis on the ability of the Drude model to reproduce the gas phase QM data. In addition, the performance of the presently developed Drude force field is compared to that of the C36 additive model.

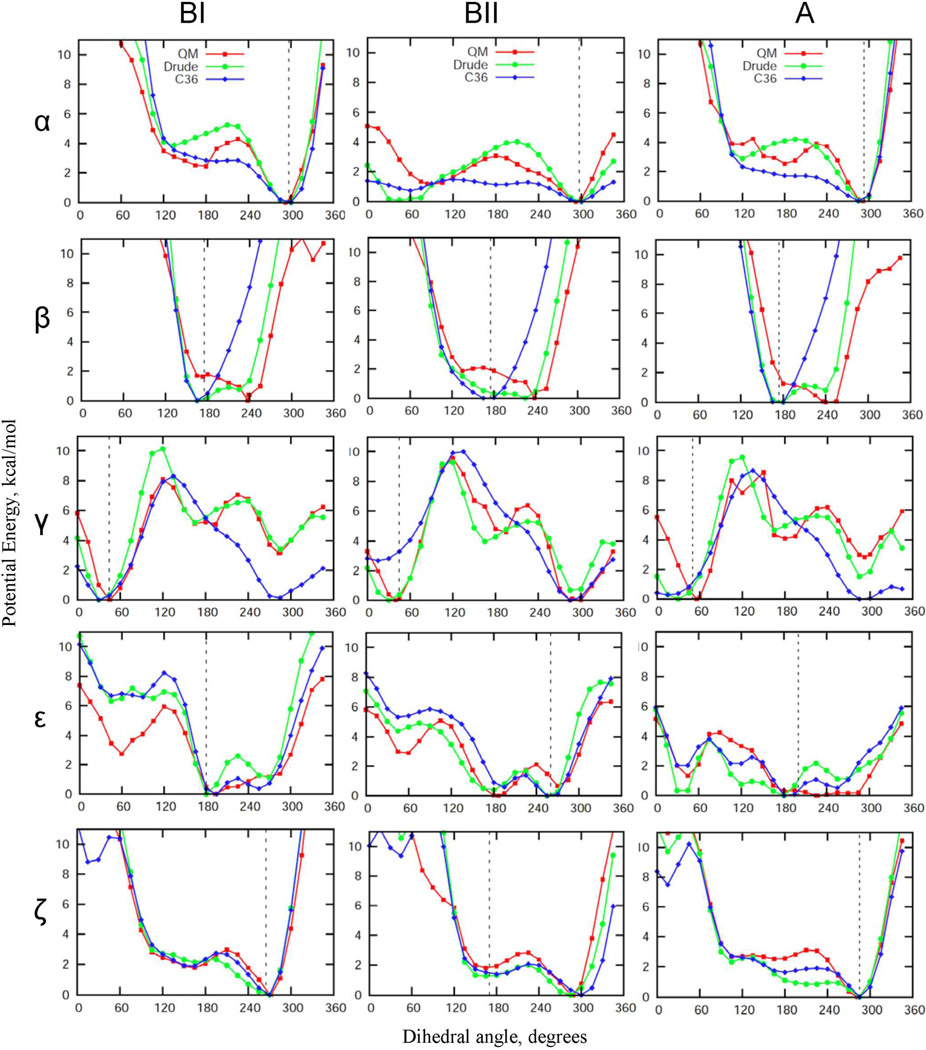
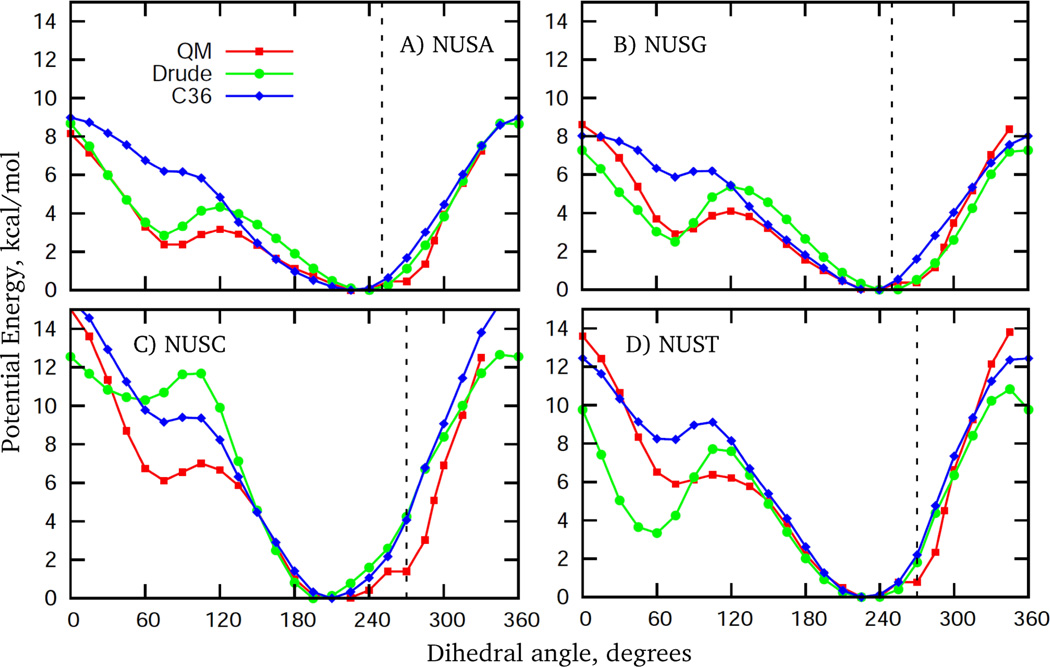
Model compound 1, comprised of two furanoses connected by a phosphodiester linkage, was previously designed as a model of the intrinsic conformational properties of the phosphodiester backbone,⁴⁰ analogous to the alanine dipeptide in the context of the polypeptide backbone,²⁰ and subjected to extensive QM calculations. The energetics of the compound was shown to be representative of the DNA backbone in duplexes. Accordingly, compound 1 represents an ideal starting point for the optimization of the backbone-associated parameters. QM energy profiles as a function of backbone dihedral angles for 1, along with the corresponding MM profiles generated by the final Drude and C36 FFs are plotted in the Fig. 3. In general, the overall shape of the empirical and QM surfaces are similar; however the Drude model is typically in better agreement with the QM data as compared to the additive results. This is particularly true for α, β and γ in all three conformations of 1 corresponding to BI, BII and A forms DNA. Although some of these improvements occur in ranges of the dihedrals not sampled in canonical DNA, their improved treatment is anticipated to be important when modeling structural transformations involving sampling of distorted backbone conformations. For example, in studies on DNA base flipping various phosphodiester backbone dihedral angles were shown to significantly deviate from canonical values.^91–93 The better performance of the Drude model compared to the additive is expected since the ability of atoms to polarize allows for more accurate treatment of conformational energetics in different environments, in this case the gas phase environment at the model compound level and the aqueous, condensed phase environment of duplex DNA, as will be shown below.

Figure 3.

QM and empirical potential energy profiles as functions of the key backbone phosphodiester dihedral angles obtained for model compound 1 with the remainder of the rotatable bonds maintained at dihedral angles corresponding to the BI, BII, or A canonical conformations. Noticeable deviations from QM surfaces come from the empirical adjustment of these backbone dihedral angles undertaken to improve the agreement with the crystal survey distributions (see also Fig. S1 of the Supporting Information section). Vertical dashed lines indicate the position of the maxima in the corresponding dihedral angle distributions from the crystal survey data on all structures in the BI, BII and A forms, respectively.

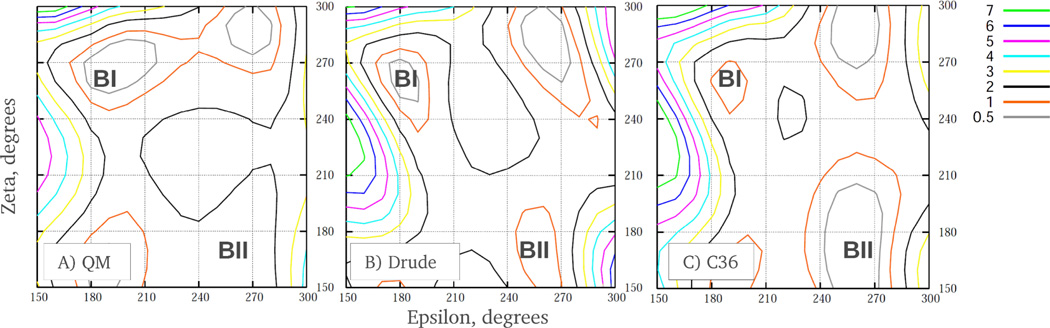
Of particular interest are the conformational properties of the ε and ζ torsions due the highly correlated motions of these dihedrals, which define the BI/BII conformations of DNA. ε and ζ potential surfaces for 1 are included in the Fig. 3. In spite of the overall similarity between empirical and QM profiles, differences are evident associated with the relative energies of the BI and BII minima, as well as in the energy barrier between BI and BII. As with the other backbone torsions, empirical adjustments for ε and ζ dihedral parameters were undertaken to improve agreement between DNA duplex simulations and the crystal survey data. In addition, the 1D PES for 1 were used as a consistency check, while optimization of the ε and ζ interaction parameters was primarily guided by the 2D QM energetic landscape for these angles using 2 due to the ε and ζ torsions varying in DNA in a concerted fashion. Correlations between ε and ζ dihedral angles are manifested by their bimodal distributions, as seen from the crystal survey data. The peaks in these distributions correspond to BI (ε∼190°, ζ∼270°) and BII (ε∼260°, ζ∼180°) DNA states. Shown in Fig. 4 are QM and empirical potential energy surfaces of ε vs. ζ. Notable are the relative energies of the minima and the topology of the low energy pathways connecting BI and BII states. In all the surfaces, the energies of the accessible regions of the torsions vary between 0 and 2 kcal/mol, suggesting frequent BI/BII transitions in DNA. ε and ζ time series of a selected base step in EcoR1 demonstrate that BI/BII transitions occur on a time scale of ∼200 ps (see Fig. 5). Consistent with these data are results of an earlier study which estimated the free energy barrier to be in the range of 2.6 to 3.1 kcal/mol based on potential of mean force calculations between the A and B forms of DNA.⁹⁴ Alternatively, results form ³¹P NMR experiments indicated that the free energy barrier for BI/BII transitions might be in the range of 12–15 kcal/mol,⁷⁵ predicting the transition time scale to be on the order of milliseconds. However, those estimates are based on the assumption of a two state model, which may not be appropriate given the significant sampling of intermediate states in both ε and ζ in MD simulations of DNA (Fig. 5). Alternatively, the experimental estimate of >12 kcal/mol may be because of more global structural phenomena (base stacking, sugar puckering etc.) contributing to the observed barrier, if the model used to make the experimental estimates is appropriate. Future studies are required to address this issue. Finally, we note that the BII minimum is not present on the 2D QM surface indicating that many-body effects in duplex DNA are not captured on the model compound level. However, empirical adjustment of ε and ζ parameters led to the prominent minimum for BII in the MM surfaces, with the additive FF having a significantly more pronounced BII minimum and a smaller barrier between the BI and BII states as compared to the Drude model. This further demonstrates the decreased ability of the additive FF to capture finer details of the QM potential surfaces while reaching satisfactory agreement with the experimental duplex DNA data.

Figure 4.

2D potential energy surfaces of ε vs. ζ for the (A) QM MP2/6–31+G(d) model chemistry, the (B) Drude force field, and (C) additive C36 force field for model compound 2. Energies are in kcal/mol. Approximate locations of the potential energy minima for the BI and BII states are shown.

Figure 5.

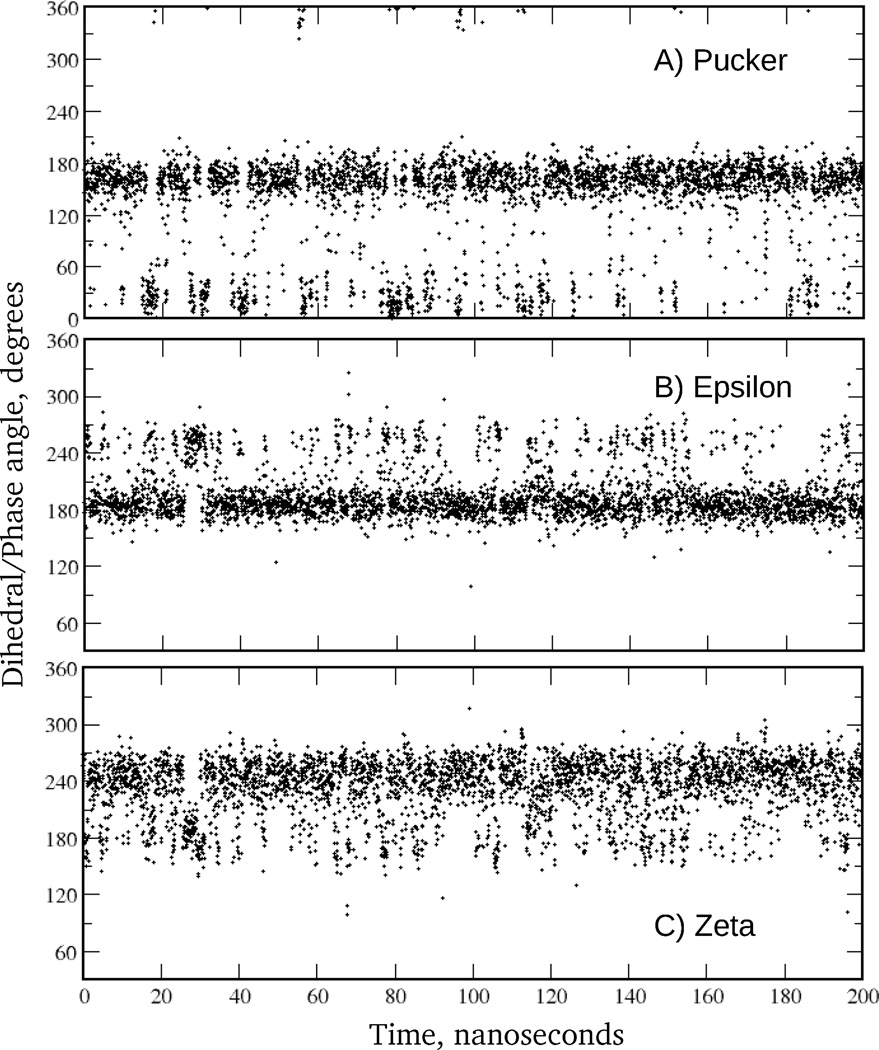
Time series from EcoR1 Drude MD simulation for (A) sugar puckering of strand 1, nucleotide 3, (B) ε of strand 1, nucleotide 4, and (C) ζ of strand 1, nucleotide 4. Data points are shown for every 50 ps. In the BI state ε and ζ are approximately 190° and 270°, respectively, and in the BII state they are approximately 270° and 180°, respectively. The pseudorotation angle characterizing the conformation of the sugar moiety assumes values of approximately 175° and 15° when the sugar is in the south and north states, respectively.

Sugar puckering in nucleosides was studied using model compounds 3–6. Use of a nucleoside as the model for the gas phase QM calculation is necessary to account for the impact of the ring substituents on the conformational properties, as previously discussed.⁴⁵ Puckering of the sugar moiety in DNA is a highly cooperative process that needs to be considered together with accompanying local motions, including rotations of the bases about the glycosidic linkage. When the sugar is in the N conformation the glycosyl dihedral angle χ takes values of ∼200°, while with the S sugar conformation that value is ∼240°. Because of these correlations, we evaluate the performance of the Drude and additive FFs applied to 3–6 on the basis of two complementary sets of QM data on these model compounds: (1) 1D potential energy scans for the χ torsions in all 4 types of nucleosides, with the sugar moiety being constrained in the S conformation, and (2) complementary data on QM energy calculations for selected nucleoside conformations typically sampled in canonical A and B form DNA as well as non-canonical nucleoside conformations, as listed in the Methods section. As discussed above, simultaneous analysis of these data allows for estimation of the energetics of the sugar repuckering in DNA on the nucleotide level.

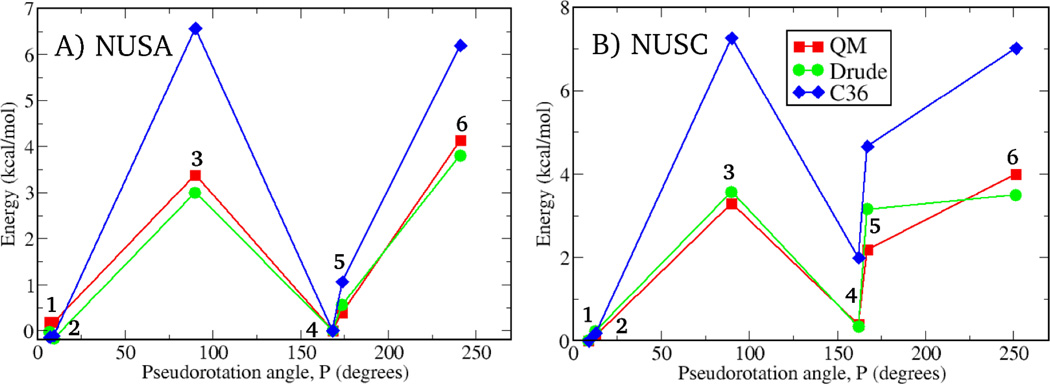
The QM and MM χ potential energy surfaces for 3–6 are presented in Fig. 6. As previously shown, these QM profiles correctly predict the positions of the corresponding χ distributions from crystal survey data.⁷ For the glycosyl surfaces in the A and G nucleosides the Drude MM results are more consistent with the QM data as compared to the additive model, although the level of agreement is similar for the C and T nucleosides. However, the situation is dramatically different when QM and empirical results are compared for energies calculated on different conformations of the sugar moiety in combination with various relative orientations of the base (Fig. 7). Qualitative differences between the Drude and additive results are evident. There is almost perfect agreement between the QM and Drude energies, while additive results significantly deviate from the QM data. For example, in the additive model, for the C nucleoside the energy of the N conformation with χ∼200° relative to the S conformation with χ∼240° is underestimated by ∼2.5 kcal/mol compared to the QM data. While such overstabilization of the north pucker conformation was necessary in the additive model to reproduce the experimentally observed enhanced sugar puckering of cytosine in DNA,⁶⁰ the consistency with experiment was achieved in duplex DNA while maintaining better agreement at the model compound level with the Drude model, which underestimates the N conformation by only ∼0.8 kcal/mol (see Table 2). As seen from Fig. 7, the additive FF also significantly overestimates energies of all non-canonical conformations in nucleosides for both the purine and pyrimidine bases, while the Drude results are in near quantitative agreement with QM data.

Figure 6.

Potential energy surfaces as a function of the glycosyl torsion χ for model compounds 3–6, with the remaining dihedrals being restrained to conformations corresponding to canonical B form DNA, as elaborated in the Methods section. Vertical dashed lines indicate the position of the maxima in the corresponding dihedral angle distributions from the crystal survey data on all structures in the BI conformation. As in Figure 3, deviations from QM data are attributed to the empirical adjustments of the χ torsions to improve consistency with the crystal survey data, as well with NMR experiments on sugar repuckering in cytosine.

Figure 7.

Relative potential energies for various conformations of model compounds 3 (A) and 4 (B) – nucleosides of adenine and cytosine, respectively. Six conformations for each model compound were considered to probe energetics of the A-to-B DNA transition on the nucleoside level. Conformations 2 and 5 are those sampled in canonical A and B form DNA, respectively. Conformations 1 and 4 differ from 2 and 5, respectively, by values of the glycosidic torsion χ (B-like for 1, and A-like for 4). 3 and 6 are non-canonical conformations with the sugar moiety being in the O4’-endo and planar conformation, respectively. See Methods section for details.

Table 2.

Relative Energies of the Conformations of the Nucleosides of Adenine and Cytosine (Model Compounds 3 and 4) Sampled in Canonical A and B forms DNA ^a

Level of theory	A form: north sugar, χ = 200°		B form: south sugar, χ = 240°
	phase angle	ΔE	phase angle	ΔE
NUSA
QM	9.35	−0.21	173.85	0.00
Drude	9.31	−0.75	173.81	0.00
C36	9.26	−1.26	172.96	0.00
NUSC
QM	12.65	−2.05	167.00	0.00
Drude	12.68	−2.92	166.94	0.00
C36	12.75	−4.52	166.53	0.00

^aValues presented for conformations 2 (A form) and 5 (B form) in Fig. 7. Energies in kcal/mol and angles in degrees. Sugar pucker phase angle calculated on the basis of the method of Altona and Sundaralingam¹⁰⁴ with QM data at the RIMP2/cc-pVTZ//MP2/6–31(+)G(d) level. β, γ and ε dihedral angles, and two of the five sugar torsions, ν₀ and ν₄, were restrained to the values corresponding to either A or B forms DNA. See Methods section.

It is also of interest to test the Drude model against QM data on a simpler model compound, 2-deoxyribofuranose, which is an analog of 3 lacking a base. This system was subjected to extensive QM calculations with emphasis on energetics of the sugar puckering.⁷⁶ Fig. S2 shows 2D energy surfaces for the Drude model along with the QM data. Notably, while the barrier between S and N states is overestimated in the Drude model, the same Drude parameters generate sub-nanosecond time scale A-to-B transitions in the DNA MD simulations (Fig. 5), consistent with NMR experiments and the puckering energies in 3 (Figs. 6, 7). This is another clear demonstration that simple model compounds may not include the functional groups necessary to mimic the correlated properties occurring in duplex DNA. In particular, the sugar moiety, including the hydroxyl groups, along with the nucleic acid base is required to model puckering of the sugar moiety in DNA.

Validation of the Drude Force Field Based on Condensed Phase MD Simulations

DNA duplexes subjected to MD simulations in solution are listed in Table 1. Of these, EcoR1 and 1ZF1 were used extensively during the iterative optimization process. Thus, these systems do not represent true validation of the model. However, the remaining sequences were not included during the optimization of the model and therefore can be considered a test set for validation of the model.

Overall DNA Conformation and the A vs B Conformational Equilibrium

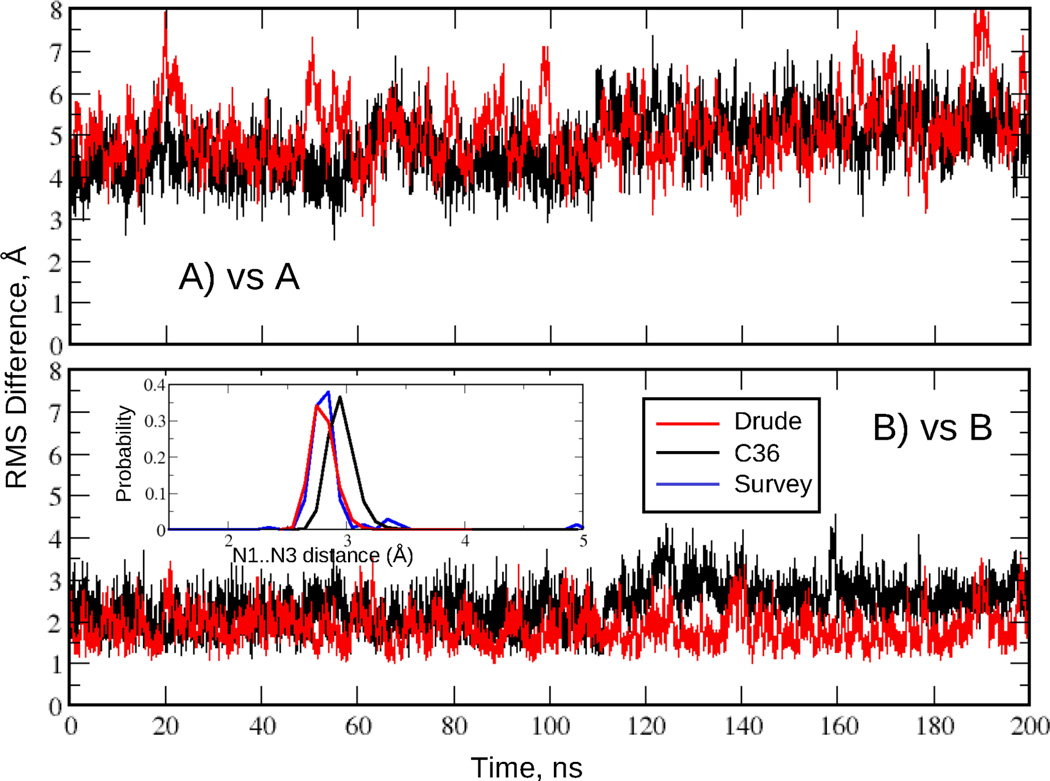
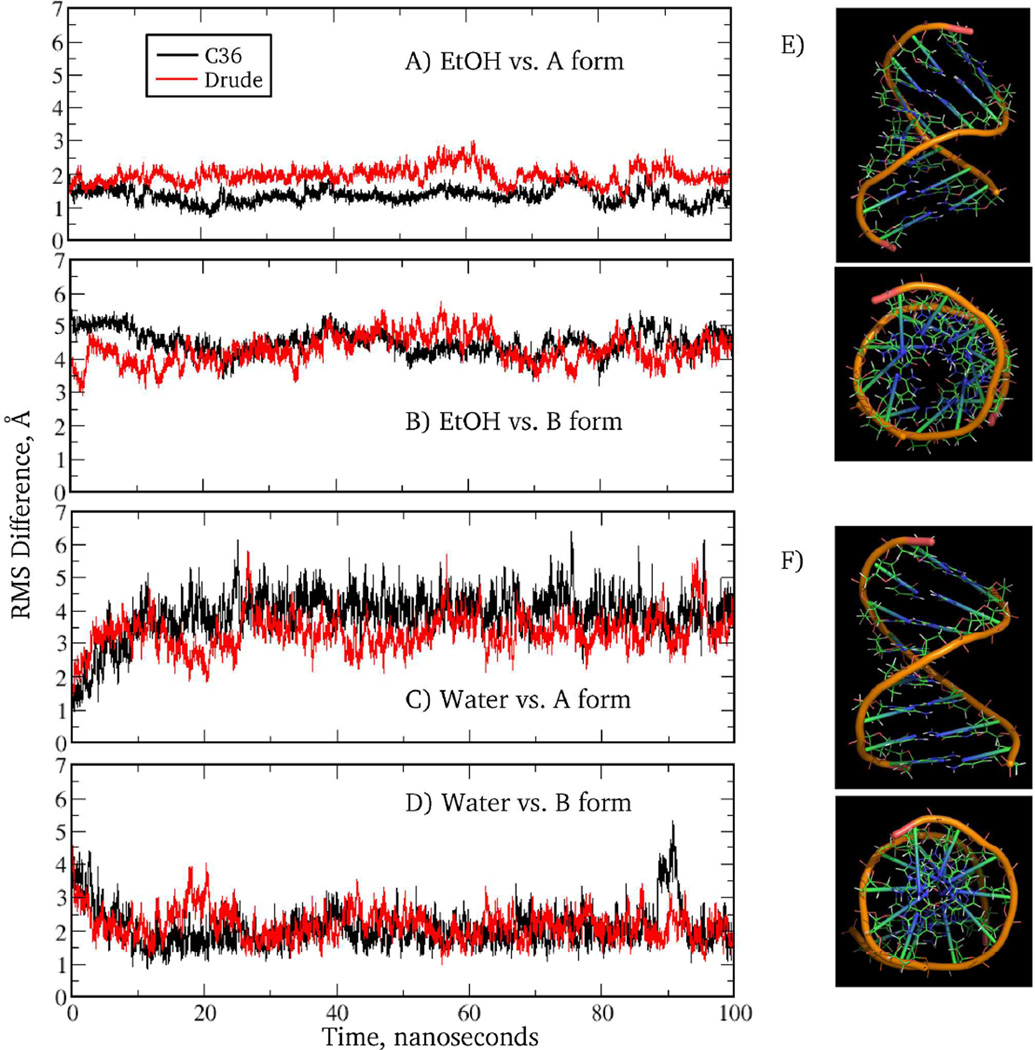
The overall DNA conformation was characterized by the time course of RMS deviations from canonical A and B structures and by Watson-Crick base pair interactions based on the N1…N3 distance distributions. These are shown in the Fig. 8 for the EcoR1 dodecamer simulated for 200 ns with the additive C36 and Drude force fields. The duplex remained stable and close to the B form throughout the simulation. Watson-Crick base pairing was also well maintained based on the N1…N3 distance time series for all non-terminal base pairs (Fig. S3) and the corresponding distance distribution (inset of Fig. 8). Notably the Drude N1…N3 distribution is in near perfect agreement with the crystal survey data while the C36 distribution has a maximum at a slightly longer distance (by 0.1 Å). Also, there is extensive base pair opening taking place in the terminal base steps in the C36 model (Fig. S3). This may contribute to the different extents of the sugar repuckering and populating of the BII state in the two models, as discussed below. N1…N3 distance time series and RMS deviations for the other DNA sequences are shown in the Fig. S4 and S5, respectively, of the Supporting Information. As seen from those figures and Table 3, in all cases the simulated outcomes are consistent with experimental data: all DNA sequences are stable and sample conformations closer to the B versus the A form. In addition, Watson-Crick base pair interactions are well maintained. These results indicate that the presented Drude DNA model properly represents the equilibrium between the A and B forms in high water activity.

Figure 8.

RMS difference versus time for the EcoR1 dodecamer in solution. RMS differences vs the (A) canonical A form and (B) canonical B form of DNA for all non-hydrogen atoms in the nonterminal residues. Data are shown for every 4 ps. Results are for the C36 (black) and Drude (red) force fields. Inset: Watson-Crick base pair interaction based on the N1…N3 distance distributions for the two force fields and data from the survey of B form DNA crystal structures (blue).

Table 3.

Average RMS Differences (Å) with respect to the Canonical Forms of DNA for the Drude and CHARMM36 Simulations ^a

DNA system	Drude		C36
	vs A	vs B	vs A	vs B
EcoR11	4.93 ± 0.67 4.00 ± 0.68	1.85 ± 0.39 1.73 ± 0.37	4.61 ± 0.651 3.54 ± 0.461	2.29 ± 0.501 1.88 ± 0.361
JunFos	6.19 ± 0.60 5.33 ± 0.55	1.89 ± 0.35 1.68 ± 0.29	6.06 ± 0.69	2.61 ± 0.57
3BSE	6.29 ± 0.67 5.75 ± 0.68	2.32 ± 0.55 1.89 ± 0.44	5.21 ± 0.65	3.71 ± 0.91
1AXP	5.20 ± 0.67 3.63 ± 0.49	2.26 ± 0.63 2.04 ± 0.56	4.02 ± 0.57	2.42 ± 0.58
1ZF7	4.24 ± 0.66 3.04 ± 0.47	1.49 ± 0.26 1.27 ± 0.25	4.23 ± 0.57	2.07 ± 0.51
2L8Q	5.73 ± 0.73 4.58 ± 0.59	1.77 ± 0.42 1.55 ± 0.29
1ZF1(EtOH)	1.95 ± 0.24 1.64 ± 0.20	4.23 ± 0.42 3.31 ± 0.36	1.34 ± 0.22	4.43 ± 0.31
1ZF1(H2O)	3.32 ± 0.56 2.35 ± 0.39	2.21 ± 0.48 1.81 ± 0.36	4.06 ± 0.50	2.07 ± 0.52

^aResults over all non-hydrogen atoms obtained by excluding one terminal residue (first row) and the first two terminal residues (second row) on each end of the DNA molecule from the analysis. Errors represent the RMS fluctuations about the average. Data are based on 100 ns MD simulations for all systems except EcoR1. For EcoR1 sequence RMSD is calculated based on 200 ns simulations. (1) Additive C36 results for EcoR1 are from MD simulations carried out in this study. All other C36 results are from Ref.⁸

Simulations were also undertaken to see if the Drude model can model the shift to the A form of DNA in low water activity, as observed for selected sequences. Previously, this aspect of DNA structural behavior was addressed with versions 27 and 36 of the additive CHARMM force field^8,69 and with the AMBER Parm94 force field.^95,96 To investigate this, the 1ZF1 sequence was simulated in two solutions, water and 75% ethanol, with both simulations being initiated from A form DNA. Shown in the Fig. 9 are RMS deviations for 1ZF1 system simulated for 100ns along with the averaged DNA structures maintained in the two solutions. It is seen that in 75% ethanol the Drude model samples conformations close to the canonical A form, as expected for the GC-rich duplex in a low water-activity environment. In contrast, in aqueous (0% ethanol) solution the DNA oligomer quickly deviates from the initial conformation and converts to a structure close to the B form. This critical test indicates that the Drude force field is sensitive to the changes in the water activity of the environment.

Figure 9.

RMS difference versus time for 1ZF1 for C36 (black) and Drude (red) models from MD simulations in a 75% ethanol solution (A, B) or aqueous solution (C, D) versus the canonical A (A, C) and B (B, D) forms of DNA. Data from 100 ns MD simulations are shown for every 4 ps. Also shown are the side and top views of the averaged over MD trajectory snapshots DNA structures maintained in the 75% ethanol (E) and pure water (F) solutions. Only nonterminal residues in (E, F) are shown. An open cylindrical core is clearly seen in the top view of the structure (E), which is a characteristic feature of the A-form DNA.

Analysis of the DNA Helicoidal Parameters

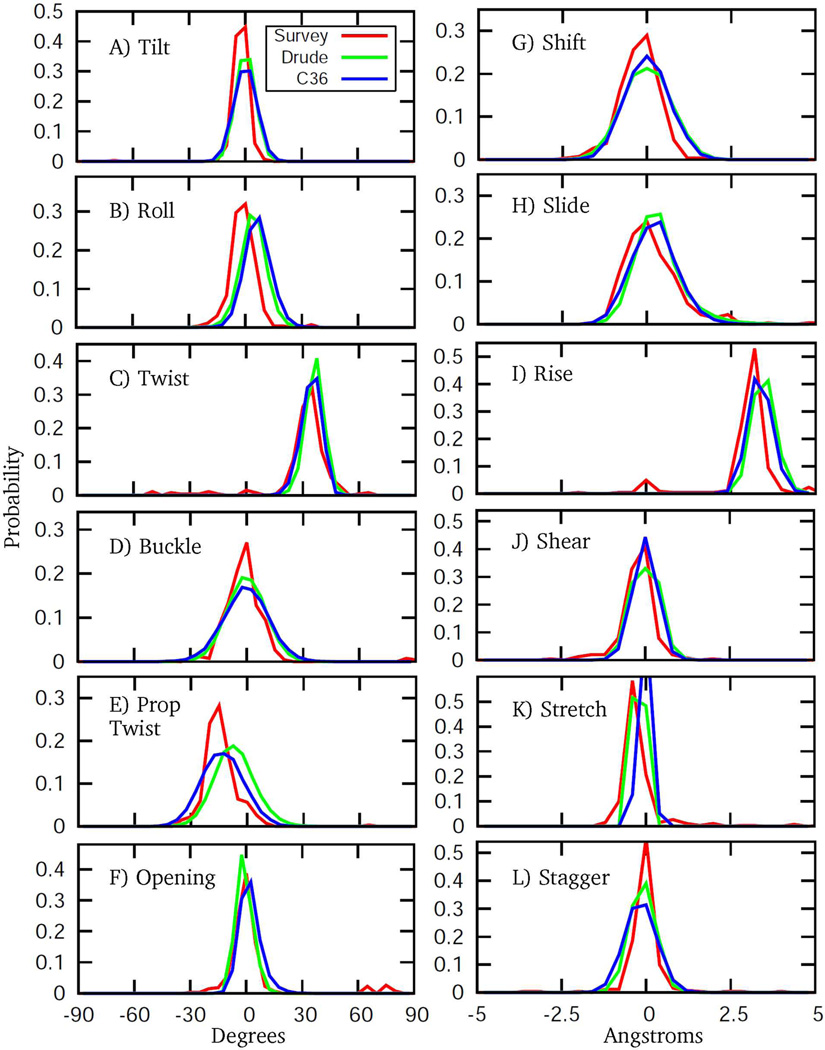
To further characterize the conformational properties of the DNA we computed various helicoidal parameters, which are commonly used to define the orientations of bases relative to the helical axis.^55–57 Notably, these terms, in contrast to the dihedral angles, were not directly targeted during optimization of the Drude model. Selected helicoidal probability distributions obtained from the MD simulation of EcoR1 were compared with a survey of crystallographic B DNA structures. The results are presented in the Fig. 10. Overall good agreement between simulation and experiment is obtained for the studied helicoidal characteristics. The quality of the Drude results is very similar to that of the C36 model. Deviations from crystallographic distributions are evident for some helicoidal parameters, such as rise, roll, and propeller twist. However, one should bear in mind that DNA properties in solution may deviate from the averages obtained from crystal survey data. For example, a noticeable shift in the distribution for propeller twist may be a result of accumulation of several small deviations of other related characteristics, such as the sequence-specific sugar puckering associated with the sampling of the A-like χ conformation.

Figure 10.

Helicoidal parameter probability distributions from the 200 ns MD simulations of EcoR1 using the C36 (blue) and Drude (green) force fields. Included are corresponding distributions from a NDB survey (red) of all B form structures with a resolution ≤ 2.5 Å. Drude and C36 distributions are based on analysis of MD trajectory snapshots saved every 4 ps (50,000 frames in total); bin sizes for distances and angles are 0.4 Å and 5 degrees, respectively.

Conformational Analysis of the DNA Backbone, Sugar Moiety and Glycosidic Linkages

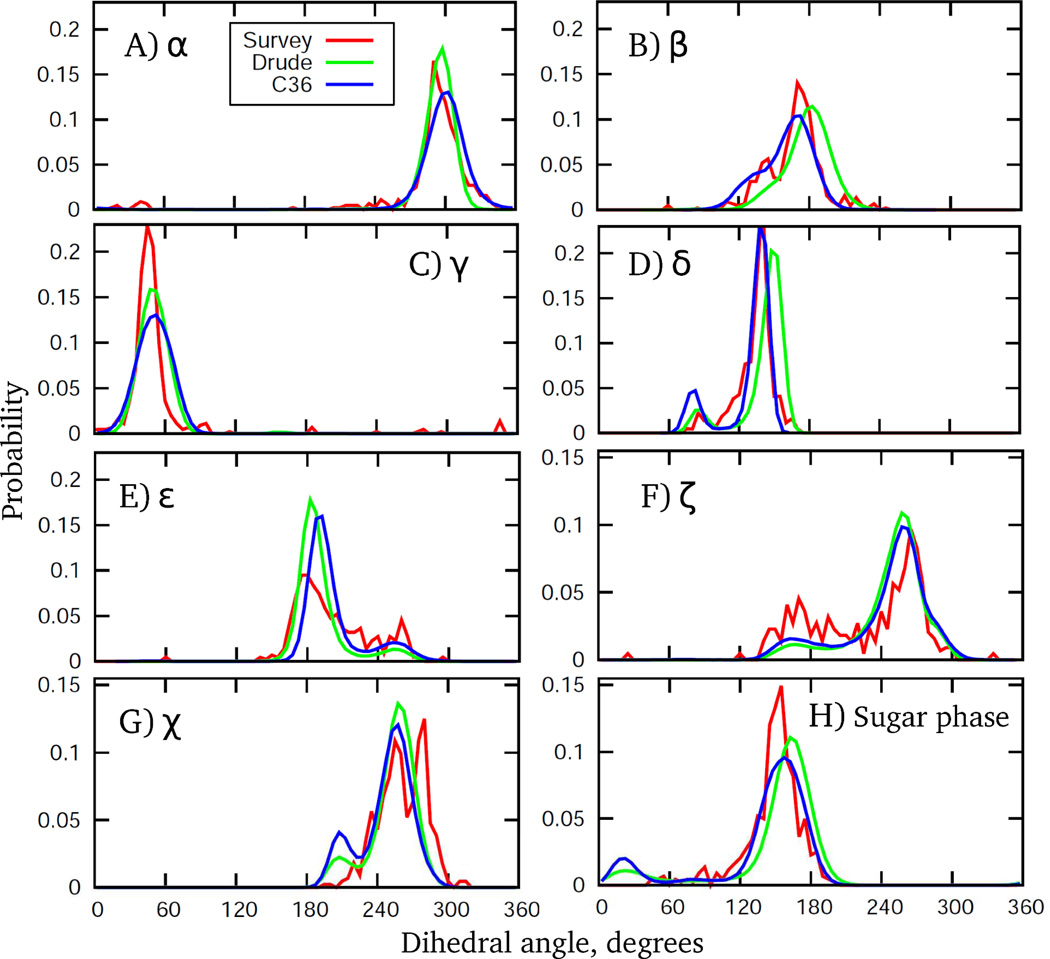
A more detailed analysis of the DNA structure in solution involved examination of probability distributions of dihedral angles in the backbone, of the glycosidic linkage, and of the sugar puckering. Comparisons involved probability distributions from the MD simulations with those from the crystal survey data. It should be noted that these distributions were targeted directly during optimization of the force field in the context of the EcoR1 and 1ZF1 sequences. The final distributions are presented in Fig. 11 for the EcoR1 dodecamer. Distributions for all other DNA systems maintaining the B form in aqueous solution, as well as for 1ZF1 in 75% ethanol, are shown in Figs. S6 and S7 of the Supporting Information. Additionally, distributions collected over all the B form DNA simulations are presented in Fig. S8 to facilitate comparison with the survey data based on crystal structures. From these figures it is evident that the Drude force field satisfactorily reproduces the crystal distributions with respect to both the location and ranges, capturing all critical aspects of DNA structural behavior. An important feature from the B form simulations is the sampling of the BII sub-state, with the BI being the dominant state. In addition, sugar repuckering from the S to N conformations occurs, which is accompanied by the rotation of the base around glycosidic linkage, as discussed above. As seen from Figs. 11, S6 and S8, bimodal distributions for the ε and ζ torsions are present that correspond to BI and BII states. For the β distribution, a prominent shoulder in the vicinity of 140° is present associated with sampling of the BII state, consistent with the previously reported correlation between BI, BII and β torsion.⁷³ As for the sugar pucker distributions, their bimodal character reflects sampling of the dominant S conformation and occasional sampling of N conformations. Interestingly, the NDB survey shows no sampling in the north region, although sampling is observed in the vicinity of 90° for δ (associated with north sugar pucker) in the survey. Detailed analysis indicates that subtle differences in the nature of the sugar puckering (i.e., associated with differences in the five furanose ring dihedrals that define the pucker) in A vs. B form crystal structures when δ is ∼90° are present, leading to the apparent lack of north sampling in the sugar phase in the survey data.

Figure 11.

Dihedral angle and pseudorotation angle probability distributions from 200 ns MD simulations of EcoR1 using the C36 (blue) and Drude (green) force fields. Included are corresponding distributions from a NDB survey of all B form structures with a resolution ≤ 2.5 Å. Drude and C36 distributions are based on analysis of MD trajectory snapshots saved every 4 ps (50,000 frames in total); dihedral angle bin size on all curves is 5 degrees.

Concerning other details of dihedral and pucker distributions, there is a slight shift in the β, δ, and sugar pucker distributions toward higher values as compared to both the crystal survey and C36 additive distributions. At the same time, the Drude model generates a distribution for ε whose primary peak is positioned at slightly lower values of the dihedral angle, which is consistent with the survey data. In the glycosidic χ distribution, the Drude FF samples a minor but distinct population for χ ∼ 200°, representing A-like χ conformation. As in the C36 model, this sampling is slightly overstabilized in the Drude FF in order to obtain sufficient sampling of the north sugar pucker observed in experiments. Importantly, this has not destabilized the B form DNA in EcoR1, 1AXP, 1ZF7, 3BSE, Junfos and 2L8Q systems.

For 1ZF1 in 75% ethanol solution, the Drude MD simulations sample DNA conformations that nicely reproduce all of the crystal survey distributions from A form duplexes (Fig. S7). In particular, sampling of δ around 90° and population of the north pucker conformation, as well as their correlation with the sampling of χ = ∼200°, are evident. Another important feature is a suppression of the BII state as follows from ε and ζ distributions, consistent with the anti-correlated fashion of sampling of the BII and the north sugar pucker. Finally, the Drude model reproduces the shift in the location of the maxima in the ε and ζ distributions as observed in the survey data (i.e., compare survey results in Figure S7 and S8), further indicating the DNA conformational properties to be sensitive to changes in the environment.

Analysis of the DNA Sequence Specific Effects

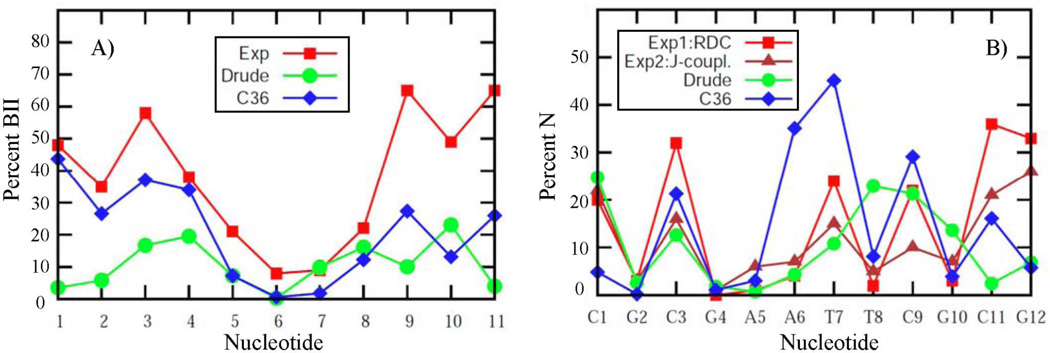
A more stringent test of the Drude model includes its ability to reproduce sequence specific effects, such as the extent of the BII population and sugar puckering. Experimental data on the sequential percent of BII are available for EcoR1⁷⁵ and JunFos,⁷¹ with a comparison of the calculated and experimental results shown in Figs. 12a and S9, respectively. Additionally, BI and BII populations averaged over all base steps for these and other DNA sequences are presented in the Table 4. Given that experimental studies indicate the overall population of the BII state to be 37% in EcoR1 and 27% in JunFos, we find that sampling of BII in the Drude model is reasonably well represented, though underestimated by almost a factor of 2 and 3 for EcoR1 and JunFos, respectively. While this indicates a limitation of the force field, the method of analysis may also contribute to the difference. In particular, analysis of MD simulations was based on direct counting of the amount of BI and BII (i.e., based on BI being defined as ε – ζ < 0) from which the relative probabilities of the two states were obtained. Alternatively, in the ³¹P NMR analysis,⁷¹ the chemical shift is converted to an average ε – ζ value that is used to identify the percent BI by interpolation between ε – ζ = 90° (0% BI) and ε – ζ = –90° (100% BI). While the results are similar for the two analyses, the more approximate interpolation method tends to overestimate the amount of BII, as was demonstrated for JunFos during development of the additive C36 model.⁸ From that analysis the interpolation method overestimates the percent BII by approximately 10% relative to the counting method. For the sequence specific percent BII, correlation between MD simulations and experiment is evident. For example, in EcoR1 there is increased sampling of BII towards the termini of the duplex with the central residues remain primarily in the BI state. Similarly, in JunFos there is a strong residual inhomogeneity with a tendency of the simulated results to follow the experimental peaks and minima for the sampling of BII (Fig. S9). Convergence of the results for sequential percent of the BII was judged based on comparison of the outputs from the two halves of the MD trajectory. Presented in the Fig. S10 are BII fractions computed for two strands of EcoR1 from the first and last 100 ns of the 200 ns long simulations using Drude and C36 force fields. It is seen that C36 results are characterized by significantly larger variations compared to polarizable outcomes, especially towards the termini of the molecule, and may indicate that a longer equilibration is needed for the additive model. As can be seen from Fig. S3 this may be associated with the opening of the terminal base pairs, which is largely absent in the Drude model. Related to this is the observation that the biggest deviations from experimental points as well as from C36 results are for the two terminal residues in both EcoR1 and JunFos polarizable models. This is caused by the end-effects present in majority of simulations. It is speculated that even the third and forth nucleotides from the termini may be affected.⁹⁷ Interestingly, when two terminal residues are excluded from the analysis of the overall population of the BII in EcoR1 and JunFos, the difference between the experimental estimates and MD simulations becomes smaller with factors of 1.4 and 1.5, respectively (see Table 4). A similar analysis approach was adopted in a recent study on the improvement of BII treatment in the AMBER force field for nucleic acids.⁹⁷ It is also worth mentioning that because of exclusion of the terminal residues from the analysis of dihedral angle distributions, there are only small differences between the additive C36 and Drude distributions for ε and ζ in the Fig. 11.

Figure 12.

Analysis of DNA sequence specific effects. (A) Percent BII conformation and (B) percent north conformation of the sugar moiety, as functions of nucleotide for EcoR1 from experiments and from the MD simulations using the C36 (blue) and Drude (green) force fields. Data for the symmetrically related base-pair steps have been combined.

Table 4.

Populations of the BII State for the Drude and CHARMM36 Simulations ^a

DNA	Drude		C36		Exp
	BII	BII2	BII	BII2	BII	BII2
EcoR11	0.10	0.11	0.213	0.173	0.38	0.31
JunFos	0.13	0.12	0.24	0.16	0.30	0.22
3BSE	0.25	0.29	0.30
1AXP	0.28	0.32	0.30
1ZF7	0.15	0.17	0.45
2L8Q	0.20	0.25
1ZF1(EtOH)	0.05	0.05	0.09

^aResults obtained over 100 ns MD simulations of all sequences except EcoR1 (200 ns). (1) Statistical analysis for EcoR1 based on four 50 ns blocks form which the averages and standard deviations were obtained (%BII, average ± standard deviation): Drude, 10.5 ± 1.26; C36, 21 ± 3.5%. (2) The second column of Drude and C36 simulation and experimental results is obtained by excluding first 2 terminal residues on both ends of the molecule from analysis. (3) Additive C36 results for EcoR1 are from MD simulations carried out in this study (200 ns). Additive results for JunFos are from Ref.⁸

Analysis of the sequence specific sugar puckering has been performed on EcoR1, for which deoxyribose pucker equilibria were obtained from NMR J-coupling⁵⁸ and RDC⁵⁹ experiments. The sugar moiety N populations from experiments and MD simulations are shown in Fig. 12b. It is seen that simulation results are in a good agreement with both J-coupling and RDC-derived data. In particular, all non-terminal purine residues have low N populations between 0% and 5%. An exception is G10, whose N population is overestimated in the simulation by ∼7%. Also, T8 demonstrates an enhanced sampling of the N state that differs from experimental estimates. As for the terminal C11 and G12 residues, ³J(H,H) and RDCs consistently predict a high N populations of ∼25%. In contrast, their N populations are much lower in the MD simulation. This again may be caused by the end-effects leading to a poor representation of the terminal residues in the Drude model. What is important, however, is that data for the two non-terminal cytosines, C3 and C9, and also for the terminal cytosine C1, are in near quantitative agreement with experiments. In the MD simulation, 25%, 15% and 24% were obtained for C1, C3 and C9, respectively; N populations are closer to ³J(H,H)-derived values for C1 and C3, but closer to the RDCs for C9. These results are consistent with the hypothesis of an increased sampling of N puckers in cytosine, irrespective of sequence content. The increased sampling of N by cytosine is supported by a ¹³C spin relaxation NMR study that characterized the internal motions of the DNA deoxyribose and base moieties on the pico- and nanosecond time scales.⁶⁰ The data from that study includes NMR-derived order parameters for C1’, C3’, C6 and C8 sites in the EcoR1 duplex, providing an excellent opportunity to probe the dynamical aspect of the Drude model by comparing these quantities with predictions from MD simulation.

Sequence Dependent Dynamic Behavior

The ability of the model to quantitatively model DNA dynamics was based on reproduction of NMR order parameters for the C1', C3', C6 and C8 atoms in EcoR1 (Table 5). Experimental values are not available for all atoms,⁶⁰ while simulation results are presented for individual palindromic strands in the duplex to probe the convergence of the results. There are two general trends observed in the experimental data that are faithfully captured by the Drude model. First, there is an increase in motional amplitudes from the base to the phosphodiester backbone: values of the order parameter decrease from an average of 0.882 for bases (C6/C8 atoms) to 0.799 for C1' atoms, down to 0.765 for C3' sites in the deoxyribose. Second, increased motions for the deoxyribose C1'/C3' atoms are observed in all cytosines (order parameters are smaller for residues C1, C3, C9 and C11). The nature of such an enhanced sugar flexibility in cytosine can be elucidated from the above analysis of the sequence specific sugar puckering: experimentally observed increased reorientations of the C1’-H1 and C3'-H3 vectors correlate with substantially increased N populations in all cytosine residues of EcoR1 (see Fig. 12b). Hence, the motional mode corresponding to NMR-derived order parameters is the sugar puckering in a two-state fashion, from S to N conformation, occurring on time scales between 60 ps and 250 ps. Time series for the sugar puckering in selected residues of EcoR1 from MD simulation (Fig. 5), and computed from them autocorrelation functions (not shown), indicate that the lifetime of a distinct sugar conformation is on the ∼250 ps time scale, in near quantitative agreement with the experimental data. Overall, the Drude results are in better agreement with the experimental data as compared to the additive model, as follows from the difference and correlation analysis presented in Table 5. Such an improvement may be associated with the better ability of the Drude FF to model the conformational energetics of the individual dihedrals as evidenced by the closer agreement with the gas phase QM model compound energy surfaces, as discussed above.

Table 5.

Order Parameters, S², for EcoR1 from NMR Experiments and MD Simulations ^a

C1’ atom Base #	Exp		Drude		C36
	S2	SD	s1	s2	s1	s2
1	0.52	0.02	0.54	0.50	0.57	0.31
2	0.78	0.03	0.77	0.80	0.81	0.78
3	0.74	0.03	0.62	0.66	0.60	0.58
4	0.88	0.03	0.83	0.83	0.82	0.81
5	0.84	0.03	0.87	0.88	0.85	0.87
6	N.A.	N.A.	0.84	0.85	0.58	0.60
7	0.92	0.02	0.71	0.71	0.68	0.67
8	0.86	0.02	0.64	0.69	0.82	0.79
9	0.68	0.03	0.63	0.61	0.51	0.56
10	0.85	0.02	0.73	0.74	0.71	0.81
11	0.71	0.02	0.76	0.78	0.66	0.62
12	N.A.	N.A.	0.77	0.79	0.54	0.68
Difference analysis
Average all			−0.07	−0.06	−0.08	−0.10
Average non-terminal			−0.08	−0.06	−0.09	−0.08
Correlation coefficient all			0.70	0.72	0.64	0.71
C3’ atom Base #	Exp		Drude		C36
	S2	SD	s1	s2	s1	s2
1	0.39	0.02	0.50	0.46	0.58	0.33
2	N.A.	N.A.	0.72	0.77	0.83	0.79
3	N.A.	N.A.	0.57	0.60	0.53	0.50
4	N.A.	N.A.	0.82	0.82	0.83	0.83
5	0.90	0.02	0.86	0.87	0.84	0.86
6	0.79	0.03	0.79	0.81	0.36	0.39
7	N.A.	N.A.	0.66	0.72	0.48	0.47
8	0.79	0.03	0.45	0.57	0.78	0.74
9	0.67	0.04	0.45	0.43	0.33	0.42
10	N.A.	N.A.	0.55	0.57	0.58	0.80
11	N.A.	N.A.	0.73	0.76	0.49	0.51
12	0.43	0.05	0.66	0.67	0.48	0.61
Difference analysis
Average all			−0.04	−0.03	−0.10	−0.10
Average non-terminal			−0.15	−0.11	−0.21	−0.18
Correlation coefficient all			0.73	0.84	0.76	0.72
C6/C8 atom Base #	Exp		Drude		C36
	S2	SD	s1	s2	s1	s2
1	0.77	0.04	0.73	0.71	0.69	0.32
2	0.81	0.07	0.84	0.85	0.87	0.85
3	0.92	0.04	0.86	0.85	0.85	0.84
4	N.A.	N.A.	0.89	0.88	0.89	0.89
5	N.A.	N.A.	0.89	0.89	0.90	0.90
6	N.A.	N.A.	0.90	0.90	0.90	0.90
7	0.83	0.02	0.88	0.87	0.86	0.86
8	0.87	0.04	0.85	0.85	0.85	0.85
9	0.79	0.06	0.86	0.87	0.85	0.85
10	0.88	0.04	0.87	0.88	0.88	0.88
11	0.88	0.08	0.85	0.85	0.83	0.83
12	0.91	0.08	0.82	0.82	0.59	0.74
Difference analysis
Average all			−0.01	−0.01	−0.04	−0.07
Average non-terminal			0.00	0.00	−0.01	−0.01
Correlation coefficient all			0.44	0.41	0.11	0.10

^aResults from MD simulations are presented individually for strand 1 (s1) and strand 2 (s2). Experimental data from Duchardt et al. SD indicates the standard deviation in the experimental values. Differences and correlation coefficients calculated over nucleotides for which experimental data are available, excluding the terminal nucleotides.

Dipole Moment Analysis of the Nucleic Acid Bases and the Water in the Minor and Major Grooves

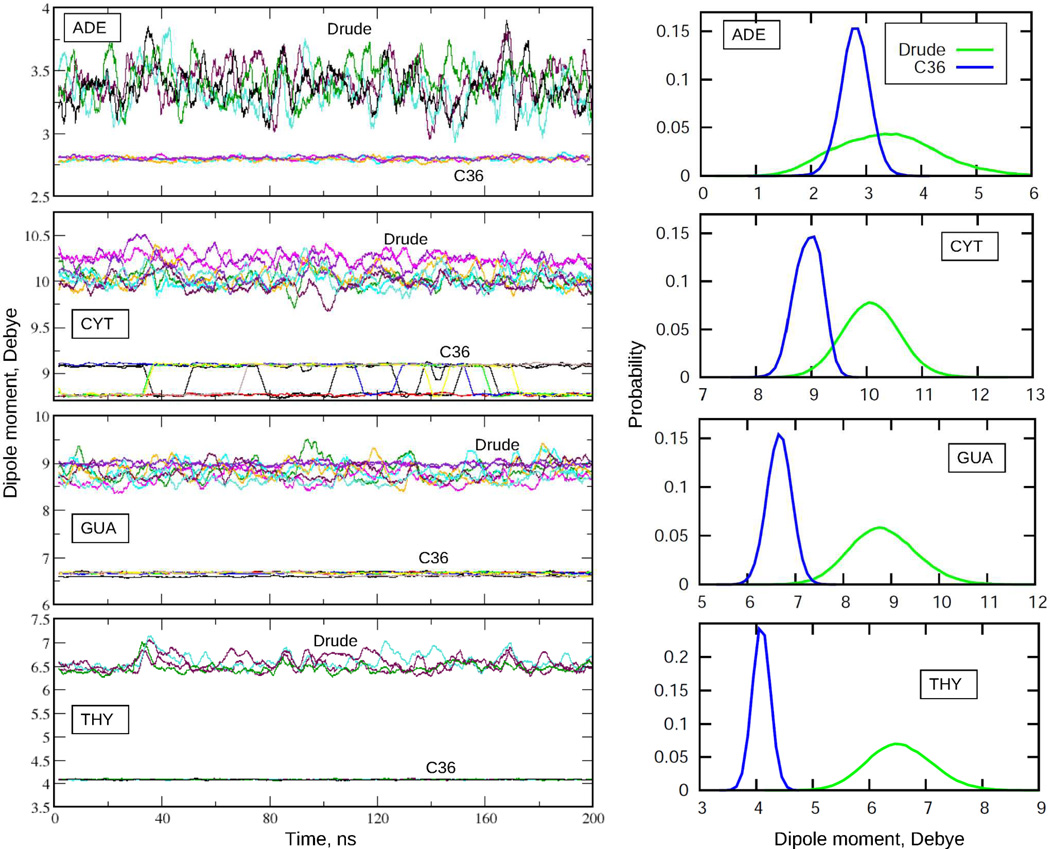
The extensive validation of the Drude force field presented so far reveals that the Drude model achieves a level of agreement with a range of experiments comparable to that of the additive C36 model. At the same time, the microscopic physical forces driving the dynamics and structure of the system differ among the two models due to the use of an electrostatic model that includes explicit induced polarization in the Drude model. This is evident in Fig. 13, which shows the impact of the variation in the electronic structure on the evolution of the dipole moments of the nucleic acid bases in the EcoR1 dodecamer. Compared to the additive results, the Drude model is characterized by significant variability of the dipole moments of the individual bases during the MD simulation indicating sensitivity of the base electronic distribution to changes in the local environment. In contrast, only small variations of the dipoles in the C36 model occur, associated with changes in the internal geometry of the largely rigid nucleic acid bases. In addition, the dipole moments are systematically higher in the Drude model, despite the fact that the dipole moments in the additive force field were systematically overestimated in order to account for the polar environment in a mean-field manner. This is an important observation indicating such an overestimation in the additive model is insufficient to account for the correlation effects in the condensed phase environments encountered by the nucleic acid bases. We note that in the gas phase, the Drude model yields dipole moments for the bases in good agreement with gas phase experimental and QM values as well as being smaller than those in the C36 FF. Importantly, because the polarizabilities for nucleic acid bases were scaled down relative the QM estimates by a factor of 0.85,⁶² it is unlikely that the current Drude model is inherently overpolarized. Similar observations have been made for the Drude polarizable protein FF.²⁰

Figure 13.

Dipole moments of the nucleic acid bases as functions of simulation time (left) and the corresponding probability distribution functions (right) from MD simulations of EcoR1 using C36 and Drude force fields. Time series are running averages over 200 windows, each of 1 ns. Distribution functions are from the actual MD simulation time series (time interval 4 ps, bin size for dipole moments 0.1 D). Data presented for 4 adenine, 8 cytosine, 8 guanine, and 4 thymine bases.

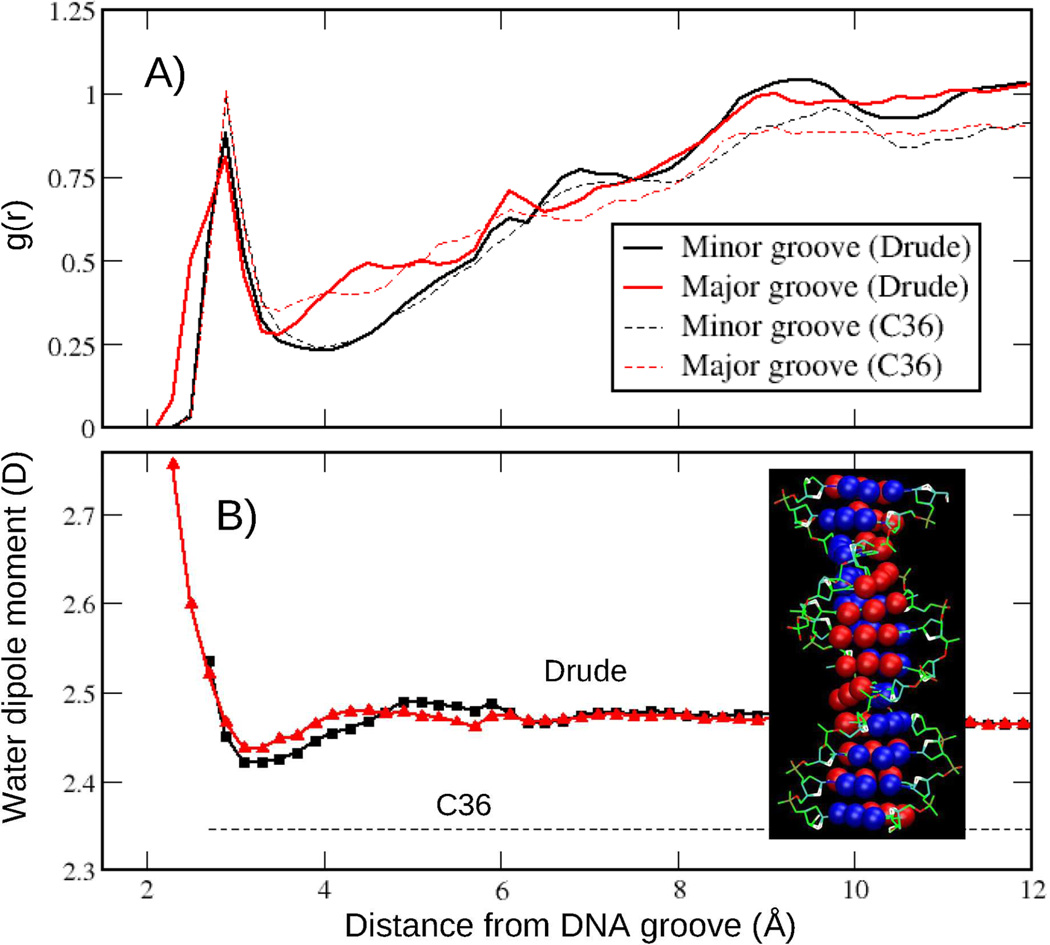
The different nature of the underlying physics in the additive and Drude models can also be visualized by the change in the dipole moment of water as a function of distance from DNA minor and major grooves. For example, previous studies have shown the dipole moments of water to be perturbed in the vicinity of the protein in polarizable force field simulations.^20,98,99 To understand whether such dipole changes associated with alteration of the water structure in the vicinity of DNA, we also compared water-DNA radial distribution functions (RDF) for both models. Presented in the Fig. 14a are the water-DNA RDFs computed on the basis of the closest approach of the water oxygen to the atoms defining the respective grooves. To ensure proper normalization of the RDF, water-DNA distance histograms were scaled with the volume Jacobian computed numerically as a function of the closest distance from the grooves, as previously performed to compute distributions of mobile ions around DNA.^100,101 The definitions for the minor and major grooves are provided in Fig. 14. As seen from the figure, water distributions around DNA are very similar in the Drude and additive models. Based on water-DNA RDF, an average dipole moment of water as a function of the distance from DNA groove was computed (Fig. 14b). Notably, there is a perturbation of the water dipole moment in the vicinity of DNA in the Drude model. In both major and minor grooves the dipole moment is enhanced at the contact distance and has a pronounced minimum just beyond the peak in the g(r) followed by an increase to the bulk value of 2.46 D at longer distances. A similar water behavior was observed in the vicinity of the charged groups of the protein simulated with the Drude-2013 force field.²⁰

Figure 14.

Radial distribution function, g(r), and average dipole moments for water molecules around minor and major DNA grooves from the Drude and C36 MD simulations of EcoR1 (200 ns). Distances are based on the closest separation between oxygen atoms of the water and the atoms defining the grooves. Accordingly, g(r) is normalized by the volume Jacobian calculated numerically as a function of the closest distance between the groove surface and water oxygen. See the text for details. DNA grooves are defined as follows (inset of B). Major groove (atoms in red): GUA(N7,O6), CYT(N4), ADE(N7,N6), and THY(O4); Minor groove (atoms in blue): GUA(N3,N2), CYT (O2), ADE(N3, C2), and THY(O2).

CONCLUSIONS

In the present study we report on the development of the first generation of the CHARMM Drude polarizable force field for DNA. The auxiliary Drude particle and real atoms are treated on equal footing, dynamically, within the framework of extended Lagrangian formalism, allowing for efficient MD simulations.^21–23 The Drude model also includes lone pairs and anisotropic polarizabilities on selected atoms, typically hydrogen bond acceptors, allowing accurate treatment of nonbond interactions as a function of orientation.¹⁶ In addition, the use of atom-pair specific LJ parameters¹⁰² and through-space (ie. non-bond) Thole scaling¹⁰³ allows for further fine tuning of specific nonbond interactions. Thus, the Drude model provides a more approximate description of some finer and higher-order electrostatic effects, such as atomic multipoles, while allowing for computational efficiency required to perform MD simulations of macromolecules in aqueous solution on the 100 ns timescale. As of the writing of this manuscript implementations of the Drude model were available in CHARMM,²⁵ NAMD²⁴ and the ChemShell QM/MM package,²⁶ with implementations in the OpenMM GPU toolkit²⁸ and Gromacs²⁷ ongoing. In addition, the availability of the Drude Prepper facility in the CHARMM-GUI³⁶ allows for rapid conversion of DNA containing systems equilibrated with the additive model to the Drude model along with input files for polarizable simulations using CHARMM and NAMD.

The goal of the present study was to develop a polarizable DNA model that would faithfully capture a number of critical condensed phase properties of DNA, while adequately reproducing the underlying intrinsic conformational energetics of the biopolymer based on QM data on model compounds. Comparison of the accuracy of the Drude and additive C36⁸ models demonstrated that inclusion of polarization effects was an important prerequisite for achieving such dual consistency, where the Drude model more accurately reproduces the QM data on the model compounds as well as reproducing a range of condensed phase properties of duplex DNA. From a physical viewpoint, explicit inclusion of polarizability allowed for a better representation of many-body effects in the DNA polyanion, whose conformational behavior is driven by a subtle interplay between various local degrees of freedom. It should be noted that, compared to the additive model, addition of the extra layer of complexity in the system's description made empirical parameter adjustment in the present study far more challenging due to unexpected non-additive phenomena that occurred in the Drude model upon combining parameters from small model compounds into those for the DNA polymers.

We focused on the two main aspects of DNA structural behavior in solution – an adequate modeling of the equilibrium between A and B forms DNA and satisfactory treatment of the BI/BII conformational equilibrium. Multiple DNA sequences maintained the B form in aqueous solution demonstrating the overall ability of the model to reproduce a collection of experimental data. Those data included crystal survey data on dihedral angle and sugar pucker distributions, NMR data on the overall and sequence-specific populations of the BII sub-state and of the deoxyribose N conformation; NMR order parameters characterizing kinetics of internal motions of selected sites in the DNA backbone, deoxyribose and bases, and crystal survey distributions for selected DNA helicoidal parameters. Improved agreement of the Drude model with NMR order parameters over the C36 additive model indicates that improved agreement in the treatment of the individual degrees of freedom based on QM data on model compounds contributes to more accurate treatment of dynamics of the DNA duplex. Importantly, the Drude force field is sensitive to changes in the environment as evidenced by stabilization of A form DNA in a low-water activity (ethanol) solution. When in the A form the Drude model reproduces A form crystal survey data for dihedral angles and sugar pucker distributions. While the presented model reproduces a range of QM and experimental target data, limitation in the model are present including some underestimation of the BII population and representation of the terminal DNA nucleotides. In addition, simulations of a Z-form DNA duplex in a low water activity environment gave large RMS deviations after a few ns of simulation time (see Fig. S11).

In summary, presented is the first generation CHARMM Drude polarizable force field for DNA. The model is shown to adequately model B form DNA, the equilibrium of the BI and BII states of DNA, the equilibrium between the N and S sugar puckers and to stabilize the A form of DNA in low water activity conditions. Thus, the model will be useful for computational studies of a range of DNA sequences under varying conditions on the 100+ ns time scale. We anticipate that such studies will yield a better understanding of the physical forces dictating the structural and dynamical properties of DNA and their relationship to its biological functions. In addition, given the availability of Drude polarizable parameters for proteins,²⁰ lipids,²⁹ carbohydrates,^30,31 atomic ions^14,24 and other entities, the presented model may be used in modeling and simulation studies of heterogeneous systems.