Structural and Energetic Analysis of 2-Aminobenzimidazole Inhibitors in Complex with the Hepatitis C Virus IRES RNA Using Molecular Dynamics Simulations

Abstract

Despite the many biological functions of RNA, very few drugs have been designed or found to target RNA. Here we report the results of molecular dynamics (MD) simulations and binding energy analyses on hepatitis C virus internal ribosome entry site (IRES) RNA in complex with highly charged 2-aminobenzimidazole inhibitors. Initial coordinates were taken from NMR and crystallography studies that had yielded different binding modes. During MD simulations, the RNA–inhibitor complex is stable in the crystal conformation but not in the NMR conformation. Additionally, we found that existing and standard MD trajectory postprocessing free energy methods, such as the MM-GBSA and MM-PBSA approaches available in AMBER, seem unsuitable to properly rank the binding energies of complexes between highly charged molecules. A better correlation with the experimental data was found using a rather simple binding enthalpy calculation based on the explicitly solvated potential energies. In anticipation of further growth in the use of small molecules to target RNA, we include results addressing the impact of charge assignment on docking, the structural role of magnesium in the IRES–inhibitor complex, the entropic contribution to binding energy, and simulations of a plausible scaffold design for new inhibitors.

Introduction

RNA performs a vast array of functions in biological systems, including genetic encoding, regulation, and catalysis,¹⁻³ and yet very few small-molecule drugs that target RNA exist.⁴ This may be the result of many factors, including the relatively recent discovery of RNA’s many biological roles and the difficulty in preventing RNA degradation during experiments, particularly by ribonucleases.^5,6 Likewise, computational investigations of RNA–ligand binding are comparatively rare (a PubMed search of “protein binding simulations” as of January 2014 yielded 7633 results, and a search of “rna binding simulations” yielded 488 results).^7,8 In order to address this paucity, the current study reports the results of molecular dynamics (MD) simulations on a specific RNA–ligand system and aims to provide a more reliable foundation for future studies involving highly charged RNA–ligand complexes such as those described here.

The target of this research is the domain IIa RNA sequence from the hepatitis C virus internal ribosome entry site (HCV IRES).⁹ Experimental structures exist for the unbound (or free) structure^10,11 and also of the RNA in complex with 2-aminobenzimidazole inhibitors.^12,13 These RNA–inhibitor complexes are attractive structures to study because they involve a relatively short RNA sequence bound to druglike molecules. This contrasts with typical structures that are often larger and more complex, such as RNA or riboprotein molecules in complex with aminoglycosides.^14,15 Moreover, a distinct structural difference between the free and bound HCV IRES is observed, and this is most notably characterized by the loss of a critical bend in the RNA upon ligand binding that explains the inhibition mechanism.¹⁶ Biologically, the structure is of interest because of both the high degree of sequence conservation in IRES elements and its importance in HCV genome translation and viral replication.¹⁷ Rather than using the 5′ cap-dependent mechanism to initiate translation at the ribosome, as is typical in eukaryotes, the HCV IRES element is responsible for recruiting the 40S ribosomal subunits. Thus, the development of inhibitors of the IRES machinery could be useful in treating hepatitis C virus infections.

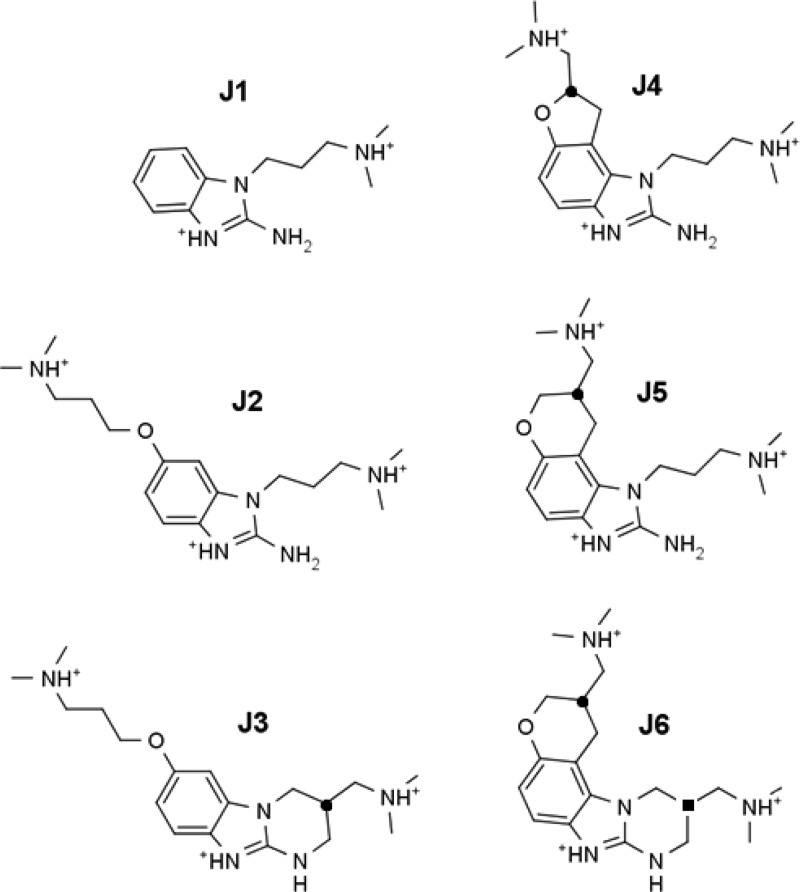
The 2-aminobenzimidazole inhibitors used in the experimental structures were developed by Isis Pharmaceuticals, Inc. using a structure–activity relationship (SAR) by mass spectrometry guided approach. These RNA binding inhibitors were confirmed to reduce HCV RNA levels in a viral RNA replication assay.¹⁸ As part of the exploration of SARs, a number of different derivatives were synthesized and binding constants estimated (those studied in this work are described in Figure 1 and Table 1). This provides a series of related inhibitors studied by the same laboratory with equivalent and comparable experiments that can be investigated by simulations to assess biomolecular simulation protocols. There are some drawbacks to this experimental data set, including the following: (1) the protonation state of the inhibitor upon binding is unknown; (2) several inhibitors were synthesized as mixtures of enantiomers or diastereomers, and the experimental binding data published do not distinguish the effects from individual stereoisomers; and (3) the errors in the binding measurements were not reported. These challenges do not preclude computational assessment. For example, the protonation states can be estimated with reasonable accuracy using pK_a estimation software (see Methods), and such calculations suggest that the inhibitors are all fully protonated in solution at physiological pH as depicted in Figure 1. With regard to stereochemistry, it is very easy to perform separate calculations on each of the enantiomers and diastereomers and, as an approximation, to report the mean value for comparison with experimental data for the mixture. The lack of error analysis in the experimental results, however, does suggest the use of caution when making certain conclusions on the basis of a comparison of the experimental and computational results.

Figure 1.

Structures of previously identified inhibitors,¹⁸ which are studied further in this work, that bind to the HCV IRES subdomain IIa. Twelve stereochemically distinct inhibitors can be derived from the six structures shown here. The protonation states used in the simulations are as depicted. The locations of the stereocenters in J3, J4, and J5 are indicated by a ● symbol on the chiral carbon. We refer to the identity of the stereoisomer by adding R or S to the name designator (i.e., J3R, J3S, J4R, J4S, J5R, and J5S). The two carbon stereocenters of the J6 diastereomers are indicated with the ● and ■ symbols, and denoted by appending R or S to J6 in that respective order (J6●■): J6RR, J6RS, J6SR, and J6SS. Note: the J4 inhibitor was used in the NMR study,¹² whereas the J5 inhibitor was used in the crystallography study.¹³

Table 1. Experimental Dissociation Constants (μM) and the Corresponding Binding Free Energies (kcal/mol) Determined Previously by Mass Spectrometry¹⁸.

inhibitor	KD (μM)	ΔGbinding (kcal/mol)a
J1	>100.00	–5.45b
J2	17.00	–6.50
J3	3.50	–7.44
J4	1.70	–7.87
J5	0.86	–8.27
J6	0.72	–8.37

^aThe free energy of binding was calculated according to the relation ΔG = RT ln K_D at 298.15 K.

^bThe exact dissociation constant is not known for J1, and thus, −5.45 kcal/mol represents the lower bound for the binding energy.

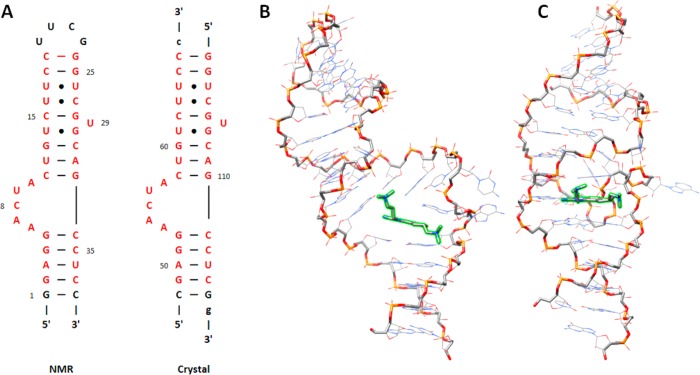
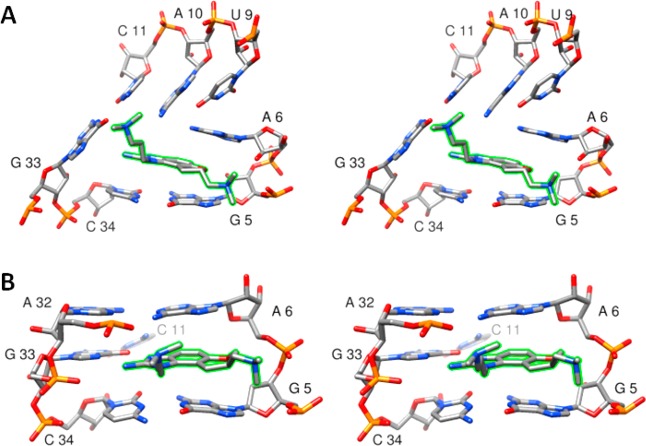
The available experimental structures of the RNA–inhibitor complexes derived from NMR data¹² and X-ray crystallography¹³ exhibit distinctly different binding modes. These differences cannot easily be attributed to the identity of the two different inhibitors used in the separate investigations, as they differ by only a single −CH₂– group (J4 for NMR and J5 for X-ray; see Figure 1). The differences also cannot be attributed to the slight change in RNA sequence in the NMR structure versus the crystal structure, as the sequence changes are found only at the ends of the molecule, as shown and discussed in Figure 2A. Rather, the differences must lie in either the experimental conditions or the structure refinement procedures used in the two experimental methods. The NMR structure can be described as an open conformation with stacking contacts formed below the inhibitor. Contacts to the RNA binding site are formed by both dimethylamino arms of the inhibitor: one to the phosphate group of G5 and one to the junction of the C11:G33 base pair (Figures 2B and 3A). Hydrogen-bonding contacts between the benzimidazole ring donor sites and the RNA are not observed. In contrast, the crystal structure is characterized by a compact binding site in which stacking interactions are formed both above and below the inhibitor. Both dimethylamino groups of the inhibitor interact with the RNA phosphate backbone, and two critical hydrogen bonds are formed between the benzimidazole ring and residue G33 (Figures 2C, 3B, and 4). Dibrov et al.¹³ suggest that these hydrogen bonds explain the observation that the C11G:G33C base pair mutant does not bind the benzimidazole inhibitors.

Figure 2.

Despite similar sequences, the reported conformations of the inhibitor-bound HCV IRES domain IIa determined by NMR analysis and X-ray crystallography differ. (A) Secondary structure diagrams of the domain IIa constructs used in the NMR¹² and crystallography¹³ studies. The hairpin sequence from the NMR study was used for all of the simulations in this study. The residues colored in red show the portions of the RNA that are identical in the two published structures. (B, C) Representative models depicting the global structures of the NMR ensemble and the crystal structure, respectively. In each structure, the RNA backbone is emphasized with heavier width, and the inhibitor is highlighted in green. The structural orientations were chosen to emphasize the global differences in the binding conformations.

Figure 3.

Stereoviews (wall-eyed) of the inhibitor binding conformations observed in (A) the experimental NMR ensemble and (B) the crystal structure. The inhibitor is highlighted in green.

Figure 4.

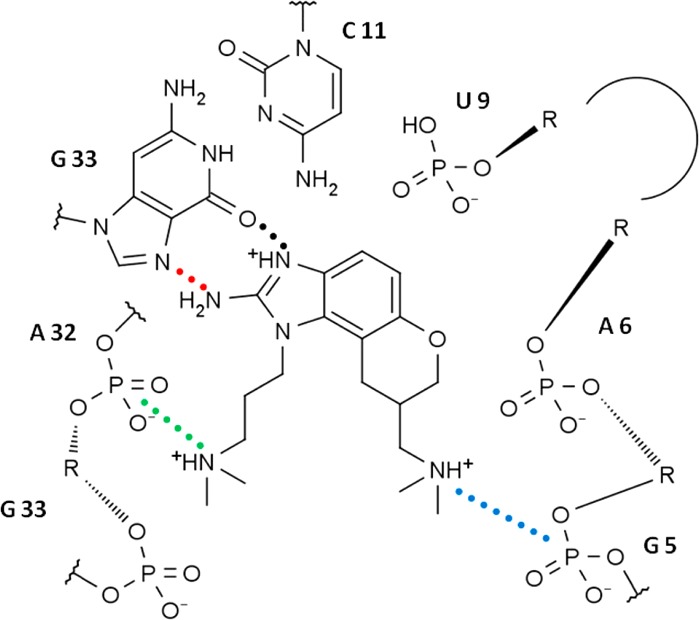
Schematic of the crystal structure binding site in the plane of the J5 inhibitor. Residue labels are numbered according to the NMR hairpin sequence (Figure 2A). Critical contacts are indicated by colored dotted lines, and the colors correspond to the distances depicted in SI Figure S2.

In addition to the differences in the conformations of the NMR and crystal structures, there are potentially conflicting reports regarding the cation requirements necessary for the formation of the inhibitor-bound complex. Magnesium is observed at core positions in both the unbound and bound crystal structures.^11,13 It has also been found that removal of magnesium from the Förster resonance energy transfer (FRET) binding assay of the crystal structure yields an approximately 30-fold decrease in binding affinity.¹³ Although these findings are consistent with the well-known relationships between RNA structure and cation binding,^19,20 they should not be interpreted to suggest that coordinated magnesium exclusively performs the stabilization role.²¹ A variety of RNA tertiary structures are known to form in moderate levels of monovalent salt,²² and magnesium is known to compete with monovalent cations in stabilizing RNA.²³ In the case of the HCV IRES domain IIa RNA, although the addition of magnesium stabilizes the unbound solution structure,¹⁰ no changes were observed in the NMR spectra of the bound complex upon addition of magnesium to a solution with a relatively high monovalent salt concentration.¹² Also, the first reported dissociation constants for the benzimidazole inhibitors were determined in the absence of magnesium with modest levels of ammonium acetate.¹⁸ These values (Table 1) are comparable to those determined by FRET assays using the crystallography construct with magnesium. Additionally, a fluorescence binding assay of the NMR sequence conducted in 0.15 M KCl and 0.15 M NaCl using the J4 inhibitor (Figure 1) yielded a dissociation constant of 2.4 μM,¹² which is in the equivalent range as the value determined by a FRET assay for the crystal sequence bound to the J5 inhibitor in 2 mM Mg²⁺ (EC₅₀ = 3.4 μM).¹³

The goal of this work is to validate the computational methods we plan to employ for HCV IRES inhibitor discovery and/or optimization. As an initial step in this process, we report results that attempt to answer the following questions: (1) Which of the two published IRES–inhibitor structures is best supported by MD simulations? (2) Can MD simulations further inform whether the magnesium ions identified in the crystal structure are required for inhibitor binding? (3) Is the MM-GBSA/MM-PBSA method sufficiently accurate to predict the relative order of binding affinity of several 2-aminobenzimidazole inhibitors? (4) Is there a significant difference in docking results when using the partial charges assigned by the rigorous RED method²⁴ versus the more approximate AM1-BCC method?^25,26 (5) Do the MD simulations of various 2-aminobenzimidazole inhibitors suggest alternative inhibitor scaffolds that can be validated using further MD simulations?

Methods

Ligand Parametrization

All of the inhibitors in this study were protonated at the dimethylamino and benzimidazole positions as indicated in Figure 1. The fully protonated state at pH 7.0 is consistent with pK_a estimates by two different pK_a prediction programs, SPARC²⁷ and Marvin Sketch (www.chemaxon.com/products/marvin). Charge derivation was performed in a very careful manner because of the highly charged nature of the inhibitors: (1) A hand-built inhibitor model was geometry-optimized at the quantum-mechanical (QM) HF/6-31G* level consistent with the AMBER ff10 and ff12SB force fields, after which the initial atomic charges were determined by restrained electrostatic potential (RESP)²⁸ charge fitting; (2) 50 ns of implicit-solvent generalized Born (GB) MD using the Hawkins, Cramer, and Truhlar model²⁹ was performed at 400 K to sample relevant inhibitor conformations, and the resulting trajectory was clustered³⁰ into 20 clusters by the “averagelinkage” algorithm using AMBER’s Ptraj program; (3) the representative structures from clusters whose occupancies were greater than 2% were then geometry-optimized at the QM HF/6-31G* level; and (4) optimized structures whose energies were within ∼0.5 kcal/mol of the minimum-energy structure were used in a multiconformation, multiorientation RESP fit using the RED program²⁴ to generate the final charges used in this study. Enantiomers were fit simultaneously to ensure identical charges. Bonds, angles, torsions, improper torsions, and Lennard-Jones parameters were assigned from the general AMBER force field (GAFF) using the Antechamber and Parmchk programs.^31,32 Some torsion and improper torsion parameters were modified because the default parameters did not maintain planarity at C2 of the 2-aminobenzimidazole ring. MOL2 files with GAFF atom types and charges as well as “frcmod” files with the modified torsion parameters are provided in the Supporting Information (SI). All of the QM calculations were performed using Gaussian 09 (www.gaussian.com), and all of the MD simulations were performed using AMBER12.³³

In addition to the more detailed approach to generate high-quality atom charges discussed above, we were interested in the performance of more approximate charge parametrization methods. To test this, we performed molecular docking studies (discussed below) using both the RESP charges from the above procedure and AM1-BCC^25,26 charges produced by AMBER’s Antechamber program. In the latter case, charges were determined separately for each inhibitor stereoisomer studied.

Initial RNA–Inhibitor Conformations

Experimentally determined atomic-resolution structures exist for HCV IRES RNA complexed with the J4R and J4S inhibitors (NMR structures) and also for the J5R inhibitor (crystal structure). To facilitate comparisons between the MD simulations, the crystal structure duplex was converted into a hairpin of identical sequence to the NMR structure. To accomplish this, the 3′ dangling bases were removed, the C:G base pair at the base of the lower stem was converted to a G:C base pair, and a UUCG tetraloop was added to the opposite stem (Figure 2A). With the exception of J4R and J4S bound in the NMR conformation and J5R in the crystal conformation, binding poses for the inhibitors in our test set were not available. In preliminary MD simulations, we noticed that the flexible portions of the inhibitor scanned the nearby RNA contacts on a short (ns) time scale, suggesting a dynamic binding mode. While the core aromatic ring atoms of each inhibitor are presumed to bind identically, the best pose for the flexible regions is not obvious. Thus, we chose the following procedure to eliminate bias in building the initial poses. In order to generate a diverse set of binding conformations for the inhibitors in Figure 1, the 20 representative conformations of each inhibitor identified by clustering during the charge derivation procedure were root-mean-square (RMS)-fit to the benzimidazole core atoms of the existing experimental structure, either NMR or crystal. For the NMR structure, the first model from the Protein Data Bank 2KU0 ensemble¹² was used as the reference structure. This procedure resulted in the generation of 20 “NMR-like” RNA–inhibitor conformations and 20 “crystal-like” RNA–inhibitor conformations for each of the 12 stereochemically distinct inhibitors. The selection of these conformations as initial structures for the various simulation sets in this work is described in the following section. The simulation that included magnesium used the exact coordinates from the crystal structure for all of the atoms of the J5R inhibitor, magnesium, and RNA, except for the necessary sequence modifications to the RNA helix termini required to match the NMR sequence. In the case of the novel ligands, a single inhibitor conformation was chosen and RMS-fit to the benzimidazole core atoms in the experimental crystal structure.

Simulation Sets

As described in Table 2, several sets of simulations were performed. For RNA–inhibitor studies, two strategies were employed: single long simulations and multiple short simulations. For the single long simulation sets (NMR1 and CRY1), a single initial structure was selected from the 20 initial conformations for each of the 12 inhibitors on the basis of the minimum GB energy of the complex. For the multiple simulation set (CRY2), all 20 initial conformations were used. In a few cases, bad initial conformations with severe atom overlap were replaced with good conformations.

Table 2. MD Simulations Performed in This Work.

simulation set	system contents	no. of ligands tested	no. of ligand poses	total no. of simulations	simulation length (ns)e
NMR1	RNA,a ligand,c K+, Cl–, TIP3P	12	1	12	232
CRY1	RNA,b ligand,c K+, Cl–, TIP3P	12	1	12	218+
CRY2	RNA,b ligand,c K+, Cl–, TIP3P	12	20	240	2
MG	RNA,b J5R, Mg2+, K+, Cl–, TIP3P	1	1	1	232
RDC	RNA,b J4R, K+, Cl–, TIP3P	1	1	1	5
NOV	RNA,b ligand,d K+, Cl–, TIP3P	4	1	4	70
LIG	ligand,c K+, Cl–, TIP3P	12	1	12	594+

^aRNA receptor in the NMR conformation.

^bRNA receptor in the crystal conformation.

^cThe 12 ligands are those described in Figure 1.

^dThe four ligands are those described in Figure 11.

^eSimulation length represents the simulation time for each simulation (the product of the total number of simulations and the simulation length yields the aggregate time). “+” indicates that the stated time is the minimum from among the simulation set.

Construction of Solvated Models

The domain IIa RNA was parametrized using AMBER’s ff12SB force field, which includes a recent update of the backbone and χ torsion parameters.³⁴⁻³⁶ The initial RNA–inhibitor conformations were first minimized for 2500 cycles using the steepest-descent algorithm in implicit GB solvent, and the resulting geometries were solvated. All of the simulations described in Table 2 were performed in TIP3P water³⁷ with net-neutralizing potassium ions and an additional ∼200 mM KCl as parametrized by Joung and Cheatham.³⁸ The number of waters added was chosen to yield a periodic truncated octahedron with an approximately 12 Å minimum water shell between the solute and the box edge. In order to facilitate energetic comparisons of inhibitors, the numbers of solvent atoms for the systems in each simulation set were made to be identical using an in-house Perl script coupled to AMBER’s LEaP program. In the case of the J1 inhibitor, which has a net charge of +2 rather than +3, direct energetic comparisons with the other inhibitors were not performed. Following solvation, the monovalent ion positions were randomized with AMBER’s Ptraj program using the “randomizeions” command to remove bias from the initial ion placement. In the case of the MG simulation (Table 2), the crystallographic magnesium ions and water molecules were included using the magnesium parameters of Allnér, Nilsson, and Villa³⁹ in addition to 200 mM KCl.

Molecular Dynamics Simulations

All of the solvated simulations used a similar minimization, heating, and equilibration procedure: (1) the entire system was minimized for 1000 steps using the steepest-descent algorithm followed by 1000 steps of conjugate-gradient minimization while 25 kcal mol^–1 Å^–2 positional restraints were enforced on the RNA and inhibitor benzimidazole core atoms; (2) the system was heated from 10 to 150 K at constant volume with the Langevin thermostat over the course of 100 ps with 25 kcal mol^–1 Å^–2 positional restraints on the RNA and benzimidazole core atoms; (3) further heating from 150 to 298 K and initial equilibration were performed using constant pressure and the Langevin thermostat over the course of 100 ps with 5 kcal mol^–1 Å^–2 positional restraints on all of the solute atoms; and (4) final equilibration at 298 K was performed for 2 ns using constant pressure and the Langevin thermostat with 0.5 kcal mol^–1 Å^–2 positional restraints on the RNA and benzimidazole core atoms. Production simulations were performed at 298 K at constant pressure using the weak-coupling algorithm for the thermostat and barostat.⁴⁰ The pressure relaxation times were 1 ps for the initial equilibration step, 5 ps for the final equilibration step, and 10 ps for production. For heating and both equilibration steps, a collision frequency of 2 ps^–1 was used for the Langevin thermostat. For production, the time constant of heat bath coupling was 10 ps using the weak-coupling algorithm. For all heating, equilibration, and production steps, the time step was 2 fs, the direct space sum used a cutoff of 8.0 Å, and SHAKE was applied to all bonds involving a hydrogen atom.⁴¹ The default particle-mesh Ewald⁴² settings (which correspond to a grid spacing of ∼1 Å and a direct space tolerance of 10^–6) were used to determine long-range charge interactions. Coordinates were recorded every picosecond during production simulations. With the exception of the simulation performed with residual dipolar coupling (RDC) restraints, all of the production simulations were unrestrained and performed using either the CPU or GPU version of the PMEMD program in AMBER12.³³ A single simulation of the crystal conformation with the NMR RDC restraints enforced was performed using AMBER’s Sander program (the use of RDC restraints is not yet implemented in the faster PMEMD program). A short minimization was performed on the equilibrated, solvated structure to best fit the RDC alignment tensor. The relative weighting of the alignment restraint was chosen to be 0.08 kcal/Hz², which represents an empirical determination of the largest value that did not produce simulation instability (e.g., integration errors).

Energy Analysis

MM-GBSA and MM-PBSA are well-known postprocessing techniques for computing binding energies from simulation trajectories.⁴³⁻⁴⁵ In this work, MM-GBSA and MM-PBSA analyses were performed with the MMPBSA.py program in AMBER12 using the single-trajectory approach. For MM-GBSA, the Hawkins, Cramer, and Truhlar GB model²⁹ was used for implicit solvation with a salt concentration of 200 mM approximated using Debye–Huckel screening. For MM-PBSA, the following options were used: a level-set-based dielectric model, a two-term nonpolar solvation free energy term based on a cavity and dispersion calculation,^46,47 an ionic strength of 200 mM, a solvent probe of 1.4 Å, a grid spacing of 0.25 Å, and a value of 6.0 for the ratio between the longest grid dimension and the solute. Radii for inhibitors were chosen from a set of optimized radii to best match the atom types present.⁴⁶ For MM-GBSA, all of the frames from the trajectory were used, but for MM-PBSA only every 100th frame was used for computational efficiency reasons. Solute entropy estimates were calculated separately (see below) and were not included in the MM-GBSA/MM-PBSA values.

In addition to the MM-GBSA/MM-PBSA framework of energy analysis, we also calculated relative binding enthalpies that included the full explicit solvent effects. The instantaneous enthalpy for any given simulation frame is defined as

where U_pot is the potential energy, E_K is the kinetic energy, p is the pressure, and V is the volume. When the binding enthalpy was computed, the kinetic energy and pressure–volume terms were assumed to be negligible because of the use of the thermostat and barostat. Thus, the relative binding enthalpy was calculated by subtracting the solvated-inhibitor mean potential energy (obtained using simulations of the free ligands in explicit solvent, denoted as LIG) from the solvated RNA–inhibitor mean potential energy (obtained from the CRY1 and CRY2 simulations):

The inhibitor J1 was excluded from these calculations because its net charge differs from those of the other inhibitors, which complicated direct comparisons because of differences in the numbers of counterions.

We also performed two types of entropy analysis. In both cases, only the inhibitor entropy was considered, and entropy changes were computed by subtracting the entropy of the free inhibitor from that of the complexed inhibitor. The RNA–inhibitor and free-inhibitor conformations were taken from the CRY1 and LIG simulation sets, respectively. The first method, quasi-harmonic analysis,⁴⁸ was computed using AMBER’s Ptraj program. The second method, first-order configurational entropy analysis based on bond/angle/torsion probability distribution functions, was computed using the ACCENT program developed by Gilson and co-workers.⁴⁹ Both methods ignore rotational and translational contributions to the entropy. Because of the accumulative nature of these values and the difficulty we had in converging them, error bars are not given for the entropy estimates, and the data are not used in combination with the other energetic analyses presented here.

Finally, unbound-inhibitor solvation enthalpies were estimated by subtracting gas-phase average potential energies from either GB implicit solvation energies or from potential energies of explicitly solvated trajectories. Although one could compute the gas-phase energies from solvated trajectories by stripping the solvent, we performed 100 ns gas-phase simulations for each of the 12 inhibitors represented in Figure 1 in order to ensure the independence of these values.

Error Analysis

Two approaches were used to estimate the error, depending on the simulation set. For the single long simulation sets, a previously described reblocking procedure was used.⁵⁰ Briefly, a data set plotting the standard error of the mean (SEM) versus increasing block size was computed. Given sufficient sampling, the plot plateaus at a value that corresponds to the SEM. The data can be fit with a trend line to predict this value, but the fit is not always accurate because of specific assumptions about the type of correlation in the data. To be conservative, we used the maximum value observed in the plot. An example of this error analysis is given in SI Figure S1. For the multiple short simulation set (CRY2), we considered the average values from the 20 separate simulations to be independent, uncorrelated data points and computed the SEM in the traditional way by dividing the sample standard deviation by the square root of the number of data points (i.e., the number of simulations). The error combining rules were as follows: when the difference of two mean values was computed, the errors were added; when the average of two or more mean values was computed, the errors were averaged.

Grid Analysis

The regions of highest magnesium ion occupancy were determined using the “grid” command in AMBER’s Ptraj program.⁵¹ The simulation trajectory frames were centered, imaged, and RMS-fit using the heavy atoms of residues 5, 11, 33, and 34 that form the binding region. Occupancy was determined by a three-dimensional histogram approach using a 75 Å × 75 Å × 75 Å box with 0.5 Å × 0.5 Å × 0.5 Å resolution. The results were visualized on the average RNA–inhibitor structure from the simulation using the UCSF Chimera package.⁵² To choose the density surface contour level to be displayed, the contour level was increased until magnesium occupancy in the bulk solvent region was no longer observed, thus suggesting stable binding locations.

Docking

Docking was performed on the crystal receptor structure (modified to match the full NMR sequence; Figure 2A) using Dock 6.5.⁷ The top and bottom helical portions of the receptor were excluded from consideration as they are known not to contain the binding site. This exclusion did not inappropriately limit docking poses to the known binding cavity since the entire backside region of the receptor was explored for docking. In order to include various ring pucker conformations in some of the inhibitors, for which Dock 6.5 is not able to search automatically, all of the inhibitor conformational clusters whose occupancy was greater than 2% (identified during the charge derivation procedure) where used as initial seed structures for docking. Two schemes were used to assign charges to the inhibitor for use during docking. The first scheme simply used the RESP charges that were derived for use in the MD simulations. In the second scheme, which resembles a more typical docking procedure, charges were derived for each inhibitor conformation using the semiempirical AM1-BCC charge model, which can be accessed through AMBER’s Antechamber program. The default grid-based method in Dock 6.5 was assigned as the primary scoring function. All other settings are listed in SI Table S1.

NMR Spectroscopy

NMR data were acquired on 500 and 600 MHz Varian NMR spectrometers using RNA-optimized pulse sequences from the standard Varian Biopack pulse sequence library (www.agilent.com). The F1-filtered/F2-filtered nuclear Overhauser spectroscopy (NOESY) measurements were performed as described by Zwahlen et al.⁵³ The NMR sample conditions and data acquisition were as described by Paulsen et al.,¹² and the data were processed using standard VNMR processing software and then visualized in SPARKY (www.cgl.ucsf.edu/home/sparky).

Results

MD Simulations

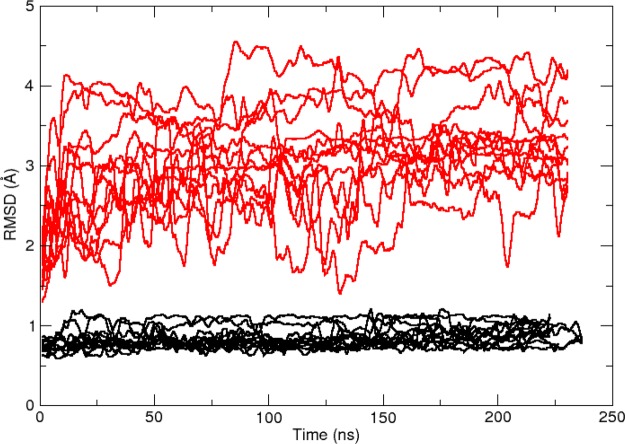
The NMR1 and CRY1 simulation sets (Table 2) were intended to evaluate the simulation stability of the two available experimental conformations in the context of 12 related inhibitors over a fairly long time scale (200+ ns). Visual inspection of the simulation trajectories reveals a stark contrast in the stability of the binding region. A quantitative measure of this difference is shown in Figure 5, where the binding region RMS deviation (RMSD) is plotted versus simulation time using the initial conformation of each production simulation as a reference. For all 12 simulations in the CRY1 simulation set (shown in black) the RMSD value is low and very steady. The small fluctuations arise from inhibitor ring transitions and conformational searching by the dimethylamino groups. Throughout the CRY1 simulations, all of the critical contacts depicted in Figure 4 are maintained in each simulation. In contrast to the CRY1 results, the NMR1 RMSD results (shown in red) reveal a high degree of fluctuation and departure from the initial structure. A variety of RNA–inhibitor poses are adopted during the 12 NMR1 simulations and do not point to a consensus alternative to the original NMR pose. Much of the structural instability is due to conformational transitions in the bulge residues 6–10. To visualize the structural difference between the NMR1 and CRY1 simulation sets, the final frames of each simulation were overlaid to produce an ensemble (Figure 6). As a result of unfolding of the bulge residues, many of the NMR1 conformations do not retain the linear RNA orientation known to inhibit viral replication but rather adopt an “L-shaped” conformation similar to the unbound structure (Figure 6A). Additionally, the inhibitor poses are smeared into a variety of orientations (Figure 6C). In contrast, the CRY1 simulations maintain the linear orientation and produce a rather tight ensemble of structures and inhibitor poses (Figure 6B,D). We conclude from these data that the NMR conformation is highly unstable in the context of the force field energy landscape, whereas the crystal conformation appears to be in an energetically favorable minimum. Therefore, the crystal conformation is preferred for subsequent analysis.

Figure 5.

Plot of binding region RMSD vs simulation time, which reveals that the 12 simulations in the CRY1 simulation set (black) are much more stable than those of the NMR1 set (red). The simulation sets contain 12 simulations, one each for the 12 inhibitor-RNA complexes (Figure 1) bound in either the crystal conformation (CRY1) or the NMR conformation (NMR1). The atoms considered in the binding region are defined to be the heavy atoms in residues 5, 6, 32, 33, and 34 and the inhibitor. The first frame of each production simulation was used as the RMSD reference structure for that simulation. For clarity, the RMSD values have been smoothed with a 2500 data point running average.

Figure 6.

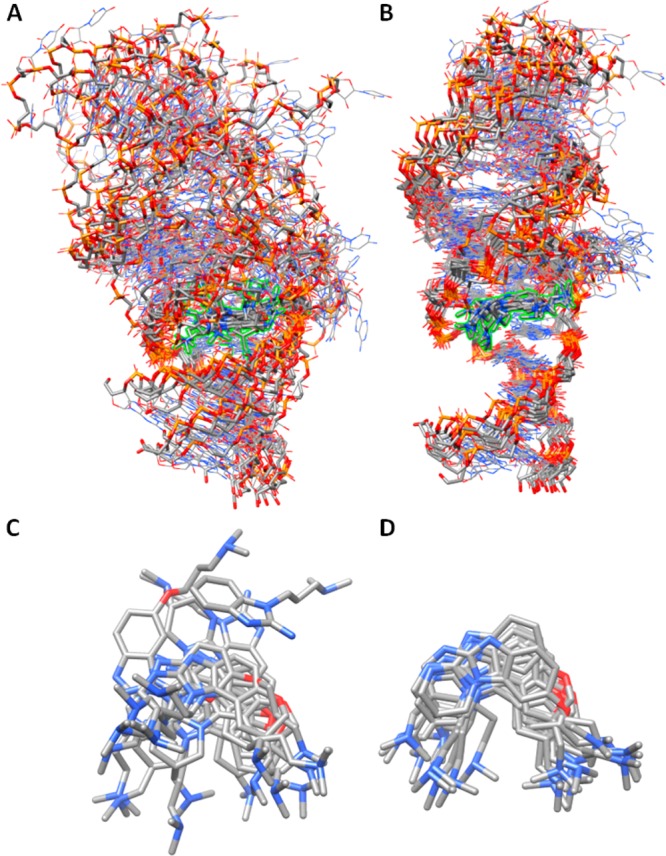
(A, B) Structural ensembles made from the final frames of the 12 simulations in the (A) NMR1 and (B) CRY1 simulation sets as defined in Table 2. The inhibitors are highlighted in green. The ensembles were generated by RMS fitting of residues 5, 6, 33, and 34 of each frame. (C, D) Final inhibitor position in each simulation for the (C) NMR1 and (D) CRY1 simulation sets using the same RMS fits as for the full ensembles.

One of the NMR1 simulations, the complex with the J5S inhibitor, is notable because it partially converts to the conformation of the crystal structure. All of the critical contacts in Figure 4 are observed, including the hydrogen bonds between the inhibitor and G33 and the contacts between the dimethylamino groups and the phosphate backbone (SI Figure S2A). These distances are similar to those observed in the CRY1 simulation set (SI Figure S2B). The only interaction that is not formed is the base-triple interaction between residue A6 and the Hoogsteen edge of A32, which forms a “roof” above the inhibitor. After 232 ns of simulation, the conformation of residues 7–9 continues to restrain the flexibility of A6 in such a way as to prevent the full formation of the base triple, although A6 and A32 are near enough to form direct contacts. Other simulations in the NMR1 set also partially adopt the crystal-like binding mode, usually by forming the hydrogen bonds between the inhibitor and G33, but none are as stable as the aforementioned simulation with J5S. Further research, likely involving enhanced sampling, is necessary to determine whether a complete transition is accessible on a reasonable time scale.

In addition to using long simulations, we also investigated whether using many shorter simulations with diverse initial inhibitor conformations could produce comparable data. Because of the instability of the NMR conformation in the simulations, we discuss this approach only for the crystal conformation, and we term this the CRY2 simulation set. This simulation set is primarily used for comparisons in the energetic analysis portion of the results, but we also wanted to determine whether the RMSD spaces explored by the inhibitor in the two approaches were different. SI Figure S3 compares the mean RMSD values of the binding region, as well as the maximum and minimum values, for the CRY1 and CRY2 simulation sets using the same reference structure for each simulation of a given inhibitor. For most of the inhibitors, the mean, minimum, and maximum RMSD values are similar. Only in the case of the weak-binding J1 inhibitor does a large difference in the maximum RMSDs appear. These results do not guarantee that exactly the same conformations are sampled by the two approaches, nor does it indicate that the proportions of conformations sampled are similar. However, the results do indicate that long simulations do not explore RMSD space that is significantly farther away (i.e., has higher RMSD values) than that sampled with an ensemble of diverse short simulations.

It is important to note that the published crystal structure contains six magnesium ions, five of which are near the binding region.¹³ The authors note three specific magnesium ions that seem particularly important structurally and also note that the binding affinity dramatically decreases in the absence of magnesium. We chose not to include magnesium ions in this study, with the exception of the MG simulation (Table 2), because previous NMR data¹² and binding assays¹⁸ have indicated that moderate levels of monovalent salt are sufficient to stabilize the RNA. To investigate whether simulations with magnesium differed from those without, a single 232 ns simulation was performed using the experimental coordinates for the J5R inhibitor, magnesium ions, crystallographic waters, and RNA (with the necessary sequence modifications to create a tetraloop consistent with the NMR structure). In addition to the crystallographic magnesium ions, 200 mM KCl was included in the bulk solvent. No changes in the ligand binding mode were observed upon the inclusion of coordinated magnesium ions within the RNA structure. SI Figure S4 compares the regions of highest magnesium ion occupancy with the crystallographic locations of the magnesium ions. Although qualitatively similar, none of the highest-occupancy locations observed in the simulation reproduce the exact coordination contacts observed in the crystal structure. The magnesium coordinated to atom N7 of A6 in the crystal structure moves to coordinate the phosphate groups of G30 and C31 in the simulation. The magnesium coordinated to both O4 of U14 and OP1 of U9 in the crystal structure loses the interaction to the phosphate and forms an interaction with O2 of C8 instead. Finally, both magnesium ions located near G5 in the crystal structure move elsewhere and are replaced, to some extent, by potassium ions. These results, combined with the observation of stable simulations without magnesium ions, suggest that magnesium is not critical in simulations with moderately high concentrations of monovalent salt (i.e., both had 200 mM KCl). This is consistent with in vitro binding assays at relatively high concentrations of monovalent salt with no magnesium where high-affinity binding was detected.^12,18

Our simulation results support the crystal structure as the predominant conformation in solution. However, specific interactions indicated by the NMR data are inconsistent with the crystal structure, indicating that under the NMR solution conditions alternative binding modes may be significantly populated. In the following section, we attempt to reconcile the NMR data with the key binding interactions identified in the crystal structure.

Are the Differences between the NMR Data and the Crystal Structure Reconcilable?

We were first curious whether the crystal structure was actually compatible with the NMR data and therefore that the NMR refinement procedure was to blame for the inconsistency in conformation. One way to investigate this is to determine whether the NMR distance restraints are satisfied by the crystal structure. To determine this, the r⁶-averaged distances for all of the atom pairs that were assigned NOE distance restraints were computed for the 200+ ns simulation of J4R from the CRY1 simulation set (this inhibitor structure is identical to that of the published NMR structure). A rotating structure with indications of NOE violations greater than 1.0 Å is provided as a movie file in the SI, and a list of all restraint violations is given in SI Table S3. The results suggest that the crystal structure and several NMR restraints are incompatible. Most of the large violations occur between inhibitor and RNA atom pairs, with the largest being those between the dimethylamino arms of the inhibitor and RNA residues A6, C11, and U12. Next, we attempted to perform MD simulations where we gently enforced the NMR distance restraints on the crystal conformation RNA. Inevitably, the crystal-like binding pocket conformation was destroyed, including the hydrogen bonds between the ligand and residue 33. We also tested this same approach starting with the conformation from the NMR1 J5S simulation (which partially converted to the crystal conformation). The same loss of crystal-like conformation was observed. This procedure was further repeated, except that all of the ligand restraints to residue A6 were removed, and again the crystal-like conformation was lost.

From our attempts to reconcile the NMR and crystal structures, we concluded that the two distance restraints between the ligand and residues C11 and U12 are the key driving forces in maintaining the NMR conformation during the refinement procedure. To confirm this, we performed simulated annealing using two distance restraint sets. In one trial we included all of the NOE distance restraints, and in the other we removed the two restraints between the ligand and residues C11 and U12. These simulated annealing calculations differed from the originally published approach in two ways. First, in order to simplify the procedure, only the distance restraints were used while torsion and RDC restraints were ignored. Second, in the original NMR refinement, the ligand cyclic ring was protonated on the primary amine rather than the more favorable secondary amine. That error was corrected in this work. The annealing results clearly confirmed that the two restraints between the ligand and residues C11 and U12 are a key determinant in the conformational outcome. With all of the distance restraints included, the ligand is unable to form hydrogen bonds with residue 33, and the resulting binding pocket resembles that in the published NMR structure. When these two restraints are excluded, the hydrogen bonds between the ligand and residue 33 are clearly formed, and the binding pocket resembles that in the crystal structure.

In addition to the fine details of local structure, we were interested in whether the crystal conformation was consistent with the RDC data published with the NMR structure.¹² To test this, we performed a 5 ns simulation with RDC restraints enforced on the crystal conformation. No significant changes in the global structure or inhibitor binding contacts were observed. This suggests that although significant NOE distance violations are observed for the crystal conformation, its global conformation is consistent with the RDC data.

Finally, we were interested in the possibility of a second binding site. The conditions necessary to saturate the RNA–ligand complex and minimize exchange broadening of the NMR spectra required significant excess ligand, creating the possibility of an RNA with multiply bound ligands. To test this, we extracted conformations of the RNA–ligand complex from the CRY1 J4R and J4S simulations and performed docking of a second J4R or J4S ligand. In all cases, the best-scoring docking pose was in a pocket near residues C11 and U12, which also happens to be a magnesium ion binding site in the crystal structure. The exact pose of the second ligand was dependent on the specific receptor conformation, but the result raises the possibility that at high concentrations a second highly charged ligand could bind in the region near residues C11 and U12 and produce additional NOE signals.

The base conformation of residue A6 and its relationship to the restrained dimethylamino chain of either inhibitor J4 or J5 is another key difference between the NMR and crystal structures. In the NMR structure, the A6H2 proton is proximal to the dimethylamino group, while in the crystal structure the A6H8 proton is proximal. A careful analysis of the NMR data for selectively isotopically labeled RNA–J4 complexes appears to uphold the original NMR report and suggests that there is a fundamental difference between the orientations of A6 in solution and in the solid state. SI Figure S5A shows that there are strong NOEs from A6H2 to the methyl protons and to the methylene protons on the dihydrofuran side chain, while the corresponding NOEs to H6–H8 are weak. This pattern is inconsistent with the crystal structure. The assignment of these NOEs to A6H2 is corroborated by ¹H–¹³C HSQC data (SI Figure S5B,C), which show no adenosine H8 protons resonating at 7.92 ppm. While the problematic NOEs to C11 and U12 could result from binding of a second ligand to the RNA, the extremely weak NOE from A6H8 to the ligand is incompatible with the crystal structure, suggesting that the conformation at this site under solution conditions differs from that solved by crystallography.

Taken together, at present the data suggest the following. At least two NMR distance restraints are incompatible with the crystal structure and may have arisen from a second binding mode. However, the overall conformation of the crystal structure is consistent with the RDC alignment restraints derived from NMR analysis. The NMR NOE data involving residue A6 indicate that its conformation in solution differs from the form captured in the crystal. This could result from the effect of magnesium, a second ligand, or some combination of the two. Further work to address these issues is underway in our laboratories.

Energy Analysis

A major goal of this study was to determine whether energetic binding analyses of the simulation trajectories could reproduce the experimental trends in binding energy. This is a challenging problem because of the highly charged ligands and the relatively tight range of K_D or ΔG_binding values estimated in the experiments. Given the instability of the NMR1 simulation sets, we considered only simulations performed with the crystal conformation. One of the quickest methods for obtaining binding energy data from MD simulations is to perform MM-GBSA/MM-PBSA analyses using the single trajectory method. From the MM-GBSA (Figure 7) and MM-PBSA (SI Figure S6) results for both the CRY1 and CRY2, several observations can be made. First, the magnitudes of the binding energies are significantly larger than those observed experimentally. For MM-GBSA, the range of binding energies for the various inhibitors is around −45 to −65 kcal/mol. For MM-PBSA, the magnitude is slightly smaller, with binding energy ranges of around −30 to −55 kcal/mol. Obviously there is a significant difference between these values and the −5 to −8 kcal/mol range identified experimentally (Table 1). A variety of corrections can be considered to address this discrepancy. One explanation is that the free energy change upon RNA reorganization that accompanies inhibitor binding is not taken into account in the single-trajectory approach. We performed MD simulations and MM-GBSA analysis on the apo-RNA using the published NMR structure¹⁰ as the initial conformation and can estimate that this would add around +10 kcal/mol to the MM-GBSA binding energies. An additional energetic component that we did not include in our MM-GBSA/MM-PBSA results is the change in solute entropy upon binding. We attempted to estimate the conformational entropy change for the inhibitors alone (the estimates are between 0 and 25 kcal/mol, as discussed below), but the size of the RNA presents a challenge to obtaining a full solute estimate. Additionally, the rotational and translational entropy loss upon ligand binding would likely add in the range of 3–12 kcal/mol.⁵⁴⁻⁶⁰ Together, these corrections are in the range of +13–47 kcal/mol and could, in theory, bring at least the MM-PBSA results close to the experimental ranges. However, the raw binding energies from MM-GBSA/MM-PGBSA analyses have not only a large magnitude but also a large spread in the values. For example, if we exclude the results for the J1 inhibitor (because of uncertainty about its exact experimental binding energy), the range for MM-GBSA is ∼10 kcal/mol and for MM-PBSA around ∼20 kcal/mol. Given the similarity of the ligands and their binding mode with the RNA, it is unlikely that the aforementioned corrections for receptor reorganization and solute entropy could account for the large range in values. Finally, even if we ignore the incorrectly large range of binding energies, the relative trend in binding energy does not match what is observed experimentally (Table 1). The weakest binder, J1, can be distinguished from the other inhibitors, although less so with MM-PBSA than MM-GBSA. As for the other inhibitors, the computed values do not correlate well with experiment. In particular, both MM-GBSA and MM-PBSA rank J2 as having a binding energy equal to or lower than that of the J5 enantiomers, despite the fact that experimentally J2 is among the weakest binders while J5 is among the strongest binders. It is not immediately clear why the MM-GBSA/MM-PBSA results do not match the experimental data, but this outcome may be related to the failure of implicit solvent models to model highly charged systems accurately. In fact, it is known that the Hawkins, Cramer, and Truhlar GB model does not produce accurate values for salt bridges⁶¹ and incorrectly models DNA helices.⁶²

Figure 7.

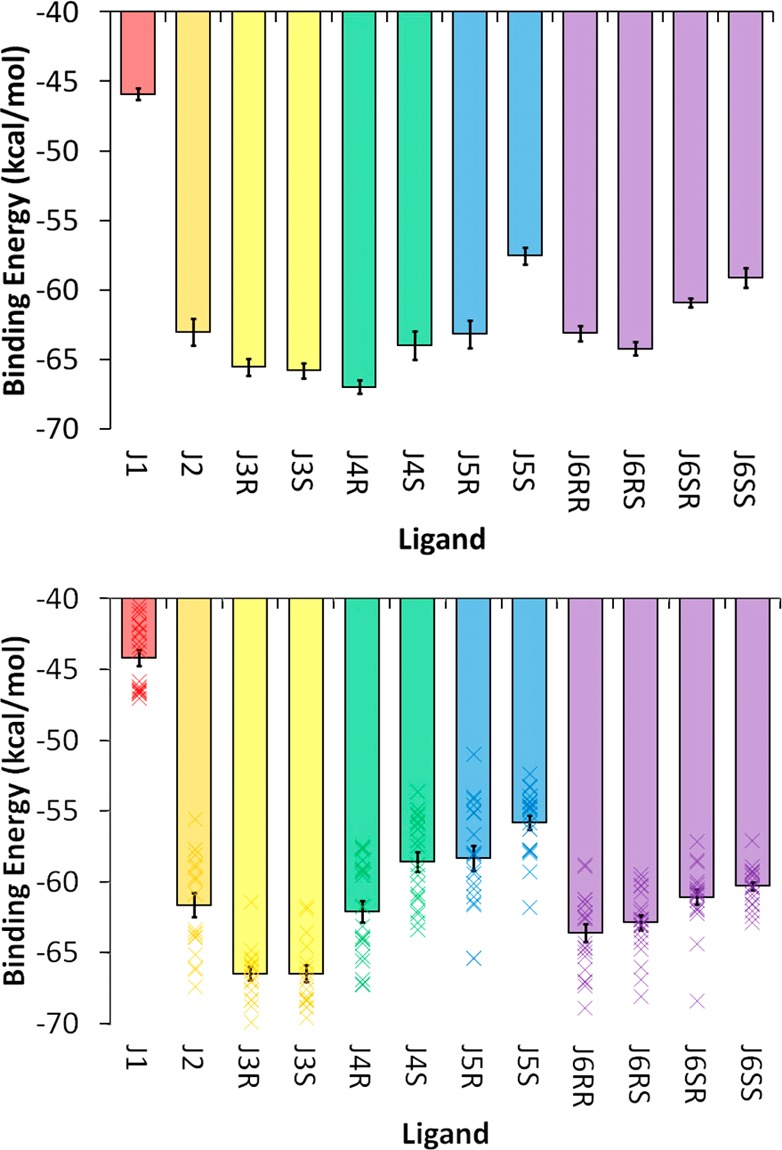
MM-GBSA binding energy results for the (top) CRY1 and (bottom) CRY2 simulation sets. The mean values for the 20 individual CRY2 simulations are depicted by the “×” symbols (bottom), whereas the bar shows the overall mean value. All of the data are in units of kcal/mol, and the specific values for both panels are given in SI Table S4. Stereoisomers/diastereomers are grouped by color.

Given the poor performance of these implicit models, it is reasonable to seek an alternative calculation of the binding energy that explicitly includes solvent contributions. We performed a relative binding enthalpy analysis on the explicitly solvated RNA–inhibitor systems using the total potential energy of the explicitly solvated trajectories directly. This was possible because all of the systems in the CRY1 and CRY2 simulation sets, with the exception of J1, had by design identical numbers of atoms (excluding the inhibitor atoms). Likewise, the LIG simulation set, which contained just the free inhibitors and solvent, also contained identical numbers of solvent atoms. Since the J1 inhibitor has a different charge and therefore a different number of counterions, it was excluded from consideration. The relative energetic contributions to binding for the trivalent inhibitors (J2–J6) can be calculated by subtracting the average potential energy of the free-inhibitor simulations (LIG set) from the average potential energy of the bound-inhibitor simulations (CRY1 or CRY2 set). Only the single long simulation strategy was used for the free inhibitor simulations (LIG) because the potential energies were tightly converged. Confirmation of this is demonstrated by the fact that the mean potential energies of all the enantiomers are within the expected error of one another (SI Table S5, fourth column). The results for the binding enthalpy are shown in Figure 8. It should be noted that the absolute value of the binding enthalpy is meaningless because it represents the force field energy difference of two systems with unequal atoms (i.e., ligand in solution and ligand bound to RNA). However, the relative enthalpy differences can be compared because the relative differences between the systems are identical with the exception of the inhibitor atoms of interest. Several observations suggest that the relative binding enthalpy values are a better predictor of binding free energy than the MM-GBSA or MM-PBSA values. First, the range of binding enthalpies is much smaller (∼6–7 kcal/mol). Second, the binding enthalpies calculated from the CRY1 and CRY2 simulation sets are within the error of one another, except for J6SS, which has a 0.9 kcal/mol difference between the error bounds. This was not the case for the implicit solvent approach, although it should be noted that the error values are larger for calculations involving explicit solvent. Third, the binding enthalpies are internally consistent: the four J6 diastereomers, which contain two constrained rings, of which one each is present in the J3 and J5 enantiomers, produce a binding trend that can be predicted from the J3 and J5 results. The binding enthalpy of the S enantiomer is preferred for J5, whereas the R enantiomer is preferred for J3. Consistent with expectations, the J6SR inhibitor has the lowest binding enthalpy. The lone exception to this internal consistency is again J6SS of the CRY1 simulation set (the prediction is correct in the CRY2 results). Finally, if one averages the values of the enantiomers/diastereomers as an approximation of the experimental conditions (where stereochemistry was not considered), the trends match well with experiment (Figure 9). The range of the binding enthalpies calculated from simulation is somewhat larger than the range of binding energies from experiment (∼4 vs ∼2 kcal/mol, respectively). However, the correct trend as well as agreement between the single long trajectory and multiple short trajectory approaches is observed. This last observation is critical given the small number of data points. Two completely independent approaches produce very similar results, suggesting that adequate sampling was obtained and that the results accurately reflect the underlying force field terms used to model the system.

Figure 8.

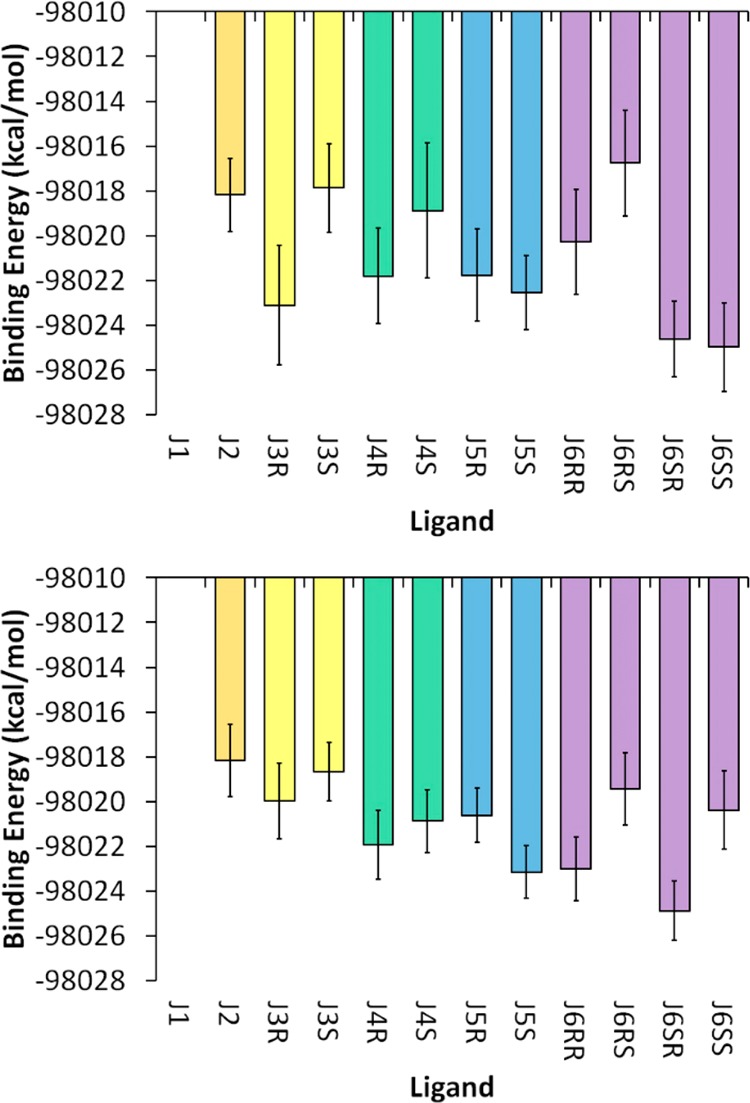
Relative binding enthalpies calculated using the solvated potential energy difference (see the text) from the (top) CRY1/LIG and (bottom) CRY2/LIG simulation sets. Data for the J1 inhibitor are not shown because it has a different charge than the rest of the inhibitors, which prevents a direct comparison of the results. All of the data are in units of kcal/mol, and the specific values for both panels are given in SI Table S5. Stereoisomers/diastereomers are grouped by color.

Figure 9.

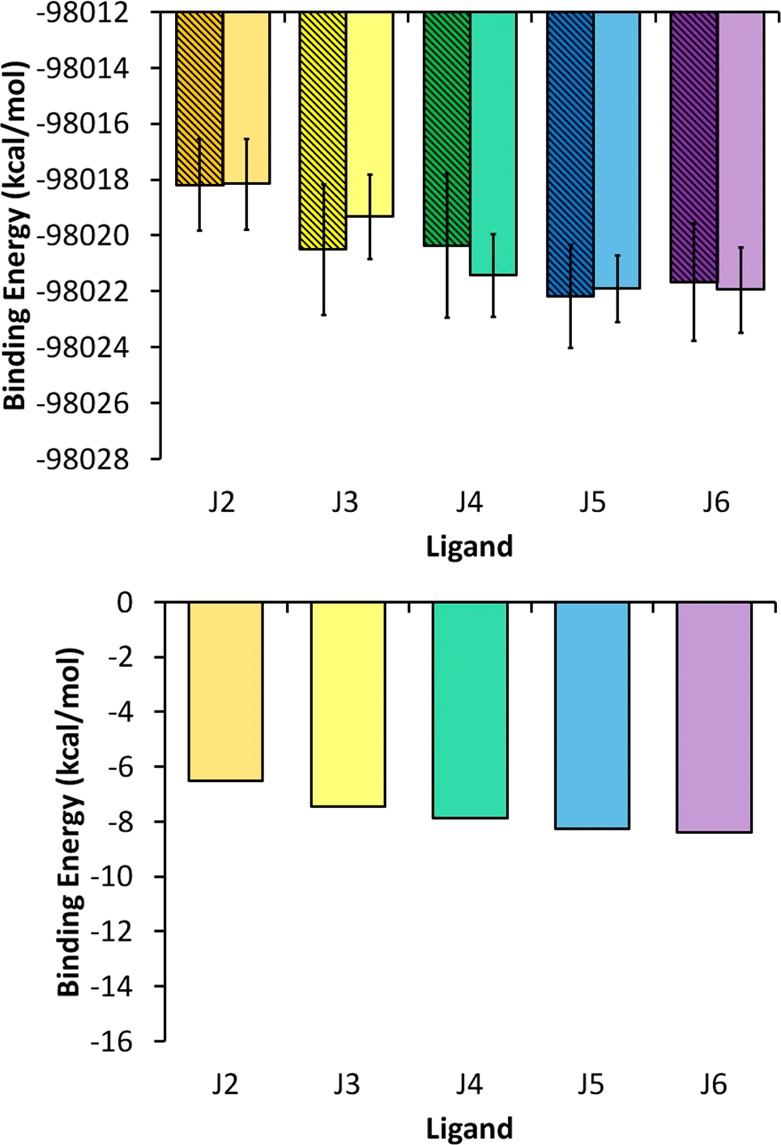
(top) Stereochemically averaged relative binding energies calculated using the solvated potential energy difference (see the text) for the CRY1/LIG (striped bars) and CRY2/LIG (solid bars) simulation sets. Data for the J1 inhibitor are not shown because it has a different charge than the rest of the inhibitors, which prevents a direct comparison of the results. (bottom) Previously reported experimental binding energies.¹⁸ All of the data are in units of kcal/mol, and the specific values for both the top and bottom charts are given in SI Table S6. Color scheme follows Figures 7 and 8

The difference between the implicit solvation and explicit solvation results can be highlighted by looking at cases where the inhibitor was improperly bound to the RNA. As noted in Methods, the initial inhibitor poses were not chosen via a docking algorithm but rather by a simple RMS fit of the benzimidazole core atoms. While this ensured that critical hydrogen bonds were formed between the inhibitor and residue G33, it did nothing to prevent unfavorable clashes of the flexible inhibitor arms with the RNA. In nearly every initial inhibitor conformation, potential clashes were eliminated during the minimization step, and the resulting geometry resembled a reasonable binding pose. However, in a few cases, one of the inhibitor arms was improperly inserted through the back of the binding cavity. Despite the apparent strain in the geometry, some of these cases produced stable simulations without integration errors or energy instability. These cases were not included in the previously discussed energy analysis, but they provide a useful test case in that an accurate representation of the system energy should distinguish highly strained systems from those with an expected binding conformation. One such case of an improper binding mode occurred with the J2 inhibitor. For the multiple short simulation set CRY2, the range of mean GB total potential energies of J2 in normal binding poses was −7891 to −7913 kcal/mol. The mean GB total potential energy of the incorrect strained conformation was −7916 kcal/mol, suggesting that it was actually a lower-energy conformation. The MM-GBSA binding energy computed using this strained conformation was −77 kcal/mol, indicating stronger binding by about 15 kcal/mol compared with the average MM-GBSA binding value for J2 from the CRY2 simulation set. Apparently, some portion of the implicit solvation model incorrectly modeled this interaction. In contrast, using explicit-solvent potential energies accurately identifies the strained J2 conformation as a high-energy outlier. The range of mean explicit-solvent potential energies for J2 from the CRY2 simulation set was −118766 to −118790 kcal/mol, whereas the mean explicit-solvent potential energy for the strained conformation was −118761 kcal/mol. This trend in which explicit-solvent potential energies more reliably predicted strained conformations than implicit-solvent potential energies was true for other cases of strained RNA–inhibitor conformations as well.

In order to understand whether solvation energies played a role in the errors of the MM-GBSA/MM-PBSA results, we performed further analysis of the LIG simulation set (in which the inhibitor was simulated freely in explicit solvent without RNA). After postprocessing of the LIG trajectories to extract the GB potential energy, a comparison of the explicitly solvated and GB-solvated ligand potential energies was made (SI Figure S7, top). As indicated by the trend line fit, the relative potential energies are similar whether explicit solvent energies or GB solvent energies are used. An RMS fit of explicit-solvation energy values onto the implicit-solvation values reveals that the differences between the two methods range from 0.06 to 1.60 kcal/mol. First, this shows that the MM-GBSA values are primarily enthalpic since they are similar to the explicit results, which are purely enthalpic. Second, it suggests that the likely origin of the errors in the implicit solvation model is found not in computing the solvation energy of the ligand alone but in calculating the solvation energy of the ligand in complex with the RNA. Similarly, when the solvation enthalpy is computed (by subtracting the gas-phase inhibitor energies from the solvated energies, either explicit or implicit GB), very similar trends for the explicit and implicit solvation models are observed (SI Figure S7, bottom). The origin of the large difference (∼13 kcal/mol) between the solvation enthalpies for the J2 and J3 and those for the rest of the inhibitors is unclear. The distinguishing feature of the two sets of inhibitors is the absence or presence of a cyclic ring connection formed on the oxygen side of the benzimidazole group.

As a final piece of energy analysis, we note that the experimental binding energy trends suggest that the use of ring constraints to reduce the flexibility improves the binding energy. Thus, it is reasonable to expect that entropic considerations play a role in the inhibitor binding free energy. Because of the difficulty in converging entropy estimates for large molecules, only the inhibitor was considered in the following entropy calculations, and the receptor entropy contribution is assumed to be nearly identical for the inhibitors we evaluate. Two methods were used: quasi-harmonic analysis⁴⁸ and a configurational estimate based on bond, angle, and torsion probability distributions.⁴⁹ The entropic energy penalties upon binding of the various inhibitors based on calculations from the CRY1 and LIG simulation sets are given in SI Figure S8. Convergence plots for these values are shown SI Figures S9 and S10. The convergence plots demonstrate that the estimates are not reliably converged, even at greater than 700 ns for the free ligands, and thus must be interpreted very conservatively. One observation that is clear is that the quasi-harmonic estimates have a much larger magnitude (approximately 5 to 25 kcal/mol) than the conformational entropy estimates (0 to 5 kcal/mol). The large values produced by the quasi-harmonic approximation are likely due to an overestimation of the harmonic potential width for the free inhibitors because no attempt was made to differentiate between conformational energy minima, which necessarily results in a wider estimated width in order to cover a broader space. In contrast, the configurational estimate using probability distributions distinguishes both well-width and conformational differences. In this case, the drawback is that individual degrees of freedom (bonds, angles, and torsions) are assumed to be uncorrelated when only the first-order approximation is used, as was done here. It is important to note that neither of these estimation techniques include the entropy loss due to changes in translational and rotational entropy upon ligand binding, which can be estimated to add an additional 3–10 kcal/mol.⁵⁴⁻⁵⁹ In view of the assumptions made in the estimates and the lack of clear convergence, it is unwise to treat these values as anything more than qualitative observations. Given that caveat, we do find that the average entropic penalty upon binding is smaller for the fully constrained inhibitors (J6 diastereomers) than for the less constrained ones (J2, J3, J4, and J5).

Molecular Docking

In order to test whether high-throughput computational techniques could be used to predict accurate conformations for binding between highly charged ligands and RNA, we used Dock 6.5 to perform docking analysis of the inhibitors shown in Figure 1 on the crystal RNA conformation. With the exception of the weakest-binding inhibitor considered, J1, the docking pose with the best score for each inhibitor was consistent with the crystal structure binding mode and formed all of the critical binding contacts (Figure 10A,B). The J1 inhibitor binds incorrectly to a major groove pocket on the opposite side of the correct RNA ligand pocket. It is unclear why J1 was so poorly docked, but this may reflect its weak binding value. Not surprisingly, the trend in docking scores did not match the experimental binding energy trend (SI Table S9). However, the docking results suggest that fairly accurate binding poses can be obtained for highly charged systems at low computational cost. Given the somewhat elaborate procedure we used to obtain charges for the inhibitors, we were interested in whether similar docking results could be obtained using a more traditional approach in which the semiempirical AM1-BCC charge model was used to assign atomic charges to the inhibitors. The results suggest that the more rigorous RESP approach does yield a significant improvement in the results (Figures 10C and S11). This consideration is likely to be more important for multivalent and highly charged ligands such as those studied in this work. Taken together, the results show that methods such as Dock 6.5 using reliable scoring functions can be applied to generate reasonable binding modes. The resulting structures can then be further explored using more detailed simulation and energetic analyses such as those presented in this work.

Figure 10.

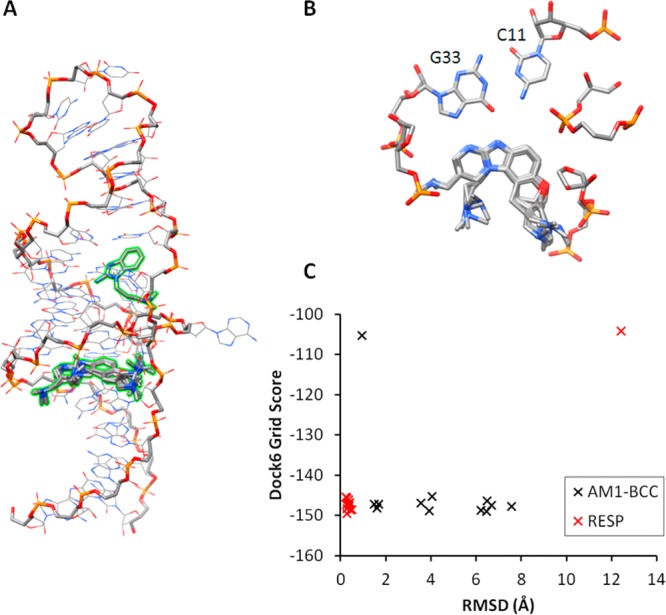
Docking results using the crystal structure receptor conformation. (A) Overlay of the best-scoring docking poses using RESP charges for each of the 12 stereochemically distinct inhibitors on the crystal structure receptor RNA. The only inhibitor that did not bind in the expected orientation was the weakest binder, J1. (B) Close-up view of the inhibitor docking poses in the binding site (using RESP charges). (C) Comparison of the AM1-BCC (black) and RESP (red) charge methods. The best-scoring pose for each of the 12 inhibitors is plotted with its corresponding RMSD value (using the experimental crystal structure as the reference, benzimidazole core atoms only). The outlier data point for the RESP values (red) is for the weak-binding J1 inhibitor.

Novel Ligands

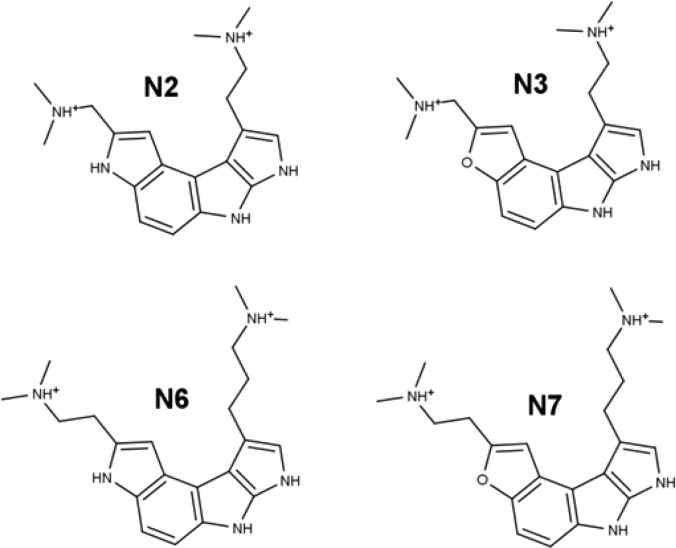
Given the robustness of the crystal conformation across simulations of all the inhibitors in Figure 1, we were interested in how well ligands with a different scaffold could be accommodated by the binding site. We designed four novel ligands that both exploit the known inhibitor interactions and, in certain respects, reduce the complexity of the ligand (Figure 11). These novel ligands have several advantages: less positive charge, fully aromatic rings that are less flexible, and no chiral centers. One of these ligands, N7, was particularly stable in the receptor binding site during a 130 ns simulation (SI Figure S12). MM-GBSA analysis on that trajectory yielded a binding energy of −61 kcal/mol, which is in the same approximate range as those of the known inhibitors, although our caution regarding implicit solvent models applies. Additionally, the N2 and N3 ligands were moderately stable and maintained most of the critical binding contacts. Visual inspection of the simulation trajectories suggests that further optimization of the dimethylamino arm length and orientation would likely further improve the binding.

Figure 11.

Novel ligands investigated in the NOV simulation set.

Discussion

The presented results are relevant for computational drug development targeting the HCV domain II site as well as for research on RNA–ligand binding in general. First, we have demonstrated that the crystal structure of the RNA–inhibitor complex is strongly supported over the NMR conformation by simulation using the AMBER ff12SB force field in explicit solvent. This result highlights the need for accurate initial structures when performing MD simulations. Because of the rugged energy landscape of RNA, highly incorrect initial structures will likely not reach the global minimum on tractable time scales. Since this concern is coupled with known force field flaws for RNA (a subject of ongoing research in our lab), it necessitates caution when performing MD simulations. In this case, the force field does not predict that the NMR conformations are near a local energy minimum. The result is a quick degradation of the initial structural contacts during the simulation. In contrast, the crystal structure is clearly in a minimum of the force field energy landscape and yields extremely stable simulations that maintain fidelity in the binding region.

It still remains unclear how best to resolve the apparent contradictions between the NMR data and the crystal structure. The low proton density of RNA compared with proteins presents a challenge in the use of NMR spectroscopy for high-resolution RNA structure determination. The addition or exclusion of just a few atom-pair restraints can make a large difference in the resulting structural refinement. In this case, close contacts that would result in detectable NOEs between RNA residue G33 and the inhibitor do not exist, so there was no justification during the original NMR refinement to enforce the hydrogen-bonding interactions observed in the crystal structure. In regard to NOE distance restraints that are violated by the crystal structure, possible explanations include the presence of an additional inhibitor binding site near the primary site or, alternatively, a third unidentified conformation that is present in solution. At present, use of the crystal conformation is recommended for simulation studies.

Even if a simulation model maintains structural fidelity, drug development efforts require accurate estimates of relative binding energy. Traditionally, MM-GBSA/MM-PBSA trajectory postprocessing techniques have been moderately successful at predicting the binding free energies of protein–ligand systems, but studies with highly charged ligands and highly charged receptors (e.g., RNA) are rare. As has been noted elsewhere,⁶³ the binding free energy is largely determined by the difference between the desolvation energy and the energy of the bound complex. For a highly charged ligand–receptor interaction, both of these values will be very large, and thus, errors in the method will dwarf the binding energy value. In this case, the error is likely not related to insufficient sampling (our estimated errors are reasonably small) but rather is due to an error in the model used to describe the desolvation energy and the energy of the bound complex. As additional evidence, we have obtained very poor results from MD simulations of various RNA structures when using the Hawkins, Cramer, and Truhlar GB implicit solvent model (data unpublished). This could explain why the binding energies calculated from the explicit-solvent systems compare more favorably to experiment than the binding energies obtained from implicit-solvent approximations. In view of the relative success of explicit solvent in comparison to implicit solvent for MD simulations of RNA, it is not surprising that energetic results utilizing the former solvation terms would produce better results. Similarly, the charge parametrization method appears to be crucial for at least docking studies but likely simulations as well. This is not surprising given the large net charge of the inhibitors used in this study; the careful procedure reported here provides a useful framework for future charge parametrization on highly charged ligands. The docking results suggest that methods such as Dock 6.5 with good scoring functions can accurately predict ligand binding modes when care is taken with ligand charge derivation.

The data suggest that the multiple short simulation approach offers efficiency benefits over the single long simulation approach for energetic analysis. The mean explicit-solvent binding enthalpy values computed using the two approaches were within the error of each other for 10 out of the 11 inhibitors considered. In the case that differed, it seemed likely that the multiple simulation approach was correct on the basis of the argument for internal consistency of stereochemical binding. The aggregate simulation time for the multiple simulation approach was only 480 ns (CRY2 set), which is significantly less than the 2616 ns of aggregate time used for the single simulation approach (CRY1 set). The drawback to the multiple simulation approach is that it does not ensure binding stability over longer time scales. The 2 ns trajectories used are not long enough to allow large structural transitions. Thus, if we had used only 2 ns trajectories, even 240 of them, the difference in stability between the NMR conformation and the crystal conformation would not have been as clear. In view of the ongoing questions about possible differences between the binding modes for the crystal and solution conditions, the use of longer simulations may be justified when analyzing highly charged RNA–ligand complexes.

Finally, we conclude that computational simulations are not intended to replace or “compete” with experimental observations. Rather, they should aid in the evaluation of existing data and improve the accuracy of hypotheses and predictions for future efforts. The data presented in this work should suggest several avenues for additional research, both experimental and computational.

Supporting Information Available

Figures S1–S12, Tables S1–S9, a rotating movie of NMR distance violations (MPG), and a zip file containing the AMBER force field input files for the ligands in this paper. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^† Niel M. Henriksen, Skaggs School of Pharmacy and Pharmaceutical Sciences, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA.

This work was supported by the National Institutes of Health (R01-GM081411 to T.E.C.), the Eccles Foundation (N.M.H.), and the American Foundation for Pharmaceutical Education (N.M.H.) as well as computing allocations from the National Science Foundation (XSEDE-MCA01S027 to T.E.C.), friendly user time on the Keeneland System at the Georgia Institute of Technology and the National Institute for Computational Sciences (T.E.C.), and the University of Utah Center for High Performance Computing (T.E.C.).

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States