Filming Biomolecular Processes by High-Speed Atomic Force Microscopy

1. Introduction

In the history of science and technology, researchers have always undertaken endeavors to enhance the degree of “directness of measurement”. With “directness of measurement”, we conceptualize that the essence of the object under investigation, the structure, dynamics, and function of biological samples in the scope of this Review, is entirely and straightforwardly assessed by the measurement, bypassing hypotheses and intricate data analysis. When the degree of measurement directness is low, conclusions derived from the gleaned data often differ depending on the formulation of hypotheses, analysis models, and the data interpretation. That is why conceptual consensus about a specific issue of the studied object is rarely reached based on indirect data. This is often the case for studies of structure–function relationship of proteins. Previously, scientists had to understand distinct qualities of proteins by measuring a sample containing a huge number of molecules. The results are ensemble-averaged quantities (often at equilibrium) that provide only limited information on the proteins of study. Proteins are dynamic in nature and work at the single-molecule level. Protein molecules fluctuate, undergo structural changes, bind to and dissociate from interaction partners, and traverse a range of energy and chemical states during molecular action. Most, if not all, of these dynamics and their statistical distributions are convoluted and hidden in ensemble averaging measurements.

To overcome the limitations of ensemble measurements, single-molecule biophysics was developed more than two decades ago, with the use of fluorescence microscopy,^1,2 optical spectroscopy,^3,4 and optical and magnetic tweezers,^5,6 whose performances were further improved by the advancements of improved optical microscopes, lasers, electronics, computers, and high-sensitivity video cameras and sensors. Using these techniques, our understanding of the functional mechanism of proteins has made significant steps forward. Moreover, super-resolution optical microscopy techniques bypassing the diffraction limit for fluorophore localization have recently been added to fluorescence microscopy.⁷⁻⁹ However, the degree of directness of measurement is still limited, because the protein molecules themselves are invisible in these single-molecule measurements. Protein structure is typically studied by X-ray crystallography, electron microscopy (EM), and nuclear magnetic resonance (NMR) spectroscopy. To date, these techniques have revealed detailed three-dimensional structures of over 94 000 proteins (Protein Data Bank (PDB), http://www.rcsb.org/pdb/home/home.do), with a growth rate of about 8000 novel structures per year (2010–2013). Yet, these techniques make use of ensemble averaging, and, more seriously, the obtained structures are merely limited to static snapshots of fixed conformations. Thus, the simultaneous and direct observation of structure, dynamics, and function of single protein molecules has long been infeasible, and hence the materialization of a technique allowing such an observation has long been awaited in biological sciences.

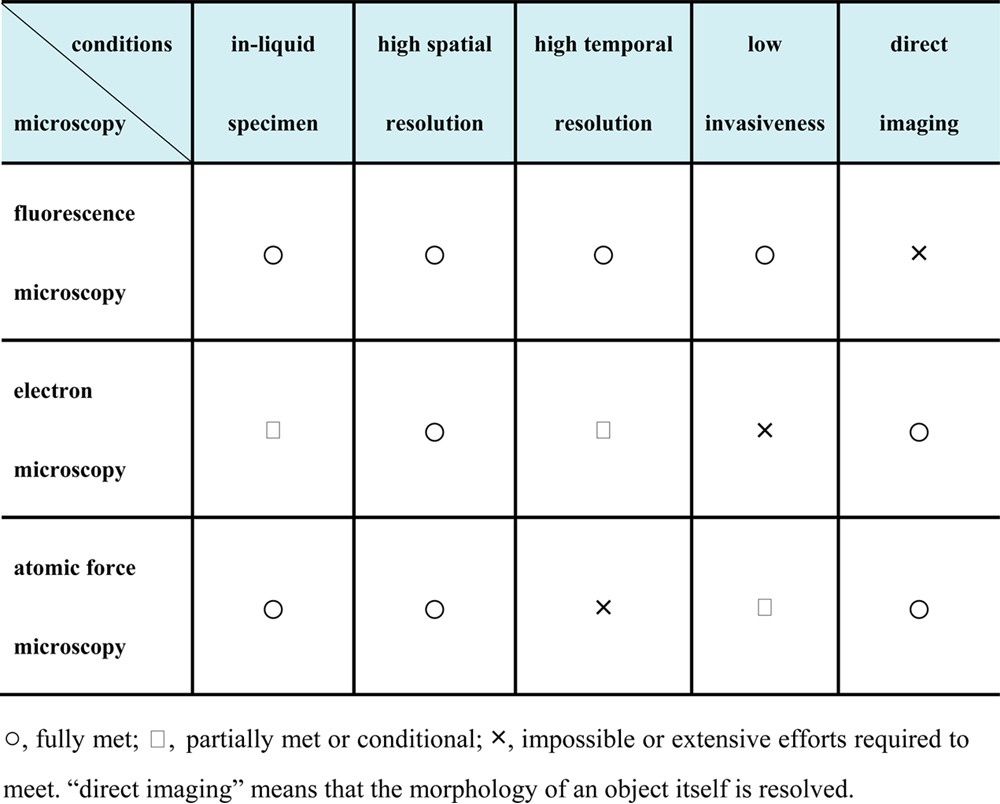
An ideal microscopy technique that allows simultaneous observation of structure, dynamics, and function of single protein molecules has to meet all of the following conditions (see Table 1): (i) in-liquid specimen imaging, (ii) high spatial resolution, (iii) high temporal resolution, (iv) low invasiveness to the specimen, and (v) direct imaging of the specimen without the use of markers (in other words, resolving the structure of the specimen itself). Although efforts have been made to develop environmental electron microscopy techniques capable of observing unstained biological specimens in solutions,¹⁰ the strong electron dose that is required to achieve high contrast and spatial resolution instantaneously denatures the sample. Achieving the above-described goals by EM is a highly difficult, if not impossible, task. Conventional atomic force microscopy¹¹ (AFM) meets most of the above-mentioned conditions, except for the third condition, that is, high temporal resolution, and the fourth condition, that is, low invasiveness, is only moderately satisfied.

Table 1. Feasibility Comparison of Three Types of Microscopy.

AFM was originally invented to visualize atoms on solid surfaces.¹¹ The basic principle of AFM imaging is that a sharp tip attached to the free end of a microcantilever probes the sample surface, while this tip is being scanned over the sample surface (more details are given in the next section). Today, AFM can be used for a wide range of specimen made of any material in any environment (vacuum, air, and liquids). When used for measuring biological samples in liquid, the tip is brought into contact with the sample, and the mechanical response of the cantilever upon this contact is measured. The sample stage (or the cantilever base) is moved in the Z-direction to keep constant the cantilever’s mechanical state (and hence, the mechanical tip–sample interaction force) at a given condition, that is, a set point, through feedback control. This series of operation is repeated many times, so that the tip traces the whole sample surface to provide the sample surface topography. AFM is now routinely used in biological sciences (see reviews^12,13) not only for high-resolution imaging of biological samples under physiological conditions,^14,15 but also for force measurements to estimate the strength of intra- and intermolecular bonds at the single-molecule level^16,17 and the elasticity of biological objects.¹⁸⁻²⁰ However, as mentioned above, the AFM’s low imaging rate (about 1 min is required to capture an image) has precluded the analysis of the vast majority of dynamic biological processes and therefore limited its usefulness for biological studies.

This shortcoming of AFM imaging can in principle be significantly improved. Encouraged by this expectation and motivated by the desire to visualize single protein molecules in action, attempts to increase the AFM imaging rate were initiated around 1993 by the Hansma and Ando groups independently, and later by the Miles group. Through the development of new devices and techniques (see reviews²¹⁻²⁴) and the improvement of the first version of prototypic instruments,^25,225 HS-AFM was realized around 2008²³ (for the history of development of HS-AF techniques, see review²²). Now in 2013, state of the art HS-AFM can capture dynamic images of biomolecules at sub-100 ms temporal and submolecular lateral resolution. Importantly, the function of fragile molecules is not disturbed by the interaction with the cantilever tip (detailed in section 4, Minimizing Invasiveness: The Tip–Sample Interaction). This performance made it possible to directly observe the structural dynamics and dynamic processes of biomolecules in action, providing a straightforward understanding of how the biomolecules operate to function.²⁶⁻²⁸ In the past few years, various biomolecular systems and their dynamic events have been studied using HS-AFM, continuously demonstrating the innovative power of this novel microscopy to reveal details of molecular action inaccessible to other approaches.²⁹⁻⁶⁶ Very recently, the analysis of dynamic events occurring in live cells has also become possible.⁶⁷⁻⁷⁰ Most of the biological HS-AFM studies on proteins and cells performed since 2006 are listed in Table 2.

Table 2. HS-AFM Imaging Studies on Proteins and Cells.

year	targets and subjects	substrate surfaces
2006	actin filament gliding on myosin and GroEL–GroES interaction24	bare mica
	conformational change of GroEL and GroEL–GroES interaction29	bare mica
2007	DNA translocation and looping by type III restriction enzyme30	bare mica
2008	identification of intrinsically disordered regions of FACT protein31	bare mica
	DNA–BAL 31 nuclease interaction32	bare mica
	anisotropic diffusion of point defects in streptavidin 2D crystals33	streptavidin 2D crystals
2009	dynamic equilibrium at the edge of bR 2D crystals34	native membrane
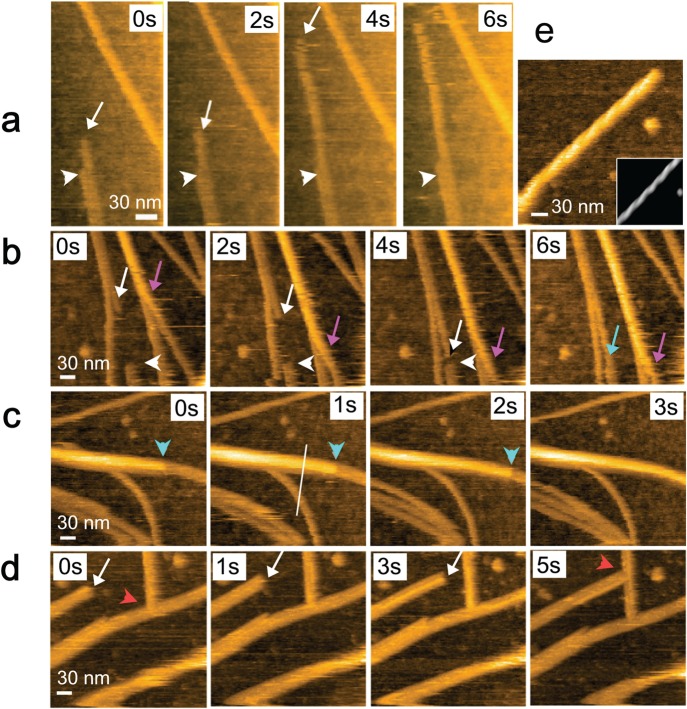
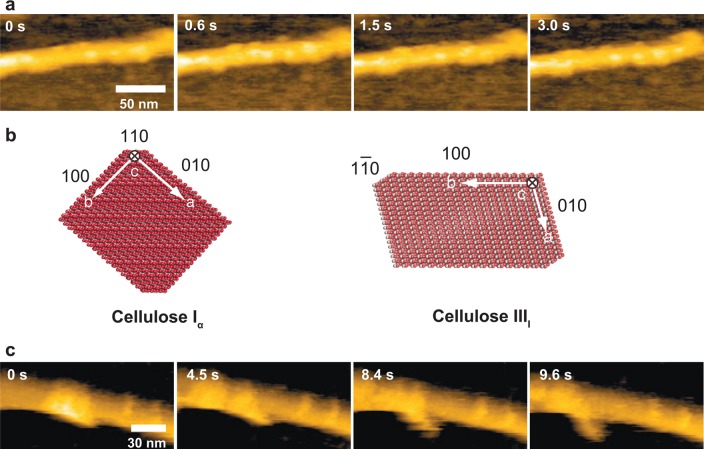
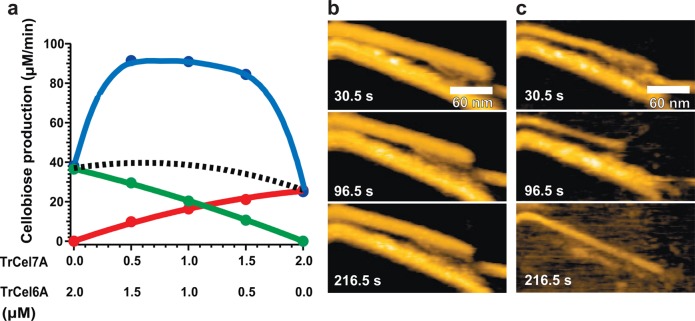
	unidirectional translocation of cellulase along cellulose fibers35	HOPG
	ATP-induced conformational change in P2X4 receptor36	bare mica and SLB
	structural change of CaM and actin polymerization on streptavidin 2D crystals37	streptavidin 2D crystals
	purple membrane in contact-mode HS-AFM41	native membrane
	translocation of EcoRII restriction enzyme along DNA39	bare mica
2010	structural change of bR trimer in a stretched membrane40	native membraneb
	membrane-mediated protein–protein interaction38	native membrane
	height change of acid-sensing ion channel 1a upon acidification42	SLB
	photoinduced structural change in bR43	native membrane
	process of forming supported planar lipid bilayers44	bare mica
	effect of ClpX on FtsZ polymerization45	bare mica
	self-assembly of amyloid-like fibrils46	bare mica
	myosin V walking on an actin filament47	SLB
	time course of cell death by antimicrobial peptide67	live cella
2011	bR in response to alternate two-color illumination48	native membrane
	height change in sarcoplasmic reticulum Ca2+-ATPase49	native membrane
	structural fluctuations of CENP-W complexed with CENP-T50	bare mica
	rotary catalysis of rotorless F1-ATPase51	modified mica
	pathways of ATP-independent unwrapping of nucleosomes52	modified mica
	concerted DNA cleavage by Type IIF Restriction Enzyme SfiI53	modified mica
	slide and hopping motion of Rad54 on DNA54	bare mica
	dynamics of synthetic proteo-nucleic building blocks55	bare mica
	unidirectional movement and traffic jams of cellulases hydrolyzing cellulose56	HOPG
2012	formation of synthetic DNA–protein complex formation57	modified mica
	diffusion and interaction of OmpF molecules in crowded condition58	SLB
	cooperative interaction dynamics of aquaporin-0 in eye lens cell membranes59	native membrane
	diffusion of crowded porin molecules on live bacterial cell68	live cella
	formation of complexes between DNA and single-stranded DNA-binding protein64	modified mica
	dynamics of DNA cytosine deaminase bound to single-stranded DNA66	modified mica
2013	structural changes of NMDA receptors60	SLB
	photoactivated structural changes in isolated bacteriorhodopsin trimers61	native membranea
	phosphorylation-coupled intramolecular dynamics of unstructured FACT protein62	bare mica
	dynamic processes in bacteriolysis and endocytosis in live cells69	live cellsa
	diffusion and interaction of AQP0 on live cells70	live cellsa
	oligomerization of DNA cytosine deaminase on single-stranded DNA65	modified mica
	self-assembly of sphingomyelin-specific toxin63	SLB

^aNative membranes and live cells are placed on chemically modified mica surfaces.

^bNative membranes are suspended over nanowells. In the other cases, native membranes are placed and SLBs are formed on bare mica surfaces. Streptavidin 2D crystals are formed on biotin-containing SLBs.

This Review focuses on application studies of HS-AFM, in which dynamics of proteins and live cells are visualized. For application studies of HS-AFM on the dynamics of DNA and DNA-binding proteins, see ref (71). Here, we also describe the HS-AFM setup, substrate surfaces, and precautions to be considered in HS-AFM imaging experiments.⁷² Before these topics are described, the physical backgrounds of the high imaging rate and low invasiveness are explained. In the last part of this Review, future prospects of HS-AFM studies are briefly outlined.

2. Principle of AFM Imaging

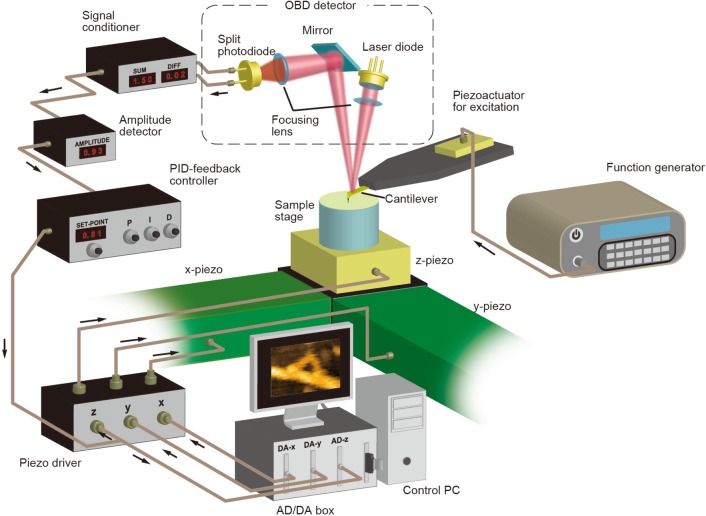
AFM can be operated in several imaging modes.^73,74 These are generally classified into contact mode, intermittent contact mode, noncontact mode, and other modes. Figure 1 shows a typical experimental setup for intermittent contact mode AFM. For HS-AFM imaging of biological samples, the intermittent contact mode is predominantly used, which will be detailed below. However, first, brief descriptions are given of the contact and noncontact modes; other modes are out of the scope of this Review.

Figure 1.

Schematic of experimental setup for intermittent contact mode AFM.

In contact mode, the cantilever tip is always in contact with the sample while scanned across the sample surface during topography acquisition. The cantilever is deflected by the tip–sample interaction. The extent of cantilever deflection, and hence the tip–sample interaction force, is kept constant during scanning by feedback control. The force applied on the sample can be minimized by the use of contact mode cantilevers with small spring constants with respect to bending by the normal force. In contrast, the spring constant is high for cantilever bending and twisting caused by lateral friction forces. Therefore, when the sample surface roughness is relatively large, high lateral friction forces are exerted by the dragging tip onto the sample, eventually resulting in significant deformation and damage of biological samples or displacement of samples that are weakly attached to the substrate surface. Therefore, this mode has been most successfully used for firmly immobilized samples with small surface roughness such as bacteriorhodopsin (bR) embedded in the crystalline purple membrane.⁷⁵

In noncontact mode, the so-called frequency-modulation (FM) mode is typically used.⁷⁶ In the FM mode, the cantilever is always oscillated at its first resonant frequency, using a self-oscillation circuit. The self-oscillation means that the cantilever deflection signal is used to generate the cantilever excitation signal, so that the frequency of the excitation signal is the same as the cantilever resonance frequency that varies upon tip–sample interaction. The gradient of the tip–sample interaction force in Z-direction, k, induces a shift (Δf_c) of the cantilever resonance frequency, approximately by

1

where k_c and f_c are the spring constant and the original resonance frequency (under free oscillation while the tip is very far from the surface) of the cantilever, respectively. This is because the apparent spring constant of the cantilever is changed from k_c to k_c – k by the tip–sample interaction. In the attractive regime, k is positive, and hence, Δf_c < 0, whereas in the repulsive regime, k is negative, and hence, Δf_c > 0. Before imaging, a set point frequency is defined, which is shifted with respect to the original resonance frequency. During scanning, the feedback control tries to get the actual frequency back to the set point frequency by driving the Z-scanner, which restores the desired tip–sample interaction corresponding to the set point frequency. The true noncontact condition is achieved only in vacuum or in air, because a high quality factor of the cantilever oscillation Q_c is required for highly sensitive detection of Δf_c at any instant during the scanning. In solution, Q_c is small because of damping of the cantilever oscillation due to the viscous drag effect of the solution. Moreover, to obtain a relatively large Δf_c, the oscillating cantilever tip must always be close to the sample surface where the force gradient is steep, meaning that the cantilever oscillation amplitude must be kept very small (<0.2 nm). Nevertheless, FM-mode AFM has recently been used also in aqueous solutions to obtain high-resolution images of biological samples⁷⁷⁻⁷⁹ under conditions where the oscillating tip makes contact with the sample. Liquid FM-AFM is, however, limited to samples with small surface roughness (<1 nm). Because of this limitation, the FM-mode is generally inappropriate for biological HS-AFM that is desired to be applicable to a wide range of samples.

In intermittent contact mode, also called tapping mode or amplitude modulation (AM) mode,⁸⁰ the cantilever is excited to oscillate at or near its first resonance frequency. The excitation frequency is fixed at a constant value. The oscillating tip interacts with the sample surface at its bottom swing (about 10% of the oscillation cycle), by which the oscillation amplitude is reduced. This amplitude reduction is not only due to energy dissipation. As will be described later, the cantilever resonance frequency shift (and hence a phase shift relative to the excitation signal) also results in amplitude reduction, depending on the excitation frequency used. During scanning, the oscillation amplitude A is kept constant at the amplitude set point A_s by feedback control. The cantilever deflection is measured typically by the optical beam deflection (OBD) system (see Figure 1). The laser beam reflected back by the cantilever is guided to the segmented (bicell or quadrant) photodiode sensor. The output signals from the photodiode sensor are conditioned to produce a differential signal (S₁ – S₂) or a normalized differential signal (S₁ – S₂)/(S₁ + S₂) corresponding to the cantilever deflection. Either one of these two signals is fed into the deflection-to-amplitude convertor, followed by subtraction of its output amplitude signal from a set point voltage corresponding to the set point amplitude. The resulting signal (i.e., feedback error) is fed into the proportional-integral-derivative (PID) feedback controller. The PID controller’s output signal is input to the Z-piezodriver for signal amplification to displace the Z-scanner so that the feedback error approaches zero. The output from the PID controller represents the sample height, because the Z-scanner movement driven by the amplified PID output signal traces the sample surface, although its movement is the inverse of the sample height. Therefore, the PID output signal is used to construct the sample topography in a computer. The signals for displacing the X- and Y-scanners, defining the scan area under investigation, are generated by the computer through a two-channel digital/analog (D/A) converter and fed into the respective piezodrivers.

3. Speed Limits of AFM Imaging

The input to the feedback loop is the change in sample height under the cantilever tip, which is caused by lateral scanning of the sample stage relative to the cantilever. The final output from the feedback loop is the displacement of the Z-scanner. If it was possible to keep the cantilever oscillation amplitude precisely constant at its set point value by feedback control, the sample surface would look perfectly flat when viewed from the cantilever. In reality, however, this is not the case because of an inevitable time delay in feedback control. Several electronic and physical devices are contained in the feedback loop, each of which responds to the corresponding input with a certain time delay, and, therefore, the Z-scanner cannot move “at the same time” as the change of sample height.

Here, we briefly discuss how the imaging speed limit of AFM is determined by the time delay τ₀ of the feedback loop.²⁷ For simplicity, the sample surface is assumed to have a sinusoidal shape with a periodicity λ in the X–Z plane (Figure 2a). This assumption is a justified generalization of the real situation because any sample surface can be expressed as a Fourier integral of sine and cosine functions. When the sample stage is scanned in the X-direction at velocity V_s, the sample height under the tip changes with time at frequency f = V_s/λ. Therefore, the Z-scanner is moved at the same frequency f in the direction opposite to the sample height, with a phase delay θ = 2πfτ₀ with respect to the change of the sample height under the tip during scanning (Figure 2a). Because of this feedback error, in the uphill region of the sample the cantilever oscillation amplitude A is smaller than A_s, whereas in the downhill region A is larger than A_s. Therefore, in the uphill region the tip is pushed more strongly into the sample than the set point force F_s, while in the downhill region the interaction force is smaller than F_s (Figure 2b). F_s is determined by A₀, A_s, k_c, and Q_c, and approximately expressed as⁸¹

2

where α (0 < α < 1) represents the ratio of amplitude reduction caused by the cantilever resonance frequency shift over the total amplitude reduction. As described in the next section, α is approximately 0.5 for short cantilevers optimized for HS-AFM. When the excessive force in the uphill region is too excessive, the biological sample is deformed and its biological activity is compromised or completely lost. When A_s is set closer to A₀ so that F_s becomes smaller, the tip–sample interaction force becomes zero in the downhill region (Figure 2c), meaning that the tip loses contact with the sample surface at its bottom swing, resulting in inability to acquire the sample height information. Once the contact is lost, the error signal (A – A_s) is saturated at a small value of (A₀ – A_s), irrespective of how far the tip is apart from the sample surface at its bottom swing. Therefore, once the contact is lost, it takes long to bring the tip back to sample interaction (i.e., “parachuting”). The maximum possible phase delay not causing parachuting is approximately 10 times smaller than the phase delay limit acceptable for not producing excessive force of disturbing protein functions in the uphill region.^27,72 Thus, maybe counterintuitively, tip parachuting is the major obstacle in simultaneously achieving both high-speed and low-invasive performances of AFM.

Figure 2.

Effects of feedback delay on the tip force exerted onto the sample. (a) Movement of Z-scanner (red line) tracing sinusoidally shaped sample surface (black line) with periodicity λ and amplitude h₀/2, when no parachuting occurs. Because of the delay of the Z-scanner movement, tracing error (blue line) is produced. (b) Tip force (blue line) exerted onto the sample when the set point force (black line) corresponding to the set point amplitude is relatively large. (c) Tip force (blue line) exerted onto the sample when the set point force (black line) is set at a small value.

This problem has been solved by a new feedback control technique called “dynamic PID control”, in which a false error signal proportional to the real error signal is automatically added to the real error signal when A exceeds A_s (i.e., when the downhill region of the sample is being scanned).⁸² This has proven efficient to bring the tip back into sample contact even at very high scan velocities. Therefore, to estimate the limits of speed and invasiveness, we focus on the effect of feedback phase delay on the sample damage. Denoting θ_max as the maximum allowable phase delay at which the sample is not affected by excessive force, the highest possible feedback frequency f_max is given by f_max = θ_max/(2πτ₀), and hence the highest possible scan velocity in the X-direction V_s^max is given by V_s^max = λθ_max/(2πτ₀). When the scan size in the X-direction is W and the number of scan lines is N, the highest possible imaging rate R_max frames/s (fps) is given by R_max = λθ_max/(4πNWτ₀). Instead of using τ₀, we can use a more practical parameter, the feedback bandwidth f_B at which π/4 phase delay occurs, that is, f_B = 1/(8τ₀). Thus, R_max is finally expressed as

3

f_B varies depending on the ratio between sample height h₀ and the cantilever free oscillation amplitude A₀ but is generally ∼100 kHz when proteins with height 1–5 nm are imaged, in our HS-AFM instrument.²³ According to our experiences of HS-AFM imaging of proteins, θ_max is approximately π/9.⁷² Therefore, under the conditions of N = 100, W = 150 nm, and λ = 10 nm, R_max is about 14.8 fps.

4. Minimizing Invasiveness: The Tip–Sample Interaction

For HS-AFM imaging, small cantilevers with high resonant frequencies in water f_c of 400 kHz to 1.2 MHz are used. Therefore, the sample is tapped many times by the oscillating cantilever tip during successive image acquisition. Here, we estimate the actual numbers of tapping for two cases. When an image of a sample area W_x × W_y nm² is captured at an imaging rate R fps, a molecule with a top surface area (A_top nm²) perpendicular to the tip is tapped f_c/R × A_top/(W_xW_y) times per frame. Under the conditions (f_c ≈ 1.2 MHz, R = 12.5 fps, and W_x × W_y = 45 × 22 nm²) used for the noninvasive imaging of the α₃β₃ subcomplex of the F₁-ATPase,⁵¹ one α₃β₃ subcomplex (A_top ∼100 nm²) is tapped approximately 9600 times per frame and ∼5 million times in total during the 40 s of successive imaging. Under the conditions (f_c ≈ 1.2 MHz, R = 7 fps, and W_x × W_y = 150 × 75 nm²) used for the noninvasive imaging of tail truncated myosin V moving on an actin filament,⁴⁷ one of the myosin’s two motor domains (A_top ∼25 nm²) is tapped with the tip ∼380 times per frame and ∼60 000 times in total during the 23 s movie acquisition time. The α₃β₃ subcomplex and the myosin V did not show any activity loss throughout the image acquisition periods. Thus, the energy transferred from the oscillating cantilever to the sample does not accumulate in the biological sample but dissipates quickly, within a time range much shorter than the oscillation period of the cantilever of ∼1 μs, into many degrees of freedom of many atoms including those of surrounding water molecules.

The other mechanical parameters of small cantilevers used in these imaging studies are k_c ≈ 0.2 N/m and Q_c ≈ 2 in water. The free oscillation amplitude A₀ and set point amplitude A_s were set approximately at 1 nm and 0.8–0.9 nm, respectively. Therefore, according to eq 2, the set point force F_s is approximately 30–42 pN. However, due to the phase delay in feedback control the actual applied force is higher; a maximum force as large as ∼80 pN must sometimes have been exerted during the scanning over the uphill regions of the samples. Why does this magnitude of force not disturb the function of these biomolecules? We should first note that the mechanical quantity that affects the sample (i.e., causes a change in momentum) is not the force but the impulsive force (i.e., the product of the force acting on the sample and the time during which this force is applied). The time during which the force acts is short (∼100 ns or less, i.e., ∼10% of the oscillation cycle of ∼1 μs) for small cantilevers with 1.2 MHz resonance frequency in water. Thus, the magnitude of the impulsive force is small, in the atto-Newton second range (∼5 × 10^–18 N s).

The low-invasiveness can also be considered in terms of energy. An oscillating cantilever loses part of its oscillation energy during every tap by (1 – α) × k_c(A₀² – A_s²)/(2Q_c) on average. For the same conditions as those detailed in the aforementioned imaging studies, this energy loss only amounts to 1.2–2.2 k_BT (when α = 0.5), where k_B is the Boltzmann constant and T is the temperature of 300 K in the experiments. Even when the oscillation energy is completely lost at once by the tip–sample interaction, it amounts only to 24 k_BT (when α = 0), comparable to the energy of ATP hydrolysis ∼20 k_BT. In actual imaging experiments, such events of complete oscillation energy loss happen only very rarely, if at all.

5. Small Cantilevers

For the above-mentioned imaging studies, custom-made small cantilevers (Olympus BL-AC7DS-KU5) have been used that are 6–7 μm long, 2 μm wide, and 90 nm thick (Figure 3a). They have a resonance frequency f_c ≈ 1.2 MHz in water (3.5 MHz in air), a quality factor Q_c ≈ 2 in water, and typical spring constant k_c ≈ 0.2 N/m. The commercially available small cantilevers are 9–10 μm long, 2 μm wide, and 130 nm thick, and have f_c ≈ 0.6 MHz in water (1.5 MHz in air), Q_c ≈ 2 in water, and k_c ≈ 0.1 N/m (Olympus BL-AC10DS-A2), or 6 μm long, 2 μm wide, and 200 nm thick, and have f_c ≈ 0.4 MHz in water (1.2 MHz in air), Q_c ≈ 2 in water, and k_c ≈ 0.15 N/m (NanoWorld UCS-1.2, Neuchâtel, Switzerland). Small cantilevers have advantages in addition to their fast response to tip–sample interaction. As indicated by eq 1, the cantilever resonance frequency is increased by repulsive tip–sample interaction, and this increase becomes greater with increasing ratio f_c/k_c. Small cantilevers designed for HS-AFM have large f_c/k_c ratios, approximately 1000 times larger as compared to conventional cantilevers. Therefore, with small cantilevers an increase of the resonance frequency results in a decrease (or increase) of the oscillation amplitude depending on the excitation frequency used f_ex, as shown in Figure 4. The resonance frequency increase also results in a phase advance relative to the excitation signal, as shown in the bottom of Figure 4. Roughly speaking, the amplitude decreases when the excitation frequency is lower than the free oscillation resonance frequency f_c, and vice versa. The most effective excitation frequency f_ex^m for gaining the largest amplitude decrease is approximately expressed as f_ex^m = f_c × (1 – 0.35/Q_c).⁸³ Thus, there are two types of amplitude decreases: one due to energy dissipation and another due to the resonance frequency change. These decreases are most effectively added when the excitation frequency f_ex^m is used, providing high sensitivity for tip–sample interaction detection. According to measurements with small cantilevers, the tip–sample contact induces phase advances by ∼11° under the practical conditions used for noninvasive imaging of proteins. From a numerical analysis, this amount of phase advance contributes to the measured amplitude decrease by approximately 50%, when f_ex is optimized at f_ex^m.

Figure 3.

Small cantilever. (a) Scanning electron microscopy (SEM) image of small cantilever. The inset shows an electron-beam-deposited (EBD) tip grown on an original bird-beak-shaped tip. (b) Magnified SEM image of EBD tip.

Figure 4.

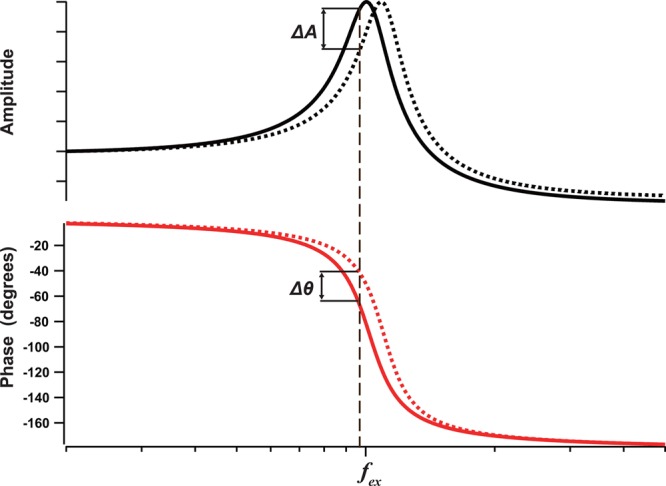
Amplitude and phase response curves of a cantilever as a function of excitation frequency when the cantilever is freely oscillating (solid line) and when the cantilever tip is influenced by negative force gradient (repulsive regime of tip–sample interaction) without energy dissipation (broken line). This interaction increases the cantilever’s resonant frequency. When the cantilever is excited at frequency f_ex, the resonant frequency shift results in amplitude reduction by ΔA and in phase advance by Δθ.

Another advantage of small cantilevers is the small thermal noise effect on amplitude detection. According to the equipartition theorem, the average cantilever deflection by thermal excitation is a function of only temperature T and the spring constant k_c:

4

where Δz is the cantilever deflection at the free end. The averaged thermal deflection amounts to 0.14–0.2 nm at 300 K for a cantilever with a spring constant k_c = 0.1–0.2 N/m. The average deflection values of 0.14–0.2 nm are comparable with the amplitude damping (A₀ – A_s) = 0.1–0.2 nm used for noninvasive imaging of proteins. However, the thermal noise density is distributed over a large frequency range from 0 to approximately 2f_c, that is, 0–2 MHz. Therefore, the thermal noise density is small for small cantilevers because f_c is high, as compared to conventional cantilevers where the total thermal noise density is accumulated within a narrow frequency range of about 0–30 kHz. In oscillating AM mode, the frequency region used for imaging is approximately the feedback frequency f centered on the resonance frequency f_c. Thus, a band-pass filter cleans the differential output signal of the segmented photodiode sensor by eliminating the thermal noise substantially. Thus, for a cantilever with a higher f_c, the thermal noise has less effect on the cantilever amplitude measurement.

The last advantage of small cantilevers is that they enhance the sensitivity of cantilever deflection detection by the OBD detection method. The deflection of a cantilever alters the angle of its free end (Δφ), which is detected by the OBD detector (see Figure 1). For a given displacement Δz of the cantilever free end in Z-direction, a shorter cantilever results in a larger angle change following Δφ = 3Δz/2L, and thus gives higher displacement detection sensitivity. Because of this high sensitivity and the strongly diminished thermal noise effect with short (6–10 μm) cantilevers, the displacement as small as ∼0.1 nm can be detected even with high bandwidth detection (a few MHz). This high detection sensitivity allows better force control and hence greatly contributes to the low-invasive performance of HS-AFM.

In AFM, the spatial resolution in the lateral direction depends largely on the cantilever tip apex radius. The tip apex radius of commercially available small cantilevers is not necessarily small enough to acquire high-resolution images. Now short cantilevers with sharp electron beam deposited (EBD) or carbon nanofiber tips are commercially available. They are however expensive and not of perfect reproducible quality. When a scanning electron microscope (SEM) and a plasma etcher are available, sharp EBD tips can be fabricated in the laboratory, and, moreover, used short cantilevers featuring EBD tips can be recycled many times, followed by cleaning in the plasma etcher. As a sublimate for growing EBD tips, phenol powder is used to control the chemistry of the deposit.⁷²

A small amount of the phenol powder is placed in a container with holes of ∼0.1 mm in diameter in the lid located inside the SEM chamber. Short cantilevers are placed on the lid, near the holes to favor deposition of decomposed phenol vapors onto the HS-AFM tip. A spot-mode electron beam is focused onto each original HS-AFM cantilever tip, which produces the growth of a stylus composed of amorphous carbon at a growth rate of ∼17 nm/s. The focused electron beam is irradiated onto the original tip for ∼1 min typically, which results in ∼1 μm length of an EBD tip with an apex radius of 15–25 nm, hence providing an excellent aspect ratio. The EBD tip can then be sharpened by argon or oxygen plasma etching, which reduces the apex radius to 4–5 nm (Figure 3b). In the best case, it can be reduced to <1 nm, although this occurs rarely, ∼10% of the etching procedures.⁷² The mechanical durability of this sharp tip is not superb but still good enough to perform several experiments. It is notable that the EBD tip can be completely removed by oxygen plasma etching over one day. Therefore, a small cantilever chip can be reused many times as long as the cantilever is intact and new EBD tips can be grown onto it and sharpened.

6. Hydrodynamic Pressure

In our HS-AFM instrument,²³ which is now commercially available (HS-AFM 1.0, RIBM, Tsukuba, Japan), the sample stage (and not the cantilever tip) is scanned in all three dimensions (lateral dimensions X, Y and vertical dimension Z), which simplifies the instrument structure and gives additional stability to the OBD detection. In HS-AFM imaging of proteins, the Z-scanner is displaced at 20–100 kHz. This high-frequency displacement produces and exerts high hydrodynamic pressure, particularly to the cantilever and its supporting base positioned near the sample stage surface.⁸⁴ Under such hydrodynamic pressure, the cantilever and the chip itself tend to move, often deteriorating the dynamic performance of the cantilever response to relevant tip–sample interactions.⁷² In the worst case, the cantilever response delay becomes longer than the minimized delay of the feedback loop, meaning that the hydrodynamic perturbation becomes a major limiting factor for HS-AFM operation. To minimize the hydrodynamic pressure, the dimensions of the sample stage must be designed as small as possible, 1–2 mm in diameter.^72,84,85 To further circumvent disturbance by hydrodynamic pressure, the lateral overlap between the sample stage and the cantilever chip must be minimized, meaning that only objects placed at the peripheral regions of the sample stage should be imaged.^72,85 Moreover, the cantilever tip (tip together with EBD tip) should be longer than 2.5 μm. When the tip is shorter than this value, the cantilever gets close to the sample surface in a distance range where the solution confined between them is significantly “squeezed” at the bottom of cantilever swing, resulting in oscillation damping as well as in a blunt change of the oscillation amplitude upon weak tip–sample interaction. This leads to a drastic deterioration of the cantilever deflection detection sensitivity during imaging.^72,85 Commercially available short cantilevers do not sufficiently consider the problem raised by hydrodynamic perturbation and the tip length is only ∼1 μm, highlighting the necessity for EBD tip growth in laboratories to achieve successful HS-AFM operation.

7. Substrate Surfaces

The choice of substrate surfaces on which samples are placed is a key to successful dynamic imaging by HS-AFM. Unlike single-molecule fluorescence microscopy, the surface roughness should be small enough to identify molecules of interest that have typically single nanometer dimensions, and in the most demanding cases the surface should be atomically flat. Moreover, because AFM can visualize the sample only from one direction perpendicular to the substrate surface, sample molecules sometimes have to be attached to the surface in a specific orientation so that their characteristic structural features and portions of interest of the molecules can be visualized. These requirements are common in both static and dynamic AFM imaging. However, in dynamic AFM imaging, sample molecules should not strongly interact with a surface so as to be kept functionally intact. Nevertheless, when the interaction is too weak, the molecules detach from the surface or move too fast along the surface to be clearly imaged with HS-AFM. When dynamic events of the interaction between two different species of molecules are to be imaged, selective immobilization is often required, meaning that only one species of molecules are immobilized onto the surface without loss of biological activity, while the other species of molecules should be free from the surface and interact only with the surface-immobilized partner. Thus, establishment of various substrate surface (as well as the sample) conditions is required depending not only on the properties of molecules to be imaged but also on the nature of the dynamic events to be studied.

Thus far, five types of surfaces have been used for HS-AFM imaging of biological molecules: (i) bare or chemically modified mica, (ii) supported lipid bilayers (SLBs) formed on mica, (iii) two-dimensional (2D) crystals of streptavidin grown on planar lipid bilayers containing biotin lipid,^33,37,86 (iv) highly oriented pyrolytic graphite (HOPG),^35,56 and (v) DNA origami tiles placed on mica surface.⁷¹ Native membranes are usually placed on bare mica surface, very similar to condition (ii). In a rare case, membrane samples are placed on a substrate surface with nanowells, so that narrow portions of the membranes are suspended.⁴⁰ Live cells are often attached to chemically modified mica surfaces.⁶⁷⁻⁷⁰ Characteristics and use of these surfaces are summarized in this section except for (iv) (briefly described in section 8.8.1) and (v) (described in detail in a complementary review article⁷¹). More details about imaging studies on surface conditions (i–iii) are also described elsewhere.^37,72,86,87

7.1. Mica Surfaces

The surface of freshly cleaved natural muscovite or synthetic fluorophlogopite mica has frequently been used for AFM imaging because it provides atomically flat surfaces over large areas. The mica surface is negatively charged in aqueous solution because K⁺ ions located between the cleaved layers are desorbed from the surface upon cleavage and contact with water. Therefore, the cleaved surface facilitates electrostatic adsorption of positively charged molecules. Monovalent cations (K⁺, Na⁺, and Li⁺) weaken the adsorption affinity for many proteins in the order K⁺ > Na⁺ > Li⁺. In analogy, strongly negatively charged molecules such as DNA can be adsorbed on bare mica surface through the addition of divalent cations including Mg²⁺, Ca²⁺, Ni²⁺, or Zn²⁺ in the buffer. Because electrostatic adsorption is nonspecific, proteins adsorbed on the bare mica surface cannot be expected to have specific orientations on the surface but some proteins do so. For example, GroEL, a barrel shaped molecule with a double-ring structure, tends to bind to the surface in the end-up orientation.^24,29 Probably such preferential adsorption orientation is due to specific uneven charge distribution on the surface of the biological molecule. The bare mica surface is particularly useful for fractionated native membranes or SLBs containing membrane proteins because a thin water layer (∼1 nm thick) separates the lower membrane surface from the mica surface,^88,89 sometimes resulting in no direct interaction of the proteins with the mica surface. In fact, as observed on bR in the purple membrane and outer membrane F (OmpF) in reconstituted membranes, molecules in the noncrystallized regions rapidly diffuse in such supported membranes.^34,58,61

The mica surface can be functionalized in several ways. The surface contains silanol Si–OH, which can react with organosilanes to form siloxane bonds Si–O–Si, and hence various functional groups can be introduced to the surface.⁹⁰ 3-Aminopropyltriethoxysilane (APTES) has frequently been used to graft NH₂ groups to the mica surface, affording a positively charged surface. However, caution has to be taken in the preparation because APTES contains three ethoxy groups and can therefore polymerize laterally and vertically in aqueous solution, often resulting in increased surface roughness. 1-(3-Aminopropyl)silatrane (APS) also can be used for the same purpose.^65,91 APS is less reactive than APTES and resistant to hydrolysis and polymerization at neutral pH, which guarantees smooth surfaces.⁸⁷ The NH₂-functionalized surfaces can be reacted with various chemicals for further functionalizations. For example, the reaction with the homobifunctional reagent glutaraldehyde can provide an amino-reactive surface, onto which proteins can be covalently immobilized, often in specific orientations. This strategy was used for HS-AFM observation of F₁-ATPase⁵¹ and isolated bR trimers,⁶¹ as described in sections 8.3 and 8.5.2, respectively.

7.2. Lipid Bilayer Surfaces

The surfaces of self-assembled monolayers (SAMs) and bilayers of lipids have been used as substrate surfaces not only for AFM imaging but also for various other purposes.⁹² The lipid SAMs have been prepared using the Langmuir–Blodgett method; a monomolecular layer of lipids is first formed on the water–air interface and then transferred to a solid substrate surface by pulling the surface out of the liquid phase. This method requires a special apparatus and skills. In comparison with this method, SLB artificial membranes on a solid surface can be prepared more easily and are more amenable for biological studies than lipid SAMs.^93,94 Deposition of small unilamellar vesicles (SUVs, or small liposomes) on the bare mica surface leads to the rupture of liposomes by electrostatic interactions with the surface, followed by fusion of the small SLB patches and resulting in the formation of a SLB with negligible surface roughness covering essentially the entire mica support. The surfaces of SLBs formed with lipids having electrically neutral zwitterionic polar head groups, such as phosphatidyl choline (PC) and phosphatidyl ethanolamine (PE), are known to be unfavorable for nonspecific binding of proteins.^95,96 Starting from a PC or PE SLB, various types of surfaces can be prepared by including different types of lipids in the electrically neutral SLB.^97,98 Therefore, the surface of SLBs can be used for electrostatic adsorption or specific immobilization of proteins.⁸⁶ Unlike the bare mica surface, the surface charge density and polarity can easily be controlled using the lipid bilayer strategy, facilitating the adjustment of its affinity for proteins. For example, lipids with the following charged head groups are available: negatively charged head groups phosphatidylserine (PS), phosphoric acid (PA), and phosphatidylglycerol (PG); positively charged head groups trimethylammoniumpropane (TAP) and ethylphosphatidylcholine (EPC). Importantly, various lipids having functional groups, such as biotin and Ni-nitrilotriacetic acid (NTA), at their polar heads are commercially available. They enable specific attachment of streptavidin- or His-tag-conjugated proteins to the surface of SLBs.⁸⁶ When streptavidin is immobilized on the biotinylated lipid bilayer, biotinylated proteins can further be immobilized on top of the streptavidin.

SLBs are highly fluid when lipids with unsaturated alkyl chains such as DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) are their main constituents. When protein molecules are bound with low surface density to the surface of such SLBs, they diffuse too fast to be imaged even with HS-AFM.⁸⁶ However, when the surface density of proteins is high enough for neighboring protein molecules to interact with each other, the molecular diffusion is significantly decreased. In some cases, proteins form 2D crystals.⁹⁹ When dense protein packing or 2D crystallization is achieved, only a specific protein surface is exposed, and hence high-resolution imaging is possible, as demonstrated with 2D crystals of streptavidin¹⁰⁰ and annexin V¹⁰¹ formed on the surfaces of fluid SLBs that contain biotinylated lipids or negatively charged lipids, respectively. When proteins bound to a SLB surface at low density are to be observed, lipids with saturated alkyl chains such as DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine) should be used as a main component of the SLB to attain low fluidity. For example, low fluidic SLBs with biotin lipid were used to immobilize partially biotinylated actin filaments in the HS-AFM imaging study of myosin V walking on the filaments.⁴⁷

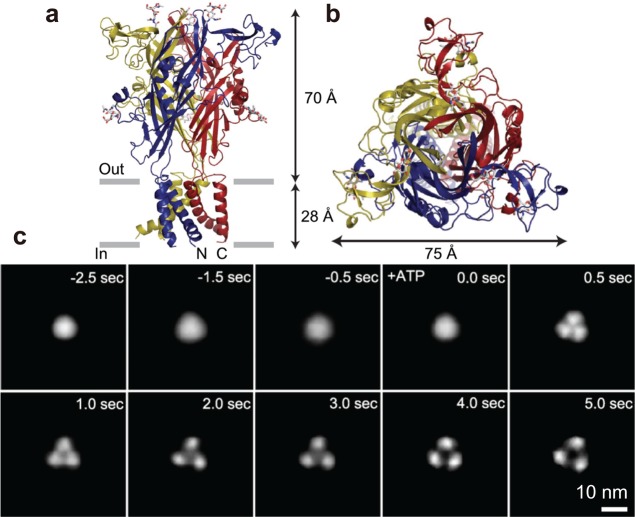
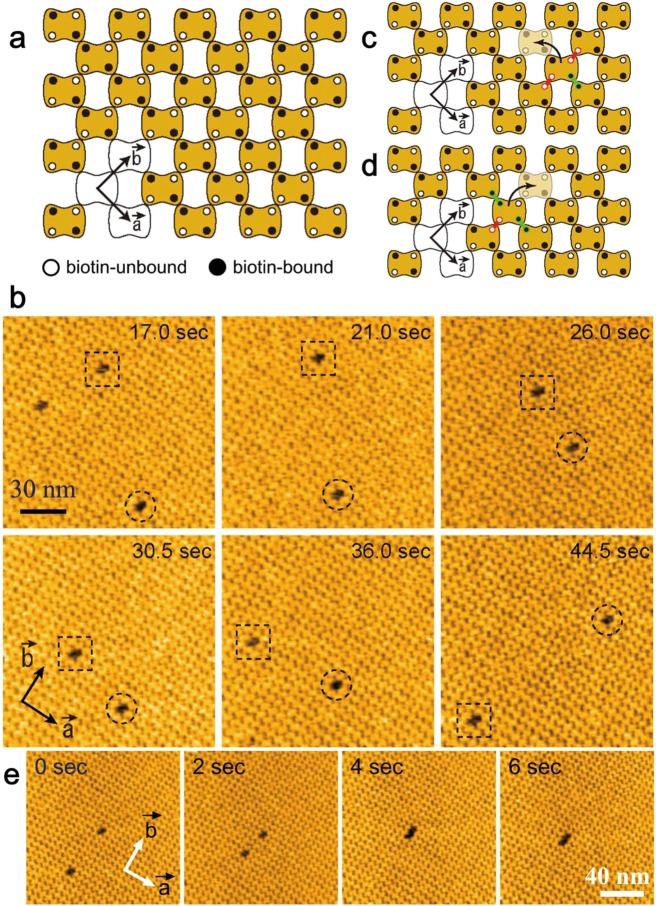
7.3. Surface of 2D Crystals of Streptavidin

Streptavidin is a homo tetramer with dihedral D2 symmetry (Figure 5a). Importantly, it is not favorable to nonspecific binding of many proteins, while each subunit has a high affinity biotin binding site. Streptavidin 2D crystals are easily formed on the surface of a fluid SLB containing biotin-lipid. These 2D crystals are monomolecular layers with surface roughness <0.2 nm (Figure 5b), given appropriate 2D crystallization conditions (pH and ionic strength) have been chosen.^37,86 On the SLBs, two of the four biotin binding sites of streptavidin face the lipid bilayer and are occupied by biotin, whereas the other two are exposed to the aqueous environment and accessible (Figure 5a). Therefore, biotinylated samples can be specifically immobilized on the surface of streptavidin 2D crystals.^37,86 This surface is particularly useful for selective immobilization of homooligomeric proteins such as actin filaments, GroEL, and ATPases associated with diverse activities (AAA) proteins because a stable pinning of the complexes at multiple biotinylated sites is possible. In fact, the 2D crystal surface has been used for HS-AFM imaging of actin polymerization processes at the plus and minus ends of an actin filament,³⁷ dynamic association and dissociation between GroEL and GroES,³⁷ Ca²⁺-induced conformational changes of calmodulin,³⁷ and ATP-invoked structural changes of an AAA ATPase, p97.¹⁰² For monomeric proteins, the tethering to the surface through a single biotin binding site is locally fixed but can result in a rotational motion around the link. This mobility can however be reduced using reactive dibiotin compounds. Moreover, His-tag-conjugated proteins can be specifically immobilized on the surface of streptavidin 2D crystals by the attachment of biotin-NTA to the surface.

Figure 5.

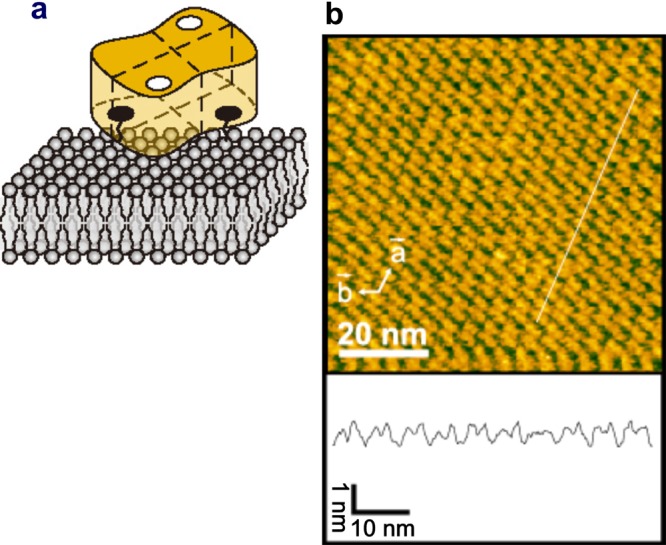
Streptavidin and its 2D crystal. (a) Schematic of streptavidin molecule placed on biotin lipid-containing lipid bilayer surface. ○, biotin-binding sites unoccupied with biotin; ●, biotin-binding sites occupied with biotin. (b) AFM image of streptavidin 2D crystal formed on biotin-containing SLB (top) and height profile along the white line shown in the AFM image (bottom).

8. Dynamic Imaging of Proteins

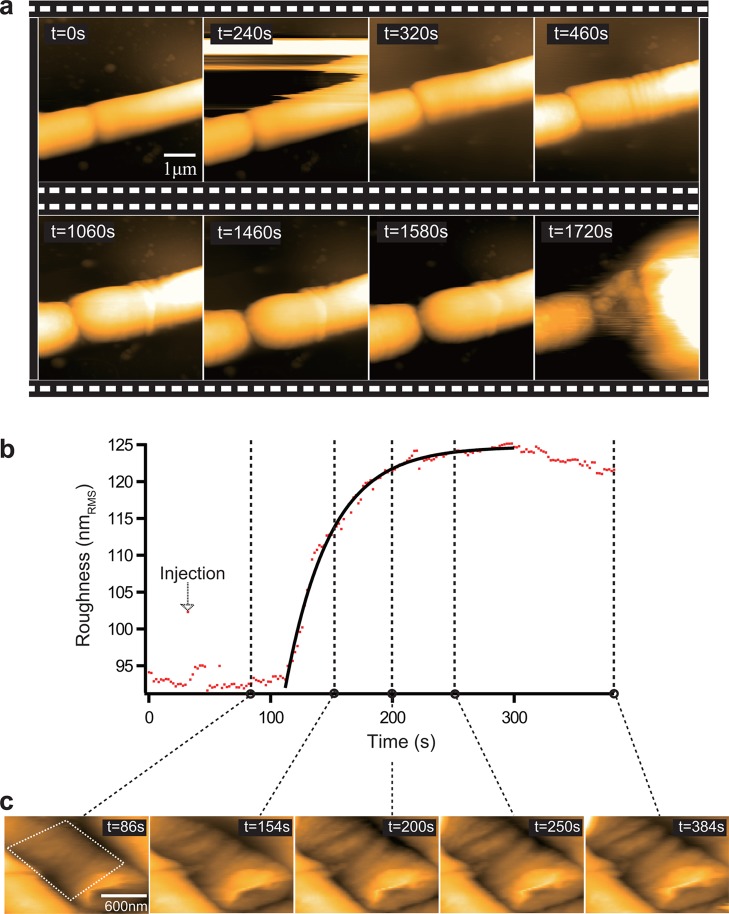
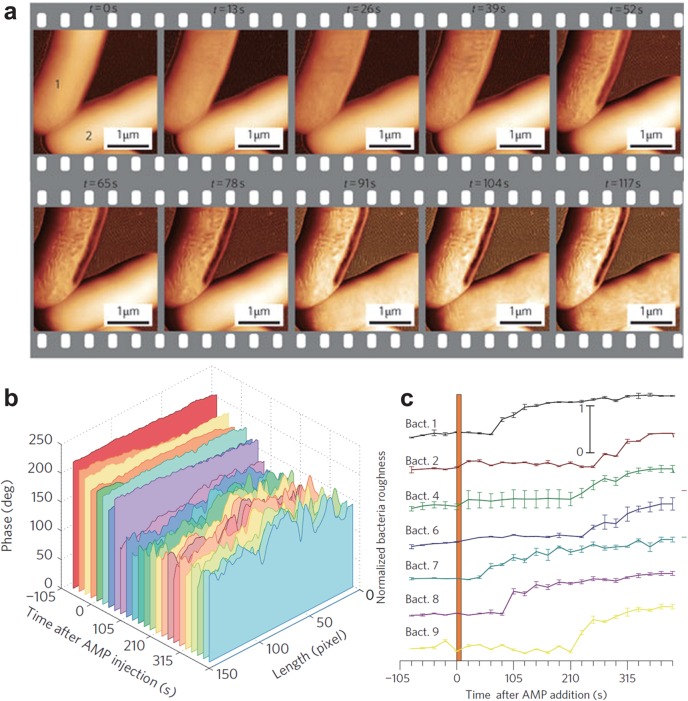
In this main section of this Review, we show various types of molecular imaging on proteins (and one case of lipids) by HS-AFM, which have been conducted in the past few years. The variety of studies could be classified in several ways: according to phenomena such as structural changes and diffusional processes or according to the nature of the proteins, soluble or membrane associated. Here, we have decided to discuss the HS-AFM achievements in topical groups of (i) motor proteins (myosin V and F₁-ATPase), (ii) structural changes of membrane proteins (bR, Ca²⁺-pump, P2X₄ receptor), (iii) diffusion and dynamic interaction of membrane proteins (bR, c-rings of ATP-synthase, aquaporin-0 (AQP0), and OmpF), (iv) self-assembly processes (amyloid-like fibril formation, 2D crystallization of annexin A5, SLB formation), and (v) other topics (cellulase enzymatic action, intrinsically disordered proteins, and diffusion of point vacancy defects in 2D protein crystals). These are described below in this order. Application studies on live cells, which have become possible only very recently thanks to the development of fast wide-area scanners and the integration of optical microscopy with HS-AFM, are shown in the following section. DNA and DNA–protein complexes are also important targets of HS-AFM. In fact, several HS-AFM studies have already been performed on these systems mainly by the Takeyasu, Lyubchenko, and Sugiyama groups.^{30,32,39,53,54,57,64−66,103} However, we do not describe these studies here as they are reviewed elsewhere.⁷¹ Movies of molecular actions captured by HS-AFM have corroborated several previous reports or reinforced speculated phenomena concerning the structure and dynamics of proteins. However, the dynamic molecular images have provided not only corroborative “direct visual evidence” for inferences but also solved long-standing questions that have previously been difficult or impossible to address by other approaches. Therefore, HS-AFM has successfully provided more and deeper insights into how the proteins operate to function. We emphasize this aspect in each application study described below, willing to attract broad interest of chemical biologists and biophysicists for the use of HS-AFM to unravel biological questions.

8.1. General Remarks on Dynamic Structural Study of Motor Proteins

Quite a while ago, myosin and dynein were the only proteins called motor proteins. These motors were shown to hydrolyze ATP to convert the chemical energy of ATP into mechanical work. During the ATPase cycle, myosin interacts with actin filaments to cause muscle contraction, while dynein interacts with microtubules to beat cilia and flagella. Along with the progress of cell biology and molecular biology, actin¹⁰⁴ and many classes of myosins were found in all eukaryotes and discovered to be responsible for several types of cellular motilities.¹⁰⁵ Kinesin was first described in the squid giant axon¹⁰⁶ and then in all eukaryotes as a motor responsible for cargo transport along microtubules and other mechanical functions. F₁-ATPase was found to be a rotary motor that links ATP generation or hydrolysis to the directional transmembrane passage of protons or ions.¹⁰⁷ Functionally diverse AAA (or AAA+) proteins were also found, which function by exerting force on substrate proteins or protein aggregates to degrade, translocate, or disaggregate them.¹⁰⁸ DNA-dependent ATPases such as condensin, cohesion, and helicases were found to mechanically act on DNA to transform its structure or assemblies. GTPases of the dynamin superfamily were also found to mechanically act on membranes to perform remodeling of their morphology.¹⁰⁹ Thus, the definition of motor proteins has now been remarkably extended. All proteins that perform mechanical work by hydrolyzing nucleotides or using electrochemical energy are considered to be motor proteins. During the chemical reaction cycle, they globally change their structure in a large extent as well as the mode of interaction with partner or substrate proteins, DNA, or subunits that they are constituted of. These dynamic changes produce mechanical actions, such as pushing, pulling, unwinding, winding, rotating, squeezing, transporting, and sliding. These mechanical actions in themselves are their biological function. Therefore, the direct visualization of these dynamic changes at the single molecular level is considered to show their functions themselves on screen. As such, these diverse motor proteins are excellent targets for HS-AFM analysis.

There are many ring-shaped motor proteins comprising multiple ATPase subunits, represented by F₁-ATPase, GroEL, and AAA proteins. The ATP-binding sites of these proteins are typically positioned at the interface between adjacent subunits, suggesting coupling of ATP binding and hydrolysis events with changes of intersubunit interactions followed by a synchronized global change in the ring structure; the chemical state of individual subunits would be influenced by the intersubunit interactions and vice versa. Therefore, the interplay between subunits is expected to elicit cooperative ATP binding and hydrolysis and possibly rotational propagation of the chemical and conformational states over the ring, which drive the mechanical actions tightly linked to the function of these proteins.^108,110 Detailed analysis of individual subunits and their structural changes by HS-AFM hence represents a powerful novel approach to unraveling expected but so far unstudied dynamic events. If an ATP analog visualizable even with AFM is available, HS-AFM should also be able to visualize the expected cooperative binding and hydrolysis of the ATP analog and concomitant structural changes at the subunit level. Once simultaneous detection by HS-AFM of the chemical and conformational states of an ATPase becomes possible, our understanding of the fundamental problem of biological energy transduction to mechanical work in ATPase motors will be greatly enhanced: How is the chemical energy liberated by ATP hydrolysis used to execute mechanical work? However, without this simultaneous detection, HS-AFM imaging of myosin V (M5), which will be described in detail below, has elucidated the essence of this fundamental problem with nearly ultimate clearness.

8.2. Myosin V Walking on Actin Filament

The double-headed motor protein, M5 (Figure 6a,b), is a member of the myosin superfamily and functions as a cargo transporter in cells (see review¹¹¹). Each “head” contains an N-terminal motor domain and a long neck domain consisting of six IQ motifs, to each of which calmodulin is attached (in some cases a calmodulin-like light chain). After the neck region, M5 is dimerized by a coiled-coil tail, which is followed by a C-terminal globular tail domain able to bind to various cargos via adapter proteins. Unlike muscle myosin (i.e., myosin II), M5 does not self-assemble into oligomers but operates as a single molecule. Remarkably, M5 moves highly processively on actin filaments over long distances,^112,113 facilitating the observation of individual M5 molecules at work. M5 movement and motor mechanism have extensively been studied by single-molecule fluorescence microscopy and optical-trap nanometry. Using these technologies, it has been shown that M5 moves along actin filaments toward the plus end¹¹² in a “hand-over-hand” manner,^114,115 advancing 36 nm^112,116 per ATP hydrolysis cycle.¹¹⁷ The 36 nm stride corresponds to a half pitch of the right-handed, double-helical structure of an actin filament, and, therefore, M5 moves approximately on a plane (only slightly biased for a left-handed spiral).¹¹⁸ “Hand-over-hand” means that the two heads step alternately, exchanging leading and trailing roles with each step, very much like “bi-pedal walking”. In addition, the mechanism underlying the alternate steps was suggested to arise from asymmetric kinetics of ADP dissociation from the two heads; ADP dissociation at the trailing head is more accelerated than at the leading head¹¹⁹ and/or ADP dissociation at the leading head is decelerated.^{117,119−121} However, despite numerous and extensive studies, the heart of the motor mechanism, that is, how the tension for the forward step is generated in the molecule, coupled with the ATPase reaction, and how the energy liberated by ATP hydrolysis is used, has remained elusive. These central questions were previously studied to a great extent on muscle myosin mostly by ensemble-averaging techniques (see reviews^122,123) and considered to have reached a consensus to some extent (although direct and irrefutable evidence has been lacking). The chemo-mechanical coupling and nature of the chemical energy usage in M5 has been considered to be the same as (or very similar to) that in muscle myosin (see reviews^124,125). Yet, actual attempts to examine these central issues have not been carried out until the recent HS-AFM study on M5.⁴⁷ Before describing this HS-AFM study in detail, the prevailing view of the chemo-mechanical coupling in an ATP hydrolysis cycle in myosin is summarized below.

Figure 6.

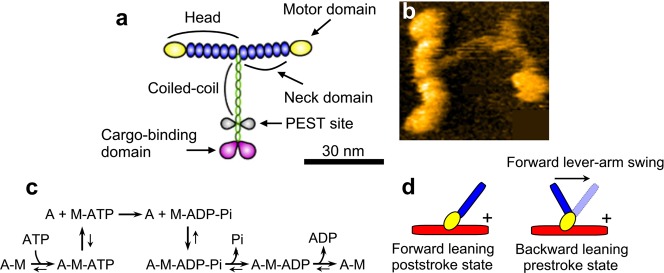
Structure of myosin V, actomyosin ATPase reaction scheme, and prevailing view on conformational states of myosin. (a) Schematic of molecular structure of myosin V. (b) AFM image of myosin V. (c) Reaction scheme of actomyosin ATPase. (d) Schematic for backward leaning prestroke and forward leaning poststroke conformations. The mark “+” indicates the plus end of an actin filament (red). The motor domain (yellow) binds to an actin filament in the same orientation, in both conformational states, while the neck (blue) is leaned in different directions. The forward lever-arm swing is supposed to occur on the actin-bound head when Pi is released from myosin. The backward lever-arm swing is supposed to occur on the detached head when ATP is hydrolyzed to ADP–Pi.

The simplest scheme of the actomyosin ATPase cycle is shown in Figure 6c. The nucleotide-free head tightly bound to actin detaches from the actin immediately after binding to ATP, quickly followed by hydrolysis of the bound ATP to ADP–Pi. When the ADP–Pi bound head is attached to actin, the bound Pi dissociates from the head, which is followed by the formation of a strongly bound tertiary complex A–M–ADP (A and M denote actin and myosin, respectively) and then by ADP dissociation, completing one ATPase cycle. The main role of actin in the ATPase reaction is to accelerate the otherwise very slow Pi and ADP dissociation from a myosin head. The degree of acceleration for Pi and ADP dissociation varies among the classes of myosin. The processivity and nonprocessivity are determined, respectively, by whether or not the lifetime of the strongly bound A–M–ADP is predominant over the other states (except for the A–M state waiting for ATP binding).¹²⁶ That is, in nonprocessive myosins, Pi-release is the rate-limiting step, while in processive myosins, ADP-release is rate-limiting.¹²⁶

The key idea in the prevailing view on the chemo-mechanical coupling in myosin motility, which has been mainly derived from muscle myosin studies, is that the myosin head is supposed to take two different conformations, prestroke and poststroke conformations corresponding to different angles between the motor domain and the neck domain (often called “lever-arm”), depending on the nucleotide states (Figure 6d); the head assumes the prestroke conformation in the ADP–Pi bound state, while it assumes the poststroke conformation in the ADP-bound state as well as in the ATP-bound state. As such, the detached ATP-bound head swings back the lever-arm upon ATP hydrolysis (i.e., ATP→ADP–Pi), while upon the chemical transition from ADP–Pi to ADP, the actin-bound head is supposed to swing the lever-arm (around the neck–motor domain junction) from the backward leaning orientation to the forward leaning orientation, resulting in exertion of sliding force to the bound actin filament in the backward direction (Figure 6d).^122−125 The angle between the motor and neck domains that is taken by the prestroke conformation facilitates the binding of the ADP–Pi-bound head to actin in the backward leaning orientation and at the same time impedes its binding to actin in the forward leaning orientation. The A–M–ADP–Pi state with the prestroke conformation is considered to be a higher-energy state; that is, the energy liberated by ATP hydrolysis is stored in the myosin head. Upon Pi release, the myosin head is supposed to use the stored energy by swinging the lever-arm forward to execute a powerstroke, after which a lower-energy state of A–M–ADP is supposed to be formed. For processive myosins, this scheme has to be modified because there is a large chance that both heads are attached to actin. After Pi release, the leading head cannot swing the lever-arm that is pulled back by the actin-bound trailing head. In this two-headed bound state where both heads are bound to ADP, intramolecular tension is generated. As such, the energy liberated by ATP hydrolysis is considered to be stored in the tension-generating state and eventually used for lever-arm swing at the leading head that takes place following trailing head detachment from actin. Direct HS-AFM imaging of processive M5 has considerably shaken this concept, as detailed below.

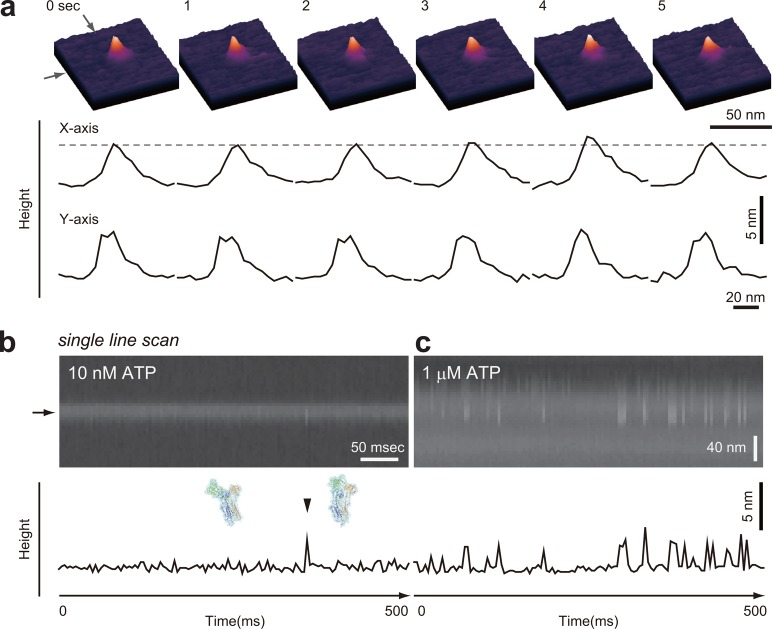
8.2.1. Visualization of Lever-Arm Swing

The lever-arm swing as powerstroke in muscle myosin was proposed by Huxley in 1969.¹²⁷ Since then, numerous studies were performed to obtain evidence for this hypothesis, not only for muscle myosin but also for M5. Nevertheless, even with the use of single-molecule techniques, no unambiguous experimental evidence for this mode of action was attained. Instead, other models were proposed, which brought long lasting debate and confusion^128,129 (although at a higher level) in the fields of muscle contraction and myosin motor action in general. The confusion was gradually cleared up with time, but the swinging lever-arm hypothesis has remained a proposal lacking solid data as it was before, until its visualization by HS-AFM.⁴⁷ This example of the long lasting divergence of myosin functional hypotheses clearly indicates a general difficulty of obtaining clinching evidence for dynamic actions of proteins even with the use of well-disseminated single-molecule techniques. In other words, the degree of directness of measurement was not yet high enough. Therefore, M5 lever arm motion was naturally chosen as a paradigm target to illustrate the power of HS-AFM in providing unambiguous direct data of complex molecular processes.⁴⁷

To visualize moving M5 molecules on actin filaments, actin filaments had to be immobilized on a surface, whereas M5 molecules had to be free enough from the surface to interact with the immobilized actin filaments. To this end, the surface of an SLB containing DPPC and biotin-cap-DPPE in a weight ratio of 9:1 was first used as a substrate surface. Partially biotinylated actin filaments were immobilized on the surface through streptavidin that were attached beforehand to the SLB with a low surface density. The tail-truncated M5 (M5-HMM) was not found to adhere to this surface but only interacted with the actin filaments, on which it moved unidirectionally. In various concentrations of ATP, M5-HMM moved with velocities V that followed a modified Michaelis–Menten relationship as a function of ATP concentration:

5

where d_s is the step size, k₁ is the second-order ATP binding rate constant, and k₂ is the first-order ADP dissociation rate constant. This relationship holds because ADP release is the major rate-limiting step,¹²⁶ ATP binding is also a rate-limiting step at low ATP concentrations (other chemical steps occur much faster), and each discrete translocation step is tightly coupled to one ATP hydrolysis.¹¹⁷ The observed step size was d_s = 37.2 ± 12.5 nm, irrespective of the ATP concentrations. The estimated values of the maximum velocity V_max (≡k₂d_s) = 403 ± 7 nm s^–1, K_m for ATP (≡k₂/k₁) = 5.4 ± 0.5 μM, k₁ = 2.0 ± 0.9 μM^–1 s^–1, and k₂ = 10.8 ± 3.8 s^–1 were identical to those measured by total internal reflection fluorescence microscopy (TIRFM) under the same buffer and temperature conditions,^115,130 indicating no effects of the tip–sample and surface–sample interactions on motor activity. However, as shown in Figure 7a, most of the molecules moved perpendicularly to the substrate surface, so that their characteristic structure was not well resolved.

Figure 7.

Tail-truncated myosin V (M5-HMM) movement on actin filament captured by HS-AFM. All of the images were taken at a frame rate of 7 fps. (a) Successive AFM images showing processive movement of M5-HMM in 1 μM ATP when positively charged lipid is absent in the planar lipid bilayer (PLB) surface. The arrowhead indicates one of the streptavidin molecules attached to the PLB surface. (b) Successive AFM images showing processive movement of M5-HMM in 1 μM ATP when positively charged lipid is present in the PLB. The arrows indicate the coiled-coil tail pointing to the minus end of actin. The arrowhead indicates one of the streptavidin molecules attached to the PLB surface. (c) Clips of successive images showing long processive run of M5-HMM in 1 μM ATP (14 steps are recorded). (d) Schematic explaining structural features of two-headed bound M5-HMM observed in the presence of nucleotides. (e) Successive AFM images showing stepping process in 1 μM ATP. The swinging lever is highlighted with a thin white line.

To facilitate weak sideways attraction of M5-HMM onto the SLB surface, 5% of a positively charged lipid DPTAP (1,2-dipalmitoyl-3-trimethylammonium-propan) was added to the SLB. Although the maximum translocation velocity was reduced by the addition of DPTAP to 73% of the full velocity observed without DPTAP, characteristic moving M5-HMM could clearly be visualized in a sideways view, as shown in Figure 7b. This reduction of velocity was mainly caused by the apparent reduction of the second-order ATP binding rate constant. The scan size was set to a small range (typically to about 130 × 65 nm²) to achieve a relatively high imaging rate (7 fps) and a minimum mechanical load to M5-HMM molecules. However, processive runs (4–16 steps corresponding to 144–576 nm translocation) in 0.1–2 μM ATP were observed, during which the moving molecules were tracked by manual shift of the narrow scan area (Figure 7c). The occasional failure of continual tracking occurred when the target molecule collided with another M5 ahead on the actin filament, when a portion of discontinuous substrate surface was encountered, or when the manual tracking was not appropriately performed. The sideways HS-AFM imaging of two-headed bound M5-HMM consistently exhibited the following structural features. The neck–motor domain junction appears smooth in the leading head but is V-shaped in the trailing head without exception (Figure 7d). The short coiled-coil tail is mostly tilted toward the minus end of the actin filament (Figure 7b, arrows). These features are consistent with electron microscopy observations¹³¹ and could be used to determine the actin polarity when bound M5-HMM was stationary.

Despite the successful visualization of moving M5-HMM molecules, no detailed molecular behavior during a step could be resolved because single steps were completed faster than the acquisition time of an individual frame (1/7 s). To slow the step movement of M5, additional streptavidin molecules were placed on the substrate surface (the biotinylated SLB) as moderate obstacles to the walking of M5-HMM. This method allowed the visualization of stepping processes as shown in Figure 7e. After trailing head detachment, the leading head appeared to spontaneously rotate from the backward leaning orientation toward the forward leaning orientation. Before completing this rotation, the leading head briefly halted by colliding with a streptavidin molecule placed in the way of its natural path, and the detached trailing head could be visualized in a conformation far away from the actin filament and slightly rotated around the neck–neck junction. The leading head then overcame the streptavidin blockade and completely rotated to the forward leaning orientation. Accompanied by this further rotation, the trailing head attached to a forward site of the actin filament to become the new leading head, completing one step. Thus, dynamic processes in the forward step were directly visualized at high spatial resolution. The observed rotation of the leading head corresponds to the swinging lever-arm motion to propel the molecule forward.¹²⁷ Hence, by direct imaging, HS-AFM could provide irrefutable evidence for the Huxley’s hypothesis. It is noteworthy that before completing a step the detached trailing head never interacted with actin and hence passively moved forward, driven by the rotating leading head, ruling out some models that had suggested myosin motility to occur in the “inchworm” like model considered for kinesin¹³² or in the “biased diffusion” model proposed for single-headed myosin II and for single-headed myosin V,¹³³ in which the trailing head was considered to slide on the actin filament to get close to and pass beyond the leading head.

8.2.2. Directional Rule

After the imaging of many unidirectionally moving M5-HMM molecules, a “directional rule” was noticed regarding the relationship between the moving direction and the direction from which M5-HMM was bound to an actin filament. M5-HMM molecules that were moving from left to right were bound to actin filaments from top, while those moving from right to left were bound to actin from bottom as shown in Figure 8a. This rule was unrelated to the previously observed tendency of moderate left-handed spiral motion of walking M5 around a freely suspended actin filament,¹¹⁸ because this directional rule held even in the absence of ATP, where the actin polarity could be judged from the above-mentioned structural features of two-head bound M5-HMM. The directional rule suggested a geometry-specific positioning of the motor domain on the actin filaments. As seen in AFM images of two-headed bound M5-HMM (e.g., Figure 8a), the motor domain looked brighter than actin, meaning that the bound motor domain is taller than the top surface of the actin filament. Hence, as shown in Figure 8b, the directional rule indicated that the motor domains are bound to actin at their left flank, provided that the M5-HMM molecule faces the advancing direction. If an actin filament was rotated about its long axis on the substrate surface, the outer surface of the motor domains would hit the substrate surface at some angle, as shown in Figure 8c. Thus, the directional rule originates from the steric hindrance effect of the surface, which is reinforced by a weak attractive surface–sample interaction. An important conclusion derived here is as follows: when M5 stands on an actin filament and faces the advancing direction, the motor domains do not grasp the top surface of the actin filament but grasp the right flank of the filament, as shown in Figure 8b. Although not explicitly described before in electron microscopy 3D reconstruction studies of the actin-bound M5 head, this conclusion is consistent with the 3D structure of the binary complex.¹³⁴

Figure 8.

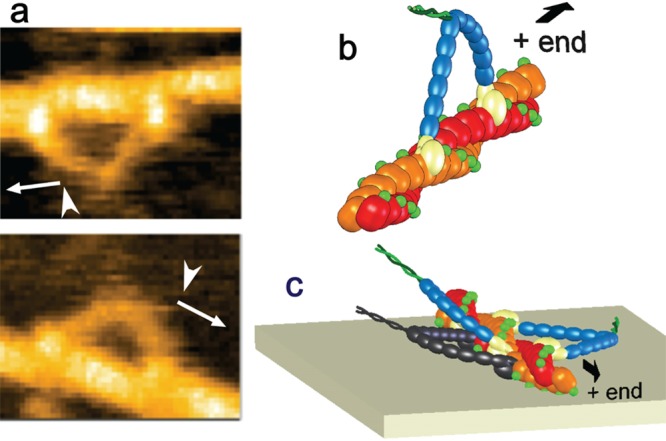
Directional rule and its mechanism. (a) Typical HS-AFM images of two-headed M5-HMM showing the directional rule; there is a fixed relationship between the moving direction (arrows) and the direction (arrowheads) from which M5-HMM bind to an actin filament. (b) Schematic showing M5-HMM bound to actin at the left flanks of the motor domains. (c) Schematic showing the reason for the directional rule. In the M5-HMM shown in black, which does not follow the directional rule, the motor domains have to get into the narrow space between the actin filament and the substrate surface, which hardly occurs.

8.2.3. Foot Stomp and Tension Generation

Interestingly, while M5-HMM was in the two-headed bound state in ATP containing buffer, the motor domain of the leading head frequently exhibited brief dissociation and reassociation on the same actin filament, whereas the molecule remained at approximately the same position on the filament, as shown in Figure 9a. Similarly, it was observed that the motor domain of the trailing head exhibited a brief translocation approximately by ±5 nm along the actin filament. These behaviors were termed “foot stomp”. The foot stomp of the leading head was observed about 3 times more often than stomping of the trailing head. Although not well documented, a foot-stomp-like behavior was previously suggested by fluorescence microscopy observations of walking M5 molecules.¹³⁵ More recently, the foot stomp was further confirmed by the observation of walking M5 by high-speed single-molecule polarized fluorescence microscopy.¹³⁶ Thus, the foot stomp is an inherent behavior of M5.

Figure 9.

M5-HMM’s foot stomping at the leading head, unfolding of coiled-coil tail, and conformational transition of the leading head captured by HS-AFM. (a) Successive AFM images showing foot stomp at the leading head in the presence of 1 μM ATP. As pointed by the arrowheads, the leading head are briefly detached from actin. Because the detached head is moving fast, it does not appear in the images. Frame rate, 7 fps. (b) Unfolding of the coiled-coil tail of two-headed bound M5-HMM. Left images, before unfolding; right images, after unfolding. (c) HS-AFM images showing conformational transition between straight and bent conformations of the leading head in the presence of 0.1 μM ADP. The symbol “+” indicates the plus ends of actin filaments (b, c).

The foot stomp at the leading head raised an important question as to the chemo-mechanical coupling in this motor. The briefly detached leading head does not carry bound Pi because Pi has already been released from the ADP–Pi-bound head since initial attachment of the head to actin. It is well-known that Pi release occurs immediately after the binding of an ADP–Pi-bound head to actin.¹²⁶ Nevertheless, the detached only ADP-bound leading head rebound to actin still in the backward leaning orientation, and then swung the lever-arm forward following trailing head detachment, like in a normal step process. This indicated that tension generation for forward movement can occur without transitioning through the ADP–Pi bound state, but directly in the ADP-bound state. Thus, as a major surprise, the tension generation for forward movement does not seem to require chemical energy be supplied by ATP hydrolysis.

This external energy-less tension generation was further confirmed by the HS-AFM observation of two-headed bound M5-HMM in the presence of ADP; sometimes the short coiled-coil tail unwound, after which the monomerized leading head immediately rotated toward the forward leaning orientation, similar to the swinging lever-arm motion (Figure 9b). The coiled-coil region unwinding suggested again that the distortion of the actin-bound leading head, which is caused just by binding to actin without any chemical transition, is the source of the intramolecular tension generation for forward movement.

From these HS-AFM observations, the following scenario was drawn as to the tension generation and the lever-arm swing to propel the molecule forward. In the two-headed bound state, the trailing head is in the forward leaning orientation, which is natural at least for the ADP-bound or nucleotide-free head. On the other hand, the leading head is not in the natural orientation (i.e., it is in the backward leaning orientation) and therefore pays an energy cost that generates the intramolecular tension. The energy cost is not supplied by the ATPase reaction. Upon trailing head detachment, the constraint keeping the bound leading head in the unnatural orientation is released, and hence the leading head spontaneously rotates forward. This scenario is not consistent with the commonly accepted view of chemo-mechanical coupling in myosin motors detailed above. According to this formerly prevailing view, the leading head of M5-HMM, in the first place, would not bind to actin without going through the M–ADP–Pi state, and in the second place, tension would not be generated without transitioning from A–M–ADP–Pi to A–M–ADP; the transition has been supposed to be an important step in which the chemical-to-mechanical energy transduction occurs. Before discussion of how the prevailing view has to be changed based on HS-AFM observations (section 8.2.5), more details of the foot stomp are described below.

The foot stomp was observed not only in the presence of ATP but also in the presence of ADP only and under nucleotide-free condition, always with higher frequencies at the leading head. In ADP and under nucleotide-free condition, detachment of the trailing head, which was followed by a forward step, was only rarely observed; that is, the foot stomp at the trailing head mostly occurred as brief translocation along the actin filament. The higher frequency of foot stomp at the leading head in any nucleotide condition implied that the leading head’s affinity for actin is lower than the trailing head’s affinity. This is consistent with the fact that when binding to actin, the leading head has to pay an energetic cost by generating intramolecular tension. Interestingly, the foot stomp was frequently accompanied by a change in the head separation (the distance between the attached motor domains). The direction of the change was well correlated with the head separation before the foot stomp, as shown in Figure 10a (for foot stomp at the leading head in 1 μM ATP) and Figure 10b (for foot stomp at the trailing head in 1 μM ATP). That is, a shorter head separation before foot stomp tended to result in a longer one after foot stomp, and vice versa. Histograms of the displacement accompanied by a foot stomp had three peaks separated by ∼5 nm, which was approximately the distance between adjacent actin monomers in one strand of an actin filament (righthand panels in Figure 10a and b). Very similar relationships were also observed in the presence of ADP and under nucleotide-free condition. These results indicated that both heads have a propensity of searching for the energetically favorable binding sites on an actin filament, but the leading head does that more often because its binding affinity is diminished due to the molecular stress (enabling the next forward step) that it features.

Figure 10.

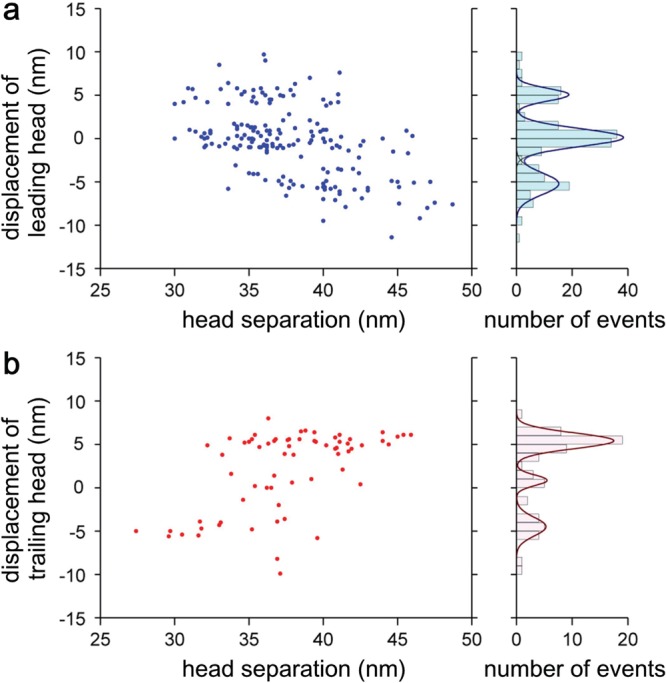
Displacement of motor domain of leading (a) and trailing (b) heads after foot stomping as a function of head separation before the foot stomping. Each right-hand figure shows the histogram of displacement.

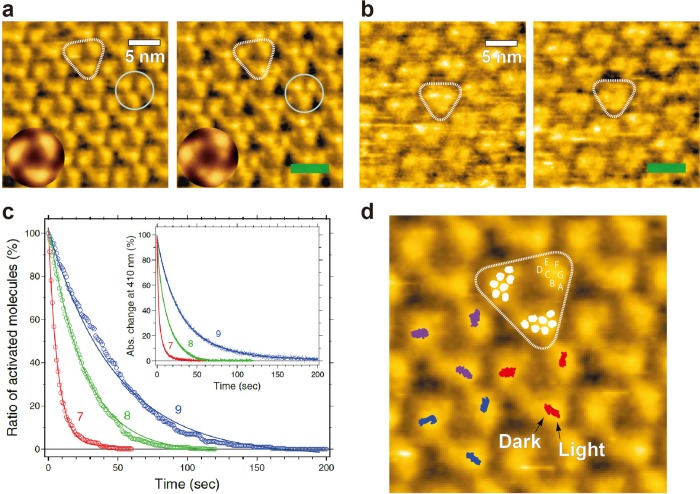
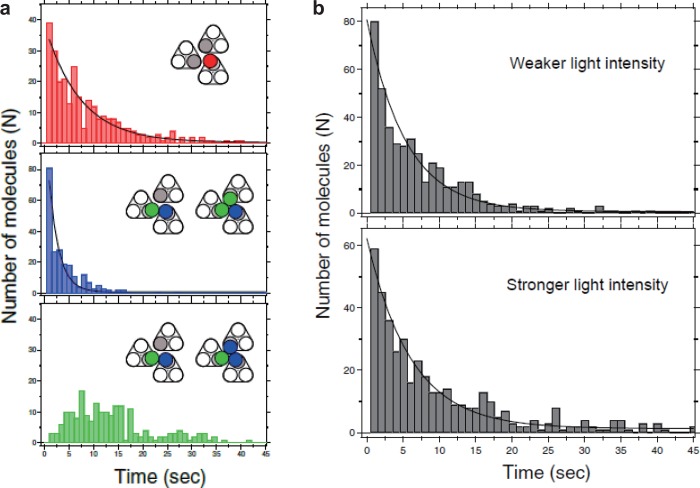
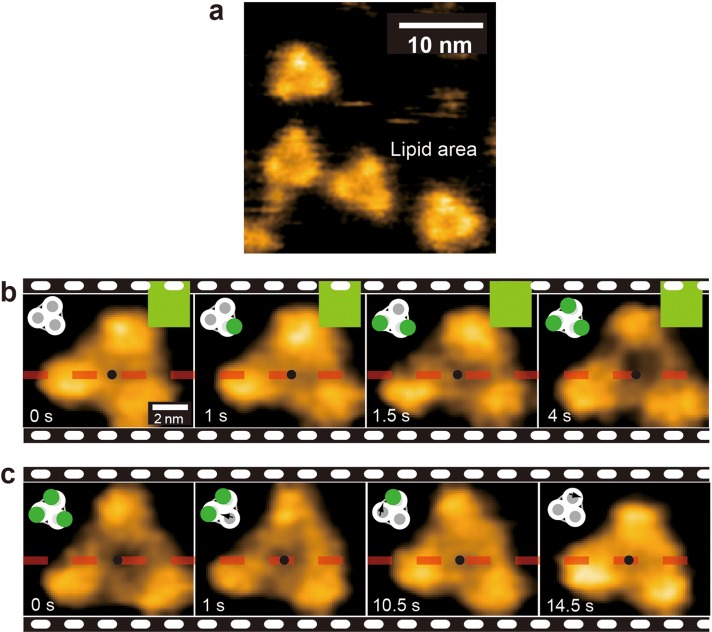
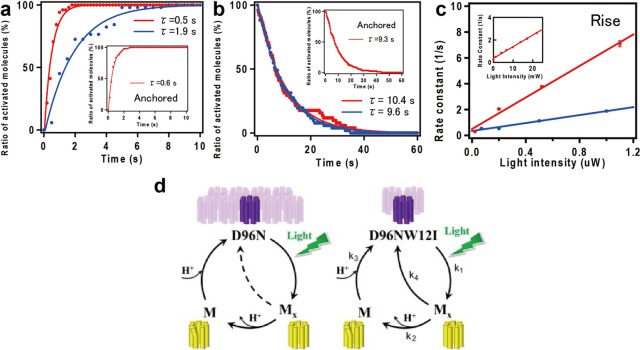
8.2.4. Asymmetric ADP Dissociation Kinetics

Even under the nucleotide-free condition, both heads of M5-HMM were bound to the same actin filament. However, unlike in the presence of nucleotides, where the leading head almost always (>95%) took a nearly straight conformation (slightly curved outward), the leading head often exhibited a sharply kinked conformation and alternated back and forth between this conformation and the nearly straight conformation (Figure 9c), indicating that these conformations are in equilibrium. The hinge portion on the neck where the kink occurs was very close to the motor domain. Although the structure was not well resolved in the AFM image, the kink appeared to occur at the neck–motor domain junction, as suggested by electron micrographs.¹³⁷ In the sharply kinked conformation, both heads had the forward leaning orientation around the motor domain, and thus both necks appeared to emerge from the front of the respective motor domains. The sharp kink is likely to occur to release the large strain accumulated in the neck, suggesting that the neck–motor domain junction is stiffer in the absence of nucleotides than that of the nucleotide-bound head.

To examine the nucleotide-dependent flexibility of the neck–motor junction, the distribution of forward leaning orientation of single-headed M5 (Figure 11a) was compared between the nucleotide-free and ADP-bound conditions. Under nucleotide-free conditions (Figure 11b,c), the orientation angle relative to the long axis of the actin filament was 34 ± 10°. In ADP (Figure 11d,e), however, the angle distribution was wider with two peaks at 29 ± 11° and 51 ± 15°, which may be relevant to two different ADP-bound states in equilibrium.¹²² Therefore, the hinge around the neck–motor domain junction of the ADP-bound head is more flexible than that of the nucleotide-free head. This result may be related to the angle distributions measured by electron spin resonance for a spin probe introduced to the regulatory light chain of myosin in rigor and contracting muscle fibers.¹³⁸

Figure 11.

Angle distributions of actin-bound single-headed M5. The single-headed M5 is formed by natural uncoiling of the short tail of two-head bound M5-HMM. (a) Schematic showing the angle measured. (b,d) HS-AFM images of bound single-headed M5 under the nucleotide-free condition (b) and in 1 mM ADP (d). The plus ends of actin filaments, which are judged from the directional rule shown in Figure 8, are indicated with “+”. The measured angles are shown in the images. Imaging rate, 3 fps. Scale bar, 30 nm. (c,e) Histograms of the angle measured for bound single-headed M5 under nucleotide-free condition (c) and in 1 mM ADP (e). The red curves represent the results of the best fit to the sum of two Gaussian distributions.

The sharply kinked conformation that was often adopted by the leading head under the nucleotide-free condition could provide a useful indicator of whether or not the leading head contained a nucleotide. Even in the presence of 0.1 μM ATP, the leading head neck was mostly straight (>98%), suggesting that the leading head almost always retains ADP until the trailing head binds to ATP and then detaches from actin. In the presence of low concentrations of ADP, the leading head exhibited alternate switching between the straight and sharply kinked conformations. From the proportion (Figure 12a) and the lifetime (Figure 12b) of the straight leading head as a function of ADP concentration, the kinetic parameters for ADP binding/dissociation on the leading head were estimated: the ADP dissociation constant, K_d = k₂/k₁ = 0.075 ± 0.013 μM; the ADP dissociation rate constant, k₂ = 0.100 ± 0.004 s^–1; the second-order ADP binding rate constant, k₁ = 1.3 ± 0.3 μM^–1 s^–1. The value of k₂ is 70 times smaller than the corresponding rate for the trailing head estimated above from the dependence of the translocation velocity on the ATP concentration (k₂ = 7.2 ± 1.5 s^–1). This degree of asymmetry between the two heads is similar to that previously reported.¹²⁰ The value of k₁ is 10 times smaller than the corresponding value, 12.6 μM^–1 s^–1, previously measured in a solution study on single-headed M5.¹²⁶ The ADP dissociation rate constant of 0.1 s^–1 means that, on average, one ADP is released from the leading head every 10 s. However, M5-HMM walks many steps during 10 s. Thus, the sequential events of ADP release, the subsequent ATP binding, and the resulting head dissociation take place solely at the trailing head, which is the basis underlying the processive hand-overhand stroke generation. This mechanism had been inferred from various indirect experiments^119−121 but was clearly and directly demonstrated by the HS-AFM observation.

Figure 12.

Leading head conformations and their dependence on nucleotides. (a) Population of straight and sharply bent conformations under different nucleotide conditions. The numbers in (frames) and [molecules] represent those of examined images and molecules, respectively. (b) Average lifetime ⟨τ_ST⟩ during which the leading head assumes the straight conformation in various ADP concentrations (the number of events used to obtain the average is shown in ⟨events⟩). The error bar indicates standard error. The line curve indicates the best fit result obtained by analyzing the data using the following equation: ⟨τ_st⟩ = n_NF/k_S–B + n_ADP/k_–, where k_S–B represents the spontaneous transition rate of the nucleotide-free leading head from the straight conformation to the sharply bent conformation, k_– represents the ADP dissociation rate constant for the leading head, and n_NF and n_ADP are, respectively, the fractions of nucleotide-free and ADP-bound leading head under a given ADP concentration, which can be calculated using the ADP dissociation constant K_d of 0.075 μM estimated from the data shown in (a).

Because ADP never dissociates from the leading head while the M5-HMM molecule is walking in the presence of ATP, the sharp kinking of the leading head in the nucleotide-free condition has no relevance to powerstroke generation. Moreover, the brief detachment of the leading head observed as a foot stomp in the presence of ATP is not caused by ATP binding to the head because the sharply kinked conformation was never observed before the brief detachment of the leading head.

8.2.5. Chemo-mechanical Coupling in Walking Myosin V

How can the prevailing view of the chemo-mechanical coupling in myosin motors be changed or modified to be reconciled with the novel results that emerged most straightforwardly from the HS-AFM observations described above?

According to the prevailing view, the leading head of M5-HMM would not be able to bind to actin when the leading head is in the ADP-bound or nucleotide-free states because both heads are supposed to assume a poststroke conformation (i.e., straight neck–motor domain junction). Moreover, the trailing head of M5-HMM would not be able to bind to actin when AMPPNP (mimicking the posthydrolysis ADP–Pi) is bound to the trailing head because the head is supposed to assume a prestroke conformation (i.e., bent neck–motor domain junction). In reality, both heads were bound to an actin filament in the nucleotide-free and ADP-bound states as well as even in the AMPPNP-bound state. The distinct prestroke and poststroke conformations have been derived from electron microscopy and X-ray crystallography studies of nucleotide-free and nucleotide-bound heads of myosins from various sources.^{134,139−143} Most of these numerous studies agree that the neck–motor domain junction is bent in the ADP–Pi state, so that the lever-arm swings back toward the motor domain (i.e., direction opposite to the forward lever-arm swing) upon ATP hydrolysis. Although this back swing to form a prestroke conformation facilitates the leading head of M5 to bind to actin in the backward leaning orientation, this conformation also occurs in the flexible ADP-bound head (otherwise, two-headed binding to actin could not occur in the presence of ADP). The previous static structural studies have often been interpreted as if a tight one-to-one relationship would exist between the chemical and conformational states.^122−125 This view has to be changed as follows: a myosin head adopts two (or more) conformations even under a given nucleotide (chemical) condition, and goes back and forth between different conformations, but its dynamic equilibrium is biased to one side depending on the nucleotide condition. As described in the supplementary data in a cryoelectron microscopy study by Volkmann et al.,¹³⁴ both bent and straight conformations appeared in the actin-bound single-headed M5 in the presence of AMPPNP or ADP·AlF₄, without a large population difference. This means that the energy difference and the energy barrier between the two conformational states is < ∼2 k_BT (T = 300 K), much smaller than the chemical energy to be liberated by ATP hydrolysis (∼20 k_BT). Thus, the following conclusion can be formed: although the conformational change of the myosin head caused by the back swing of the lever-arm is an effective strategy for facilitating its binding to actin in the backward leaning orientation, the energy required to produce the prestroke conformation is much less than that provided by ATP hydrolysis.

According to the prevailing view, the chemical energy liberated by ATP hydrolysis is supposed to be converted to mechanical energy and stored in the actin-bound leading head of M5 with ADP. This state of the leading head is supposed to be formed only through Pi release at the head. The Pi release is supposed to induce a pre- to poststroke conformational change in the leading head, which generates intramolecular tension for forward movement. In this view, the chemical energy liberated by ATP hydrolysis is supposed to be transduced to mechanical energy in the form of intramolecular tension. Nevertheless, HS-AFM observations indicated that the intramolecular tension can be directly generated by the binding of the ADP-bound leading head to actin without passing through the Pi-releasing step at the leading head. Thus, the energy liberated by ATP hydrolysis is not used for the tension generation. Therefore, the way in which the ATP hydrolysis energy is actually used for myosin V walking (perhaps also for mechanical work performed by all members of the myosin superfamily) must be reconsidered. Because the strained (tension-generating) two-head bound state can be formed without the use of ATP hydrolysis energy, the molecule is supposed to spontaneously move forward once the trailing head detaches from actin upon ATP binding. Energy is required to break the rigor bond formed by the actin-trailing head complex. Therefore, ATP binding itself should supply the energy for breaking the rigor bond of the trailing head.

How much energy is required for this bond to break? The unbinding (rupture) force was previously measured to be 15 pN using AFM.¹⁶ The rupture distance was also estimated to be 1.7–2.5 nm in this study. This rupture distance is unusually long as compared to, for example, the 0.23 nm for an antigen–antibody,¹⁴⁴ the 0.15–0.3 nm for streptavidin–biotin,¹⁴⁵ and the 0.05–0.3 nm for α-actinin–actin dissociation.¹⁴⁶ This long rupture distance is consistent with the fact that actin–myosin interfaces contain bonds formed between flexible loops.^147,148 From the values of rupture force and rupture distance, the energy required to rupture a single actin–myosin rigor bond is 6–9 k_BT (T = 300 K), which is 30–45% of the chemical energy of ATP hydrolysis (∼20 k_BT). This mechanically estimated value is in good agreement with the value of 9 k_BT estimated biochemically for the free-energy change in the dissociation A–M → A + M.¹⁴⁹ For the ATP (T)-induced dissociation A–M + T → A + M–T, the free-energy change is biochemically estimated to be ∼10 k_BT,¹⁴⁹ which is again similar to that for the mechanical dissociation A–M → A + M. However, one may argue that ATP is not yet hydrolyzed in the step where a rigor actin–myosin complex dissociates, and, therefore, the energy of ATP hydrolysis is not yet used during this phase. However, the account balance of energy should be considered for the whole cycle of the ATPase reaction, and hence the ATP-binding energy can be used as a main part of the energy of ATP hydrolysis.

8.2.6. Remaining Issues in the Walking Mechanism of Myosin V

The above argument on the chemo-mechanical cycle in walking M5 puts forward a new principle for the energy transduction and motor function mechanism of M5, which is summarized below and can probably be extended to all myosins with slight modifications.

(i) Only a very small fraction of the chemical energy liberated by ATP hydrolysis is used for the back swing of the lever-arm to form the prestroke conformation. Even without any chemical energy input, the back swing can occur thermally, but its probability is somewhat smaller than that of the chemically induced case.

(ii) No energy is used for the generation of intramolecular tension for forward movement (i.e., no chemical-to-mechanical energy transduction takes place in tension generation).

(iii) The forward lever-arm swing of the leading head spontaneously occurs upon trailing head detachment, without any chemical transitions at the leading head.

(iv) The chemical energy of ATP hydrolysis is mainly used to dissociate the rigor complex of actin and the trailing head.

(v) The main role of ATP hydrolysis does not lie in supplying energy but in ensuring the unidirectional mechanical cycle by shifting the conformational equilibrium to either of the pre- and poststroke conformations.

The most striking feature in this novel view is that the strained two-headed bound molecule can be formed without a chemical energy input and that M5 moves spontaneously forward once the trailing head detaches from actin. If this was really the case, we would, however, appear to encounter a perpetuum mobile problem. Even in the presence of ADP, the foot stomp occurs at both leading and trailing heads of a two-headed bound molecule, with more frequent occurrence at the leading head than at the trailing head. When the trailing head detaches from actin, the molecule would take a forward step by the spontaneous swing performed by the leading head. On the other hand, when the leading head detaches from actin, the molecule would not take a backward step because the trailing head is bound to actin in a stable orientation (i.e., the forward leaning orientation). Thus, without any energy input, the M5 molecule appears to step forward many times (albeit slowly), even with the less frequent occurrence of foot stomps at the trailing head. This is forbidden perpetuum motion. However, in this gedanken experiment, two factors are not well taken into consideration: (i) a single-headed bound myosin V undergoes rotational Brownian motion around the average position biased to the forward direction, which is due to the flexible neck–motor domain junction, and (ii) the population of two conformations of the ADP-bound detached head is biased toward the poststroke conformation. Considering these factors, the detached trailing head can have two possibilities of binding to the original or frontward actins, while the detached leading head can have two possibilities of binding to the original or backward actins. Thus, the principle of detailed balance would hold between the forward step after trailing head detachment and the backward step after leading head detachment, resulting in no net movement of the molecule. The ratio of foot stomp occurrence between the leading and trailing heads was observed to be 4:1 in the presence of 1 mM ADP. This ratio of 4:1 appears to be insufficient for the detailed balance. However, as described in section 8.2.3, the foot stomp at the trailing head mostly occurs as a brief translocation approximately by ±5 nm along the actin filament, which does not allow the forward swing of the leading head. Therefore, when the brief translocation is omitted and only the events of brief detachment from actin are counted as foot stomp, the ratio of foot stomp occurrence between the two heads becomes much larger, guaranteeing the detailed balance.

The novel principle mentioned above predicts that even in the presence of saturated ADP, M5 would processively move forward if the trailing head is repeatedly detached by some means instead of ATP. If each head of M5 was labeled with a chromophore and the photoexcited chromophore temporarily altered the conformation of the head to dissociate it from actin, light pulses illuminating only the trailing head should make the molecule step forward, because the strain stored in the leading head would induce a forward step. Repetition of this directed illumination only at the trailing head would have to be expected to result in a long-distance forward movement of the molecule. Instead of this method, the AFM cantilever tip, replacing the action of ATP binding, could be used to detach the trailing head by injecting mechanical energy into the head. Such guided manipulation of a single molecule by HS-AFM is a future challenge, which certainly will provide novel insights into the chemo-mechanical coupling in M5 as well as motor proteins in general.

8.3. Rotary Catalysis of α₃β₃ Subcomplex of F₁-ATPase

F₁-ATPase is the soluble part of the F_oF₁-ATP synthase and works as an ATP-driven rotary motor.^150,151 The F₁-ATPase consists of five kinds of subunits with a stoichiometry of α₃β₃γ₁δ₁ε₁. The α₃β₃γ subcomplex of F₁-ATPase is a minimum stable complex with the full ATPase and motor activities; the γ subunit rotates in the stator α₃β₃ ring while ATP is hydrolyzed by the ring.^152−154 The concept of the “rotary catalysis” of F₁ was first proposed by Boyer as a natural consequence of elaborate biochemical studies on the “binding change mechanism” for the ATP synthase.¹⁵⁵ In the binding change mechanism, all three nucleotide-binding subunits in F_oF₁-ATP synthase are always in different states and alternately exchange the states during ATP synthesis and hydrolysis. The physical rotation of the γ subunit within the α₃β₃ ring was postulated for explaining the binding change mechanism.¹⁵⁵ Later, the first crystal structure of bovine mitochondrial F₁-ATPase revealed by Walker and colleagues showed that the α and β subunits are arranged alternately, forming a ring, while the central γ subunit forms the central shaft deeply penetrating into the ring’s central hole, and that the catalytic sites of ATP synthesis and hydrolysis are located at the α–β interfaces, mainly on the β subunits.¹⁵⁶ Thus, the postulation of a rotating γ subunit seemed to be a structurally supported realistic concept. Biochemical^157,158 and optical¹⁵⁹ analyses also implied the rotation of the γ subunit, and, finally, the unidirectional and counterclockwise rotation was directly observed by single-molecule optical imaging, in which a fluorophore-labeled actin filament attached to the γ subunit was visualized to rotate around the center of the stator α₃β₃ ring.^107,160 To achieve this unidirectional, successive rotation, the three catalytic β subunits must undergo cooperative and sequential conformational changes, coupled to ATP hydrolysis. However, before the advent of HS-AFM, no experiments were able to be conducted to examine how cooperative catalysis in the F₁-ATPase took place.

In Walker’s crystal structure mentioned above, three catalytic sites are in different nucleotide-bound states (Figure 13a): one ATP-bound (α_TP–β_TP interface), one ADP-bound (α_DP–β_DP interface), and one nucleotide-free (α_E–β_E interface). The structure taken by both β_TP and β_DP, in which their C-terminal domains swing toward γ, is designated as the closed conformation, while the structure taken by β_E, in which the C-terminal domain swings away from γ, is designated as the open conformation. The rotation of the γ subunit has been considered to be driven by the open/close bending motion of the β subunits because the two conformational states appear to push or be pushed by the γ subunit in the crystal structure. Wang and Oster proposed that interactions with the γ subunit would control the conformational and catalytic states of individual β subunits to sequentially generate torque.¹⁶¹ This proposal appeared reasonable because the γ subunit is asymmetric around its long axis, and hence at any instance the β–γ interaction is always distinct among the three β subunits. In fact, some biochemical studies suggested that the α₃β₃ ring would not possess intrinsic cooperativity on its own,^154,162,163 supporting the contention that the γ subunit would mediate the interplay among β subunits. The view that the γ subunit is a “dictator” was reinforced by studies showing that backward mechanical rotation of the γ-subunit using external force reverses the chemical reaction toward ATP synthesis,^164,165 whereas forced forward rotation accelerates ATP binding.¹⁶⁶

Figure 13.

HS-AFM imaging of α₃β₃ subcomplex of F₁-ATPase under different nucleotide states. (a) Crystal structure of α₃β₃γ subcomplex. The α-, β-, and γ-subunits are shown in cyan, pink, and yellow, respectively. (b) Typical HS-AFM image of α₃β₃ subcomplex immobilized on a chemically treated mica surface without nucleotide (150 × 150 pixels; imaging rate 1 fps). (c) Filtered HS-AFM image of C-terminal side of the α₃β₃ subcomplex without nucleotide. (d) C-terminal side of crystal structure of the nucleotide-free α₃β₃ subcomplex. The α and β subunits are colored in cyan and pink, respectively. The C-terminal DELSEED motif of the β subunits corresponding to the high protruding portions is highlighted in red. (e) Simulated AFM image constructed from the structure in (d). (f) Filtered AFM image of the N-terminal side of the α₃β₃ subcomplex without nucleotides. (g) N-terminal side of the crystal structure of the α₃β₃ subcomplex. (h) Simulated AFM image constructed from the structure in (g). (i) Filtered AFM image of the C-terminal side of the α₃β₃ subcomplex at 1 mM AMP-PNP. (j) Crystal structure of the α₃β₃ subcomplex with bound nucleotides. This structure is obtained by removing γ from the crystal structure of α₃β₃γ subcomplex. (k) Simulated AFM image constructed from the structure in (j).

However, a few biochemical studies suggested the intrinsic cooperativity of α₃β₃ ring^167,168 even though they were not widely accepted. Furthermore, the “γ-dictator” model was recently challenged by the finding that even when the most interaction sites between β and γ are abolished, F₁ retains its active catalytic power and capability to rotate the shortened γ subunit unidirectionally.^169,170 To make it clear whether intrinsic cooperativity exists within the α₃β₃ ring itself, the three β subunits in the α₃β₃ ring alone (i.e., γ is absent) undergoing conformational changes should be examined. However, the observation of the rotational conformational changes by optical microscopy requires the attachment of an optical probe to the γ subunit.¹⁷¹ In one experiment, the polarization imaging of a single fluorophore firmly attached to a single β subunit in F₁-ATPase has successfully revealed the conformational change of the β subunit coupled with rotation of the γ subunit.¹⁷² However, it is rather difficult or impossible to simultaneously observe the conformations of all three β subunits in a single α₃β₃ ring using optical techniques. Thus, HS-AFM imaging of the α₃β₃ subcomplex in ATP was carried out to verify this issue that had remained unanswered by other approaches.⁵¹

On bare mica surface, all molecules of the α₃β₃ subcomplex rapidly diffused on the surface, which made it difficult to image them clearly. Therefore, the subcomplex had to be immobilized somehow. To observe the C-terminal face of the α₃β₃ subcomplex, the subcomplex had to be placed on a substrate surface with the C-terminal side up. To force the molecules into this orientation, a Lys₇-tag was introduced at the N-terminus of each β subunit, and the mica surface was made amino-reactive using APTES and glutaraldehyde.

Figure 13b shows a typical HS-AFM image of the α₃β₃ subcomplex without nucleotides. A filtered image (3 × 3 pixel median average filter) of the α₃β₃ showed a pseudo-6-fold symmetric ring. Each subunit had an externally protruding portion at the distal region of the ring as well as an upwardly protruding portion at the inner top side of the ring. Yet three of these upward protrusions were higher at alternately arranged three subunits than the other three (Figure 13c). The simulated AFM image (Figure 13e, section A.3 in Appendix) of the C-terminal side of the subcomplex constructed from the crystal structure of nucleotide-free α₃β₃ subcomplex shown in Figure 13d corresponded well to the observed image, indicating that the N-terminal side was selectively attached to the mica support. By comparison between the observed and simulated images, the three subunits with higher protrusions were identified as the β subunits. However, the selective attachment to the mica was not perfect; about 30% of the molecules showed a smaller ring without externally protruding portions, which corresponded to the N-terminus face (Figure 13f–h).

In the presence of a nonhydrolyzable ATP analog, AMPPNP, the ring became triangular because two of the alternately arranged three subunits showed inwardly retracted distal portions. These two retracted subunits also showed lower protrusions, and consequently the ring showed a single high protrusion (Figure 13i). A simulated AFM image constructed from the crystal structure of the F₁-ATPase obtained in ATP¹⁵⁶ from which the γ subunit was removed showed an asymmetric ring very similar to the observed image (Figure 13j and k). By comparison between the observed and simulated images again, the subunit with the high protrusion was identified to be an empty β subunit, and the two retracted subunits with low protrusions were identified to be AMPPNP-bound β subunits.

Under the nucleotide-free condition and in the presence of AMPPNP, the observed structures were always stationary, whereas in the presence of ATP, distinct dynamic changes in the conformation of the three β subunits occurred (Figure 14a). Each β subunit underwent a conformational transition between the outwardly extended high state (E state) and the retracted low state (R state). The outwardly extended and inwardly retracted conformations were well correlated with the high and low protrusion states, respectively (Figure 14b). The most prominent features were that only a single β-subunit adapted the E state, as statically observed in the presence of AMPPNP, and that when the E-to-R transition occurred at one β subunit, the opposite R-to-E transition usually occurred simultaneously with its counterclockwise neighbor β subunit. Consequently, the E state conformation propagated in the counterclockwise direction, with a discrete angle of 120° (Figure 14c).

Figure 14.

HS-AFM imaging of α₃β₃ subcomplex in ATP. (a) Clips of successively captured HS-AFM images of the C-terminal side of α₃β₃ subcomplex in 2 μM ATP (imaging rate, 12.5 fps). The highest pixel in each image is indicated by the red circle. (b) Tight correlation between two types of conformational changes in β subunits observed in ATP; different heights of protrusion (“H”, high; “L”, low) and extended/retracted (“E”/”R”) conformations of the distal region. (c) Time course of cumulated angle of the highest pixel. The inset shows a trajectory, superimposed on an AFM image, of the highest pixels corresponding to the high protrusions of extended β subunits (412 frames). The center of rotation is defined by the averaged X- and Y-positions of the highest pixels, and the cumulated angles are calculated relative to the first frame.

In the above statement, the different conformations of the β-subunits were described only on the basis of their appearances, without quantitative measure. For quantitative descriptions, a two-dimensional correlation coefficient can be used to evaluate the image similarity or dissimilarity between a given image and a reference image (section A.4 in Appendix). Figure 15a shows the histograms of the correlation coefficients calculated for the successive images of each β subunit observed in 2 μM ATP using an image of a β subunit in the E state as a reference. The correlation coefficients distributed around two distinct peaks. The peaks at larger and smaller coefficients correspond to the E and R states, respectively. Typical time courses of the conformational states taken by individual β-subunits within an α₃β₃ subcomplex observed in the presence of 2 μM ATP are shown in Figure 15b. In all images observed in the presence of 2–4 μM ATP (8746 images in total), the RRE state was dominant (82% of total). The REE state was also observed (14.5%). Other states, RRR (3%) and EEE (0.5%), were rare. When “+1” was given for a counterclockwise shift of the RRE state, while “–1” was given for a clockwise shift of the RRE state, the cumulated number exhibited the rotary propagation of the RRE state (Figure 15c). The propagation was unidirectional, rotating counterclockwise with an efficiency of 83% (in 2 μM ATP) over the total shift events examined (n = 371) (Figure 15d).

Figure 15.

Analysis of HS-AFM images of α₃β₃ subcomplex of F₁-ATPase using correlation coefficient. (a) Correlation coefficient histograms calculated for each β subunit (n = 220) observed in 2 μM ATP. An AFM image of an extended β subunit was used as a reference for the analysis of each β subunit. (b) Time courses of correlation coefficients. The white and gray backgrounds represent periods of extended high and retracted low states, respectively. Solid lines show the mean correlation coefficient for each period. (c) Time evolution of cumulated number of counterclockwise shifts of the RRE state. “○” and “×” correspond to RRE and other states (REE, EEE and RRR), respectively. The increase in the cumulated number indicates that the extended β subunit in RRE shifts counterclockwise. (d) Distributions of the number of successive shifts of the “RRE” state in clockwise (top) and counterclockwise (bottom) directions at 2 μM ATP. The values for “mean” indicate the average number of successive shifts, and the values for “s.d.” indicate the standard deviations.

The dwell times in the E and R states of each β subunit decreased with increasing ATP concentration from 2 to 4 μM (Figure 16a–c). This fact indicated that ATP binding is rate-limiting in this range of ATP concentrations, consistent with the Michaelis–Menten constant of 12 μM for ATP hydrolysis determined biochemically. The histograms of dwell times of the E state followed single exponential functions (Figure 16a–c, upper panels), whereas those of the R state were well fitted with the model of two consecutive ATP binding events at the other two β subunits triggering the transition of the β subunit from the R state to the E state (Figure 16a–c, lower panels). The rate constants of the counterclockwise shift of the RRE state were comparable with the initial rates of ATP hydrolysis measured biochemically (Figure 16d). Therefore, the E-to-R transition occurs when ATP is bound to an empty β, while the R-to-E transition occurs when an ADP-bound β releases ADP. As such, the empty, ADP-bound, and ATP-bound β subunits are arranged counterclockwise in this order, and hence the observed conformational propagation demonstrated rotary catalysis by the α₃β₃ subcomplex alone without the γ shaft.

Figure 16.

Kinetics analysis of conformational change of α₃β₃ subcomplex. Histograms of dwell times for the E (top) and R (bottom) states in various concentrations of ATP (a, 2 μM, n = 266; b, 3 μM, n = 426; c, 4 μM, n = 374). Dwell time distributions for the E state fit well with single exponential decay functions (solid lines on top). The distributions for the R state fit with functions representing consecutive reactions with two identical time constants: A × t × exp(−t/τ) (solid lines on bottom). (d) ATP concentration dependence of the rate of conformational change of β subunit determined by fitting the dwell-time histograms of the E and R states, shown in (a)–(c), and the initial rate of ATP hydrolysis determined by biochemical assay at three different ATP concentrations.

The HS-AFM observations of the α₃β₃ subcomplex directly indicated that the intrinsic cooperativity responsible for torque generation to rotate the γ subunit is elicited through the β–β interplay alone. Because direct interactions between β subunits in the α₃β₃ ring are considered to be infeasible from the crystal structure, the β–β interplay is very likely to take place via the intervening α subunits. This inference could be corroborated by the following observations, in addition to the observation showing conformational changes of the α subunits that were less visible than those of the β subunits. During HS-AFM imaging, a single subunit rarely dissociated from the α₃β₃ ring (Figure 17), presumably due to imperfect covalent binding of the ring to the mica surface and transient, overly strong tip–sample interaction. When either a single β subunit or a single α subunit was lost from the α₃β₃ ring, the rotary propagation completely halted, although some cooperative conformational transitions still occurred between the remaining β subunits.

Figure 17.

Cessation of rotary conformational change propagation by loss of a single subunit. (a,d) AFM images before and after loss of (a) β₁ or (d) α₁ within α₃β₃ subcomplex in 2 μM ATP. Imaging rate, 12.5 fps. (b,e) Time courses of correlation coefficients for the three β subunits designated in (a) and (d), respectively. Solid horizontal lines show the mean correlation coefficients for the periods of E and R states. The states are judged by examining whether the correlation coefficients are above or below a threshold (0.978). β₁ was lost at 16.2 s (b) and α₁ was lost at 9.4 s (e) as indicated by the vertical broken lines. (c,f) Cumulated angles of open β subunit positions measured using the highest pixel position in each frame. (c) and (f) correspond to (b) and (e), respectively.

The results of HS-AFM observations on the α₃β₃ ring in ATP definitely excluded the “γ-dictator” model¹⁶⁹ that only the interaction with the γ subunit would determine the conformational and catalytic states of β subunits.^173,174 However, the rate constant of ATP binding for the α₃β₃ subcomplex estimated from the ATP concentration-dependent dwell time of the E state was ∼1 × 10⁶ M^–1 s^–1, which is more than 10 times lower than that for a subcomplex containing the γ subunit, α₃β₃γ.¹⁷⁵ Moreover, without γ, propagation of the conformational states occasionally occurred in the opposite direction. Thus, the γ subunit plays a role in establishing an oligomeric structure with the full ATPase activity and reinforcing the cooperativity elicited by the β–β interplay.

Because the γ subunit passively rotates, an object (not necessarily made of polypeptides) that can be inserted into the central hole of the α₃β₃ would be able to rotate driven by the rotational conformational changes of the β subunits. This experiment is a future challenge. Moreover, it is also an intriguing challenge to examine the chemo-mechanical coupling in F₁-ATPase using another approach. Because there is a strong chemo-mechanical coupling in the β subunits (i.e., the chemical states determine the respective conformational states), an opposite direction of coupling (i.e., determination of the chemical states by the mechanical states) is likely to occur, which is reminiscent of the fact that the forced clockwise rotation of the γ subunit by external force can reverse the chemical reaction to ATP synthesis^164,165 but different from it. The β subunits take the E (outwardly extended high) and R (inwardly retracted low) conformational states corresponding to the nucleotide-free and nucleotide-bound states, respectively. In a buffer solution containing ADP (without ATP), the protrusion of one β subunit in the E conformational state (i.e., in the nucleotide-free state) can be pushed using a cantilever tip, which may convert the conformation to that of the R state, triggering ADP binding to the subunit as well as ADP dissociation from one of the neighboring β subunits. As a result, ATP-less rotation of the γ subunit would occur, similar to the ATP-less walking of M5 on actin filaments, as predicted above.

8.4. General Remarks on Membrane Proteins

Membrane proteins have been, and are still to some extent, the orphans of structural and molecular biology. Membrane proteins must, to adopt their native fold within the hydrophobic lipid membrane core, expose hydrophobic amino acids, in stark contrast to soluble proteins that bury hydrophobic amino acids within the protein interior. On both membrane-protruding faces, typically termed intracellular and extracellular surfaces, membrane proteins are hydrophilic, exposing polar or charged amino acids. This general architecture is the basis of their amphiphilic nature. It is this feature that rendered biochemical, functional, and structural characterization of membrane proteins difficult for a long time. It took 25 years from the first soluble protein (myoglobin) structure solved¹⁷⁶ to the first membrane protein (reaction center) atomic structure determination.¹⁷⁷ At the date this Review is written, scientists dispose of 1264 membrane protein structures of 406 unique proteins,¹⁷⁸ while a total of 91 022 structures are disposed of the PDB.¹⁷⁹ Hence, the structural information on membrane proteins of ∼1% of all structures is still in unfavorable relation to the ∼25% of all genes coding for membrane proteins.¹⁸⁰ The majority of the membrane protein structures have been solved by X-ray crystallography, a minor fraction by EM crystallography (e.g., ref (181)) and NMR spectroscopy (e.g., ref (182)). Anyway, regarding the difficulties in analyzing membrane protein structures, alternative techniques that provide structural information, even at medium resolution, were strongly welcomed. Such data can be provided by single particle EM (e.g., ref (183)) and AFM (e.g., ref (184)). Beyond structural analysis, the analysis of membrane protein dynamics is of key importance for the understanding of membrane complexes. Several levels of dynamics of membrane proteins can be distinguished, such as conformational changes, diffusion, and interaction. We will treat these aspects individually below. However, it must readily be highlighted that the concomitant analysis of structure and dynamics necessitates the use of a technique with high spatial and temporal resolution. This has not been possible so far, and the HS-AFM allowing imaging of single molecules at high spatiotemporal resolution is opening novel ways to assess superstructure/structure/function relationships of membrane proteins.

In contrast to what a single crystallographic protein structure might suggest, only very few proteins accommodate a single fixed conformation, such as proteins that serve rather as scaffolds than as functional entities, for example, light-harvesting complexes that hold pigments in place.^15,185 The majority of membrane proteins occur in at least two relatively stable conformations, activated and inactivated for receptors,¹⁸⁶ inside-open and outside-open for transporters,¹⁸⁷ and of course the short-lived intermediates between these conformations. Thinking the concept of protein conformational changes to the end, one must conclude that many proteins are actually in a permanent change of conformations, such as the mitochondrial ATP synthase. Indeed, the ATP synthase is subject to the proton gradient across the inner mitochondrial membrane during its entire “life span” and is therefore probably in continuous rotation (if it is not complexed with its inhibitory subunit), highlighting the importance of assessing protein conformational dynamics beyond static structure analysis. It is very challenging to study these conformational changes. Techniques that do not allow in situ structure assessment typically need to block the proteins in both conformations. HS-AFM, although limited to surface contouring and to a ∼30 ms dynamic range, opens a novel avenue for the direct visualization of membrane protein conformational dynamics. In this feat, it combines two additional advantages; first single molecules can be analyzed and hence the process action of individual proteins can be studied, and second studying proteins in a close-to-native environment brushes aside any interpretational doubt that could emerge, for example, for proteins subject to intermolecular contacts in crystals.

8.5. Structural Changes of Membrane Proteins

8.5.1. Bacteriorhodopsin Responding to Light

A paradigm membrane protein system is the bacterial light-driven proton pump bR in the purple membrane of Halobacterium (H.) salinarum.^188,189 It was identified and functionally characterized in the early 1970s,¹⁹⁰ and is nowadays perhaps the best characterized membrane protein. Its natural tendency to form highly ordered 2D arrays has been advantageous for structural studies, kick-starting EM crystallography.¹⁹¹ It was in these studies that the first experimental proof was acquired that membrane proteins actually cross the membrane as α-helix bundles.¹⁹¹ Over the following about 25 years, the entire photocycle of bR was characterized functionally in detail,¹⁸⁹ and high-resolution X-ray structures were determined.¹⁹²

A bR monomer comprises seven transmembrane α-helices (named A–G) enclosing the chromophore retinal.^193,194 bR assembles into trimers, which are packed into 2D hexagonal lattices.¹⁹⁰ In the photocycle, photoisomerization from all-trans to 13-cis conformation of the retinal takes place with subsequent primary proton transfer from the Schiff base to Asp85, which triggers a cascade of changes in the bR structure. A series of intermediates designated J, K, L, M, N, and O are defined by spectroscopy, and the M (M₄₁₀ with the light-absorption peak at 410 nm) is the only intermediate containing a deprotonated Schiff base.¹⁸⁹ The M and N states have long lifetimes, whereas the other states have much shorter lifetimes. The light-induced conformational changes in bR have been investigated by various methods.^188,195 In particular, crystallographic structures in the frozen activated state of the wild type (WT) and bR mutants have been solved at the atomic resolution.^195−198 The common view that has been reached through these studies on the bR structure during the photocycle is that the proton channel on the cytoplasmic surface is opened by the tilting of helix F away from the protein center.¹⁹⁶ This alteration is followed by rearrangement of the interhelix E–F loop, thus resulting in relatively global conformational changes in the M and N intermediates.^199−201 Despite the consensus on the qualitative description of conformational changes, no agreement was reached for the quantitative aspect (reported changes were small, ranging from 0.1 to 0.3 nm) because of the lack of techniques enabling direct visualization of the conformational change of bR under physiological condition.

The 2D character of purple membrane promoted the beginnings of high-resolution AFM imaging and the assessment of image resolution and quality.²⁰² Following the pioneering AFM study of bR in the purple membrane by Engel’s group,²⁰² bR has been repeatedly imaged to demonstrate the increasing high-resolution power of AFM. In fact, unprecedented high-resolution images capable of distinguishing the individual interhelix loops of bR were obtained again by Engel’s group.^75,203 Nevertheless, until recently the physiologically relevant structural changes in bR (i.e., response to light) have never been studied using AFM because of its lack in temporal resolution. It was natural that this intriguing topic was studied soon after the advent of HS-AFM, although it appeared as a challenging task to study the bR photocycle by HS-AFM. The findings obtained thereby surprisingly provided novel unexpected insights into the bR photocycle, so far unappreciated by other technical and structural approaches.⁴³ The observation successfully revealed the conformational changes much larger than 0.3 nm as well as the cooperative interplay between excited bR molecules in the 2D crystal.^43,48 Moreover, the trimer–trimer interaction energy was quantitatively estimated by the observation of dynamic interaction between diffusing trimers and the crystalline lattice edge in the membrane.³⁴ Finally, HS-AFM imaging of various bR mutations was performed to identify the amino acids responsible for the interaction between trimers leading to lattice assembly, revealing the purposes for bR assembly into regular lattices.⁶¹ All of these HS-AFM studies are described as topics of this section (structural changes of membrane proteins), except for the study of the trimer–trimer interaction energy (described in section 8.6.1).

The photocycle of wild type bR takes place within about 10 ms at neutral pH; hence bR in the photoexcited state is too short-lived to be observed even using HS-AFM. Therefore, the purple membrane containing D96N bR mutant was used. This mutant is known to have a longer photocycle (∼10 s) but retains an ability of proton pumping.²⁰⁴ D96N bR lacks the proton donor residue (Asp96) for the Schiff base, rendering the M-intermediate very long and hence the photocycle so slow; the proton for reprotonation of the Schiff base during the decay of the M state has to be supplied from the aqueous milieu. A state exactly the same as the N state of the wild-type bR, which follows the M state and contains a protonated Schiff base, has been considered not to exist in the excited D96N bR. To avoid photoactivation of bR with the laser light used in the OBD detection, an infrared laser (980 nm) was used for the OBD detector. The HS-AFM observation was performed in a solution of pH 7, 8, 9, or 10 to have different photocycle times.

Figure 18a shows two images of D96N bR clipped from successive images at the cytoplasmic surface captured at an imaging rate of 1 fps, under repeated dark–illumination cycles. Individual bR molecules within individual trimers were clearly resolved (left panel in Figure 18a; captured under dark), as observed on the cytoplasmic surface with conventional slow contact-mode AFM.²⁰⁵ During illumination with green light (532 nm, 0.5 μW; green bars in Figure 18a), the bR molecules drastically changed their structure (right panel in Figure 18a). After the light was switched off, the excited bR molecules returned back to the unphotolyzed-state conformation in a few seconds. The conformational changes were highly reproducible in repeated dark–illumination cycles. On the other hand, discernible conformational changes were never observed at the extracellular surface (Figure 18b). To ensure that the conformational changes observed here were not artifacts such as a tip-force-induced conformational change,²⁰³ the decays of the excited state after flash illumination at various pH values were analyzed (Figure 18c). It is well-known that the lifetime of the M-intermediate of D96N is prolonged at alkaline pH²⁰⁴ as observed with UV–visible spectroscopy (the inset in Figure 18c). The decay detected by HS-AFM also showed strong pH dependence, similar to that measured by UV–visible spectroscopy. This agreement indicated that the conformational change observed by HS-AFM is surely an intrinsic nature related to the bR photocycle. Moreover, the fact that the conformational change observed with green light illumination was not observed when red or blue light was used for illumination reinforces this conclusion. Note that the conformational change rarely occurred under blue light illumination because the ground state having an absorption peak at 570 nm absorbs blue light slightly.

Figure 18.

HS-AFM imaging of D96N bR mutant. (a,b) HS-AFM images of the cytoplasmic side (a) and the extracellular side (b) of D96N bR mutant (imaging rate, 1 fps) under dark (left panels) and green light illumination (right panels) (λ = 532 nm, 0.5 μW). bR trimers are highlighted by the white triangles. The insets in (a) display respective averaged images of trimers. The light-blue circles in (a) indicate a trefoil, and the green bars in (a) and (b) indicate green light illumination. (c) Decay after flash-illumination of the activated bR molecules observed at different pH values (7, 8, and 9). The exponential decay constants (τ) at pH 7, 8, and 9 are 6.7, 25, and 48 s, respectively. The inset shows the absorbance change at 410 nm (that is, decay of the M-intermediate) after flash illumination of D96N measured at various values of pH (7, 8, or 9). (d) Traces (red, blue, and purple marks) of the centers of mass of bR molecules under dark–illumination cycles are superimposed on the image of D96N in the dark. A bR trimer is encircled with the white triangle, and the positions of the α-helical ends facing the cytoplasmic surface (labeled with A–G) are derived from an atomic model of the unphotolyzed state.

Figure 18d shows the trajectories that the centers of mass of bR molecules took during the dark–illumination cycles (red, blue, and purple marks), which are superimposed on an AFM image captured under the unphotolyzed state. Here, the “center of mass” for each bR monomer was calculated from the corresponding surface area and height distribution in the HS-AFM topograph. The trajectories were highly centrosymmetric and oriented outward from the trimer centers under the light illumination condition. All activated bR monomers exhibited a displacement of 0.7–0.8 nm on average, which is much larger than those estimated before from electron microscopy and X-ray crystallography.^197,198 In comparison to the atomic model of the α-helical cytoplasmic ends in the unphotolyzed state (A–G in Figure 18d), the protruding areas around helices E and F shifted outward from the trimer center under illumination. In addition, a previous AFM imaging study of bR has assigned the prominent protrusion on the cytoplasmic face in AFM images of bR to the cytoplasmic E–F loop.^203,205 Therefore, the bR movement visualized here is considered to represent the displacement of the E–F interhelical loop. This displacement was clearly seen in the averaged image of the excited state bR (compare the averaged images under dark and illumination, which are inset in Figure 18a).

As a consequence of the outward displacement of the E–F loop in each bR monomer, the three nearest-neighbor bR monomers, each belonging to a different adjacent trimer, always transiently assembled. The triad of the nearest-neighbor monomers was designated as “trefoil” to distinguish it from the original trimer (trefoils under dark and illumination conditions are indicated by light-blue circles in the left and right panels in Figure 18a). Interestingly, this transient assembly in trefoils altered the decay kinetics of the activated state. The decay kinetics of the activated bR monomers in three different situations are shown in Figure 19a. Under weak illumination, only one monomer in each trefoil was activated in most cases. When only one monomer was activated in a trefoil, it decayed with a time constant of 7.3 ± 0.58 s (see top panel in Figure 19a). In contrast, under stronger illumination, two or three monomers within a trefoil tended to be activated together. Interestingly, the decay of each activated monomer within a trefoil was altered depending on the order of its activation. The monomer that was activated latest among the activated monomers in the trefoil decayed with a shorter time constant of 2.0 ± 0.16 s (see middle panel in Figure 19a). On the other hand, the decay kinetics of the early activated monomers did not follow a single exponential, and the averaged decay time lengthened to about 13 s (see bottom panel in Figure 19a). This observation indicated that the early activated monomers do not return to the ground state as long as the adjacent monomers within the trefoil are in the active state. Thus, the transient assembly of excited bR molecules within a trefoil elicits both positive and negative cooperative effects in the decay kinetics as the initial bR recovers. Some cooperativity regarding the photoexcitation of bR was previously proposed and considered to occur within a trimer.^206,207 However, the HS-AFM observation revealed that the cooperative effects are caused by bR–bR interactions within a trefoil, not within a trimer, shading a completely novel view onto the assembly of bR trimers in the hexagonal lattice.

Figure 19.

Cooperative effects on the decay kinetics of D96N. (a) The top figure shows the decay of activated bR monomers (as depicted by the red circle), while the other monomers (the gray circles) within the respective trefoils are not in the activated state. The exponential decay constant is 7.3 ± 0.58 s. On the other hand, when one or two nearest neighbor molecules (as depicted by green circles in the middle figure) in a trefoil are already activated, the bR monomer activated latest (as depicted by the blue circles in the middle figure) decays faster. The exponential time constant is shortened to 2.0 ± 0.16 s. In contrast, the early activated molecules within a trefoil (as depicted by green circles in the bottom figure) show a nonexponential broad distribution of decay time with an average of 13.3 s. (b) Decay rate of activated D96N under different light intensities. The upper graph shows the decay of activated molecules under weak illumination. The decay constant is 5.4 ± 0.34 s. The lower graph shows the decay of activated molecules under relatively strong illumination. The decay constant is 6.1 ± 0.37 s.

When all of the activated molecules were counted regardless of their activation order and of the number of activated monomers in a trefoil, the lifetimes of the activated state were well fit to single exponential functions under both weak and strong light illumination conditions, and their decay constants were nearly identical, irrespective of the intensity of illuminated light (Figure 19b). This was explained by the coexistence of the positive and negative cooperativity effects under strong light intensity. The two cooperative effects are nearly canceled out with each other on averaging, resulting in an approximately constant decay rate independently of the light intensity. Under a conceivable assumption that the conformational change turnover of an activated bR monomer is tightly coupled with proton transfer by the bR monomer, the average rate of proton-pumping by activated bR would be nearly conserved regardless of light intensity. As a result of the cancelation effect, the cooperative effects are hardly detected by ensemble averaging approaches. As such, this discovery of cooperative effects in a trefoil best exemplifies the importance of closely looking at individual molecules by HS-AFM. Even for extensively studied biomolecular systems such as bR, undisclosed important mechanisms still exist to be discovered, some of which can be newly disclosed by HS-AFM imaging, thanks to the directness of the acquired data of single-molecule imaging.

It is known that the all-trans to 13-cis isomerization of retinal can be reversed by a second illumination with a different wavelength.²⁰⁸ After the retinal is isomerized to the 13-cis form by green illumination, blue light (λ = 408 nm) illumination induces a back reaction of the retinal to the ground state (all-trans form). However, it has not yet been evident whether the protein structure would tightly be coupled to the isomerization of the retinal molecule because the spectroscopically detected reversal does not necessarily indicate the reversal of the entire protein conformation. This issue was addressed by the direct visualization of D96N bR under alternate illumination of green and blue light.⁴⁸ Figure 20a shows the displacement of the centers of mass, as a function of time, for three different bR monomers at pH 8. Once bR molecules were activated by green light illumination, the activated state was mostly maintained even after the light was turned off (Figure 20a). This was because the lifetime of the activated state of D96N bR at pH 8 is much longer than the duration used (10 s) for green light illumination. In the case of alternative illumination, bR molecules underwent alternate conformational changes between the excited and ground states synchronized with the switching between green and blue light illumination (Figure 20b). The blue light-induced conformational change back to the ground state is caused by the photoback-reaction, not by the normal turnover of the photocycle. Because bR in the ground state also slightly absorbs blue light, deactivated bR was sometimes reactivated under the blue light (blue arrows in Figure 20b). The number of activated molecules rapidly decreased nearly to zero after the brief blue light illumination (Figure 20c). These observations clearly showed that the bR protein structure is completely governed by the conformational state of the retinal molecule in its core.

Figure 20.

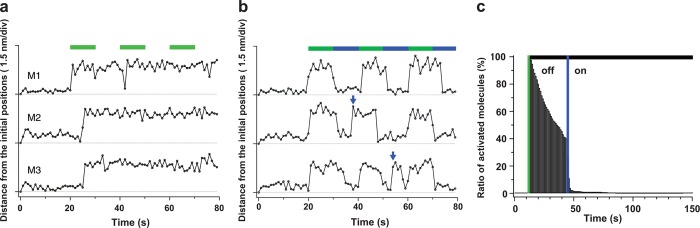
Effect of alternate two-color illumination on the conformation of D96N bR observed by HS-AFM. (a) Displacement of centers of mass for three D96N bR molecules within a trimer measured as a function of time at pH 8 on the cytoplasmic side. The green bars show the periods of green light illumination. (b) Displacement of centers of mass for three D96N bR molecules within a trimer measured as a function of time at pH 8 on the cytoplasmic side. The green and blue bars show the periods of illumination of green and blue light, respectively. The average displacement induced by green light is 0.80 ± 0.13 (mean ± s.d.) nm. (c) Decay of the activated state of D96N bR at pH 8 detected by HS-AFM. Green and blue regions indicate application of green and blue light, respectively. Illumination periods of both green and blue light are 3 s.

8.5.2. Role of Trimer–Trimer Interaction in bR Function

It has long been a question: For what purpose is bR assembled into a crystal lattice in the native state? As described in section 8.5.1, the conformational change of bR during the photocycle elicits cooperative effects due to interactions between excited bR molecules within trefoils. This suggests that the lattice formation would have a role in the physiological function of bR. Thus far, only a few studies have been presented for the elucidation of the origin of the trimer–trimer interaction leading to the crystal lattice and for the estimation of the energy involved in the interaction.^209−212

Amino acid residues in bR responsible for trimer–trimer association leading to lattice assembly were recently identified by the combination of HS-AFM imaging and directed mutagenesis. A previous neutron diffraction study has suggested that some of the aromatic residues (W10, W12, Y131, and F135) located vertically no farther than 5 Å into the extracellular side of the membrane and laterally at the outer rim of the trimers are involved in lattice formation.²¹⁰ To more specifically identify essential amino-acid residues for the lattice assembly, five bR mutants (W10I, Y131I, W12I, F135I, and W12F) were prepared and imaged by HS-AFM.⁶¹ Figure 21 shows images of these bR mutants. As can be seen in these AFM images, the W10I and Y131I mutants formed a lattice (Figure 21a and b). On the other hand, the lattice was not formed in the cases of W12I and F135I mutants (Figure 21c and d), but as indicated by the dotted triangles in the images trimers were visualized as isolated entities diffusing fast within the membrane. These results indicated that both W12 and F135 residues play an essential role in assembling bR trimers. The W12F mutant also formed a crystal lattice, as shown in Figure 21e, indicating that aromatic residues at positions 12 and 135 associate with each other (homotopically or heterotopically) possibly through a hydrophobic stacking interaction mediated by the sugar moieties of glycolipids contained in the membrane.^210,213

Figure 21.

HS-AFM images of cytoplasmic surfaces of purple membranes containing bR mutants (a, W10I; b, Y131I; c, W12I; d, Y135I; e, W12F). Imaging rates: (a, b, and e) 1 fps, (c and d) 33 fps.

Because the bR trimer isolation method was established by the above study, the question, “for what purpose bR is assembled into a crystal lattice in the native state?”, was addressed by HS-AFM imaging.⁶¹ Double mutations, D96N and W12I, were introduced to bR to obtain isolated trimers with a slow photocycle. Because D96N/W12I bR trimers diffused fast in the membrane, they were immobilized on a mica surface treated with APTES and then activated with glutaraldehyde (Figure 22a). Upon green light illumination, the D96N/W12I bR mutant exhibited conformational changes similar to that observed with the D96N bR mutant (i.e., outward movement of the E–F loops; Figure 22b; imaging rate, 2 fps). After light was turned off, the excited-state conformation returned back to the ground-state conformation within a few seconds (Figure 22c).

Figure 22.

HS-AFM imaging of isolated D96N/W12I bR trimers. (a) HS-AFM image under dark of D96N/W12I bR trimers anchored on chemically modified mica substrate (imaging rate: 1 fps). (b,c) Clips of successively captured HS-AFM images of a D96N/W12I bR trimer (b) under green light illumination (indicated by green rectangles) and (c) after the light was turned off (imaging rate: 2 fps). The insets are schematic illustrations of the observed bR conformations. The gray and green circles indicate the conformations of bR monomers in the ground and excited states, respectively.

The kinetics of photoactivation during continuous green illumination, as well as the decay kinetics after light-off, was analyzed to see a possible effect of lattice disruption on the photoreaction cycle, especially because the results presented above strongly suggested that the cooperativity measured on the single-molecule level should be lost when bR was unable to form a lattice. Figure 23a shows the population of activated D96N and D96N/W12I bR molecules as a function of time after the start of continuous illumination. The rise time constant of D96N/W12I bR was estimated to be τ = 1.9 ± 0.06 s, which was 4-fold longer than that of D96N bR (τ = 0.49 ± 0.01 s) under the same light intensity. On the other hand, the decay kinetics after light-off was almost identical for both mutants (τ ≈ 10 s), on average over many bR molecules (Figure 23b). As expected, the decay kinetics of three bR molecules within an isolated D96N/W12I bR trimer was confirmed to be independent of their activation order, like the case of three bR molecules within a D96N bR trimer, but unlike the case of three bR molecules within a D96N bR trefoil. A possible effect of anchoring the molecules onto the chemically modified mica on the activation and decay kinetics was excluded because D96N bR immobilized onto the chemically modified mica showed kinetics with time constants similar to those for D96N bR simply physisorbed on a bare mica surface (insets in Figure 23a and b). Therefore, the chemical anchoring has no significant effect on the photocycle, and, consequently, the rise delay observed with D96N/W12I bR is intrinsically caused by lattice disruption. Because the rise rate linearly increased with increasing illumination intensity (Figure 23c), the retardation was likely to be attributable to a lower efficiency of the conformational change or to a smaller optical absorption cross section of the D96N/W12I mutant. The latter was, however, ruled out because the difference spectrum between the ground and 100% excited states of D96N/W12I bR measured at low temperature (210 K) was identical to that of D96N bR. Therefore, the reduction of the rate at which the excited state conformation is accumulated during continuous illumination should be attributed to a reduced efficiency of adopting the activated conformation in D96N/W12I bR. This suggested that a nonproductive photoreaction pathway would additionally occur in disassembled D96N/W12I bR, through which the initial photoactivated state (this unspecified state is designated M_X) would be de-excited to the ground state G without passing through the M state (see Figure 23d). In addition to HS-AFM observations, spectroscopic and proton pumping assay investigations were carried out for both D96N and D96N/W12I samples to find the origin of the reduced rate of M state accumulation, but details of these studies are omitted here.

Figure 23.

Effects of lattice disassembly on the photoreaction kinetics of bR. (a) Time courses of accumulation of activated bR molecules detected by HS-AFM after the start of continuous light illumination (0.2 μW). Red plots, unanchored D96N bR; blue plots, anchored D96N/W12I bR. The exponential time constants (τ) of D96N and D96NW12I are 0.49 ± 0.01 and 1.9 ± 0.06 s, respectively. The inset shows the time course of the accumulation of activated bR in an anchored D96N bR sample. The exponential time constant is 0.58 ± 0.01 s. (b) HS-AFM-detected decay of activated states of unanchored D96N bR (red plots) and anchored D96N/W12I bR in full active trimers (blue plots) after light (0.2 μW) was switched off. The exponential time constants of D96N and D96NW12I are 10.4 ± 0.10 s and τ = 9.6 ± 0.04 s, respectively. The inset shows the decay of activated molecules for anchored D96N after light was turned off. The exponential time constant was 9.3 ± 0.04 s. (c) Rate constants of rise phase as a function of light intensity for D96N (red plots) and D96NW12I (blue plots) measured by HS-AFM. The inset shows the rate constants of the rise phase as a function of light intensity for D96N measured by UV–visible spectroscopy. (d) Models of photocycles in D96N bR and D96N/W12I bR. Upper illustrations indicate the lattice-assembled D96N bR (left) and disassembled D96N/W12I bR (right). The bottom schematics show the modeled photocycles in D96N bR (left) and D96N/W12I bR (right). In the photocycle of D96N bR, the presence of a direct recovery pathway to the ground state from M_X with no E–F loop displacement is minor as indicated by the dashed arrow. The rate constants, k₁, k₂, k₃, and k₄, for transitions between different states are assigned as shown in the right bottom schematic. Numerical analysis of HS-AFM detected conformational change kinetics based on this model gives k₁ = 2.04 s^–1, k₂ = 100.0 s^–1, k₃ = 0.1 s^–1, and k₄ = 0 s^–1 (for D96N bR) or 370.4 s^–1 (for D96N/W12I bR).

The results obtained from HS-AFM imaging, optical spectroscopy, and proton pumping assay are summarized as follows: (i) the M state with an outwardly displaced E–F loop exists in the photocycle of both D96N bR and D96N/W12I bR; (ii) after the start of continuous illumination, the M state accumulation of disassembled D96N/W12I bR occurs with a rate ∼4-times lower than that of assembled D96N bR; (iii) the accumulation rate of both samples linearly increases with increasing light intensity; (iv) the optical absorption cross section is very similar between D96N bR and D96N/W12I bR; and (v) the introduction of W12I mutation into WT bR does not appear to affect the proton pumping activity of bR within experimental accuracy. Taking these results into consideration, a novel model of the photo reaction was proposed (Figure 23d); the lattice disruption causes the photoreaction pathway to branch into two (the original productive pathway and a new nonproductive pathway). In the nonproductive pathway, no significant structural change occurs in bR and no proton is pumped out; however, the kinetics of this pathway is much faster than that of the original pathway. All of the results obtained in this study were quantitatively well explained by mathematical simulations based on this model.⁶¹ Thus, trimer–trimer association plays an essential role in providing bound retinal with an appropriate environment to maintain its full photoreactivity and in maintaining the natural photoreaction pathway. The bR lattice in purple membrane is not formed nonspecifically for the improvement of packing density. It is formed because the photocycle is more efficient in this assembly. These findings illustrate the fantastic power of HS-AFM’s direct acquisition of dynamic data at the single-molecule level and how this power could contribute to the discovery of important novel aspects in one of the best-studied membrane protein system.

8.5.3. Up–Down Motion of Ca²⁺-ATPase

Ca²⁺ is a regulator of muscle contraction. Skeletal muscle contracts when Ca²⁺ is released from the sarcoplasmic reticulum (SR) into the cytoplasm. During this activation, Ca²⁺ binds to troponin associated with actin filaments and tropomyosin, and thereby the inhibition of actomyosin ATPase activity by troponin-tropomyosin is removed.²¹⁴ Ca²⁺ is pumped back into the lumen of the SR by the action of Ca²⁺-ATPase (an energy driven Ca²⁺-pump) existing in the SR membrane, resulting in muscle relaxation.^215−217 Two Ca²⁺ ions are transported per ATPase cycle.²¹⁷ The Ca²⁺-ATPase, sarcoplasmic reticulum Ca²⁺-ATPase 1a (SERCA), is a member of the P-type ATPase superfamily, which forms a phoshoprotein intermediate and undergoes large conformational changes during the course of ATP hydrolysis.²¹⁶ SERCA has been well characterized structurally and functionally.^218,219 The reaction mechanism of P-type ATPase is commonly interpreted according to the Albers-Post scheme.^220,221 In this scheme, the ATPase has two distinct groups of states during the catalytic cycle, which are traditionally designated as E1 and E2 (Figure 24a).²²² In the E1 state, the ATPase has a high affinity for Ca²⁺, whereas in the E2 state, it has a low affinity for Ca²⁺. The ion-binding sites, which are located within the transmembrane domain, are open toward the cytoplasm in the E1 state and toward the lumen of the SR (or extracellular side) in the E2 state. Crystal structures of SERCA have been determined for various physiological states.^223,224 The basic structure of SERCA comprises a large cytoplasmic headpiece, a transmembrane domain made of 10 (M1-M10) α-helices, and short lumenal loops (inside the sarcoplasmic reticulum). Four of the transmembrane helices, M2-M5, have long cytoplasmic extensions. The cytoplasmic headpiece consists of three domains, which are referred to as actuator (A), nucleotide binding (N), and phosphorylation (P) domains. A large global conformational change takes place during the reaction cycle: the three cytoplasmic domains (A, N, and P domains) are separated in the E1·2Ca²⁺ state into a Y-shaped conformation (left schematic in Figure 24b) but tightly packed in a compact conformation in the other states (right schematic in Figure 24b).

Figure 24.

ATPase reaction and structure of sarcoplasmic reticulum Ca²⁺-ATPase 1a (SERCA). (a) Simplified Albers–Post scheme for Ca²⁺-ATPase reaction. (b) 3D structures of E1Ca²⁺ and E2(TG) forms of SERCA in lipid bilayer: Reprinted with permission from ref (224). Copyright 2003 John Wiley & Sons, Inc.

From this global structural change, the height of the E1·2Ca²⁺ intermediate is smaller (short (S) state) than those of the other intermediates (tall (T) states). According to the simplified Albers–Post scheme (Figure 24a), the S → T transition is expected to take place depending on the ATP concentration, while the T → S transition is expected to take place depending on the Ca²⁺ concentration. To clear these issues experimentally, Yokokawa and Takeyasu observed the dynamic height changes of SERCA in real time, using HS-AFM.⁴⁹

Purified SR vesicles containing SERCA were briefly treated with a detergent, deocycholate (DOC), to break the vesicles. The DOC-treated SR sample was adsorbed on a bare mica surface. The resulting membrane fragment had a thickness of 5.1 ± 0.6 nm on mica surface. The SR membrane contained well-isolated SERCA molecules with a density less than a few molecules per μm². The molecules in the membrane were essentially immobile (very slowly diffusing) with an averaged 2D diffusion coefficient of 0.4 ± 0.2 nm²/s, although the reason for this immobility was unspecified. The immobility allowed the repeated height measurements of a single molecule for relatively long time periods with single-line scanning^225,29 and imaging by HS-AFM.

Figure 25a shows successive AFM images of a SERCA molecule in the membrane captured at an imaging rate of 1 fps in the presence of both 10 nM ATP and 100 μM free Ca²⁺. The cross sections along the X- and Y-axes vaguely showed height and shape changes between the T and S states of the SERCA molecule, likely corresponding to compact and Y-shaped conformations, respectively. The single line scanning, in which an AFM tip was repeatedly scanned along the X-axis only, now clearly displayed rapid up-and-down motion of SERCA as a spike wave with an average lifetime of 0.15 ms (Figure 25b, arrowhead in the lower panel). As expected, when the ATP concentration was increased to 1 μM, the frequency of spike wave appearance was significantly increased (Figure 25c), whereas the lifetime of individual spike waves was independent of the ATP concentration. The short-lived SERCA in the T state was 2.3 ± 0.4 nm taller than that in the S state (n = 65). This value of height increase is consistent with the height difference between the E1·2Ca²⁺ form and the other more compacted forms of SERCA (E1ATP, E1P, E2P, and E2) in the X-ray crystallographic structures.²²³ To confirm this correspondence, the height of SERCA from the membrane surface was analyzed to produce histograms (Figure 26). The average height was 5.4 ± 0.8 nm in the presence of 100 μM free Ca²⁺ without ATP (Figure 26a), which is in good agreement with the height of the cytoplasmic domain estimated from the X-ray crystallography data of the E1·2Ca²⁺ form (S state). At a lower free Ca²⁺ concentration (10 nM), the height was similar to that measured in 100 μM free Ca²⁺ without ATP (Figure 26b). In contrast, in the presence of 10 μM thapsigargin (TG), which is known to retain SERCA in a form analogous to E2,²²⁶ the histogram showed two peaks around 5.4 ± 0.7 and 7.2 ± 1.0 nm (Figure 26c). These results strongly supported the inference that the height change observed in the presence of ATP and Ca²⁺ is caused by the conformational change between E1·2Ca²⁺ and the other compact forms of SERCA during the ATPase reaction cycle.

Figure 25.

HS-AFM imaging of SERCA dynamics in the presence of nucleotide and Ca²⁺. (a) Successive HS-AFM images in the presence of 10 nM ATP and 100 μM free Ca²⁺ captured at a frame rate of 1 fps. The cross sections along the X- and Y-axes are shown in the corresponding lower panels. The broken line indicates a height of 5.5 nm from the membrane surface. (b,c) Single line scan (2D observation) HS-AFM images of SERCA in the presence of 100 μm free Ca²⁺ and in the presence of (b) 10 nM and (c) 1 μM ATP, respectively. The lower panels show the X-axis cross sections positioned at the line indicated by the arrow beside the 2D HS-AFM images. Reprinted with permission from ref (49). Copyright 2011 John Wiley & Sons, Inc.

Figure 26.

Histograms of the height differences between the top of SERCA and the surface of the membrane. Statistical section analyses of SERCA were performed with the data obtained in the presence of (a) 100 μM free Ca²⁺ (n = 78), (b) 10 nM free Ca²⁺ (n = 54), and (c) 10 nM free Ca²⁺ and 10 μM TG, after 30 min incubation (n = 82). The lines are Gaussian fits for the histograms. Reprinted with permission from ref (49). Copyright 2011 John Wiley & Sons, Inc.

The height change of SERCA molecules was measured in the presence of various ATP concentrations and two different free Ca²⁺ concentrations (Figure 27a). In lower Ca²⁺ concentration (10 nM), spike waves (quick up-and-down changes) were only rarely observed; instead, the lifetime of the elevated conformation became remarkably longer (>200 ms) provided that a concentration of ATP > 10 nM was present. The long lifetime of the elevated conformation at low Ca²⁺ concentration could have resulted from lowered ATPase activity in low Ca²⁺ concentrations.²²⁷ On the other hand, in higher Ca²⁺ concentration (100 μM), the number of spike waves increased with increasing ATP concentration. Therefore, as expected, the T → S transition occurred depending on Ca²⁺ concentration, meaning that this transition takes place at the Ca²⁺-binding step (E1 → E1Ca²⁺ transition), and that the E1 state, whose conformation has not yet been resolved, also has an elevated conformation.

Figure 27.

Typical single line scan height data of SERCA obtained with different solution conditions. (a) Representative single line scan data obtained at increasing ATP concentration in the range 0–100 μM and in the presence of 10 nM and 100 μM free Ca²⁺. (b) Single line scan data for ∼2 s in the presence of both 1 mM ATP and 100 μm free Ca²⁺. The lower and higher broken lines indicate heights of 5.5 and 8.0 nm measured from the membrane surface, respectively (a, b). Reprinted with permission from ref (49). Copyright 2011 John Wiley & Sons, Inc.

Under near physiological conditions (1.0 mM ATP and 100 μM free Ca²⁺), SERCA molecules appeared to maintain the elevated conformation for a long time without T → S transition (Figure 27b). Spikes were not observed even with a much faster X-line scanning rate up to 1 kHz, which corresponded to a time resolution of 50 μs (i.e., the cantilever tip stayed on the molecule for 50 μs). This fact suggested two possible explanations: one is that the lifetime of E1Ca² is <50 μs; the other is that SERCA has no shorter conformation under high ATP concentrations (> ∼1 mM). Considering the activation effect of high concentrations (> ∼1 mM) of ATP on the ATPase activity and the Ca²⁺ uptake²²⁸ as well as the ATP concentration-independent lifetime of the elevated conformation, it was proposed that SERCA would not transit through the E1Ca²⁺ state at ATP concentrations higher than ∼1 mM, and hence would follow a catalytic pathway different from the ordinary Albers–Post scheme. However, the possibility that the lifetime of E1Ca² is much shorter than 50 μs, or the possibility that the chemical state of E1Ca²⁺ does exist but there is not sufficient time for E1Ca²⁺ to take a shorter conformation, cannot be ruled out.

8.5.4. P2X₄ Receptor in Response to ATP

P2X receptors are ATP-gated membrane cation channels transferring cations across the membrane from the extracellular side to the cytoplasmic side. Seven subtypes of subunits (P2X₁–P2X₇) have been identified.²²⁹ The channels are formed as multimers (mainly trimers) of subunits, homomeric or heteromeric channels.²³⁰ Each subunit has a large extracellular domain capable of binding ATP, two transmembrane domains responsible for the formation of the channel gate, and small N and C terminal intracellular domains.²²⁹ All P2X receptors are permeable to small monovalent cations, and some have significant Ca²⁺ or anion permeability.²³¹ P2X receptors are abundantly distributed and involved in diverse physiological processes from synaptic transmission to inflammation and sensation of taste and pain.²³¹ The crystal structure of the zebrafish P2X₄ receptor (P2X₄R) in the resting closed-channel state was recently solved (Figure 28a,b).²³² The three ATP binding sites are located at the intersubunit interfaces within the trimer, suggesting that ATP binding promotes subunit rearrangement and ion channel opening. The ion channel opening of P2X₄R is regulated by the extracellular Ca²⁺ level.²³³ Electrophysiology studies have shown that P2X₄R opens a small cation-permeable channel pore at a high concentration of Ca², whereas in the absence of Ca²⁺, it forms a large pore allowing permeation of large cationic molecules.²³⁴ However, structural studies on the channel opening and Ca²⁺ effects on it have been absent until the following HS-AFM study by Shinozaki and collaborators.³⁶

Figure 28.

Structure of P2X₄ receptor. (a) Atomic structure of N and C termini deletion mutant of homotrimeric P2X₄ receptor viewed parallel to the membrane. Each subunit is depicted in a different color. The gray bars suggest the boundaries of the outer (out) and inner (in) leaflets of the membrane bilayer. (b) Atomic structure of N and C termini deletion mutant of homotrimeric P2X₄ receptor viewed from the molecular 3-fold axis (from the extracellular side). Reprinted with permission from ref (232). Copyright 2009 Nature Publishing Group. (c) Successive AFM images showing ATP-induced structural changes of P2X₄ receptor. Before activation, P2X₄ receptor was in circular shape and exhibits some fluctuation (−2.5 to ∼0.0 s). Caged ATP (200 μM) was uncaged at 0 s, after which the structure of P2X₄ receptor changed to a trimer structure within 0.5 s. P2X₄ receptor then exhibited a further structural change and adopted a pore dilation-like conformation. Note that the images are not directly captured ones but are those obtained by averaging images of 10 P2X₄ receptor particles to reconstruct 3-fold symmetric images at given elapses of time.

First, isolated (membrane-dissociated) P2X₄R attached to polylysine-coated mica was imaged in the absence of ATP and Ca²⁺. The still images showed circular, ellipsoid, or triangular particles, although their sizes were approximately similar to each other (12.6 ± 0.2 nm in diameter and 2.3 ± 0.1 nm high). The height value of 2.3 nm is much smaller than the values of either the height or the width of the molecule estimated from the atomic structure of P2X₄R:²³² the distance between the ends of the extracellular and intracellular parts (9.8 nm); the width of the extracellular top face (7.5 nm). The reason for this large discrepancy is unclear. Moreover, the orientation of observed P2X₄R molecules on the polylysine-coated mica surface could not be judged from their images and size values. When 100 μM ATP was added, no significant changes appeared in the P2X₄R images, but addition of 1 mM ATP induced large structural changes of P2X₄R after several to 30 min. The reason such a long incubation time and high concentrations of ATP were required for evoking the large structural changes was claimed to be due to ATP adsorption on the polylysine-coated surface. Yet this is unlikely, considering the ATP binding capacity of the surface. In 1 mM ATP, most of the molecules appeared to be trimers with a diameter of 14.2 ± 0.2 nm, a height of 3.0 ± 0.1 nm, and a distance between lobes of 8.7 nm ± 0.1 nm. The trimer appearance implied that the molecules would mostly stand on the substrate with the extracellular top face up, which would be however hardly understood because the observed height (3.0 nm) was much smaller than the distance between the extracellular and intracellular ends (9.8 nm) and because the smaller surface (∼3 nm in diameter) of the N- and C-terminal intracellular domains would hardly bind to mica surface preferentially. The imaged trimers did not exhibit a three-fold axis of symmetry but heterogeneous asymmetric shapes. This appearance suggested that the molecules do not stand upright but lean on the substrate surface.

For time-lapse imaging of P2X₄R at 2 fps, the sample was placed on a bare (i.e., no polylysine-coated) mica surface and imaged. Under this condition, many P2X₄R molecules shifted position during imaging, but some were successfully imaged. The images again often showed asymmetric shapes, indicating that the molecules leaned sideward on the mica surface. To observe the time course of ATP-induced structural changes of P2X₄R, flash photolysis of caged ATP was used (200 μM). Upon flash photolysis, individual subunits became visible, and the subunit–subunit distance gradually increased, but the images were blurry. Because symmetric molecules were not observed and the images were blurry, a single-particle correlation averaging method was applied to reconstruct 3-fold-symmetric images. The symmetrized images showed that the trimeric structure became more evident with time and that the central pore was being dilated with time (0–5 s) after uncaging of caged-ATP without Ca²⁺ (Figure 28c).

Next, P2X₄R reconstructed in a lipid bilayer on a mica surface was imaged. In the absence of ATP, the appearance of P2X₄R was circular with 11.4 ± 0.3 nm diameter and protruding 1.8 ± 0.1 nm high from the lipid bilayer surface. This height value was again too small as compared to the height of the extracellular part in the atomic structure (7 nm). In the presence of ATP, P2X₄R showed a trimeric structure with 13.3 ± 0.3 nm diameter and 2.1 ± 0.1 nm high from the lipid bilayer surface. The trimeric structure was more apparent as compared to that observed with isolated P2X₄R but was asymmetric again. The reconstructed 3-fold-symmetric images of P2X₄R in ATP again showed pore dilation. On the other hand, in the presence of 2 mM Ca²⁺, no pore dilation occurred in the 3-fold-symmetrized images that were reconstructed from raw images obtained several seconds after uncaging of caged-ATP. To confirm the Ca²⁺-dependence of large molecule permeation through P2X₄R reconstructed in a lipid bilayer, an ethidium bromide (EtBr)-uptake assay was performed as follows. The lipid membrane containing P2X₄R was suspended over a 500 μm hole filled only with a buffer solution. In the external side, an EtBr solution with or without Ca²⁺ was placed. In the absence of Ca²⁺, the red fluorescence of EtBr started increasing in the hole within a few seconds after the addition of ATP and then increased gradually. On the other hand, in the presence of 2 mM Ca²⁺ in the external solution, no increase of fluorescence was observed. Thus, the P2X₄R sample reconstructed in the lipid membrane was confirmed to be active. Therefore, the ATP induced pore dilation observed in the absence of Ca²⁺ was verified to be relevant to the conformational change of P2X₄R responsible for the permeation activity. Nevertheless, two issues remain elusive in this HS-AFM imaging study. First, the observed heights of the isolated P2X₄R and the exposed part of the membrane embedded P2X₄R do not compare favorably with those revealed by the atomic structure of P2X₄R published after this HS-AFM study. It has often been recognized that the height of protein molecules appears smaller than the real height when they are strongly adsorbed on substrate surfaces. However, it seldom occurs when protein molecules are placed on or embedded in inert lipid bilayers. Second, it is unclear whether the observed asymmetric structures are inherent to this receptor protein.

8.6. Diffusion and Interaction of Membrane Proteins

The diffusion and interaction dynamics of membrane proteins are emerging topics in membrane biology. Their importance has been recognized with the paradigm shift of the scientists’ view of the membrane superstructure (e.g., ref (235)): In the early 1970s biologists conceptualized the cell membrane as a 2D fluid of lipid molecules in which the relatively few membrane proteins freely diffuse.²³⁶ This concept has been amended over the last 30 years (e.g., ref (237)), because indirect experimental evidence accumulated that the membrane features a highly heterogeneous, complex, and intricate superstructure, laterally compartmentalized, densely packed, locally even rigid, and organized. It goes far beyond the objective of this Review to overview the data that led to this conceptual change, but the major contributions came from optical microscopy showing anomalous diffusion behavior of membrane constituents trapped in compartments and/or assembling into clusters, biochemical data showing the existence of supercomplexes of membrane proteins of very high molecular weight and nonsolubilizable membrane domains, and from freeze-fracture and tomography EM analyses revealing densely grained membrane areas. It has, however, so far remained impossible to visualize a native membrane at molecular resolution and describe the structure, dynamics, and interactions of membrane proteins within it at high spatial and temporal resolution. Conventional AFM has been successful in some cases and provided high-resolution views, which was however limited to highly specialized membranes with exceptional protein arrangement and density such as photosynthetic membranes or lens membranes.^15,238 Light microscopy has undergone dramatic progress in the recent years, with a significant improvement of the localization resolution of membrane constituents under native conditions.²³⁹ However, the resolution is molecular at best and is based on the high spatial localization of a single labeled protein, implying that one cannot see a second protein in close proximity to the first. Electron microscopy has equally progressed for superstructural analysis notably with the development of tomography of vitrified samples.²⁴⁰ This technique however analyzes samples at low temperatures and in ultrahigh vacuum and is therefore unable to observe dynamics. Furthermore, it is a somewhat less powerful technique for the observation of membrane integral constituents, because the contrast between the atoms of the transmembrane proteins and the lipids is limited. Biologically, the diffusion and interactions of membrane proteins are of crucial importance. These features facilitate the cell to reorganize proteins in space and in time, to form temporal functional units to perform a particular biochemical function,, or to modulate the function of a membrane protein.²⁴¹ HS-AFM appears therefore as a particularly promising tool for the study of membrane protein structure, dynamics and interactions: (i) its high signal-to-noise ratio allows direct visualization of individual membrane proteins without labeling, (ii) the label-free submolecular resolution imaging quality warrants additionally the analysis of the molecular environment in the field of exploration, and (iii) the high spatiotemporal resolution of about 1 nm and 30 ms allows the assessment of characteristic physical parameters of diffusion and interaction like diffusion constants and properties, and interaction strength and geometry in great detail. Indeed, while optical microscopy works at comparable frame rate, only the high-resolution imaging capacity of HS-AFM allows the direct visualization of the molecule itself and the partner molecules, opening a novel avenue of structural and dynamical studies of protein–protein interaction in lipid membranes, which will be described below.

8.6.1. Interaction between bR Trimers in 2D Crystal Lattice

By observing bR trimers diffusing in the noncrystalline area in the purple membrane and their temporal interaction with the crystal edges using HS-AFM, the energy for association between bR trimers through hydrophobic stacking interaction between aromatic residues was estimated.³⁴ Successive HS-AFM images of the purple membrane frequently showed repeated association and dissociation of bR trimers at the crystal edges (Figure 29a), indicating that the bR crystal is in dynamic equilibrium with bR molecules located in the noncrystalline area. In Figure 29a, bR trimers in the crystal are highlighted by the thin-lined triangles. At 0.6 s, two bR trimers (red triangles) were newly bound to the crystal edge. At 2.1 s, two bR trimers (white triangles) dissociated, and another trimer (red triangle in the top of image) was bound to the crystal edge. One of the two dissociated trimers remained in the crystal edge for ∼0.9 s. Not only bR trimers but also bR dimers and monomers were observed to bind to and dissociate from the crystal edge, these much less frequently than trimers. The bound lifetimes of bR monomers and dimers were shorter than that of trimers. Among many observed binding events, the binding of trimeric bR occurred predominantly (82%), indicating that trimers are mostly formed and stable in the noncrystalline region.

Figure 29.

Association and dissociation of bR molecules at crystal edges captured by HS-AFM. (a) Clips of successive HS-AFM images on the borders between the bR crystal and noncrystalline areas (imaging rate, 3.3 fps). The bR trimers in the crystal are encircled by thin lined triangles. Newly bound (0.6 s) and dissociated (2.1 s) trimers are indicated by red and thick lined white triangles, respectively. (b) Schematic representing the binding manner of a trimer at the crystal edge (I, II, and III) and in the crystal interior (VI). Roman numerals indicate the number of interaction bonds (dotted lines) containing W12 residue. (c) Histograms showing lifetimes for the type II and III binding events. The histograms were fitted with single-exponential functions (dotted lines).

The intertrimer interaction energy was estimated from the bound lifetime of newly associated bR trimers at the crystal edge and its dependence on the number of interaction sites. From the packing arrangement of bR trimers in the 2D crystal, each trimer appears to interact with the surrounding trimers through six sites, as illustrated by the dotted lines in Figure 29b (see the case marked with “VI”). As exemplified in Figure 29a, successive AFM images showed many association and dissociation events, in which bR trimers were bound to different sites at the border between the crystal and noncrystalline areas. These events were classified into types “I”, “II”, and “III” depending on the number of interaction sites involved. Type II binding events were predominant (74%), whereas type I (6%) and type III (20%) events were less frequent. The type I binding events occurred with too short bound lifetimes to appear in clear images, preventing reliable statistics. Figure 29c shows histograms of the lifetimes of type II and type III bindings that were measured using HS-AFM images taken at an imaging rate of 10 fps. Each histogram was well fitted by a single exponential function. The average lifetimes τ₂ of type II binding and τ₃ of type III binding were estimated to be 0.19 ± 0.01 and 0.85 ± 0.08 s, respectively. The longer lifetime of type III binding than that of type II obviously arises from a relationship of E₃< E₂< 0, where E₂ and E₃ are the association energies responsible for type II and type III interactions, respectively. The average lifetime ratio, τ₂/τ₃, is given by τ₂/τ₃ = exp[(E₃ – E₂)/k_BT] (T is room temperature in Kelvin). Because the type II and III bonds involve two and three elementary bonds, respectively, the energy difference E₃– E₂ should correspond to the association energy of the single elementary bond formed by hydrophobic stacking interaction between W12 and F135.⁶¹ This elementary association energy was estimated to be about −1.5 k_BT from the ratio of τ₂/τ₃ = 0.22. This value approximately coincides with that measured by differential scanning calorimetry.²⁰⁹

8.6.2. Interaction of C-Rings in Purple Membrane

Although less abundant than bR, the purple membrane of H. salinarum also contains an ATP synthase that uses the transmembrane proton gradient generated by bR to produce ATP. Little is known about this ATP synthase: It is an A-ATP synthase (A for archaea), but sequence analysis indicates similarities to both F- and V-type ATP synthases.²⁴² Despite extensive studies of purple membranes using conventional AFM,²⁰⁵ these molecules have long escaped being observed, probably due to their mobility outside the crystalline bR arrays. Taking advantage of the fast frame acquisition rate of HS-AFM, A-ATP synthase c-rings were observed in the lipid bilayer regions at the edges of bR 2D lattices (Figure 30).³⁸ Mass spectroscopy of the investigated sample corroborated the presence of proteins with a mass of 7517 and 7618 Da corresponding to the native c-ring sequence.²⁴³ C-rings occurred as rings with 6.5 ± 0.5 nm diameter and 1.8 nm protrusion height, which formed dimers in the membrane. Dimer formation has been described for mitochondrial ATP synthases, but the prokaryotic homologues have been thought to be monomers. The data hence suggested that the A-ATP synthase forms superstructures reminiscent of those found in mitochondria.^244,245 The dynamic HS-AFM imaging allowed one to monitor the interaction of the c-rings in the membrane plane at 5.35 fps.³⁸ The c-ring interaction was highly dynamic; the center-to-center distance changed as a function of time (Figure 30a), and sometimes one c-ring even dissociated from the assembly (Figure 30a, arrows). Hence, three different c-ring association states occurred (Figure 30b): the monomer, when one c-ring was found without a partner molecule, the close dimer, when two c-rings were in direct contact and the center-to-center distance was between 8.0 and 10.0 nm, and the elongated dimer, when two c-rings were separated with center-to-center distances of about 12.0 nm. The mean square displacement (MSD) as a function of the lag-time Δt revealed different diffusion regimes for the c-ring monomer and dimer states. Fitting the generalized diffusion equation MSD ∝ Δt^α to the experimental data, the exponent α reported free diffusive and subdiffusive behavior for the monomer and dimer, respectively. The corresponding diffusion constants D were 125 and 1.5 nm²/s, following MSD = 4DΔt. From the dynamic description of the c-ring interaction, a distance-dependent probability density function could be derived (Figure 30c, left) that could be translated into an interaction energy profile, p(d) = p_∞ exp[−E(d)/k_BT] (Figure 30c, right), where p(d) is the distance dependent probability, E(d) is the related interaction energy, and T is 300 K. This energy landscape described the c-ring interaction with a maximum strength of −3.5 k_BT at a center-to-center distance of about 10.3 nm. At shorter distances, soft hard-body repulsion occurred, probably originating from the contact and intercalation of exposed amino acid side chains. Center-to-center distances shorter than 8.0 nm were never observed. From the favorable center-to-center distance of 10.3 nm, the interaction energy landscape described an attractive regime that extended by a radius of about 3.5 nm in the membrane plane. Membrane-mediated protein–protein interaction has been intensively studied by theory and computation, depicting an interaction profile with an attractive well at short distance (about 5 nm around a protein) that can be extended by a faint attractive regime at larger distance.²⁴¹ The general idea has emerged that the membrane protein perturbs the lipid bilayer structure and that the proteins associate to each other to minimize the energetic cost of this perturbation. Typically, the membrane proteins force the bilayer to bend so as for it to adapt to the rigid hydrophobic core of their transmembrane segments; this bending is predicted to relax over a distance comparable to the bilayer thickness. In agreement, HS-AFM measurements showed that the lipid bilayer between the two c-rings, even if these were in an elongated dimer conformation with up to 3 nm lipid bilayer space between them, adapted to the hydrophobic thickness of the protein and was 0.5–1.0 nm thicker, as compared to the bilayer environment far from the c-rings. Furthermore, the interaction energy landscape showed that at a center-to-center separation of 12.5 nm, hence at an elongation distance of about 4 nm from protein–protein contact (in good agreement with the bilayer thickness), the attraction was only about −1 k_BT, and hence thermal motion could separate the two proteins, in good agreement with theoretical considerations.

Figure 30.

H. salinarum ATP-synthase c-ring motion monitored by HS-AFM and energy profile of interaction between c-rings. (a) A series of HS-AFM images over a time span of 1309 ms (clipped from a longer movie) for two ATP synthase c-rings in dynamic interaction (imaging rate, 5.35 fps). Two c-rings assembled in a dimer that dynamically changed the center-to-center distance. Rarely, the dimer dissociated and a monomeric c-ring remained (t = 561) until a diffusing c-ring approached the attractive regime of the monomeric c-ring (t = 748 and 935 ms) and associated (t = 1122 ms). Arrows indicate diffusing c-ring monomers. (b) Three examples of ATP-synthase c-ring assemblies. (Left to right) Close dimer (center-to-center distance 80 Å); elongated dimer (center-to-center distance 120 Å); and monomer. (c) Interaction between ATP synthase c-rings as a function of center-to-center distance: (left) histogram (n = 91) of the center-to-center distance of c-rings; (right) energy landscape of membrane-mediated interaction between c-rings.

8.6.3. Interaction of AQP0 in Native Eye Lens Membrane

As seen in the above analysis of bR and A-ATP synthase c-rings in native purple membranes, HS-AFM has proven powerful in revealing the interaction dynamics and energy and conformational changes of bacterial membrane proteins.^34,38 However, a step toward a deeper understanding of membrane structure and membrane protein interaction can be gained from eukaryotic systems. In eukaryotic cell membranes, a variety of phospholipids are found, and, importantly, nonphospholipid membrane constituents such as cholesterol are evidenced to drive membrane superstructure.²⁴⁶ The variety of constituents with different physicochemical properties leads to a natural segregation of the membrane constituents, given that not all interactions are in the range of k_BT. Indeed, this led to the concept of mosaicity of the membrane, supported by indirect biochemical and biophysical data.^235,237 This vision of the membrane comprises both structural and dynamic aspects. Therefore, HS-AFM appeared to be a most promising tool to investigate membrane constituent segregation in eukaryotic systems.²³⁷ This is, however, not so easy, because the membranes must be purified from a mammalian tissue, and sufficient purity must be achieved for analysis by HS-AFM while it must be assured that the native assembly of the membranes remains unaltered. In mammalian eye lens cell membranes, membrane channels form supramolecular domains termed junctional microdomains responsible for metabolite flux, ion and water transport, and cell–cell adhesion.^247,248 Junctional microdomains are mainly constituted of lens-specific aquaporin-0 (AQP0) and connexins (Cx), the first forming stable tetramers and the second hexamers termed connexons. AQP0 and Cx constitute about 60% and 15%, respectively, of the entire membrane protein amount. Conventional AFM allowed the characterization of the supramolecular arrangement of these proteins in junctional microdomains at high resolution, showing the AQP0 assembly in regular square arrays edged and separated by densely but nonregularly packed connexons.²³⁸ Both of these membrane proteins are not only channels, but act as cell adhesion molecules by means of their extracellular loops that interact homotypically with the proteins from the neighboring cell; two head-to-head assembled AQP0 tetramers form a so-called thin-junction, and two head-to-head assembled Cx hexamers form a so-called gap-junction.^249,250 HS-AFM provided novel insights into both the vertical (cell–cell adhesion) and the lateral (domain formation) associations of these junctional microdomain proteins.⁵⁹ The lens cell membrane preparations maintained the native double membrane architecture of the junctional microdomains (Figure 31a, frame t = 0.0 s). Taking advantage of the nanomanipulation capacity of the cantilever tip, HS-AFM in contact mode under application of additional forces allowed the dissection of junctional microdomains (Figure 31a). Analysis of the junctional microdomain areas and circumference as a function of time during microdomain dissection revealed that the adhesion function of the proteins was cooperative; entire membrane patches dissociated at once (Figure 31a, compare frames t = 14.7 and 19.6 s). From this study, the size of adhesive units could be determined as about 100 × 100 nm² assembly of about 250 AQP0 tetramers, in agreement with imaging of the junctional microdomain architecture. Additionally, by imaging of the double layer (prior to dissection) and the single layer (following dissection), junctional microdomains proved to be the homotypic head-to-head association of AQP0 and connexons for cell–cell-adhesion (numbered (1) and (2) in Figure 31a). After junctional microdomain dissection, the extracellular face of the proteins could be studied on the single layers at high resolution. AQP0 was arranged in a characteristic square lattice with 6.3 ± 0.1 nm unit cell dimension and about 1 nm protrusion height, edged by connexon rings that were nonordered and protruded further by about 2 nm. HS-AFM medium resolution observations readily revealed protein motion at the edges of the junctional microdomains. Following, high spatial and temporal resolution HS-AFM imaging (single-molecule resolution at 4 fps) of the junctional microdomains depicted the assembly of AQP0 and connexons to and their disassembly from junctional microdomains (Figure 31b). Following the same statistical analysis of the image series as has been performed on bR,³⁴ the molecules associating with and dissociating from the microdomain edge were classified according to the number of their intermolecular contacts (Figure 31b, arrows), although only relevant statistics for molecules making one and two neighbor contacts could be assessed, and their residence lifetimes at these positions were evaluated. Lifetimes of τ₂ = 9.8 ± 0.5 s and τ₁ = 0.7 ± 1.0 s were found for AQP0 with two and one neighbors, respectively. Using τ₁/τ₂ = exp[(E_(two bonds) – E_(one bond))/k_BT], an interaction energy of −2.7 k_BT was determined for a single AQP0–AQP0 interaction. To test these experimental results, a single parameter Monte Carlo simulation was run following p_(diss) = exp[(n × E_(bond)/k_BT)], where p_(diss) was the probability of an AQP0 to dissociate, n is the number of neighbors, and E_(bond) is the energy per single bond. Such simulations (over 300 000 simulation steps) with the use of the experimentally determined energetic term of −2.7 k_BT (independent of the molecular concentration at the beginning of the simulation) showed AQP0 assembly in silico forming junction microdomains. In contrast, simulations at lower −1.7 k_BT or higher −3.7 k_BT interaction energies either prohibited formation of domains or formed domains with noncharacteristic morphology. Finally, connexons were revealed to have a different association behavior; their final arrangement was nonordered. Additionally, connexons associated and dissociated so rarely that the dynamics could only sporadically be observed by HS-AFM, precluding determination of an energy term that should be higher than that of AQP0. However, this stability might well be related to their function as molecules sustaining relevant forces in cell–cell adhesion.²⁵¹

Figure 31.

HS-AFM analysis of vertical and lateral association of lens-specific AQP0 in native eye lens membranes. (a) Contact mode HS-AFM imaging of eye lens junctional microdomains during nanodissection captured at 1.02 fps. Initially two stacked membrane layers were images (frame t = 0.0 s) from which the top layer is sequentially removed in distinct membrane fractions of area of about 10 000 nm² (from t = 4.9 s to t = 38.2 s). Finally, the entire top membrane of the junctional microdomain was removed (t = 70.5 s), revealing that the bottom layer comprised protein domains of the same shape and localization as the top layer (labeled with 1 and 2, in frames t = 0.0 s and t = 70.5 s). (b) High-resolution HS-AFM visualization of AQP0 tetramers in dynamic association to and dissociation from square AQP0 array (imaging rate, 4 fps). The assembly and disassembly of AQP0 occurring at the edge of the junctional microdomain array were observed (see arrows in frames t = 0.0 s and t = 2.5 s).

8.6.4. Diffusion and Interaction of OmpF

HS-AFM imaging of the diffusion and interaction of OmpF provided the most detailed information and maybe the most general insights to date about membrane protein interactions in the lipid plane.⁵⁸ OmpF and its homologues are widely distributed on the cell surface of many bacteria, where they act as an ion and solute channel and for phage recognition, and form a transient translocon complex with vitamin B12 receptor BtuB for colicin import.^252−254 In the outer membrane of E. coli, there are about 10⁵ OmpF copies inserted, covering at least 50% of the cell surface.^255,256

OmpF were reconstituted at a realistic protein density of about 50% membrane coverage into a bilayer containing all of the lipid constituents of the native E. coli system. In particular, the presence of lipopolysaccharides associated in complex with OmpF was assured. HS-AFM allowed the analysis of the structure and dynamic aspects of about 70 OmpF trimers in each frame at high spatial and temporal resolution; individual subunits were resolved, and movie acquisition rates were 2–5 fps. From a static point of view, the proteins embedded at low 50% density in the fluidic lipid bilayer were found to be loosely distributed over the membrane at any instant during the observation (Figure 32a). To assess the protein distribution quantitatively, fractal analysis, using the box method, was performed. In this in silico procedure, the individual protein outlines were compared to overlaid square boxes of various sizes. Boxes that fall into the field of the protein outlines were scored. The logarithm of the number of boxes within the protein regions then was plotted versus the logarithm of the size of the boxes to quantify the fractal dimension D defined by the slope of the plot. The OmpF distribution in the membrane had a high value of D ≈ 1.7, while a simulation of OmpF arranged in a 2D-crystal gave D ≈ 1.0. Such a high fractal dimension is characteristic of diffusion-limited aggregation;²⁵⁷ hence the molecular movements result in a dynamic equilibrium and arrange at any instant for the proteins to be exposed to a wide variety of molecular surfaces in the membrane plane. Beyond this case example, the calculation of the fractal dimension appears to be an appealing quantity to assess membrane protein assembly, as it reports in a single number the complexity of the molecular distribution mosaicity. Moving from static to dynamic analysis, a wide distribution of dynamic behaviors of individual proteins was observed; some molecules participated in stable associations with others (Figure 32a, outline 1), while some diffused in less dense membrane regions between the aggregates (Figure 32a, outline 2). The effect of the local membrane crowding on the dynamics of the molecules, which was determined by Voronoi tessellation, showed that diffusion scaled roughly in inverse relation to the local protein density (Figure 32b). The Voronoi cell area histogram described roughly a Gaussian distribution with smallest Voronoi cells of about 7000 Ų and largest cells of about 20 000 Ų, peaking at about 12 000 Ų (Figure 32b). In comparison, OmpF packed in 2D crystals within a membrane area of 5500 Ų per trimer.²⁵⁸ In agreement with the membrane area dispersion, some molecules displayed corralled subdiffusive behavior (Figure 32b, outline 1), and others diffused freely (Figure 32b, outline 2) with a slope of 1.1 in a log(MSD) versus log(Δt) plot and with a maximum displacement velocity of about 25 nm/s. Because the diffusion behavior and the local membrane density were coupled, averaging of the local molecule velocities showed that certain membrane areas were favorable for molecular motion while others were in a static phase. Close inspection of the molecules that remained stable over 2 min of HS-AFM movie recording showed that these proteins were associated with other channels in specific aggregation conformations using specific surface interactions. Interestingly, these interactions often implied a symmetry relation with the neighbor molecule, such as dimers arranged in a p2 symmetry with 72 Å center-to-center distance or trimers arranged in a lattice of p3 symmetry reminiscent of that adopted by bR, with 86 Å center-to-center distance. Statistical analysis of the interaction between the proteins that were in dynamic encounter and dissociation from each other showed that OmpF channels followed a specific interaction pathway. It appeared that the interaction contact sites at the periphery of the molecule were the last stable contact points before dissociation and could mediate processes into stable assembly. Indeed, the interaction pathway implied sliding and rotational motion of OmpF on the surface of the neighbor molecule; the molecules were going from the closest association with a center-to-center distance of ∼7.2 nm (where the two flat surfaces of the proteins were intercalated into each other with p2 symmetry over an asymmetric association) to another configuration with p2 symmetry, where the partners were only in contact at the periphery of the molecules with a large center-to-center distance of ∼10 nm. This finding was similar to the HS-AFM observation of specific interactions of bR molecules via exposed aromatic residues,⁶¹ an aspect that should be tested further in future experiments. Coarse-grained molecular dynamics simulations²⁵⁹ have been used to analyze the interaction pathway computationally, which further underlines the importance of angular lipids in the membrane protein–protein interactions. HS-AFM imaging and such simulations agreed with each other in that several stable association patterns occurred and were dynamically adopted. The patterns ranged from an energetically favored association minimizing interaction distance and maximizing protein–protein interfaces to make protein–protein contacts via peripheral portions strongly mediated by the membrane lipids. This series of events and variety of conformations are in a dynamic equilibrium maintained by thermal energy, probably assuring the versatile functionality of OmpF in recognition and transport.

Figure 32.

HS-AFM analysis of the diffusion and interaction dynamics of trimeric OmpF. (a) High-resolution HS-AFM visualization of the dynamic movement of about 70 OmpF trimers in the membrane (imaging rate, at 2.1 fps). The resolution is high enough to allow determining the lateral position and the rotational angle of every single channel. (b) The effect of local membrane crowding on the diffusion behavior of individual OmpF trimers. The average position (black star) and positional standard deviation (black error bars) were determined for each molecule by the lateral and angular tracking of the proteins in subsequent frames (colored lines and arrows). From the average positions, the Voronoi tessellation of the membrane surface was calculated (black meshwork) depicting the free membrane area that each molecules experiences. Molecules housed in large Voronoi cells (i.e., large free membrane space) revealed high mobility, while molecules in locally and densely packed regions were essentially immobile. Four trimers in a rather solid association are outlined (1) in correspondence to the molecules outlined (1) in frame t = 1908 ms in (a). A highly mobile single molecule is outlined (2) corresponding to the molecule outlined (2) in frame t = 2385 ms in (a).

8.7. Self-Assembly Processes

Self-assembly is universal in biological systems and underlies the formation of a wide variety of ordered biological architectures. This strategy that nature has adopted is largely different from that we do to produce man-made machines, in which we need blueprints as well as process charts. In biological self-assembly, the blueprints and process charts are mostly encoded in the elements themselves to be assembled. Although molecular self-assembly is an excellent strategy for automated and energy-saved construction of large ordered structures in most cases, it sometimes works in a wrong way to produce substances detrimental to health, as typically exemplified in prion-related diseases. Thus, self-assembly of proteins in particular has been an important topic not only in biophysical studies and engineering applications but also in the studies of the pathogenesis of diseases and their prevention and treatment.^260,261

As is generally seen in self-assembly, protein self-assembly starts from the formation of nucleation clusters, which provide a low-energy barrier pathway to further growth. Multiple intermediates often appear during growth, and hence the growth process toward the final ordered structure usually proceeds through multiple sequential and parallel (i.e., branched) pathways with different kinetics.²⁶² Conformational transformations possibly occur in the intermediates, which control the self-assembly pathways and kinetics.²⁶³ As in the cases of polymerization of actin to actin filaments and tubulin to microtubules, small ligand molecules (e.g., ATP in the case of actin and GTP in the case of tubulin) and their chemical reactions are sometimes involved in protein self-assembly.²⁶⁴ Moreover, polarity or anisotropy exists in the assembled structures of proteins, and hence the assembly kinetics differs from one place to others in the growing structures. Thus, self-assembly of proteins is highly complex, and hence it is difficult to decipher the entire molecular process using static, nonvisualization, or ensemble-averaging approaches. HS-AFM can simultaneously visualize several assembly processes that are ongoing sequentially and in parallel at different portions of growing structures, and therefore is the most powerful approach to studying self-assembly of proteins as well as other molecules. Here, three examples of HS-AFM observations on self-assembly processes are described.^44,46,85

8.7.1. Amyloid Fibril Formation

Amyloids are fibrous protein aggregates, and their deposition is often found in tissues from patients with different types of diseases and disorders. Therefore, amyloids are associated with various diseases, particularly neurodegenerative diseases such as Alzheimer’s, Huntington’s, Parkinson’s, Creutzfeldt–Jacob, and prion diseases,^265,266 although in some cases amyloids are functional in living organisms.²⁶⁷ Rather than precipitated insoluble aggregates, intermediate aggregated species have recently been implicated in cellular toxicity and are likely to be the source of aberrant pathology in amyloid diseases.²⁶⁸ About 30 different proteins including peptides have been identified as the major components of the deposits associated with diseases. The propensity of proteins to aggregate into amyloid-like structures has been experimentally shown to be well correlated with a decreased conformational stability in the native state.²⁶⁹ Therefore, misfolding (or conformational changes) is believed to be prerequisite to amyloidogenesis in most cases. The structures of proteins in amyloid, intermediate species occurring in the growth process, and the outline of the growth kinetics have been well studied. Nonetheless, the dynamic processes and multiple pathways through which the fibers are formed have largely been elusive. Polarity/anisotropy-dependent growth kinetics has also been elusive because of a lack of useful techniques.

Lithosthatine (also named Reg-1) of 144 amino acids is a member of proteins that generate amyloid-like fibers. It is produced by pancreas acinar cells and secreted into pancreatic juice. It tightly binds to calcium carbonate and may act as an inhibitor of calcium carbonate precipitation to prevent clogging of pancreatic duct.²⁷⁰ In chronic calcifying pancreatitis, the protein forms deposits in the pancreatic duct. Lithosthatine is also expressed in other organs including stomach and brain. Lithosthatine is susceptible to self-proteolysis under specific pH conditions, producing a soluble N-terminal undecapeptide and a C-terminal fragment of 133 amino acids. The cleaved protein (called S1) forms protease-K-resistant fibrils²⁷¹ that deposit in the brain of patients with Creutzfeldt–Jacob disease and Gertsmann–Sträussler–Scheinker syndrome, especially during the very early stages.

HS-AFM was used to observe the fibrillization process carried out by lithosthatine.⁴⁶ Upon 15 min incubation of the S1 form of lithosthatine generated by tryptic digestion of the full-length protein, globular structures with 15–28 nm in diameter appeared. They seemed to be small assemblies of lithosthatine tetramers with 9 nm in diameter and 2.5 nm in thickness. After 30 min incubation, protofibril formation and its growth to longer protofibrils and thicker fibrils were observed (Figure 33). Because no entities (monomers or small oligomers) to be added to the growing ends were visible, they must be floating and diffusing in the bulk solution. Lengthening of protofibrils took place at 27–52 nm/s, in two ways: (i) addition of lithosthatine oligomers to the ends of protofibrils (white arrows in Figure 33a, b, and d) and (ii) fusion of a growing protofibril to a pre-existing protofibril (light-blue arrow in Figure 33b). Interestingly, one end of each of some pre-existing protofibrils did not change its position (white arrowheads in Figure 33a and b), suggesting a marked difference in the oligomer addition rate at the two ends of a protofibril and therefore the existence of polarity in the protofibril. Thus, the fusion of a growing protofibril to a pre-existing nongrowing protofibril (light-blue arrow in Figure 33b) is very likely to take place by head-to-tail connection. This issue may be able to be verified directly by cutting across a protofibril using a cantilever tip and by the following observation of elongation at the exposed ends, as has been done for an actin filament.³⁷

Figure 33.

High-speed AFM images showing the time lapse of lithosthatine protofibril elongation and association. Elongation of single protofibrils is shown by white arrows in (a), (b), and (d). Some protofibrils did not grow in length, as indicated by white arrowheads in (a) and (b). Interestingly, the end of an elongating protofibril was fused with one end of a pre-existing protofibril, forming a continuous structure, as marked with a light-blue arrow in (b). Protofibrils were often laterally associated with another, at least for one part of their length. The complete sideways association between two protofibrils occurred in a zipper-like mechanism (pink arrows). Elongation of a protofibril also occurred, being stacked on a fibril, as indicated with the light-blue arrowheads in (c). The growth of a protofibril or fibril was stopped when the growing end encounters a side edge of a second fibril, forming a false branching point with a certain range of contact angle, as indicated with red arrowheads in (d). Winding of two protofibrils formed helical fibrils (e) (the inset is a filtered image).

Elongation of fibrils appeared to occur separately at each constituent protofibril. In fact, a protofibril was elongated on the top of laterally associated protofibrils (light-blue arrowheads in Figure 33c). The lateral association of protofibrils to fibrils took place in a zipper-like mechanism (pink arrows in Figure 33b). In the initial stage, two protofibrils made contact with each other in a small region, showing a Y shape. The separated protofibrils were getting closer to each other by a gradual increase of the contact region, and eventually the two protofibrils were completely associated to form a helical fibril similar to other amyloid ß fibrils (Figure 33e). It was also clear that a branched structure previously observed with lithosthatine fibrils²⁷² is a false structure. The growth of a protofibril or fibril was stopped when the growing end encountered a side edge of a second fibril, forming a false branching point with a certain range of contact angles (red arrowheads in Figure 33d).

Thus, the dynamic visualization of lithosthatine fibrillization revealed various elementary processes contained in the fibrillization, including the existence of polarity in a protofibril (and hence also in a matured fiber) with markedly different elongation rates at the head and tail ends of a protofibril.

8.7.2. 2D Crystallization of Annexin A5

Annexins are a class of soluble proteins comprising more than 150 members, which bind in a Ca²⁺-dependent manner to anionic phospholipids, particularly those containing serine at the polar heads. Because of this property, annexins are involved in many membrane-related functions: certain exocytic and endocytic transport, anchoring other proteins including actin cytoskeleton to the cell membrane, organization of membrane domains including rafts, and the regulation of ion flux across the cell membrane.²⁷³ Annexins not only bind to the cytosolic surface of cell membranes as single molecules but also form lateral assemblies at least on model membranes.²⁷⁴ In the early stage in apoptosis, the lipid compositions in the inner and outer membrane leaflets of the bilayer are altered. In particular, a fraction of phosphatidylserine increases at the outer leaflet, which recruits extracellular annexins to form 2D crystals of annexins on the surface.²⁷⁵ The crystals are supposed to induce membrane indentation and subsequent inward vesicle budding and change membrane curvature and therefore cell shape.²⁷⁶ Among many types of annexins, 2D crystallization of annexin A5 on model membranes has been well characterized by cryo-electron microscopy and AFM.^101,277,278 In the 2D crystals, trimers represent the fundamental oligomeric state, which is stabilized by the contact between trimers.

HS-AFM observations provided novel insights into several dynamic events concerning 2D crystallization of annexin A5.⁸⁵ As a model membrane, a lipid bilayer consisting of DOPC, DOPS, and DOPE at ratio 5:2:3 w/w formed on bare mica was used. The observed crystallization process is shown in Figure 34 (scan range, 400 × 400 nm²; imaging rate, 1 fps). In the initial stage of the observation, CaCl₂ was omitted from the observation buffer. Under this condition, images with many spike noises appeared (see the image at t = 0 s), which is due to annexin A5 molecules rapidly diffusing on the lipid bilayer surface. The image gradually changed with time after the injection of CaCl₂ (final concentration, 3 mM) at t = 7 s. As shown in the image at t = 31 s, much less mobile small particles appeared, indicating the first stage of self-assembly (likely to be trimer formation). The size of the particle then increased with time as shown by the image at t = 3 min and 39 s, indicating the formation of precursor clusters by monomer addition to the initial clusters from surrounding diffusing monomers. However, the energy barrier in this addition process seemed still high because the growth rate was low. As seen at the top left of the images at t = 3 min and 39 s, 4 min and 24 s, and 5 min and 6 s, the growth rate was much higher for a larger cluster, which already had shown a well-ordered crystal structure. During this rapid growth of the crystal with a much lower energy barrier for monomer addition, the precursor clusters were engulfed into the growing crystal, as seen in the images at t = 5 min and 6 s and 5 min and 25 s. As seen in the image at t = 6 min and 13 s, the lipid bilayer surface within the observation area of 400 × 400 nm² was finally covered by the crystal.

Figure 34.

Dynamic process of 2D crystal formation of annexin A5 captured by HS-AFM. The image at t = 0 s shows the lipid bilayer surface on which annexin A5 molecules are diffusing. The diffusion appeared as large noise. After a CaCl₂ solution was injected at t = 7 s, 2D crystals were formed through initial nucleation step, gradual assembling of nuclei, and rapid growth of crystal patches by the addition of molecules to the crystal edges. Scan area, 400 × 400 nm²; imaging rate, 1 fps.

After completion of crystallization, a highly ordered structure with p6 symmetry appeared as previously reported²⁷⁹ (Figure 35a; scan range, 150 × 150 nm²; imaging rate, 2 fps). In the p6 crystal, the A5 trimers are arranged in a hexagonal honeycomb pattern as shown in Figure 35b. Each “hole” in the honeycomb structure tended to be occupied with a relatively mobile trimer (colored by pink in Figure 35b). The caged central trimer underwent a more relaxed interaction with its surrounding cage than trimers forming a part of the honeycomb lattice. Because of this mobility, the caged trimer has shown a less sharply defined density in the EM images of the crystal.^279,280 The hole indicated by the arrow at t = 0 s in Figure 35a was occupied by a trimer in the next frame. This trimer was weakly bound and then soon dissociated at t = 1 s. The resulting hole was filled again with a trimer at t = 1.5 s, but this trimer was now bound more stably. The hole formation and filing occurred at several places in the crystal (images between 18 and 23.4 s). Because surface unbound molecules had been washed away, this observation indicated that trimers not incorporated in the crystal exist on the crystal surface and are rapidly diffusing on it. HS-AFM imaging also revealed rotational diffusion of a caged trimer weakly bound to the surrounding cage (Figure 36; scan range, 50 × 50 nm²; imaging rate, 5 fps). The caged trimer encircled in the image at t = 0 s rotated counterclockwise by a 60° step. In the cage surrounded with six trimers, the central trimer can assume six stable positions with identical association energy. This rotational motion indicated the association energy to be approximately −1 k_BT.

Figure 35.

Dynamics occurring in annexin A5 crystal captured by HS-AFM. (a) Binding and dissociation dynamics of annexin A5 trimer on the 2D crystal (scan area, 150 × 150 nm²; imaging rate, 2 fps). The hole in the honeycomb lattice indicated by the arrow in the image of t = 0 s was filled at 0.5 s by a trimer that had been diffusing on the crystal surface. In the next 0.5 s, the trimer was dissociated. Similar events occurred at several places in the crystal. (b) Model of the 2D crystal of annexin A5. The caged central trimer in the honeycomb structure is colored in pink.

Figure 36.

Successive HS-AFM images showing rotational diffusion of a trimer trapped in a lattice cage of 2D annexin A5 crystal. Scan area, 50 × 50 nm². Imaging rate, 5 fps.

The disassembly process of the 2D crystal was also monitored by HS-AFM following chelation of Ca²⁺ ions. Figure 37 shows HS-AFM images clipped from the successive images (scan range, 500 × 500 nm²; imaging rate, 1 fps). At t = 8 s after the injection of an EGTA solution into the observation buffer at t = 0 s (during imaging), the 2D crystal form was still maintained. After a while, some trimers, especially weakly bound trimers caged in the holes, were removed from the lipid membrane. Once a disrupted region appeared, the 2D crystal rapidly collapsed from there, indicating strong cooperative interactions between molecules in the crystal. Finally, the entire crystal disappeared within a few minutes.

Figure 37.

Disassembly process of 2D annexin A5 crystal captured by HS-AFM. An EGTA solution was injected into the sample chamber at 0 s. Scan area, 500 × 500 nm². Imaging rate, 1 fps.

8.7.3. Supported Lipid Bilayer Formation

The supported lipid bilayer (SLB) formation occurs by self-assembly of lipids, which is considered to proceed in three steps:²⁸¹ (i) small lipid vesicles (small unilamellar vesicles (SUVs)) are attached to a mica surface and then rupture because the vesicles are largely deformed by the electrostatic interaction with the negatively charged mica, (ii) upon rupture, small patches of SLB are formed, and then (iii) the patches are fused into larger SLBs, and eventually the entire mica surface is completely covered by the bilayers. However, when this entire process was imaged for the first time using HS-AFM, unexpected phenomena appeared,⁴⁴ which are described below.

The lipid composition of small vesicles used was DOPC, DOPS, and biotin-cap-DPPE in ratio 3:1:1 (w/w). The vesicles were suspended in a buffer solution of pH 7.4 containing 2 mM CaCl₂. Images clipped from successive HS-AFM images captured over 25 min after the deposition of the vesicles onto a mica surface are shown in Figure 38a (imaging rate, 1.03 fps; scan size, 800 × 800 nm²). One of the unexpected phenomena observed was the formation of lipid nanotubes (LNTs) with a uniform diameter of ∼20 nm. Note that lipid nanotubes were recently observed (by fluorescence microscopy) to be formed from giant vesicles containing biotin-lipid when the vesicles were exposed to streptavidin.²⁸²

Figure 38.

HS-AFM imaging of dynamic events occurring in the process of SLB formation on mica. (a) Clips of successive HS-AFM images captured at 1.03 fps for a scan size of 800 × 800 nm² over 25 min (Z color scale, 25 nm). The white arrows indicate rapidly growing lipid nanotubes with ∼20 nm height. The light-blue arrow indicates the interaction between a patch of SLB and one end of a lipid nanotube. The arrowheads indicate liposomes with 7.5–30 nm. (b) Successive HS-AFM images showing fusion of two lipid nanotubes at the ends. (c) A HS-AFM image showing bending of a nanotube interacting with the sideways edge of a SLB patch at the longitudinal side. (d) Clips of successive HS-AFM images showing the interaction of a lipid nanotube with the edge of SLB patch at one of the ends. The size of the SLB patch is getting smaller, while the length of the nanotube is becoming shorter.

Short LNTs had already been formed in the vesicle sample before the deposition onto mica surface as they appeared together with small globular vesicles in the AFM images immediately after the deposition. Unlike the globular vesicles, the short LNTs did not rupture on the mica surface and grew longer with time. However, the growth rate was markedly different from one LTN to another. The reason for this difference was unclear. The fastest one was the LNT that appeared at the top right and was growing toward left at ∼10 nm/s (marked with the arrow in the image at 5.3 min). When a growing end encountered the side of a pre-existing LNT, the growth was stopped. The difference in the growth rate between the two ends of a LNT was uncertain because the two ends were in somewhat different environments, and because the growth rate was markedly different among LNTs. The growth mainly occurred by the addition of free lipids to the free ends but sometimes occurred by the end-to-end fusion of LNTs, as shown in Figure 38b.

The LNTs also interacted with the sideways edge regions of SLB patches either at their longitudinal sides or at one of the free ends. When interacting at the longitudinal side, the LNT sometimes bent along the sideways edge of the SLB, as shown in Figure 38c. The longitudinal contact rarely resulted in collapse of the LNT followed by fusion with the interacting SLB patch. When an LNT interacted with the edge of a SLB patch at one of the free ends, the size of the patch was often getting smaller with time, and, more surprisingly, the length of the LNT became shorter, as shown in Figure 38d.

With further lapse of time, the length and density of LNTs increased, and the size of SLB patches also increased. As a result, long LNTs were jammed into narrow spaces between large SLB patches, thus pushing each other (images at 20 and 20.9 min in Figure 38a). Some LNTs were collapsed in this congested condition to give larger SLB patches, whereas other LNTs quickly disappeared, very likely to be detached from the surface because exposed mica surface became unavailable for their attachment.

The high stability of LNTs can be accounted for by the smaller surface curvature (and hence smaller surface tension), as compared to that of small globular liposomes. In the sideways surfaces of the edge regions of SLB patches and the ends of LNTs, the polar head groups rather than alkyl chains are exposed. The arrangements of lipid molecules at these surfaces are energetically unfavorable as compared to those in the flat surface area of SLB patches and the longitudinal surfaces of LNTs. Therefore, to reduce the fraction of these unfavorable surfaces, SLB patches and LNTs grow by incorporating free lipids and by fusing with the respective kind of partners. As mentioned above, when one of the ends of an LNT was brought into contact with a sideways edge of an SLB patch, the area of the patch became smaller with time, and the length of the LNT also became shorter with time. The SLB patches are thin (a few nanometers) while the LNTs are ∼20 nm in diameter, so that the arrangements of lipids facing at the sideways edges of SLB patches are energetically unfavorable, as compared to those of lipids at the ends of LNTs. This energetic difference would result in lipid transfer from the SLB to the LNT, explaining the size reduction of the SLB. Nonetheless, it is hard to understand the shortening of the LNT.

8.8. Other Topics on Protein Dynamics

8.8.1. Cellulase

Cellulose is a predominant component of plant cell walls,²⁸³ and therefore the most abundant biomass and component of feed crops used in the livestock industry. Therefore, the efficient conversion of cellulose to fuels and the improvement of cellulose digestibility particularly for ruminants are important issues in agricultural industries. Cellulose is a linear polymer of β-1,4-linked glucose units.²⁸³ Cellulose chains are packed into ordered arrays to form insoluble microfibrils, which are stabilized by cross-links involving intermolecular hydrogen bonds.²⁸⁴ To degrade cellulose, many organisms produce cellulases. Cellulase hydrolyzes β-1,4-glucosidic linkages of the polymer. While all types of cellulases can hydrolyze amorphous cellulose, only a limited number of cellulases can hydrolyze crystalline cellulose.²⁸⁵ The enzymes that hydrolyze crystalline cellulose are called cellobiohydrolases (CBHs) because the major product of the reaction is cellobiose, a soluble β-1,4-glucosidic dimer.²⁸⁶ CBHs consist of two-domain structures: a catalytic domain (CD) and a cellulose-binding domain (CBD) (Figure 39a).^287−289 The two domains are connected by a flexible polypeptide linker rich in serine and threonine residues that are O-glycosylated.^290−292 In general, the CBD is known to enhance cellulose hydrolysis by increasing the effective enzyme concentration on the surface of the insoluble substrate²⁹³ because loss of the CBD causes a significant decrease in the crystalline cellulose degradation rate, but has a less effect on the hydrolysis of soluble or amorphous cellulose. As such, in the initial step of cellulose hydrolysis, the cellulases adsorb onto the surface of crystalline cellulose through the CBD. The CD has a relatively long tunnel formed by surface loops with catalytic amino acids extending from the central fold of the CD. A cellulose chain threads through the tunnel and is hydrolyzed.^291,292 Therefore, it has been considered that CBHs hydrolyze crystalline cellulose chains in a processive manner, making consecutive cuts without releasing the chain.^294,295 The CBHs are generally categorized into two main types: CBH I works processively from the reducing end of cellulose, while CBH II works processively from the nonreducing end of cellulose.²⁹⁶ The CD of CBH I belongs to the glycoside hydrolase (GH) family 7, and the CD of CBH II belongs to the GH family 6.

Figure 39.

Unidirectional processive run of cellulase on crystalline cellulose fiber captured by HS-AFM. (a) Schematic of cellulase (cellobiohydrolase: CBH) with two-domain structure attached onto the surface of crystalline cellulose. (b) Clips of successive AFM images showing processive and unidirectional movement of TrCel7A on crystalline cellulose I_α. Imaging rate, 3.3 fps. Two molecules are marked with the arrows with different colors. (c) Intermittent “go and stop” movement of TrCel7A molecules on cellulose I_α. The movements of seven molecules are shown with the marks with different colors. (d) Velocity distribution of the linear movement of TrCel7A on crystalline cellulose I_α (n = 188). The histogram was approximated by the combination of two Gaussian distribution curves (blue line) with mean ± SD values of −0.32 ± 3.4 (red) and 7.1 ± 3.9 nm/s (green). (e) Successive AFM images showing traffic jam of TrCel7A bound to crystalline cellulose I_α. Imaging rate, 3.3 fps. The congestion is marked with the arrows.

Despite numerous studies, the mechanism of the enzymatic digestion of crystalline cellulose has remained a major unsolved problem in agricultural science and technology. For example, it has been known that the hydrolysis rate decreases rapidly with time,²⁹⁷ but its mechanism has not yet been understood. Furthermore, several studies have indicated that CBH I and CBH II types of enzymes exhibit strong synergy for the hydrolysis of cellulose,^298,299 but the reason for the synergy effect has been elusive. The main reason for the difficulty in understanding these issues is the lack of experimental methods to monitor the enzymatic reaction at the single molecular level. With the hope of deciphering these persistent unsolved issues, HS-AFM imaging was recently carried out on CBHs hydrolyzing crystalline cellulose fibers.^35,56

For HS-AFM observations, crystalline cellulose fibrils were immobilized on the hydrophobic surface of HOPG. The fibrils are expected to orient with their hydrophobic surfaces in contact with the HOPG surface. By the symmetry of crystalline cellulose, the opposite hydrophobic surfaces appear on the top, being exposed to the solution. Cellulases bind to these exposed hydrophobic surfaces through CBD’s hydrophobic binding capability. As such, the use of HOPG has an advantage against the use of mica. During HS-AFM imaging of cellulose fibrils on the HOPG surface, a solution containing cellulase was injected into the observation chamber.

The CBH I (TrCel7A) belonging to GH family 7 (Cel7) is secreted by the industrially important cellulolytic ascomycete fungus Trichoderma reesei. TrCel7A is one of the best-studied CBHs. Figure 39b shows clips of successive HS-AFM images of TrCel7A molecules on the crystalline cellulose I_α prepared from the cell wall of green algae. It was evident that TrCel7A was moving unidirectionally and processively on the cellulose surface, making a line. The movement of TrCel7A was observed only on the hydrophobic top surface of the cellulose crystal.

Figure 39c shows displacements of seven TrCel7A molecules as a function of time. In this analysis, the center of mass of each molecule was tracked over consecutive images (section A.5 in Appendix). Interestingly, the movement of molecules sometimes halted or was slowed (the open green and closed red plots in Figure 39c) probably due to the presence of obstructions on the crystalline cellulose surface, whereas some molecules moved continuously without halt. A histogram of the measured velocity for 188 molecules comprised two Gaussian distributions with average velocities of −0.32 ± 3.4 and 7.1 ± 3.9 nm/s (Figure 39d). This may be consistent with the view that TrCel7A has two modes of adsorption on a cellulose surface: the productive adsorption mode in which both CD and CBD contribute to the binding and the nonproductive adsorption mode in which the enzyme binds only via the CBD.²⁹³ The overall average velocity for the seven molecules was 5.3 ± 4.9 nm/s. From this velocity, the hydrolysis rate was estimated to be 5 s^–1, taking into account that one hydrolysis drives the movement by 1 nm, which is the length of cellobiose. Surprisingly, this hydrolysis rate is 500 times larger than that (0.01 s^–1) estimated biochemically.³⁰⁰ This large discrepancy is probably because in the biochemical estimation, it has been assumed that all molecules productively work on the cellulose surface. However, in reality the number of reduced ends available for TrCel7A binding is limited, and moreover the movement of molecules is often hampered by traffic jams as seen in Figure 39e.

The fabric form of cellulose I_α can be converted to cellulose III_I polymorph by supercritical ammonia treatment. This conversion dramatically enhances the cellulose hydrolysis by TrCel7A.³⁰¹ A biochemical analysis has indicated that TrCel7A has a higher affinity for cellulose III_I than for cellulose I_α, but its maximum hydrolysis rate is only slightly higher than cellulose I_α.³⁰¹ Figure 40a shows clips of successive HS-AFM images of TrCel7A molecules processively moving on a cellulose III_I surface. The number of molecules on the cellulose III_I surface appeared larger than that on the cellulose I_α surface, as shown in Figure 40a, but the velocity of the molecules was similar for both surfaces. In the case of cellulose I_α, the molecules moved only along limited lanes, whereas, on cellulose III_I, TrCel7A molecules moved over almost the whole surface. This explains the biochemically obtained affinity difference between cellulose I_α and III_I. It also agrees with previous studies^284,302 showing that cellulose I_α has a hydrophobic surface at (110) surface (Figure 40b, the left schematic), whereas cellulose III_I has a hydrophobic surface not only at (110) surface but also at (100) surface (Figure 40b, the right schematic). Therefore, cellulose III_I has more lanes available for cellulase binding and movement than cellulose I_α.

Figure 40.

HS-AFM imaging of TrCel7A moving on crystalline cellulose III_I. (a) Clips of successive AFM images of TrCel7A on crystalline cellulose III_I. Imaging rate, 3.3 fps. (b) Schematics of sections of crystalline cellulose I_α and cellulose III_I. (c) Clips of successive HS-AFM images showing fibrillation of crystalline cellulose III_I after congestion of TrCel7A molecules. Imaging rate, 3.3 fps.

When a molecule halted, many following molecules stacked behind it on the cellulose III_I surface, causing a traffic jam. However, after several additional molecules were blocked at this place, the molecules restarted to move. In this occasion, a cellulose bundle was peeled off from the crystalline cellulose III_I, as shown in Figure 40c. These observations suggested the following sequential events to occur: (i) an obstruction on the surface of crystalline cellulose (and hence a rough surface) is formed during the digestion, (ii) a single TrCel7A molecule is unable to overcome the obstacle by its own generating force and is therefore halted, and (iii) the accumulated molecules at the obstacle work together with increased force to get the obstacle out of the way (i.e., pealing of a cellulose bundle), resulting in restarting linear movement. The traffic congestion is very likely to be the mechanism underlying the rapid reduction with time of cellulose hydrolysis rate. The distance between neighboring traffic lanes is smaller than the size of a TrCel7A molecule. Therefore, the enzyme molecules moving along neighboring lanes have a large chance to collide with each other. When a TrCel7A molecule is hydrolyzing one lane of cellulose, it is likely that the molecule partially peels lanes adjacent to the lane that the molecule is hydrolyzing. This peeling results in the production of rough surfaces and obstacles. Note that before the addition of TrCel7A, the surface of crystalline cellulose fibers was smooth.

It is known that the mixture of two major CBHs, TrCel7A and TrCel6A, synergistically enhances the hydrolysis of cellulose III_I (Figure 41a). This effect has been called the exo–exo synergy.³⁰⁰ Either of these two enzymes has an active site located in a tunnel that passes through the whole CD. The active site tunnel of TrCel6A is formed by two surface loops and is about 20 Å long, whereas that of TrCel7A is approximately 50 Å long, comprising six loops.^{290−292,303} Previous transmission electron microscopic observations of crystal cellulose partially hydrolyzed by both TrCel6A and TrCel7A suggested that the enzyme cocktail degraded the cellulose from both ends of the crystal. TrCel7A degrades the crystal from the reducing end, leading to fibrillation, thinning of the crystal, or narrowing of the crystal end, whereas TrCel6A hydrolyzes the crystal from the nonreducing end, less processively than TrCel7A, thereby sharpening the crystal tip.^304,305 It is however difficult to explain this type of synergistic action based on their exoenzymatic activities. To clarify this issue, the hydrolysis process of crystalline cellulose III_I in the presence of both TrCel6A and TrCel7A was imaged.

Figure 41.

Synergistic hydrolysis by TrCel6A and TrCel7A visualized by HS-AFM. (a) Synergy, measured biochemically, between TrCel6A and TrCel7A in cellobiose production from cellulose III_I. The green and red plots show the rates of cellobiose production by TrCel6A alone and TrCel7A alone, respectively, and the blue plot shows the synergy between the two enzymes. The dotted line indicates the simple sum of cellobiose production calculated from the green and red plots. (b) Clips of successive AFM images of cellulose III_I after injection of TrCel6A at 0 s. The degradation of cellulose was not discernible even at 8 min. (c) Clips of successive AFM images after the additional addition of TrCel7A at 0 s (at 8.4 min after the initial addition of TrCel6A). The cellulose was rapidly degraded and almost disappeared at 8 min. Imaging rate, 3.3 fps for (b) and (c).

Figure 41b shows clips of successive HS-AFM images taken for cellulose III_I in the presence of TrCel6A alone. The appearance of the cellulose crystals did not significantly change during incubation over 8 min, even though many enzyme molecules were observed on the cellulose surfaces. Upon addition of TrCel7A at 8.3 min, the enzyme molecules started moving from many points on the cellulose surfaces, and the degradation of crystalline cellulose was dramatically faster than the case with TrCel6A alone (Figure 41c). Eventually, the cellulose crystals almost disappeared at ∼4 min after the addition of TrCel7A. The observed synergy was independent of the order of the addition of TrCel6A and TrCel7A. A very similar synergy was also observed when both TrCel6A and TrCel7A were added simultaneously. The HS-AFM observation showed that TrCel6A was randomly bound to the cellulose fibril but not the end of the fibril, and the movement was less processive. Therefore, the synergy observed could be rather called the endo–exo synergy,³⁰⁶ although TrCel6A has generally been defined as an exoglucanase. One possible mechanism of the synergetic degradation is that the two loops forming the active site tunnel of TrCel6A can open, allowing generation of nicks in the middle of crystalline cellulose, and that these nicks become starting and ending points for the TrCel7A activity.

8.8.2. Intrinsically Disordered Proteins

It has recently been recognized that a new class of functional proteins exist, which lack a well-defined ordered structure in the entire length or in large domains under native conditions.^307−310 These proteins are generically called intrinsically disordered proteins (IDPs). According to computational predictions based on genomes, ∼30% of eukaryotic proteins are mostly disordered, and more than 50% eukaryotic proteins have long disordered regions consisting of more than 40 consecutive amino acid residues.³¹¹ IDPs contrast strikingly with a classical structure–function paradigm of proteins. In a classical view, the structure of all functional proteins must be well ordered, and forming defined tertiary structures is considered to be a unique strategy for establishing specific interactions with ligands and partner proteins (lock-and-key model); as such, proteins with largely disordered structures have been considered to be denatured and dysfunctional, until the discovery of a large group of IDPs. The thin and flexible intrinsically disordered regions (IDRs) contained in IDPs take a structural ensemble consisting of a large number of random conformers. Upon binding to a target molecule, the disordered structure is converted to a defined ordered structure or remains partially or even fully disordered. When folded into an ordered structure, this folding is termed “coupled folding”.³¹² Certain IDPs can promiscuously interact with several target proteins, and the corresponding coupled folding results in different ordered structures adapted to the target proteins.^313,314 This adaptation furnishes such IDPs with multifunctionality. IDPs are often involved in transcription, translation, and cellular signal transduction. The adaptability, multifunctionality, and promiscuity are IDPs’ attributes essential for functioning in diverse biological processes as regulators.

Despite increasing recognition of the functional importance of IDPs, the analysis of their disordered structures has been difficult. The local structure of IDPs with molecular weights less than ∼50 kDa (usually less than ∼20 kDa) can be determined by NMR, but the overall random structure cannot be revealed by this method. Electron microscopy cannot visualize the thin and random structures. X-ray crystallography is entirely useless for IDPs because IDPs cannot be crystallized. Except for computational predictions, there have been no effective means to identify the overall random structure of IDRs until the advent of HS-AFM. It was recently demonstrated that HS-AFM could visualize the thin and random structures of IDRs, using Drosophilamelanogaster FACT (facilitates chromatin transcription) protein (dFACT) overexpressed in E. coli, as a test sample.³¹ A chromatin remodeler, FACT, is a heterodimer complex consisting of SSRP1 and SPT16 subunits.^315−317 HS-AFM images of dFACT showed two wiggling tail-like segments with different lengths that protruded from the main body of dFACT; their contour lengths were 17.5 and 27.5 nm on average. HS-AFM images of mutants, M1 and M2, in which either predicted IDRs were deleted, confirmed that these wiggling segments are IDRs, and that the longer ID region belongs to the SSRP1 subunit while the shorter one belongs to the SPT16 subunit. Note that it is hard to visualize IDRs using conventional AFM even when the sample is dried in air and immobilized onto a substrate surface because thin IDRs (∼1 nm thick) become thinner under this condition.

Interestingly, both IDRs showed a similar macroscopic flexibility (or stiffness). The stiffness of a polymer chain can be quantified by the persistence length p of the chain, that is, the length over which the average correlation in the tangential direction decays by 1/e. In 2D, the mean-square point-to-point distance ⟨r²⟩ of a uniform chain is given by

6

where l is the contour length between two points on the chain.³¹⁸ In the AFM images obtained for the tail-like structures of dFACT, their polypeptide chains were not resolved. Therefore, the persistence lengths that can be obtained from the images are those for overall (macroscopic) string structures. The analysis of AFM images of the ID regions with eq 6 gave a persistence length of 11–12 nm for both ID regions. Microscopic persistence length L_p can be approximately determined on the basis of an assumption that the polypeptide chain length L is a multiple of the number of amino acids and the likely average distance between adjacent amino acid residues (∼0.34 nm) and on the relationship:

7

where R is the end-to-end distance. This equation holds, provided that L is much longer than L_p. Note that unlike the macroscopic persistence length, the microscopic persistence length does not correspond to the stiffness of a polypeptide chain but represents the degree of its folding; a shorter microscopic persistence length reflects a higher degree of folding. The microscopic persistence length was ∼1.1 nm for both ID regions (slightly shorter with the longer ID region, likely due to the presence of the ordered high-mobility group (HMG) domain in the longer ID region within the SSRP1 subunit). Microscopic persistence lengths of structured and randomly coiled proteins have previously been estimated by the measurement of force–extension curves using AFM.^319−321 The microscopic persistence length of the PEVK region (186 amino acid residues), which is responsible for the elastic property of titin and thought to form a random coil, is reported to show a wide range of L_p (0.4–2.5 nm; 0.93 nm on average).³²⁰ On the other hand, for proteins with ordered structures, the reported values for the microscopic persistence length are within a range of 0.36–0.5 nm.^319,321 Thus, the long microscopic persistence length (∼1.1 nm) of the IDRs of dFACT protein is a fingerprint of their very loose structures. A recent HS-AFM study on other proteins’ IDRs has further confirmed long persistence lengths.³²² The nature of higher looseness of IDRs than entropically folded random coils reflects the electrostatic repulsion between charged amino acids rich in IDRs, which reduces the entropy-driven folding.

The interaction of IDRs with target proteins and DNA can be modulated by post-translational modifications, including phosphorylation, acetylation, methylation, sumoylation, and ubiquitination.^323−325 A recent study has shown that extensive phosphorylation of the IDR belonging to the SSRP1 subunit of dFACT inhibits the formation of a stable complex of dFACT and nucleosomal DNA.³²⁶ The phosphorylated sites reside on an acidic ID segment adjacent to an HMG domain-flanking basic ID segment of the SSRP1 subunit. The phosphorylation increases the number of negative charges in the acidic segment. Therefore, the DNA binding inhibition is conceived to be caused either by an increased repulsive interaction between the acidic ID segment and DNA or by the association between the acidic and basic ID segments. To elucidate the inhibitory mechanism, HS-AFM imaging was carried out for dFACT (from which the shorter IDR (888–1044) and the N-terminal amino peptidase like domain (1–401) in the SPT16 subunit were deleted) expressed in Sf9 insect cells, in fully phosphorylated (WT) and nonphosphorylated forms.⁶² The nonphosphorylated form was obtained by site-directed mutagenesis to Ala at 10 phosphorylation sites (Ser/Thr) contained in the acidic ID segment of the SSRP1 subunit.

HS-AFM images captured at 15 fps showed a similar structure on the whole for phosphorylated WT dFACT (dFACT-WT) and dephosphorylated mutant (dFACT-10SA) (Figure 42a,b); a large globular domain (GD₁) was connected to a tail-like structure (i.e., IDR of SSRP1), as previously observed.³¹ However, in both constructs, two small globular domains, termed GD₂ and GD₃, were found on the IDR in the middle and at the distal end of the IDR, respectively (Figure 42a,b). Therefore, the entire IDR was divided into two (IDR_1–2 and IDR_2–3); IDR_1–2 connects GD₁ and GD₂, while IDR_2–3 connects GD₂ and GD₃ (Figure 42c). GD₃ located at the distal end of the IDR was consistently observed, without any appearance differences between the two constructs, whereas GD₂ located in the middle of the IDR appeared temporally and vanished, with different lifetimes between the two constructs; the GD₂ of dFACT-WT exhibited a longer lifetime than that of dFACT-10SA. Moreover, the length of the entire IDR appeared to be shorter in dFACT-WT than in dFACT-10SA. This length difference was reflected from the much shorter length of IDR_1–2 in dFACT-WT. The length of IDR_2–3 was similar between the two constructs. To express these structural features quantitatively, the parameters of end-to-end distance and height shown in Figure 42c were obtained for both constructs by analyzing many successive HS-AFM images captured for three molecules of each construct. The most distinct difference between the two constructs occurred in the end-to-end distance D_1–2 between GD₁ and GD₂ (Figure 42d); the distance was shorter in dFACT-WT by ∼2 nm. The next distinct difference occurred in the height H₂ of GD₂ (Figure 42e); dFACT-WT predominantly took a high globular state (1.6–1.7 nm), while dFACT-10SA took a low state (∼1.1 nm). However, these structural states were not static but dynamic. The shorter GD₁–GD₂ distance state and the lower GD₂ states were taken even by dephosphorylated dFACT-10SA. Moreover, the position of GD₂ was consistent with the position of the HMG domain, the height ∼1.1 nm corresponded to the size of HMG (∼1 nm), and the height of the IDRs was 0.4–0.6 nm. Thus, the following conclusions were derived:⁶² (i) the acidic segment of SSRP1’s IDR electrostatically interacts with both the region containing the basic segment of SSRP1’s IDR and the HMG domain to evoke partial folding of the IDR, (ii) the folded and unfolded states are in dynamic equilibrium, (iii) extensive phosphorylation of the acidic segment of the IDR shifts the equilibrium toward the folded state, and (iv) this structural bias to the folded state blocks the binding of nucleosomal DNA to the region containing the basic IDR segment and the HMG domain.

Figure 42.

Intrinsically disordered dFACT protein and effect of phosphorylation on the structure visualized by HS-AFM. (a,b) Clips of successive HS-AFM images of phosphorylated dFACT-WT (a) and dephosphorylated dFACT-10SA (b). Imaging rate, ∼14 fps; scan area, 100 × 100 nm² with 80 × 80 pixels; Z-scale, 4.0 nm. The observed molecular features of dFACT are schematized according to the definitions in (c). These schematics were drawn freehand by tracing the AFM images by visual estimation. (c) Schematics representing the characteristics of dFACT observed by HS-AFM (upper schematic) and its side-view (lower schematic). Gray-colored ellipses and black-colored thick solid lines represent the globular domains (GD) and the intrinsically disordered regions, respectively. (d) Histograms of distance D_1–2 indicated in (c) measured for dFACT-WT (upper) and dFACT-10SA (bottom). (e) Histograms of height H₂ indicated in (c) measured for dFACT-WT (upper) and dFACT-10SA (bottom). The histograms appear to have two peaks at 1.6–1.7 and ∼1.1 nm, which correspond to HMG associated with an IDR and HMG alone, respectively.

As demonstrated above, high-speed AFM is powerful in identifying and characterizing IDRs of proteins. In conventional methods, even the identification of IDRs is difficult and time-consuming. Moreover, high-speed AFM can detect order–disorder transitions of IDRs that occur naturally with free IDRs or are biased to the ordered state either by post-translational modification or by interaction with target molecules. In the near future, high-speed AFM will visualize the dynamic processes in which IDRs are folded into ordered structures upon interaction with their target molecules and drugs.

8.8.3. Dynamics of Vacancy Defects in 2D Crystals of Proteins

In 2D crowded conditions, protein molecules frequently interact with each other even under a very weak attractive force between the molecules, which sometimes results in the formation of 2D crystals. The 2D crystallization of proteins occurs naturally as seen in bR in the purple membrane and AQP0 in the intercellular junctional microdomains, as well as artificially as seen in electron crystallographic studies.^99,327,328 When vacancy defects are present in the 2D crystal of a protein, the defects are very likely to move in the crystal because proteins molecules facing a vacancy defect lose some of intermolecular bonds, and therefore tend to move into the defect, leaving a new vacancy defect behind. In fact, this phenomenon was observed by HS-AFM in the orthorhombic C222 crystals of streptavidin formed on biotin-containing SLBs.³³ Note that the 2D crystal has P2 symmetry,³⁷ but here the notation C222 for the symmetry group follows a previous report.³²⁸

The lipid composition used was DOPC, DOPS, and biotin-cap-DOPE (7:2:1 w/w). The C222 crystal of streptavidin with lattice constants a = 5.9 nm, b = 5.9 nm, and γ = 90° (Figure 43a) was prepared using a relatively high ionic buffer solution containing 2 mM CaCl₂ (pH 7.4). Monovacancy defects in the streptavidin 2D crystals were produced by increasing the tapping force exerting from the oscillating tip to the sample. The imaging was carried out at 2 fps over 150 × 150 nm² scan areas. Monovacancy defects were mobile, with an anisotropic feature with respect to the two axes of the crystalline lattice: larger mobility along the b axis than the a axis (Figure 43b). The a axis includes the rows of contiguous biotin-bound subunits, whereas the b axis includes the rows of contiguous biotin-unbound subunits (Figure 43a). The linear relationship between the MSDs and time intervals gave the diffusion rate constants of D_a = 20.5 nm²/s for the a-axis component of diffusion and D_b = 48.8 nm²/s for the b-axis component of diffusion. This anisotropy in the mobility (D_b > D_a) arises from a free energy difference between the biotin-bound subunit–subunit interaction and biotin-unbound subunit–subunit interaction. When a streptavidin molecule adjacent to a monovacancy defect moves to the defect site along the a axis, two intermolecular bonds between biotin-unbound subunits (“u–u bond”) and one intermolecular bond between biotin-bound subunits (“b–b bond”) are broken (see Figure 43c). On the other hand, when it moves to the defect site along the b axis, one u–u bond and two b–b bonds are broken (see Figure 43d). Therefore, the difference in the activation energies E_a and E_b for the step movement of a monovacancy defect along the respective a and b axes simply corresponds to the difference between the free energy changes G_u–u and G_b–b produced by the formation of the respective u–u bond and b–b bond: E_b – E_a = G_u–u – G_b–b. Therefore, the observed relationship D_b > D_a indicates G_u–u < G_b–b; that is, the u–u bond affinity is higher than that of the b–b bond. The ratio of the two diffusion rate constants (D_b/D_a) can be expressed by D_b/D_a = exp[−(E_b – E_a)/(k_BT)]. Thus, from the observed value of D_b/D_a = 2.4, the free energy difference G_u–u – G_b–b was estimated to be approximately −0.88 k_BT (T ≈ 300 K), which corresponds to −0.52 kcal/mol.

Figure 43.

Migration of monovacancy defects in streptavidin 2D crystal captured by HS-AFM. (a) Schematic of streptavidin arrays in a C222 crystal. Unit lattice vectors are indicated: the a-axis includes rows of contiguous biotin-bound subunits, while the b-axis includes rows of contiguous biotin-unbound subunits. (b) High-speed AFM images of streptavidin 2D crystal and monovacancy defects therein. The monovacancy defects are enclosed by dashed squares and circles. The directions of the lattice vectors of the crystal are also indicated. Imaging rate, 2 fps; scan area, 150 × 150 nm²; the number of pixels, 200 × 200. (c) Schematic showing a streptavidin molecule being transferred to the neighboring monovacancy defect along the a-axis. (d) Schematic showing a streptavidin molecule being transferred to the neighboring monovacancy defect along the b-axis. The “u–u bonds” are shown in red, while the “b–b bonds” are shown in green (c and d). (e) Clips of successive HS-AFM images showing fusion of two monovacancy defects into a divacancy defect. Imaging rate, 2 fps; scan area, 140 × 140 nm²; pixels, 200 × 200.

This free energy difference must affect the 2D crystal growth, resulting in asymmetric crystal growth rate along perpendicular axes, hence in an anisotropic crystal morphology.³²⁸ In fact, the streptavidin C222 crystals formed under biotinylated lipid layers are known to have X-, H-, and rectangle-shaped morphologies.^329,330 The anisotropy estimated from the aspect ratios of the C222 crystals has been reported to be 2–3 (about 2 at neutral pH),³³¹ coinciding with the diffusion constant ratio (D_b/D_a= 2.4). Supposing that the aspect ratio of a crystal is proportional to the ratio of the free energies of attractive interactions that occur along the crystal axes (Wulff’s rule),³³²G_u–u/G_b–b is approximately 2. This relationship and G_u–u – G_b–b ≈ −0.88 k_BT result in G_b–b ≈ −0.88 k_BT and G_u–u ≈ −1.76 k_BT. The small free energy G_b–b ≈ −0.88 k_BT suggests that the C222 crystal could be disrupted when all of the biotin binding sites are bound to biotin because the number of b–b bonds per molecule in the C222 crystal lattice is two; hence the association free energy per molecule amounts to only −1.8 k_BT. This was confirmed by the observation that the ordered lattices were immediately disrupted when the crystals were exposed to free biotin in the bulk solution.³³

The monovacancy defects sometimes fused into a divacancy defect (Figure 43e). Through several fusions, larger multivacancy defects were formed.³³ As the size increased, the diffusivity of multivacancy defects increased for both crystal axes, except for the case of divacancy defects. For example, D_a and D_b of tetra-vacancy defects increased ∼3.5 times and ∼2.5 times, respectively, as compared to those of monovacancy defects. The higher mobility of larger point defects increases their probability to encounter other point defects to form larger point defects with further higher mobilities. During the crystal growth in the presence of free streptavidin in the bulk solution, this acceleration effect should promote the removal of point defects from the crystalline regions. This would be one of the mechanisms for defect-free crystal formation not only in 2D crystals but also in 3D crystals. This issue should be examined in the future by imaging the crystal growth in the presence of free streptavidin in the bulk solution. The mechanism underlying the larger mobility of larger multivacancy defects is at a glance considered to be contrary to the fact that many intermolecular bonds have to be broken for a large multivacancy defect to move. However, this seemingly peculiar tendency was rationally interpreted by the consideration of two factors.³³ One factor is the lower stability of the crystal regions adjacent to a larger point defect in comparison with the crystal regions adjacent to a smaller defect. Another is that there are multiple paths along which a multivacancy defect migrates to one of their nearest-neighbor positions.

9. Dynamic Imaging of Live Cells

One of the prospective high-impact applications of HS-AFM is real-time monitoring of dynamic phenomena occurring in live cells and isolated intracellular organelles, including morphological changes of cells, filopodium formation and retraction, phagocytic and endocytic processes, fusion and fission of mitochondria, synaptic formation in neurons, and enlargement of spines associated with memory and learning. Furthermore, HS-AFM would offer a unique opportunity to visualize dynamic events of membrane proteins occurring on the surfaces of live cells and isolated intracellular organelles. However, imaging of these phenomena has been one of the largest challenges for HS-AFM. The larger size and extremely soft surfaces of these objects require a large scan range and high sensitivity for tip–sample interaction detection, respectively. Recently, fast scanners covering an XY scan range of up to 10 × 10 μm² and even up to 46 × 46 μm² have been developed.^67,69,333 Despite their noncompact structures due to the use of large piezo actuators as well as displacement magnification mechanisms, the high-speed scan performance is only slightly inferior to the fast scanners with a much smaller maximum scan range. Using these wide-area scanners, HS-AFM imaging of live cells has just recently been embarked on. Thus far, the number of successful studies is still very limited, and even these successful studies do not yet fully solve biological questions of importance. However, it is worthwhile to look at the current state of live cell imaging by HS-AFM to know its potential as well as techniques that should be further developed or combined with the current HS-AFM to facilitate this endeavor.

9.1. Bacterial Cell Surfaces

9.1.1. Bacteriolysis of Bacillus subtilis Subjected to Lysozyme

Because of the nonpathogenicity and amenability to genetic manipulation, Bacillus (B.) subtilis has been widely used as a model system for investigating the roles of autolysins (i.e., bacteriolysis caused by digestion of the cell wall peptidoglycan of bacteria by enzymes that are produced from the bacteria themselves) in the cell wall metabolism of endospore-forming Gram-positive bacteria, and the structure of peptidoglycan and spores.^334,335 It is well-known that B. subtilis is also susceptible to the antibacterial action of lysozyme, which hydrolyzes 1,4-beta linkages between N-acetyl glucosamine and N-acetyl muramic acid, leading to degradation of peptidoglycan in the cell wall.³³⁴ This degradation process of peptidoglycan induced by lysozyme was captured by HS-AFM.⁶⁹

The B. subtilis bacteria were immobilized on a glass stage coated with poly-l-lysine. HS-AFM imaging was conducted in a culture medium to maintain bacteria alive. Figure 44a shows time-lapse images of the bacterium before and after the addition of lysozyme (imaging rate, 0.05 fps; scan size 5 × 5 μm² with 256 × 256 pixels). Before the injection of lysozyme (t = 0 s), the cell surface appeared smooth. At t = 240 s, lysozyme (final concentration, 80 μM) was injected into the observation solution, and therefore the imaging was somewhat disturbed. After t = 320 s, the surface morphology gradually became varied, and wrinkle structures perpendicular to the long cell axis appeared. At the same time, the cell gradually swelled (t = 1060, 1460, and 1580 s), indicating lowered resistance to osmotic pressure due to the degradation of the hard cell wall. Finally, at t = 1720 s, the cell exploded by osmolysis, resulting in partial exposure of the intracellular contents. The detailed morphological change induced by lysozyme at higher final concentration of 200 μM was also observed at a faster imaging rate 0.5 fps for a 2 × 1.5 μm² area with 120 × 90 pixels (Figure 44c). The cell surface roughness increased rapidly with a time lag of ∼90 s after the injection of lysozyme at t = 32 s (Figure 44b). Here, the surface roughness was expressed by the root-mean-square (RMS) roughness of the area indicated by the white rectangle in Figure 44c. The roughness was almost constant (∼93 nm) before the injection of lysozyme, whereas it increased to ∼125 nm after the injection. The increase in the surface roughness was well fitted by a single exponential function with a time constant of τ = 36.8 s, as indicated by the solid line in Figure 44b. High-resolution imaging on the bacterial cell surface was also carried out before and after the addition of lysozyme, at an imaging rate 0.5 fps for a 500 × 500 nm² area with 200 × 200 pixels (Figure 45). Fine structures on the cell wall were clearly visible, as shown in Figure 45a (t = 0 s). Soon after the injection of lysozyme, the fine structure on the cell surface became blurry due to the degradation of the cell wall, and a wrinkled structure with a periodicity of about 300 nm appeared (Figure 45b).

Figure 44.

Process of lysozyme-induced bacteriolysis captured by HS-AFM. (a) Time-lapse images of bacteriolytic process of B. subtilis subjected to lysozyme. Lysozyme was injected at t = 240 s. Scan range, 5 × 5 μm²; imaging rate, 0.05 fps (20 s/frame); pixels, 256 × 256. (b) Time course of RMS roughness of the outer surface of B. subtilis subjected to lysozyme. Lysozyme was injected at t = 32 s. Solid line shows the result of best fitting (time constant, τ = 36.8 s) by a single exponential function for the time course between t = 112 s and t = 300 s. (c) Corresponding clips of successive AFM images of the outer surface of B. subtilis at different time lapses. Values of RMS roughness were calculated for the area encircled by the white broken line shown in the image at t = 86 s.

Figure 45.

Bacterial surface change by lysozyme captured by HS-AFM. (a,b) Magnified views of outer surface of B. subtilis (a) before and (b) after the injection of lysozyme. Scan range, 500 × 500 nm²; imaging rate, 0.5 fps; pixels, 256 × 256.

9.1.2. Surface Change of E. coli Subjected to Antimicrobial Peptide

Antimicrobial peptides (AMPs) produced by a vast array of organisms comprise a diverse class of natural antibiotics, which are considered to be a major part of the innate immune system of a host (a first line of defense against pathogenic invasion by microbes). The peptides display a wide range of antimicrobial activities against bacteria, viruses, and fungi. The binding of these peptides to a bacterium is followed by the disruption of cytoplasmic membranes, leading to bacterial cell death.³³⁶ Because antimicrobial peptides have a potential as therapeutic alternatives to current antibiotics, numerous studies have been conducted to understand how AMPs interact with and act on cell membranes. However, there have been no direct studies to elucidate the early stage kinetics of the membrane disruption in live cells at high spatiotemporal resolution. Fantner and colleagues studied this issue by imaging surface morphological changes of bacterial cells subjected to an AMP using a HS-AFM instrument and small cantilevers developed by them.⁶⁷

E. coli cells were immobilized on a cover slide coated with poly-l-lysine and then imaged in water. CM15, which is a linear, synthetic hybrid AMP composed of the first seven residues of the cecropin A and residues 2–9 of the bee venom peptide mellitin, was added to the HS-AFM fluid cell to a final concentration of 50 μg/mL using a flow-through fluid exchange system with a dual syringe pump. HS-AFM images were captured at 0.077 fps for 3 × 3 μm² areas. For the HS-AFM observation, the phase of the cantilever oscillation relative to the excitation signal was used as the imaging signal (rather than the topography) because the fine structures of the bacterial surface were more conspicuous than the height image. This is because the topography contains a large height background against small surface corrugations of the bacteria surface. Figure 46a shows time-lapse phase images of the surfaces of E. coli cells after the addition of CM15 at t = −6 s. The surface of the cell marked with “1” changed from smooth to rough with time due to the CM15 action. The surface roughness increase of the cell induced by CM15 is consistent with an electron microscopy study.³³⁷ Interestingly, the cell “1” started changing within 13 s after the addition of CM15 and the change was completed in ∼60 s, whereas the cell “2” did not start changing until ∼80 s, and the surface alterations were not completed in ∼120 s, suggesting that the two cells are not in the same stage in the cell cycle, or revealing individuality concerning their sensitivity to CM15. Correlation between the degree of surface roughness increase and the cell death was confirmed by HS-AFM-combined fluorescence microscopy using a fluorescent indicator of cell viability.

Figure 46.

Process of antimicrobial peptide-induced bacteriolysis captured by HS-AFM. (a) Clips of successive HS-AFM images of E. coli subjected to CM15 antimicrobial peptide. CM15 was injected at t = −6 s. Imaging rate, 0.08 fps (12.5 s/frame); pixels, 1024 × 256. (b) Cross sections along the long axis of a bacterium showing the time progression of the surface variation. (c) Averaged surface variations of individual bacterial cells as a function of time after injection of CM15. Reprinted with permission from ref (67). Copyright 2010 Nature Publishing Group.

Time evolution of the surface roughness along the long axis of several bacteria (assessed by the phase signal) was analyzed to quantify the kinetics of the change. Figure 46b shows representative cross sections of a single bacterium surface at different incubation stages. The marked increase of the surface roughness appeared at ∼80 s after the addition of CM15. Figure 46c shows the normalized RMS roughness for nine cells as a function of incubation time. The onset time of the roughness change depended largely on individual cells, ranging from 40 s (bacterium 7) to more than 4 min (bacterium 2), with an average of 155 ± 89 s. The time for each bacterium to complete the change (smooth to corrugated) was more consistent; 50% of the maximum roughness increase occurred within 52 ± 16 s after the onset of roughness change.

On the basis of these results, it was proposed that sterilization of bacteria by CM15 is a two-stage process, that is, incubation and execution phases, and that the bulk sterilization rate is dominated by the incubation phase, rather than the execution phase.

9.1.3. Imaging of Single Molecules on Live Bacteria Surfaces

Dynamics of membrane proteins in isolated native membrane fragments and those reconstituted in synthetic membranes can be visualized at high resolution with HS-AFM.^{34,36,40−43,48,49,58,60} However, it would be more ideal to visualize membrane proteins in live cell membranes at the single-molecule level, using HS-AFM. Little is known about dynamic actions of membrane proteins in real environments, where membrane proteins interact with other proteins and are influenced by membrane potential and ionic species partitioned across the membrane. Therefore, such in situ dynamic imaging will certainly expand the usefulness of HS-AFM in biological studies. Previously, visualization of the molecular organization on live cell surfaces was performed for the hexagonal S-layer of Corynebacterium glutamicum,³³⁸ the peptidoglycan organization of Lactococcus lactis,³³⁹ and the germinating spores of B. atrophaeus.³⁴⁰ However, only a few attempts of HS-AFM visualization have thus far been made on molecules on live cell surfaces.^68,70 The first attempt was carried out for a bacterium,⁶⁸ which will be described below.

The magnetotactic spirillum Magnetospirillum (M.) magneticum AMB-1 was used as a test sample.⁶⁸ The cells were chemically immobilized on mica, which had been covered with poly-l-lysine and then treated with glutaraldehyde. The viability of the immobilized cells was assessed using a fluorescent indicator of bacterial viability. Most of the cells were alive for at least 1 h after the immobilization. Figure 47a and b shows the cell surface captured for scan ranges of 150 × 150 nm² (imaging rate, 0.5 fps) and 100 × 100 nm² (imaging rate, 1.43 fps), respectively. The cell surface was coarse and covered all over with regularly arranged particles with similar size (Figure 47a). The magnified image (Figure 47b) showed reticulate structures with a dent in each central region, which were irregularly moving, indicating that the overall structure is loosely packed. Many particles were seen on the embankments surrounding dents (Figure 47b, arrows). The central positions of 23 dents in the reticulate structure were tracked. The trajectories of four of the 23 dents are shown in Figure 47c. Despite the highly crowded condition, their MSDs were approximately linear as a function time (Figure 47d, inset), from which diffusion constants were estimated. Figure 47d shows a histogram of the diffusion constants, which could be fitted with a log-normal distribution, resulting in a mean diffusion constant of 3.2 ± 0.4 nm²/s.

Figure 47.

Molecular imaging of bacterial outer surface by HS-AFM. (a,b) HS-AFM images of the outer surface of live M. magneticum AMB-1 for (a) 150 × 150 nm² area and (b) 100 × 100 nm² area, captured at 0.5 and 1.43 fps, respectively. Small indents and particles surrounding the indents were seen over the entire cell surface. Compactly arranged particles forming a reticulate structure were seen at the rims of these indent (arrows in (b)). (c) Trajectories of four reticulate structures superimposed on HS-AFM image (200 × 200 pixels, 2 fps). These trajectories were drawn by tracing the movement of each indent. (d) Distribution of diffusion constants for individual trajectories. The data followed a log-normal distribution characterized by a mean diffusion constant D = 3.2 ± 0.4 nm²/s (red solid line). Inset shows MSDs of individual trajectories as a function of time.

M. magneticum AMB-1 belongs to α-proteobacteria, and is enveloped by the outer and cytoplasmic membranes. To identify the composition of the reticulate structure, the outer membrane of M. magneticum AMB-1 was isolated, placed on a bare mica surface, and observed by HS-AFM. The HS-AFM images showed a reticulate structure very similar to that observed on live cell surfaces (Figure 48a). As previously demonstrated,^{37,70,341,342} the cantilever tip can be used to manipulate and dissect samples by increasing the loading force, and the treated samples can be imaged with the same tip at the same or lower loading force. The change of the reticulate structure during the dissection is shown in Figure 48b. By the increased loading force during imaging (frames 3–7), the reticulate structure was disrupted, resulting in appearance of diffusing triangular-shaped molecules in the membrane patch (frame 13 in Figure 48b). Most of the molecules showed a trimeric form (Figure 48c). To identify the trimeric protein, proteins contained in the outer membrane fraction were analyzed by sodium dodecyl sulfate-polyacrylamide gel electrophoresis and then by matrix-assisted laser desorption/ionization time-of-flight tandem mass spectrometry of the trypsin-digested gel slices. The most abundant protein in the outer membrane fraction was a 40-kDa protein (∼80% of the total protein content), which was identified as a porin homologue (amb0025: Msp1). Therefore, it was concluded that the major fraction of the molecules densely covering the outer membrane of M. magneticum AMB-1 is porin trimers.

Figure 48.

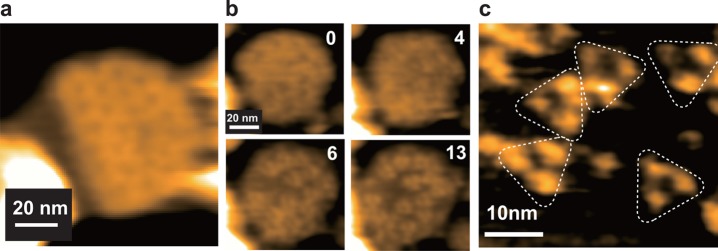
HS-AFM images of isolated outer membrane of M. magneticum AMB-1 adsorbed on mica. (a) Reticulate structure similar to those observed on the bacterial outer surface. (b) HS-AFM observation of tip-induced dissection process of the reticulate structure in an outer membrane patch. Numbers indicate the frame number. Triangle-shaped molecules were seen after the dissection of the reticulate structure. (c) Highly magnified HS-AFM image of trimeric molecules observed after dissection. Imaging rates, 1.0 fps; pixels, 100 × 100 (a and b) and 160 × 160 (c).

9.2. Dynamic Phenomena Occurring on Eukaryotic Cell Surfaces

Imaging of plasma membranes of live eukaryotic cells with AFM is more challenging than that of outer membranes of live bacteria cells because the plasma membranes are extremely soft and hence easily deformed by the contact of the AFM tip. An attempt to observe by HS-AFM dynamic events taking place on the plasma membranes of live eukaryote cells was recently made.⁶⁹

As a test sample, HeLa cells, one of the most commonly used immortal cell lines derived from human cancer cells, were imaged. The HeLa cells were cultured on a poly-l-lysine-coated glass rod at 37 °C in 5% CO₂. The glass rod was the sample stage routinely used for HS-AFM imaging. For positioning of the AFM tip on a defined place of a large HeLa cell, a simple fluorescent microscope system was incorporated into the HS-AFM system. Figure 49a shows a fluorescent image of a HeLa cell in which GFP was overexpressed. The cantilever could be seen as a dark shade (arrow in Figure 49a), and hence the cantilever tip position could be easily adjusted on a target region of the cell surface.

Figure 49.

Dynamics occurring on the apical surface of HeLa cell captured by HS-AFM. (a) Fluorescence microscopic image of GFP-transfected HeLa cells. The cantilever is indicated by the white arrow. (b) Clips of successive HS-AFM images of the apical surface of a live HeLa cell. Growth of a filopodium is indicated by arrows. Scan range, 5 × 5 μm²; imaging rate, 0.2 fps; pixels, 200 × 200.

Numerous actin-based filopodia dynamically repeat extension and retraction at the apical surface of a live HeLa cell.³⁴³ Dynamic morphological changes at the apical surface of the cell cultured on the glass rod were captured by HS-AFM at 0.2 fps for 5 × 5 μm² with 200 × 200 pixels (Figure 49b). HS-AFM cannot image filopodia perpendicularly extending from the cell surface due to the tip force. Indeed, even during imaging at low interaction forces, the surface morphology was deformed. Nonetheless, the dynamic growth of some filopodia was visualized as shown with arrows in Figure 49b.

Next, the tip was positioned at the peripheral region of the cell where the cell is much thinner and hence the effective stiffness is higher due to the underlying hard substrate. At a peripheral region of the HeLa cell, sheet-like structures with ∼100 nm height were captured at 0.2 fps for 5 × 5 μm² with 200 × 200 pixels (Figure 50a). Interestingly, the HS-AFM movie clearly showed a continuous flow of small objects directed from the cell periphery toward the center of the cell body (Figure 50a). On the other hand, after bath application of cytochalasin D (an inhibitor of actin polymerization), the continuous flow ceased completely (Figure 50b). This indicated that the flow observed in the HS-AFM movies is the actin retrograde flow. As a matter of course, the flow is occurring in the cell interior. HS-AFM visualizes the dynamics of cytoskeleton in the cell interior as convolution between the surface morphology and the local mechanical differences.³⁴⁴

Figure 50.

Dynamics observed by HS-AFM on the peripheral surface of HeLa cell. (a,b) Topographic image of HeLa cell at an peripheral region (a) before and (b) after the addition of cytochalasin D. Thin black lines in (a) indicate flow of small objects. Black dots in (b) show that no flow is occurring. Scan range, 5 × 5 μm²; imaging rate, 0.2 fps; pixels, 200 × 200. (c) Clips of successive images showing the process of endocytosis. Initially formed pits are highlighted by the dotted circles. Scan range, 5 × 5 μm²; imaging rate, 0.2 fps; pixels, 200 × 200.

Endocytosis is a cellular process, in which a cell brings molecules or substances into the cell interior from the exterior by engulfing them with the cell membrane. The engulfment typically begins with the formation of nanoscale pits on the cell surface. Recently, this pit formation and disclosure have been directly visualized on Cos-7 cells by using scanning ion conductance microscopy (SICM; see section 10), which can operate in noncontact condition.³⁴⁵ Even with tapping mode HS-AFM, this process was successfully captured using HeLa cells at an imaging rate 0.1 fps for 5 × 5 μm² with 200 × 200 pixels,⁶⁹ as shown in Figure 50c. In the HeLa cell, mEGFP-Rab5(Rab5Q79L)-CAAX was overexpressed. The small GTPase Rab5 is known to be crucial in regulation of endocytosis, and its constitutive active mutant Rab5(Rab5Q79L) stimulates endocytosis.^346−348 Replacement of the C-terminus of Rab5 with a CAAX box derived from k-Ras enhances the plasma membrane localization of Rab5. As seen in Figure 50c, each of the two pits encircled by broken lines was capped by a membrane protrusion that grew with time from the membrane surrounding each pit.

9.3. Diffusion and Interactions of Membrane Proteins on Eukaryotic Live Cells

Indirect evidence has been accumulated that membrane proteins and lipids in eukaryotic cells are organized in functional rafts, work together in multiprotein assemblies, modulate their function by interaction, temporally associate in signal or transport complexes, etc.³⁴⁹ Direct visualization of a native cell surface under physiological conditions allowing the stimulation and the observation of a dynamic membrane rearrangement would provide tremendous advances for the understanding of membrane related processes. Most recently, first breakthrough experiments have been reported, indicating the feasibility of high speed and high resolution imaging on eukaryotic cells using HS-AFM techniques.^69,70 First, the development of a wide-range scanner that can overview an entire cell while maintaining high-resolution capacity has already proven powerful to visualize dynamic cellular processes on live eukaryotic cells at high resolution, as described above.⁶⁹ In another approach, the integration of optical microscopy devices into a HS-AFM setup allowed the placement of the HS-AFM tip onto areas of interest on a cell and subsequent high-resolution high-speed imaging using a fast narrow-area scanner. With this latter technology, HS-AFM has been used to visualize individual water channels AQP0 binding to and dissociating from junctional microdomains directly on lens fiber cells.⁷⁰ As has been demonstrated for dissected AQP0 junctional microdomains by conventional and HS-AFM,^59,238,350 imaging AQP0 on a live cell corroborated their assembly in square arrays with approximate 6.5 nm unit cell dimensions, but importantly revealed novel insights into their physiological function: although only very slowly (D = 0.5 nm²/s), the junctional microdomains diffused freely in the lens cell membrane. This motional freedom of the junctional microdomains is the key to an understanding of the maintenance of adhesion between lens cells while the lens tissue undergoes elastic deformation when focusing to different distances. This pilot study of HS-AFM on live cells addressed a highly specialized membrane system of a highly specialized cell. However, the tremendous potential of HS-AFM for cell biology applications was shown by the proof of concept that individual membrane proteins could be imaged even in the membranes of live eukaryotic cells. Numerous questions concerning membrane superstructure and domain formation, and their related dynamics and responses to environmental stimuli, await to be investigated.³⁵¹

10. Perspectives

HS-AFM just recently opened a new avenue to directly and closely look at biological molecules in action and even dynamic events occurring in live cells. What biological questions of importance will be further addressed and solved by HS-AFM imaging? How extensively will this new microscopy be used in biological science? Are higher imaging rates achievable? Is it possible to combine other techniques with HS-AFM to make it more useful? Perspectives on these issues are briefly described below.

Nils Walter predicted as follows: “In a decade or two from now, each static structure from X-ray crystallography in our biochemistry textbooks may be accompanied by a dynamic video of the same biopolymer in actual biological action.”³⁵² Thus far, we have videos of only four proteins that can be placed in such textbooks: bR,^43,48 myosin V,⁴⁷ F₁-ATPase,⁵¹ and P2X₄R.³⁶ In other HS-AFM imaging studies conducted so far, protein structures are not well resolved (for example, cellulase,⁵⁶ Ca²⁺ pump,⁴⁹ NMDA receptor,⁶⁰ restriction enzymes^30,39,53), or diffusion and interaction processes of proteins are imaged instead of biological actions while their structures are resolved (for example, c-rings,³⁸ OmpF,⁵⁸ and aquaporin-0^59,70). There are countless proteins that are interesting to be investigated using HS-AFM: condensin assembling chromatins into a chromosome, helicase unwinding a double-stranded DNA, RecBCD unwinding a double-stranded DNA and digesting the resulting single strands, proteasomes digesting polyubiquitinated proteins, E3 ubiquitin ligase self-ubiquitinating or ubiquitinating substrate proteins, dynein moving on microtubules, AAA proteins disaggregating aggregated proteins, ABC transporters transporting substrates, dynamin squeezing membrane tubes, protein transport apparatuses transporting proteins, MreB and ParM in polymerization, many channel proteins opening and closing their channels during gating, DNA polymerase synthesizing a complementary DNA strand, and ribosome synthesizing a polypeptide. These are limited examples of important biomolecular systems that have been untouched by HS-AFM. In principle, any biomolecular action that occurs in the milliseconds to seconds time range is a potential target for HS-AFM structural and dynamics analysis. The limited number of systems studied so far is solely because the number of HS-AFM users is limited. This situation will quickly change because HS-AFM instruments with high-speed (>10 fps) and low-invasiveness performances are now commercially available, and small cantilevers optimized for HS-AFM are also commercially available. By a synergy effect of increasing number of HS-AFM users and concomitant accumulation of the know-how to conduct successful HS-AFM imaging (preparations of substrate surfaces and samples), the number of dynamic videos to be placed in future biochemistry textbooks will increase. Furthermore, the equipment will become handier by future enhanced development and less costly. The latter is also true for consumables like the small cantilevers. As such, Nils Walter’s prediction will surely come true.

The speed performance of the current HS-AFM instrument including small cantilevers will not be significantly improved. Maybe 100 fps could be achieved, but even to reach this rate the imaging area will have to be narrowed to ∼20 × 20 nm². This is because the small cantilevers represent the current speed limit. Generally, to increase the resonant frequency, one must compromise with the cantilever stiffness and vice versa. The currently most advanced small cantilevers (resonant frequency 1.2 MHz in water, spring constant 0.2 N/m) deem to have almost achieved the ultimate goal of balancing these two mechanical quantities. Much smaller cantilevers might be fabricated, but building a reliable and sensitive OBD detector for such very tiny cantilevers seems very difficult. Contact mode HS-AFM⁴¹ could potentially circumvent the limitations imposed by the cantilever resonant frequency. It would, however, only be applicable to solid, well adhering, and flat samples because high friction forces are unavoidable.

Short cantilever HS-AFM can also be used as a force measurement tool for high-speed force spectroscopy (HS-FS). The fast response time of the cantilever, and the fast piezo elements and electronics will allow force measurements on biomolecules with orders of magnitude faster rates than conventional AFM.³⁵³ In particular, the small cantilevers feature several advantages: high force sensitivity (as discussed above in the context of imaging), fast response, and low hydrodynamic drag. We anticipate that HS-FS will have a wide range of biological applications, notably allowing force application on molecules with speeds comparable to molecular dynamics simulations.

SICM, originally developed by Hansma,³⁵⁴ could be an alternative to HS-AFM for live cell imaging if the scan speed was increased to that of the current HS-AFM. Instead of a cantilever, SICM uses an electrolyte-filled glass capillary with an Ag/AgCl electrode inserted from the back, and measures an ionic current going through a small pore at the apex.³⁵⁵ When the tip apex is placed close to the sample surface, the impedance for the ionic current is increased. Therefore, the sample surface can be detected under noncontact condition by solely measuring the ionic current. The achieved highest spatial resolution of SICM is laterally 3–6 nm.³⁵⁶ This resolution was obtained by the advanced fabrication technique for producing very sharp capillaries with a small pore at the apex, notably by the use of a computer controlled puller equipped with a CO₂ laser to melt the capillary and the use of quartz capillaries with a high melting point.³⁵⁷ High-speed SICM with a noncontact imaging capability would be useful for observing the surface of extremely soft surfaces of live eukaryotic cells.

The information that can be acquired with HS-AFM is limited, particularly in imaging of live eukaryotic cells and isolated intracellular organelles. Only dynamic events occurring at their outer surfaces are observable. Dynamic events occurring there are often linked with dynamic events occurring in their interiors, which can be observed with fluorescence microscopy. Therefore, HS-AFM should be combined with powerful fluorescence microscopy. The current HS-AFM instrument employs the sample-stage scan mode. This design is inadequate for making simultaneous HS-AFM and florescence-microscopy observations possible, because the sample stage moves relative to the objective lens for fluorescence microscopy and a crucial area to be imaged simultaneously by fluorescence microscopy is blocked by the cantilever, although sufficient fluorescence microscopy optical signal can be acquired so as to guide the HS-AFM observation at specific loci of cells.^69,70 To have high performance optical microscopy together with HS-AFM, a HS-AFM instrument is needed that employs the tip-scan mode (the cantilever chip is scanned at least in the X- and Y-directions). Very recently, a tip-scan HS-AFM instrument was developed and combined with an inverted fluorescence microscope.³⁵⁸ This new instrument removed the limitation imposed to the sample-stage scan HS-AFM that only a small sample stage can be used to achieve high speed scanning of the sample stage. One can now use large samples. When the fluorescence microscope combined with the tip-scan HS-AFM instrument is operated in the total internal reflection mode, simultaneous single-molecule HS-AFM/fluorescence microscopy observations can be performed, as demonstrated.³⁵⁸ Therefore, in addition to imaging of live eukaryotic cells and isolated intracellular organelles, this combined system allows simultaneously observing, for example, the dynamic binding and dissociation events of fluorescent ligands on single protein molecules and the structural changes of the molecules concomitantly occurring with the ligand binding and dissociation.

Tip-scan mode HS-AFM combined with optical microscopy allows the full use of the light microscope; not only TIRFM observations but also confocal and super-resolution fluorescence microscopy observations can be performed simultaneously with HS-AFM imaging. Moreover, optical tweezers can be installed in the combined system. Therefore, HS-AFM can visualize biological molecules under external force. In the current single-molecule AFM-FS, only the magnitude of force applied to a protein molecule and the extension of the molecule under force can be measured,³⁵⁹ meaning that the molecular structure deformed or unfolded by the applied force cannot be visualized. This is also the case in the current optical trap FS.³⁶⁰ The HS-AFM visualization of molecules under external force will provide a new opportunity to study the effect of applied force on the action of the molecules as well as detailed unfolding and refolding processes of the molecules.

Tip-enhanced fluorescence microscopy has resolution <10 nm.³⁶¹ This technique is based on the highly enhanced electric field close to a laser-illuminated metal or silicon tip,^362,363 and can be installed in a tip-scan mode HS-AFM setup to materialize super-resolution/high-speed fluorescence microscopy combined with HS-AFM. Unlike some of current super-resolution fluorescence microscopy systems, no significant background fluorescence appears even when relatively high concentrations of fluorophores exist in the bulk solution because only fluorophores very close to the cantilever tip can be detected.

11. Concluding Remarks

The advent of AFM was hailed with acclamations by biologists. This is because AFM is the first and unique microscopy that allows high-resolution visualization of active biological samples in aqueous solutions. However, in contrast to the initial excitement, the enthusiasm for bio-AFM imaging gradually subsided. This is because biologists could not be satisfied only with still images. In 1992, one of the inventors of AFM, Gerd Binnig, predicted that “in biology, use of the force microscope will probably become quite common because of its ability to deliver films of processes.”³⁶⁴ However, AFM was too slow to film biological processes. The efforts to increase the imaging rate of bio-AFM started around 1993 and continued (see review³⁶⁵), which were, however, not so visible for biologists for a while. However, tremendous strides were recently accomplished in developing biocompatible HS-AFM providing high spatial and temporal resolution and low-invasiveness. Consequently, proteins in native biological action were readily captured on video. Gerd Binnig’s prediction has now partially come true; unlike his prediction, HS-AFM has not yet become “quite common”. Yet it is most certainly just a matter of time.

After describing the basic principle of AFM imaging, we quantitatively discussed how fast successive imaging could be performed by HS-AFM. The highest possible imaging rate was shown to be a function of several parameters. We found that the magnitude of maximum applied tip-force endurable by the sample most severely restricts the imaging rate. The tip-force that exceeds the set point force is caused by the delay in the feedback control. This delay is minimized in HS-AFM but never vanishes completely because of the “chasing-after” nature of the feedback control. The spatial frequency of the sample surface corrugation to be imaged was also shown to be a key parameter for the determination of the maximum possible imaging rate. Even for the same sample surface corrugation, the detectable highest spatial frequency depends on the sharpness of the cantilever tip. The higher spatial frequency can be detected by the sharper tip, which however results in the necessity of taking the images at lower rates.

We did not describe the HS-AFM instrumentation in detail, but rather focused on small cantilevers, sample stages, substrate surfaces, and their associated issues, which HS-AFM users themselves must deal with. The substrate surfaces are a key element for successful HS-AFM imaging. Because proteins have multifarious faces, we should be able to prepare many different substrate surfaces depending on the target proteins and molecular processes to be visualized. Despite the necessity of having a variety of substrate surfaces, its menu is still limited because of the limited number of proteins attempted to be visualized by HS-AFM. This issue will be improved along with increasing number of HS-AFM studies.

We started the main part of this Review (i.e., application studies on proteins) with walking myosin V and described this HS-AFM study quite in detail. This is because we feel that it is the most impressive and representative demonstration of the ability of HS-AFM to provide impregnable evidence for the nature of the dynamic molecular structural changes involved in a crucial biological mechanism. This study best exemplified the most impactful feature of HS-AFM that direct observation of single protein molecules in biological action immediately and straightforwardly recounts in detail and provides great insights into how the protein functions. In addition to several HS-AFM studies of isolated proteins, we also reviewed two HS-AFM studies of in situ imaging of protein molecules in live cells. Because molecular processes on the membrane surfaces of live cells and the surfaces of intracellular organelles are largely unknown, HS-AFM will certainly also be intensely applied to provide novel insight into these topics in the near future.

A Nobel laureate, Sydney Brenner, mentioned “progress in science depends on new techniques, new discoveries, and new ideas, probably in that order.” New discoveries are often made using new techniques, which often leads to the creation of new ideas. In this sense, new techniques most contribute to the progress in science. We hope that HS-AFM will be one of such new techniques and that this Review will provide biological researchers with a chance of considering the use of HS-AFM in their studies to directly observe their molecular and cellular phenomena under study at unprecedented high spatiotemporal resolution.

Glossary

Abbreviations

AAA

ATPases associated with diverse cellular activities

ADP

adenosine diphosphate

AM

amplitude modulation

AMP

antimicrobial peptide

AMPPNP

adenylyl-imidodiphosphate

APS

1-(3-aminopropyl)silatrane

APTES

3-aminopropyltriethoxysilane

AQP0

aquaporin-0

ATP

adenosine triphosphate

A5

annexin 5

bR

bacteriorhodopsin

CBH

cellobiohydrolases

CBD

cellulose-binding domain

CD

catalytic domain

D/A

digital to analog

DNA

deoxyribonucleic acid

DOC

deocycholate

DOPC

1,2-dioleoyl-sn-glycero-3-phosphocholine

DPPC

1,2-dipalmitoyl-sn-glycero-3-phosphocholine

DPPE

1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine

EBD

electron beam deposition

EGTA

ethylene glycol tetraacetic acid

EM

electron microscopy

EPC

ethylphosphatidylcholine

FACT

facilitates chromatin transcription

fps

frames per second

FM

frequency modulation

GFP

green fluorescent protein

GH

glycoside hydrolase

HMG

high-mobility group

HMM

heavy mero myosin

HOPG

highly ordered pyrolytic graphite

IDP

intrinsically disordered protein

IDR

intrinsically disordered region

mEGFP

monomeric enhanced GFP

M5

myosin V

MSD

mean square displacement

NMR

nuclear magnetic resonance

NTA

nitrilotriacetic acid

OBD

optical beam deflection

OmpF

outer membrane protein F

PC

phosphatidyl choline

PDB

protein data bank

PE

phosphatidyl ethanolamine

PG

phosphatidylglycerol

PID

proportional integral derivative

PS

phosphatidylserine

RMS

root-mean-square

SAM

self-assembled monolayer

SERCA

sarcoplasmic reticulum Ca²⁺-ATPase

SICM

scanning ion conductance microscopy

SLB

supported lipid bilayer

SR

sarcoplasmic reticulum

SSRP

structure specific recognition protein

TAP

trimethylammoniumpropane

WT

wild type

Biographies

Toshio Ando studied physics, applied physics, and biophysics at Waseda University and received his Dc. Sci. degree in 1980 from Waseda University. After working on the mechanism of muscle contraction and fluorescence techniques for six and half years as a postdoctoral fellow and then an assistant research biophysicist at UC San Francisco (Manuel Morales’s lab), he was appointed to the faculty at Kanazawa University, where he is currently a Full Professor of Physics and the Director of the Bio-AFM Frontier Research Center. His research interests include the elucidation of functional mechanism of proteins, particularly of motor proteins, and the instrument development of high-speed scanning probe microscopes. He has received many awards for his development of high-speed AFM and its biological applications.

Takayuki Uchihashi received his B.Sc., M.Sc. in Physics from Hiroshima University, Japan in 1993 and 1995, respectively. In 1998, he obtained his Dc.Eng. in Electronics from Osaka University, Japan. From 1998 to 2000, he worked at the Joint Research Center for Atom Technology (JRCAT) in Tsukuba as a research associate. In 2000, he joined the Department of Electronic Engineering, Himeji Institute of Technology. In 2002, he moved to Trinity College in Dublin and worked as a senior researcher. In 2004, he joined the Department of Physics, Kanazawa University, and since 2006 he has been an associate professor. His research interests include the instrumentation of scanning probe microscopy and its application to biological science.

Simon Scheuring is the founder and head of the “Bio-AFM-Lab” laboratory U1006 INSERM/Université Aix-Marseille. He is a trained biologist from the Biozentrum at the University of Basel, Switzerland (1992–1996). During his Ph.D. in the laboratory of Andreas Engel (1997–2001), he learned electron microscopy and atomic force microscopy, and got interested in membrane proteins. During this period he worked on the structure determination of aquaporins in collaboration with Peter Agre. During his postdoc at the Institut Curie in Paris, France, in the laboratory of Jean-Louis Rigaud (2001–2004), he learned membrane physical chemistry and developed atomic force microscopy for the study of native membranes. As a permanent researcher (2004–2007) and junior research director (2007–2012), he set up his lab at the Institut Curie in Paris, France. He has been awarded an INSERM Avenir grant (2005) and the “Médaille de la Ville de Paris” (2007). He then moved to Marseille (2012) where he built a larger laboratory named “Bio-AFM-Lab” administrated by INSERM and Université Aix-Marseille, where he was promoted to senior research director (2012). His objective is to head a dynamic young research team with members from different scientific fields ranging from biology, physics, and engineering to develop and use atomic force microscopy to provide novel insights into the processes taking place in biological membranes. Simon Scheuring has been awarded a European Research Council (ERC) grant (2012).

Appendix

A.1. Resolution

Very different resolution ranges are attained by various techniques used in structural biology, as summarized in Table 3. The assessment of resolution of AFM topographs is a more complex problem than one could initially anticipate, and often AFM users describe their molecular imaging assessment with qualitative terms such as “high-resolution” or “submolecular resolution”, although sometimes the same qualitative terms have been used for completely different structural details analyzed by other techniques.

Table 3. Resolutions Achieved by Different Structural Biology Techniques.

technique	sample	information	resolution range	“high-resolution”	refs
X-ray diffraction	3D crystal	3D electron density	0.5–8.0 Å in x, y, z	0.5–1.0 Å in x, y, z	(366,367)
NMR	protein in solution	3D distance constraints	0.1–1.0 Å distance constraints	0.1–0.5 Å distance constraints	(182,368)
EM crystallography	2D crystal	2D or 3D nuclear density	1.8–25 Å in x, y dimensions, lower resolution in z dimension	1.8–4.0 Å in x, y dimensions, lower resolution in z dimension	(250,369)
EM single particle	protein in solution	3D nuclear density	5.0–25 Å	3–5 Å	(183,370)
fluorescence microscopy	proteins in cells	fluorescent label localization	200–1000 nm	10 nm spatial localization	(239)
AFM	adsorbed proteins	surface topography	1–50 nm in x, y dimensions, 0.1–1.0 nm in z dimension	1–2 nm in x, y dimensions, 0.1–0.2 nm in z dimension

The assessment of the resolution in AFM is a difficult task. On the one hand, the scanning process, with the fast and slow scan axes, results in an inhomogeneous resolution in X and Y dimensions. On the other hand, the tip radius crucial for surface contouring is often unmeasured. For this reason, and for others like the unknown contribution of electrostatic, chemical, and van der Waals forces, the image contrast transfer function is not definable. Today, AFM scientists still debate about image resolution. Initially, the imaging of membrane protein 2D crystals has suggested by the visual inspection of diffraction spots in calculated power spectra that the AFM could acquire topography details with down to 6 Å resolution.³⁷¹ It has however been shown that the surface convolution by the AFM tip of radius comparable to the features or unit cell of the proteins (nanometer scale) imperatively results in higher order diffraction spots not corresponding to realistic image resolution, and hence in overestimation of the imaging resolution.³⁷² An approach closer to the genuine resolution assessment like the one that has been used in single particle electron microscopy appeared more appropriate.^372,373 Sometimes it was proposed that like for optical microscopy, the capability of separating two features from each other could be used as resolution assessment in AFM. However, this leads to an underestimation of the imaging resolution. This is because AFM contours topography and does not transform a point signal into a point spread function like an optical microscope does. For example, AFM can contour a most protruding surface feature and at the same time document information about the asymmetric nature of the surrounding lower topography protein structure; see the HS-AFM topography of the α₃β₃ subcomplex of F₁-ATPase (Figure 13). When one follows the logics of distinguishing intensity peaks, a low resolution (of about 3 nm) would be estimated on these molecules from the distance between the peaks of the subunits. This is certainly not the case, because the resolution was high enough to unambiguously distinguish between the conformational states of the molecules by cross-correlation comparison with a surface rendering of the atomic structure.⁵¹ Indeed the AFM contouring is structurally dependent on objects that are larger than the radius of the tip, where a structure oriented resolution assessment similar to single particle electron microscopy is most appropriate. However, when contouring objects of size similar to the tip radius or smaller, then obviously the tip convolutes the features in a point spread function manner. Recently, FM-AFM has reported the resolution of substructure on individual lipid headgroups in supported lipid bilayers.³⁷⁴ This finding remains controversial because of the documented diffusion of lipids even in gel phase bilayers.³⁷⁵ Such a high resolution could so far only be acquired on crystalline lipids in a regular arrangement, and certainly not on a protein. Taking together, the highest AFM imaging resolution on protein molecules is of about 1 nm in lateral dimensions and 0.1 nm in vertical dimension. This is in agreement with both (i) comparison with atomic structure surfaces rendered to different resolutions and (ii) theoretical considerations concerning the tip radius. The AFM imaging resolution has not been improved since pioneering works of high-resolution imaging by contact mode AFM on bR and aquaporins.^202,371,376 However, HS-AFM in AM mode, which has now achieved the same resolution and documented protein dynamics,⁴³ is much less invasive⁵¹ and can achieve such high resolution on highly corrugated and relatively loosely attached molecules.⁴⁷

A.2. Software

HS-AFM data visualized must be analyzed. A hopefully helpful but certainly not complete list of software that can be used to analyze AFM data in general and HS-AFM data in particular is given in Table 4.

Table 4. Software Packages That Allow Image Processing.

software name	webpage	access	applications
imageJ	http://rsb.info.nih.gov/ij/	free	single pixel manipulation, various operations (Java-based plugins can be downloaded for a wide range of image processing tasks)
photoshop	http://www.adobe.com/products/photoshop.html	commercial	single pixel manipulation
gwyddion	http://gwyddion.net	free	various scanning probe microscopy specific image visualization and analysis operations
image SXM	http://www.liv.ac.uk/∼sdb/ImageSXM/	free	single pixel manipulation, various scanning probe microscopy specific image visualization and analysis operations
2dx	http://2dx.org/	free/open source	2D-crystal processing
EMAN2	http://blake.bcm.edu/emanwiki/EMAN2	free/open source	2D-crystal processing, single particle averaging
IMAGIC	http://imagescience.de/imagic/	commercial nonprofit prices	2D-crystal processing, single particle averaging
MRC	http://www2.mrc-lmb.cam.ac.uk/image2000.html	free for academia	2D-crystal processing
SIMPLE	http://simple.stanford.edu	free/open source	single particle averaging

Typically, images are briefly pretreated (mostly flattened for scan line non-horizontality) by the AFM-specific data acquisition software. After transformation to a more general file format (tiff, stack of tiffs), images can be contrast adjusted and filtered using any pixel-oriented image treatment software. Of course, care must be taken to consider that contrast adjustment means changing the height scale in AFM topographs and such alterations must be reliably tracked to maintain the scientific meaning of the image.³⁷² In any case, filtering results in altered (diminished) image resolution. One may choose a soft mean or median filter to decrease imaging noise and/or scan related noise (scan lines), which enhances the visibility of the object to be analyzed. However, only features visible in the original raw data set should be scientifically interpreted. For molecular imaging, several image processing packages “inherited” from EM can be used to average and analyze images of molecules; when the molecules are ordered in 2D crystals, lattice oriented algorithms can be used, while when the molecules are randomly arranged, single particle averaging approaches can be used.³⁷⁷ These methods function typically well, but care must be taken not to over-interpret the resolution. This is mainly due to the fact that EM-specific program algorithms have been designed to work with a large amount of well-defined (white) noise overlaid to the molecule images. In AFM, the signal-to-noise ratio is much higher, and the noise is of different nature. Hence, AFM images produce high signal diffraction spots at high resolution when analyzed using EM software packages as shown³⁷⁸ and discussed.³⁷² Importantly, dynamic processes must be tracked in the analysis of successive HS-AFM images. For this purpose, single particle tracking software packages or plugins developed for fluorescence optical microscopy can be “inherited”.³⁷⁹ Again, these programs function relatively well for HS-AFM particle tracking data analysis. Yet there are some limitations; for example, fluorescence particles can “blink” (disappear and reappear in subsequent frames), and the scan line noise is present in AFM images, which might influence the tracking algorithm.³⁸⁰ Clearly, there is still a lot of work to be done by and a major interest for the HS-AFM community (and the AFM community in general) to gather efforts to standardize image processing and analysis tools adapted to the specificities of the microscopy technique. Typically, standardization of processes, analysis, and statistical assessment provide a major increase in the credibility of a technical approach and will therefore boost the esteem and use of AFM and HS-AFM in biological sciences in general.

A.3. Simulation of AFM Image

Construction of simulated AFM images from protein crystal structures can be performed using software, for example, the SPM simulator (Advanced Algorithm Systems Co., Tokyo, Japan). The cantilever tip is modeled as a circular cone of various angles with a small sphere of various radiuses at the apex. Each atom in a protein is modeled as a hard sphere with a corresponding van der Wars radius. The simulated images are processed by a low-pass filter with an appropriate cut-off wavelength that is adjusted to be similar to the spatial resolution of experimentally obtained AFM images. By the comparison of experimentally obtained images to images simulated with various cone angles and tip apex radiuses, one can approximately determine the cone angle and the tip apex radius used in the experiment. The procedure is exemplified here on the α₃β₃ subcomplex of F₁-ATPase, as illustrated in Figure 51 (the cone angle was fixed at 10°).

Figure 51.

Simulated AFM images of the C-terminal side of α₃β₃ subcomplex obtained using different tip apex radiuses indicated at the top of the corresponding images.

A.4. Correlation Coefficient Analysis

A 2D correlation coefficient calculation can be performed to assign HS-AFM images of a protein to specific conformational states of the protein or a subunit in the protein. For a series of HS-AFM images of the protein, a reference frame and ROIs are chosen; the ROI in each image fully contains the protein molecule or the subunit to be analyzed. The 2D correlation coefficient r defined below is calculated frame-by-frame for each ROI. The 2D correlation coefficient r is defined as:

8

Here, I_mn and R_mn are intensities at pixel point (m, n) in a ROI to be analyzed and those in the reference ROI in the reference frame, respectively. I̅ and R̅ are mean values of the intensity matrices I and R, respectively. When the analyzed image and the reference one are the same, the correlation coefficient r becomes 1. If they are completely different, the correlation coefficient r becomes zero. Therefore, one can evaluate the similarity of two images from the value of r. Of course, to assign an AFM image to one of the specific conformational states, the conformational state of the protein (or the subunit) contained in the reference ROI should be determined anyhow. This determination can be made again by this correlation coefficient analysis, when crystal structures of the protein are available for its specific conformational states. In this case, using the correlation coefficient analysis, the ROI of the reference image experimentally obtained is compared to ROIs of the simulated images constructed as mentioned above. The procedure is exemplified for the β subunits within the α₃β₃ subcomplex of F₁-ATPase, as shown in Figure 52, and its results are shown in Figure 15.

Figure 52.

Correlation coefficient analysis of AFM images. (a) Experimentally acquired AFM image of α₃β₃ subcomplex in nucleotide-free condition that was chosen as a reference image and ROIs therein used in the two-dimensional correlation coefficient analysis for the determination of conformational states of each β subunit. The transparent boxes represent ROIs for three β subunits. (b) Simulated AFM image of α₃β₃ subcomplex in the presence of ATP and the ROI (encircled with the white rectangle) containing a β subunit in the E conformational state (i.e., nucleotide-free state). Scale bar, 5 nm. (c) A clip from successively acquired HS-AFM images of α₃β₃ subcomplex in the presence of ATP and the ROI (encircled with the white rectangle). Scale bar, 5 nm. (d) Time course of correlation coefficients calculated to determine the conformational states of the β subunit shown in the ROI of (c). For this calculation, the simulated AFM image and the ROI as a reference shown in (b) were used. Bimodal change of the correlation coefficient is clearly seen: the larger r (0.98) and smaller r (around 0.95) represent the E and R conformational states, respectively.

A.5. Tracking Analysis of Proteins Moving along a Filament

For statistical analysis of velocities of individual molecules linearly moving on a filamentous structure, the center of mass of each molecule can be tracked semi-automatically for its successive AFM images. Because AFM images sometimes contain spike noises due to instant adsorption of other molecules to the filaments, fully automatic tracking is difficult. Here, the semi-automatic tracking procedure is shown below for the case of cellulase molecules moving on crystalline cellulose fibers, but applicable to other systems where objects to be analyzed are moving approximately in a linear path.

(1) To reduce spike noises in the AFM images, all raw images are processed by a 2 × 2 pixel averaging filter before the analysis. An example is given for the first frame as shown in Figure 53a (raw image) and Figure 53b (filtered image).

Figure 53.

Tracking procedures for a cellulase molecule linearly moving along a cellulose fibril (see text).

(2) A single cellulase molecule in the first frame is selected, and a ROI is drawn by encircling the molecule with a rectangle (Figure 53c).

(3) Within the ROI, the image is compensated for the height slope by first-order plane fitting, and then the center of mass in the ROI is calculated (red dot, Figure 53c). This height slope compensation is sometimes required especially when the height of the filamentous structure is not uniform.

(4) In the last frame of the successive images, the same molecule is encircled with a rectangle, followed by the height slope compensation and then calculation of its center of mass of the molecule (Figure 53d). Next, the determined centers of mass of the target molecule in the first and last frames are connected by a linear line, which gives the first approximation for the trajectory (Figure 53e). An average translocation velocity of the molecule is determined using the distance between the centers of mass in the first and last frames and the time interval between them.

(5) In the second frame, the ROI made in the first frame is translated along the linear trajectory obtained above by the distance expected from the average translocation velocity determined above. The 2D correlation coefficient r for the ROI in the second frame is calculated, in which the ROI of the first frame is used as the reference image. To find the ROI position that gives the maximum value of r, the ROI of the second frame is translated within tolerance of 5 × 5 pixels. At the ROI position where the maximum value of r is obtained, the position of ROI in the second frame is fixed. Next, the center of mass of the molecule is calculated within the ROI, which represents the position of molecule in the second frame.

(6) The same procedures described above are repeated for the remaining frames (Figure 53f).

The authors declare no competing financial interest.