Abstract
One of the most fundamental concepts of microscopy is that of resolution–the ability to clearly distinguish two objects as separate. Recent advances such as structured illumination microscopy (SIM) and point localization techniques including photoactivated localization microscopy (PALM), and stochastic optical reconstruction microscopy (STORM) strive to overcome the inherent limits of resolution of the modern light microscope. These techniques, however, are not always feasible or optimal for live cell imaging. Thus, in this review, we explore three techniques for extracting high resolution data from images acquired on a widefield microscope–deconvolution, model convolution, and Gaussian fitting. Deconvolution is a powerful tool for restoring a blurred image using knowledge of the point spread function (PSF) describing the blurring of light by the microscope, although care must be taken to ensure accuracy of subsequent quantitative analysis. The process of model convolution also requires knowledge of the PSF to blur a simulated image which can then be compared to the experimentally acquired data to reach conclusions regarding its geometry and fluorophore distribution. Gaussian fitting is the basis for point localization microscopy, and can also be applied to tracking spot motion over time or measuring spot shape and size. All together, these three methods serve as powerful tools for high-resolution imaging using widefield microscopy.
As scientists who use microscopes to address biological questions, we strive to acquire ever better images and push the limits of resolution. The image formed of a specimen by a light microscope occurs as the combination of light diffracted by the specimen, the interference of these light rays, and the collection of these light rays by the objective lens. The ability to detect objects–the image contrast–depends on the signal-to-noise ratio. In order to clearly identify an object, its signal intensity must be high enough over the background noise. The level of detail in an image, or alternatively the ability to distinguish two objects as separate, is its resolution limit. The limits of resolution (the ability to distinguish as separate two points of light) were first described by Ernst Abbe, and are dependent on both the sample and the microscope hardware (Abbe, 1873). As a result of the wavelength of the light and its diffraction by the microscope optics, a single point of light will not appear as a spot but instead as a hazy circle surrounded by diffraction rings in the focal plane. In three dimensions, this blurring is termed the point spread function (PSF) and defines the limits of resolution (Fig. 1A). The lateral dimensions of this hazy blurring can be described mathematically as an Airy pattern (Airy, 1835), and the bright central region (Airy disk) has a radius determined by the wavelength of light (λ) and numerical aperture (NA) of the objective lens (Inoué, 2006; Waters, 2009),
Fig. 1.
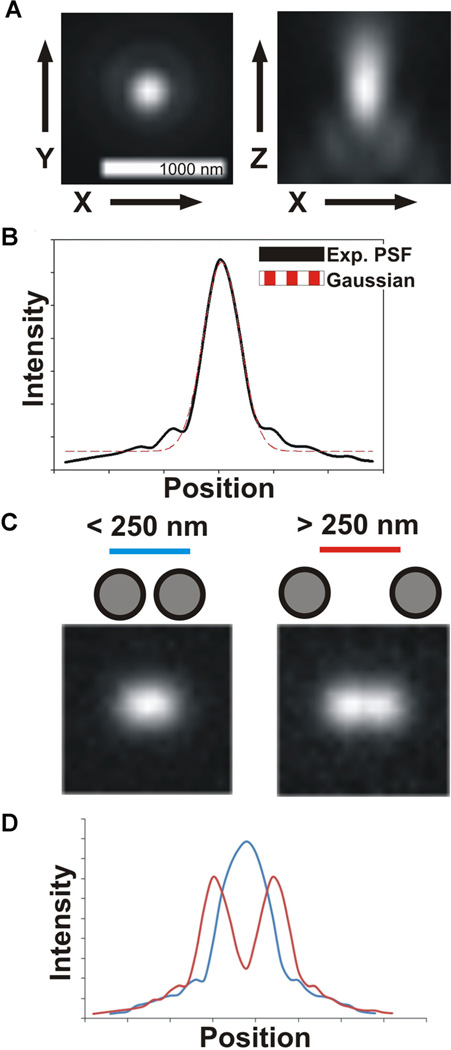
A: Experimental images of a sub-resolution bead illustrating the characteristic blurring of a point source of light by a widefield microscope. In X and Y (left), the bead appears as a bright central spot surrounded by more faint rings, termed the Airy disk and Airy rings. In X and Z (right), the light is flared along the z-axis. B: The blurring of light by the microscope, the point spread function (PSF), can be approximated by a Gaussian distribution. C: Examples of two point sources of light less that ~250nm apart (left) and more than ~250nm apart (right). At smaller separating distances, the two spots appear as one. D: A linescan illustrating the intensity profile of the images in (C). The spots in close proximity appear as a single, higher peak, whereas the two more separated spots appear as two distinct peaks.
The Airy disk can be approximated by a Gaussian distribution (Fig. 1B). By the Rayleigh criterion, two point objects are said to resolvable when they are separated by a distance equal to or greater than the radius of the Airy disk (Rayleigh, 1896). For example, in order to be able to distinguish two separated sister kinetochores in the budding yeast mitotic spindle, these must physically be separated by at least 222 nm, assuming they are labeled with GFP and imaged with a 1.4 NA objective lens. Otherwise, they are said to be within a single diffraction limited spot (Fig. 1C,D). As we shall see, even this fundamental limit is being pushed by advancements in methods of image acquisition and mathematical image processing.
So how can we image two objects that are close together or more precisely find the position of a single point of light? Newer imaging technologies have emerged that use a range of methods to improve the resolution of a light microscopy image (Inoué, 2006; Weisshart et al., 2013). Modern confocal microscopy is based on the principles first described in 1957 by Marvin Minsky and use a combination of pinholes to illuminate a smaller area of the total sample and eliminate the collection of out of focus (scattered) light rays (Minsky, 1988). Multi-photon microscopy (MPM) utilizes the simultaneous absorption of two (or more) photons to excite a single fluorophore as an alternative method to confine excitation to a smaller area of the sample and allowing for deeper penetration into thick samples. In structured illumination microscopy (SIM), a sample is illuminated with highly structured light that has passed through a grating. This process effectively allows the microscope to capture finer details in the sample and can double resolution of a typical widefield microscope. Photoactivated localization microscopy (PALM), stochastic optical reconstruction microscopy (STORM), and a wide range of similar techniques utilize specialized fluorophores or modulate fluorophore behavior (e.g., photoactivation and photoswitching) to sequentially image and precisely localize subsets of fluorophores (Betzig et al., 2006; Rust et al., 2006; Schermelleh et al., 2010; Sengupta et al., 2012).
However, these techniques are not always optimal for imaging in vivo dynamic events in budding yeast. Imaging live cells requires trade-offs to optimize imaging parameters for a given experiment. These include total time imaged (timelapsing), z-axis resolution, image acquisition speed, and signal to noise. Confocal and multi-photon microscopy require greater excitation intensity to collect a similar number of photons per second as compared to widefield microscopy. This increased intensity can lead to cell damage and death, hampering the ability to collect data for longer periods of time. SIM requires the collection of multiple images with different grating patterns to reconstruct a single plane, drastically increasing total imaging time (preventing rapid acquisition) and this increased photobleaching reduces total images that can be acquired over time. The extensive rounds of imaging required for PALM/STORM image reconstruction is not feasible in live and dynamic cells. Thus, for imaging relatively thin, highly dynamic and rapidly photobleaching samples like budding yeast, we prefer widefield microscopy.
In this review, we will outline three post-acquisition methods to improve the spatial resolution of a widefield microscopy image, and their applications to yeast cell biology. Deconvolution utilizes mathematical algorithms to remove or reverse image blurring and improve contrast. Image analysis by model convolution allows the user to examine how computer generated geometrical structures are blurred by the microscope and compare these to experimentally obtained images. Gaussian fitting of single point objects allows for sub-pixel localization of structures of interest and can be used to precisely track motion over time. In order to maximize signal to noise and reach spatial resolution limited by the physics and optics of the microscope, it is essential to properly prepare samples. Discussions of optimizing sample preparation and imaging parameters, however, are beyond the scope of this article (Rines et al., 2002; Cannell et al., 2006; Dailey et al., 2006; Waters, 2009; Goldman et al., 2010).
Deconvolution Putting Light (Back) in Its Proper Place
The observed image generated by the microscope is generated from the actual image convolved by the PSF and contains noise (Biggs, 2010; Fig. 2A, left). Thus, although the image is degraded, it occurs in a mathematically predictable manner. Image restoration is achieved either by removal (deblurring) or reassignment (deconvolution) of blurred light, based on knowledge of how the image was degraded during acquisition. In this section, we discuss measurement of the PSF, briefly outline the various techniques used in image deconvolution, and highlight some applications of image deconvolution to the study of mitosis in budding yeast.
Fig. 2.
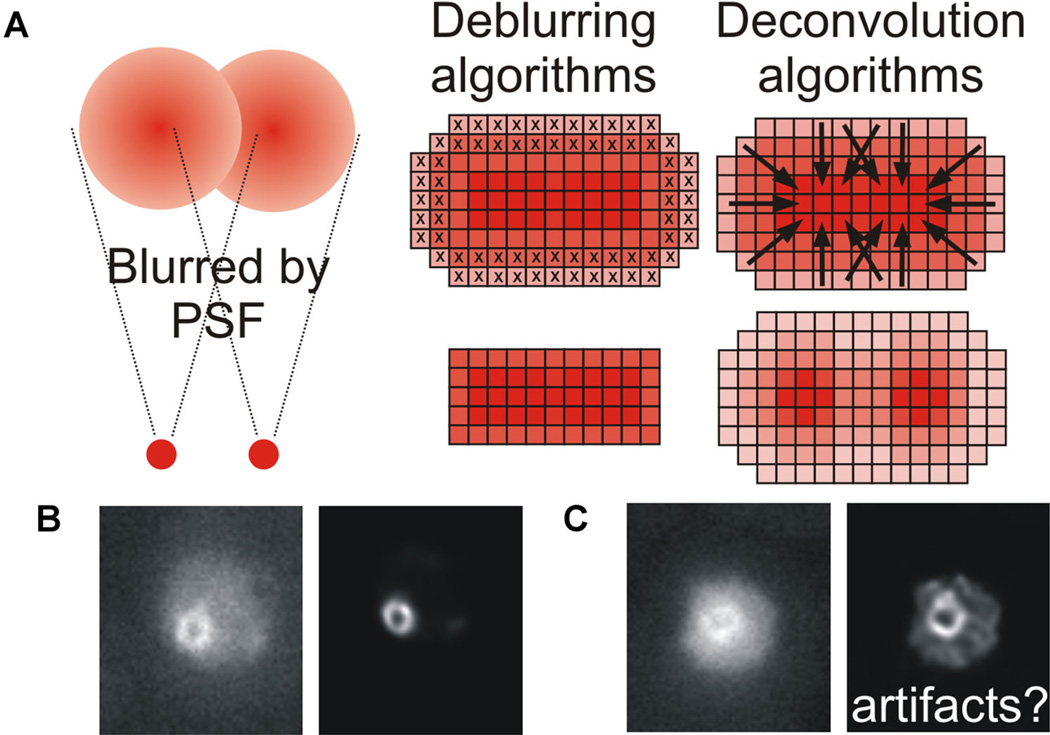
A: Point sources of light are significantly blurred by both the point spread function (PSF) of the microscope and noise. Two distinct methods exist for post-acquisition processing of a blurred image. Deblurring algorithms remove out of focus planes, producing a sharper image but reducing the total information available and thus rendering the image unquantifiable. Deconvolution algorithms preserve the information, and restore the blurred fluorescence to the original point source using a range of methods as described in the text. B,C: Cohesin forms a barrel-like structure during metaphase in budding yeast, which appears as a doughnut when viewed end-on and bilobed when viewed side-on (Yeh et al., 2008; Stephens et al., 2011). Original and deconvolved images of cohesin (SMC3-GFP) illustrating how both input image quality and deconvolution algorithm parameters can lead to very different output images and potentially introduce artifacts.
The PSF forms the basis for image deconvolution and depends on the microscope (objective lens properties) and imaging conditions. The PSF can be estimated mathematically or measured under experimental conditions (Gibson and Lanni, 1991; Wallace et al., 2001; Cannell et al., 2006; Swedlow, 2007). Measurement of the PSF is most commonly done using sub-resolution (100–200 nm) fluorescent beads under identical conditions as the experiment by imaging through the axial (z) direction (Biggs, 2010). Adding these fluorescent beads to the experimental slide further ensures PSF measurements are consistent (Cannell et al., 2006). It is important to image multiple beads throughout the field of view to ensure that the measured PSF is consistent throughout and detect any possible aberrations in the imaging set up (e.g., coma, astigmatism, spherical and chromatic) that may alter the PSF. The shape of the PSF is especially sensitive to spherical aberrations of the objective lens, as these cause oblique light rays to be focused at a different focal plane than the central light rays. The PSF can be translated to frequency, or Fourier, space to ease mathematical analysis, as convolution functions translate to multiplication in the frequency domain (Biggs, 2010). The Fourier transform of the PSF is termed the optical transfer function (OTF; Sibarita, 2005).
Deblurring algorithms–including nearest neighbor, no neighbor, multi-neighbor–improve image appearance by removing or reducing blur but the resulting image cannot be used for subsequent quantification (Agard, 1984; Agard et al., 1989; Wallace et al., 2001; Sibarita, 2005; Swedlow, 2007; Biggs, 2010; Fig. 2A, center). These analyses have the benefit of being computationally simple and fast, but since these do not use all out of focus planes their application is limited.
In contrast, fully three dimensional deconvolution algorithms reassign blurred light preserving signal intensity and include linear (Weiner) filters and nonlinear (iterative) filters (Wallace et al., 2001; Biggs, 2010; Fig. 2A, right). Wiener and other linear filters are a direct method of image reconstruction and are very sensitive to PSF measurements. Linear filters are limited by noise and errors in reconstruction (Sibarita, 2005; Cannell et al., 2006). The application of constraints or limitations during reconstructions can limit noise (Wallace et al., 2001). More recently, nonlinear iterative deconvolution has become standard and linear deconvolution can be used as a first approximation for these iterative processes (Sibarita, 2005).
Nonlinear iterative deconvolution algorithms are based on repeatedly generating a reconstructed image until the reconstruction reaches a level acceptable to the user or software chosen by the user (Swedlow, 2007). Classical iterative methods are based on the Jansson Van-Cittert and Gold algorithms (Gold et al., 1964; Agard et al., 1989; Shaw, 2006; Jansson, 2012). Reconstruction can be slow and unsatisfactory if the raw data is too noisy (Sibarita, 2005). Thus, deconvolution becomes a balance between removing noise by filtering and a less sharp final image due to increased smoothing. Statistical iterative deconvolution is similar to classical algorithms and improves image quality by reducing noise. The metric to be applied depends on the source of the noise and its distribution (Gaussian or Poisson; Richardson, 1972; Lucy, 1974; Sibarita, 2005; Biggs, 2010). Blind deconvolution, also called adaptive PSF deconvolution, is iterative reconstruction of both the image and the PSF from an estimated starting point with constraints (Holmes, 1992; Krishnamurthi et al., 1995; Holmes et al., 2006; Biggs, 2010). This method has the advantage of not requiring measurement of the PSF but tends to be slower than non-blind iterative methods (Holmes et al., 2006).
Image restoration by deconvolution is a powerful tool to improve image quality but does have inherent limitations. Deconvolved images provide a high resolution, high contrast image that can provide additional information about biological structures. If done with certain algorithms, the resulting images can be quantitatively analyzed (Wallace et al., 2001). Advances in computing power will continue to increase speed and ease of deconvolution, making it an attractive option for improving image quality. Imaging followed by deconvolution is a good option for live cell imaging where cell viability must be balanced against exposure time and light intensity. However, it is essential that deconvolved images be compared to raw data, and if a structure is present in the deconvolved image, it should also be visible in the raw data (Sibarita, 2005). One must exercise caution to avoid artifacts or aberrations in the reconstructed image (Wallace et al., 2001; Murray, 2005; Fig. 2B,C).
Model Convolution Blurring the Lines Between Reality and Simulation
Model convolution is an approach used to understand the possible distributions of fluorophores that give rise to an experimentally acquired image. Model convolution takes the opposite approach of deconvolution. Instead of trying to deduce fluorophore positions/distribution from a noise-filled experimental image, model convolution uses computer simulated fluorophore positions/distributions then generates a noise-filled simulated image. This is accomplished by attaching the experimentally determined PSF of the microscope to each of the fluorophores to recapitulate the spread of fluorescence through the microscope objective (Fig. 3A). The convolution of the entire fluorophore geometry or distribution is the summarization of the contributions of the fluorescence from each simulated fluorophore position in x, y, and z to the image plane (Agard et al., 1989; Sprague et al., 2003). Image(x,y,z) = ΣFluorophore matrix (x,y,z) × PSF(x,y,z). Signal to noise ratios can be recapitulated by adding in the experimentally measured background, brightest intensity, and noise variation. Simulated images from model convolution can then be compared directly to experimental microscopy images in a statistically rigorous fashion to determine a best fit.
Fig. 3.
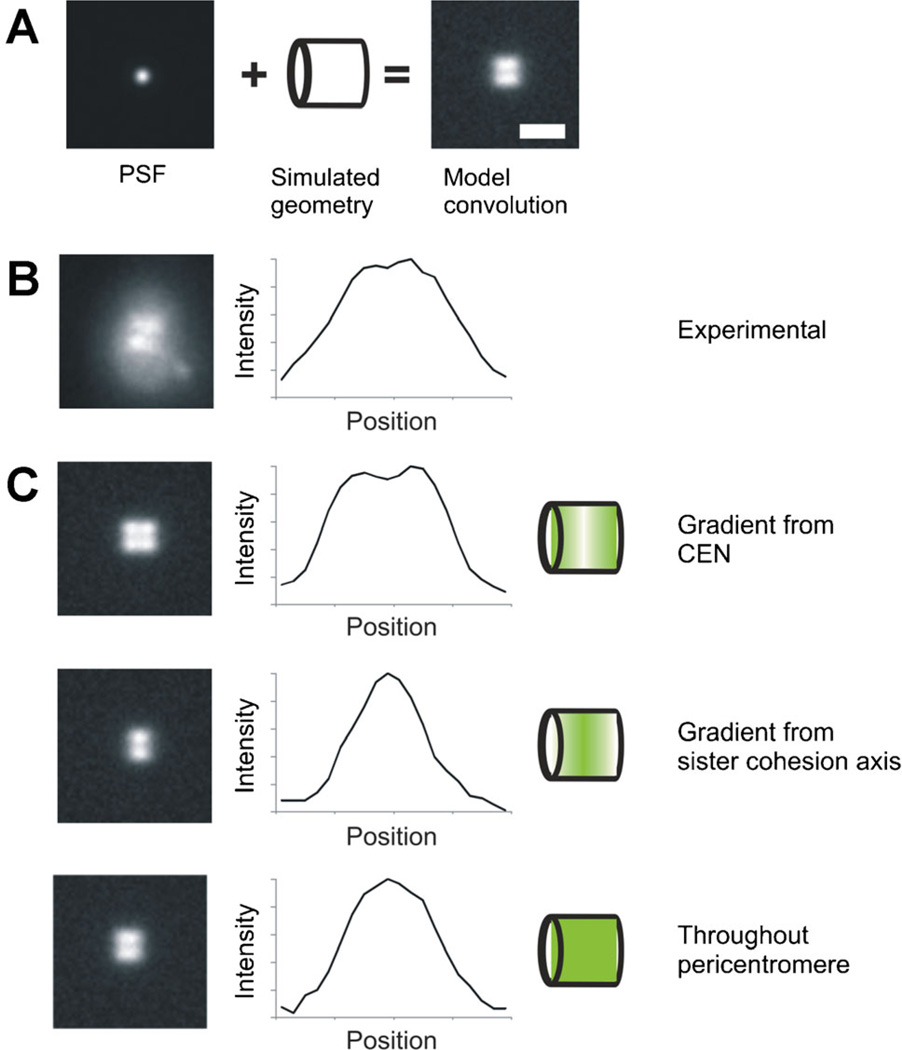
A: Model convolution requires knowledge of the point spread function (PSF) and a simulated geometry to produce an image that can then be compared to experimentally acquired data. B: Experimental image of cohesin (SMC3-GFP) viewed side-on appears bilobed. C: In order to further understand the distribution and organization of cohesin during metaphase, we compared the experimental distribution to various modeled geometries. Introducing a gradient from either the centromere or the center (sister chromatid cohesion axis), resulted in intensity profiles that did not match the experimental data in (B). When cohesin distribution was modeled as distributed throughout the pericentromere region, the intensity profile matched experimental data, showing that cohesin distribution is not characterized by a concentration gradient.
Model convolution has various positives and negatives as compared to deconvolution. Deconvolution methods are centered on producing a clearer image of a fluorescently labeled structure. However, when trying to use deconvolution algorithms to determine correct fluorophore positions in a structure, poor signal to noise ratios can impede deconvolution or introduce artifacts (Gardner et al., 2010). Alternatively, model convolution can be used to determine the distribution of fluorophores in a structure through running possible iterations and finding the best match. This approach relies on knowing how many fluorescent molecules are in the structure. Modeling can provide information about gradients, clustering, and/or random dispersion of the fluorophores within the structure. The limitation of model convolution is that you are still subject to the resolution of your microscope - the ability to discriminate two objects or fluorophores. However, modeling intensity changes over a structure along with the ability to alter fluorophore positions with sub-pixel accuracy makes model convolution a useful tool to analyze experimental data at the resolution limit.
Model convolution has been instrumental in determining the shape, size, and distribution of molecules in the pericentric cohesin and condensin structures that are two major components of the mitotic chromatin spring. While deconvolution was effective in determining shape and size of the cohesin barrel (Fig. 2B), model convolution allowed insight into the distribution of fluorophores (Fig. 3B,C). Using the measured number of fluorophores for cohesin we simulated different gradients from a major loading site, the centromere, and major site of function, the sister cohesion axis (Fig. 3C). Interestingly, the simulated sister cohesin axis gradient accurately recapitulated experimental size measurements but failed to match the intensity distributions throughout the structure. Instead, cohesin randomly distributed throughout the structure recapitulated fluorescence intensity along the cohesin barrel. This approach of matching changes in intensities is the cornerstone of model convolution. Model convolution allows one to determine how fluorophores are distributed within a structure and assess the validity of mathematical models of biological processes by comparing simulated and experimental images.
As scientists and researchers we love to see an image, because seeing is believing. However, when you consider the PSF and Abbe diffraction limit, what you see might not be what you get. This is where model convolution excels. The output of a microscope image may not align with your preconceived notion of the underlying structure. However, with this technique we can explore possible structures and distributions and analyze how they are changed by the spreading of light through the microscope. One example of failed intuition is that two smaller hollow cylinders will look like one line, while one larger hollow cylinder will look like two lines. This occurs because the two smaller cylinders are too close to differentiate, while for the larger cylinder we only see the top and the bottom of the cylinder in focus. Model convolution goes beyond measurements by allowing us to understand how a defined geometry or distribution of fluorophores results in the blurred image we see in the microscope.
The other place that model convolution excels is in computer modeling. In the quest to understand the biology of life computer models are being used to investigate complex cellular process. Microscopy holds a wealth of data that is necessary to incorporate into modeling approaches. Through the use of programs such as Microscope Simulator 2.0, we can produce fluorescence simulated images from computational models to compare to experimental data (Quammen et al., 2008; Stephens et al., 2013).
Gaussian Fitting Cutting Through the Haze
As described above, point sources of light are blurred in a characteristic manner by the widefield light microscope, termed the PSF. In the image plane, the point of light appears as a bright maximum cone of light surrounded by concentric diffraction rings. The shape of this maximum cone, the Airy disk, can be approximated by a Gaussian fit (Fig. 1B). The fitting of a single molecule’s Airy disk with a Gaussian function to identify its centroid with nanometer resolution forms the basis of PALM/STORM microscopy, which relies on various techniques (e.g., photoactivation and photoswitching) to sequentially image subsets of fluorophores (Betzig et al., 2006; Rust et al., 2006; Schermelleh et al., 2010; Sengupta et al., 2012). Here, we outline sub-diffraction particle localization methods, and the application of Gaussian fitting to track motion or localize proteins within a complex structure in vivo.
The shape of the theoretical PSF can be approximated by either a Gaussian function or center of mass calculation in order to localize the sub-resolution position of the fluorophore (Cheezum et al., 2001; Thompson et al., 2002; Levi and Gratton, 2007; Deschout et al., 2012). Approximation of the PSF by a Gaussian function is relatively simple, quick computationally, and more robust under conditions of low signal to noise than the center of mass method (Santos and Young, 2000; Cheezum et al., 2001; Thomann et al., 2002; Levi and Gratton, 2007; Stallinga and Rieger, 2010; Churchman and Spudich, 2012). The approximation of position by center of mass does not rely on a normal distribution of fluorescence intensity, making it a better choice for larger or asymmetric particles, and has been shown to more accurately estimate lateral motion (Levi and Gratton, 2007; Deschout et al., 2012). It is also important to note that computationally a Gaussian fitting can be done by either least squares fitting or maximum likelihood estimation. Maximum likelihood estimation is a more accurate method, but more complex than least squares fitting (Larson et al., 2010; Laurence and Chromy, 2010; Mortensen et al., 2010; Smith et al., 2010). Close proximity of fluorophores or structures can confound the precision localization of basic Gaussian fitting methods. Advancements in mathematical processing of PALM/STORM datasets has allowed for localization analysis of fluorophores in close proximity (Holden et al., 2011; Huang et al., 2011; Babcock et al., 2012; Cox et al., 2012). With the advancement of computational power, the development of more robust algorithms for particle localization will continue to be developed and more precise localization may be possible.
Precise tracking of motion by Gaussian fitting has been used to address a wide range of biological questions including nucleocytoplasmic transport, myosin V motor motion, organelle dynamics and chromatin motion (Churchman et al., 2005; Levi and Gratton, 2007; Jaqaman et al., 2008; Goryaynov et al., 2012). We have developed a methodology for tracking chromatin motion to quantify confinement and physical properties such as spring constant. As mentioned previously, imaging setup is essential to obtain images with good signal to noise for sufficiently long timelapses. Once images are acquired, we perform a 2D Gaussian fitting by least squares using a custom MatLab (The Mathworks, Natick, MA) script (Wan et al., 2008; Wan et al., 2009; Fig. 4A). We assume that the labeled chromatin array forms a close to diffraction limited spot, and the program is able to account for small asymmetries by the incorporation of a rotation transformation (Wan et al., 2008).
Fig. 4.
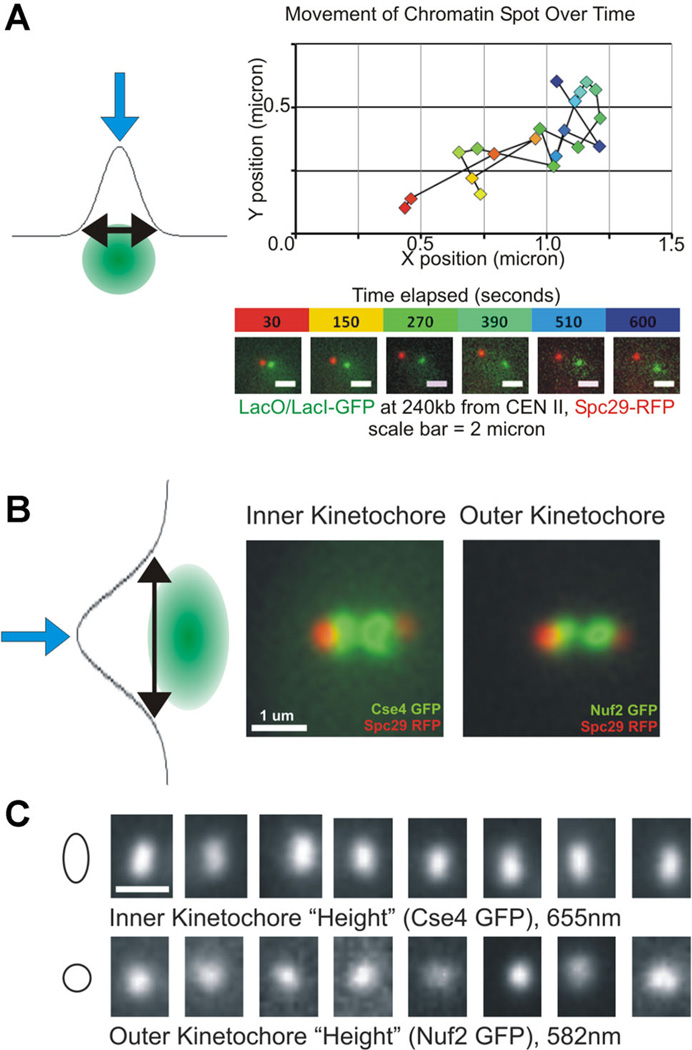
A: The precise localization of a blurred point source of light can be achieved by fitting the fluorescent signal with a Gaussian distribution, as illustrated by the blue arrow at the apex. An example of precise localization of a labeled chromatin spot performed over time is shown, and these data can be used to perform mean square displacement (MSD) analysis or examine viscoelastic properties of the polymer. B: In addition to measuring precise localization (blue arrows), fitting with Gaussian distributions can be used to measure spot size (black arrows). This method reveals differences in kinetochore spot shape between the inner (Cse4) and outer (Nuf2) kinetochores (adapted from Haase et al., 2012). C: Various individual images illustrating the increased spot size along the vertical axis of the inner kinetochore (mean = 655nm) not present when examining outer kinetochore spots (mean = 582 nm; adapted from Haase et al., 2012).
In addition to tracking particles over time, Gaussian fitting has been used to characterize the architecture of the kinetochore and measure the number of proteins within this complex. The kinetochore is a large multi-protein complex that mediates the attachment of the centromere to the microtubule during chromosome division (Bloom and Joglekar, 2010). Essential to further understanding the role of the kinetochore in establishing and maintaining proper attachment is the development of a precise map of protein numbers and organization. Measurement of signal intensity by Gaussian fitting to determine number of proteins in a single focus within the kinetochore has been performed in a range of yeast species (Joglekar et al., 2006, 2008a,b). These have revealed a conserved fundamental building block present in both point and regional centromeres. Protein numbers are reported as ratio values to a known standard, as a wide range of factors can influence signal intensity including inherent properties of the fluorophore and imaging conditions. Due to the stereotypic nature of the budding yeast point centromere, the fluorescence intensity of Cse4p (HsCENP-A) has been used as a standard. Recent studies using a variety of imaging and molecular techniques have shed new light on the number of Cse4p molecules in the single focus and further work will be needed to clarify the use of Cse4p as an imaging standard for counting by fluorescence intensity (Lawrimore et al., 2011; Coffman and Wu, 2012; Shivaraju et al., 2012; Aravamudhan et al., 2013; Padeganeh et al., 2013a,b).
Precision localization by Gaussian fitting can also be used to determine distances between kinetochore components. The SHREC (single molecule high-resolution colocalization) method serves as a basis for this methodology, and is based on imaging two points of interest within the same protein labeled with two different fluorophores and precisely localizing these using least squares fit to a 2D Gaussian curve (Churchman et al., 2005). This approach has been expanded to incorporate distance measurements throughout the human kinetochore, which suggested an intra-kinetochore tension-sensing mechanism important for cell cycle regulation (Wan et al., 2009). Work examining the distances between different kinetochore proteins using 2 color imaging and fitting to a Gaussian function by maximum likelihood estimation has revealed that distances within the budding yeast kinetochore have also been shown to change upon loss of tension, perhaps serving a similar role in cell cycle checkpoint signaling during mitosis (Joglekar et al., 2009).
The architecture of the budding yeast kinetochore has further been characterized by Gaussian fitting to describe kinetochore spot shapes and possible positions within the stereotypical mitotic spindle structure. By measuring kinetochore spot sizes during metaphase along defined axes during metaphase, we have shown that the proteins of the inner kinetochore (adjacent to the chromatin) are anisotropic and elongated along the axis perpendicular to the spindle (Haase et al., 2012; Fig. 4B,C). These measurements were done by rotating the fluorescent images using the spindle pole body markers to bring the spindle axis to a horizontal level (y-axis). After rotation, we measured the full width-full maximum of the Gaussian fit to the kinetochore signal along the spindle axis (y-axis) and along the x-axis. In addition to characterizing the shape of individual kinetochore foci, the precise measurement of coordinates by Gaussian fitting can be used to examine the distribution of possible positions occupied by the protein of interest. In order to normalize the data across many individual cells, the spindle pole body coordinates are set to (0,0) and positions of kinetochore proteins or labeled chromatin measured in many cells are plotted relative to the normalized spindle pole body (Haase et al., 2012). The resulting heat map illustrates the average position as well as the spread of possible positions.
Conclusion
In this review, we have highlighted three methods that can be used to extract greater detail from widefield images– deconvolution, model convolution, and precision localization by Gaussian fitting. These methods can be used independently or together in order to best address the scientific questions of interest. Acquiring a good image (i.e., good signal to noise, maintaining cell viability, fully capturing processes of interest) is only part of the battle; for the image to be of value it must also be analyzed in a quantitative and rigorous manner. We would encourage any researcher to experiment with various analysis techniques and software packages to determine which is most suitable for the problem at hand.
Acknowledgments
We thank members of the Bloom laboratory for discussion, advice, and critical readings of the manuscript. J.S.V. would like to thank the instructors, vendor-instructors, and fellow students of the 2013 Cold Spring Harbor Laboratory Quantitative Imaging: From Cells to Molecules course. This work was funded by the National Institutes of Health R37 grant GM32238 (to K. Bloom).
Literature Cited
- Abbe E. Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung. Archiv für Mikroskopische Anatomie. 1873;9:413–418. [Google Scholar]
- Agard DA. Optical sectioning microscopy: Cellular architecture in three dimensions. Annu Rev Biophys Bioeng. 1984;13:191–219. doi: 10.1146/annurev.bb.13.060184.001203. [DOI] [PubMed] [Google Scholar]
- Agard DA, Hiraoka Y, Shaw P, Sedat JW. Fluorescence microscopy in three dimensions. Methods Cell Biol. 1989;30:353–377. doi: 10.1016/s0091-679x(08)60986-3. [DOI] [PubMed] [Google Scholar]
- Airy GB. On the diffraction of an object-glass with circular aperture. Trans Camb Philos Soc. 1835;5:283. [Google Scholar]
- Aravamudhan P, Felzer-Kim I, Joglekar AP. The budding yeast point centromere associates with two Cse4 molecules during mitosis. Curr Biol. 2013;23:770–774. doi: 10.1016/j.cub.2013.03.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babcock H, Sigal YM, Zhuang X. A high-density 3D localization algorithm for stochastic optical reconstruction microscopy. Opt Nanosc. 2012;1:1–10. doi: 10.1186/2192-2853-1-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, Hess HF. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- Biggs DSC. 3D deconvolution microscopy. Curr Protoc Cytom. 2010;52:12.19.1–12.19.20. doi: 10.1002/0471142956.cy1219s52. [DOI] [PubMed] [Google Scholar]
- Bloom K, Joglekar A. Towards building a chromosome segregation machine. Nature. 2010;463:446–456. doi: 10.1038/nature08912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannell MB, McMorland A, Soeller C. Handbook of biological confocal microscopy. New York, NY: Springer; 2006. Image enhancement by deconvolution; pp. 488–500. [Google Scholar]
- Cheezum MK, Walker WF, Guilford WH. Quantitative comparison of algorithms for tracking single fluorescent particles. Biophys J. 2001;81:2378–2388. doi: 10.1016/S0006-3495(01)75884-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchman LS, Spudich JA. Colocalization of fluorescent probes: Accurate and precise registration with nanometer resolution. Cold Spring Harb Protoc. 2012;2012:141–149. doi: 10.1101/pdb.top067918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchman LS, Okten Z, Rock RS, Dawson JF, Spudich JA. Single molecule high-resolution colocalization of Cy3 and Cy5 attached to macromolecules measures intramolecular distances through time. Proc Natl Acad Sci USA. 2005;102:1419–1423. doi: 10.1073/pnas.0409487102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coffman VC, Wu JQ. Counting protein molecules using quantitative fluorescence microscopy. Trends Biochem Sci. 2012;37:499–506. doi: 10.1016/j.tibs.2012.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox S, Rosten E, Monypenny J, Jovanovic-Talisman T, Burnette DT, Lippincott-Schwartz J, Jones GE, Heintzmann R. Bayesian localization microscopy reveals nanoscale podosome dynamics. Nat Methods. 2012;9:195–200. doi: 10.1038/nmeth.1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dailey ME, Manders E, Soll DR, Terasaki M. Handbook of biological confocal microscopy. New York, NY: Springer; 2006. Confocal microscopy of living cells; pp. 381–403. [Google Scholar]
- Deschout H, Neyts K, Braeckmans K. The influence of movement on the localization precision of sub-resolution particles in fluorescence microscopy. J Biophotonics. 2012;5:97–109. doi: 10.1002/jbio.201100078. [DOI] [PubMed] [Google Scholar]
- Gardner MK, Sprague BL, Pearson CG, Cosgrove BD, Bicek AD, Bloom K, Salmon ED, Odde DJ. Model convolution: A computational approach to digital image interpretation. Cell Mol Bioeng. 2010;3:163–170. doi: 10.1007/s12195-010-0101-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson SF, Lanni F. Experimental test of an analytical model of aberration in an oil-immersion objective lens used in three-dimensional light microscopy. JOSA A. 1991;8:1601–1613. doi: 10.1364/josaa.9.000154. [DOI] [PubMed] [Google Scholar]
- Gold R Atomic Energy Commission, Argonne National Laboratory. An iterative unfolding method for response matrices. Argonne, Ill: Argonne National Laboratory; 1964. [Google Scholar]
- Goldman RD, Swedlow J, Spector DL. Live cell imaging: A laboratory manual. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 2010. [Google Scholar]
- Goryaynov A, Ma J, Yang W. Single-molecule studies of nucleocytoplasmic transport:From one dimension to three dimensions. Integr Biol (Camb) 2012;4:10–21. doi: 10.1039/c1ib00041a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haase J, Stephens A, Verdaasdonk J, Yeh E, Bloom K. Bub1 kinase and Sgo1 modulate pericentric chromatin in response to altered microtubule dynamics. Curr Biol. 2012;22:471–481. doi: 10.1016/j.cub.2012.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holden SJ, Uphoff S, Kapanidis AN. DAOSTORM: An algorithm for high-density super-resolution microscopy. Nat Methods. 2011;8:279–280. doi: 10.1038/nmeth0411-279. [DOI] [PubMed] [Google Scholar]
- Holmes TJ. Blind deconvolution of quantum-limited incoherent imagery: Maximum-likelihood approach. JOSA A. 1992;9:1052–1061. doi: 10.1364/josaa.9.001052. [DOI] [PubMed] [Google Scholar]
- Holmes TJ, Biggs D, Abu-Tarif A. Handbook of biological confocal microscopy. New York, NY: Springer; 2006. Blind deconvolution; pp. 468–487. [Google Scholar]
- Huang F, Schwartz SL, Byars JM, Lidke KA. Simultaneous multiple-emitter fitting for single molecule super-resolution imaging. Biomed Opt Express. 2011;2:1377–1393. doi: 10.1364/BOE.2.001377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inoué S. Handbook of biological confocal microscopy. New York, NY: Springer; 2006. Foundations of confocal scanned imaging in light microscopy; pp. 1–19. [Google Scholar]
- Jansson PA. Deconvolution of images and spectra. Mineola, NY: Dover Publications; 2012. [Google Scholar]
- Jaqaman K, Loerke D, Mettlen M, Kuwata H, Grinstein S, Schmid SL, Danuser G. Robust single-particle tracking in live-cell time-lapse sequences. Nat Methods. 2008;5:695–702. doi: 10.1038/nmeth.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joglekar AP, Bouck DC, Molk JN, Bloom KS, Salmon ED. Molecular architecture of a kinetochore-microtubule attachment site. Nat Cell Biol. 2006;8:581–585. doi: 10.1038/ncb1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joglekar AP, Bouck D, Finley K, Liu X, Wan Y, Berman J, He X, Salmon ED, Bloom KS. Molecular architecture of the kinetochore-microtubule attachment site is conserved between point and regional centromeres. J Cell Biol. 2008a;181:587–594. doi: 10.1083/jcb.200803027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joglekar AP, Salmon ED, Bloom KS. Counting kinetochore protein numbers in budding yeast using genetically encoded fluorescent proteins. Methods Cell Biol. 2008b;85:127–151. doi: 10.1016/S0091-679X(08)85007-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joglekar AP, Bloom K, Salmon ED. In vivo protein architecture of the eukaryotic kinetochore with nanometer scale accuracy. Curr Biol. 2009;19:694–699. doi: 10.1016/j.cub.2009.02.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnamurthi V, Liu Y-H, Bhattacharyya S, Turner JN, Holmes TJ. Blind deconvolution of fluorescence micrographs by maximum-likelihood estimation. Appl Opt. 1995;34:6633–6647. doi: 10.1364/AO.34.006633. [DOI] [PubMed] [Google Scholar]
- Larson ME, Harrison BD, Bloom K. Uncovering chromatin’s contribution to the mitotic spindle: Applications of computational and polymer models. Biochimie. 2010;92:1741–1748. doi: 10.1016/j.biochi.2010.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurence TA, Chromy BA. Efficient maximum likelihood estimator fitting of histograms. Nat Methods. 2010;7:338–339. doi: 10.1038/nmeth0510-338. [DOI] [PubMed] [Google Scholar]
- Lawrimore J, Bloom KS, Salmon ED. Point centromeres contain more than a single centromere-specific Cse4 (CENP-A) nucleosome. J Cell Biol. 2011;195:573–582. doi: 10.1083/jcb.201106036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levi V, Gratton E. Exploring dynamics in living cells by tracking single particles. Cell Biochem Biophys. 2007;48:1–15. doi: 10.1007/s12013-007-0010-0. [DOI] [PubMed] [Google Scholar]
- Lucy L. An iterative technique for the rectification of observed distributions. Astronom J. 1974;79:745. [Google Scholar]
- Minsky M. Memoir on inventing the confocal scanning microscope. Scanning. 1988;10:128–138. [Google Scholar]
- Mortensen KI, Churchman LS, Spudich JA, Flyvbjerg H. Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat Methods. 2010;7:377–381. doi: 10.1038/nmeth.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray JM. Confocal microscopy, deconvolution, and structured illumination methods. In: Goldman RD, Spector DL, editors. Live cell imaging–A laboratory manual. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press; 2005. pp. 239–279. [DOI] [PubMed] [Google Scholar]
- Padeganeh A, De Rop V, Maddox PS. Nucleosomal composition at the centromere: A numbers game. Chromosome Res. 2013a;21:27–36. doi: 10.1007/s10577-012-9335-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padeganeh A, Ryan J, Boisvert J, Ladouceur AM, Dorn JF, Maddox PS. Octameric CENP-A nucleosomes are present at human centromeres throughout the cell cycle. Curr Biol. 2013b;23:764–769. doi: 10.1016/j.cub.2013.03.037. [DOI] [PubMed] [Google Scholar]
- Quammen CW, Richardson AC, Haase J, Harrison BD, Taylor RM, II, Bloom KS. FluoroSim: A visual problem-solving environment for fluorescence microscopy. Eurographics Workshop Vis Comput Biomed. 2008;2008:151–158. doi: 10.2312/VCBM/VCBM08/151-158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rayleigh L. XV. On the theory of optical images, with special reference to the microscope. Philos Mag Ser 5. 1896;42:167–195. [Google Scholar]
- Richardson WH. Bayesian-based iterative method of image restoration. JOSA. 1972;62:55–59. [Google Scholar]
- Rines DR, He X, Sorger PK. Quantitative microscopy of green fluorescent protein-labeled yeast. Methods Enzymol. 2002;351:16–34. doi: 10.1016/s0076-6879(02)51839-5. [DOI] [PubMed] [Google Scholar]
- Rust MJ, Bates M, Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM) Nat Methods. 2006;3:793–796. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santos A, Young IT. Model-based resolution: Applying the theory in quantitative microscopy. Appl Opt. 2000;39:2948–2958. doi: 10.1364/ao.39.002948. [DOI] [PubMed] [Google Scholar]
- Schermelleh L, Heintzmann R, Leonhardt H. A guide to super-resolution fluorescence microscopy. J Cell Biol. 2010;190:165–175. doi: 10.1083/jcb.201002018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengupta P, Van Engelenburg S, Lippincott-Schwartz J. Visualizing cell structure and function with point-localization superresolution imaging. Dev Cell. 2012;23:1092–1102. doi: 10.1016/j.devcel.2012.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw PJ. Handbook of biological confocal microscopy. Springer; 2006. Comparison of wide-field/deconvolution and confocal microscopy for 3D imaging; pp. 453–467. [Google Scholar]
- Shivaraju M, Unruh JR, Slaughter BD, Mattingly M, Berman J, Gerton JL. Cell-cycle-coupled structural oscillation of centromeric nucleosomes in yeast. Cell. 2012;150:304–316. doi: 10.1016/j.cell.2012.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sibarita JB. Deconvolution microscopy. Adv Biochem Eng Biotechnol. 2005;95:201–243. doi: 10.1007/b102215. [DOI] [PubMed] [Google Scholar]
- Smith CS, Joseph N, Rieger B, Lidke KA. Fast, single-molecule localization that achieves theoretically minimum uncertainty. Nat Methods. 2010;7:373–375. doi: 10.1038/nmeth.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprague BL, Pearson CG, Maddox PS, Bloom KS, Salmon ED, Odde DJ. Mechanisms of microtubule-based kinetochore positioning in the yeast metaphase spindle. Biophys J. 2003;84:3529–3546. doi: 10.1016/S0006-3495(03)75087-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stallinga S, Rieger B. Accuracy of the gaussian point spread function model in 2D localization microscopy. Opt Express. 2010;18:24461–24476. doi: 10.1364/OE.18.024461. [DOI] [PubMed] [Google Scholar]
- Stephens AD, Haase J, Vicci L, Taylor RM, II, Bloom K. Cohesin, condensin, and the intramolecular centromere loop together generate the mitotic chromatin spring. J Cell Biol. 2011;193:1167–1180. doi: 10.1083/jcb.201103138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens AD, Haggerty RA, Vasquez PA, Vicci L, Snider CE, Shi F, Quammen C, Mullins C, Haase J, Taylor RM, II, Verdaasdonk JS, Falvo MR, Jin Y, Forest MG, Bloom K. Pericentric chromatin loops function as a nonlinear spring in mitotic force balance. J Cell Biol. 2013;200:757–772. doi: 10.1083/jcb.201208163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swedlow JR. Quantitative fluorescence microscopy and image deconvolution. Methods Cell Biol. 2007;81:447–465. doi: 10.1016/S0091-679X(06)81021-6. [DOI] [PubMed] [Google Scholar]
- Thomann D, Rines DR, Sorger PK, Danuser G. Automatic fluorescent tag detection in 3D with super-resolution: Application to the analysis of chromosome movement. J Microsc. 2002;208:49–64. doi: 10.1046/j.1365-2818.2002.01066.x. [DOI] [PubMed] [Google Scholar]
- Thompson RE, Larson DR, Webb WW. Precise nanometer localization analysis for individual fluorescent probes. Biophys J. 2002;82:2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace W, Schaefer LH, Swedlow JR. A workingperson’s guide to deconvolution in light microscopy. Biotechniques. 2001;31:1076–1078. 1080. doi: 10.2144/01315bi01. 1082 passim. [DOI] [PubMed] [Google Scholar]
- Wan X, Salmon ED Department of Biomedical Engineering, University of North Carolina at Chapel Hill. Asymmetric chromosome oscillation during mitosis and protein architecture of the human kinetochore measured by K-SHREC Kinetochore-Speckle High Resolution Co-Localization. Chapel Hill, NC: University of North Carolina at Chapel Hill; 2008. p 1 electronic text PDF (2.63 MB) [Google Scholar]
- Wan X, O’Quinn RP, Pierce HL, Joglekar AP, Gall WE, DeLuca JG, Carroll CW, Liu ST, Yen TJ, McEwen BF, Stukenberg PT, Desai A, Salmon ED. Protein architecture of the human kinetochore microtubule attachment site. Cell. 2009;137:672–684. doi: 10.1016/j.cell.2009.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waters JC. Accuracy and precision in quantitative fluorescence microscopy. J Cell Biol. 2009;185:1135–1148. doi: 10.1083/jcb.200903097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisshart K, Dertinger T, Kalkbrenner T, Kleppe I, Kempe M. Super-resolution microscopy heads towards 3D dynamics. Adv Opt Technol. 2013;2:211–231. [Google Scholar]
- Yeh E, Haase J, Paliulis LV, Joglekar A, Bond L, Bouck D, Salmon ED, Bloom KS. Pericentric chromatin is organized into an intramolecular loop in mitosis. Curr Biol. 2008;18:81–90. doi: 10.1016/j.cub.2007.12.019. [DOI] [PMC free article] [PubMed] [Google Scholar]