Abstract
Background
We compared the functional brain connectivity produced during resting-state in which subjects were not actively engaged in a task with that produced while they actively performed a visual motion task (task-state).
Material/Methods
In this paper we employed graph-theoretical measures and network statistics in novel ways to compare, in the same group of human subjects, functional brain connectivity during resting-state fMRI with brain connectivity during performance of a high level visual task. We performed a whole-brain connectivity analysis to compare network statistics in resting and task states among anatomically defined Brodmann areas to investigate how brain networks spanning the cortex changed when subjects were engaged in task performance.
Results
In the resting state, we found strong connectivity among the posterior cingulate cortex (PCC), precuneus, medial prefrontal cortex (MPFC), lateral parietal cortex, and hippocampal formation, consistent with previous reports of the default mode network (DMN). The connections among these areas were strengthened while subjects actively performed an event-related visual motion task, indicating a continued and strong engagement of the DMN during task processing. Regional measures such as degree (number of connections) and betweenness centrality (number of shortest paths), showed that task performance induces stronger inter-regional connections, leading to a denser processing network, but that this does not imply a more efficient system as shown by the integration measures such as path length and global efficiency, and from global measures such as small-worldness.
Conclusions
In spite of the maintenance of connectivity and the “hub-like” behavior of areas, our results suggest that the network paths may be rerouted when performing the task condition.
MeSH Keywords: Brain, Connectome, Functional Neuroimaging, Magnetic Resonance Imaging, Models, Statistical
Background
The characterization of brain function depends not only on the activity in specific brain regions, but also on understanding the patterns of connectivity among them. Examining the brain as an integrative network of functionally interacting areas can provide new insights into large-scale neuronal communication [1]. Brain connectivity patterns are mostly described by two methods: structural connectivity, typically focusing on the large white matter tracts, describes the presence of physical links among brain areas, and functional connectivity (fcMRI) which measures the functional association among brain regions, that is, the degree to which the activity in one region resembles activity in another. fcMRI correlations among brain regions are likely to reflect a combination of direct anatomic connections as well as indirect connections that lead to functional coupling [2].
fcMRI studies have shown that spontaneous, low-frequency variations (<.1 Hz) in blood oxygen level dependent responses (BOLD) exhibit correlations related to functional associations among brain areas (see [3] for a review). One prominent example is the co-activation of a network of cortical regions of interest (ROIs) during rest (when the subject performs no external task), known as the default mode network (DMN) [4]. The DMN involves a set of cortical and subcortical regions, including the posterior cingulate/precuneus cortices (PCC/PrCC), medial prefrontal cortex (MPFC), orbital frontal gyrus, and lateral parietal cortex [5]. It has been defined as a network of areas engaged during mind wandering, prospective and retrospective self-reflection and memory retrieval, and it suggests that the ‘default mode’ involves on-going processing of information relevant to the self [6].
The cognitive tasks associated with the DMN raise the question of whether this network is exclusively engaged at rest, and whether its properties fundamentally change when subjects participate in active, external tasks. Previous studies have explored several hypotheses in an attempt to explain task vs. rest connectivity. For example, it has been suggested that tasks which are not trivially easy [7], or that contain behavioral and memory-related components (instead of simple action-perception) [8], result in a higher default mode network activity. Other studies have using ROI-to-voxel correlations argued that the DMN is attenuated and the signal fluctuations persist and reorganize with the workload during task [9]. Yet other studies have suggested that DMN activity is anti-correlated between rest and cognitive task performance [10–12]. Here, we use a combination of ROI-to-voxel, ROI-to-ROI and graph theoretical approaches to investigate how functional brain networks, both those restricted to the DMN and those spanning the entire cortex, change between rest-state and active-task fMRI. By using established and robust neuroimaging analysis methods, we were able to explore the overall structure of the brain network with a high level of spatial detail [13,14]. We conducted a whole-brain analysis of connections among anatomically defined ROIs and compared network statistics including path length and efficiency, regional measures such as degree (number of connections) and betweenness centrality (number of shortest paths of which an ROI is a member), and global measures such as small-worldness. We found that connections among the DMN areas were enhanced, rather than suppressed, during active task processing, and that global regional measures across the cortex such as degree and betweenness centrality were stronger during task processing than at rest, suggesting increased inter-regional coupling. Despite the higher regional connectivity present during task processing, we found no increase in global or local efficiency, which suggests that increased connectivity does not imply a more efficient processing system, and instead supports the view that the brain switches between several similarly efficient cognitive states in response to whatever are the current behavioral demands.
Material and Methods
Subjects
Eight, right-handed, healthy volunteers (3 female, mean age 19.8±2.0) with normal or corrected-to-normal vision and naïve as to the purpose of the study, participated in fMRI scans of resting state and a high-level visual motion task. None of the subjects had any history of neurological or psychiatric diseases, and were not on any recreational drugs. The study was approved by the ethics committees at the Boston University and the Martinos Center for Biomedical Imaging at Massachusetts General Hospital and all subjects gave written informed consent.
Stimulus and tasks
Resting state
In the resting state scans, subjects were shown a gray screen without fixation and were instructed to keep their eyes open while blinking normally, keep their head as still as possible, and stay awake throughout the data acquisition. Five of the eight subjects had 2 resting state runs.
Task (gap closure)
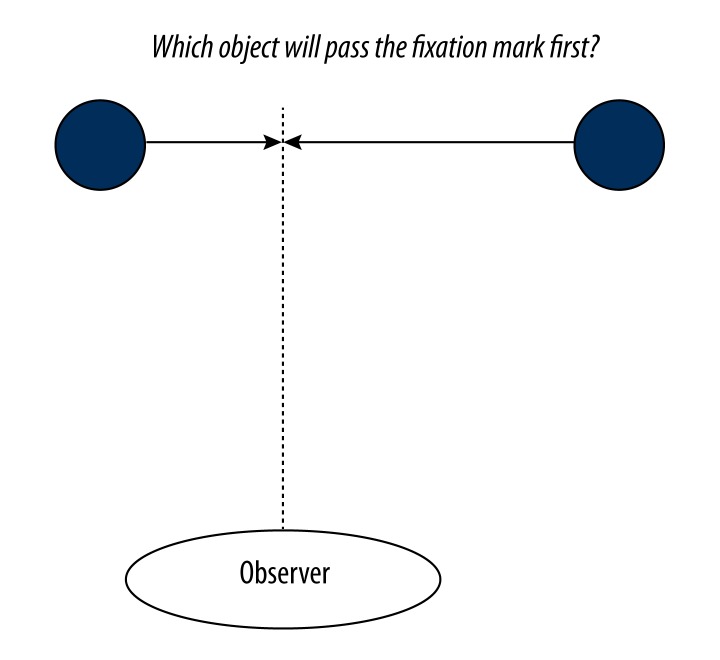
The stimulus used for this task was based on a previous psychophysical study in carried out in our laboratory [15]. As seen in Figure 1, the stimulus consisted of two spheres, 1.5° in diameter, positioned along the horizontal midline at randomly chosen eccentricities ranging between 2.8 and 9.5° on either side of a central red dot (20×20 arcmin). During each trial, the spheres moved towards the fixation mark such that they would reach fixation 1.0 sec and 1.3 sec after stimulus onset respectively. The object which would arrive first was selected randomly on each trial. The stimulus was visible for 500 ms, so that the collision with the fixation mark occurred 500–800 ms after the completion of the trial, forcing subjects to interpolate the motion in order to determine which would collide first (i.e., the collision itself was not shown). Spheres had a mean luminance of 28 cd/m2 on a background of 0.3 cd/m2. Subjects were instructed to fixate on a central red dot and report which of the two spheres would have crossed the medial plane first. Subjects completed two 5 minute runs, consisting of 80 trials each. Trials were presented based on event related timing sequence, generated using the optseq2 tool [16,17], with the time between trials varying from 2 to 14 sec. Overall, subjects performed the task with 91.1% accuracy (with a standard deviation among subjects of 5.4%).
Figure 1.
Gap-closure stimulus schematic. Screen shot of the gap-closure psychophysical motion test, showing two spheres on either side of a central fixation mark.
Imaging data acquisition
All structural and functional images were acquired at Massachusetts General Hospital – Martinos Center for Biomedical Imaging on a 3-Tesla whole-body scanner (Siemens, Trio, Erlangen, Germany) and a standard 8 channels head coil. Earplugs were used to reduce the acoustic scanning noise. A capsule of vitamin E was taped to the subject’s right temple in to enable definitive determination of the right side in the image data. Head motion was minimized using tightly packed foam pads on either side of the head.
Resting-state functional images (the imaging protocol was provided by Randy Buckner) were acquired using a gradient echo, echoplanar (EPI) sequence (repetition time TR=5000 ms, echo time TE=30 ms, flip angle=90°, T1=−1 msec, 128×112×55 matrix/2×2×2 mm, field of view 128 mm) for measurement of BOLD signal. Acquisitions consisted of 76 time points, for a total duration of 380 sec.
Task functional volumes were acquired using an interleaved, gradient echo EPI sequence every 2 seconds for each 5 min acquisition (TR 2000 ms, 150 TRs; TE 30 ms, flip angle 90°, distortion factor=20%, phase=100). At the least, two acquisitions were obtained for each subject. We acquired 33 slices of 3.6 mm thickness with in-plane sampling of 64×64 (resolution of 3.125×3.125 mm). Slice positions were based on the AutoAlign sequence [18].
Structural MRI images were acquired through two T1-weighted magnetic resonance (MR) images, magnetization-prepared rapid-acquisition gradient echo (MPRAGE; TR=2.53 s, TE=3.28 ms, flip angle=7°, T1=1, 100 ms, 128 slices with a 256×256 matrix; voxel size 1.00×1.00×1.33 mm3).
Data pre-processing
Pre-processing of both rest and task state data was performed using Freesurfer 4.5 (http://surfer.nmr.mgh.harvard.edu/). The technical details of these procedures are described in several publications [19–32]. Briefly, the first 4 volumes of each scan were discarded to allow for T1-equilibration effects. Pre-processing included motion correction, slice time correction, volume based intensity normalization and removal of non-brain tissue using a hybrid watershed/surface deformation procedure, segmentation of the subcortical white matter and deep gray matter volumetric structures along with automated topology correction. Normalization to the MNI 305 space was achieved by first registering the functional runs with a 6 DOF linear (affine) transformation matrix to map between the individual’s functional data and the Freesurfer structural/anatomical data. The functional data was then resampled to the MNI 305 brain with 2mm thickness and registered to the MNI 305 space using a 12 DOF transformation matrix. No additional spatial smoothing was applied in order to minimize artificial local spatial correlations in the whole-brain analysis [33–37]. Both rest and task state data sets were upsampled to a TR of 1 and band-pass filtered to allow for the timecourses to be compared directly. We were interested in comparing the resting state frequencies in both the data sets. Since there is higher frequency information available in the task signal compared to the rest-state signal, we applied the same filtering to both the upsampled rest-state and task signals, thus ensuring the same frequency content in both the data. For the resting state and gap-closure fMRI data, we used a band-pass temporal filtering to remove constant offsets and linear trends over each run while retaining frequencies between 0.009 Hz< f <0.08 Hz. There is broad agreement that low frequencies are typical for revealing connectivity in resting state fMRI data [11]. However, since the temporal characteristics of event-related data may change the frequency profile of the BOLD signal (likely increasing the high frequency content), we investigated the implications of filtering fcMRI timecourses. Overall, connectivity in the DMN and in whole brain networks was stronger in the fullband (unfiltered) condition compared to the bandpass version of the analysis (see Supplement Tables 2 and 3). For consistency, and for using a conservative method that prevents any increase in task connectivity to be attributed to less restrictive temporal filtering, in all subsequent analyses we used the band-pass filtered fcMRI data, identical to the filter used with the resting state data. This also ensured that any interpolated data due to the upsampling step was accounted for.
We used the CONN functional connectivity toolbox (version 12p http://web.mit.edu/swg/software.htm) [38] to implement noise reduction, segment the gray matter/white matter/Cerebrospinal Fluid (CSF) and to isolate the areas of BOLD signal. These steps are implemented by CONN toolbox using SPM8 (Wellcome Department of Imaging Neuroscience, London, UK; www.fil.ion.ucl.ac.uk/spm).
Selection of regions of interest (ROIs)
For the DMN analysis, we used the FMRIB Software Library (FSL), [39] to define a 12-mm diameter spherical seed in the Precuneus (centered at MNI: 0, −53, 26), which has been consistently demonstrated as being a part of the DMN [3]. We also used five additional pre-defined DMN seeds in order to compare the relative correlation strengths of the ROIs in the DMN during resting-state and task performance [3]. Since the choice of coordinates for a seed can affect the results of seed-correlation analysis, we picked the seeds from a study which validated the choice of seeds using ICA [3,6]. In the whole brain analysis, 90 ROIs based on Brodmann Areas were chosen using the WFU_PickAtlas tool [40, 41] implemented in Statistical Parametric Mapping (SPM) package. ROIs were resampled into the MNI 305 2mm space from the ICBM 152 space using FSL and Freesurfer (http://surfer.nmr.mgh.harvard.edu/). For every subject and every ROI, the representative time series of each ROI was obtained by averaging the BOLD time series of all voxels in that ROI.
There could be co-activation confounds from task activation/co-activation because the BOLD signal may have a similar shape between different ROIs and therefore a correlation may be observed even if there is no communication between those ROIs. However, our study was not designed to account for this co-activation/activation in the task condition. Consequently, we do not make any claims about the significance or strength of correlation of either the resting state or task conditions. Our interest in this study was to conduct a comparative analysis between connectivity in the rest-state and task and, therefore we investigated the relative connectivity between resting state and task in DMN and in the whole-brain networks.
Connectivity: Bivariate correlation
We used the CONN toolbox (version 12p http://web.mit.edu/swg/software.htm) [38] to calculate the strength and significance of bivariate Pearson correlation among pairs of ROIs within each subject’s data. For ROI-to-ROI connectivity, significant connections were identified by computing the FDR-corrected two-sided p-value (q) at q<0.05 thresholds. The resulting connections were then converted to a normal distribution using Fisher’s z transform and averaged across subjects to produce a single measure characterizing the average correlation [42].
To perform a correlation analysis between a given ROI and every other voxel (ROI-to-voxel maps), the beta (Fisher transformed z-score) maps were converted to z-scores by dividing by the square root of the variance (1/sqrt (n-3), where n is the number of degrees of freedom in the measurement) [11]. Since individual time points in the BOLD signal are not statistically independent, the degrees of freedom were corrected using the Bartlett correction factor [42], which is computed as the mean (across voxels) of the sum (across TRs) of the squares of the autocorrelation functions [3]. The Bartlett correction factors were 3.4197 and 4.0143 for task and rest respectively. This process was used to correct individual z-scores, after which the group z-score significance map was generated by calculating a voxel-wise two-tailed t-test on the z-scores of the 8 participants and computing a -log(p-value) score for each voxel in the corrected z-score map. Volume clusters based on the z-score maps (minimum cluster-size=200 contiguous voxels, minimum significance threshold p<0.05) [11] were generated using the cluster detection tools included in the FreeSurfer software package.
Graph theory analysis
To analyze the characteristics of the whole brain networks, we computed several graph theoretical measures for task and resting-state data. We first computed degree, which is a measure of the number of connections incident upon a specific node (ROI). The degree distribution shows how many nodes exist in the network with each degree value. The existence of high-degree nodes may indicate nodes that are of critical importance to the flow of information within the network. Second, the closeness centrality (CC) of a given ROI was computed as the inverse of the sum of the lengths of the shortest paths starting from a given ROI and is normalized by a fraction of the maximum possible CC – the given ROI connected to all other ROIs 2*(N-1). Third, we computed betweenness centrality (BC), which considers the fraction of the shortest paths connecting every pair of ROIs (geodesics) that contain a given ROI [43]. For computing BC, the geodesic for every pair of ROIs is identified, and an ROI’s BC is defined as the number of geodesics of which the ROI is a member. To normalize for network size, we present BC as a fraction of the maximum possible BC (N-1)*(N-2), where N is the number of nodes in the network; i.e., a BC=1 would indicate that the node falls along the geodesic between every pair of nodes in the network).
We further computed global efficiency, which is the average of the inverse shortest path lengths for all ROI-ROI pairs in the network and provides a measure of the network’s overall connectedness. A network with a low characteristic path length is characterized by short distances between any pair of nodes, and would therefore have a high global efficiency. To compute global efficiency, we found the lengths of all shortest paths and took the mean of their inverses. We also computed the local efficiency defined as the average of the inverse shortest path lengths among the ROIs in the immediately connected neighborhood of a ROI. The mean local efficiency between all the ROIs in a network is used for measuring how well, on average, the network communicates when one of the ROIs is eliminated [34]. It is important to note that local efficiency and closeness centrality (CC) are directly proportional to each other by a constant scaling factor and therefore these measures can be used interchangeably. Both these measure give us a qualitative measure of the spread of information in the immediate neighborhood from a given ROI.
Efficiency as a function of “cost” (K) of a graph is defined as the inverse of the mean of the minimum path lengths between each pair of nodes normalized by the maximum possible number of (undirected) edges (N2-N)/2, where N is the number of brain regions. Comparing efficiency among networks with different numbers of edges (connections) is problematic because increasing the number of edges in a network would likely result in shorter path lengths, and therefore higher values of efficiency. Thus, we compared efficiency for each value of cost (number of connections), such that the number of edges was constant, rather than for each significance threshold (which would produce different numbers of edges in each network). The efficiency of each network is measured as a function of variable cost in the range 0.01<K<0.5 (i.e., 1–50% of all possible edges in a fully connected).
Taking into account the graph theory measures described above we computed the small-worldness of the network. A network is defined to be small-world when it has a global efficiency greater than a regular lattice network with the same number of vertices, but less than a random network, and local efficiency greater than a random network, but less than a regular lattice in the connection cost range of 0.34≤K≤0.5 [34]. Thus a small-world network has both high local and global efficiencies. This reflects highly clustered networks with a small characteristic path length, allowing for fast communication between any two ROIs in the network.
Results
To determine how functional brain networks change when participants actively perform a perceptual task relative to their resting state in which they have no goal-directed behavior, we investigated the similarities and differences in the functional connectivity between resting state data and the gap-closure motion task. We compared connectivity within the default mode network (DMN) in resting state and task networks, by first using a seed-based connectivity approach applied to both conditions. In order to compare resting state and task networks beyond the DMN and to capture the task-dependent global tendencies of connectivity, we applied a whole-brain connectivity analysis to each condition (rest and task). We characterize each network by comparing measures of integration such as path length, global and local efficiency, regional measures such as degree and betweenness centrality, and global measures such as small-worldness.
Connectivity of the Default Mode Network during task processing
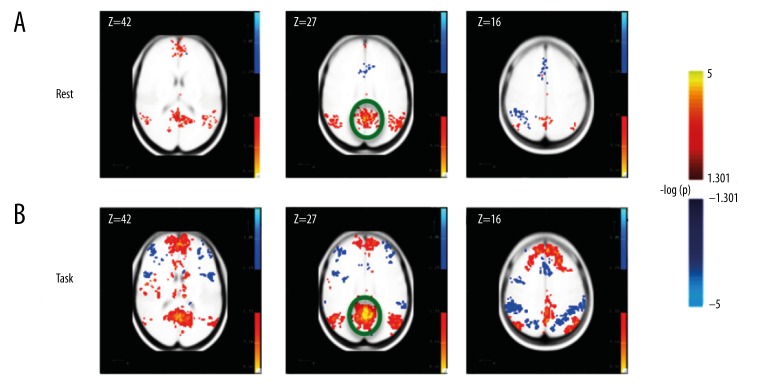
We performed a seed-based DMN analysis, by defining a seed ROI on the precuneus and then we computed the correlation of this seed ROI to every voxel in the cortex (see Connectivity: Bivariate Correlation section in Methods). The clusters of voxels significantly correlated to the Precuneus matched previous descriptions of the DMN [4,11], and were present in both the rest and visual task conditions (see Supplement Table 1 and Supplement Figure 1, and Figure 2). These data suggest that the activation of the DMN network is not specific to the resting-state condition, but that a similar set of voxel clusters are correlated to the Precuneus (the seed used) in the task (Figure 2).
Figure 2.
Voxels significantly correlated to the Precuneus ROI (circled in green) for (A) resting state data and (B) task data.
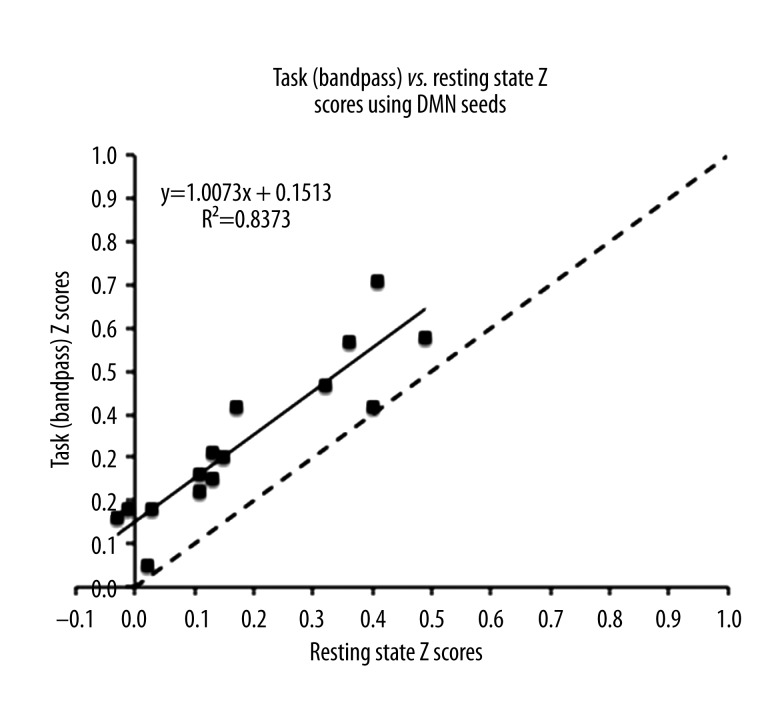
To quantitatively assess how the strength of connections among DMN areas changed when observers actively performed the gap-closure psychophysical task, we computed the Fisher transformed (r-to-z) correlation strengths among the six pre-defined DMN ROIs regions as reported in a previous study (see Connectivity: Bivariate Correlation section in Methods) [3]. This resulted in a network with 15 possible ROI-ROI connections. Figure 3 shows the Fisher transformed correlation strengths among the DMN ROIs for both the task and the resting state data. Each value in Figure 3 represents the z-score correlation strength between two DMN ROIs. The black dotted line is a reference line with slope 1 and represents equal functional connectivity between the resting state and task networks. There was a positive correlation between resting state and task (R2=0.83, t28=12.0041, p<0.001, 95% confidence interval of the slope 0.8354 to 1.1792), which suggests that the more connected a pair of ROIs was at rest, the more connected it was in the task (Figure 3). Most of the z-score correlation strengths were greater in task condition than in resting state condition (i.e., they fell above the slope=1 line), as indicated by a significant offset (t28=7.3135, p<0.001) in Figure 3. This suggests an increase in connectivity within the DMN during task-related processing with correlation strengths significantly greater in the task data than at rest. These results suggest a more general-purpose role for the DMN, not limited to resting state modes, such as introspection, or mind wandering in the absence of an active task.
Figure 3.
Task vs. resting state connectivity in DMN seeds. The Task vs. resting state Fisher Transformed Z scores of the DMN seeds as chosen from Van Dijk et al. (2010) respectively. The black dotted line is a line with slope=1 representing equal connectivity.
Changes in whole-brain connectivity networks between task and rest
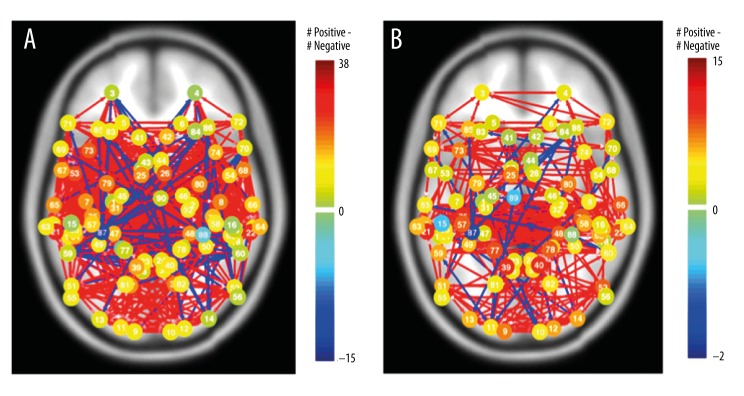
In the previous section we addressed how connections within the DMN network change with rest state and task. Here, we are interested in determining how large-scale networks spanning the entire cortex are altered in the task-condition compared to the resting state-condition. Identifying properties of the “whole brain” network allows us to examine the overall structure of neuronal communication among spatially precise regions. To study connections spanning the cortex, we defined 90 anatomical ROIs based on Brodmann Areas spanning both the right and left cortical hemispheres using the WFU_PickAtlas toolbox [44]. Connections among these ROIs were used to compute network statistics to capture global tendencies of connectivity in resting-state and task networks, and to characterize the consistencies and differences in the behavior of individual cortical areas using graph theoretical measures. Figure 4 illustrates the whole-brain networks of the resting state (Figure 4A), and task (Figure 4B) networks with Brodmann areas as the ROIs. The connections represent bivariate correlations with p<0.05 (FDR Corrected), and node color indicates the difference between the positive and negative connections (green to dark blue indicating increasing negative total connections respectively, green to dark red indicating increasing positive total connections). In the following sections, we discuss the quantitative properties of these networks.
Figure 4.
Whole-brain networks of the resting state (A) and task (B) networks. 90 Brodmann Areas were chosen spanning the whole brain. The networks were generated using the CONN-fMRI toolbox. The node color indicates the difference between the positive and negative connections (green to dark blue indicating increasing negative total connections respectively, green to dark red being indicating increasing positive total connections).
Degree distribution
Degree measures the number of connections at a particular node, and the mean degree across all nodes (referred to as the average degree) measures the extent to which the graph is connected [45]. To illustrate changes in connection density (i.e., network connectedness), we computed the mean degree in both resting state and task networks by selecting connections passing an FDR-corrected bivariate correlation threshold of p<0.05. The connectedness, as assessed by the average degree across nodes, increased during the task-condition with nodes having, on average, more than double the number of significant connections during task than at rest (4.24±2.24 connections per node in resting state to 9.88±4.24 in task processing; 2-sample, 2-tailed t-test comparing connections for each node between rest and task showed these were significantly different: t178=11.16, p<0.001).
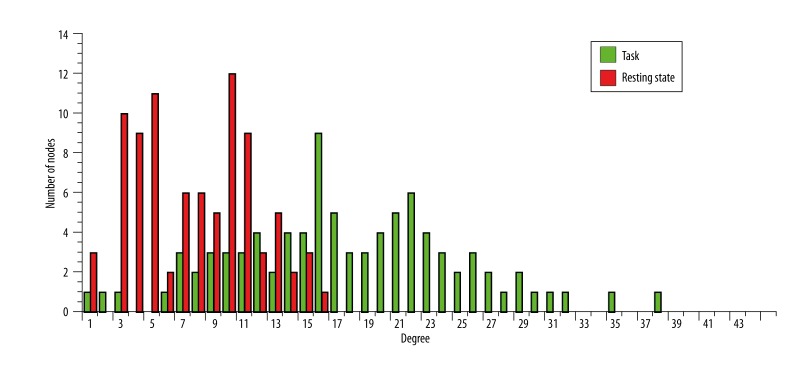
In addition to the mean of all nodes’ degrees, we also computed the degree distribution of the network, i.e., a histogram of the frequency of every degree value [13]. Degree distributions provide a summary of the connectivity in networks by providing a snapshot of the connectedness of all nodes. Figure 5 shows the degree distribution of both the resting state (red) and task (green) networks. Consistent with the increase in mean degree shown in Figure 4, we found that in task processing the distribution of degree values are shifted higher, indicating that the overall whole-brain network is more connected during task processing. This can be interpreted as an overall increase in the significance of connections, more connections reached the significance threshold, thus resulting in a more densely connected network.
Figure 5.
The degree distribution of the networks Degree is a measure of the number of connections at a particular node. Degree distribution plots show the number of nodes with a particular degree. The green and red bar plot shows the degree distribution of the task and resting state network respectively.
This result has implications on other network measurements such as centrality and global efficiency, since those metrics depend on the network size and number of edges [46]. For example, increasing the number of connections in a network will likely decrease the average path length in that network, even if it does not increase its global efficiency (see Graph Theory Analysis section of Methods). Due to the increase in average degree of the task-network, in the following sections, instead of applying a fixed significance threshold which considers a limited (and variable) number of connections in the network, we used a threshold of p<=1 (i.e., all connections included), or computed network properties for all values of cost (i.e., computed as a function of the number of connections in the network, rather than as a function of a fixed significance threshold), as appropriate.
Betweenness centrality and degree
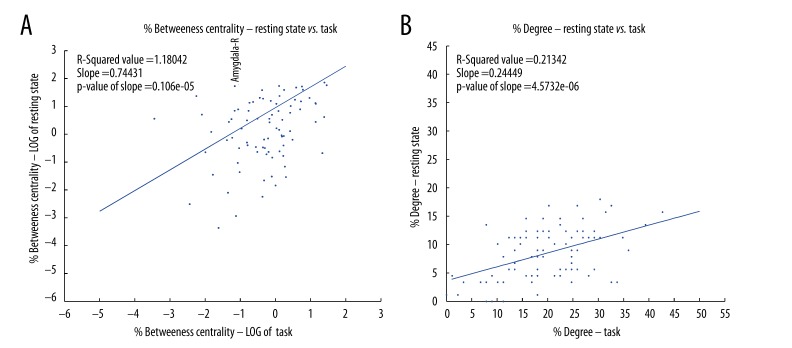
Betweenness centrality measures the influence a particular region has over the spread of information throughout the network [47]. In order to investigate the relative importance of particular areas between the resting state and task networks, and how the role of an area changes between conditions, we computed for both conditions the weighted degree, which is the sum of the strengths of connections from one ROI to every other ROI, and the betweenness centrality, that is the number of weighted shortest paths that pass through a certain ROI from all the ROIs towards all other ROIs. These measurements provide an indication of how well connected each ROI is, and of its importance to the information flow through the network. To obtain a value invariant to network size, both degree and betweenness centrality (BC) were normalized by the maximum possible value, 2*(N-1) for degree, i.e., connected to all other ROIs, and (N-1)*(N-2) for BC, i.e., falling along the route from every ROI, except the one being considered, to every other ROI. To characterize how similar each ROI’s behavior was in task and resting state conditions, we calculated the linear regression and variance (correlation coefficient of the line) of the relationship between task and resting state networks. For example, a slope of 1 with no variance in the regression would indicate that nodes that were highly connected or central in the resting state network are equally connected/central in the task state network. Figure 6A, 6B show the scatter plots of the percent of the log of the percent betweenness centrality and the weighted degree for every ROI between the resting state and task network respectively. The blue dotted lines represent the 95% confidence intervals of the slope of regression fit.
Figure 6.
(A) shows the log of percent weighted betweenness centrality and (B) the percent weighted degree of each node of the resting state, and task networks plotted against each other for each of the 90 Brodmann Areas. The degree centrality was normalized by the total number of degree possible, and betweenness centralities were normalized by the total number of connections possible in the network. In A and B – the axes represent the % degree and the log of % betweenness centrality respectively. The blue line represents linear least-squared regression best-fit line.
We found a significant positive correlation between task and resting state for both degree (slope=0.55, 95% confidence interval=0.41 to 0.6975, t88=7.655, p<0.001, Figure 6A) and betweenness centrality (slope=0.20, 95% confidence interval=0.0182 to 0.3824, t88=2.1862, p=0.0314, Figure 6B). These positive correlations suggest that ROIs highly connected (degree) or highly central (BC) maintain these properties during both, resting state and task processing. While the degree data had a high correlation coefficient between the resting state and task (R2=0.39, Figure 6A), the correlation coefficients for betweenness centrality were weak (R2=0.05, Figure 6B). This suggests that although number of synchronized brain areas through each node (degree) was increased linearly, the influence of a particular ROI on the flow of information in a network becomes irregular, likely indicating a shift in the most efficient paths through the network. Furthermore, since the slopes for both task and resting state data were significantly less than 1, the volume of information flow and influence of an ROI over the flow of information were observed to be higher during task than at rest.
Measures of integration
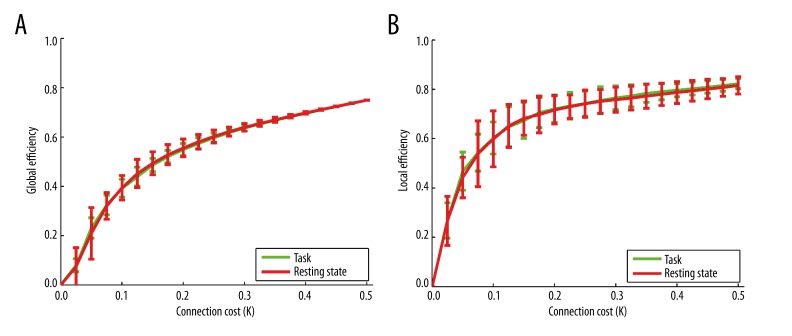
Measures of integration allow the determination of how efficiently information travels through a network [13]. We computed global and local efficiency measures to determine how integration among cortical ROIs changes in task and resting state networks. Global efficiency is a measure of the network’s capacity for parallel information transfer between nodes via multiple series of edges, while local efficiency is a measure of how fault tolerant the network is, (i.e., by indicating the efficiency of the network when one ROI is removed) [34]. To control for the number of connections, we computed the global and local efficiency with respect to the connection cost of the network, the average edge density across all ROIs and subjects for all possible significance thresholds. By computing these measures as a function of the number of edges, rather than the significance threshold for each particular edge, differences in efficiency cannot arise simply due to changes in the number of connections in the network (as we have already observed in the task data). Instead, this computation provides an assessment of the network’s efficiency that is independent of the significance threshold selected and applied to individual connections. As illustrated in Figure 7, we compared task and rest states and found no significant differences in either local or global efficiency (two-tailed, two-sample t-test for global efficiency: t40=−0.02, p=0.98; and local efficiency: t40=0.09, p=0.92). The variance of local efficiency (error bars in Figure 7B) among subjects was lower in the task network than resting state for every cost value (two-tailed, two-sample t-test, 11.29<t14 <21.95, 0<p<20.4e-9 across all values of cost), indicating that there was more inter-subject variability in the effectiveness of short-range communication between brain regions at rest condition than during task processing. However, we did not find a similar trend in the inter-subject variance of global efficiency (−1.21<t14<1.18, 0.25<p<0.86) (error bars in Figure 7A).
Figure 7.
(A) global efficiency vs. connection cost (K), and (B) local efficiency vs. connection cost (K) of the task network shown in green, and the resting state network shown in red. The lines represent the mean connection cost at each node across all subjects, and the error bars represent the standard error across all subjects calculated at p>1.
Small worldness
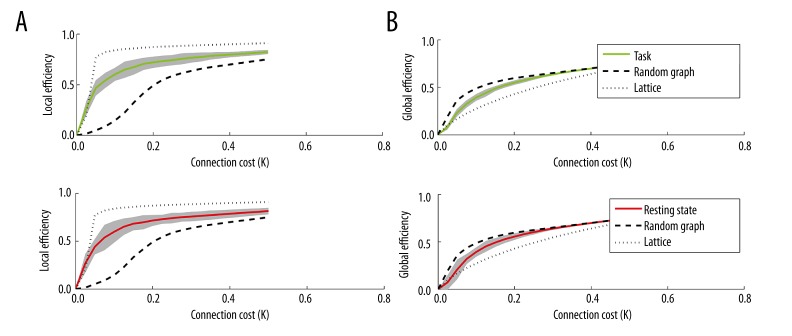
Small-world networks are a class of networks that exhibit efficient long-distance communication and tightly interconnected local neighborhoods [48]. A small-world network has a global efficiency greater than a regular lattice but less than a random network in the range 0.34< cost (K) <0.5 [34]. Figure 8 shows the global and local efficiency vs. connection cost of the task and resting state networks. Both networks exhibit small-worldness characterized by high global and local efficiency, thus enabling an efficient model of communication with low cost of transmitting information from one ROI to another.
Figure 8.
Local efficiency (left) and global efficiency (right) vs. connection cost (K) of the task network shown in green (A), and the resting state network shown in red (B). The thick black dotted line represents the global efficiency vs. cost of a random network, while the thin black dotted line represents that of a regular lattice. Small world networks are defined as networks with higher global efficiency than a lattice but lower global efficiency than a random graph.
Discussion
We used connectivity derived from fMRI data to characterize and compare in the same subjects the brain networks underlying both task and resting state brain activity. We first investigated the implications of applying narrow bandpass filtering (0.009 Hz <f<0.08 Hz) to event-related task connectivity data similar to that typically used in the analysis of resting state data. We found that the fullband task data showed stronger connectivity than its bandpass counterpart (see Validation section of the Supplement). This suggests that bandpass filtering might cause some task-relevant connections to be lost, thus reducing the filtered network connectivity compared to the unfiltered network connectivity. Since we were interested in comparing task and rest state networks, we used only the bandpass filtered data in order to maintain methodological consistency (for comparison with the full band task network data, see Supplementary Table 4 and Supplementary Figures 3–6).
Bivariate correlations among time courses extracted from brain regions involved in the default mode network (DMN) showed that the interregional correlations was greater during task processing than during the resting state (Figure 3). There are several possible explanations for this finding. First, the activity in the DMN may persist through both task and rest conditions if the experiment is not sufficiently challenging [7]. We chose task conditions based on previous data and the difficulty of the task was chosen so that subjects’ performance was good (91.6% accuracy), albeit not perfect, but it may not have been difficult enough to prevent activation of the DMN. Thus, the connectivity we observe during the task may be a superposition of both rest and task state connectivity. An alternative explanation may be that the DMN areas may play a role in the gap-closure psychophysical task. It has been shown that the resting DMN areas PCC and MFG/vACC are functionally connected when subjects perform a working memory task, possibly to facilitate or monitor performance [49]. Likely, working memory is involved in the gap-closure task, in which subjects simultaneously monitor and compare the trajectories of two objects in order to make their decision. All the above explanations support a framework in which the DMN is not fully suppressed during task processing, but either continues to operate, or is even actively engaged by task demands. Although our data do not specifically indicate any one of these explanations, they do support the general point that the DMN continues to operate even while subjects are actively engaging in a perceptual task. Yet, there could be another explanation for our results, which is methodological. We compared rest state data that is continuous to task, which was an event related design and hence it alternates between stimulus and blank periods. This could not be ruled out on the basis of the experimental paradigm we used in this study, and we plan to carefully investigate this possibility in a study, which is underway.
To explore changes in the global behavior of brain networks associated with the cognitive state, we used a graph theoretical approach similar to those described in recent studies [8,36,37,50]. We assessed the relationship in the regional network measures between the rest-state and task, by computing the line of best fit through linear least squares (Figure 6). A significantly positive slope would indicate that ROIs with a relatively high network measure value in rest-state would tend to remain unchanged during task. Similar to previous studies which showed a correlation in voxel-wise degree between task and rest [8], we found a significantly positive slope of the ROI-wise degree line (Figure 6B). Similarly, there was also a significant positive slope of the betweenness centrality measure line (Figure 6A). The positive slope indicates that regions that exhibit “hub-like” behavior (i.e., highly connected) tend to remain “hub-like” independent of the cognitive brain state (rest state or task). However, the R-squared correlation measure in the BC between the rest-state and task conditions is lower than that in the degree, suggesting that in spite of the maintenance of connectivity and the “hub-like” behavior of areas, the network paths may be rerouted when performing the task condition.
In order to explore whether the increases in the correlation strengths in the DMN connectivity were proportionally similar, or whether the DMN connectivity increased to a proportionally smaller or larger extent compared to whole-brain connectivity between the resting state and task conditions, we computed a permutation test between the z-score correlation strengths of the two experimental conditions. The permutation test produces a distribution of the slope and intercept values of random combinations of the correlation strengths between conditions. The results showed that the DMN intercept value was significantly larger than the permuted population revealing that the DMN has a proportionately larger increase in connectivity compared to the connectivity among whole brain areas.
Our results show an overall higher level of connection strength and network density during task processing than rest, yet we found that when controlling for connection cost (i.e., number of connections) there was no change in local or global efficiency of the networks (Figure 7). We also found that both networks (rest-state and task) demonstrated small-worldness, which implies the coexistence of both modular and distributed processing dynamics [50]. Although the efficiency measures and small-worldness of the two networks (rest-state and task) are very similar, the finding that centrality is less correlated than the degree between task and rest state conditions suggests a rewiring of the brain network between rest-state and task while maintaining efficiency and the small-world topology.
Conclusions
We computed the functional brain connectivity among brain areas in a resting state, and during active performance of a visual motion psychophysical experiment (gap closure). A comparison of connectivity within the DMN and across the entire cortex showed increased communication during the visual motion task, suggesting a superposition of task and resting state networks. Graph theoretic measures computed for the whole brain network suggest that although the brain recruits more areas during task processing leading to greater connectivity, the efficiency of the network does not differ significantly between rest state and gap-closure task processing. One commonality between the function of the rest state DMN and the neuronal network underlying the gap-closure task is that both involve areas involved in working memory. This is consistent with the increase we have seen in the connectivity of DMN areas.
The global statistics of the network (efficiency, relative degree, relative centrality) were similar between rest-state and task. Our results support a view of cognitive processing in which although the underlying network structure does not fundamentally change with the subject’s cognitive state (rest-state or task), the brain switches among several pathways of comparable efficiency as required by the current cognitive demands.
Supplement
Validation
In order to determine whether our resting state data is consistent with previous studies, we investigated the presence and detectability of the Default Mode Network (DMN). The DMN has been defined as the areas showing correlated activity during resting state (no task), and includes the posterior cingulate cortex (PCC), precuneus, medial prefrontal cortex (MPFC), lateral parietal cortex, and the hippocampal formation [3]. Using the method described in VanDijk et al. [3] we computed a spatial map of the correlation between a seed placed on the precuneus (average BOLD time course from a 12 mm diameter sphere centered on MNI co-ordinate: 0, −53, 26) and every other voxel in the cortex. The population based −log(p) z-score significance map was computed by applying a t-test on the subject-wise z-score maps obtained from Beta correlation values (see Methods). The Freesurfer fMRI data analysis package was used to generate volume clusters from the correlation maps (minimum cluster-size =200 contiguous voxels, minimum threshold =−log(0.05)) [11]. As seen in Supplemental Figure 1A, positive values, shown in an orange to yellow scale, represent areas significantly correlated with the Precuneus, whereas negative values, shown on a light to dark blue scale represent areas significantly anticorrelated with the Precuneus. The resting state fMRI correlation maps shows correlation with the Superior Temporal Gyrus, Medial Frontal Gyrus, and the Angular Gyrus. Our results are consistent with those reported by other studies [3,11].
Presence of DMN ROIs during task
Previous studies have reported that the default mode network (DMN) shows correlations in task conditions, but at an attenuated level relative to resting state [9]. In order to find if brain regions in the DMN (correlated to the Precuneus) were also correlated during task processing, we identified clusters of voxels with significant Fisher-transformed correlations to precuneus signal during the task (using the same statistics as described above). Significance maps (Supplement Figure 1) show the −log(p) values after applying a two-tailed t-test on the z-scores obtained from each subject. The columns in Supplement Figure 1 represent the significance of correlation with the precuneus-seed (circled in green) for the same slices (Z=42, 27 and 16) for the resting state and task data. Supplement Tables 1–3 show the significantly correlated anatomical areas found in resting state, as well as task data after clustering. The anatomical areas were defined through a lookup of the mean Talairach coordinate of the cluster (http://www.talairach.org, [51] using Freesurfer. We found that the DMN areas were more significantly correlated to the Precuneus seed in the task condition as compared to resting state. This result is different from the usually reported anti-correlations between resting state and task conditions [11]. In Supplemental Figure 1, we illustrate the significance of the connections with the precuneus (circled in green), and not the strengths of the connections, and hence we only show the areas that are connected during resting state and task.
Voxels significantly correlated to the precuneus ROI (circled in green) for (A) resting state data, (B) bandpass filtered task data, and (C) fullband filtered task data.
Shows the task fullband and task bandpass vs. resting state connectivity in DMN seeds. (A) and (B) shows the task fullband vs. resting state and task bandpass vs. resting state Fisher Transformed Z scores of the DMN seeds as chosen from Van Dijk et al. [3] respectively. The black dotted line in each figure is a line with slope=1 representing equal connectivity.
(A–C) show the whole-brain networks of the Resting state, Task bandpass, and task fullband networks respectively. 90 Brodmann Areas were chosen spanning the whole brain and the CONN-fMRI toolbox was used to generate the networks. The node color indicates the difference between the positive and negative connections (green to dark blue indicating increasing negative total connections respectively, green to dark red being indicating increasing positive total connections).
The degree distribution of three networks that were explored. Degree is a measure of the number of connections at a particular node. Degree distribution plots show the number of nodes with a particular degree. The red, green and blue bar plot shows the degree distribution of the task (fullband), task (bandpass) bandpass and the resting state network respectively.
The figures below show the % weighted degree and % weighted betweenness centrality of each node of the resting state, gap closure task (bandpass), and gap closure task (fullband) networks plotted against each other for each of the 90 Brodmann Areas. The degree centrality was normalized by the total number of degree possible, and betweenness centralities were normalized by the total number of connections possible in the network. In (A, C, and E) – the axes represent the % Degree; whereas in (B, D, and F), they represent the log of the% betweenness centrality. The blue line represents linear least-squared regression best-fit line, and the dotted black line represents a reference slope=1 line. In (B, D, and F), the best-fit line and reference slope=1 line are calculated in linear space, but plotted in log-log space.
Shows the global and local efficiency vs. connection cost (K) of the task network with fullband processing shown in blue (A), task network with bandpass processing shown in green (B), and the resting state network shown in red. The thick black dotted line represents the global efficiency vs. cost of a random network, while the thin black dotted line represents that of a regular lattice. Small world networks are defined as networks with higher global efficiency than a lattice but lower global efficiency than a random graph.
Supplement Table 1.
Shows the clusters found in the default mode network connectivity maps in the resting state network.
| Size (n) | Size (mm3) | MNI X | MNI Y | MNI Z | TAL X | TAL Y | TAL Z | Max -log(p) value | Cerebrum | Lobe | Anatomical area | Brodmann area | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1707 | 13656 | −10 | −51 | 27 | −10 | −48 | 27 | 5.83732 | Left cerebrum | Parietal lobe | Precuneus | Brodman area 31 |
| 2 | 772 | 6176 | −42 | −57 | 27 | −42 | −54 | 28 | 5.10571 | Left cerebrum | Temporal lobe | Superior temporal gyrus | Brodman area 39 |
| 3 | 708 | 5664 | −12 | 65 | 7 | −12 | 63 | 3 | 4.71252 | Left cerebrum | Frontal lobe | Media frontal gyrus | Brodman area 10 |
| 4 | 602 | 4816 | 52 | −65 | 31 | 51 | −62 | 32 | 4.07893 | Right cerebrum | Parietal lobe | Angular gyrus | Brodman area 39 |
| 5 | 319 | 2552 | 56 | −45 | 41 | 55 | −42 | 40 | −3.88219 | Right cerebrum | Parietal lobe | Inferior parietal lobule | Brodman area 40 |
| 6 | 313 | 2504 | −8 | 25 | 27 | −8 | 25 | 24 | −3.78081 | Left cerebrum | Limbic lobe | Anterior cingulate | Brodman area 32 |
Supplement Table 2.
Shows the clusters found in the default mode network connectivity maps in the task (bandpass) network.
| Size (n) | Size (mm3) | MNI X | MNI Y | MNI Z | TAL X | TAL Y | TAL Z | Max −log(p) value | Cerebrum | Lobe | Anatomical area | Brodmann area | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6190 | 49520 | 2 | −45 | 29 | 2 | −42 | 29 | 7.51287 | Right cerebrum | Limbic lobe | Cingulate gyrus | Brodman area 31 |
| 2 | 12646 | 101168 | 0 | 57 | 15 | 0 | 56 | 11 | 6.4667 | Left cerebrum | Frontal lobe | Media frontal gyrus | Brodman area 10 |
| 3 | 2011 | 16088 | 54 | −65 | 31 | 53 | −62 | 32 | 5.96842 | Right cerebrum | Parietal lobe | Angular gyrus | Brodman area 39 |
| 4 | 312 | 2496 | −6 | −15 | 13 | −6 | −14 | 13 | 5.54662 | Left cerebrum | Sub- lobar | Thalamus | Medial dorsal nucleus |
| 5 | 2031 | 16248 | −62 | −15 | −13 | −61 | −15 | −10 | 5.47374 | Left cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 6 | 1398 | 11184 | −46 | −75 | 31 | −46 | −71 | 32 | 5.22169 | Left cerebrum | Temporal lobe | Angular gyrus | Brodman area 39 |
| 7 | 574 | 4592 | 26 | −21 | −17 | 26 | −21 | −13 | 4.78953 | Right cerebrum | Limbic lobe | Parahip-pocampal gyrus | Brodman area 35 |
| 8 | 366 | 2928 | 16 | −69 | 45 | 16 | −65 | 45 | −4.7328 | Right cerebrum | Parietal lobe | Precuneus | Brodman area 7 |
| 9 | 1782 | 14256 | −44 | −59 | −31 | −44 | −58 | −23 | −4.45789 | Left cerebrum | Posterior lobe | Tuber | * |
| 10 | 507 | 4056 | −38 | 55 | 21 | −38 | 54 | 17 | −4.36372 | Left cerebrum | Frontal lobe | Superior frontal gyrus | Brodman area 10 |
| 11 | 455 | 3640 | 44 | −81 | −25 | 44 | −80 | −17 | −4.20093 | Right cerebrum | Posterior lobe | Declive | * |
| 12 | 422 | 3376 | 64 | −13 | −13 | 63 | −13 | −10 | 3.9602 | Right cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
Supplement Table 3.
Shows the clusters found in the default mode network connectivity maps in the task (fullband) network.
| Size (n) | Size (mm3) | MNI X | MNI Y | MNI Z | TAL X | TAL Y | TAL Z | Max −log(p) value | Cerebrum | Lobe | Anatomical area | Brodmann area | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 7528 | 60224 | 2 | −55 | 27 | 2 | −52 | 27 | 7.75249 | Left cerebrum | Limbic lobe | Cingulate gyrus | Brodman area 31 |
| 2 | 1110 | 8880 | 44 | −19 | 53 | 44 | −16 | 50 | 7.07843 | Right cerebrum | Frontal lobe | Precentral gyrus | Brodman area 4 |
| 3 | 10199 | 81592 | 6 | 57 | 31 | 6 | 57 | 26 | 6.10365 | Right cerebrum | Frontal lobe | Superior frontal gyrus | Brodman area 9 |
| 4 | 973 | 7784 | 50 | −59 | 35 | 50 | −56 | 35 | 5.4246 | Right cerebrum | Parietal lobe | Inferior parietal lobule | Brodman area 40 |
| 5 | 486 | 3888 | −60 | −15 | −13 | −59 | −15 | −10 | 5.08472 | Left cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 6 | 2987 | 23896 | 42 | 19 | 3 | 42 | 19 | 2 | −5.01401 | Right cerebrum | Sub- lobar | Insula | * |
| 7 | 699 | 5592 | 28 | −41 | −31 | 28 | −41 | −24 | −4.55969 | Right cerebrum | Anterior lobe | Culmen | * |
| 8 | 229 | 1832 | −6 | −9 | 13 | −6 | −8 | 12 | 4.18239 | Left cerebrum | Sub- lobar | Thalamus | * |
| 9 | 278 | 2224 | −54 | 7 | −29 | −53 | 6 | −25 | 4.05919 | Left cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 10 | 374 | 2992 | 68 | −31 | −3 | 67 | −30 | −1 | 4.04834 | Right cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 11 | 383 | 3064 | −48 | 41 | 19 | −48 | 41 | 15 | −3.84668 | Left cerebrum | Frontal lobe | Middle frontal gyrus | Brodman area 46 |
| 12 | 407 | 3256 | −20 | −59 | −31 | −20 | −58 | −23 | −3.59756 | Left cerebrum | Anterior lobe | * | Dentate |
| 13 | 665 | 5320 | 52 | 43 | 9 | 51 | 42 | 6 | −3.41915 | Right cerebrum | Frontal lobe | Inferior frontal gyrus | Brodman area 46 |
| 14 | 269 | 2152 | −54 | −57 | −9 | −53 | −56 | −5 | −3.29778 | Left cerebrum | Temporal lobe | Inferior temporal gyrus | Brodman area 37 |
| 15 | 265 | 2120 | 62 | −13 | −13 | 61 | −13 | −10 | 3.27451 | Right cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 16 | 395 | 3160 | −22 | −17 | −21 | −22 | −17 | −17 | 3.16681 | Left cerebrum | Limbic lobe | Parahip-pocampal gyrus | Brodman area 28 |
Supplement Table 4.
Shows the mean degrees of the resting state, gap closure task (fullband) and gap closure task (bandpass) networks.
| Networks | Mean degree |
|---|---|
| Task (fullband) | 10.5243 |
| Task (bandpass) | 9.8876 |
| Resting rate | 4.2447 |
Acknowledgements
This work was supported by NIH grant RO1NS064100 to L.M.V. We thank Dr. Susan Whitfield-Gabrieli and members of her laboratory for providing the CONN fMRI toolbox and for the generous help with the numerous questions we had during the course of this project. This research was carried out in part at the Athinoula A. Martinos Center for Biomedical Imaging at the Massachusetts General Hospital, using resources provided by the Center for Functional Neuroimaging Technologies, P41RR14075, a P41 Regional Resource supported by the Biomedical Technology Program of the National Center for Research Resources (NCRR), National Institutes of Health. This work also involved the use of instrumentation supported by the NCRR Shared Instrumentation Grant Program and/or High-End Instrumentation Grant Program; specifically, grant number S10RR021110.
Footnotes
Source of support: This work was supported by NIH grant RO1NS064100 to L.M.V.
References
- 1.van den Heuvel MP, Hulshoff Pol HE. Exploring the brain network: a review on resting-state fMRI functional connectivity. Eur Neuropsychopharmacol. 2010;20(8):519–34. doi: 10.1016/j.euroneuro.2010.03.008. [DOI] [PubMed] [Google Scholar]
- 2.Friston KJ, Jezzard P, Turner R. Analysis of functional MRI time series. Human Brain Mapping. 1994;1:153–71. [Google Scholar]
- 3.Van Dijk KR1, Hedden T, Venkataraman A, et al. Intrinsic functional connectivity as a tool for human connectomics: theory, properties, and optimization. J Neurophysiol. 2010;103(1):297–321. doi: 10.1152/jn.00783.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Greicius MD, Srivastava G, Reiss AL, Menon V. Default-mode network activity distinguishes Alzheimer’s disease from healthy aging: evidence from functional MRI. Proc Natl Acad Sci USA. 2004;101(13):4637–42. doi: 10.1073/pnas.0308627101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jiao Q, Lu G, Zhang Z, et al. Granger causal influence predicts BOLD activity levels in the default mode network. Hum Brain Mapp. 2010;32(1):154–61. doi: 10.1002/hbm.21065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cole DM, Smith SM, Beckmann CF. Advances and pitfalls in the analysis and interpretation of resting-state FMRI data. Front Syst Neurosci. 2010;4:8. doi: 10.3389/fnsys.2010.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Greicius MD, Menon V. Default-mode activity during a passive sensory task: uncoupled from deactivation but impacting activation. J Cogn Neurosci. 2004;16(9):1484–92. doi: 10.1162/0898929042568532. [DOI] [PubMed] [Google Scholar]
- 8.Buckner RL1, Sepulcre J, Talukdar T, et al. Cortical hubs revealed by intrinsic functional connectivity: mapping, assessment of stability, and relation to Alzheimer’s disease. J Neurosci. 2009;29(6):1860–73. doi: 10.1523/JNEUROSCI.5062-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fransson P. How default is the default mode of brain function? Further evidence from intrinsic BOLD signal fluctuations. Neuropsychologia. 2006;44(14):2836–45. doi: 10.1016/j.neuropsychologia.2006.06.017. [DOI] [PubMed] [Google Scholar]
- 10.Raichle ME, MacLeod AM, Snyder AZ, et al. A default mode of brain function. Proc Natl Acad Sci USA. 2001;98(2):676–82. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fox MD, Snyder AZ, Vincent JL, et al. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci USA. 2005;102(27):9673–78. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Greicius MD, Krasnow B, Reiss AL, Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci USA. 2003;100(1):253–58. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rubinov M, Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage. 2010;52(3):1059–69. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- 14.Behrens TE, Sporns O. Human connectomics. Curr Opin Neurobiol. 2012;22(1):144–53. doi: 10.1016/j.conb.2011.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Calabro FJ, Vaina LM. Detection of object motion during self-motion: psychophysics and neuronal substrate. Vision Science Society Annual Meeting. 2011 [Google Scholar]
- 16.Burock MA, Buckner RL, Woldorff MG, et al. Randomized event-related experimental designs allow for extremely rapid presentation rates using functional MRI. Neuroreport. 1998;9(16):3735–39. doi: 10.1097/00001756-199811160-00030. [DOI] [PubMed] [Google Scholar]
- 17.Burock MA, Dale AM. Estimation and detection of event-related fMRI signals with temporally correlated noise: a statistically efficient and unbiased approach. Human Brain Mapping. 2000;11:249–60. doi: 10.1002/1097-0193(200012)11:4<249::AID-HBM20>3.0.CO;2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.van der Kouwe AJ, Benner T, Fischl B, et al. On-line automatic slice positioning for brain MR imaging. Neuroimage. 2005;27(1):222–30. doi: 10.1016/j.neuroimage.2005.03.035. [DOI] [PubMed] [Google Scholar]
- 19.Dale A, Sereno M. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: A linear approach. J Cog Neurosci. 1993;5:162–76. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
- 20.Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage. 1999;9(2):179–94. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- 21.Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci USA. 2000;97(20):11050–55. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fischl B, Liu A, Dale AM. Automated manifold surgery: constructing geometrically accurate and topologically correct models of the human cerebral cortex. IEEE Trans Med Imaging. 2001;20(1):70–80. doi: 10.1109/42.906426. [DOI] [PubMed] [Google Scholar]
- 23.Fischl B, Salat DH, Busa E, et al. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–55. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- 24.Fischl B, Salat DH, van der Kouwe AJ, et al. Sequence-independent segmentation of magnetic resonance images. Neuroimage. 2004;23(Suppl 1):S69–84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 25.Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999;9(2):195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- 26.Fischl B, Sereno MI, Tootell RB, Dale AM. High-resolution intersubject averaging and a coordinate system for the cortical surface. Hum Brain Mapp. 1999;8(4):272–84. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fischl B, van der Kouwe A, Destrieux C, et al. Automatically parcellating the human cerebral cortex. Cereb Cortex. 2004;14(1):11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
- 28.Han X, Jovicich J, Salat D, et al. Reliability of MRI-derived measurements of human cerebral cortical thickness: the effects of field strength, scanner upgrade and manufacturer. Neuroimage. 2006;32(1):180–94. doi: 10.1016/j.neuroimage.2006.02.051. [DOI] [PubMed] [Google Scholar]
- 29.Jovicich J, Czanner S, Greve D, et al. Reliability in multi-site structural MRI studies: effects of gradient non-linearity correction on phantom and human data. Neuroimage. 2006;30(2):436–43. doi: 10.1016/j.neuroimage.2005.09.046. [DOI] [PubMed] [Google Scholar]
- 30.Ségonne F, Dale AM, Busa E, et al. A hybrid approach to the skull stripping problem in MRI. Neuroimage. 2004;22(3):1060–75. doi: 10.1016/j.neuroimage.2004.03.032. [DOI] [PubMed] [Google Scholar]
- 31.Reuter M, Rosas HD, Fischl B. Highly accurate inverse consistent registration: a robust approach. Neuroimage. 2010;53(4):1181–96. doi: 10.1016/j.neuroimage.2010.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Reuter M, Schmansky NJ, Rosas HD, Fischl B. Within-subject template estimation for unbiased longitudinal image analysis. Neuroimage. 2012;61(4):1402–18. doi: 10.1016/j.neuroimage.2012.02.084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Achard S, Salvador R, Whitcher B, et al. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J Neurosci. 2006;26(1):63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Achard S, Bullmore E. Efficiency and Cost of Economical Brain Functional Networks. PLoS Comput Biol. 2007;3(2):e17. doi: 10.1371/journal.pcbi.0030017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Salvador R, Suckling J, Schwarzbauer C, Bullmore E. Undirected graphs of frequency-dependent functional connectivity in whole brain networks. Philos Trans R Soc Lond B Biol Sci. 2005;360(1457):937–46. doi: 10.1098/rstb.2005.1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wang J, Zuo X, He Y. Graph-based network analysis of resting-state functional MRI. Front Syst Neurosci. 2010;4:16. doi: 10.3389/fnsys.2010.00016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Liao W, Ding J, Marinazzo D, et al. Small-world directed networks in the human brain: multivariate Granger causality analysis of resting-state fMRI. Neuroimage. 2011;54(4):2683–94. doi: 10.1016/j.neuroimage.2010.11.007. [DOI] [PubMed] [Google Scholar]
- 38.Whitfield-Gabrieli S, Nieto-Castanon A. Conn: a functional connectivity toolbox for correlated and anticorrelated brain networks. Brain Connect. 2012;2(3):125–41. doi: 10.1089/brain.2012.0073. [DOI] [PubMed] [Google Scholar]
- 39.Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–19. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- 40.Maldjian JA, Laurienti PJ, Kraft RA, Burdette JH. An automated method for neuroanatomic and cytoarchitectonic atlas-based interrogation of fMRI data sets. Neuroimage. 2003;19(3):1233–39. doi: 10.1016/s1053-8119(03)00169-1. [DOI] [PubMed] [Google Scholar]
- 41.Maldjian JA, Laurienti PJ, Burdette JH. Precentral gyrus discrepancy in electronic versions of the Talairach atlas. NeuroImage. 2004;21(1):450–55. doi: 10.1016/j.neuroimage.2003.09.032. [DOI] [PubMed] [Google Scholar]
- 42.Jenkins G, Watts D. Spectral Analysis and its Applications. San Francisco: Holden-Day; 1968. [Google Scholar]
- 43.Baria AT, Baliki MN, Parrish T, Apkarian AV. Anatomical and functional assemblies of brain BOLD oscillations. J Neurosci. 2011;31(21):7910–19. doi: 10.1523/JNEUROSCI.1296-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lancaster JL, Woldorff MG, Parsons LM, et al. Automated Talairach atlas labels for functional brain mapping. Hum Brain Mapp. 2000;10(3):120–31. doi: 10.1002/1097-0193(200007)10:3<120::AID-HBM30>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wang J, Wang L, Zang Y, et al. Parcellation-dependent small-world brain functional networks: a resting-state fMRI study. Hum Brain Mapp. 2009;30(5):1511–23. doi: 10.1002/hbm.20623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.van Wijk BC, Stam CJ, Daffertshofer A. Comparing brain networks of different size and connectivity density using graph theory. PLoS One. 2010;5(10):e13701. doi: 10.1371/journal.pone.0013701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Newman MEJ. A measure of betweenness centrality based on random walks. Social Networks. 2005;27(1):39–54. [Google Scholar]
- 48.Hayasaka S, Laurienti PJ. Comparison of characteristics between region-and voxel-based network analyses in resting-state fMRI data. Neuroimage. 2011;50(2):499–508. doi: 10.1016/j.neuroimage.2009.12.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hampson M, Driesen NR, Skudlarski P, et al. Brain connectivity related to working memory performance. J Neurosci. 2006;26(51):13338–43. doi: 10.1523/JNEUROSCI.3408-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bassett DS, Bullmore E, Verchinski BA, et al. Hierarchical organization of human cortical networks in health and schizophrenia. J Neurosci. 2008;28(37):9239–48. doi: 10.1523/JNEUROSCI.1929-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Talairach J, Tournoux P. Co-planar stereotaxic atlas of the human brain. New York: Thieme Medical Publishers; 1988. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Voxels significantly correlated to the precuneus ROI (circled in green) for (A) resting state data, (B) bandpass filtered task data, and (C) fullband filtered task data.
Shows the task fullband and task bandpass vs. resting state connectivity in DMN seeds. (A) and (B) shows the task fullband vs. resting state and task bandpass vs. resting state Fisher Transformed Z scores of the DMN seeds as chosen from Van Dijk et al. [3] respectively. The black dotted line in each figure is a line with slope=1 representing equal connectivity.
(A–C) show the whole-brain networks of the Resting state, Task bandpass, and task fullband networks respectively. 90 Brodmann Areas were chosen spanning the whole brain and the CONN-fMRI toolbox was used to generate the networks. The node color indicates the difference between the positive and negative connections (green to dark blue indicating increasing negative total connections respectively, green to dark red being indicating increasing positive total connections).
The degree distribution of three networks that were explored. Degree is a measure of the number of connections at a particular node. Degree distribution plots show the number of nodes with a particular degree. The red, green and blue bar plot shows the degree distribution of the task (fullband), task (bandpass) bandpass and the resting state network respectively.
The figures below show the % weighted degree and % weighted betweenness centrality of each node of the resting state, gap closure task (bandpass), and gap closure task (fullband) networks plotted against each other for each of the 90 Brodmann Areas. The degree centrality was normalized by the total number of degree possible, and betweenness centralities were normalized by the total number of connections possible in the network. In (A, C, and E) – the axes represent the % Degree; whereas in (B, D, and F), they represent the log of the% betweenness centrality. The blue line represents linear least-squared regression best-fit line, and the dotted black line represents a reference slope=1 line. In (B, D, and F), the best-fit line and reference slope=1 line are calculated in linear space, but plotted in log-log space.
Shows the global and local efficiency vs. connection cost (K) of the task network with fullband processing shown in blue (A), task network with bandpass processing shown in green (B), and the resting state network shown in red. The thick black dotted line represents the global efficiency vs. cost of a random network, while the thin black dotted line represents that of a regular lattice. Small world networks are defined as networks with higher global efficiency than a lattice but lower global efficiency than a random graph.
Supplement Table 1.
Shows the clusters found in the default mode network connectivity maps in the resting state network.
| Size (n) | Size (mm3) | MNI X | MNI Y | MNI Z | TAL X | TAL Y | TAL Z | Max -log(p) value | Cerebrum | Lobe | Anatomical area | Brodmann area | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1707 | 13656 | −10 | −51 | 27 | −10 | −48 | 27 | 5.83732 | Left cerebrum | Parietal lobe | Precuneus | Brodman area 31 |
| 2 | 772 | 6176 | −42 | −57 | 27 | −42 | −54 | 28 | 5.10571 | Left cerebrum | Temporal lobe | Superior temporal gyrus | Brodman area 39 |
| 3 | 708 | 5664 | −12 | 65 | 7 | −12 | 63 | 3 | 4.71252 | Left cerebrum | Frontal lobe | Media frontal gyrus | Brodman area 10 |
| 4 | 602 | 4816 | 52 | −65 | 31 | 51 | −62 | 32 | 4.07893 | Right cerebrum | Parietal lobe | Angular gyrus | Brodman area 39 |
| 5 | 319 | 2552 | 56 | −45 | 41 | 55 | −42 | 40 | −3.88219 | Right cerebrum | Parietal lobe | Inferior parietal lobule | Brodman area 40 |
| 6 | 313 | 2504 | −8 | 25 | 27 | −8 | 25 | 24 | −3.78081 | Left cerebrum | Limbic lobe | Anterior cingulate | Brodman area 32 |
Supplement Table 2.
Shows the clusters found in the default mode network connectivity maps in the task (bandpass) network.
| Size (n) | Size (mm3) | MNI X | MNI Y | MNI Z | TAL X | TAL Y | TAL Z | Max −log(p) value | Cerebrum | Lobe | Anatomical area | Brodmann area | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6190 | 49520 | 2 | −45 | 29 | 2 | −42 | 29 | 7.51287 | Right cerebrum | Limbic lobe | Cingulate gyrus | Brodman area 31 |
| 2 | 12646 | 101168 | 0 | 57 | 15 | 0 | 56 | 11 | 6.4667 | Left cerebrum | Frontal lobe | Media frontal gyrus | Brodman area 10 |
| 3 | 2011 | 16088 | 54 | −65 | 31 | 53 | −62 | 32 | 5.96842 | Right cerebrum | Parietal lobe | Angular gyrus | Brodman area 39 |
| 4 | 312 | 2496 | −6 | −15 | 13 | −6 | −14 | 13 | 5.54662 | Left cerebrum | Sub- lobar | Thalamus | Medial dorsal nucleus |
| 5 | 2031 | 16248 | −62 | −15 | −13 | −61 | −15 | −10 | 5.47374 | Left cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 6 | 1398 | 11184 | −46 | −75 | 31 | −46 | −71 | 32 | 5.22169 | Left cerebrum | Temporal lobe | Angular gyrus | Brodman area 39 |
| 7 | 574 | 4592 | 26 | −21 | −17 | 26 | −21 | −13 | 4.78953 | Right cerebrum | Limbic lobe | Parahip-pocampal gyrus | Brodman area 35 |
| 8 | 366 | 2928 | 16 | −69 | 45 | 16 | −65 | 45 | −4.7328 | Right cerebrum | Parietal lobe | Precuneus | Brodman area 7 |
| 9 | 1782 | 14256 | −44 | −59 | −31 | −44 | −58 | −23 | −4.45789 | Left cerebrum | Posterior lobe | Tuber | * |
| 10 | 507 | 4056 | −38 | 55 | 21 | −38 | 54 | 17 | −4.36372 | Left cerebrum | Frontal lobe | Superior frontal gyrus | Brodman area 10 |
| 11 | 455 | 3640 | 44 | −81 | −25 | 44 | −80 | −17 | −4.20093 | Right cerebrum | Posterior lobe | Declive | * |
| 12 | 422 | 3376 | 64 | −13 | −13 | 63 | −13 | −10 | 3.9602 | Right cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
Supplement Table 3.
Shows the clusters found in the default mode network connectivity maps in the task (fullband) network.
| Size (n) | Size (mm3) | MNI X | MNI Y | MNI Z | TAL X | TAL Y | TAL Z | Max −log(p) value | Cerebrum | Lobe | Anatomical area | Brodmann area | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 7528 | 60224 | 2 | −55 | 27 | 2 | −52 | 27 | 7.75249 | Left cerebrum | Limbic lobe | Cingulate gyrus | Brodman area 31 |
| 2 | 1110 | 8880 | 44 | −19 | 53 | 44 | −16 | 50 | 7.07843 | Right cerebrum | Frontal lobe | Precentral gyrus | Brodman area 4 |
| 3 | 10199 | 81592 | 6 | 57 | 31 | 6 | 57 | 26 | 6.10365 | Right cerebrum | Frontal lobe | Superior frontal gyrus | Brodman area 9 |
| 4 | 973 | 7784 | 50 | −59 | 35 | 50 | −56 | 35 | 5.4246 | Right cerebrum | Parietal lobe | Inferior parietal lobule | Brodman area 40 |
| 5 | 486 | 3888 | −60 | −15 | −13 | −59 | −15 | −10 | 5.08472 | Left cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 6 | 2987 | 23896 | 42 | 19 | 3 | 42 | 19 | 2 | −5.01401 | Right cerebrum | Sub- lobar | Insula | * |
| 7 | 699 | 5592 | 28 | −41 | −31 | 28 | −41 | −24 | −4.55969 | Right cerebrum | Anterior lobe | Culmen | * |
| 8 | 229 | 1832 | −6 | −9 | 13 | −6 | −8 | 12 | 4.18239 | Left cerebrum | Sub- lobar | Thalamus | * |
| 9 | 278 | 2224 | −54 | 7 | −29 | −53 | 6 | −25 | 4.05919 | Left cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 10 | 374 | 2992 | 68 | −31 | −3 | 67 | −30 | −1 | 4.04834 | Right cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 11 | 383 | 3064 | −48 | 41 | 19 | −48 | 41 | 15 | −3.84668 | Left cerebrum | Frontal lobe | Middle frontal gyrus | Brodman area 46 |
| 12 | 407 | 3256 | −20 | −59 | −31 | −20 | −58 | −23 | −3.59756 | Left cerebrum | Anterior lobe | * | Dentate |
| 13 | 665 | 5320 | 52 | 43 | 9 | 51 | 42 | 6 | −3.41915 | Right cerebrum | Frontal lobe | Inferior frontal gyrus | Brodman area 46 |
| 14 | 269 | 2152 | −54 | −57 | −9 | −53 | −56 | −5 | −3.29778 | Left cerebrum | Temporal lobe | Inferior temporal gyrus | Brodman area 37 |
| 15 | 265 | 2120 | 62 | −13 | −13 | 61 | −13 | −10 | 3.27451 | Right cerebrum | Temporal lobe | Middle temporal gyrus | Brodman area 21 |
| 16 | 395 | 3160 | −22 | −17 | −21 | −22 | −17 | −17 | 3.16681 | Left cerebrum | Limbic lobe | Parahip-pocampal gyrus | Brodman area 28 |
Supplement Table 4.
Shows the mean degrees of the resting state, gap closure task (fullband) and gap closure task (bandpass) networks.
| Networks | Mean degree |
|---|---|
| Task (fullband) | 10.5243 |
| Task (bandpass) | 9.8876 |
| Resting rate | 4.2447 |