Developmental Reversals in Risky Decision Making: Intelligence Agents Show Larger Decision Biases Than College Students

Abstract

Intelligence agents make risky decisions routinely, with serious consequences for national security. Although common sense and most theories imply that experienced intelligence professionals should be less prone to irrational inconsistencies than college students, we show the opposite. Moreover, the growth of experience-based intuition predicts this developmental reversal. We presented intelligence agents, college students, and postcollege adults with 30 risky-choice problems in gain and loss frames and then compared the three groups’ decisions. The agents not only exhibited larger framing biases than the students, but also were more confident in their decisions. The postcollege adults (who were selected to be similar to the students) occupied an interesting middle ground, being generally as biased as the students (sometimes more biased) but less biased than the agents. An experimental manipulation testing an explanation for these effects, derived from fuzzy-trace theory, made the students look as biased as the agents. These results show that, although framing biases are irrational (because equivalent outcomes are treated differently), they are the ironical output of cognitively advanced mechanisms of meaning making.

Risky decision making is a central phenomenon of economic and psychological theory (Fox & Tannenbaum, 2011). Some people take risks with disastrous consequences; adolescents and young adults, for example, are disproportionately prone to crime, reckless driving, and unprotected sex (Figner & Weber, 2011; Reyna, Chapman, Dougherty, & Confrey, 2012). Other people avoid risks, for example, holding on to lower-risk financial instruments despite the prospect of better lifetime returns from higher-risk investments (Benartzi & Thaler, 1995). Intelligence agents are an important group of professionals who weigh risky options routinely, and their decisions have serious consequences for national security (Heuer, 1999). We investigated whether intelligence agents who make decisions about national security are subject to the same decision biases as college students or whether, as predicted by the growth of experience-based intuition, they are more biased.

Although the merits of risk seeking or risk avoiding are debatable under different circumstances, a fundamental tenet of most decision theories is that risk preferences for the same circumstances should be consistent (Kahneman & Tversky, 2000). Framing effects—decision makers’ shifts from risk seeking to risk avoiding when options are equivalent—challenge that fundamental tenet of consistency. People who choose inconsistently should have difficulty achieving their goals (Fischhoff, 2008). Nevertheless, reversals in risk preference are easily demonstrated with college students (Kahneman, 2003; Stanovich & West, 2008).

According to fuzzy-trace theory (FTT), which is grounded in research on memory and narrative, decision makers simultaneously encode two perspectives on risky-choice problems: a verbatim representation of quantities (which they combine multiplicatively, trading off risk and outcomes, as in expected-value or expected-utility theory) and gist representations of qualitative meaning (Kühberger & Tanner, 2010). Although people encode both types of representations of decision options, the decision-making process begins with the simplest qualitative distinctions (a fuzzy-processing preference); decision makers rely on finer distinctions only if the simplest gist representations of the options are identical (because it is impossible to choose between options mentally represented as identical).

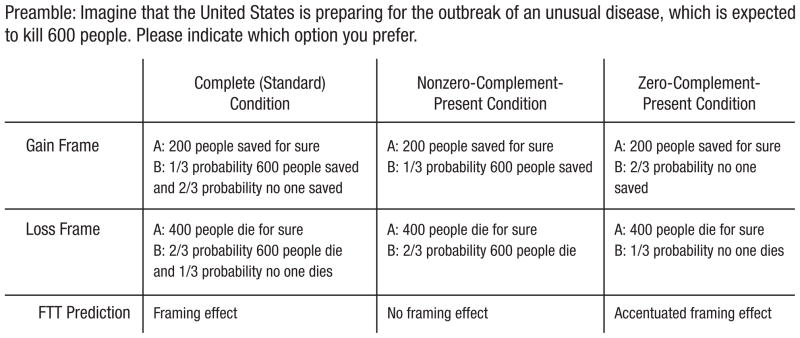
In framing problems involving sure and risky options (including a zero outcome, such as “no people saved”), the simplest (categorical) contrast between something and nothing is pivotal. Consider the problem presented in Figure 1. In this problem, 600 lives are at stake, and the possible outcome of 600 people saved is encoded qualitatively as “some saved” and “all saved.” However, the mental representation “all saved” requires that three distinctions be made to represent the gain-frame outcomes: “all” (600), “some” (200), or “none” saved; in contrast, categorizing both 600 and 200 people saved as “some saved” produces a simple dichotomy between “some” and “none.” Decision making gravitates to the simplest bottom-line gist of options, which boils down, in the gain frame, to saving some people versus either saving some people or saving no one (Reyna, 2012). If decision makers value human life, they choose the sure option because saving some lives is better than saving none. Conversely, in the loss frame, the options boil down to “some people die” versus “either some die or none die.” Valuing “none die” above “some die,” decision makers choose the risky option, which offers the categorical possibility that none die. Thus, gist-based categorical distinctions account for framing effects.

Fig. 1.

Example of the risky-choice problems used in this study, with predictions for framing effects. Across subjects, each problem was presented in three truncation conditions, with both gain and loss framing. The standard framing effect is risk avoidance in the gain frame (i.e., choosing the sure option) and risk seeking in the loss frame (i.e., choosing the risky option). For any given problem, the sure options were equivalent in all versions: In the specific example of the dread-disease problem shown here, because there is a total of 600 people, saving 200 lives is equivalent to 400 people dying. Similarly, the risky options of a given problem were equivalent in all versions: In the case of the dread-disease problem, the expected value of 1/3 probability of all 600 people being saved (200 saved) is equal to the expected value of 2/3 probability of all 600 people dying (400 die). Moreover, the sure and risky options of a given problem were equivalent in expected value. Subjects were instructed that the missing part of a truncated option was the complement of the presented part (complementarity was explained with examples). Presenting only the nonzero complement eliminates the some-none categorical contrast that underlies the framing effect (making equivalence of options salient). Presenting only the zero complement emphasizes this contrast and leads to an accentuated framing effect. Presenting both complements creates a conflict between equivalence and contrast, which leads to the standard framing effect. FFT = fuzzy-trace theory.

Such gist-based categorical distinctions are reflected in medical decisions (the categorical possibility of rare, incurable brain cancer discourages patients’ risk taking regarding medications for rheumatoid arthritis), insurance choices (the categorical possibility of rare, catastrophic loss encourages purchasing expensive insurance), and moral reasoning (the categorical possibility of murdering a single person discourages action even when that action would save more lives; Fraenkel et al., 2012; Reyna, 2008; Reyna & Casillas, 2009). According to FTT, gist-based thinking often determines judgments and decisions, and empirical results are consistent with this formulation (Brainerd, Reyna, Wright, & Mojardin, 2003; Kühberger & Tanner, 2010; Reyna & Brainerd, 2008).

Moreover, FTT makes the counterintuitive prediction that reliance on gist-based thinking increases with development. That is, with increasing experience and expertise, people are less likely to engage in literal, verbatim-based analysis and more likely to use simple semantic gist in memory, judgment, and decision making (Brainerd, Reyna, & Zember, 2011; Reyna & Brainerd, 2011). For example, “remembering” the gist of events as directly experienced increases from childhood to adulthood, such that net memory accuracy is lower in adults than in children. Although verbatim memory for words increases from childhood to adulthood, “false” memory for meaning-consistent words increases even faster, an effect that has been replicated in 53 of 55 experiments. This is called a developmental- reversal effect because it violates the usual expectation that adults should outperform children on cognitive tasks.

Developmental reversal of framing effects has been documented, and these reversals are also driven by age-related changes in reliance on gist versus verbatim memory representations (Reyna & Ellis, 1994). According to FTT, children are more likely than adults to focus on verbatim details, treating decisions between sure options and gambles like math problems. Thus, in framing tasks, when extraneous performance factors (e.g., memory for problem information) were controlled, young children were able to combine the magnitudes of outcomes and probabilities multiplicatively, trading off risk and reward (Levin & Hart, 2003).

Contrary to traditional assumptions about the development of cognitive capacity, the literature shows that framing biases emerge with age, appearing in attenuated form in early adolescence (see also Reyna et al., 2011). The explanation, according to FTT, is that reliance on simple, categorical gist in decision making increases from childhood to adulthood (whereas reliance on verbatim numbers decreases), just as the emphasis on gist in memory increases during this same period. Other biases and heuristics show a similar developmental trajectory (De Neys & Vanderputte, 2011; Furlan, Agnoli, & Reyna, in press; Reyna & Farley, 2006, Table 3).

In addition, FTT predicts that individuals with autism will show decreased framing biases (and other gist-based biases; Reyna & Brainerd, 2011) relative to the general population. Autism spectrum disorders have been analyzed as arising not from a lack of intelligence, but from a verbatim-based, analytical information-processing style. According to this account, they should perform worse when accurate reasoning requires nonliteral gist thinking and better when nonliteral gist thinking is the source of reasoning biases. Indeed, empirical studies have demonstrated this pattern (De Martino, Harrison, Knafo, Bird, & Dolan, 2008; Morsanyi, Handley, & Evans, 2010).

Most relevant to the current research, studies of adults ranging from novices in a domain (e.g., medical students) to experts (e.g., cardiologists) have shown that the latter are more likely to base decisions on categorical gist as opposed to verbatim details (Reyna & Lloyd, 2006). (Experts’ use of configural pattern matching or gist should be distinguished from their ability to discriminate categories; Weiss & Shanteau, 2003.) Like children learning about life, novices lack background knowledge and experience that would allow them to “connect the dots” in a novel domain (Lloyd & Reyna, 2009). Ironically, therefore, experts should be more susceptible than novices to effects of meaning and context and, hence, to gist-based illusions or biases in their domains of experience (see also Doherty, Campbell, Tsuji, & Phillips, 2010).

However, there are uncertainties about how judgment and decision making might change in adulthood. The development of professional expertise typically begins after college, and yet many phenomena have been studied primarily with college students (Henrich, Heine, & Norenzayan, 2010). Studies rarely directly compare college students with postcollege professionals or experts. Therefore, we compared college students with experts in an important domain of risky decision making: intelligence.

The intelligence establishment of the United States is a vast enterprise consisting of roughly 100,000 employees (Sanders, 2008). The intelligence professionals whom we studied routinely make risky decisions, ranging from whether to draw a weapon to how to combat terrorism. They also analyze risky situations and make recommendations based on the relative risks of different options. Despite the consequential nature of their jobs, little is known about how they make decisions (Fischhoff & Chauvin, 2011).

We studied how such intelligence professionals make risky decisions—in particular, whether they show framing effects—for several reasons. Framing effects are interesting because they violate the most basic assumption of otherwise powerful economic theories, because they motivate one of the most popular psychological alternatives to these theories, and because they show that small wording differences produce dramatic differences in risk preferences, which govern decisions in finance, medicine, law enforcement, and other domains. Would professionals immersed in making risky decisions in real life be susceptible to superficial changes in wording, or would they recognize that the consequences of these choices were the same regardless of such wording changes?

Although many theorists might expect that intelligence professionals would be more likely than college students to take a rational (System 2; Stanovich & West, 2008) approach (and thus censor their intuitions), FTT predicts a developmental-reversal effect—that professionals with greater experience making risky decisions would be more likely to display framing effects. This predicted growth of the framing bias would be a continuation of the developmental “progression” from no framing bias in childhood to the emergence of framing biases in adolescence and young adulthood to even greater biases among experts with even greater experience making risky decisions.¹

Our use of the term expert is relative (i.e., intelligence professionals are more expert than college students at making risky decisions) and broadly conforms to definitions of expertise in intelligence used elsewhere (specialized training and “time spent working on particular places, people, or problems” in intelligence; Fingar, 2011, p. 9). However, intelligence professionals are also generally older than college students. Therefore, in order to control for age differences, we also recruited a sample of postcollege adults that was comparable socioeconomically to the college students (many were parents, family members, or other social contacts of the students, and some were recruited during alumni weekends and, hence, were graduates of the same university). All but one of the intelligence professionals were college educated.

We experimentally manipulated the key factors predicted by FTT to cause framing effects in order to determine whether we could mimic developmental effects on framing biases. If our theory is correct, one should be able to induce greater framing effects in college students, so that they resemble experts, by emphasizing categorical something-nothing contrasts; conversely, one should be able to make framing effects go away by emphasizing verbatim quantities. To create this waxing and waning of framing effects, we used truncation manipulations—constructed to test FTT’s predictions—in which a redundant portion of the risky option in a problem is deleted (Kühberger & Tanner, 2010; Reyna, 2012; Reyna & Brainerd, 1991). For example, for the dread-disease problem in Figure 1, all subjects received the same background information (600 people are expected to die if nothing is done), and each subject received all three versions of the problem in one of the two framing conditions (gain, loss). The versions were a standard, complete presentation of the choice options and truncated presentations in which either the zero complement was deleted (i.e., 2/3 probability that no one is saved was deleted, but 1/3 probability that 600 are saved was presented) or the nonzero complement was deleted (i.e., 1/3 probability that 600 are saved was deleted, but 2/3 probability that no one is saved was presented).

According to FTT, on the one hand, because the zero (or nothing) outcome is crucial to the categorical something-nothing contrast between options, removing the zero complement should eliminate framing. Removing this outcome literally removes nothing in prospect theory, cumulative prospect theory, or expected-utility theory, all of which predict that this manipulation should have no effect on framing. On the other hand, according to FTT, removing the nonzero complement (leaving outcomes of 200 saved vs. 2/3 probability that no one is saved) should accentuate the categorical something-nothing contrast between options, increasing framing effects. Thus, the latter manipulation (truncating the nonzero complement) should cause college students to resemble experts under standard complete-problem conditions—because removing the nonzero complement induces a greater categorical contrast between something and nothing (e.g., between saving some people vs. saving no one).

Method

Subjects

Sixty-three undergraduates were recruited from Cornell’s Ithaca campus and from the New York City area (age range = 18–22 years, M = 19.74, SD = 1.20; 59% female, 41% male; 66% Caucasian, 27% Asian, and 7% African American; 6% of this group was Hispanic). Fifty-four postcollege adults were recruited through student contacts (age range = 22–56 years, M = 30.83, SD = 9.90; 57% female, 43% male; 53% Caucasian, 30% Asian, 13% African American, and 4% Native American; 2% of this group was Hispanic). Thirty-six intelligence professionals were recruited from a federal agency (age range = 27–60 years, M = 35.87, SD = 7.39; 22% female, 78% male; 69% Caucasian, 6% Asian, 17% African American, and 8% Asian Indian; 14% of this group was Hispanic). Gender was included as a factor in all analyses and was not significant; the analyses reported here were collapsed across this factor.²

All of the undergraduates were working toward a university degree. Most of the postcollege adults were understood to have a university degree, although this was confirmed with a subset only. All but 1 of the intelligence agents were college educated. Five of the agents did not provide detailed demographic information (they also did not provide confidence ratings in this study); among the 86% of the intelligence agents who provided detailed demographic information, 34% had a postbaccalaureate degree.

Neither the college nor the postcollege group had specialized training in law enforcement or intelligence activities. The intelligence agents had an average of 7.09 (SD = 4.87) years of experience working for the agency. Of the 86% of intelligence agents who provided detailed information, 77% were special agents, 7% were special officers, and 16% were administrators.

Materials and procedure

Sixty decision problems about human lives and other valued outcomes were divided into two stimulus sets. Each subject received one set of 30 problems (15 in the gain frame and 15 in the loss frame) in random order with the constraint that the gain and loss versions of the same scenario were presented to different subjects. The 15 gain and 15 loss problems were equally divided among the three truncation conditions (i.e., each subject received problems in all three conditions): complete, nonzero complement present, and zero complement present. (The college and postcollege groups received additional problems involving choices about money, but results for the problems discussed here did not differ significantly from results for the additional problems about money.)

Subjects were instructed that part of the risky option would sometimes be deleted from a problem (examples were given) and were told to assume that the missing part was simply the complement of the presented part. They were tested to establish that they understood this instruction. For each problem, subjects were asked to choose the option that they would prefer in real life, and to rate how confident they were in their choice, on a scale ranging from 1 (not at all) to 5 (completely). Finally, they completed Zuckerman’s (2007) 19-item sensation-seeking scale (a risk-preference predictor) and provided demographic and other background information.

Results and Discussion

We performed a 3 (group: college students, postcollege adults, intelligence agents) × 2 (stimulus set) × 3 (truncation condition: complete, zero complement present, nonzero complement present) analysis of variance on each of two dependent measures: choices (0 for the sure option, 1 for the risky option) and a transformed measure of signed confidence (confidence ratings were given a negative sign if the sure option was chosen and a positive sign if the risky option was chosen, so the scale ranged from −5 to +5). Unsigned confidence was also analyzed (see later in this section). Groups did not differ significantly in sensation seeking.

Framing bias for choices was measured by subtracting the proportion of risky choices in the gain frame from the proportion of risky choices in the loss frame. This score could vary from −1.0 (all risky choices in the gain frame and no risky choices in the loss frame) to 1.0 (all risky choices in the loss frame and no risky choices in the gain frame—the standard framing-effect pattern of results). For signed confidence, the average signed confidence in the gain frame was subtracted from the average signed confidence in the loss frame, which resulted in a range of −10 (maximum confidence in choices opposite to the standard framing effect) to 10 (maximum confidence in choices consistent with the standard framing effect).

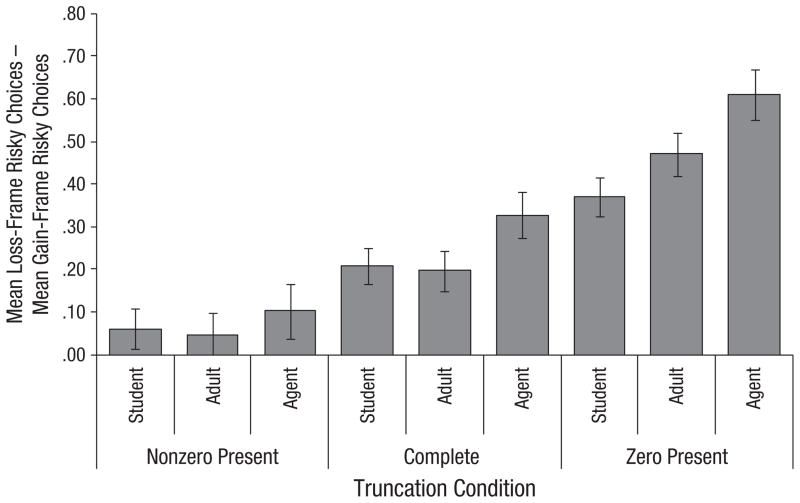
In the choice analyses, significant main effects on framing bias were obtained for group, F(2, 147) = 3.18, p = .044, η_p² = .041, and for truncation condition, F(2, 294) = 68.106, p < .0001, η_p² = .317 (Fig. 2). Consistent with developmental reversal, pairwise tests revealed that the framing effect was smaller in college students (M_students = .212, SE = .033) compared with intelligence agents (M_agents = .346, SE = .043). Postcollege adults (M_adults = .237, SE = .037) did not differ from college students and differed marginally from intelligence agents (p = .057). As predicted by FTT, framing effects were smallest in the nonzero-complement-present condition (M_{nonzero complement} = .069, SE = .032), intermediate in the complete condition (M_{both complements} = .244, SE = .028), and largest in the zero-complement-present condition (M_{zero complement} = .483, SE = .03); all comparisons were significant, p < .0001. Although these differences in framing bias across conditions seemed to diverge for college students (Δ = .308), postcollege adults (Δ = .425), and intelligence agents (Δ = .508), the Group × Truncation Condition interaction was nonsignificant. Analyses conducted separately for each condition showed that framing effects were not significant in the nonzero- complement-present condition, but were significant in both the complete and the zero-complement-present conditions. Framing bias for college students in the zero-complement-present condition (M_{students, zero complement} = .369, SE = .045) resembled that for intelligence agents in the complete condition (M_{agents, both complements} = .328, SE = .055).

Fig. 2.

Mean framing bias as a function of group (college students, postcollege adults, intelligence agents) and truncation condition (nonzero complement present, complete, zero complement present). Framing bias could vary from −1.0 (all risky choices in the gain frame and no risky choices in the loss frame) to 1.0 (all risky choices in the loss frame and no risky choices in the gain frame—the standard framing-effect pattern). Error bars represent ±1 SE.

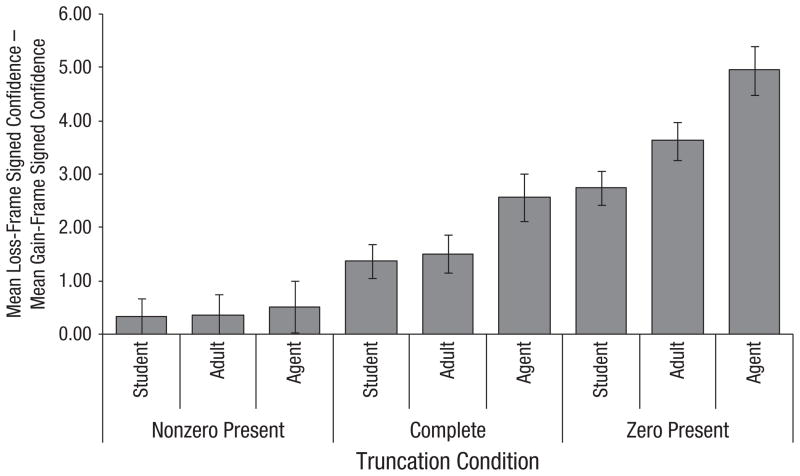
In the signed-confidence analyses, significant main effects reflecting framing bias were again obtained for group, F(2, 142) = 4.101, p = .019, η_p² = .055, and for truncation condition, F(2, 284) = 81.839, p < .0001, η_p² = .366 (Fig. 3). (Technically, framing bias was not a factor in these analyses, but because loss-gain difference scores were used, main effects refer to framing effects.) Consistent with developmental reversal, pairwise tests revealed that the framing effect was smaller in college students (M_students = 1.487, SE = 0.239) compared with intelligence agents (M_agents = 2.676, SE = 0.34). Postcollege adults (M_adults = 1.834, SE = 0.266) did not differ from college students and differed marginally from intelligence agents (p = .053). As predicted by FTT, framing effects were smallest in the nonzero-complement-present condition (M_{nonzero complement} = 0.404, SE = 0.235), intermediate in the complete condition (M_{both complements} = 1.820, SE = 0.214), and largest in the zero-complement-present condition (M_{zero complement} = 3.773, SE = 0.224); all comparisons were significant, p < .0001. Analyses conducted separately for each condition showed that framing effects were not significant in the nonzero-complement-present condition, but were significant in both the complete and the zero-complement-present conditions.

Fig. 3.

Framing confidence as a function of group (college students, postcollege adults, intelligence agents) and truncation condition (nonzero complement present, complete, zero complement present). Framing confidence could range from −10 (maximum confidence in choices opposite to the standard framing effect) to 10 (maximum confidence in choices consistent with the standard framing-effect pattern). Error bars represent ±1 SE.

Furthermore, group and truncation condition interacted, F(4, 284) = 2.441, p = .047, η_p² = .033: The differences in the framing effect across conditions diverged for college students (Δ = 2.410), postcollege adults (Δ = 3.263), and intelligence agents (Δ = 4.435). Within each group, all pairwise comparisons between conditions were significant, p < .006. Within the nonzero-complement- present condition, the groups did not differ from one another (and none showed a framing effect). Within the complete condition, the framing effect was smaller in college students (M_students = 1.375, SE = 0.311) compared with intelligence agents (M_agents = 2.570, SE = 0.443). Postcollege adults (M_adults = 1.514, SE = 0.346) did not differ from college students and differed marginally from intelligence agents (p = .062). Within the zero-complement-present condition, the framing effect was smaller in college students (M_students = 2.747, SE = 0.325) compared with intelligence agents (M_agents = 4.946, SE = 0.463). Postcollege adults (M_adults = 3.625, SE = 0.362) differed marginally from college students (p = .073), but they differed significantly from intelligence agents (p = .026). Framing bias for college students in the zero-complement-present condition (M_{students, zero complement} = 2.747, SE = 0.325) resembled that for intelligence agents in the complete condition (M_{agents, both complements} = 2.570, SE = 0.443). Truncation condition also interacted with stimulus set, F(2, 284) = 4.529, p = .012, η_p² = .031; although truncation effects were present for both stimulus sets, the effect was larger in one set than the other. All other effects were similar for the two stimulus sets.

Unsigned confidence ratings ranging from 1 to 5 were analyzed in a 3 (group: college students, postcollege adults, intelligence agents) × 2 (stimulus set) × 3 (truncation condition: complete, zero complement present, nonzero complement present) × 2 (frame: gain, loss) analysis of variance. A main effect of group was found, F(2, 142) = 4.62, p = .011, η_p² = .061; intelligence agents showed higher confidence in their decisions (M_agents = 3.850, SE = 0.135) than both postcollege adults (M_adults = 3.487, SE = 0.106; p = .036) and college students (M_students = 3.349, SE = 0.095; p = .003). Adults and college students did not differ significantly. Thus, not only did intelligence agents show larger framing effects than the other groups, but they were also more confident in their biased decisions (De Neys, Cromheeke, & Osman, 2011).

Truncation condition also had a significant effect on unsigned confidence ratings, F(2, 284) = 3.73, p = .025, η_p² = .026: Confidence was higher in the zero-complement-present condition (M_{zero complement} = 3.618, SE = 0.065) than in the nonzero-complement-present condition (M_{nonzero complement} = 3.542, SE = 0.068; p = .024) and in the complete condition (M_{both complements} = 3.528, SE = 0.072; p = .013). Thus, removing complementary information increased confidence in the condition that highlighted categorical contrasts. Finally, subjects were more confident when problems were in the gain frame (M_gain = 3.645, SE = 0.066) compared with the loss frame (M_loss = 3.480, SE = 0.069), F(1, 142) = 23.94, p < .001, η_p ² = .144. This result is consistent with prospect theory because the loss frame involves avoid-avoid conflict between loss aversion (avoiding the sure loss) and risk aversion (avoiding the gamble), whereas the gain frame involves no such conflict (only avoiding the gamble). Overall, subjects were moderately to highly confident about their decisions, despite their shifting risk preferences.

Conclusions

According to common sense and most theories, experienced intelligence professionals should be less prone to irrational inconsistencies than college students are. Intelligence agents have more experience thinking about risks involving human lives (and other valued assets) than do college students, and their training should reduce biases. During the course of this study, these agents expressed motivation to demonstrate their professional expertise in decision making. Although 1 agent in our study reported not having completed a 4-year degree, none of the students had completed their 4-year degrees, and a substantial number of the agents had postbaccalaureate degrees. Nevertheless, the intelligence agents exhibited larger decision biases than the college students, treating equivalent outcomes differently on the basis of superficial differences in wording. In particular, the agents were more willing to take risks with human lives when outcomes were framed as losses rather than as gains. These effects were found in both choices and confidence ratings, and indeed, agents “doubled down” on their choices by expressing higher confidence in them relative to either students or other adults.

Postcollege adults occupied an interesting middle ground between college students and agents. They were often as biased as college students (but sometimes more biased), and occasionally less biased than agents. Thus, the pattern of framing biases observed for college students, postcollege adults, and intelligence agents echoes findings for children, adolescents, and adults showing that more developmentally “advanced” reasoners were more likely to exhibit reasoning biases, a developmental-reversal effect (Reyna & Ellis, 1994; Reyna et al., 2011; for a similar pattern, see Schurr, 1987).

According to FTT, these biases reflect the growth of gist-based intuition as reasoners gain experience in a domain (much as some perceptual illusions emerge with experience; Doherty et al., 2010). Although the explanation of framing biases was supported, how life experience produces greater reliance on fuzzy processing is not fully understood. Rote experience, without insight, should not make information processing more gist based. Intelligence agents deal with the danger or exploit the opportunity of risks (Heuer & Pherson, 2011); experience with losses may predominate, but the something-nothing distillation applies to both gains and losses.

Framing biases are technically irrational (because equivalent outcomes are treated differently and not just slightly differently, as the confidence ratings confirmed), but they are the ironical output of cognitively advanced mechanisms of meaning making (Gaissmaier & Schooler, 2008) that generally facilitate expert performance (Reyna & Lloyd, 2006). Meaning making also explains why people show greater framing bias when they process information in their native tongue rather than a foreign one; they grasp the meaning of the information better (Keysar, Hayakawa, & An, 2012; this effect of language is also observed in gist-based false memories).

Our experimental manipulations induced behavior in college students that resembled developmental patterns, wiping out the framing effect by emphasizing quantitative trade-offs between risks and outcomes (so that the students mimicked the behavior of children) and augmenting the framing effect by emphasizing categorical contrasts (so that the students mimicked the behavior of experts). This difference between processing verbatim quantities and processing qualitative categories has been identified as an important dimension of cognitive development in many other tasks. In contrast, a personality measure that has been shown to predict real-life risk taking (i.e., impulsive sensation seeking) did not differ among our groups (and, hence, could not explain group differences). Expected-utility and prospect theory also cannot explain why the truncation manipulations worked; for example, removing the zero complement should have no effect according to those theories (zero adds nothing to quantitative perceptions), and yet framing effects disappeared in the nonzero-complement-present condition, as predicted by FTT. Moreover, focusing on “nothing” (zero-complement-present condition) augmented framing, which confirmed another of FTT’s predictions.

These results shed light on the mechanisms of decision making in intelligence agents who identify and mitigate risks to national security. Like results from some other laboratory gambling tasks, framing effects have been shown to predict real-world behavior (Reyna et al., 2011). As demonstrated in many studies, framing bias occurs in high-stakes real-world decisions, such as judicial, surgical, and investment decisions. Taken together, all of these results suggest that meaning and context play a larger role in risky decision making as experts gain experience, which enhances global performance but also has predictable pitfalls.