Motion Planning for Concentric Tube Robots Using Mechanics-based Models

Abstract

Concentric tube robots have the potential to enable new minimally invasive surgical procedures by curving around anatomical obstacles to reach difficult-to-reach sites in body cavities. Planning motions for these devices is challenging in part due to their complex kinematics; concentric tube robots are composed of thin, pre-curved, telescoping tubes that can achieve a variety of shapes via extension and rotation of each of their constituent tubes. We introduce a new motion planner to maneuver these devices to clinical targets while minimizing the probability of colliding with anatomical obstacles. Unlike prior planners for these devices, we more accurately model device shape using mechanics-based models that consider torsional interaction between the tubes. We also account for the effects of uncertainty in actuation and predicted device shape. We integrate these models with a sampling-based approach based on the Rapidly-Exploring Roadmap to guarantee finding optimal plans as computation time is allowed to increase. We demonstrate our motion planner in simulation using a variety of evaluation scenarios including an anatomy-based neurosurgery case that requires maneuvering to a difficult-to-reach brain tumor at the skull base.

I. Introduction

Concentric tube robots are needle-like devices that can be controlled to trace curved paths through open air [1]–[3]. The ability to control the curvilinear shape of these devices enables them to avoid obstacles and reach targets in tight spaces. These continuum robots are composed of thin nested tubes where each tube is pre-curved, shaped for example as a straight transmission segment followed by a segment with constant curvature. Each tube, typically composed of nitinol, can be controlled independently by two degrees of freedom: it can be (1) rotated axially, and (2) pushed/retracted through the containing tube. These degrees of freedom could be robotically actuated or directly controlled by a human operator. When rotating or telescopically extending any of the component tubes of the robot, the device’s entire shape changes due to interactions among the pre-curvatures of the individual tubes.

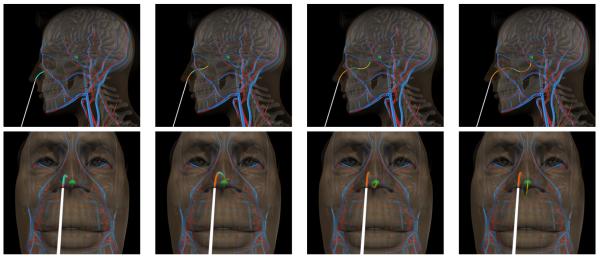
Paired with effective motion planning algorithms, concentric tube robots have the potential to enable new minimally invasive procedures, such as endoscopic access to the brain [4], the lung [5], [6], and the heart [2]. We illustrate in Fig. 1 the potential of these devices for accessing tumors in the brain near the pituitary gland via the nasal cavity while avoiding critical blood vessels, nerves, and bones.

Fig. 1.

Virtual simulation of a concentric tube robot executing a motion plan for neurosurgery at the skull base. The robot is inserted through the nostril and guided toward the pituitary gland (highlighted in green) in the skull base while avoiding skin, bone, blood vessels, and healthy brain tissue. The component tubes of the robot are colored gray, orange, cyan, and yellow.

The power and flexibility of concentric tube robots comes at the cost of modeling and planning complexity. The shape of a concentric tube robot is a function of the control inputs, which are the rotation and extension of each of the component tubes. The shape is governed by the interplay of beam mechanics and torsional effects among the tubes [5], [7]. There is no known closed-form solution to the kinematics of concentric tube robots. Because of these challenges, prior work in motion planning for concentric tube robots in anatomically complex environments has largely focused on simplified kinematic models of the devices at the expense of accuracy. Furthermore, although computationally intensive accurate models of robot shape have been developed, their accuracy typically decreases as the inserted length of the robot increases [8]. In real world scenarios there is uncertainty in actuation and in the kinematic model of the robot which can result in deviations from the predicted motion; this motion uncertainty must be considered in order to maximize the probability of successfully performing a task.

We propose a sampling-based motion planning algorithm that computes the control inputs that guide the robot to a goal point while minimizing the probability of collision with obstacles in the environment. Obstacle avoidance in a minimally-invasive procedure is essential as critical structures like nerves and blood vessels could be damaged if contacted by the device. Unlike prior motion planners, our planner uses a highly accurate kinematic model of concentric tube robots. The planner also considers the effect of uncertainty in the estimated shape of the concentric tube robot; using recent results in optimal motion planning, our planner computes plans that minimize the estimated probability of colliding with sensitive structures.

II. Related Work

Planning motions for concentric tube robots requires that we have the ability to estimate the robot’s shape as a function of its control inputs. Kinematic modeling of concentric tube robots began with geometric and torsionally-rigid models [1], [2], [9]. The model has been improved to consider torsion in straight segments [3], [10], torsion in curved segments [7], [11], and the effect of external loading on the tubes [8], [12]. However, increasing model complexity has also led to longer computation times to estimate the device’s shape. In this paper we use a highly accurate model which considers tube bending interactions, tube material properties, and torsional deformation in straight and curved sections of the tubes [11].

Motion planning for concentric tube robots has only addressed special cases of the general problem. Sears et al. formulated the inverse kinematics of concentric tube robots with simplifying physical assumptions [2], [9]. Dupont et al. used a Fourier approximation over a grid of precomputed forward kinematics solutions to approach inverse kinematics for a model of concentric tube robots that fully handles torsional effects on the tubes [7]. Rucker et al. compute inverse kinematics of the externally loaded model of the device by computing the manipulator Jacobian of the robot [13]. These previous approaches do not explicitly consider obstacle avoidance in reaching a target.

Lyons et al. applied optimization-based motion planning in order to find a plan to reach a target point while avoiding obstacles [6], [14] but only considered the simpler kinematic models of concentric tube robots that neglect torsional effects on the tubes. These models allow for the simplifying assumption that any given collision free concentric tube robot configuration can also serve as a collision free motion plan if the appropriate insertion/rotation strategy is used, which enables us to treat the device like a point robot for planning. However, these models sacrifice accuracy for model simplicity. During medical applications, such inaccuracies can lead to significant side effects or procedure failures. The more accurate model we use in this paper invalidates the assumption that inner tube movement does not affect global device shape, which complicates the motion planning process and eliminates the feasibility of using direct configuration optimization methods.

Concentric tube robots with a sufficient number of tubes can be seen as redundant manipulators, which are difficult to plan motions for due to the lack of closed-form inverse kinematics. Weghe et al. and Bertram et al. investigated probabilistic sampling-based approaches in [15], [16] but do not guarantee globally optimal solutions. Recently developed sampling-based algorithms like RRT* [17] can provide probabilistic convergence to an optimal solution; this useful property however is accompanied by a considerable increase in computation time for real-world problems. We base our motion planner on the Rapidly-Exploring Roadmap (RRM) [18] that guarantees probabilistic convergence to the optimal solution but saves computation time by focusing expensive path refinement procedures on paths that can reach the goal region.

Motion planning for a variety of needle-like devices has been addressed for minimally invasive procedures. Optimization-based planning has been used for sti, symmetric-tip needles in 2D [19] and 3D [20]. Planners have also been developed to maneuver flexible, bevel-tip steerable needles around obstacles in 2D soft tissue [21]–[26]. However, needles can be approximated as a point robot (i.e. the needle tip) moving through soft tissue since the path of the rest of the needle shaft follows the tip. This approximation does not hold for concentric tube robots operating in open air cavities where robot shape can change globally with tube rotation and extension.

Uncertainty in robot motion is significant in medical applications because of the miniaturization of devices and the complexity of tool/tissue interactions. The effect of uncertainty has been well-studied for bevel-tip steerable needles [22], [23], [26]. The planners described above, however, cannot be directly applied to the case of concentric tube robots. The Stochastic Motion Roadmap presented in [22] assumes a discrete set of possible actions at any given robot state, which is not necessarily true when planning for concentric tube robots. The LQG-based method used in [26] introduces an estimation of the probability of collision during plan execution, but assumes that the robot’s tip acts independently of the rest of the shaft. Although we cannot directly use these planners, our goal is to maximize the same metric: the probability of successfully reaching the target while avoiding obstacles.

In this paper we present a motion planning method for concentric tube robots which considers a more accurate kinematic model than in previous work. We present a plan quality metric which seeks to minimize the probability of colliding with obstacles under motion uncertainy. To efficiently compute a plan which optimizes this metric, we extend the RRM with a goal bias while maintaining the RRM’s convergence to optimality. Lastly, we demonstrate the effectiveness of our planner by comparing its performance to other sampling-based planners and by generating a motion plan for an anatomy-based neurosurgery procedure.

III. Problem Formulation

A. Modeling Assumptions

We consider a concentric tube robot with N nested tubes numbered in order of decreasing cross-sectional radius. Each tube i consists of a straight transmission segment of length L_i followed by a pre-curved portion of length C_i, i = 1, … , N. The pre-curved portions of the tubes are curved with constant radii of curvature of r_i, i = 1, … , N. We assume that the device is inserted at a point x_start in 3D space and oriented along the vector v_start.

Each tube contributes two degrees of freedom to the entire concentric tube robot, as shown in Fig. 2. Each tube may be (1) inserted or retracted from the previous tube, and (2) axially rotated. We therefore define a configuration of a concentric tube robot as a 2N dimensional vector q = (θ_i, l_i : i = 1, … , N) where θ_i is the axial angle at the base of the i’th tube and l_i > 0 is the length of insertion of tube i past the tube just before it (and l₁ is the length of the first tube past the insertion point x_start).

Fig. 2.

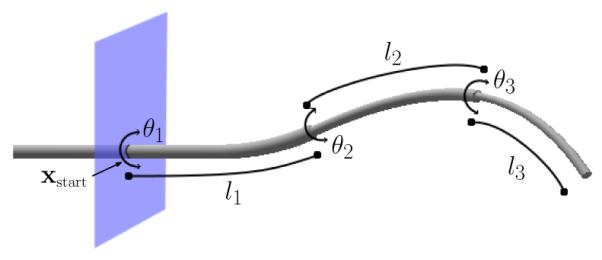
Configuration q = (θ₁, l₁, θ₂, l₂, θ₃, l₃) for a concentric tube robot with N = 3 nested tubes.

For a given configuration q_i, we define the device’s shape using $\mathbf{x}(\mathbf{q},s):{\mathbb{R}}^{2N}\times \mathbb{R}\mapsto {\mathbb{R}}^3$. The function x is a 3D space curve parameterized by arc length s in the domain [0, t], where t is the arc length of the innermost tube past the insertion point (equivalent to ${\sum }_i{l}_i$). We note x(q, 0) maps to x_start and x(q, t) maps to the 3D position of the tip of the concentric tube robot. The space curve x defines only the centerline of the backbone shape of the concentric tube robot. We also define R(q, s) as the cross-sectional radius of the tube at arc length s. To estimate the device’s shape x(q, s) we use the mechanics-based model developed by Rucker et al. [11].

We define environmental obstacles using a set O of size M, O = O₁, O₂, … , O_M. Obstacles can be defined in any geometric representation, as long as it is possible to compute d(x, O_j), the Euclidean distance between a point x in space and the obstacle O_j. In our work we consider spherical obstacles as well as obstacles defined by general 3D polygonal meshes.

B. Planning Problem Formulation

We define a path in configuration space as a sequence of robot configurations (q₁, q₂, … , q_n). A collision free path is a path where, for i = 1, … , n, the shape of the robot corresponding to q_i does not collide with any obstacles in the environment.

We desire that the robot tip reach a point within a distance of r_tol of a goal point x_goal. We assume that the start location x_start and initial orientation v_start are fixed and correspond to the opening through which the device may be deployed based on the constraints of the procedure. From the start location and orientation, we can trivially determine the start configuration q₁.

Given the concentric tube robot’s properties, the start configuration q₁, the goal coordinate x_goal, and the set of obstacles O, we formulate the motion planning problem as a search for a path Π = (q₁, … , q_n) where:

1. $\parallel \mathbf{x}({\mathbf{q}}_n,t)-{\mathbf{x}}_{\text{goal}}\parallel \le r_{\text{tol}}$

2. Each configuration along Π is collision free;

3. Π is of maximal quality as defined in the next subsection.

C. Quantifying Plan Quality

Our motion planning method allows us to select optimal plans based on any quality metric that is smooth and can be represented as a summation along transitions between configurations in Π. The choice of metric should ultimately depend on the clinical task. In prior work, we considered minimizing control effort as defined by the total Euclidean distance in configuration space traveled by the path [18].

When planning motions for a physical implementation of a robot, uncertainty in control inputs and in the kinematic model of the robot can cause deviations from the predicted shape. During plan execution, errors in predicted shape can accumulate and possibly lead to the failure of a plan to be collision free or to reach the goal. In a medical procedure, obstacle collisions can result in significant harm to the patient, e.g. a vital blood vessel may be punctured by the robot. We therefore consider a metric that minimizes the estimated probability of colliding with sensitive structures.

For a given path Π = (q₁, … , q_n), we define its probability of clearance P_clear(Π) as the probability that all of its configurations q_i are collision free. We denote the probability of configuration q_i being collision free as P_clear(q_i).

For a given robot configuration q_i, we characterize its probability of being collision free as the probability that the shape of the concentric tube robot at configuration q_i is free of collision with any of the obstacles O_j, j = 1, … , M. A configuration q_i is collision free only if for every 3D point x(s) on the space curve defining the robot’s shape and for every obstacle O_j, the distance between x(s) and O_j is greater than the radius of the concentric tube robot at s. We discuss in the next section how the planner estimates the probability of clearance for a configuration q.

IV. Motion Planning Algorithm

We use a sampling-based approach to solve the motion planning problem formulated in Sec. III-B. Our planner combines probabilistic completeness for finding a path that avoids obstacles with the property that it converges to the optimal solution (under a metric such as minimizing control effort or maximizing estimated probability of clearance) as computation time is allowed to increase.

A. Rapidly-Exploring Roadmaps

Our motion planner is based on the Rapidly-Exploring Roadmaps method [18] that provides both probabilistic completeness and convergence to optimality guarantees while efficiently only optimizing paths that can feasibly reach the goal. The RRM algorithm generates a weighted, directed graph whose vertices represent robot configurations and weighted edges correspond to the cost associated with moving from one configuration to another. The algorithm begins with a vertex at the start configuration q₁. It expands in an RRT-like manner by adding vertices and edges toward randomly sampled points in the configuration space. Once there exists at least one sequence of connected vertices from the start vertex to the goal region, the RRM then at each iteration either continues random exploration or refines an existing path to the goal to obtain a better solution. The user-specified parameter w_refine ∈ [0, 1) weighs these two options; the RRM algorithm will explore the configuration space with probability (1 − w_refine) and will refine with probability 1 − w_refine. The algorithm avoids wasteful refinement by only refining paths that can feasibly reach the goal. Once the algorithm has run for a certain number of iterations, then the method uses Dijsktra’s shortest path algorithm to find the path with lowest total cost from the start configuration to a goal configuration.

B. Goal Bias

To reduce planning computation time, we extend the RRM method by introducing a goal bias. Goal bias can significantly speed up sampling based planners by checking for connections to the goal rather than requiring that a configuration be sampled inside the goal region. To introduce a goal bias into RRM, we define another weighting parameter w_goal so that, at each iteration of the RRM algorithm, we have the choice of the following actions:

1. Explore: Rapidly explore with probability (1 − w_refine − w_goal).

2. Goal bias: Check for a connection to the goal with probability w_goal.

3. Refine: Refine a feasible path with probability w_refine

To perform a goal biasing step, we need to generate configurations that result in the robot tip position x(q, t) being inside the goal region around x_goal. This is an inverse kinematics problem, and it is made difficult because there is no known closed-form solution to the kinematics of concentric tube robots (using accurate beam mechanics models and torsion). We can however utilize the robot’s manipulator Jacobian to approximate a change in configuration inputs that will result in the robot’s tip moving closer to the goal. The manipulator Jacobian relates a differential change in the robot’s configuration to a differential change in the position of the end e ector of the robot.

At each goal biasing step we select the vertex q_near in the RRM that has a tip position closest to x_goal and was not previously selected or created as part of a goal bias operation. We define our desired change in robot tip position to be Δx_tip = x_goal − x(q_near, t). We then compute the manipulator Jacobian J(q_near) using a second-order finite difference approximation. By taking the pseudoinverse of the Jacobian J⁺ we can then get a linear approximation of the required change in configuration Δq which will bring the tip of the robot closer to the goal (Δq ≈ J⁺Δx_tip). At each goal biasing step we iteratively apply this operation, taking small steps in configuration space and adding these intermediate configurations to the RRM graph until we either collide with an obstacle or stop making positive progress toward the goal. Our approach to the goal bias is similar to that of the JT-RRT algorithm [15], with the exception that we use pseudoinverses of the Jacobian instead of transposes for better performance with concentric tube robots.

C. Computing Path Cost

As discussed in Sec. III-C, our motion planning method can support a variety of metrics for quantifying the quality of paths. We would like to minimize the probability that this uncertainty results in collision with obstacles.

We first estimate the probability of a given robot configuration being collision free. For a given robot configuration q we can calculate the shape of the robot x(q, s) parameterized by arc length s. We discretize this space curve into a finite sequence of 3D points (x₁, … , x_n) such that x₁ = x(q, 0) and x_n = x(q, t), i.e. x₁ corresponds to the insertion point x_start and x_n corresponds to the position of the tip of the robot. Uncertainty in the positions of these points x_i as a result of the factors previously described create a non-zero probability of colliding with an obstacle and causing a failure in the procedure. We model this uncertainty as a normal distribution about each x_i’s position in 3D space. As inspired by [27], we define the probability of x_i being in collision as the likelihood of its 3D position varying by more than its distance from the closest obstacle in the environment. We therefore approximate the probability of a robot configuration q being collision free as

$$P_{\text{clear}}\left(\mathbf{q}\right)=\underset{i}{\Pi }{\left[P_{\text{clear}}\left({\mathbf{x}}_i\right)\right]}^{\frac{1}{n}}$$ (1)

where the probability P_clear(x_i) of a point x_i being collision free is estimated by a chi distribution of standard deviation σ(s) about x_i’s distance from the nearest obstacle. We take a geometric mean in (1) so as to make the probability invariant to the discretization resolution of the robot’s shape. The standard deviation σ(s) is dependent on the arc length parameter of x_i because uncertainty in the shape of the robot typically increases with the arc length along the robot toward the tip [8].

We experimentally characterized σ(s) by executing randomized motion plans with Gaussian noise in actuator inputs, material properties of the tubes, and orientation of tubes as they exit outer tubes. The variation in 3D position due to noise of each point x_i on the cannula shaft was collected. We fit the experimental data to a chi distribution using the parameter estimation method in [28].

Lastly, we need to restate our problem of maximizing the probability of clearance of a path in terms of minimizing the summation of edge costs in the RRM graph. The estimated probability of clearance for an entire path, P_clear(Π), can be computed as the product of the P_clear(q_i) for all configurations q_i in path. To express this product as a summation we use a negative log transformation; we therefore assign each edge cost as

$$E({\mathbf{q}}_i,{\mathbf{q}}_j)=-\log \left[P_{\text{clear}}\left({\mathbf{q}}_j\right)\right]$$ (2)

where E(q_i, q_j) is the weight of the edge connecting configurations q_i and q_j. With edge weights defined this way, graph paths with smaller edge weights correspond to paths with a higher estimated probability of clearance.

D. Convergence to Optimality

Our planning algorithm always converges in the limit to a globally optimal solution if one exists. In [18] it is shown that a RRM will always converge to an optimal solution in the limit as long as the RRM executes path refinement at least as often as it randomly explores the configuration space. We will now show that, under certain conditions, we can still meet this convergence property with the incorporation of the goal bias that we added in this paper.

The RRM algorithm keeps a list of vertices that still require refinement, U. Convergence to a globally optimal solution requires that |U| does not grow unbounded as the number of iterations executed approaches infinity. In the standard algorithm, at each iteration the RRM can either explore and add a node to U or refine and remove a node from U. With the addition of a goal biasing step, the RRM has an additional choice of extending toward the goal and adding up to a specified maximum number of nodes. Depending on the likelihood of the RRM to randomly explore, perform a goal biasing step, or perform refinement, we can find a maximum number of nodes to allow the RRM to add at each goal biasing step to maintain the convergence to global optimality.

Let X_k be the number of vertices added to U and U_k be the total number of vertices in U at the k’th iteration of the RRM. As previously defined, the probabilities of refining, goal bias, and exploration as w_refine, w_goal, and (1 − w_refine − w_goal), respectively. Given a maximum number of nodes added during the goal bias step, G, we can calculate the expected values of X_k and U_k at the k’th iteration of the RRM:

$$\begin{array}{cc}\hfill E\left(X_i\right)& =(1-w_{\text{refine}}-w_{\text{goal}})+w_{\text{goal}}G-w_{\text{refine}}\hfill \\ \hfill E\left(U_k\right)& =1+E(X_1+X_2+\dots +X_k)=1+\sum _{i}E\left(X_i\right)\hfill \\ \hfill & =1-2k{w}_{\text{refine}}+k{w}_{\text{goal}}(G-1)+k\hfill \end{array}$$ (3)

Because we are interested in determining the maximum number of vertices G to add at each goal biasing step to make U empty in the limit, we take the limit of E(U_k) as k approaches infinity, set it to zero, and solve for G:

$$G=\frac{2w_{\text{refine}}-1}{w_{\text{goal}}}+1.$$ (4)

Therefore, given values for w_refine and w_goal, we can use (4) to calculate the maximum number of nodes to add during a goal biasing iteration while still maintaining the theoretical convergence to optimality a orded by the RRM.

V. Results

For our experiments we simulated a concentric tube robot with the following tube parameters: straight tube section lengths L_i of 12.5 cm, 25 cm, and 37.5 cm; pre-curved section lengths C_i of 5 cm, 10 cm, and 15 cm; cross-sectional radii R_i of 0.125 cm, 0.0875 cm, and 0.05 cm; and radii of curvature r_i for all pre-curved sections of 10 cm. The material properties of the tubes were defined to be equivalent to those of nitinol. The growth of the σ(s) function described in Sec. IV-C was found to be linear with a coefficient of 0.03559.

A. Spherical Obstacle Environment

In our first set of experiments we generated four environments with a goal region and arbitrarily dispersed spherical obstacles to obstruct the motion of the simulated concentric tube robot. The four environments are demonstrated in Fig. 3. In each experiment we ran our planner for 10,000 iterations using w_explore = 0.7 and w_goal = 0.01 (i.e. we performed random exploration 70% of the time, biased toward the goal 1% of the time, and performed refinement 29% of the time). For comparison, we also ran an RRT planner and an RRG planner [17]. The RRT reflects a planner with no refinement and the RRG eagerly performs all possible refinement at each iteration.

Fig. 3.

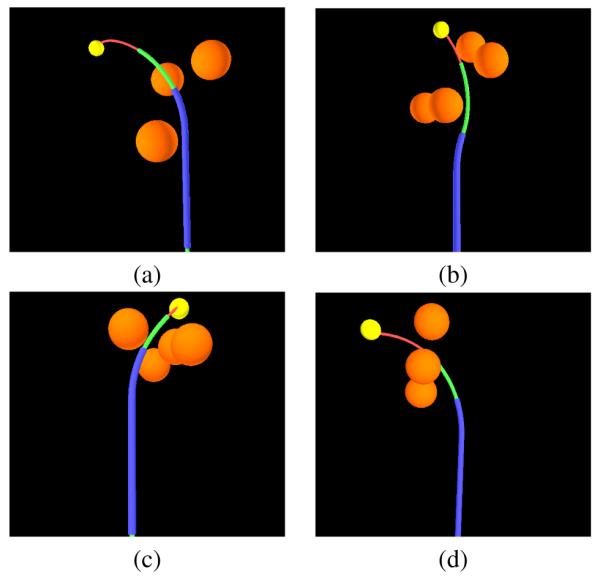
Four test environments, each containing spherical obstacles.

As long as we employed a goal bias, our planner never failed to find a collision free path to the goal in environments where such a path was known to exist. We also ran experiments using a planner without a goal bias and even after upwards of 60,000 iterations a path was never found for any of the environments; therefore our incorporation of a goal bias was essential to the effectiveness of our planner. We show a comparison of the run times for RRT, RRG, and RRM in Fig. 4.

Fig. 4.

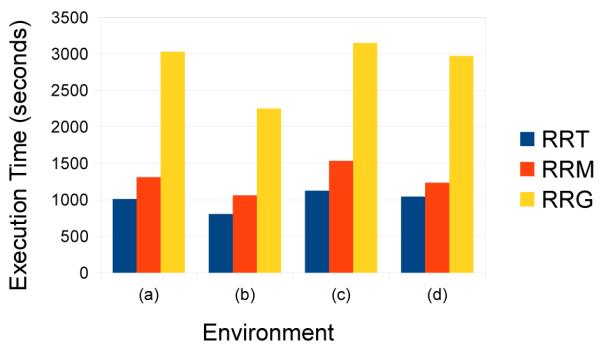
Execution times in the test environments shown in Fig. 3 for each evaluated planning algorithm. We also note that the quality metric values of plans generated by the RRM were always better than RRT plans and always within 1% of the RRG plans.

To verify the correlation of our estimated P_clear metric with the actual probability of clearance of a plan under uncertainty, we executed each of the generated plans 100 times with small amounts of Gaussian noise in the kinematic model computations to test the plans’ robustness to uncertainty. A run was considered “clear” if the robot did not collide into any obstacles. For comparison, we also ran the above experiments on a set of plans generated by a metric that minimizes control effort. In Fig. 5, we compare the clearance rates obtained by minimizing control effort to the clearance rates of plans generated using the P_clear metric. The clearance rate for plans computed using the P_clear metric was higher than that of the plans that minimized control effort.

Fig. 5.

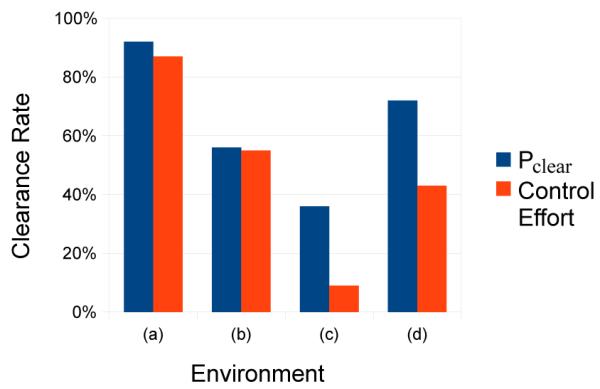
Clearance rates of Monte Carlo simulations of plans computed for the four test environments with spherical obstacles. Plans were a result of 10,000 iterations of our algorithm using both the P_clear metric and a minimal control effort metric.

B. Neurosurgery Environment

Tumors located at the skull base (in or near the pituitary gland) are difficult to safely access, making surgical removal a challenge. Rather than cutting through healthy brain tissue to access these tumors, a preferred route is through the nasal cavity (an endonasal approach). However, current surgical tools provide limited ability to access sites at the skull base. Concentric tube robots have the potential to help physicians performing these procedures by entering a nostril, curving through the nasal cavity, drilling a small hole through bone at the skull base, and then entering the tumor site in the brain while avoiding critical nerves and blood vessels.

We evaluate our planner in a realistic anatomical environment that includes the skull, critical blood vessels, and healthy brain tissue. In our planner implementation, we use PQP [29] for distance queries between our concentric tube robot and obstacles in the anatomical environment. The planner required 1077 seconds of computation time. As shown in Fig. 6, the plan cleanly avoids bone, critical blood vessels, and healthy brain tissue en route to the skull base tumor. With the dexterity of concentric tube robots and guidance by our motion planner, we can find a path that reaches the tumor while minimizing the probability of damaging vital structures during execution.

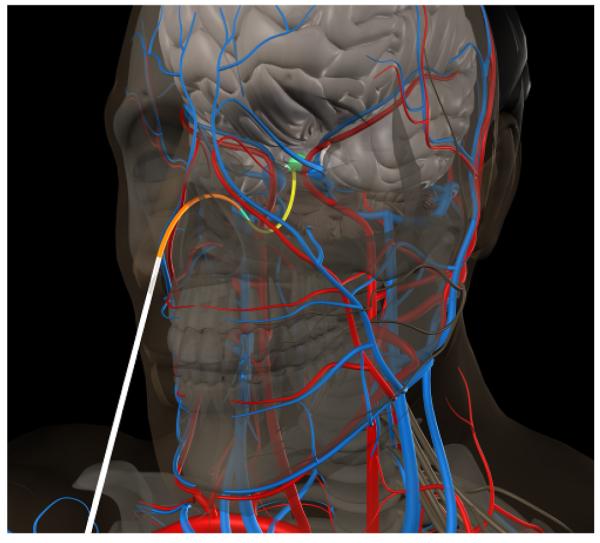
Fig. 6.

A step-by-step illustration of our simulation of the minimally invasive procedure discussed in V-B. The concentric tube robot is inserted based on a motion plan that reaches a clinical target at the skull base while avoiding obstacles including skin, bone, blood vessels, and healthy brain tissue. The same procedure is shown from two perspectives.

VI. Conclusion

We proposed a motion planning algorithm for guiding concentric tube robots around obstacles to goal regions. Our algorithm is based on Rapidly-Exploring Roadmaps (RRM) and a mechanically accurate kinematic model of concentric tube robots. Given a goal location, the starting position and orientation, and a geometric representation of the environmental obstacles, our algorithm computes a sequence of rotation angles and insertion lengths for each tube of the concentric tube robot such that the device follows a collision free path to the goal. The path computed by our planner probabilistically converges to a globally optimal solution. We presented a metric of path optimality which is based on the probability of safely avoiding obstacles during plan execution. In this way we compute plans which are more robust to uncertainty in the predicted shape of the concentric tube robot compared to plans computed by a standard metric that minimizes control effort.

In future work, we will investigate new difficult surgical procedures that would benefit from the dexterity and minimal invasiveness of concentric tube robots. Finally, we plan to integrate our motion planner with concentric tube robot hardware and image-guided sensing to fully evaluate the exciting potential of these devices with integrated motion planning software.